Table of contents

The purpose of this paper is to highlight students' misconceptions of the kinematics of rolling movement and to show mechanisms that can help the student to overcome them. In particular, it focuses on the relationship between the angular and linear acceleration of a rigid body that moves without slipping. Frequently, physics books show particular examples of rolling movement instead of treating the underlying physics. Consequently, students can develop misunderstandings that lead to errors when solving more general cases. In this paper, I suggest how the physics teacher can deal with these problems. First, I discuss how to best teach the kinematics of the plane movement in a rigid body. Second, I propose several examples that can point out the misconceptions to the students and help them to restructure their knowledge.

We introduce here the concept of relative space, an extended 3-space which is recognized as the only space having an operational meaning in the study of the space geometry of a rotating disc. Accordingly, we illustrate how space measurements are performed in the relative space, and we show that an old-aged puzzling problem, Ehrenfest's paradox, is explained in this purely relativistic context. Furthermore, we illustrate the kinematical origin of the tangential dilation which is responsible for the solution of Ehrenfest's paradox.

The standard (unperturbed) Kepler problem is expressed in Kustaanheimo–Stiefel form and solved utilizing the algebra of quaternions. This provides the necessary background to understand some of the new techniques of celestial mechanics.

Einstein was the first to discuss and resolve the 'twin paradox', which in 1905 he did not consider paradoxical and treated as a consequence of lack of simultaneity. He maintained this view until at least 1914. However, in 1918 Einstein brought forward arguments about accelerated frames of reference that tended to overshadow his initial resolution. His earlier arguments were gradually rediscovered during the subsequent controversy about this 'paradox'.

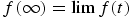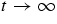A suggestion relevant to teaching the use of Laplace transforms in a basic course of engineering mathematics (or circuit theory, automatic control, etc) is made. The useful 'final-value' theorem for a function f(t), , , makes sense only if , , exists. A generalization of this theorem for time functions for which 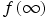does not exist, but the time average exists, states that as 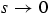, . This generalization includes the case of periodic or asymptotically periodic functions, and almost-periodic functions that can be given by finite sums of periodic functions.

The proofs include the case of f(t) tending to f_as(t) exponentially, which is realistic for the main physics and circuit applications.

Extension of the results to discrete sequences, treatable by the z-transform, is briefly considered.

The generalized form of the final-value theorem should be included in courses of engineering mathematics. The teacher can introduce interesting new problems into the lesson, and provide a better connection with the (usually later) study of the Fourier series and Fourier transform.

The PDF file provided contains web links to all articles in this volume.