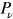Matter and waves
Published March 2024
•
Copyright © 2024 The Editors. Published by IOP Publishing Ltd.
Pages 3-1 to 3-114
You need an eReader or compatible software to experience the benefits of the ePub3 file format.
Download complete PDF book, the ePub book or the Kindle book
Abstract
Chapter 3 presents an introduction and sections on: quantum many-body systems and emergent phenomena; the search for new materials; manipulating photons and atoms: photonics and nanophysics; extreme light; systems with numerous degrees of freedom;

Original content from this work may be used under the terms of the Creative Commons Attribution NonCommercial 4.0 International license. Any further distribution of this work must maintain attribution to the editor(s) and the title of the work, publisher and DOI and you may not use the material for commercial purposes.
All rights reserved. Users may distribute and copy the work for non-commercial purposes provided they give appropriate credit to the editor(s) (with a link to the formal publication through the relevant DOI) and provide a link to the licence.
Permission to make use of IOP Publishing content other than as set out above may be sought at permissions@ioppublishing.org.
The editors have asserted their right to be identified as the editors of this work in accordance with sections 77 and 78 of the Copyright, Designs and Patents Act 1988.
3.1. Introduction
Kees van Der Beek1
1Institut Polytechnique de Paris, Paris, France
The scales of length, time, and energy that are intermediate between the infinitely small and the infinitely large define the world we live in and that we experience. The relevant fundamental forces that act on these scales are, for nearly all phenomena, the gravitational, and the electromagnetic forces. At the energy scales that characterise our world, the relevant physical approaches take atoms, ions, and electrons as fundamental building blocks of matter, and photons as those of light. This chapter considers how these constituents, in the unimaginable vastness of their numbers and the fantastic variety of their possible arrangements, lead to the astounding complexity of our world and the dazzling phenomena it harbours. The world we experience is also the world on which we may intervene. When done in a controlled manner, this intervention—or experiment—belongs to the realm of science and technology. But even when we do not strive to control, our actions are still controlled by the physical workings of the world's constituent building blocks and their interactions.
When one comes to think of it, an atom itself is a hugely complex system. Mathematics abdicates when faced with the problem of providing an exact description of more than three interacting objects; all atoms are in this situation: quarks make up hadrons, hadrons make up the atomic nuclei, and nuclei and, for most elements, numerous electrons make up the atom. The internal organisation of the atom is the result of 'correlations'. The simultaneous presence of several and often many interacting particles lead to the organisation of matter. This is even truer when one assembles atoms into molecules, atoms, and molecules into liquids and solids, and liquid, and solid components into complex systems. What we witness is the result of this internal, physical organisation, the forces that objects around us exert on each other and the phenomena we witness as the net result of this organisation. The myriad particles involved and the manner in which they can interact and made to interact vow for this complexity.
Section 3.2, 'Quantum many-body systems and emerging phenomena', treats this organisation of matter and of the excitations the constituents matter can undergo when stimulated by light or other, impinging, particles, how we can understand it, and how we may describe it. It describes how highly complex behaviour can emerge from the interaction of many constituent particles, and how the quantum mechanical nature of our world determines the nature of the objects that constitute it, even though we may not at all be aware of such. It also describes when a quantum description is needed, that is, when the conditions of observation are such that coherent interactions and propagation of light and particles are guaranteed. When the quantum mechanical coherence of light and matter is disturbed in the process at hand, we may resort to what has become known as the 'classical description'.
Section 3.3, 'The search for new materials', details how our—even limited—understanding of the organisation of matter can help us fashion materials and tools needed to tackle the world's challenges and problems. While in principle there is nothing new—did not the smithies and rock-hewers of prehistoric and early historic times draw on their experience to fashion stone and metal tools?—the formidable scientific progress made in the last two centuries allows for mankind to imagine and make materials according to need, in a sustainable and controlled manner, taking into account availability of material and energetic resources, and designing those material assemblies and those processes that are most appropriate for a given application from the many millions of materials that nature would allow. Nowhere does the force of science have an impact as great as when matter and light are manipulated on the smallest of scales—the nanometer (i.e., 10−9 m) or below. Section 3.4, 'Manipulating photons and atoms: photonics and nanophysics', explains how today's and tomorrow's technologies allow us to dive into the smallest length scales defining materials and the systems they can build and, indeed, back into the quantum realm. It explains how interactions between particles manifest themselves differently depending on the length scale we are working on, how the quantum mechanical nature of these interactions can be brought out, and how both can be put to work to define entirely new tools and systems.
What goes for matter also goes for light, and what goes for space also goes for time. Section 3.5 on 'Extreme light' provides an account of the astounding advances made in fashioning extremely bright light beams, extremely short light pulses, or a combination of both. Extreme brightness allows us to examine the structure of matter, its organisation, and its response to excitation in the very finest details—for it is those details that most often give away the fundamentals at stake in determining the nature of the studied object in the first place. Ultra-short and bright pulses allow one to make 'movies of matter'. Much as stroboscopic illumination of moving beings can reveal the gestures in motion, pico- and femtosecond illumination of matter unveil the dance of electrons in matter: how matter is excited, how matter reacts, how matter transforms. Extremely spectacular results with high-stake implications in many fields (chemistry, biology, medicine, etc) are to be expected here. Moreover, being able to intervene at the rhythm of matter itself allows us to reorganise it, yielding yet another tool for the creation of new (quantum) states of matter designed as tools to face the challenges of humankind.
Finally, section 3.6 'Systems with numerous degrees of freedom' reflects on the multiplicity of interactions in systems that are not necessarily characterized atomic length and timescales and quantum coherence. This opens the way for the most complex of organisations of matter as we know it: life itself, to be treated in chapter 4.
3.2. Quantum many-body systems and emergent phenomena
Lucia Reining1
1Laboratoire des Solides Irradiés, CNRS, École Polytechnique, CEA/DRF/IRAMIS, Institut Polytechnique de Paris, F-91128 Palaiseau, France European Theoretical Spectroscopy Facility (ETSF)
The development of theoretical and experimental approaches to understanding many-body effects in both soft and hard condensed matter, but also in dilute matter, atomic, and molecular systems, as well as in atomic nuclei, remains one of the key challenges in physics today. A proper description of the effects of interaction and inter-particle correlation is key to the understanding of materials properties, their quantum states, as well as the outcome of experiments that probe them, modern spectroscopies, scattering, or collisions. Beyond phenomenology, the adequate description of quantum many-body phenomena will allow the understanding of emergent states of matter and new physics associated with these. Recent advances have concerned novel types of charge and spin order, new magnetic and superconductive systems (see section 3.3), as well as multiferroic systems, the switching between different orders by the tuning of a parameter (e.g., pressure, density, electronic excitation by radiation) but also the absence of order in a number of key systems. The advent of new states of matter will open the way to novel applications in the field of electronics, thermodynamics, sensors, biology (see section 3.3.2.3.4), health and medicine, and it will provide us with new understanding that may go well beyond condensed matter. In this section, we will introduce the main concepts and challenges and explain their consequences on materials science.
3.2.1. General overview
The quantum many-body problem has been one of the most challenging topics of physics for decades. In spite of much progress, all evidence indicates that it will still remain a challenge for a while, both intellectually and because of its potential impact on applications. It turns an old subject, condensed matter theory, into an exciting adventure of unpredictable outcome and potentially highest impact. If we want to understand what is measured in laboratory spectroscopy experiments, if we want to draw maximum benefit from large instruments such as synchrotrons, if we want to use known materials for new purposes or design new materials to solve long-standing problems, we must adapt our thinking to the many possible stories written by a system that is composed of numerous interacting particles in a quantum state.
In order to appreciate the depth and breadth of the problem and its implications, let us first analyse its ingredients. What is the quantum many-body problem?, or, to be more precise, what is the quantum interacting many-body problem? and why does it lead to new emergent phenomena? We will explain each term, and immediately point out why each of the ingredients is so important, both for the whole and for particular applications. Further reading can be found in the references; we cite texts that give an overview, that conveniently illustrate a particular aspect, or that are particularly accessible, whereas we do not claim to cite all, and not even a significant fraction of, the first or the most forefront works in the field.
3.2.2. Quantum
Our mind is classical, which means that we describe the world in terms of our observations: an object is in a given place, or it moves from one place to another with a given speed that may change with time. This makes it difficult to understand or even simply to describe the quantum world, where an object is in a given state, or where it changes state with time. For simplicity, let us think that our problem is static. We may, for example, have two positive charges. Let us say, two protons (depicted by the blue balls in figure 3.1) that create a potential (depicted by the blue lines) which is attractive for negative charges. In the classical world, if we place a negative charge (red ball in the upper row) directly into one minimum of the potential, it will stay there. The two possibilities (charge on the right and charge on the left) are shown on the left and right side, respectively. If we place the charge not in the minimum, but somewhere in that region, it will fall into a minimum, and then it will oscillate around that minimum by converting potential into kinetic energy, if there is not too much friction. In the quantum world (treating for the moment the potential as given), we place the negative charge into a quantum state. If we put the charge into an eigenstate, which is a special state of the system, it will remain there forever. We could also put it into another state that is a mixture, a superposition, of eigenstates: in that case, the wavefunction will oscillate. So, the eigenstates play the role of the minimum positions, and other states somehow play the role of places away from the minima—somehow, because the states do not at all, in general, correspond to a position. This is depicted in the bottom row of figure 3.1, where the red shaded regions represent the eigenstates. To be precise, the red line is the wavefunction of a given state, and there are two of them (on the left and right, respectively). The wavefunction is a probability amplitude, and its square gives the probability to find the particle in a given place. Both states are extended over the whole region: we cannot see such thing as a well-defined position. There is, instead, a well-defined shape of the wavefunction.
Figure 3.1. Schematic view of a system with two protons and one electron, a model for the molecule. Light blue balls, the two positive charges (e.g., protons). Blue lines: attractive potential created by the protons. Red ball in the upper row: the electron, understood as a classical particle. It can be captured by the left or right potential minimum with the same probability. Red line with shaded area in the lower row: the quantum state represents a probability amplitude. The probability to find the electron on the right or left side is the square of the wavefunction, and it is the same in the two quantum states, since the shaded area indicates the regions of positive and negative sign.
Download figure:
Standard image High-resolution imageOf course, one may object that looking at the picture it is clear that we can build a state, superposition of the two eigenstates, which privileges a position: this state is the simple sum (appropriately normalized) of the wavefunction in the left panel and the one in the right panel. The sum cancels the portion of the wavefunction in the right minimum, so now the square of this new wavefunction is localized on the left: our particle is confined on the left side. However, because the superposition is not an eigenstate, there is oscillatory behavior in which the electron explores the possible realisations of the superposition state, and some time later we will find the charge on the right side. Moreover, the localization is not perfect, meaning that even at the start we do not know exactly where the charge is, and at intermediate times, the wavefunction is again delocalized over both potential wells.
This simple example illustrates the difference between the information of classical and of quantum mechanics: classical mechanics tells in which position you are, quantum mechanics tells in which state you are. It is unambiguous about the state-information, but when you ask the question about position, there are only probabilities.
We now have a choice: we can accept this fact and follow the mathematical rules given by quantum mechanics to calculate the properties of the system using wavefunctions. Or we can try to project the quantum world onto our classical world in a way that allows us to interpret and maybe even predict what is going on. Usually one will do both, but here we will avoid mathematics and try to give a feeling of how one may look at the situation. Of course, many books have been written about the interpretation of quantum mechanics, and the debates are fascinating; here our purpose is just to highlight certain aspects. In particular, if we want to use a classical way to look at the problem—for example, we would like to talk about positions, we will have to admit that not knowing where a particle is forces us to ask the question what if? For example, suppose we add a second negative charge to our model system. If it gets close to the first one, there will be a strong Coulomb repulsion energy. But since we do not have a well-defined and ever-lasting position, we have to consider different scenarios, where the two charges come close, or where they do not. The outcome of an experiment will be the sum of all possible stories of what could happen, so in this case, we should measure at least two peaks in a spectroscopy experiment: one at an energy where the particles meet, one where they do not. This is a first challenge: to take into account in our reasoning, and in the theory that we build, all or at least the most important, of the possible stories that a system can write.
Why is this important? The importance of this fact is not limited to esoteric questions of quantum mechanics. It determines our daily life. As an example, take two helium atoms. They both have a nucleus in the center and a spherical wavefunction of two electrons around it. These are two charge neutral and perfectly symmetric objects, and in principle they should not interact (i.e., they should not 'see' each other via the Coulomb interaction). However, this consideration interprets the square of the spherical wavefunction as a classical charge distribution that would stay the same forever. This classical interpretation (which is used, for example, in one of the first approximations to the interacting electron problem, the one by Hartree [1]) tries to give charges a well-defined position, and it does not take into account the probability aspect. To respect quantum mechanics, we have to write the possible stories of these objects, meaning we have to consider all possible positions of the two electrons of one atom (with a probability that is spherically symmetric) and the reaction of the electrons of the other atom to this particular distribution. Now, as soon as the distribution that we consider is not symmetric, the other atom starts to see a dipole or higher multipoles, so it will itself polarize. This fact, schematized in the left panel of figure 3.2, leads to an attractive potential, so the atoms bind together. The effect is called the van der Waals dispersion interaction. Note that the dipole–dipole interaction or the coupling of oscillations also exist in classical physics, but of course only when the classical picture predicts that electrostatic dipoles or oscillating charges are present. The van der Waals dispersion interaction is a quantum effect, because it is due to the coupling of fluctuations that exist only on the quantum level.
Figure 3.2. Quantum mechanical aspects of binding. Left: schematic picture of fluctuating dipoles in neutral atoms or molecules, leading to weak bonding. This is a pure quantum effect. Right: alanine helix structures in alanine polypeptides. The α-helix structure is favoured by the weak van der Waals dispersion interaction. In experiment, it is stable up to 725 K. The figure shows snapshots from computer simulations using density functional molecular dynamics, at the start (top) and after 30 ps (bottom). At 700 K inclusion of the van der Waals contribution preserves the α-helix (bottom left), whereas the structure opens when this contribution is neglected (bottom right). Results from reference [2] with permission from APS, figure in right panel from [3] with permission from Cambridge University Press.
Download figure:
Standard image High-resolution imageOne may not care whether helium atoms can bind or not (although it is interesting to know that solid helium can exist), but one should care about this effect in general. The weak van der Waals dispersion interaction is often important in biology, for example, where it is in particular an ingredient of protein folding. The left panel of figure 3.2 shows results of a computer simulation of an alanine helix structure [2]. In the computer, one can switch off the van der Waals dispersion interaction artificially. The simulation shows that after some time, the resulting conformation is completely different.
This is but one example. One may imagine how rich the world becomes by writing all the possible stories. 'Quantum' or 'Quantum Materials' has become a hot topic over the last years [4]. The terms are maybe not always perfectly well defined, but they are essentially saying that one is interested in materials that have very particular properties stemming from the fact that quantum mechanics does not fix classical observables, but quantum mechanical states.
3.2.3. Interacting
In the discussion above, we have already anticipated that particles interact. This is true in the classical and in the quantum world. We can see it all around us. Take a drop falling on a water surface: as depicted on the left side of figure 3.3, the water reacts and concentric waves form. This means that the water 'sees' the drop; in other words, the water molecules that form the drop and that form the water interact. Both objects, the drop and the water, are affected by the interaction, and the result of the drop falling on the surface is different from having simply more water at the end.
Figure 3.3. Left: Water drop falling on water surface. Because of the interaction between water molecules, the small drop has a visible effect over a large range. Right: Two coupled pendula. The motion of the coupled object is more complicated than the motion of each pendulum alone.
Download figure:
Standard image High-resolution imageAnother good example is the coupled motion of two pendula. A single pendulum has its well-known regular left-right oscillatory motion. When we couple two identical pendula by a weak spring, as schematized on the right side of figure 3.3, each of the two pendula oscillates with an amplitude that changes over time, and there are moments where one of the two even stands still. The amplitudes of the right and left pendula are out of phase, so when the left one stands still the right one moves strongly, and vice versa.
Why is this important? The fact that two or more objects in interaction behave differently than just the sum of the two is of utmost importance. Take chemistry: it is not rare to hear people asking the question carbon and oxygen molecules are not toxic, so how can carbon monoxide be toxic? To scientists, this may seem a naive question, but it is not naive when asked by someone who is not used to thinking about effects of interactions. We have to imagine pictures like the one in figure 3.4, where carbon atoms (blue), oxygen molecules (yellow), and carbon monoxyde (violet/yellow gradients) are schematized. We have to explain that two oxygen atoms influence each other, so if we break the molecule into two atoms there is a first change, and then, oxygen influences the carbon atom and carbon influences oxygen, so together they form a new and completely different object. The fact that a composed object is potentially completely different from the sum of its constituents is sometimes phrased as emergent behavior, because new properties seem to emerge without obvious explanation. It implies, for example, that one has to be extremely careful when evaluating the impact of chemicals, such as drugs or pesticides, because investigating them in a situation where they are isolated from other drugs or chemicals and from the environment where they will be used may lead to dramatically wrong conclusions, positive or negative.
Figure 3.4. Neither carbon nor oxygen molecules are toxic, but CO is: interactions can change everything.
Download figure:
Standard image High-resolution imageIt also means that experiments are in general difficult to interpret. For example, in a photoemission experiment ultraviolet (UV) light or x-rays are sent on a material and their energy absorbed by electrons, which are then ejected from the material and their energy measured in a detector [5]. In a naive picture one would think that each electron in the materials has its own energy, so we would measure a spectrum with sharp peaks. Instead, such spectra are in general very complex, with broad peaks and many extra features, called satellites and incoherent background, that cannot be explained by considering the material as a sum of independent nuclei and electrons [3]. Figure 3.5 shows the photoemission spectrum of a very simple metal, aluminum [6]. The horizontal axis represents the momentum of the electrons in the crystal, and the vertical axis, energy. The relatively sharp lines close to the top are the energy bands that one would naively expect for electrons sitting in the allowed energy levels of aluminum. These can be well described by relatively simple band structure calculations, where interaction effects only lead to quantitative, not qualitative, changes. All the rest of the spectrum is exclusively due to interactions, either between electrons and nuclei that vibrate around their ideal crystal position because of temperature, or, most importantly, among the electrons. In more complex systems, the situation is correspondingly even more intricate, and a close collaboration between experiment and theory is often necessary to extract sound information from the measurements. Photoemission is one of the key techniques used to study interaction effects in materials, because the spectra display these effects in such a dramatic way.
Figure 3.5. Angle-resolved photoemission spectrum of bulk aluminum. The relatively sharp lines close to the top are the energy bands that one would naively expect for electrons sitting in the allowed energy levels of aluminum. All the rest is exclusively due to interactions. Results from [6], figure courtesy of F Sirotti.
Download figure:
Standard image High-resolution image3.2.4. Quantum and interacting
If we adopt for a moment the point of view that quantum mechanics leads us to write all possible stories, and if we take into account at the same time that particles are interacting, an additional difficulty arises: to describe the state of a system, we cannot treat particles separately. The what if?—aspect that was worked out in the first example of implies that while the state of the system with all its particles is expressed by the wavefunction, this wavefunction cannot be simply the product of single-particle wavefunctions. If it were, then the probability to realize a certain event would be the product of independent probabilities from the state of each single particle, but asking what if? means we must have conditional probabilities. In other words, in classical mechanics the state of a static system is well described by telling separately where each particle is, but in a quantum many-body system, we cannot consider particles one by one, or mathematically speaking, the wavefunction is not a product of the wavefunctions of individual particles.
Why is this important? Due to this fact, strictly speaking, even when they are very far away particles are not independent. This entanglement leads to some of the most discussed aspects of quantum mechanics and to some of the most recent promising applications, in particular, in quantum computing [7]. It is also the major difficulty when one tries to develop efficient numerical approaches to predict materials properties, because treating all particles at the same time—writing all possible stories of all particles, with all their what if?—is simply impossible [8]. The box summarizes ways to deal with the problem that are used in practice; more information and references can be found in [3, 9].
3.2.4.1. What do we do in practice?
Experimentally,
- Scattering experiments such as x-ray diffraction or neutron scattering detect patterns of charge and spin.
- Spectroscopy probes the electronic structure and response. Prototypical examples are direct and inverse photoemission and scanning tunneling spectroscopies that give insight about the density of electronic states as a function of energy, optical measurements such as reflection or ellipsometry experiments probing electronic excitations in the visible and UV range, or inelastic x-ray scattering and electron energy loss measurements, which can access excitations that are visible with higher momentum. Another way to make otherwise undetectable excitations visible are resonant spectroscopies such as resonant photoemission or resonant inelastic x-ray scattering. Spectroscopic experiments can be resolved in time, up to attosecond resolution.
Theoretically,
- The solution of models, such as the Hubbard model or the Anderson impurity model, yields precious insight about general tendencies and can also predict parameter ranges where interesting phenomena may occur.
- Wavefunction-based approaches approximate the many-body wavefunction while still yielding a good description of observables. Prototypical examples are stochastic (Quantum Monte Carlo) approaches and expansions in finite basis sets such as Configuration Interaction.
- Density functional theory (DFT) relies on the fact that the density of a system in its lowest energy (ground) state contains in principle all the information necessary to predict ground state observables. First principles DFT calculations are today widely used. They are very successful, in spite of the fact that in most cases it is not known in which way observables depend on the density; in other words, the functionals are unknown and must be approximated. DFT has an extension to the time-dependent case (TDDFT). In linear and higher-order response, this also yields compact expressions to describe spectroscopy.
- Approaches based on Green's functions, similarly to DFT, avoid wavefunctions by expressing observables in terms of more compact quantities. One-body and higher-order Green's functions are more complicated objects than the density, but much more compact than the many-body wavefunctions. Also in this case, most functionals are unknown. Major approximations are perturbation expansions in the Coulomb interaction (Many-Body Perturbation Theory) and expansions around a local problem, such as Dynamical Mean Field Theory. Green's functions describe the propagation of particles. They are therefore helpful for finding approximations that are intuitive, because they naturally write the possible stories of the system.
3.2.5. Many-body
In the examples above we were looking at systems composed of few objects, such as two hydrogen atoms or two pendula, and others composed of many molecules or electrons and nuclei, such as liquid water or bulk aluminum. The drop-on-the-water observation is stunning, if you think about it. Liquid water is a disordered ensemble of a huge number of molecules, but when the drop hits the surface, these molecules somehow coordinate and give rise to a beautifully symmetric pattern. Such a collective behaviour of a many-body system is not determined if you just have all the detailed information of every one of its particles; it is determined if, to this, one adds the interaction and information such as the average distance between particles. Collective effects are very important for the understanding of materials, and they also happen at the quantum level. Probably the most well-studied collective effect of the many-electron system is the plasmon. Plasmons are collective oscillations of an electron gas and have been first studied theoretically for a homogeneous distribution of electrons [10, 11], but they also occur in real, inhomogeneous materials. The plasmon frequency is the resonance frequency of an electron gas, and it depends on its density and shape. Real materials show regions of different densities and can therefore have plasmon spectra with more than one resonance. Moreover, as in classical mechanics the double, triple, etc, frequency can be excited [12]. Plasmons are measured as sharp spectral peaks in experiments such as inelastic x-ray scattering, where an x-ray scatters from the sample but loses energy and momentum to excitations of the material [13], or electron energy loss spectroscopy, where an electron beam (e.g., in an electron microscope) is transmitted or reflected, again losing energy and momentum by exciting the material [14].
Why is this important? Because collective motion gives rise to sharp spectral features corresponding to long-lived excitations, they are interesting for applications. Plasmons, for example, have created an own field of research called plasmonics [15]. It is mostly concerned with the nanoscale, where it considers resonances of metallic particles (see, e.g., the example of photography below) or at metal-dielectric interfaces. It aims to establish the generation, manipulation, and detection of optical signals. Potential applications are found in optical communication, microscopy, and more general imaging, for example, of biological materials.
The response of a system at resonance is strong. This is used in string instruments, where the body and the air inside the sound box have characteristic resonance frequencies that determine the sound of the instrument. The response can be so strong that it becomes destructive. This may be a problem, for example, for the stability of buildings or vehicles, but it can also be used on purpose, for example, to destroy tumors. More generally, the violent response of materials at certain frequencies allows one to change their properties in a targeted way, for example, using visible light.
A nice example is the first colour photography by E Becquerel. His technique did not meet great success. The colours could be captured (see his first attempt to capture the colours of the rainbow in figure 3.6), but the process could not be stopped, so the photography has to be kept in the dark to avoid further evolution. Nevertheless, the approach he proposed is interesting, and the origin of the colours in this material has long been debated, not least because a better understanding can result in better conservation of the fragile pictures. A collaboration of researchers and the National Museum for Natural History in Paris has found that the explanation is given by plasmon resonances [16]: Becquerel's material is composed of silver chloride crystals that contain small, nano-sized, silver particles of various sizes. This is schematically represented by the crystal (green/blue) and two different nanoparticles (light blue circles) in the leftmost part of figure 3.7. According to the size of the nanoparticles and their shape, their plasmon resonance frequencies differ. Therefore, they absorb light of different colours. In the beginning of the process, all resonance frequencies are present and the visible light is completely absorbed: the material appears to be black, whereas pure silver chloride would be white. Now suppose you shine red light (represented by the red arrow) on it: this will be absorbed by those nanoparticles that have a resonance frequency corresponding to the wavelength of red light. The violent reaction of the electron system perturbs these nanoparticles to the point that they explode or, at least, change shape (middle panel). Visible light (represented by the red and blue arrows in the right panel) is now absorbed at all frequencies except red, since the corresponding particles no longer exist. Red light is transmitted and reflected, and therefore the object is seen as red in the places where the nanoparticles have absorbed red light. Such changes form the principle of photochromic materials, which change colour when exposed to light. In many applications, such as automatically darkening sun-glasses, one needs a reversible process. For example, some organic molecules are photochromic because they respond to UV light by changing shape and subsequently absorb light also in the visible range. When there is no longer any UV radiation, they return to their original shape.
Figure 3.6. Solar spectrum, Edmond Becquerel 1848, Musée Nicéphore Niépce, Chalons-sur-Saône (France).
Download figure:
Standard image High-resolution imageFigure 3.7. Schematic view of a photochromic material. When light of a certain wavelength is absorbed, the absorbing object may undergo changes. Subsequently, light of that same wavelength will be transmitted and reflected.
Download figure:
Standard image High-resolution imageIn large (bulk) materials, typical plasmon frequencies of the weakly bound outer valence electrons lie well above the range of visible light. However, another kind of many-body resonance exists at lower frequencies, often in the visible range: these are excitons. As in the case of plasmons, one cannot understand excitons within an independent-particle picture, in which electrons absorb photons and transit between single-particle states independently. Instead, the whole system of the order of electrons is promoted from its initial state, which, as pointed out earlier, corresponds to a wavefunction describing all particles at the same time, to a new many-body state. Whereas it is impossible to give a simple picture of the initial and final states, one can more easily describe the final state with respect to the initial one. This is schematized in figure 3.8: an electron (red) is displaced and leaves a hole (white) behind. The electron carries a negative charge, and the hole, or 'missing' electron, acts correspondingly like a positive charge, so it creates an attractive potential for the electron. If the interaction is strong enough, the electron is captured in this potential and we have a bound electron–hole pair called exciton. The whole system participates to this situation, in particular, all electrons contribute to screen the Coulomb interaction between electron and hole, so the interaction responsible for the exciton binding depends on the material. The pair of a positive and a negative charge has some similarity with a hydrogen atom. Therefore, bound excitons create very characteristic features in optical absorption experiments, sometimes extremely similar to the Rydberg series of optical absorption of the hydrogen atom. The right panel of figure 3.8 shows an example.
Figure 3.8. An exciton is a bound electron–hole pair. Left, schematic representation of an exciton. Right, schematic view on the absorption spectrum of copper oxide Cu2O. The typical hydrogen-like series of bound exciton peaks is observed. Figure representing results published in [17].
Download figure:
Standard image High-resolution imageExcitons are important in many applications, such as solar cells, or photocatalysis, as illustrated in figure 3.9. One can easily imagine why: on one side, when an electron and a hole travel together they form an overall neutral object, which reduces the interaction with the lattice compared to a charge travelling alone. On the other side, when one wants to separate the positive and negative charges, as is the case, for example, in photovoltaics, strong exciton binding can be an obstacle. Other examples of applications where excitons play a role are UV excitonic lasers, tuneable UV photodetectors, or LEDs.
Figure 3.9. Excitons are important in photovoltaics (left illustration) or photocatalysis (right illustration), where electron–hole pairs are created by light absorption and where the transport, separation of charges, and migration of electrons and holes to the desired places is crucial. Theory can help to get insight into these complex processes.
Download figure:
Standard image High-resolution image3.2.6. Tiny differences, large effects: symmetry breaking
One of the reasons why the waves in figure 3.3 do not surprise us is because they are concentric, meaning, they are perfectly symmetric. We expect that in the absence of a clear reason no particular direction is privileged. In quantum mechanics, this translates into the fact that a Hamiltonian (the quantum mechanical operator describing the system) with certain symmetries will also lead to properties with that symmetry. For example, in figure 3.1 the potential is left-right symmetric, and the two eigenstates are, respectively, symmetric and anti-symmetric, so the square of the wavefunction is symmetric in both cases. We would expect that this is true independently of the distance between the two atoms, and this is indeed so on paper. In reality, the two hydrogen atoms are not alone, but surrounded by other objects—or even the vacuum—in a continuously changing universe, which leads to fluctuations of the potential. These may be very small, and their effect negligible. However, while we separate the protons more and more, the energy difference between the two eigenstates of the molecule becomes smaller and smaller, and eventually smaller than the fluctuations. At this stage, a fluctuation that breaks the symmetry will win and localize the electron on the side with lower energy. Even when the fluctuation ceases and the molecule experiences again a symmetric potential, such that the localized state of the electron is no longer an eigenstate of the system, it will stay where it is for a long time, because the oscillation of the composite quantum state that follows has a period that is inversely proportional to the energy difference between the eigenstates. For an observer who is not aware of the tiny fluctuations, this will appear as if the system had decided to break the symmetry spontaneously. This spontaneous symmetry breaking is therefore a consequence of degeneracy, which means energy differences between eigenstates becoming smaller than typical fluctuations. After all, this is not too mysterious: even in the classical world, such things occur. For example, if you place a ball exactly on top of a fixed sphere, it will stay there, because there is no reason to fall down in any particular direction. However, the slightest disturbance is enough to make the ball fall.
Why is this important? In the above classical example, it is important to note that it is impossible to predict in which direction the ball will move, unless you have perfect control over the fluctuations of the surroundings of the sphere, for example, the vibrations of the table where you have put it. What you can predict, on the other hand, is that it will eventually fall down. At this stage, one may understand that this can trigger fundamental discussions about the question whether one can ever predict what will happen to a system even if one knows all its constituents and fundamental interactions (i.e., the reductionalist hypothesis), or whether other ways to approach the problem, or even additional knowledge, are needed [18]. To understand the practical consequences for materials, we first have to see how situations of degeneracy and spontaneous symmetry breaking can come into play in large systems.
3.2.7. More can be very different
More is different—with this famous expression P W Anderson [19] meant to stress the ongoing excitement of condensed matter theory, and the fact that one can discover radically new effects even when all constituents have been known for a long time. This is actually something that even children know—in the movie Finding Nemo, for example, a school class of small fish learns how to self-organize in order to simulate one large fish that could frighten an enemy [20].
One would immediately object that small fish can think and decide to do this, while electrons or protons cannot. Still, they form patterns. Take, for example, a crystal: if you start from empty space and throw in a bunch of atoms, at low temperature they may form a crystal. In a large homogeneous environment this crystal would have the same probability to sit in whatsoever place—this is a very degenerate problem. However, the crystal will 'decide' to form somewhere. Of course, space is usually not empty and homogeneous, but even if it were, the crystal position would be pinned by the small fluctuations as introduced earlier. Electrons can also form crystals, although this is less common. A homogeneous electron gas at very low density crystallizes; this is called a Wigner crystal [21]. The left panel of figure 3.10 shows the electron density that one obtains by an analytic calculation on paper for many electrons in a completely flat potential, taking into account the translational invariance: it shows no feature whatsoever. The result in the right panel was obtained for the same system numerically, using the Quantum Monte Carlo method, a stochastic approach to optimizing the many-body electronic ground state wavefunction by minimizing its energy [3]. One can clearly see a crystal structure. The difference between the results of the analytical and the numerical calculation is huge. This does not mean that one of them is wrong; they are both correct. However, the analytic calculation is done in unrealistic conditions, because the tiny fluctuations of the environment are missing. Therefore, the system cannot break the symmetry. The calculation, instead, involuntarily contains fluctuations, through initial conditions of the simulation, its finite length, and the random number generator that is used. In a sense, one would not call this realistic either: why should this simulation noise have anything to do with a natural environment? Indeed, if one repeats the very same calculation, one will most likely obtain a completely different picture. Or, to be precise, one will find the crystal in a different position and with a different orientation. However, it will be the same crystal, with the same shape of the unit cell and the same periodicity. This means that the particular realization is meaningless, but the pattern is meaningful.
Figure 3.10. A Wigner crystal breaks the symmetry of a homogeneous electron distribution. Left: Analytic solution for the electron density in a homogeneous potential. Right: Solution obtained by path-integral Quantum Monte Carlo calculations. Figure by D Ceperley, published in [3], copyright (2016) with permisssion from Cambridge University Press.
Download figure:
Standard image High-resolution imageThere is still a piece missing in the puzzle: the example of the molecule cannot explain the formation of a regular pattern as the one we observe here, and one would think that tiny irregular local fluctuations should lead to an irregular picture. Somehow the information of how to organize is spread throughout the whole system: the density fluctuations are correlated. Indeed, one can define a correlation function that gives the probability to find a density change in one place together with another density change in a second place [3]. For the Wigner crystal, one finds that this correlation function diverges for a wavevector leading to the density changes that have the periodic pattern seen in figure 3.10. There is a direct link to the , though: the probability amplitudes calculated in such a correlation function are inversely proportional to energy differences, so divergence of the correlation function is directly related to degeneracy. Degeneracy, in turn, is likely to arise in infinitely extended systems where the energy spectrum becomes continuous in the so-called thermodynamic limit. The correlation functions express the capability of the system to respond to an external perturbation, and a divergence implies that even the most tiny fluctuation will lead to a sizeable response—right as the Wigner crystal example shows.
Why is this important? There are many examples of the formation of patterns in many-body systems: in ferromagnetic materials, small magnetic moments are aligned in a given direction, and there is no apparent reason why the moments point in this, and not in opposite direction: ferromagnetism breaks a mirror symmetry. In antiferromagnetic materials, small magnetic moments are periodically aligned in alternating direction, and this can break the translational invariance of the ideal crystal structure. Charge density waves can stabilize patterns in materials, similar to the Wigner crystal in the homogeneous electron gas. Nematic order occurs in liquids, but also in some superconductors: in this case, translational invariance is not broken, but the electron cloud is deformed locally, for example, around an atom, such that some of the original rotational symmetries around each atom are broken and the material may become anisotropic. These are symmetry breakings that one can visualize quite easily. But there are other, less evident symmetry breakings that lead to exotic behaviour of great interest. A superconductor, for example, breaks electromagnetic gauge symmetry, and this gives the material extraordinary properties, the most well known being zero resistance at non-zero temperature. Similarly, superfluids can creep up walls like magic.
One can easily understand that these drastic changes of the material are very important for applications. More is different can open new avenues to design materials with non-toxic, earth-abundant elements, to replace compounds with harmful properties or at the origin of conflicts. Finally, symmetry and symmetry breaking is an important concept all over physics. Therefore, the study of symmetry-broken phases of condensed matter may also shine light on fields where experimental data are more difficult to obtain, and condensed matter analogues for high-energy physics is a fascinating topic [22].
What to look at? From what we have seen up to now, it becomes clear that the goal cannot be to describe every possible story of every single particle in materials with a number of particles of the order of , neither theoretically nor experimentally: it would not be possible, and even it it were possible, it would not be meaningful. What is important are not the details of a single realization, but averages and patterns, in the widest sense. The former are the expectation values that are measured experimentally with good statistics, and calculated using increasingly complex and accurate approaches from quantum chemistry, stochastic methods, or functional approaches such as density functional theory or functionals of Green's functions.
Most often materials are interesting even in the absence of challenging symmetry breaking: the interaction between electrons and of electrons with the lattice still determines their properties. Some of them can be explained in terms of single-particle features that are simply renormalized by the presence of all particles. Others are due to collective effects such as plasmons or excitons, or such as magnons, which are collective spin excitations, or phonons, stemming from lattice vibrations. These are excitations that appear as quite sharp features in the spectra, which means that they live a long time before they decay into the continuum of incoherent excitations of the many-body system [3]. This means that their characteristics to some extent resemble those of independent particles, although they are different from the bare electrons and nuclei that constitute the system. They are therefore called quasiparticles [23]. This is an important concept: while the behaviour of a material cannot be understood in terms of the motion of each of its constituent particles, it can be understood in terms of these quasiparticles. We have seen examples above: the sharp bands of aluminum correspond to quasiparticles, where the removal of an electron from the system can be described in terms of the hole left behind. This hole is surrounded by a cloud of electrons that are attracted by its effective positive charge, an effect called screening, which changes the energies but still leaves the material with a clearly visible band structure. The importance of these quasiparticles reflects itself in the fact that they have launched new directions of research and applications that are named after them, such as plasmonics [15] that is based on plasmons and that was already mentioned above, excitonics [24] where ultra-small optical switches, solar energy production, or low-consumption solid-state light sources are based on excitons, or magnonics [25], where, for example, magnetic materials are to be used in miniaturized programmable devices. Even for complex materials, much can be understood in these terms, especially by combining experiments with electronic structure calculations.
In the more difficult case, when degeneracies determine the materials properties, still much can be done: fluctuations are naturally present in experiment, and symmetry breaking can be induced in calculations by adding small perturbations [26]. However, the tendency of a material to organize in a pattern can be more directly understood by looking at correlation functions: in an antiferromagnet, for example, the spin–spin correlation function would tell us that every spin prefers to have an opposite spin as next neighbour, whereas in a ferromagnet, a neighbour of same spin is preferred. The Wigner crystal, in turn, can be deduced from a density–density correlation function. It is important to note that the 'will' to self-organize is already encoded in such a correlation function that would be calculated or measured in the symmetry-unbroken state, and it is therefore independent of any particular realization of the symmetry breaking. The tendency to organize appears as a divergence of the correlation function at a parameter that corresponds to the pattern, for example, a wavevector related to the period of a translationally broken symmetry. As pointed out earlier, this divergence, in turn, stems from division by an energy difference that vanishes, hence from degeneracy. Correlation functions actually help us out of the dilemma: we may admit that it is impossible to predict a particular Wigner crystal or to reproduce the very same Wigner crystal by two subsequent experiments, but it is possible and pertinent to measure or calculate the density–density correlation function and therefore, what kind of pattern will be formed—even with pen and paper, in principle.
3.2.8. Challenges and opportunities
No doubt, this is a fertile field, where new discoveries are made every day. Above, we have outlined the complexity of the quantum many-body problem. Most importantly, we have explained to which extent potential surprises and yet unpredicted properties are inherent in its very nature. In particular, emergent phenomena due to spontaneous symmetry breaking are not exotic singularities, but common in condensed matter. Their importance for fundamental insight and technological applications has been widely acknowledged—maybe the fact that a large portion of what used to be called condensed matter physics is now called the study of quantum materials [27] is just reflecting that fact. It should not make us forget that even 'simple' metals or semiconductors may have interesting properties and lead to crucial technological breakthrough.
In the following, we will not try to predict what we cannot even dream of today. We shall simply remind the reader that we can only be ready for new discoveries, and be humble enough to admit that some ideas or observations put forward recently may seem of modest interest right now, but could have huge impact tomorrow. We have described the basic ingredients above in simple terms, using prototypical illustrations, but the consequences in real materials are so multifaceted that it is impossible to give an exhaustive summary. Valuable roadmaps exist and are regularly updated, where one can monitor progress and have a glimpse at the possible future (see, e.g., [28]).
What we can do is, however, to ask questions. Many new materials will be synthesized, and in particular the combination of different materials is a vast playground. So, for example, we can ask How can we use the two-dimensional electron gas that forms at the interface between two insulating oxides [29]? or How much is still to be discovered in low-dimensional systems, in particular quasi one-dimensional ones, knowing that the effective Coulomb interaction is stronger in lower dimensions? And What about combinations of such low-dimensional systems? For example, layers of two-dimensional crystals are often kept together by the weak van der Waals dispersion interaction explained above. Therefore, they can be stacked in many ways. The stacking can be twisted, and we know today that such twisted systems at 'magic' angles have very unconventional properties [30–33]. On the other hand, still new classes of materials are discovered and/or characterized, leading to questions such as What will be future research in, and applications of, spin liquids [34], where, for example, magnetic excitations with unconventional statistics may be found. Spin liquids belong to the wider class of topological materials, a field of research that by itself is not very recent [35], but the importance of which is increasingly acknowledged [36]. Topological phases, such as topological insulators [37], though clearly distinct from other phases of matter, cannot be described by conventional spontaneous symmetry breaking. Still, they are distinct phases and can be described by an order parameter which plays the role of conventional symmetry-breaking order parameters (e.g., magnetization is the order parameter when the spins order). In topological phases the order parameters are certain integrals over the momentum frequency space that do not depend on details of the integrand, which makes it more difficult to imagine than quantities such as the magnetization. So, what other order parameters and related phases may we find in the future? Also, superconductivity remains in the focus of interest. Superconductivity in cuprates has been studied since the 1980s, but still, new features are discovered, such as a pattern of the charge density (called charge order, a reminder of the Wigner crystal) that has been measured using different techniques such as inelastic x-ray scattering [38] and that does not come with spin order, which is quite unusual. What is the relation between different forms of symmetry breaking in superconductors? is a question that is not yet satisfactorily answered. At the same time, superconductors are used to push quantum technologies, and there is a dream to develop quantum computing based on superconducting qbits [39]. Can materials science lead to the breakthrough of quantum computing?
While this admittedly very partial list of questions develops, and while it is clear that every single research group or even every single researcher would have at least one more important question to suggest, some broad directions of search can be distilled from the discussion above.
The search for new quasiparticles: We have pointed out the importance of quasiparticles, such as plasmons or excitons, for the understanding of materials and for whole classes of applications. There are in principle infinitely many possibilities for such collective effects, and quasiparticles with very exotic properties may exist. Hunting for such quasiparticles is a lively field of research. For example, zero-energy modes which exist at the ends of one-dimensional conductors that are in a topological superconducting state [40], called Majorana fermions, have attracted much effort. Also skyrmions, chiral magnetic objects that are expected to be stable, localized in a few nanometers, and easily manipulable by weak electric or magnetic stimuli, are intensively studied for their promises ranging from low-power applications [41] to neuromorphic computing [42].
The exploration of new couplings: 'More is different' always applies, when one brings together particles such as electrons and nuclei, when one combines different atoms, different crystalline layers, or other pieces of matter, and also when one couples matter to photons. A strongly coupled photon–electron system can give rise to new quasiparticles that are detected in experiment. A convenient theoretical formulation is the Floquet approach [43]. The strong electron–photon coupling can, for example, lead to replica of the energy bands called Floquet bands, which are found in experiment [44]. One can understand them in a similar way as the replica of the energy bands in aluminum that can be observed in figure 3.5, the only difference being that there, the hole coupled to plasmons, whereas here, the coupling is to photons. Both can be described by a model of fermion–boson coupling, but of course, with different parameters. The most puzzling observation is probably that even a molecule in vacuum is coupled to vacuum fluctuations, which can be observed when putting the molecule into a cavity. In that case, the coupling to something that is seemingly nothing (but that actually consists of photons) can significantly alter the properties of the molecule [45]. This motivates the search for new couplings, involving potentially more than just two ingredients, with infinite possibilities of combining pieces of matter and electrons, holes, plasmons, excitons, magnons, lattice vibrations (phonons), photons, etc.
A new dimension: time: Time adds a new dimension to possible studies, and the typical timescales of lattice vibrations (picoseconds) and electrons (femto- and attoseconds) are now accessible experimentally. Experimental developments such as free-electron lasers are tools that have yet been used only to a fraction of their potential, and that will without doubt challenge our understanding. Time-dependent perturbations can be used both to probe and to create: they can drive a system out of equilibrium, and it can be very instructive to see how the system evolves. They may also allow one to bring a system into a new state; one prominent example is light-induced superconductivity [46]. Theoretical efforts, for example, with new developments in the framework of TDDFT or non-equilibrium Green's function theory and real-time propagation of Green's functions, are already paying off, especially with joint experimental–theoretical studies, and open new persepctives such as coherent manipulation of the excitonic properties on ultrafast timescales [47].
Additional parameters: Many more parameters influence materials: for example, these can be pressure, an environment such as a substrate or a solvent, external electric or magnetic fields, doping, or temperature. Often it is not easy to take this additional information into account, but in order to exploit the full range of possibilities for understanding and designing materials, we have to face the challenge. Changing the parameters can lead to new observations, such as phase transitions (e.g., a transition from one crystal structure to another). Temperature is a good example: often calculations suppose that the lattice is frozen and that the electrons are in their ground state, whereas in reality there is thermal motion and the electrons occupy also higher states with a thermal distribution. This may require to take disorder into account, entropy, exchange of energy between electrons and lattice vibrations, thermal fluctuation of magnetic moments, etc, on a level that is more than just taking averages. For example, some materials above a certain critical temperature appear to be metallic when one neglects magnetic moments by considering that they are zero on average, whereas these materials are paramagnetic insulators in nature, and they can only be described correctly by taking the fluctuating magnetic moments into account [3].
Order parameters: As we have seen, while symmetry is a fundamental constraint underlying all domains of physics, symmetry breaking occurs (though for good reasons) and leads to the most amazing phenomena. Much more remains to be discovered and understood. Investigations are already ongoing on topics such as understanding the interplay of distortions and superconductivity [48], or the formation of time crystals [49], where a periodicity in time of a driven system is superseeded by a different time periodicity. We will have to be creative and imagine new forms of symmetry breaking, with new order parameters (including those not related to global symmetry breaking such as the topological ones, see in the questions above) that can bring us to unexplored territory. It will also be interesting to find new ways to suppress certain symmetry breakings, since different forms of symmetry breaking, such as magnetism and superconductivity, can be in competition. From the theoretical and numerical point of view, the example of the Wigner crystal shouldn't give the impression that having a noisy method or computer is enough to find everything that might possibly occur, since the computational choices that are made still restrict the range of what one could possibly find. We will have to improve theory for the calculation of correlation functions, and set up correlation functions for new kinds of fluctuations. We will also have to include potential symmetry breaking in the functional approaches, which is especially delicate when going to infinite systems, where the order of limits may seem to be a mathematical subtlety, but strongly impacts the physics that one may find.
Machine learning and data science: Experiments, theory, and computation see constant progress, which should be acknowledged. However, recently a new tool has emerged that may well change our way of working in a fundamental way and therefore merits special mention. Computers can not only perform electronic structure calculations, but they can handle large amount of data in an efficient way. This leads to several possibilities that find exponentially growing use today and may well completely transform our field by the horizon 2050. First, databases allow us to profit from existing knowledge and in such a way avoid huge waste [50, 51]. Today, materials databases exist with millions of entries, where one can find information about a given material, or materials with desired properties. Second, computers can perform nonlinear interpolations and extrapolations in huge parameter spaces. This is the essence of machine learning, which allows us to predict properties of materials knowing the properties of a set of other materials [52]. Third, they can recognize patterns and correlations, which, although the computer does not 'know' the reason for correlations, can be of tremendous help for modeling, developing theory (functionals), and classifying materials to make predictions [53]. Many difficulties remain, and in particular in materials science, the absence of clean, unified, and abundant data is a challenge. Nevertheless, machine learning can be a plus also for experimental data, in particular imaging [51], even today, and the future is promising. Needless to say, be it with or without machine learning, computational materials design is an increasingly important branch of condensed matter physics, and collaboration with mathematicians and computer scientists will be needed in order to use the expanding computing capacities in the best possible and responsible way.
Much of our discussion reflects the very essence of science: trying to discover what is not yet known, and not even thought of. To do so, we have to continuously find new ways to think and imagine, and we have to be ready for surprises. As a final remark, we may be proud of the fact that the investigation of materials on a quantum level can respond to many of the grand challenges of humankind, such as the development of renewable energies, or of new drugs. However, the complexity of the field may also serve to remind us that scientists have the mission to learn and transmit to society ways to structure, understand, and solve problems that are too difficult for any of us. And that, yes, 'more is different', and we will solve those problems only collectively, or not at all.
Stimulating discussions with many members of the Palaiseau Theoretical Spectroscopy Group are gratefully acknowledged.
3.3. The search for new materials
Claudia Draxl1 and José María de Teresa2
1Professor of Physics at the Humboldt-Universität zu Berlin, Berlin, Germany
2Research Professor at CSIC and Leader of the Nanofabrication and Advanced Microscopies Group at the Institute of Nanoscience and Materials of Aragón (INMA, CSIC-University of Zaragoza), Zaragoza, Spain
3.3.1. General overview
Ever since Homo sapiens started to create tools and develop technologies, new materials that could improve the quality of life have been discovered and deliberately fashioned. New elements, metals, alloys, molecular assemblies, and compounds have contributed to create additional functionalities or implement better physical properties. Today as well, there is an intense research activity aiming to create new substances, expanding the palette of materials available for higher efficiency and quality of life.
Apart from the material composition, the dimensions and microstructure of materials are crucial for the physical properties they exhibit, especially when the nanometer scale is approached. As a consequence, it is important to control the conditions by which crystals, polycrystals, or amorphous states of a bulk material are synthesized, as well as to investigate their properties not only in bulk form but also when grown as thin films, nanoparticles, nanowires, aerosols, etc.
In certain cases, the discovery of a new material or a new form of a material entails its prompt technological application, which explains the healthy state of research on new materials. Sometimes, a targeted application can guide what material to search for, whereas in other serendipitous cases, a new material brings about unexpected applications and technological developments.
In the following sections, the three main aspects of state-of-the art research on new materials will be addressed: synthesis, physical properties, and applications. Moreover, we shall discuss aspects of data-centric materials science. The focus will first be on the present understanding of the topic; in the second part of this chapter the challenges and opportunities on the Horizon 2050 will be tackled. As materials research is an extremely wide area, we will focus on some—subjectively chosen—examples rather than covering the whole field.
3.3.2. Present understanding and applications
3.3.2.1. Synthesis
Once a researcher, guided by, perhaps, theoretical predictions, by previous experience, by experiments, or by intuition has decided to prepare a new material, it is very important to choose an appropriate synthesis method. This task is not obvious. To synthesize new materials, one can rely on either physical or chemical methods, or a combination thereof—the variety of existing growth methods is immense. An optimized synthesis method will depend on multiple variables such as the equipment available or the budget, the required bulk, thin-film, or nanostructured form of the material, its single-crystalline, polycrystalline, or amorphous nature, the desired throughput, the accuracy of the stoichiometry that is needed, and so forth. Moreover, if the new material is intended to be used commercially, one should also consider other requirements such as the cleanliness and sustainability of the synthesis method, the potential for large-scale synthesis, the availability of the starting materials, etc. Given the breadth of the topic and space limitations, we shall restrict the discussion to the most common physical methods for the synthesis of new materials and provide a few examples.
For bulk materials, most of the synthesis routes are based on chemical methods, but in some particular examples physical routes can be more convenient. For example, the semiconductor industry relies on single-crystal Si wafers that are grown by means of the Czochralski method. In this method, the necessary elements are molten and the surface of the liquid is put in contact with a small crystalline seed that is pulled and serves as a guide for obtaining a large single crystal [54]. More generally, the use of molten metal fluxes allows the synthesis of novel materials in the form of single crystals, which are ideal to investigate the intrinsic physical properties of a new material [55]. A recent example is the synthesis of a new class of Fe-based superconductors [56]. The arc-melting growth method is of interest for the synthesis of ingots of metallic materials. In this method, stoichiometric amounts of the required elements are molten by the electrical arc discharge from terminals submitted to a high voltage. In this way, multielement alloys can be grown; a recent prominent example is that of high-entropy alloy systems [57]. The growing interest for the fabrication of materials with arbitrary shapes and resolution down to the micrometer range and for manufacturing objects that cannot be machined or assembled otherwise has boosted the use of additive printing techniques [58].
In many applications, the new material will need to be grown in the form of a thin film of sub-micrometer thickness. Such films are usually not self-supporting, therefore synthesis is directly performed on a support substrate. A wide variety of physical techniques are available to achieve the required stoichiometry, crystallinity, and roughness; these include sputtering, thermal, or electron-beam evaporation, molecular beam epitaxy (MBE), pulsed laser deposition (PLD), and physico-chemical techniques such as chemical vapour deposition (CVD) and atomic layer deposition (ALD). Each of these techniques has proven to be very successful in the growth of particular thin films.
We will provide a few examples to give the reader the flavour of the topic. Sputtering techniques use targets composed of the elements or compounds required for synthesis. A plasma maintained in the deposition cell provides for ion bombardment of the targets, which results in the sputtering of their constituent elements and their subsequent deposition on the substrate. In some cases elements present in the plasma such as oxygen or nitrogen are incorporated in the process. This is the general technique of choice in the magnetic storage- (memory) and magnetic sensor-industry [59]. Thermal or electron-beam evaporation is convenient to produce thin films from small molecules [60] or from elements and compounds; these can even be mixed after annealing processes [61]. On the other hand, MBE uses the evaporation of elementary components under ultra-high vacuum conditions to achieve an accurate stoichiometry, which has been extremely useful to grow high-quality semiconductors [62] and devices based on multilayers of high-quality semiconductors [63]. The PLD technique, which uses a laser to vaporize material from a target onto a substrate under high-vacuum conditions, is frequently used to grow high-quality multicomponent oxide films [64]. CVD, where appropriate precursor gases are mixed on a chamber and made to react on a heated substrate, is a widely used growth technique for films [65]; it has recently allowed the synthesis of graphene films on large areas, thus opening the route for many applications [66]. Finally, ALD, where precursor gases are brought into the chamber sequentially and react to grow a film layer by layer with great control, has found applications in the semiconductor industry to grow high-dielectric-constant gate oxides [67].
In those cases where nano-structured materials (nanowires, nanoparticles, flakes, etc) need to be synthesized, it is possible to either grow the material in the form of a thin film and subsequently carry out a nanolithography process to pattern it into small structures [68] or to directly grow it in its nano-structured form (see figure 3.11 with ZnO nanostructures as an example). In general, for direct growth of the nanostructures, chemical synthesis routes are used. However, other methods benefitting from physical–chemical phenomena have been used. For example, the Vapour–Liquid–Solid (VLS) technique, in which a metal nanoparticle such as Au acts as a catalyser and forms a liquid droplet that contains the incoming gas to produce a growing nanowire [69], is very convenient to synthesize high-quality Si nanowires or other types of semiconducting, oxide, and nitride nanowires [70]. Another popular nanowire growth method is electrodeposition on appropriate membranes with small tubular structures [71], which allows the exploration of new and multicomponent stochiometries [72]. Moreover, focused ion- or electron beam-induced deposition techniques (FIBID or FEBID), where a precursor gas is delivered onto the substrate surface and decomposed by an impinging focused electron or ion beam, produce nano-deposits with metallic, magnetic, optical, or superconducting functionality [73]. Moreover, FEBID and FIBID techniques allow for the growth of three-dimensional nanostructures in a single step, which is convenient to explore novel physical effects [74].
Figure 3.11. Different morphologies of ZnO. From left to right and from top to bottom: Quantum dot. Nanotubes. Nanowires. Nanobelts. Nanoring. Nanocombs. Tetrapod. Nanoflowers. Hollow spheres. Sponge-like film. Nanosphere. Nanoplates. Copyright (2017) John Wiley & Sons [75].
Download figure:
Standard image High-resolution imageInterestingly, it is possible to exfoliate certain materials and produce flakes down to thicknesses of an atomic monolayer or a few atomic layers. In this way, graphene flakes were grown and studied for the first time, opening the important research field of 2D materials [76]. Moreover, deterministic transfer techniques allow the synthesis of multilayer-like systems with various flakes one on top of another, including control of the rotation angle of the flakes [77].
It is also worth discussing some emerging synthesis techniques for new materials not mentioned so far. For instance, self-organization and self-assembly are useful strategies to synthesize unconventional nano-patterns, as shown by the example of polymethyl methacrylate–polystyrene block copolymers [78]. Also, the combination of various synthesis and/or patterning techniques is common to fabricate novel structures and devices [79]. In this direction, smart combinations of materials and structures can give rise to metamaterials with new physical properties, such as the ability to cloak objects from electromagnetic fields [80]. The synthesis of topological materials (section 3.2) is also an intense field of research guided by theoretical predictions [81]. In such materials, symmetries in the electronic structure produce robustness against smooth topological variations and the materials show unusual physical properties. Thus, bulk, thin films, and nanowires of topological materials have been recently synthesized and their properties thoroughly studied [82].
Beyond the technical aspects of materials synthesis, we call the reader's attention to the important aspect of sustainability of the synthesis process, especially if it is intended to be commercially used on a large scale. First, the synthesis process should be clean, avoiding the release of contaminant products. Second, scarce materials should be avoided and recycling processes developed. For example, the use of rare-earth materials in permanent magnets raises important questions regarding strategic dependence on a single provider; alternative materials and strategies are under investigation [83]. Similarly, the increasing dependence on Li for its use in batteries and the difficulty in recycling them has raised concerns on the sustainability of this technology [84].
3.3.2.2. Physical properties of new (or improved) materials and their applications
It is not only our inherent human nature that makes us strive for steady advancements in all aspects of our life. Fast progress is also owed to the pressing needs to meet the enormous challenges arising from the world's tremendously increasing energy consumption and environmental problems, to a large extent caused by the rapid growth of the population and of industry in the absence of sustainability concepts or collective responsibility of the current 'throwaway society'. Materials are an essential part of our prosperity and lifestyle. In fact, there is hardly any sector where they do not play a crucial role, be it energy, environment, information technology (IT), mobility, or health. Sustainable energy involves photovoltaics, thermoelectricity, batteries, catalysis, solid-state lighting, and superconductivity. IT is concerned with electronic devices, data storage, sensors, switches, touch screens, and alike. Mobility and infrastructure are based on robust materials, in terms of being strong, hard, non-corrosive, heat-resistant, or inflammable. This also applies to various tools. Finally, the health sector is dealing with biocompatible, non-toxic components for implants or drug delivery, but is equally concerned with a huge variety of medical instruments that, in turn, not only require proper materials for their functions but also, again, electronics and IT. Below, we illustrate the crucial nature of materials development with a few examples, discussing where we are now and where improvements are needed.
The key components in electronics are semiconductors. These are materials that typically exhibit a band gap (range of forbidden electron energies) in the infrared (IR) and visible part of the energy spectrum. Their behaviour is tuned by the selective addition of impurity atoms. These introduce 'free' charge carriers (i.e., not bound to a particular atom) that make the material electrically conducting, in the form of either negatively charged electrons (n-doping) or positively charged holes (p-doping, see section 3.2). The material's electrical conductivity can also be controlled by external stimuli, such as electric or magnetic fields, by exposure to light or heat, or by mechanical deformation. The prime materials in electronic devices are silicon, germanium, and gallium arsenide; silicon is by far the most common. It is used, for instance, in MOSFETs (metal–oxide–semiconductor field-effect transistors) of which no less than several trillion have been made to date. Despite this obvious success, and their widespread application in light-absorbing or -emitting devices, neither Ge nor Si are optimal materials for the semiconductor industry, because of the 'indirect' nature of their band gaps. The excitation of electrons to higher energy levels in these materials requires the electron to interact not only with light (photons) to gain energy, but also with lattice vibrations (phonons, see section 3.2) in order to gain or lose momentum. Such indirect processes happen at much lower rates and are thus less efficient than direct processes. Despite this disadvantage, Si is hard to beat on the market as it is abundant on the Earth's surface and thus rather cheap; there are well-established processing techniques that ensure its high quality and purity. The total production volume of silicon worldwide in 2020 amounted to about eight million metric tons (https://www.statista.com/topics/1959/silicon/).
Inorganic semiconductors rule today's electronics and optoelectronics industry. While GaAs is the main player in red-light emitting devices and lasers, GaN plays the same role for the blue and green colours—and, as a consequence, for the generation of white light. In 2014, Isamu Akasaki, Hiroshi Amano, and Shuji Nakamura were awarded the Nobel Prize for Physics for 'for the invention of efficient blue light-emitting diodes which has enabled bright and energy-saving white light sources'. A long process requiring many years of in-depth investigations towards a full understanding and a full development of the material preceded its use in such applications. Today, LEDs are omnipresent in TV screens and cover walls and buildings as giant advertisements. Most important, LEDs are a true game changer towards more efficient lighting devices, compared to traditional lightbulbs. The latter waste about 90% of the energy as heat could be considered 'heating devices' rather than light sources. Nevertheless, ample room for improvement remains, as LEDs too should become more efficient.
On the other hand, organic semiconductors have been studied for several decades as potential replacements for inorganic components. Besides their extraordinary electro-optical properties, they combine several advantages such as mechanical flexibility, a huge variety of building blocks, and low production costs. Therefore, all kinds of opto-electronic devices have been demonstrated. On the downside are their inferior thermal stability and low charge-carrier mobilities. Therefore, this class of materials is only used on a large scale in very distinct applications such as organic light-emitting diodes (OLEDs). How to compensate for major disadvantages by forming organic/inorganic hybrid interfaces will be discussed in section 3.3.3.
Over 40% of current energy consumption is wasted in the form of heat, be it in industrial ovens, chemical plants, exhaust pipes, engines, or computers. The thermoelectric effect allows the conversion of heat into electricity using thermoelectric generators. Thus, such devices have great potential to reduce the world's energy consumption. However, today's thermoelectric materials are not efficient enough to make this concept economically viable. Designing high-performance thermoelectric materials that could boost their widespread deployment is a difficult task. Since the thermoelectric efficiency depends on the ratio of charge and heat transport, the goal is to maximize the former and minimize the latter at the same time. As the enhancement of one goes typically hand in hand with that of the other, a real breakthrough is a great challenge. One way out of this dilemma is the development of complex crystals. Such compounds typically have a cage-like crystal structure formed by atoms with covalent bonds to ensure a high performance in their electronic properties, while guest atoms inside their cavities ensure low thermal transport. Typical examples for such inclusion compounds are skutterudites and clathrates. Such structures offer a playground for tuning their properties to the optimal performance. Still, their figure of merit ZT—a measure for the usefulness of the material in thermoelectric applications—hardly exceeds values of about 1, whereas a value larger than 2 would be required for use on a large scale. Another approach to reaching high ZTs is the reduction of dimensionality or nanostructuring via superlattices, quantum dots, nanowires, and nanocomposites [85–88]. When the distance between nanostructured interfaces is shorter than the mean free path of phonons but still larger than that of the electron, the engineered interfaces enhance phonon scattering, thereby impeding heat transport, without affecting electron-mediated electrical transport. For the quantum-well superlattices Bi2Te3/Sb2Te3, a high ZT of 2.4 has been achieved [89]. More recently, simpler structures consisting of weakly bound 2D layers have gained a lot of attention. For example, SnSe2 shows a remarkable low thermal conductivity of 0.4 W m−1 K−1 and a ZT of 2.6 [90]. These properties are realized over a wide temperature range.
It is not only the direct consumption of fuel and electricity that needs to be reduced to facilitate the transition to a carbon-neutral economy. Consider how much energy is lost because all our means of transportation are heavy, being mainly made of steel. Clearly, heavy is considered synonymous to robust and strong, which is a requirement for cars, trains, and airplanes to be safe. On the other hand, strength is not the only prerequisite. It is their ductility that prevents materials from breaking. How to make materials extremely strong and simultaneously ductile when, typically, one property can only be improved at the expense of the other? This question has triggered generations of researchers and engineers. The situation is getting even more puzzling when one also needs to reduce weight (e.g., by reducing thickness). Airplanes, cars, and trains would consume so much less energy if they were lighter. One solution of this problem may be found in high-entropy alloys, a currently booming field of research [91].
Another solution lies in materials that involve only light chemical elements such as aluminium and titanium. Aluminium, being super light, lacks strength and is also extremely expensive to produce—in terms of energy consumption. Titanium—more than an order of magnitude less abundant than Al—is, on the positive side, heat-resistant, tough (but weaker than heat-treated steel), and non-magnetic, and also shows low thermal expansion. On the downside, it is difficult and expensive to manufacture. The intermetallic compounds TiAl, lightweight and resistant to oxidation, find use in aircrafts, jet engines, and automobiles. Its ɤ-phase has excellent mechanical properties and is oxidation- and corrosion resistant, to temperatures well above 600 °C. It is therefore discussed as a possible replacement for traditional Ni-based superalloys. In this context, we briefly address another problem. Turbine blades operate at temperatures higher than their melting point. Therefore, they require coatings. Such 100 μm to 2 mm thick layers of thermally insulating materials reduce the temperature of the underlying metal, thereby also providing protection against oxidation and corrosion by high-temperature gases. The prototypical material here is Y-stabilized ZrO2. Since this material undergoes a phase transformation at elevated temperatures, active research is currently dedicated to adequate replacements.
3.3.2.3. Selected emerging applications and the need for new materials
As shown in the previous section, new materials have applications in numerous fields. In the present section, we will focus our attention only on emerging applications related to the digital world as well as energy. In the first case, we have chosen emergent technologies that largely depend on new or improved materials and allow for improved or energy-efficient computing and sensing. In the second case, we have chosen materials that could help methods that lower our carbon footprint such as solar energy, energy harvesting, and thermoelectricity. Without being exhaustive, this approach should permit the reader to appreciate how new materials can impact our future lives.
3.3.2.3.1. Quantum computing, neuromorphic computing
Quantum computing has the potential to tackle difficult or long computational problems that are tedious, intractable, or impossible using classical computation [92]. Recent demonstrations even suggest that quantum supremacy has been achieved in a particular case [93]. Various technologies have been put forward to perform quantum computation, but the one based on superconducting qubits is so far the most promising [94]. Other proposals for quantum computing make use of topological materials, photonic structures, molecular magnets, etc. This is an open and exciting field of research fed by the use of new or improved materials.
Inspired by the low energy consumption of the human brain (20 W), an emergent field of research is neuromorphic computing. Here, the use of materials and devices that mimic the behaviour of neurons and synapses is pursued. Neuronal computation is performed through the generation of spikes, depending on the integrated input coming from other neurons. The synapses, or connections between neurons, contribute to the computation by changing their connection strength as a result of neuronal activity, which is known as synaptic plasticity. Synaptic plasticity is the mechanism that is believed to underlie learning and memory of the biological brain [95]. Materials with phase change, memresistors, ferroelectric materials, spintronic oscillators, etc, are currently being studied for this application [96] and proof-of-concept results indicate the potential of this technology for language recognition [97].
3.3.2.3.2. Low-power, flexible, high-frequency electronics
One of the main paradigms of the 21st century society is the existence of electronic devices and their connectivity. The underlying hardware supporting this technology is silicon-based microelectronics, which is sustained by two main pillars: the materials involved in microelectronics (semiconducting, metallic, insulating, magnetic, etc) and the lithography techniques allowing one to reach the required small dimensions (below 10 nm). These techniques comprise optical and electron-beam lithography, focused ion beams, and nanoimprinting, among others. Future developments in electronics are expected to come, within Moore's approach, from improvements in the materials used or in the lithography processes; alternatively, they can come from new applications of microelectronic chips (More-than-Moore), or from different approaches beyond standard paradigms of the semiconductor industry (Other-than-Moore) [98]. Within the new context of More-than-Moore and Other-than-Moore approaches, intense research is being carried out to target novel electronic devices harnessing low power, flexible, and high-frequency properties [99]. Whereas low power is required to comply with today's and tomorrow's energy requirements, flexibility is needed in wearable and implantable devices; high-frequency response allows for fast data collection, treatment, and communication. Given their intrinsic flexibility and low power consumption due to their one-atom-thick nature, as well as the absence of the working-frequency limitations of Si, Graphene, and other two-dimensional (2D) materials such as transition-metal dichalcogenides (TMDs) are expected to excel in these applications [100]. An example is shown in figure 3.12, where a device based on graphene transistors has been implanted in a rat brain for mapping its neuronal activity.
Figure 3.12. (a) Schematic of the graphene-based transistor and its equivalent circuit. (b) Transistor characteristics. (c) Illustration of the rat with the untethered recording system implanted. (d) Graphene transistor array device implanted in the rat cortex. (e) Photograph of the wireless headstage. (f) Photograph of the graphene transistor array mounted on a customized connector and zoomed image of the probe active area (right). This figure has been obtained from reference [101] and is subject to a free license under a Creative Commons Attribution 4.0 International License.
Download figure:
Standard image High-resolution image3.3.2.3.3. Ubiquitous sensing and in situ and operando characterization
Today's digital society and modern industry require ubiquitous sensing. Many sensors are based on physical (i.e., optical, magnetic, electrical, mechanical, etc) effects. They can be carried by objects (vehicles, electrical appliances, etc) or by humans (cell phones, smart watches, etc), placed in an industrial environment (for the monitoring of manufacturing, fabrication by robotic machines, etc), in the workplace, or at home (for purposes of security, safety, comfort, etc) [102]. A particular requirement of sensors is their capability to give an accurate output in an energy-efficient way [103]. If we take the example of CO2 monitoring, extremely important in closed spaces during the COVID-19 pandemic, technology has evolved from bulky, heavy sensors to small portable sensors that are fabricated in clean rooms in a manner similar to microchips. Using the same physical principles as the old bulky CO2 sensors (i.e., the absorption of infrared light by CO2 molecules), new materials for semiconductor diodes providing emission of light at the required wavelength, for miniaturized waveguides coated with efficient light reflection, and for solid-state photodiodes have paved the way for these modern CO2 sensors (see figure 3.13).
Figure 3.13. (a) Simple design of a CO2 sensor, with a single reflection. The light emitted by the light emitting diode (LED) is absorbed at particular infrared wavelength by CO2, which leads to a decrease in the light intensity detected by the photodetectors (PD). (b) Optimized design of the pathway travelled by light, which includes multiple reflections between LED and PD. (c) Wireless self-powering LED/PD-based CO2 sensor. (d) Battery-based LED/PD-based CO2 sensor. Images have been taken from the article reference [104] through Creative Commons CC BY license.
Download figure:
Standard image High-resolution image3.3.2.3.4. Materials for improved energy production
Clean and renewable energy sources are increasingly used in the energy mix of most countries. New materials can help us find more efficient and cleaner processes for energy production and reduce CO2 emissions (https://www.elsevier.com/connect/net-zero-report). This hot topic is also very broad, so, we will just mention a few examples.
Solar cells for photovoltaic energy production have a quite long history. We draw the reader's attention to the well-known chart provided by NREL (https://www.nrel.gov/pv/cell-efficiency.html) that shows the efficiency of solar cells over the years. Also in this area, silicon has long dominated the market. In the last two decades, a great many new or improved materials are investigated for their application in solar cells, photovoltaic cells, solar absorbers, heat storage materials, photocatalysis, light trapping, solar concentrators, and so forth. A huge boost was achieved in recent years with the advent of hybrid halide perovskites that, so far, keep breaking all records in terms of efficiency [105]. Unless replacement elements are found, the widespread application of these materials is likely to be halted because they contain the toxic element lead. Another example is that of electro-chromic materials. These change the absorption of light under small electric fields and are used as chromogenic materials [106].
As described in the previous section, an interesting way to produce energy is to use the waste heat of other energy sources to feed thermoelectric devices, which relies on materials with good electrical conduction but bad heat transport, with great expectations from nanostructured materials and new compounds [107]. Energy harvesting from friction, vibration, RF sources, etc, is also intensively studied to power small (electronic) devices [108]. Future energy sources such as fusion energy call for the investigation of materials that could stand the stress and hard radiation inside the fusion reactor [109]. This topic will be later discussed in more detail.
3.3.2.4. Data-centric materials research
While Make and Measure—synthesizing materials, characterizing them with various experimental probes, and computing and analyzing their properties—represents the current state-of-the art of materials research, there is an urgent need of speeding up the process by complementary approaches. 'Twice as fast at a fraction of the cost compared to traditional methods' was also the aim of President Obama's Materials Genome Initiative (MGI) (https://www.mgi.gov/about), launched in 2011. In fact, data-centric science—combining emerging techniques of machine learning and other methods of artificial intelligence (AI) with the Big Data that the community is producing on an everyday basis—is currently establishing the fourth pillar of materials research. This is evidenced by the increasing number of publications and the advent of new journals emphasizing the importance of data, but also by the many workshops and sessions at international conferences dedicated to this topic. To mention an example, the 2021 spring conference of the American Physical Society (APS) counted 51 sessions with either Data Science, Machine Learning, Deep Learning, or Artificial Intelligence in the session title. One might get the impression here that data-centric materials science is already fully established. How huge the challenges truly are will be discussed below.
A popular approach among data-driven efforts is high-throughput screening (HTS). It has led, for instance, to the establishment of large-scale US-based computational data collections (http://aflow.org, https://materialsproject.org, http://oqmd.org) already before the MGI; and all over the world, there is a rapidly growing number of other small and large databases (see also [110]), examples being the Computational 2D Materials Database (C2DB) [111] (https://cmr.fysik.dtu.dk/c2db/c2db); the HybriD3 materials database (https://materials.hybrid3.duke.edu)—a collection of experimental and theoretical halide-perovskite data; the experimental metal–organic framework database CoRE MOF [112], just to mention a few examples. Systematically replacing atomic species in known materials or combining them in new ways such to create novel structures offers a huge playground for exploring materials and their properties before they are even synthesized. There are also more and more experimental initiatives of this kind, examples being the high-throughput platforms for catalysis (https://www.hte-company.com/en/company/high-throughput-experimentation) or photovoltaics (https://data.nrel.gov/submissions/75, https://www.hi-ern.de/hi-ern/HighThroughputPV/node.html). We note that HTS has by no means always been a computational approach. The most famous example may be the ammonia catalyst demonstrated by Fritz Haber in 1909; this was followed by systematic testing of about 20 000 materials by Alwin Mittasch in Carl Bosch's group at BASF.
However, all these efforts are insufficient when it comes to exploring the infinite amount of possible materials that can be created, considering the building blocks provided by the periodic table of elements (PTE) and the many ways of combining them, in terms of composition and configuration. To reach the ambitious goal—phrased in reference [113]—of creating 'materials maps' from which one can read in what region of 'materials space' one is likely to find promising candidates for a given application, HTS and Big Data must be accomplished by novel AI concepts and tools. This issue will be addressed below.
First, we discuss the current limitations of data-centric materials research (i.e., the facts that are hampering fast success). A first problem concerns scientific bias introduced by our publication culture. Published success stories show what works and may lead us to comprehend why. However, this procedure alone does not provide us with the full picture (i.e., it does not allow us to understand why alternative approaches or materials do not work). This problem is particularly critical in materials synthesis. Even publicly accessible databases such as Landolt–Börnstein (SpringerMaterials, https://materials.springer.com), which provide comprehensive information about materials properties, lack information on synthesis. A recent effort is placed on scanning literature for synthesis recipes and parameters [114]. However, this information cannot be complete as unsuccessful synthesis attempts are typically not published.
The second showstopper concerns the amount and description of shared research data. The materials science community is steadily producing enormous volumes of valuable data, be it with the diverse experimental techniques and instruments or the large variety of computational methods. Eventually, papers are published that report on the gained knowledge in a very compact form. Most of the information inherent in the data is, typically, 'forgotten' and might even be discarded rather than published and made available for future use. However, even if data are kept, they are often insufficiently described, rendering them of little value. This problem is less severe in theoretical research. As long as the input and output files and the computer programme (and its version) are known, calculations can be verified. Nevertheless, for comparison with other results, the meaning of the data must be uniquely described in terms of metadata. The in-depth annotation of measured data is an even bigger issue as the full information on the sample (including preparation), the apparatus, and the measurement type and conditions is required.
Sharing and publishing research data also implies 'sustainability'. For instance, doubling of identical calculations or measurements can be avoided, leaving time and resources for work beyond. This topic brings us back to HTS. Typically, those materials that fulfil the required criteria are investigated and well characterized, while all others are not further pursued. Obviously, while they may not be useful for the purpose of the particular research pursued, they may be extremely valuable in other contexts.
To harvest all this currently disregarded information, research data—but also workflows and tools—must follow the FAIR principles [115]. What does FAIR—Findable, Accessible, Interoperable, and Reusable—mean in the context of our field? Certainly, publicly available data stores fulfil the F and to a large extent also the A as uploaded data can be inspected and, possibly, also downloaded. This is the prerequisite also for the R —re-using or re-purposing data. The latter refers to what was mentioned above, namely that research results can be useful for a purpose that is different from the original intention. The I (interoperability) is the most critical and largely unresolved issue. This applies in particular when data from different sources are brought together. For the experimental characterization, there exist a few benchmark databases, an example being the EELS Atlas (https://eels.info/atlas). However, many more well-characterized data obtained from state-of-the-art instruments would be needed. On the theory side, reproducibility [116] and benchmarking for solids [117–120] have become an issue only rather recently.
An early data infrastructure, following FAIR principles even before the term FAIR was introduced is the NOMAD Laboratory (https://nomad-lab.eu). Being an open platform for sharing data within the entire community, it is different from other data collections in computational materials science. Information about its services, comprising the NOMAD Repository, the Encyclopædia, and the AI Toolkit, can be found in [121, 122]. Its extension to data from sample synthesis and experimental characterization is described elsewhere [123]. Likewise, the Open Access to Research (OAR) data infrastructure at NIST [124] is built to allow NIST scientists and others to share research data using standards and best practices adopted in the scientific community. Given the pressing needs, many such initiatives are currently established or will follow.
3.3.3. Challenges and opportunities on the Horizon 2050
As discussed in the previous section, in the next years and decades, a great many bottlenecks must be overcome as far as materials exploration and development is concerned. Clearly, innovative solutions and ideas and therefore 'thinking out of the box' is required. Which are the most promising material classes for what kind of applications? A first example is that of nanostructured and composite materials; these will certainly help us tailor and tune desired properties. The introduction of interfaces allows us to exploit the advantages of pristine components while getting rid of their disadvantages. This may apply to the transition from pure organic electronics to hybrid electronics (e.g., in light-harvesting or light-emitting device, where, one may want to make use of the superior light–matter interaction of organic components with the advantageous higher charge-carrier mobilities and weaker electron–hole binding of inorganic semiconductors). This concept of combining the best of two worlds applies to other interfaces and nanostructures as well. In addition, data-driven approaches (see above) is expected to bring 'outliers' to light (i.e., materials that have not been considered for a given application so far). These may well be 'simpler' materials and therefore less involved as far as synthesis is concerned.
The development of technologies based on new or improved materials will surely have a great impact in our lives on the Horizon 2050, no matter the technology at hand: information technologies, transport, energy production, health, and more. In what follows, we shall focus our attention on materials for a digital and energy-efficient world in 2050. Unfortunately, many topics will remain unaddressed, but we think that most of the profound changes in the coming decades will come from the increasingly digitalized society and the evolution of our means of producing energy.
3.3.3.1. Materials for a digital world
The control of information (storage, processing, and transmission) shapes every aspect of our daily life, thus permeating cultural and social changes. The digitalization of information, which started around 50 years ago, is accelerating and it is reasonable to suppose that by 2050 the relevant information in our society will be digital and in most cases only digital. A multi- and cross-disciplinary approach is needed to cover the present challenges in this field, ranging from more technological aspects to social ones. The current digital transformation is enabled by developments in physics and engineering and concerns several fields including electronics, optics, material science, and quantum technologies. Today's challenges include sustainable and energy-efficient electronics, integrated photonics with new functionalities, quantum computing, machine learning, and operation within the Internet of Things [125].
Materials for ubiquitous sensing. The future is that of an omni-connected society, where sensors will play a key role and represent an unavoidable interface amongst humans, objects, and the environment (see also section 3.3.2.3.3). Sensors are needed for monitoring of the environment (gas concentrations, radiation, etc), for energy-efficient control of autonomous cars and drones, for the precise localisation of persons and objects, for safety and security applications, and so on. Sensors are more efficient if they are integrated with the electronics handling the obtained data into a single device (system), which requires micro/nano-fabrication techniques. Sensing matter at the micro- and nano-scale allows, on the one hand, to probe new physical states endowed with novel properties and allowing the development of new devices and, on the other hand, the detection of biological objects and processes with high spatial and temporal resolution. In addition, new tools such as artificial intelligence and machine learning can help design a new generation of smart nano-sensors that process the data and communicate them more efficiently in order to provide a faster and energy-saving response. In sensors, one of the most important constituents (if not the most important) is the material that shows the functional response: optical, electrical, magnetic, mechanical, etc. Also, the material into, or onto which the sensor is integrated (the substrate) is of utmost importance; their physical properties determine their applicability: flexibility, optical transparency, heat or electrical conductivity, etc. These are some of the challenges and opportunities in this field on the horizon 2050:
- –Functional properties of materials. With respect to electrical conductors, good electrical contacts and materials at the nanoscale are required in the pursuit of ever-increasing miniaturization of electronic devices. This opens opportunities to achieve improved metallic contacts by resorting to new materials such as graphene and other 2D materials that do not suffer from electro-migration issues when their dimensions are decreased to the nanoscale. As for magnetic materials, in the case of permanent magnets it is important to decrease our dependence on rare-earth elements, all the while not losing performance. In nano-magnetism and spintronics applications, the challenge is to find suitable magnetic materials and architectures that decrease power consumption. The purpose of spin-orbitronics is to obtain materials or combinations of materials that produce topological magnetic structures (skyrmions, etc) or useful three-dimensional magnetic textures. In the field of nano-optics, superb opportunities exist for the fabrication of smaller optical components; even if the light wavelength is intrinsically large (in the order of half a micrometer), it is possible to exploit plasmonic effects to reduce the working wavelength to smaller values (see also section 3.2.5).
- –Integration of materials in suitable electronics platforms. Flexible electronics is a very important development field for electronic devices on clothes, on our skin or inside our body (such as neuro-chips). In this application, the added value of other substrate properties such as optical transparency or electrical conductivity is very relevant. The realization of hybrid fabrication processes combining functional materials with semiconductor-based platforms, which are generally very strict with respect to compatible materials, offers important opportunities.
- –Working range of materials. The tendency in telecommunications is to work at high frequencies, which opens the need for (conductive, magnetic, optical, etc) materials that are (energy-)efficient at GHz and THz frequencies. Here, graphene and other 2D materials as well as superconducting materials are very promising. For superconducting materials, the Holy Grail is to find superconductivity at room temperature and ambient pressure, perhaps in materials where it is today unsuspected. Extending the temperature range in which sensors work is very important in applications where substantial heating is produced; one cannot forget that the increasing electronic miniaturization is generally accompanied by a large Joule heating in a small volume space.
- –Biocompatibility of materials. Whereas for in vitro and point-of-care biosensors any material can be used, biosensors that are to be implanted inside the body or will be in contact with the skin must be biocompatible. This poses strict requirements on the materials used, especially in the case of implanted biosensors that track disease markers. Given the overall requirements of biosensors in terms of sensitivity and specificity, this implies significant challenges. For example, the biosensor must be able to operate within the therapeutic range of the target substance whilst in the presence of complex solutions (e.g., interstitial fluid or blood). It must be biostable and biocompatible, since negative immune reactions may cause the device to become non-functional. It must be self-sufficient in terms of power supply and control from external devices; as far as data transmission is concerned: the signal output transmitted to an external communication device should arrive in a meaningful form for ease of use for the patient/clinician [126].
- –Energy efficiency of materials. Ubiquitous sensing has a pitfall: the need for energy to power the sensors, to process the data, and to transmit them. Power can be provided to the sensor by batteries, through energy harvesting, or via wireless means. Thus, improved materials for batteries and energy harvesters will remain necessary for decades to come. In addition to the intense search for materials that could serve as efficient thermoelectric convertors that was already mentioned, similar searches are conducted for materials for power supply and for detection.
- –Scarcity of materials. There is plenty of room for the substitution of scarce/strategic materials with more abundant ones, provided that the performance of the sensors is not jeopardized. Just to have an overall picture, a mobile phone contains up to 64 elements, many of which could be unavailable in a few years (https://www.bbc.com/future/article/2014031414-the-worlds-scarcest-material). Besides the long-standing problem of the scarcity of rare earths for permanent magnets and that of Li for batteries, some heavily used metals are also scarce, such as Ta, Co, Pd, Cu, In, Pt, Ag, Rh, Au, Al, etc. In this topic, another interesting avenue is the development of recycling processes that could reduce this problem.
Materials for quantum technologies (see also section 3.2). Quantum technologies comprise quantum computing, quantum communication, and quantum sensing and hold potential for paradigm shifts across several disciplines. Huge research investments have been announced in this field by the main players in technology, which include the most important technological companies as well as entire nations and clusters of nations. The treasure hunt is on for a disruptive technology that can beat semiconductor-based computation in specific applications. Although promises in this field have already existed for a few decades, the current state-of-the-art in this discipline as well as the incoming investments are expected to pay off by 2050.
- –Quantum computing. The challenge is to develop robust platforms with a sufficient number of qubits allowing fault-tolerant computation. Although superconducting platforms based on Josephson Junctions are currently leading the race, as recently demonstrated by Google [39], an intense research using other platforms also exists. In particular, semiconductor-based platforms are very promising, such as single-spin qubits hosted in quantum dots. Another emerging platform is that of topological qubits based on Majorana quasiparticles occurring on topological superconductors [127]. Basic research is also underway regarding the use of molecular and magnetically based qubits [125]. In all these platforms, one can foresee a tremendous research effort in the next decades to implement new or improved materials and their integration in optimized electronic platforms.
- –Quantum communications. Today, we already use a quantum effect whenever we use a navigation system: an atomic clock. In the future, our communications will be private thanks to quantum encryption, the technical name of which is quantum key distribution (QKD). This technology is protected by the very laws of physics: the mere fact of observing a quantum object perturbs it in an irreparable way (section 3.2). The span of current QKD systems is limited by the transparency of optical fibres and typically reaches one hundred km, which opens opportunities for improved optical fibres and optical platforms that could extend the working range of this technology. By 2050, it is expected that various ambitions of quantum connectivity will be achieved [128].
- –Quantum sensing. In our tireless effort to probe matter with the highest sensitivity and the highest spatial and temporal resolution, quantum sensors are expected to contribute enormously. For instance, the most advanced detectors of magnetic flux today are quantum ones, such as SQUIDs (superconducting quantum interference devices) or SNVM (scanning nitrogen-vacancy microscopy) [129]. Sensors able to detect such magnetic fields with nanometre spatial resolution enable powerful applications, ranging from the detection of magnetic resonance signals from individual electron or nuclear spins in complex biological molecules to readout of classical or quantum bits of information encoded in an electron or nuclear spin memory [130].
Materials for neurotechnologies. Interfacing with the brain (brain–machine interfaces, BMIs) is one of the most exciting opportunities of today's technologies, but there are many challenges to overcome before the technology is ready for broad use. For certain applications, the external detection of the weak electric fields produced by the brain activity will be sufficient, such as in videogames, communication with our mobile phone, treatment of certain brain disorders, or neurostimulation (https://www.bitbrain.com/#). However, implanted BMIs are more powerful and even have the potential to produced enhanced human beings (https://neuralink.com/). Whereas advancements in BMI for electrophysiology, neurochemical sensing, neuromodulation, and optogenetics are revolutionizing scientific understanding of the brain and enabling treatments, there are many gaps in the technology. The grand challenge in neural interface engineering is to seamlessly integrate the interface between neurobiology and engineered technology to record from and modulate neurons over chronic timescales. However, the biological inflammatory response to implants, neural degeneration, and long-term material stability diminishes the quality of the interface over time [131]. Recent advances in functional materials are aimed at engineering solutions for chronic neural interfaces, yet, the development and deployment of neural interfaces designed from novel materials have introduced new challenges that have been largely unaddressed. Many aspects of this topic are related to the use of suitable materials, such as the optimization of the individual electrodes and probes, including their softness and flexibility, and other critical multidimensional interactions between different physical properties of the device that contribute to overall performance and biocompatibility. Before regulatory approval for use in human patients is achievable, the behaviour of these new materials and of the overall device must be addressed. By 2050, we predict that significant progress will have taken place and some of these BMIs will be available for broad use. Hopefully, this disruptive technology will develop following appropriate regulations (neurorights) [132] that avoid the existence of neuronal paradises (https://nanofab-deteresa.com/science-popularization/).
3.3.3.2. Materials for energy production (see also section 3.3.2.3.4)
Crucially important for the production of chemicals and fuels is the sustainable production of hydrogen. For this, photo-catalytic water splitting could become a key technology. So far, limitations in suitable catalyst materials render this process unfeasible. To trigger the chemical reaction requires a stable semiconductor to harvest the solar energy as well as an efficient catalyst to split the water molecules and evolve hydrogen and oxygen from the electron–hole pairs that are created by sunlight. As such, identification of a better catalyst for water splitting has enormous potential in carbon-dioxide management and hydrogen-based energy technology.
On the longer-term perspective, our cars and trucks may run on hydrogen. For the time being, society and industry rely more on electric drive. Thus, batteries are a critical player here (see section 3.3.3.1).
Also, we should not forget the energy losses caused by transmission which amount to about 6% in average in Europe. Superconductors would be the ideal solution as they transport current without losses; these materials can operate so far, however, only at low temperatures and/or high pressures. Yet, we are far from room-temperature superconductivity at ambient conditions, but the huge progress in identifying materials with high superconducting transition temperatures and high critical currents over the last years has given rise to big hopes. The highest temperatures so far have been achieved in pressurized superconducting hydrides (see, e.g., [133] and references therein).
Making current technologies more energy efficient by improving or replacing the underlying materials will be essential for the period leading up to 2050 and beyond. We should, however, also look ahead towards a possible additional source of energy—nuclear fusion. The idea is to replicate the fusion processes of the Sun to create energy on the Earth. To this extent, the thermonuclear fusion reactor ITER is built as a collaborative megaproject of (in alphabetic order) China, the European Union, India, Japan, Russia, South Korea, and the USA; other partners being the UK, Switzerland, Australia, Canada, Kazakhstan, and Thailand. ITER will have the capability to produce 500 MW of power with a necessary input power of 50 MW for more than 300 s [134]. This reactor, is, however, not built for energy supply but for technology demonstration and can be considered as the world's largest plasma physics experiment. Besides being an incredible engineering effort, it also poses severe challenges to materials science. Interestingly, construction of the ITER complex started in 2013, while the choice of most crucial materials was not made. Issues here are, for instance, temperature and radioactive contamination. Components must withstand extremely high temperatures up to 1200 °C, or even possibly 3000 °C. An obvious candidate here is tungsten, exhibiting a melting point of 3422 °C. A severe drawback of this material is that it turns brittle above room temperature. Therefore, for instance, doping elements must be found to remedy the situation. As a very promising candidate for the reactor walls, carbon-based materials like CC fiber composites or SiC were discussed. Unfortunately, it turned out that they would quickly absorb all tritium from the plasma, making the reactor walls highly contaminated. Overall, the case is still not settled today.
3.3.3.3. New knowledge from research data
What do we need to enhance our research by the fourth paradigm? These are basically two aspects: FAIR data and the corresponding data infrastructure, including tools for processing, storing, and accessing data; and novel AI methods that allow us to turn data into knowledge. All this is in the making, but we are still far from a real breakthrough.
Let us focus on FAIR data first. It is clear that the big picture can only be realized when bringing together data from different sources, essentially, from all over the world. This comes with challenges with respect to all 4V of Big Data. The incredible Volume of materials data requires a distributed data infrastructure that allows for accessing its content with standardized protocols. A first example for a specification of a common REST API has been developed by the OPTIMADE consortium (https://www.optimade.org/) [135]. Such tools are indispensable as the community, and every sub-community, is using and building very different tools in their daily research. This means that, in the first place, we need to overcome the issue of Variety without forcing people to drastically change their habits but rather supporting them with appropriate tools. Variety not only concerns different instruments and measurement modes for one specific type of experiment or one specific calculation method that can be applied by different software packages. Overall, we are hit by variety as the community is dealing with an enormous number of different theoretical and experimental characterization techniques that should be dealt with on equal footing. This variety comes with Veracity, the uncertainty in the data. Veracity also has different faces. On the one hand, calculations can be based on one or another method and approximation; likewise, different instruments may have different resolutions, and measurements can be carried out at different temperatures. On the other hand, even measured with the same instrument under the same conditions, different samples may give rise to different results. Finally, theory and experiment need to be reconciled. In contrast to other fields, like high-energy physics, Velocity may be least critical in materials research. The emerging new (time-resolved) measurement techniques producing enormous amounts of data in short time, may pose, however, challenges in the future.
From the above, it is clear that veracity and variety largely hamper interoperability if the data are not fully annotated. If data can be misinterpreted because their meaning and quality are not known or not considered, even the most innovative AI method can be misled. Therefore, the description of the data by rich metadata is key for interoperability and for the success of data-centric approaches. Metadata should capture all parameters that may influence the results. The establishment of metadata schema for each synthesis route, experimental probe, and theoretical approach, possibly connected by a 'materials ontology', is the most critical step towards FAIR handling of all materials science data. An example for how such data infrastructure can be built by the community is described in reference [123].
Let us now turn to the role of AI. Machine learning methods are applied to many problems of materials research (see, e.g., [136, 137]) to predict stable structures and materials properties. Most of them are very successful as long as it concerns interpolation of data or classification problems. To go beyond interpolation, dedicated data analysis and AI tools are yet to be developed. Most crucial thereby is the representation of a material in terms of descriptors—the most relevant parameters behind a certain property or function [138–141]. Obviously, having such methods in hand along with the right data is key for their success. Right in this context means certainly Big, as the complex interplay of interactions taking place in materials can only be learned and trends can only be identified from a large amount of data. Right, however, also means that the data need to be well characterized (as noted above) and need to carry the required information. In that sense, just increasing the amount of data does not help. How to obtain and choose those very precious data that enable exceptional findings is another big challenge.
To summarize, as often stated, research data are a goldmine of the 21st century. Turning it into gold, however, means refining the feedstock and enhancing it by novel tools. On the Horizon 2050, big steps toward this goal can and will be realized.
3.3.4. Final considerations
Role of theory. Last but not least, we should consider the role of theory, which is invaluable for the characterization of materials as well as for data-centric approaches. For instance, a big bottleneck in superconductivity research is that a full theoretical understanding of unconventional superconductivity is lacking [142]. Theoretical concepts overall, and in particular, ab initio methods, have advanced during the last decades as a stable pillar of materials research. Density-Functional Theory, Green-function-based methods, (ab initio) Molecular Dynamics, and Monte Carlo Simulations are state-of-the art techniques that are able to describe and predict materials properties with high accuracy. For details, we refer to the section 3.2 by L Reining. We note though that significant advances in methodology are needed to arrive at a fully quantitative description such to enhance their predictive power. While first principles theory is well advanced in capturing electron–electron, electron–lattice, electron–hole, etc interactions very well, their interplay is often less well understood. This is partly owing to the very complex formalisms and partly to the computational costs that render such calculations infeasible for more complex and even so for rather simple materials. Here, also new computing technology may be one way out.
Societal aspects. There are practical and political aspects to be considered. It is not always the best material that provides the best solution to a problem. We always need to keep a bigger picture in mind; for instance, the whole life cycle of a product and the side effects it may cause. Many questions may arise here: Is it better to use cheap and easy to produce, but imperfect materials than the best possible, most efficient ones that are expensive? Are good products recyclable? If yes, are, for instance, contaminations of an alloy with all kinds of elements and deviations from the desired composition still acceptable such to be able to produce the product in mind? Can toxic elements be tolerated if they are kept in the circle such to avoid contamination by waste? Is industry reluctant to switch to new materials as a redesign of production lines costs enormous amounts of money that has to be compensated by higher gain and/or possible competitive advantage? On the political side, a big issue is the dependence on third countries: Just to give one example, China is by far the world's largest producer of silicon. Around 5.4 million metric tons of silicon were produced in China in 2020, which accounted for about two-thirds of the global silicon production that year. In 2017, the European Union identified 27 critical raw materials among 78 candidates to be critical [143]. This situation requires rethinking in view of our global goals and even more careful assessment of what material to choose for what purpose.
Acknowledgments
CD acknowledges helpful discussions with J Spitaler, L Romaner, and R Pippan and funding from the DFG through the NFDI consortium FAIRmat, project 460197019. JMDT acknowledges funding from Gobierno de Aragón (grant E13_23R)
3.4. Manipulating photons and atoms: photonics and nanophysics
Jean-Jacques Greffet1, Antoine Browaeys1, Frédéric Druon1 and Pierre Seneor2
1Université Paris-Saclay, Institut d'Optique Graduate School, CNRS, Laboratoire Charles Fabry, Palaiseau, France
2Université Paris-Saclay, Thales, CNRS, Unité Mixte de Physique, Palaiseau, France
Our knowledge on the physics of atoms and light has been revolutionized by the advent of quantum mechanics during the first 30 years of the 20th century. It was Planck who first postulated the fundamental principle that energy exchange between light and matter can only be provided by electromagnetic energy quanta, a postulate needed to explain the form of the high-energy spectrum emitted by incandescent blackbodies. The very existence of the photon with quantized electromagnetic energy was the basis of the explanation of the photoelectric effect given by Einstein, an achievement for which he was awarded the Nobel Prize. The origin of the narrow spectral lines of atoms was finally understood in the framework of quantum theory. After these first achievements, quantum mechanics became the basis for understanding molecules and solid-state properties with seminal contributions in the middle of the 20th century. During all these years, quantum mechanics was used to describe physical systems with a macroscopic number of particles, on the order of the Avogadro number.
A revolution started in the mid 1980s: understanding and manipulating light and matter at the nanoscale and even at the level of single atoms and single photons. The road there was long and full of obstacles, but was adorned with many achievements in the last 30 years, celebrated by over 20 Nobel Prizes in physics and chemistry. We will briefly sketch this long journey, highlighting a few examples for the sake of brevity. Let us start with a description of the state of the art in the middle of the 20th century.
3.4.1. The landscape in the 1960s
To realize why manipulating individual atoms and photons is a revolution—after all, in the mid-20th century quantum mechanics was already believed to be the theory of single quantum objects—let us quote a few sentences written in 1952 by Erwin Schrödinger, one of the founding fathers of quantum mechanics [144]:
... it is fair to state that we are not experimenting with single particles, any more than we can raise Ichthyosauria in the zoo.
... we never experiment with just one electron or atom or (small) molecule. In thought-experiments we sometimes assume that we do; this invariably entails ridiculous consequences ...
A few years later, in 1960, Richard Feynman gave a famous speech at a meeting of the American Physical society entitled 'There is plenty of room at the bottom' [145]. He argued that the physics at the scale of only hundreds or thousands of atoms had not yet been explored. It was a genuine scientific terra incognita with real challenges for new physics and many practical applications.
Atoms on a small scale behave like nothing on a large scale, for they satisfy the laws of quantum mechanics. So, as we go down and fiddle around with the atoms down there, we are working with different laws, and we can expect to do different things.
The principles of physics, as far as I can see, do not speak against the possibility of manoeuvring things atom by atom. It is not an attempt to violate any laws; it is something that can be done; but, in practice, it has not been done because we are too big.
In 2022, physicists perform experiments with single atoms emitting single photons despite the fact that physicists are still too big. They invented advanced tools to manipulate single atoms, to detect single electrons and single photons. They build materials by depositing atomic layers. This may sound like science fiction happening only in advanced laboratories, but the fabrication of materials by depositing individual monoatomic layers is state of the art in today's industry. What was deemed impossible and ridiculous in 1952, 'futuristic' in 1960, has become today the basis of widely spread technology. Every person using a GPS or checking the time on its smart phone is relying on atomic clocks, every person storing information on a hard disk or using a LED relies on devices fabricated with nanometer-scale precision.
3.4.2. Nanophysics: there is plenty of room at the bottom
3.4.2.1. What are nanosciences and nanotechnologies?
The pioneering vision put forward by Richard Feynman in 1960 became what is known today as nanotechnology. LEDs and hard disks are examples of what has been called nanotechnology. Why do we speak of nanotechnologies and never of micro-technologies or mega-technologies? What is so special about the nanometer scale?
As pointed out by Feynman, an important part of the answer is that quantum mechanical rules come into play. This is definitely the basis of all quantum technologies. Yet, so many nanoscale devices exist where quantum is not the key word. Why not? To address that question a simple example is enlightening. When measuring the electrical resistance R of a wire with a length L, the measurement can be fitted with a simple Ohm's law depending on L. This formula is valid if L is 1 km, 1 m or 1 μm. However, as soon as the length becomes smaller than 100 nm 1 , the wire enters the nanoscale regime and the formula does not work anymore. Why is this? It turns out that when electrons move in a metal, they typically have collisions with defects or phonons and the mean displacement between two collisions (the so-called mean free path) is on the order of 100 nm. Hence, when a wire becomes smaller than 100 nm, the electrons can travel ballistically, that is, without collisions (see figure 3.14). In this regime, their fate is described by quantum mechanics: electrons cannot be viewed any longer as particles bouncing back and forth; they have to be described as a wave trapped in a wire which plays the role of an optical fibre. This intermediate regime between the microscopic and the macroscopic world is denoted by the mesoscopic regime.
Figure 3.14. Illustration of diffusive (a) versus ballistic electron (b).
Download figure:
Standard image High-resolution imageLet us take another simple example: the colour of a gold layer. Depositing a layer of gold on a substrate will make it bright and yellow independent of the layer thickness. But if this thickness becomes smaller than 100 nm, gold is no longer opaque and becomes semitransparent and green in transmission. Here, we compare the thickness of the layer gold with the attenuation length (called the skin depth) of light in a metal. Nanoscale gold nanorods may be either blue or green. This behaviour is not due to quantum effects.
From these two examples, we conclude that the behaviour of a physical system changes when its size is reduced as compared to some typical length of a physical phenomenon. This often happens at the nanoscale but not always. This often happens because of quantum effects but not always. Nanoscience is the study of all new laws at the nanoscale. Nanotechnology uses these new laws to design new devices.
During the last 30 years, physicists and chemists have learnt how to control light–matter interactions at the nanoscale and even at the atomic scale and have learnt how to design new devices using them. In what follows, a few examples will illustrate these ideas.
3.4.2.2. Seeing the atoms: novel microscopies
Looking at ever smaller objects has always been a challenge in physics. In the 19th century, optical microscopy was well understood and the resolution limit derived by Ernst Karl Abbe provided a fundamental limit in terms of the wavelength used. Hence, two tiny particles separated by 200 nm can be distinguished if a wavelength of 400 nm or less is used.
The introduction of electron microscopes was a revolution. These microscopes are based on the fact that in quantum mechanics, electrons are described by a wave. It was possible to develop lenses for electron beams and assemble them to make a microscope. The tremendous advantage is that the electron wavelength can be made much smaller than 200 nm by accelerating the electron. Ruska received the 1986 Nobel Prize for this invention. Another Nobel Prize was given in 2017 in chemistry to Dubochet, Frank, and Henderson who managed to adapt the electron microscope to image molecules of biological interest noninvasively (i.e., without destroying them). Their technique, now known as cryo-electron microscopy, provides a sharp three-dimensional image with atomic resolution of biomolecules such as proteins and surfaces of viruses.
The 1986 Nobel Prize was shared by Binnig and Rohrer who introduced a totally different design of a microscopy that allowed observing and manipulating single atoms. The basic idea is very simple: a tip attached to a cantilever is brought in close distance to an electrically conducting surface. Before the tip actually touches the sample surface, a tiny current is established between the tip and the surface through the insulating vacuum by means of the so-called tunnelling effect, a purely quantum phenomenon. An image of the surface is then produced by scanning the tip above the surface, while keeping the current intensity constant and recording the vertical position of the tip. This technique, known as scanning tunnelling microscopy (STM), reveals the structure of the crystal with atomic resolution. It was the first time that individual atoms could be directly observed. A few years later, it was shown that atoms could be moved one by one, and then observed as shown in figure 3.15 [146].
Figure 3.15. Image showing Xe atoms on a Ni surface. The atomic structure of Ni is not resolved. The size of a letter is 5 nm from top to bottom. Reproduced from [144] with permission from Oxford University Press.
Download figure:
Standard image High-resolution imageThe STM technique had initially been envisioned as a means to study the electronic properties of surfaces rather than to use it as an imaging technique. As a matter of fact, the atomic resolution was quite unexpected. This observation triggered the development of a large number of novel microscopy designs, known as near-field microscopes based on scanning tips brought close to surfaces to detect different signals such as forces (atomic force microscopy with many variants such as magnetic force, electrostatic forces, Kelvin probes, etc), heat flux (scanning thermal microscopy), etc. These instruments can be used to measure different physical quantities with nanometer resolution. While the dream of developing nanotechnology had been put forward by Feynman in the 1960s, its real implementation by the scientific community was boosted by the advent of near-field microscopies that provided some of the tools needed to measure and manipulate at the nanoscale. It is the development of these tools that, among others, enabled to a large extent the development of nanosciences and nanotechnology.
3.4.2.3. Detecting single molecules and super-resolution imaging
The imaging techniques described above are based on electrons and forces. They do not use light. Hence, the Abbe resolution limit is not beaten but circumvented. Today, several types of optical microscopy can produce images with resolution much better than the Abbe limit. The first breakthrough was the demonstration of an image performed with a sub-wavelength aperture in a metallic screen. This aperture was used to illuminate very locally a sample so that light transmitted or reflected could only originate from this small area. With this scheme, the resolution does not depend on the wavelength but only on the size of the aperture. This simple idea was first demonstrated experimentally in 1972 by Ash and Nicolls, using microwaves [147]. Yet, the implementation of the idea in the wavelength regime of visible light was deemed to be impossible as it implied bringing a nanoscale aperture at a nanoscale distance from the sample. The first experimental evidence was reported in the 1980s by D Pohl [148] in the visible using a scanning tip to hold a tiny aperture producing a light spot on the order of 100 nm. The Scanning Near-Field Optical Microscope was born.
It was later shown that imaging beyond Abbe's resolution limit could even be achieved without using a near-field technique. The idea is based on the possibility of detecting light emitted by a single molecule. While the image of a point is blurred and has a spatial extension on the order of half a wavelength, it is possible to determine its centre position with much better accuracy. By operating in conditions where the molecules can be detected separately, it becomes possible to locate their positions. If they are attached to an object, its structure can be reconstructed. Betzig [149], Hell [149], and Moerner [150] were awarded the 2014 Nobel Prize in Chemistry for the development of super-resolved fluorescence microscopy. These techniques can be designed in standard microscopes objectives and do not require scanning a tip. They have become very popular for biological applications (figure 3.16).
Figure 3.16. Image of a cellular cytoskeleton with the STED super-resolution technique (top) and a diffraction limited confocal microscope (bottom). Adapted from [151], SPIE (1963), with permission from Nobel Foundation.
Download figure:
Standard image High-resolution imageAs we mentioned, a key asset for these techniques is the ability to detect optically a single molecule using its fluorescence [152]. Very sensitive detectors have been developed so that even a single photon can be detected. Hence, detecting a molecule standing alone in vacuum is not so difficult. The formidable challenge is to distinguish the faint signal emitted by a single molecule in a solid or a liquid because its contribution has to be distinguished from the background due to billions of surrounding molecules. This was achieved at low temperature with molecules embedded in a matrix taking advantage of the fact that the interactions with the local environment shifts the fluorescence line so that each molecule emit at a different frequency with a very narrow spectral width. By combining a narrow spectral filter with a microscopic technique isolating light coming from a tiny volume, it is possible to reduce the background and isolate the light emitted by single molecules.
3.4.2.4. Manipulating single atoms with light. Cooling and optical tweezers
Is it possible to grab a single atom and move it around? It can be done with light using so-called optical tweezers. Arthur Ashkin (Nobel Prize 2018) predicted and demonstrated that a dielectric particle can be captured at the focus of a laser beam that acts as an optical trap [153]. It is then possible to move the beam to displace the particle trapped at its focus. This technique was later extended to single atoms in a dilute vapour of atoms. Figure 3.17 shows an Eiffel tower made of single Rubidium atoms spatially arranged using focused lasers. This method can be used to explore the interactions between atoms and forms the basis of a platform needed for the development of quantum computers.
Figure 3.17. Image of an Eiffel tower made of N rubidium atoms trapped by optical tweezers. The height of this atomic Eiffel tower is 90 μm. Courtesy of A Browaeys.
Download figure:
Standard image High-resolution imageAnother important example of using light to apply a force on an atom is the technique of laser cooling. The idea is to reduce the velocity of an atom by making it absorb photons propagating in the direction opposite to its movement. Due to the recoil associated with each frontal collision, the atom experiences on average a drag force so that its kinetic energy is rapidly reduced. This technique is called laser cooling. With this type of technique, atoms can be almost stopped and stored in a trap. Further cooling techniques can be applied and temperatures as low as microKelvins can be attained. The Nobel Prize 1997 was awarded for the prediction and development of these techniques. A further development enabled by laser cooling was the observation of a so-called Bose–Einstein condensate, a state of matter predicted already in 1924 but never observed before, in which thousands of atoms all occupy the exact same quantum state. This offers the possibility to fashion an 'atom laser' out of atoms, such as was done with photons, with a minimum uncertainty in energy and momentum.
While these techniques were initially developed by curiosity-driven research, they have paved the way for novel and future technologies. They are at the heart of new quantum technologies with numerous applications such as atomic clocks, enabling accurate positioning systems, or ultrasensitive gravitational sensors.
3.4.2.5. The advent of spintronics: electronics using the electron spin
The discovery of giant magneto-resistance has been a revolution in electronics. For the first time in the history of electricity, the electrical resistance was tailored through the spin of the electrons. Electrons are elementary particles with a mass, a charge, and a spin. The spin is an intrinsic quantum property of the electron. While quantum in nature, it is also the ultimate constituent of the magnetism observed every day in magnets at the macroscopic scale. In a normal metal or a semiconductor, the electrical resistance, originating from collisions, depends on the charge and on the mass but not on the spin of the electron. However, if the conducting medium is magnetic, such as is the case of iron, for example, a propagating electron experiences collisions that now depend on its spin orientation. This leads to the electrical current in the magnetic medium being spin polarized and, hence, the creation of an electronic spin source. One may then take advantage of this effect to control the electron flow and hence the electrical resistance. This effect, named giant magneto-resistance (GMR), was first observed by A Fert and P Grünberg in 1988. They were awarded the Nobel Prize in 2007. As is often the case in nanoscience, this breakthrough in fundamental physics was made possible because of the development of a new technology. Here, it was molecular beam epitaxy, or MBE (see section 3.3.2.1) that allowed one to produce magnetic multilayers superposing high-quality layers of different materials, only a few atoms thick. In turn, this breakthrough in fundamental physics became the starting point for novel applications. The discovery of GMR has found a major application in data storage and has contributed to the digital age and big data revolution, which is ever expanding with data centre-based cloud applications. Indeed, today digital information is still stored in hard disks drives using the orientation of the magnetisation of nanometer-scale magnetic materials. Remarkably, hard disks relying on GMR-based technology for the read-out the orientation of magnetic domains were released in 1997, less than ten years after the discovery of the effect.
On a broader perspective, GMR has been the starting point of a new type of electronics based on the spin in addition to the electronic charge. This field is called spintronics [154, 155].
3.4.3. Photonics: let there be light
Until the middle of the 20th century, light sources had slowly evolved from candles to incandescent light bulbs and fluorescent lamps. A first revolution came in the 1960s, with the advent of the laser. For the first time, it was possible to produce a coherent light source, i.e., a source such that all the energy is concentrated in a given direction and emitted at a very well-defined frequency, due to the light propagating perfectly in phase. Since then, light has become a powerful tool to probe material properties and lasers have played a key role in the subsequent development of physics and chemistry. They also became the basis of many technologies, ranging from cutting and soldering materials to the design of telecommunication through optical fibres.
In the quest of mastering light emission, three breakthroughs were achieved in the last 30 years. The first was the ability to emit light at a single-photon level in a controlled way. This is much more than doing optics with extremely dimmed light. It is about manipulating quantum properties with light, and has paved the way for an entirely new field that started in the 1970s: quantum optics. This field is now mature in the sense that the textbook experiments reported in the 1980s can now be reproduced in laboratory classes. A major output of quantum optics has been to understand the implications of the concept of quantum entanglement, and to initiate a second 'quantum revolution'. This strange feature is the cornerstone of all applications of quantum physics to quantum computing, and will be explained in more detail below. Today's state-of-the art in this quantum revolution is undoubtedly at the level that will allow the development of the quantum technologies of the future. A second breakthrough is the development of semiconductor light sources. The development of solid-state devices requires exquisite control of materials (section 3.3.2.1). This was made possible by a major effort in material sciences and nanofabrication. A ubiquitous consequence of this great success is the development of LEDs with unprecedented energy conversion efficiency. The third breakthrough, started in the 1980s, is the ability to generate extremely short light pulses (section 3.5.3). This enables one to observe ultrafast phenomena that were impossible to study before. One can now follow, in real time, atomic dynamics and chemical reactions. Progress has been astonishing: from picosecond pulses in the late 1970s, one has gone to femtosecond pulses in the 1980s, and finally attoseconds in the late 1990s. Another consequence of short light pulses is the possibility to generate extremely large laser powers during short times. This paves the way for many applications ranging from laser surgery to new particle accelerators (see section 3.5).
3.4.3.1. Single photons and single atoms
Controlling light at the level of a few photons forms the basis of quantum optics. If the concept of quantization of the energy of light was first introduced by Planck and Einstein in the beginning of the 20th century to explain the spectrum of blackbody radiation, it is only in the 1960s that a general framework of quantum optics was finally introduced by Glauber (Nobel Prize 2005), largely motivated by a new generation of experiments made possible by the introduction of the laser. The challenge of the last 30 years in quantum optics has been the control of light with very few photons and the exploration of their unique properties. We will briefly quote three examples here: the experimental observation of wave-particle duality, the generation of entangled photons, and the realization of atomic systems interacting with a single photon.
In the late 1980s, it became possible to generate single photons and observe wave-particle duality. Reconciling the wave model of light with the particle point of view had been a major issue in the early days of quantum mechanics. A spectacular experiment, performed in 1985, was to observe interferences with single photons, which highlights one of the central concepts of quantum physics, that is, the superposition principle. This concept states that a quantum object can be in different states at the same time. Its validity has been tested extensively, and although quite counterintuitive, it is one of quantum physics' cornerstones. Single photons are ideal to illustrate both particle-wave duality and the superposition principle.
Producing single photons, which are truly quantum objects, was an experimental challenge before 1980 but has now become nearly routine. The basic scheme consists of exciting an atom with a short laser pulse. The atom then releases its energy with a time delay given by the atom lifetime, on the order of a nanosecond. A lens collects the emitted photons, which can then be sent into an interferometer and then detected at the output by single-photon counter (that also had to be developed). Over the years, photon sources have improved considerably. Starting from faint atomic beams where one tried to isolate the light coming from a single atom, or the use of exactly one atom trapped in a laser beam, one has gone to the use of bright quantum dots (see figure 3.18) that finally turned out to be the most practical solution. It is now possible to produce solid-state sources emitting single photons into optical fibres on demand.
Figure 3.18. Single quantum dots in a semiconducting cavity heterostructure.
Download figure:
Standard image High-resolution imageAs mentioned above, the concept of interference is crucial in quantum physics, but there is more to it than wave-particle duality. Take, for example, a beam splitter that reflects 50% of the incident power and transmits 50%. Send two photons, one in each input port, as shown in figure 3.19. Amazingly enough, the two photons always exit the beam splitter in the same direction. This observation, called the Hong–Ou–Mandel effect, cannot be understood either by considering the photons as pure waves or by pure particles! This effect only occurs when the two photons are in a quantum state in which they are truly indistinguishable. The Hong–Ou–Mandel effect is now often used as a diagnostic for single-photon sources to check that they really produced exactly identical photons.
Figure 3.19. Principle of the Hong–Ou–Mandel experiment.
Download figure:
Standard image High-resolution imageThe superposition principle leading to interferences is the first important concept that one encounters when learning quantum mechanics. Applied to, for example, two photons that can each be in two polarization states (horizontal: H or vertical: V), it leads to the existence of quantum correlations. To illustrate this concept, we consider a superposition state where both photons 1 and 2 have a vertical polarization (1V, 2V) or both photons have a horizontal polarization (1H, 2H). Such a state is called an entangled state. Measuring the polarization of the first photon will result in random observations of horizontal and vertical polarization. However, once this measurement is performed, the state is no longer a superposition but either (1V, 2V) if the result was V or (1H, 2H) if the result was H. Hence, measuring the polarization of the second photon yields the same result as for the first one. In such an entangled state, the polarization of one photon is not defined, but the state exhibits strong correlations between the two photons. What is amazing is that those correlations are stronger than any classical correlations in a sense that was made clear by J Bell in 1964. From the philosophical debate between Bohr and Einstein, which revealed the intrinsic and surprising absence of reality in quantum mechanics, we have reached the stage where entanglement has become a fundamental resource for quantum technologies, following experimental tests starting in the early 1980s, for which J Clauser, A Aspect and Z Zeilinger were awarded the 2022 Nobel prize in physics.
One of the most fundamental physical processes is the interaction between light (i.e., a train of photons) and atoms. As soon as experimental techniques were devised that made it possible to isolate individual atoms, it became tempting to study these processes at the level of just one atom interacting with just one photon. These studies started in the late 1980s and led to the Nobel Prize of Serge Haroche in 2012. The basic idea was to send an attenuated beam of excited atoms through a microwave cavity, which isolates a single mode of the field. With the cavity initially empty, the excited atom drops the photon in the cavity, and is able to reabsorb it after the photon has bounced onto the cavity mirrors, leading to a periodic exchange of energy (called Rabi oscillation) between the atom and the cavity involving exactly one photon and one atom! Pushing the technique, it was even possible to entangle two atoms via the single photon of the cavity.
3.4.3.2. Semiconductor light sources
The advent of lasers and semiconductor light sources has deeply modified our playground. Telecommunication infrastructures rely heavily on the interplay between photons and semiconductors. On the one hand, processors manipulate electrons, and information is exchanged via electrical currents that circulate within the processor. On the other hand, information exchange over large distances is achieved using photons propagating in optical fibres. Sending light over hundreds of km was made possible by the development of extremely low absorption materials (2009 Nobel Prize C K Kao). It is thus critical for information devices to be able to convert, with high quality, an optical signal into an electrical current and vice versa. Another fundamental issue is the energy required for lighting. The incandescent light bulbs that have been used for decades typically deliver 3 W of optical power at the cost of 100 W of electrical power (see also section 3.3.2.1).
Both optical communication and lighting have been impacted by the development of light-emitting diodes. An LED is a remarkable device that provides energy to an electron and converts this electrical energy into light with efficiency larger than 30% for commercially available lamps. This was made possible by significant progress in materials science, which has enabled the design of materials with high-purity and high-light emission efficiency. For instance, GaAs is a very good emitter whereas silicon is a very poor emitter of light. In order to convert electric energy to light inside this material, an electric current is injected. Light can be emitted by an electron within a very thin region only. In order to favour the emission of light, so-called nanoscale heterostructures have been introduced (Nobel Prize 2009 awarded to Z I Alferov and H Kroemer). They can be viewed as traps capturing the electrons in those regions where light emission can take place. These heterostructures are made of alternate layers of semiconductors with thicknesses on the order of 10 nm. This type of nanotechnology is the key to efficient lighting. For decades, LEDs emitted red light but could not produce the much more desired white light because no material was known to emit in the blue part of the spectrum. This finally became possible with the advent of GaN, a semiconductor with a relatively large gap of 3.4 eV, more than three times the gap of Silicon. (Nobel Prize 2014 awarded to I Akasaki, H Amano, and S Nakamura.)
Artificial atoms called quantum dots were discovered in the 1980s (2023 chemistry Nobel prize, M Bawendi, L Brus, A Yekimov). Physically, they are realised as semiconductor nanocrystals with a typical radius on the order of a few nanometers. They can be grown at the interface between two semiconductors or be synthesized chemically as semiconductor nanocrystals in a solution. These nanocrystals emit light and behave as artificial atoms. Remarkably, by tuning their size, it is possible to tune the emission frequency with high accuracy. They are currently used in display technology to produce high-quality colour rendering.
3.4.3.3. Extreme light: attosecond and petawatt
Imaging on a very short timescale is fundamental to understand the processes involved in matter at molecular and atomic scales. Just like high-speed photography has facilitated the capture of the movement of a horse at the turn of the 19th century, one can now capture the movement of an electron by illuminating it with ultrashort pulses. In the 1980s, the development of ultrafast lasers producing flashes of light on the femtosecond (fs) scale revolutionized our understanding of molecular vibrations. This work has provided the basis for femtochemistry research and led to Ahmed Zewail receiving the Nobel Prize for Chemistry in 1999 (see section 3.5).
Since then, ultrafast lasers have continued to improve and electronic motion in atoms, molecules, or solids can now be observed in situ. A significant step was taken to reach attosecond (as) resolution (an attosecond duration amounts to one second divided by a billion and again by a billion), an achievement recognized by the 2023 Nobel prize in physics awarded to Anne L'Huillier, Pierre Agostini and Ferenc Krausz. This was made possible by an additional nonlinear process producing x-rays and ultraviolet (UV) light via the generation of high harmonics (HHG) using intense ultrafast lasers. This nonlinear process is based on a second advantage of ultrafast lasers: the ability to concentrate a large number of photons over ultrashort times. This amount of energy (from micro-Joules to hundreds of Joules) compressed to an ultra-short duration (about 20 fs) gives rise to extreme peak powers, typically in the range of giga watts (GW) and even peta watts (PW). If the laser is focused as well, light intensities are typically in the range of 1013–1023 W cm−2. This increase in the intensity of ultrafast lasers has been made possible by a technological breakthrough. The laser intensity is increased by propagation through an amplifying medium. Yet, beyond some threshold, the amplifying medium is damaged so that further amplification is not possible. To circumvent this limit, Gérard Mourou and Dona Strickland introduced a technique consisting of stretching the pulse duration before sending it through the amplifier and then compressing it in time as it propagates in a vacuum so that there is no damage threshold. They were awarded the Nobel Prize in 2018 for this invention, known as chirped pulse amplification (CPA).
The development of intense and femtosecond-laser pulses has enabled new sources producing attosecond pulses by sending them on gas atoms. Ultrafast pulses interact with gas atoms in the following way: First, the electric field pulls an electron out of the atom via the tunnelling effect; during the next half-period of the laser's electric field, this electron is accelerated back to the ion. Finally, the recombination of the fast electron with its ion results in the emission of an attosecond pulse in the XUV. At the current state of the art, the shortest light pulses have a duration of 43 attoseconds, which is the shortest physical event ever produced in the laboratory.
Increasing the laser intensity even more allows for other interesting applications. For example, the ultrafast ionization enabled by femtosecond-laser/matter interactions can create an athermal ablation process that leads to precise micromachining. This athermal micromachining can be used for industrial and medical applications such as LASIK (laser-assisted in situ keratomileusis). Pushing the laser energy even further may result in what is called ultra-high intensity laser-matter interaction, in which the electromagnetic field is so intense that the acceleration of the electrons leads to relativistic velocities. In these relativistic regimes, the electron can be accelerated in the laser-wakefield (LWFA) up to the GeV range in relatively short distances since the electric field is about tens of GeV m−1. Moreover, when an ultraintense laser interacts with a solid target, this ultrafast bunch of electrons creates a high-space-charge-field zone in which protons and ions can be accelerated. Finally, due to the betatron effect, the relativistic and nonlinear motion of the electrons creates x-rays and gamma rays. All these effects in the relativistic (1018 W cm−2) to ultra-relativist (1023 W cm−2) regimes for laser-matter interaction can then lead to remarkable ultrafast 'secondary' sources of light and particles.
3.4.4. Challenges and opportunities
In summary, during the last 30 years, the physics community has explored the light–matter interaction at the nanoscale, in the regime where few photons and few atoms are involved. It is now possible to observe and manipulate single atoms and single photons. It has also explored regimes of interaction at extremely short times and at very large powers. Theoretical tools are now available to model these systems. But this is by no means the end of the road. A challenge for the years to come is to increase the size of the systems while keeping them under control. Increasing the size of the systems from a few particles to thousands or billions of particles introduces complexity. Complexity has often been regarded as a source of disorder and noise. But if complexity can be controlled, it may become an opportunity. Complexity of classical systems allows us to revisit optical devices and components. Complexity of quantum systems may offer an opportunity to take advantage of the exponentially growing number of degrees of freedom of a quantum system.
3.4.4.1. Classical complexity: complex media and metasurfaces
A good example of a complex system is light propagation in a cloud. The latter consists of a myriad of water droplets randomly located. As the sunlight illuminates a cloud, the light is scattered by these droplets and the transmitted light becomes isotropic. When using a laser beam to illuminate a slab containing randomly located particles of TiO2 forming a white powder, the transmitted intensity shows fluctuations known as speckle (figure 3.20(a)). They are due to interference between the light emitted by the particles which behave as secondary sources with random phase. Although a microscopic theory is available, solving the equations becomes computationally very challenging when the number of particles increases. Even more challenging is the idea of taking advantage of such a complex medium to control light. Figure 3.20(a) suggests that a large number of particles just generates a random pattern. Yet, complexity can be viewed as an opportunity to benefit from many degrees of freedom to control light–matter interaction. Taming complexity to take advantage of this large number of degrees of freedom is a challenge.
Figure 3.20. (a) Light transmission of a laser beam through a strongly scattering system. As expected, a properly shaped beam can be focused through the sample as seen in (b). Adapted from [156] with permission from OSA, CC BY 3.0.
Download figure:
Standard image High-resolution imageA beautiful and counterintuitive example is the possibility of focusing light through a random medium made of TiO2 particles forming a white powder as seen in figure 3.20(b). The key to achieving such unexpected behaviour is to try to shape the phase of each pixel of the incident beam such that it compensates the random action of the slab. Surprisingly, it is possible to obtain a nicely focused beam out of a random system as opposed to our daily experience: You can't see through the fog.
If this is possible, why not use a very complex system to design optical devices instead of always using perfect mirrors, lenses, and beam splitters? Not only the direction but also the spectrum and the polarization of the light have to be controlled. The motivation to use complexity is that a complex system contains a very large number of degrees of freedom (e.g., the positions of the particles) that all control the propagation of the light. This leads to a paradigm shift. Currently, optical systems use optical components such as lenses, mirrors, polarisers, and prisms. Each component has a single function so that an optical system is obtained by adding several independent components. The art of optical engineering is to efficiently design these multicomponent systems. The new paradigm is completely different. It amounts to taking a slab of material and considering removing material at arbitrary places and replacing with other materials using numerical simulations to find out if some combination of the modifications could end up in a useful system. The success of this approach obviously relies heavily on numerical solutions.
Let us give two more examples of this type of approach. Figure 3.21 shows a recently developed method to separate three beams with different wavelengths propagating in a silicon wire (called a waveguide) on a substrate. We want to guide them into three different waveguides. Classically, one would use a combination of lenses and prisms to achieve this goal. Here, a rectangular intermediate region with micrometer size is defined (see figure 3.21(b)). To achieve the required objective, silicon is replaced by silicon dioxide in some areas, shown in white. The figure shows the result of a purely numerical optimization solving Maxwell equations, which rule the fate of light. Although at first glance, the distribution of the white areas is reminiscent of droplets scattering light in all directions, the system is remarkably efficient at sorting out the different frequencies and focusing them at the right points. The fabricated sample is shown in figure 3.21(c). The length scale shows that the system is extremely compact. It fits inside a square of 40 μm, roughly the size of a hair's diameter.
Figure 3.21. Example of the numerical design of a microscale optical system separating different spectral waves and funneling them into different waveguides. Adapted from [149], SPIE (1963) with permission from ACS.
Download figure:
Standard image High-resolution imageA second example of intelligent complexity to control light with extremely compact systems is a metasurface. It consists of an array of resonant scatterers distributed over a surface. These metasurfaces have a thickness on the order of a micrometer. They can be used to mimic optical components and, more importantly, combinations of optical components (i.e., optical systems). A major advantage is to be able to design the ultrathin optical systems that are the premises of a new generation of optical systems. In this section, we have considered systems that have a number of parameters that is very large but can still be described with a deterministic approach. We have referred to them as complex using the layman meaning of the word. In physics, a complex system is beyond any deterministic calculation. An example of complex behaviour is the phase transition (see section 3.2) between liquid water and ice. At the melting point, an ensemble of water molecules can move from a very ordered crystal form to a disordered liquid form, spontaneously. This type of transition phenomena is observed in many fields of physics. It is often beyond our current simulation possibilities. However, this situation could change with quantum computers.
3.4.4.2. From quantum complexity to quantum technologies
One of the ultimate goals of physics is to understand matter and waves and more generally to understand the natural phenomena that one observes in Nature. Today, our understanding of the laws of physics is based on quantum mechanics, which allows the superposition of states. It is a huge challenge to predict the behaviour of N interacting quantum particles even if we assume that each particle only has two possible quantum states denoted 0 or 1. In practice, the 0 or 1 could be the polarization states of a photon (V or H), or two atomic states of an atom or the spin states of an electron. A possible state for the system of N particles is thus a list of N values (0, 0, 0, 1, 0, 1, 1, ...) specifying the state of each of them. Owing to the superposition principle, the quantum state of the N particles is a superposition of all the 2N possible states with a complex amplitude for each of them. Hence, a single quantum state of a physical system is defined by 2N complex numbers. This exponential scaling means that beyond typically 50 particles we cannot even store all these numbers, on any computer we have today or that we can hope to develop soon, thus thwarting the numerical solution of Schrödinger's equation beyond this number. Simply adding one extra particle doubles the time of a calculation! But a single milligram of matter already contains 1020 atoms—therefore, any ab initio calculation is thus completely out of reach! Over the 100 years that have lapsed since the beginning of quantum physics, physicists have of course devised sophisticated approximations methods to understand and capture complexity, such as the spontaneous replica breaking method in statistical physics by Giorgio Parisi and rewarded by the Nobel Prize of 2022. They obtained great successes in doing that, but many situations remain very hard to understand. This is the case, for example, of high-Tc superconductivity, many-body Anderson localization, the magnetic properties of oxides, or the conduction properties of materials. As the understanding of all these cases could lead to important technological developments, our impossibility to model them ab initio is problematic, etc. Usually, the failure of the approximation methods in such situations originates from the very strong interactions between the particles.
The idea to move forward was once again proposed by Richard Feynman in the early 1980s: We need a quantum machine to solve a quantum problem! If the machine is ruled by quantum physics, the superposition principle tells us that N atoms with two states can encode 2N numbers, and we would need 2N classical bits of information! Feynman's suggestion was the birth of the concept of quantum computer that is today actively investigated experimentally and theoretically. It relies on the superposition principle, quantum interference, and entanglement. Indeed, as the quantum state of N two-state particles encode 2N numbers at the same time owing to the superposition principle, a quantum calculation on this state would also operate on the 2N numbers simultaneously. However, one would then also obtain a superposition of all the results! This is where quantum interferences play a role: the quantum algorithm is designed such that all the paths interfere destructively, except the one leading to the desired result. In doing so the quantum computer generates a huge amount of entanglement.
Building such a quantum computer that operates on thousands of quantum bits (the superposition of two states) is a formidable task, as one has to fight decoherence (i.e., the tendency of any superposition state to collapse into one of the states of the superposition, and then behave classically). This decoherence originates from the fact that any system is not perfectly isolated but does interact (even very weakly) with its environment. Unfortunately, decoherence gets worse when the number of particles increases. Strategies to mitigate the role of decoherence are being devised at the same time as physicists are developing better-controlled quantum systems. These systems can be photons, atoms, and ions that are 'naturally quantum', but physicists have also designed what are called artificial atoms. A prominent example is a superconducting loop, which consists of a huge number of atoms, but which behaves as a two-state 'real' atom: the current through the loop can flow clockwise (state 1), anti-clockwise (state 2), or both at the same time in the same way a photon can be in a superposition of two polarizations. Today's systems already contain a few dozen quantum bits and roadmaps predict several thousands soon.
Even if, in terms of technological complexity, the quest for a quantum computer resembles the challenge of landing a man on the Moon and could take decades to reach, the quantum machines that exist in the laboratory today are already at the stage where they can be useful. For example, we have mentioned that a quantum computer generates a large amount of entanglement: this entanglement can be used as a resource to improve the accuracy of atomic clocks by many orders of magnitude, leading to extremely precise sensors or geo-localisation devices. Moreover, the elementary quantum processors already available are solving open scientific questions related to the conductivity of materials or the magnetic properties of matter. Amazingly enough, they can also be used to optimize industrial processes: finding the lowest energy state of an ensemble of interacting particles turns out to be equivalent to minimizing a cost function. Applications in logistic, finance, and in the optimisation of industrial processes are already actively being developed!
3.4.4.3. Extreme light
The emblematic challenge for ultrahigh-power lasers is to reach the so-called Schwinger intensity of 1029 W cm−2 at which electron–positron pairs can be created from the vacuum subject to the ultraintense electromagnetic fields. To achieve this value, several orders of magnitude in intensity need to be gained. One technological breakthrough would consist of generating high-energy attosecond pulses by sending a multi-PW laser onto a solid target, thereby creating a surface plasma mirror oscillating at a speed close to that of light. This relativistically oscillating mirror induces a Doppler effect on the reflected laser beam, which temporally compresses parts of the laser field, producing attosecond x-rays, thus reducing the duration and potential focus of the beam and finally allowing access to tremendous intensities (see section 3.5).
Currently, 100 PW lasers are under development. These lasers (compact compared to a synchrotron) pave the way, with new laser-acceleration concepts, to the possibility of reaching 100 GeV, and even TeV for acceleration lengths of a few meters instead of several tens of km today.
In order to study light–matter interaction with increased temporal and spatial resolution, attosecond pulses operating at shorter wavelengths in the XUV range are needed. Moreover, extending the XUV range will open up new applications such as in biology where the 200–400 eV photon energy is targeted since this energy band corresponds to a water-transparent window. Another important issue concerning the generation of XUVs attosecond pulses concerns the low photon flux. This is crucial for extending the range of application of these relatively compact XUV coherent sources such as for photoemission spectroscopy with pulses of 10–50 eV or photolithography with pulses of 100 eV.
3.4.4.4. Spintronics: toward all-spin systems
Sparked by the initial discovery of GMR, spintronics now pushes to provide new energy-conserving solutions to the existing silicon technology known as CMOS (complementary metal-oxide semiconductor). A good example of the potential of spintronics is the ultrafast and low-power non-volatile magnetic random access memories (MRAMs) based on the tunnelling of spins—a quantum property where electrons can pass through walls when these are thin enough (i.e., of the order of few atoms) between magnetic layers. We then speak of magnetic tunnel junctions. It is also possible to envision a sustainable post-CMOS technology based on spin as the information carrier. Thanks to magnetism's intrinsic non-volatility 2 , it could deliver quantum information (a single spin is the perfect quantum variable) using ultrafast and low-power electronics while giving access to stochastic and neuromorphic computing, ultimately offering compatibility with optical transmission by exploiting the properties of circularly polarized light.
Achieving all-spin logics integration is one of the key remaining challenges. It requires the ability to transport and process spin information. Indeed, while spin information can be stored on the long term through magnetism (a magnet stays on a fridge forever) it quickly vanishes when carried away for processing: this is the spintronics paradox. Along this way, several paths are now being actively followed; these include the recently discovered 2D materials for efficient electronic spin transport, or, again, the development of radiofrequency communication between oscillator spin devices via spin wave technologies (magnonics).
3.5. Extreme light
Franck Lépine1, Jan Lüning2, Pascal Salières3, Luis O Silva4, Thomas Tschentscher5 and Antje Vollmer2
1CNRS-ILM-Lyon, Lyon, France
2Helmholtz Zentrum, Berlin, Germany
3Université Paris-Saclay, CEA, LIDYL, Gif-sur-Yvette, France
4Instituto Superior Técnico, Universidade de Lisboa, Lisbon, Portugal
5European XFEL, Hamburg, Germany
Ever since the discovery of x-rays by W G Röntgen in December 1895, the use of energetic radiation to interrogate matter has been a key tool for science, industry, medicine, and society at large. The invention of the laser by Theodore H Maiman on May 16, 1960 has increased the impact and applications of the light–matter interaction manifold still. Over the decades, light sources have been developed to access ever-shorter wavelengths, higher energies, higher powers, shorter pulse durations, and higher repetition rates. Such light sources are electron-accelerator based synchrotron radiation and free-electron laser sources, as well as laser-based attosecond and ultrahigh-intensity sources, considered 'extreme' with respect to what had been possible only two or three decades before today (2022).
It is safe to say that the development of these extreme sources of light, providing radiation across the electromagnetic spectrum, has been a critical ingredient in solving scientific and societal problems over the last century, and that this will continue for many decades and even centuries to come. 'We are in a climate and environmental emergency' is a quote from Frans Timmermans, the Executive Vice-President of the European Commission in 2019 [157]. With climate change, sustainable energy supply, environment, biodiversity, clean water, food, health, digital transformation, and pandemics, humankind is confronted with unprecedented challenges. Light sources and radiation facilities, operating as national/international research units, each providing light with unique properties, are highly versatile tools that continue to prove their importance for an ever-expanding range of scientific fields. Starting from physics, chemistry, materials science, biology, and life sciences, they now encompass fields such as environmental science and the study of artefacts of cultural interest. The manifold examples of breakthrough experiments [158] advancing our knowledge on new energy sources, on the environment, and in the sector of health and medicine clearly demonstrate how extreme light sources instigate strategies and provide solutions to societal challenges.
Below, we present the realisation and prospects for extreme light sources, as well as their scientific and societal impact (note that single-photon sources are discussed in section 1.2.5). In order to respond to the current and forthcoming societal challenges as well as to lead the harvest of new knowledge in many fields, it is imperative that Europe as a leading industrialised area stays on the forefront of the development of new methods and techniques and maintains its own array of cutting-edge analytical research tools.
3.5.1. Synchrotron radiation
Synchrotron radiation facilities have proven to provide eminent and highly relevant analytical tools to advance our understanding of materials and, more generally, to find solutions for pressing societal challenges [158]. This is also reflected by the spread and use of the facilities themselves. Starting from three synchrotron radiation facilities worldwide in the 1960s, today, in Europe alone, fourteen synchrotron sources are operated as user facilities in ten European countries, together serving more than 25 000 users per year. In a synchrotron radiation source, a high-energy (GeV, i.e., a billion electron-volts) and finely focused electron beam propagating in an alternating magnetic field serves as a source of extremely bright radiation. The spectrum of the emitted radiation depends on the electron beam and magnetic field parameters and may range from the THz and infrared via the range of visible light, visible-to-ultraviolet (VUV) radiation, to soft and hard x-rays from which specific energies can be selected. In addition, full control of the polarization of the light is provided. At the same time, the radiation is pulsed, allowing time-resolved studies down to the picosecond (10−12 s) range.
The remarkable success of synchrotron radiation facilities fuels continuous interest in the further development of their capabilities. On the one hand, the increasing relevance of materials and devices that are spatially inhomogeneous on the nanometer (nm) length scale, whether due to the material's underlying physical properties or to tailored structuring, continuously drives the improvement of the spatial resolution that can be achieved. On the other hand, there is an ever-increasing user demand for new analytical capabilities, with a notable shift of interest from understanding a material's static ground state properties towards its behaviour in operation under application relevant conditions. Time-resolved experiments that probe local properties study how fundamental properties as well as properties relevant for applications evolve, thereby yielding the insight necessary for application specific tailoring of materials. This has lead to advances in situ or operando experimental techniques, experiments on liquids, on biological objects, and yet more, which, in turn, stimulate a broadening of the user communities themselves.
To address these needs, synchrotron radiation facilities continuously improve the performance of their light-generating accelerators. The much-discussed transition from the third to the fourth generation of synchrotron sources is characterised by a radical increase in brightness, which is the main performance parameter describing the beam quality of an accelerator-based light source; this has become possible with the recent advent of a novel technique, the so-called multibend achromat (MBA) storage ring design (figure 3.22). The increase in brightness goes along with an increase in the spatial coherence of the emitted light, which dramatically improves focusing capabilities and the application of novel imaging techniques. The new Max IV source in Sweden has pioneered the implementation of the MBA design. Essentially all facilities worldwide currently envision an upgrade of their accelerator to this technology [159], with the ESRF [160] having been the first to do so (in 2020), thus becoming the world's brightest synchrotron light source. As an illustration, the upgrade to a fourth-generation source increased the brightness of ESRF's x-ray beam by a factor 100 over the previous upgrade completed in 2015; the source, which feeds 40 beamlines, is now 10 000 times stronger than when it was first inaugurated in 1994!
Figure 3.22. The diffraction limited photon energy is shown versus the circumference of the accelerator for synchrotron radiation facilities based on the double-bend-achromat (DBA, third generation) and the multibend-achromat (MBA, fourth generation) accelerator lattice design. The comparison highlights the jump-like boost in brightness and coherence gain by transition from the third to the fourth generation sources.
Download figure:
Standard image High-resolution image3.5.2. X-ray free-electron lasers—studying the dynamics of atomic and electronic structures
While synchrotron radiation sources had matured by around 2000, new developments allowed the conception of a new type of electron accelerator-driven x-ray light source. Compared to (synchrotron) storage rings, free-electron lasers use an electron beam with narrower collimation, a much smaller bandwidth, and a much higher peak current to create laser-like (i.e., intrinsically coherent) x-ray radiation. The free-electron laser (FEL) process uses a resonance in the x-ray generation process—the self-amplified spontaneous emission or SASE process—to produce slices in the electron bunches coherently emitting x-rays. The FEL process shows an exponential gain along many thousands of magnetic periods (so-called undulators), until saturation is reached (see figure 3.23). Due to the high peak current and the ultra-short electron bunches, FEL pulses can be very energetic (of the order of several mJ) and very short (of the order of tens of femtoseconds, or 10−14 s). Their wavelength is governed by the same equation as undulator radiation and can be tuned by the electron energy and the magnetic field of the undulators. The concept of FELs was proposed in the 1970s [161], but only the small emittance of modern accelerators and the single-pass self-amplified spontaneous emission or SASE principle [162] has allowed physicists to reach the conventional x-ray regime with wavelengths shorter than 0.1 nm.
Figure 3.23. Scheme of SASE FEL process using alternating magnetic fields to initially create synchrotron radiation, which then acts back on the electron beam producing density modulations within the electron bunches. In the final section of very long undulators (typically 1000 periods; shown are five periods) the electron bunch is fully structured and electrons emit radiation coherently.
Download figure:
Standard image High-resolution imageSince the slices do not emit coherently between them, the temporal coherence of x-ray FELs is not complete. The development of fully coherent sources is an area of active research and has already provided fully coherent FEL radiation for wavelengths exceeding 1 nm.
The properties of FEL radiation offer unique possibilities for following the time-dependent evolution of geometric and electronic structures of atoms, ions, molecules, clusters, nano- and bio-particles, as well as those of bulk materials. Sometimes called 'taking the molecular movie', the application of ultra-short and intense XFEL pulses allow the detection of atomic-scale movements as well as extremely rapid electronic structure changes (e.g., during a chemical reaction [163], a phase transition of a solid [164], or a magnetic recording [165]). Such rapid transient states regularly occur in reality, but cannot be observed using conventional x-ray sources. XFEL pulses can also be used to record the structure of very short-lived states, such as in matter exposed to extreme electromagnetic fields relevant to materials research and to the geo- and planetary sciences [166]. While most FEL applications apply conventional x-ray techniques, the intense and coherent FEL radiation also allows one to develop and employ new, nonlinear x-ray spectroscopy methods [167].
The first user facility based on the SASE FEL principle FLASH at DESY (Hamburg, Germany) opened to a broad scientific community in 2005. Now, about ten facilities for the wavelength regime from the VUV to very hard x-ray radiation operate worldwide and serve a growing community of scientists. Their operation is similar to that of synchrotron radiation facilities, and the scientific applications and user communities employ the complementary features of x-ray radiation provided by these two types of extreme light sources. The international network of FEL facilities collaborations with the goal to expand scientific applications and to further develop FEL sources and techniques. The most important of these developments are the increased application of high repetition rate FELs with pulse rates from 0.1 to above 1 MHz [168], the development of methods to provide attosecond (10−18 s) pulse duration and attosecond pulse trains [169–171], the generation of fully coherent FEL pulses [172], as well as the development of nonlinear x-ray spectroscopy [173]. Some of the first FEL facilities are in the process of upgrading in order to improve the quality of FEL radiation. In addition, a second generation of FEL facilities is either under construction or has been proposed. Already, present-day facilities are characterised by an extreme data rate, related to the fact that each x-ray pulse basically corresponds to a full experiment for which the corresponding scattering and emission signals are recorded. With increasing repetition rates and more complex and larger x-ray detection schemes this issue will become more and more important.
3.5.3. Attosecond light sources
The quest for ultrashort light sources has been triggered by the dream to follow and control physical/chemical/biological processes at the level of the fundamental constituents of matter, from molecules and atoms, down to electrons. Tabletop lasers have been instrumental in this endeavour. Indeed, the rapid development in laser technology from 1960 has made it possible to produce shorter and shorter light pulses, down to a few femtoseconds in the 1980s, reaching the single-cycle limit in the visible/infrared (IR) range. Such ultrashort laser pulses allow the observation of atomic motion within molecules, which has spawned the field of femtochemistry [174] and was rewarded with a Nobel Prize to A Zewail in 1999. In order to follow the electronic motion within atoms, molecules, and solids, attosecond pulses are required 3 . The production of attosecond flashes of light is confronted with a fundamental difficulty. Namely, the Fourier transform link between time and frequency implies a very broad spectrum extending from the visible to the extreme ultraviolet (XUV), with different spectral frequencies all in phase (i.e., one requires coherent broadband XUV radiation). A solution was identified in the 1990s: the interaction of intense femtosecond IR laser pulses with atomic gases results in a huge broadening of the laser spectrum due to strongly nonlinear optical processes in the form of the generation of a whole set of high-order harmonics of the laser frequency [175, 176]. As these harmonics inherit the coherence of the fundamental laser, the Fourier conditions are met: there is a parallel increase in central frequency/bandwidth and a concomitant decrease in pulse duration. The clarification of the underlying physics [177–180] confirmed the possibility to generate attosecond pulses, and soon after, at the dawn of the 21st century, attosecond metrology techniques required for such short pulses were developed [181, 182].
At the time of writing, huge progress has been accomplished in both the generation and the characterization of isolated attosecond pulses [183, 184]. While all the initial studies were performed using Titanium:Sapphire laser drivers (λ = 0.8 μm), the recent use of few-cycle driving pulses in the mid-IR (λ = 1–2 μm) has yielded XUV pulse durations as short as 50 attoseconds [185, 186]; the central frequency was also increased to reach the so-called 'water window' [187]. Using a λ = 3.9 μm driving wavelength, the high harmonic generation process was extended to orders greater than 5000, reaching a 1600 eV photon energy and providing a record 700 eV spectral bandwidth [188]. While the latter would be compatible with the generation of pulses as short as 2 attoseconds, close to the zeptosecond (10−21 s) range, these are still to be demonstrated, and will require significant progress both in spectral phase management, and in metrology techniques. Coherently mixing IR and mid-IR pulses allows sub-cycle control of the driving light wave, providing μJ energies in a single attosecond pulse centred at 30 eV photon energy [189]. The corresponding gigawatt (GW) peak power results in focused intensities in the 1013–1014 W cm−2 range, large enough to induce multiphoton transitions. In terms of repetition rate and average power, bright prospects are brought by the new Ytterbium laser technology. As compared to the typical 1–10 kHz repetition rate of standard Titanium:Sapphire lasers, Yb lasers hold the promise of attosecond sources with repetition rates in excess of 100 kHz and average powers reaching 0.1 μW eV−1 at 90 eV [190]. Finally, advanced control over the spatial, temporal, and polarisation/angular momentum properties of the attosecond beams has been achieved.
These exquisitely controlled tabletop attosecond sources have spread in laboratories all around the world, with Europe keeping the lead after having pioneered the field (as illustrated by the 2023 Physics Nobel Prize awarded to A L'Huillier, P Agostini and F Krausz). The European attosecond community has been structured thanks to a number of (Marie Curie) European Networks that have trained young researchers, starting as early as 1993. Furthermore, the cluster of European laser facilities Laserlab-Europe encompasses several attosecond facilities offering beam time to international users since 2006. Finally, important investments worldwide are currently devoted to the construction and operation of large-scale attosecond facilities, such as the European Extreme Light Infrastructure—Attosecond Light Pulse Source (ELI-ALPS) in Szeged-Hungary, the NSF National Extreme Ultrafast Science Facility (NeXUS) at Ohio State-USA, and a number of new projects are blooming (e.g., in China).
In parallel, two new sources of attosecond pulses have emerged. First are the x-ray FELs [170, 171] that provide extremely powerful—100 GW—tunable pulses extending to the x-ray spectral region and discussed above. Second, high harmonic beams generated from the laser–plasma interaction at very high intensity (>1018 W cm−2 instead of typically 1014 W cm−2 for gas harmonics, see discussion below) present promising properties, in particular for high-energy pulses. Both attosecond pulse trains [191] and isolated pulses [192] have been demonstrated for these plasma sources.
3.5.4. Attosecond applications—imaging at the attosecond scale
The stability of matter is the result of the complex interplay between interacting microscopic constituents: electrons and nuclei. The complexity involved has its origin in the electronic correlations (see section 3.2) that determine how electrons interact quantum mechanically with each other. The difficulty to account for electronic correlations theoretically limits the accurate prediction of physical and chemical properties. While the description of static properties of matter has made enormous progress, our knowledge on how electronic correlations influences out-of-equilibrium properties is still in its infancy. Attosecond science allows one to measure and manipulate electrons on the quantum level, using the coherent properties of light. Over the past 20 years, a large effort was dedicated to the investigation of small quantum systems (atoms and small molecules) in the gas phase [193]. This has constituted a first playground to test state-of-the-art quantum theories and has allowed the investigation of the stability of excited electronic states [194].
Accessing processes on the attosecond timescale has revealed the complexity of seemingly trivial issues. One example is the well-known photoelectric effect, with the question 'how much time does it take for an electron to escape an atom, a molecule or a surface, after the absorption of a photon?' This simple question hides profound interrogations on the quantum mechanical properties of matter, on causality, and on the concept of measurement in quantum mechanics, time not being an observable. It involves discussion of the 'Wigner delay' semi-classical concept and its connection to the scattering phase acquired by the electron. Experimentally, the temporal dynamics of the scattering process has become accessible in atoms, molecules, and solids [195]. Recent investigations include the study of resonance effects [196–198], of single vs. multiphoton transitions [199], of electron scattering in nanoparticles [200] as well as in liquids [201]. The high coherence of the attosecond sources gives direct access to the phase and amplitude of the ejected electron wave packets, allowing the dynamical reconstruction of the formation of quantized structures such as Fano resonances [202], or resonant two-photon transitions [203] (figure 3.24).
Figure 3.24. Space-time movie of the 2-photon XUV+IR ionization of a helium atom through the intermediate 1s3p and 1s4p bound states [204]: time dependence of the complex-valued atomic ionization rate (amplitude in polar coordinates, color-coded phase).
Download figure:
Standard image High-resolution imageAttosecond molecular physics has emerged as a major field of interest, with, notably, the attosecond control of molecular reactions using the coherent manipulation of their electronic degrees of freedom [204]. The first demonstration was performed on H2 through the quantum manipulation of electronic localization following molecular dissociation [205]. Light controlled with attosecond precision has now allowed the modification of the absorption and dissociation of larger molecules such as N2, CO2, and C2H4 [206], as well as to trigger coherent charge oscillations across the molecular backbone of amino-acids such as phenylalanine [207]. The modification of molecular reactivity by directly acting on the electronic localization questions the role played by electronic correlations [208] and the complex interaction between electrons and nuclei. In these experiments, the electronic charges are manipulated faster than the timescale on which any nuclear motion can occur, so that the nuclear structure has to re-adapt to the new charge configuration. This new paradigm was called 'charge driven reactivity'. In the past years, tremendous work has been done to reveal the role of coherent hole dynamics [207], non-adiabatic relaxation [209], and structural rearrangements [210].
While attosecond pump–probe schemes initially used electron spectroscopy, other promising spectroscopic techniques are currently being developed. For instance, attosecond transient-absorption spectroscopy has been performed on dense jets and solids, with demonstrated control of the absorption processes using the interaction with strong field-controlled IR pulses. It has thus been possible, for example, to drive insulator-to-conductor transitions in crystals [211] and to study exciton dynamics [212].
3.5.5. Laser–plasma interaction and the ultra-relativistic limit
3.5.5.1. The present
The invention of chirped pulsed amplification, or CPA (figure 3.25), recognized with the 2018 Nobel Prize awarded to Gérard Mourou and Donna Strickland [213], has triggered an exponential increase in laser intensity and a concomitant decrease in the achievable brevity of pulse duration, with a celerity that recalls Moore's law in electronic transistors.
Figure 3.25. Chirped pulsed amplification (CPA)—a short laser pulse (left) is stretched spatially by a pair of gratings with a well-defined spectral encoding (low frequencies first, high frequencies of the pulse in the back of the stretched pulse). The longer pulse can then be safely amplified without damaging the amplifier and/or significant nonlinear effects. The amplified stretched pulse can then be compressed with another pair of gratings, and the frequencies properly combined to recover the original short pulse length.
Download figure:
Standard image High-resolution imageAs the laser intensity increases, novel regimes of physics can be explored in existing laser laboratories worldwide [214]. Notably, matter irradiated by intense laser light becomes fully ionized and forms a plasma. At intensities in excess of 1023 W cm−2 [215], the electrons in the plasma quiver in the laser field with velocities very close to the speed of light; the plasma response to the laser light is highly nonlinear and determined by special relativity.
At the same time, we are witnessing a golden age for plasma kinetic simulations. Taking advantage of the largest supercomputers in the world, these are able to capture the physics in these novel relativistic and ultra-relativistic regimes, and complement experimental advances with unprecedented detailed synthetic diagnostics. This virtuous combination has propelled exciting advances in laser–plasma interactions.
The most prominent are associated with the development of the entirely new concept of compact advanced laser–plasma accelerators (figure 3.26) [216]. Here, an intense laser pulse propagating through a transparent plasma excites a trail of plasma oscillations with their associated periodic, intense electric field. These oscillations propagate close to the speed of light, much in the way a boat drives a wake in a lake. The intense electric field oscillations accelerate the charged particles of the plasma. Thus, recent experiments have delivered electron beams of energy close to 10 GeV, propelling charges of up to a fraction of a nanoCoulomb (nC, or 10−9 C) in pulses of duration of a mere few femtoseconds. Thus, laser–plasma acceleration has demonstrated ultrahigh accelerating gradients in excess of 1 GeV cm−1. The properties of electron beams generated in this manner are continuously optimized. In particular, high-quality beams with energy spread ΔE/E as low as 0.1% have been demonstrated. Critical advances on laser technology (such as stability, reproducibility, and repetition rate) and on targets (plasma channels of controlled length and density) have been (and are) the main stepping stones for further advances.
Figure 3.26. Schematic of laser wakefield acceleration. A strong laser pulse (depicted at the right of the simulation window in red) propagates in the plasma—the radiation pressure is strong enough to expel the electrons from the wakefield region, forming a bubble/electron cavity. The ions in the plasma column thus create an electric field that pulls electrons in, closing the bubble, but that also provides electron acceleration. Inside the bubble, electrons (coloured according to their energy) can accelerate and gain energy. Image courtesy of Samuel F Martins GoLP/IPFN/Instituto Superior Tecnico.
Download figure:
Standard image High-resolution imageElectron beams generated by the laser–plasma interaction are now routinely used as compact drivers for betatron sources of (incoherent) x-rays [217]. These sources provide a unique source for high-resolution, high-contrast coherent diffraction imaging with a wide range of applications going from biology and biomedicine to materials science (figure 3.27). A demonstration of free-electron lasing driven by a laser–plasma accelerator in the x-ray range [211] has just been achieved, holding the promise to further increase the impact of laser–plasma accelerators as compact drivers for ultrafast (duration of a few fs) x-ray sources unleashing a wide range of applications across many scientific fields.
Figure 3.27. Imaging with betratron-generated x-rays, illustrating several applications of betatron sources [218] probing different targets/materials. Image courtesy of Nelson Lopes (Imperial College, London and GoLP/IPFN/Instituto Superior Tecnico). Reprinted from [219], copyright (2020) by permission from Springer Nature.
Download figure:
Standard image High-resolution imageAdvances on ion acceleration have been steady with the exploration of several laser-driven proton/ion acceleration mechanisms and their optimization. For ion acceleration, the laser hits a solid (or near solid) density target where its energy is predominantly absorbed by the electrons. The dynamics of the hot electrons then generates electric fields, via different mechanisms, that can pick up and accelerate the protons. Many conceptual studies have been performed, targeting proton therapy with these unique beams, and addressing the distinct features of ultrashort, but high-intensity, doses. As laser technology progresses and novel targets are engineered it is expected that one of the key milestones for proton therapy, proton acceleration to energies in the 200–250 MeV range, can be achieved within the next few years.
Fundamental studies of laser–plasma interactions have an important impact in laser fusion. The laser energy to be deposited in the fuel must first propagate through very long transparent and semi-transparent plasmas, in which different types of plasma instabilities can develop. Progress in computer modelling has underscored the importance of controlling deleterious laser–plasma instabilities by careful engineering of the spectral content of the lasers. This will become even more relevant as laser fusion moves to the burning plasma and ignition domain, triggered by the recent results at the Lawrence Livermore National Laboratory announced in late 2022, and recently published. These conditions provide an important test bed for burning plasma conditions, of relevance for any other fusion device, but also can give additional momentum to the more energy-efficient direct-drive laser fusion, based on shock ignition, and other advanced concepts such as fast ignition.
The first steps on the manipulation of light beyond the damage threshold of conventional materials have been taken. These most notably involve plasma mirrors that are now routinely used to improve the intensity contrast of lasers. Extensive theoretical and numerical work has explored the combination of intense lasers and plasmas. We cite laser–surface interactions and relativistic plasmonics and novel routes, based on strong coupling with the plasma, to amplify or to focus laser light in order to achieve ultra-high intensities in excess of 1026 W cm−2.
These advances are touching other fields of physics. The confluence of high-intensity lasers, relativistic dynamics, and optics allows the study of laser–plasma interactions with exotic beams. These feature, for example, a phase velocity opposite the group velocity, or a superluminal moving focus. The detailed control of the phase of the laser light, as well as its orbital angular momentum, is opening novel directions for fundamental studies and for laser–plasma accelerators and fine-tuned secondary sources.
Exciting developments at the interface between high-intensity lasers and plasma astrophysics are starting to shed light on fundamental processes in astrophysics. This emerging field of laboratory astrophysics has seen important developments in recent years. One example concerns shock waves. These are pervasive in the Universe and are thought to be the site for the acceleration of cosmic rays, the most energetic particles in the Universe. These shock waves are collisionless, in the sense that the mean free path of the particles is much longer than the shock wave thickness—the shock structure is determined by collective plasma processes. High-intensity lasers provide a unique tool to drive these shocks in the laboratory, generating collisionless conditions and sub- to near-relativistic plasma flows. Recent experiments, supported by extensive theoretical and numerical work, have demonstrated the formation of laser-driven collisionless shock waves, spanning from electrostatic to fully electromagnetic shocks (figure 3.28). The exploration of the acceleration mechanisms in these experiments has provided first hints on possible proton acceleration and Fermi acceleration— i.e., the key mechanism for cosmic ray acceleration—in laboratory shocks [219]. The first studies on magnetized plasmas driven by lasers demonstrate a possibility of studying jets, magnetogenesis, and magnetized turbulence, providing yet stronger connections with plasma astrophysics.
Figure 3.28. Numerical simulation of a laser-driven collisionless shock driven by two ablated plasmas, originating from the left-hand side and the right-hand side of the simulation window. In the centre, the compressed density, permeated by magnetic filaments, originates the collisionless shocks propagating from the central region (red corresponds to the regions of higher density—downstream, while blue represents the lower region—upstream region of the shock). Image courtesy of Frederico Fiuza (SLAC/Stanford University).
Download figure:
Standard image High-resolution imageFor many years, electron–positron plasmas have been addressed theoretically and numerically, motivated by their relevance in high-energy astrophysics (most notably associated with pulsars), and also due to their (apparent) simplicity. Recent experiments resorting to high-intensity lasers have not only generated copious amounts of electrons and positrons but have also been able to produce a quasi-neutral electron–positron plasma plume. The interaction of energetic electrons (accelerated via the laser wakefield) with a solid target of high mass number ('high Z') atoms generates gamma rays, via bremsstrahlung. In turn, these can generate electron–positron pairs through scattering on the high Z nuclei. The road is now open to the experimental study of plasma properties of relativistic fireballs, thought to be a key ingredient to the understanding of gamma ray bursters, including the onset of plasma instabilities, the self-consistent generation of magnetic fields, radiation from fireballs, and the formation of collisionless relativistic shocks.
These studies highlight the convergence of high-intensity lasers, quantum electrodynamics, and plasma physics. These opportunities have triggered several experimental directions, as described previously, but have also motivated new theoretical directions. As the laser intensity increases, a plethora of quantum electrodynamics processes starts to play an important role. The quantum electrodynamics of ultrahigh-intensity laser fields poses highly challenging theoretical questions [220]—ranging from radiation reaction, multiphoton processes in the ultra-relativistic regime, to vacuum birefringence—but the very possibility to generate very large numbers of secondary particles (e.g., electron–positron pairs, gamma rays) via cascade or avalanche processes can trigger further QED processes and might provide an alternative route to the generation of even higher density electron–positron(-photon) plasmas, with densities comparable to those of solids. Collective plasma dynamics in such conditions is unexplored and has strong connections with extreme astrophysical phenomena. Laser experiments are on the brink of reaching the quantum regime. Experiments on the collision of high-intensity lasers and electron beams have started to explore the transition between radiation reaction in the classical regime and in the quantum regime. It is clear, however, that this is a first step in the pursuit of even more extreme conditions, where fully developed electron–positron cascades can develop, providing a test bed for fundamental processes of relevance in astrophysics (figure 3.29).
Figure 3.29. Electron–positron cascades driven by two counter-propagating ultraintense laser pulses (field lines of the beating structure are depicted as well as the amplitude of the beating pattern in the plane). In the interaction region the strongly accelerated electrons (green) radiate photons (in yellow) that in turn interact with the ultrastrong laser field and generate copious amounts of pairs (electrons—green and positron—red) in a cascade process. Image courtesy of Thomas Grismayer GoLP/IPFN/Instituto Superior Tecnico.
Download figure:
Standard image High-resolution imagePlanned or commissioned laser facilities will move into these exciting new directions, pursuing both fundamental science and applications across multiple disciplines. These facilities include the EU-wide Extreme Light Infrastructure, Apollon (France), EPAC (UK), or, more focused on laser fusion, the Laser MJ (France) or the EU-wide effort on laser–plasma accelerators EUPRAXIA or HIPER+ on laser fusion.
3.5.6. Challenges and opportunities
3.5.6.1. Synchrotrons and free-electron lasers
About 30 years before today (2022) x-ray FELs and their scientific use had not yet been proposed and synchrotron radiation sources had just started into a new era. Looking 30 years ahead, it is certain that electron accelerator-based synchrotron radiation sources and x-ray FELs will have developed into x-ray light sources with full control of all kinds of radiation parameters in a mature way.
The jump in source performance provided by the MBA synchrotron source technology will provide the basis for entirely new experimental capabilities, enabling new discoveries and insights in a broad range of scientific fields, serving existing as well as new research communities. Higher brightness allows for unprecedented improvement in spatial resolution for microscopy, imaging, tomography, and diffraction, enabling novel types of experiments, and drastically speeding up experiments. Better performance and higher throughput will be beneficial for both the quality and the quantity of experimental results and with this for the amount of created knowledge.
Therefore, after ESRF, all other European facilities, such as the Spanish synchrotron ALBA ('dawn', inaugurated in 2010, with eight beamlines), BESSYII at the Helmholtz Zentrum in Berlin (with 46 beamholes), the DIAMOND [221] light source in Didcott (UK), ELETTRA [222] (Italy), PETRA III [223] (Jordan), the Swiss Light Source [224], and SOLEIL [225] (France) (in alphabetical order) are each planning their upgrades so as to deliver radiation with a brightness improved by at least two orders of magnitude. Similar projects are pursued by the leading facilities outside of Europe.
The improvement of the coherence of synchrotron light concomitant with MBA will allow the application of 3D microscopy with nanometer spatial resolution as a routine analytical tool, using dedicated sample environments for in situ and operando studies, in a broad range of research fields, with time resolution as a fourth dimension.
X-ray FELs will provide extreme light with wavelengths down to 0.02 nm, pulse durations ranging from attoseconds to picoseconds, arbitrary pulse shapes, and full coherence that users will be able to select. These features will enable new applications in a vast range of scientific domains. In addition, alongside attosecond and femtosecond lasers, laser-driven Compact-FELs will complement accelerator-driven facilities and will contribute to the worldwide network of FEL infrastructures, large laser installations, and synchrotron radiation sources. Compact-FELs may feature reduced power and peak performances, but their reduced size, operation effort, and cost will allow to use them for specific applications or to install them in regions without access to x-ray sources. There is a possibility that Compact-FELs will become the preferred technology for the UV to soft x-ray (>1 nm) spectral range.
The current development of applying new data science technologies both to the operation and experiments of both synchrotron and FEL facilities will have a huge impact, similar to the evolution of the instruments themselves. In addition to improving photon beam parameters, rigorous digitalization of the facilities and the experiment offers unique opportunities to improve efficiency. Applying artificial intelligence will allow the operation of more stable, more performant, and more energy-efficient light sources. Software developments will not only mitigate today's increasing challenges to deal with huge data rates and volumes, but they will likely change our way of doing science: data algorithms will be looking for patterns in huge datasets, and will find new correlations, which will become experimental observations.
The implementation of remote access to the infrastructures is a very important step towards making the facilities even more open, accessible, and inclusive, to a much wider user community, and thus increase their relevance. Recording, storing, and instantaneous data analysis will provide real-time guidance for experiments, ideally coupled with autonomous decision taking. The growing scientific community and the expansion of research fields also presents synchrotron radiation and FEL facilities with new challenges. Tailored sample environments, multimodal measurements, and offline instruments complementing synchrotron radiation-based techniques allow for higher throughput and more efficient experiments, thus increasing the attractiveness and outreach of synchrotron research even further.
3.5.6.2. Attosecond light sources
Predicting the properties of attosecond sources on the Horizon 2050 is challenging. Thirty years ago, the high-order harmonic generation process had just been observed, x-ray FELs did not exist yet, and the production of attosecond pulses was not even envisioned. The rate at which advances are currently being made means both the ultrafast laser and x-ray FEL fields are in full evolution, meaning that different complementary paradigms are evolving rapidly. All in all, we may expect that in 2050 attosecond light sources are available as routine tools for scientific research; tabletop laser sources and large-scale accelerator-driven x-ray FELs will, together, provide a wide spectrum of attosecond light source properties, including a wide wavelength spectrum from the XUV to very hard x-rays, pulse energies in the millijoule range, high repetition rates, full coherence, and polarization control, as well as access to the entire attosecond range and even to pulse durations entering the zeptosecond regime. A particularly interesting recent prospect is opened by tabletop laser sources relying on the generation of attosecond pulses by solid materials such as crystals instead of gas jets or cells [184]. This may lead to further integration and compactness, key to cost-efficient highly reliable systems that could then spread in laboratories and industries and be used by researchers/engineers from other fields. Attosecond techniques could become an everyday tool for applications in chemistry, materials science, or spectroscopy labs in general. In parallel, the accelerator-driven FELs will offer the most extreme characteristics for pioneering scientific studies, in particular requiring high flux. The best possible vision is doubtlessly that which is fuelled by outstanding scientific challenges, as we now outline.
3.5.6.3. Taking movies of molecules and real materials as they function
As to the most important scientific applications of ultrafast x-ray sources in decades to come, we first note that we are currently witnessing a phase of exploratory experiments, during which new methods and techniques are developed and tested on prototypical or highly standard sample systems. The results of these experiments largely serve to qualify experimental results. Their success will lead to a maturing of methods and techniques and to their application to less standard, more complex, but also more relevant scientific or technological problems. Therefore, in 30 years, one is likely to see many instruments specialized in specific methods and applying these to specific classes of material samples. At the same time, the development of methods will continue in order to enable new applications of extreme, ultrafast x-ray light sources.
A highly promising scientific application of ultrafast x-ray sources will be to take molecular movies in the very broadest sense. Employing the unique properties of x-ray FELs to adjust spatial and temporal resolution, such movies will allow one to follow atomic motion and electronic excitations from the shortest (attosecond) time regime to the rearrangement of macroscopic numbers of atoms in the millisecond regime. Probed samples will range from small molecules, via complex bio-systems, to real materials, and investigations will be performed under operando conditions. Understanding and describing a probed volume at all length scales, from the atomic to the macroscopic regime, and being able to dial in to the relevant voxels will employ techniques developed at synchrotron sources today, and will imply a huge data management and software challenge. Materials' research will benefit the most from these movies, as they will allow to develop a profound understanding of the dynamic processes responsible for specific materials' characteristics. Such will contribute to the development of new energy conversion materials, catalytic systems, and entire systems such as batteries. The investigation of the dynamics and behaviour of hard materials will also benefit from this 'four-dimensional atomic resolution microscopy' (time being the fourth dimension). A very important area of application will be the investigation of stochastic processes such as crack propagation, defect formation, or crystallisation. These require special techniques to observe the spontaneous and usually non-ergodic events. Nonetheless, the majority of experiments will apply deterministic and tailored drive pulses with THz to x-ray wavelengths, available at each FEL instrument or multicolour FEL operation to initiate and probe specific dynamic processes of samples mimicking nature.
Another field where x-ray FELs will have a big impact is the investigation of the nature and dynamics of liquids allowing one to understand their behaviour and physical properties, and thereby allowing one to design new liquids with designed physical properties. The emergence of fully coherent FEL radiation and the development of nonlinear x-ray spectroscopy in the next decades will open the route towards new scientific applications which in 30 years may just transit from the prototypical phase to applications with direct relevance to societal challenges. In particular, in the area of quantum optics completely new insights are to be expected. With the transition to mature FEL applications for specific scientific problems the presence of industrial applications of x-ray FELs will have significantly increased compared to today. Following trials to use FEL for 13.6 nm lithography during the last decade, x-ray FELs might turn out to be the light source providing powerful, stable, and coherent radiation enabling lithography in the regime of 1 nm or even below.
3.5.6.4. Future applications of attophysics
Like femtosecond technology before, we expect that attosecond technologies and their applications will swiftly evolve in the coming years [167]. Femtosecond science has demonstrated the new possibilities offered by ultrashort broadband coherent light pulses and has progressively evolved from the investigation of basic concepts such as the dynamics of nuclear wave packets to increasingly more complex spectroscopic approaches, including multidimensional spectroscopy and coherent imaging, and has progressively found industrial applications such as surgery and in material structuring. At the time of writing, attosecond science has unveiled new questions on the nature and dynamics of all phases of matter, from atoms and molecules in the gas phase, to liquids and solids. Augmented spectroscopies and the control of material properties and chemical reactions have already emerged as addressing very fundamental aspects of quantum mechanics. They have pushed experimental performances and precision, broadened the community of interest, and touched possible applications.
Overall, manipulating light with ultrahigh accuracy has clearly pushed our understanding and capacity to control nature and create new generations of technologies. The prime requirements have been to adapt light technologies and spectroscopic methods to the frontier of new temporal resolutions. In the next decades, small quantum systems could be interrogated with unprecedented accuracy in order to perform 'complete experiments' where, electrons, nuclei, and photons could be all measured, together with their 3D properties (position, velocity, spin, etc). We foresee experiments in which the complete, phase, and amplitude-resolved reconstruction of electronic and nuclear wave packets and the elucidation of their properties over the wide spectral range from UV to x-ray, including coincidence between these particles, will be possible. Such would present a major test for quantum theories, and would provide crucial information for a universal description of electron correlations. It would provide a quantum mechanical view of non-equilibrium processes occurring at microscopic scales.
The use of attosecond pulses to study and control molecules will be further pushed towards larger and more elaborate complexes, including isolated fragile biomolecules, metal-complexes, molecules in an environment, and exotic ions. This opens the perspective to investigate and control elementary processes in complex biomolecules such as proteins, in which radiation damage could be investigated at its ultimate timescale. By doing so, attosecond science will address questions beyond proof of principle, and connect to research fields such as radiolysis, photocatalysis, and biochemistry. It will be possible to control phase transitions in molecular materials and the material bulk by acting coherently on electrons and holes. The recent application of ultrashort XUV pulses to materials has emerged as a new frontier, and one may expect that the usual technologies that are available at synchrotrons or at femtosecond labs will also be used and coupled to attosecond light sources in order to address correlated materials, topological insulators, complex nanostructures, molecules in liquid samples and so forth. Proof-of-principle experiments are already being carried out at time of writing using electron energy- and momentum spectroscopy (ARPES, 3D PEEM). While already used with femtosecond and UV pulses, they might soon become also common tools in attosecond science, providing detailed dynamical information on molecules and nanostructures at interfaces with e.g., metallic surfaces. Applications will cover spintronics as well as plasmonics, in which 3D fields will be resolved with attosecond precision. Combining light control with attosecond precision and microscopy techniques will allow ultrafast microscopy in the XUV or x-ray domain with ultrahigh time and space resolution. Proposals are also emerging in which attosecond light control will allow laser machining with higher (nano-scale) spatial resolution.
Attosecond science offers the capacity to manipulate quantum properties of matter. Because attosecond pulses can act on the timescale where the atomic nuclei are essentially frozen, one might expect that it will teach us how to manipulate matter using its quantum properties on ultrashort timescales, even in complex systems. This might open new areas where quantum states are not only measured but also manipulated, and electron quantum currents in vacuum or in a mesoscopic or nanoscopic circuits controlled, thus providing new tools for quantum computation, quantum microscopy, and quantum detectors in general. These developments will address increasingly specialized and diverse research topics, for which attosecond technology will become a tool among others. Here again, the complementarity between tabletop sources and large-scale installations will play an important role in disseminating attosecond techniques and contributing to these research programs. Finally, with the progress made in attosecond sources and technologies, zeptosecond resolution will be reachable, which opens the possibility to track particles on sub-Angstrom dimensions, thus, perhaps, connecting attosecond physics to nuclear physics.
3.5.6.5. Ultraintense beams and laser–plasma accelerators
In the next 30 years, laser technology at the intensity frontier will continue to evolve, moving towards higher focused intensities (beyond 1024 W cm−2), higher pulse energies (in excess of several MJ), shorter pulse durations (of a few fs or lower), and a wider spectrum of laser wavelengths (moving towards the mid-infrared). The combination of these laser parameters allows for a broad range of novel physics and applications across many fields of science. Furthermore, it is now very likely, as demonstrated by ongoing projects or planned facilities, that an even stronger impact can be achieved from the combination/co-location of ultraintense laser beams and high-intensity charged particle beams, either generated from conventional accelerators or from laser–plasma accelerators, where beams in excess of 10 GeV in bunch durations of, typically, dozens of femtoseconds, will be within reach of the next generation of lasers. This combination opens the way for even more exciting physics, associated with intense sources of low-energy photons, high-energy (secondary) photons, and multi-GeV electron beams. State-of-the-art numerical tools, critical to the pursuit of extreme light-plasma studies, will strongly benefit from progress in machine learning, through the convergence of data from experiments and simulations, as well as quantum computing, as novel algorithms are deployed to future quantum computers.
3.5.6.6. Secondary sources and applications
Many experimental advances will rely on fully developed strategies for laser control and delivery of secondary sources on demand, with fine-tuned control of secondary sources with unique properties. The availability in the laboratory of such sources, with the potential for co-location of synchronous generation, of high-brightness photons, high-energy electron, proton, and neutron beams, until now only available at large-scale facilities, will revolutionize a broad range of fields, from fundamental science to applications.
3.5.6.7. Plasma optics
Taming plasma properties for the manipulation of light is a critical and challenging aspect of the road to ultrahigh intensities. Conventional materials cannot sustain the intensities of state-of-the-art lasers. Therefore, optics at ultrahigh intensities will have to rely on plasmas to steer, focus, and shape light. Relativistic plasmonics will thus become a central question to address the manipulation of extreme light. As we envisage moving to even higher laser intensities, even the laser amplification process itself will have to rely on the nonlinear properties of the plasma to transfer light from long lasers pulses to ultrashort and ultrahigh laser intensities pulses, via Raman or Brillouin amplification. Further manipulation of the topological properties of light with angular momentum resorting to the unique topological plasma response provides an additional exciting direction, with deep and fundamental consequences for laser–plasma interactions and their applications.
3.5.6.8. Quantum-electrodynamics; applications to particle- and astrophysics
Lasers (and particle beams) at the intensity frontier will first provide a unique stage to explore fundamental quantum electro-dynamical phenomena in the novel regime of multiphoton processes, driven by (a very large number of) low- energy photons. These will also provide a unique path to the exploration of the transition from the classical to quantum physics in the relativistic regime. The envisaged intensities can eventually approach the regime in which it has been conjectured that quantum electrodynamics might 'break down'; a strongly non-perturbative field theory would then be needed, which would move into QED regimes that remain hitherto theoretically and experimentally unexplored.
The density of the electron–positron plasma generated at such laser intensities via QED processes (from laser-beam or laser-target collisions) will exceed the plasma density of solids and will therefore itself affect the interaction of light with the target and the plasma and laser dynamics. A new fundamental direction for laser–plasma interactions will be opened up, in which QED processes determine collective plasma dynamics, and even brighter gamma ray and electron–positron sources can be designed for a multitude of applications. It is even possible to conceive the generation and exploration of secondary sources of pions and muons generated via laser–plasma interactions. This is now only possible at a few very large accelerator facilities worldwide.
Similar electromagnetic intensities and extreme electron–positron plasmas are also present in extreme astrophysical scenarios such as gamma ray bursts, pulsars, magnetars, and black holes. Therefore, laser–plasma interactions in the ultrarelativistic limit opens a novel path for the convergence of ultrahigh laser intensity physics with laboratory astrophysics in the high-energy regime, and with ultrastrong (electro)magnetic fields, where numerical tools and experiments commonly associated with laboratory experiments can shed light on some of the fundamental processes underpinning the scientific mysteries of the most exotic objects in the Universe.
As the laser energy increases and laser facilities are complemented with ultra-strong magnetic fields or relativistic particle beams, the next 30 years will also witness further developments on laboratory astrophysics, driven by high-intensity/high-energy lasers, of collisionless shock waves and their physics and impact on cosmic ray acceleration, magnetized relativistic flows and the formation of jets, fundamental magnetogenesis processes, and the long-term evolution of turbulence in magnetized plasma, a fundamental question underpinning many astrophysical questions.
Plasma acceleration is expected to reach two key milestones. For electrons, the realm of high-energy physics will be within reach, with high-energy, high-current beams, high-brightness beams, and moderate repetition rate (kHz), determined by the laser technology. For protons, acceleration beyond 200 MeV will further place laser–plasma interactions as a route for compact proton accelerators for proton therapy and other applications.
As the world addresses climate change, the quest for clean energy sources is at the forefront of the scientific and technology challenges of the 21st century. One of the possible directions, still requiring major scientific and technological advances and the development of new large-scale facilities, is laser fusion, or its combination with other clean technologies. This is a very long-term, very high-risk endeavor but humanity just cannot leave a direction filled with outstanding scientific and technological challenges and a possible path to achieve a commercial clean energy source unexplored.
3.6. Systems with numerous degrees of freedom
Marco Baldovin1,2, Giacomo Gradenigo3 and Angelo Vulpiani4
1Université Paris-Saclay, Orsay, France
2CNR - Instute for Complex Systems, Rome, Italy
3Gran Sasso Science Institute, L'Aquila, Italy
4Università 'Sapienza', Rome, Italy
3.6.1. Introduction
Hamiltonian systems have great relevance in many fields, from celestial mechanics to fluids and plasma physics. Not even to mention the importance of the Hamiltonian formalism for quantum mechanics and quantum field theory [226]. The aim of this contribution is to discuss the relation between the dynamics of Hamiltonian systems with many degrees of freedom and the foundations of statistical mechanics [227–229]. In particular, we want to address the problem of thermalization in integrable and nearly integrable systems, questioning the role played by chaos in this processes. The problem of thermalization of high-dimensional integrable Hamiltonian systems is, in our opinion, a truly non-academic one and is today of groundbreaking importance for one main reason: it has a direct connection with the problem of quantum systems thermalization. The analogy between the problem of thermalization in high-dimensional integrable Hamiltonian systems and thermalization of quantum many-body systems would make it possible to exploit the rich conceptual and methodological framework already developed for classical systems for the investigation of the quantum ones. The point of view we want to promote here is that the presence or absence of thermal equilibrium is not an absolute property of the system but depends on the set of variables chosen to represent it. We will present some examples supporting the idea that the notion of thermal state strongly depends on the choice of the variables used to describe the system. One could ask at this point what makes the study of thermalization still such an interesting problem. The answer is that the most recent technologies allow now for manipulation of quantum mesoscopic systems in an uprecedented way, so that many foundational questions gain renewed importance and are today crucial for experimental purposes. Last but not least, the interplay between the absence of thermalization in quantum many-body systems and the processing (storage/transmission) of information in quantum devices is of paramount importance for all applications to quantum computing.
The discussion develops through sections as follows: in section 3.6.2 the standard viewpoint, according to which chaos plays a key role to guarantee thermalization, is summarized; in section 3.6.3 we present three counter-examples to the above view and provide a more refined characterization of the central point in the 'thermalization problem', namely the choice of the variables used to describe the system; in section 3.6.4 we discuss the analogies between the problem of thermalization in classical and quantum mechanics and we compare the scenarios established, respectively, by the Khinchin's (classical) ergodic theorem [230] and the quantum ergodic theorem by Von Neumann [231–233]. An account of open questions and future perspectives follows at the end.
3.6.2. The role of Kolmogorov–Arnold–Moser (KAM) and chaos for the timescales
It is usually believed that ergodicity is a necessary condition to observe thermal behaviour in a given Hamiltonian system [229]. The ergodic hypothesis, first introduced by Boltzmann, states that a Hamiltonian system with energy E, during its motion, will visit the whole hypersurface of constant energy E in the phase space; in each region of the hypersurface the system will spend an amount of time which is proportional to the volume of the region itself (i.e., its Lebesgue measure). In modern terms, the assumption of ergodicity amounts to asking for the phase space to not be partitioned in disjoint components which are invariant under time evolution [227, 234]. Indeed, if dynamics can explore the whole hypersurface, the latter cannot be divided into measurable regions that are invariant under time evolution without resulting in a contradiction. The existence of conserved quantities different from energy implies in turn the existence of other invariant hypersurfaces, which prevent the system from being ergodic.
The claim that thermalization is related to ergodicity summarizes the viewpoint of those who think that invariant manifolds in phase space, which work as obstructions to ergodicity, are the main obstacle to thermal behaviour. The problem of 'thermalization' can be thus reformulated as the determination of the existence of integrals of motion other than energy. This was solved by Poincaré in his celebrated work on the three-body problem [227, 228]. Consider the following Hamiltonian
where H depends on a set of 'angles' , with , and on their conjugate momenta, the 'actions' . Actions and angles are the canonical coordinates which are typically chosen to describe the motion of an integrable system, which is the limiting case of the above Hamiltonian. In that case, the actions are constant in time (since the angles do not appear in the Hamiltonian) and the angles increase with constant velocities. There are therefore conservation laws and the motion takes place on -dimensional invariant tori.
If is small but non-vanishing, we are in an 'almost' integrable situation. Poincaré showed that, for , excluding specific cases, there are no conservation laws apart from the trivial ones (i.e., energy and total momentum). In 1923 Fermi generalized Poincaré's theorem, showing that, if , it is not possible to have a foliation of phase space in invariant surfaces of dimension embedded in the constant-energy hypersurface of dimension . From this result Fermi argued that generic Hamiltonian systems are ergodic as soon as . At that time it was believed that global invariant manifolds were the main obstruction to thermalization; as a consequence, Fermi's mathematical proof appeared to imply that good thermal behaviour should have been expected for non-integrable systems. It was then a numerical experiment realized by Fermi himself in collaboration with J Pasta, S Ulam, and M Tsingou (who did not appear among the authors) which showed that this was not the case [235]. Fermi and coworkers studied a chain of weakly nonlinear oscillators, finding that the system, despite being non-integrable, was not showing relaxation to a thermal state within reasonable times when initialized in a very atypical condition. This observation raised the problem that while the absence of globally conserved quantities guarantees that no partitioning of phase space takes place, on the other hand, it does not tell anything on the timescales to reach equilibrium [236]. A first understanding of the slow FPUT timescales from the perspective of phase-space geometry came from the celebrated Kolmogorov–Arnold–Moser (KAM) theorem, sketched by A N Kolmogorov already in 1954 and completed later [227, 228]. The theorem says that for any value of , even very small, some tori of the unperturbed system, the so-called resonant ones, are completely destroyed, and this prevents the existence of analytical integrals of motion. Despite this, if is small, most tori, slightly deformed, survive; thus the perturbed system (for 'non-pathological' initial conditions) has a behaviour quite similar to an integrable one.
3.6.2.1. KAM scenario, chaos, and slow timescales
After the discovery of the KAM theory it became clear that also in weakly nonlinear systems the phase space is characterized by the presence of invariant manifolds which, even if not partitioning it into disjoint components, might crucially slow down the dynamics. The foundational problem of statistical mechanics thus turned from 'do we have a partitioning of phase space?' to 'how long does it take to thermalize in the large-N limit?'.
A crucial role to answer this question was then played by the notion of chaos. Very roughly, chaos means exponential divergence of initially nearby trajectories in phase space. The rate of divergence of nearby orbits is the inverse of a quantity known as the first (maximal) Lyapunov exponent [237] : . Of course, the behaviour of nearby trajectories may, and actually does, depend on the phase space region they start from. In fact, for a system with N degrees of freedom one finds N independent Lyapunov exponents: in the multiplicity of Lyapunov exponents is encoded the property that the rate of divergence of nearby orbits has fluctuations in phase space. This is indeed the picture which comes from both the KAM theorem and the evidence of many numerical experiments: at variance with dissipative systems (characterized by a sharp threshold from regular to chaotic behavior) Hamiltonian systems are characterized at any energy scale by the coexistence of regular and chaotic trajectories. In particular, one has in mind that fast thermalization takes place in chaotic regions while the slow timescales are due to the slow intra-region diffusion. The slow process is thus controlled by the location and structure of invariant manifolds which survive in the presence of nonlinearity. The whole issue of determining on which timescale the system exhibits thermal properties boils down to estimating the timescale of diffusion across chaotic regions in phase space: this is the so-called Arnold's diffusion.
3.6.2.2. Arnold's diffusion
Arnold's diffusion is the name attached to the slow diffusion taking place in a phase space characterized by the coexistence of chaotic regions and regular ones [227, 228]. Typically, chaotic regions in high-dimensional phase spaces do not have a smooth geometry and are intertwined in a very intricate manner with invariant manifolds. Diffusion across the whole phase space is driven by chaotic regions, but their complicated geometry, typically fractal, slows down diffusion at the same time [238]. From this perspective, let us try to have a look at the scenario for diffusion in phase space in the case of weakly non-integrable systems in the limit of large [239–241]. Is it compatible with the appearance of a thermal state?
Let us consider the generic Hamiltonian for a weakly nonintegral system. This is a system with N degrees of freedom where, after introducing the Liouville–Arnold theorem's action-angle variables , the symplectic dynamics is defined as follows:
where , is the term which breaks integrability and is a dimensionless coefficient which we assume to be small. Let us note that a symplectic map with degrees of freedom can be seen as the Poincaré section of a Hamiltonian system with degrees of freedom. The key point for the purpose of our discussion is to understand what happens to invariant manifolds in the large-N limit. Several numerical works (see, e.g., [239]) showed that the volume of regular regions decreases very fast at large N. In particular, the normalized measure of the phase space, where the numerically computed first (maximal) Lyapunov exponent is very small, goes to zero exponentially with N:
At a first glance such a result sounds quite positive for the possibility to build the statistical mechanics on dynamical bases, since, no matter how small is, the probability to end up in a non-chaotic region () becomes exponentially small with the size of the system.
At this stage the problem of dynamical justification of statistical mechanics may seem to be solved. On the one hand, it is true that a set of manifolds of finite measure which are invariant along the dynamics can always be found, even for non-integrable systems (KAM theorem), and this invariance may possibly spoil the relaxation to equilibrium; on the other hand, however, very reasonable estimates also assure that in the large-N limit, the probability to end up in a non-chaotic region is negligible.
But this is not the end of the story. Indeed, the presence of chaos is not sufficient to avoid the long timescale correlations in the motion of the system. From a mere analysis in terms of Lyapunov exponents it is indeed only possible to conclude that almost all trajectories have the 'good' statistical properties we expect in statistical mechanics. The main reason is that the time , which is related to the trajectory instability, is not the unique relevant characteristic time of the dynamics. There might be more complicated collective mechanisms which prevent a fast thermalization of the system which are not traced by the Lyapunov spectrum. Think for instance to the mechanism of ergodicity breaking in systems such as spin glasses [242].
The trajectories of an N-dimensional system lie on a dimensional hypersurface in the phase space (i.e., the phase-space region with constant energy), while the KAM tori have dimension N. If , a 1D torus can thus separate the 2D hypersurface it lies on into an 'inner' and an 'outer' portion. As soon as , instead, a constant-energy hypersurface cannot be separated into disjoint components by a torus and, as we have said, ergodicity is guaranteed asymptotically from the point of view of dynamics. A trajectory initially closed to a KAM torus may visit any region of the energy hypersurface, but, since the compenetration of chaotic regions and invariant manifolds typically follows the pattern of a fractal geometry, the diffusion across the isoenergetic hypersurface is usually very slow; as we said, such a phenomenon is called Arnol'd diffusion [227, 240]. The important and difficult problem is therefore to understand the 'speed' of the Arnold diffusion, i.e., the time behaviour of
where the denotes the averages over the initial conditions. There are some theoretical bounds for , as well as several accurate numerical simulations, which suggest a rather slow 'anomalous diffusion':
where and depend on the system's parameters. We can say that in a generic Hamiltonian system Arnold diffusion is present and, for small , it is very weak. It can thus happen that different trajectories, even with a rather large Lyapunov exponent, maintain memory of their initial conditions for considerably long times. See, for instance, the results of [239] discussed below in section 3.6.3. The existence of Arnold's diffusion is a hint that chaos is sometimes not sufficient to guarantee thermalization.
3.6.2.3. Lyapunov exponents in the large-N limit
Although we are going to depart from this point of view, let us put on the table all evidences that chaos is apparently a good property to justify a statistical mechanics approach. For instance, in a chaotic system it is possible to define an entropy directly from the Lyapunov spectrum [237]. In any Hamiltonian (symplectic) system with degrees of freedom we have Lyapunov exponents which obey a mirror rule, i.e.,
and the Kolmogorov–Sinai entropy is
Regarding statistical mechanics, the natural question is about the asymptotic behaviour of for . There is clear numerical evidence [243, 244] and analytical results for a few special cases [245] that at large one has
where as . Such a result implies that the Kolmogorov–Sinai entropy equation (3.8) is proportional to the number of degrees of freedom:
where does not depend on N. The extensivity of H in the thermodynamic limit resonates with the properties of entropy in statistical mechanics, but it should not be overestimated, as we will discuss in the next section.
3.6.3. Challenging the role of chaos
The previous section was entirely dedicated to present evidences in favour of chaos being a sufficient condition for an equilibrium behaviour in the large-N limit and the possibility to apply a statistical mechanics description. In the present section we present counter-examples to this point of view. These examples suggest that in the large-N limit a statistical mechanics description holds for almost all Hamiltonian systems irrespective of the presence of chaos. First, we will quote two results showing that, even in the presence of finite Lyapunov exponents, there are clear signatures of (weak) ergodicity breaking and of the impossibility to establish a statistical mechanics description on finite timescales [239, 246]. Conversely, we can also present the examples of an integrable system, the Toda chain [247], which shows thermalization on short timescales notwithstanding all Lyapunov exponents are zero. Clearly, in the case of an integrable system, thermalization takes place with respect to some observables and not with respect to others. But this is the point of the whole discussion we want to promote: thermal behaviour is not a matter of dynamics being regular or chaotic, it is just a matter of choosing the description of the system in terms of the appropriate variables. And, as we will see, this is also the case for quantum mechanics (which has important similarities with classical integrable systems); almost all choices of canonical variables are good while only very few are not good. In the case of an integrable system, in order to detect thermalization the canonical variables which diagonalize the Hamiltonian must be, of course, avoided.
3.6.3.1. Weak ergodicity breaking in coupled symplectic maps
We start our list of 'counter-examples' to the idea that chaotic properties guarantee fast thermalization by recalling the results of [239]. In [239] the authors studied the ergodic properties of a large number of coupled symplectic maps (3.1) and (3.2) where one considers periodic boundary conditions, i.e., , and nearest-neighbour coupling:
represented by following system of discrete time update equations:
Skipping all the details of the analysis let us move straight to the main results of [239]. The authors perform a numerical mesure of the Lyapunov spectrum and provide an estimate for the size of 'regular regions', which is a way to refer to the measure of KAM tori, by looking at the fraction of Lyapunov exponents compatible with zero within error bars.
As anticipated above, reference [239] shows that the volume of phase space filled with invariant manifolds decreases exponentially with system size, as shown in figure 3.30. This is a remarkable evidence that in the large- limit the probability that thermalization is obstructed by KAM tori is exponentially (in system size) small. The system has good chaotic properties. This notwithstanding, at the same time there are clear signatures of a phenomenon analogous to the so-called weak-ergodicity breaking of disordered systems. The terminology weak-ergodicity breaking is jargon indicating the situations where, despite relaxation being always achieved asymptotically, at any finite time memory of the initial conditions is preserved [248]. Let us define as the time elapsed since the beginning of the dynamics, is a later time, and is the time auto-correlation (averaged over an ensemble of initial conditions) of some relevant observable of the system. Weak ergodicity breaking is then expressed by the condition
The dependence on waiting times encoded in equation (3.11) represents the fact that we do not find only one characteristic timescale emerging at the macroscopic level (which is the standard behaviour at thermodynamic equilibrium): on the contrary, a broad distribution of timescales can be appreciated even macroscopically. In jargon, we say that the probability distribution of characteristic timescales is not self-averaging (i.e., it cannot be approximated with a Dirac delta in the thermodynamic limit). A clear signature of a situation with the features of weak ergodicity breaking is revealed by the study of how the distribution of the maximum Lyapunov spectrum depends on the system size [239]. While the probability distribution of the exponents peaks at a value of order with respect to , still the scaling of the variance is anomalous (i.e., it decays much slower than : this is the distinguishing feature of a probability distribution which is not self-averaging. One of the main results of [239] is, in fact, that the variance of the Lyapunov exponent distribution, in particular its asymptotic estimate , scales as
where , so that for small , is much larger than .
since
Figure 3.30. Fraction of maximal Lyapunov exponents smaller than as a function of for (a) and (b) , , averaged over initial conditions. Reprinted figure with permission from [239], Copyright (1991) by the American Physical Society.
Download figure:
Standard image High-resolution image3.6.3.2. High-temperature features in coupled rotators
Another example of a system which does not show thermal behaviour despite having positive Lyapunov exponents is represented by the coupled rotators at high energy studied in [246]. The Hamiltonian of this system reads as:
where are angular variables and are their conjugate momenta. The specific heat can be easily computed from the partition function as
with , being Boltzmann's constant and the temperature. In particular, the expression of the specific heat reads in terms of a modified Bessel function as
It is possible to compare the analytical prediction of equation (3.17) with numerical simulations by estimating in the latter the specific heat from the fluctuations of energy in a given subsystem of rotators, with :
where is the Hamiltonian of the chosen subsystem and the 'ensemble' average in equation (3.18) includes averaging over initial conditions and averaging along the symplectic dynamics for each initial condition. The result of the comparison is presented in figure 3.31. From the figure it is clear that, while at small and intermediate energies the canonical ensemble prediction for the specific heat equation (3.17) matches the quantity (3.18) observed in numerical simulations, it fails at high energies. What is remarkable is that in the high-temperature regime where statistical mechanics fails, the value of the largest Lyapunov exponent is even larger than in the intermediate-small energy regime where the equilibrium prediction works well. This is one of the strongest hints from the past literature that the chaoticity of orbits has nothing to do with the foundations of statistical mechanics. In practice, it happens that for rotators a sort of 'effectively integrable' regime arises at high energy. In this regime each rotator is spinning very fast, something which guarantees the chaoticity of orbits, but the individual degrees of freedom do not interact with each other, which causes the breakdown of thermal properties of the system. This very simple mechanism is a concrete example (and often examples are more convincing than arguments) of how absence of thermalization and chaos can be simultaneously present. In the next example, the role of chaos for thermalization will be challenged even further: we are going to present the case of a system which, despite being all Lyapunov exponents equal to zero, presents fast relaxation to equilibrium when the appropriate variables are considered.
Figure 3.31. Specific heat versus temperature in the rotator model. The continuous line represents the analytic prediction from equation (3.17). Empty symbols represent the results of numerical simulations, respectively, for a subsystem with (circles) and (diamonds) rotators, in a chain of and particles, respectively. The dashed line is the maximal Lyapunov exponent as a function of the temperature (specific energy) measured in units of the coupling constant [see equation (3.15)]. Reprinted by permission from Springer Nature [246], copyright (1987).
Download figure:
Standard image High-resolution image3.6.3.3. Toda lattice: thermalization of an integrable system
We present here the example of an integrable system which shows very good thermalization properties. In some sense we find that the statement 'the system has thermalized' or 'the system has not thermalized' depends, for Hamiltonian systems, on the choice of canonical coordinates in the same way as the statement 'a body is moving' or 'a body is at rest' depend on the choice of a reference frame. In this respect, it is true that, if a system is integrable in the sense of the Liouville–Arnold theorem and we choose to represent it in terms of the corresponding action-angle variables, we will never observe thermalization. But there are infinitely many other choices of canonical coordinates which allow one to detect a good degree of thermalization. Let us be more specific about this and recall the salient results presented in [249] on the Toda chain.
It is well known that the Toda lattice,
where is the Toda potential,
admits a complete set of independent integrals of motion, as shown by Henon in his paper [247]. This result can also be understood in light of Flashka's proof of the existence of a Lax pair related to the Toda dynamics [250]. The explicit form of such integrals of motion is rather involved, and their physical meaning is not transparent; one may wonder whether the system is able to reach thermalization under a different canonical description, such as the one which is provided by the Fourier modes,
A typical test which can be performed, inspired by the FPUT numerical experiment, is realized by considering an initial condition in which the first Fourier mode is excited, and for all ; the system is evolved according to its Hamiltonian dynamics, and the average energy corresponding to each normal mode,
is studied as a function of time. It is worth noticing that in the limit of small energy , the Toda Hamiltonian is well approximated by a harmonic chain in which the 's are conserved quantities; it is therefore not surprising that, for , it takes very long times to observe equipartition of harmonic energy between the different modes (figure 3.32). This ergodicity-breaking phenomenology has been studied, for instance, in reference [236] to underline relevant similarities with the FPUT dynamics.
Figure 3.32. Normalized harmonic energy as a function of the Fourier mode number , for different values of the averaging time, in a Toda dynamics (3.19) with FPUT initial conditions. Here , total energy .
Download figure:
Standard image High-resolution imageThe scenario completely changes when specific energies of order or larger are considered. In figure 3.31 the distribution of the harmonic energy among the different Fourier modes is shown for several values of the averaging time ; no ergodicity breaking can be observed, and in finite times the harmonic energy reaches equipartition.
3.6.4. From classical to quantum: open research directions
After the examples of the previous section we feel urged at this point to draw some conclusions. We started our discussion from wondering how much having a phase space uniformly filled by chaotic regions is relevant for relaxation to equilibrium and we came to the conclusion, drawn from the last set of examples, that in practice chaos does not seem to be the crucial point for relaxation to equilibrium. What is then the correct way to frame the 'foundation of statistical mechanics' problem? It seems that the correct paradigm to understand the results of section 3.6.3 is the one established by the ergodic theorem by Khinchin [230]: in order to guarantee a thermal behaviour, i.e., that dynamical averages correspond to ensemble averages, it is sufficient to consider appropriate observables for large enough systems. That is, the regime is mandatory. As anticipated in section 3.6.3 by our numerical results, one finds that the hypothesis under which the Khinchin ergodic theorem is valid are for instance fulfilled even by integrable systems. In a nutshell we can summarize his approach by saying that it is possible to show the practical validity of the ergodic hypothesis when the following three conditions are fulfilled:
- the number of the degrees of freedom is very large
- we limit the interest to 'suitable' observables
- we allow for a failure of the equivalence of the time average and the ensemble average for initial conditions in a 'small region'
The above points will be clarified in the following.
3.6.4.1. The ergodic problem in Khinchin's perspective
Let us see in practice what the theorem says. Consider a Hamiltonian system with canonical variables . Let be the flow under the symplectic dynamics generated by . The time average for given initial datum is defined as
while the ensemble average is defined with respect to an invariant measure in phase space:
Let us define as sum function any function reading as
For such functions Khinchin [230] was able to show that for a random choice of the initial datum the probability that the time average in equation (3.23) and the ensemble average in equation (3.24) are different is small in , that is,
where and are constants with respect to . This is the well-known Khinchin's theorem. We can note that many, but not all, relevant macroscopic observables are sum functions. While the original result of Khinchin was for non-interacting system, i.e., systems with Hamiltonian:
Mazur and van der Linden [251] were able to generalize it to the more physically interesting case of (weakly) interacting particles:
From the results by Khinchin, Mazur, and van der Linden we have the following scenario: although the ergodic hypothesis mathematically does not hold, it is 'physically' valid if we are tolerant, namely if we accept that in systems with ergodicity can fail in regions sampled with probability of order (i.e., vanishing in the limit . Let us stress that the dynamics has a marginal role, while the very relevant ingredient is the large number of particles.
Whereas it is possible, on the one hand, to emphasize some limitations of the Khinchin ergodic theorem, as for instance the fact that it does not tell anything about the timescale to be waited for in order to have equation (3.26) reasonably true, let us stress here its goals. For instance, let us highlight the fact that the Khinchin ergodic theorem guarantees the thermalization even of integrable systems! In fact, if we consider the Toda model discussed in the previous section, the conditions under which the Khinchin ergodic theorem was first demonstrated perfectly apply to it. In fact, integrability, proved first by Hénon in 1974 [247], guarantees the existence of action-angle variables such that the Hamiltonian reads as:
which is precisely the non-interacting-type of Hamiltonian considered in first instance by Khinchin. The results presented in [249] on the fast thermalization of the Toda model have been in fact proposed to re-establish with the support of numerical evidence the assertion, hidden between the lines of the Khinchin theorem and perhaps overlooked so far, that even integrable systems do thermalize in the large- limit. The phase-space of Toda chain is in fact completely foliated in invariant tori. But, according to the Khinchin theorem and our numerical results, this foliation of phase space in regular regions is not an obstacle as long as the 'thermalization' of sum functions is considered (for almost all initial data in the limit ).
3.6.4.2. Quantum counterpart: Von Neumann's ergodic theorem
The observation that 'even integrable systems thermalize well in the large- limit' becomes particularly relevant as soon as we regard, in the limit of large , the dynamics of a classical integrable system as the 'classical analog' of quantum system dynamics. In quantum systems one finds in fact the same 'ergodic problem' of classical mechanics: is it possible to replace time averages with ensemble averages? Let us say a few words on the quantum formalism in order to point out the similarities between the ergodic theorem by Khinchin and the one by Von Neumann for quantum mechanics. As it is well known, due to the self-adjointness of the Hamiltonian operator, any wavevector can be expanded on the Hamiltonian eigenvectors basis:
where denotes the discrete spectrum of the Hamiltonian operator . The projection on a limited set of eigenvalues defines the quantum microcanonical ensemble. Since it is reasonable to assume that also in a quantum system the total energy of an -particle system is known with finite precision (i.e., usually we know that it takes values within a finite shell with and , one defines the microcanonical density matrix as the projector on the eigenstates pertaining to that shell:
where is the number of eigenvalues in the shell. The microcanonical expectation of the observable thus reads:
Clearly in the limit where the eigenvalues are densely distributed on the real line one has that even in a finite shell . By preparing a system in the initial state the expectation value of a given observable at time reads as:
Quantum ergodicity amounts then to the following equivalence between dynamical and ensemble averages:
The reader can easily convince himself of the fact that, if for almost all times the expectation of on the initial state is typical, namely one has , then the quantum ergodicity property as stated in equation (3.34) is realized. The fact that for almost all times is ususally called 'normal typicality': it is discussed thoroughly in [232]. Similarly to the scenario later proposed by Kinchin for classical systems, already in 1929 Von Neumann proposed a quantum ergodic theorem which proves the typicality of without making any reference to quantum chaos properties. The definition of quantum chaos, which will be formalized much later [252], is to have a system characterized by a Hamiltonian operator, , such that its eigenvctors behave as random structureless vectors in any basis. This property, notwithstanding the different formalism of quantum and classical mechanics, has a deep analogy with the definition of classical chaos [228, 253]: a quantum system is said to be chaotic when a small perturbation of the Hamiltonian, , produces totally uncorrelated vectors, , in the same manner that a small shift in initial conditions produces totally uncorrelated trajectories in classical chaotic systems.
Quite remarkably, Von Neumann's ergodic theorem does not make any explicit assumption of the above kind on the Hamiltonian's eigenvalues structure. Here follows a short account of the theorem; mathematical details can be found in the recent translation from German of the original paper [231] and in [232, 233]. Let be the dimensionality of the energy shell , namely , where is the Hilbert space spanned by the eigenvectors such that , and define a decomposition of in orthogonal subspaces each of dimension :
Then define as the projector on subspace . It is mandatory to consider the large system size limit where . It is then demonstrated that, under quite generic assumptions on the original Hamiltonian and on the orthogonal decomposition , for every wavefunction and for almost all times one has normal typicality, i.e.,
where is the microcanonical density matrix in equation (3.31). A crucial role is played by the assumption that the dimensions of the orthogonal subspaces of are macroscopically large (i.e., .) In this sense the projectors correspond to macroscopic observables. From this point of view, Von Neumann's quantum ergodic theorem is constrained by the same key hypothesis of Khinchin's theorem: the limit of a very large number of degrees of freedom. At the same time, Von Neumann's theorem does not make any claim on chaotic properties of the eigenspectrum, in the very same way as the Khinchin's theorem does not make any claim on chaotic properties of trajectories.
For completeness we also need to mention what is regarded today as the 'modern' version of Von Neumann's theorem, namely the celebrated eigenstate thermalization hypothesis (ETH) [254]. By expanding the expression of as
it is not difficult to figure out that ergodicity, as expressed in equation (3.34), is guaranteed if suitable hypotheses are made for the matrix elements . For instance, it can be assumed that:
- The off-diagonal matrix elements are exponentially small in system size, with beingthe microcanonical entropy and .
- The diagonal elements are a function of the initial-condition energy, .
The hypothesis guarantees that for large enough systems relaxation to a stationary state is achieved within reasonable time, still leaving open the possibility that stationarity is different from thermal equilibrium. In fact, it is thanks to the exponentially small size of non-diagonal matrix elements that in the large- limit one does not need to wait the astronomically large times needed for dephasing in order to have
Hypothesis then guarantees that relaxation is towards a state well characterized macroscopically, i.e., a state which depends solely on the energy of the Hilbert space vector and not on the extensive number of coefficients :
Though inspired from the behaviour of (quantum) chaotic systems, ETH is clearly a different property since it makes no claim on the structure of energy eigenvectors. For this reason and also because a necessary condition for ETH to be effective is a large- limit, ETH is rather close in spirit to Von Neumann's theorem. Then, we must say that a complete understanding of the reciprocal implications of quantum chaos and the ETH is still an open issue which deserves further investigations. In this respect let us recall the purpose of this chapter, namely to furnish reasons to believe that an investigation aimed at challenging the role of chaos in the thermalization of both quantum and classical systems is an interesting and timely subject. For instance, a deeper understanding of the mechanisms which trigger, or prevent, thermalization in quantum systems is crucial to estimating the possibilities of having working scalable quantum technologies, like quantum computers and quantum sensors.
An interesting point of view which emerged from the results on the Toda model discussed in section 3.6.3.3 and which can be traced back to both Khinchin and Von Neumann's theorem is the following: the presence (or absence) of thermalization is a property pertaining to a given choice of observables and cannot be stated in general (i.e., solely on the basis of the behaviour of trajectories or the structure of energy eigenvectors). We have in mind the choice of the projectors in Von Neumann's theorem and the choice of sum functions in Khinchin's theorem. This perspective of considering 'thermal equilibrium as a matter of observables choice' is in our opinion a point of view that deserves careful investigation.
3.6.4.3. Summary and perspectives
Let us try to summarize the main aspects here discussed. At first, we stressed that the ergodic approach, even with some caveats, appears the natural way to use probability in a deterministic context. Assuming ergodicity, it is possible to obtain an empirical notion of probability which is an objective property of the trajectory. An important aspect often not considered is that both in experiments and numerical computation one deals with a unique system with many degrees of freedom, and not with an ensemble of systems. According to the point of view of Boltzmann (and the developments by Khinchin, Mazur, and van der Linden) it is rather natural to conclude that, at the conceptual level, the only physically consistent way to accumulate a statistics is in terms of time averages following the time evolution of the system. At the same time ergodicity is a very demanding property and, since in its definition it requires to consider the infinite time limit, physically it is not very accessible.
We then presented strong evidence from a numerical study of high-dimensional Hamiltonian systems that chaos is neither a necessary nor a sufficient ingredient to guarantee the validity of equilibrium statistical mechanics for classical systems. On the other hand, even when chaos is very weak (or absent), we have shown examples of a good agreement between time and ensemble averages [249]. The perspective emerging from our study is that the choice of variables is crucial to saying whether a system has thermalized or not. We have found that this point of view emphasizes the commonalities between classical and quantum mechanics for what concerns the ergodic problem. This is particularly clear by comparing the assumptions and conclusions of the ergodic theorems of Khinchin and Von Neumann, where, without any assumption on the chaotic nature of dynamics, it is shown that for general enough observables a system has good ergodic properties even in the case where interactions are absent, provided that the system is large enough.
This brought us to underline as a possibly relevant research line the one dedicated to find 'classical analogs' of thermalization problems in quantum systems and to study such problems with the conceptual tools and the numerical techniques developed for classical Hamiltonian systems.
The ability to control and exactly predict the behavior of quantum systems is in fact of extreme relevance, in particular for the great bet presently made by the worldwide scientific community on quantum computers. In particular, understanding the mechanisms preventing thermalization might certainly help to improve the function of quantum processors and to devise better quantum algorithms.
In summary, we tried to present convincing motivations in favour of a renewed interest towards the foundations of quantum and statistical mechanics. This is something which in our opinion should be pursued while approaching the one century anniversary of the two seminal papers by Heisenberg [255] and Schrödinger [256] on quantum mechanics. How much over the past 100 years has the quantum mechanics revolution influenced not only the understanding of the microscopic world, but even the thermodynamic properties of macroscopic systems? This is a key question for future research.
References
- [1]Hartree D R 1928 The wave mechanics of an atom with non-Coulombic central field: parts I, II, III Proc. Cambridge Phil. Soc. 24 89,111,426
- [2]Tkatchenko A, Rossi M, Blum V, Ireta J and Scheffler M 2011 Unraveling the stability of polypeptide helices: critical role of van der waals interactions Phys. Rev. Lett. 106 118102
- [3]Martin R M, Reining L and Ceperley D M 2016 Interacting Electrons (Cambridge: Cambridge University Press)
- [4]Keimer B and Moore J E 2017 The physics of quantum materials Nat. Phys. 13 1045–55
- [5]Hüfner S 2003 Photoemission Spectroscopy: Principles and Applications (Berlin: Springer)
- [6]Sky Zhou J et al 2020 Unraveling intrinsic correlation effects with angle-resolved photoemission spectroscopy Proc. Natl Acad. Sci. 117 28596–602
- [7]Fitzgerald R 2000 What really gives a quantum computer its power? Phys. Today 53 20–2
- [8]Kohn W 1999 Nobel lecture: electronic structure of matter—wave functions and density functionals Rev. Mod. Phys. 71 1253–66
- [9]Martin R M 2020 Electronic Structure: Basic Theory and Practical Methods 2nd edn (Cambridge: Cambridge University Press)
- [10]Bohm D and Pines D 1953 A collective description of electron interactions. 3. Coulomb interactions in a degenerate electron gas Phys. Rev. 92 609–25
- [11]Pines D and Bohm D 1952 A collective description of electron interactions.2. Collective vs individual particle aspects of the interactions Phys. Rev. 85 338–53
- [12]Huotari S, Sternemann C, Schülke W, Sturm K, Lustfeld H, Sternemann H, Volmer M, Gusarov A, Müller H and Monaco G 2008 Electron-density dependence of double-plasmon excitations in simple metals Phys. Rev. B 77 195125
- [13]Schülke W 2007 Electron dynamics by inelastic x-ray scattering Oxford Series on Synchrotron Radiation (Oxford: Oxford University Press)
- [14]Egerton R F 2009 Electron energy-loss spectroscopy in the TEM Rep. Prog. Phys. 72 016502
- [15]Yu H, Peng Y, Yang Y and Li Z-Y 2019 Plasmon-enhanced light–matter interactions and applications npj Comput. Mater. 5 45
- [16]de Seauve V, Languille M-A, Kociak M, Belin S, Ablett J, Andraud C, Stéphan O, Rueff J-P, Fonda E and Lavédrine B 2020 Spectroscopies and electron microscopies unravel the origin of the first colour photographs Angew. Chem. Int. Ed. 59 9113–9
- [17]Kazimierczuk T, Fröhlich D, Scheel S, Stolz H and Bayer M 2014 Giant Rydberg excitons in the copper oxide Cu2O Nature 514 343–7
- [18]Laughlin R B 2005 A Different Universe: Reinventing Physics from the Bottom Down (New York: Basic Books)
- [19]Anderson P W 1972 More is different Science 177 393–6
- [20]Unkrich L and Stanton A 2003 Finding Nemo (Pixar Animation Studios)
- [21]Wigner E 1934 On the interaction of electrons in metals Phys. Rev. 46 1002–11
- [22]Novoselov K, Geim A and Morozov S et al 2005 Two-dimensional gas of massless dirac fermions in graphene Nature 438 197–200
- [23]Pines D 1997 The Many Body Problem (Advanced Book Classics, originally published in 1961) (Reading, MA: Addison-Wesley)
- [24]David P 2009 Excitonics heats up Nat. Photonics 3 604–4
- [25]Kruglyak V V, Demokritov S O and Grundler D 2010 Magnonics J. Phys. D 43 264001
- [26]Zhao X-G, Wang Z, Malyi O I and Zunger A 2021 Effect of static local distortions vs. dynamic motions on the stability and band gaps of cubic oxide and halide perovskites Mater. Today 49 107–22
- [27]Editorial 2016 The rise of quantum materials Nat. Phys. 12 105
- [28]Giustino F et al 2020 The 2021 quantum materials roadmap J. Phys.: Mater. 3 042006
- [29]Ohtomo A and Hwang H Y 2004 A high-mobility electron gas at the LaAlO3/SrTiO3 heterointerface Nature 427 423–6
- [30]Bistritzer R and MacDonald A H 2011 Moiré bands in twisted double-layer graphene Proc. Natl. Acad. Sci. 108 12233–7
- [31]Cao Y et al 2018 Correlated insulator behaviour at half-filling in magic-angle graphene superlattices Nature 556 80–4
- [32]Cao Y, Fatemi V, Fang S, Watanabe K, Taniguchi T, Kaxiras E and Jarillo-Herrero P 2018 Unconventional superconductivity in magic-angle graphene superlattices Nature 556 43–50
- [33]Lopes dos Santos J M B, Peres N M R and Castro Neto A H 2007 Graphene bilayer with a twist: electronic structure Phys. Rev. Lett. 99 256802
- [34]Savary L and Balents L 2016 Quantum spin liquids: a review Rep. Prog. Phys. 80 016502
- [35]Volkov B A and Pankratov O A 1985 Two-dimensional massless electrons in an inverted contact JETP Lett. 42 178
- [36]Wang J and Zhang S-C 2017 Topological states of condensed matter Nat. Mater. 16 1062–7
- [37]Qi X-L and Zhang S-C 2011 Topological insulators and superconductors Rev. Mod. Phys. 83 1057–110
- [38]Ghiringhelli G et al 2012 Long-range incommensurate charge fluctuations in (Y,Nd)Ba2Cu3O6+x Science 337 821–5
- [39]Arute F et al 2019 Quantum supremacy using a programmable superconducting processor Nature 574 505–10
- [40]Lejinse M and Flensberg K 2012 Introduction to topological superconductivity and Majorana fermions Semicond. Sci. Technol. 27 124003
- [41]Zázvorka J et al 2019 Thermal skyrmion diffusion used in a reshuffler device Nat. Nanotechnol. 14 658–61
- [42]Song K M et al 2020 Skyrmion-based artificial synapses for neuromorphic computing Nat. Electron. 3 148–55
- [43]Bukov M, D'Alessio L and Polkovnikov A 2015 Universal high-frequency behavior of periodically driven systems: from dynamical stabilization to floquet engineering Adv. Phys. 64 139–226
- [44]Mahmood F, Chan C-K, Alpichshev Z, Gardner D, Lee Y, Lee P A and Gedik N 2016 Selective scattering between Floquet–Bloch and Volkov states in the topological insulator Bi2Se3 arXiv:1512.05714 [cond-mat.mes-hall]
- [45]Flick J, Ruggenthaler M, Appel H and Rubio A 2017 Atoms and molecules in cavities, from weak to strong coupling in quantum-electrodynamics (QED) chemistry Proc. Natl Acad. Sci. 114 3026–34
- [46]Fausti D, Tobey R I, Dean N, Kaiser S, Dienst A, Hoffmann M C, Pyon S, Takayama T, Takagi H and Cavalleri A 2011 Light-induced superconductivity in a stripe-ordered cuprate Science 331 189–91
- [47]Mor S, Gosetti V, Molina-Sánchez A, Sangalli D, Achilli S, Agekyan V F, Franceschini P, Giannetti C, Sangaletti L and Pagliara S 2021 Photoinduced modulation of the excitonic resonance via coupling with coherent phonons in a layered semiconductor Phys. Rev. Res. 3 043175
- [48]Sachdev S 2003 Colloquium: order and quantum phase transitions in the cuprate superconductors Rev. Mod. Phys. 75 913–32
- [49]Sacha K and Zakrzewski J 2017 Time crystals: a review Rep. Prog. Phys. 81 016401
- [50]Vergniory M G, Elcoro L, Felser C, Regnault N, Andrei Bernevig B and Wang Z 2019 A complete catalogue of high-quality topological materials Nature 566 480–5
- [51]Zhang T, Jiang Y, Song Z, Huang H, He Y, Fang Z, Weng H and Fang C 2019 Catalogue of topological electronic materials Nature 566 475–9
- [52]Schmidt J, Marques M R G, Botti S and Marques M A L 2019 Recent advances and applications of machine learning in solid-state materials science NPJ Comput. Mater. 5 83
- [53]Schleder G R, Padilha A C M, Acosta C M, Costa M and Fazzio A 2019 From DFT to machine learning: recent approaches to materials science—a review J. Phys.: Mater. 2 032001
- [54]Canfield P C and Fisk Z 1992 Growth of single crystals from metallic fluxes Phil. Mag. B 65 117
- [55]Kanatzidis M G et al 2005 The metal flux: a preparative tool for the exploration of intermetallic compounds Angew. Chem. Int. Ed. 44 6996
- [56]Stewart G R 2011 Superconductivity in iron compounds Rev. Mod. Phys. 83 1589
- [57]Tong C-J et al 2005 Microstructure characterization of Al x CoCrCuFeNi high-entropy alloy system with multiprincipal elements Metall. Mater. Trans. A 36 881
- [58]Ligon S C et al 2017 Polymers for 3D printing and customized additive manufacturing Chem. Rev. 117 10212
- [59]Parkin S S P et al 2004 Giant tunnelling magnetoresistance at room temperature with MgO (100) tunnel barriers Nat. Mater. 3 862
- [60]Hoppe H et al 2004 Organic solar cells: an overview J. Mater. Res. 19 1924
- [61]Priyadarshini P et al 2021 Structural and optoelectronic properties change in Bi/In2Se3 heterostructure films by thermal annealing and laser irradiation J. Appl. Phys. 129 223101
- [62]Strite S and Morkoç H 1992 GaN, AlN, and InN: a review J. Vac. Sci. Technol. B 10 1237
- [63]Faist J et al 1994 Quantum cascade laser Science 264 553
- [64]Zheng H et al 2004 Multiferroic BaTiO3–CoFe2O4 nanostructures Science 303 661
- [65]Özgür Ü et al 2005 A comprehensive review of ZnO materials and devices J. Appl. Phys. 98 041301
- [66]Li X et al 2009 Large-area synthesis of high-quality and uniform graphene films on copper foils Science 324 1312
- [67]George S M 2010 Atomic layer deposition: an overview Chem. Rev. 110 111
- [68]De Teresa J M (ed) 2020 Nanofabrication: Nanolithography Techniques and Their Applications (Bristol: IOP Publishing)
- [69]Wagner R S and Ellis W C 1964 Vapor–liquid–solid mechanism of single crystal growth Appl. Phys. Lett. 4 89
- [70]Law M et al 2004 Semiconductor nanowires and nanotubes Ann. Rev. Mater. Res. 34 83
- [71]Nietsch K et al 2000 Uniform nickel deposition into ordered alumina pores by pulsed electrodeposition Adv. Mater. 12 582
- [72]Fert A and Piraux L 1999 Magnetic nanowires J. Magn. Magn. Mater. 200 338
- [73]Utke I et al 2008 Gas-assisted focused electron beam and ion beam processing and fabrication J. Vac. Sci. Technol. B 26 1197
- [74]Córdoba R et al 2019 Three-dimensional superconducting nanohelices grown by He+-focused-ion-beam direct writing Nano Lett. 19 8597
- [75]Laurenti M et al 2017 Surface engineering of nanostructured ZnO surfaces Adv. Mater. Interfaces 4 1600758
- [76]Novoselov K S et al 2004 Electric field effect in atomically thin carbon films Science 306 666
- [77]Cao Y et al 2018 Unconventional superconductivity in magic-angle graphene superlattices Nature 556 43
- [78]Lopes W et al 2001 Hierarchical self-assembly of metal nanostructures on diblock copolymer scaffolds Nature 414 735
- [79]Lu W and Lieber C 2007 Nanoelectronics from the bottom up Nature 6 841
- [80]Pendry J B et al 2006 Controlling electromagnetic fields Science 312 1780
- [81]Bradlyn B et al 2017 Topological quantum chemistry Nature 547 298
- [82]Xu S-Y et al 2015 Discovery of a Weyl fermion semimetal and topological Fermi arcs Science 349 613
- [83]Cui J et al 2018 Current progress and future challenges in rare-earth-free permanent magnets Acta Mater. 158 118
- [84]Larcher D and Tarascon J M 2015 Towards greener and more sustainable batteries for electrical energy storage Nat. Chem. 7 19
- [85]Chen Z-G et al 2012 Nanostructured thermoelectric materials: current research and future challenge Prog. Nat. Sci. Mater. Int 22 535
- [86]Dresselhaus M S et al 2007 New directions for low-dimensional thermoelectric materials Adv. Mater. 19 1043
- [87]Bux S K et al 2010 Nanostructured materials for thermoelectric applications Chem. Commun. 46 8311
- [88]Szczech J R et al 2011 Enhancement of the thermoelectric properties in nanoscale and nanostructured materials J. Mater. Chem. 21 4037
- [89]Venkatasubramanian R et al 2001 Thin-film thermoelectric devices with high room-temperature figures of merit Nature 413 597
- [90]Zhao L-D et al 2014 Ultralow thermal conductivity and high thermoelectric figure of merit in SnSe crystals Nature 508 373
- [91]George E P et al 2019 High- entropy alloys Nat. Rev. Mater. 4 515
- [92]Bennett C H and DiVincenzo D P 2000 Quantum information and computation Nature 404 247
- [93]Arute F 2019 Quantum supremacy using a programmable superconducting processor Nature 574 505
- [94]Wendin G 2017 Quantum information processing with superconducting circuits: a review Rep. Prog. Phys. 80 106001
- [95]Kuzum D et al 2013 Synaptic electronics: materials, devices and applications Nanotechnology 24 382001
- [96]Saïghi S et al 2015 Plasticity in memristive devices for spiking neural networks Front. Neurosci. 9 51
- [97]Torrejón J et al 2017 Neuromorphic computing with nanoscale spintronic oscillators Nature 547 428
- [98]Clark R et al 2018 Perspective: new process technologies required for future devices and scaling APL Mater. 6 058203
- [99]Nomura K et al 2004 Room-temperature fabrication of transparent flexible thin-film transistors using amorphous oxide semiconductors Nature 432 488
- [100]Kim K S et al 2009 Large-scale pattern growth of graphene films for stretchable transparent electrodes Nature 457 7230
- [101]Garcia-Cortadella R et al 2021 Graphene active sensor arrays for long-term and wireless mapping of wide frequency band epicortical brain activity Nat. Commun. 12 211
- [102]Baselt D R et al 1998 A biosensor based on magnetoresistance technology Biosens. Bioelectron. 13 731
- [103]Klauk H et al 2007 Ultralow-power organic complementary circuits Nature 445 745
- [104]Gibson D and MacGregor C 2013 A novel solid state non-dispersive infrared CO2 gas sensor compatible with wireless and portable deployment Sensors 13 7079
- [105]Yin W-J et al 2015 Halide perovskite materials for solar cells: a theoretical review J. Mater. Chem. A 3 8926
- [106]Lampert C M 2004 Chromogenic smart materials Mater. Today 7 28
- [107]Sootsman J R et al 2009 New and old concepts in thermoelectric materials Angew. Chem., Int. Ed. 48 8616
- [108]Harb A 2011 Energy harvesting: state-of-the-art Renew. Energy 36 2641
- [109]Ehrlich K 2001 Materials research towards a fusion reactor Fusion Eng. Des. 56–7 71
- [110]Himanen L et al 2019 Data-driven materials science: status, challenges, and perspectives Adv. Sci. 6 1900808
- [111]Haastrup S et al 2018 The computational 2D materials database: high-throughput modeling and discovery of atomically thin crystals 2D Mater. 5 042002
- [112]Chung Y G et al 2019 Advances, updates, and analytics for the computation-ready, experimental metal–organic framework database: CoRE MOF 2019 J. Chem. Eng. Data 64 5985
- [113]Draxl C and Scheffler M 2019 Handbook of Materials Modeling , ed W Andreoni and S Yip (Cham: Springer)
- [114]Kim E et al 2017 Materials synthesis insights from scientific literature via text extraction and machine learning Chem. Mater. 29 9436
- [115]Wilkinson M D et al 2016 The FAIR Guiding Principles for scientific data management and stewardship Sci. Data 3 160018
- [116]Lejaeghere K et al 2016 Reproducibility in density functional theory calculations of solids Science 351 aad3000
- [117]Gulans A et al 2018 Microhartree precision in density functional theory calculations Phys. Rev. B 97 161105(R)
- [118]Jensenet S R et al 2020 Polarized Gaussian basis sets from one-electron ions J. Chem. Phys. Lett. 152 134108
- [119]Nabok D et al 2016 Accurate all-electron G0W0 quasiparticle energies employing the full-potential augmented plane-wave method Phys. Rev. B 94 035418
- [120]Rangel T et al 2020 Reproducibility in G0W0 calculations for solids Comput. Phys. Commun. 255 107242
- [121]Draxl C and Scheffler M 2018 NOMAD: the FAIR concept for big data-driven materials science MRS Bull. 43 676
- [122]Draxl C and Scheffler M 2019 The NOMAD laboratory: from data sharing to artificial intelligence J. Phys.: Mater. 2 036001
- [123]Scheffler M et al 2022 FAIR data enabling new horizons for materials research Nature 604 635
- [124]Greene G et al 2019 Building open access to research (OAR) data infrastructure at NIST CODATA Data Sci. J. 18 30
- [125]Zambrini R and Rius G 2021 Digital and Complex Information (: CSIC)
- [126]Gray M et al 2018 Implantable biosensors and their contribution to the future of precision medicine Vet. J. 239 21
- [127]Qi X L 2011 Topological insulators and superconductors Rev. Mod. Phys. 83 1057
- [128]Kimble H J 2008 The quantum internet Nature 453 1023
- [129]Marchiori E et al 2022 Nanoscale magnetic field imaging for 2D materials Nat. Rev. 4 49
- [130]Maze J R et al 2008 Nanoscale magnetic sensing with an individual electronic spin in diamond Nature 455 644
- [131]Wellman S M et al 2018 A materials roadmap to functional neural interface design Adv. Funct. Mater. 28 1701269
- [132]Goering S et al 2021 Recommendations for responsible development and application of neurotechnologies Neuroethics 14 365
- [133]Errea I 2022 Superconducting hydrides on a quantum landscape J. Phys.: Condens. Matter 34 231501
- [134]Hawryluk R and Zohm H 2019 The challenge and promise of studying burning plasmas Phys. Today 72 34
- [135]Andersen C W et al 2021 OPTIMADE, an API for exchanging materials data Sci. Data 8 217
- [136]Tanaka I, Rajan K and Wolverton C 2018 Data-centric science for materials innovation MRS Bull. 43 659
- [137]Botti R S and Marques M 2021 Roadmap on machine learning in electronic structure Electron. Struct. 4 2021 023004
- [138]Ghiringhelli L M, Vybiral J, Levchenko S V, Draxl C and Scheffler M 2015 Big data of materials science: critical role of the descriptor Phys. Rev. Lett. 114 105503
- [139]Isayev O et al 2017 Universal fragment descriptors for predicting properties of inorganic crystals Nat. Commun. 8 15679
- [140]Jäckle M, Helmbrecht K, Smits M, Stottmeister D and Groß A 2018 Self-diffusion barriers: possible descriptors for dendrite growth in batteries? Energy Environ. Sci. 11 3400
- [141]Ward L, Agrawal A, Choudhary A and Wolverton C 2016 A general-purpose machine learning framework for predicting properties of inorganic materials npj Comput. Mater. 2 16028
- [142]Zhou X et al 2021 High- temperature superconductivity Nat. Rev. Phys. 3 462
- [143]European Commission 2020 Study on the EU's list of critical raw materials Final Report
- [144]Schrödinger E 1952 Are there quantum jumps? (Part II) Br. J. Philos. Sci. III 233
- [145]Feynman R P 1960 There is plenty of room at the bottom Eng. Sci. XXIII 22
- [146]Eigler D M and Schweizer E K 1990 Positioning single atoms with a scanning tunnelling microscope Nature 344 524
- [147]Ash E A and Nicholls G 1972 Super-resolution aperture scanning microscope Nature 237 510
- [148]Pohl D W, Denk W and Lanz M 1984 Optical stethoscopy: image recording with resolution l/20 Appl. Phys. Lett. 44 651
- [149]Betzig E Single Molecules, Cells, and Super-Resolution Optics (: Nobel Lectures) https://nobelprize.org/prizes/chemistry/2014/betzig/lecture/
- [150]Moerner W E Single-molecule Spectroscopy, Imaging and Photocontrol: Foundations for Super-Resolution Microscopy (: Nobel Lecture) www.nobelprize.org/prizes/chemistry/2014/moerner/lecture/
- [151]Hell S 2014 Nanoscopy with Focused Light (: Nobel Lectures) www.nobelprize.org/prizes/chemistry/2014/Hell/lecture/
- [152]Orrit M and Bernard J 1990 Single pentacene molecules detected by fluorescence excitation in a p-terphenyl crystal Phys. Rev. Lett. 65 2716
- [153]Ashkin A 1970 Acceleration and trapping of particles by radiation pressure Phys. Rev. Lett. 24 156
- [154]Fert A The Origin, Development and Future of Spintronics (: Nobel Lectures) www.nobelprize.org/prizes/physics/2007/fert/lecture/
- [155]Grünberg P A From Spinwaves to Giant Magnetoresistance (GMR) and Beyond (: Nobel Lecture) www.nobelprize.org/prizes/physics/2007/grunberg/lecture/
- [156]Vellekoop I M and Mosk A P 2007 Focussing coherent light through opaque scattering media Opt. Lett. 32 2309
- [157]European Commission 2019 The European Green Deal sets out how to make Europe the first climate-neutral continent by 2050, boosting the economy, improving people's health and quality of life, caring for nature, and leaving no one behind (press release) https://ec.europa.eu/commission/presscorner/detail/en/IP_19_6691
- [158]Fan C and Zhao ZSee books such as 2018 Synchrotron Radiation Applications, or Synchrotron Radiation in Materials Science: Light Sources, Techniques, and Applications (: Wiley)
- [159]Eriksson M 2016 The multi-bend achromat storage rings AIP Conf. Proc. 1741 020001
- [160]European Synchrotron Radiation Facility (https://esrf.eu/about/upgrade)
- [161]Madey J M J 1971 Stimulated emission of bremsstrahlung in a periodic magnetic field J. Appl. Phys. 42 1906
- [162]Pellegrini C, Marinelli A and Reiche S 2016 The physics of x-ray free-electron lasers Rev. Mod. Phys. 88 015006
- [163]Kim J G et al 2020 Mapping the emergence of molecular vibrations mediating bond formation Nature 582 520
- [164]Buzzi M, Först M and Cavalleri A 2019 Measuring non-equilibrium dynamics in complex solids with ultrashort X-ray pulses Phil. Trans. R. Soc. A 377 20170478
- [165]Büttner F et al 2021 Observation of fluctuation-mediated picosecond nucleation of a topological phase Nat. Mater. 20 30
- [166]Cerantola V et al 2021 New frontiers in extreme conditions science at synchrotrons and free electron lasers J. Phys.: Condens. Matter 33 274003
- [167]Young L et al 2018 Roadmap of ultrafast x-ray atomic and molecular physics J. Phys. B: At. Mol. Opt. Phys. 51 032003
- [168]Tschentscher Th 2023 Investigating ultrafast structural dynamics using high repetition rate x-ray FEL radiation at European XFEL Eur. Phys. J. Plus 138 274
- [169]Huang S et al 2017 Generating single-spike hard x-ray pulses with nonlinear bunch compression in free-electron lasers Phys. Rev. Lett. 119 154801
- [170]Duris J et al 2020 Tunable isolated attosecond x-ray pulses with gigawatt peak power from a free-electron laser Nat. Photonics 14 30–6
- [171]Praveen Kumar M et al 2020 Attosecond pulse shaping using a seeded free-electron laser Nature 578 386–91
- [172]Huang Z and Ruth R R 2006 Fully coherent x-ray pulses from a regenerative-amplifier free-electron laser Phys. Rev. Lett. 96 144801Kwang-je Kim Y, Shvyd'ko and Reiche S 2008 A proposal for an x-ray free-electron laser oscillator with an energy-recovery linac Phys. Rev. Lett. 100 244802
- [173]Rouxel J R et al 2021 Hard X-ray transient grating spectroscopy on bismuth germanate Nat. Photonics 15 499
- [174]Zewail A H 2000 Femtochemistry: atomic-scale dynamics of the chemical bond J. Phys. Chem. A 104 5660–94
- [175]Ferray M, L'Huillier A, Li X F, Lompre L A, Mainfray G and Manus C 1988 Multiple harmonic conversion of 1064 nm radiation in rare gases J. Phys. B 21 L31–5
- [176]McPherson A, Gibson G, Jara H, Johann U, Luk T S, McIntyre I A, Boyer K and Rhodes C K 1987 Studies of multiphoton production of vacuum-ultraviolet radiation in the rare gases J. Opt. Soc. Am. B 4 595–601
- [177]Schafer K J, Yang B, DiMauro L F and Kulander K C 1993 Above threshold ionization beyond the high harmonic cutoff Phys. Rev. Lett. 70 1599–602
- [178]Corkum P B 1993 Plasma perspective on strong field multiphoton ionization Phys. Rev. Lett. 71 1994–7
- [179]Lewenstein M, Balcou P, Ivanov M Y, L'Huillier A and Corkum P B 1994 Theory of high-harmonic generation by low-frequency laser fields Phys. Rev. A 49 2117–32
- [180]Salières P et al 2001 Feynman's path-integral approach for intense-laser-atom interactions Science 292 902–5
- [181]Krausz F and Ivanov M 2009 Attosecond physics Rev. Mod. Phys. 81 163–234
- [182]Paul P M et al 2001 Observation of a train of attosecond pulses from high harmonic generation Science 292 1689–92
- [183]Chang Z 2016 Fundamentals of Attosecond Optics (Boca Raton, FL: CRC Press)
- [184]Li J, Lu J, Chew A, Han S, Li J, Wu Y, Wang H, Ghimire S and Chang Z 2020 Attosecond science based on high harmonic generation from gases and solids Nat. Commun. 11 2748
- [185]Li J et al 2017 53-Attosecond X-ray pulses reach the carbon k-edge Nat. Commun. 8 186
- [186]Gaumnitz T, Jain A, Pertot Y, Huppert M, Jordan I, Ardana-Lamas F and Wörner H J 2017 Streaking of 43-attosecond soft-X-ray pulses generated by a passively cep-stable mid-infrared driver Opt. Express 25 27506–18
- [187]Johnson A S et al 2018 High-flux soft x-ray harmonic generation from ionization-shaped few-cycle laser pulses Sci. Adv. 4 eaar3761
- [188]Popmintchev T et al 2012 Bright coherent ultrahigh harmonics in the kev x-ray regime from mid-infrared femtosecond lasers Science 336 1287–91
- [189]Takahashi E J, Lan P, Mücke O D, Nabekawa Y and Midorikawa K 2013 Attosecond nonlinear optics using gigawatt-scale isolated attosecond pulses Nat. Commun. 4 2691
- [190]Klas R, Eschen W, Kirsche A, Rothhardt J and Limpert J 2020 Generation of coherent broadband high photon flux continua in the XUV with a subtwo- cycle fiber laser Opt. Express 28 6188–96
- [191]Nomura Y et al 2009 Attosecond phase locking of harmonics emitted from laser-produced plasmas Nat. Phys. 5 124–8
- [192]Wheeler J A, Borot A, Monchocé S, Vincenti H, Ricci A, Malvache A, Lopez-Martens R and Quéré F 2012 Attosecond lighthouses from plasma mirrors Nat. Photonics 6 829–33
- [193]Lépine F, Sansone G and Vrakking M J J 2013 Molecular applications of attosecond laser pulses Chem. Phys. Lett. 578 1–14
- [194]Drescher M, Hentschel M, Kienberger R, Uiberacker M, Yakovlev V and Scrinzi A 2002 Time-resolved atomic inner-shell spectroscopy Nature 419 803–7
- [195]Pazourek R, Nagele S and Burgdörfer J 2015 Attosecond chronoscopy of photoemission Rev. Mod. Phys. 87 765
- [196]Kotur M et al 2016 Spectral phase measurement of a Fano resonance using tunable attosecond pulses Nat. Commun. 7 10566
- [197]Nandi S et al 2020 Attosecond timing of electron emission from a molecular shape resonance Sci. Adv. 6 eaba7762
- [198]Cattaneo L, Pedrelli L, Bello R Y, Palacios A, Keathley P D, Martín F and Keller U 2022 Isolating attosecond electron dynamics in molecules where nuclei move fast Phys. Rev. Lett. 128 063001
- [199]You D et al 2020 New method for measuring angle-resolved phases in photoemission Phys. Rev. X 10 031070
- [200]Seiffert L et al 2017 Attosecond chronoscopy of electron scattering in dielectric nanoparticles Nat. Phys. (N.Y.) 13 766–70
- [201]Jordan I, Huppert M, Rattenbacher D, Peper M, Jelovina D, Perry C, von Conta A, Schild A and Wörner H J 2020 Attosecond spectroscopy of liquid water Science 369 974–9
- [202]Gruson V et al 2016 Attosecond dynamics through a Fano resonance: monitoring the birth of a photoelectron Science 354 734–8
- [203]Autuori A et al 2022 Anisotropic dynamics of two-photon ionization: an attosecond movie of photoemission Sci. Adv. 8 eabl7594
- [204]Lépine F, Ivanov M Y and Vrakking M J J 2014 Attosecond molecular dynamics: fact or fiction? Nat. Photonics 8 195–204
- [205]Sansone G et al 2010 Electron localization following attosecond molecular photoionization Nature 465 763–6
- [206]Neidel C et al 2013 Probing time-dependent molecular dipoles on the attosecond time scale Phys. Rev. Lett. 111 033001
- [207]Calegari F et al 2014 Ultrafast electron dynamics in phenylalanine initiated by attosecond pulses Science 346 336–9
- [208]Barillot T et al 2021 Correlation-driven transient hole dynamics resolved in space and time in the isopropanol molecule Phys. Rev. X 11 031048
- [209]Hervé M et al 2021 Ultrafast dynamics of correlation bands following XUV molecular photoionization Nat. Phys. (N.Y.) 17 327–31
- [210]Attar A R, Bhattacherjee A, Pemmaraju C D, Schnorr K, Closser K D, Prendergast D and Leone S R 2017 Femtosecond x-ray spectroscopy of an electrocyclic ring-opening reaction Science 356 54–9
- [211]Schultze M et al 2013 Controlling dielectrics with the electric field of light Nature 493 75–8
- [212]Moulet A, Bertrand J B, Klostermann T, Guggenmos A, Karpowicz N and Goulielmakis E 2017 Soft x-ray excitonics Science 357 1134–8
- [213]The Nobel Prize organisation 2018 https://nobelprize.org/prizes/physics/2018/summary/
- [214]Danson C et al 2019 Petawatt and exawatt class lasers worldwide High Power Laser Sci. Eng. 7 E54
- [215]Yoon J W, Y G K, Choi I W, Sung J H, Lee H W, Lee S K and Nam C H 2021 Realization of laser intensity over 1023W/cm2 Optica 8 630–5
- [216]Joshi C 2021 New ways to smash particles Sci. Am. 55
- [217]Kneip S et al 2010 Bright spatially coherent synchrotron X-rays from a table-top source Nat. Phys. 6 980–3
- [218]Fiuza F, Swadling G F and Grassi A et al 2020 Electron acceleration in laboratory-produced turbulent collisionless shocks Nat. Phys. 16 916–20
- [219]Wang W, Feng K and Ke L et al 2021 Free-electron lasing at 27 nanometres based on a laser wakefield accelerator Nature 595 516–20
- [220]Silva L O 2017 Boiling the vacuum: in silico plasmas under extreme conditions in the laboratory and in astrophysics Europhys. News 48 For a popular account see 34–7Marklund M and Shukla P Kfor comprehensive reviews, see 2006 Nonlinear collective effects in photon-photon and photon-plasma interactions Rev. Mod. Phys. 78 591Di Piazza A, Müller C, Hatsagortsyan K Z and Keitel C H 2012 Extremely high-intensity laser interactions with fundamental quantum systems Rev. Mod. Phys. 84 1177Gonoskov A, Blackburn T G, Marklund M and Bulanov S S 2022 Charged particle motion and radiation in strong electromagnetic fields arXiv:2107.02161
- [221]Diamond Light Source 2022 https://diamond.ac.uk/Home/About/Vision/Diamond-II.html
- [222]Elettra Sincrotrone Trieste 2023 https://elettra.eu/images/Documents/ELETTRA%20Machine/Elettra2/Elettra_2.0_CDR_abridged.pdf
- [223]Deutsches Elektronen-Synchrotron DESY 2019 PETRA IV, Upgrade of PETRA III to the Ultimate 3D X-ray Microscope, Conceptual Design Report https://bib-pubdb1.desy.de/record/426140/files/DESY-PETRAIV-Conceptual-Design-Report.pdf
- [224]Paul Scherrer Institute 2022 SLS 2.0 https://psi.ch/en/sls2-0
- [225] Source Optimisée de Lumière d'Energie Intermédiaire du LURE (https://synchrotron-soleil.fr/en/news/conceptual-design-report-soleil-upgrade)
- [226]Lee T D 1981 Particle Physics and Introduction to Field Theory (New York: Harwood Academic Publishers)
- [227]Castiglione P, Falcioni M, Lesne A and Vulpiani A 2008 Chaos and Coarse Graining in Statistical Mechanics (Cambridge: Cambridge University Press)
- [228]Cencini M, Cecconi F and Vulpiani A 2009 Chaos: From Simple Models to Complex Systems (Singapore: World Scientific)
- [229]Oono Y 2013 The Nonlinear World (Berlin: Springer)
- [230]Khinchin A I 1949 Mathematical Foundations of Statistical Mechanics (New York: Dover)
- [231]Von Neumann J 2010 Proof of the Ergodic theorem and H-theorem in quantum mechanics Eur. Phys. J. H 35 201
- [232]Goldstein S, Lebowitz J L, Mastrodonato C, Tumulka R and Zanghì N 2010 Normal typicality and von Neumann's quantum ergodic theorem Proc. R. Soc. A 466 3203–24
- [233]Goldstein S, Lebowitz J L, Tumulka R and Zanghí N 2010 Long-time behavior of macroscopic quantum systems Eur. Phys. J. H 35 173
- [234]Emch G and Liu C 2002 The Logic of Thermo-Statistical Physics (Berlin: Springer)
- [235]Gallavotti G (ed) 2008 The Fermi-Pasta-Ulam Problem: A Status Report (Berlin: Springer)
- [236]Benettin G, Chrisodoulidi H and Ponno A 2013 The Fermi–Pasta–Ulam problem and its underlying integrable dynamics J. Stat. Phys. 152 195–212
- [237]Pikovsky A and Politi A 2016 Lyapunov Exponents, A Tool to Explore Complex Dynamics (Cambridge: Cambridge University Press)
- [238]Kaneko K and Bagley R J 1985 Arnold diffusion, ergodicity and intermittency in a coupled standard mapping Phys. Lett. A 110 435
- [239]Falcioni M, Marini Bettolo Marconi U and Vulpiani A 1991 Ergodic properties of high-dimensional symplectic maps Phys. Rev. A 44 2263
- [240]Yamagishi J F and Kaneko K 2020 Chaos with a high-dimensional torus Phys. Rev. Res. 2 023044
- [241]Hurd L, Grebogi C and Ott E 1994 On the tendency toward ergodicity with increasing number of degrees of freedom in Hamiltonian systems Hamiltonian Mechanics , ed J Siemenis (New York: Plenum) p 123
- [242]Mézard M, Parisi G and Virasoro M-A 1987 Spin Glass Theory and Beyond (Singapore: World Scientific)
- [243]Kaneko K and Konishi T 1987 Transition, ergodicity and Lyapunov spectra of Hamiltonian dynamical systems J. Phys. Soc. Japan 56 2993
- [244]Livi R, Politi A and Ruffo S 1986 Distribution of characteristic exponents in the thermodynamic limit J. Phys. A: Math. Gen. 19 2033
- [245]Bunimovich L A and Sinai G 1993 Statistical mechanics of coupled map lattices Theory and Applications of Coupled Map Lattices , ed K Kaneko (New York: Wiley) p 169
- [246]Livi R, Pettini M, Ruffo S and Vulpiani A 1987 Chaotic behavior in nonlinear Hamiltonian systems and equilibrium statistical mechanics J. Stat. Phys. 48 539
- [247]Hénon M 1974 Integrals of the Toda lattice Phys. Rev. B 9 1921
- [248]Cugliandolo L F and Kurchan J 1995 Weak ergodicity breaking in mean-field spin-glass models Philos. Mag. B 71 501–14
- [249]Baldovin M, Vulpiani A and Gradenigo G 2020 Statistical mechanics of an integrable system arXiv:2009.06556
- [250]Flaschka H 1974 The Toda lattice. II. Existence of integrals Phys. Rev. B 9 1924–5
- [251]Mazur P and van der Linden J 1963 Asymptotic form of the structure function for real systems J. Math. Phys. 4 271
- [252]Bohigas O, Giannoni M and Schmit C 1984 Characterization of chaotic quantum spectra and universality of level fluctuations law Phys. Rev. Lett. 52 1
- [253]Vulpiani A 1994 Determinismo e Caos Carocci Editore (: Roma)
- [254]Rigol M and Srednicki M 2012 Alternatives to Eigenstate thermalization Phys. Rev. Lett. 108 110601
- [255]Heisenberg W 1925 Über quantentheoretische Umdeutung kinematischer undmechanischer Beziehungen Z. Phys. 33 879
- [256]Schrödinger E 1926 An ondulatory theory of the mechanics of atoms and molecules Phys. Rev. 28 1049
Footnotes
- 1
One nanometer—1 nm or 10−9 m—is equal to one billionth of a meter.
- 2
Note here the key importance of stabilizing ultimately small magnetic structures. This is one of the very active research fields of magnetism with magnetic textures such as Skyrmions that resembles a hedgehog of spins that is said to be 'topologically protected'.
- 3
To give an idea of the involved timescale, in the Bohr model of the hydrogen atom, the characteristic time associated with the journey of the electron on the first orbit around the nucleus is 150 attoseconds


























































































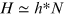


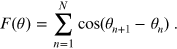





















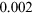

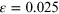

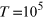









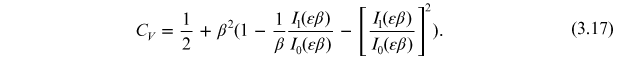


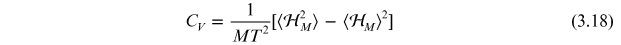



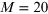




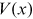
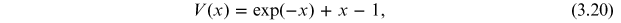



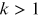

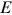
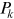



































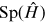
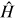
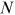
![${ {\mathcal I} }_{E}\in [E-\delta E,E+\delta E]$](https://content.cld.iop.org/books/10__1088_978-0-7503-6342-6/revision9/bk978-0-7503-6342-6ch3ieqn157.gif)





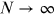








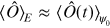




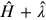
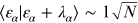

![${ {\mathcal I} }_{E}=[E-\delta E,E+\delta E]$](https://content.cld.iop.org/books/10__1088_978-0-7503-6342-6/revision9/bk978-0-7503-6342-6ch3ieqn180.gif)