What is computation?

The most familiar computations are the numerical calculations that we all do in everyday life: adding up prices, multiplying the length and width of a room to compute its surface, dividing a quantity into equal parts, etc. Most people today have even more occasions for doing numerical calculations in their professional lives. Basic arithmetic on anything that can be quantified is so fundamental that it takes up a significant part of training in the first years of school. Mechanical aids for numerical operations, such as the abacus, have been used for at least 2000 years and perhaps even for much longer.

We do not think much about how we do simple arithmetic operations on small numbers, and in fact we often just recall the result that we have internalized due to frequent use. But as soon as we work on larger numbers, mental calculation becomes a mechanical activity based on rules we have learned. An example for such a rule is: to multiply a number by 9, multiply it by 10 and then subtract the original number.

When operations become too complex to be handled in the head, we turn to pen and paper for a more reliable record of the intermediate results in our calculations. A large number of calculation techniques with pen and paper has been developed in the course of the centuries, ranging from addition via long division to the calculation of cube roots.

As a simple example, consider adding the numbers 173 and 51. One way to do it systematically starts by writing one below the other, adding zeros to the left of the smaller number to make the number of digits equal:

We then process the digits from right to left, starting by adding 3 and 1. We 'know' that the result is 4, because we have done this so often. But for the slightly more complex operation of multiplication, most readers probably remember how they memorized multiplication tables in school—tables that were actually printed in books. To be precise in our description of addition, we will use an equally explicit addition table for one-digit integers:

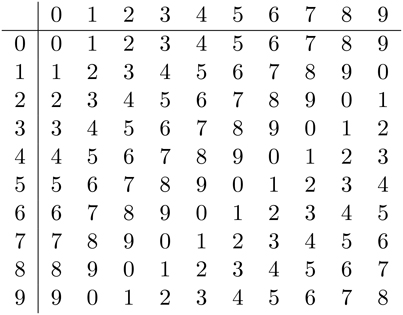
We actually need two such tables, the second one being for the 'carry' digit, which is 1 when the sum of the two digits is 10 or more, and which is 0 otherwise. We note the one-digit sum and the carry digit, and move on to the left to handle the next digit:

This method, and all the other arithmetic operations we use, rely on the positional notation for numbers that is used all around the world today. Any natural number can be written as a sequence of the digits 0 to 9. Another symbol, the minus sign, takes care of negative integers, and one further symbol, either the decimal point or the division slash, makes it possible to express fractions. The rules for arithmetic can then be formulated as rules for manipulating sequences of symbols, as shown above for addition, which can be applied mechanically.

It is indeed important to realize that the method outlined above does not work on numbers, but on a specific representation for numbers. Numbers are an abstract concept, which cannot be manipulated using mechanical rules. Different representations lead to different methods for doing arithmetic. Even though the decimal character string '42', the roman-numeral character string 'XLII', and the English-language character string 'forty-two' refer to the same number, they cannot be manipulated in the same way. In fact, our recipe for addition never refers to numbers. It takes two sequences of digits as input, and produces one sequence of digits as output. Applying the recipe does not require any knowledge of numbers, only the capacity to work with a finite set of symbols and apply rules to them.

A recipe for solving a specific problem by manipulating symbols is called an algorithm. The word is derived from the name of the Persian mathematician al-Khwārizm, who lived in the 9th century. His book describing the 'Indian numbers', which today we call Arabic numerals, introduced our modern decimal notation and its rules for arithmetic into Europe [1]. The use of this system was called 'algorism' in the late middle ages, and later the spelling and meaning transformed into today's 'algorithm'. The positional notation for numbers transformed arithmetic from a difficult craft performed by trained specialists into a routine task that could be mastered by almost everyone.

Today the decimal representation of numbers seems so obvious to us that we often make no difference between a number and its decimal representation. This phenomenon is not limited to numbers. We rarely distinguish carefully between a word and its meaning either, and in quantum physics, to cite an example from science, the confusion between a quantum state and one of its many possible representations is very common. When thinking about computation, it is often important to recall that the Universe of symbols and the Universe of meanings are separate. In computer science, this is known as the distinction between syntax and semantics. Syntax defines which sequences of symbols a particular algorithm deals with, for example 'a sequence of any number of the digits 0 to 9'. Semantics defines how such sequences of symbols are interpreted, such as 'a natural number'. No knowledge of semantics is needed to apply our algorithm for adding two natural numbers, but it is essential to understand what the algorithm does, and in particular which problems it can help to solve.

A symptom of the confusion between numbers and their representations is the popular saying that 'computers work only on numbers'. This is patently false: what today's digital computers work on is sequences of bits, a bit being a symbol from an alphabet containing two symbols. We often choose the digits 0 and 1 to represent this alphabet, suggesting an interpretation as binary numbers, i.e. numbers represented in a positional notation with base 2. The idea that computers work on numbers is mistaken because bits can equally well represent information other than numbers. It is also misleading in another way because it suggests that any number-related problem can be solved by a computer. However, most numbers cannot be represented by sequences of bits and therefore cannot enter in any computation.

It is easy to see that bits can represent any information that can be written as sequences of symbols at all. Suppose we have an alphabet with N symbols, for example the N = 26 letters of the English alphabet. We can then make up a translation table that assigns a unique set of values for five bits to each symbol in our alphabet. With five bits, we have ${2}^{5}=32$ distinct values, so six values will be left unused. Our translation table allows us to encode any English word in terms of bit sequences.

It is less obvious and perhaps even surprising to many readers that most numbers cannot be represented as bit sequences. For natural numbers, there is no problem: any sequence of bits can be interpreted as a natural number in base 2 notation. Inversely, every natural number can be written in base 2 notation, and therefore as a sequence of bits. It is thus possible to define a one-to-one correspondence between natural numbers and bit sequences. In mathematical terminology, the set of natural numbers is isomorphic to the set of bit sequences. Since we can perform computations on sequences of bits, we can perform computations on natural numbers. In fact, any set of values that we wish to do computations on must be isomorphic to the set of bit sequences, or equivalently to the set of natural numbers, or to a subset of such a set. Such sets are called countable. All finite sets are countable: just write down the elements in some order and then write a number below to each element, starting from 1. Infinite sets that are countable are called countably infinite sets.

It is straightforward to see that integers are still countable: use one bit for the sign, and then a natural-number bit sequence for the absolute value. It takes a bit more effort to show that the rational numbers, i.e. the set of all quotients of integers, are countable. By the definition of countability, this requires the assignment of a unique natural number to each rational number. The standard procedure is based on a two-dimensional matrix-like arrangement of the rational numbers:

The entries of this infinite matrix can now be enumerated along diagonals:

A more sophisticated enumeration scheme would skip over each number that is equal to one that already received an index earlier. For example, $2/2$ would be skipped because it is equal to $1/1$.

The proof that the set of real numbers is not countable is more involved, and I will not reproduce it here. Like many other proofs concerning infinite sets, it goes back to Georg Cantor, a German mathematician who laid the foundations of set theory in the late 19th century, and actually provided the first rigorous definition of the real numbers. The complex numbers, being a superset of the real numbers, are also uncountable. There are, however, countable number sets larger than the rational numbers. A well-known one in mathematics is the set of algebraic numbers, defined as the roots of polynomials with integer coefficients. In the context of computation, the largest useful countable subset of the real numbers is the set of computable numbers, which was introduced by Alan Turing in the same 1936 publication as the Turing machine. I will come back to this subject in chapters 2 and 3, because it is of central importance for the use of computation in science.

We can now write down a first definition of computation, which will be refined in chapter 3:

Computation is the transformation of sequences of symbols according to precise rules.

What will need refinement is the 'precise rules', which must be expressed so precisely that a machine can apply them unambiguously.

Once we get rid of the idea that computation is about numbers, we can easily identify other operations that qualify as computations. One example is solving equations by algebraic manipulations. The steps leading from

$$\begin{eqnarray*}&&y+2x=z\end{eqnarray*}$$

to

$$\begin{eqnarray*}&&x=\frac{1}{2}(z-y)\end{eqnarray*}$$

are completely mechanical and can be formulated as an algorithm. The practical evidence is that computers can do the job. Software packages that implement such operations are called computer algebra systems, emphasizing algebraic manipulations. However, computer algebra systems also perform other non-numerical algorithms, for example finding the derivative or integral of an elementary function. The algorithm for computing derivatives is simple and taught in every calculus course. In contrast, the algorithm for computing indefinite integrals is very complicated [2] and was implemented as a computer program only in 1987 [3].

A perhaps more surprising use of computation in mathematics is the validation of proofs. A proof is a sequence of deduction steps, each of which establishes the truth of a statement based on other statements already known to be true and a finite set of rules of logic deduction. In textbooks and mathematical publications, proofs are written concisely for human readers who have a prior knowledge of mathematics. But when all the details are spelled out, proofs consist of nothing but applications of a finite set of deduction rules. These rules are applied to statements that must respect the rules of a formal language. The use of computers to check such detailed proofs is becoming more and more common, both in mathematical research and in industrial applications. This involves writing the proof in some formal language, as a sequence of symbols. The 'proof checking' computation transforms this sequence of symbols into a 'true' or 'false' statement about the proof's validity.

Leaving the narrow scope of mathematics, we find a huge number of domains where computation is applied to textual data. Finding a word in a text is a computation: it transforms the input data (the text and the word to look for) into output data (the position in the text where the word occurs), both of which can be encoded as sequences of symbols. Likewise, aligning two DNA sequences, translating a sentence from English to French, or compiling a Fortran program, are computations in which the data being processed are text. In fact, numbers and text are the two kinds of elementary data from which almost everything else is made up by composition: images are represented as two-dimensional arrays of numbers, dictionaries as sets of word pairs, etc. However, this fundamental role of numbers and text is due to their importance to humans, not computers.

Another kind of data that are becoming increasingly important for scientific computation are graphs, in particular when used to describe networks. Traffic flow, protein interactions in a cell, and molecular structures are all examples of what can be described by graphs. An example of a computation on graphs is a check for cycles. This transforms the input data (a graph) into output data (a list of all cycles in the graph). Encoding graphs, cycles, and lists as sequences of symbols is not as obvious as encoding numbers and text. Humans already represented numbers and text by sequences of symbols long before thinking about computers and computation. The human representation of graphs, on the other hand, takes the form of two-dimensional drawings. The precise techniques for representing graphs as sequences of symbols are beyond the scope of this book, but I will come back to the general question of information representation in computers in section 5.3.2.