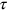The Beer–Lambert law and the gain coefficient
Published August 2022
•
Copyright © IOP Publishing Ltd 2022
Pages 5-1 to 5-11
You need an eReader or compatible software to experience the benefits of the ePub3 file format.
Download complete PDF book, the ePub book or the Kindle book
Abstract
In this chapter, the basic experiment in photonics, the absorption of radiation by any material, is described which follows the Beer–Lambert law. Description of how the absorption coefficient of a material is related to the strength of its gain coefficient is given here. Besides explaining the gain saturation, its application in cavity-ring-down spectroscopy is highlighted.
The amount of light absorbed by a medium can be estimated by measuring the transmission of collimated light. Spontaneous emission spreads in all directions. Therefore, interrelating the quantities associated with the processes of absorption and emission is useful to obtain the decay rates of the excited energy states. This introduces the requirement for a relation between Einstein's A and B coefficients. Since we will deal with the energy density as well as the absorption and emission rates, we will work out the rate equations in this chapter. The measurement of the absorption spectrum of a material—a basic experiment for a student of spectroscopy—is introduced in this chapter. Knowledge of the absorption strength–known as the absorption cross section—is important in establishing whether a material is suitable for use as a gain medium in lasers.
Learning objectives
After reading this chapter, the learner will be able to:
State the concept of absorption and the Beer–Lambert law;
Describe the absorption coefficient;
Define a gain medium;
Explain population inversion and the small-gain coefficient;
Relate the round-trip gain to gain saturation;
Understand the technique of cavity ring-down spectroscopy.
5.1. The Beer–Lambert law
As mentioned in chapter 2, spectroscopy has contributed immensely to the development of modern science, in particular, in ground-breaking experiments in the late 19th and early 20th centuries. One spectroscopic technique deals with the measurement of absorption spectra. For a two-level system, for example with  , the Boltzmann law suggests that at a given temperature, the largest population of molecules lies in the lower energy state (
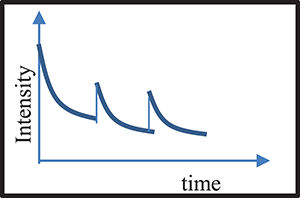
, the Boltzmann law suggests that at a given temperature, the largest population of molecules lies in the lower energy state ( ). Let us look at the experiment shown in figure 5.1. A broadband light source of various frequencies with a constant intensity
). Let us look at the experiment shown in figure 5.1. A broadband light source of various frequencies with a constant intensity  is incident on the sample. The selection of a frequency is achieved using either a prism or a grating spectrograph (known as a monochromator). The sample is considered to be made of infinitesimally thin sheets of thickness
is incident on the sample. The selection of a frequency is achieved using either a prism or a grating spectrograph (known as a monochromator). The sample is considered to be made of infinitesimally thin sheets of thickness  .
.
Figure 5.1. A collimated light beam of intensity  and frequency
and frequency  falls on a detector after passing through the sample with a thickness of
falls on a detector after passing through the sample with a thickness of  .
.
Download figure:
Standard image High-resolution image♣ The term intensity is defined as the power per unit solid angle per unit area of the source (♠ see chapter 10 for details of the solid angle). On the other hand, irradiance is the total power per unit area incident on the body.
The change of intensity  for subsequent sheets of the sample is proportional to their thickness (
for subsequent sheets of the sample is proportional to their thickness ( ) and the incident intensity at the particular sheet (
) and the incident intensity at the particular sheet ( ):
):
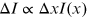
or
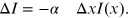
Here,  is the proportionality constant known as the absorption coefficient (in cm−1). It is related to the absorption strength of a material. For a sample in liquid form, it is further described as the product of the concentration (C) and the extinction coefficient (
is the proportionality constant known as the absorption coefficient (in cm−1). It is related to the absorption strength of a material. For a sample in liquid form, it is further described as the product of the concentration (C) and the extinction coefficient ( ) of the sample. The absorbing medium causes a loss of photons from an incident beam of initial intensity
) of the sample. The absorbing medium causes a loss of photons from an incident beam of initial intensity  . The detector is used to monitor the transmitted light intensity (I).
. The detector is used to monitor the transmitted light intensity (I).
♣ In practice, with the help of a beam splitter, two beam paths are generated from the same source for the sample and the reference to measure I and I0, respectively.
We can rearrange the above equations as
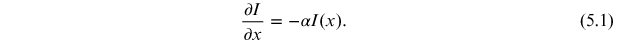
On integrating we obtain the following form of the equation, known as the Beer–Lambert law.

Here,  for liquid solutions. The quantity
for liquid solutions. The quantity  is also known as the optical density (OD) of the sample.
is also known as the optical density (OD) of the sample.
The basic idea is to measure the light transmitted by the sample to find its absorption strength across the frequencies of interest. The effect of the EM wave incident on the medium is schematically shown in figure 5.2. We can see that the amplitude of the incident light wave is reduced after passing through an absorbing medium.
Exercise 5.1. An optical density of unity is obtained for a sample that has a concentration of 0.1 M when the path length used is 1 mm. What are the other values of thickness and concentration that could be be selected to obtain samples with the same optical density?
Solution: The optical density (OD) is defined as  . For the path length (
. For the path length ( ) and the concentration (
) and the concentration ( ) of a sample, we know that its extinction coefficient (
) of a sample, we know that its extinction coefficient ( ) is a fixed quantity (
) is a fixed quantity ( ). Equation (5.2) can be rewritten as
). Equation (5.2) can be rewritten as  , and we see that to maintain the same value of OD, the parameters
, and we see that to maintain the same value of OD, the parameters  and
and  have to be adjusted suitably. Therefore, for the given situation, OD = 1 can be obtained, for example, using (i)
have to be adjusted suitably. Therefore, for the given situation, OD = 1 can be obtained, for example, using (i)  = 0.5 M with a sample path length of 0.2 mm, or (ii)
= 0.5 M with a sample path length of 0.2 mm, or (ii)  = 0.01 M with a path length of 10 mm, and so on.
= 0.01 M with a path length of 10 mm, and so on.
Figure 5.2. Effect of absorption by a medium on the amplitude of an incident EM wave.
Download figure:
Standard image High-resolution image5.2. Absorption coefficient
The irradiance  of a light source at a photon frequency is the power delivered by the source (or energy crossing in unit time) to the unit area of a body. Therefore, in terms of the energy density of the photons
of a light source at a photon frequency is the power delivered by the source (or energy crossing in unit time) to the unit area of a body. Therefore, in terms of the energy density of the photons  , the speed of light
, the speed of light  , and the refractive index
, and the refractive index  of the medium, it is also written as
of the medium, it is also written as  . A change in the irradiance,
. A change in the irradiance,  , is defined as the total number (M) of photons delivered by a source of an area (
, is defined as the total number (M) of photons delivered by a source of an area ( ) per unit time (
) per unit time ( ), as follows:
), as follows:
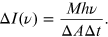
The energy density ( ) of M photons for a volume V, is given by
) of M photons for a volume V, is given by
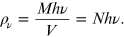
Here,  is number of photons per unit volume. For sufficiently small
is number of photons per unit volume. For sufficiently small  , we can rewrite the change in irradiance within the light beam as
, we can rewrite the change in irradiance within the light beam as
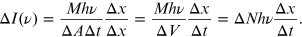
By replacing  by
by  , which denotes the emission frequency between the two levels, we can express
, which denotes the emission frequency between the two levels, we can express  as
as
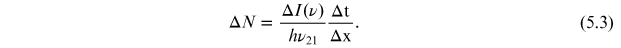
The beam travels through a volume element that has a thickness of  and a unit sectional area of
and a unit sectional area of  . As described in chapter 4, after stimulated absorption rate
. As described in chapter 4, after stimulated absorption rate  ), the molecules from the higher energy state decay to the lower state with a spontaneous emission rate of (
), the molecules from the higher energy state decay to the lower state with a spontaneous emission rate of ( ) and a stimulated emission rate of (
) and a stimulated emission rate of ( ). As shown in figure 5.3, assuming that the spontaneous emission coefficient
). As shown in figure 5.3, assuming that the spontaneous emission coefficient  is very small compared to that due to stimulated emission (
is very small compared to that due to stimulated emission ( ), the net rate of photon loss from the beam per unit volume is given by the following:
), the net rate of photon loss from the beam per unit volume is given by the following:
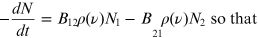
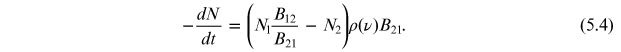
Figure 5.3.
Stimulated absorption and absorption between two energy states  and
and  ;
; 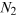 and
and  , respectively, are the corresponding populations.
, respectively, are the corresponding populations.  and
and 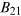 are the coefficients of stimulated absorption and stimulated emission, respectively. The contribution of spontaneous emission has been neglected.
are the coefficients of stimulated absorption and stimulated emission, respectively. The contribution of spontaneous emission has been neglected.
Download figure:
Standard image High-resolution imageEquation (5.3) can be rewritten as
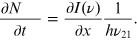
Using equation (5.1), we can rewrite this as
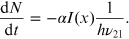
Placing the value of irradiance  , we get,
, we get,
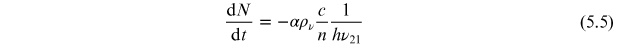
Comparing equations (5.4) and (5.5), and by using  , the absorption coefficient (α) can be written as
, the absorption coefficient (α) can be written as
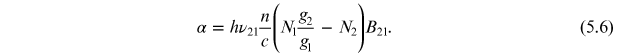
Equation 5.6 relates α to the coefficient of stimulated emission, (B21). We already know from equation (4.13) that B21 is related to the spontaneous emission rate coefficient, (A21).Therefore, if we know the decay time of spontaneous emission ( ) of the system, the stimulated parameters can be estimated. From this relation, it is obvious that for a higher value of the absorption coefficient, the probability of stimulated emission is higher.
) of the system, the stimulated parameters can be estimated. From this relation, it is obvious that for a higher value of the absorption coefficient, the probability of stimulated emission is higher.
5.3. Gain media
We now know that atoms or molecules in the forms of gases, liquids, or solids give rise to spontaneous/stimulated emission when excited. Any suitable material which is capable of emitting with a high quantum yield, and can therefore be used to generate photons, is known as a gain medium. Examples of popular gain media are He–Ne (gas), dye solutions (liquid), and Nd+3:yttrium aluminum garnet (YAG) (solid).
Equation (5.6) gives the absorption coefficient in terms of the populations of the two states involved in the transitions. This equation, when used in combination with the Beer–Lambert law, gives rise to an interesting insight about gain media. We see that the value of  is positive for
is positive for  and becomes negative for
and becomes negative for  . The latter is the situation for population inversion (see the next chapter). For instance, if we replace the negative value of
. The latter is the situation for population inversion (see the next chapter). For instance, if we replace the negative value of  with
with  in equation (5.2), we obtain,
in equation (5.2), we obtain,
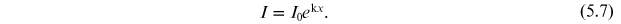
Equation (5.7) indicates that the irradiance increases exponentially with the thickness of the medium for a given value of  . Here
. Here  is known as the small-gain coefficient, i.e. the gain at a given frequency of the emission spectrum.
is known as the small-gain coefficient, i.e. the gain at a given frequency of the emission spectrum.
5.4. Gain coefficient
Let us now consider figure 5.4 in view of equation (5.7) for negative values of the absorption coefficient ( By comparing this figure with figure 5.2, we can schematically observe that the transmitted EM wave has an increased amplitude compared to that of the incident wave.
By comparing this figure with figure 5.2, we can schematically observe that the transmitted EM wave has an increased amplitude compared to that of the incident wave.
Figure 5.4. Schematic of the effect of a negative value of  on the amplitude of the incident EM wave. Compare this with figure 5.2.
on the amplitude of the incident EM wave. Compare this with figure 5.2.
Download figure:
Standard image High-resolution imageWe know that when the absorption strength (also known as the oscillator strength) of the system is high, the amplitude of the interacting incident light is exponentially reduced by passing through the medium, as shown in figure 5.2. In contrast, for negative values of  , the transmitted light gains photons from the gain medium, as shown in figure 5.4. The greater the oscillation strength, the larger the number of photons transmitted by the system. This point shows the importance of a prior estimate of the absorption parameters of a system in order to establish whether it is a suitable laser material for the given wavelength range.
, the transmitted light gains photons from the gain medium, as shown in figure 5.4. The greater the oscillation strength, the larger the number of photons transmitted by the system. This point shows the importance of a prior estimate of the absorption parameters of a system in order to establish whether it is a suitable laser material for the given wavelength range.
♣ Richard Tolman proposed the idea of negative absorption in 1924.
♣ In terms of the transition dipole moment (♠ see equation (2.8)), the oscillator strength (f) is a dimensionless quantity given by  . Here,
. Here,  is the extinction coefficient and the integration is performed over the absorption band.
is the extinction coefficient and the integration is performed over the absorption band.
To obtain a negative value of  (i.e. a positive value of k), we can rewrite equation (5.6) for a particular frequency
(i.e. a positive value of k), we can rewrite equation (5.6) for a particular frequency  as follows:
as follows:
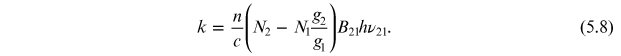
Note that the difference between the populations (assuming an inverted population between  and
and  ) is now given by
) is now given by  . It should be noted that the transmitted amplitude has a net gain of photons and is now given by equation (5.7). This indicates that the amplitude is enhanced exponentially (i.e. amplified!). While k is known as small-gain coefficient, the exponential factor
. It should be noted that the transmitted amplitude has a net gain of photons and is now given by equation (5.7). This indicates that the amplitude is enhanced exponentially (i.e. amplified!). While k is known as small-gain coefficient, the exponential factor  is termed the overall gain coefficient (
is termed the overall gain coefficient ( ) or simply the gain.
) or simply the gain.
From equation (5.8), the stimulated emission cross section ( ) is introduced, as follows:
) is introduced, as follows:
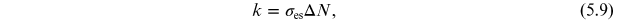
where  . It can also be written in terms of
. It can also be written in terms of  from equation (4.13). Therefore, equation (5.7) can now be rewritten as
from equation (4.13). Therefore, equation (5.7) can now be rewritten as
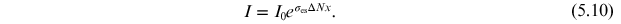
Lasers are also known as optical amplifiers 1 . We note here that an ideal laser requires a single optical transition between two energy levels. In practice, a correction by a spectral width factor is included in equation (5.8) (♠ see the next chapter).
Exercise 5.2. The stimulated emission coefficient of a gain medium is of the order of 10−19 cm2. Assuming no losses, what is the value of the small-gain coefficient if the population inversion in the two states is equal to 1019 cm−3 ?
Solution: Using equation 5.9, we see that the value of k is 1 cm−1.
5.5. Round-trip gain
The value of the small-gain coefficient
 is defined for a stimulated emission transition between two levels. As shown in figure 5.5, we now place the emitter in between two mirrors—a 2D cavity of length L. The reflectivities of the cavity mirrors (1 and 2) are
is defined for a stimulated emission transition between two levels. As shown in figure 5.5, we now place the emitter in between two mirrors—a 2D cavity of length L. The reflectivities of the cavity mirrors (1 and 2) are  and
and  , respectively. Let the initial photon density at mirror 1 be
, respectively. Let the initial photon density at mirror 1 be  . As shown below, after the first reflection, the photon density
. As shown below, after the first reflection, the photon density  is given by the product of
is given by the product of  and the reflectivity of the first mirror:
and the reflectivity of the first mirror:

After traveling the length L, the photon flux ( ) includes the gain of the medium and is given by
) includes the gain of the medium and is given by
Figure 5.5. Schematic of a round trip in a cavity of length L with mirrors (denoted by 1 and 2) of reflectivities  and
and  , respectively. As explained in the text,
, respectively. As explained in the text,  and
and  are the photon fluxes at the mirrors.
are the photon fluxes at the mirrors.
Download figure:
Standard image High-resolution imageSimilarly, after the second reflection at mirror 2, on reaching mirror 1 (by completing a full round trip), the photon flux ( is given by
is given by
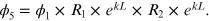
For sustained lasing, the initial and final photon densities must at least be identical. We can now define the round-trip gain (G) as the ratio of the initial and final photon densities, as follows:

Exercise 5.3. Find the length of the gain medium required to provide an overall gain of three for a small-gain coefficient value (k) of 0.4 cm−1 at a given frequency. If the length of the gain medium is doubled, what is the overall gain?
Solution: In the absence of losses, the (overall) gain coefficient is given by  .
.
Using the given values, 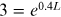 , we obtain
, we obtain 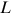 = 2.75 cm. Furthermore, if the gain length (L) is doubled, the value of
= 2.75 cm. Furthermore, if the gain length (L) is doubled, the value of  is 9.02.
is 9.02.
5.6. Gain saturation
Losses in the laser cavity arise from several factors. A few of them are: (i) reflection losses at the mirrors, (ii) scattering and absorption due to impurities in the active medium, and (iii) external parameters. The threshold value of the pump rate includes some of these losses. As a consequence, the value of  is reduced. If we denote all such losses by γ, then the net value of the small-gain coefficient (
is reduced. If we denote all such losses by γ, then the net value of the small-gain coefficient ( ) can be written as
) can be written as
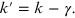
According to equation (5.12), if the value of 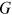 is more than one, the oscillations will grow. However, if
is more than one, the oscillations will grow. However, if  is less than one, the oscillations will die out. Therefore, for the steady state and for continuous-wave operation of the laser, the value of G is taken to be unity. Therefore, equation (5.12) yields
is less than one, the oscillations will die out. Therefore, for the steady state and for continuous-wave operation of the laser, the value of G is taken to be unity. Therefore, equation (5.12) yields
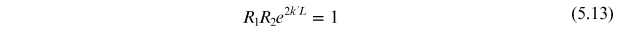
The situation in which the value of  is unity is known as the condition of gain saturation. At the point of gain saturation, the number of photons extracted from the excited population is insignificant in comparison to the number of the excited molecules. This can be further understood as follows: as shown in figure 5.6, at the commencement of laser operation, the round-trip gain is greater the threshold value (indicated by
is unity is known as the condition of gain saturation. At the point of gain saturation, the number of photons extracted from the excited population is insignificant in comparison to the number of the excited molecules. This can be further understood as follows: as shown in figure 5.6, at the commencement of laser operation, the round-trip gain is greater the threshold value (indicated by  in the figure). At the onset of the process of stimulated emission, the population inversion value starts to decrease. The existing losses in the cavity further decrease the gain. These processes affect the net value of the gain. As a result, the net round-trip gain may vary, as shown in figure 5.6. When the gain just balances the losses and the value of
in the figure). At the onset of the process of stimulated emission, the population inversion value starts to decrease. The existing losses in the cavity further decrease the gain. These processes affect the net value of the gain. As a result, the net round-trip gain may vary, as shown in figure 5.6. When the gain just balances the losses and the value of  remains at unity over a period of time, the power stabilizes.
remains at unity over a period of time, the power stabilizes.
Figure 5.6. The output power stabilizes at a gain of unity due to a balance between the losses and the small-gain coefficient in the cavity.
Download figure:
Standard image High-resolution imageFor  , equation (5.13) can be rewritten as
, equation (5.13) can be rewritten as  . In view of equation (5.9), in terms of population inversion, we have
. In view of equation (5.9), in terms of population inversion, we have  , so that
, so that  . Here,
. Here,  is known as the critical inversion.
is known as the critical inversion.
Exercise 5.4. A He–Ne laser tube is 50 cm long and the reflectivities of the two mirrors are 100% and 99%, respectively. Assuming no losses, what is the value of the small-gain coefficient?
Solution: Assuming no losses, the small-gain coefficient is given by
 . For the given values of
. For the given values of  = 50 cm,
= 50 cm,  = 1, and
= 1, and  = 0.99, we obtain the value of
= 0.99, we obtain the value of 
5.7. Applications of the Beer–Lambert law
The absorption coefficient (i.e. the parameter  ) contains vital information about the sample. The absorption strength of the sample (and hence the strength of the transition from the lower to the higher energy level) as well as the population in the upper level immediately after absorption can be estimated from
) contains vital information about the sample. The absorption strength of the sample (and hence the strength of the transition from the lower to the higher energy level) as well as the population in the upper level immediately after absorption can be estimated from  . A number of modern sensing technologies for toxic and explosive materials are based on the measurement of
. A number of modern sensing technologies for toxic and explosive materials are based on the measurement of  . Therefore, the Beer–Lambert law has tremendous application in science and industry. Notice that the thickness of the sample plays an important role. In practical terms, the thickness should be sufficiently small that the intensity at the first layer (
. Therefore, the Beer–Lambert law has tremendous application in science and industry. Notice that the thickness of the sample plays an important role. In practical terms, the thickness should be sufficiently small that the intensity at the first layer ( ) of the sample can be considered to be the same as that at the final layer of the sample. For this reason, the value of the optical density (OD) is generally kept at less than one. However, for extremely weakly absorbing systems, the thickness used can be as large as several meters. As mentioned above, α is a function of the concentration (C) and the extinction coefficient (
) of the sample can be considered to be the same as that at the final layer of the sample. For this reason, the value of the optical density (OD) is generally kept at less than one. However, for extremely weakly absorbing systems, the thickness used can be as large as several meters. As mentioned above, α is a function of the concentration (C) and the extinction coefficient ( ) of the sample. This means that the concentration or thickness of the sample can (and should) be controlled to achieve an OD value near unity. Therefore, by making use of capillaries several meters long or passing the light through the sample multiple times, it is possible to measure the absorption parameters of extremely dilute samples. The technique of cavity ring-down spectroscopy (CRDS), which is based on absorption coefficient, is used to detect explosives at the ppm level (♠ see question 7).
) of the sample. This means that the concentration or thickness of the sample can (and should) be controlled to achieve an OD value near unity. Therefore, by making use of capillaries several meters long or passing the light through the sample multiple times, it is possible to measure the absorption parameters of extremely dilute samples. The technique of cavity ring-down spectroscopy (CRDS), which is based on absorption coefficient, is used to detect explosives at the ppm level (♠ see question 7).
♣ Cavity ring-down spectroscopy (CRDS) measures the decay of light intensity using multiple passes through the sample.
Questions and problems
- 1.(a). What is the significance of the thickness of the sample in Beer–Lambert's law?(b). The optical density of a sample is 0.5 for a path length of 1 cm and a concentration of 1 M. What is the molar extinction coefficient?
- 2.What is a gain medium? In a gain medium, the ratio of the inverted population of the two levels after optical pumping is
 . At 300 K, what wavelength of light can be emitted by the system?
. At 300 K, what wavelength of light can be emitted by the system? - 3.Can absorption by a system be related to amplification by the same system?
- 4.If γ represents the total loss of the resonator, how is the threshold gain coefficient modified in terms of the length of the medium (L) and the reflectivity of the resonator mirrors R1 and R2?
- 5.For a dye laser at 540 nm, the stimulated emission cross section is
 cm−2. The population inversion is
cm−2. The population inversion is  cm−3. Calculate the small-gain coefficient, provided that there are no losses.
cm−3. Calculate the small-gain coefficient, provided that there are no losses. - 6.Define the term 'gain saturation'.
- 7.CRDS is a technique based on the phenomenon of absorption. It is used to quantitatively detect atomic or molecular species with high sensitivity [4]. The sample chamber made of a high finesse cavity (♠ see next chapter) is scanned repetitively thousands of times by a laser pulse. The intensity decay of the tunable transmitted laser pulse, i.e. the ring-down decay time (
 ) decreases exponentially. The decay time, as shown in the figure, is monitored through one of the mirrors. The rate of decrease is proportional to the reflectivity of the mirrors (
) decreases exponentially. The decay time, as shown in the figure, is monitored through one of the mirrors. The rate of decrease is proportional to the reflectivity of the mirrors ( ), the length of the sample chamber, and the absorption coefficient. The ring-down time
), the length of the sample chamber, and the absorption coefficient. The ring-down time  in a round trip
in a round trip  is given by
is given by  . Here, (1 − R) is the reflection loss. Furthermore, a plot of
. Here, (1 − R) is the reflection loss. Furthermore, a plot of  vs laser frequency shows that the sample's
vs laser frequency shows that the sample's  is of the order of
is of the order of  . Calculate the value of
. Calculate the value of  for a length of 0.5 m for a cavity with no absorption (
for a length of 0.5 m for a cavity with no absorption ( What will happen if there are
What will happen if there are  reflections?
reflections?

References
- [1]Rabek J F 1991 Photochemistry and Photophysics vol III (Boca Raton, FL: CRC Press)
- [2]Tolman R C 1924 Duration of molecules in upper quantum states Phys. Rev. 23 693–709
- [3]Berden G, Peeters R and Meijer G 2000 Cavity ring-down spectroscopy: experimental schemes and applications Int. Rev. Phys. Chem. 19 565–607
- [4]O'Keefe A and Deacon D A G 1988 Cavity ring-down optical spectrometer for absorption measurements using pulsed laser sources Rev. Sci. Instrum. 59 2544–51
- [5]Stelmaszczyk K, Fechner M and Rohwetter P et al 2009 Towards supercontinuum cavity ring-down spectroscopy Appl. Phys. B 94 369–73
Footnotes
- 1
In libraries, the books related to lasers can be found categorized as electrical amplifiers in the electrical section.