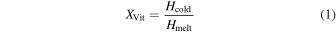Abstract
The analysis of micrometer-sized ice grains emitted into space by Saturn's moon Enceladus suggests that the moon's subsurface ocean may be habitable. However, the formation conditions of these ice grains are largely unknown. Upon cooling, ocean droplets may supercool and then form a crystalline or glassy state, or a mixture of both. To investigate the processes of supercooling and glass formation in Enceladus's ice grains, we performed differential scanning calorimetry experiments with Enceladus-relevant salt mixtures at cooling rates ranging from 5 K minute−1 to ∼1227 K minute−1 and extrapolated our results to faster cooling rates. We modeled the freezing of these solutions and associated mineral assemblages using the thermodynamic chemistry packages PHREEQC and Reaktoro. Our results indicate supercooling of ∼25–30 K upon freezing from Enceladus's saline ocean. Freshly formed ice grains should be predominantly crystalline but contain up to 5% glass. Fast cooling rates and high salt concentrations favor the formation of glasses, potentially enabling the preservation of organics and cells, if present. Salts in the grains crystallize in the following sequence: first phosphate, followed by carbonates, and then chlorides. We find that the recently detected phosphates in Enceladus's ice grains are likely Na2HPO4:12H2O. The pH values appear to vary among individual ice grains, depending on the stage of the freezing process, and these values may slightly differ from the pH of the moon's bulk ocean. Our experiments and models are relevant to other icy worlds with salty water reservoirs in their subsurfaces, such as Jupiter's moon Europa or the dwarf planet Ceres.

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Saturn's moon Enceladus emits into space a plume of gas and ice grains sourced from a global subsurface ocean through near-parallel cracks, named tiger stripes, in the moon's south polar region (C. C. Porco et al. 2006; P. C. Thomas et al. 2016). The emitted material can be sampled within minutes after eruption using mass spectrometry during spacecraft flybys, as was performed by the Cassini mission. An in situ analysis of the plume composition represents a cost-effective means to assess the composition of the moon's subsurface ocean.
Individual micrometer-sized ice grains emitted from Enceladus were measured by Cassini's Cosmic Dust Analyzer, an impact ionization mass spectrometer (R. Srama et al. 2004). These analyses revealed that Enceladus's ocean is salty, likely slightly lower in salinity than Earth's oceans (F. Postberg et al. 2009). However, individual salts (NaCl being the most abundant) appear to partition into different ice grains, with salt concentrations in individual grains ranging from 0.05 M to at least 0.6 M (F. Postberg et al. 2022, 2023). This compositional diversity probably does not reflect the chemical diversity in Enceladus's subsurface ocean, but instead fractionation during droplet freezing inside Enceladus (M. G. Fox-Powell & C. R. Cousins 2021; M. Koga & Y. Sekine 2024).
The ocean is determined to be alkaline, with a pH between ∼8.5 and 10.5 (F. Postberg et al. 2009; C. R. Glein & J. H. Waite 2020; L. M. Fifer et al. 2022), with its fluids reacting hydrothermally with the moon's tidally heated and permeable rocky core (H. W. Hsu et al. 2015; G. Choblet et al. 2017). The ocean contains a diverse complement of organic compounds, with organic mass concentrations detected in individual grains ranging from the parts per million- to the percent-level (F. Postberg et al. 2018; N. Khawaja et al. 2019). These organics include low-mass, volatile, mostly aliphatic organic compounds as well as hydrophobic macromolecules with a variety of functional groups. Recent discoveries of phosphates in emitted ice grains (F. Postberg et al. 2023) and hydrogen cyanide in the gas phase of the plume (J. S. Peter et al. 2023) further enhance the moon's astrobiological potential.
Laboratory experiments predict that even traces of cellular material, if entrapped and preserved, could be detected on Enceladus using single ice grain analysis (F. Klenner et al. 2024). However, while the compositions of the ice grains can be analyzed in some detail, little is known about the formation conditions of these grains, in particular, the liquid–solid phase transition and associated formation of crystalline or glassy amorphous phases. Potential future mission concepts, such as the Enceladus Orbilander (S. M. MacKenzie et al. 2021), will shed more light on Enceladus's potential to host life and the processes occurring in the interior of the moon, including physical and chemical fractionation processes and the formation of ice grains from the moon's ocean. Until then, we can use a combination of experimental and computational studies to better understand the associated physical and chemical processes.
In the 2030s, ice grains from Jupiter's moon Europa will be analyzed by the SUrface Dust Analyzer instrument (S. Kempf et al. 2025) on NASA's Europa Clipper mission (R. T. Pappalardo et al. 2024). Europa harbors a global liquid water ocean (M. G. Kivelson et al. 2000) and likely brine pockets with high concentrations of salts (J. J. Buffo et al. 2020; G. Steinbrügge et al. 2020; E. Lesage et al. 2022; N. S. Wolfenbarger et al. 2022) under or within its ice shell. These salt-rich water reservoirs are potential sources of icy material on the moon's surface. The types of salts and their concentrations in these reservoirs are yet to be constrained, but spectral features in the near UV or visible light at the surface, geochemical modeling, and thermodynamic constraints suggest that NaCl is abundant (M. Y. Zolotov & E. L. Shock 2001; E. C. Thomas et al. 2017; S. K. Trumbo et al. 2019; M. Melwani Daswani et al. 2021; B. Journaux et al. 2023). Other objects in the solar system with potentially NaCl-rich water reservoirs include Jupiter's moon Ganymede (F. Tosi et al. 2023), which is the main target of ESA's Jupiter Icy Moons Explorer (Juice) mission (O. Grasset et al. 2013), and the dwarf planet Ceres (M. C. De Sanctis et al. 2020).
The salt-rich portion of ice grains emitted from Enceladus is believed to form via flash-freezing of ocean droplets (F. Postberg et al. 2009). The cooling rates of these droplets are poorly constrained (see Methods section: Cooling Rate Considerations), but potentially play a major role in controlling the ice grains' potential for cryopreservation (e.g., A. D. Bravenec & D. C. Catling 2023). Cryopreservation is a process of preserving structurally intact organics as well as cells or other biological samples by cooling them to subzero temperatures (e.g., D. E. Pegg 2015; K. A. Murray & M. I. Gibson 2022). On Earth, cryopreservation is a technique commonly used to store and transport cells, tissues, or organs for transplantation or even safeguarding biodiversity (M. J. Taylor et al. 2019; M. Hagedorn et al. 2024).
Different cooling rates tend to lead to different phase states (crystalline, amorphous, or a mixture of both) of the sample (K. A. Murray & M. I. Gibson 2022). Slow cooling rates (for example, <1 K minute−1) favor the formation of ice crystals and can lead to the dehydration of cells or intracellular ice formation, eventually resulting in irreversible cell damage. In contrast, fast cooling rates (for example, >100 K minute−1) are favorable for the formation of amorphous, glassy phases.
Bulk vitrification of pure water, which is full transformation of the sample into a glassy state, requires extremely fast cooling rates (at least 106–107 K minute−1; I. Kohl et al. 2005; M. Warkentin et al. 2013; V. M. Silonov & V. V. Chubarov 2015). For aqueous single solute solutions, the critical cooling rate for bulk vitrification appears to follow an exponential function, with higher solute concentrations leading to lower critical cooling rates. For example, bulk vitrification of a 2 M NaCl solution may only occur at cooling rates exceeding 104–105 K minute−1 (M. Warkentin et al. 2013). Partial vitrification can occur at slower cooling rates, even under dilute conditions. K. Imrichová et al. (2019) observed partial vitrification of dilute NaCl solutions (up to 0.06 M) for cooling rates >100 K minute−1.
However, vitrification is strongly influenced by solute composition. J. D. Toner et al. (2014) reported bulk vitrification of aqueous solutions of 4 molal Ca(ClO4)2 as well as 3.4 and 4.2 molal Mg(ClO4)2 at a cooling rate of only 1 K minute−1. Vitreous MgSO4 hydrates form when 0.1 M MgSO4 solutions are frozen at rates > 10 K min−1 (P. V. Johnson & T. H. Vu 2022).
For successful cryopreservation, bulk vitrification is not necessary. J. Huebinger et al. (2016) demonstrated that cells tolerate the presence of micrometer-sized crystals in their vicinity upon freezing and subsequent warming. Importantly, J. Huebinger et al. (2016) conducted their study with live cells, and, for Enceladus ice grains, even tiny fragments of structurally intact cellular material (∼0.01% of a single cell) within a single grain would be identifiable as biosignatures in spacecraft flybys (F. Klenner et al. 2024).
On Enceladus, there is evidence for both phase states (crystalline and amorphous). While the moon's tiger stripes show a relatively high degree of crystallinity, the region surrounding the tiger stripes shows the largest amount of amorphous ice on the entire surface of the moon (S. F. Newman et al. 2008). However, postdepositional processes, such as micrometeoroid bombardment and radiation, can affect the phase state of ices on the surfaces of solar system objects (M. Famá et al. 2010; R. M. E. Mastrapa et al. 2012).
Measurements by Cassini's Visible and Infrared Mapping Spectrometer (VIMS; R. H. Brown et al. 2004) indicate that the bulk icy material in Enceladus's plume is predominantly crystalline (D. Dhingra et al. 2017). Importantly, VIMS had a low spatial resolution of typically 0.5 mrad per pixel. Most of the time it was not capable of discerning the material erupted from different tiger stripes, nor did this instrument provide information about individual ice grains.
Laboratory experiments by M. G. Fox-Powell & C. R. Cousins (2021) provide evidence that freshly formed ice grains from Enceladus may contain both crystalline phases and glasses that partition during freezing. However, this study did not quantify the amount of glass that formed upon freezing of individual ice grains. Constraining the degree of vitrification of freshly frozen ice grains on Enceladus—that is the amount of glass relative to the amount of crystalline material—will advance our understanding of the ice grains' potential to preserve complex organic structures or cells that may be present in the ocean.
Differential scanning calorimetry (DSC) can be used to measure the heat flow into or out of a sample as a function of temperature or time, thereby recording thermograms from which kinetic and thermodynamic parameters can be derived, such as crystallization and glass transition temperatures. DSC experiments were recently applied to Mars by studying concentrated brines of single-salt perchlorate compositions at cooling rates ranging from 1 to 150 K minute−1 (A. D. Bravenec & D. C. Catling 2023). These brines showed bulk vitrification after staying liquid down to 100 K below the respective liquidus temperature (i.e., supercooling).
Crystalline mineral assemblages that form upon the freezing of ice grains from Enceladus or other icy worlds with liquid reservoirs can be predicted using thermodynamic chemistry packages, such as FREZCHEM (G. M. Marion & J. S. Kargel 2008), PHREEQC (D. L. Parkhurst & C. A. J. Appelo 2013), or Reaktoro (A. M. M. Leal 2015). M. G. Fox-Powell & C. R. Cousins (2021) modeled the freezing of an Enceladus simulant solution at pH 9 and 11 using FREZCHEM and found that, in both cases, the crystallization of H2O ice is followed by sodium carbonates and then chlorides. PHREEQC was recently applied to model the freezing sequence of salts in intrusions in Europa's ice shell (M. Naseem et al. 2023).
In the present study, we use DSC experiments to provide the first comprehensive experimental constraints on the supercooling and glass formation ability of ice grains upon freezing from Enceladus's salty ocean water or NaCl-rich brines on icy worlds. To investigate the formation of salts upon ice grain formation, we model the freezing process of these grains and associated mineral assemblages using two different and complementary thermodynamic chemistry packages, PHREEQC and Reaktoro.
2. Methods
Here, we provide some constraints on the cooling rates of Enceladus's ice grains. We then describe our laboratory experiments and modeling approaches.
2.1. Cooling Rate Considerations
The timescale over which droplets freeze depends on their size (e.g., T. E. Hoffer 1961). Most ice grains emitted from Enceladus are 1–5 μm in diameter (S. Kempf et al. 2018; A. Ershova et al. 2024). However, larger grains may initially form from the ocean spray droplets (D. Cordier et al. 2024), and mechanical or physical splitting may subsequently lead to smaller grains in the observed size range (F. Postberg et al. 2022; M. Koga & Y. Sekine 2024).
Water droplets with a diameter of 12–16 μm can achieve cooling rates of up to 106 K minute−1 when injected into a vacuum (J. D. Smith et al. 2006). While droplets from Enceladus's ocean are likely formed at the triple point of water (6.1 mbar), the environment farther up above the water table, where the droplets freeze, is unlikely to be a vacuum. Bursting gas bubbles (C. C. Porco et al. 2017), boiling (A. P. Ingersoll & M. Nakajima 2016), and/or volatile exsolution (K. L. Mitchell et al. 2024) will produce a mixture of water vapor and gases above the water table that drags the droplets upward though fissures in the moon's ice crust.
Calculations by J. H. Waite et al. (2017) indicate that ice grains (of 1 μm radius) may freeze from evaporative cooling in a vapor in less than 1 ms after droplet formation from Enceladus's ocean. According to different models (M. Nakajima & A. P. Ingersoll 2016; L. M. Fifer et al. 2022), the initial velocity of material forming from Enceladus's ocean is below 5 m s−1. This means that ice grains may freeze within <0.5 cm above the water table. However, the vertical temperature gradient from the water table (∼273 K) to the tiger stripes (∼197 K; J. D. Goguen et al. 2013) through 2–4 km deep fissures in the ice crust (M. Nakajima & A. P. Ingersoll 2016) is relatively gentle, and droplets may stay in a supercooled liquid state for several meters or more.
To account for various possible cooling rates of ice grains that form from Enceladus's ocean and other water reservoirs in the solar system, we consider a wide range of cooling rates from 5 up to 106 K minute−1 for our experiments and models.
2.2. Differential Scanning Calorimetry Experiments
We performed experiments using a DSC Q2000 manufactured by TA Instruments operating at atmospheric pressure from room temperature down to 113.15 K. These low temperatures were achieved by cooling the DSC using the TA Instruments's Liquid Nitrogen Cooling System accessory. The DSC has a sample holder for two samples, used to compare the heat flow into or out of an analyte sample with that of a reference sample. We used helium to purge the sample holder at a flow rate of 25 ml minute−1. The purge gas removes moisture or oxygen that may accumulate over time, and it eliminates localized hot spots.
We prepared fresh aqueous measuring solutions in deionized water according to mass using an analytical balance. Solutions were made in large volumes (50 mL) to ensure high accuracy despite the small sample sizes (typically <100 μL) used in DSC experiments. The following compounds were used for our experiments: NaCl, KCl, Na2CO3, NaHCO3, NH4OH, Na2HPO4, and K2HPO4. More information about the vendors and purities of these compounds can be found in Table A1.
Two salt solutions were prepared, where solution I was relatively dilute compared to solution II. Salt concentrations in solution I (Table 1) were chosen to fall into the lower range of concentrations estimated for Enceladus's ocean based on up-to-date constraints provided by both Cassini measurements and modeling efforts. The moon's ocean is dominated by sodium chloride (100–200 mM NaCl) and 2–5 times less sodium carbonate/bicarbonate (F. Postberg et al. 2009). Concentrations of potassium salts are not well constrained, with Na+-to-K+ ratios ranging in Enceladus's ice grains from ∼3 (L. Nölle et al. 2023) to ∼100 (F. Postberg et al. 2009). We here adopt the cosmic abundance ratio of Na+/K+ = ∼10 (E. Anders & N. Grevesse 1989) for our experiments. NH4++NH3 concentrations are likely between 10 and 100 mM (L. M. Fifer et al. 2022). The recent detection of phosphates in ice grains from Enceladus suggests that phosphate concentrations in the ocean are between 1 and 21 mM (F. Postberg et al. 2023). According to these constraints, the salinity (grams of salt per kilogram of water) of Enceladus ocean lies between ∼8 and 26 g kg−1. For comparison, the salinity of Earth's oceans is ∼35 g kg−1. The salinity of solution I is 14.7 (±0.1) g kg−1.
Table 1. Aqueous Measuring Solutions (20 μL Samples) Used in the DSC Experiments
| Solution No. | Ionic Concentrations | pH | Investigated Cooling Rates | ||||||
|---|---|---|---|---|---|---|---|---|---|
| (mM) | (K minute−1) | ||||||||
| Na+ | K+ | NH4++NH3 | Cl− | HCO3− | CO32− | PO43− | |||
| I | 205 | 20 | 10 | 150 | 45 | 5 | 10 | 9.68 ± 0.03 | 10, 50, 75, 100, 125, 150, 1227 |
| II | 2050 | 200 | 100 | 1500 | 450 | 50 | 100 | 9.15 ± 0.03 | 5, 10, 50, 75, 100, 125, 150, 1227 |
Note. For reference, the pH of Enceladus's ocean is likely between ∼8.5 and 10.5.
Download table as: ASCIITypeset image
Solution II was prepared at salt concentrations 10 times higher than solution I, but in the same abundance ratios of the salts. Experiments with solution II account for ice grain formation from salty, NaCl-rich brines as may occur on Europa, Ceres, or other solar system bodies. The salinity of solution II is 147.0 (±0.2) g kg−1 (Table 1). pH values of both solutions were measured at room temperature using the edge pH meter manufactured by Hanna Instruments.
Aqueous solutions were pipetted into aluminum sample pans (Tzero Alodine) manufactured by TA Instruments. Sample volumes were 20 (±0.2) μL. The pans were hermetically sealed with aluminum lids and weighed before and after each DSC run to an accuracy of ±0.01 mg to ensure the pans remained sealed over the course of the DSC run. Pans that showed leakage were discarded. An example DSC thermogram is shown in Figure 1.
Figure 1. Example thermogram of solution II (Enceladus ocean simulant with 10× solute concentrations), with the lower panel showing expanded detail. The cooling rate was 10 K minute−1. Indicated events (red) are also observed in solution I (our standard Enceladus ocean simulant), but are less pronounced. The melting temperature is the temperature at which a horizontal line (drawn from a local maximum before the second melting valley) intersects with a tangential line drawn from an inflection point within the second melting valley where the derivative equals zero (black lines). Melting of the H2O phase of the sample is included in the second melting valley.
Download figure:
Standard image High-resolution imageTo investigate the effect of different sample volumes on the supercooling and glass forming ability, we additionally performed DSC experiments with both solutions using several sample volumes ranging from 4 to 40 μL at a cooling rate of 150 K minute−1.
The DSC was programmed to automatically load the prepared pans in the sample holder next to an empty reference pan and carry out a typical temperature profile (cooling rate of 10 K minute−1 as example; see Figure 1):
- i.sample equilibrates at 298.15 K,
- ii.cooling ramp with 10.00 K minute−1 to 113.15 K,
- iii.isothermal for 3.00 minutes for sample to equilibrate at 113.15 K,
- iv.heating ramp with 10.00 K minute−1 to 298.15 K,
- v.sample equilibrates at 298.15 K.
We performed our DSC experiments at controlled cooling rates ranging from 5 to 150 K minute−1, where 150 K minute−1 is the maximum achievable cooling rate in the DSC. We additionally achieved a much faster cooling rate by drop quenching the sample pan into liquid nitrogen. The cooling rate of our 20 μL samples was estimated as per M. G. Fox-Powell & C. R. Cousins (2021) by calculating the theoretical heat loss assuming conductive cooling from a 20 μL droplet at room temperature (293 K) that is injected into liquid nitrogen (77 K). This calculation results in a cooling rate of ∼1227 K minute−1. Because our sample pans sank immediately after dropping them into liquid nitrogen, the inverse Leidenfrost effect (R. S. Hall et al. 1969), where rapidly boiling liquid nitrogen may form an envelope of insulating gas around the samples before they sink does not apply to our experiments. When samples were flash frozen, the DSC was programmed to execute steps I (equilibrating at 298.15 K) and II (cooling ramp) of the aforementioned temperature profile with a dummy pan. After completion of step II, we opened the DSC sample holder manually, immediately replaced the dummy pan with the flash frozen sample, and closed the DSC sample holder manually. Steps III (maintaining isothermal at lowest temperature), IV (heating ramp), and V (equilibrating at 298.15 K) were then executed with the flash frozen sample. The DSC records one data point per 0.2 s, and, thus, slow heating rates result in a higher resolution providing more detailed thermograms than fast heating rates. This is why the heating scans of the DSC runs were always performed at 10 K minute−1.
During the DSC runs, the sample pans may cause a thermal lag. Because the capacitance and thermal resistance as a function of the temperature of each pan type are built into the TA Instruments's measurement software, thermal lags caused by the pans were addressed by that software. In the DSC Q2000, all scanning rate dependent thermal lag is automatically corrected. Fast heating rates can cause broadening and distortion of peaks, an effect that persists even in corrected thermograms. To help account for this effect, control DSC runs were performed with pure deionized water (20 μL) at the beginning of each measurement day at three different cooling rates of 10, 50, and 150 K minute−1.
Supercooling is a phenomenon where a material stays liquid below its nominal melting temperature, meaning the degree of supercooling is the temperature difference between the nucleation temperature and the melting temperature of the same sample indicating the metastability of the measured system (e.g., I. Shamseddine et al. 2022).
Cold crystallization is an exothermic event taking place when an amorphous phase crystallizes upon heating and, thus, is often preceded by glass transition features in DSC data (e.g., B. Wunderlich 1958; B. Chen & J. M. Torkelson 2021; K. Ishino et al. 2021). Therefore, the degree of vitrification can be estimated by comparing the enthalpy of cold crystallization (glasses) with that of the melting events of all solid phases (crystals and glasses; Figure 1). A similar approach was applied by K. Imrichová et al. (2019) who performed DSC experiments with NaCl-solutions at concentrations of up to 0.06 M. We calculate the enthalpies by integrating the areas of the reaction peaks (cold crystallization and/or melting events) in the thermograms using the TRIOS software (v5.7) provided by TA instruments. While this method only approximates the enthalpy of material, it is sufficient for showing relative trends given the same instrument conditions. We then calculate the degree of vitrification as follows:
where XVit is the degree of vitrification, Hcold is the enthalpy of the cold crystallization event, and Hmelt is the total enthalpy of all melting events.
2.3. Modeling of Mineral Assemblages
To assess what solid phases were likely present in our DSC experiments, we modeled equilibrium mineral assemblages associated with ice grain formation from Enceladus's ocean or NaCl-rich brines using the thermodynamic chemistry packages PHREEQC (v3; D. L. Parkhurst & C. A. J. Appelo 2013) and Reaktoro (A. M. M. Leal 2015). PHREEQC implements the Pitzer equations that describe ion interactions depending on temperature and composition (K. S. Pitzer 1973). The package models aqueous systems based on equilibrium constants and may encounter buffer under- or overflow at low water content for systems at very low temperatures. Thus, trouble in computing equilibria may occur when the aqueous phase vanishes, for example, when it fully evaporates or fully freezes. To address this potential issue, we also model the freezing process using Reaktoro.
Reaktoro is a modern computational framework for modeling geochemical processes, with support for numerous thermodynamic databases, including those provided by SUPCRT (J. W. Johnson et al. 1992), SUPCRTBL (K. Zimmer et al. 2016), PHREEQC (D. L. Parkhurst & C. A. J. Appelo 2013), NASA-CEA (S. Gordon et al. 1984; B. J. McBride & S. Gordon 1996), and ThermoFun (G. D. Miron et al. 2023). It also offers various thermodynamic activity models for aqueous solutions, such as Davies, Debye–Hückel and its variants, Helgeson-Kirkham-Flowers, Pitzer, and Extended UNIQUAC (see A. M. M. Leal et al. 2025), and equations of state for gases, including Peng–Robinson, Redlich–Kwong, and Soave–Redlich–Kwong. Reaktoro calculates the chemical equilibrium of geochemical systems using a Gibbs energy minimization algorithm (A. M. M. Leal et al. 2017), which can potentially handle the complete disappearance of an aqueous phase due to either evaporation or freezing. It is developed in C++ for performance reasons, with a Python interface provided for convenience. In this study, we utilized the Python interface of Reaktoro for the simulations.
For our models, we used the frezchem.dat database (J. D. Toner & R. S. Sletten 2013), which is a direct conversion of sulfate, chloride, carbonate, and proton-hydroxide data from the FREZCHEM software, a geochemical model for aqueous subzero temperature chemistry (G. M. Marion & J. S. Kargel 2008). Because the frezchem.dat database lacks phosphorus and some nitrogen species, both of which appear to exist in Enceladus's ocean (L. M. Fifer et al. 2022; F. Postberg et al. 2023), we added the following solid phases to the frezchem.dat database for use in our models: Na(H2PO4), Na(H2PO4)(H2O), Na(H2PO4)(H2O)2, Na2(HPO4), Na2(HPO4)(H2O)2, Na2(HPO4)(H2O)7, Na2(HPO4)(H2O)12, Na3PO4, NH4Cl, NH4HCO3, NH3(H2O), and NH3(H2O)2. Analytical expressions for the temperature dependence of equilibrium constants of sodium phosphate species were taken from J. D. Toner & D. C. Catling (2020). Pitzer parameters of phosphorus-containing ion interactions were taken from T. Scharge et al. (2013) and T. Scharge et al. (2015). Analytical expressions for the temperature dependence of equilibrium constants and Pitzer parameters of nitrogen-containing species were taken from G. M. Marion et al. (2012). Enthalpies, activity-coefficient parameters, and analytical expressions for the temperature dependence of equilibrium constants of associated solution species were taken from other established PHREEQC databases, namely, minteq.dat (J. D. Allison et al. 1991) and wateq4f.dat (J. W. Ball & D. K. Nordstrom 1991). As nitrogen may be abundant in Enceladus's ocean as a dissolved gas, we added NH3 data from the phreeqc.dat database. The NH3 data set includes analytical expressions for the temperature dependence of the equilibrium constants, critical temperature and pressure, and the acentric factor of the gas. Our newly extended frezchem.dat database can be found in the online repository Zenodo via doi:10.5281/zenodo.15009033.
Using our extended database, we modeled the freezing process of 1 kg of both solution I and solution II at pressures from 6.1 mbar (triple point of water) to 20 bar in steps of 0.055 K in PHREEQC and in steps of 0.070 K in Reaktoro. The charge balance in our PHREEQC simulations was achieved by allowing the pH—the balance of H+ and OH− in the system—to equilibrate. With our simulations, we can track the precipitation of compounds from the solutions, the evolution of the pH in the liquid solutions, and the amount of residual liquid water in the system.
3. Results
3.1. Supercooling
Nucleation temperatures and the degree of supercooling were derived from the recorded thermograms at cooling rates from 10 to 150 K minute−1. The degree of supercooling is the temperature difference of the nucleation temperature and the melting temperature (Figure 1). Because of the applied measurement protocol for the flash frozen samples (see Methods: Differential Scanning Calorimetry Experiments; Figure A1), no meaningful cooling ramp and, thus, no nucleation temperature, was recorded for the flash frozen samples. With an increasing cooling rate, the nucleation temperature of solution I and solution II decreases, and the degree of supercooling increases (Table 2). We note that, at the fastest cooling rate of 150 K minute−1, the nucleation temperature increased, and the degree of supercooling decreased compared to the preceding measurement at a cooling rate of 125 K minute−1. The same behavior was also observed in pure H2O samples (Table A2). We cannot rule out that this behavior is due to an instrumental effect of our DSC because faster cooling rates are generally expected to produce higher degrees of supercooling (B. J. Mason 1958; I. Shamseddine et al. 2022). However, a similar behavior with faster cooling rates leading to lower degrees of supercooling as compared to slower cooling rates of H2O was also reported in another study (N. R. Gokhale 1965).
Table 2. Cooling Rate versus Nucleation Temperature and Degree of Supercooling for Solution I and Solution II (20 μL Sample)
| Cooling Rate | Nucleation Temperature | Degree of Supercooling | ||
|---|---|---|---|---|
| (K minute−1) | (K) | (K) | ||
| Solution I | Solution II | Solution I | Solution II | |
| 10 | 253.90 | 248.93 | 16.26 | 10.43 |
| 50 | 253.39 | 248.58 | 16.80 | 10.77 |
| 75 | 253.10 | 248.37 | 17.05 | 10.98 |
| 100 | 253.10 | 248.35 | 17.14 | 11.00 |
| 125 | 253.07 | 248.07 | 17.17 | 11.16 |
| 150 | 253.44 | 248.33 | 16.86 | 11.07 |
Note. The degree of supercooling refers to the second melting valley (see Figure 1). The uncertainty of the nucleation temperatures is ±0.01 K. The uncertainty of the degrees of supercooling is ±0.15 K.
Download table as: ASCIITypeset image
Higher salt concentrations generally lead to lower nucleation temperatures, so 10 times higher salt concentrations in solution II lead to ∼5 K lower nucleation temperatures than in solution I. The higher the salt concentration in the sample, the lower the degree of supercooling of the measured sample (Tables 2, A2).
Different sample volumes were tested during this study (4–40 μL), which influenced the degree of supercooling, with smaller samples having a higher degree of supercooling than larger samples. To bring our experiments into better context with ice grains that form from Enceladus's ocean droplets, we calculated the diameter of our liquid samples assuming a spherical shape. We find that the increase in supercooling with decreasing droplet diameter follows a linear function for both solution I and solution II (Figure 2). Assuming the droplets are a maximum of a few hundred micrometers in diameter upon freezing (D. Cordier et al. 2024), they should experience a degree of supercooling of ∼25–30 K (Figure 2).
Figure 2. Degree of supercooling of solution I and solution II as a function of droplet diameter derived from DSC experiments with a cooling rate of 150 K minute−1. The uncertainty of the degrees of supercooling is ±0.15 K. The droplet diameter was calculated with an accuracy of ±0.03 mm.
Download figure:
Standard image High-resolution image3.2. Glass Formation
We observe cold crystallization events in thermograms recorded from both solutions I and II at all investigated cooling rates (Figure 1). The degree of vitrification (glass formation) depends on the applied cooling rate and the salinity of the solution (Figure 3). Fast cooling rates produce more glass in our samples than slow cooling rates. Solution II (more salt) forms more glass than solution I (less salt) at all investigated cooling rates.
Figure 3. Degree of vitrification as a function of cooling rate and salinity. The salinity of solution I is ∼14.7 g kg−1. The salinity of solution II is ∼147 g kg−1. Data points are fitted and extrapolated to faster cooling rates using exponential functions (orange and light blue curves). For reference, the estimated salinity range of Enceladus's ocean lies between ∼8 and 26 g kg−1.
Download figure:
Standard image High-resolution imageIn our experiments, the differences in glass content between both solutions decrease with increasing cooling rate. For example, at a cooling rate of 10 K minute−1, solution II forms ∼230 times more glass than solution I, at a cooling rate of 100 K minute−1; it is 38 times more glass, and for the flash frozen sample (1227 K minute−1), it is 29 times more glass (Figure 3). In other words, salinity affects the glass content more at slow cooling rates.
For Enceladus, the glass content in individual, freshly formed grains ranges from approximately 0.3%–5% correlated with the cooling rate of the grains (light blue curve in Figure 3). Ice grains that form from a high-salinity, NaCl-dominated water reservoir, as it possibly occurs on Europa, Ceres, or other icy bodies, can have a glass content of 15%–35% or more, depending on the salinity of the reservoir and the cooling rate (orange curve in Figure 3).
The degree of vitrification was not significantly affected using different sample volumes from 4 to 30 μL (Table 3). A notable increase in glass content was observed from 30 μL to the largest sample volume of 40 μL: while the degree of vitrification increased by ∼100% in solution I, it increased by ∼17% in solution II.
Table 3. Sample Volume versus Degree of Vitrification of Solution I and Solution II at a Cooling Rate of 150 K minute−1
| Sample Volume | Solution I—Degree of Vitrification | Solution II—Degree of Vitrification |
|---|---|---|
| (μl) | (%) | (%) |
| 4 | 0.41 ± 0.15 | 20.8 ± 0.5 |
| 10 | 0.67 ± 0.15 | 20.9 ± 0.5 |
| 20 | 0.59 ± 0.15 | 20.4 ± 0.5 |
| 30 | 0.60 ± 0.15 | 20.6 ± 0.5 |
| 40 | 1.23 ± 0.15 | 24.1 ± 0.5 |
Note. Uncertainties are from the peak integrations using the TRIOS software, i.e., where the user defines the onset and end points for each integration (see Methods section: Differential Scanning Calorimetry Experiments).
Download table as: ASCIITypeset image
We note that a melting event occurs in thermograms of all flash frozen samples at ∼139 K (Figure A1). This melting event is not observed for any of the slower cooling rates.
3.3. Mineral Assemblages
To predict mineral assemblages precipitating from Enceladus's ocean upon ice grain formation, we modeled the freezing process of both solution I and solution II with PHREEQC and Reaktoro. In the investigated pressure range (6.1 mbar–20 bar), the precipitation temperatures of individual salts vary by less than 0.3 K (Figure A2). Thus, we only describe in detail the results for an example pressure of 3.1 bar, which represents the case of ice grain formation in the shallow subsurface of an icy moon.
Both the PHREEQC and Reaktoro modeling approaches produce consistent results (Figures 4, 5). In contrast to PHREEQC, Reaktoro could produce extremely small amounts of minerals (<10–16 mol). These values should be interpreted from a mathematical point of view in most cases, as Reaktoro calculations strive to produce an exact mass conservation for chemical elements and electric charge. In both solutions, the precipitation of salts follows the same sequence, which is first Na2HPO4:12H2O (disodium phosphate dodecahydrate), followed by the carbonates NaHCO3 (nahcolite) and Na2CO3:10H2O (natron), and then NaCl:2H2O (hydrohalite) and KCl (sylvite). H2O ice starts to crystallize at 272.37 K (PHREEQC) or 272.34 K (Reaktoro) in solution I and at 266.26 K (PHREEQC) or 266.25 K (Reaktoro) in solution II. For both solutions, no nitrogen-bearing phase precipitates until the simulation stops. PHREEQC's simulations stop at a temperature of 246.66 K for both solutions while Reaktoro's simulations stop at a temperature of 246.65 for both solutions.
Figure 4. Precipitating mineral assemblages (top), pH evolution (center), and residual liquid water (bottom) upon freezing of solution I at 3.1 bar. Left panels show PHREEQC simulations; right panels show Reaktoro simulations.
Download figure:
Standard image High-resolution imageFigure 5. Precipitating mineral assemblages (top), pH evolution (center), and residual liquid water (bottom) upon freezing of solution II at 3.1 bar. Left panels show PHREEQC simulations; right panels show Reaktoro simulations.
Download figure:
Standard image High-resolution imageIn solution II, disodium phosphate dodecahydrate is saturated, and, thus, this salt precipitates immediately when the simulations start at 278.15 K. Interestingly, disodium phosphate dodecahydrate is the only phosphate that precipitates from both solutions. Only for acidic compositions with pH values below 4, Na(H2PO4):2H2O would precipitate instead of disodium phosphate dodecahydrate (Table A4, Figure A3).
The predicted pH values of solution I and II at the start of the simulations (at 278.15 K) are 9.64 and 9.25, respectively. For comparison, the measured pH values of the freshly prepared solutions in the laboratory were 9.68 ± 0.03 and 9.15 ± 0.03 (Table 1).
The pH values of the liquid solutions change throughout the freezing process when different phases crystallize. In solution I, the pH rises by ∼0.1 when the liquid solution cools. As soon as the first phase crystallizes (H2O ice), the ionic strength of the solution increases, and the pH drops by ∼0.3 within 6 K. Following crystallization of nahcolite starting at 266.20 K (PHREEQC) or 266.18 K (Reaktoro), the pH rises by ∼0.25 within 3 K. Then, natron precipitates, and the pH continues to rise. The pH of solution I at the end of the simulations is 9.90 (Figure 4).
In solution II, the pH continuously rises throughout the freezing process. The end pH is 9.90. The steepest increase in pH (∼0.25 within 3 K) is observed when H2O ice and nahcolite precipitate simultaneously (Figure 5).
As expected, the amount of residual water decreases throughout the freezing process, with the most notable decrease occurring in the late stage of the crystallization for temperatures <250 K. We note that ∼4 g of solution I and 36 g of solution II (out of 1000 g) are still liquid when the simulations stop. These remaining liquids near complete freeze have very high ionic strengths (Figures A4, A5).
4. Discussion
4.1. Supercooling and Cooling Rates
In our experiments, we systematically measured the degree of supercooling of NaCl-dominated solutions and investigated the effects of sample volume, salinity, and cooling rate on the supercooling ability. We find that the degree of supercooling depends linearly on the sample volume, with smaller samples having a higher degree of supercooling than larger samples (Figure 2).
Because the samples are in contact with the pans during the DSC experiments, the mode of nucleation is heterogeneous and specific to the DSC pans. Thus, in our experiments, the degree of supercooling scales linearly with the exposure of the sample to the DSC pan. The formation of ice grains on Enceladus might involve both heterogeneous and homogeneous nucleation, depending on the ice grain type and the underlying formational processes. However, we note that, in nature, heterogeneous nucleation often dominates homogeneous nucleation (e.g., X. Y. Liu 2000).
In the framework of classical nucleation theory, one would expect that a higher salinity generally leads to a higher degree of supercooling of water. However, for our samples, we find that a higher salinity leads to a lower degree of supercooling before freezing (Table 2). A possible explanation for this observation is that the nucleating phase (and/or the phase represented by the second melting valley; see Figure 1) is not pure H2O ice but rather contains a salt-bearing solid. This explanation is supported by the broad appearance of the second melting valley, possibly representing different phases (including salts and H2O). Another possible explanation could be interactions with our DSC pans (see Section 2.2), meaning that surface interactions are at play that stimulate heterogeneous nucleation. We note that, in the presence of nucleation substrates, select solutes are found to decrease the degree of supercooling of water (K. E. Blow et al. 2024). Interestingly, in soil, an increase in salinity lowers the degree of supercooling because salt ions can promote the growth of crystal embryos (K. Li et al. 2024).
The difference in supercooling ability between samples of different salinities decreases with decreasing sample volume so that the degree of supercooling in small samples (<300 μm in diameter) is nearly identical in experiments with both solutions (Figure 2). Cooling rates only marginally influence the degree of supercooling (Table 2), with faster cooling rates resulting generally in a slightly higher degree of supercooling than slower cooling rates. Importantly, the degree of supercooling for both solutions increases by less than 1 K at the cooling rates achieved with our DSC (from 10 to 150 K minute−1).
D. Cordier et al. (2024) calculated that droplets that form from Enceladus's ocean can reach sizes of tens to hundreds of micrometers before freezing. Therefore, ice grains from Enceladus, and probably also other icy worlds, should experience a similar degree of supercooling that does not depend on the salinity of the water reservoir. According to our experiments, Enceladus's ocean droplets that are <500 μm in size will experience supercooling of 25–30 K (Figure 2).
Cooling rates of droplets from Enceladus's ocean are poorly constrained, but likely play an important role in assessing the ice grains' potential for cryopreservation (e.g., A. D. Bravenec & D. C. Catling 2023). Considering the degree of supercooling that these droplets experience before freezing, we can describe two different scenarios for ice grain formation: rapid freezing versus slow freezing.
For the rapid freezing scenario, we adopt the approach from J. H. Waite et al. (2017) to calculate the freezing time of ocean droplets that cool evaporatively, but we consider that ocean droplets from Enceladus are likely to be tens of micrometers in diameter before freezing (D. Cordier et al. 2024): The net evaporative flux of water at 273.15 K is 0.1 kg m−2 s−1 (J. H. Waite et al. 2017). Therefore, based on the surface area of a spherical droplet of 10–100 μm in diameter, which is 3.1 × 10–10–3.1 × 10–8 m2, respectively, the droplets' evaporation rate is 3.1 × 10−11–3.1 × 10−9 kg s−1. Because the enthalpy of vaporization of water (2257 kJ kg−1) is ∼7 times larger than the enthalpy of fusion at 273.15 K (334 kJ kg−1), 14% of the droplet's mass will evaporate before freezing. The resulting evaporated mass is 7.3 × 10–14–7.3 × 10–11 kg. Taking the evaporated masses and the calculated evaporation rates, the droplets freeze within 2.4–24 ms. Assuming the droplets experience 25–30 K supercooling before freezing (see Results section: Supercooling), the cooling rate for droplets from Enceladus's ocean upon ice grain formation would be 6.3 × 104–7.5 × 105 K minute−1.
In the slow freezing scenario, we consider that the droplets/ice grains experience a linear temperature gradient from the water table (273 K) to the tiger stripes (197 K; J. D. Goguen et al. 2013) over 2–4 km, which is the approximate distance for droplets/ice grains to travel through Enceladus's ice shell to the plume outlet (M. Nakajima & A. P. Ingersoll 2016). If droplets supercool by 25–30 K before freezing, and assuming they remain in thermal equilibrium with the temperature gradient, they will stay in a liquid metastable state for ∼700–1600 m. While the initial velocity of the droplets is relatively low, probably 2–3 m s−1 (M. Nakajima & A. P. Ingersoll 2016; L. M. Fifer et al. 2022), ice grains are launched from Enceladus's tiger stripes at speeds of around 100–200 m s−1 (J. Schmidt et al. 2008; M. M. Hedman et al. 2009; A. Ershova et al. 2024). However, within the first half of their travel distance (1–2 km), the droplets or ice grains' velocity only increases up to ∼10 m s−1 (M. Nakajima & A. P. Ingersoll 2016). Assuming the droplets pass the region in which they cool and freeze with an average velocity of, for example, 6 m s−1, they will travel for 117–267 s before they freeze completely, resulting in a cooling rate of 6–15 K minute−1.
Perhaps the real cooling rates of ice grains from Enceladus's ocean lie between the two described scenarios. In our DSC experiments, we covered a wide range of cooling rates ranging from 5 to 1227 K minute−1. This range covers the cooling rates that we calculated for the slow freezing scenario and up to 2 orders of magnitude faster cooling rates. Faster cooling rates, including those calculated for the rapid freezing scenario, must be extrapolated.
Our laboratory experiments are only the first step toward understanding the cooling rate of ice grains from Enceladus and other icy worlds. Critical information about the cooling rate of the grains can be acquired in the future with, for example, capable spaceborne instrumentation conducting nondestructive spectroscopic measurements of the emitted plume material. These measurements will also help determine the degree of vitrification of the emitted ice grains in much more detail than it was achieved with Cassini's VIMS instrument (D. Dhingra et al. 2017).
4.2. Vitrification and Cryopreservation
While supercooling is primarily controlled by the sample volume, the degree of vitrification depends mostly on the cooling rate and the salinity of the water reservoir. The salinity of Enceladus's ocean is likely in the range of 8–26 g kg−1 (see Methods: Differential Scanning Calorimetry Experiments), and, thus, we estimate the degree of vitrification of individual ice grains that are freshly formed from Enceladus's ocean droplets to be between 0.3% and 5%, depending on the true cooling rate (Figure 3). Our experiments demonstrate that these ice grains are mostly crystalline (at least 95%), which agrees with Cassini VIMS measurements of ice grains in Enceladus's plume (D. Dhingra et al. 2017). The salinity of the solution appears to control the degree of vitrification much stronger at relatively slow cooling rates (≤100 K minute−1) than at fast cooling rates (>100 K minute−1). For example, solution II forms ~40× more glass than solution I at a cooling rate of 100 K minute−1, but only ~20× more glass at a cooling rate of 104 K minute−1 (Figure 3).
Our results are relevant to other icy worlds where ice grain formation from NaCl-dominated brines may occur, such as Jupiter's moon Europa (J. J. Buffo et al. 2020; G. Steinbrügge et al. 2020; E. Lesage et al. 2022; N. S. Wolfenbarger et al. 2022) or dwarf planet Ceres (M. C. De Sanctis et al. 2020). According to our experiments, these ice grains should have a higher degree of vitrification of at least 15%–35%, or more if the salinity is greater than 147 g kg−1 and the grains cool fast (Figure 3).
Bulk vitrification of pure H2O requires very fast cooling rates of at least 106–107 K minute−1 (I. Kohl et al. 2005; M. Warkentin et al. 2013; V. M. Silonov & V. V. Chubarov 2015). Therefore, it is likely that the H2O phase in our samples (and probably also on an icy world) freezes in a crystalline form, and the salts, or a subset of the salts, account for the amorphous component. This interpretation is supported by the observation that solution II is driven to a higher degree of vitrification than solution I.
On an icy world, the degree of vitrification in freshly formed ice grains can be modified when the grains rise through the fissures in the ice shell (as is the case for Enceladus), for example, due to water vapor that condenses onto the grains. The glass content can also be modified after the grains are exposed to space (in the plume or at an icy world's surface), for example, due to radiation. While water vapor that slowly condenses onto the grains may reduce the ratio of glassy phases to crystalline phases, radiation is likely to increase that ratio (M. Famá et al. 2010).
Time can modify the phase state of ices on bodies in the solar system. Down to ∼75 K—which is the average temperature on Enceladus's surface (J. R. Spencer et al. 2006) and the minimum temperature achieved in our experiments—ice would always convert into a crystalline state over time (R. M. E. Mastrapa et al. 2012). At solar system surfaces with even lower temperatures, such as Neptune's moon Triton (B. Conrath et al. 1989), amorphous ice should remain in an amorphous state over solar system-relevant timescales (R. M. E. Mastrapa et al.2012).
For cryopreservation of complex organic structures or even cells, the formation of glassy phases is advantageous over crystalline phases (e.g., K. A. Murray & M. I. Gibson 2022). The identification of various organic compounds with different functional groups in Enceladus's ice grains (F. Postberg et al. 2018; N. Khawaja et al. 2019) demonstrates that at least some structural information of these compounds is incorporated and preserved in the grains upon formation and eruption. Studies show that biologically important molecules, such as amino acids or fatty acids (e.g., F. Klenner et al. 2020), and even cellular material (M. Dannenmann et al. 2023; F. Klenner et al. 2024) would be identifiable in emitted ice grains using mass spectrometry, providing that these compounds exist in Enceladus's ocean and get incorporated into the grains.
U. Demirci & G. Montesano (2007) demonstrated that cells survive in bulk vitrified droplets down to 77 K. In their experiments, the authors encapsulated between one and four cells in 70 μm diameter droplets and successfully vitrified these droplets via ejection into liquid nitrogen. After thawing, >90% of all cells were viable (U. Demirci & G. Montesano 2007). However, for cryopreservation of cells, bulk vitrification is not necessary because cells tolerate the presence of tiny crystals (up to ∼2 μm) in their vicinity (J. Huebinger et al. 2016). Under conditions relevant to icy moons, the presence of hydrated salts in ice grains appears to be favorable for the survival of organic structures (T. H. Vu et al. 2023) and cells (C. W. Parker et al. 2023). Indeed, laboratory experiments suggest that rapidly freezing droplets can incorporate cells (M. G. Fox-Powell et al. 2022).
According to our experiments, very large droplets that are a few millimeters in diameter may be slightly more likely to form ice grains with higher degrees of vitrification than smaller droplets of only a few μm in diameter (Table 3), perhaps due to the freeze concentration of salts to promote glass formation (e.g., G. M. Fahy & B. Wowk 2015). Larger droplets also provide the better ability to preserve larger fragments of cells or even whole cells upon ice grain formation. Most of the ice grains with radii of >3 μm cannot escape Enceladus's gravity and instead fall back onto the surface of the moon (M. M. Hedman et al. 2009; A. Ershova et al. 2024) after being ejected to altitudes of between approximately 10–50 km (W. Degruyter & M. Manga 2011). To sample a larger portion of ice grains and possibly larger cellular fragments or cells, we therefore recommend potential future flyby missions (e.g., K. Reh et al. 2016; O. Mousis et al. 2022) to target low plume regions (<50 km altitude) and potential future lander missions (e.g., S. M. MacKenzie et al. 2021) to target regions near the tiger stripes.
Our results demonstrate that ice grains that form from high-salinity water reservoirs should have a higher degree of vitrification, meaning that they are more likely to preserve biosignatures, than ice grains that form from low-salinity water reservoirs (Figure 3). Complementarily, high concentrations of salts can increase the likelihood of cell survival by suppressing intracellular ice formation down to 190 K (S. Gault et al. 2024), which is even lower than the temperatures measured at Enceladus's tiger stripes (J. D. Goguen et al. 2013).
4.3. Salt Formation in Freshly Frozen Ice Grains
At least 95% of the mass of individual grains freshly formed from Enceladus's ocean are crystalline, highlighting the importance of better understanding the formation of salt assemblages that are associated with the freezing process. FREZCHEM simulations combined with microscopy and X-ray spectroscopy show that, when droplets from Enceladus's ocean freeze, water ice should form first, followed by sodium carbonates and then chloride salts; and that the salts will partition within the same droplet (M. G. Fox-Powell & C. R. Cousins 2021). However, these experiments and simulations neither included phosphate, a compound recently found in ice grains from Enceladus and important for understanding the moon's habitability (F. Postberg et al. 2023), nor accounted for relatively high concentrations of ammonia/ammonium that are likely to be present in the moon's ocean (L. M. Fifer et al. 2022).
We performed freezing simulations using an extended database for aqueous subzero temperature chemistry within the thermodynamic chemistry packages PHREEQC and Reaktoro. Our simulations included phosphates, higher concentrations of NH4+/NH3, and more nitrogen-bearing species (see Methods: Modeling of Mineral Assemblages). We find that PHREEQC and Reaktoro produce very consistent results. Both modeling approaches demonstrate that different salts precipitate at different temperatures, meaning that salts would likely form individual brine pockets within single droplets upon freezing from Enceladus's ocean water. The crystallization sequence of the salts predicted by our simulations generally agrees with the simulations made by M. G. Fox-Powell & C. R. Cousins (2021). Up to 20 bar (and probably beyond), the precipitation of salts does generally not depend on pressure (Figure A2).
No nitrogen-bearing phase precipitates throughout the simulations, but the NH4+ and NH3 concentrations in the solutions increase when the freezing process evolves, with NH4+ concentrations being 3 orders of magnitude higher than NH3 concentrations when the simulations stop (Figure A4). For both solutions, saturation indices of NH4Cl are the highest among all nitrogen-bearing species in the late-stage brine, meaning NH4Cl would be the likeliest compound to precipitate just before the eutectic is reached (Figure A5). Disodium phosphate dodecahydrate is the only form of phosphate that forms upon freezing over a wide range of pH values and Enceladus-relevant compositions (Figure 4, Table A4). Therefore, the orthophosphates that were detected in ice grains from Enceladus (F. Postberg et al. 2023) are probably disodium phosphate dodecahydrate.
With our simulations, we can track the pH evolution of the liquid solutions (Figures 4, 5). In both solution I and solution II, the pH generally increases by up to 0.6 throughout the freezing process, meaning that the pH of freshly frozen salt-water assemblages (ice grains) varies throughout the freezing process and may differ from the pH of the remaining liquid solutions (ocean droplets).
Although the pH variation is as low as 0.6 throughout the freezing process, the changing pH values are likely to be reflected in compositionally different ice grains that form from Enceladus's ocean or salty brines. In particular, the precipitation of nahcolite leads to a sudden increase in pH in the remaining liquid solution. This finding has implications for the formation of gases via droplet degassing (e.g., L. M. Fifer et al. 2022). The ratio of CO2/H2O between the liquid droplet and the gas that forms from it is suggested to be preserved (C. R. Glein & J. H. Waite 2020). Our results indicate that the ratios of species that exsolve from droplets with varying pH values should vary during the droplet freezing process. As a result, pH-dependent species like CO2 may exsolve more readily at the onset of the freezing process (when pH of the droplet is lower), whereas NH3 could exsolve more readily when freezing nears completion (and pH is higher). The tendency of gases to exsolve from droplets will also depend on the kinetics of pH-dependent speciation compared to the freezing timescales. These findings highlight the important role of fractionation processes that occur upon the freezing of salty water on icy worlds.
PHREEQC and Reaktoro models help in understanding the formation of salts that are associated with freezing on Enceladus, Europa, Ceres, and other solar system bodies, but the chemistry packages have limitations. Most importantly, these packages model equilibrium conditions. If a system is cooled past its eutectic temperature in equilibrium and completely frozen, the eutectic temperature represents the melting temperature. The melting temperatures measured with DSC are 244.71 K (solution I) and 246.78 K (solution II; Table A3). While the end temperature of our solution II models (Figure 5) matches the measured melting temperature relatively well, the end temperature of our solution I freezing models (Figure 4) is ∼2 K higher than the measured melting temperature, meaning that our freezing simulations seem to stop shortly before the eutectic temperature is fully reached. This finding is supported by the fact that ∼4 g of solution I and 36 g of solution II (out of 1000 g) are still liquid when the simulations stop (Figures 4, 5). Both modeling codes are unable to find a numerical solution for the equilibrium state of solutions I and solution II as the temperature approaches the measured melting temperature. We believe this is because Pitzer parameters and logK values for some species in the used database were not well calibrated for very low temperatures and at high ionic strengths. This means for Enceladus's ice grains that the results of our work do not rule out the crystallization of additional phases, such as NH4Cl or halite, shortly before the eutectic is reached, and freezing is complete.
The modeling results depend inherently on the phases present in the chosen database. In our models, we included species for which literature data are currently available. More experimental work is needed to fully characterize other salty phases (see, e.g., P. V. Johnson et al. 2019; B. Journaux et al. 2023) that can then be fed into the database. We modeled two different NaCl-dominated scenarios, and future work needs to investigate the formation of salts and the evolution of pH values upon freezing from water reservoirs that are dominated by other salts, such as MgSO4.
In our DSC experiments, we observed a melting event at 139 K for all flash frozen samples (Figure A1), but not for any of the slower cooling rates. Because this event is more pronounced (higher enthalpy) in thermograms of solution II than those of solution I, we hypothesize that this event is due to the melting of a salty phase that only forms at fast cooling rates. In a recent study, B. Journaux et al. (2023) discovered two hyperhydrated sodium chloride hydrates that are stable under icy moon conditions, namely, 2NaCl:17H2O and NaCl:13H2O. In another study, R. E. Hamp et al. (2024) report the discovery of a metastable sodium chloride dihydrate that can be produced via flash-freezing of NaCl solutions. Studies of the freezing of likely Europa ocean solutions at different rates also revealed distinct mineral formation sequences (e.g., P. V. Johnson et al. 2019). These studies, together with our observation (Figure A1), imply the existence of other salty phases that may be involved in the formation of ice grains from Enceladus's ocean or liquid reservoirs on other icy worlds.
5. Conclusions
We performed DSC experiments and simulations using PHREEQC and Reaktoro to constrain supercooling, glass formation, and mineral assemblages upon freezing of salt-rich ice grains from Enceladus's ocean droplets. We find that droplets that form from Enceladus's ocean water should experience 25–30 K supercooling before freezing, providing some constraints on the cooling rate of the droplets/ice grains. When the grains form, they contain up to 5% glassy phases that are potentially advantageous to the cryopreservation of complex organic structures or even cellular material. Upon freezing, crystalline salts are predicted to precipitate individually at different temperatures; and the crystallization follows a particular sequence, which is first Na2HPO4:12H2O (disodium phosphate dodecahydrate), followed by the carbonates NaHCO3 (nahcolite) and Na2CO3:10H2O (natron). Then, NaCl:2H2O (hydrohalite) and KCl (sylvite) precipitate sequentially. The pH of the remaining salty water droplet varies by ∼0.6 throughout the freezing process.
We also performed DSC experiments and geochemical simulations using PHREEQC and Reaktoro with a solution at 10 times higher salt concentrations than estimated for Enceladus's ocean. Ice grain formation from such high-concentrated salt water may occur on Europa, Ceres, Ganymede, or other icy worlds with subsurface water reservoirs. Such grains should have a higher degree of vitrification of 15%–35% or even more. Thus, our results inform not only future Enceladus models as well as potential future Enceladus mission concepts, such as the Enceladus Orbilander, but also models for and current missions to other icy worlds, such as NASA's Europa Clipper or ESA's Juice.
Acknowledgments
We acknowledge support from NASA Habitable Worlds Program grant No. 80NSSC19K0311. PHREEQC input files and our newly extended database for modeling the freezing process of solution I and solution II can be found in the online repository Zenodo via doi:10.5281/zenodo.15009033.
Competing Interests
The authors declare no competing interests.
Appendix
Here we provide supplementary information for our DSC experiments (Figure A1, Table A1, Table A2, Table A3) and modeling efforts (Figure A2, Figure A3, Figure A4, Figure A5, Table A4).
Figure A1. Thermogram of solution II, flash frozen (1227 K minute−1). Melting of a salty, yet unidentified compound is observed in the heating ramp at ∼139 K.
Download figure:
Standard image High-resolution imageFigure A2. Precipitation of salts from solution I and solution II at 6.1 mbar and 20 bar, respectively, simulated with PHREEQC. For both solutions, the precipitation temperatures of the individual salts vary by less than 0.3 K in the investigated pressure range.
Download figure:
Standard image High-resolution imageFigure A3. Mineral assemblages precipitating at 3.1 bar from NaCl-dominated water reservoirs at low pH, simulated with PHREEQC. The pH was adjusted by adding 80 mM chlorine ions to solution I and 780 mM chlorine ions to solution II (Table A4). In solution II, disodium phosphate dodecahydrate (red) redissolves when Na(H2PO4):2H2O (olive) precipitates.
Download figure:
Standard image High-resolution imageFigure A4. NH4+ and NH3 concentrations in solution I and solution II during freezing at 3.1 bar, simulated with PHREEQC.
Download figure:
Standard image High-resolution imageFigure A5. Saturation indices of nitrogen-bearing species in solution I and solution II during freezing at 3.1 bar, simulated with PHREEQC. A saturation index of 0 would mean that the respective species is saturated in solution.
Download figure:
Standard image High-resolution imageTable A1. Vendors and Purities of Compounds Used to Prepare the Samples for the DSC Experiments
| Compound | Vendor | Purity |
|---|---|---|
| (%) | ||
| NaCl | Sigma-Aldrich | ≥99.5 |
| KCl | Fisher chemical | 99.6 |
| Na2CO3 | Fisher chemical | ≥99.9 |
| NaHCO3 | Sigma-Aldrich | ≥99.7 |
| NH4OH (aqueous solution) | Sigma-Aldrich (Supelco) | 28.0–30.0 NH3 |
| Na2HPO4 | J.T.Baker | ≥99 |
| K2HPO4 | Fisher chemical | 98 |
Download table as: ASCIITypeset image
Table A2. Cooling Rate versus Nucleation Temperature and Degree of Supercooling of Deionized H2O (20 μL Sample)
| Cooling Rate | Nucleation Temperature | Degree of Supercooling |
|---|---|---|
| (K minute−1) | (K) | (K) |
| 10 | 254.65 | 18.39 |
| 50 | 253.70 | 19.40 |
| 150 | 253.90 | 19.22 |
Note. The uncertainty of the nucleation temperatures is ±0.01 K. The uncertainty of the degrees of supercooling is ±0.15 K.
Download table as: ASCIITypeset image
Table A3. Melting Temperatures of Solution I and Solution II Measured with DSC
| Composition | Melting Temperatures |
|---|---|
| (K) | |
| Solution I | 244.71 |
| Solution II | 246.78 |
Note. Solution I and solution II were initially frozen at a cooling rate of 10 and 5 K minute−1, respectively.
Download table as: ASCIITypeset image
Table A4. Phosphates Precipitating from NaCl-dominated Water Reservoirs during Freezing at Variable Solution pH Values, Simulated in PHREEQC
| Composition | Solution pH | Precipitating Phosphates | Temperature |
|---|---|---|---|
| (K) | |||
| Solution I − 100 mM Cl− | 13.16 | No phosphate precipitates | N/A |
| Solution I − 75 mM Cl− | 12.82 | Na2HPO4:12H2O | 255.20 |
| Solution I − 50 mM Cl− | 11.73 | Na2HPO4:12H2O | 270.17 |
| Solution I − 25 mM Cl− | 10.41 | Na2HPO4:12H2O | 271.11 |
| Solution I | 9.64 | Na2HPO4:12H2O | 271.05 |
| Solution I + 25 mM Cl− | 7.12 | Na2HPO4:12H2O | 270.61 |
| Solution I + 50 mM Cl− | 6.25 | Na2HPO4:12H2O | 269.78 |
| Solution I + 70 mM Cl− | 5.34 | Na2HPO4:12H2O | 268.24 |
| Solution I + 73 mM Cl− | 4.92 | Na2HPO4:12H2O | 266.87 |
| Solution I + 75 mM Cl− | 3.95 | Na2HPO4:12H2O and NaH2PO4:2H2O | 256.96 and 243.42 |
| Solution I + 80 mM Cl−a | 2.58 | NaH2PO4:2H2O | 242.38 |
| Solution I + 82 mM Cl− | 2.43 | NaH2PO4:2H2O | 240.62 |
| Solution I + 85 mM Cl− | 2.26 | No phosphate precipitates | N/A |
| Solution I + 100 mM Cl− | 1.82 | No phosphate precipitates | N/A |
| Solution II − 1000 mM Cl− | 13.72 | No phosphate precipitates | N/A |
| Solution II − 750 mM Cl− | 13.36 | Na2HPO4:12H2O | 255.20 |
| Solution II – 500 mM Cl− | 11.56 | Na2HPO4:12H2O | 275.51 |
| Solution II − 250 mM Cl− | 10.12 | Na2HPO4:12H2O | 278.15 |
| Solution II | 9.25 | Na2HPO4:12H2O | 278.15 |
| Solution II + 250 mM Cl− | 7.01 | Na2HPO4:12H2O | 278.15 |
| Solution II + 500 mM Cl− | 6.63 | Na2HPO4:12H2O | 278.15 |
| Solution II + 700 mM Cl− | 5.78 | Na2HPO4:12H2O | 275.4 |
| Solution II + 730 mM Cl− | 5.34 | Na2HPO4:12H2O | 270.28 |
| Solution II + 750 mM Cl− | 3.89 | Na2HPO4:12H2O and NaH2PO4:2H2O | 256.96 and 243.42 |
| Solution II + 780 mM Cl−a | 2.19 | Na2HPO4:12H2O and NaH2PO4:2H2O | 243.97 and 243.59 |
| Solution II + 800 mM Cl− | 1.89 | NaH2PO4:2H2O | 242.38 |
| Solution II + 820 mM Cl− | 1.66 | NaH2PO4:2H2O | 240.62 |
| Solution II + 850 mM Cl− | 1.38 | No phosphate precipitates | N/A |
| Solution II + 1000 mM Cl− | 0.65 | No phosphate precipitates | N/A |
Notes. The pH was adjusted by adding or removing Cl− ions. Solution pH refers to the pH of the solution at the start of the simulations (reaction step 1). Temperature refers to the temperature when the precipitations of the phosphates start.
aMineral assemblages are shown in Figure A3.Download table as: ASCIITypeset image