Abstract
We compute the inertial modes of a freely rotating two-layer planetary model with an ellipsoidal inviscid fluid core and a perfectly rigid mantle. We present a method to derive analytical formulae for the frequencies of the free core nutation (FCN) and Chandler wobble (CW) that are valid to all orders of the dynamical flattening of the core and mantle, and we show how the FCN and CW are the direct generalization of the purely fluid spin-over mode and of the Eulerian wobble to the case where the mantle can oscillate freely around a state of steady rotation. Through a numerical computation for an axisymmetric (oblate spheroidal) planet, we demonstrate that all other inertial modes of the steadily rotating fluid core are also free modes of the freely rotating two-layer planet.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The rotation of a planet depends on its internal structure via its moments of inertia. In particular, the misalignment between the rotation axis of a planet and its moment of inertia axis, along with the misalignment between the rotation axis of a planet and of its liquid core, give rise to two free modes of rotation known as the Chandler wobble (CW) and the free core nutation (FCN), respectively. In the planetary reference frame, the CW, if excited, is a long-period prograde rotation of the instantaneous axis of rotation around the principal axis of largest moment of inertia of the planet, while the FCN, if exited, is a retrograde motion of nearly diurnal frequency around the same axis.3 When taking the gravitational pull on the planet from the Sun, the moon, and other planets into account, these two modes can resonantly amplify the planet's forced nutation. Concerning the Earth, nutations are observed by using very long baseline interferometry and modeled precisely, accounting for deformation and coupling mechanisms at the core–mantle boundary (CMB) such as pressure and electromagnetic couplings. A solid deformable inner core inside the liquid core is also accounted for; see, e.g., Dehant & Mathews (2015). Concerning the planet Mars, which possesses precession and nutations as well, the joint efforts of the current RISE (Folkner et al. 2018) and future LaRa (Dehant et al. 2020) lander missions aim to detect such amplification in the nutation signal of Mars measured directly from its surface. Such a detection would allow an estimate of Mars's FCN frequency, from which Mars' polar moment of inertia can be deduced; this can then be used to build radial profiles of the density structure of the planet, and in particular constrain its core size (Dehant et al. 2020). Usually, such a computation is based on the formalism of Sasao et al. (1980) in which the rotational dynamics of the fluid core is described in terms of its angular momentum, which is assumed to be proportional to a mean flow resembling a solid-body rotation (see Section 2.3). This has a couple of important advantages, such as that of being easily adaptable to accommodate the existence of a nonrigid (elastic) mantle. However, as we show in the present work, it is, by design, valid only to first order in the planet's dynamical flattening parameters. This casts doubts on the results of previous studies attempting to push the formalism of Sasao et al. (1980) beyond first order to evaluate the effects of trixiality (Van Hoolst & Dehant 2002; Chen & Shen 2010; Dehant & Mathews 2015; Shen et al. 2019; Guo & Shen 2020).
In addition to the FCN and CW, the liquid core of a rotating star or planet is known to support the existence of oscillations known as inertial modes caused by the restoring effect of the Coriolis force. Experimental studies in laboratory have shown that these inertial modes can be excited by the action of tidal deformation at the fluid boundary; see, e.g., Malkus (1968), Aldridge & Toomre (1969), Kelley et al. (2007), and Morize et al. (2010). However, the role of the inertial modes on the rotation of planets and other astrophysical objects remains unclear. The main reason for this being that most studies, so far, have focused on the response of the fluid core in situations where the rotation of the planet is prescribed, i.e., known a priori. Therefore, they have disregarded the action of the fluid core on the rotation via the forces acting at the CMB; see Le Bars et al. (2015) for a review. In a previous work, we included the action of the fluid core on the free rotation of a two-layer planet with a viscous liquid core (Triana et al. 2019). We showed that the FCN and CW naturally emerge among the spectrum of inertial modes and that complex interactions between the eigenmodes take place when the moment of inertia of the mantle varies. Due to the difficulty in dealing with both the presence of a thin viscous boundary layer and the ellipticity of the CMB, we could not explore the regime of very low viscosity relevant to planetary and astrophysical objects.
In the present work, we complement the analysis of Triana et al., focusing specifically on the effects of the pressure torque between the fluid core and the solid mantle. We do so by computing the free modes of rotation of a two-layer ellipsoidal planet model with a perfectly rigid mantle and an inviscid fluid core. When one sets the viscosity of the fluid to zero, the viscous boundary layer at the CMB and the various shear layers that it generates inside the core disappear and the flow pattern inside the core becomes smooth. This enables us to derive the free modes of rotation at all values of the core and mantle's ellipticities.
Previous studies have attempted to mathematically model the rotational modes of a terrestrial planet based on the displacement field approach whereby the motion of the core and mantle are computed using the set of gravito-elastic equations that follow from the local conservation of momentum (Smith 1974, 1977; Rogister 2001; Rochester et al. 2014; Seyed-Mahmoud et al. 2017). However, these are limited to considering planetary models that are only slightly aspherical. There is also some doubt regarding the ability of these works to adequately capture the effects of the presence of a solid inner core, which is known to generate singularities within the displacement field (Rieutord et al. 2000).
This work is structured as follows. In Section 2, we present the two-layer planet model and its equations of motion. We then consider the special case of a core flow with a uniform vorticity and derive analytical formulae for the FCN and CW frequencies. In Section 3, we numerically compute the inertial modes of a two-layer planet with an axisymmetric CMB using the set of oblate spheroidal coordinates, and compare the value of the FCN frequency to the analytical expressions of Sasao et al. (1980) and our own formalism. Results are discussed in Section 4.
2. Model
Figure 1 represents the planetary model used throughout this work. The usual way to compute the rotation of this two-layer model is via the system of equations expressing the conservation of angular momentum for each layer. In the reference frame attached to the mantle rotating at angular velocity  relative to the inertial frame, and in the absence of external forces, these read:
relative to the inertial frame, and in the absence of external forces, these read:
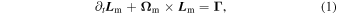

where 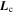 and
and  denote the angular momentum of the core and mantle, respectively, and
denote the angular momentum of the core and mantle, respectively, and  represents the total torque that the fluid core exerts on the mantle. All these quantities are measured relative to the inertial frame. In the absence of other external torques, this must be balanced by the torque from the core on the mantle. The addition of Equations (1) and (2) then yields:
represents the total torque that the fluid core exerts on the mantle. All these quantities are measured relative to the inertial frame. In the absence of other external torques, this must be balanced by the torque from the core on the mantle. The addition of Equations (1) and (2) then yields:

where  is the total angular momentum of the planet. Traditionally, one chooses to solve Equations (2) and (3). The difficulty then lies in the determination of
is the total angular momentum of the planet. Traditionally, one chooses to solve Equations (2) and (3). The difficulty then lies in the determination of  , which expresses the coupling between the core and the mantle. For the case of a perfect fluid with zero viscosity and in the absence of magnetic field, the only contribution comes from the pressure forces at the CMB, which give rise to the pressure torque:
, which expresses the coupling between the core and the mantle. For the case of a perfect fluid with zero viscosity and in the absence of magnetic field, the only contribution comes from the pressure forces at the CMB, which give rise to the pressure torque:

where P is the pressure inside the fluid and  is the position vector. The integration runs over the whole surface of the CMB, and
is the position vector. The integration runs over the whole surface of the CMB, and  denotes the radially outward normal vector to this surface. In principle, one should add the increment of gravity resulting from the change in the repartition of mass to Equation (4). In our simple model, however, this contribution is zero, as the distribution of masses is kept constant due to the perfect rigidity of the mantle and the incompressibility of the fluid core. Sasao et al. (1980) have shown how to avoid the computation of the pressure torque explicitly by replacing Equation (2) with an equation involving the mean rotation of the fluid. This approach, however, is only valid in the limit of small flattening of the CMB (see Section 2.3). In the present work, we use a different approach based on the equation giving the evolution of the flow inside the fluid core. In the special case where the flow vorticity is spatially uniform, the problem reduces to determining the evolution of the components of the vorticity in time. We can do so analytically by working from the equation of vorticity (the curl of the momentum equation) in a way that is formally similar to the formalism of Sasao et al. but has the advantage of being valid for all values of the flattening.
denotes the radially outward normal vector to this surface. In principle, one should add the increment of gravity resulting from the change in the repartition of mass to Equation (4). In our simple model, however, this contribution is zero, as the distribution of masses is kept constant due to the perfect rigidity of the mantle and the incompressibility of the fluid core. Sasao et al. (1980) have shown how to avoid the computation of the pressure torque explicitly by replacing Equation (2) with an equation involving the mean rotation of the fluid. This approach, however, is only valid in the limit of small flattening of the CMB (see Section 2.3). In the present work, we use a different approach based on the equation giving the evolution of the flow inside the fluid core. In the special case where the flow vorticity is spatially uniform, the problem reduces to determining the evolution of the components of the vorticity in time. We can do so analytically by working from the equation of vorticity (the curl of the momentum equation) in a way that is formally similar to the formalism of Sasao et al. but has the advantage of being valid for all values of the flattening.
Figure 1. Two-layer planet model with an ellipsoidal core and surface. Cartesian basis  is aligned with the principal axes of inertia of the core and the rigid mantle. Here,
is aligned with the principal axes of inertia of the core and the rigid mantle. Here,  is the rotation vector of the mantle relative to the inertial frame of reference and is related to the polar figure axis,
is the rotation vector of the mantle relative to the inertial frame of reference and is related to the polar figure axis,  , by Equation (9), where
, by Equation (9), where  .
.
Download figure:
Standard image High-resolution imageIn the remainder of this section, we present the equations governing the dynamics of the fluid core coupled to planetary rotation. We then present their analytical resolution in the special case of a flow with uniform vorticity and provide a comparison to the formalism of Sasao et al.
2.1. Equations for a General Flow
We focus on the small departures of the flow from a solid-body rotation and write:

where  and
and  denote the velocity field measured in the inertial frame and the mantle frame, respectively. Assuming that the fluid is incompressible and has zero viscosity, the equation of motion in the mantle frame and to first order in
denote the velocity field measured in the inertial frame and the mantle frame, respectively. Assuming that the fluid is incompressible and has zero viscosity, the equation of motion in the mantle frame and to first order in  reads (Triana et al. 2019):
reads (Triana et al. 2019):

where ρ denotes the fluid density and we have identified the reduced pressure, p, as:

where the second term represents the centrifugal potential—which, in the absence of external forces, is the only contribution to the total potential. The flow must satisfy the no-penetration condition at the CMB:

In this work, we focus on the small oscillations of the planet about a steady rotation, whereby  can be decomposed as:
can be decomposed as:

where the Cartesian basis vector, 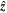 , is chosen as the mean axis of rotation (see Figure 1) and we have
, is chosen as the mean axis of rotation (see Figure 1) and we have  . In what follows, we set
. In what follows, we set  for simplicity, which amounts to measuring frequencies in cycles per day. As we are looking for solutions that are oscillatory, we use the following Fourier decomposition:
for simplicity, which amounts to measuring frequencies in cycles per day. As we are looking for solutions that are oscillatory, we use the following Fourier decomposition:



where a * denotes the complex conjugation and where we have used the same symbol to denote a quantity and its Fourier component at frequency  for simplicity. Inserting Equations (9) and (10)—(12) into Equation (A1), keeping terms up to first order in
for simplicity. Inserting Equations (9) and (10)—(12) into Equation (A1), keeping terms up to first order in  and
and 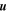 yields:
yields:

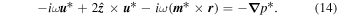
From Equation (13), we can isolate 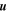 and express it in terms of in terms of p and
and express it in terms of in terms of p and 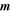 only. Upon using the incompressibility condition (
only. Upon using the incompressibility condition ( ), and the condition of no-penetration Equation (8), we then arrive respectively to (see Appendix A):
), and the condition of no-penetration Equation (8), we then arrive respectively to (see Appendix A):

which is valid inside the whole core, and

which must be satisfied at the CMB. When the mantle is in steady rotation, one has  . Equation (15) then reduces to the well-known Poincaré equation, the solutions of which are global oscillations of the flow called inertial modes and their frequencies satisfy
. Equation (15) then reduces to the well-known Poincaré equation, the solutions of which are global oscillations of the flow called inertial modes and their frequencies satisfy 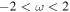 (see, e.g., Section 8.3.3 of Rieutord 2015). In his classic paper, Bryan (1889) gave the general analytical implicit expression of the inertial modes frequencies for an axisymmetric ellipsoid (those are reproduced in Appendix A). His work was later extended by that of Hough (1895) to the geometry of the triaxial ellipsoid. In both cases, the pressure field associated with each mode can be represented as a polynomial function in the Cartesian coordinates (Kudlick 1966; Zhang et al. 2001; Vantieghem 2014; see also Rekier et al. 2018). The inertial mode of lowest degree is called the spin-over mode (SO), and when observed from the mantle frame, its flow resembles a solid-body rotation around an axis perpendicular to the rotation vector of the mantle. It is the only inertial mode that carries a net amount of total angular momentum when integrated over the whole core; it is therefore especially important for rotation, as we show later.
(see, e.g., Section 8.3.3 of Rieutord 2015). In his classic paper, Bryan (1889) gave the general analytical implicit expression of the inertial modes frequencies for an axisymmetric ellipsoid (those are reproduced in Appendix A). His work was later extended by that of Hough (1895) to the geometry of the triaxial ellipsoid. In both cases, the pressure field associated with each mode can be represented as a polynomial function in the Cartesian coordinates (Kudlick 1966; Zhang et al. 2001; Vantieghem 2014; see also Rekier et al. 2018). The inertial mode of lowest degree is called the spin-over mode (SO), and when observed from the mantle frame, its flow resembles a solid-body rotation around an axis perpendicular to the rotation vector of the mantle. It is the only inertial mode that carries a net amount of total angular momentum when integrated over the whole core; it is therefore especially important for rotation, as we show later.
In order to obtain the evolution of  , we must use Equation (1) and express the angular momentum of the mantle in terms of its tensor of inertia,
, we must use Equation (1) and express the angular momentum of the mantle in terms of its tensor of inertia, 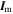 , and its angular velocity:
, and its angular velocity:

To obtain the right-hand side of Equation (1), we must write the pressure torque Equation (4) in terms of the reduced pressure,  and the increment of angular velocity
and the increment of angular velocity  . From the definition of Equation (7), one has, to first order in
. From the definition of Equation (7), one has, to first order in  :
:
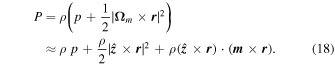
In Section 3, we numerically solve Equations (1), (15), and (16) for an axisymmetric oblate ellipsoidal fluid core using a set of oblate spheroidal coordinates, in a manner similar to what we presented in Rekier et al. (2018). In the remainder of the present section, we focus on the special case where the flow inside the core has a uniform vorticity for which the free modes of the two-layer planet can be computed analytically.
2.2. Flow with a Uniform Vorticity
In his classic paper, Poincaré (1885) looked for solutions of the fluid flow in an ellipsoid characterized by a spatially uniform (yet possibly time-dependent) vorticity. Denoting this vorticity as  , the velocity field,
, the velocity field,  , is written as:
, is written as:

where ψ is explicitly expressed in terms of  and the ellipsoid dimensions (a, b, c). This scalar function is there to adjust the flow to the no-penetration boundary condition Equation (8) and is zero for a spherical core. The explicit expressions of
and the ellipsoid dimensions (a, b, c). This scalar function is there to adjust the flow to the no-penetration boundary condition Equation (8) and is zero for a spherical core. The explicit expressions of  and ψ are given in Appendix B. We obtain the equation giving the time evolution of the vorticity by taking the curl of Equation (A1):
and ψ are given in Appendix B. We obtain the equation giving the time evolution of the vorticity by taking the curl of Equation (A1):

This has the advantage of making the gradient of pressure vanish and the whole influence of the mantle on the fluid core is accounted for entirely via the variations of  . Under the assumption of uniform vorticity, the computation of the fluid flow inside the core reduces to the resolution of Equation (20) for the three Cartesian components of
. Under the assumption of uniform vorticity, the computation of the fluid flow inside the core reduces to the resolution of Equation (20) for the three Cartesian components of  . In order to obtain the coupled motion of the core and mantle, we must add another equation giving the evolution of
. In order to obtain the coupled motion of the core and mantle, we must add another equation giving the evolution of  . We choose to use Equation (3), as it does not require any explicit computation of the torque at the CMB. It does, however, require us to evaluate the angular momentum of the whole planet relative to the inertial frame,
. We choose to use Equation (3), as it does not require any explicit computation of the torque at the CMB. It does, however, require us to evaluate the angular momentum of the whole planet relative to the inertial frame,  . Using Equation (5), this is written as:
. Using Equation (5), this is written as:

where the first term is proportional to the total tensor of inertia of the whole planet and the integral runs over the whole volume of the core. As the mantle is taken to be perfectly rigid, we can always chose the coordinates of the mantle frame to be aligned with the principal axes of inertia of the core and mantle at all times, and parameterize the tensor of inertia as:

In Appendix B, we give the explicit expressions of the components of the core angular momentum. In what follows, we parameterize the moments of inertia in terms of the following dynamical flattening parameters (see p.154 of Dehant & Mathews 2015):

for the fluid core and
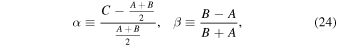
for the whole planet.
As we are interested in the small oscillations of the flow around the axis of rotation, we write, in analogy with Equation (12) and consistent with the notation of Sasao et al. (1980):

and we assume  . The system of Equations (3) and (20) in the first order in
. The system of Equations (3) and (20) in the first order in  and
and 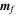 can be put in the following matrix form from which the components of these vectors in the z-direction decouple completely:
can be put in the following matrix form from which the components of these vectors in the z-direction decouple completely:

The problem of finding the free-mode frequencies, ω, then reduces to solving the polynomial equation, which results from imposing:

This polynomial equation is in fact biquadratic in the frequency ω, and so its roots come in pairs that have the same magnitude and opposite signs. The set of individual modes associated with each root can be classified into prograde and retrograde motions (relative to the mean planetary rotation). In the end, there are only two independent physical motions, as a prograde (respectively retrograde) mode of frequency ω < 0 is equivalent to a retrograde (respectively prograde) mode of ω > 0. Here, we follow the convention of Dehant & Mathews (2015) and others, and represent the retrograde modes using negative frequencies.
The explicit expressions of the two independent frequencies are too lengthy to reproduce here. Instead, we provide the expressions of their Taylor expansions in the dynamical flattening parameters:
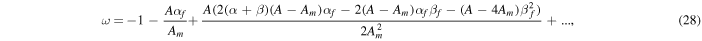

We identify these frequencies as those of the FCN and CW, respectively. The former presents a nearly diurnal retrograde nutation as measured in the planetary frame of reference. The latter is a prograde nutation of small frequency (and thus long period) in that same frame.
In anticipation of the next section, we now turn to the special case where the planet and its liquid core are axisymmetric around the mean rotation axis,  . In such a case,
. In such a case,  and Equation (26) can be further simplified in terms of the following variables:
and Equation (26) can be further simplified in terms of the following variables:

and analogous expressions for the components of  . These new variables are the components of
. These new variables are the components of  in the Cartesian canonical basis; see, e.g., p. 193 of Trinh (2019). The equations for
in the Cartesian canonical basis; see, e.g., p. 193 of Trinh (2019). The equations for  and
and  on the one hand, and for
on the one hand, and for  and
and  on the other hand, decouple completely. Thus, we end up with:
on the other hand, decouple completely. Thus, we end up with:
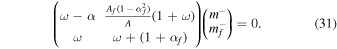
Setting the determinant of the above matrix to zero gives the following two independent frequencies:
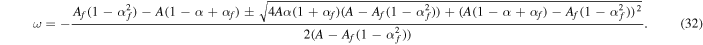
By taking the series expansion of Equation (32) in α and αf, assuming that these two parameters are small quantities of the same order, one recovers more familiar expressions for the FCN and the CW in the axisymmetric case:
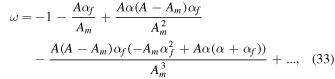

From Equation (33), one sees that the FCN has an exactly diurnal frequency in the case where the fluid core is spherical (αf). This is true to all orders in α and αf, as can be shown by working directly from Equation (32). From Equation (34), we see that the frequency of the CW remains proportional to the dynamical flattening of the whole planet, α, in that same limit. In Section 3, we demonstrate the validity of Equation (32) by comparing it to the result of a direct numerical integration of Equation (15). We also provide a comparison to the formula obtained using the formalism of Sasao et al. (1980), to which we now turn.
2.3. The Inertial Torque Approximation
Rather than working directly from the vorticity Equation (20), most studies prefer to compute the motion of the fluid core from the conservation of angular momentum. In theory, this amounts to solving Equation (2), which requires the computation of the pressure torque contribution Equation (4) to  . In practice, however, Sasao et al. (1980) have shown how Equation (2) can be replaced by the following:
. In practice, however, Sasao et al. (1980) have shown how Equation (2) can be replaced by the following:

where  denotes the angular velocity of the Tisserand frame of the fluid core, which is defined via
denotes the angular velocity of the Tisserand frame of the fluid core, which is defined via

The right-hand side of Equation (35) only involves terms that are second-order or more in the flattening parameters αf and βf, here assumed to be proportional to a single small parameter  ; see p. 271 of Dehant & Mathews (2015), and p. 79 of Trinh (2019) for more details. The usage of Equation (35) over Equation (2) is usually referred to as the inertial torque approximation. From the Cartesian components of the core angular moment, one can verify that, for all considerations of angular momentum,
; see p. 271 of Dehant & Mathews (2015), and p. 79 of Trinh (2019) for more details. The usage of Equation (35) over Equation (2) is usually referred to as the inertial torque approximation. From the Cartesian components of the core angular moment, one can verify that, for all considerations of angular momentum,  is equivalent to
is equivalent to 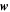 to first order in the flattening, such that the latter can be used in place of the former in Equation (35) (Appendix B). In this approximation, Equation (26) is replaced by:
to first order in the flattening, such that the latter can be used in place of the former in Equation (35) (Appendix B). In this approximation, Equation (26) is replaced by:
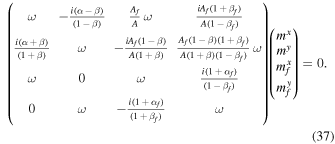
The frequencies, ω, derived from Equation (37) are equivalent to those derived from Equation (26) only to first order in the flattening parameters, α, β, αf, and βf.
2.4. The Spin-over Mode
In Section 2.2, we have seen how the FCN and CW wobble are natural oscillations of the two-layer system when the "wobbly" motion of the mantle is coupled to a core flow of uniform vorticity. From Equation (26), we can illustrate the relation between the FCN and the SO by considering the special case where  . Physically, this corresponds to the situation where the mantle is forced to remain in a state of steady rotation at all times. Mathematically, this amounts to ignoring the first two rows and columns of M, such that Equation (26) reduces to:
. Physically, this corresponds to the situation where the mantle is forced to remain in a state of steady rotation at all times. Mathematically, this amounts to ignoring the first two rows and columns of M, such that Equation (26) reduces to:

This gives a single independent frequency (using the same convention of sign as in Section 2.2):
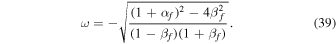
Upon using Equations (C4) and (C5) expressing αf and βf in terms of the dimensions of the ellipsoidal core (a, b, c), we arrive at the more familiar expression (see, e.g., Equation (3.21) of Vantieghem 2014 or Equation (A.23) of Rekier et al. 2018):

Note that carrying the same exercise with Equation (37) gives a different—and incorrect—expression for the SO frequency, which matches Equation (39) only up to first order in the flattening parameters.
We see that, strictly speaking, the SO is a mode of the two-layer system only in the limit where the rotation of the mantle is steady. When this is not the case, such as in the context of planetary nutations, the SO is replaced by the FCN. The flow inside the core is similar for both modes, having a uniform vorticity. The main difference is that the FCN is a combined motion of the core and mantle. When the core is axisymmetric (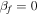 ), Equation (39) reduces to:
), Equation (39) reduces to:

In Section 3, we use Equation (41) to evaluate the discrepancy between the frequencies of the SO and the FCN numerically as a function of the core flattening, and we compare it to the analytical expression Equation (32).
3. Results
In this section, we present the results from the direct numerical integration of Equations (1), (15), and (16) for an axisymmetric oblate ellipsoidal fluid core. This computation is based on spectral decomposition introduced in Rekier et al. (2018), in which the reduced pressure field is developed onto the basis of spheroidal harmonics of the form:

where 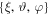 are the set of oblate spheroidal coordinates and L is the degree of truncation. Rekier et al. have shown how to use these coordinates to compute the inertial modes of a steadily rotating axisymmetric ellipsoid numerically by using the expansion Equation (42) and a decomposition of the
are the set of oblate spheroidal coordinates and L is the degree of truncation. Rekier et al. have shown how to use these coordinates to compute the inertial modes of a steadily rotating axisymmetric ellipsoid numerically by using the expansion Equation (42) and a decomposition of the  over the basis of Chebyshev polynomials,
over the basis of Chebyshev polynomials,  :
:

where N is the degree of truncation. Here,  denotes the normalized ξ-coordinate and
denotes the normalized ξ-coordinate and  is the value of ξ at the CMB. With an appropriate choice of normalization,
is the value of ξ at the CMB. With an appropriate choice of normalization,  is a constant that depends only on the polar flattening. It can be shown that the component of the pressure torque Equation (4) in the z-direction vanishes in these coordinates, due to axial symmetry in the azimuthal φ-coordinate. The other components in the Cartesian canonical basis reduce to:
is a constant that depends only on the polar flattening. It can be shown that the component of the pressure torque Equation (4) in the z-direction vanishes in these coordinates, due to axial symmetry in the azimuthal φ-coordinate. The other components in the Cartesian canonical basis reduce to:

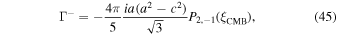
where a and c are the semimajor and semiminor axes of the core, respectively, and the  are the spheroidal harmonics components of the physical pressure field, with
are the spheroidal harmonics components of the physical pressure field, with 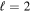 and
and  at the CMB. These should not be confused with the components of the reduced pressure,
at the CMB. These should not be confused with the components of the reduced pressure,  , to which they are related via Equation (18), which gives:
, to which they are related via Equation (18), which gives:

From Equations (44) and (45), we see that the geometry of the CMB restricts the family of flows coupled to the planetary rotation to those with a nonvanishing  and
and  pressure component at the CMB. In particular, this limits the analysis to the set of modes that are antisymmetric with respect to the equatorial plane.
pressure component at the CMB. In particular, this limits the analysis to the set of modes that are antisymmetric with respect to the equatorial plane.
Equations (1), (15), and (16) form a closed system of equations in p and  that we solve numerically as a (polynomial) eigenvalue problem in the frequency ω. For definiteness, we arbitrarily assume that the two layers of the planet have the same density and that the semimajor axes of the fluid core and of the whole planet are in a 1/2 ratio. We also set the exterior flattening to zero, α = 0), i.e., the outside surface of the planet is spherical. This leaves αf as the only free parameter. In Appendix C, we provide the detailed expressions of the different moments of inertia involved in this computation.
that we solve numerically as a (polynomial) eigenvalue problem in the frequency ω. For definiteness, we arbitrarily assume that the two layers of the planet have the same density and that the semimajor axes of the fluid core and of the whole planet are in a 1/2 ratio. We also set the exterior flattening to zero, α = 0), i.e., the outside surface of the planet is spherical. This leaves αf as the only free parameter. In Appendix C, we provide the detailed expressions of the different moments of inertia involved in this computation.
Figure 2 represents the partial spectrum of eigenvalues of modes with the azimuthal wavenumber m = 1 as a function of αf.
Figure 2. Partial spectrum of eigenfrequencies of the two-layer planet as a function of the polar flattening of the fluid core. Blue circles are the frequencies of the inertial modes computed numerically for a planet in steady rotation ( ). Red dots are the same thing for a planet with a nonsteadily rotating (wobbly) mantle (
). Red dots are the same thing for a planet with a nonsteadily rotating (wobbly) mantle ( ). Eigenvalues corresponding to the frequencies of inertial modes are the same in both cases—except for the SO, which gets replaced by the FCN. Blue dashed lines represent the analytical frequencies of the inertial modes of a steadily rotating planet (see Appendix A). These are labeled with the ℓ-number of their highest-degree component. Red curve represents the frequency of the FCN computed from Equation (47). We have subtracted the value of the SO frequency Equation (41) from all eigenvalues, to accentuate the discrepancy with the FCN. All frequencies in the figure correspond to modes with the azimuthal wavenumber m = 1.
). Eigenvalues corresponding to the frequencies of inertial modes are the same in both cases—except for the SO, which gets replaced by the FCN. Blue dashed lines represent the analytical frequencies of the inertial modes of a steadily rotating planet (see Appendix A). These are labeled with the ℓ-number of their highest-degree component. Red curve represents the frequency of the FCN computed from Equation (47). We have subtracted the value of the SO frequency Equation (41) from all eigenvalues, to accentuate the discrepancy with the FCN. All frequencies in the figure correspond to modes with the azimuthal wavenumber m = 1.
Download figure:
Standard image High-resolution imageThe blue circles are the inertial modes frequencies when the planet is in steady rotation ( ). The red dots are the same thing for a planet with a nonsteadily rotating (wobbly) mantle (
). The red dots are the same thing for a planet with a nonsteadily rotating (wobbly) mantle ( ). The blue dashed lines represent the analytical frequencies of the inertial modes of a steadily rotating planet (see Appendix A). These are labeled with the ℓ-number of their highest-degree component. The frequencies are the same in both cases—the only exception being the SO, which disappears from the spectrum when the planet has a nonsteady rotation and is then replaced by the FCN. In order to accentuate the discrepancy in the frequencies of these two modes, we have subtracted the SO frequency Equation (41) from all the frequencies in the plot. The red curve represents the frequency of the FCN computed from Equation (32), which, for α = 0), simplifies to:
). The blue dashed lines represent the analytical frequencies of the inertial modes of a steadily rotating planet (see Appendix A). These are labeled with the ℓ-number of their highest-degree component. The frequencies are the same in both cases—the only exception being the SO, which disappears from the spectrum when the planet has a nonsteady rotation and is then replaced by the FCN. In order to accentuate the discrepancy in the frequencies of these two modes, we have subtracted the SO frequency Equation (41) from all the frequencies in the plot. The red curve represents the frequency of the FCN computed from Equation (32), which, for α = 0), simplifies to:

This is in very good agreement with the values computed numerically, even for large values of αf. We observe that the nonsteady rotation of the mantle has no effect on the frequencies of the inertial modes other than the SO. This can be confirmed by looking at the ratio of the kinetic energy densities of the mantle and the core measured from the steadily rotating reference frame (see Appendix D) as shown in Figure 3.
Figure 3. Ratio of the kinetic energy densities of the mantle and the fluid core as measured from the steadily rotating frame. Red line corresponds to the analytical value computed for the solution of Equation (31) with α = 0) and with a frequency given by Equation (47).
Download figure:
Standard image High-resolution imageAs we can see, the ratio is strictly zero for all modes other than the FCN. The red line corresponds to the analytical value computed from the resolution of Equation (31) with α = 0) and with a frequency equal to Equation (47). It is in good agreement with the numerical computation, even for large values of the flattening.
We can further illustrate the agreement between the numerical and analytical computations by looking at Figure 4, which shows the same thing as Figure 2 but focuses on the frequency of the FCN up to very large values of the core flattening, 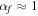 . The red curve represents the frequency obtained from Equation (47) and the dots show the numerical computation. The blue dashed line represents the value of the frequency computed using the inertial torque approximation described in Section 2.3, which, for α = 0), predicts:
. The red curve represents the frequency obtained from Equation (47) and the dots show the numerical computation. The blue dashed line represents the value of the frequency computed using the inertial torque approximation described in Section 2.3, which, for α = 0), predicts:

We see that, in the example of the figure, the numerical computation starts to deviate markedly from Equation (48) for 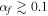 . The precise value of this threshold depends on the values of the moments of inertia,
. The precise value of this threshold depends on the values of the moments of inertia,  and
and  . We also see that Equation (47) agrees well with the numerical computation for all values of αf, thus proving the validity of the computation of Section 2.2 based on the vorticity equation.
. We also see that Equation (47) agrees well with the numerical computation for all values of αf, thus proving the validity of the computation of Section 2.2 based on the vorticity equation.
Figure 4. Frequency of the FCN as a function of the core flattening. Red dots are the results from direct numerical integration. Red curve corresponds to the analytical formula of Equation (47). Numerical and analytical results agree well for all values of αf. Blue dashed line represents the value of the frequency computed using the inertial torque approximation Equation (48), which predicts the wrong value of the FCN frequency for large values of the flattening.
Download figure:
Standard image High-resolution image4. Discussion
We have presented a method to compute the free rotation of a simplified two-layer planet with an inviscid and incompressible fluid core and a perfectly rigid ellipsoidal mantle. This method is based on the resolution of the modified Poincaré Equation (15) coupled to the Liouville Equation (1), which describes the "wobbling" motion of the mantle subjected to the pressure torque from the fluid at the CMB. We have found that the inertial modes of the fluid core enclosed in a steadily rotating mantle are also modes of the freely rotating two-layer planet. The only exception being the SO—the simplest of the inertial modes—which disappears from the spectrum and is replaced by the FCN (Figure 2). The fact that this is the only mode that can influence the rotation of the planet (or be influenced by it) can be traced back to the fact that it is the only inertial mode that exerts a net pressure torque at the CMB, something that was already noted by Toomre (1974). This can be verified by looking at Equations (44), (45), and (46), after realizing that the reduced pressure components  and
and  are zero at the CMB for all modes except the spin-over. This result demonstrated here for a freely rotating spheroid remains valid for a triaxial ellipsoid or when there are external tidal forces acting on the planet. In the latter case, the torque from the external potential must be added to the total torque Equation (4), but it must also be included in the definition of the reduced pressure Equation (7) so that nothing is changed.
are zero at the CMB for all modes except the spin-over. This result demonstrated here for a freely rotating spheroid remains valid for a triaxial ellipsoid or when there are external tidal forces acting on the planet. In the latter case, the torque from the external potential must be added to the total torque Equation (4), but it must also be included in the definition of the reduced pressure Equation (7) so that nothing is changed.
Looking at Figure 2, which shows the evolution of the spectrum of eigenvalues as a function of the core flattening, we observe that the frequency of the FCN crosses paths with that of the other inertial modes when αf varies. In their study of the completeness of the set of inertial modes in a steadily rotating ellipsoid, Backus & Rieutord (2017) showed that the modes remain orthogonal even when such accidental degeneracies happen. In the same paper, the authors also demonstrated that the Poincaré Equation (15) and the boundary condition Equation (16) form a self-adjoint system4
when  , thus providing the mathematical explanation for the realness of the eigenfrequencies. Our work extends their conclusions to the case where the motion of the mantle is nonsteady. Triana et al. (2019) have shown that the pictures drawn out from Figure 2 change significantly when the viscosity of the fluid is taken into account. The eigenvalues are then complex numbers and their imaginary parts represent the damping of the corresponding eigenmodes. Instead of crossing, the eigenvalues avoid each other in the complex plane in a complicated manner that is not yet fully elucidated (see their Figures 3 and 4). A similar example of this phenomenon referred to as avoided crossing was previously given by Rogister & Valette (2009), who studied the influence of a thermally stratified liquid core on the rotational modes of the Earth. In both cases, avoided crossings result from the introduction of a nonadiabatic diffusion term in the dynamical equations (respectively viscous or thermal), which breaks their "self-adjointness." Birch (2002) gave a similar interpretation in a study of the magnetohydrodynamical equations for a one-dimensional stratified medium where the avoided crossings result from the introduction of radiative cooling into the model. It should be noted that avoided crossings can also take place in systems that are self-adjoint. This is the case, for example, for the eigenfrequencies of the spheroidal oscillations of stars both in the adiabatic and nonadiabatic cases. See, e.g., chapter 5 of Christensen-Dalsgaard (2014) or Section 11.3 of Smeyers & Van Hoolst (2010) for a review. See also Triantafyllou & Triantafyllou (1991) for a more general description of the phenomenon and applications to problems in engineering.
, thus providing the mathematical explanation for the realness of the eigenfrequencies. Our work extends their conclusions to the case where the motion of the mantle is nonsteady. Triana et al. (2019) have shown that the pictures drawn out from Figure 2 change significantly when the viscosity of the fluid is taken into account. The eigenvalues are then complex numbers and their imaginary parts represent the damping of the corresponding eigenmodes. Instead of crossing, the eigenvalues avoid each other in the complex plane in a complicated manner that is not yet fully elucidated (see their Figures 3 and 4). A similar example of this phenomenon referred to as avoided crossing was previously given by Rogister & Valette (2009), who studied the influence of a thermally stratified liquid core on the rotational modes of the Earth. In both cases, avoided crossings result from the introduction of a nonadiabatic diffusion term in the dynamical equations (respectively viscous or thermal), which breaks their "self-adjointness." Birch (2002) gave a similar interpretation in a study of the magnetohydrodynamical equations for a one-dimensional stratified medium where the avoided crossings result from the introduction of radiative cooling into the model. It should be noted that avoided crossings can also take place in systems that are self-adjoint. This is the case, for example, for the eigenfrequencies of the spheroidal oscillations of stars both in the adiabatic and nonadiabatic cases. See, e.g., chapter 5 of Christensen-Dalsgaard (2014) or Section 11.3 of Smeyers & Van Hoolst (2010) for a review. See also Triantafyllou & Triantafyllou (1991) for a more general description of the phenomenon and applications to problems in engineering.
We have given the exact analytical expressions of the FCN and the CW frequencies of a triaxial two-layer planet. To second order in the flattening, these are given as Equations (28) and (29), which derive from the joint resolution of the Liouville equation for the mantle Equation (1) and the equation of vorticity for the fluid core Equation (20), based on the assumption that flow vorticity is uniform throughout the core. The task then reduces to solving Equation (26). We have shown that the resulting formula for the FCN is valid to all orders in the flattening parameters, by comparing it to the numerical solution for a spheroidal core. This is illustrated in Figure 4, where we have also plotted the same result based on the formalism of Sasao et al. (1980) as summarized in Section 2.3. In the same section, we have shown how that formalism, based on Equation (35), is only valid to first order in the flattening parameters.
Based on Equation (26), valid for core flows of uniform vorticity, we have shown how the FCN reduces to the SO in the limit where the rotation of the mantle is steady. We can understand this by considering the fact that the pressure torque Equation (4) vanishes identically when the CMB is spherical. This limit is equivalent to setting a = c in Equations (44) and (45) for an axisymmetric core. The motion of the mantle then becomes independent of that of the fluid core and vice versa, and the motion of the planet is derived from Equation (26) after setting 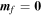 . The solution is that of a fully rigid solid-body rotation with frequency:
. The solution is that of a fully rigid solid-body rotation with frequency:
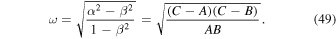
We recognize the expression on the right-hand side as the frequency of the free Euler wobble (EW). If we imagine increasing the flattening of the CMB from zero, the core and mantle become coupled and the EW and SO disappear from the solutions to be replaced by the CW and the FCN. Both of these are coupled motions of the core and mantle, even though the CW is mostly a motion of the mantle and the FCN is (as its name indicates) mostly a motion of the fluid core.
In Section 2.4, we have shown that, while the SO and FCN share a similar type of motion in the fluid core (one of uniform vorticity), it is improper to speak of the SO of a freely rotating planet. Some publications prefer to use the term tilt-over mode (TOM; Toomre 1974; Noir et al. 2003; Cébron et al. 2010), but this has the disadvantage of being easily confused with yet another mode of the same name that results from the mismatch between the polar axis of a planet and its instantaneous rotation axis (Dehant & Capitaine 1996). This mode has a purely diurnal frequency in the mantle frame, regardless of the planet's internal structure. We give a short mathematical description of the TOM in Appendix D, in which we derive the expression for the mantle's rotation vector with respect to the steadily rotating frame.
At present, the main interest of the results presented here is purely conceptual because our model cannot, at the moment, account for the elasticity of the mantle, which induces corrections to the FCN and CW frequencies that are first-order in the core ellipticity and therefore dominate over the second-order corrections computed here. As it stands now, our model can nevertheless provide a useful baseline for comparison with studies performed in triaxial geometries.
Other possible extensions to the present work include taking into consideration the effects of density stratification inside the core. Toomre (1974) argued that a radial density profile could lead to coupling the rotation to inertial modes other than the SO. For the Earth, the inclusion of a magnetic field can also potentially alter the spectrum of inertial modes. This is especially important for the Earth, as the ohmic power dissipation is estimated to be one of the main sources of damping of the FCN (Koot et al. 2010). Finally, the presence of a solid inner core should be taken into account in order to model the free inner core nutation of the Earth. This proves to be a significant numerical challenge, as it no longer permits the usage of a single set of oblate spheroidal coordinates covering the whole volume of the core. Concerning the planet Mars, it is considered (but not yet demonstrated) that there is no inner core and that the main dissipation mechanism at the CMB will be induced by the viscosity, also thought to be a very important factor for the Earth (S. A. Triana et al. 2020, in preparation). Furthermore, even in the simplified spherical shell geometry, the elliptical nature of the Poincaré equation is known to cause singularities in the fluid velocity (and pressure) field (Rieutord et al. 2000). These singularities can be regularized by reintroducing viscosity into the picture, with the well-known numerical limitations that it entails.
The authors would like to thank T. Van Hoolst for useful discussions in the writing of this work. We also extend our gratitude to the two reviewers, M. Efroimsky and M. Dumberry, whose comments helped to improve its presentation significantly. The research leading to the results presented here has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (advanced grant agreement No. 670874).
Appendix A: Derivation of the Poincaré Equation and Solutions for the Fluid Spheroid
From the momentum Equation (13):
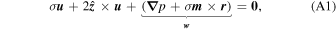
where we have set 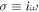 for simplicity. Taking the cross product of Equation (A1) with
for simplicity. Taking the cross product of Equation (A1) with 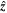 and injecting the result back into Equation (A1), we find:
and injecting the result back into Equation (A1), we find:

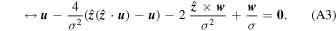
From Equation (A1), we also have:

which can then be used to rewrite the second term of Equation (A3). This allows us to isolate  :
:

Equations (15) and (16) follow immediately from the condition of incompressibility and the no-penetration condition respectively.
In Section 3, we compare the inertial modes of the freely rotating two-layer planet with an axisymmetric fluid core to those of a fluid core in steady rotation around the polar axis,  . Those are the results of Equations (15) and (16) with
. Those are the results of Equations (15) and (16) with  . In such a case, Bryan (1889) showed that the inertial modes can be written as a sum of product of two associated Legendre polynomial; see Equation (A.13) of Rekier et al. (2018). The frequencies of the inertial modes, ω, then derive from the solutions of:
. In such a case, Bryan (1889) showed that the inertial modes can be written as a sum of product of two associated Legendre polynomial; see Equation (A.13) of Rekier et al. (2018). The frequencies of the inertial modes, ω, then derive from the solutions of:

where  denotes the associated Legendre polynomial of degree ℓ and order m, and where we wrote
denotes the associated Legendre polynomial of degree ℓ and order m, and where we wrote
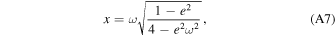
with  denoting the (geometrical) eccentricity of the fluid core.
denoting the (geometrical) eccentricity of the fluid core.
Appendix B: The Poincaré Flow and its Associated Angular Momentum
Equation (19) gives the general expression of a flow with a uniform vorticity. The scalar function, ψ, must be chosen so as to accommodate the no-penetration boundary condition at the CMB; see Equation (8). Following Poincaré (1885), we do so by operating the following coordinates transform:

where a, b, and c denote the dimensions of the core (Figure 1). If one defines the rescaled position vector in terms of its Cartesian coordinates as  , the implicit equation of the ellipsoid surface reduces to
, the implicit equation of the ellipsoid surface reduces to 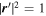 . The most general flow of uniform vorticity satisfying Equation (8) is then:
. The most general flow of uniform vorticity satisfying Equation (8) is then:

where  is a constant vector in space related to the flow vorticity,
is a constant vector in space related to the flow vorticity,  , through the condition that
, through the condition that  . In components, this yields
. In components, this yields



from which we obtain the expression of ψ by comparison with Equation (19):
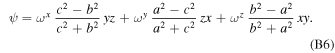
Using Equations (B3) to (B6), we can finally compute the angular momentum of the core from its definition as measured from the inertial frame:
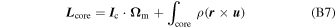

where  denotes the tensor of inertia of the fluid core and the integrals run over the whole volume of the core. In Cartesian components, this yields :
denotes the tensor of inertia of the fluid core and the integrals run over the whole volume of the core. In Cartesian components, this yields :



Using the definitions of the dynamical flattening parameters Equations (23), these read:
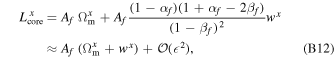


where, in the rightmost equalities, we have assumed that αf and βf are small quantities proportional to a single parameter  .
.
Appendix C: Tensor of Inertia
The principal moments of inertia of the fluid ellipsoid of equation  and with a homogeneous density
and with a homogeneous density  are:
are:



After introduction into the definitions of the dynamical flattening parameters Equations (23), we find :

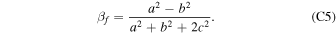
Substituting Equations (C4) and (C5) into Equations (C1) to (C3) yields:



We can obtain the expressions of the moments of inertia of the mantle by working directly from the above expressions. If we define the ratio between the semimajor axes of the core and of the whole planet as η, the principal moments of inertia of the mantle read:
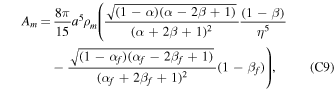


Appendix D: The Steadily Rotating Frame and the Tilt-over Mode
In Figure 3, we have represented the ratio between the kinetic energy density of the mantle and that of the fluid core as measured in the steadily rotating frame, which corresponds to the frame rotating with a constant velocity around the mean axis of rotation of the planet. In their Appendix C, Triana et al. (2019) gave some details on how the values of the quantities computed in that frame relate to their value in the mantle frame. We now provide a more detailed explanation.
We can think of the z-axis in the inertial frame, which we denote by  , as the mean rotation axis of the planet perpendicular to the equator (at J2000). The angular velocity of the mantle relative to the steadily rotating frame therefore reads (assuming Ω0 = 1):
, as the mean rotation axis of the planet perpendicular to the equator (at J2000). The angular velocity of the mantle relative to the steadily rotating frame therefore reads (assuming Ω0 = 1):

where  denotes the instantaneous z-axis of the mantle frame. In order to write this in coordinates, we need to express
denotes the instantaneous z-axis of the mantle frame. In order to write this in coordinates, we need to express  in the mantle's coordinates. We can do this by using the three Euler angles that relate the mantle to the steadily rotating frame. We use the following convention:
in the mantle's coordinates. We can do this by using the three Euler angles that relate the mantle to the steadily rotating frame. We use the following convention:

where the Ri denotes the ordinary (three-dimensional) rotation matrices around the axis i. The arguments of these matrices define the Euler angles α, β, and γ, which are all harmonic functions of t with frequency ω, and should not be confused with the flattening parameters of Equations (24). From the transformation matrix, T, we can construct the antisymmetric rotation tensor:
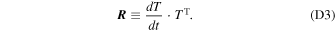
The dual vector of  then defines the angular velocity of the rotation (see, e.g., p. 46 of Lai et al. 2010), which must be equal to the angular velocity of the mantle. In components, and assuming that α, β, and γ are small, this gives:
then defines the angular velocity of the rotation (see, e.g., p. 46 of Lai et al. 2010), which must be equal to the angular velocity of the mantle. In components, and assuming that α, β, and γ are small, this gives:

In order to obtain the components of  in the mantle frame, we use the transformation matrix:
in the mantle frame, we use the transformation matrix:
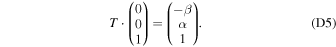
Finally, after solving Equation (D4) for α and β, we obtain the expression of the angular velocity of the mantle relative to the steadily rotating frame in the mantle's coordinates (in terms of  and m−):
and m−):

Equation (D6) presents a clear resonance when 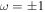 . These values can be interpreted as new eigenfrequencies, which are added to the spectrum when we solve the first two equations of Equation (D4) for α and β simultaneously with Equations (26). They correspond to the motion known as the tilt-over mode, which has a purely diurnal frequency independent of the interior structure of the planet.
. These values can be interpreted as new eigenfrequencies, which are added to the spectrum when we solve the first two equations of Equation (D4) for α and β simultaneously with Equations (26). They correspond to the motion known as the tilt-over mode, which has a purely diurnal frequency independent of the interior structure of the planet.
Footnotes
- 3
This motion is sometimes referred to as the nearly diurnal free wobble (NDFW) in the planetary frame of reference.
- 4
For an introductory discussion on the "self-adjointness" of differential operators and its implications, see, e.g., Sections 10.1 and 10.2 of Arfken & Weber (2005).







