Abstract
In this work, we divide the classic "lunar megaregolith" layer into three distinct regions: (1) a Surficial Regolith layer, about 5–20 m in depth, consisting of loose, unconsolidated fines and breccia, and characterized by frequent overturn and comminution caused by small impacts; (2) an Upper Megaregolith layer, about 1–3 km in depth, consisting of depositional layers of brecciated and/or melted material, and characterized by the transport and deposition of material via either transient crater gravitational collapse or impact ejecta ballistic sedimentation; and (3) a Lower Megaregolith layer, about 20–25 km in depth, consisting of bedrock that has been fractured in place, and characterized by a fracture-density and fragment-size distribution that decreases rapidly with increasing depth. The objective of this study is to model the formation of the lunar Upper Megaregolith layer, the least well characterized of these three layers, using modern scaling relationships and a three-dimensional terrain, Monte Carlo cratering model. We first developed a model impactor population that accurately reproduces the Lunar Highlands crater population, which is assumed to originate in the Main Asteroid Belt. We then applied this impactor population in multiple full-scale lunar surface simulations, producing an Upper Megaregolith depth of 1.4 ± 1.0 km at the point of best χ2 fit between model and actual crater counts. This Upper Megaregolith layer consists of ∼60% crater collapse deposits and ∼40% impact ejecta deposits. We find that a total delivered impactor mass of 3.72 ± 1.14 × 1019 kg, or 0.0506 ± 0.0156 lunar weight percent (wt%), is required to reproduce the observed Lunar Highlands cratering record.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Background and Objectives
1.1. Definition of the "Lunar Megaregolith"
In 1971, D. Nash, J. Conel, and F. Fanale of the Jet Propulsion Laboratory were advocating for a series of lunar rover missions to follow up on the then-ongoing crewed Apollo missions to the Moon (Nash et al. 1971). As part of their argument for a more limited, but highly mobile exploration of the lunar surface (as opposed to a highly detailed, but stationary site exploration), they hypothesized the following structure for the upper lunar crust (Nash et al. 1971): "Present data suggest a complicated history of discontinuous mare filling, over an extensive period of time, which produced stratigraphic sequences of flows, multiple regoliths and possibly intercalated intrusive layers. Beneath the mare fill and in the highlands we might expect a "mega-regolith" perhaps kilometers in thickness, created by the final stages of the lunar accretion flux. This larger regolith may be compatible with the essentially saturated distribution of 10–100 km craters on the highlands and far side; mare flows may merely represent islands of consolidated material within this regolith."
In Hartmann (1973), this hypothesis was reintroduced, proposing "that the roughly 5 m of post mare regolith is only a small fraction of the total fragmental material distributed in the lunar stratigraphic column. A surface megaregolith of depth on the order 2 km should exist in the terrae." Hartmann (1973) based this 2 km estimate on a model of impact cratering excavation and ejecta blanketing depths for large basins, which complemented a report from Short & Forman (1972), wherein they computed the total volume of ejecta from visible craters and basins to obtain 1.9 ± 0.5 km "for the depth of pre-mare debris still exposed on the present-day terra surfaces."
However, Hartmann (1973) also quoted new Apollo Passive Seismic Experiment (PSE) results that had been recently presented in Latham et al. (1972), which stated: "Lunar seismic signals differ greatly from typical terrestrial seismic signals. It now appears that this can be explained almost entirely by the presence of a thin dry, heterogeneous layer which blankets the Moon to a probable depth of few km with a maximum possible depth of about 20 km. Seismic waves are highly scattered in this zone." Continued PSE data collection, including from Saturn V third stage and Lunar Module impacts on the surface, confirmed a 20–25 km depth for this highly fractured zone of the upper lunar crust, presumably due to the Moon's long and heavy bombardment history (Dainty et al. 1974; Toksoz et al. 1974). In this way, the term "lunar megaregolith" began to be applied to the entire cross section of the upper lunar crust that has been heavily affected by impact cratering (Hartmann 2019), without distinguishing between different formation processes or characteristics, and as a result, has become a rather nebulous term in application.
In order to alleviate this confusion, in this work we divide the classic, broadly defined "lunar megaregolith" layer into three distinct regions based upon their different formation processes and characteristics, as shown in Figure 1. These are:
- 1.
- 2.an Upper Megaregolith layer, about 1–3 km in depth (Short & Forman 1972; Hoerz et al. 1976; Aggarwal & Oberbeck 1979; Thompson et al. 1979), consisting of depositional layers of brecciated and/or melted material, and characterized by the transport and deposition of material via either transient crater gravitational collapse or impact ejecta ballistic sedimentation; and
- 3.a Lower Megaregolith layer, about 20–25 km in depth (Dainty et al. 1974; Toksoz et al. 1974; Wiggins et al. 2019), consisting of bedrock that has been fractured in place by impacts, but not transported, and characterized by a fracture-density and fragment-size distribution that decreases rapidly with increasing depth.
Figure 1. Cross sectional diagram of the upper lunar crust (not to scale), in which we divide the classic "lunar megaregolith" layer into three distinct regions: (1) a Surficial Regolith layer, about 5–20 m in depth, consisting of loose, unconsolidated fines and breccia, and characterized by frequent overturn and comminution caused by small meteoritic impacts; (2) an Upper Megaregolith layer, about 1–3 km in depth, consisting of depositional layers of brecciated and/or melted material, and characterized by the transport and deposition of material via either transient crater gravitational collapse or impact ejecta ballistic sedimentation; and (3) a Lower Megaregolith layer, about 20–25 km in depth, consisting of bedrock that has been fractured in place, and characterized by a fracture-density and fragment-size distribution that decreases rapidly with increasing depth.
Download figure:
Standard image High-resolution imageThis type of division was also suggested by Heiken et al. (1991), who likewise divided the broadly defined "lunar megaregolith" into three regions: (1) an uppermost regolith layer, which is meters thick and composed of fine-grained heavily reworked material; (2) a "large-scale ejecta layer," which is composed of material ejected during the formation of large basins, and which is approximately a few kilometers thick; and (3) an "in situ fragmentation layer," composed of material fractured or fragmented by impacts but not ejected (Wiggins et al. 2019).
1.1.1. Surficial Regolith
The uppermost Surficial Regolith layer, a term coined by Hartmann (1973) to expand upon the term "regolith" from Shoemaker et al. (1967), has received a significant amount of study due to being directly sampled by the Apollo astronauts (King et al. 1971). This layer is characterized by a high degree of overturn, mixing, and further comminution due to small meteoritic impacts, in a process known as "impact gardening" (Ross 1968; Shoemaker et al. 1970; Soderblom 1970; Gault et al. 1974). Because the impactor population in this size range (<100 m diameter) has a steep, negative power-law size distribution, it has many more smaller than larger impactors (Neukum & Ivanov 1994; Neukum et al. 2001), such that the uppermost portions of this layer undergo the highest degree of mixing and further comminution, with the overturn rate rapidly decreasing with increasing depth.
The depth of this Surficial Regolith layer can be observationally determined by measuring the morphology of craters whose excavation penetrated this overlying, extremely weak, surficial regolith layer to expose an underlying, stronger substrate layer beneath: that is, by examining so-called "concentric craters" formed in a dual-strength layered target. This measurement method was pioneered by Quaide & Oberbeck (1968) and Oberbeck & Quaide (1968), who examined 12 of the potential Apollo landing sites during the 1966–1967 Lunar Orbiter missions, finding that "each of the sites analyzed has one of four type of thickness distributions characterized by approximate median values of 3.3, 4.6, 7.5, and 16 m. The regolith thickness correlates directly with cratering density." Concurrent with these measurements, Shoemaker et al. (1969) developed an analytical model of the formation of this surficial regolith layer that yielded similar values to these observations: a regolith layer 4.5–23 m in depth. Following up on their observational work, Oberbeck et al. (1973) developed a numerical Monte Carlo model of the formation of this regolith layer, obtaining model depths of 3.3–15 m.
More recently, Bart et al. (2011) applied the Quaide & Oberbeck (1968) "concentric crater" technique to 143 images returned by the Lunar Reconnaissance Orbiter Camera (LROC), finding that "median regolith depths in the mare regions are typically 2–4 m, whereas median regolith depths on the lunar far side and non-mare nearside areas are typically 6–8 m." This "concentric crater" technique has also been recently used to examine the potential Chinese Chang'e 5 landing site in Oceanus Procellarum, wherein Yue et al. (2019) found that the Surficial Regolith layer in the landing area ranges in depth from 0.7 to 18 m, with a mean of 7.2 m.
Additionally, seismic refraction experiments were used to study the characteristics of the lunar near-surface at the Apollo 14, 16, and 17 landing sites. The results of these active seismic experiments, together with passive recordings of Apollo Lunar Module (LM) ascent stage impacts, permitted an interpretation of the seismic velocity structure of the shallow lunar surface layers. At the Apollo 14 landing site, the uppermost ∼0.1 km s−1 seismic velocity layer was found to be 8.5 m thick (Kovach & Watkins 1972), while at the Apollo 16 landing site, this surficial layer has a depth of 12.2 m (Kovach et al. 1973). At the bottom of this Surficial Regolith layer, the seismic body-wave velocity transitions sharply to ∼0.3 km s−1, increasing rapidly with depth to a value of ∼4 km s−1 at a depth of about 5 km (Kovach et al. 1973).
1.1.2. Upper Megaregolith
The presence of an Upper Megaregolith layer is strongly inferred by the Lunar Highlands (lunar terrae) crater population (Nash et al. 1971), which exists in a state of crater density equilibrium (empirical saturation) for craters ≲250 km in diameter (Hartmann 1984, 1988, 1995; Hartmann & Gaskell 1993, 1997). The surface overturn depths, ejecta blanket depths, and crater collapse deposit depths associated with this heavy cratering record have been modeled multiple times and consistently point to an Upper Megaregolith layer about 1–3 km deep. As mentioned above, Short & Forman (1972) computed the total volume of ejecta from visible craters and basins to obtain an Upper Megaregolith depth of 1.9 ± 0.5 km. Hartmann (1973) estimated an Upper Megaregolith depth of 2 km based upon analytical computations of excavation and ejecta blanketing depths for large basins. Hoerz et al. (1976) performed Monte Carlo computer simulations of Lunar Highland impacts to predict that 50% of the highlands is cratered to a depth of 2–3 km. Finally, Aggarwal & Oberbeck (1979) performed detailed Monte Carlo computer simulations of the Lunar Highlands cratering record, with a specific focus on differing crater morphologies, to find an Upper Megaregolith depth of about 1.9–2.0 km.
In addition, a singular attempt was made to observationally ascertain the depth of the lunar Upper Megaregolith by Thompson et al. (1979), in which they investigated systematic terra-mare differences in radar and infrared images of impact craters to find: "Fresh terra craters smaller than 12 km were less likely to be infrared and radar anomalies than comparable mare craters: but terra and mare craters larger than 12 km had similar infrared and radar signatures. Also, there are many terra craters which are radar bright but not infrared anomalies. Our interpretation of these data is that while the maria are rock layers (basaltic flow units) where craters eject boulder fields, the terrae are covered by relatively pulverized megaregolith at least 2 km deep, where craters eject less rocky rubble."
More recently, results from the lunar Gravity Recovery and Interior Laboratory (GRAIL) mission are consistent with the existence of an Upper Megaregolith layer, such that an alternate stratification solution for the upper lunar crust's porosity-density gradient assumes a surface bulk density of 2600 kg m−3 with a large surface porosity of 0.30–0.35 in a thin porous layer limited to the top 3 km of the crust (Han et al. 2014). Although it is not the primary solution (discussed in Section 1.1.3), this alternative stratification model does satisfy the GRAIL observations within the wavelength band of 30–100 km, beyond which the interior geophysical processes and data noise hamper the analysis (Han et al. 2014).
1.1.3. Lower Megaregolith
Following the establishment of the first station of the Apollo Lunar Surface Experiment Package (ALSEP), which included a lunar PSE component, seismologists were faced with meteoritic impact seismic signals that were unlike anything encountered in terrestrial seismology. In Latham et al. (1970a, 1970b), the Apollo seismic experiment team wrote: "Seismometer operation for 21 days at Tranquility Base revealed, among strong signals produced by the Apollo 11 lunar module descent stage, a small proportion of probable natural seismic signals. The latter are long-duration, emergent oscillations which lack the discrete phases and coherence of earthquake signals. From similarity with the impact signal of the Apollo 12 ascent stage, they are thought to be produced by meteoroid impacts or shallow moonquakes. This signal character may imply transmission with high Q and intense wave scattering, conditions which are mutually exclusive on Earth."
With the establishment of a network of five such ALSEP stations at the Apollo 11, 12, 14, 15, and 16 landing sites, both the naturally occurring meteoritic impactor flux (Duennebier & Sutton 1974; Duennebier et al. 1975) and the upper lunar crust (Dainty et al. 1974; Toksoz et al. 1974) were well characterized via this network. As mentioned in Section 1.1, the upper lunar crust was found to be a highly fractured and therefore highly scattering medium with respect to seismic energy, such that seismic wave propagation in the upper 20–25 km of the lunar crust is best modeled as a diffusion process, rather than by direct wave propagation (Dainty et al. 1974). It was also found that beneath this highly fractured and scattering layer, more typical seismic wave propagation does occur (Dainty et al. 1974; Toksoz et al. 1974).
Although modeling attempts were made to push the depth of large lunar basin deposits (from either crater collapse or ejecta blanketing) down to this 20–25 km level, these attempts largely fell short. For example, Cashore & Woronow (1985) and Cashore (1987) performed Monte Carlo computer simulations of megaregolith formation to find only "29.7% of the surface being cratered to 1 km or greater for the observed highlands crater density; for 2 times the observed highlands crater density 50% is cratered to 2 km or greater and 20% is cratered to 16 km or more; for 5 times the observed highlands crater density 50% is cratered to 7 km or greater and 20% is cratered to 37 km or more." The scientific consensus therefore converged upon the alternate theory that this Lower Megaregolith layer consists of bedrock that has been fractured in place by impacts, but not transported, and is characterized by a fracture-density and fragment-size distribution that decreases rapidly with increasing depth (Heiken et al. 1991).
In more recent modeling work, Wiggins et al. (2019) implemented the Grady–Kipp model for dynamic fragmentation (Grady & Kipp 1987) into the iSALE shock physics code (Amsden et al. 1980; Melosh et al. 1992; Ivanov et al. 1997; Collins et al. 2004; Wünnemann et al. 2006), performing simulations of impacts into the upper lunar crust. They found that for impactors 1 km in diameter or smaller, a hemispherical zone centered on the point of impact contains meter-scale fragments and extends to depths of 20 km. At larger impactor sizes, overburden pressure inhibits fragmentation and only a near-surface zone is fragmented, such that for a 10 km diameter impactor, this surface zone extends only to a depth of ∼20 km (as before) but does extend out to lateral distances ∼300 km from the point of impact. "This suggests that impactors from 1 to 10 km in diameter (producing craters about 13.5–135 km in diameter) can efficiently fragment the entire lunar crust to depths of ∼20 km, implying that much of the modern-day (lower) megaregolith can be created by single impacts rather than by multiple large impact events" (Wiggins et al. 2019).
In addition to supporting the existence of an Upper Megaregolith layer, as discussed in Section 1.1.2, results from the lunar GRAIL mission also support the existence of a Lower Megaregolith layer in that the primary stratification solution for the upper lunar crust's porosity-density gradient assumes a surface bulk density of 2400 kg m−3 and a surface porosity of 0.10–0.20, where this porosity decreases exponentially with depth down to about 10–20 km in depth (Besserer et al. 2014; Han et al. 2014).
1.2. Objectives
The purpose of this study was to model the formation of the lunar Upper Megaregolith layer, the least well characterized of the three layers shown in Figure 1, using modern scaling relationships and computing technology. As mentioned previously, the most detailed numerical modeling investigation of this layer was performed by Aggarwal & Oberbeck (1979), using a matrix only 361 × 361 pixels in size (130321 total). By contrast, our Small Body Cratered Terrain Evolution Model (SBCTEM), described in Section 2, has a matrix of 2000 × 2000 pixels in size (4 × 106 total) and can simulate the entire lunar surface area at a resolution of 3.08 km per pixel. In order to model the formation of the lunar Upper Megaregolith properly, however, we must first be able to accurately model the Lunar Highlands cratering record. Therefore, in Section 3.1, we describe the development of an impactor population that accurately reproduces the Lunar Highlands crater population, both for craters ≲250 km diameter, which are in a state of crater density equilibrium, and craters ≳250 km diameter, which are not. In Section 3.2, we apply this impactor population in multiple simulations of Upper Megaregolith growth on the lunar surface in order to produce a good statistical sample, given the Monte Carlo nature of this model, particularly at large basin sizes.
2. Methodology
2.1. Small Body Cratered Terrain Evolution Model
The primary tool for this investigation is the Small Body Cratered Terrain Evolution Model (SBCTEM), initially introduced in Richardson (2009) in a study of crater saturation and equilibrium conditions. Monte Carlo (or stochastic) cratering models have long been a mainstay in the investigation of cratered terrains. The majority of these models have been geometric in nature, with crater rims represented by circles in a two-dimensional matrix, and employ parameterized mathematical functions to determine the effects of ejecta blanket coverage and the erasure of existing craters by subsequent craters (Woronow 1978; Chapman & McKinnon 1986; Hartmann & Gaskell 1997; Richardson et al. 2005). In Richardson (2009), we presented a new Cratered Terrain Evolution Model (CTEM) that took advantage of advances in (1) the impact cratering scaling relationships, particularly as applied to small bodies (Richardson et al. 2007; Richardson 2011) and (2) our understanding of seismically induced crater degradation (Richardson et al. 2004, 2005) to produce a fully three-dimensional numerical model of crater production and erasure on a given target surface, including automatic crater counting. Several small body specific improvements were introduced in Richardson (2013), designed to better model impact-produced seismic shaking and regolith growth. Substantial improvements in code modularization, parallelization, and running efficiency were introduced in Minton et al. (2015), wherein the model was applied to the lunar cratering record specifically. Finally, breccia lens creation and improved crater forms are introduced in this work.
Each SBCTEM simulation uses Monte Carlo sampling of
- 1.
- 2.
- 3.a user-supplied impactor population, developed in Section 3.1
to bombard an initially clean bedrock target surface as a function of time and then generate surface terrain maps, regolith depth maps, and crater counts at specified time intervals throughout the model run (Figure 3). At each time step, the model crater size–frequency distribution (SFD) is compared to the observed crater SFD for the target body, using a χ2 goodness of fit test. This surface is usually 1000 × 1000 or 2000 × 2000 pixel elements in size, with a user-specified pixel scale (meters per pixel). This simulated surface is continuous in nature, possessing periodic boundary conditions from side-to-side and top-to-bottom. The user also specifies a mean surface gravity, g (as corrected by the mean rotational force on the surface); a mean target body radius, rt (which becomes the model depth); surface material properties for both the "bedrock" substrate and generated "regolith" layer (density, ρt; effective strength,  ; and scaling-law constants μ, and K1); and bedrock seismic propagation properties (impact seismic efficiency, η; seismic quality factor, Q; P-wave velocity, vs; and mean free path for scattering, ls). These values are selected or estimated from the scientific literature relative to the body or type of body under study in order to achieve the most accurate simulation possible. Note that the body under study is represented as a continuous terrain map having a uniform surface gravity, g, rather than as a three-dimensional polygon shape-model, because a generalized approach is needed to facilitate the simulation of millions of successive impacts on the model surface within a reasonable amount of computation time.
; and scaling-law constants μ, and K1); and bedrock seismic propagation properties (impact seismic efficiency, η; seismic quality factor, Q; P-wave velocity, vs; and mean free path for scattering, ls). These values are selected or estimated from the scientific literature relative to the body or type of body under study in order to achieve the most accurate simulation possible. Note that the body under study is represented as a continuous terrain map having a uniform surface gravity, g, rather than as a three-dimensional polygon shape-model, because a generalized approach is needed to facilitate the simulation of millions of successive impacts on the model surface within a reasonable amount of computation time.
Figure 2. (left) Impact velocity distribution used in these lunar surface simulations, derived from an N-body simulation of the dynamical diffusion of Main Belt asteroids into the Near Earth region (Minton & Malhotra 2010). The rms velocity of this distribution is 18.3 km s−1. (right) The impact angle distribution used in these lunar surface simulations, described in Gilbert (1893), Shoemaker (1962), and Pierazzo & Melosh (2000) for an isotropic population of impactors striking the surface of a spherical target body.
Download figure:
Standard image High-resolution imageFigure 3. Example of the SBCTEM output from a full-scale lunar surface simulation, 6160 km per side (3.794 × 107 km2 surface area), with a pixel resolution of 3.08 km. (left) The terrain map (Digital Elevation Map) from lunar surface simulation Luna 14 (Section 3), showing a contrast-enhanced crater population in a state of empirical saturation for craters ≲250 km diameter. This particular simulation produced a single South Pole-Aitken (SPA) basin-like impact shown in the upper left and a single Imbrium basin-like impact shown in the lower left. The elevation range in this simulation is 18 km, similar to the Moon's actual elevation range of ∼19 km. (right) A regolith distribution map from simulation Luna 14, showing regolith depth on a linear, rainbow color scale. The depth ranges from 0 m (black–violet) to 5931 m (red), with a mean depth of 1290 ± 954 m. The deepest depths occur inside the SPA-like impact basin, which occurred relatively early in the simulation.
Download figure:
Standard image High-resolution imageA key component of the SBCTEM is the inclusion of downslope regolith migration, triggered either by slope instability or by the seismic motion generated by nearby impacts, thus incorporating crater degradation as a function of age and local impact history within the model (Richardson 2009, 2013). Following each impact, the simulation enters an Eulerian phase, wherein seismic shaking–induced, loose regolith flow between matrix pixels occurs, implemented in finite-differencing fashion using topographic diffusion theory (Culling 1960; Nash 1980; Richardson et al. 2005; Richardson 2009, 2013). Additionally, the affected area around each new impact crater is checked for slopes above the angle-of-repose, which are then collapsed to below the angle-of-stability (user-supplied parameters).
An SBCTEM simulation has three methods for covering a pixel area with new regolith and two methods for removing that regolith. With respect to covering a pixel with new regolith, regolith can be (1) generated by crater breccia lens creation, which occurs when the transient crater created by an impact gravitationally collapses into its final form (Melosh 1989; Hirabayashi et al. 2017); (2) deposited by impact ejecta emplacement (ballistic sedimentation); or (3) created by the downslope motion of regolith from upslope of the pixel in question. With respect to removing regolith from a pixel, regolith can be removed by (1) the process of crater excavation or (2) the gravitationally driven motion of regolith to regions downslope of the pixel in question. Note that upturned crater rims are not considered to be regolith in the model, but instead act as a source region for loose regolith, since this rock has been uplifted, broken, and is severely weakened. To be considered as "regolith" in this model, material must be transported, either ballistically or via mass wasting.
To achieve automatic crater tracking and counting, the SBCTEM uses three auxiliary matrix layers to track the creation and degradation of each pixel in a particular crater, where layer (a) contains a unique crater identifier, layer (b) contains the original crater profile (in meters of height) relative to the mean topographic surface present at the time of the crater's formation, and layer (c) contains the deviation of the current crater surface (in meters of height) from its original profile position. As specified by a user-supplied parameter, when a particular crater pixel deviates by more than 80%–100% from its original profile elevation, that crater pixel is permanently "erased" from the three tracking layers. Due to the ability of smaller craters to be nested within larger craters, a total of 7 sets of 3 auxiliary tracking layers (21 total) are employed by the model, in order to ensure that all crater pixels are tracked properly. In order for a crater to be considered "observable" or "countable," at least 40%–50% of a crater's original pixel area must remain, as determined by a second user-supplied parameter. Although SBCTEM does create and track craters down to a single pixel in diameter, such that "sandblasting"—the erasure of large craters by small craters—is included in the model (see Section 1.1 of Richardson 2009), only craters of at least three pixels in diameter (≥8 km) are used in the crater counts presented in this study.
As currently configured, the SBCTEM utilizes the IDL package (Harris Geospatial Solutions) for overall simulation control and display, while the program engine is written and compiled in Fortran 90/95. This program engine utilizes the OpenMP (Open Multi-Processing) Application Programming Interface to parallelize the engine modules wherever possible (Minton et al. 2015). Running on a 16 processor LINUX modeling computer, a particular simulation may take from a few days up to a few weeks to complete, depending upon the mesh resolution specified by the user and the degree to which impact-induced seismic shaking affects the small body under study, wherein each simulation generally involves thousands to millions of individual impacts.
The SBCTEM is a separate code branch from the CTEM described in Minton et al. (2015) and thus differs from the Purdue University CTEM in the following ways: (1) SBCTEM uses a simplified crater counting routine (described above), (2) SBCTEM uses a simplified complex crater size computation (described in Section 2.2), (3) SBCTEM uses an improved impact-induced seismic shaking routine (described in Richardson 2013) instead of the "terrain softening" routine described in Minton et al. (2015), and (4) SBCTEM now includes improved complex crater forms, including terrace zone, breccia lens, and central peak creation (described in Section 2.4), developed as part of this particular study.
The following sections describe the manner in which crater size scaling (Section 2.2), ejecta velocity and volume scaling (Section 2.3), and crater form and breccia lens computations (Section 2.4) are handled within the SBCTEM. The equations here are described, but not derived; for the full derivations, please see the referenced publications.
2.2. Crater Diameter Scaling
In order to estimate the size of the crater produced by a particular impact, we make use of the general solution to the crater volume scaling relationship developed in Holsapple (1993), which contains the effects of both gravity and strength:

where Vt is the volume of the transient crater; ρi, ai, and mi are the impactor's bulk density, mean radius, and mass, respectively; vi is the vertical component of the impact velocity (as determined by the randomly selected impact angle (Figure 2 (right)); ρt is the target's density; and K1, μ, and  are experimentally derived impact crater scaling-law properties of the target material. In practice, the effective target strength
are experimentally derived impact crater scaling-law properties of the target material. In practice, the effective target strength  is roughly a measure of cohesion and usually lies somewhere between the laboratory-measured tensile and shear strengths of the material (Holsapple 1993; Holsapple & Housen 2007), for low- to medium-porosity targets. In high-porosity targets, the effective target strength
is roughly a measure of cohesion and usually lies somewhere between the laboratory-measured tensile and shear strengths of the material (Holsapple 1993; Holsapple & Housen 2007), for low- to medium-porosity targets. In high-porosity targets, the effective target strength  can be thought of in broader terms: as the energy per unit volume (rather than the force per unit area) required to both crush pore spaces and to break the material apart for excavation.
can be thought of in broader terms: as the energy per unit volume (rather than the force per unit area) required to both crush pore spaces and to break the material apart for excavation.
Since the SBCTEM employs and tracks two different target materials, "bedrock" and "regolith," the target density ρt and effective strength  values used in Equation (1) depend upon whether the impactor penetrates the existing regolith layer or not. This is found using the impactor "equivalent depth of burial" equation from Melosh (1989):
values used in Equation (1) depend upon whether the impactor penetrates the existing regolith layer or not. This is found using the impactor "equivalent depth of burial" equation from Melosh (1989):

where ρt here is the "regolith" density supplied by the user. If the impactor penetrates the regolith layer, then "bedrock" values are used; if not, then "regolith" values are used.
The transient crater volume Vt can be related to the more easily measured transient crater (rim-to-rim) diameter Dt or radius Rt by
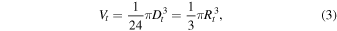
where we assume that the transient crater depth Ht is roughly 1/3 its diameter, Dt: in experiments, this is somewhat variable, between 1/4 and 1/3 (Schmidt & Housen 1987; Melosh 1989).
Note that the above expressions yield only a transient crater size: that is, the crater's momentary diameter prior to gravitational collapse. In order to compute a final crater diameter, Df, from the transient crater diameter, Dt, two expressions are used: one for small, simple craters, and one for large, complex craters—see the discussion in Chapman & McKinnon (1986) for more details. For simple craters, the transient crater is approximately 85% the diameter of the final crater, and the conversion factor is linear:

as described in Chapman & McKinnon (1986) and Melosh (1989). For complex craters this conversion factor follows a power-law, as described in Croft (1981), Chapman & McKinnon (1986), Melosh (1989), and Schenk et al. (2004). This power-law begins at a simple crater diameter known as the simple-to-complex transition point Dtr, and where this transition point varies inversely with the surface gravity of the body involved (Dtr ∝ 1/g). The simple-to-complex crater transition point fir a silicate rock target is found by fitting the data presented in Figure 18 of Schenk et al. (2004):

where the gravity g is given in terms of m s−2, and the transition crater diameter Dtr is given in terms of meters. Finally, for craters where the simple crater diameter Ds (Equation (4)) is greater than the transition crater diameter Dtr (Equation (5)), we compute the size of the final complex crater using the expression:

where the silicate rock target, power-law exponent in Equation (6) is taken from Croft (1981) and Chapman & McKinnon (1986).
2.3. Ejecta Velocity and Volume Scaling
The application of a general solution to the crater volume scaling relationship permits us to also utilize the general solution to the ejecta velocity scaling relationships developed by Richardson et al. (2007). These new ejecta scaling relationships permit us to directly compute surface ejection velocity as a function of projectile and target material properties, impact parameters, and distance from the impact site, all the way out to the transient crater rim. This analytical solution is applied to a discretized model of the excavation flow-field's hydrodynamic streamlines (Maxwell & Seifert 1974; Maxwell 1977), in order to compute excavated mass as a function of distance from the impact site and ejection velocity. Finally, these discrete, ejected mass segments are followed in post-ejection flight through a set of ballistics equations in order to compute ejecta blanket thickness as a function of distance from the final crater rim, as described in Richardson (2009). In addition to correctly duplicating the ejecta plume evolution observed on Tempel 1 as a result of the Deep Impact collision (Richardson et al. 2007; Richardson & Melosh 2013), the efficacy of this model has been verified through direct comparison to the laboratory-impact ejecta plume behavior experiments conducted by Cintala et al. (1999), Anderson et al. (2003, 2004), and Barnouin-Jha et al. (2007), as described in Richardson (2011).
The ejecta velocity scaling relationships developed by Richardson et al. (2007) takes advantage of a basic concept described in the Maxwell Z-model of ejecta behavior (Maxwell & Seifert 1974; Maxwell 1977); namely, that the ejecta flow emerging from the surface at some radius r from an impact site represents a hydrodynamic streamline, which is in a steady-state condition and incompressible. If we also assume that frictional forces beyond those implicit in Equation (9) (below) are small compared to the forces of inertia, gravity, and strength (that is, inviscid flow), we can use Bernoulli's principle at the point of ejecta emergence to form an energy balance equation:

where ve is the emergence velocity (after losses due to friction), and vef is the effective ejection velocity that we desire (after losses due to gravity and strength). Beginning on the left, the first two terms describe the kinetic energy (or stagnation pressure) of the excavation flow in a single streamline, assuming that upon emergence, the hydrostatic pressure in the flow is zero. The third term describes the mean amount of gravitation potential energy needed to loft each unit volume in the flow (a function of surface radius r), and the fourth term describes the amount of energy needed to fracture or "break loose" each unit volume in the flow (a function of effective target strength  ). Solving for constants Kg and Ks yields the following equation for the final "effective" ejecta velocity vef as a function of distance r from the impact site (Richardson et al. 2007):
). Solving for constants Kg and Ks yields the following equation for the final "effective" ejecta velocity vef as a function of distance r from the impact site (Richardson et al. 2007):

where ρt is the target density, g is the gravitational acceleration, and 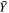 is the effective target strength with respect to crater excavation. The uncorrected ejection speed ve is given by the gravity-scaled ejecta speed equation derived by Housen et al. (1983):
is the effective target strength with respect to crater excavation. The uncorrected ejection speed ve is given by the gravity-scaled ejecta speed equation derived by Housen et al. (1983):
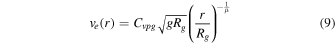
where Rg is the gravity-scaled transient crater radius: that is, the radius that would result if the target was strengthless. μ is a commonly used exponential material constant (Holsapple 1993), and the constant Cvpg is given in Richardson et al. (2007) as

This expression contains constant CTg, which has an experimentally determined value of 0.8–0.9 (Schmidt & Housen 1987; Holsapple & Housen 2007) as discussed in Section 2.2 of Richardson et al. (2007).
The constant Cvps in the strength term of Equation (8) is given by

where Rs is the transient crater radius due to the effects of both gravity and strength. The transition strength Yt (between gravity and strength dominated cratering) is expressed as

where vi is the vertical component of the impactors speed, ai is the impactor's mean radius, and ρi is the impactor density.
Given the above method for determining the ejection velocity vef at some given distance r from the impact site, we next calculate the mass of ejecta expelled at that distance r by dividing the excavated portion of the transient crater into a large number of N concentric, paraboloid shells: where each thin shell approximates a Maxwell Z-model streamtube of thickness dr = RsN−1, such that all the material in a given streamtube emerges from the surface at distance r and at speed vef(r). The volume of material Vi contained in a particular paraboloid shell is given by

where  (Equation (10)), and i runs from 0 to N − 1. The value of Kgr here represents a mean streamline excavation depth (from Equation (8)) and ranges from r/9.0 (at μ = 0.40) to r/5.8 (at μ = 0.55) for a CTg value of 0.85. This implies a maximum streamline excavation depths of r/4.5 to r/2.9, which is reasonable; usual values range from r/5 to r/4 (Melosh 1989). This paraboloid shell approach represents an approximation of the more accurate method for computing the excavated mass via numerical integration between streamtubes within the Maxwell Z-model itself. Comparison between these two methods, however, has shown that the paraboloid shell approximation yields results that are within 3%–4% of the numerical Z-model integration (depending upon Z value), such that the added accuracy of a full integration was deemed not worth the additional computation time.
(Equation (10)), and i runs from 0 to N − 1. The value of Kgr here represents a mean streamline excavation depth (from Equation (8)) and ranges from r/9.0 (at μ = 0.40) to r/5.8 (at μ = 0.55) for a CTg value of 0.85. This implies a maximum streamline excavation depths of r/4.5 to r/2.9, which is reasonable; usual values range from r/5 to r/4 (Melosh 1989). This paraboloid shell approach represents an approximation of the more accurate method for computing the excavated mass via numerical integration between streamtubes within the Maxwell Z-model itself. Comparison between these two methods, however, has shown that the paraboloid shell approximation yields results that are within 3%–4% of the numerical Z-model integration (depending upon Z value), such that the added accuracy of a full integration was deemed not worth the additional computation time.
In order to estimate the ejecta blanket thickness at some distance l from the impact site, we utilize a set of simple ballistics equations to compute landing distances for the material ejected at distances ri and ri+1. Since the vast majority of impact ejecta will land within 1–3 crater radii of the impact site, and most craters in the model will be significantly smaller than the radius of curvature of the target body under study, we assume flat-plane geometry to obtain

for the horizontal ejection velocity and

for the vertical ejection velocity, where ejection angles gradually drop from 55° to 35°, consistent with the experimental findings of Cintala et al. (1999; see Richardson et al. 2007 for a full discussion). The above two equations are used to find the ejecta landing distances li and li+1 for the ejecta launched at distances ri and ri+1, respectively, using the simple ballistics equation:
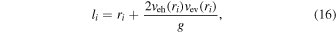
assuming no horizontal motion once the ejecta have landed. The surface area occupied by the landed ejecta can be found by
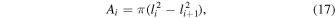
with the ejecta blanket thickness bi at some distance li from the impact site estimated by

For each impact in the model, the above equations are used to produce a variably sized look-up table of ejecta blanket thickness as a function of distance from the impact site, which is automatically scaled to the size of the resulting impact crater and the extent of ejecta coverage on the surface. This look-up table is kept to a fine enough resolution to permit linear interpolations between each data point, when points on the Digital Elevation Map (DEM) fall between look-up table distances from the impact site. It should be noted that post-landing, horizontal ejecta movement, and its scouring effects on existing terrain (Melosh 1989), are not included in the model at this time. More importantly, ejecta volume bulking (a porosity increase) is not included in the ejecta volume calculation (Equation (13)) to prevent the possibility of cascade (runaway) bulking of the uppermost regolith layers that undergo continuous turnover due to "impact gardening" (Ross 1968; Shoemaker et al. 1970; Soderblom 1970; Gault et al. 1974).
2.4. Crater Form Computation
2.4.1. Crater Interior Form
Following the random selection of an impactor size, impactor velocity, impact angle, and impact site on the matrix, and the computation of the resulting crater dimensions and ejecta blanket coverage, the program surveys the area where the crater is to be placed, determining this area's mean elevation and slope. This survey is used to produce a "reference plane," upon which the new crater is superimposed.
For simple craters, this new crater follows a standard, parametric, paraboloid shape, with its depth to a diameter ratio  designated by a user input parameter. For simple craters (Ds ≤ Dtr), the depth ds is given by Pike (1977):
designated by a user input parameter. For simple craters (Ds ≤ Dtr), the depth ds is given by Pike (1977):
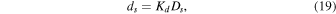
where a value of Kd = 0.19 is used in these simulations Pike (1977).
For complex craters (Ds > Dtr), we performed a fit to the lunar depth to diameter data plotted in Figure 1 of Pike (1977) in order to create a more general equation that could be applied to other planetary bodies as a function of surface gravity g. This fit yields a maximum depth dc of
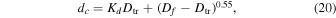
where the maximum complex crater depth dc acts as a flat-floored limit on the depth of a standard paraboloid shape having diameter Df and depth KdDf. The blue line in Figure 4 plots the computed crater depth, using Equations (19) and (20), as a function of the final crater diameter, Equations (4) and (6), and compared it to the maximum depth versus diameter study of lunar craters shown in Figure 1 of Pike (1977) (open red circles).
Figure 4. Plot of SBCTEM computed maximum lunar crater depth (blue line) and breccia lens depth (dashed, dark green line), as compared to the maximum depth vs. diameter study of lunar craters by Pike (1977) (open red circles) and the maximum breccia lens depth vs. diameter study of terrestrial craters by Orphal (1979) (filled purple triangles).
Download figure:
Standard image High-resolution imageBeginning with this work, SBCTEM includes the addition of a breccia lens to each crater, which is composed of "regolith" material (Hirabayashi et al. 2017). For simple craters ( ), the maximum breccia lens depth bs is given by Orphal (1979):
), the maximum breccia lens depth bs is given by Orphal (1979):

where a value of Kb = 0.32 is used in these simulations Orphal (1979).
Due to a lack of data regarding complex crater breccia lens thicknesses on the lunar surface, and only a few, very scattered data points regarding terrestrial complex craters, for complex craters in our model (Ds > Dtr), we adopt the conservative stance that the breccia lens thickness will continue to have roughly the same fraction of crater's maximum depth as it has in the case of a simple crater. That is, the maximum breccia lens depth bc is assumed to be

where a value of (Kb/Kd) = (0.32/0.19) = 1.68421 is used in these simulations; that is, the breccia lens has a maximum thickness that is 68.4% of the maximum crater depth. The dashed, dark green line in Figure 4 plots the computed breccia lens depth, using Equations (21) and (22), as a function of final crater diameter, Equations (4) and (6), and compared it to the maximum breccia depth versus diameter study of small terrestrial craters shown in Figure 1 of Orphal (1979) (filled purple triangles).
As a rough check on Equations (20) and (22), we applied these expressions in the terrestrial environment, where the simple-complex transition diameter Dtr = 1.6 km, and we compared the results to the handful of terrestrial craters for which borehole breccia lens thicknesses have been obtained:
- (a)For the 1.2 km diameter Meteor Crater, Roddy et al. (1975) found an average crater collapse breccia lens thickness of 175 m; our model estimates a breccia lens thickness of 156 m.
- (b)For the 3.8 km diameter Brent crater, Grieve (1978) states that the melt-bearing breccias occupy the uppermost 160 m of the breccia lens, which has a maximum thickness of 630 m; our model estimates a breccia lens thickness of 252 m.
- (c)
- (d)
- (e)For the ∼200 km diameter Sudbury crater, French (1967), Dressler et al. (1996), and Abramov & Kring (2004) describe an usually thick breccia layer, the Onaping formation, "which is a 1.4 km thick sequence of fragmental and minor intrusive rocks, which are thought to represent fallback and washback breccia"; our model estimates a breccia lens thickness of 765 m.
Although our expression for complex crater breccia lens thickness (Equation (22)) does produce estimates that are within a factor of two of the borehole measured values, there is significant variation in the measured breccia thickness at the above terrestrial craters, due to variations in borehole locations and processes not operating on the Moon (such as the presence of water in the target). For example, Chicxulub and Sudbury have roughly similar diameters, but have significantly different observed breccia lens thicknesses. Unfortunately, the sparse terrestrial crater data set, with its high degree of data scatter, prevents further refinement of this expression. As such, Equation (22) represents the largest source of error in our lunar Upper Megaregolith formation modeling (Section 3.2).
Complicating the above, large complex craters also include bedrock that has been melted in place and thus is not part of the crater excavation flow or crater collapse breccia lens. This is particularly important for large basins, because melt production increases dramatically with basin diameter (Grieve & Cintala 1992; Pierazzo et al. 1997; Cintala & Grieve 1998). Such melt sheets, consisting primarily of melted in situ bedrock material, are not included in this model, and are more properly considered to be part of the Lower Megaregolith layer described in Section 1.1.3.
For simple craters, the computed breccia lens will follow the paraboloid shape of the pre-collapse transient crater, with diameter Dt (Equation (3)) and depth bs (Equation (21)), until it intersects the final crater paraboloid form (diameter Ds and depth ds). Since the transient crater has a diameter Dt that is ∼85% of the final crater Ds, the formation of a breccia lens will leave a "bare" crater wall occupying the outermost ∼15% of the crater's radius.
For complex craters, the sides of the computed breccia lens will follow the paraboloid shape of the pre-collapse transient crater (diameter Dt and depth bs) until it too intersects the final crater paraboloid form (diameter Df and depth ds), while having a ceiling formed by the actual complex crater depth dc (Equation (20)) and a floor formed by the actual complex crater breccia lens depth bc (Equation (22)). Similar to simple craters, the transient crater has a diameter Dt that is ∼85% that of the final crater Df, such that the formation of a breccia lens will leave a "bare" terrace zone occupying the outermost ∼15% of the crater's radius.
If the crater is complex (Ds > Dtr), a central peak is also added to the crater form. The maximum height hp of this central peak is given by Hale & Grieve (1982) as

The sides of this central peak are given a slope of 18°, about 1/2 the typical angle-of-repose. The breccia lens beneath this central peak is thinned by the same amount that the terrain above is uplifted, thus imparting this uplift to both breccia lens and bedrock layer. Note that although a central peak is included in the model, peak rings and annular troughs for the largest basins are not, given their relative scarcity compared to the much more common crater forms.
Figure 5 shows four example crater profiles of the crater forms automatically generated within the model, beginning with a simple crater and progressing up to a large basin. Labels point out the primary features described in this section, along with the ejecta blanket described in Section 2.3.
Figure 5. Four example crater cross sections, showing the crater forms automatically generated within the SBCTEM (axes have a 1:1 scale, without vertical exaggeration), beginning with a simple crater and progressing up to a large basin. The fractured bedrock substrate is shown in gray, with impact-generated regolith, both breccia lens and ejecta blanket, shown in black. The impactor diameters used to generate these craters are 0.5 km (9.3 km crater), 1.0 km (17.1 km crater), 4.0 km (65.5 km crater), and 16.0 km (240.1 km crater), with the impactor striking the surface at a speed of 17.0 km s−1.
Download figure:
Standard image High-resolution image2.4.2. Crater Exterior Form
The height of a simple, paraboloid crater's rim above the surrounding reference plane is designated by a rim height to diameter ratio (hrs/Ds), also user input designated input parameter. For simple craters (Ds ≤ Dtr), the rim height is given by Pike (1977):

where a value of Kd = 0.04 is used in these simulations. For complex craters (Ds > Dtr), the rim height is given by Pike (1977):

where a value of Kd = 0.04 is used in these simulations.
Outside of the crater's rim, the degree of surface uplift falls off rapidly as a function of distance from the impact site by a power-law factor of about hrimdrop = −3 to −4, where this falloff exponent is poorly quantified due to its burial beneath the crater's ejecta blanket (Shoemaker 1963; McGetchin et al. 1973; Settle & Head 1977; Melosh 1989). For these lunar surface simulations, a value of hrimdrop = −3 was used.
Note that the uplifted (or upturned) ground associated with the crater rim is in addition to the material laid down in the ejecta blanket. Because the user selects the parameters that determine the height hrs and fall off with distance hrimdrop of the upturned crater rim, and both add positive topography to the simulation, these parameters must be selected with care. Ideally, the mean elevation of the cratered terrain either remains relatively constant or very slowly deflates over time and impacts, as material is lost to space due to ejection at greater than the target's escape velocity. That is, because crater form and landed ejecta production are handled separately within the model, it is incumbent upon the user to be mindful of model surface mass conservation and to choose these parameters accordingly. This feature thus provides a check on the validity of these parameters when their cumulative effect over thousands to millions of impacts becomes evident. As an aid to the user, the depth of surface terrain lost to space (due to ejecta escape) and the mean terrain map elevation are both computed and displayed following each simulation time step, where these two values should track with each other.
Table 1 lists the values of the SBCTEM user input parameters used in these lunar surface simulations, selected based upon our previous lunar surface studies (Richardson 2009; Minton et al. 2015). For a full description of the impact-induced seismic shaking module currently used by SBCTEM, which will gradually the smooth terrain around each newly formed impact crater, see Richardson (2009, 2013). The selected Upper Megaregolith density ρt = 2500 kg m−3 is consistent with the GRAIL results of Han et al. (2014), Besserer et al. (2014), while the selected underlying bedrock density of ρt = 3500 kg m−3 is consistent with the Apollo seismic experiment results of Toksoz et al. (1974). With respect to crater diameter scaling (Equation (1)), the most important parameter is the selected bedrock effective target strength 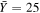 MPa, which can be used to shift a crater diameter distribution (such as that shown in Figure 7) either left or right (toward either smaller or larger crater sizes) when the target surface gravity g and the impactor population are held constant. As described in Richardson (2009), a value of
MPa, which can be used to shift a crater diameter distribution (such as that shown in Figure 7) either left or right (toward either smaller or larger crater sizes) when the target surface gravity g and the impactor population are held constant. As described in Richardson (2009), a value of  does the best job of aligning the crater count curve inflection points in the produced model crater population with the Lunar Highland's observed crater population, when a Main Asteroid Belt (MAB) impactor population is assumed to be the primary source of impactors (Section 3.1).
does the best job of aligning the crater count curve inflection points in the produced model crater population with the Lunar Highland's observed crater population, when a Main Asteroid Belt (MAB) impactor population is assumed to be the primary source of impactors (Section 3.1).
Table 1. SBCTEM Lunar Surface Input Parameters
| Grid length | 2000 |
| Pixel scale | 3080.0 m |
| Surface gravity g | 1.62743 m s−2 |
| Target radius rt | 1737.35 × 103 |
| Bedrock density ρt | 3500.0 kg m−3 |
Bedrock strength 
|
25.0 MPa |
| Regolith density ρt | 2500.0 kg m−3 |
Regolith strength 
|
0.5 MPa |
| Impactor density ρi | 2500.0 kg m−3 |
| Scaling-law μ | 0.55 |
| Scaling-law K1 | 0.20 |
| Crater depth ds/Ds | 0.19 |
| Breccia depth bs/Ds | 0.32 |
| Rim height hrs/Ds | 0.04 |
| Rim falloff hrimdrop | −3.0 |
| Crater profile fraction | 1.00 |
| Crater count fraction | 0.45 |
| Seismic quality factor Q | 3000.0 |
| Impact seismic efficiency η | 1.0 × 10−6 |
| P-wave velocity vs | 3000.0 m s−1 |
| Mean free path for scattering ls | 500.0 m |
Download table as: ASCIITypeset image
3. Lunar Surface Simulations
3.1. Impactor Population Determination
A long-standing debate in the cratering community has been in regard to the primary source of impactors for the inner solar system, and the Lunar surface in particular: is it either cometary or asteroidal in origin? In an attempt to answer this question, Strom et al. (2005) showed that when mapped through the impact crater scaling relationships (Section 2.2) to form a "production population," a crater SFD directly reflective of the impactor SFD, the modern-day asteroid population yields a very good match to the cratering record on the Lunar surface, thus pointing to the asteroid belt as the primary source of impactors in the inner solar system. In that same year, O'Brien & Greenberg (2005) and Bottke et al. (2005) published the results of collisional evolution models for the Main Belt asteroids, showing that while greatly depleted over the time since its formation, the Main Belt continues to reflect its early SFD; that is, it displays a "fossilized" SFD. This is because the shape of the SFD curve for a collisionally evolved population (such as the asteroids) is more determined by material properties and impact parameters than by the starting, or original, SFD of the population (Bottke et al. 2005).
In Richardson (2009), we performed a preliminary test of the Strom et al. (2005) hypothesis as part of a much larger paper concerning crater population saturation and equilibrium, and we concluded then that the MAB did indeed appear to be a very good match to the cratering record of the Lunar Highlands. However, a much more detailed investigation of this hypothesis, described in Minton et al. (2015), revealed that although the Lunar Highlands crater SFD could be correctly matched using an MAB SFD for craters ≲200 km in diameter, doing so consistently created too many large basins ≳1000 km in diameter, when compared to the actual lunar surface (only 5% of our CTEM runs produced the correct number of large basins). This implies that while relatively close, the modern-day MAB SFD is different from the impactor SFD that actually produced the Lunar Highlands cratering record, having either too few impactors in the 0.5–20 km diameter range or too many impactors in the 20–200 km diameter range (or both).
Therefore, the first task of this study was to develop a custom-built impactor population that correctly reproduces the Lunar Highlands crater SFD, and assumed to have originated in the Main Belt region of the solar system, and thus possessing the impact velocity distribution developed in Minton & Malhotra (2010) and shown in Figure 2 (left). Over the course of several SBCTEM lunar surface simulations (Luna 1–13), we began with the model MAB SFD produced by Bottke et al. (2005) and then customized it to more accurately reproduce the Lunar Highlands crater population, both with respect to craters ≲250 km diameter, which are in a state of crater density equilibrium, and craters ≳250 km diameter, which are not. Particular attention was paid to the production of very large basins ≳1024 km in diameter, such that over the course of a given simulation, no more than two such basins would be produced, consistent with the presence of Mare Imbrium (1145 km diameter) and the South Pole-Aitken basin (∼2500 km diameter). Note that although Strom et al. (2005) also included Mare Frigoris (1445 km diameter) in his lunar crater SFD, most sources are uncertain as to its having an impact origin, and we thus did not include it in our desired production limit for basins ≳1024 km.
Figure 6 shows our final custom Lunar Highlands impactor population (named LH Custom) compared to previous model Main Belt asteroid populations from O'Brien & Greenberg (2005), Bottke et al. (2005), and Minton et al. (2015). As mentioned above, we used the Bottke et al. (2005) model Main Belt asteroid population as our starting point and then attempted to keep our LH Custom impactor population as consistent with all three previous model populations as possible, while still reproducing the Lunar Highlands crater population accurately. The cumulative SFD plot shown in Figure 6 (left) is placed in terms the number of impacts per year per km2 on the surface of a body exposed to the mean Main Belt impactor flux: that is, the impactor flux experienced if the target body was in the center of the MAB (which our Moon obviously is not). Note that all flux exposure ages in this work are placed in terms of MAB exposure age and therefore do not represent an actual exposure age. This standardized flux exposure rate is thus used as a way to compare one model run to another in a relative fashion, in addition to tracking the total number of impacts and the total impacted mass delivered.
Figure 6. O'Brien & Greenberg (2005), Bottke et al. (2005), Minton et al. (2015), and our LH Custom MAB impactor population plotted in the form of (left) a cumulative SFD, and (right) a relative SFD (Crater Analysis Techniques Working Group et al. 1979).
Download figure:
Standard image High-resolution imageFigure 6 (right) shows the O'Brien & Greenberg (2005), Bottke et al. (2005), Minton et al. (2015), and LH Custom asteroid impactor populations in a relative SFD plot (relative density, or R-plot) fashion, which is given by (Crater Analysis Techniques Working Group et al. 1979)

where Ni is the number of craters in bin i, Acnt is the surface area of the portion of the surface where crater counts were conducted, Di and Di − 1 are the crater diameters at the bin boundaries, and  is the geometric mean crater diameter of the bin, given by
is the geometric mean crater diameter of the bin, given by

wherein the crater counts presented in this study, we use the standard bin size  specified in Crater Analysis Techniques Working Group et al. (1979). The primary advantage in using a relative density plot is that most crater populations have cumulative SFD slope indices within the range of −2 ± −1; therefore, they will plot as non-sloping (horizontal) or moderately sloping lines on an R-plot. The shallow average slopes of the lines on an R-plot thus make any changes in the SFD more obvious and facilitate identifying differences in the distribution function and densities among crater populations (Crater Analysis Techniques Working Group et al. 1979). The other advantage of the relative density plot is that when a crater population reaches a state of crater density equilibrium (empirical saturation), the R-values will generally fall between 0.1 and 0.3, and have an overall horizontal (∼−2 cumulative power-law) R-plot slope (Gault 1970; Richardson 2009).
specified in Crater Analysis Techniques Working Group et al. (1979). The primary advantage in using a relative density plot is that most crater populations have cumulative SFD slope indices within the range of −2 ± −1; therefore, they will plot as non-sloping (horizontal) or moderately sloping lines on an R-plot. The shallow average slopes of the lines on an R-plot thus make any changes in the SFD more obvious and facilitate identifying differences in the distribution function and densities among crater populations (Crater Analysis Techniques Working Group et al. 1979). The other advantage of the relative density plot is that when a crater population reaches a state of crater density equilibrium (empirical saturation), the R-values will generally fall between 0.1 and 0.3, and have an overall horizontal (∼−2 cumulative power-law) R-plot slope (Gault 1970; Richardson 2009).
As Figure 6 (right) shows, our LH Custom impactor population requires (a) an increase in the number of impactors in the 0.5–20 km diameter range as compared to that of Bottke et al. (2005), up to the number used by Minton et al. (2015) and (b) roughly the same number of impactors in the 20–200 km diameter range as that of Bottke et al. (2005), but less than the number used by Minton et al. (2015). Note that this LH Custom Main Belt asteroid impactor population retains the double-peaked shape of a silicate rock, collisionally processed SFD, as initially described in Bottke et al. (2005) and O'Brien & Greenberg (2005) and also remains within the amplitude boundaries of the other Main Belt asteroid model populations: O'Brien & Greenberg (2005), Bottke et al. (2005), and Minton et al. (2015).
The Lunar Highlands crater count resulting from our customized MAB impactor population is shown in Figure 7, for the five final SBCTEM lunar surface simulations, Luna 14–18, conducted for this study (using five sequential, Monte Carlo integer seeds, without cherry-picking). Figure 7 (left) shows the crater counts produced as a function of MAB exposure time in simulation Luna 15, as compared to the Lunar Highlands craters counts presented in Strom et al. (2005). The best χ2 R-value fit countable crater numbers are indicated by the blue line, while the total number of craters in each size bin actually produced over the course of the simulation is shown by the dashed green line (the "production function"). Note that because this production function has a cumulative power-law slope of −2.1 (averaged over the full range of impactors used in this model: 0.15–310 km), it is tilted upward at smaller crater sizes, such that crater density equilibrium (empirical saturation) will be reached first at smaller crater sizes and then progress left to right as larger crater sizes also reach crater density equilibrium (Gault 1970; Richardson 2009). At the point of best χ2 R-value fit between the model crater population and the Strom et al. (2005) crater counts, craters ≲250 km diameter are in a state of crater density equilibrium, while craters ≳250 km diameter are not.
Figure 7. (Left) Crater counts produced as a function of Main Asteroid Belt (MAB) exposure time in SBCTEM simulation Luna 15, as compared to the Lunar Highlands craters counts presented in Strom et al. (2005). The best-fit countable crater numbers are indicated by the blue line, while the total number of craters in each size bin actually produced over the course of the simulation are shown by the dashed green line. (Right) The best χ2 R-value fit between the model crater population and the Strom et al. (2005) crater counts for all five final SBCTEM simulations (Luna 14–18), including a comparison to the Lunar Highlands crater counts from Head et al. (2010).
Download figure:
Standard image High-resolution imageFigure 7 (right) shows the best χ2 R-value fit between the model crater population and the Strom et al. (2005) crater counts for all five final SBCTEM simulations (Luna 14–18). This plot also includes the Lunar Highlands crater counts produced via the Lunar Orbiter Laser Altimeter (LOLA) aboard the Lunar Reconnaissance Orbiter (LRP) spacecraft (Head et al. 2010). It is important to note that in attempting to match these observed Lunar Highlands crater counts, there is a built-in tension between trying to match the number of basins in the 512–1024 km diameter size range, wherein Strom et al. (2005) has a total of 15 basins, and the 1024–3000 km diameter size range, wherein Strom et al. (2005) has a total of 3 basins (and we only count 2 basins, as discussed previously). Using only a double-peaked asteroidal impactor population (Figure 6 (right)), one cannot satisfy both basin constraints simultaneously. We therefore opted to make the larger basin (>1024 km diameter) constraint the higher priority, producing a mean of 1.8 ± 0.4 in our five final simulations, which left these simulations falling a bit short with respect to the number of countable basins 512–1024 km in diameter, producing a mean of 10.4 ± 2.3. It is possible that the actual lunar surface experienced a higher number of impacts in this 512–1024 km diameter size range due to the small number (Poisson) statistical nature of both the naturally occurring and simulated impactor flux in this large size range. However, it is always safer to assume that the observed counts are typical, rather than atypical, such that there remains room for further, minor improvements in determining the SFD shape of the asteroidal impactor population that actually produced the Lunar Highlands crater population SFD.
Table 2 lists various crater-related values from our five final SBCTEM lunar surface runs, at the point of best χ2 R-value fit between the model crater population and the Strom et al. (2005) crater counts. In Table 2, TC is the total crater number (down to a single pixel remaining), OC is the observable (countable) crater number, and SR is the "saturation ratio" (TC/OC), first with respect to craters ≥8 km diameter (about 3 pixels in diameter) and second with respect to basins ≥256 km diameter. It is important to point out that this work does not explore the actual timing of the accumulated bombardment at all, where we instead place all ages in terms of an MAB exposure age, as discussed in Section 3.1. Rather than this arbitrary "age," the key parameters from this modeling are the total mass delivered to the surface, and the total number of craters produced as a result, required to accurately reproduce the observed Lunar Highlands cratering record (Figure 7).
Table 2. SBCTEM Lunar Run Crater Data
| Run | Age (Gy) | Mass (kg) | Lunar wt% | TC ≥ 8 km | OC ≥ 8 km | SR ≥ 8 km | TC ≥ 256 km | OC ≥ 256 km | SR ≥ 256 km |
|---|---|---|---|---|---|---|---|---|---|
| Luna 14 | 2.07 | 3.209 × 1019 | 0.0437 | 60204 | 25071 | 2.40 | 58 | 39 | 1.49 |
| Luna 15 | 2.67 | 4.994 × 1019 | 0.0680 | 78337 | 26581 | 2.95 | 69 | 29 | 2.38 |
| Luna 16 | 3.03 | 4.818 × 1019 | 0.0656 | 86412 | 27909 | 3.10 | 68 | 35 | 1.94 |
| Luna 17 | 2.90 | 3.224 × 1019 | 0.0439 | 85291 | 27377 | 3.12 | 58 | 29 | 2.00 |
| Luna 18 | 2.80 | 2.342 × 1019 | 0.0319 | 82456 | 27990 | 2.95 | 61 | 36 | 1.69 |
| Mean | 2.69 | 3.717 × 1019 | 0.0506 | 78540 | 26986 | 2.9 | 62.8 | 33.6 | 1.9 |
| StdDev | 0.37 | 1.144 × 1019 | 0.0156 | 10714 | 1209 | 0.3 | 5.4 | 4.4 | 0.3 |
Download table as: ASCIITypeset image
The impact crater "saturation ratio" is the ratio between the total number of impact craters produced on the surface (the production function) and the total number of observable or countable craters on the surface once crater density equilibrium (empirical saturation) has been reached. As discussed in Section 3 of Chapman & McKinnon (1986) and Section 1 of Richardson (2009), the degree to which the Lunar Highlands represent an equilibrium crater population is a long-standing issue in the cratering community. In Section 4 of Richardson (2009), we showed that (a) the Lunar Highlands cratering record does indeed represent a crater population in a state of crater density equilibrium for craters ≲250 km diameter, and (b) even after crater density equilibrium has been reached, the crater population will continue to follow (reflect) the shape of the production population that created it, verifying the modeling results of Chapman & McKinnon (1986). With this current work, we find that the saturation ratio for all craters ≥8 km diameter for the Lunar Highlands is 2.9 ± 0.3 (Table 2), as shown by the difference between the solid blue and dashed green curves in Figure 7 (left). This result is consistent with the much simpler Monte Carlo model shown in Figure 22 of Chapman & McKinnon (1986), in which they found a saturation ratio of about 2–3 for the Lunar Highlands.
An additional, available constraint is to compare the total number of basins ≥256 km in diameter produced, including those which have been buried, softened, or otherwise degraded to the point of no longer being considered "countable," to the total number of countable basins ≥256 km in diameter at the point of best χ2 R-value fit. As listed in Table 2, the total number of basins ≥256 km in diameter, regardless of degradation state, is 62.8 ± 5.4 on average, whereas the total number of countable basins ≥256 km in diameter is 33.6 ± 4.4 on average, for a basin saturation ratio of SR = 1.9 ± 0.3. Neumann et al. (2015) used a combination of GRAIL and LOLA data to identify ∼53 lunar basins ≥256 km in diameter, about 10 of which had not been previously identified, given the 43 countable basins ≥256 km in diameter identified by Strom et al. (2005) using standard crater counting techniques, yielding an observed lunar basin saturation ratio of SR ≈ 1.2. The difference in these saturation ratios, 1.9 versus 1.2, is most likely due to the ability of visual crater counters to detect and measure large basins with a lower percentage of the basin's recognizable surface area remaining, as compared to the single, user-supplied value (generally 40%–50%) employed by SBCTEM for all crater sizes. Nevertheless, the 62.8 ± 5.4 basins ≥256 km in diameter present at the end of these simulations, regardless of their degradation state, compares favorably (within factor of ∼1.2) with the ∼53 basins identified on the actual lunar surface using GRAIL and LOLA data (Neumann et al. 2015).
The total mass of the impactors bombarding the surface over the course of the simulation is of particular interest, as a fraction of this mass is retained on Moon and becomes part of the upper lunar crust, leaving behind a chemical remnant signal (Mojzsis et al. 2019). In these five final simulations, we estimate a total impactor mass of 3.72 ± 1.14 × 1019 kg, or 0.0506 ± 0.0156 lunar weight percent (wt%), about 1.6 times higher than the 0.032 lunar wt% assumed for this bombardment in Mojzsis et al. (2019). Because the total impactor mass is dominated by the mass of the largest impactors (Minton et al. 2015), and the number of visible large basins on the lunar surface is well constrained (Strom et al. 2005; Head et al. 2010), we suspect that this factor of 1.6 difference is due to the amount of impactor material that is lost back to space as part of the impact-produced vapor plume and high-speed ejecta (Melosh 1989; Zhu et al. 2019). The implication from these SBCTEM simulations is that only about 2/3 of a large impactor's mass is retained by the lunar surface following the impact cratering process (Zhu et al. 2019).
3.2. Upper Megaregolith Modeling
Figure 8 plots the modeled lunar Upper Megaregolith growth as a function of an MAB exposure age for simulations Luna 14–18, which reach a mean depth of 1.4 ± 1.0 km at the point of best χ2 crater count R-value fit (Figure 7), at an MAB exposure age of 2.69 ± 0.37 Gy, as listed in Table 2. In Figure 8, large upward step changes in regolith depth are the result of large basin-forming impacts, which can cause the mean lunar Upper Megaregolith depth increase by up to 200–400 m due to a single impact. These Upper Megaregolith formation results are summarized in Table 3. Because SBCTEM has the user-determined ability to turn crater breccia lens creation off and on, we reperformed simulation Luna 14 without breccia lens creation to determine the contribution of impact ejecta deposits alone to the lunar Upper Megaregolith. This simulation produced a regolith layer 512 ± 417 m in depth (ejecta deposits only), as compared to a regolith 1290 ± 954 m in depth (ejecta deposits and breccia lenses), such that when both are included, impact ejecta deposits comprise ∼40% of the resulting Upper Megaregolith layer.
Figure 8. Plots of modeled lunar Upper Megaregolith growth as a function of MAB exposure age for simulations Luna 14–18, which reach a mean depth of 1.4 ± 1.0 km at the point of best χ2 crater count R-value fit (see Figure 7), at an MAB exposure age of between 2 and 3 Gy (see Table 2). A single simulation (Luna 15) was extended to an MAB exposure age of 10 Gy, revealing an equilibrium Upper Megaregolith depth of 1.9 ± 1.0 km beginning at an MAB exposure age of about 8–9 Gy.
Download figure:
Standard image High-resolution imageTable 3. SBCTEM Lunar Run Upper Megaregolith (UMR) Data
| Run | UMR Mean (m) | UMR Std (m) | UMR Max (m) |
|---|---|---|---|
| Luna 14 | 1290.18 | 954.04 | 5930.67 |
| Luna 15 | 1523.26 | 1029.58 | 6216.79 |
| Luna 16 | 1495.80 | 1012.95 | 6241.49 |
| Luna 17 | 1371.47 | 915.55 | 5721.53 |
| Luna 18 | 1312.95 | 866.72 | 5302.49 |
| Mean | 1398.73 | 955.77 | 5882.59 |
| StdDev | ⋯ | ⋯ | 388.99 |
Download table as: ASCIITypeset image
On the lunar surface, impact cratering is the primary means by which regolith is both produced, via ejecta deposits and crater collapse, and lost, via ejecta launch to space (Sullivan et al. 1996; Richardson et al. 2005). On such bodies, the regolith layer depth generally increases over time until it reaches an equilibrium state, wherein the losses to space from frequent small impacts (which fail to penetrate the regolith layer) are offset by infrequent large impacts, which do penetrate the regolith layer and thus produce fresh regolith. In Figure 8, we show the result of extending SBCTEM simulation Luna 15 out to an MAB exposure age of 10 Gy, wherein the simulated Upper Megaregolith depth gradually reaches a plateau of 1.9 ± 1.0 km at an MAB exposure age of about 8–9 Gy. At 8–9 Gy MAB exposure age, which corresponds to a cratering saturation ration of 6.2–7.5. the crater counts are in a state of crater density equilibrium at all sizes. The problem in considering the possibility that the lunar surface may have experienced such a significantly increased bombardment level, and thus possesses an Upper Megaregolith that is in a state of regolith depth equilibrium, is that the number of large basins produced in that 8–9 Gy MAB exposure is much too high, with about 40–46 basins 512–1024 km in diameter produced and about 9–10 basins >1024 km in diameter produced. As previously discussed in Section 3.1, the actual number of recognized lunar basins in the 512–1024 km diameter size range is 15, with only 2–3 recognized basins >1024 km in diameter (Strom et al. 2005; Head et al. 2010; Minton et al. 2015). We therefore conclude that the lunar Upper Megaregolith is not currently in a state of regolith depth equilibrium and would have continued to grow by another ∼0.5 km or so, had the bombardment that produced it continued.
To illustrate the high degree of local variability present in lunar Upper Megaregolith depths, from 0 km in a few places (usually crater walls and terrance zones, see Section 2.4.1), up to a maximum of 5.9 ± 0.4 km (Table 3), Figure 9 shows a cross section through a segment of SBCTEM lunar surface simulation Luna 14. The region depicted is a 1000 × 300 pixel (3080 × 924 km) portion of the fully simulated lunar surface, 2000 × 2000 pixels (6160 × 6160 km), at a resolution of 3.08 km/pixel. The dashed, horizontal white line through the center of the terrain map indicates the location of the cross section shown beneath the terrain map. Compare this cross section to Figure 1. This shaded-relief terrain map also shows an overhead view of the automatically generated crater forms described in Section 2.4 and shown in Figure 5. Note that because these full-scale lunar simulation only involve impactors ⪆150 m in diameter (capable of producing a 1 pixel, 3.08 km diameter crater), small-scale "impact gardening" and Surficial Regolith generation is not simulated.
Figure 9. Cross section (lower panel) through a 3080 × 924 km (1000 × 300 pixel) portion of SBCTEM lunar surface simulation Luna 14 (upper panel). The dashed, horizontal white line through the terrain map indicates the location of the cross section. The cross section is displayed using a vertical scale exaggeration of 20:1, with the fractured bedrock substrate shown in gray and the overlying, accumulated Upper Megaregolith layer shown in black.
Download figure:
Standard image High-resolution imageFigure 10 shows a histogram of lunar Upper Megaregolith depth for SBCTEM simulation Luna 15, in which depths of <1.0 km were produced over ∼36% of the surface, depths of 1.0–3.0 km were produced over ∼55% of the surface, and depths of >3.0 km were produced over ∼9.0% of the surface at the point of best χ2 fit between model and actual crater count R-values (Figure 7 (left)). This histogram analysis compares favorably with the early Monte Carlo modeling work of Aggarwal & Oberbeck (1979), who found that 50% of the highlands is cratered to a depth of 1 km; Hoerz et al. (1976), who found that 50% of the highlands is cratered to a depth of 2–3 km; and Cashore (1987), who found that at a saturation ratio of 2 times the observed highlands crater density, 50% of the surface is cratered to 2 km or greater. Overall, these SBCTEM simulations, which produced a mean Upper Megaregolith depth of 1.4 ± 1.0 km, provide an updated validation of the observational findings of Thompson et al. (1979), who found an Upper Megaregolith at least 2 km deep, as well as earlier modeling results, which estimated an Upper Megaregolith depth of 1.9 ± 0.5 km (Short & Forman 1972), about 2–3 km (Hoerz et al. 1976), and about 1.9–2.0 km (Aggarwal & Oberbeck 1979).
Figure 10. Normalized histogram of Upper Megaregolith depth for SBCTEM simulation Luna 15 (4 × 106 surface elements), using a bin width of 200 m. Depths of 1.0–3.0 km were produced over 55.4% of the surface, depths of <1.0 km were produced over 35.6% of the surface, and depths of >3.0 km were produced over 9.0% of the surface.
Download figure:
Standard image High-resolution image4. Conclusion
In Section 1, we divide the classic "lunar megaregolith" layer into three distinct regions: (1) a Surficial Regolith layer, about 5–20 m in depth (Oberbeck & Quaide 1968; Quaide & Oberbeck 1968; Bart et al. 2011; Yue et al. 2019), consisting of loose, unconsolidated fines and breccia, and characterized by frequent overturn and comminution caused by small meteoritic impacts; (2) an Upper Megaregolith layer, about 1–3 km in depth (Short & Forman 1972; Hoerz et al. 1976; Aggarwal & Oberbeck 1979; Thompson et al. 1979), consisting of depositional layers of brecciated and/or melted material, and characterized by the transport and deposition of material via either transient crater gravitational collapse or impact ejecta ballistic sedimentation; and (3) a Lower Megaregolith layer, about 20–25 km in depth (Dainty et al. 1974; Toksoz et al. 1974; Wiggins et al. 2019), consisting of bedrock that has been fractured in place, and characterized by a fracture-density and fragment-size distribution that decreases rapidly with increasing depth.
The purpose of this study was to model the formation of the lunar Upper Megaregolith layer, the least well characterized of the three layers listed above, using modern scaling relationships and a three-dimensional terrain, Monte Carlo cratering model. Our first task was to accurately model the Lunar Highlands cratering record. In Section 3.1, we described the development of an impactor population that accurately reproduces the Lunar Highlands crater population, both for craters ≲250 km diameter, which are in a state of crater density equilibrium, and craters ≳250 km diameter, which are not. This model impactor population is assumed to be asteroidal in nature, originating in the Main Belt, possesses the general SFD shape of a collisionally evolved population, and is consistent with previously developed MAB population models (Bottke et al. 2005; O'Brien & Greenberg 2005; Minton et al. 2015). Based upon these lunar surface simulations, we estimate that a total delivered impactor mass of 3.72 ± 1.14 × 1019 kg, or 0.0506 ± 0.0156 lunar weight percent (wt%), is required to reproduce the observed Lunar Highlands cratering record. The model's final crater saturation ratio (total produced/final countable) for all craters >8 km diameter is 2.9 ± 0.3, consistent with the value of 2–3 obtained from the early Monte Carlo simulation work of Chapman & McKinnon (1986).
In Section 3.2, we applied this developed impactor population in five simulations of Upper Megaregolith growth on the lunar surface, in order to produce a good statistical sample, given the Monte Carlo nature of this model, particularly at large basin sizes. Our five final lunar surface simulations yield an Upper Megaregolith depth of 1.4 ± 1.0 km at the point of best χ2 R-value fit between the model crater population and the Strom et al. (2005) Lunar Highlands crater counts. This Upper Megaregolith layer consists of ∼60% crater collapse deposits and ∼40% impact ejecta deposits and possesses a high degree of local variability, from 0 km in a few places up to a maximum of 5.9 ± 0.4 km, with depths of 1–3 km produced over ∼55% of the modeled lunar surface. These results provide an updated validation of earlier modeling results that estimated an Upper Megaregolith depth of 1.9 ± 0.5 km (Short & Forman 1972), about 2–3 km (Hoerz et al. 1976), and about 1.9–2.0 km (Aggarwal & Oberbeck 1979), as well as the observational results of Thompson et al. (1979), who found an Upper Megaregolith layer at least 2 km in depth. Our simulations also indicate that the current lunar Upper Megaregolith is not in a state of regolith depth equilibrium.
This work was funded by NASA Grant 80NSSC17K0732, Integrated Modeling of Early Impact Bombardments, and NASA Grant 80NSSC19K0032, Constraining Lunar Bombardment History by Modeling Age Distributions of Ancient Impact Melts. We would also like to thank both William Hartmann and H. Jay Melosh for their informative discussions regarding the planetary science history of the enigmatic "lunar megaregolith."













