Abstract
The spin properties of merging black holes observed with gravitational waves can offer novel information about the origin of these systems. The magnitudes and orientations of black hole spins offer a record of binaries' evolutionary history, encoding information about massive stellar evolution and the astrophysical environments in which binary black holes are assembled. Recent analyses of the binary black hole population have yielded conflicting portraits of the black hole spin distribution. Some works suggest that black hole spins are small but nonzero and exhibit a wide range of misalignment angles relative to binaries' orbital angular momenta. Other works conclude that the majority of black holes are nonspinning while the remainder are rapidly rotating and primarily aligned with their orbits. We revisit these conflicting conclusions, employing a variety of complementary methods to measure the distribution of spin magnitudes and orientations among binary black hole mergers. We find that the existence of a subpopulation of black holes with vanishing spins is not required by current data. Should such a subpopulation exist, we conclude that it must contain ≲60% of binaries. Additionally, we find evidence for significant spin–orbit misalignment among the binary black hole population, with some systems exhibiting misalignment angles greater than 90°, and see no evidence for an approximately spin-aligned subpopulation.

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The spins of black holes in merging binaries detected with gravitational waves promise to illuminate open questions in massive stellar evolution and compact binary formation. The orientations of component black hole spins may differentiate between binaries formed via isolated stellar evolution and those formed dynamically in clusters or the disks of active galactic nuclei, and additionally offer a means of measuring natal kicks that black holes receive upon their formation (Rodriguez et al. 2016; Vitale et al. 2017; Farr et al. 2017; Gerosa & Berti 2017; O'Shaughnessy et al. 2017; Gerosa et al. 2018; Liu & Lai 2018; Wysocki et al. 2018; Fragione & Kocsis 2020; McKernan et al. 2020; Callister et al. 2021a; Abbott et al. 2021a; Steinle & Kesden 2021). Spin magnitudes, meanwhile, are determined by poorly understood angular momentum processes operating in stellar cores and may be further affected by binary processes such as tidal torques or mass transfer (Qin et al. 2018; Bavera et al. 2020, 2021; Steinle & Kesden 2021; Zevin & Bavera 2022). Black holes with large spin magnitudes might also point to hierarchical assembly in dense environments, involving component black holes that are themselves the products of previous mergers (Gerosa & Berti 2017; Rodriguez et al. 2019; Kimball et al. 2020, 2021; Doctor et al. 2020; Gerosa & Fishbach 2021).
Despite the large astrophysical interest, spin measurements are hampered by the fact that spin dynamics have a relatively weak imprint on the gravitational-wave signal. The main effect of spins (anti)parallel to the Newtonian orbital angular momentum is to (speed up) slow down the binary inspiral and merger. Spins in the plane of the orbit, on the other hand, give rise to precession that modulates the amplitude and phase of emitted gravitational waves. Even with informative measurements of these effects, however, it is not straightforward to constrain all six spin degrees of freedom independently.
Recent work (Abbott et al. 2021a; Galaudage et al. 2021; Roulet et al. 2021) has yielded conflicting conclusions regarding the distribution of spins among the binary black hole population witnessed by Advanced LIGO (Aasi et al. 2015) and Virgo (Acernese et al. 2015). Specifically:
- 1.Do binary black holes have small but nonzero spins that may be misaligned significantly with the Newtonian orbital angular momentum, i.e., with spin–orbit misalignments >90°?
- 2.Or, do a majority of binaries have spins that are identically zero or, if nonzero, preferentially aligned with the Newtonian orbital angular momentum, i.e., with misalignments <90°?
These questions highlight the subtleties and difficulties inherent in statistical analysis of weakly informative measurements. This debate also hinges on a variety of technical difficulties related to hierarchical inference of narrow population features using discretely sampled data.
The two possibilities listed above carry considerably different astrophysical implications for the assembly and evolution of binary black hole mergers. Systems arising from isolated binary evolution are traditionally expected to have spins preferentially parallel to their orbital angular momenta (Belczynski et al. 2008; Qin et al. 2018; Zaldarriaga et al. 2018; Bavera et al. 2020). Significant spin–orbit misalignment, in contrast, is considered difficult to achieve under canonical isolated binary evolution and so would indicate either the presence of alternative formation channels or a change in the paradigm of isolated binary evolution (Rodriguez et al. 2016; Farr et al. 2017; Callister et al. 2021a; Steinle & Kesden 2021; Tauris 2022). The degree to which black holes are observed to be primarily spinning or nonspinning, meanwhile, would support or refute theories positing highly efficient angular momentum transport in stellar interiors (Spruit 1999; Fuller et al. 2015; Fuller & Ma 2019).
Our goal in this paper is to revisit these incompatible conclusions. In Section 2 we review recent literature and describe in more detail what is known, unknown, and still debated about binary black hole spins. We then employ a string of increasingly sophisticated analyses to study the population of binary black hole spins and determine what we can and cannot robustly conclude about the magnitudes and orientations of black hole spins. We begin in Section 3 with a simple counting argument, which demonstrates that the fraction of black holes that are nonspinning is consistent with zero. We then turn to full hierarchical analyses of the binary black hole population, studying the distributions of effective inspiral spins (Section 4) and component spin magnitudes and orientations (Section 5). In all cases, we find that the fraction of nonspinning black holes can comprise up to 60%–70% of the total population, but that this fraction cannot be confidently bounded away from zero. Overall, the inferred spin-magnitude distribution is consistent with a single population extending smoothly from zero up to magnitudes of approximately 0.4. Additionally, we find a preference for considerable spin–orbit misalignments among the binary black hole population, with some spins inclined by more than 90° relative to their orbits.
2. The Spins of Black Holes in Binaries
Each component black hole in a binary has dimensionless spin vectors χ 1 and χ 2. Six parameters are needed to fully specify these two spins, with each spin vector characterized by a magnitude 0 ≤ χi ≤ 1, tilt angle θi , and azimuthal angle ϕi , where i ∈ {1, 2}.
Not all spin degrees of freedom are as dynamically important in a gravitational-wave signal, however. While the two spin magnitudes are conserved throughout the binary evolution (modulo horizon absorption effects; Poisson 2004; Chatziioannou et al. 2013), the four spin angles vary due to spin precession. A combination known as the effective inspiral spin is conserved under spin precession to at least the 2PN order 5 (Racine 2008):
where q = m2/m1 < 1 is the mass ratio. Though not conserved under spin precession, the effective precessing spin,
reflects the degree of in-plane spin and characterizes spin-precession dynamics (Schmidt et al. 2015). 6 Although modern waveform models make use of the full six-dimensional spin parameter space (Khan et al. 2019; Varma et al. 2019; Ossokine et al. 2020; Pratten et al. 2021), earlier versions were constructed in terms of χeff and χp, leveraging their relevance in binary dynamics.
At current signal strengths, it is not possible to meaningfully constrain all six spin parameters. When exploring the population of compact binary spins, we therefore generally work in one of two lower-dimensional spaces.
- 1.The most straightforward approach is to constrain the distribution of "effective" spin parameters. Though the χeff and χp distributions do not unambiguously reveal information about individual component spins, they do enable categorical conclusions to be made regarding compact binary spins. A nonvanishing χp distribution, for example, indicates that spins are not perfectly aligned with binary orbits, while the identification of negative χeff requires at least some component spins to be inclined by more that θi = 90°. A common approach, and the baseline model that we will extend below, is to treat the marginal distribution of χeff as a truncated Gaussian (Roulet & Zaldarriaga 2019; Miller et al. 2020). We refer to this as the Gaussian model; see Appendix A.1.
- 2.Going one step beyond the effective spin parameters, we can directly model the distribution of component spin magnitudes and tilt angles. A popular choice is to treat the component spin magnitude distribution as a Beta distribution, while spin tilts are drawn from a mixture between two components, an isotropic component and a preferentially aligned component (Talbot & Thrane 2017; Wysocki et al. 2019). The azimuthal spin angles are ignored and presumed to be uniformly distributed as ϕ1, ϕ2 ∼ U[0, 2π] (this assumption was relaxed in Varma et al. 2022). We assume that component spin magnitudes and tilts are independently and identically distributed within this model and refer to it as the Beta+Mixture model, 7 discussed further in Appendix A.2.
2.1. What We Know about Black Hole Spins
Before proceeding to explore the prevalence of zero-spin events and extreme spin–orbit misalignment (i.e., spin tilts larger than 90°), it is useful to first examine the conclusions that are broadly and robustly recovered by different analyses and authors.
(i.) Black hole spins are not all maximal. Following the first four binary black hole detections by Advanced LIGO, Farr et al. (2017), and Farr et al. (2018) determined that if all component spins are aligned (), then their magnitudes must be small, χi ≲ 0.3. If spins were assumed to be isotropically oriented, though, near-extremal spins were still allowed. Tiwari et al. (2018) conducted a similar analysis using an expanded catalog and also found large spins to be disfavored, regardless of their orientation. The degeneracy between spin magnitude and orientation was later broken by efforts to simultaneously measure these two properties. Using the Default model, Wysocki et al. (2019) and Abbott et al. (2019a) found that typical spin magnitudes are small, with 50% of black holes having χ ≲ 0.3. Abbott et al. (2019a) furthermore revisited the analysis of Farr et al. (2018), now finding that large spin magnitudes are moderately disfavored assuming isotropic orientations. Roulet & Zaldarriaga (2019), meanwhile, studied the χeff distribution, leveraging the Gaussian model to conclude that effective spins are concentrated about zero. They argued that, if component spins are aligned, then the measured χeff distribution implies that component spin magnitudes are χ ≲ 0.1. Roulet & Zaldarriaga (2019) additionally measured the fraction of binaries whose secondaries have maximal spins due to tidal spin-up; they found the fraction to be consistent with zero and bounded to <0.3. To date, no confident detection has exhibited unambiguously large χ ≳ 0.5.
(ii.) Black hole spins are not all zero. Despite evidence pointing toward preferentially small spin magnitudes, not all black holes can be nonspinning. Using the Gaussian effective spin model, Roulet & Zaldarriaga (2019) and Miller et al. (2020) concluded that the χeff distribution is inconsistent with a delta function at zero; hence, the χeff distribution possessed either a nonzero mean or nonzero width. This conclusion was bolstered by Abbott et al. (2021a), who found that the χeff distribution is centered at ∼0.05 with a nonzero width ≥0.08 and that the component spin magnitude distribution peaks at small values but also with a nonvanishing width of ∼0.15. Several individual events such as GW151226 (Abbott et al. 2016) and GW190517 (Abbott et al. 2021c) are also confidently known to possess spin, although their component spins are individually poorly measured (see e.g., Figure 11).
(iii.) Black holes exhibit a range of spin–orbit misalignment angles. Because spin precession is a subtle effect, the spin tilts of individual binaries are highly uncertain. Analyses of the population, however, indicate that spins are not purely aligned but instead exhibit a range of misalignment angles. In their analysis of the χeff distribution, Tiwari et al. (2018) reported evidence against pure spin–orbit alignment. Abbott et al. (2021a) later employed the Default model to directly measure the distribution of misalignment angles, recovering a possible preference for alignment but ruling out perfect alignment at high credibility. Abbott et al. (2021a) furthermore extended the Gaussian model to jointly measure the mean and variance of both χeff and χp. They found a delta function at χp = 0 to be disfavored, indicating the presence of spin–orbit misalignment in the population. Galaudage et al. (2021), meanwhile, used an extended version of the Default model to measure the maximum spin–orbit misalignment angle among the binary black hole population, finding that the observed population requires some misalignment angles exceeding θ ≳ 65° () at 99% credibility. Evidence for spin precession identified in individual events is also under active investigation (Abbott et al. 2020a; Chia et al. 2022; Hannam et al. 2021; Islam et al. 2021; Mateu-Lucena et al. 2021; Hoy et al. 2022b; Estellés et al. 2022; Vajpeyi et al. 2022).
2.2. What Is under Debate about Black Hole Spins?
(i.) Do most black holes have zero spin? Although it is agreed that not all black holes can possess zero spin, a debated question is whether most do. Using both the Default and Gaussian models, Abbott et al. (2021a) found no indication of an excess of zero-spin systems; predictive checks designed to test the goodness-of-fit of these models found these continuous unimodal distributions to be good descriptors of the observed population. In the context of hierarchical black hole formation, Kimball et al. (2020, 2021) directly measured the fraction of "first-generation" black holes with zero spin, finding this fraction to be consistent with zero. A different conclusion was drawn in Roulet et al. (2021), who modeled the χeff distribution not as a single Gaussian but via a mixture of three components,
corresponding to a half-Gaussian encompassing χeff > 0, a half-Gaussian encompassing χeff < 0, and a Gaussian centered at zero. This third component was intended to capture systems with χeff = 0; its finite standard deviation (fixed to 0.04) was chosen to mitigate sampling effects, a technical issue we discuss further below. Roulet et al. (2021) argued that a significant fraction of observed binaries are possibly associated with this zero-spin subpopulation. They reported a maximum-likelihood value of ζ0 ≈ 0.5, although ζ0 remained consistent with zero. A similar but stronger conclusion was forwarded by Galaudage et al. (2021). Working in the component spin domain, they extended the Default model to include an additional subpopulation whose spin magnitudes are identically zero for both binary components. Galaudage et al. (2021) concluded that of binaries are members of the zero-spin subpopulation at 90% credibility. 8
(ii.) Do some black holes have large spin magnitudes? Abbott et al. (2021a) performed a series of predictive checks, testing the goodness of fit of their models against observation. They concluded that black hole spins are well described by a single unimodal distribution concentrated at small but nonzero values. In contrast, Galaudage et al. (2021) argued that, although they infer most binary black holes to be nonspinning, the remaining binaries are members of a distinct rapidly spinning subpopulation. This secondary population is claimed to exhibit a broad range of spin magnitudes, centered at χ ≈ 0.45 but extending to maximal spins. Hoy et al. (2022a) noted that some individual events exhibit more confidently positive spin than others, speculating that they comprise a secondary population of more rapidly spinning events. However, their results are based on the inspection of individual posteriors and not hierarchical inference of the underlying population, and so it is unclear how their conclusions compare to those of Galaudage et al. (2021).
(iii.) Do extreme spin–orbit misalignments exist? Although all analyses agree that at least a moderate degree of spin–orbit misalignment exists, the question of extreme misalignments, i.e., θ > 90°, remains. Using the Gaussian model, Abbott et al. (2021a) inferred that at least 12% of binaries have negative χeff, possible only if one or both component spins have θ > 90°. To determine whether this conclusion was a proper measurement or simply an extrapolation of their model, Abbott et al. (2021a) introduced a variable lower bound on the Gaussian χeff distribution, finding the data to require at 99% credibility. Roulet et al. (2021), however, found that this support for negative effective spins is diminished when allowing for the possibility of a zero-spin population as in Equation (3). Galaudage et al. (2021), meanwhile, explored another variant of the Default component spin model, now introducing a variable truncation bound on the spin tilt distribution. They found this minimum to be consistent with zero. Motivated by these analyses, Abbott et al. (2021b) further extended the Gaussian model to include both a variable truncation bound and a possible zero-spin subpopulation. They recovered diminished evidence for negative effective spins but still recovered a preference for , now at 90% credibility. To date, no individual events discovered by the LIGO–Virgo–KAGRA Collaboration have confidently negative χeff or component spins unambiguously inclined by more than 90° (Abbott et al. 2021d). Independent reanalyses of LIGO/Virgo data have identified several candidates with confidently negative χeff (Venumadhav et al. 2020; Olsen et al. 2022), although most of these candidates do not pass the significance threshold adopted in Roulet et al. (2021).
3. A Counting Experiment
The central question of whether the majority of detected black hole binaries have vanishing spins admits a quick back-of-the-envelope estimate. Fully marginalized likelihoods 9 have been obtained for every event in GWTC-2 (Abbott et al. 2021c; Kimball et al. 2021) under two different prior hypotheses: (i) Both binary components are nonspinning (NS), with spin magnitudes fixed to χ1,2 = 0, and (ii) the black holes are spinning (S), with spin magnitudes and cosine tilts distributed uniformly across the intervals 0 ≤ χ1,2 ≤ 1 and . The ratio of the fully marginalized likelihoods gives the Bayes factor between the nonspinning and spinning hypotheses. Such Bayes factors serve as a primary input in the analysis of Galaudage et al. (2021), which makes use of parameter estimation samples obtained under both nonspinning and spinning priors; the Bayes factors between hypotheses is critical in determining how to properly combine these samples.
We start by considering a simple one-parameter model for the fraction of nonspinning binaries, ζ. Given a catalog of Nobs observations and data {d}, the likelihood of {d} is
where in the second line we have written the likelihood for each individual event as the sum of two terms corresponding to the nonspinning (NS) and the spinning (S) hypothesis. By definition, p(NS∣ζ) = ζ and p(S∣ζ) = 1 − ζ. Substituting these expressions into Equation (4) gives
where the likelihood ratio p(di ∣NS)/p(di ∣S) is the nonspinning versus spinning Bayes factor .
The Bayes factors computed in Abbott et al. (2021c) and used by Galaudage et al. (2021) were obtained via nested sampling (Skilling 2004, 2006; Speagle 2020). To evaluate Equation (5), we instead use posterior samples under the spinning hypothesis to calculate via a Savage–Dickey density ratio. The Bayes factors we compute generally agree with those used as inputs in Galaudage et al. (2021), although with some notable exceptions that may contribute to the discrepancies between their results and our own; see Appendix G.
The solid curve in Figure 1 shows our resulting posterior on ζ using only GWTC-2 events for which such Bayes factors are available. We find that zero-spin fractions ζ ≳ 0.8 are excluded at high credibility. It also appears that ζ = 0 is disfavored, which would imply the presence of at least a few zero-spin systems. However, note that the spinning hypothesis (S) requires that spin magnitudes be distributed uniformly up to , a possibility that is heavily disfavored as discussed in Section 2. What happens if we adopt a more plausible prior distribution for the spinning hypothesis? To answer this question, the dashed and dotted curves in Figure 1 show the ζ posterior given by Equation (5) if we recompute but now assume maximum spin magnitudes of and 0.8, respectively, among the "spinning" population. We see that even these small adjustments to further rule out large ζ and increasingly support ζ = 0.
Figure 1. Posterior on the fraction ζ of binary black holes in which both components have zero spin, as obtained in the simple counting experiment of Section 3. This counting experiment uses only events detected through GWTC-2 (Abbott et al. 2021c) and furthermore only relies on the fully marginalized likelihoods for each binary under spinning () and nonspinning (χ1 = χ2 = 0) priors. Values of ζ ≳ 0.8 are definitively ruled out. Whether or not ζ is consistent with zero, however, depends more sensitively on assumptions regarding the distribution of black hole spin magnitudes. If we assume that black hole spins range uniformly up to , ζ = 0 is disfavored. At the same time, relaxing to slightly smaller values yields posteriors increasingly consistent with zero, which would indicate no distinct subpopulation of nonspinning systems.
Download figure:
Standard image High-resolution imageIf, rather than our Savage–Dickey estimates, we instead use the same nested sampling Bayes factors adopted by Galaudage et al. (2021), we now much more strongly rule out ζ = 0. In Appendix G we track the origin of this behavior to one event, GW190408_181802, whose nested sampling Bayes factor appears significantly overestimated. This system is reported to have a large Bayes factor in favor of the nonspinning hypothesis, but this conclusion is not supported by the posterior on this system's spins (and thus the Savage–Dickey density ratio); see Figure 14. When we exclude GW190408_181892 from our sample, we obtain consistent p(ζ) posteriors from both sets of Bayes factors. When including this event, however, the nested sampling Bayes factors cause p(ζ = 0) to be underestimated by a factor of ∼102 relative to the result obtained with Savage–Dickey ratios (again see Figure 14). This could account for the nonzero fraction of nonspinning events found in Galaudage et al. (2021).
The initial check presented in Figure 1 suggests that the conclusion that most binary black holes comprise a distinct nonspinning subpopulation is inconsistent with the parameter estimates for individual binary black systems. At the same time, however, we saw that exact quantitative conclusions depend sensitively on assumptions regarding other aspects of the binary black hole population. We therefore need to undertake a more complete hierarchical analysis, measuring the zero-spin fraction ζ while simultaneously fitting the distribution of black hole spin magnitudes and orientations.
4. No Sharp Features in the Effective Spin Distribution
Going beyond our simple counting experiment, we next consider hierarchical inference of the effective spin distribution. An excess of events with vanishing spins would have stark implications for the distribution of effective spin parameters. In Figure 2 we compare the χeff distribution implied by the results of Galaudage et al. (2021) and Abbott et al. (2021b). If most black holes are indeed nonspinning, we should correspondingly see a prominent spike at χeff = 0, and if such a spike exists it should be robustly measurable using an appropriate model.
Figure 2. Marginal posterior distribution for χeff using results from Abbott et al. (2021b) that have no excess of zero-spin events (blue) and results from Galaudage et al. (2021) that imply that ∼50% of binaries have zero spins (red). The solid lines trace the mean distribution inferred by each model while shaded regions denote the 90% credible regions; the light traces trace individual draws from the population posterior under each model. We see that, if a significant fraction of binary black holes are indeed nonspinning, this should be clearly identifiable through their χeff distribution. This figure is modeled after Figure 5 of Galaudage et al. (2021).
Download figure:
Standard image High-resolution imageThere are two benefits to searching for this excess of zero-spin systems in the χeff domain before proceeding to more carefully explore the distribution of component spins. First, inference of the χeff distribution offers an independent and complementary check on the existence of a prominent zero-spin population: such a feature should be detectable either in the space of component spins or effective spins. Second, by analyzing χeff and not the higher-dimensional space of spin magnitudes and tilts, we can more easily avoid systematic uncertainties due to finite sampling effects. As detailed in Appendix B, the core ingredients in any hierarchical analysis are the posteriors p(λi ∣di ) on the properties λi of our individual binaries (labeled by i ∈ [1, Nobs]). In general, however, we do not have direct access to these posteriors, but instead have discrete samples {λi,j } drawn from the posteriors, where j ∈ [1, Ni ] enumerates the samples from posterior i and Ni is the total number of samples for this event. We therefore ordinarily replace integrals over p(λi ∣di ) with Monte Carlo averages over these discrete samples. The fundamental assumption underlying this approach is that the posterior samples are sufficiently dense relative to the population features of interest. In this paper, however, we are concerned with very narrow features in the binary black hole spin distribution; see Figure 2. In this case, we cannot automatically assume that Monte Carlo averages over posterior samples will yield accurate results.
Analysis of the χeff distribution allows us to circumvent these sampling issues by alternatively representing each event's posterior as a Gaussian kernel density estimate (KDE) over its posterior samples. This approach effectively imparts a finite "resolution" to each posterior sample, and allows us to assess the likelihood of arbitrarily narrow population features that would otherwise cause the typical Monte Carlo procedure to break down. Further details about the KDE representation of posteriors are provided in Appendix E.
Motivated by Figure 2, we attempt to measure the presence of any zero-spin subpopulation by modeling the χeff distribution as a mixture between a broad "bulk" population, centered at μeff with width σeff, and a narrow "spike" centered at zero,
We call this the GaussianSpike model; see Appendix A.1 for further details. Leveraging the KDE posterior representation introduced above, we take  = 0, such that the spike is infinitely narrow at χeff = 0. We hierarchically infer the parameters of this model using every binary black hole detection in GWTC-3 (Abbott et al. 2021d) with a false-alarm rate below 1 yr−1; see Appendix B for further details on the data we use.
= 0, such that the spike is infinitely narrow at χeff = 0. We hierarchically infer the parameters of this model using every binary black hole detection in GWTC-3 (Abbott et al. 2021d) with a false-alarm rate below 1 yr−1; see Appendix B for further details on the data we use.
The blue curve in Figure 3 shows our resulting marginal posterior on the fraction ζspike of binary black holes comprising a zero-spin spike. We find that ζspike remains consistent with zero, indicating no evidence for an over-density of events at χeff = 0. For reference, the "zero-spin" fraction measured by Roulet et al. (2021) (ζ0 in Equation (3)) is shown as a dashed black curve. The results from Roulet et al. (2021) are qualitatively consistent with our own; exact agreement is not expected due to the different models and different data employed in each analysis.
Figure 3. Marginalized posterior on the fraction ζspike of binary black holes comprising a distinct subpopulation with χeff = 0. The blue curve shows the results obtained through analysis of the binary black holes in GWTC-3 (Abbott et al. 2021d). We find ζspike to be consistent with zero, indicating no evidence for an excess of zero-spin systems. Nevertheless, p(ζspike) peaks suggestively at ζspike ≈ 0.5. We demonstrate that this is not unexpected by repeatedly generating and analyzing mock catalogs of χeff measurements, drawn from an intrinsically spikeless population described by a simple Gaussian. These catalogs yield posteriors similar to our own, often (and incorrectly) disfavoring ζspike = 0. As discussed in the main text, this behavior is due to a degeneracy between ζspike and the inferred mean of the spinning "bulk" population. For reference, the black dashed line shows the posterior on the zero-spin fraction ζ0 inferred in Roulet et al. (2021), which is qualitatively consistent with both our GWTC-3 measurement and the simulated spikeless measurements.
Download figure:
Standard image High-resolution imageAlthough ζspike is not bounded away from zero, a nonzero value is nevertheless preferred, with a maximum posterior value of ζspike ≈ 0.5. We demonstrate that this behavior is not unexpected from intrinsically spike-less populations. We perform a series of null tests, repeatedly simulating and analyzing catalogs of events drawn from a spikeless population and with uncertainties typical of current detections; see Appendix F for further details on the simulations. The gray curves in Figure 3 show the posteriors on ζspike given by these synthetic catalogs. Despite being drawn from a spikeless population, the simulated catalogs generically yield posteriors morphologically similar to the those obtained using actual observations, with some posteriors that even more extremely (and incorrectly) disfavor ζspike = 0.
The cause of this behavior is a degeneracy between μeff and ζspike. The mock catalogs that strongly disfavor ζ = 0 are typically those that have events with moderately high, well-measured effective spins. The presence of such events increases the inferred mean μeff of the "bulk" population, pulling the bulk away from those events near χeff ≈ 0 and leaving them to be absorbed into a zero-spin subpopulation. We have verified that removing the most rapidly spinning events from these mock catalogs indeed acts to resolve the apparent tension in Figure 3; see Appendix F. This demonstration further emphasizes the need for additional caution when drawing strong astrophysical conclusions based on narrow population features, particularly in the regime when uncertainties on individual events are much larger than the features of interest.
Going beyond the question of a narrow spike at zero, we now more generally ask if there is evidence for any bimodality in the χeff distribution of binary black holes. We explore this question using the BimodalGaussian model (see Appendix A.1) in which the "spike" in Equation (6) is replaced with a second, independent Gaussian with a variable mean and width. The χeff distribution inferred under this model is shown in Figure 4, where light traces show individual draws from our population posterior and the slide lines mark 90% credible bounds. We find no evidence that the effective spin distribution deviates from a simple unimodal shape. For reference, the dashed black line marks the mean distribution inferred using a simple Gaussian model. Inference using the more complex BimodalGaussian remains extremely consistent with this simple result, with both models yielding consistent means ( and under the Gaussian and BimodalGaussian models, respectively) and standard deviations ( and ).
Figure 4. The χeff distribution as inferred by a BimodalGaussian effective spin model, defined as the sum of two Gaussians (see Appendix A). Solid blue lines denote the 90% credible intervals, while blue light curves are select individual draws from the posterior. For reference, the dashed black curve shows the mean χeff distribution as inferred using a single Gaussian. Both results are consistent with one another, indicating no evidence for bimodal features, narrow or otherwise, in the binary black hole χeff distribution.
Download figure:
Standard image High-resolution imageAn alternative way to test for the presence of additional structure in the χeff distribution is to ask about the predictive power of our models: Are there systematic residuals between the χeff values we observe and those predicted by each model? In Appendix C we subject the Gaussian, GaussianSpike, and BimodalGaussian models to predictive tests, finding that all three models, once fitted, successfully predict the observed χeff values among GWTC-3. The fact that the simple Gaussian model passes this check once more points to the lack of observational evidence for additional structure in the binary black hole χeff distribution, whether a spike, a secondary mode, or still other feature.
5. The Population of Spin Magnitudes and Tilts
Preliminary results so far, based on the Bayes factor counting experiment in Section 3 and hierarchical χeff analyses in Section 4, do not point to an excess of zero-spin events. Here we confirm these conclusions via a more complete inference of the component spin magnitude and tilt distributions under a series of increasingly complex models.
As a baseline model (Talbot & Thrane 2017; Wysocki et al. 2019; Abbott et al. 2021a, 2021b), we take each component spin magnitude to be distributed following a Beta distribution,
where c(α, β) is a normalization constant. Every spin tilt, meanwhile, is distributed as a mixture between an isotropic component and a preferentially aligned component, modeled as a half-Gaussian centered at :
We refer to Equations (7) and (8) as the Beta+Mixture model. A related version of this model in which both component spin tilts are together drawn from either the isotropic or the aligned component is also called the Default spin model in Abbott et al. (2021a, 2021b).
Galaudage et al. (2021) explored an extension to the Default model that allowed for an excess of systems with zero spin and a variable bound on the spin tilt distribution; it was termed the Extended model in that study. Motivated by these extensions, we introduce the possibility of a zero-spin "spike" in the spin magnitude distribution, modeled as a half-Gaussian with finite width  spike centered at zero:
spike centered at zero:
Following Galaudage et al. (2021) we also introduce a variable truncation bound zmin on the spin-tilt distribution:
for . We refer to Equations (9) and (10) together as the BetaSpike+TruncatedMixture model. To better understand how conclusions regarding a zero-spin excess and the prevalence of spin–orbit misalignment are related, we also consider variants of this model in which only one extended feature is present: a zero-spin spike but no truncation (BetaSpike+Mixture) or a truncation but no spike (Beta+TruncatedMixture). See Appendix A.2 for further details.
Our full BetaSpike+TruncatedMixture model differs from the Extended model of Galaudage et al. (2021) in two ways. First, we do not fix the width  spike of the vanishing spin subpopulation, but instead treat it as a free parameter to be inferred from the data. This allows us to test whether a narrow subpopulation is actually preferred by the data, similar to our investigation with the BimodalGaussian model in Section 4 above. We adopt a prior requiring
spike of the vanishing spin subpopulation, but instead treat it as a free parameter to be inferred from the data. This allows us to test whether a narrow subpopulation is actually preferred by the data, similar to our investigation with the BimodalGaussian model in Section 4 above. We adopt a prior requiring  spike ≥ 0.03. This lower limit is motivated by tracking our number of effective posterior samples per event (see further discussion below), and by the effective population resolution of our catalog, which we estimate as
spike ≥ 0.03. This lower limit is motivated by tracking our number of effective posterior samples per event (see further discussion below), and by the effective population resolution of our catalog, which we estimate as
where and are the variances of the spin magnitude posteriors for each event i. We find σobs = 0.02, approximately equal to our lower bound on  spike.
spike.
Second, the Extended model does not allow for independently and identically distributed spin magnitudes and orientations. Instead, component spin magnitudes are either both vanishing or both nonvanishing in a given binary. This choice precludes astrophysical scenarios such as tidal spin-up, which is expected to affect only one component spin in a given binary. Similarly, within the Extended model, the spin tilts are both either members of the isotropic component or the preferentially aligned component in Equation (10). Here, we instead assume that all component spin magnitudes and tilts are independently drawn from Equations (9) and (10).
When hierarchically analyzing the χeff distribution above, we relied on a KDE representation of individual-event likelihoods p(di
∣λi
) to mitigate sampling uncertainties and evaluate population models with narrow features. This trick cannot be straightforwardly applied to inference of the component spin distribution, due to both the increased dimensionality and the fact that the sharp feature of interest (a spike at χ1 = χ2 = 0) lies on the boundary of parameter space, rather than the center. We will therefore return to standard Monte Carlo averaging over posterior samples when hierarchically inferring the component spin distribution. To diagnose possible breakdowns in our inference due to finite sampling effects, we monitor the effective number of posterior samples, Neff, informing our Monte Carlo estimates for each event's likelihood. As discussed in Appendix D, we explicitly track , the minimum effective sample count across all events for a proposed population Λ, and use this quantity to define which regions of parameter space we can and cannot make claims about. In particular, we find that we expect reliable population inference when  spike > 0.03.
spike > 0.03.
Figure 5 shows the measured spin magnitude and tilt distributions under our four component spin models, and we show the posteriors obtained on the hyperparameters of each model in Figure 6. To hierarchically measure the component spin distribution, we again use all binary black holes in GWTC-3 with false-alarm rates below 1 yr−1; see Appendix B for details.
Figure 5. Inferred distributions of component spin magnitudes (left), spin–orbit tilts (middle), and effective inspiral spins (right) of binary black holes under the various component spin models considered in this paper. Solid black lines denote the median and the 90% credible intervals, while red/green light curves correspond to individual draws from the posterior for each model. Among models that allow for a distinct subpopulation of nonspinning systems (bottom two rows), we infer that the fraction of binaries in such systems is consistent with zero. Meanwhile, we find that the distribution confidently extends to negative values; models that allow for a sharp truncation in the distribution require this truncation to occur at . Despite the varying component spin magnitude and tilt distributions recovered by these different models, all yield similar χeff distributions. For reference, the dashed black curves in the right-hand column show the mean χeff distribution obtained by direct inference with the BimodalGaussian model of Section 4; all four component spin models give χeff distributions that are consistent with this result.
Download figure:
Standard image High-resolution imageFigure 6. One- and two-dimensional marginalized posteriors for the parameters of each component spin model we consider (see Appendix A.2). These posteriors correspond to the measured distributions of component spin magnitudes and tilts shown above in Figure 5. Some parameters are defined only for a subset of component spin models. The shaded region in the joint μχ –σχ posterior is the region excluded by the prior cut on the shape parameters of the spin magnitude Beta distribution; see Appendix A.2. We find that the fraction fspike of black holes comprising a zero-spin subpopulation is consistent with zero. The data also require that at least some spins are misaligned by more than 90° relative to their Newtonian orbital angular momentum; among models that include a variable truncation bound zmin on the distribution, this bound is inferred to be confidently ≤ 0, regardless of assumptions about a possible zero-spin subpopulation. Allowing such a truncation bound, meanwhile, significantly impacts constraints on fiso, the fraction of binaries with isotropically oriented spins, as well as σt , the width of a preferentially spin-aligned mixture component (see Equation (8)). As seen in Figure 5, the introduction of a truncation bound yields a significantly flatter distribution, corresponding here to larger values of fiso and σt .
Download figure:
Standard image High-resolution imageFor those models allowing a distinct zero-spin spike, the left panels of Figure 5 indicate that such a feature is not required to exist. We instead see inferred spin magnitude distributions consistent with a single, smooth function that remains finite at χ = 0, with most events having spin magnitudes in the χ ∈ (0, 0.3) range. Correspondingly, the posteriors on fspike in Figure 6 are consistent with zero. Compared to the fraction ζspike with χeff = 0 (see Figure 3), we find that fspike is more consistent with zero. We interpret this variation as reflective of the systematic uncertainty in exactly how the question "does there exist an excess of zero-spin systems?" is posed: whether in the component spin or effective spin domains, with a delta function at zero or a finite-width spike, etc. Despite these differences, all results indicate that the presence of a zero-spin population is not required by the current data. A zero-spin population is not precluded, though: both sets of results bound any zero-spin fraction to ≲60%, suggesting that a distinct zero-spin population could yet emerge in future data.
The fraction fspike is primarily correlated with μχ , the mean of the "bulk" spin magnitude population. Larger μχ values reduce the capability of this "bulk" Beta distribution to accommodate events with small spin; these events will therefore necessarily be assigned to the "spike" and thus increase the value of fspike. This is similar to the phenomenon identified in Section 4 above. Additionally, all four component spin models yield similar spin magnitude distributions above χ ≳ 0.4, suggesting that the data are robustly consistent with the absence of large spin magnitudes. Table 1 lists the 1st and 99th spin magnitude percentiles (χ1% and χ99%, respectively) under each model; our most conservative estimate gives.
Table 1. Median and 90% Credible Intervals on Various Physical Quantities of Interest under Various Component Spin Models
| Model | fspike | z1% | χ1% | χ99% | χeff,1% | χeff,99% | |
|---|---|---|---|---|---|---|---|
| Beta+Mixture | ⋯ | ⋯ | |||||
| BetaSpike+Mixture | ⋯ | ||||||
| Beta+TruncatedMixture | ⋯ | ||||||
| BetaSpike+TruncatedMixture |
Note. From left to right, we present the fraction of black holes that belong in the (finite-width) zero-spin spike (fspike; see Figure 6 for the posterior), the minimum value of the spin tilt ( Figure 6 for the posterior), 1% lower value of the spin-tilt posterior distribution (z1%), the 1%/99% lower/upper values of the spin-magnitude posterior distribution (χ1%/χ99%), and the 1%/99% lower/upper values of the effective-spin distribution (χeff,1%/χeff,99%). We choose to report 1% and 99% values because 1/Nobs = 0.014 ≃ 1% for our Nobs = 69 events.
Download table as: ASCIITypeset image
In contrast to Galaudage et al. (2021), we left the width  spike of our "spike" population as a free parameter in order to test whether the data indeed require a narrow feature at χ = 0. Although we recover largely uninformative constraints on
spike of our "spike" population as a free parameter in order to test whether the data indeed require a narrow feature at χ = 0. Although we recover largely uninformative constraints on  spike, Figure 6 in fact shows a slight preference for large
spike, Figure 6 in fact shows a slight preference for large  spike, further indicating that no narrow features are confidently present in the spin magnitude distribution. Our conclusions regarding small
spike, further indicating that no narrow features are confidently present in the spin magnitude distribution. Our conclusions regarding small  spike, however, are limited by the finite sampling effects discussed above. In Appendix D we study the number Neff of effective posterior samples as a function of
spike, however, are limited by the finite sampling effects discussed above. In Appendix D we study the number Neff of effective posterior samples as a function of  spike. We find that Neff depends sensitively on
spike. We find that Neff depends sensitively on  spike, and we caution that values of
spike, and we caution that values of  spike ≲ 0.04 are possibly subject to significant Monte Carlo uncertainty. Even with this restriction, however, we find no preference for a small
spike ≲ 0.04 are possibly subject to significant Monte Carlo uncertainty. Even with this restriction, however, we find no preference for a small  spike in the posterior. This conclusion is further bolstered by the analysis of the effective spin distribution in Section 4 above, which was not subject to finite sampling effects and which similarly found no evidence for an excess of zero-spin systems.
spike in the posterior. This conclusion is further bolstered by the analysis of the effective spin distribution in Section 4 above, which was not subject to finite sampling effects and which similarly found no evidence for an excess of zero-spin systems.
Irrespective of modeling assumptions regarding a zero-spin subpopulation, all four component spin models exhibit significant support at negative in Figure 5. Models that allow for a truncation in the spin tilt distribution consistently infer this truncation to be at negative values; in Figure 6 we correspondingly see that at high significance. This result signals the presence of events with spins misaligned by more than 90° from their Newtonian orbital angular momentum. Table 1 gives the first percentile (z1%) on inferred by each model, with in the most conservative case. Notably, the addition of truncation in the spin tilt distribution significantly "flattens" the recovered distribution, no longer requiring any peak at . This behavior is due to the fact that the data disfavor an equal density of events at and . Because an isotropic distribution is necessarily symmetric at , models that allow for a mixture of isotropic and aligned spin tilts must compensate by adding more weight to the "primarily aligned" Gaussian component in Equation (8). No such compensation is necessary if the spin tilt distribution is allowed to truncate. In models including a zmin truncation, all events are either assigned to the "isotropic" (but now truncated) component, or the Gaussian component itself is stretched to near-isotropy; in Figure 6 we see that fiso becomes consistent with unity and σt shifts to prefer large values when a truncation is included in the model.
This result indicates the presence of events with tilt angles greater than 90°, and hence the possibility of binaries with effective spins χeff < 0. The third column in Figure 5 shows the χeff distributions implied by each component model. Despite the wide range of possible features possessed by each model, they all yield similar χeff distributions that exhibit asymmetry about zero but that extend to negative values. As a consistency check, we also compare these implied χeff distributions to our result obtained through direct inference on χeff. The dashed curve in each panel shows the mean obtained under the BimodalGaussian effective spin model. Each of the four component spin models yields consistent χeff distributions, although they are suggestive of possible additional skewness (Abbott et al. 2021a, 2021b). As an additional consistency check and safeguard against erroneous conclusions due to poorly-fitting models, we subject each of the component spin models to predictive checks, as introduced in Section 4 above. The results, shown in Appendix C, indicate that all four models provide a good fit to observation.
As a proxy for the minimum χeff values implied by our component spin results, Figure 7 shows posteriors on the first percentile (χeff,1%) of the effective spin distribution corresponding to each model. Under the BetaSpike+TruncatedMixture model, for example, we find and bound χeff,1% < 0 at 98.8% credibility. This finding is consistent with the conclusions drawn by Abbott et al. (2021a, 2021b), who added a lower truncation in the χeff distribution and inferred at ∼90% credibility. Our conclusions are also consistent with Roulet et al. (2021), who modeled the χeff distribution as the sum of a positive component, a negative, and a "near-zero" component whose 2σ width spanned −0.08 < χeff < 0.08; see Equation (3). This near-zero component is broad enough to likely encompass the negative, but near-zero, χeff,1% values we report here.
Figure 7. Posterior for the first percentile (χeff,1%) of the χeff distributions implied by each of our component spin models, as shown in the right-hand column of Figure 5. The median values and 90% credible intervals for χeff,1% are also reported in Table 1. Each of our component spin models require the binary black hole population to contain spins misaligned by more than 90° relative to their Newtonian orbital angular momentum. Correspondingly, χeff,1% is inferred to likely (although not necessarily) be negative. The χeff,1% values recovered here are consistent with the minimum χeff values measured by Abbott et al. (2021a, 2021b).
Download figure:
Standard image High-resolution imageFinally, Figures 5 and 6 reveal how questions regarding zero-spin subpopulations and spin–orbit misalignment are potentially related. The inclusion or exclusion of a zero-spin subpopulation (Beta+TruncatedMixture versus BetaSpike+TruncatedMixture) has a negligible effect on our conclusions regarding the location of zmin. On the other hand, the introduction of a spin tilt truncation (BetaSpike+Mixture versus BetaSpike+TruncatedMixture) more noticeably impacts the inferred fspike posterior, resulting in less support for zero. As discussed above, though, the spin tilt truncation has a much larger effect on fiso, which becomes consistent with 1 (i.e., no excess of spin-aligned events) when a spin tilt truncation is included in the model. This same effect can be seen in Figure 4 of Galaudage et al. (2021).
6. Discussion and Conclusions
In this paper we have sought to explore the three open questions posed in Section 2.2 via three complementary routes: a counting experiment using only the fully marginalized likelihoods for each event, hierarchical analysis of the binary black hole effective spin distribution, and hierarchical analysis of the binaries' component spin distribution. Each of these three routes yielded consistent conclusions, which we summarize below.
(i.) We find no evidence for an excess of zero-spin events . Using each of our three methods we find that the fraction of black holes in a distinct zero-spin subpopulation is consistent with zero. We furthermore verified that this behavior is common among analyses of synthetic populations lacking a zero-spin excess. We therefore conclude that the observational data do not presently support the notion that the majority of black holes in merging binaries are nonspinning. Given current observations, a nonspinning population can comprise at most ≲60%–70% of merging binary black holes.
(ii.) The inferred population is consistent with less than 1% of spin magnitudes above χ ∼ 0.6. In each of the component spin models explored in Section 5, the inferred population is nearly identical for spin magnitudes χ ≳ 0.4, falling rapidly, with negligible support for χ ≳ 0.6. This conclusion is robust against modeling systematics, including a possible truncation in the spin tilt distribution or a zero-spin subpopulation.
(iii.) Binary black holes exhibit a broad range of spin–orbit misalignment angles, with some angles greater than 90°. In all models, we find a preference for a flat and broad distribution of spin–orbit misalignment angles. When we introduce a lower truncation bound on the distribution, we confidently infer that this truncation bound must be negative, thus requiring the presence of systems with antialigned spins among the binary black hole population. Additionally, the minimum χeff among the binary black hole population is inferred to be confidently negative under each component spin model.
Our conclusions are consistent with the findings of Abbott et al. (2021a, 2021b), who reported evidence for spins misaligned by more than 90° and no modeling tension that would indicate the existence of a large zero-spin subpopulation. Our conclusions are moreover in broad agreement with Roulet et al. (2021). Figure 3 shows the inferred fraction of events with χeff = 0 from this work and the inferred fraction of events in the "zero-spin" subpopulation (ζ0 in Equation (3)) from Roulet et al. (2021). Both results are in qualitative agreement, consistent with a zero-spin fraction of zero but peaking at ∼0.5. As demonstrated in Section 4, posteriors of this form arise generically when analyzing mock catalogs of events drawn from a population lacking a zero-spin subpopulation.
Roulet et al. (2021) find that the fraction of events in their "negative-spin" subpopulation is consistent with zero; this too is consistent with our result. As discussed in Section 5, we infer χeff,1% to be negative but small in magnitude. Because Roulet et al.'s (2021) "zero-spin" subpopulation has a broad standard deviation of 0.04, events with negative but small-in-magnitude χeff are counted as members of this zero-spin subpopulation, rather than associated with the "negative-spin" subpopulation. Indeed, Roulet et al. (2021) conclude that the sum of their "zero-spin" and "negative-spin" subpopulations is nonzero. This is evident from Figure 3 of Roulet et al. 2021, in which ζpos is inconsistent with 1.
Shortly after the initial circulation of our study, an independent and complementary study of binary black hole spins was presented by Mould et al. (2022). They sought to explore evidence for mass ratio reversal in compact binary formation, employing models in which component spins are not independently and identically distributed. As in our study, though, they additionally considered the possibility of zero-spin spikes appearing in the spin-magnitude distribution. Their findings corroborate our own, indicating that <46% of black hole primaries and <36% of secondaries have vanishing spins.
At the same time, our conclusions are generally inconsistent with those reported by Galaudage et al. (2021). Although our posterior distributions do overlap with those of Galaudage et al. (2021) to within statistical uncertainty, differences between them result in qualitatively different conclusions regarding the nature of binary black hole spins. Below, we detail several differences between our analyses and those of Galaudage et al. (2021) and comment on whether each could be contributing to the discrepancy.
First, an important categorical difference between our analyses and those conducted in Galaudage et al. (2021) is the sample of gravitational-wave events analyzed. While our counting experiment in Section 3 uses only GWTC-2 (Abbott et al. 2021c) events, the hierarchical analyses in Section 4 and Section 5 make use of the full GWTC-3 catalog (see Appendix B for the exact event selection criteria). Galaudage et al. (2021), meanwhile, analyzed only GWTC-2 events, as GWTC-3 had not yet been released at the time of their study. To gauge whether our differing data sets contribute to the disagreement between our own conclusions and those of Galaudage et al. (2021), in Appendix H we show results obtained using only GWTC-2 events. Our results are qualitatively unchanged, with GWTC-2 yielding no evidence for a distinct subpopulation of nonspinning black holes. Additionally, GWTC-2 contains spin–orbit misalignment greater than 90°, though at a slightly reduced credibility compared to GWTC-3 (97.1% versus 99.7% quantiles).
Unlike our analyses, which use a single set of posterior samples for each event, Galaudage et al. (2021) make use of two distinct sets of samples for each binary, obtained under spinning and nonspinning parameter estimation priors. In order to perform inference with both sets of samples, it is necessary to quantify the Bayes factors between these priors for each event. As we mentioned in Section 3 and illustrate further in Appendix G, there is at least one event whose fully marginalized likelihood under the nonspinning hypothesis is significantly overestimated in the data set used by Galaudage et al. (2021). This could cause Galaudage et al. (2021) to spuriously confirm the existence of a distinct nonspinning subpopulation.
Another factor may be the demand by Galaudage et al. (2021) that the zero-spin subpopulation have a vanishing width. In Section 5, we did not fix the width  spike of our approximate zero-spin spike, but let it vary as another free parameter to be inferred from the data. In addition to concluding that the fraction fspike of events occupying this spike is consistent with zero, we also found no preference for the spike to be narrow, even if it were to exist. If we nevertheless require
spike of our approximate zero-spin spike, but let it vary as another free parameter to be inferred from the data. In addition to concluding that the fraction fspike of events occupying this spike is consistent with zero, we also found no preference for the spike to be narrow, even if it were to exist. If we nevertheless require  spike to be small, however, we do see an increased preference for larger fspike. It is therefore possible that the strict delta-function model adopted by Galaudage et al. (2021) is systematically affecting their results. We note, however, that our posteriors in the region
spike to be small, however, we do see an increased preference for larger fspike. It is therefore possible that the strict delta-function model adopted by Galaudage et al. (2021) is systematically affecting their results. We note, however, that our posteriors in the region  spike ≤ 0.04 may be subject to elevated Monte Carlo variance (see Appendix D) and so we cannot confidently conclude that the demand of
spike ≤ 0.04 may be subject to elevated Monte Carlo variance (see Appendix D) and so we cannot confidently conclude that the demand of  spike = 0 is responsible for the discrepant conclusions.
spike = 0 is responsible for the discrepant conclusions.
Although we may be able to reproduce Galaudage et al.'s (2021) measurement of fspike by artificially demanding small  spike, we are unable to reproduce their conclusions regarding zmin, the lower truncation bound on the component spin distribution. While we infer zmin to be confidently negative, indicating spins misaligned by more than 90°, Galaudage et al. (2021) infer this parameter to be consistent with zero or positive values. Qualitatively, binaries with large in-plane spins are difficult to distinguish from binaries with very small or vanishing aligned spins—both give the same χeff values. Therefore, if Galaudage et al. (2021) are overestimating the fraction fspike of nonspinning systems, they may correspondingly be underestimating the prevalence of systems with significant spin–orbit misalignments. This said, neither Galaudage et al.'s (2021) results nor our own exhibit any significant correlation between zmin and fspike.
spike, we are unable to reproduce their conclusions regarding zmin, the lower truncation bound on the component spin distribution. While we infer zmin to be confidently negative, indicating spins misaligned by more than 90°, Galaudage et al. (2021) infer this parameter to be consistent with zero or positive values. Qualitatively, binaries with large in-plane spins are difficult to distinguish from binaries with very small or vanishing aligned spins—both give the same χeff values. Therefore, if Galaudage et al. (2021) are overestimating the fraction fspike of nonspinning systems, they may correspondingly be underestimating the prevalence of systems with significant spin–orbit misalignments. This said, neither Galaudage et al.'s (2021) results nor our own exhibit any significant correlation between zmin and fspike.
Finally, although our spin models were heavily inspired by those of Galaudage et al. (2021), ours do not reduce to theirs in the limit  spike = 0. Our component spin models assume that individual spins are independently and identically distributed between spike and bulk subpopulations, whereas Galaudage et al. (2021) assume that both spins in a given binary together lie in the spike or the bulk of the component spin distribution. Similarly, Galaudage et al. (2021) require that both spins are together members of the isotropic or preferentially aligned components of the spin tilt distribution. We have verified that this modeling choice is not responsible for the different conclusions regarding fspike, as can be seen in Figure 17 in Appendix H. In fact, we find that fspike is constrained to even smaller values if we alternatively adopt Galaudage et al.'s (2021) modeling convention. This is expected: under the convention of Galaudage et al. (2021), a component spin can only contribute to fspike if its companion is also consistent with zero spin. Under our assumption of independent and identically distributed spins, in contrast, a component spin can be identified as a member of the zero-spin spike regardless of its companion's spin measurement. Such differing conventions and how they impact population measurements are further elaborated upon in Appendix H.
spike = 0. Our component spin models assume that individual spins are independently and identically distributed between spike and bulk subpopulations, whereas Galaudage et al. (2021) assume that both spins in a given binary together lie in the spike or the bulk of the component spin distribution. Similarly, Galaudage et al. (2021) require that both spins are together members of the isotropic or preferentially aligned components of the spin tilt distribution. We have verified that this modeling choice is not responsible for the different conclusions regarding fspike, as can be seen in Figure 17 in Appendix H. In fact, we find that fspike is constrained to even smaller values if we alternatively adopt Galaudage et al.'s (2021) modeling convention. This is expected: under the convention of Galaudage et al. (2021), a component spin can only contribute to fspike if its companion is also consistent with zero spin. Under our assumption of independent and identically distributed spins, in contrast, a component spin can be identified as a member of the zero-spin spike regardless of its companion's spin measurement. Such differing conventions and how they impact population measurements are further elaborated upon in Appendix H.
Overall, we find a component spin distribution that is consistent with a single, smooth function. Our results suggest that the spin distribution is possibly nonzero at χ = 0, but without a requirement for a distinct and discontinuous subpopulation of nonspinning black holes (see Figure 5). Such a behavior cannot be easily captured by the common modeling choice of a nonsingular Beta distribution, which is constrained to vanish at χ = 0. This tension is illustrated in the joint μχ –σχ posterior of Figure 6, which shows the inferred mean and variance of the spin magnitude distribution railing against the prior cut that ensures nonsingular behavior. When the spin magnitudes are modeled with a single Beta distribution (green posteriors in Figure 5), μχ must be small in order to accommodate events with small but finite spins. Events with larger spins, meanwhile, can nominally be captured with a large σχ . However, σχ cannot be large when μχ is small, as seen by the prior cut in Figure 6. The introduction of a zero-spin "spike" relieves this tension (even if no such spike is actually present in the data). Small-spin events can now be captured by the spike, allowing the Beta distribution to shift to higher μχ and σχ to accommodate higher-spin events. This phenomenon can also be seen in the correlation, noted above, between fspike and μχ : the spin magnitude distribution is best described either as a single Beta distribution that peaks at low values (small fspike and μχ ), or a "spike" combined with a Beta distribution that peaks at higher values (large fspike and μχ ). The combination of these two effects yields a smooth spin magnitude distribution that does not exhibit distinct subpopulations. This discussion suggests that a Beta distribution might be a suboptimal model for spin magnitudes going forward.
The observed presence or absence of a distinct zero-spin subpopulation, rapidly spinning black holes, and/or significantly misaligned black hole spins would all carry considerable theoretical implications for the formation channels and astrophysical processes driving compact binary evolution. At the same time, hierarchical inference of the compact binary spin distribution is technically difficult, relying on a large number of highly uncertain measurements that are themselves finitely sampled. When drawing observational conclusions about the nature of compact binary spins, ensuring that results are reproducible under different complementary approaches can help mitigate these concerns and determine which conclusions are driven by priors, which by modeling systematics, and which by the data itself.
It certainly remains possible that the binary black hole mergers witnessed by Advanced LIGO and Virgo contain subpopulations of nonspinning and/or nearly aligned binaries, but this scenario is not presently required by gravitational-wave observations. If such subpopulations were to appear in an analysis of future data, they could be taken as evidence toward the hypothesis that merging black holes are born in the stellar field, with spins acquired primarily through tidal spin-up (Belczynski et al. 2021; Galaudage et al. 2021; Olejak & Belczynski 2021; Mandel & Farmer 2022; Shao & Li 2022; Stevenson 2022). Such astrophysical conclusions are currently unsupported by the data, however. Further detections made in the upcoming O4 observation run and beyond will shine further light on the nature of compact binary spins and, consequently, the evolutionary origin of the black hole mergers we see today.
We thank our anonymous referee, the AAS Data Editors, and Ilya Mandel for their valuable comments on our manuscript, as well as Eric Thrane, Colm Talbot, and Shanika Galaudage for numerous discussions about these results. We also thank Javier Roulet for sharing data from Roulet et al. (2021) with us and for insightful feedback on this study, and Christopher Berry, Charlie Hoy, Vaibhav Tiwari, and Mike Zevin for their thoughtful comments. This research has made use of data, software, and/or web tools obtained from the Gravitational Wave Open Science Center (https://www.gw-openscience.org), a service of LIGO Laboratory, the LIGO Scientific Collaboration and the Virgo Collaboration. Virgo is funded by the French Centre National de Recherche Scientifique (CNRS), the Italian Istituto Nazionale della Fisica Nucleare (INFN) and the Dutch Nikhef, with contributions by Polish and Hungarian institutes. This material is based upon work supported by NSF's LIGO Laboratory, which is a major facility fully funded by the National Science Foundation. The authors are grateful for computational resources provided by the LIGO Laboratory and supported by NSF grants PHY-0757058 and PHY-0823459.
Software: astropy (Astropy Collaboration 2013, 2018), emcee (Foreman-Mackey et al. 2013), h5py (Collette et al. 2021), jax (Bradbury et al. 2018), matplotlib (Hunter 2007), numpy (Harris et al. 2020), numpyro (Phan et al. 2019; Bingham et al. 2019), scipy (Virtanen et al. 2020).
Data & Code Availability
The code used to produce the results of this study is available via Github (https://github.com/tcallister/gwtc3-spin-studies) and a copy is available on Zenodo (Callister & Miller 2022). Our data, meanwhile, can be obtained on Zenodo: https://doi.org/10.5281/zenodo.6555145.
Appendix A: Spin Population Models
We employ two broad categories of parameterized models for the black hole spins: models on the effective spin parameters and models on the spin components. A summary of all models, their corresponding parameters, and their priors is presented in Tables 2 and 3. All component spin models ignore the azimuthal spin angles, assuming they are distributed according to the uniform prior used during the original parameter estimation (Abbott et al. 2021c). As measurements of compact binary spins and mass ratios are generally correlated, we hierarchically measure the distribution of binary mass ratios alongside spins, assuming that the secondary mass distribution follows
and inferring the power-law index βq . We adopt a Gaussian prior N(0, 3) on βq . The distributions of primary masses and redshifts, in contrast, have a negligible impact on conclusions regarding spin. We assume that primary masses follow the PowerLaw+Peak model (Talbot & Thrane 2018), with parameters fixed to their (one-dimensional) median values as inferred in Abbott et al. (2021b). Following the notation of Abbott et al. (2021b), we take α = 3.5, , , λpeak = 0.03, μm = 33.6, σm = 4.7, and δm = 4.9. Meanwhile, we assume that the source-frame binary black hole merger density rate evolves as
where is the differential comoving volume per unit redshift.
Table 2. Summary of Effective Spin Models We Employ, Including Their Names, an Example p(χeff) Plot, Parameters, Priors, and Comments
| Model Name | p(χeff) | Parameter | Prior | Comments |
|---|---|---|---|---|
| Gaussian |

| μeff | U(−1,1) | Simplest Gaussian model |
| σeff | LU(0.01,1) | |||
| GaussianSpike |

| μeff | U(−1,1) | Mixture of a Gaussian "bulk" with a distinct "spike" subpopulation of nonspinning systems |
| σeff | LU(0.01,1) | |||
| ζspike | U(0,1) | |||

| δ(0) | |||
| BimodalGaussian |

| μeff,a | U(−1,1) | Mixture of two Gaussians with variable means and widths |
| μeff,b | U( − 1, 1) | |||
| σeff,a | LU(0.01,1) | |||
| σeff,b | LU(0.01,1) | |||
| ζa | U(0.5,1) | |||
Note. denotes a uniform prior between xmin and xmax, signifies a log-uniform prior across the same bounds, and δ(0) a delta function prior at zero.
Download table as: ASCIITypeset image
Table 3. Summary of Component Spin Models We Employ, Including Their Names, an Example χ and Plot, Parameters, Priors, and Comments
| Model Name | p(χ) | Parameter | Prior | Comments | |
|---|---|---|---|---|---|
| Beta+Mixture |

|

| μχ | U(0,1) | Simplest component spin model; additional prior requirement that α, β > 1, see Equation (A7) |
| σχ | U(0.07,0.5) | ||||
| σt | U(0.1,4) | ||||
| fiso | U(0,1) | ||||
| Beta+TruncatedMixture |

|

| μχ | U(0,1) | Introduces a truncation in the distribution at some minimum value (maximum misalignment angle) |
| σχ | U(0.07,0.5) | ||||
| σt | U(0.1, 4) | ||||
| fiso | U(0,1) | ||||
| zmin | U(−1,1) | ||||
| BetaSpike+Mixture |

|

| μχ | U(0,1) | Spin-magnitude distribution modified to include Beta distribution "bulk" and a finite-width "spike" at approximately zero spin |
| σχ | U(0.07,0.5) | ||||
| fspike | U(0,1) | ||||
 spike spike
| U(0.03, 0.1) | ||||
| σt | U(0.1,4) | ||||
| fiso | U(0,1) | ||||
| BetaSpike+TruncatedMixture |

|

| μχ | U(0,1) | Most complex component spin model; includes both the multiple two-spin-magnitude subpopulations and the truncation in the spin-tilt distribution |
| σχ | U(0.07,0.5) | ||||
| fspike | U(0,1) | ||||
 spike spike
| U(0.03, 0.1) | ||||
| σt | U(0.1, 4) | ||||
| fiso | U(0,1) | ||||
| zmin | U(−1,1) | ||||
Note. denotes a uniform prior between xmin and xmax, while signifies a log-uniform prior.
Download table as: ASCIITypeset image
A.1. Effective Spin Models
In this subsection, we list the various models considered when exploring the distribution of effective inspiral spins among binary black hole mergers. See Table 2 for illustrations of each model, as well as the priors adopted for each parameter.
Gaussian. Our simplest model assumes effective inspiral spins to be Gaussian-distributed with mean μeff and variance ,
where denotes a Gaussian distribution truncated within [a, b]. Our priors on μeff and σeff are listed in Table 2. This model was proposed in Roulet & Zaldarriaga (2019) and Miller et al. (2020) and has been employed and extended in Abbott et al. (2021a, 2021b), Callister et al. (2021b), Biscoveanu et al. (2022), and Bavera et al. (2022).
GaussianSpike.
To initially assess the prevalence of identically nonspinning black holes, we extend the Gaussian model to include a narrow "spike" centered at χeff = 0 with width  ≪ 1,
≪ 1,
The fraction of binary black holes comprising the zero-spin spike is given by ζspike. A similar model was studied by Abbott et al. (2021b), who imparted a finite width to the zero-spin spike population. In this work, we fix  = 0 following the modeling choice of Galaudage et al. (2021), leveraging the kernel density estimation trick discussed in Appendix E to accurately and stably evaluate the likelihood for this delta-function spike.
= 0 following the modeling choice of Galaudage et al. (2021), leveraging the kernel density estimation trick discussed in Appendix E to accurately and stably evaluate the likelihood for this delta-function spike.
BimodalGaussian. Given the inferred absence of a zero-width spike with GaussianSpike, we introduce this model to more generally assess any potential multimodality. We model the distribution of χeff as a mixture of two Gaussians with arbitrary means and standard deviations:
The mixing fraction ζa is constrained to be ≥0.5, solving the "label-switching" problem by demanding that μeff,a and σeff,a are the mean and standard deviation of the dominant subcomponent. No further prior constraints are placed on μeff,a and σeff,a or μeff,b and σeff,b .
A.2. Component Spin Models
We next list the various models used to study the distribution of component spin magnitudes and orientations among binary black holes. See Table 3 for illustrations and priors.
Beta+Mixture: In our simplest component spin model, we assume that spin magnitudes are independently drawn from identical Beta distributions,
where c(α, β) normalizes the distribution to unity. The two shape parameters α and β are constrained such that α, β > 1 to ensure that the distribution is bounded. This choice of parameters requires that p(χi = 0) = p(χi = 1) = 0, thus a priori assuming that there are no systems with exactly vanishing spin. We sample not in α and β directly but rather in the mean μχ and standard deviation σχ of the Beta distribution. The shape parameters α and β are calculated from μχ and σχ through
The region of the μχ and σχ parameter space excluded by restriction α, β > 1 can be seen in Figure 6. The spin-tilt distribution is a mixture between two components: a uniform isotropic component and a preferentially aligned component,
Here, fiso is the fraction of events comprising the isotropic subpopulation, while the second term is a half-Gaussian peaking at . Each component spin tilt is independently drawn from Equation (A8). A model of this form was introduced in Talbot & Thrane (2017) and Wysocki et al. (2019), with the restriction that both spin tilts together lie in either the isotropic or the preferentially-aligned component, and is referred to as the Default model in Abbott et al. (2021a, 2021b), and Galaudage et al. (2021).
BetaSpike+Mixture.
In order to assess the presence of nonspinning black hole binaries, we emulate Galaudage et al. (2021) and extend the Beta+Mixture model include a half-Gaussian "spike" that peaks at χi
= 0 but has a finite width  spike:
spike:
A fraction fspike of the population falls in this (approximately) zero-spin spike while 1 − fspike lives in the bulk, parameterized again by a Beta distribution. Unlike Galaudage et al. (2021), we do not require both black holes in a given binary to occupy the same subpopulation, but instead assume that component spins are independently and identically drawn from Equation (A9). The spin tilt distribution is the same as that in the Beta+Mixture model, given by Equation (A8).
Beta+TruncatedMixture. Further motivated by Galaudage et al. (2021), we alternately extend the Beta+Mixture model by instead modifying the distribution, augmenting it with a tunable lower truncation bound zmin:
with for . The spin magnitude distribution is the same as that in the Beta+Mixture model, given in Equation (A6).
BetaSpike+TruncatedMixture. Finally, we consider both extensions together, incorporating both the (finite-width) zero-spin subpopulation in Equation (A9) and the truncated spin tilt distribution in Equation (A10).
Appendix B: Hierarchical Inference and Data Analyzed
In this appendix, we briefly describe our hierarchical inference framework as well as the exact data we use in this study. Given a catalog of gravitational-wave events with data , the likelihood that such events arise from a population with parameters Λ is (Loredo 2004; Fishbach et al. 2018; Mandel et al. 2019; Vitale et al. 2020)
where λi denotes the parameters (masses, spins, etc.) of each individual binary, and we have marginalized over the overall rate of binary mergers assuming a logarithmically-uniform prior. The detection efficiency ξ(Λ) is the fraction of events that we expect to successfully detect given the proposed population Λ. If Pdetection(λ) is the probability that an event with parameters λ is successfully recovered by detection pipelines, then
In order to evaluate Equation (B1), we require the likelihood p(di ∣λi ) for each detection. In most cases, however, we do not have access to these likelihoods, but rather the posterior p(λi ∣di ) obtained using some default prior ppe(λ). In this case, we rewrite Equation (B1) as
Furthermore, we generally do not know p(λi ∣di ) itself, but instead have a discrete set of independent samples drawn from p(λi ∣di ), where Ni is the number of posterior samples used for event i. The standard course of action is to approximate the integral within Equation (B3) via a Monte Carlo average over these posterior samples,
We can similarly recast the detection efficiency (Equation (B2)) as a Monte Carlo average. Given a number Ninj of injected signals drawn from some reference distribution pinj(λ), the detection efficiency may be approximated via
summing over the Nfound injections that pass our detection criteria.
The fundamental assumption made in Equations (B4) and (B5) is that posterior samples (and recovered injections) are sufficiently dense relative to the population features of interest. In this paper, however, we are concerned with very narrow features in the binary black hole spin distribution: Gaussians of width  ≪ 1 or even true delta functions. We cannot therefore be automatically assured that Equations (B4) and (B5) will accurately represent our likelihood and detection efficiency. In Appendix D we will further assess the accuracy of these Monte Carlo averages, and in Appendix E describe how to bypass them completely.
≪ 1 or even true delta functions. We cannot therefore be automatically assured that Equations (B4) and (B5) will accurately represent our likelihood and detection efficiency. In Appendix D we will further assess the accuracy of these Monte Carlo averages, and in Appendix E describe how to bypass them completely.
For this study, we consider the subset of black holes among GWTC-3 with false-alarm rates below 1 yr−1 (Abbott et al. 2021d). We do not include GW190814 (Abbott et al. 2020b) or GW190917 (Abbott et al. 2021e), both of which have secondary masses m2 < 3 M⊙ and are outliers with respect to the binary black hole population (Abbott et al. 2021a, 2021b). This leaves us with a total of 69 binary black holes in our sample. We use parameter estimation samples made publicly available through the Gravitational-Wave Open Science Center 10 (Vallisneri et al. 2015; Abbott et al. 2021f). For events first published in GWTC-1 11 (Abbott et al. 2019b), we use the "Overall_posterior" parameter estimation samples. We adopt the "PrecessingSpinIMRHM" samples for events first published in GWTC-2 12 (Abbott et al. 2021c) and GWTC-2.1 13 (Abbott et al. 2021e), and for new events in GWTC-3 (Abbott et al. 2021d) use the "C01:Mixed" samples. 14 These choices correspond to a union of samples obtained with different waveform families. All samples include spin precession effects, while the PrecessingSpinIMRHM and C01:Mixed samples from GWTC-2, GWTC-2.1, and GWTC-3 additionally include the effects of higher-order modes (parameter estimation accounting for higher-order modes was not available in GWTC-1). We evaluate the detection efficiency using the set of successfully recovered binary black hole injections, provided by the LIGO–Virgo–KAGRA collaborations, spanning their first three observing runs. 15
Appendix C: Model Checking
In order to trust physical conclusions drawn from phenomenological models, we must be sure that the models themselves provide a reasonable fit to observation. A particularly powerful means of model checking is to perform predictive tests: comparing the predictions made by a fitted model to our actual observed data. In this section, we subject each of the effective and component spin models used in this paper to such predictive tests.
Figure 8 compares predicted and observed χeff values under the Gaussian, GaussianSpike, and BimodalGaussian models explored in Section 4. The ensemble of traces in each panel reflects the uncertainties in the hyperparameters of each model, as well as our uncertainties in the observed properties of each event. Specifically, these figures are generated via the following algorithm:
- 1.Perform hierarchical inference using the model in question, as described in Appendix B, to obtain posteriors on the hyperparameters Λ of the model.
- 2.From the posterior on Λ, draw a single hyperparameter sample Λi .
- 3.Use this Λi to define a new prior p(λ∣Λi ) on the properties of individual events. Reweight the posterior of each observed binary to this new prior, as in e.g., Miller et al. (2020), and randomly select a single sample λj from each event. The resulting set {λ}obs constitutes one realization of "observed" values. 16
- 4.Similarly, reweight the set of successfully found injections described above to the proposed prior p(λ∣Λi ). Randomly select Nobs values from these injections; the resulting set {λ}inj is one realization of "predicted" values. Drawing predicted values from found injections, rather than directly from the proposed population Λi , serves to accurately capture relevant selection effects.
- 5.Independently sort {λ}obs and {λ}inj and plot them against one another, yielding a single "Observed versus Predicted" trace as in Figure 8.
- 6.Repeat Steps 1–4.
Figure 8. Predictive checks of the three effective spin models explored in Section 4. Under each model, we repeatedly generate sets of "Observed" χeff values drawn from our binary black hole observations, and sets of "Predicted" values according to the fitted models; see Appendix C for further details. Each trace among the three subplots represents one such realization, with the spread among traces reflecting both our uncertainty in the properties of each observed binary as well as the uncertainty in model hyperparameters. A model that provides a good fit to observation will yield an ensemble of traces centered symmetrically around the diagonal, whereas any systematic departure from the diagonal would indicate model failure. No such departures are seen, and so all three effective spin models are able to successfully reproduce observation.
Download figure:
Standard image High-resolution imageA model that accurately captures features in our observed data will yield an ensemble of traces centered on the Predicted χeff = Observed χeff diagonal, shown as a dashed black line. Systematic departures away from the diagonal, on the other hand, would indicate a failure of the fitted model to reflect true features in the data. All three effective spin models show good predictive power in Figure 8, yielding traces distributed symmetrically about the diagonal. Note that the large variance in the BimodalGaussian results reflects our correspondingly large uncertainty about the χeff distribution at very negative and very positive values. The elevated variance is symmetric about the diagonal, though, and so is not a sign of model failure.
Figure 9 shows analogous predictive checks using the four component spin models explored in Section 5. We investigate each model's ability to predict observed spin magnitudes (first and second columns), spin tilts (third and fourth columns), and effective spins (final column). Each model shows good predictive power, with no significant departures from the diagonal that would indicate model failure. The Beta+Mixture and BetaSpike+Mixture models, though, may show slight signs of tension in their ability to predict and χeff. For each model, 70% of traces lie above the diagonal at −0.5, possibly indicating a tendency to overpredict the occurrence of large and negative values. Accordingly, both models slightly overpredict the prevalence of large negative χeff, with ∼75% of traces rising above the diagonal at Predicted χeff = −0.2. This behavior is consistent with the preference for a truncation at −0.5 found using the Beta+TruncatedMixture and BetaSpike+TruncatedMixture models. These tendencies are slight, however, and so cannot yet be taken as an indicator of model failure; more data will be required to better resolve the underlying spin distributions and determine which (if any) models can no longer provide a good descriptor of observation.
Figure 9. As in Figure 8 above, but for the component spin models studied in Section 5. We explore each model's ability to predict the observed spin magnitudes (first and second columns), spin tilts (third and fourth columns), and effective spins (fifth column). Again, we see no clear departures from the diagonal, such that none of the four models can be rejected as a poor descriptor of our data. The Beta+Mixture and BetaSpike+Mixture models may exhibit slight tension with observation, possibly overpredicting the occurrence of very negative and χeff, but additional data are required to confirm the significance of this tendency.
Download figure:
Standard image High-resolution imageAppendix D: Effective Samples
In order to identify and mitigate possible issues due to such finite sampling effects when estimating Equation (B4), we track the number of "effective samples" informing the Monte Carlo estimates of the likelihood for every event. Given a set of Ni posterior samples for each event i, the number of "effective samples" under a proposed population Λ is
where wi,j (Λ) = p(λi,j ∣Λ)/ppe(λi,j ). Small Neff,i (Λ) indicates that the given event is sparsely sampled in the region where the population p(λ∣Λ) is concentrated, and hence the likelihood may be dominated by sampling variance. In these regions, we should not necessarily trust the results of Monte-Carlo-based hierarchical inference. To avoid such regions, Abbott et al. (2021b) impose a data-dependent prior cut, rejecting those Λ for which falls below some threshold value. We avoid imposing such a cut, which amounts to an implicit (and often stringent) prior on Λ. Instead, we compute and track for each component spin population model we consider. Additionally, for models with distinct "spike" and "bulk" spin subpopulations (i.e., the half-Gaussian at zero and the Beta distribution, respectively), we track the minimum effective sample count within each of these subpopulations.
Our primary concern in tracking Neff is to calibrate the allowed width  spike of a possible zero-spin spike in the component spin distribution. Due to finite sampling effects, we cannot let this spike width be arbitrarily small, but must bound
spike of a possible zero-spin spike in the component spin distribution. Due to finite sampling effects, we cannot let this spike width be arbitrarily small, but must bound  spike to sufficiently large values to ensure reasonable Neff. Essick & Farr (2022) argue that Neff ∼ 10 per event is sufficiently high to ensure accurate marginalization over each event's parameters. Figure 10 illustrates how varies as a function of
spike to sufficiently large values to ensure reasonable Neff. Essick & Farr (2022) argue that Neff ∼ 10 per event is sufficiently high to ensure accurate marginalization over each event's parameters. Figure 10 illustrates how varies as a function of  spike; each point represents a posterior sample drawn from the BetaSpike+TruncatedMixture results in Figure 6. The left panel shows Neff as computed across the full spin distribution, while the center panel shows the effective sample count taken just over the "bulk" Beta distribution (via fixing fspike = 0 when computing Equation (D1)). The effective sample counts across the total population and in the bulk are largely uncorrelated with
spike; each point represents a posterior sample drawn from the BetaSpike+TruncatedMixture results in Figure 6. The left panel shows Neff as computed across the full spin distribution, while the center panel shows the effective sample count taken just over the "bulk" Beta distribution (via fixing fspike = 0 when computing Equation (D1)). The effective sample counts across the total population and in the bulk are largely uncorrelated with  spike > 0.03 and are everywhere large, with .
spike > 0.03 and are everywhere large, with .
Figure 10. Scatter plot of the minimum (across events) number of effective samples and the width of the zero-spin spike  spike for the BetaSpike+TruncatedMixture model. Each point represents a single draw from the posterior shown in Figure 6. Left panel: the minimum number of effective samples as computed across the entire population model. Middle panel: the minimum number of effective samples in the "bulk" (Beta distribution) spin magnitude subpopulation.. Right panel: the minimum number of effective samples in the "spike" (zero-spin half-Gaussian) spin magnitude subpopulation. Dashed vertical lines denote
spike for the BetaSpike+TruncatedMixture model. Each point represents a single draw from the posterior shown in Figure 6. Left panel: the minimum number of effective samples as computed across the entire population model. Middle panel: the minimum number of effective samples in the "bulk" (Beta distribution) spin magnitude subpopulation.. Right panel: the minimum number of effective samples in the "spike" (zero-spin half-Gaussian) spin magnitude subpopulation. Dashed vertical lines denote  spike = 0.03, the lower limit we impose on this parameter in our prior. Although the minimum sample count in the spike appears unacceptably low, the minimum is driven by events that are confidently spinning and which therefore do not impact our inference regarding the zero-spin spike (see the left panel of Figure 11). Red points illustrate the minimum effective samples when excluding events these events that are confidently spinning. Green points show the minimum effective sample count if we further exclude events that are "likely" spinning (e.g., middle panel of Figure 11), focusing only on those events that are well described by zero spin. To ensure a reasonable number of effective samples among these remaining events, we bound
spike = 0.03, the lower limit we impose on this parameter in our prior. Although the minimum sample count in the spike appears unacceptably low, the minimum is driven by events that are confidently spinning and which therefore do not impact our inference regarding the zero-spin spike (see the left panel of Figure 11). Red points illustrate the minimum effective samples when excluding events these events that are confidently spinning. Green points show the minimum effective sample count if we further exclude events that are "likely" spinning (e.g., middle panel of Figure 11), focusing only on those events that are well described by zero spin. To ensure a reasonable number of effective samples among these remaining events, we bound  spike > 0.03 and note that the region
spike > 0.03 and note that the region  spike ≲ 0.04 may be subject to elevated Monte Carlo variance.
spike ≲ 0.04 may be subject to elevated Monte Carlo variance.
Download figure:
Standard image High-resolution imageThe right panel of Figure 10, meanwhile, shows the number of effective samples contained in the zero-spin spike (obtained by fixing fspike = 1 in Equation (D1)). The number of effective samples in the spike is extremely correlated with  spike. This is expected, as a wider spike will encompass more posterior samples and thus have a larger . The blue points show taken across all events. This minimum sample count is unacceptably low (Essick & Farr 2022), with every population sample yielding at least one binary with only ∼1 effective sample. However, we argue that this is not in fact concerning.
17
The events with a very low number of effective samples in the spike are the same events that are unambiguously spinning and hence confidently belong in the bulk and not the spike. Their extremely low number of effective samples in the spike, therefore, does not affect inference. The left-hand panel in Figure 11 illustrates the component spin magnitude posterior for one such "confidently spinning" event that unambiguously rules out χ1 = χ2 = 0. The red dots in Figure 10 show the minimum effective sample count if we now exclude these confidently spinning events (GW190517, GW190412, GW151226, and GW191204, specifically). This minimum count still contains events that are likely (but not necessarily unambiguously) nonspinning, such as the event shown in the center panel of Figure 11. The most critical measure of stability is whether Neff is large for events such as GW150914 (right panel of Figure 11) whose posteriors are finite up to and including χ1 = χ2 = 0. The green points in Figure 10, therefore, show the minimum sample count when we further exclude "likely nonspinning" events, defined as any event with less than 1/200 of its samples in the region χ1, χ2 < 0.1. The minimum number of effective samples across remaining events now rises to ∼5 at
spike. This is expected, as a wider spike will encompass more posterior samples and thus have a larger . The blue points show taken across all events. This minimum sample count is unacceptably low (Essick & Farr 2022), with every population sample yielding at least one binary with only ∼1 effective sample. However, we argue that this is not in fact concerning.
17
The events with a very low number of effective samples in the spike are the same events that are unambiguously spinning and hence confidently belong in the bulk and not the spike. Their extremely low number of effective samples in the spike, therefore, does not affect inference. The left-hand panel in Figure 11 illustrates the component spin magnitude posterior for one such "confidently spinning" event that unambiguously rules out χ1 = χ2 = 0. The red dots in Figure 10 show the minimum effective sample count if we now exclude these confidently spinning events (GW190517, GW190412, GW151226, and GW191204, specifically). This minimum count still contains events that are likely (but not necessarily unambiguously) nonspinning, such as the event shown in the center panel of Figure 11. The most critical measure of stability is whether Neff is large for events such as GW150914 (right panel of Figure 11) whose posteriors are finite up to and including χ1 = χ2 = 0. The green points in Figure 10, therefore, show the minimum sample count when we further exclude "likely nonspinning" events, defined as any event with less than 1/200 of its samples in the region χ1, χ2 < 0.1. The minimum number of effective samples across remaining events now rises to ∼5 at  spike = 0.03 and ≳10 at
spike = 0.03 and ≳10 at  spike = 0.04. Given this, we choose to limit
spike = 0.04. Given this, we choose to limit  spike ≥ 0.03, and caution that the region
spike ≥ 0.03, and caution that the region  spike < 0.04 may be subject to increased Monte Carlo averaging error.
spike < 0.04 may be subject to increased Monte Carlo averaging error.
Figure 11. Spin magnitude posterior samples demonstrating the three classes of events discussed in Figure 10 above. The left-hand panel illustrates a confidently spinning binary, which is clearly identified as a member of the spinning "bulk" population and whose low effective sample count in the spike is therefore unimportant. The middle panel illustrates a "likely" spinning event, defined by having less than a fraction 1/200 of its posterior samples in the region χ1, χ2 < 0.1. The right panel, finally, shows an event belonging to neither category; these remaining events are used to generate the green points in Figure 10 above.
Download figure:
Standard image High-resolution imageAppendix E: Avoiding Samples with Likelihood KDEs
Our ordinary population likelihood, Equation (B4), relies on Monte Carlo averages over posterior samples, an approach that can behave poorly when evaluating narrow population features as described above. Within the GaussianSpike effective spin model, for example, in the limit that  → 0 there will be precisely no posterior samples falling in the zero-spin spike, and hence we will be unable to precisely evaluate the model's likelihood. This limitation is not physical, but purely due to our representation of each event's posterior as a set of discrete samples. As an alternative approach, we can abandon samples altogether and instead represent the likelihoods of individual events as Gaussian KDEs. This alternative representation remains well behaved even when the population features of interest are narrow, provided that there are enough samples in the neighborhood of the narrow feature to estimate the KDE.
→ 0 there will be precisely no posterior samples falling in the zero-spin spike, and hence we will be unable to precisely evaluate the model's likelihood. This limitation is not physical, but purely due to our representation of each event's posterior as a set of discrete samples. As an alternative approach, we can abandon samples altogether and instead represent the likelihoods of individual events as Gaussian KDEs. This alternative representation remains well behaved even when the population features of interest are narrow, provided that there are enough samples in the neighborhood of the narrow feature to estimate the KDE.
For convenience, let represent all individual-event parameters except χeff. Under the discrete sample representation, the ordinary Monte Carlo average in Equation (B4) is obtained by identifying individual events' likelihoods as a sum of delta functions located at each posterior sample j:
In the KDE approach, we impart a finite "resolution" to each posterior sample, replacing the delta functions with Gaussians of width σkde:
Equation (E2) is now a continuous function of χeff,i and hence allows us to evaluate the likelihood of a population with arbitrarily narrow features. This comes at a cost. As shown in Equation (B1), evaluation of a population likelihood requires evaluation of the integral . This integration is trivial when the likelihoods are composed purely of delta functions, as in Equation (E1), but not necessarily straightforward using Equation (E2).
Fortunately, both the individual-event likelihoods and our population models are mixtures of Gaussians in χeff, and so we can analytically carry out the required integration over χeff. For the GaussianSpike model, for example, the result is
with
and
In an exactly analogous fashion, when computing the detection efficiency ξ (Λ) we can replace a Monte Carlo average over successfully found injections [as in Equation (B5)] with a KDE over injections:
As above, the integration can be carried out analytically when (as in our case) the population model p(χeff∣Λ) is a mixture of Gaussians.
As a demonstration and validation of this approach, we revisit inference of the GWTC-3 effective spin distribution via the GaussianSpike model, but now fix the "spike" at χeff = 0 to have a finite width  > 0. We repeat the analysis in two ways: (i) using the ordinary Monte Carlo representation of Equations (B4) and (B5), and (ii) using the KDE representation of Equations (E3) and (E6). Figure 12 shows the marginal posterior for ζspike for different choices of
> 0. We repeat the analysis in two ways: (i) using the ordinary Monte Carlo representation of Equations (B4) and (B5), and (ii) using the KDE representation of Equations (E3) and (E6). Figure 12 shows the marginal posterior for ζspike for different choices of  . When
. When  is large (i.e., the "spike" is broad compared to the typical intersample spacing), the two methods give identical results. As we let
is large (i.e., the "spike" is broad compared to the typical intersample spacing), the two methods give identical results. As we let  approach zero, however, the Monte Carlo average produces divergent results, while the KDE likelihood representation yields stable and converging posteriors.
approach zero, however, the Monte Carlo average produces divergent results, while the KDE likelihood representation yields stable and converging posteriors.
Figure 12. Validation of the KDE likelihood approach discussed in Appendix E. Each subplot shows the marginalized posterior for the fraction of events contained within a narrow spike at χeff = 0. Solid lines show posteriors computed using the KDE method, while dashed lines show posteriors obtained using ordinary Monte Carlo averaging (Appendix B). Results are shown for a variety of spike widths, from broad spikes with standard deviation  = 0.03 to narrow spikes with
= 0.03 to narrow spikes with  = 10−4. We see that the KDE method yields consistent and convergent results as
= 10−4. We see that the KDE method yields consistent and convergent results as  approaches zero, while the Monte Carlo averaging gives increasingly divergent results for small spike widths due to growing Monte Carlo errors.
approaches zero, while the Monte Carlo averaging gives increasingly divergent results for small spike widths due to growing Monte Carlo errors.
Download figure:
Standard image High-resolution imageAppendix F: Mock Injection Campaign
In Figure 3 in the main text, we showed posteriors on ζspike obtained by analyzing mock catalogs of binary black holes drawn from an intrinsically spikeless population. In this appendix, we describe our procedure for generating and analyzing these mock catalogs.
To generate mock χeff measurements, we assume an underlying astrophysical distribution following the Gaussian effective spin model, with mean μeff = 0.06 and standard deviation σeff = 0.09. These values are chosen to match the median measurements of μeff and σeff obtained when hierarchically analyzing GWTC-3 with the Gaussian effective spin model. For each mock catalog, we draw 69 "true" spin values from this Gaussian population:
We then add a random measurement uncertainty to each mock event. Assuming Gaussian likelihoods for each χeff measurement, "observed" maximum-likelihood values are generated via
where σobs is the standard deviation of each event's likelihood. These uncertainties are themselves randomly distributed to match the range of uncertainties exhibited by real measurements. The χeff likelihoods among binary black holes in GWTC-3 have log standard deviations that are approximately normally distributed, with a mean of −0.9 and a standard deviation of 0.3. When drawing mock observed values in Equation (F2), we therefore assign each event a random measurement uncertainty according to
Because both our population model and our mock likelihoods are Gaussian, the hierarchical likelihood for μeff and σeff can be calculated analytically, exactly as was done in Appendix E above. Specifically, the likelihood p({d}∣μeff, σeff) of our mock catalog is of the same form as Equation (E3), with the observed χeff,obs values in place of χeff,i,j
, the measurement uncertainties σobs in place of  , and ignoring the summation over j.
, and ignoring the summation over j.
As highlighted in Section 4, many of our mock catalogs exhibit ζspike posteriors qualitatively similar to the posterior obtained using real data, encompassing zero but peaking at ζspike ≈ 0.5. Some mock catalogs even more confidently (and incorrectly) appear to rule out the injected value of ζspike = 0. We find that this elevated "false-alarm probability" can be explained by a degeneracy between ζspike and μeff that occurs when analyzing relatively small number of individually uncertain measurements. To illustrate this behavior, we choose the mock catalog whose ζspike posterior most strongly rules out zero in Figure 3. The left-hand panel in Figure 13 shows the joint posterior on ζspike and μeff given by this catalog. These parameters are correlated: if the Gaussian "bulk" is shifted to a larger mean, events located at negative or near-zero χeff values are left behind and must be absorbed into the zero-spin spike. To test this intuition, we show in the middle panel of Figure 13 the individual likelihoods that comprise this mock catalog. The event with the largest χeff (and hence the event pulling μeff to large values) is highlighted. If we remove this high-spin event and redo the hierarchical inference on this catalog, we obtain the blue ζspike posterior shown in the right-hand panel of Figure 13. After removing the high-spin event, we now find ζspike to be considerably more consistent with zero.
Figure 13. Follow-up exploration of the injected mock catalog that most strongly (and incorrectly) excludes ζspike = 0 in Figure 3. Left: the joint posterior on ζspike and μeff from the selected catalog. In general, we find significant correlations between ζspike and the mean μeff of the spinning "bulk" population. Mock catalogs that most strongly disfavor ζspike = 0 are generally those that have the largest inferred μeff. Middle: the individual events comprising the selected catalog. The event with the largest measured χeff (and hence the event that most strongly influences μeff) is highlighted. Right: the solid blue curve shows the updated ζspike posterior after removing the highlighted high-spin event. Compared to the original ζspike measurement (dashed black curve), the updated posterior is now more (correctly) consistent with ζspike = 0.
Download figure:
Standard image High-resolution imageAppendix G: Bayes Factors through the Savage–Dickey Density Ratio
Our initial counting experiment in Section 3 uses only the Bayes factors for each event in GWTC-2 between the nonspinning (χ1 = χ2 = 0) and spinning (χ1, χ2 ≥ 0) hypotheses. Such Bayes factors also act as inputs in the analysis of Galaudage et al. (2021). Galaudage et al. (2021) form Bayes factors via the ratios of fully marginalized likelihoods computed for each event via nested sampling under nonspinning and spinning priors (Abbott et al. 2021c; Kimball et al. 2021). Instead, we compute Bayes factors directly from the posterior samples for each event. For nested models where the simpler model (e.g., the nonspinning model) is contained within a more complex model (the spinning model with χ1 = χ2 = 0), the Bayes factor between models is given through the Savage–Dickey density ratio (Verdinelli & Wasserman 1995),
where p(χ1 = 0, χ2 = 0∣d) and p(χ1 = 0, χ2 = 0) are the posterior and prior densities at χ1 = χ2 = 0, respectively. See Appendix B of Chatziioannou et al. (2014) for a proof of this equation when the more complex model has additional parameters (here, the spin angles) that are absent from the simpler model. For every binary black hole in GWTC-2, the left panel of Figure 14 shows the probability that the event is nonspinning,
as implied by both sets of Bayes factors. We find general agreement, within numerical uncertainties, between our Bayes factors computed via Savage–Dickey density ratios and those computed via nested sampling (Abbott et al. 2021c). We note that Savage–Dickey density ratios, which rely on KDEs over posterior samples, may be less reliable for events with very little support at (χ1 = 0, χ2 = 0). In these cases, however, a Savage–Dickey density ratio would still conclude that pNS → 0 consistently.
Figure 14. Left panel: the probabilities pNS for each binary black hole in GWTC-2 to be nonspinning, as computed in two different ways: through a Savage–Dickey density ratio and using fully marginalized likelihoods computed via nested sampling and reported in Abbott et al. (2021c). The circles denote GW190408_181802 and GW190828_063405, whose nested sampling results appear to be outliers. Center panel: the spin magnitude posterior for GW190408_181802. Nested sampling yields a Bayes factor of in favor of the hypothesis that this event is nonspinning. This would require the spin magnitude posterior to be ∼130 times larger than the (flat) prior at χ1 = χ2 = 0. This is inconsistent, though, with the true posterior on the spin magnitudes of GW190408_181802, suggesting that the nested sampling Bayes factor in favor of the nonspinning hypothesis is significantly overestimated. Right panel: as a consistency check, we repeat the counting experiment from Section 3 using the nested sampling Bayes factors serving as input to Galaudage et al. (2021), rather than our Savage–Dickey estimates. We show posteriors obtained using the entire GWTC-2 catalog (solid blue curve) and results after excluding GW190408_181802 from our sample (dashed blue). As mentioned in Section 3, we obtain much closer agreement with the Savage–Dickey result (gray curve) after excluding GW190408_181802.
Download figure:
Standard image High-resolution imageThere are two significant outliers, however. Nested sampling returns in favor of the nonspinning hypothesis for the event GW190408_181802. If this Bayes factor were correct, then GW190408_181802 is almost certainly nonspinning, guaranteeing that a nonzero number of events will be placed in a nonspinning subpopulation. This is indeed the conclusion drawn by Galaudage et al. (2021) with the nested sampling Bayes factors. Such a large preference for vanishing spins is not supported by this event's spin magnitude posteriors (right panel); it would require that the posterior is ∼130 times larger than the prior at (χ1 = χ2 = 0). A Savage–Dickey density ratio instead gives an agnostic for GW190408_181802. The opposite situation is encountered for GW190828_063405, which is reported to have from nested sampling. Inspection of the posterior again shows that the posterior and the Bayes factor are inconsistent, as the former remains finite at χ1 = χ2 = 0. Although these two outliers were identified by comparison of nested sampling and Savage–Dickey density ratio results, the conclusion that the nested sampling Bayes factors are misestimated can be drawn through visual inspection of the posterior samples alone.
Appendix H: Different Catalogs and Model Variations
All results in Sections 4 and 5 of the main text rely on the latest GWTC-3 catalog of gravitational-wave detections(Abbott et al. 2021d), as detailed in Appendix B. However, the results of Galaudage et al. (2021) (to which we frequently compare) instead made use of GWTC-2 (Abbott et al. 2021c), because GWTC-3 results were published only after their study. Moreover, our model differs slightly from ours in how component spin magnitudes and tilt angle are paired. We assume that spin magnitudes χ1 and χ2 are independently and identically distributed (IID), as are tilt angles and . In our BetaSpike+TruncatedMixture model, for example, one component spin could lie in the zero-spin spike while its companion spin could lie in the Beta distribution "bulk." Galaudage et al. (2021), on the other hand, adopt preferential pairing and require that both component spins in a given binary occupy the same mixture component (bulk or spike; aligned or isotropic). In order to enable a more direct comparison between our results, in this appendix we show results obtained using only binary black holes among GWTC-2, as well as results generated with an alternative pairing model that directly matches that of Galaudage et al. (2021).
Figure 15 illustrates the fraction of binary black holes inferred to be nonspinning using the GaussianSpike effective spin model (see Sections 4 and A.1) and analyzing data from GWTC-2. Like our results with GWTC-3, results using only GWTC-2 are consistent with ζspike = 0, indicating no evidence for a distinct subpopulation of nonspinning events. Similarly, Figure 16 shows results when analyzing GWTC-2 binary black holes with the BetaSpike+TruncatedMixture component spin model. We again find consistent results between GWTC-2 and GWTC-3 events. When analyzing only events in GWTC-2, we infer the fraction fspike of approximately nonspinning systems to be consistent with zero and find no requirement for the width of this possible subpopulation to be narrow (small  spike). Using GWTC-2, we also conclude that the distribution of spin–orbit misalignment angles extends beyond 90°, with the truncation zmin on the distribution inferred to be negative (97.1% credibility), although with slightly decreased certainty compared to GWTC-3 (99.7% credibility).
spike). Using GWTC-2, we also conclude that the distribution of spin–orbit misalignment angles extends beyond 90°, with the truncation zmin on the distribution inferred to be negative (97.1% credibility), although with slightly decreased certainty compared to GWTC-3 (99.7% credibility).
Figure 15. The fraction of binary black holes among GWTC-2 (solid blue line; Abbott et al. 2021c) with χeff = 0, inferred using the GaussianSpike effective spin model. For comparison, the dashed black curve shows the result obtained using GWTC-3 (Abbott et al. 2021d); this is the same result shown in Figure 3 in the main text. Both results are consistent with one another, showing no evidence for a distinct subpopulation of events with χeff = 0, although the GWTC-3 result more strongly favors ζspike = 0.
Download figure:
Standard image High-resolution imageFigure 16. Posterior on the parameters of the BetaSpike+TruncatedMicture component spin model, now using only GWTC-2 events (purple). The shaded region in the μχ –σχ two-dimensional posterior is the region excluded by the prior cut on the shape parameters of the beta distribution α, β > 1. For reference, results using the full GWTC-3 event list are shown in orange; the GWTC-3 result is identical to the one presented in Figure 6. We find broadly consistent results between the two catalogs, including no requirement for a zero-spin subpopulation as well as a preference for spins misaligned by more than 90° relative to binaries' Newtonian orbital angular momentum.
Download figure:
Standard image High-resolution imageFinally, Figure 17 shows results obtained under an alternative version of our BetaSpike+TruncatedMixture model that directly matches the pairing function used by Galaudage et al. (2021) in their Extended model. Explicitly, spin magnitudes are jointly distributed as
and the joint tilt angle distribution is
Figure 17 shows results from this alternative model using both GWTC-2 and GWTC-3. For reference, the dashed black distributions show results from our usual BetaSpike+TruncatedMixture model. Compared to BetaSpike+TruncatedMixture, the Extended model has more support at fspike = 0, strengthening the conclusion that the fraction of black holes with negligible spin is consistent with zero. For the tilt angle distribution, we find that data still has a strong preference for negative zmin under the Extended model, but with decreased confidence (84.6% credibility for GWTC-2 and 90.4%credibility for GWTC-3) compared with BetaSpike+TruncatedMixture. Perhaps the starkest difference between results generated with the Extended and sBetaSpike+TruncatedMixture models is that under Extended, the data even more strongly prefer isotropically distributed tilt angles over aligned, as seen by the fiso peaking strongly at unity. This again indicates no strong preference, given current data, that black hole spins are collectively nearly aligned with their orbital angular momenta.
Figure 17. Posterior on the parameters of the Extended component spin model (Equations (H1) and (H2)) using GWTC-3 data (orange) and just GWTC-2 data (purple). The one-dimensional marginalized posteriors for the BetaSpike+TruncatedMicture model for GWTC-3 are shown in black dashed lines for comparison; this result is identical to that shown in Figures 6 and 16. The Extended model infers a population with smaller fspike and larger fiso than BetaSpike+TruncatedMicture; it also has more support for than BetaSpike+TruncatedMicture, although the zmin posterior peaks at a negative value for both cases. The posteriors for the remaining population parameters are qualitatively similar between the two models.
Download figure:
Standard image High-resolution imageFootnotes
- 5
An NPN order is defined as being proportional to compared to its leading-order term, where u is a characteristic velocity of the system and c is the speed of light.
- 6
- 7
- 8
During the late stages of preparation of this study, the exact numerical results of Galaudage et al. (2021) were updated to account for an analysis bug, though their main conclusions remain unchanged. Numbers in this manuscript correspond to their updated results.
- 9
Sometimes known as "evidence," though in this paper we reserve this term for nontechnical use.
- 10
- 11
GWTC-1 samples available at https://dcc.ligo.org/LIGO-P1800370/public.
- 12
GWTC-2 samples available at https://dcc.ligo.org/LIGO-P2000223/public.
- 13
GWTC-2.1 samples available at https://zenodo.org/record/5117703.
- 14
GWTC-3 samples available at https://zenodo.org/record/5546663.
- 15
- 16
Note that reweighting single-event posteriors following Steps 1 and 2 avoids any "double counting" of information (Callister 2021).
- 17
If one wishes to avoid this argument altogether, the alternative method discussed in Appendix E and used to infer the binary χeff distribution is accurate in the presence of narrow population features, producing results that agree with those discussed in this section.



































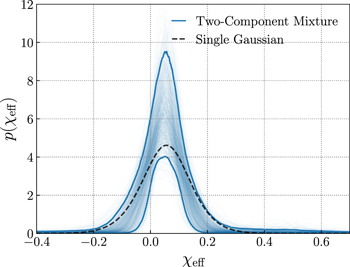











![$\min \left[{N}_{\mathrm{eff},i}({\rm{\Lambda }})\right]$](https://content.cld.iop.org/journals/2041-8205/937/1/L13/revision2/apjlac847eieqn31.gif)






























































![${{ \mathcal N }}_{[a,b]}$](https://content.cld.iop.org/journals/2041-8205/937/1/L13/revision2/apjlac847eieqn88.gif)



























![$\min \left[{N}_{\mathrm{eff},i}({\rm{\Lambda }})\right]$](https://content.cld.iop.org/journals/2041-8205/937/1/L13/revision2/apjlac847eieqn101.gif)
![$\min \left[{N}_{\mathrm{eff},i}({\rm{\Lambda }})\right]$](https://content.cld.iop.org/journals/2041-8205/937/1/L13/revision2/apjlac847eieqn102.gif)
![$\min \left[{N}_{\mathrm{eff},i}\right]$](https://content.cld.iop.org/journals/2041-8205/937/1/L13/revision2/apjlac847eieqn103.gif)


![$\min \left[{N}_{\mathrm{eff},i}\right]$](https://content.cld.iop.org/journals/2041-8205/937/1/L13/revision2/apjlac847eieqn105.gif)
![$\min \left[{N}_{\mathrm{eff},i}\right]$](https://content.cld.iop.org/journals/2041-8205/937/1/L13/revision2/apjlac847eieqn106.gif)
![$\min \left[{N}_{\mathrm{eff},i}\right]$](https://content.cld.iop.org/journals/2041-8205/937/1/L13/revision2/apjlac847eieqn107.gif)


































