Abstract
The Voyager 1 magnetometer has detected several shock waves in the very local interstellar medium (VLISM). Interplanetary shock waves can be transmitted across the heliopause (HP) into the VLISM. The first in situ shock observed by Voyager 1 inside the VLISM was remarkably broad and had properties different than those of shocks inside the heliosphere. We present a model of the 2012 VLISM shock, which was observed to be a weak, quasi-perpendicular, low magnetosonic Mach number, low beta, and subcritical shock. Although the heliosphere is a collisionless environment, we show that the VLISM is collisional with respect to the thermal plasma, and that the thermal collisions introduce dissipative terms such as heat conduction and viscosity. The structure of the VLISM shock is determined by thermal proton–proton collisions. VLISM pickup ions (PUIs) do not introduce a significant pressure or dissipation through the shock transition, meaning that the VLISM shock is not mediated by PUIs but only by the thermal gas and magnetic field. Therefore, VLISM shocks are controlled by particle collisions and not by wave–particle interactions. We find that the weak VLISM shock is very broad with a thickness of about 0.12 au, corresponding to the characteristic thermal heat conduction scale length.
Export citation and abstract BibTeX RIS
1. Introduction
The Voyager 1 spacecraft crossed into the very local interstellar medium (VLISM) after passing the heliopause (HP) on 2012 August 25. Anomalous cosmic rays and termination shock particles, which are dominant in the inner heliosheath (IHS), vanished abruptly and the galactic cosmic-ray flux increased significantly. The Voyager 1 magnetometer detected a change in the magnetic field strength (Krimigis et al. 2013; Stone et al. 2013; and Webber & McDonald 2013). Voyager 1 is now making in situ measurements of the interstellar medium. Although the plasma instrument on Voyager 1 stopped working in 1980, the electron number density can be estimated from the frequency of electron plasma oscillations (Gurnett et al. 2013). A remarkable discovery made by Voyager 1 was the observation of shock waves in interstellar space (Burlaga et al. 2013). The shocks seen in the VLISM are due to interplanetary shocks that propagate through the supersonic solar wind, collide with the heliospheric termination shock (HTS), and then propagate through the inner heliosheath until the HP, where the shocks are partially reflected and transmitted into the VLISM (Whang & Burlaga 1994; Zank & Müller 2003; Washimi et al. 2011; Zank 2015).
The interstellar shocks are surprising in the regard that they possess properties quite different than those of heliosphere shocks (Burlaga et al. 2013). The 2012 VLISM shock was observed (Burlaga et al. 2013) to have a weak jump in the magnetic field, 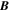 (compression ratio of about B2/B1 ≈ 1.4 where 2/1 refers to the downstream/upstream state of the shock), and appeared to correspond to a weak, low beta, and subcritical shock (Mellott & Greenstadt 1984). Burlaga et al. (2013) showed that the shock is quasi-perpendicular (the angle between shock normal and
(compression ratio of about B2/B1 ≈ 1.4 where 2/1 refers to the downstream/upstream state of the shock), and appeared to correspond to a weak, low beta, and subcritical shock (Mellott & Greenstadt 1984). Burlaga et al. (2013) showed that the shock is quasi-perpendicular (the angle between shock normal and 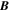 is about 85°). The significant property of the shock is its very smooth nature with very large width, being about 104 times broader than a shock with similar properties at 1 au. Thus far there is no theoretical explanation for such a broad shock structure in the VLISM. Here we present a theory describing the VLISM that accounts for the structure of VLISM shocks, and we model the VLISM shock observed at the end of 2012 by Voyager 1. We show that the electron and proton collisional timescale in the VLISM is much smaller than the characteristic dynamical timescale in the VLISM with corresponding short collisional mean free paths. Consequently, the VLISM is collisional with respect to the thermal plasma. Thermal collisions introduce heat conduction and viscosity (dissipation) into the system, and these processes are responsible for determining the structure of VLISM shocks. Fast and hot neutral atoms created in the supersonic solar wind and IHS are deposited in the VLISM (Zank et al. 1996; Zank et al. 2014, 2016), which, through secondary charge exchange, leads to the creation of suprathermal PUIs in the VLISM. The VLISM PUIs contribute a very small pressure in the VLISM due to their small number density compared to that of the thermal gas. Although the primary dissipation mechanism at the HTS is reflected PUIs (Zank et al. 1996; Richardson et al. 2008), they are insufficient to provide the dissipation for VLISM shocks.
is about 85°). The significant property of the shock is its very smooth nature with very large width, being about 104 times broader than a shock with similar properties at 1 au. Thus far there is no theoretical explanation for such a broad shock structure in the VLISM. Here we present a theory describing the VLISM that accounts for the structure of VLISM shocks, and we model the VLISM shock observed at the end of 2012 by Voyager 1. We show that the electron and proton collisional timescale in the VLISM is much smaller than the characteristic dynamical timescale in the VLISM with corresponding short collisional mean free paths. Consequently, the VLISM is collisional with respect to the thermal plasma. Thermal collisions introduce heat conduction and viscosity (dissipation) into the system, and these processes are responsible for determining the structure of VLISM shocks. Fast and hot neutral atoms created in the supersonic solar wind and IHS are deposited in the VLISM (Zank et al. 1996; Zank et al. 2014, 2016), which, through secondary charge exchange, leads to the creation of suprathermal PUIs in the VLISM. The VLISM PUIs contribute a very small pressure in the VLISM due to their small number density compared to that of the thermal gas. Although the primary dissipation mechanism at the HTS is reflected PUIs (Zank et al. 1996; Richardson et al. 2008), they are insufficient to provide the dissipation for VLISM shocks.
The paper is organized as follows. We first derive the basic equations describing the VLISM environment and the structure of shock waves therein. In Section 3, we model the VLISM shock and compare it with the observations (Burlaga et al. 2013). Finally, we discuss and summarize our results.
2. Model
The VLISM is comprised of thermal electrons and protons, suprathermal PUIs, and interstellar neutral atoms. In the VLISM, for the scales of interest here, the charge exchange mean free path of protons and hydrogen is sufficiently large that we can neglect their coupling. Zank et al. (2014) discussed collisions between PUIs and thermal VLISM electrons and protons, showing that the collisional mean free path is very large with the implication that PUIs are not equilibrated with the thermal VLISM on scales of less than 75 au. PUIs are scattered by both in situ and self-excited magnetic field fluctuations and therefore experience pitch-angle scattering. A collisionless Chapman–Enskog expansion (Zank et al. 2014, 2016) shows that PUIs can be described by an isotropic pressure, PI, stress tensor, 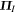 , and heat flux, qI, given by
, and heat flux, qI, given by
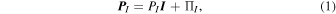
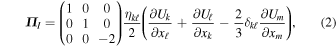
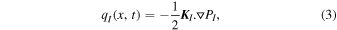
where 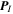 is the PUI pressure tensor, η is the PUI viscosity,
is the PUI pressure tensor, η is the PUI viscosity,  is a spatial PUI diffusion tensor, and
is a spatial PUI diffusion tensor, and  is the bulk flow velocity.
is the bulk flow velocity.
Consider now the thermal VLISM electrons and protons, and assume both have a nearly Maxwellian distribution. The collisional streaming or frictional timescale for a charged particle a colliding with a stationary background population of charged particles b is given by (e.g., Zank 2014)
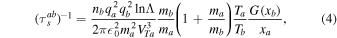
where G(x) is the Chandrasekhar function,
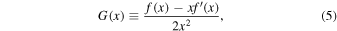
xa/b ≡ v/VTa/b, and f(x) is the error function. The n, q, m, and T for particles a and b denote number density, charge, mass, and temperature, respectively.  is the thermal speed, KB is Boltzmann's constant, and
is the thermal speed, KB is Boltzmann's constant, and 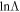 is the Coulomb logarithm.
is the Coulomb logarithm.
The VLISM is collisionally equilibrated, with electrons and protons having the same temperature of about 7500 K (McComas et al. 2015). The electron and proton thermal speeds are 477 km s−1 and 11 km s−1, respectively. The Voyager 1 magnetometer measured the magnetic field magnitude upstream of the VLISM shock to be about 0.38 nT (Burlaga et al. 2013). Based on electron plasma oscillations observed in the vicinity of the 2012 VLISM shock, the electron density upstream of the shock is about 0.06 cm−3 (Gurnett et al. 2013, 2014). For these parameters, we can evaluate the proton–proton (pp), electron–electron (ee), electron–proton (ep), and proton–electron (pe) collisional frictional timescales and the mean free paths (Zank 2014).
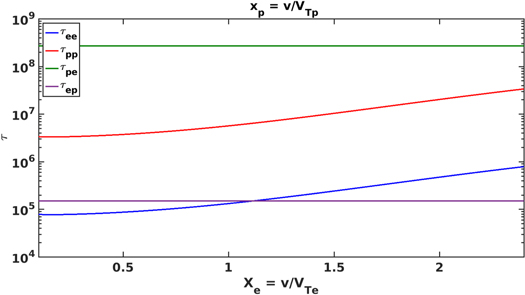
These are illustrated in Figure 1, which shows that the ep and pe collisional timescales are constant and independent of the velocity,
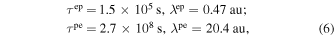
where τ is the collisional timescale and λ is the mean free path. The timescales for ee and pp collisions are not constant and depend on the velocity. The collisional heat conduction and viscous coefficients depend on the collisional scattering timescales, τs, (see, for example, Section 4.8 of Zank 2014). Therefore, we need to estimate τs for the pp and ee collisions and we approximate an appropriate collisional time,  , as follows. The coefficient of viscosity, η, can be estimated as (Zank et al. 2014)
, as follows. The coefficient of viscosity, η, can be estimated as (Zank et al. 2014)
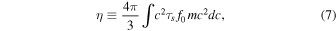
where 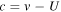 is the random velocity.
is the random velocity. 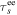 and
and 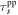 can be approximated as fifth degree polynomial curves from Figure 1 and f0 is a Maxwellian distribution. Integrating from 0 to 2.5VT, we obtain the viscosity coefficient, η, for ee and pp collisions. Using the pressure upstream of the VLISM shock and the relation
can be approximated as fifth degree polynomial curves from Figure 1 and f0 is a Maxwellian distribution. Integrating from 0 to 2.5VT, we obtain the viscosity coefficient, η, for ee and pp collisions. Using the pressure upstream of the VLISM shock and the relation  , we derive the most probable estimates
, we derive the most probable estimates

The VLISM is collisional with respect to the thermal plasma since the electron and proton collisional mean free paths are small compared to the almost featureless VLISM. Therefore, dissipation terms such as thermal heat conduction, Kg, and viscosity, ηg, associated with Coulomb collisions (see Zank 2014) determine the structure of VLISM shocks. In the Appendix, we show that the structure of the observed VLISM shock in the absence of the collisional viscous term is not smooth, meaning that heat conduction alone is insufficient to determine the shock structure and an extra dissipation term (viscosity) is necessary to insure a smooth solution (see also Mostafavi et al. 2017a, 2017b).
Figure 1. pp, ee, ep, and pe collisional timescales for the thermal VLISM plasma. Note that these collisional timescales do not apply to the PUI collisional interactions with the thermal plasma.
Download figure:
Standard image High-resolution imageTo describe shock waves in the VLISM, we ideally need to consider a multi-fluid system of equations for thermal electrons, protons, and non-thermal PUIs. Solving such a system of equations is complicated, but we can reduce the model to a single-fluid-like system of equations while retaining the effects of an equilibrated thermal plasma and non-equilibration with the PUI components. Since PUIs are not equilibrated with the background plasma in the VLISM (Zank et al. 2014, 2016), they should be treated as a separate pressure component, PI, in the system. The reduced single-fluid model comprises the continuity, momentum, and energy equations, together with Maxwell's equations, (see Zank et al. 2014 and Mostafavi et al. 2017a, 2017b)
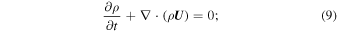
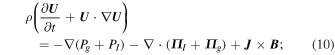
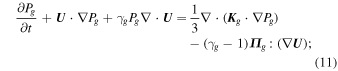
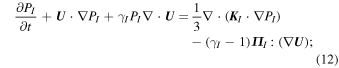
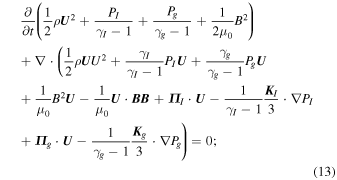
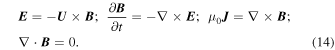
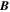 and
and 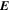 denote the magnetic and electric fields, Pg is the thermal gas (protons and electrons) pressure, ρ is the total density, and
denote the magnetic and electric fields, Pg is the thermal gas (protons and electrons) pressure, ρ is the total density, and 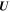 is the bulk flow velocity. We denote all quantities pertaining to PUIs and thermal gas with the subscripts I and g. γg/I are the adiabatic indices of the thermal plasma/PUIs. The collisional thermal plasma stress tensor and PUI stress tensor in a 1D form may be expressed as
is the bulk flow velocity. We denote all quantities pertaining to PUIs and thermal gas with the subscripts I and g. γg/I are the adiabatic indices of the thermal plasma/PUIs. The collisional thermal plasma stress tensor and PUI stress tensor in a 1D form may be expressed as 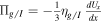 , where ηg is the thermal collisional viscosity coefficient and ηI is the collisionless PUI viscosity coefficient associated with magnetic fluctuations (Jokipii & Williams 1992; Zank et al. 2014).
, where ηg is the thermal collisional viscosity coefficient and ηI is the collisionless PUI viscosity coefficient associated with magnetic fluctuations (Jokipii & Williams 1992; Zank et al. 2014).
A 1D steady-state model in which all physical quantities depend on the x Cartesian coordinate is used and U = (Ux, 0, 0) and B = (0, 0, Bz). The 1D form of Equations (10)–(12) in normalized form is
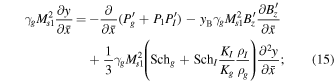
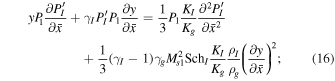
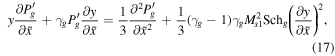
where  is the thermal gas Mach number of the flow,
is the thermal gas Mach number of the flow, 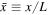 , L ≡ Kg/U1,
, L ≡ Kg/U1, 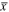 is distance normalized to the diffusion length scale, and
is distance normalized to the diffusion length scale, and 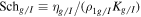 is the Schmidt number of the thermal plasma/PUI. The inverse compression ratio is y = Ux/Ux1 and
is the Schmidt number of the thermal plasma/PUI. The inverse compression ratio is y = Ux/Ux1 and  ,
, 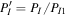 ,
, 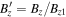 and
and 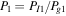 . The inverse Alfvén Mach number squared of the flow far upstream is
. The inverse Alfvén Mach number squared of the flow far upstream is 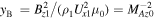 .
.
Based on the thermal collisional term scales derived above from the expressions in Zank (2014), the dominant collisional terms in a collisional magnetized plasma can be estimated. The small mass of electrons compared to protons means they do not contribute significantly to either the thermal heat conduction or thermal viscosity. Proton–electron collisions are negligible since the mean free path is very large compared to that of proton–proton collisions. The dominant collisional terms derive from proton–proton collisions. The diffusion coefficient associated with proton–proton collisions, Kpp, upstream of the observed VLISM shock is about 1015 m2 s−1, and the thermal viscosity is 2.5 × 10−8 kg m−1 s−1, giving a thermal Schmidt number of about 0.25. Energetic PUIs outside the heliosphere are generated by secondary charge exchange, and their number density is very small in the VLISM (np ≈ 5 × 10−5 cm−3; Zirnstein et al. 2014), therefore they contribute a very small pressure compared to the thermal plasma (PI1/Pg1 ≈ 0.05). A characteristic value for the PUI heat conduction, KI, in the VLISM is ∼10 14 m2 s−1. The pitch-angle scattering timescale in the VLISM is taken to be  , giving 5.17 × 102 s, which gives a value for the PUI viscosity, ηI, as ∼3.57 × 10−13 kg m−1 s−1, making the PUI Schmidt number about 10−3. The PUI Schmidt number is much smaller than that of the thermal gas (
, giving 5.17 × 102 s, which gives a value for the PUI viscosity, ηI, as ∼3.57 × 10−13 kg m−1 s−1, making the PUI Schmidt number about 10−3. The PUI Schmidt number is much smaller than that of the thermal gas (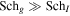 ), thus PUIs and the dissipation associated with them cannot mediate the VLISM shock, as shown by Mostafavi et al. (2017a, 2017b). Consequently, we can neglect PUI dissipation terms in favor of the corresponding thermal gas terms. Unlike the HTS, PUIs will therefore behave adiabatically,
), thus PUIs and the dissipation associated with them cannot mediate the VLISM shock, as shown by Mostafavi et al. (2017a, 2017b). Consequently, we can neglect PUI dissipation terms in favor of the corresponding thermal gas terms. Unlike the HTS, PUIs will therefore behave adiabatically, 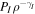 is constant through a broad VLISM shock, and the thermal gas will be heated preferentially. Recall that PUIs were predicted (Zank et al. 1996) and observed (Richardson et al. 2008) to be heated preferentially at the HTS, with the thermal plasma component remaining relatively unheated. The physical processes determining the structure of the HTS and the VLISM shocks are therefore different.
is constant through a broad VLISM shock, and the thermal gas will be heated preferentially. Recall that PUIs were predicted (Zank et al. 1996) and observed (Richardson et al. 2008) to be heated preferentially at the HTS, with the thermal plasma component remaining relatively unheated. The physical processes determining the structure of the HTS and the VLISM shocks are therefore different.
We use the 1D form of the model equations to determine the structure of the VLISM shock observed by Burlaga et al. (2013). Equations (15)–(17) can be rewritten as a second-order equation,
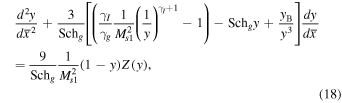
where
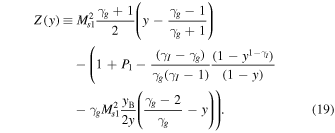
Equation (18) is the shock structure equation in the presence of both the thermal gas heat flux and viscosity.
3. Results
To model the VLISM shock observed by Burlaga et al. (2013), we assume the shock is perpendicular. Upstream of the VLISM shock, the Alfvén speed is VA1 = 34 km s−1 and the sound speed is Cs1 = 14 km s−1 (VA > Cs). The magnetoacoustic speed of the ambient medium is about 36.7 km s−1, similar to that estimated by Gurnett et al. (2013), and yields a subcritical shock. The upstream plasma beta β1 =Pg1/PB1 ≃ 0.2 < 1. Such a quasi-perpendicular, low beta, low magnetosonic Mach number shock has traditionally been designated a laminar shock (e.g., see Figure 1 of Mellott 1985). Burlaga et al. (2013) showed that Voyager 1 (which is moving relative to the Sun at 17 km s−1) moved past the broad 2012 VLISM shock in about 8.7 days. We need to estimate the shock propagation speed to simulate the VLISM shock. Since a subcritical shock has a magnetosonic Mach number less than about two, the upstream flow speed in the shock frame should be less than 72 km s−1 and therefore, the shock speed in the stationary Sun frame should be less than 52 km s−1 (assuming the post-bow shock/wave VLISM flows toward the Sun with a speed of 20 km s−1; Zank et al. 2013). Kim et al. (2017) used the Multi-Scale Fluid-Kinetic Simulation Suite (MS-FLUKSS) to model shock propagation beyond the HP using near-Earth solar wind data, finding that the 2012 VLISM shock had a compression ratio of about 1.65 and shock speed of about 50 km s−1 in a frame in which the Sun is stationary (T. Kim 2018, private communication). Here we adopt a shock speed of 40 km s−1 with respect to the stationary Sun and, therefore, Voyager 1's traversal of the shock in 8.7 days corresponds to a thickness of about 0.12 au. The thickness of the shock is much greater than that expected for a shock with similar properties in the solar wind at 1 au (Burlaga et al. 2013). The thermal heat conduction length scale, K/U1, and the viscous length scale, 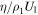 , associated with proton–proton collisions is about 0.115 au and 0.03 au, respectively.
, associated with proton–proton collisions is about 0.115 au and 0.03 au, respectively.
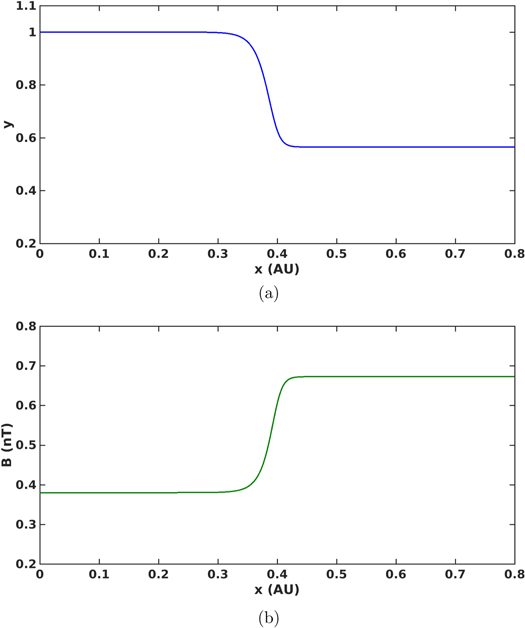
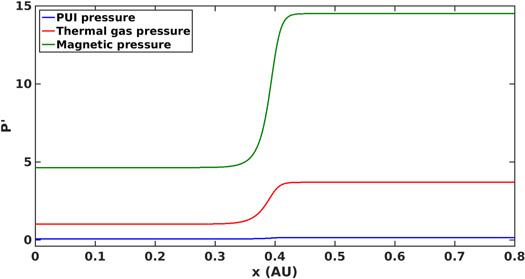
To model the VLISM shock, we use the upstream parameters Ms1 = 4.17, yB = 0.31, PI1/Pg1 = 0.05, γI = γg = 5/3 and solve Equation (18) in the stationary frame of the shock. Figure 2(a) shows the inverse compression ratio as a function of unnormalized distance (au), being a smooth transition connecting the upstream to the downstream state. The VLISM shock compression ratio is ∼1.67. The shock thickness is about 0.12 au and is determined by proton–proton collisions. Figure 2(b) illustrates the change in magnetic field through the shock. The normalized pressure is shown in the Figure 3. The shock is mediated by the thermal gas and magnetic field pressure, which are the dominant components downstream of the shock. PUIs do not contribute a large downstream pressure. The fast magnetosonic Mach number shows that the flow changes from supersonic to subsonic (Figure 4). Since PUIs do not contribute a large pressure through the shock, their inclusion in the sound speed (i.e., the long wavelength sound speed  Zank et al. 2014) scarcely change the magnetosonic Mach number.
Zank et al. 2014) scarcely change the magnetosonic Mach number.
Figure 2. (a) Inverse compression ratio as a function of unnormalized distance (au) showing that the shock is smoothed. (b) Unnormalized magnetic field (nT) through the shock as a function of unnormalized distance (au) showing a weak compression in the magnetic field. Here γg = γI = 5/3, PI1/Pg1 = 0.05, yB = 0.31, and Ms1 = 4.17.
Download figure:
Standard image High-resolution imageFigure 3. PUI, thermal gas, and magnetic pressure normalized to the thermal gas pressure far upstream as a function of unnormalized distance (au).
Download figure:
Standard image High-resolution imageFigure 4. Magnetosonic Mach number as a function of unnormalized distance (au). The thermal gas magnetosonic Mach number (blue line) and the combined effective thermal gas and PUI magnetosonic Mach number (red line) show that the flow changes from supersonic to subsonic.
Download figure:
Standard image High-resolution image4. Conclusions
The VLISM is collisional with respect to the thermal plasma since the electron and proton collisional mean free paths are small compared to the almost featureless VLISM. The dominant proton–proton collisions yields a thermal collisional heat flux and viscous dissipation terms. VLISM PUIs are created by secondary charge exchange, experience pitch angle scattering by magnetic fluctuations, and contribute a collisionless heat flux and collisionless viscosity. However, the thermal gas Schmidt number is much greater than the PUI Schmidt number which ensures that we can neglect the PUI dissipation terms. We have shown that the structure of the interstellar shock observed by Burlaga et al. (2013) is determined by interstellar proton–proton collisions, making the shock the first in situ observed example of a classical collisional subcritical shock. Thus, the shock structure is not controlled by wave–particle interactions but by particle collisions. The weak shock is dominated by the magnetic field and thermal gas pressure and PUIs do not contribute a large pressure through the shock transition. The overall thickness of the shock transition is about 0.12 au, which corresponds to the VLISM heat conduction length scale of K/U1 ∼ 0.115 au.
P.M. acknowledges the support of a NASA Earth and Space Science Fellowship Program grant 16-HELIO16F-0022. G.P.Z. acknowledges the support of NASA grants NNX14AC08G, NNX15AI65G, NNX17AB04G, NNX14AJ53G, and the NSF EPSCoR RII-Track-1 Cooperative Agreement OIA-1655280. We thank Dr. Tae Kim for useful discussions.
Appendix
If we neglect thermal viscosity, that PUIs behave adiabatically, and that the only dissipation term in the VLISM is the thermal heat flux, then the 1D shock structure equation is now
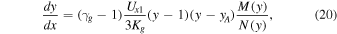
where
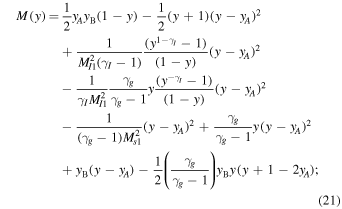
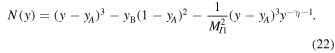
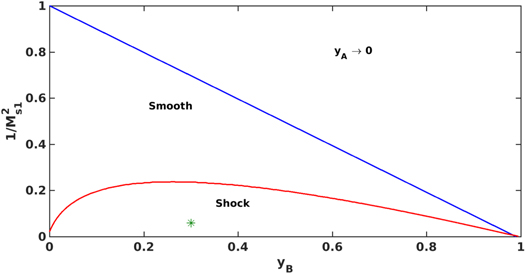
Equation (20) admits two solutions. One regime yields smooth transitions from an upstream state to a downstream state, i.e., solutions mediated completely by the thermal gas heat flux. The second regime corresponds to double-valued solutions that are not physical, and a smooth transition from upstream to downstream is impossible. Thermal heat conduction is insufficient to smooth the shock, and an additional thermal dissipation (thermal viscosity) is required for a smooth shock transition. Figure 5 plots 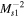 as a function of yB for quasi-perpendicular shocks (
as a function of yB for quasi-perpendicular shocks ( ), identifying the smoothed and sub-shock regimes. The observed VLISM shock parameters,
), identifying the smoothed and sub-shock regimes. The observed VLISM shock parameters, 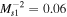 and yB = 0.31, show that the 2012 VLISM shock is located in the sub-shock region. Thermal viscosity is therefore necessary to ensure a smooth shock transition.
and yB = 0.31, show that the 2012 VLISM shock is located in the sub-shock region. Thermal viscosity is therefore necessary to ensure a smooth shock transition.
Figure 5. Initial upstream values 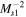 plotted as a function of yB for a quasi-perpendicular shock. Here, γI = γg = 5/3 and PI1/Pg1 = 0.05. The green star corresponds to the parameters of the 2012 VLISM shock.
plotted as a function of yB for a quasi-perpendicular shock. Here, γI = γg = 5/3 and PI1/Pg1 = 0.05. The green star corresponds to the parameters of the 2012 VLISM shock.
Download figure:
Standard image High-resolution image