Phase Mixing of Propagating Alfvén Waves in a Single-fluid Partially Ionized Solar Plasma

The problem of plasma heating in the solar atmosphere is one of the most enigmatic questions that still eludes a definite answer. The formation conditions of many spectral lines observed by various instruments show that the temperature in the solar atmosphere undergoes a gradual increase from the temperature minimum in the photosphere to the chromosphere, a very steep increase in the narrow transition region, and reaches values of several million degrees in the solar corona. The energy in the upper part of the solar atmosphere is lost due to radiation and this needs to be compensated for by mechanisms that can balance the radiative loss.

Several proposed mechanisms can generate the required energy in the chromosphere and/or corona (see, e.g., Erdélyi & Ballai 2007), but none of these have received unequivocal observational proof. All the proposed mechanisms are likely to work simultaneously under different circumstances.

One category of heating mechanisms involves energy derived from damping magnetohydrodynamic (MHD) waves. Such waves are generated by various sources (e.g., the buffeting of magnetic structures by granular motion) in the dense solar photosphere, propagate along the magnetic field, and can dissipate their energy. Although waves can lose their energy due to, e.g., viscosity, magnetic resistivity, and thermal conduction, etc., these effects are not very efficient, as they require long temporal and spatial scales. It is widely accepted that to have an effective energy transfer from MHD waves to smaller scales, one needs large transversal gradients in the background plasma over small spatial scales, e.g., in the ambient Alfvén speed. In such conditions, the mechanisms of resonant absorption and phase mixing become ideal wave-based heating candidates.

Resonant absorption, first proposed by Ionson (1978) as a heating mechanism for coronal loops, is based on the fact that in a plasma with transversal inhomogeneity, the spectrum of waves becomes continuous. An effective wave energy transfer occurs between incident waves and the plasma if the frequency of the wave lies in the frequency continuum of the plasma. In this situation, the energy of the wave is transferred to the local perturbations in the inhomogeneous regions of the magnetic structure, leading to a growth in the amplitude (see, e.g., Davila 1987; Sakurai et al. 1991a, 1991b; Goossens & Ruderman 1995; Goossens et al. 1995; Erdélyi et al. 1999; Cally & Andries 2010, etc.). The growth of the amplitude leads to the nonlinear behavior of waves near the resonant point that can be balanced by dissipative processes that do not need to be excessively large for resonant absorption to work. The theory of resonant absorption predicts a damping time of kink waves that is proportional to the period of waves and was proposed by Ruderman & Roberts (2002) to explain the rapid damping of kink oscillations of coronal loops. For a review of the theory of resonant absorption of kink waves, see, e.g., Goossens et al.(2011).

Phase mixing is a mechanism, like resonant absorption, that requires transversal inhomogeneity, but it operates based on a different consideration (see, e.g., Heyvaerts & Priest 1983; Ireland & Priest 1997; Mocanu et al. 2008; Ruderman & Petrukhin 2017, 2018; Prokopyszyn & Hood 2019, etc.). In particular, for the phase mixing of Alfvén waves to occur, they require an inhomogeneity of the local Alfvén phase speed across the background magnetic field. As a result, the perturbations on different magnetic surfaces become out of phase while propagating. As the phase mixing evolves, even with a small amount of viscosity or resistivity, the dissipation mechanisms become important and could eventually transform the wave energy into heat.

The phase mixing of Alfvén waves was first proposed as a possible heating mechanism of the solar corona by Heyvaerts & Priest (1983), who predicted a damping time proportional to the period of the wave and a damping length inversely proportional to the cube root of the magnetic Reynolds number. Although phase mixing is a viable mechanism that can damp waves, its efficiency (at least under coronal conditions) is questionable. Indeed, the studies by Ofman & Aschwanden (2002) and Mocanu et al. (2008) showed that under coronal conditions, the damping length of shear Alfvén waves is of the order of a few solar radii, and for an effective damping one needs dissipative coefficients that are several orders of magnitude larger than formulas predict (see, e.g., Hood et al. 2002; Mocanu et al. 2008; Cargill et al. 2016; Pagano & De Moortel 2017; Ruderman & Petrukhin 2018; Prokopyszyn & Hood 2019; Van Damme et al. 2020, etc.).

Here we will study the problem of phase mixing for plasma conditions relevant to the solar chromosphere, which is markedly different from the corona, since it is partially ionized, meaning that electrons, positive ions (mostly protons), and neutral atoms interact via long-range collisions (i.e., Coulomb collisions) or short-range encounters (the binary interaction of neutrals with other species). These collisions provide a very effective channel for momentum and energy transfer between species, but also ensure a certain level of coupling. Based on standard solar atmospheric models, e.g., the AL c7 model (Avrett & Loeser 2008), the ratio between the number density of ions to neutrals varies between 10⁻⁴ in the solar photosphere to 10² in the upper part of the chromosphere, i.e., over a distance of about 2.5 Mm, the plasma changes from being weakly ionized to strongly ionized.

The modeling framework of a partially ionized plasma depends very much on the frequency regime in which a certain physical mechanism is described. Here we limit ourselves to the case when the frequency of waves is much smaller than the collisional frequency of particles; therefore we employ a single-fluid description. In this framework, partial ionization appears only through the generalized Ohm's law and it describes the resistive damping (often called ambipolar diffusion or the Cowling resistivity) of currents perpendicular to the ambient magnetic field.

Ambipolar diffusion occurs within a partially ionized plasma when the neutrals are not fully coupled to the charged component. While the charged fluid is subject to the Lorentz force, the decoupled neutral particles undergo a Brownian motion, while still being affected by the close-range collisions with ions. These collisions result in frictional effects between the two components, providing a mechanism for magnetic and mechanical energy to be dissipated, and hence creating a source of localized atmospheric heating (see, e.g., Forteza et al. 2007; Shelyag et al. 2012; Khomenko et al. 2018). Studies by Khomenko et al. (2018) and Popescu Braileanu & Keppens (2021) demonstrated that ambipolar diffusion greatly enhances the damping of waves in photospheric and chromospheric regions where the magnetic field is strong.

The last decade has seen an increased number of studies on the properties of waves in partially ionized plasma. Zaqarashvili et al. (2011) and Soler et al. (2013) discussed the solutions of the dispersion relation for Alfvén waves in a two-fluid plasma and found that high-frequency waves (with frequencies higher than the ion-neutral collisional frequency) have vastly different damping rates than the single-fluid model's approach. These studies showed that the efficiency of damping increases for smaller wavelengths. The nonlinear propagation of waves in a three-dimensional stratified solar flux tube in the presence of ambipolar diffusion was considered by Shelyag et al. (2016) and showed that up to 80% of the Poynting flux associated with these waves can be dissipated and converted into heat, providing an order-of-magnitude larger energy supply to the chromosphere compared to the dissipation of stationary currents modeled by Khomenko & Collados (2012). Ballai et al. (2019) investigated the formation of dispersive shock waves in partially ionized plasmas, in the presence of ambipolar diffusion. These authors showed that the width of the shocks increases with the number of neutrals in the system.

The phase mixing of Alfvén waves in a partially ionized plasma, to the best of our knowledge, has so far been neglected. Hence, the present study aims to address this shortcoming by investigating the efficiency of phase-mixed Alfvén waves in a partially ionized chromospheric plasma and how the damping length of waves depends on the ionization degree of the plasma. The paper is organized as follows: the physical and mathematical background behind the mechanism of phase mixing is presented in Section 2, where we derive the governing equations for phase-mixed Alfvén waves in partially ionized plasmas. These equations are solved analytically for a simplified case and numerically for a general setup and a sinusoidal driver in Sections 3 and 4. Finally, our results are summarized and concluded in Section 5.

Our analytical analysis is analogous to the model of Heyvaerts & Priest (1983), but for a partially ionized—instead of a fully ionized—plasma, and the numerical investigation will be similar to the methodology of Hood et al. (2002).

Since the temperature of the solar photosphere and chromosphere is not high enough to ensure a full ionization of the plasma (here assumed to be made up of hydrogen), the plasma will consist of a mixture of protons, electrons, and neutral atoms that interact through collisions. In order to describe the ionization degree of the plasma, we introduce the relative densities of ions and neutrals (denoted ρ_i and ρ_n , respectively) as

$$\begin{eqnarray}&&{\xi }_{i}=\displaystyle \frac{{\rho }_{i}}{\rho }\approx \displaystyle \frac{{n}_{i}}{{n}_{i}+{n}_{n}},\ \ \ {\xi }_{n}=\displaystyle \frac{{\rho }_{n}}{\rho }\approx \displaystyle \frac{{n}_{n}}{{n}_{i}+{n}_{n}},\end{eqnarray} \tag{ 1 }$$

so that ξ_i + ξ_n = 1. With these quantities, we can define the ionization degree of the plasma as

$$\begin{eqnarray}&&\mu =\displaystyle \frac{1}{1+{\xi }_{i}},\end{eqnarray} \tag{ 2 }$$

which means that ξ_i = (1/μ) − 1 and ξ_n = 2 − 1/μ. The quantity μ will play an important role in our investigation when we discuss the efficiency of the phase mixing in terms of the ionization degree of the plasma. The parameter μ varies between the values of 1/2 (fully ionized plasma) to 1 (fully neutral fluid). In addition, we will use the ratio σ = ξ_i /ξ_n ≈ n_i /n_n as a measure of the ion number density relative to the neutral number density, so that

$$\begin{eqnarray*}&&\sigma =\displaystyle \frac{1-\mu }{2\mu -1}.\end{eqnarray*}$$

The degree of ionization of the solar atmospheric plasma can be derived from standard solar atmospheric models. Here we employ the AL c7 model (Avrett & Loeser 2008) that provides values of neutral hydrogen and electron number densities with height and temperature. The AL c7 model predicts that in the solar photosphere, there are 10⁴ more neutrals than ions, while at the top of the chromosphere, ions are more abundant. The ionization degree as a function of height for the AL c7 model is shown in Figure 1.

Zoom In Zoom Out Reset image size

In the AL c7 model, the ionization degree is a multivalued function at heights of about 2.1 Mm above the solar surface, as seen in Figure 1, i.e., for two different heights, we obtain two identical ionization degrees of the plasma. The discrepancies between the values at the top of the chromosphere are due to various non–local thermodynamic equilibrium effects that were considered by the study by Avrett & Loeser (2008). With regard to the present phase-mixing study, the different dissipative coefficients will result in different damping lengths for the same ionization degree. However, in our analysis, we are going to choose particular values of the ionization degree that avoid these peculiarities.

The qualitative and quantitative description of the dynamics in a partially ionized plasma depends on the frequency regime of interest. Accordingly, for temporal changes of the same order as the collisional time between particles (or frequencies of the same order as the collisional frequency), an accurate description of the dynamics requires a multifluid model. In the present analysis, we assume that the temporal changes are much larger than the collisional time between particles; hence we use a single-fluid description, and the partial ionization effects are cast in specific transport mechanisms.

We consider a plasma permeated by a homogeneous magnetic field oriented in the z-direction, and the plasma density varies in the x-direction, i.e., ρ₀ = ρ₀(x). We consider a stationary and static equilibrium and the perturbations of the velocity and magnetic field are denoted by $v(x,z,t)\hat{y}$ and $b(x,z,t)\hat{y}$, respectively. Neglecting the effects of gravity and considering the cold and incompressible plasma approximation, the linearized momentum equation is given by

$$\begin{eqnarray}&&{\rho }_{0}\displaystyle \frac{\partial {\boldsymbol{v}}}{\partial t}=\displaystyle \frac{1}{{\mu }_{0}}({\rm{\nabla }}\times {\boldsymbol{b}})\times {{\boldsymbol{B}}}_{0}+{\rho }_{0}{\nu }_{v}{{\rm{\nabla }}}^{2}{\boldsymbol{v}},\end{eqnarray} \tag{ 3 }$$

where B ₀ is the equilibrium magnetic field oriented in the z-direction, μ₀ is the magnetic permeability of free space, and ν_v is the coefficient of viscosity. The interaction between the magnetic field and fluid is described by the induction equation that in the linear approximation takes the form

$$\begin{eqnarray}\begin{array}{rcl}\displaystyle \frac{\partial {\boldsymbol{b}}}{\partial t} & = & {\rm{\nabla }}\times ({\boldsymbol{v}}\times {{\boldsymbol{B}}}_{0})+\eta {{\rm{\nabla }}}^{2}{\boldsymbol{b}}\\ & & +{\rm{\nabla }}\times \left\{\displaystyle \frac{{\eta }_{C}-\eta }{{\left|{\boldsymbol{B}}\right|}^{2}}\left[\left({\rm{\nabla }}\times {\boldsymbol{b}}\right)\times {{\boldsymbol{B}}}_{0}\right]\times {{\boldsymbol{B}}}_{0}\right\},\end{array}\end{eqnarray} \tag{ 4 }$$

where η is the magnetic diffusivity (also known as the Spitzer resistivity) and η_C is the Cowling resistivity. The quantity η_C − η often is replaced by η_A , the coefficient of ambipolar diffusion. Equations (3) and (4) contain a degree of simplification that will allow us to make analytical progress and the omitted ingredients may play an important role. Gravitational effects are neglected, despite the wavelengths we are going to discuss being large enough that they might cover several gravitational scale heights. In addition, we will consider that dissipative coefficients are all z-independent.

The ambipolar diffusion term in the induction equation is a consequence of considering the effects of neutrals in a single-fluid partially ionized plasma and it is due to neutrals not experiencing the magnetic field and, hence, the Lorentz force. As a result, the neutrals become decoupled from the magnetic field and the magnetic field diffuses through the neutral gas without any perturbation caused by the neutrals. For a hydrogen plasma, the coefficient of ambipolar diffusion is given by

$$\begin{eqnarray}&&{\eta }_{A}=\displaystyle \frac{{\xi }_{n}^{2}{v}_{A}^{2}}{{\nu }_{{in}}+{\nu }_{{en}}},\end{eqnarray} \tag{ 5 }$$

where v_A is the Alfvén speed. The magnetic diffusivity coefficient is dependent on the collisional frequencies of electrons with ions and neutrals and in partially ionized plasma, whose value is given by

$$\begin{eqnarray}&&\eta =\displaystyle \frac{{m}_{e}({\nu }_{{ei}}+{\nu }_{{en}})}{{e}^{2}{n}_{e}{\mu }_{0}},\end{eqnarray} \tag{ 6 }$$

where m_e and e are the electron mass and charge and n_e is the electron number density. In the above relations, ν_ab denotes the collisional frequency between species a and b and their expression is given by Braginskii (1965):

$$\begin{eqnarray*}&&{\nu }_{{in}}=4{n}_{n}{\sigma }_{{in}}{\left(\displaystyle \frac{{k}_{B}T}{\pi {m}_{i}}\right)}^{\tfrac{1}{2}},\quad {\nu }_{{en}}={n}_{n}{\sigma }_{{en}}{\left(\displaystyle \frac{8{k}_{B}T}{\pi {m}_{e}}\right)}^{\tfrac{1}{2}},\end{eqnarray*}$$

$$\begin{eqnarray}&&{\nu }_{{ei}}=\displaystyle \frac{{n}_{e}{e}^{4}{\rm{\Lambda }}}{3{m}_{e}^{2}{\epsilon }_{0}^{2}}{\left(\displaystyle \frac{{m}_{e}}{2\pi {k}_{B}T}\right)}^{3/2}={\nu }_{{ii}}{\left(\displaystyle \frac{{m}_{i}}{{m}_{e}}\right)}^{1/2},\end{eqnarray} \tag{ 7 }$$

where m_i is the ion (proton) mass, ₀ is the electric permittivity, k_B is the Boltzmann constant, T is the temperature, and

$$\begin{eqnarray}&&{\rm{\Lambda }}=\mathrm{ln}\left[\displaystyle \frac{8.48\pi }{{n}_{i}^{1/2}}{\left(\displaystyle \frac{{\epsilon }_{0}{k}_{B}T}{{e}^{2}}\right)}^{3/2}\right]\end{eqnarray} \tag{ 8 }$$

is the Coulomb logarithm describing the cumulative effect of many small-angle deflective collisions. Here, n_i is the ion number density.

The collisional cross sections that appear in the above relations are height-dependent due to the fact that these values depend on the energy of colliding particles, i.e., their temperature (see, e.g., Vranjes & Krstic 2013). However, for the sake of the present analysis, we are going to consider them as constant and here these take the values σ_in = 3.5 × 10⁻¹⁹ m², σ_en = 10⁻¹⁹ m².

Since we assume a quasi-neutral hydrogen plasma, n_e = n_i , all number densities are given in m⁻³ and temperatures in K. As we consider elastic collisions between particles, the momentum conservation requires that ν_ab m_a n_a = ν_ba m_b n_b .

Assuming that flow speeds are comparable with the particles' thermal speed, viscosity can be understood as the flux of momentum. In a plasma, where the direction of the magnetic field defines a preferential direction, the viscosity tensor is more complicated, as the transport of momentum occurs at different rates in different directions. In a magnetically dominated plasma, Alfvén waves are affected by shear viscosity that originates from random walk transport of momentum with a step size equal to the Larmor radius.

In a partially ionized plasma, the viscosity of the fluid contains contributions from each species. However, in unithermal plasmas, the electron shear viscosity can be negligibly small (proportional to m_e /m_i ). In addition, under chromospheric conditions, the neutral shear viscosity is at least 5 orders of magnitude larger than the corresponding value for ions; therefore the ion shear viscosity will also be neglected. As a result, the shear viscosity coefficient used in the present study is (Vranjes 2014)

$$\begin{eqnarray}&&{\nu }_{v}=\displaystyle \frac{{n}_{n}{k}_{B}T{\tau }_{n}}{2}\displaystyle \frac{{\rm{\Delta }}\gamma +{\left({\omega }_{{ci}}{\tau }_{i}\right)}^{2}}{{{\rm{\Delta }}}^{2}+{\left({\omega }_{{ci}}{\tau }_{i}\right)}^{2}},\end{eqnarray} \tag{ 9 }$$

where ${\omega }_{{ci}}={{eB}}_{0}/{m}_{i}={v}_{A}{\left({e}^{2}{\mu }_{0}{n}_{i}/{m}_{i}\right)}^{1/2}$ is the ion cyclotron frequency, and

$$\begin{eqnarray*}\begin{array}{rcl}{\rm{\Delta }} & = & 1-\displaystyle \frac{1}{(3{\nu }_{{ii}}/{\nu }_{{in}}+4)(3{\nu }_{\mathrm{nn}}/\sigma {\nu }_{{in}}+4)},\\ \gamma & = & 1+\displaystyle \frac{\sigma }{3{\nu }_{{ii}}/{\nu }_{{in}}+4},\end{array}\end{eqnarray*}$$

with

$$\begin{eqnarray*}&&{\nu }_{\mathrm{nn}}=4{n}_{n}{\sigma }_{\mathrm{nn}}{\left(\displaystyle \frac{{k}_{B}T}{\pi {m}_{n}}\right)}^{1/2}\end{eqnarray*}$$

being the neutral–neutral collisional frequency and σ_nn being the collisional cross section of this collision—we take this value to be σ_nn = 2.6 × 10⁻¹⁹ m².

The variation of the Spitzer resistivity, ambipolar resistivity, and viscosity with height is shown in Figure 1. Specific plasma parameters were taken from the AL c7 atmospheric model (Avrett & Loeser 2008), and the magnetic field varies with height as ${B}_{0}=1000\exp (-z/660)$ G and z is measured in kilometers. Therefore, the magnetic field used to calculate the dissipative coefficients decays by a factor of e over 660 km. The governing equation derived by Heyvaerts & Priest (1983) was obtained using simplifications, such as neglecting terms containing the products of dissipative coefficients (in the fully ionized solar corona, this assumption might be valid), so that all terms containing the products of dissipative coefficients and derivatives of equilibrium quantities are neglected and the dissipative coefficients are constant quantities.

In the partially ionized solar chromosphere, the dissipative coefficients are much larger than in the solar corona, therefore the first simplifications made by Heyvaerts & Priest (1983) regarding the omission of some terms based on the smallness of dissipative coefficients in the governing equations cannot be applied. Nevertheless, in order to highlight the impact of transport coefficients in partially ionized plasmas and to define a proof-of-concept benchmark, we are going to apply the above simplification. The obtained results could only constitute a qualitative indication of the efficiency of phase mixing in a partially ionized plasma. The proper treatment of the problem will be carried out numerically later.

Let us define the small parameter = l_inh/l_ss ≪ 1, where l_inh is the characteristic spatial scale of inhomogeneity and l_ss is a spatial scale of the problem (say, the wavelength of waves). With the inclusion of constant (height-independent) resistivity, viscosity, and ambipolar diffusion, the linearized incompressible MHD equations reduce to

$$\begin{eqnarray}&&\displaystyle \frac{\partial v}{\partial t}=\displaystyle \frac{{B}_{0}}{{\mu }_{0}{\rho }_{0}}\displaystyle \frac{\partial b}{\partial z}+{\nu }_{v}\left(\displaystyle \frac{{\partial }^{2}v}{\partial {x}^{2}}+\displaystyle \frac{{\partial }^{2}v}{\partial {z}^{2}}\right),\end{eqnarray} \tag{ 10 }$$

$$\begin{eqnarray}&&\displaystyle \frac{\partial b}{\partial t}={B}_{0}\displaystyle \frac{\partial v}{\partial z}+\eta \left(\displaystyle \frac{{\partial }^{2}b}{\partial {x}^{2}}+\displaystyle \frac{{\partial }^{2}b}{\partial {z}^{2}}\right)+{\eta }_{A}\displaystyle \frac{{\partial }^{2}b}{\partial {z}^{2}}.\end{eqnarray} \tag{ 11 }$$

We can combine these two equations and eliminate the velocity perturbation, v, to obtain a single governing equation describing the evolution of a magnetic field perturbation in the form

$$\begin{eqnarray}\begin{array}{rcl}\displaystyle \frac{{\partial }^{2}b}{\partial {t}^{2}} & = & {v}_{A}^{2}(x)\displaystyle \frac{{\partial }^{2}b}{\partial {z}^{2}}\\ & & +\left[(\eta +{\nu }_{v})\displaystyle \frac{{\partial }^{2}}{\partial {x}^{2}}+({\eta }_{C}+{\nu }_{v})\displaystyle \frac{{\partial }^{2}}{\partial {z}^{2}}\right]\displaystyle \frac{\partial b}{\partial t}+{ \mathcal O }({\epsilon }^{2}),\end{array}\end{eqnarray} \tag{ 12 }$$

where the Alfvén speed is defined as ${v}_{A}{(x)={B}_{0}/({\mu }_{0}{\rho }_{0}(x))}^{1/2}$. Similar to the study by Heyvaerts & Priest (1983), we consider that $({\nu }_{v}{\partial }^{2}/\partial {z}^{2})/({\nu }_{v}{\partial }^{2}/\partial {x}^{2})={ \mathcal O }({\epsilon }^{2})$; therefore we neglect the viscous term connected to the z-derivative. Keeping only the terms of the same order, our governing equation reduces to

$$\begin{eqnarray}&&\displaystyle \frac{{\partial }^{2}b}{\partial {t}^{2}}={v}_{A}^{2}(x)\displaystyle \frac{{\partial }^{2}b}{\partial {z}^{2}}+\left[(\eta +{\nu }_{v})\displaystyle \frac{{\partial }^{2}}{\partial {x}^{2}}+{\eta }_{C}\displaystyle \frac{{\partial }^{2}}{\partial {z}^{2}}\right]\displaystyle \frac{\partial b}{\partial t}.\end{eqnarray} \tag{ 13 }$$

This equation has been obtained using the approximation of Heyvaerts & Priest (1983) that assumes that due to the very high Reynolds numbers as in the solar corona (very small dissipative coefficients), all terms containing the products of dissipative coefficients are negligibly small. Due to the dependence of the Alfvén speed on the x-coordinate, each field line will oscillate with its own frequency, since the Alfvén speed varies from field line to field line; hence we satisfy the conditions for phase mixing to occur.

Following Heyvaerts & Priest (1983), we consider that the perturbation of the magnetic field can be written as $b(x,z,t)=\hat{b}(x,z){e}^{i(\omega t-{k}_{\parallel }(x)z)}$, where $\hat{b}(x,z)$ is the amplitude of Alfvén waves and k_∥(x) = 2π/λ_∥(x) = ω/v_A (x) is the parallel wavenumber. After some straightforward calculations, it follows that the amplitude of the magnetic field perturbation can be written as

$$\begin{eqnarray}&&\hat{b}(x,z)=\hat{b}(x,0)\exp \left\{-{\left(\displaystyle \frac{z}{{{\rm{\Lambda }}}_{1}}\right)}^{3}-\left(\displaystyle \frac{z}{{{\rm{\Lambda }}}_{2}}\right)\right\},\end{eqnarray} \tag{ 14 }$$

where $\hat{b}(x,0)$ is the amplitude of the perturbation at z = 0 and the quantities Λ₁ and Λ₂ are related to the waves' damping length. In the above expression, the first term in the exponent recovers the results obtained by Heyvaerts & Priest (1983), while the second term is attributed solely to the fact that the plasma is partially ionized. The expressions of these two quantities are given by

$$\begin{eqnarray}&&{{\rm{\Lambda }}}_{1}={k}_{\parallel }^{-1}{\left(\displaystyle \frac{6\omega }{(\eta +{\nu }_{v}){\left(d\mathrm{log}{k}_{\parallel }/{dx}\right)}^{2}}\right)}^{\displaystyle \frac{1}{3}},\ \ {{\rm{\Lambda }}}_{2}=\displaystyle \frac{2\omega }{{k}_{\parallel }^{3}{\eta }_{C}}.\end{eqnarray} \tag{ 15 }$$

Hence, Alfvén waves will damp due to phase mixing, such that the damping length is a superposition of the solution that has the same definition as the expression for the fully ionized case given by Heyvaerts & Priest (1983; Λ₁) and a term that is due to the ambipolar diffusion (Λ₂). One very important aspect of these quantities is that only Λ₁ depends on the gradient of the Alfvén speed, while the second one depends on the ionization degree. This qualitatively different behavior is due to the spatial derivatives associated with the dissipative coefficients. While the viscosity and Spitzer resistivity are associated with a spatial derivative that is in the direction of propagation, the Cowling resistivity is associated with derivatives perpendicular to the propagation of waves, i.e., perpendicular to the density inhomogeneity. This is a consequence of some of the earlier simplifications. We find that in the numerical case, the Cowling resistivity is very much connected to phase mixing.

In order to evidence the changes in the damping length of phase-mixed Alfvén waves in a partially ionized plasma, we perform a simple numerical investigation. For that purpose, we prescribe that the inhomogeneous Alfvén speed is given by one of the following four profiles:

$$\begin{eqnarray}\begin{array}{rcl}{P}_{1}:{v}_{A}(x) & = & {v}_{A1},\\ {P}_{2}:{v}_{A}(x) & = & {v}_{A1}\left(1+\displaystyle \frac{1}{2}\cos \left[\displaystyle \frac{2\pi }{{l}_{\mathrm{inh}}}(x-0.5{l}_{\mathrm{inh}})\right]\right),\\ {P}_{3}:{v}_{A}(x) & = & {v}_{A1}\left(1+\displaystyle \frac{1}{2}\tanh \left[\displaystyle \frac{x-0.25{l}_{\mathrm{inh}}}{0.1{l}_{\mathrm{inh}}}\right]\right),\\ {P}_{4}:{v}_{A}(x) & = & {v}_{A1}\left(1+\displaystyle \frac{1}{2}\tanh \left[\displaystyle \frac{x-0.25{l}_{\mathrm{inh}}}{0.03{l}_{\mathrm{inh}}}\right]\right),\end{array}\end{eqnarray} \tag{ 16 }$$

where l_inh is the length scale of the inhomogeneity. For illustration, we chose v_A1 = 20 km s⁻¹, l_inh = 300 km, and the factor of 1/2 is chosen in such a way that the Alfvén speed varies by a factor of 3 across the inhomogeneity, ranging from 10−30 km s⁻¹. The last two tanh profiles are reflected about the midpoint of the inhomogeneity to make them symmetric. The choice of these profiles was made to model the effectiveness of an increased local gradient in the Alfvén speed. These four profiles are converted to dimensionless form before use in the numerical study in Section 4, where the reasoning is further discussed relevant to the numerical modeling carried out. Figure 2 shows these profiles in dimensionless form.

Zoom In Zoom Out Reset image size

Since Equation (14) is not a simple exponential, we cannot define a standard e-folding distance. However, we are still going to define the damping length as the length over which the initial amplitude of the wave decays by e-times, and this distance will be determined by solving numerically the equation ${\left(z/{{\rm{\Lambda }}}_{1}\right)}^{3}\,+\,z/{{\rm{\Lambda }}}_{2}=1$. The inhomogeneity length scales and characteristic Alfvén speeds necessary to perform our investigations were taken from previous studies involving propagating Alfvén waves in an inhomogeneous partially ionized plasma in spicules and fibrils that are evidenced in abundance by observations (see, e.g., He et al. 2009; Okamoto & De Pontieu 2011; Gafeira et al. 2017; Jafarzadeh et al. 2017; Bate et al. 2022, etc.). While direct observations of transverse density inhomogeneities are almost impossible to evidence, magnetoconvection codes have been shown to produce such transversal density enhancements in fibrils and spicules due to magnetic forces (see, e.g., Martínez-Sykora et al. 2011, 2017; Leenaarts et al. 2012, 2015, etc.).

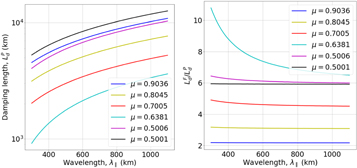
The dependence of the damping length of phase-mixed Alfvén waves propagating in a partially ionized plasma on the wavelength of waves is shown in the left panel of Figure 3 for different ionization degrees (shown by different colors). The values of the ionization degree were chosen so that these cover the whole spectrum between a strongly ionized and weakly ionized plasma. Our results show that considering either very weakly ionized or very strongly ionized plasma results in weak damping and, therefore, large damping lengths, too large to contribute to heating the solar chromosphere. This behavior can be attributed to the variation of the Cowling resistivity with the ionization degree. In both of these cases, the perpendicular currents are very small, thanks to the very small number of neutrals in the case of strongly ionized plasma, and a very high collisional frequency in the case of almost neutral plasma.

Zoom In Zoom Out Reset image size

Inspired by these results, we have investigated the number of wavelengths an Alfvén wave must propagate in order for its amplitude to decay by e-times. The results show, again, that the shortest wavelengths are the most affected by phase mixing (due to the relative differences in speed of waves in adjacent field lines) and the damping mechanisms considered in our study. For the larger wavelengths, resistivity and viscosity damp the wave most effectively. The largest number of wavelengths is required in the case of nearly fully ionized or neutral plasma.

The efficiency of phase mixing in the propagation of Alfvén waves in partially ionized plasma becomes visible when we investigate the role of neutrals in this process. For this purpose, we consider that by removing entirely the neutral species from the plasma, we have a fully ionized plasma for which the dissipative coefficients will be different and are given by Heyvaerts & Priest (1983), although the remaining plasma parameters (primarily temperature) remain relevant to the photosphere–chromosphere region. The right panel of Figure 3 shows the ratio of the damping lengths obtained in fully ionized and partially ionized plasmas in terms of the wavelength of waves. The different ionization degrees are shown by different colors. Our results show that the ratio in damping lengths is marginally larger for shorter wavelengths, meaning the neutrals play a much more important role in wave damping, approximately an order-of-magnitude reduction in damping when considering the effects of neutrals for ionization degree μ = 0.6381. This behavior is due to the Cowling resistivity found in Equations (14) and (15). For short wavelengths (large k_∥), Λ₂ is small and hence is the dominant damping mechanism. For large wavelengths (small k_∥), Λ₂ plays a smaller role and hence for larger wavelengths we find our solutions tend to a saturated ratio. This is a result of a superposition of solutions coming from the enhanced Spitzer resistivity and shear viscosity coefficients in a partially ionized plasma versus the fully ionized chromospheric plasma, i.e., the damping due to ambipolar diffusion plays a negligible role for large-wavelength Alfvén waves, at least in the weak solution.

The damping length ratio corresponding to a nearly fully ionized case (μ = 0.5001, shown by the brown line) is independent of the wavelength of waves. In this limit, the contribution due to damping length is due mainly to Λ₁, and the fact that this ratio is not 1 can be attributed to the 0.1% of neutrals still in the system. Furthermore, a similar trend for the weakly ionized cases can be recovered (blue line), which is due to the low values of the Cowling resistivity. These conclusions highlight the need for a balanced population of neutrals and ions in the process of phase mixing.

Before moving on to the full numerical study, we would like to evidence the effects of varying the Alfvén speed profile on the damping lengths of phase-mixed Alfvén waves in the "weak" solution case. We choose to showcase a single wavelength chosen to be λ_∥ = 400 km and we plot the damping length against all heights associated with ionization degrees in our range of study (μ = 0.5001–0.9036). The effect of the multivalued ionization degree is displayed here in Figure 4. There is a clear trend in Figure 4; the damping lengths are drastically reduced when the presence of an inhomogeneous Alfvén speed is introduced, highlighting the efficiency of phase mixing as a mechanism to damp Alfvén waves effectively in the solar chromosphere. The shortest damping length is attained for the steepest profile (P₄).

Zoom In Zoom Out Reset image size

The solution for propagating phase-mixed Alfvén waves in an unbounded plasma given by Equation (14) can be considered as a "weak" solution, as it was obtained by applying the same simplifications as in the study by Heyvaerts & Priest (1983) and they are connected to the small values of dissipative coefficients (or very high Reynolds numbers). While these assumptions are obvious in fully ionized coronal plasmas, in a partially ionized chromospheric plasma, the transport coefficients are large and, therefore, terms containing the products of dissipative coefficients have the potential to be not only important, but also dominant.

Under these circumstances, the governing equation describing the temporal and spatial evolution of the magnetic field perturbation in a single-fluid partially ionized plasma reduces to

$$\begin{eqnarray}\begin{array}{rcl}\displaystyle \frac{{\partial }^{2}b}{\partial {t}^{2}} & = & {v}_{A}^{2}(x)\displaystyle \frac{{\partial }^{2}b}{\partial {z}^{2}}+\left[(\eta +{\nu }_{v})\displaystyle \frac{{\partial }^{2}}{\partial {x}^{2}}+{\eta }_{C}\displaystyle \frac{{\partial }^{2}}{\partial {z}^{2}}\right]\displaystyle \frac{\partial b}{\partial t}\\ & & -{\nu }_{v}\left[\eta \displaystyle \frac{{\partial }^{2}}{\partial {x}^{2}}+{\eta }_{C}\displaystyle \frac{{\partial }^{2}}{\partial {z}^{2}}\right]{{\rm{\nabla }}}^{2}b+{ \mathcal O }({\epsilon }^{2}).\end{array}\end{eqnarray} \tag{ 17 }$$

In the above equation, simplifications were made regarding the order-of-magnitude difference between characteristic scales in the transversal and longitudinal direction; the second and third terms contain a derivative in the z-direction because the Cowling resistivity is much larger in the chromosphere than the Spitzer resistivity and/or viscosity. Given the complexity of the above partial differential equation, the solutions are determined using a numerical method analogous to that used by Hood et al. (2002). We employ a fourth-order Runge–Kutta-based time step and a second-order centered difference approximation for the spatial derivatives. In order to proceed numerically, we must first rewrite Equation (17) as a system of first-order dimensionless equations:

$$\begin{eqnarray}\begin{array}{rcl}\displaystyle \frac{\partial U}{\partial t} & = & {v}_{A}^{2}(x)\displaystyle \frac{{\partial }^{2}b}{\partial {z}^{2}}+\left[(\eta +{\nu }_{v})\displaystyle \frac{{\partial }^{2}}{\partial {x}^{2}}+{\eta }_{C}\displaystyle \frac{{\partial }^{2}}{\partial {z}^{2}}\right]U\\ & & -{\nu }_{v}\left[\eta \displaystyle \frac{{\partial }^{2}}{\partial {x}^{2}}+{\eta }_{C}\displaystyle \frac{{\partial }^{2}}{\partial {z}^{2}}\right]{{\rm{\nabla }}}^{2}b,\end{array}\end{eqnarray} \tag{ 18 }$$

$$\begin{eqnarray}&&\displaystyle \frac{\partial b}{\partial t}=U.\end{eqnarray} \tag{ 19 }$$

Following Hood et al. (2002), we write all quantities in dimensionless form. Using finite difference approximations for the spatial derivatives to tackle the system of first-order Equations (18) and (19) inevitably leads to solving a large system of linear algebraic equations, which can be written in the form

$$\begin{eqnarray}&&\begin{array}{l}\displaystyle \frac{\partial }{\partial t}\left[\begin{array}{c}b\\ U\end{array}\right]\,=\,A\left[\begin{array}{c}b\\ U\end{array}\right],\end{array}\end{eqnarray} \tag{ 20 }$$

where A denotes a tridiagonal matrix with fringes, the coefficients of which correspond to the finite difference approximations. We then use a Runge–Kutta fourth-order time step to progress forward in time. The evolution of waves is followed until they reach a steady state or the perturbation reaches the end of the domain. The peaks of the damped wave are tracked and an envelope is fitted. We then calculate the percentage reduction in amplitude after a given distance that the wave has propagated.

4.1. Sinusoidal Wave Driver

4.2. Results

Our aim is to study the damping of phase-mixed Alfvén waves generated by a sinusoidal wave driver for varying ionization degrees that is given by Equation (2). As the ionization degree varies between the limits of fully ionized (μ = 0.5) and fully neutral (μ = 1) plasmas, an increase of the ionization degree is equivalent with the case of a plasma whose temperature is decreasing (assuming that the ionization degree of the plasma is temperature-dependent only, i.e., the effect of radiation is removed).

Figure 5 shows the normalized value of the envelope in the case of an Alfvén wave generated by the four different Alfvén wave profiles considered in the present study. The waves have identical periods and the solutions are presented for the same ionization degree (μ = 0.7852). The variation in the envelope is caused by different levels of phase mixing due to the variation of the Alfvén speed profiles. The envelope is plotted by fitting a curve to the peaks of the generated Alfvén waves. The damping length is measured from the first peak, rather than from z = 0, to avoid any extrapolation errors. The horizontal red line marks the value of the normalized amplitude that corresponds to an e-fold decrease of the original value and the vertical lines mark the vertical points where the envelopes of the waves intersect with the horizontal line. The damping length is then calculated to be the distance between the first peak and the vertical line. The results show clearly that any inhomogeneous profile results in a shorter damping length, i.e., phase mixing indeed reduces the damping length of waves. Comparing these results with the profiles of the Alfvén waves shown in Figure 2, it is evident that the wave that corresponds to the steepest gradient undergoes the heaviest damping. The steep gradients enhance the contribution of the viscosity and resistivity in the Navier–Stokes and induction equation.

Zoom In Zoom Out Reset image size

The percentage reduction in the amplitude of Alfvén waves over the particular distance of 1 Mm from their first peak is displayed in Figure 6. This value was chosen somehow arbitrarily to replace the damping length, due to constraints on the size of the domain used in our numerical solver. The percentage reduction of the amplitude is a quantity that is defined as

$$\begin{eqnarray}&&P( \% )=\displaystyle \frac{A[0]-A[1]}{A[0]}\times 100,\end{eqnarray} \tag{ 21 }$$

where A[0] is the initial amplitude of the Alfvén wave and A[1] is the amplitude after the wave propagated a distance of 1 Mm. The results shown in Figure 6 show the same trend as obtained in the case of weak damping, i.e., a plasma with an ionization degree in the region of μ = 0.6381 produces the most effective damping, where for all the considered Alfvén speed profiles nearly all of the wave energy has been dissipated. For larger ionization degrees (higher relative neutral densities), we recover a similar result as shown in Figure 5, i.e., the percentage change in the amplitude of the wave increases with the steepness of the Alfvén wave profile.

Zoom In Zoom Out Reset image size

The same percentage damping of Alfvén waves after propagating 1 Mm in terms of the wavelength of waves (here in the range of 300–1100 km) is shown in Figure 7 for different ionization degrees of the plasma. First of all, Alfvén waves undergo the smallest damping (irrespective of the wavelength of waves) when the plasma is nearly neutral or nearly fully ionized. Waves propagating in a plasma with an ionization degree close to μ = 0.6381 will damp very effectively for all profiles of Alfvén speed, as at this value of ionization degree the dissipative coefficients responsible for removing energy from the wave are at their combined largest. Inhomogeneities in the plasma density are shown to enhance the dissipation of Alfvén waves in partially ionized plasmas to varying degrees. For each ionization degree considered here, the largest damping belongs to the Alfvén wave with the steepest inhomogeneous profile (shown in purple). For ionization degrees close to the fully neutral plasma, very little wave energy is dissipated due to resistivity and viscosity when considering the waves that are propagating in a homogeneous plasma, thanks to the weak transport mechanisms. As before, waves with the smallest wavelength damp the most effectively. Our results also show that the damping in the case of a homogeneous plasma (here shown in blue) and in the case of a sinusoidal inhomogeneity lead to almost identical results, meaning that here the damping is not due to the inhomogeneity; instead, it is due to the presence of neutrals.

Zoom In Zoom Out Reset image size

Let us return to the "weak" solutions obtained in Section 3 and verify our hypothesis that the "strong" solutions are more realistic in chromospheric partially ionized plasmas. In general, taking into account extra terms in the governing equation of phase-mixed Alfvén waves leads to a decrease in the damping length by a factor between 1.4 and 2.5. The weak solution captures the strong (numerical) solution most effectively for short wavelengths and steep Alfvén speed profiles, but it fails to do so for larger wavelengths. As the wavelength is increased, the weak solution tends toward capturing only 20% of the damping after 1 Mm propagated, hence using the weak solution results in an underestimate in the damping by a factor of 5. These results show that the additional terms containing the products of dissipative coefficients in Equation (17) become important in describing the damping of Alfvén waves in inhomogeneous plasmas. That is why the weak solution has provided us with an order-of-magnitude estimate for the damping of Alfvén waves in inhomogeneous plasmas, but for accurate description, the use of our full numerical solution is imperative.

Now that we have established that phase mixing in partially ionized solar plasmas has the potential to damp waves very effectively within the chromosphere, let us estimate the amount of heat produced by the damping of phase-mixed Alfvén waves that are subject to damping due to the ohmic dissipation of parallel and perpendicular currents, as well as the conversion of waves' kinetic energy into heat due to viscous damping. In this case, the heating rate, Q, is calculated as the sum of the heating due to resistive ohmic heating, Q_res, and viscous heating, Q_ν (Priest 2014; Melis et al. 2021):

$$\begin{eqnarray}\begin{array}{rcl}Q={Q}_{\mathrm{res}}+{Q}_{\nu } & = & \displaystyle \frac{1}{{\mu }_{0}}\left[\eta {\left(\displaystyle \frac{\partial b}{\partial x}\right)}^{2}+{\eta }_{C}{\left(\displaystyle \frac{\partial b}{\partial z}\right)}^{2}\right]\\ & & +\displaystyle \frac{\rho {\nu }_{v}}{2}{\left(\displaystyle \frac{\partial v}{\partial x}\right)}^{2},\end{array}\end{eqnarray} \tag{ 22 }$$

where we retained only the dominant term in the expression of viscous heating. The variation of the heating rate with respect to the ionization degree of the plasma for a given wavelength of Alfvén waves (400 km) propagating along the magnetic field line associated with the maximum gradient of the Alfvén speed profile P₄, shown in purple in Figures 2–7, is displayed in Figure 8. The amplitude of the velocity perturbation was taken to be 2.5 km s⁻¹ (Grant et al. 2018). For the sake of simplicity, we neglected the back reaction of the heating process on the values of dissipative coefficients and also the ionization degree of the plasma. Given the particular dependence of dissipative coefficients, the values we determine constitute an upper limit.

Zoom In Zoom Out Reset image size

In order to estimate the efficiency of the phase-mixed Alfvén waves to heat the plasma, we use, for comparison, the estimated average heating rate of the quiet chromosphere. The radiative losses estimated from commonly used semiempirical models of the quiet-Sun chromosphere are 4.3 kWm⁻², while in active regions, this value reaches 20 kWm⁻² (Withbroe & Noyes 1977; Vernazza et al. 1981; Yadav et al. 2022). The required heating rate to compensate for the radiative losses in the quiet chromosphere is shown by the horizontal black line in Figure 8. Our analysis reveals that the maximum heating rate produced by Alfvén waves varies considerably with the ionization degree of the plasma; in the full spectrum of the ionization, the heating rate varies by more than 1 order of magnitude and it attains its maximum value for an ionization degree of μ = 0.576. The results show that waves propagating in a partially ionized plasma with ionization degrees in the range μ = 0.518–0.657 provide sufficient heating rates to balance chromospheric radiative losses. In the AL c7 atmospheric model, these values correspond to a ratio of neutrals to ions, n_n /n_i = 0.0567–0.917, respectively.

These values of the ionization degree in the AL c7 model occur at the heights of 1916 and 2150 km above the solar atmosphere. It is instructive to compare our findings with the variation of the temperature with height in the Vernazza, Avrett, and Loeser atmospheric model (Vernazza et al. 1981, their Figure 1) together with the approximate depths where various continua and spectral lines are formed (see Figure 9). The heights in between which the heating rate obtained by us is larger than the required heating rate are shown by the vertical red lines, while the temperature at which the specific ionization degrees occur is shown by the red horizontal segments. In this way, we can define a region in the height–temperature diagram where phase-mixed Alfvén waves can provide the required heating. This domain corresponds to the region where the temperature increases dramatically and it is the location where the Lyman α and the 3 mm continuum intensity due mostly to free–free transitions of hydrogen are generated. These results show that the increases in the temperature at the transition-region level could be easily attributed to phase mixing of Alfvén waves.

Zoom In Zoom Out Reset image size

Comparing the heating rates obtained using the other three Alfvén speed profiles, we found that the ratio in heating rates, obtained by dividing the heating rate associated with P₄ by the heating rate from each of the other three profiles, varied considerably with ionization degree. The steepest profile produced as much as 2.5 times the amount of heating obtained using P₁ and approximately two times the heating obtained using the two shallower profiles, P₂ and P₃. The maximum of this ratio occurs for ionization degrees close to μ = 0.6, the value where we found optimal heating. This is due to the dissipative coefficients reaching their combined maximum close to this ionization degree. For ionization degrees tending toward fully neutral or fully ionized plasmas, this ratio approached unity. This shows the importance of both neutrals and transverse gradients in heating the partially ionized solar chromosphere.

Ever since the seminal paper by Heyvaerts & Priest (1983), the damping of phase-mixed Alfvén waves propagating along magnetic field lines has been suggested as a possible mechanism to explain the heating of the solar upper atmospheric layers. One key drawback of the phase-mixed Alfvén waves applied to the solar corona was that the dissipative coefficients are very small, leading to damping lengths that are often as large as the solar radius. This was attributed to the very small value of transport coefficients in the solar corona.

Our study aimed to address this major shortcoming by investigating the problem in the chromospheric plasma, where transport coefficients are far larger, but the plasma is partially ionized. Effective Alfvén wave damping due to phase mixing was achieved by imposing a density profile that varied in the transversal direction to the wave propagation. The main result of our research is that using realistic dissipative coefficients for the partially ionized chromospheric plasma results in an enormous reduction in the damping lengths compared to those for the fully ionized coronal case given by Heyvaerts & Priest (1983). Consequently, our estimations do not rely on turbulence to enhance transport mechanisms to bring the damping lengths to values that are important for heating. The small-scale mixing of magnetic field lines will create turbulence that can, even more, enhance transport coefficients (Magyar et al. 2017; Oppenheim et al. 2020).

Our results show that short-wavelength Alfvén waves damp much faster than longer-wavelength waves and the maximum attenuation of Alfvén waves occurs for ionization degrees close to 0.6. For steep gradients and for dissipative coefficients corresponding to our optimum ionization degree (or close to this), significant damping is seen for all wavelengths within 1 Mm of propagation. This length scale of damping could well explain a large amount of chromospheric heating, with the rest of the energy left stored in the Alfvén waves going on to the corona.

For waves with a particular wavelength of 400 km propagating in the presence of our steepest profile in the Alfvén speed, sufficient heating was generated due to the damping of phase-mixed Alfvén waves to balance radiative losses in the upper chromosphere/transition region when the ionization degree of the plasma is in the range μ = 0.518–0.657. This means that the phase mixing of Alfvén waves in partially ionized plasmas is indeed a viable mechanism for plasma heating.

Finally, we should mention that our approach used several simplifications that made the treatment of the problem of phase mixing clearer. Key ingredients were neglected (e.g., the height and time dependence of dissipative coefficients and gravitational stratification, etc.), but these might play an important role. Furthermore, as pointed out by Ofman et al. (1998) and Cargill et al. (2016), an assumed equilibrium density profile (at least in coronal plasmas) is not sustained due to the heating produced by the damping of phase-mixed Alfvén waves. Whether the same conclusion holds for chromospheric partially ionized plasma needs to be investigated by modifying our code to include a time-dependent Alfvén speed profile. It is our intention to expand the investigation of this problem and take into account the neglected processes in future analyses.

V.F., G.V., and I.B. are grateful to the STFC for grant ST/V000977/1. M.M. is grateful for the STFC studentship. V.F. and G.V. thank the Royal Society, International Exchanges Scheme, for collaborations with Pontificia Universidad Catolica de Chile, Chile (IES/R1/170301) and the Institute for Space-Earth Environmental Research (ISEE, International Joint Research Program, Nagoya University, Japan). V.F., G.V., I.B. thank the Royal Society, International Exchanges Scheme, for collaborations with the Aeronautics Institute of Technology, Brazil, (IES/R1/191114), Monash University, Australia (IES/R3/213012), Instituto de Astrofisica de Canarias, Spain (IES/R2/212183), Institute for Astronomy, Astrophysics, Space Applications and Remote Sensing, National Observatory of Athens, Greece (IES/R1/221095), Indian Institute of Astrophysics, India (IES/R1/211123), and the collaboration with Ukraine (IES/R1/211177) and for the support provided. This research has also received financial support from the European Union's Horizon 2020 research and innovation program under grant agreement No. 824135 (SOLARNET). This research was supported by the International Space Science Institute (ISSI) in Bern, through ISSI International Team project 457 (The Role of Partial Ionization in the Formation, Dynamics and Stability of Solar Prominences). The authors are grateful to the referee for the constructive comments and suggestions that helped to improve the paper. M.M. thanks S. McMurdo for the many enlightening conversations that have benefited this research.