ALMA Measurement of 10 kpc Scale Lensing-power Spectra toward the Lensed Quasar MG J0414+0534

The overall procedure of our model fitting (see Figure 3) using the ALMA data of lensed images of an extended source is described as follows: (1) We derive a best-fitted smooth model that consists of galaxy halos with smooth gravitational potentials. (2) Using the obtained smooth model, we calculate a fiducial model source intensity for a particular weighting. (3) For a given potential perturbation, we calculate the shifts of each de-lensed extended image and their effect on the positions and fluxes of the lensed images of the quasar core. (4) Based on (3), we try to minimize χ² (we call it "source plane +α χ²") defined as

$$\begin{eqnarray}&&{\chi }^{2}={\chi }_{\mathrm{ext}}^{2}+{\chi }_{\mathrm{core}}^{2}+{\chi }_{\mathrm{flux}}^{2}.\end{eqnarray} \tag{ 1 }$$

Zoom In Zoom Out Reset image size

RHS of Equation (1) consists of three terms: The first term ${\chi }_{\mathrm{ext}}^{2}$ constrains the differences between the intensities of de-lensed images of an extended source in the source plane. The second term ${\chi }_{\mathrm{core}}^{2}$ constrains the predicted positions of lensed images of a quasar core in the source plane. The third term ${\chi }_{\mathrm{flux}}^{2}$ constrains the predicted flux ratios of the lensed images of a quasar core. In what follows, we use our ALMA data, the HST/VLBA data, and the MIR data for calculating ${\chi }_{\mathrm{ext}}^{2}$, ${\chi }_{\mathrm{core}}^{2}$, and ${\chi }_{\mathrm{flux}}^{2}$, respectively.

Because of limited observable sky area of lensed images (i.e., thin arcs) compared to the sky area inside the arcs, we need to minimize a regularized ${\chi }_{\mathrm{reg}}^{2}$ instead of χ². More detailed definitions are described in the following subsections.

To apply the above procedure to MG J0414+0534, we first model the primary lensing galaxy G using an SIE and a possible companion galaxy X using a cored isothermal sphere (CIS) that can account for an absence of a bright spot in the vicinity of X. As conducted in MacLeod et al. (2013), possible effects from neighboring clusters and other large-scale structures are modeled as an ES centered at the SIE. First, we perturb our background Type A models (SIE-ES-CIS) in which object Y (see Section 6.5) is not explicitly modeled by discrete Fourier modes (see Section 4.6 for details) defined in the interior of a square that encompasses the lensed arcs. ⁸ Then, we perturb Type B models in which object Y is modeled by an SIE (SIE-ES-CIS-SIE) by the Fourier modes. From these results, we check whether these two procedures give a similar power spectra or not. In order to obtain the smooth models, we only use the HST or VLBA data for the positions of quadruply lensed images and galaxies (objects) and our Subaru and the Keck MIR data for the flux ratios of quadruply lensed images.

We use our combined ALMA Cycle 2 and Cycle 4 data as well as those used to obtain the smooth models to calculate ${\chi }_{\mathrm{ext}}^{2}$, ${\chi }_{\mathrm{core}}^{2}$, and ${\chi }_{\mathrm{flux}}^{2}$, respectively. We do not constrain the position of G and X in the final fitting procedure because we found that such constraints do not affect the fitting much. Our Fourier decomposition of gravitational perturbation can describe perturbed gravitational potentials of the primary lensing galaxy G, object X, possible substructures, and LOS structures.

Although we can obtain a model that minimizes χ² defined in Equation (1), the best-fitted model tends to yield a very large amplitude of perturbations at regions outside the lensed image because of limited sky area of lensed images. Since we aim to reconstruct a potential perturbation δ ψ defined in a region R that extends beyond the whole lensed image, we need to add a smoothing term R_s to χ², which functions as a penalty or regularization term (Treu & Koopmans 2004; Koopmans 2005). In order to ensure the smoothness of the potential perturbation δ ψ and the first and second derivatives, ⁹ we adopt a smoothing term defined as

$$\begin{eqnarray}&&{R}_{s}=\displaystyle \frac{\langle {\left(\delta \psi \right)}^{2}\rangle }{{\left(\delta {\psi }_{0}\right)}^{2}}+\displaystyle \frac{\langle {\left(\delta \alpha \right)}^{2}\rangle }{{\left(\delta {\alpha }_{0}\right)}^{2}}+\displaystyle \frac{\langle {\left(\delta \kappa \right)}^{2}\rangle }{{\left(\delta {\kappa }_{0}\right)}^{2}},\end{eqnarray} \tag{ 2 }$$

where δ ψ is the potential perturbation projected on the primary lens plane, δ α is the astrometric shift, δ κ is the convergence perturbation, and δ ψ₀, δ α₀, and δ κ₀ are the smoothing parameters. 〈〉 denotes ensemble averaging over region R. For a given set of smoothing parameters δ ψ₀, δ α₀, and δ κ₀, we minimize a regularized ${\chi }_{\mathrm{reg}}^{2}$ defined as

$$\begin{eqnarray}&&{\chi }_{\mathrm{reg}}^{2}={\chi }^{2}+{R}_{s},\end{eqnarray} \tag{ 3 }$$

where χ² is given by Equation (1). From the obtained set of solutions, we select one that satisfies a χ²/degrees of freedom (dof) ∼ 1. Thus, a set of the best-fitted model parameters and smoothing parameters, which determines the best-fitted potential perturbation δ ψ is determined. Note that we do not change the parameters of the smooth model in the fitting procedure.

In order to fit perturbed lensing models to the observed data of lensed images of an extended source, we adopt a fit in which "χ²" fit is performed in the source plane. The reason for this is as follows: first, the bias for estimating the potential perturbation in the "source plane χ²" fit is expected to be smaller than that in the traditional "lens plane χ²" fit. Owing to the strong lensing effect from a primary lens, the weak lensing effect from a potential perturbation is significantly enhanced in the lens plane. Therefore, astrometric shifts due to a potential perturbation become very anisotropic and inhomogeneous in the lens plane, which would result in a biased estimate. Second, we do not need to assume any functional forms for the source intensity. It can be obtained a posteriori rather than a priori. As we shall describe later, the source intensity of a lensed quasar can have a very complex structure, and the dynamical range can be very large. In such lens systems, the ensemble of source intensity does not necessarily obey homogeneous and isotropic Gaussian statistics, which is often assumed in the traditional "lens plane χ²" fit. Third, systematic errors due to coupling between noises at different regions or coupling between signals and noises can be significantly suppressed in the source plane. Since multiple images are generated from a single image, we expect a gain factor of $\sim \sqrt{N}$ for a de-lensed image generated from N multiple images. Moreover, de-lensed point-spread functions (PSFs) with a high magnification factor are significantly contracted (typically by a factor of ∼1/10) in one direction. Therefore, the areas of de-lensed side lobes in the source plane are reduced by ∼1/10, leading to a suppression of systematic errors.

We now derive astrometric shifts due to a potential perturbation. The lens equation for an unperturbed (background) primary lens system with a deflection angle α ₀ is

$$\begin{eqnarray}&&{\boldsymbol{y}}={\boldsymbol{x}}-{{\boldsymbol{\alpha }}}_{0}({\boldsymbol{x}}),\end{eqnarray} \tag{ 4 }$$

where x and y are the coordinates in the primary lens plane and the source plane, respectively. If the deflection angle is perturbed by δ α , then the lens equation is given by

$$\begin{eqnarray}&&\tilde{{\boldsymbol{y}}}=\tilde{{\boldsymbol{x}}}-{{\boldsymbol{\alpha }}}_{0}(\tilde{{\boldsymbol{x}}})-\delta {\boldsymbol{\alpha }}(\tilde{{\boldsymbol{x}}}),\end{eqnarray} \tag{ 5 }$$

where

$$\begin{eqnarray}&&\tilde{{\boldsymbol{x}}}={\boldsymbol{x}}+\delta {\boldsymbol{x}},\end{eqnarray} \tag{ 6 }$$

$$\begin{eqnarray}&&\tilde{{\boldsymbol{y}}}={\boldsymbol{y}}+\delta {\boldsymbol{y}},\end{eqnarray} \tag{ 7 }$$

and δ α = ∇δ ψ. ¹⁰ Equations (6) and (7) represent a relationship between the unperturbed and perturbed coordinates. Assuming that the second-order terms due to coupling between the perturbation of the deflection angle and the astrometric shifts in the primary lens plane (=d δ α ) are negligible, the lens equation for the perturbation of the coordinates is

$$\begin{eqnarray}&&\delta {\boldsymbol{y}}=\left(1-\displaystyle \frac{\partial {{\boldsymbol{\alpha }}}_{0}}{\partial {\boldsymbol{x}}}\right)\delta {\boldsymbol{x}}-\delta {\boldsymbol{\alpha }},\end{eqnarray} \tag{ 8 }$$

where 1 is a unit matrix. The choice of unperturbed coordinates x and y are arbitrary. Therefore, we need to fix a "gauge" to determine the unperturbed coordinates. In what follows, we consider gauges in which the positions of lensed images are given by a sum of singular/cored isothermal ellipsoids with an external shear, representing galaxies, and a nearby cluster, respectively. If we choose a set of unperturbed coordinates with δ y = 0, then the lens equation yields astrometric shifts in the primary lens plane,

$$\begin{eqnarray}&&\delta {\boldsymbol{x}}=\displaystyle \frac{\partial {\boldsymbol{x}}}{\partial {\boldsymbol{y}}}\delta {\boldsymbol{\alpha }}=M\delta {\boldsymbol{\alpha }},\end{eqnarray} \tag{ 9 }$$

where M is the magnification matrix. We call this the "lens plane gauge." If we choose unperturbed coordinates with δ x = 0, then the lens equation yields astrometric shifts in the source plane,

$$\begin{eqnarray}&&\delta {\boldsymbol{y}}=-\delta {\boldsymbol{\alpha }}.\end{eqnarray} \tag{ 10 }$$

We call this the "source plane gauge." Note that the above formalism applies only for the weak lensing regime: the perturbation does not change the number of lensed images, as d δ α is sufficiently small.

In terms of n-lensed images at x _i in the primary lens plane (i = 1, ⋯ ,n), the source intensity at y = y ( x _i ) can be estimated using a linear combination of intensities I_i observed in the primary lensed plane with weightings w_i ,

$$\begin{eqnarray}&&\hat{I}({\boldsymbol{y}})=\displaystyle \frac{{\sum }_{i=1}^{n}{w}_{i}{I}_{i}({{\boldsymbol{x}}}_{i}({\boldsymbol{y}}))}{{\sum }_{i=1}^{n}{w}_{i}}.\end{eqnarray} \tag{ 11 }$$

In what follows, we consider only two particular types of a priori weighting choices for de-lensing: the homogeneous weighting in which the weighting is unity (w_i = 1), and the magnification weighting in which the weighting is an absolute magnification (w_i = ∣μ_i ∣). However, analogous to the weighting scheme in interferometry, one may also introduce the "robust" weighting defined as

$$\begin{eqnarray}&&{w}_{i}=\displaystyle \frac{| {\mu }_{i}| +1}{2}+\displaystyle \frac{r(| {\mu }_{i}| -1)}{4},\end{eqnarray} \tag{ 12 }$$

where μ_tot = ∑_i ∣μ_i ∣ is the total magnification, and r is the "robust" parameter. r = − 2 and r = 2 correspond to the homogeneous weighting and the magnification weighting, respectively. The robust parameters −2 < r < 2 represent weightings between the homogeneous and magnification weightings.

Due to large magnification in strong lenses, the effective angular resolution of a source image can be significantly improved. Let us consider a system in which a point source is quadruply lensed and the PSF of lensed images is circularly symmetric and homogeneous in size and shape. As shown in Figure 4, in the source plane, the de-lensed PSFs are shrunk compared to the original PSFs. Therefore, the synthesized de-lensed PSF made from a linear combination of the de-lensed PSFs is significantly smaller than the original PSF in the lens plane, though the shape is complicated in the tail. If the fitted gravitational potential is smooth and not perfectly correct, de-lensed images would become blurred due to residual astrometric shifts of PSFs (top-right panel in Figure 4). In order to find a true gravitational potential, it is necessary to align the de-lensed PSFs on all relevant pixels in the source plane (bottom-right panel in Figure 4).

Zoom In Zoom Out Reset image size

For fold or cusp caustics, the choice of weighting scheme yields noticeable differences: the "synthesized" de-lensed PSF for the homogeneous weighting is more isotropic but larger than that for the magnification weighting. As shown in Figure 4, the de-lensed PSF shrinks more for a lensed image with larger magnification. Therefore, in the source plane, the effective angular resolution of a de-lensed image given by the magnification weighting is expected to be much better than that given by the homogeneous weighting. Moreover, the S/N of de-lensed image is expected to be significantly better for the magnification weighting because it corresponds to the inverse-variance weighted average provided that the observational noise dominates. However, the de-lensed PSF is more anisotropic because of the small effective number of de-lensed PFSs and the information of pixels with small magnification is partially lost. Thus, it is not clear whether the magnification weighting is an optimal choice for estimating lensing power spectra.

If the lens model is perfect and the S/N is sufficiently large, then the intensity of each lensed images must be equal. However, owing to finite angular resolution, errors in the intensity and the measured gravitational potential of lensing objects, the estimated source intensity on each pixel defined in Equation (11) differs from the true intensity regardless of the weighting scheme.

By minimizing the difference in the intensity at pixels in the source plane, one can obtain a more accurate gravitational perturbation toward lensed images. Suppose that a sufficiently bright region in the source plane consists of N pixels. For a given position y _j in the source plane, the positions of multiple lensed images are x ₁( y _j ), x ₂( y _j ), ⋯ , x _n ( y _j ), where n( y _j ) is the total number (even) of the lensed images. The range of subscript 1 to n( y _j )/2 corresponds to images with a positive parity and that of n( y _j )/2 to n( y _j ) corresponds to images with a negative parity. Although a statistic that can measure the difference in intensity between lensed images can have many definitions, we adopt a weighted mean of all of the lensed images with a positive parity subtracted by a weighted mean of all of the lensed images with a negative parity. The reason for this is as follows: First, the collective patterns of astrometric shifts due to perturbations depend on the parity (Inoue & Chiba 2005b). If the de-lensed images with different parity are synthesized, the signal of a source smaller than the PSF beam size may be weakened due to cancellation of perturbation. Second, for quadruple lenses with cusp or fold caustics, a pair of images with a different parity can have a significantly larger magnification than the other pair, leading to loss of information. Grouping with parity avoids such selections. Third, grouping with parity is easy to implement as the parity can be directly calculated from magnification matrices. Other selections of grouping need calculation of the boundaries at which the sign of parity changes, which results in an increase in computation time. Assuming that the correlation in flux errors at different pixels is negligible, ¹¹ ${\chi }_{\mathrm{ext}}^{2}$ defined in the "lens plane gauge" (δ y = 0) is given by

$$\begin{eqnarray}\begin{array}{rcl}{\chi }_{\mathrm{ext}}^{2} & = & \displaystyle \sum _{j=1}^{{N}_{{\rm{p}}}}\displaystyle \frac{1}{{\varepsilon }_{\mathrm{dif}}{\left({{\boldsymbol{y}}}_{j}\right)}^{2}}\left(\displaystyle \frac{{\sum }_{i=1}^{n({{\boldsymbol{y}}}_{j})/2}{w}_{i}I({{\boldsymbol{x}}}_{i}({{\boldsymbol{y}}}_{j})+\delta {{\boldsymbol{x}}}_{i}({{\boldsymbol{y}}}_{j}))}{{\sum }_{i=1}^{n({{\boldsymbol{y}}}_{j})/2}{w}_{i}}\right.\\ & & -{\left.\displaystyle \frac{{\sum }_{i=n({{\boldsymbol{y}}}_{j})/2+1}^{n({{\boldsymbol{y}}}_{j})}{w}_{i}I({{\boldsymbol{x}}}_{i}({{\boldsymbol{y}}}_{j})+\delta {{\boldsymbol{x}}}_{i}({{\boldsymbol{y}}}_{j}))}{{\sum }_{i=n({{\boldsymbol{y}}}_{j})/2+1}^{n({{\boldsymbol{y}}}_{j})}{w}_{i}}\right)}^{2},\end{array}\end{eqnarray} \tag{ 13 }$$

where I is the observed intensity, ε_dif is the error between de-lensed weighted "mean" images with different parities, δ ψ is the potential perturbation projected on the primary lens plane, δ α is the strength of deflection angle, δ κ is the convergence perturbation, and N_p is the total number of pixels.

To constrain the HST/VLBA positions of lensed images of a quasar core, we add the following constraining term defined in the "source plane gauge" (δ x = 0) as

$$\begin{eqnarray}&&{\chi }_{\mathrm{core}}^{2}=\displaystyle \sum _{({\rm{J}},{\rm{K}})}\displaystyle \frac{| \delta {\boldsymbol{\alpha }}({{\boldsymbol{x}}}_{{\rm{J}}}({{\boldsymbol{y}}}_{\mathrm{core}}))-\delta {\boldsymbol{\alpha }}({{\boldsymbol{x}}}_{{\rm{K}}}({{\boldsymbol{y}}}_{\mathrm{core}})){| }^{2}}{\langle | \delta {{\boldsymbol{x}}}_{{\rm{J}}}-\delta {{\boldsymbol{x}}}_{{\rm{K}}}{| }^{2}\rangle },\end{eqnarray} \tag{ 14 }$$

where ${{\boldsymbol{y}}}_{\mathrm{core}}$ is the fitted source position in the source plane, and δ x _J and δ x _K are the astrometric shifts at the positions J and K of a lensed core due to perturbation, respectively. The ensemble average of the shift difference 〈∣δ x _J − δ x _K∣²〉 in a lens plane can be estimated using the residual errors in the positions of the lensed images in the best-fitted smooth model. We may consider that the shift differences in the denominator should be replaced with those in the source plane $\langle | ({M}^{-1}\delta {{\boldsymbol{x}}}_{{\rm{J}}})({{\boldsymbol{y}}}_{\mathrm{core}})-({M}^{-1}\delta {{\boldsymbol{x}}}_{{\rm{K}}})({{\boldsymbol{y}}}_{\mathrm{core}}){| }^{2}\rangle$. However, we found that such a choice is too restrictive: by changing the fitted position of the quasar core ${{\boldsymbol{y}}}_{\mathrm{core}}$, the errors in the source plane can be increased if the added potential perturbation on brightest lensed images gives a similar astrometric shift in the source plane (see also Takahashi & Inoue 2014). The sum in Equation (14) is taken over four sets of closest pairs of lensed images. For MG J0414+0534, the closest pairs (J, K) are (A1,A2), (A2,B), (B,C), and (C,A1).

To constrain the MIR flux ratios of lensed images of a quasar core, we add the following constraining term:

$$\begin{eqnarray}&&{\chi }_{\mathrm{flux}}^{2}=\displaystyle \sum _{{\rm{J}}}{\left(\displaystyle \frac{{\mu }_{{\rm{J}}}+\delta {\mu }_{{\rm{J}}}}{{\mu }_{{\rm{A}}1}+\delta {\mu }_{{\rm{A}}1}}-\displaystyle \frac{{\mu }_{{\rm{J}}}}{{\mu }_{{\rm{A}}1}}\right)}^{2}/{\left({\sigma }_{{\mu }_{{\rm{J}}}{/\mu }_{{\rm{A}}1}}\right)}^{2},\end{eqnarray} \tag{ 15 }$$

where μ_J is the magnification factor at lensed image J (J = A2, B, C) of a core (or best-fitted image position of J) in the smooth model, δ μ_J is the perturbation, and ${\sigma }_{{\mu }_{{\rm{J}}}/{\mu }_{{\rm{A}}1}}$ is the observational error in the magnification ratio μ_J/μ_A1.

A gravitational potential perturbation δ ψ due to halos and voids in the vicinity of photon paths of lensed images is expanded in terms of Fourier modes. In what follows, to discretize the potential, we impose a Dirichlet boundary condition ¹² δ ψ = 0 at the boundary of a square R with a side length of L centered at (x_c1, x_c2) in the (primary) lens plane. The parameters are selected to satisfy that the entire lensed image is contained in the square. The potential perturbation δ ψ is set to zero outside the boundary. In our model, the contribution from masses inside the square is modeled as Fourier modes, and the contribution from masses outside the square is modeled as an external shear in the smooth model and low (spatial) frequency Fourier modes inside the square. We can express the core structure or distortion of the primary lens as well as halos and voids in sight lines inside the square. To take into account the gravitational effect from masses near the boundary, we need to adjust the size of the square such that the distance between the lensed arc and boundary is larger than the half of the minimum angular wavelength in the real Fourier modes.

The potential perturbation at (x₁, x₂) in the lens plane can be decomposed as,

$$\begin{eqnarray}&&\begin{array}{l}\delta \psi \,({x}_{1},{x}_{2})=\displaystyle \sum _{m,n\gt 0}\left[{{\rm{\Psi }}}_{{mn}}^{++}\cos {k}_{m}^{+}{\tilde{x}}_{1}\cos {k}_{n}^{+}{\tilde{x}}_{2}\right.\\ \quad +\,{{\rm{\Psi }}}_{{mn}}^{+-}\cos {k}_{m}^{+}{\tilde{x}}_{1}\sin {k}_{n}^{-}{\tilde{x}}_{2}+{{\rm{\Psi }}}_{{mn}}^{-+}\sin {k}_{m}^{-}{\tilde{x}}_{1}\cos {k}_{n}^{+}{\tilde{x}}_{2}\\ \quad +\,\left.{{\rm{\Psi }}}_{{mn}}^{++}\sin {k}_{m}^{-}{\tilde{x}}_{1}\sin {k}_{n}^{-}{\tilde{x}}_{2}\right],\end{array}\end{eqnarray} \tag{ 16 }$$

where ${\tilde{x}}_{1}={x}_{1}-{x}_{c1}$, ${\tilde{x}}_{2}={x}_{2}-{x}_{c2}$ are the relative positions in the lens plane of the primary lens, ${k}_{m}^{+}=(m\,\mathrm{mod}\,2)m\pi /L$ and ${k}_{m}^{-}=((m+1)\,\mathrm{mod}\,2)m\pi /L$ are the angular wavenumbers, m and n are nonzero positive integers, and ${{\rm{\Psi }}}_{{mn}}^{++},{{\rm{\Psi }}}_{{mn}}^{+-},{{\rm{\Psi }}}_{{mn}}^{-+}$, and ${{\rm{\Psi }}}_{{mn}}^{--}$ are expansion coefficients. Note that the relation between real and complex Fourier coefficients is described in Appendix B. Subsequently, the mean squared potential perturbation δ ψ is given by

$$\begin{eqnarray}\begin{array}{rcl}\langle {\left(\delta \psi \right)}^{2}\rangle & = & \displaystyle \frac{1}{4}\displaystyle \sum _{m,n\gt 0}\left[{\left({{\rm{\Psi }}}_{{mn}}^{++}\right)}^{2}+{\left({{\rm{\Psi }}}_{{mn}}^{+-}\right)}^{2}\right.\\ & & +\,{\left({{\rm{\Psi }}}_{{mn}}^{-+}\right)}^{2}\left.+{\left({{\rm{\Psi }}}_{{mn}}^{++}\right)}^{2}\right].\end{array}\end{eqnarray} \tag{ 17 }$$

Similarly, the mean squared astrometric shift $\langle {\left(\delta \alpha \right)}^{2}\rangle$ and mean squared convergence $\langle {\left(\delta \kappa \right)}^{2}\rangle$, which is equal to the mean squared shear $\langle {\left(\delta \gamma \right)}^{2}\rangle$, can be written in terms of the expansion coefficients as

$$\begin{eqnarray}\begin{array}{rcl}\langle {\left(\delta \alpha \right)}^{2}\rangle & = & \displaystyle \frac{1}{4}\displaystyle \sum _{m,n\gt 0}\left[({k}_{m}^{+2}+{k}_{n}^{+2}){\left({{\rm{\Psi }}}_{{mn}}^{++}\right)}^{2}\right.\\ & & +\,({k}_{m}^{+2}+{k}_{n}^{-2}){\left({{\rm{\Psi }}}_{{mn}}^{+-}\right)}^{2}\\ & & +\,({k}_{m}^{-2}+{k}_{n}^{+2}){\left({{\rm{\Psi }}}_{{mn}}^{-+}\right)}^{2}\\ & & \left.+\,({k}_{m}^{-2}+{k}_{n}^{-2}){\left({{\rm{\Psi }}}_{{mn}}^{++}\right)}^{2}\right],\end{array}\end{eqnarray} \tag{ 18 }$$

and

$$\begin{eqnarray}\begin{array}{rcl}\langle {\left(\delta \kappa \right)}^{2}\rangle & = & \displaystyle \frac{1}{4}\displaystyle \sum _{m,n\gt 0}\left[{\left({k}_{m}^{+2}+{k}_{n}^{+2}\right)}^{2}{\left({{\rm{\Psi }}}_{{mn}}^{++}\right)}^{2}\right.\\ & & +\,{\left({k}_{m}^{+2}+{k}_{n}^{-2}\right)}^{2}{\left({{\rm{\Psi }}}_{{mn}}^{+-}\right)}^{2}\\ & & +\,{\left({k}_{m}^{-2}+{k}_{n}^{+2}\right)}^{2}{\left({{\rm{\Psi }}}_{{mn}}^{-+}\right)}^{2}\\ & & \left.+\,{\left({k}_{m}^{-2}+{k}_{n}^{-2}\right)}^{2}{\left({{\rm{\Psi }}}_{{mn}}^{++}\right)}^{2}\right].\end{array}\end{eqnarray} \tag{ 19 }$$

Before performing mock simulations, we prepared a fiducial unperturbed smooth model based on our ALMA observations, and previous HST and VLBA observations of MG J0414+0534. The procedure is as follows:

First, we used a Type A model consisting of an SIE, an ES, and a CIS. SIE, ES, and CIS model the primary lensing galaxy G, a large-scale external shear, and object X, respectively. Using the SIE-ES-CIS model, we fitted the positions of quadruple images of a quasar core and the centroid of G and X observed in the OPT/NIR band in the CASTLES database. The assumed HST position errors are 0003 for lensed images, and the centroid of G and 02 for the centroid of X. The error for X was relaxed because X may be a lensed image of the quasar host galaxy rather than that of a companion galaxy (see Inoue et al. 2017 for details of model parameters). The size of the core of CIS was selected to best fit the observed parameters but constrained to not have an additional pair of images of a quasar core, which has not been observed in any radio bands. We did not consider any relative fluxes of lensed images for parameter fitting.

Second, we carried out continuum imaging with a Briggs weighting of robust = − 1 using the Measurement Set from mock "Cycle 4" observations. Then we rotated and translated the image to fit the positions of the lensed quasar images of the quasar core in the OPT/NIR band. We also subtracted off the lensed images of the lensed peaks using the best-fitted synthesized elliptical Gaussian beam in the lens plane. The peak intensity of the elliptical Gaussian beam at image A2 was fixed to 95% of the peak intensity at image A2. The 5% reduction is due to fluxes from an extended region. The peak intensities at other lensed images were given by the MIR flux ratios.

Third, we reconstructed the source image from the continuum image of the Cycle 4 observations, in which imaging was carried out using the natural weighting. We used the homogeneous weighting for de-lensing. To carry out de-lensing, as shown in (Figure 5, left), a square region with a side length of 2'' centered at the center of the best-fitted SIE is covered with 50 × 50 square meshes. Then, we selected all of the meshes at which the absolute magnification is larger than μ₁ = 6, and we subdivided these meshes into four square meshes. Similarly, we iterated this process with thresholds μ₂ = 18 and μ₃ = 65. This choice resulted in a similar number of meshes in each tier and the final mesh size being the same as the pixel size of the original image. We also subdivided meshes in a circular region around the center of object X into square meshes with a side length of 01 to resolve a small closed critical curve. Moreover, we omitted a region within a radius of 01 centered at the center of an SIE to avoid a singularity. Each square mesh was divided into two right triangles, and their vertices were mapped into the corresponding vertices in the source plane (Figure 5, right). The source plane was covered with square meshes, and at the center of each mesh, the number of triangles that include the center and the mapped triangles in the lens plane were computed. For a given point in the source plane, with the mesh that contains the point, the number of lensed image and the first guess of the corresponding points in the lens plane were computed. Using the first guess values, the corresponding accurate points in the lens plane were computed using Newton's method. Thus for a given point in the source plane, the corresponding lensed points in the lens plane can be numerically obtained with shorter CPU time. For brevity, we used the homogeneous weighting for de-lensing the continuum image. We found that the source (after subtracting bright spots) consists of two bright spots and a surrounding extended structure with a core (Inoue et al. 2020).

Zoom In Zoom Out Reset image size

Finally, we made a "true" source image and added a random potential perturbation to the obtained background lens potential: First, we fitted the two bright spots and extended structures observed in the Cycle 4 core-subtracted source image (Figure 6, left) with two identical spherical Gaussian functions with an FWHM of 12 pc and two-component concentric elliptical Gaussian functions, respectively (Figure 6, right). The two bright spots and extended structures represent jet/core components and cold/warm dust emissions, respectively. The amplitudes, ellipticity, and axis directions of these Gaussian functions were obtained from a χ² fit to the Cycle 4 core-subtracted source image on pixels with >3σ. Second, we added a quasar core component represented by a spherical Gaussian function with FWHM of 12 pc in the source plane. The amplitude was adjusted to recover fluxes of bright spots observed in the lens plane. Third, we added a random Gaussian perturbation consisting of 4 × 3² = 36 discrete modes to the potential of the background lens model. The side length of a square region was set to 36, and the center was set at (−04, 03) in which the centroid of G is at (0, 0). The selected parameters satisfy the condition that the distance between the boundary and the lensed arcs, objects X and Y, are longer than half of the shortest angular wavelength of 12. The "true" potential perturbation was assumed to vanish at the boundary and the outside of the square. The coefficients of the potential perturbation were assumed to obey a Gaussian distribution with a zero mean and a standard deviation of 0.57 mas². We made random 10⁵ realizations and selected one set that satisfied the constraints on the relative astrometric shifts in the OPT/NIR bands (Equation (14)) and the MIR flux ratios of the lensed quasar cores (Equation (15)).

Zoom In Zoom Out Reset image size

We carried out ALMA mock continuum observations of the lensed "true" source using the simobserve task in CASA. We used the same observation dates, antenna configuration, precipitable water vapor, and integration time as used in our actual Cycle 2 and Cycle 4 observations. We added thermal noise for a ground temperature of 271 K. The line-free bandwidth was set to 4189 MHz, approximately equal to the one for the actual observations. After the mock "Cycle 2" and "Cycle 4" observations, we concatenated the obtained Measurement Sets as was conducted for our actual data. Then continuum imaging was performed using the CLEAN algorithm (tclean in CASA) with a Briggs weighting of robust = 0.5 (Figure 7). To measure the positions of quadruple images of a quasar core, we also performed continuum imaging with a Briggs weighting of robust = − 1 using the Measurement Set from mock "Cycle 4" observations. We also subtracted off the lensed images of the mock "quasar core" using the best-fitted elliptical Gaussian beam. The peak intensity of the elliptical Gaussian beam at image A2 was set to 95% of the peak intensity at image A2. The 5% reduction is due to fluxes from an extended region. The peak intensities at other lensed images were given by the "true" flux ratios. We observed that our CLEANed image gives a ∼60% increase in intensities except for the brightest spot with S/N ≳ 50 that corresponds to the mock quasar core. Therefore, to test our mock analysis, we multiplied the mock observed intensities for peak-subtracted lensed images by a constant of 1/1.6. Such a uniform change in intensity does not much affect the reconstruction of perturbation as the scale of potential perturbation is much smaller than the whole lensed image.

Zoom In Zoom Out Reset image size

We used the SIE-ES-CIS (Type A) model to fit the positions of mock quadruple images of quasar cores and the centroids of the primary lensing galaxy G and object X (see Inoue et al. 2017 for details). Note that the positions of the centroid of G and X were also perturbed by the added potential perturbation. We assumed that the errors in the positions in the lens plane are equivalent to the values in the OPT/NIR data.

Then we performed χ² minimization numerically to obtain the best-fitted parameters for the mock smooth model. As described in Section 5.1, a square region with a side length of 2'' centered at the center of the best-fitted SIE was covered with 50 × 50 square meshes, which were subdivided iteratively. The source plane at which the estimated signal in the source plane is larger than 5σ was covered with meshes with a side length of 6.66 or 13.3 mas. The meshes cover the central and surrounding region of the core-subtracted mock source (Figure 8). The size of small meshes is smaller than the two bright spots. Since the mesh sizes are larger than the de-lensed PSF size of ∼4 mas, the effect of spatial correlation of errors is expected to be small. The mesh size is larger in the outer region since the curvature of the de-lensed intensity is smaller in the outer region.

Zoom In Zoom Out Reset image size

In order to avoid regions at which our weak lensing formalism breaks, ¹³ we excluded meshes at which the maximum absolute magnification is larger than 30. We also excluded meshes that yielded an odd number of images, due to crossing over the caustic. For each pixel, 1σ errors ε_I in the reconstructed source and ε_dif in the difference in the weighted mean de-lensed images for a positive/negative parity were measured from random translations of the mock lensed image. In order to suppress contributions from signals, we subtracted off fluxes larger than 4σ in the lens plane to estimate the errors in the source plane.

If the scale of the fluctuation in the de-lensed intensity is smaller than the fitted synthesized beam, the reconstructed intensity differs (typically smaller for brighter regions) from the true value due to the contribution within the beam. Moreover, the fitted synthesized beam may differ from the "true" PSF due to systematic errors. To take into account such effects, we modeled the "true" errors in the weighted mean de-lensed images at a pixel centered at y _j as

$$\begin{eqnarray}&&{\varepsilon }_{\mathrm{dif}}({{\boldsymbol{y}}}_{j})={\varepsilon }_{\mathrm{dif}}({{\boldsymbol{y}}}_{j};\mathrm{fid})| \hat{I}({{\boldsymbol{y}}}_{j})/{\varepsilon }_{I}({{\boldsymbol{y}}}_{j}){| }^{\beta },\end{eqnarray} \tag{ 20 }$$

where ε_dif( y _j ; fid) is the nominal value obtained from random translations of a de-lensed image, and β is a constant parameter. If the contamination is described by a Poisson process, we expect β = 0.5. In what follows, we adjusted β before χ² minimization to yield a best-fitted reduced χ² of ∼0.8–1.5.

If a potential perturbation is decomposed into N × N modes, we use modes with $3.5\lt \sqrt{{m}^{2}+{n}^{2}}\lt N+0.5$ to analyze the mock perturbation due to LOS structures or subhalos. For instance, for N = 6, we use 7 low-to-intermediate-frequency modes, 11 intermediate-to-high frequency modes, and 7 high-frequency modes for analysis of perturbation (Figure 9) in our mock simulations. This ensures an approximate rotational symmetry of the correlation and avoids degeneracy with low multipole (=monopole, dipole, and quadrupole) contributions from the galaxy of the primary lens.

Zoom In Zoom Out Reset image size

In this mock analysis, we used the same square boundary with a side length of L = 36 and N = 6. Therefore, our mock analysis is limited to systems in which the gravity of halos at the boundary does not significantly affect the lensed arcs. For comparison, we adjusted β to satisfy the condition χ²/dof = 2.0 in the initial model without any perturbation.

As shown in Table 1, the magnification weighting gives smaller β than the homogeneous weighting. This is expected because the magnification weighting corresponds to the inverse-variance weighted average, which maximizes the S/N.

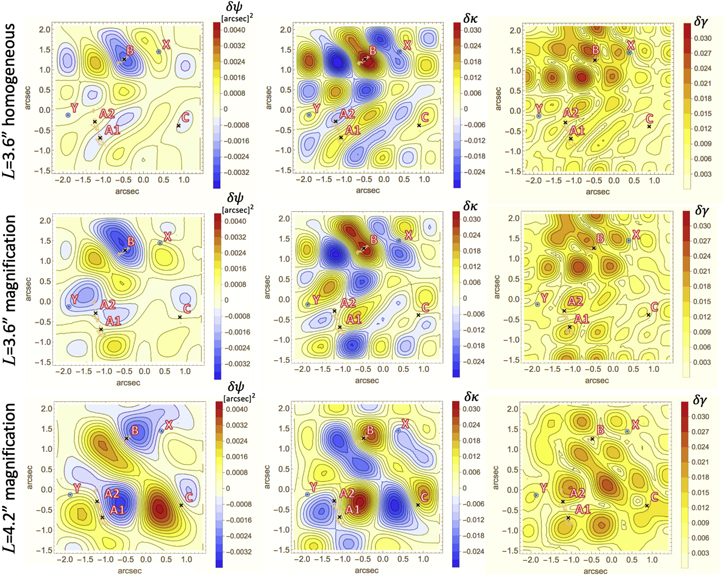
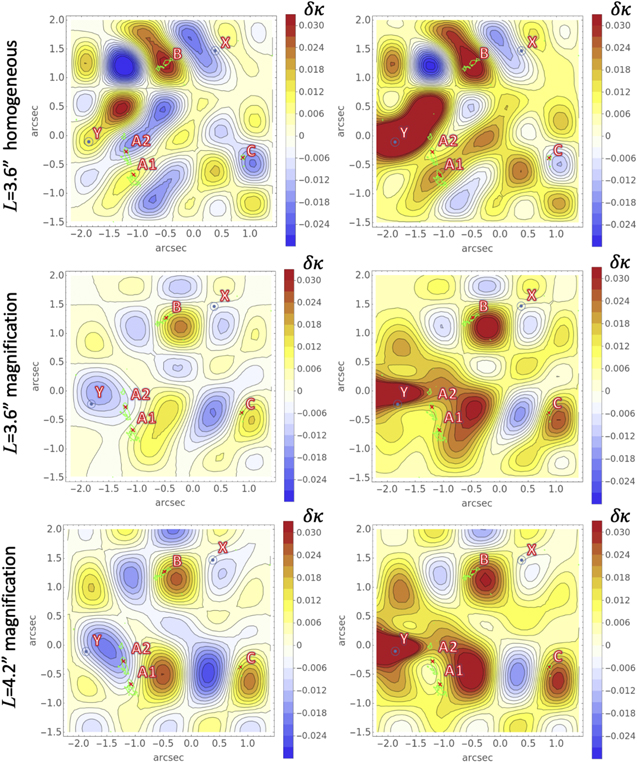
We plotted the original and best-fitted convergence perturbation δ κ in Figure 10 and their differences in Figure 11. We can see in these figures that the fidelity of convergence perturbation in the vicinity of images A1, A2, and B are better for the magnification weighting. This result is not surprising, as these images have large magnification, and thus the de-lensed images have large weighting. On the other hand, the fidelity of convergence perturbation in the vicinity of X and image C are better for the homogeneous weighting, though the fidelity in the vicinity of images A1, A2, and B is worse. This result is again not surprising as the homogeneous weighting weighs each lensed image equally. Fluctuations that are reconstructed with the magnification weighting seem to be more anisotropic than those reconstructed with the homogeneous weighting. This implies that the magnification weighting may not be an optimal choice for the purpose of reconstructing correlation functions, and lensing power spectra though the fidelity of perturbation in real space (i.e., lens plane) is better than that obtained with the homogeneous weighting.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

The magnification weighting also gives a better fidelity of intensity in the source plane. As shown in Figure 12, two bright spots with a separation of 0014, which is one-third of the beam size, were resolved for the magnification weighting. Thus "super-resolution" was achieved. However, the homogeneous weighting failed to resolve the two spots. Since de-lensed PSFs obtained with the homogeneous weighting are larger than peak structures, large residual errors remain for peaks with high S/N. The residual errors were larger than the nominal errors for larger S/N because brighter pixels affect the neighboring pixels much more than fainter pixels. Such effects were observed in both the weightings, but the difference was more prominent for the homogeneous weighting due to the sizes of the de-lensed PSFs. As shown in Figure 13, the residual error in the reconstructed mock source intensity shows a significant deviation from the best-fitted polynomial function in pixels with S/N ∼ 30 in the homogeneous weighting. Thus, the mock residual errors support our assumption on errors in intensity difference between de-lensed images: stronger S/N dependency for the homogeneous weighting than for the magnification weighting.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

In contrast, the homogeneous weighting gave much better results than the magnification weighting in reconstructing the lensing power spectra (Table 2). The relative errors ¹⁴ between the mean value of the reconstructed power spectra are 40%–80% for the magnification weighting and 20%–50% for the homogeneous weighting for three bins of angular wavenumbers centered at l = 0.74 × 10⁶, 1.08 × 10⁶, and 1.30 × 10⁶. In other words, our results suggest that the magnification weighting results in significantly large systematic errors compared with the homogeneous weighting when estimating the powers. Since the homogeneous weighting weighs the multiple lensed images equally, it is probable that the information loss of fluctuations in regions beyond the lensed images and the bias in the estimated powers were reduced. We found that the relative errors in potential and astrometric shift perturbations are much smaller than those of convergence perturbation in intermediate scales regardless of weighting scheme.

Table 2. Simulated Mock Lensing Power Spectra (See Appendix A) for Three Bins of Angular Wavenumbers Centered at l = 0.74 × 10⁶, 1.08 × 10⁶, and 1.30 × 10⁶

	${{\rm{\Delta }}}_{\psi }({\mathrm{arcsec}}^{2})$	${{\rm{\Delta }}}_{\alpha }(\mathrm{arcsec})$	Δκ	${{\rm{\Delta }}}_{\psi }({\mathrm{arcsec}}^{2})$	${{\rm{\Delta }}}_{\alpha }(\mathrm{arcsec})$	Δκ	${{\rm{\Delta }}}_{\psi }({\mathrm{arcsec}}^{2})$	${{\rm{\Delta }}}_{\alpha }(\mathrm{arcsec})$	Δκ
l[106]	0.74 ± 0.06	0.74 ± 0.06	0.74 ± 0.06	1.08 ± 0.07	1.08 ± 0.07	1.08 ± 0.07	1.30 ± 0.08	1.30 ± 0.08	1.30 ± 0.08
"True" values	0.000644	0.00214	0.00362	0.00101	0.00526	0.0138	0.00111	0.00688	0.0217
Magnification	0.00099	0.00360	0.00656	0.000637	0.00329	0.0087	0.000658	0.00410	0.0128
	±0.00012	±0.00045	±0.00083	±0.00011	±0.00056	±0.0015	±0.00014	±0.00092	±0.0029
Absolute error [1σ]	2.9	3.3	3.6	3.5	3.5	3.4	2.9	3.0	3.1
Relative error [%]	54	68	83	37	37	53	40	41	41
Homogeneous	0.000881	0.00303	0.00531	0.000851	0.00431	0.0110	0.000730	0.00456	0.0143
	±0.00018	±0.00061	±0.00110	±0.00014	±0.00070	±0.0018	±0.00017	±0.00104	±0.0033
Absolute error [1σ]	1.3	1.4	1.5	1.1	1.4	1.6	2.2	2.3	2.4
Relative error [%]	37	42	47	16	18	20	34	34	34

Note. They were calculated using the fitted seven low-to-intermediate, 11 intermediate-to-high, and seven high-frequency modes shown in Figure 9, respectively. The measured lensing power spectra within a range of 1σ error obtained with the magnification weighting and those with the homogeneous weighting are shown in the fourth and eighth rows, respectively.

Download table as:  ASCIITypeset image

To obtain background lensing models from our ALMA data, we used lensed images of a compact radio component q in the VLBA map at 5 GHz (Trotter et al. 2000) instead of the HST position of the quasar core. In a continuum map of the Cycle 4 observation in which imaging was performed with (robust = − 1), the positions of lensed images of q are shown with circles (Figure 14).

Zoom In Zoom Out Reset image size

The reason for this is as follows: first, the accuracy of the VLBA positions (≲2 mas) are better than that of the HST positions (∼3 mas). Second, as the position of the radio emission at 5 GHz is very close to the OPT/NIR emission of the quasar core (<2 mas), we can consider component q as the quasar core rather than a jet (Inoue et al. 2020).

In order to match the VLBA positions to the HST positions, we translated and rotated the coordinates of the VLBA map to best fit the positions of lensed q to the HST positions in the OPT/NIR band. The obtained rotation angle is 176 (east of north). The residual differences between the lensed q and the HST positions, A1, A2, B, and C are 0.0, 2.4, 2.0, and 1.3 mas.

Then our ALMA maps were rotated by the same angle (assuming a perfect alignment with the coordinates in the VLBA image), and the position of a local peak in image A1 was placed on the brightest image A1 of the lensed gravitational center of p and q in the corresponding VLBA data (see Figure 14). The differences between local peaks in the ALMA image and the gravitational centers of p and q for A2, B, and C were 2.3, 4.0, and 1.4 mas, which are smaller than the pixel size of 5 mas ¹⁵ used in the continuum maps. We assumed that the errors in the VLBA positions are 2 mas, which is the mean size of the synthesized beam. Although the positions of emission at 340 GHz may slightly differ from those at 5 GHz, the differences in the positions in the lens plane were found to be smaller than 4 mas. The differences in the source plane are expected to be much smaller due to demagnification.

As conducted in our mock analysis, we used the HST positions of the centroids of the primary lensing galaxy G, object X observed in the OPT/NIR band, and the MIR flux ratios observed with the Subaru and Keck telescopes (Minezaki et al. 2009; MacLeod et al. 2013). Considering a possible misalignment of ∼2 mas, the positional error of the centroid of G was assumed to be 5 mas. The positional errors of X and Y were assumed to be 01.

To obtain the best-fitted Type B model, we also used the central position of object Y observed with ALMA (see Section 6.5 for details), and assumed observational constraints for the ellipticities of G and Y. For G, the mean ellipticity of isophotes in the HST I band was measured as e_G = 0.20 ± 0.02 (Falco et al. 1997). Taking into account the misalignment between the baryonic and dark matter components and halo flattening, we adopt a conservative error value δ e_G = 0.20 for the ellipticity of the projected total matter (baryon + dark matter) in the halo of G. As the expected ellipticity of the halo of Y, we adopt a mean ellipticity ∼0.5 of projected dark matter halo measured in cluster scales (Evans & Bridle 2009; Oguri et al. 2010; Okabe et al. 2020). We assume a conservative error value δ e_Y = 0.20 for the ellipticity of Y. To include these constraints in fitting, we add a term

$$\begin{eqnarray}&&{\chi }_{e}^{2}={\left(\displaystyle \frac{0.2-{e}_{{\rm{G}}}}{0.2}\right)}^{2}+{\left(\displaystyle \frac{0.5-{e}_{{\rm{Y}}}}{0.2}\right)}^{2},\end{eqnarray} \tag{ 21 }$$

to ${\chi }_{\mathrm{tot}}^{2}$ in modeling Type B. For simplicity, we assume the same ratio between the core size r_X of X and the effective Einstein radius b_G of G as used in Type A. Therefore, r_X is fixed in Type B models. We also parameterized the redshift z_Y of object Y. The best-fitted parameters of the smooth models of Type A and B are shown in Table 3.

Table 3. Fiducial Smooth Model Parameters, χ², and Flux Ratios in Models Best-fitted to the MIR Flux Ratios, HST Positions of Galaxies, and VLBA Positions of Jet Component q

Type	bG	(ys1, ys2)	eG	ϕG	γ	ϕγ	(xG1, xG2)	bX	(xX1, xX2)	rX
A	1094	(−00562, 02654)	0.307	−879	0.0918	475	(0006, − 0009)	0219	(0445, 1483)	0018
B	1107	(−00981, 02254)	0.280	−879	0.0790	475	(−0001, − 0002)	0160	(0316, 1490)	0019
Type	zY	bY	eY	ϕY	(xY1, xY2)
A
B	0.661	0028	0.604	795	(−1850, − 0042)
Type	${\chi }_{{\rm{flux}}}^{2}$	${\chi }_{{\rm{posG}}}^{2}$	${\chi }_{{\rm{posX}}}^{2}$	${\chi }_{{\rm{posY}}}^{2}$	${\chi }_{{\rm{posq}}}^{2}$	${\chi }_{e}^{2}$	${\chi }_{{\rm{tot}}}^{2}/$ dof	A2/A1	B/A1	C/A1
A	24.09	4.58	0.45		6.58		35.7/3	1.007	0.350	0.175
B	7.014	0.264	0.555	0.645	0.018	0.427	8.92/1	0.928	0.358	0.174

Note. In Type A models, object Y is not modeled explicitly but in Type B models, Y is modeled explicitly in the smooth model. b_G is the effective Einstein radius of the primary lensing galaxy G, (y_s1, y_s2) is a set of source coordinates of the jet component q, e_G is the ellipticity of G, ϕ_G is the direction of the major axis of G, γ is the amplitude of the external shear, ϕ_γ is the direction of the external shear, (x_G1, x_G2) is a set of coordinates of the centroid of G, b_X is the Einstein radius of object X, (x_X1, x_X2) is a set of coordinates of the centroid of X, and r_X is the assumed core radius of X (see Inoue et al. 2017 for details). For simplicity, r_X is fixed in fitting. z_Y is the redshift of object Y, b_Y is the effective Einstein radius of object Y, (x_Y1, x_Y2) is a set of coordinates of the peak position of Y, e_Y is the ellipticity of Y, and ϕ_Y is the direction of the major axis of Y. ${\chi }_{{\rm{tot}}}^{2}$ is the sum of contributions from the flux ratios ${\chi }_{{\rm{flux}}}^{2}$, the positions of the lensed images of the jet component q ${\chi }_{{\rm{posq}}}^{2}$, lensing galaxy G ${\chi }_{{\rm{posG}}}^{2}$, and object X ${\chi }_{{\rm{posX}}}^{2}$. The coordinates are centered at the centroid of G (CASTLES database; Falco et al. 1997). The assumed errors are 2 mas for the VLBA positions, 5 mas, 100 mas, and 100 mas for the HST positions of the centroids of G, X, and ALMA position of Y. Here, the error in the HST position of G includes the systematic difference of ∼2 mas between the HST and VLBA maps. We assume that the central position of object Y is (−1865, − 0116; see Section 6.5).

Download table as:  ASCIITypeset image

To subtract lensed images of bright core components p and q from a continuum image, we used the best-fitted elliptical Gaussian beam obtained from CASA. We considered p and q as two pointlike sources, whose intensities are described by an elliptical Gaussian beam synthesized beam, multiplied by a constant. The intensities c_p and c_q (in units of the observed peak intensity of q at the fitted position) at the fitted positions of p and q in image A2 were selected as free parameters but constrained so as not to become negative. c_p + c_q was also constrained to be 0.95. ¹⁶ The 5% decrease accounts for emission from extended dust regions (Figure 15). Note that c_p and c_q were not fit independently as our numerical analysis showed that such fits tend to give a solution with a negative flux.

Zoom In Zoom Out Reset image size

The intensities at the positions of lensed p and q in image A1, B, and C were given by the MIR flux ratios of the quasar core and intensities at the positions of lensed p and q in image A2. If we allow for independent change in both c_p and c_q, χ² minimization would give a solution with a negative hole in the peak-subtracted image due to over subtraction. Therefore, we fixed c_p + c_q to be a constant.

We constructed multiscale meshes in the source plane in a similar manner to our mock analysis but the mesh sizes was fixed to be 6.66 mas. The mesh size was determined from the fluctuation scale of the de-lensed image in the brightest region.

We used only pixels with >3.8σ in the source plane. In order to estimate possible enhancement in the errors in the source plane due to side lobes, we subtracted off fluxes larger than 4σ in the lens plane and carried out random translations of the lens plane around the lensed image. Using the data set, we found that the absolute values of the nondiagonal components in the covariance matrix of the difference in the weighted sum of the de-lensed source intensity is ≲10% of the diagonal components. Therefore, the effect of spatial correlation of errors in the pixels in the source plane is expected to be small.

Before performing χ² analysis, we adjusted β to satisfy the condition χ²/dof ∼ 3 for an unperturbed model. As a fiducial value, we set c_q = 0.20 and c_p = 0.75. Then we minimized χ² using de-lensed images reconstructed with the magnification or homogeneous weighting as was conducted in the mock analysis.

In our algorithm, the phases of Fourier modes are fixed. Therefore, the position of the square boundary at which the gravitational potential vanishes may affect the reconstruction of potential. Moreover, lensing power spectra may depend on the scale of fluctuation. To take into account these ambiguities, we considered two types of models to describe the potential perturbation due to subhalos and LOS structures: 36 modes with L = 36 centered at (−04, 03). To test the effect of possible masses in the vicinity of object Y, we also considered another model with 36 modes with L = 42 centered at (−07, 03). In this model, the east (left) boundary of a square region was shifted toward the east by the half of the shortest wavelength (06), while the west (right) boundary was fixed. The number of modes, the size, and position of the square region satisfy the following conditions: (1) the number of modes—a squared integer should be smaller than the number of pixels in the source plane; (2) the distance between the boundary of the square region and the lensed quasar core should be larger than the half of the shortest wavelength in the Fourier modes; and (3) the square region includes the central positions of object X and Y.

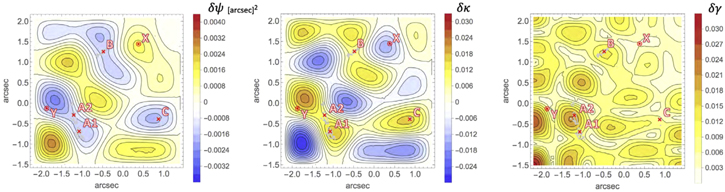
The center of the coordinates was located at the centroid of the primary lensing galaxy G. For each model, a set of parameters that gives the minimum of χ² for the image obtained with robust = 0 is given in Table 4. To analyze the perturbation in the real space, we used the magnification weighting and to analyze the lensing power spectra, we used the homogeneous weighting for de-lensing.

Table 4. Results of Source Plane Fits: Assumed Parameters, Minimized χ², Flux Ratios, and rms Perturbations in Models Best-fitted to the ALMA Data, MIR Flux Ratios, HST Positions of Galaxies, and VLBA Positions of Jet Component q

Type		N2	L	β	δ ψ0	δ α0	δ κ0	cq	χ2/dof	Np	nobs	dof	A2/A1	B/A1	C/A1	${\chi }_{\mathrm{pos}}^{2}/{\mathrm{dof}}_{\mathrm{pos}}$	dofpos	$\delta {\kappa }_{\mathrm{rms}}^{q}$	$\delta {\gamma }_{\mathrm{rms}}^{q}$
A	mag.	36	36	0.67	0.0014	0.0053	0.0090	0.324	0.80(3.0)	46	7	13	0.943	0.374	0.146	0.67(0.73)	24	0.015	0.012
A	mag.	36	42	0.67	0.00096	0.0060	0.0057	0.333	0.83(3.0)	46	7	13	0.905	0.349	0.153	0.68(0.73)	24	0.011	0.010
A	hom.	36	36	0.77	0.00065	0.0085	0.0125	0.452	1.2(2.8)	51	7	18	0.958	0.346	0.131	1.0(0.73)	24	0.018	0.011
A	hom.	36	42	0.77	0.00075	0.0065	0.0340	0.400	1.2(2.8)	51	7	18	0.952	0.369	0.132	1.0(0.73)	24	0.025	0.007
B	mag.	36	36	0.48	0.00070	0.0064	0.0058	0.229	1.0(2.4)	48	7	15	0.924	0.354	0.152	0.28(0.32)	24	0.010	0.0076
B	mag.	36	42	0.48	0.00053	0.0053	0.0070	0.134	1.0(2.4)	48	7	15	0.918	0.359	0.152	0.29(0.32)	24	0.013	0.0091
B	hom.	36	36	0.77	0.00089	0.0059	0.0066	0.306	1.0(1.7)	57	7	24	0.943	0.339	0.131	0.65(0.32)	24	0.019	0.011
B	hom.	36	42	0.77	0.00080	0.0050	0.0130	0.080	1.0(1.7)	57	7	24	0.894	0.344	0.126	0.60(0.32)	24	0.026	0.011
MIR													0.919	0.347	0.139
													±0.021	±0.013	±0.014

Note. "mag." and "hom." represent the magnification and homogeneous weighting, respectively. N² is the number of mode functions. L is the side length of a square at which the Dirichlet condition is imposed. β is the power index of the expected error as the function of signal in the source plane. The units of smoothing parameters δ ψ₀ and δ α₀ are ${\mathrm{arcsec}}^{2}$ and $\mathrm{arcsec}$, respectively. c_q is the ratio of the flux of q to the peak flux at the lensed image A2 of q. χ²/dof is the reduced χ² for the ALMA image (robust = 0), VLBA positions of q, and MIR flux ratios. N_p is the total number of pixels. n_obs is the total number of constraints for the relative angular distance (=4) and the MIR flux ratios (=3) of the lensed images of the quasar core (assumed to be q). ${\chi }_{\mathrm{pos}}^{2}/{\mathrm{dof}}_{\mathrm{pos}}$ is the reduced χ² for the positions of four VLBA jet components p, q, r, and s in which only the source positions are adjusted while the Fourier modes are fixed. Numbers in parentheses are the values for the corresponding unperturbed smooth model. The last column shows the observed MIR flux ratios (Minezaki et al. 2009; MacLeod et al. 2013).

Download table as:  ASCIITypeset image

To check the consistency with the VLBA map at 5 GHz, we further fitted the positions of lensed VLBA jet components p, q, r, and s as well as the centroids of the primary lensing galaxy G and object X using the obtained best-fitted Fourier coefficients, c_q, c_p, and the parameters for the smooth model. Considering the beam size of the VLBA observation (1.5 mas × 3.5 mas) at 5 GHz and a possible misalignment between our ALMA and the VLBA map, we assumed a positional error of 5 mas for the lensed quasar core (or q) and jet components p, r, and s.

As shown in Table 4, the reduced χ² for the best-fit Type A model based on the ALMA (Cycle 2 + Cycle 4) image reconstructed with robust = 0, magnification weighting and L = 36 or L = 42 is ${\chi }_{\mathrm{pos}}^{2}/{\mathrm{dof}}_{\mathrm{pos}}=22.5/(36-8)=0.80$. Thus, the fit to the ALMA image, VLBA position of the VLBA core component q, and HST positions of the centroids of G and X is good even without explicit modeling of object Y (Figure 16). For the four Type A models we analyzed, the rms of convergence perturbation $\delta {\kappa }_{\mathrm{rms}}^{q}$ and that of shear perturbation $\delta {\gamma }_{\mathrm{rms}}^{q}$ at the positions of the quadruple image of q are 0.017 ± 0.005 and 0.010 ± 0.002, respectively. Our result suggests that the rms convergence perturbation is significantly larger than the rms shear perturbation on the positions of the quadruple images. The Type B models fitted the data slightly better than the Type A models. Inclusion of Fourier modes yielded good fits without large ellipticity for Y (see Inoue et al. 2017). Compared with the Type A models, the a posteriori fit to the VLBA positions was slightly improved.

Zoom In Zoom Out Reset image size

We also conducted a similar analysis using the ALMA image reconstructed with robust = 0.5, but it yielded slightly worse fitting for the VLBA positions with ${\chi }_{\mathrm{pos}}^{2}/{\mathrm{dof}}_{\mathrm{pos}}=49.5/(36-8)=1.8$ and β = 0.456 in Type A models. Therefore, we used only the ALMA image reconstructed with robust = 0 in the subsequent analysis.

As shown in the middle panel in Figure 17, the differences in the weighted mean de-lensed peak-subtracted source images with the same parity were significantly reduced in the perturbed model with L = 36 and c_q + c_p = 0.95 compared with the unperturbed model (left panel in Figure 17). The difference between the unperturbed and perturbed source images depicted two brightest spots, which can be interpreted as anomalies in astrometric shifts (right panel in Figure 17). The position of r is not perfectly aligned with one side of the bipolar structure in the unperturbed model (left panel in Figure 18), but aligned in the perturbed model (middle panel in Figure 18). The misalignment may be due to errors in the fitted gravitational potential. Compared with the unperturbed model, a caustic that crosses a jet component r (triangle in Figure 18) and corresponds to a closed critical curve in the vicinity of object X (right panel in Figure 18) is shifted toward a jet component r by ∼5 mas. The shift suggests that the perturbed model has a larger core for object X with fainter fifth and sixth images around it. Since our ALMA images did not indicate the presence of bright fifth and sixth images, the perturbed model is considered to be a reasonable model.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Both the unperturbed and perturbed peak-subtracted de-lensed images show a brightest spot centered at q. The spot may be associated with dust emission from a circumnuclear disk around the quasar core. However, we cannot exclude the possibility of synchrotron emission from the quasar core due to insufficient subtraction of a pointlike source component (Inoue et al. 2020). Note that the position of the brightest spot obtained in our previous analysis that uses the HST positions of lensed core images deviates from q by ∼10 mas in the source plane (see also Figure 6). Since the accuracy of VLBA positions (≲2 mas) used in this new analysis is better than that of the HST positions (∼3 mas), we expect that our new de-lensed images yielded much better description of the source structure.

If the obtained model gives a better fit to the data, we expect that the fit to the data in the lens plane is also improved if the fluctuation scale of intensity is larger than the synthesized beam in the lens plane. ¹⁷ To observe this effect, we smoothed the intensity of the lensed de-lensed image within a pixel with a side length of 005 and subtracted it from the ALMA image. As shown in Figure 19 (left and middle), the differences in the residuals between unperturbed and perturbed models is limited to regions near the critical curve, at which the magnification is large (Figure 19, right). In the perturbed model, the fit in the lensed arc image A2 was improved at regions near the critical curve (Figure 19, middle). This result is expected as astrometric shifts of ∼0005 along the lensed arc can be enhanced as ∼0005 × μ, where μ is the magnification. In our best-fitted models, the typical magnification at images A1 and A2 is ∼15. Therefore, we expect shifts of 005–01 in the vicinity of A1 and A2, which is larger than the beam size.

Zoom In Zoom Out Reset image size

In the middle panels of Figure 20, we can see a positive peak in the convergence perturbation near image A2. In the models using the magnification weighting, the negative peak in the potential that corresponds to the positive peak in the convergence is slightly shifted from the position of object Y. However, we cannot exclude the possibility of perturbation by object Y because accurately measuring the matter distribution outside the lensed arcs is difficult. As shown in the right panels of Figure 20, images A1 and A2 are perturbed by shear possibly due to a pair of clumps or a trough.

Zoom In Zoom Out Reset image size

Our method can probe both the potential perturbation due to subhalos and LOS structures and distortion in the potential of the primary lens. Since the effect is degenerate with that of low-frequency potential perturbation due to subhalos and LOS structures, extracting only the distortion in the potential of the primary lens is difficult. Although it is somewhat ad hoc to determine the range of the "low" frequency affected by the primary lens, we adopted the lowest 6 modes with angular wavelength of 2'' ∼ 7'' as the "low-frequency" modes. ¹⁸ As shown in Figure 21, The convergence perturbation δ κ due to the low-frequency modes is less than 0.002, corresponding to ∼0.4% of the background convergence of κ ∼ 0.5 in the effective Einstein radius. This result is expected, as low-frequency modes whose fluctuation scales are larger than the effective Einstein radius of the primary lens cannot perturb quadruple images independently. Thus, it is likely that our results for intermediate- and high-frequency modes are not very sensitive to the selected low-frequency modes (including deviation from SIE), which are partly associated with the potential of the primary lens. However, note that our result cannot exclude the possibility of contribution from very small angular scale modes <10, which we did not take into account.

Zoom In Zoom Out Reset image size

We also studied perturbed Type B models in which object Y is modeled by an SIE at a redshift z_Y = 0.661 in the smooth model (Figure 22). We found that the ratio of the difference of convergence contribution δ κ between A2 and B to A1 and B as (δ κ(A2) − δ κ(B))/(δ κ(A1) − δ κ(B)) = 2.8. The value is close to the ratio of the differential extinction of A2 to that of A1, ΔA_V (A2)/ΔA_V (A1) ≈ 3.4 (Inoue et al. 2017). Therefore, the large difference in the differential extinction of A2 relative to A1 can be naturally explained by our model if the convergence is proportional to the dust column density. Owing to the presence of small clumps in the vicinity of B and A1, the perturbed Type B models fit the MIR flux ratios better than the unperturbed background Type B model. Compared with the perturbed Type A models, the perturbed Type B models fit the VLBA positions of jet components much better (see Table 4). In Figure 23, we show the best-fitted convergence perturbations in the Type B models. One can visually confirm that the fluctuation patterns are similar to those in Type A models with the same parameters (see Figure 20). This suggests that the small-scale potential fluctuations are independent of the presence or absence of object Y.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

To estimate the lensing power spectra toward MG J0414+0534, we used the homogeneous weighting, which was observed to be more suitable than the magnification weighting (Section 5.4). Similar to our mock analysis, the constant β was chosen to satisfy χ²/dof = 2.8 in the initial model without any perturbation. The 1σ errors of the powers were calculated using random Gaussian potentials that give Δχ ≤ 1 with the smoothing term R_s /dof smaller than that for the best-fitted model. We used the two models (36 modes with L = 36 and L = 42) to estimate the lensing power spectra. Table 5 shows the lensing power spectra obtained from the 22 intermediate-frequency modes as was calculated in the mock analysis. The lensing power spectra of potential perturbation Δψ and astrometric shift perturbation Δα did not depend much on the side length L. In contrast, the convergence perturbations Δψ showed a weak dependence on L: a model with smaller angular scale has a slightly larger convergence perturbation. This tendency was observed in the lensing power spectra with much smaller bins (see Figure 24). Modes with smaller angular scales have a larger power. This tendency is more apparent for convergence perturbation than astrometric shift and potential perturbations. On the smallest angular scale, the difference in powers of Type A and those of B models becomes smaller. This result suggests that the lensing powers on the smallest angular scale obtained from the seven high-frequency modes are not so sensitive to the details of object Y. Therefore, we adopt the lensing powers on the smallest angular scale as the robust ones.

Zoom In Zoom Out Reset image size

Table 5. Model Parameters and the Lensing Power Spectra Obtained from the 22 Intermediate-frequency Modes

Type	Weighting	N2	L	l[105]	δ θ	${{\rm{\Delta }}}_{\psi }({\mathrm{arcsec}}^{2})$	${{\rm{\Delta }}}_{\alpha }(\mathrm{arcsec})$	Δκ	χ2/dof	Rs /dof	dof
A	hom.	36	36	8.6 ± 2.6	$1\buildrel{\prime\prime}\over{.} {5}_{-0\buildrel{\prime\prime}\over{.} 35}^{+0\buildrel{\prime\prime}\over{.} 64}$	0.00070 ± 0.00004	0.0033 ± 0.0002	0.0079 ± 0.0005	1.2	0.12	18
A	hom.	36	42	7.4 ± 2.2	$1\buildrel{\prime\prime}\over{.} {75}_{-0\buildrel{\prime\prime}\over{.} 40}^{+0\buildrel{\prime\prime}\over{.} 75}$	0.00072 ± 0.00003	0.0030 ± 0.0002	0.0066 ± 0.0003	1.2	0.12	18

Note. They were obtained from the 22 intermediate-frequency modes, which are a subset of the 36 modes that were best-fitted to the ALMA data, MIR flux ratios, HST positions of galaxies, and VLBA positions of a jet component q. N² is the number of mode functions. L is the side length of a square at which the Dirichlet condition is imposed. l is the angular wavenumber in degrees, and δ θ is the corresponding angular wavelength. To obtain de-lensed images, the homogeneous weighting was used.

Download table as:  ASCIITypeset image

We summarize our results obtained from the source plane fit to the ALMA images as follows:

• 1.  
  Using a discrete Fourier expansion of potential perturbation δ ψ, we were able to fit the VLBA positions of lensed images of a radio core, HST positions of the centroids of the primary lensing galaxy G and object X (object Y), peak-subtracted ALMA continuum image at 340 GHz, and MIR flux ratios observed with the Subaru and Keck telescopes. Using the obtained model parameters, we were able to fit the VLBA positions of lensed images of radio-jet components using the traditional lens plane fit without changing the model parameters.
• 2.  
  The de-lensed source images show a bright spot centered at a radio core with a bipolar structure in the vicinity of the VLBA jet components.
• 3.  
  The best-fitted models show a complex mass distribution with four clumps near the quadruple images. One clump near image A2 may be associated with object Y. The detailed structure of the mass distribution depends on the choice of assumed model parameters that were fixed in fitting.
• 4.  
  The contribution to convergence from low-frequency modes is less than ∼0.4% of the background value.
• 5.  
  The range of measured convergence power within 1σ of the mean values at the two smallest angular scales l = (1.11 ± 0.07) × 10⁶ and l = (1.30 ± 0.08) × 10⁶ was Δ_κ = 0.021–0.028. The mean angular scale l ∼ 1.2 × 10⁶ of the two measurements corresponds to the effective Einstein radius b_G ∼ 11 of G. The power is significantly larger than those on larger angular scales >11. The ranges of measured astrometric shift and potential powers within 1σ of the two angular scales were Δ_α = 7–9 mas and Δ_ψ = 1.2–1.6 mas², respectively. The measured lensing powers at l ∼ 1.2 × 10⁶ were not so sensitive to the presence or absence of object Y.

As we have discussed, the effects of systematic errors due to limited sample of visibility data are significantly reduced in our partially nonparametric model fitting. However, residuals of systematic errors caused by the CLEAN deconvolution process or phase corruption may still affect the fitted models significantly. Therefore, we check one of our best-fitted model (Type A) using χ² fit in the visibility plane (Hezaveh et al. 2013, 2016b; Rybak et al. 2015; Spilker et al. 2016; Maresca et al. 2022). Direct fitting to the visibility data obtained by our Cycle 2 and 4 observations can test whether the observed astrometric shifts are due to perturbation by LOS structures/subhalos or systematic errors caused by side lobes and phase corruption.

Since our fitting formalism cannot determine the absolute fluxes of lensed images, we parameterize the overall amplitudes of the best-fitted point sources (cores p, q) and extended sources (jets r,s and dust) in the lens plane by multiplying constants a and b to the pre-fitted model visibilities of point and extended sources, respectively. In what follows, we use a Type A model that was fitted to the ALMA data with the magnification weighting (36 modes and L = 36). We describe the detailed procedure of fitting visibilities to the ALMA data in Appendix C.

As described in Section 6.2, perturbation by LOS structures/subhalos produces thin tangential arcs across a critical line. Therefore, it is likely that such a perturbation preserves the radial structure of extended source visibility components (Figure 34). Moreover, the amplitude of point-source visibilities is invariant with respect to rotation in the visibility plane. Thus, we consider that grids defined in the polar coordinates are suitable to compress the data to analyze the effects of potential perturbation efficiently.

As one can see in Figure 25, the ALMA visibilities averaged with polar grids with azimuthal separation δ θ = 90° are dominated by errors at uv distance $(=\sqrt{{u}^{2}+{v}^{2}})$ larger than ∼10,000 m that corresponds to the size of the synthesized beam. The extended components contribute to the visibilities more than the point-source components at distances smaller than ∼800 m, whereas the point-source components dominate the signal at distances larger than ∼800 m. Although the amplitudes of the total fitted model visibilities are comparable to the observed ones at distances ∼400–5000 m, we observe a slight excess in model visibilities at small distances ≲400 m possibly due to systematics in our CLEAN deconvolution process. Improvement in fitting with respect to no (null) model is more conspicuous for larger angular separations δ θ in which each grid has a larger number of samples (Figure 26). If δ θ is too small, much of the information of phase is lost, leading to a worse fit.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

For 1° ≲ δ θ ≲ 90°, our visibility fitting showed that the perturbed model fits the ALMA data better than the corresponding unperturbed smooth model (Figure 27). We found that the optimal value of azimuthal separation that gives the best fit is δ θ = 10°. This result suggests that the improvement by including Fourier modes of potential perturbation is not caused by systematics due to side lobes and phase corruption. We also found that the improvement is caused by both the extended and point-source components. In order to have the evidence of improvement due to the extended source components, we fitted model visibilities in which the point-source flux ratio of A1 to A2 is artificially fixed to be unity while the extended source components were intact. If the improvement is not caused by extended components, then we can expect that the model visibilities will not show any improvements. However, as shown in Figure 27, we found that the fit was improved to some extent. Therefore, we conclude that the fit to the extended source components was indeed improved.

Zoom In Zoom Out Reset image size

At δ θ = 10°, the coefficients of the point-source component and extended source component in the perturbed model were a = 1.8 ± 1.5 mJy and b = 0.42 ± 0.39. At δ θ = 90°, the corresponding values were a = 1.8 ± 0.8 mJy and b = 0.44 ± 0.19. The errors were obtained from a condition Δχ²/dof < 1. Thus the best-fitted values correspond to ∼20% and ∼60% decrease in overall amplitude with respect to the originally modeled intensity distribution of the point-source component and extended source component, respectively. The decrease in a is not statistically significant, but the significance of a decrease in b is at the ∼3σ level.

As we have seen in Section 5.2, our CLEAN deconvolution process gave a systematic boost in overall amplitudes of flux on large angular scales. Therefore, it can affect the model fit on large angular scales ≳07 (corresponding to a distance of ∼400 m). However, on small angular scales, especially for signals with large S/N, such systematic effects are expected to be small. The improvement of χ² fit due to the extended source components implies that the perturbation effect caused by LOS structures and subhalos is limited to intensity fluctuations on relatively small angular scales ≲07. The size of the image residual in the lens plane (Figure 19) in Section 6.2 supports this interpretation.

Thus, we conclude that our results in visibility fitting and mock analysis suggest that observed astrometric shifts are due to perturbation by LOS structures/subhalos rather than systematic errors caused by side lobes and phase corruption.

Based on the above discussions, the reconstructed potentials in the lens plane exhibit some differences depending on the choice of the center and side length L of a square at which the Dirichlet boundary condition is imposed. In order to scrutinize the effect of perturbation, particularly in the vicinity of object Y, we also performed a χ² fitting in the lens plane. We fitted the model to the positions of VLBA jet components p, q, r, and s, centroid of G and object X, and the MIR flux ratios of quadruple images with adjusting coefficients of the 22 intermediate-frequency Fourier modes and translation. ¹⁹ The positional errors are assumed to be 2 mas for q, 5 mas for p, r, s, and G, and 01 for X. The number of observed parameters is 4 × 2 × 4 + 2 × 2 + 3 = 39, and the number of fitting parameters is 22 + 2 + 8 = 32. We did not consider rotation of the potential.

If we conduct χ² fitting for the positions, significant discontinuity in the potential perturbation may occur at places farther from the position of lensed jet components, as the size of jets are much smaller than the lensed arc observed in the ALMA image. To avoid such discontinuity, we imposed an additional constraint on the smoothness of perturbation. To do so, we minimized χ² for the positions of G, X, and the VLBA jet components and MIR flux ratios plus the smoothing term R_s defined in Equation (10). We fixed the smoothing parameters δ_ψ0, δ_α0, and δ_κ0 to be the same or slightly smaller values obtained from the best-fitted models with the magnification weighting with L = 36 and N² = 36 modes. To test the smoothing effect, we considered two types of χ² fitting: with and without constraint on the smoothness of perturbation.

As shown in Table 6, the rms perturbations $\langle {\left(\delta \psi \right)}^{2}{\rangle }^{1/2}$, $\langle {\left(\delta \alpha \right)}^{2}{\rangle }^{1/2}$, $\langle {\left(\delta \kappa \right)}^{2}{\rangle }^{1/2}$ ²⁰ for fitting without constraint on smoothness are significantly larger than those for fitting with the constraint. Our results indicate that reconstructing the potential beyond the region of jet components is difficult if constraint on smoothness is not taken into account. The fit is slightly better for the model with L = 36 than that with L = 42. The obtained rms perturbations in the model with L = 36 and constraint on smoothness agree with those in the corresponding model with 36 Fourier modes obtained from the previous fits based on the ALMA image within 35%. Moreover, as shown in Figure 28, the fit to the VLBA positions of jet components p, q, and r in images A1 and A2 noticeably improved compared with the previous fit in the source plane using the ALMA data dominantly. Therefore, the obtained model may be significantly better in describing the perturbation in the vicinity of A2. As shown in Figure 29, the feature of potential perturbation δ ψ is similar to that obtained with L = 36, N² = 36 modes, and the magnification weighting (Figure 20).

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Table 6. Parameters, Minimized χ², Flux Ratios (Estimated at the Fitted Positions of q), and rms Perturbations in Type A Models Best Fitted to the MIR Flux Ratios, the HST Positions of Galaxies, and the VLBA Positions of Four Jet Components p, q, r, and s

L	δ ψ0	δ α0	δ κ0	χ2/dof	dof	A2/A1	B/A1	C/A1	${\chi }_{\mathrm{flux}}^{2}/\mathrm{dof}$	${\chi }_{\mathrm{VLBA}}^{2}/\mathrm{dof}$	${\chi }_{{\rm{X}}}^{2}/\mathrm{dof}$	${\chi }_{{\rm{G}}}^{2}/\mathrm{dof}$	$\langle {\left(\delta \psi \right)}^{2}{\rangle }^{1/2}$	$\langle {\left(\delta \alpha \right)}^{2}{\rangle }^{1/2}$	$\langle {\left(\delta \kappa \right)}^{2}{\rangle }^{1/2}$
3.6	0.0014	0.0053	0.0090	2.0	7	0.916	0.355	0.157	0.29	1.13	0.06	0.47	0.00097	0.0041	0.0092
3.6	∞	∞	∞	0.65	7	0.920	0.345	0.151	0.10	0.30	0.06	0.19	0.0031	0.0144	0.0346
4.2	0.00082	0.0051	0.0048	2.1	7	0.918	0.355	0.158	0.33	1.22	0.06	0.44	0.0011	0.0042	0.0084
4.2	∞	∞	∞	0.99	7	0.915	0.355	0.132	0.095	0.676	0.06	0.16	0.0028	0.0113	0.0238

Note. Only the 22 intermediate-frequency modes with translation were used for fitting. The parameters in the smooth model were fixed except for the position of an SIE+ES. L is the side length of a square at which the Dirichlet boundary condition is imposed. δ ψ₀, δ α₀, and δ κ₀ are smoothing parameters that control the rms values defined in the square region. χ² is the sum of ${\chi }_{\mathrm{flux}}^{2}$ for the MIR flux ratios, ${\chi }_{{\rm{X}}}^{2}$ for the HST position of X, ${\chi }_{{\rm{G}}}^{2}$ for the HST position of G, ${\chi }_{\mathrm{VLBA}}^{2}$ for the VLBA positions of four jet components. The rms perturbations $\langle {\left(\delta \psi \right)}^{2}{\rangle }^{1/2}$, $\langle {\left(\delta \alpha \right)}^{2}{\rangle }^{1/2}$, and $\langle {\left(\delta \kappa \right)}^{2}{\rangle }^{1/2}$ on the square region were obtained from the coefficients for the best-fitted 22 Fourier modes.

Download table as:  ASCIITypeset image

Interestingly, the best-fitted convergence perturbation δ κ indicates the presence of a clump in the vicinity of object Y as well as three clumps in the vicinity of image A1, B, and C. The distance between the local peak in the convergence and object Y is ∼03, which is smaller than the smallest fluctuation scale ∼09 of the fitted Fourier mode functions. Compared with the previous model in Inoue et al. (2017), the shape of the clump in the vicinity of Y is rounder. In the best-fitted models, a pair of clumps in the vicinity of B and a pair of clumps in the vicinity of A2 cause a shear perturbation δ γ at A2 and B, respectively. They probably result in an improvement in the fit to the MIR flux ratios and VLBA positions of jet components. Our results indicate that potential perturbations consisting of several halos are more realistic and robust compared with perturbations consisting of only one halo.

A faint continuum emission with a flux of 0.2–0.3 mJy at (R.A., decl.) = $({4}^{{\rm{h}}}{14}^{{\rm{m}}}37\buildrel{\rm{s}}\over{.} 818,5^\circ 34^{\prime} 42\buildrel{\prime\prime}\over{.} 810)$, in the north east of A2, was first reported by Inoue et al. (2017). We called it object Y. Using the same ALMA Cycle 2 data, Stacey & McKean (2018) pointed out that the emission disappears after self-calibration. To check the result, we added the data of our Cycle 4 (high-resolution) observations to the Cycle 2 (low resolution) data. For each data set of Cycle 2 and 4 data, we subtracted off the components of line emission and carried out phase-only self-calibration. Then we combined both of the data sets to obtain CLEANed images with various robust parameters. As shown in Table 7, with robust = 0, 0.5, we detected a faint emission with a peak flux density of 81.8, 114.5 μJy beam⁻¹ at the position of object Y. The statistical significances were 3.6σ, 3.8σ. To increase S/N, we also carried out imaging with robust = 0 using the full-band data (self-calibrated line-free and line channels) and detected faint emission with a peak flux density of 84.2 μJy beam⁻¹ at the position of object Y. The statistical significance is 3.7σ. Although the significances are not sufficiently high, as shown in Figure 30, the signals seem to be stable. In contrast, other faint spots with intensity <3.5σ are not stable. Their peak flux depends on the selected robust parameters and frequency. Note that the significance of object Y decreased to <3.0σ for the natural weighting. Thus, we cannot conclude the significance of the object Y.

Zoom In Zoom Out Reset image size

Table 7. Flux of Object Y Measured in CLEANed Images

	Line-free	Line-free	Full-band
Robust	0.5	0	0
rms errors [μJy beam−1]	22.9	30.4	22.6
Peak flux [μJy beam−1]	81.8	114.5	84.2
S/N [σ] at peak	3.6	3.8	3.7
Flux (>2σ) [μJy]	36	79	63
Peak ΔR.A. (J2000)	−1865	−1866	−1865
Peak Δdecl. (J2000)	−0116	−0116	−0118

Download table as:  ASCIITypeset image

In order to verify the weak emission from object Y, we performed visibility fitting. We used a Type A model that was best fitted to the ALMA, HST, Subaru, and VLBA data using the magnification weighting with L = 36. We added a Gaussian component at (−1865, − 0116) ²¹ in the J2000 coordinates in which the centroid of galaxy G is at (0,0). In the fitting, the flux of the Gaussian component was used as a free parameter as well as a and b that control the overall amplitudes of the pointlike and extended sources, but the position of the Gaussian source was fixed at the central position of object Y. The distance between object Y and the phase center (in the vicinity of q in A1) is $\sim 1^{\prime\prime}$, the corresponding baseline scale at ∼340 GHz is ∼40 m. The scale of the synthesized beam is 003, which corresponds to the baseline scale of ∼1500 m. Therefore, in order to retain the phase information of object Y, we needed to restrict the azimuthal separation of polar grids to $\delta \theta \lesssim \arctan (40/1500)=1\buildrel{\circ}\over{.} 5$. We plotted our result in Figure 31. The fitted flux values were 40–400 μJy and always positive. We also fitted our model to the full-band visibility data. Our fitting result showed that the fitting to the full-band data is worse than the line-free data (left panel in Figure 32). Since we did not include line components in the model, the result is not surprising. Interestingly, compared to the line-free data, the full-band data showed an enhanced improvement in fitting compared to the model without object Y (right in Figure 32). Since the S/N of emission from object Y is expected to be higher in the full-band data, the result is again not surprising. Thus, we were not able to exclude the possibility that the weak continuum emission is associated with object Y rather than systematic errors.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

However, it should be noted that the origin of the weak emission is still not confirmed. In order to confirm the weak emission, we need to carry out new ALMA observations at frequency ≳340 GHz with angular resolution ≲01 with sensitivity better than ∼10 μJy beam⁻¹.