Abstract
Ultralight bosons are a proposed solution to outstanding problems in cosmology and particle physics: they provide a dark-matter candidate while potentially explaining the strong charge-parity problem. If they exist, ultralight bosons can interact with black holes through the superradiant instability. In this work we explore the consequences of this instability on the evolution of hierarchical black holes within dense stellar clusters. By reducing the spin of individual black holes, superradiance reduces the recoil velocity of merging binary black holes, which, in turn, increases the retention fraction of hierarchical merger remnants. We show that the existence of ultralight bosons with mass 2 × 10−14 ≲ μ/eV ≲ 2 × 10−13 would lead to an increased rate of hierarchical black hole mergers in nuclear star clusters. An ultralight boson in this energy range would result in up to ≈60% more present-day nuclear star clusters supporting hierarchical growth. The presence of an ultralight boson can also double the rate of intermediate-mass black hole mergers to ≈0.08 Gpc−3 yr−1 in the local universe. These results imply that a select range of ultralight boson masses can have far-reaching consequences for the population of black holes in dense stellar environments. Future studies into black hole cluster populations and the spin distribution of hierarchically formed black holes will test this scenario.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
A number of extensions to the Standard Model of particle physics propose the existence of a theoretical ultralight boson with a mass between μ ∼ 10−33–10−10 eV (Arvanitaki et al. 2010; Arvanitaki & Dubovsky 2011; Ringwald 2013). These particles can provide solutions to outstanding problems in cosmology and fundamental particle physics such as by being viable candidates for dark matter (Hu et al. 2000; Jaeckel & Ringwald 2010; Hui et al. 2017) or solving the strong charge-parity problem (Peccei & Quinn 1977a, 1977b; Weinberg 1978). While ultralight bosons are not expected to strongly interact with particles from the Standard Model (Kim 1979; Shifman et al. 1980; Dine et al. 1981), the weak equivalence principle requires them to gravitate in a similar manner to visible matter (Detweiler 1980).
If an ultralight bosonic wave exists in the vicinity of a spinning black hole, the wave can become gravitationally bound to the black hole. The bosonic field may be amplified by the extraction of rotational energy from the black hole through a process known as superradiance (Zel'Dovich 1971; Press & Teukolsky 1972; Zel'Dovich 1972; Bekenstein 1973; Bekenstein & Schiffer 1998; Brito et al. 2015, 2020a). Superradiant amplification of the bosonic field can be unstable, leading to the exponential growth of the bosonic wave (Press & Teukolsky 1972), forming a macroscopic quantum object, or boson cloud (e.g., Balakumar et al. 2020). This superradiant instability occurs most rapidly when the Compton wavelength of the particle is comparable to the outer horizon radius of a spinning black hole, and only ceases when the angular frequency of the black hole's rotation equals the frequency of the bosonic wave (Bekenstein 1973; Bekenstein & Schiffer 1998; Arvanitaki et al. 2010; Brito et al. 2015). The final astrophysical system, following unstable black hole superradiance, is a lighter black hole with a reduced spin, surrounded by a macroscopic boson cloud (Arvanitaki & Dubovsky 2011; Brito et al. 2017a; Arvanitaki et al. 2017). This matter configuration can also lead to long-lasting, nearly monochromatic gravitational-wave radiation from the rotation of the boson cloud–black hole system (Yoshino & Kodama 2014), often referred to as a continuous gravitational-wave signal.
Searches for all-sky nearly monochromatic gravitational waves from ultralight boson clouds around black holes (Arvanitaki et al. 2015, 2017) have found no evidence for ultralight bosons and exclude ultralight boson masses from 2 × 10−13–2.5 × 10−12 eV in the Milky Way under various Galactic black hole population assumptions (Dergachev & Papa 2019; Palomba et al. 2019; Zhu et al. 2020; Abbott et al. 2021d). Directed searches for continuous waves from ultralight boson clouds around black hole merger remnants have not yet been undertaken because the signal is likely too weak to observe with current observatories (Isi et al. 2019; Sun et al. 2020). In addition, nondetections of an incoherent stochastic background from the continuous-wave emission have placed tentative constraints on boson masses of (2–3.8) × 10−13 eV given particular assumptions about the black hole formation spin distribution (Brito et al. 2017b; Tsukada et al. 2019, 2021).
Furthermore, by studying the spins of the population of resolved binary black hole mergers, constraints exclude boson masses between (1.3–2.7) × 10−13 eV assuming negligible boson self-interactions (Ng et al. 2021a, 2021b). Other observations of radial velocities and photometric data from star–black hole binaries (e.g., Mehta et al. 2020; Baryakhtar et al. 2021), particularly Cygnus X-1 (Iorio 2008; Orosz et al. 2011; Reid et al. 2011; Middleton 2016), have excluded the presence of ultralight bosons in different regions of the boson-mass parameter space. Ultimately, there is no strong evidence yet for either the existence or absence of ultralight bosons.
Details regarding the formation of the merging binary black holes detected by LIGO/Virgo are uncertain. A number of possible formation mechanisms have been proposed including isolated massive stellar binaries (Ivanova et al. 2013; de Mink & Mandel 2016; Mandel & de Mink 2016; Marchant et al. 2016; Giacobbo & Mapelli 2018), the Lidov–Kozai mechanism in hierarchical triples/quadruples (VanLandingham et al. 2016; Silsbee & Tremaine 2017; Hoang et al. 2018; Martinez et al. 2021), and dynamical formation in dense stellar environments like globular clusters and nuclear star clusters (Zwart & McMillan 2000; Portegies Zwart & McMillan 2002; Rodriguez et al. 2015). Dynamical channels have gained significant recent interest because the growing number of massive black hole binary mergers detected by LIGO/Virgo (such as GW190521; Abbott et al. 2020a, 2020b; Gayathri et al. 2020; Romero-Shaw et al. 2020) are expected to be difficult to form through standard isolated binary formation scenarios (Abbott et al. 2020b; Holgado et al. 2021). In dense stellar clusters, the merger products of binaries comprised of first-generation (1G) black holes can be retained in their host cluster postmerger and thus can potentially form new binaries and merge again, leading to mergers comprised of second-generation (2G), and higher, black holes (Zwart & McMillan 2000; Miller & Lauburg 2009; Downing et al. 2010; Rodriguez et al. 2015; Antonini & Rasio 2016; Rodriguez et al. 2016; Petrovich & Antonini 2017; Arca-Sedda & Gualandris 2018; Fragione & Kocsis 2018; Rodriguez et al. 2018; Antonini et al. 2019; Kremer et al. 2020a). Whether or not a merger remnant is retained depends primarily on the velocity kick (which in turn depends primarily upon the mass ratio and component spins of the initial merger) attained by the merger product during the merger process (Antonini et al. 2019; Gerosa et al. 2020). Thus, given that the superradiance process affects directly the spin of black holes, superradiance may plausibly play an important role in the hierarchical merger process in dense star clusters: by decreasing black hole spins through superradiance, the gravitational-wave recoil velocities are reduced (Campanelli et al. 2006, 2007a; González et al. 2007a; Campanelli et al. 2007b; González et al. 2007b; Lousto et al. 2010; Lousto & Zlochower 2013; Varma et al. 2019). Lower recoil velocities lead to a higher retention fraction of binary black hole merger remnants (Merritt et al. 2004; Varma et al. 2020), and subsequent enhancement of hierarchical black hole growth as a result (Rodriguez et al. 2018; Antonini et al. 2019; Rodriguez et al. 2019).
In general, hierarchical black hole growth is thought to be enabled most easily in the most massive star clusters with the highest escape velocities (Antonini et al. 2019). A number of recent studies have examined black hole dynamics in these clusters (Antonini et al. 2019; Rodriguez et al. 2019; Kremer et al. 2020b; Mapelli et al. 2021; Martinez et al. 2021), showing the details of hierarchical black hole growth are sensitive to a number of uncertain features including the mass and natal spin distribution of the black holes and the cluster birth properties. Of course, decoupling these uncertainties in the underlying black hole population from the uncertainties pertaining to the superradiance process is not straightforward. However, as the number of detections of merging binary black holes grows in the coming years and decades, increased constraints upon the underlying black hole formation channels may enable such studies.
The remainder of the manuscript is structured as follows. In Section 2, we discuss the theory of black hole superradiance in the context of scalar bosons and its impact on individual black holes. 6 We summarize our semi-analytic model for studying black hole mergers in dense star clusters (based on Antonini et al. 2019), in Section 3. We present results from cluster simulations in relation to both individual clusters and the population as a whole in Section 4. Finally, we outline the implications of superradiance for recently observed black hole mergers, and the possibility for the detection of ultralight bosons in this boson-mass regime in Section 5.
2. Black Hole Superradiance
In this section we summarize the key expressions from Brito et al. (2020a) to provide the relevant theory for including the effects of ultralight bosons in cluster simulations. We work with the analytic approximations for the evolution of boson clouds around spinning black holes (Ternov et al. 1978; Detweiler 1980; Baryakhtar et al. 2017), as opposed to the coupled differential equations governing the black hole–boson cloud system assuming quasi-adiabatic evolution (Brito et al. 2015). Though these approximations are accurate in the limit α ≲ 0.1, the errors are insignificant when extrapolated (Pani et al. 2012).
2.1. The Superradiant Condition
The superradiant condition is simply that the boson's angular frequency, ω = μ/ℏ, must satisfy (Bekenstein 1973; Brito et al. 2020a)
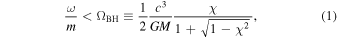
where m is the magnetic quantum number corresponding to a specific boson cloud mode and ΩBH is the angular frequency of the black hole's outer horizon (Teukolsky 2015). Furthermore, the black hole's angular frequency is a function of the its mass, M, dimensionless spin, χ, and dimensionless outer radius, 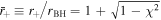 , where rBH = GM/c2 and where the characteristic black hole length scale is half the Schwarzschild radius. The energy eigenstates of the boson cloud take a similar form to those of a hydrogen atom, and are denoted by radial n, orbital l, and magnetic quantum numbers (Ternov et al. 1978; Detweiler 1980).
, where rBH = GM/c2 and where the characteristic black hole length scale is half the Schwarzschild radius. The energy eigenstates of the boson cloud take a similar form to those of a hydrogen atom, and are denoted by radial n, orbital l, and magnetic quantum numbers (Ternov et al. 1978; Detweiler 1980).
To highlight this comparison, we define the effective fine-structure constant for the "black hole atom":
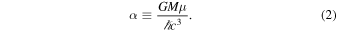
Large values of α lead to significant growth of the boson cloud. If the inequality in Equation (1) is satisfied, the boson cloud extracts rotational energy from the black hole, leading it to spin down. Unstable growth of the boson cloud ceases when the angular frequency of the bosonic wave equals mΩBH.
In order to incorporate the effect of superradiance, we compute the final mass and spin of a black hole according to Equation (1) (Brito et al. 2017a; Isi et al. 2019):
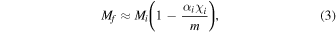
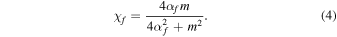
Here the subscripts i and f refer to the initial and final states of the boson cloud–black hole system, respectively, if the boson cloud is given enough time to saturate a given mode. However, the cloud saturates fully only if  . Otherwise the cloud does not grow appreciably during the lifetime of the black hole.
. Otherwise the cloud does not grow appreciably during the lifetime of the black hole.
2.2. Superradiance Timescales and Evolution
The occupation number of a given energy state grows exponentially at the rate (Ternov et al. 1978; Detweiler 1980; Baryakhtar et al. 2017)
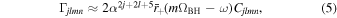
where Cjlmn is a dimensionless factor dependent on the quantum state inhabited by the ultralight bosons, and j is the total angular momentum quantum number. In the case of scalar ultralight bosons, j = l, and (Ternov et al. 1978; Detweiler 1980)
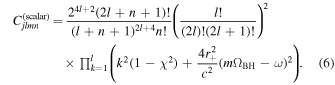
The growth rate of the occupation number can be used to approximate the timescale for the size of the cloud to grow by one e-fold, often known as the instability timescale.
Typically, the size of the boson cloud saturates at ∼180 e-folds of the instability timescale (see Equation (14) from Baryakhtar et al. 2017), which we use to compute an approximate growth timescale around a black hole (Arvanitaki et al. 2010; Arvanitaki & Dubovsky 2011; Baryakhtar et al. 2017; Ng et al. 2021a):
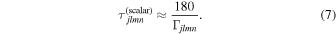
The growth timescale scales as
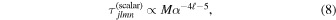
where it is clear that when α ≪ 0.1, the instability growth rate is greatly reduced (Brito et al. 2015).
Finally, due to the greatly differing timescales between states, the mode which determines the final spin of the black hole is the mode with the lowest final spin that grows within the age of the black hole, or evolution timescale, τevol (e.g., see Figure 1 in Ng et al. 2021a and Figure 3 in Baryakhtar et al. 2017). Motivated by the strong fine-structure constant dependence, and the associated strong mass dependence, the quasi-adiabatic differential equations governing the evolution of the black hole–boson cloud system can be largely ignored. We consider a black hole to have undergone superradiance only if its age exceeds the growth timescale of the fastest growing mode. For the remainder of this manuscript, we focus on the first three l = m = 1, 2, 3, n = 0, states.
An important corollary of Equations (4)–(7) is that there are regions of the mass–spin parameter space, also known as the Regge plane, where a black hole cannot exist if an ultralight boson is present (Arvanitaki & Dubovsky 2011; Brito et al. 2015, 2017a). These exclusion regions are strongly dependent of the boson's mass and the evolution timescale of the black hole population. In Figure 1, we present the exclusion regions as governed by the first three l = m = 1, 2, 3, n = 0, energy eigenstates over the black hole mass range relevant for hierarchical growth from stellar-mass black holes. Each m corresponds to a particular "bump" in the excluded region, with the m = 1 mode contributing at lower black hole masses. Furthermore, increasing the evolution timescale of the systems results in the growth of boson clouds around lower mass black holes.
Figure 1. Exclusion regions for black holes in the presence of three different scalar ultralight bosons, with masses 10−13, 3 × 10−13, and 10−14 eV (see Figure 1 from Brito et al. 2017a). The darker-colored regions bounded by the solid curves correspond to black hole mass–spin parameter space within which any black hole would be spun down via superradiance after τevol = 10 Myr. Since binary black hole merger delay time distribution has little support for systems merging within 10 Myr of formation (e.g., Britt et al. 2021), we expect all black holes to allow for superradiant cloud growth for at least 10 Myr. Therefore, the observation of a black hole within the darker region of the parameter space can rule out some range of boson mass. The lighter region bounded by the dashed curves corresponds to when the black holes are given 10 Gyr to evolve.
Download figure:
Standard image High-resolution image3. Semi-analytic Cluster Model
To model the evolution of dense stellar clusters such as nuclear star clusters, we follow Antonini et al. (2019), which applies Hénon's principle (Hénon 1975) to simulate the evolution of dense stellar environments. In this section, we briefly summarize the key components of the cluster model and the evolution of the cluster's black hole population. Please refer to Appendix A for the full details of the model.
3.1. Evolution of Cluster Properties
To model the global properties of a cluster, we assume the heating rate from black hole binaries in the core of the cluster balances the energy flow into the whole cluster, known as Hénon's principle (Hénon 1961, 1975; Gieles et al. 2011; Breen & Heggie 2013; Kremer et al. 2019). The half-mass–radius, heating rate, and escape velocity of the cluster evolve as
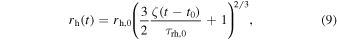
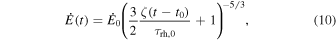
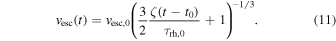
Here t0 is the time at which the first black holes begin to heat the cluster, and ζ ≃ 0.1 (Gieles et al. 2011; Alexander & Gieles 2012) is a dimensionless factor. The initial half-mass–radius, heating rate, and escape velocity are dependent only on the cluster mass, Mcl, and initial density, ρh,0,
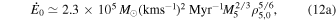
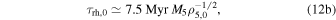
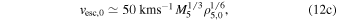
where M5 ≡ Mcl/105
M⊙ and ρ5,0 ≡ ρh,0/105
M⊙ pc−3, and  . All the quantities are dependent on only the initial density of the cluster and the cluster mass.
. All the quantities are dependent on only the initial density of the cluster and the cluster mass.
3.2. Evolving the Black Hole Population
Within our cluster model, we must first create a 1G black hole population. 1G black holes' masses are assumed to follow the inferred Power Law + Peak model (Talbot & Thrane 2018) from the second gravitational-wave transient catalog from the LIGO/Virgo Collaboration (Abbott et al. 2021a), with an additional strict mass cutoff at 45 M⊙. This model is a combination of a power-law describing low-mass black holes, and a Gaussian peak at higher masses motivated by the prediction of a pair-instability supernova upper-mass gap precluding the formation of black holes with masses between ∼45 and ∼130 M⊙ (Barkat et al. 1967; Fryer et al. 2001; Heger & Woosley 2002; Belczynski et al. 2016; Spera & Mapelli 2017; Stevenson et al. 2019).
All 1G black holes are considered to be initially nonspinning, motivated by studies which indicate that isolated black holes are likely to form with small spins (χ ≲ 0.01; Fuller & Ma 2019). The total mass of the 1G black holes within the cluster is fixed to 2% of the cluster mass (Löckmann et al. 2010; Antonini et al. 2019; Kremer et al. 2020b). Additionally, each black hole is initialized with a natal supernova kick velocity (Fryer & Kalogera 2001; Hobbs et al. 2005), though this has a minimal effect on the initial population. Finally, the black holes are deposited within the cluster at the initial half-mass–radius, rh,0. Each black hole is expected to settle within the core of the cluster on the dynamical friction timescale, τdf(rh,0, t0) (Binney & Tremaine 2011),
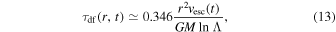
where 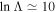 and assumes the King (1966) cluster model to relate the cluster's velocity dispersion to escape velocity.
and assumes the King (1966) cluster model to relate the cluster's velocity dispersion to escape velocity.
Once the first black holes settle within the cluster's core, a black hole binary might form through dynamical three-body interactions (Ivanova et al. 2005; Morscher et al. 2015; Park et al. 2017). We let only one black hole binary exist at any one time such that it dominates the heating of the cluster. The binary is formed according to a mass distribution given by 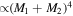 (O'Leary et al. 2016). The required heating rate of the cluster is balanced with the loss of energy from the binary in the core of the cluster (Antonini et al. 2019; Kremer et al. 2019). The timescale during which dynamical interactions dominate the energy flow of the cluster is given by
(O'Leary et al. 2016). The required heating rate of the cluster is balanced with the loss of energy from the binary in the core of the cluster (Antonini et al. 2019; Kremer et al. 2019). The timescale during which dynamical interactions dominate the energy flow of the cluster is given by
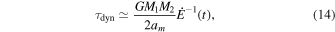
where 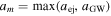 . Here aej is the binary separation at which the binary is ejected, and aGW is the separation at which gravitational-wave radiation dominates. Since we are focusing on denser stellar environments, the majority of binary systems are likely to merge within the cluster rather than be ejected. The ejection of the interloper black holes is also incorporated (see Appendix A.3). We calculate the separation at which gravitational-wave radiation dominates by equating the separation evolution due to dynamical interactions and gravitational-wave emission (Peters 1964). We compute the timescale for the binary to merge due to gravitational-wave radiation as
. Here aej is the binary separation at which the binary is ejected, and aGW is the separation at which gravitational-wave radiation dominates. Since we are focusing on denser stellar environments, the majority of binary systems are likely to merge within the cluster rather than be ejected. The ejection of the interloper black holes is also incorporated (see Appendix A.3). We calculate the separation at which gravitational-wave radiation dominates by equating the separation evolution due to dynamical interactions and gravitational-wave emission (Peters 1964). We compute the timescale for the binary to merge due to gravitational-wave radiation as 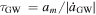 .
.
At this point in the binary's evolution, we modify the black holes' masses and spins according to Equations (4) and (3) to incorporate the effects of superradiance, ensuring each black hole's age exceeds to the growth timescale of the boson cloud. Our treatment of superradiance does not consider the impacts of dense cluster environments or binary systems on the spin-down process. It might be expected that close, hyperbolic encounters within the cluster could tidally disrupt the boson cloud. However, we can estimate the typical close-encounter timescale (Malmberg et al. 2007; Binney & Tremaine 2011) for clusters considered within this manuscript. To estimate the possibility of tidal disruption of the boson clouds, we note that the boson cloud radius is rcloud ≳ α−2 rBH (Arvanitaki et al. 2010; Arvanitaki & Dubovsky 2011). Furthermore, since the boson cloud growth follows Equation (8), we are only interested in systems where α ≳ 10−2 so that the black hole can sufficiently spin down. Therefore, we can consider the limiting case where α ∼ 10−2 and rcloud ∼ 104 rBH. We assume typical values of a half-mass–radius of 1 pc, and a cluster mass of 107 M⊙. Under these assumptions, a 50 M⊙ black hole would undergo a close encounter on the timescale of ∼400 Myr. This is longer than both the typical timescale required for the majority of black holes to be spun down via superradiance (see Figure 1; Arvanitaki et al. 2010; Arvanitaki & Dubovsky 2011; Baryakhtar et al. 2017; Ng et al. 2021a) and the typical timescale of the black hole forming a binary (Binney & Tremaine 2011; Antonini et al. 2019). Furthermore, systems with higher values of α will have less extended boson clouds, thereby reducing the possibility of tidal disruption. Therefore, close encounters within the dense stellar environment are very unlikely to impact the spin-down process.
There is also the possibility that interactions between the boson clouds and the binary system can influence the evolution of the black hole–boson cloud system (Arvanitaki & Dubovsky 2011; Baumann et al. 2019; Berti et al. 2019; Zhang & Yang 2019; Baumann et al. 2020; Ng et al. 2021a). Of particular interest are the phenomena of "floating orbits" (Zhang & Yang 2019; Baumann et al. 2020) and angular momentum transfer due to level mixing (Baumann et al. 2019; Berti et al. 2019; Zhang & Yang 2020). Floating orbits arise from a driven transition between a growing and decaying mode of the boson cloud, which can increase the angular momentum of the orbiting black holes (Zhang & Yang 2019). However, it has been shown that such orbits exist for up to ∼100 yr for the intermediate mass ratio systems which arise during hierarchical black hole growth (see Figures 16 and 17 in Baumann et al. 2020). This is a negligible correction to the dynamical merger timescales considered above. In addition, the impact of cloud disruption during the binary black hole merger event might spoil the statement that black holes possess low spins prior to merging. However, studies have shown that cloud disruption might actually lead to reduced black hole spin (Baumann et al. 2019; Berti et al. 2019; Zhang & Yang 2019; Baumann et al. 2020; Zhang & Yang 2020). Due to the selection rules governing the behavior of a black hole–boson cloud system, typically boson cloud states with negative angular momentum fall in toward the black hole (Zhang & Yang 2020; Ng et al. 2021a), which leads to the further reduced spin. Ultimately, there is rich phenomenology associated with the behavior of binary systems in the presence of ultralight bosons. However, their impact on hierarchical growth appears minimal in the regime considered and are therefore ignored for the remainder of the study.
3.3. Black Hole Merger Remnants
A vital component to the semi-analytic model is the computation of the black hole merger remnant properties. In particular, due to the conservation of linear momentum, the final remnant black hole receives a kick from the anisotropic emission of gravitational waves (Merritt et al. 2004; Campanelli et al. 2006, 2007a; González et al. 2007a; Campanelli et al. 2007b; González et al. 2007b; Lousto et al. 2010; Lousto & Zlochower 2013; Varma et al. 2019, 2020). This recoil velocity, vk , determines whether the remnant remains in the core, is ejected from the core and has to settle through dynamical friction, or is ejected from the cluster entirely. We utilize the Precession code (Gerosa & Kesden 2016) to determine the final mass (Barausse et al. 2012), spin (Barausse & Rezzolla 2009), and recoil velocity of the remnant black hole. The details of the calculation of the recoil velocity are outlined in Appendix B.
The salient features of the recoil velocity calculation for the study of hierarchical mergers arise from black hole binary spins and mass ratios. It has been found that the largest kicks are typically a result of special spin configurations known as superkicks (Campanelli et al. 2007a; González et al. 2007a) and hang-up kicks (Lousto & Zlochower 2011, 2013). These spin configurations can lead to recoil velocities up to ∼5000 km s−1. Conversely, nonspinning binaries typically lead to the smallest recoil velocities. For example, the largest recoil velocity a nonspinning binary can produce is only ∼170 km s−1 for q ≃ 1/3 (González et al. 2007b). In order to quantify the binary's total spin and explore its contribution to hierarchical mergers, we introduce a mass-weighted spin magnitude:
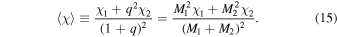
After calculating the properties of the merger remnant, we determine if or where it should be reintroduced into the black hole population. If the recoil velocity exceeds the escape velocity of the cluster at the time of the merger, vk ≥ vesc(tmerge), then the remnant is ejected from the cluster. Alternatively, if vk < vesc(tmerge), the remnant is retained and placed at a radius (Antonini et al. 2019)
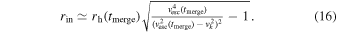
If rin < rh(tmerger)/10, a conservative estimate of the core radius (Hurley 2007; Madrid et al. 2012), then the remnant black hole remains in the core. Otherwise, the binary must first settle in the core due to dynamical friction (see Equation (13)). After the merger remnant has either been ejected (over a period τdyn) or retained (over a period of τdyn + τGW) either in the core or in the cluster, we repeat the process outlined above by generating a new black hole binary to support the heating rate condition. The simulation is concluded when either only one black hole remains, too few black holes remain for dynamical hardening, or 13 Gyr have passed.
4. Results
We create a grid of ≈1800 simulations in the space of cluster mass Mcl, initial density ρh,0, and boson mass μ. We select log-uniformly spaced cluster masses between 106 and 2 × 108 M⊙, initial densities between 103 and 107 M⊙ pc−3, and boson masses between 5 × 10−15 and 5 × 10−13 eV. We run the simulations with and without ultralight bosons. 7
4.1. Individual Cluster Simulations
In Figure 2 we plot the total mass of the binary black hole system as a function of the coalescence time. These merger evolution tracks are plotted for four different ultralight boson masses (and for the case of no ultralight boson) using two different initial cluster densities. The shape of the points contained to retained (blue squares) or ejected (red crosses) binary systems. Different initial densities lead to different escape velocities and dynamical friction timescales. The denser cluster (left), with an initial density ρh,0 = 1.9 × 106 M⊙ pc−3, has an initial escape velocity vesc,0 = 391.8 km s−1, whereas the less dense cluster (right) only has an initial escape velocity vesc,0 = 224.2 km s−1.
Figure 2. Total binary black hole merger mass vs. the coalescence time of the merger from simulations with Mcl = 1.1 × 107 M⊙ and two different initial densities. From top to bottom, each row is an increasingly large boson mass except the bottom row, which shows the results when no boson is present. The two columns show how the results change for different initial densities. The shape of the points corresponds to whether the merger remnant was ejected (red cross) or retained (blue square). Two distinct phases of dynamical interactions and hierarchical black hole growth are present. The denser cluster (left) allows for all clusters to dynamically form heavy black holes (M > 103 M⊙). The inclusion of ultralight bosons with μ = 4.1 × 10−14 eV leads to hierarchical black hole growth in less dense clusters where growth does not occur under normal circumstances (right). The fractions of simulations leading to hierarchical black hole growth (fhier) are also stated.
Download figure:
Standard image High-resolution imageThere are two distinct epochs during a black hole population's evolution in a cluster. Initially, the black hole population undergoes random, dynamical interactions which lead to mergers and formation of 2G or third-generation (3G) black holes. Since the black hole binaries formed early within the cluster have similar total masses, the chance any two black holes become a binary is small, though heavier black holes are slightly more likely to form binaries (O'Leary et al. 2016). This epoch is categorized by remnant masses typically less than ∼200 M⊙ in the early cluster evolution. Eventually, however, one black hole tends to become sufficiently massive to dominate, leading to the second evolutionary phase. Since the heavy black hole will primarily form binaries with much smaller black holes, the resulting small mass ratio can lead to significantly reduced gravitational-wave recoil velocities (González et al. 2007b). This black hole therefore seeds hierarchical growth in the cluster. This period of evolution is seen by a track of increasing total binary mass with the merger coalescence time in Figure 2.
In the left column of Figure 2, we show the binary black hole mergers which occur in a cluster simulation with Mcl = 1.1 × 107 M⊙ and ρh,0 = 1.9 × 106 M⊙ pc−3. We see that all simulations are able to support hierarchical black hole growth. However, the existence of an ultralight boson at some masses can change the time at which hierarchical growth starts to occur. This is due to the spin down of 2G+1G and 2G+2G black hole mergers (see Figure 1) when bosons of masses ∼2 × 10−14–2 × 10−13 eV exist, helping retain more merger remnants. By retaining more massive black holes, the formation of a hierarchical black hole seed is more likely to occur earlier in the simulation. The simulation result in the top panel (μ = 7.6 × 10−15 eV) is similar to the case when no ultralight boson exists because the boson cloud instability growth rate is significantly reduced for stellar-mass black holes. However, there is some indication of spin-down from superradiance in the high-mass, hierarchical-growth regime.
On the right of Figure 2, we show the results from a cluster with Mcl = 1.1 × 107 M⊙ and ρh,0 = 6.6 × 104 M⊙ pc−3. Only one particular ultralight boson, with a mass μ = 4.1 × 10−14 eV, can facilitate hierarchical black hole growth. The clear difference between this simulation and the remaining four is that the binary systems with a total mass ∼80–200 M⊙ have mass-weighted spins 〈χ〉 ≲ 0.15. The important result from these individual simulations is that the presence of ultralight bosons can impact what cluster properties support hierarchical growth. For the remainder of the manuscript, we use the scenario where μ = 4.1 × 10−14 eV as our best-case scenario example.
In Figure 3, we plot the distributions of the binary black hole merger properties for all 2G+2G and 2G+1G mergers for cluster simulations presented in Figure 2. We use the full set of 30 simulations for each set of initial cluster parameters, and show the distributions for the μ = 4.1 × 10−14 eV, 2.2 × 10−13 eV and no ultralight boson simulations. The left plot shows the distributions in the case where all clusters lead to hierarchical growth. The bulk of the kick-velocity distributions lay below the initial escape velocity, vesc,0, of the cluster. Crucially, in the μ = 4.1 × 10−14 eV results (orange), we see two spin populations corresponding to systems which have undergone substantial superradiance (〈χ〉 ≲ 0.15), and a population which has not (〈χ〉 ∼0.3–0.45). The low-spin population is entirely retained within the cluster.
Figure 3. Distributions of the total binary black hole mass, mass-weighted spin (〈χ〉), and gravitational recoil velocity (vk ) for all binaries forming a third-generation (3G) black hole, two second-generation black holes (2G+2G) and second-generation and first-generation (2G+1G) merger events. The black lines correspond to the initial escape velocity of the cluster, vesc,0. The distributions correspond to six panels in Figure 2, when μ = 4.1 × 10−14, 2.2 × 10−13 eV, and no ultralight boson is present. Of these ultralight boson masses, only μ = 4.1 × 10−14 eV (orange) facilitates hierarchical black hole growth in both example clusters considered. Therefore, black holes spinning down due to superradiance directly leads to a higher retention fraction of black holes and consequently a higher chance of hierarchical growth.
Download figure:
Standard image High-resolution imageIn the right panel, only the μ = 4.1 × 10−14 eV (orange) distribution corresponds to a system capable of hierarchical growth. In these results, the majority of black holes are spun down to the low-spin population, and are still retained. Conversely, in the cases of μ = 2.2 × 10−13 eV and no ultralight boson, the black holes are not spun down enough to reduce the velocity distribution significantly. Therefore the majority of 2G black holes are ejected upon merging with another black hole.
4.2. Hierarchical Growth in Present-day Clusters
For each set of simulations with a given ultralight boson mass and cluster properties, we compute the fraction of the repeated 30 simulations which result in the formation of a black hole with a mass ≥1000 M⊙. 8 We denote this fraction fhier (Antonini et al. 2019). We use fhier as a proxy for the fraction of simulations leading to hierarchical growth within the cluster. We compute the region within which more than 50% of the simulations for a given initial effective radius, Reff, and cluster mass undergo hierarchical growth, i.e., fhier > 0.5. We compare the region of the effective radius–cluster mass (Reff − Mcl) parameter space where clusters support hierarchical growth with a population of globular clusters (Baumgardt et al. 2019) and nuclear star clusters (Georgiev et al. 2016). For the nuclear star cluster population, we plot the 152 nuclear star clusters with cluster mass uncertainty less than an order of magnitude, and effective radius estimates with only positive radius support. However, we use the full population of 228 nuclear star clusters from Georgiev et al. (2016) in future calculations. These results are presented in Figure 4 for μ = 4.1 × 10−14 eV (orange), as well as simulations where no ultralight boson is present (hatched blue).
Figure 4. Effective radius (Reff)–cluster mass (Mcl) parameter space that can support hierarchical growth, and present-day populations for globular clusters (Baumgardt et al. 2019) and nuclear star clusters (Georgiev et al. 2016). The solid orange and hatched blue contours correspond to the regions of the parameter space where more than 50% of cluster simulations at a given point can support hierarchical growth if μ = 4.1 × 10−14 eV or if no ultralight boson exists, respectively. We assume the effective radius is approximately given by the half-mass–radius as Reff ≃ 0.75rh. Any observed cluster within this contour is capable of undergoing hierarchical black hole growth now or in the future. The dashed contours indicate the evolved state of the bounded region after 10 Gyr. A cluster under the dashed contours might have supported hierarchical growth in the two scenarios.
Download figure:
Standard image High-resolution imageThe lower-right region, corresponding to denser and heavier clusters, unsurprisingly supports hierarchical growth. Our bounds are similar to those presented in Antonini et al. (2019) for the scenario with no ultralight boson, though here we empirically compute the region of parameter space supporting hierarchical growth. The inclusion of superradiance extends the region within which hierarchical growth is supported further into the astrophysical population of clusters, though it still does not permit hierarchical growth in globular clusters. Importantly, the orange contour includes a higher percentage of the nuclear star cluster population. Furthermore, the highlighted contour region only corresponds to the initial conditions, whereas it is inevitable that the clusters have evolved since their formation. To illustrate this, we evolve clusters with initial conditions along the contour to an age of 10 Gyr, shown by the dashed curves in Figure 4. A larger proportion of the nuclear star cluster population is contained under this contour. However, given that the age of present-day clusters is not well known, it is difficult to interpret whether hierarchical growth might have previously occurred in observed clusters.
In order to interpret the significance of the difference between the hierarchical-growth regions for simulations with and without superradiance, we compute the fraction of nuclear star clusters from Georgiev et al. (2016), which presently would support hierarchical growth, fNSC, i.e., those nuclear star clusters that lie within the contours in Figure 4. See Appendix C for details about the calculation and uncertainty estimation. As an example, for the contours presented in Figure 4, the fraction of present-day nuclear star clusters which can sustain hierarchical growth is ≈4.5% in the absence of ultralight bosons and ≈7% in the presence of a boson with a mass of μ = 4.1 × 10−14 eV. The fraction in the absence of ultralight bosons is less than the value presented in Antonini et al. (2019 ; fNSC ≃ 10%) as we empirically generate the contour from simulations, as well as explicitly integrate under it to calculate fNSC. The values of fNSC for different boson masses are presented in Figure 5. The fraction peaks at μ ≃ 4.1 × 10−14 eV, corresponding to a ≈60% increase in the number of clusters capable of supporting hierarchical growth presently. There is also an increased number of clusters currently capable of supporting hierarchical growth if bosons with masses μ ∼ 2 × 10−14–2 × 10−13 eV exist.
Figure 5. The fraction (and 3σ uncertainty) of observed nuclear star clusters capable of supporting present-day hierarchical black hole growth under the assumption of the existence of different ultralight bosons. The fraction is computed from the expression in Equation (C1), using contours such as those presented in Figure 4. In the absence of ultralight bosons, we find only ≈4.5% of observed nuclear star clusters from Georgiev et al. (2016) can support hierarchical growth (black interval shown), whereas bosons with masses of μ ∼ 2 × 10−14–2 × 10−13 eV lead to an increased fraction (shown in orange).
Download figure:
Standard image High-resolution image4.3. Synthetic Present-day Black Hole Population
To understand the distribution of binary black hole mergers in present-day clusters, we generate a synthetic population, which we evolve to a similar state as the observed population. We generate cluster masses from 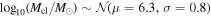 and initial densities from
and initial densities from 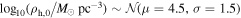 . Each cluster is evolved to an age drawn at random from
. Each cluster is evolved to an age drawn at random from 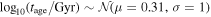 . These distributions are chosen such that the evolved population visually appears similar to the observed nuclear star cluster properties from Georgiev et al. (2016). We evolve 4.8 × 104 clusters with properties drawn randomly from these distributions, for scenarios where μ = 4.1 × 10−14 eV and no ultralight boson exists. The final merger is then included in the merger population. The individual black hole properties from both scenarios, along with the spin-down limits set by μ = 4.1 × 10−14 eV, are shown in Figure 6. The densities of the merger fraction, fm
, in mass and spin are also presented.
. These distributions are chosen such that the evolved population visually appears similar to the observed nuclear star cluster properties from Georgiev et al. (2016). We evolve 4.8 × 104 clusters with properties drawn randomly from these distributions, for scenarios where μ = 4.1 × 10−14 eV and no ultralight boson exists. The final merger is then included in the merger population. The individual black hole properties from both scenarios, along with the spin-down limits set by μ = 4.1 × 10−14 eV, are shown in Figure 6. The densities of the merger fraction, fm
, in mass and spin are also presented.
Figure 6. Distribution of the masses and spins of simulated merging black hole populations within a model cluster population visually matching the observed nuclear star cluster population from Georgiev et al. (2016) after evolution, with either an ultralight boson of mass μ = 4.1 × 10−14 eV or no ultralight boson. The red curves correspond to the τevol = 10 Myr (solid) and τevol = 10 Gyr (dashed) spin-down exclusion limits when μ = 4.1 × 10−14 eV. With the inclusion of ultralight bosons with μ = 4.1 × 10−14 eV, there is an increased number of heavy black holes in the merging population as a direct result of more clusters being able to facilitate hierarchical growth.
Download figure:
Standard image High-resolution imageFrom the one-dimensional marginal distributions, the inclusion of superradiance from bosons with μ = 4.1 × 10−14 eV clearly leads to an enhancement of the number of black holes with masses above 100 M⊙ in the population of merging binary systems. Furthermore, a distinct 2G population with spins ∼0.7 is observed. This is present regardless of the presence of the ultralight boson, as the majority of black holes in this population are not old enough to undergo any significant superradiant boson cloud growth. Additionally, the superradiant instability leads to a strong correlation between the black hole spin and mass in the mass range from ∼80–300 M⊙, as the black holes are maximally spun down through the formation of a boson cloud. Finally, there is a trend of reduced spins as the black holes become heavier. This is due to the fact that these black holes are formed through high mass ratio mergers, which typically reduce the spin of the merger remnant. This is present in both scenarios.
5. Implications
The process of black hole superradiance can increase the number of nuclear star clusters where hierarchical black hole growth occurs while impacting the black hole merger population. The signature of this distinct population may be detectable by gravitational-wave detectors such as Advanced LIGO (Aasi et al. 2015) and Advanced Virgo (Acernese et al. 2014; Abbott et al. 2020a, 2020b, 2020d).
5.1. Gravitational-wave Source Population
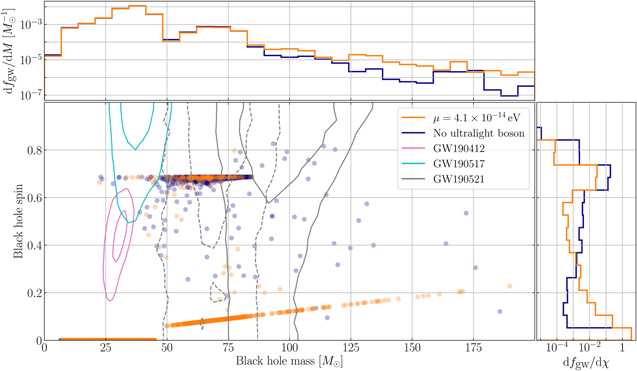
In Figure 7, we plot the mass–spin distribution while taking into account gravitational-wave detector selection biases. The primary black hole mass–spin 1σ and 2σ two-dimensional credible intervals for GW190412, GW190517, and GW190521, as well as the secondary black hole intervals for GW190521, are also shown (shown as dashed contours; Abbott et al. 2020a, 2020b, 2020d).
Figure 7. Simulated binary black hole merger population weighted by their detection probability by a single-design-sensitivity aLIGO detector (Aasi et al. 2015) for the μ = 4.1 × 10−14 eV or no ultralight boson scenarios. The 1σ and 2σ credible intervals inferred for the primary black hole properties from GW190412 (Abbott et al. 2020c), GW190517 (Abbott et al. 2020d), and GW190521 (Abbott et al. 2020a, 2020b) are shown as solid contours. The properties of GW190521's secondary black hole is given by the dashed contours. The existence of a μ = 4.1 × 10−14 eV ultralight boson would lead to an enhancement of heavier binary systems with lower spins. Currently observations from gravitational waves cannot rule out the existence of ultralight bosons in the mass range 10−14–10−13 eV.
Download figure:
Standard image High-resolution imageBy comparing the gravitational-wave detection-weighted binary black hole populations, we see a number of distinct features. First, the observed population is restricted to black holes with individual masses ∼5–200 M⊙. These selection biases are well known and consistent between both scenarios presented here (Messenger & Veitch 2013; Farr 2019). Additionally, the black hole mass–spin correlation is still observable in the population in the presence of ultralight bosons. Finally, there is an increase in the number of heavier black hole detections in the ultralight boson scenario. To quantify the increased number of heavier black hole merger populations, we compute the merger rates of both the total population, 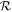 , as well as the intermediate-mass (100 <M/M⊙ < 1000) population; please refer to Appendix D for details. We summarize the merger rates calculated and present the observed rates (Abbott et al. 2020b, 2021a, 2021e) in Table 1. The values calculated in the absence of ultralight bosons are consistent with the results from Antonini et al. (2019).
, as well as the intermediate-mass (100 <M/M⊙ < 1000) population; please refer to Appendix D for details. We summarize the merger rates calculated and present the observed rates (Abbott et al. 2020b, 2021a, 2021e) in Table 1. The values calculated in the absence of ultralight bosons are consistent with the results from Antonini et al. (2019).
Table 1. Total and Intermediate Mass Black Hole Merger Rates from Observations of Gravitational Waves from Stellar-mass Black Hole Mergers (Abbott et al. 2020b, 2021a, 2021e) Compared to the Calculated Merger Rates From Our Simulated Population (with 68% Credible Intervals)
Total Merger Rate, 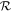
| IMBH Merger Rate, 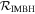
| |
|---|---|---|
| (Gpc−3 yr−1) | (Gpc−3 yr−1) | |
| Observed |
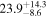
|
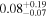
|
| No ultralight boson | ≈1.2 fnMBH | ≈0.04 fnMBH |
| μ = 4.1 × 10−14 eV | ≈0.9 fnMBH | ≈0.08 fnMBH |
Note. The observed intermediate-mass black hole (IMBH) merger rate is a single-event rate determined from GW190521 (Abbott et al. 2020b, 2021e). While the total merger rate cannot be justified by hierarchical mergers in nuclear star clusters, the observed rate of intermediate-mass mergers might be explained by such events. The inclusion of superradiance due to the existence of bosons with μ = 4.1 × 10−14 eV leads to a doubling in the IMBH merger rate for our simulated population. Here, fnMBH corresponds to the fraction of galaxies without a central massive black hole.
Download table as: ASCIITypeset image
From these calculations, nuclear star clusters, regardless of whether superradiance occurs, cannot explain the total observed merger rate from gravitational-wave detectors (Abbott et al. 2020d). This result is expected, and it is anticipated that field binaries and/or dynamical mergers in globular clusters can explain the bulk of the observed binary black hole mergers (Dominik et al. 2013; Eldridge et al. 2019; Neijssel et al. 2019; Kremer et al. 2020b; Mapelli et al. 2021; Santoliquido et al. 2020; Rodriguez et al. 2021; Wong et al. 2021; Zevin et al. 2021). However, the inclusion of superradiance leads to a doubling of the merger rate of intermediate-mass black hole (IMBH) mergers to ≈0.08 fnMBH Gpc−3 yr−1 for μ = 4.1 × 10−14 eV bosons. Both inferred values of  are consistent with the single-event merger rate determined for GW190521 (Abbott et al. 2020b, 2021e). Future gravitational-wave observations of heavy-mass binary black hole systems will continue to reduce the uncertainty in the merger rate of these heavier systems.
are consistent with the single-event merger rate determined for GW190521 (Abbott et al. 2020b, 2021e). Future gravitational-wave observations of heavy-mass binary black hole systems will continue to reduce the uncertainty in the merger rate of these heavier systems.
Finally, within our simulated population, the interpretations of gravitational-wave observations remain unchanged in the presence of ultralight bosons. For GW190521 (Abbott et al. 2020a, 2020b), we conclude that the system is likely a 2G+2G binary black hole merger (discussed in Gayathri et al. 2020, Kimball et al. 2021, and Romero-Shaw et al. 2020). Recently, Ng et al. (2021b) confirmed that the primary black holes from GW190412 (Abbott et al. 2020c) and GW190517 (Abbott et al. 2020d) exclude non-self-interacting ultralight scalar bosons with masses 1.3–2.7 × 10−13 eV. From our simulations, we suspect GW190517 might be a 2G+1G merger too light to be spun down through superradiance. This is tentatively supported by the results from Kimball et al. (2021). GW190412 is inconsistent with our simulated population irrespective of the presence of ultralight bosons—likely a direct result of our mass cutoff or spin distribution used. We can nevertheless interpret GW190412 as a direct result of hierarchical and/or dynamical formation (as in Abbott et al. 2020c, Gerosa et al. 2020, Rodriguez et al. 2020, Safarzadeh & Hotokezaka 2020, and Zevin et al. 2020). For the most impactful boson masses from our analysis, GW190412 and GW190517 do not provide any information about their presence.
5.2. Detectability
Currently, the existence of ultralight bosons is purely hypothetical. In the mass range we are focused on in this manuscript, μ ∼ 2 × 10−14–2 × 10−13 eV, their detection would likely be made by gravitational-wave detectors via either the direct observation of continuous gravitational waves, as a stochastic background, or as a feature of the population (Brito et al. 2017b; Isi et al. 2019; Tsukada et al. 2019; Sun et al. 2020; Ng et al. 2021a, 2021b; Tsukada et al. 2021). Other ultralight boson searches would likely cover a different boson-mass range, which impacts black holes of different masses. The detection of ultralight bosons in this energy range is likely only possible with future generations of gravitational-wave detectors (Isi et al. 2019; Sun et al. 2020). Isi et al. (2019) found that the horizon distance for continuous gravitational-wave emission from boson clouds with masses 10−14–10−13 eV is ≲100 Mpc for aLIGO detectors (Aasi et al. 2015). 3G gravitational-wave detectors such as the Cosmic Explorer (Reitze et al. 2019) or Einstein Telescope (Maggiore et al. 2020) would be able to detect continuous gravitational-wave emission from the desired ultralight bosons out to a horizon of ∼1 Gpc. Analyzing the mass–spin distributions of the stellar-mass black holes may be a more successful method for indirectly determining the existence of ultralight bosons (Ng et al. 2021a, 2021b). Ng et al. (2021a) found that 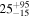 or
or  gravitational-wave detections with signal-to-noise ratios exceeding 30 were required to determine the presence of ultralight bosons with μ = 10−13 eV, for two fiducial 1G spin distributions. It is unlikely that these detection numbers can be applied to a ∼10−14 eV boson detection prediction. Finally, even though we find interesting features beyond the spin-down exclusion regions, they will likely be masked by current uncertainties in the modeling of binary black hole cluster dynamics (Rodriguez et al. 2018; Antonini et al. 2019; Rodriguez et al. 2019; Mapelli et al. 2021). Therefore, in the near future, the detection of ultralight bosons will still rely on a direct gravitational-wave measurement or on spin-population studies of gravitational-wave events (Brito et al. 2017b; Dergachev & Papa 2019; Isi et al. 2019; Palomba et al. 2019; Tsukada et al. 2019; Sun et al. 2020; Zhu et al. 2020; Abbott et al. 2021d; Ng et al. 2021a, 2021b; Tsukada et al. 2021). Our study has explored the possible differences superradiance might bring to the observed population of binary black hole mergers.
gravitational-wave detections with signal-to-noise ratios exceeding 30 were required to determine the presence of ultralight bosons with μ = 10−13 eV, for two fiducial 1G spin distributions. It is unlikely that these detection numbers can be applied to a ∼10−14 eV boson detection prediction. Finally, even though we find interesting features beyond the spin-down exclusion regions, they will likely be masked by current uncertainties in the modeling of binary black hole cluster dynamics (Rodriguez et al. 2018; Antonini et al. 2019; Rodriguez et al. 2019; Mapelli et al. 2021). Therefore, in the near future, the detection of ultralight bosons will still rely on a direct gravitational-wave measurement or on spin-population studies of gravitational-wave events (Brito et al. 2017b; Dergachev & Papa 2019; Isi et al. 2019; Palomba et al. 2019; Tsukada et al. 2019; Sun et al. 2020; Zhu et al. 2020; Abbott et al. 2021d; Ng et al. 2021a, 2021b; Tsukada et al. 2021). Our study has explored the possible differences superradiance might bring to the observed population of binary black hole mergers.
We thank Richard Brito for insightful discussions about black hole superradiance. We also thank Susan Scott and Karl Wette for helpful discussions about ultralight boson cloud detection prospects. This work is supported through Australian Research Council (ARC) Centre of Excellence CE170100004. E.P. acknowledges the support of ARC CE170100004's COVID-19 support fund. P.D.L. is supported through ARC Future Fellowship FT160100112, and ARC Discovery Project DP180103155. K.K. is supported by an NSF Astronomy and Astrophysics Postdoctoral Fellowship under award AST-2001751.
This research has made use of data, software and/or web tools obtained from the Gravitational Wave Open Science Center (https://www.gw-openscience.org), a service of LIGO Laboratory, the LIGO Scientific Collaboration and the Virgo Collaboration. Computing was performed on LIGO Laboratory computing cluster at California Institute of Technology.
Appendix A: Cluster Properties Under Hénon's Principle
A.1. Cluster Evolution
Using Hénon's principle, the heating rate from binary black hole systems in the core of the cluster is balanced against the energy flow into the cluster as a whole (Hénon 1961, 1975; Gieles et al. 2011; Breen & Heggie 2013). The rate of energy generation,  , is therefore directly related to the properties of the cluster,
, is therefore directly related to the properties of the cluster,
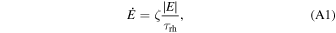
where 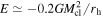 is the total energy of the cluster, Mcl is the cluster mass, rh
is the half-mass–radius, ζ ≃ 0.1 (Gieles et al. 2011; Alexander & Gieles 2012) is a dimensionless factor, and τrh is the relaxation timescale of the cluster, which can be approximated as (Spitzer & Hart 1971; Antonini et al. 2019)
is the total energy of the cluster, Mcl is the cluster mass, rh
is the half-mass–radius, ζ ≃ 0.1 (Gieles et al. 2011; Alexander & Gieles 2012) is a dimensionless factor, and τrh is the relaxation timescale of the cluster, which can be approximated as (Spitzer & Hart 1971; Antonini et al. 2019)
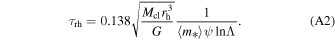
Here, 〈m*〉 is the mean stellar and compact object mass within the cluster and  is the Coulomb logarithm. The factor ψ is related to the distribution of masses within the half-mass–radius and approximated in Spitzer & Hart (1971) as
is the Coulomb logarithm. The factor ψ is related to the distribution of masses within the half-mass–radius and approximated in Spitzer & Hart (1971) as 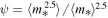 . For the remainder of the manuscript, we follow Antonini et al. (2019) and assume low-mass stars dominate the mass distribution of the cluster, such that 〈m*〉 = 0.6 M⊙, and ψ ≃ 5.
. For the remainder of the manuscript, we follow Antonini et al. (2019) and assume low-mass stars dominate the mass distribution of the cluster, such that 〈m*〉 = 0.6 M⊙, and ψ ≃ 5.
Finally, by defining the half-mass density, 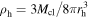 , and escape velocity,
, and escape velocity,  , we can express the initial heating rate, relaxation time, and escape velocity at t = t0 uniquely in terms of the initial cluster density and its mass. From Equations (A6) and (A7) (Antonini et al. 2019),
, we can express the initial heating rate, relaxation time, and escape velocity at t = t0 uniquely in terms of the initial cluster density and its mass. From Equations (A6) and (A7) (Antonini et al. 2019),
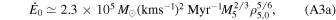
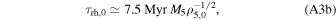
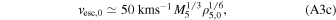
where M5 ≡ Mcl/105 M⊙ and ρ5,0 ≡ ρh,0/105 M⊙ pc−3. Here, t0 corresponds to the time at which the first black hole binaries begin to heat the cluster (i.e., when they have entered the cluster's core; Breen & Heggie 2013). Furthermore, we have implicitly assumed that mass loss of the cluster is a negligible contribution to the evolution of the cluster. Below, we explicitly require a constant Mcl in the calculation of the cluster model's evolution. The proportionality constant for the initial escape velocity is derived from the King (1966) cluster model with W0 = 7, where W0 is the central value of the dimensionless form of the cluster's gravitational potential, uniquely describing the potential's shape. This model is used throughout for the calculation of the dynamical features of the clusters.
To derive the time dependence of the cluster properties, we assume no mass loss (constant Mcl) and that the cluster is always in virial equilibrium. Under these assumptions, the rate of expansion of the cluster is related to the heating rate as (Hénon 1965)
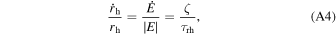
following Equation (A6). Fixing the cluster mass, we have 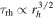 , and solve Equation (A4) for the time evolution of the half-mass–radius from t0,
, and solve Equation (A4) for the time evolution of the half-mass–radius from t0,
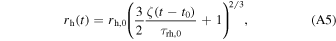
when t > t0. When t < t0, the cluster has not yet extracted energy from the binary population and is assumed to have the initial half-mass–radius. Equation (A5) can be directly substituted into the expressions for the heating rate and escape velocity to find
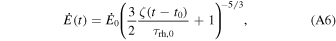
and

A.2. Binary Black Hole Evolution
After a binary black hole system has formed, the system undergoes dynamical hardening (Leigh et al. 2018). This process tightens the binary orbit while heating the cluster via Hénon's principle (Hénon 1975). This implies that the rate of energy loss from the binary is approximately equal to the heating rate of the cluster in Equation (A6):
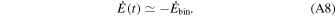
The total energy of the binary during the process of dynamical hardening is
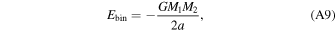
where a is the semimajor axis of the binary's orbit. Therefore, differentiating both sides of Equation (A9) and applying Equation (A8) to express the semimajor axis evolution of the binary as a function of the heating rate of the cluster leads to (Antonini et al. 2019)
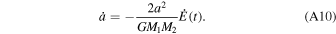
We integrate this expression with respect to the semimajor axis from the initial semimajor axis of formation, ah , to the minimum semimajor axis for which dynamical hardening dominates, am . The heating rate is assumed to be approximately constant over the binary's evolution. This defines the timescale of dynamical hardening for a binary to be
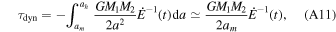
where we have used the fact that ah ≫ am , as seen in Equation (14).
The lower bound semimajor axis, am , is given by
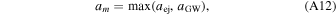
where aej is the semimajor axis for which the binary system is ejected from the cluster through binary–single interactions, and aGW is the semimajor axis at which the energy loss from dynamical hardening is equal to the energy loss from gravitational-wave emission. If the semimajor axis of the binary decreases below aej, then the binary is ejected from the cluster prior to merging (Quinlan 1996; Miller & Hamilton 2002; Miller & Lauburg 2009). The value of aej is given by (Antonini & Rasio 2016)
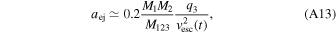
where 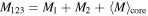 is the average total mass of the binary–single interaction, and
is the average total mass of the binary–single interaction, and 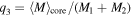 is the mass ratio of the interaction. Since we do not track the individual trajectories and interactions within the cluster, we use the average black hole mass in the core (excluding the binary),
is the mass ratio of the interaction. Since we do not track the individual trajectories and interactions within the cluster, we use the average black hole mass in the core (excluding the binary),  , to calculate aej.
, to calculate aej.
If aGW > aej, the binary will merge within the cluster. Due to the massive and dense clusters considered in this manuscript, this occurs for almost all binaries. The evolution of the semimajor axis through gravitational-wave emission is given by (Peters 1964)
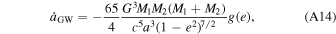
where e is the eccentricity of the binary, and
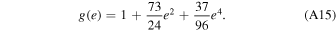
By equating Equations (A10) and (A14), solving for a leads to the expression (Antonini et al. 2019)
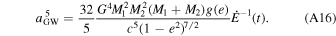
For every binary formed, we generate an eccentricity from the thermal eccentricity distribution ∝ e (Jeans 1919). The timescale for gravitational-wave emission from the binary is then given by 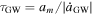 . Just prior to merger, the effects of superradiance on the individual black holes are incorporated.
. Just prior to merger, the effects of superradiance on the individual black holes are incorporated.
A.3. Interloper Ejection
Although it is very unlikely that the binary system is ejected from binary–single interactions, this is not the case for interlopers. To account for this, the expected number of ejected interlopers as (Antonini et al. 2019)
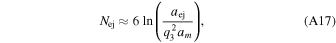
where the interloper mass ratio, q3, is calculated from the mean mass of black holes in the core. With the approximate number of ejected black hole interlopers calculated, we discard Nej black holes randomly. Generally, this process would favor the ejection of low-mass black holes. However, given that the majority of black holes in the cluster are from the first generation, this averaged procedure does not change the expected results. The key difference with the inclusion of interloper ejection is a restriction on the upper mass of the black hole formed through hierarchical black hole mergers. Since this process removes a fraction of black holes from the cluster, in some simulations this limits the available black holes for hierarchical growth.
Appendix B: Recoil Velocity Calculation
We utilize the Precession code (Gerosa & Kesden 2016) to determine the final recoil velocity of the remnant black hole. The kick-velocity-fitting formulae are constructed from mass-weighted spin vector combinations (Gerosa & Kesden 2016),
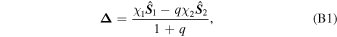
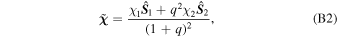
where χ1,2 are the spin magnitudes of the individual black holes, 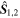 are their associated unit vectors, and q = M2/M1 is the mass ratio. These vectors can also be decomposed into the components parallel and orthogonal to the orbital angular momentum,
L
, given as
are their associated unit vectors, and q = M2/M1 is the mass ratio. These vectors can also be decomposed into the components parallel and orthogonal to the orbital angular momentum,
L
, given as 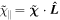 ,
, 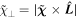 ,
, 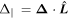 , and
, and 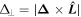 .
.
The formulation of the final magnitude of the kick velocity of the black hole, vk , is constructed from the recoil velocities from mass, vm , and spin, vs∥ and vs⊥, asymmetries in the binary system. The velocity component from mass asymmetry lies perpendicular to the orbital angular momentum vector, whereas the spin component has some contribution both parallel to the vector and in the orbital plane of the binary. This leads to the simple expression for the magnitude of the kick velocity (Campanelli et al. 2007a),

where β is the angle between the components from mass and spin asymmetry orthogonal to the orbital angular momentum. Each of the individual terms in Equation (A3) has been determined through analytical fits to numerical relativity simulations. The velocity components, vm , vs∥, and vs⊥, are calculated as
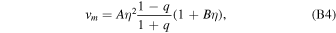
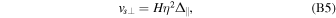
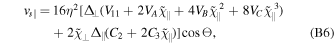
where 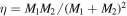 , and the coefficients have been found through fitting to numerical relativity simulations: A = 1.2 × 104 km s−1, B = −0.93 (González et al. 2007b), H = 6.9 × 103 km s−1 (Lousto & Zlochower 2008), V11 = 3677.76 km s−1, VA
= 2481.21 km s−1, VB
= 1792.45 km s−1, VC
= 1506.52 km s−1 (Lousto et al. 2012), C2 = 1140 km s−1, C3 = 2481 km s−1 (Lousto & Zlochower 2013), and β = 145° (Lousto & Zlochower 2008). Finally, Θ is the angle between
, and the coefficients have been found through fitting to numerical relativity simulations: A = 1.2 × 104 km s−1, B = −0.93 (González et al. 2007b), H = 6.9 × 103 km s−1 (Lousto & Zlochower 2008), V11 = 3677.76 km s−1, VA
= 2481.21 km s−1, VB
= 1792.45 km s−1, VC
= 1506.52 km s−1 (Lousto et al. 2012), C2 = 1140 km s−1, C3 = 2481 km s−1 (Lousto & Zlochower 2013), and β = 145° (Lousto & Zlochower 2008). Finally, Θ is the angle between  and the infall direction of the black holes at merger, with an additional offset of ∼ 200° (Brügmann et al. 2008; Lousto & Zlochower 2009). This angle is assumed to be uniformly distributed from 0 to π (Gerosa & Kesden 2016), and is therefore drawn at random for each merger calculation.
and the infall direction of the black holes at merger, with an additional offset of ∼ 200° (Brügmann et al. 2008; Lousto & Zlochower 2009). This angle is assumed to be uniformly distributed from 0 to π (Gerosa & Kesden 2016), and is therefore drawn at random for each merger calculation.
Appendix C: Calculating the Fraction of Hierarchical-growth-supported Clusters
We use Monte Carlo integration to determine the fraction of the individual nuclear star cluster property distributions, pi (Reff, Mcl), contained within the contour (which itself has uncertainty), where i indexes the cluster. To estimate the uncertainty on the contours, the uncertainty on the fraction of simulations that demonstrate hierarchical growth must first be calculated. By assuming the fraction follows a binomial distribution, the uncertainty on fhier is estimated with a Wilson score interval (Wilson 1927). The median and confidence interval are fit with a generalized extreme value (GEV) distribution following Possolo et al. (2019). This allows us to draw 1000 possible fractions at each point in the parameter space, from which we create 1000 possible hierarchical-growth contours. We fit the NNSC = 228 nuclear star cluster properties (Georgiev et al. 2016) with GEV distributions (Possolo et al. 2019) as an approximation for pi (Reff, Mcl) to generate Np = 4 × 103 plausible (Reff, Mcl) values for each cluster. We compute the integral as
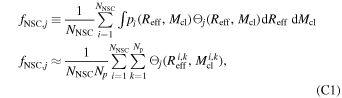
where 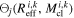 evaluates to one for a point within the jth, fhier > 50% contour, and zero otherwise. The value of fNSC is taken as the median from the distribution fNSC,j
, with an uncertainty set by the distribution.
evaluates to one for a point within the jth, fhier > 50% contour, and zero otherwise. The value of fNSC is taken as the median from the distribution fNSC,j
, with an uncertainty set by the distribution.
Appendix D: Calculating Merger Rates
From the synthetic population presented in Section 4.3, the merger rate is estimated following Antonini et al. (2019) as
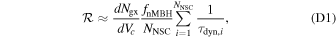
where d Ngx/d Vc ≈ 0.01 Mpc−3 (Conselice et al. 2005) is the number density of nucleated galaxies, and fnMBH is the fraction of galaxies without a central massive black hole. For each nuclear star cluster, we compute the reciprocal of the binary formation timescale, τdyn, as an approximate for the rate of binary mergers within the cluster, since a single binary dominates the cluster evolution at any one time. Here, fnMBH is kept as a parameter in the expression as its value is somewhat unconstrained, though expected to be ∼0.2–1 (Seth et al. 2008; Antonini et al. 2015; Nguyen et al. 2018). Furthermore, the merger rate for which at least one member of the binary is within the black hole mass range 102 M⊙ < M < 103 M⊙ is calculated as
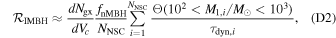
where Θ(102 < M1,i /M⊙ < 103) evaluates to one when the condition is satisfied and zero otherwise. This mass range corresponds to the lower end of the IMBH range (e.g., Greene et al. 2020). The merger remnant (and possibly also the primary black hole) for GW190521 lies conclusively within this range (Abbott et al. 2020a, 2020b). The calculation in Equation (D2) can be compared to the observed IMBH merger rates.
Footnotes
- 6
We focus on scalar (spin-0) bosons (Damour et al. 1976; Ternov et al. 1978; Detweiler 1980; Yoshino & Kodama 2014). However, the general conclusions can be applied to spin-1 (East 2017; Frolov et al. 2018; Siemonsen & East 2020) and spin-2 (Hinterbichler 2012; Brito et al. 2013; de Rham 2014; Brito et al. 2020b) bosons if efficient black hole spin-down is possible.
- 7
For each point in the grid, we run 30 subsimulations to average over random fluctuations.
- 8
This threshold is somewhat arbitrary, as we still compute similar fractions when considering a mass threshold as low as ∼400 M⊙. This is because once a ∼400 M⊙ black hole is formed, hierarchical growth almost always follows.