Abstract
We have observed the Class I protostar TMC-1A in the Taurus molecular cloud using the Submillimeter Array (SMA) and the Atacama Large Millimeter/submillimeter Array (ALMA) in the linearly polarized 1.3 mm continuum emission at angular resolutions of ∼3'' and ∼0.3'', respectively. The ALMA observations also include CO, 13CO, and C18O J = 2−1 spectral lines. The SMA observations trace magnetic fields on the 1000 au scale, the directions of which are neither parallel nor perpendicular to the outflow direction. Applying the Davis–Chandrasekhar–Fermi method to the SMA polarization angle dispersion, we estimate a field strength in the TMC-1A envelope of 1–5 mG. It is consistent with the field strength needed to reduce the radial infall velocity to the observed value, which is substantially less than the local freefall velocity. The ALMA polarization observations consist of two distinct components—a central component and a north/south component. The central component shows polarization directions in the disk minor axis to be azimuthal, suggesting dust self-scattering in the TMC-1A disk. The north/south component is located along the outflow axis and the polarization directions are aligned with the outflow direction. We discuss possible origins of this polarization structure, including grain alignment by a toroidal magnetic field and mechanical alignment by the gaseous outflow. In addition, we discover a spiral-like residual in the total intensity (Stokes I) for the first time. The C18O emission suggests that material in the spiral-like structure is infalling at a speed that is 20% of the local Keplerian speed.

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Magnetic fields are expected to play an important role in the process of star formation. During the main accretion phase, magnetic fields in protostellar envelopes regulate mass and momentum accretion onto a disk and consequently affect disk formation and disk properties, such as mass and size. Thus, magnetic fields may have an impact on the subsequent planet formation in the system, since such protostellar disks provide the initial conditions for planet formation. On the one hand, magnetohydrodynamics (MHD) simulations have suggested that magnetic fields strongly suppress disk formation in the protostellar phase through the so-called the magnetic braking (e.g., Mellon & Li 2008; Hennebelle & Ciardi 2009; Joos et al. 2012). On the other hand, theoretical studies also suggest that nonideal MHD effects (ohmic dissipation, ambipolar diffusion, and Hall effect) can weaken the effects of magnetic braking, enhancing disk formation (e.g., Inutsuka et al. 2010; Krasnopolsky et al. 2011; Dapp et al. 2012; Tomida et al. 2015; Tsukamoto et al. 2015; Zhao et al. 2018). Observations of magnetic fields are thus necessary to verify the above theoretical predictions and reveal how magnetic fields affect mass accretion onto disks in the disk formation phase.
Polarized emission from dust grains enables us to observe magnetic fields. However, recent observational studies have reported that magnetic fields are not the only source of polarized emission on disk scales in young stellar objects. For example, protoplanetary disks show polarized dust emission arising from self-scattering (Kataoka et al. 2016, 2017; Ohashi & Kataoka 2019) at millimeter wavelengths. This interpretation is based on theoretical predictions of the polarization direction and fraction: polarization directions along the disk minor axis and polarization fractions on the order of 1% independent of the polarization intensity (Yang et al. 2017). In addition to self-scattering, the mechanical momentum in the protostellar outflow can align dust grains producing polarized dust emission. If gaseous flux aligns the major axis of dust grains along the outflow direction (Gold 1952), the resultant polarization direction is parallel to the outflow axis. In contrast, if torque generated by the outflow rotates dust grains around the outflow axis, the resultant polarization direction is perpendicular to the outflow axis (Le Gouellec et al. 2019).
Recent observations toward protostars on multiple spatial scales suggest that magnetic fields affect circumstellar materials in different degrees on different spatial scales (Hull et al. 2017a, 2017b). It is, therefore, important to observationally investigate magnetic fields, along with kinematics, specifically on the protostellar envelope-disk scales in order to understand how magnetic fields regulate mass accretion onto disks.
In order to investigate the effects of magnetic fields on mass accretion onto a protostellar disk, we observed the Class I protostar TMC-1A using the SMA and ALMA with the polarized dust continuum emission at 1.3 mm. TMC-1A is a good target for this purpose because previous observational studies have already revealed the kinematics in its protostellar disk and envelope. TMC-1A is in the Taurus molecular cloud located at a distance of 130–160 pc away from us (Galli et al. 2018); we adopt 140 pc as the distance to TMC-1A in this paper. The disk in TMC-1A was identified kinematically by a power-law index of radial profiles of rotational velocity close to −0.5 (Harsono et al. 2014; Aso et al. 2015). Harsono et al. (2014) fitted a disk and envelope model to the continuum visibilities at 1.3 mm derived from observations using the Plateau de Bure Interferometer at an angular resolution of 0.7''–1.3'', estimating the disk size, disk inclination angle, and central stellar mass to be 80–100 au, 55°, and 0.53 M☉, respectively. Aso et al. (2015) reproduced, by a disk and envelope model, position-velocity (PV) diagrams along the major and minor axes of the disk in the C18O J = 2−1 line observed with ALMA at an angular resolution of ∼1'', estimating the disk size, disk inclination angle, and central stellar mass to be ∼100 au, ∼65°, and 0.68 M☉, respectively. They also suggested an radial infall velocity of ∼0.3 times the freefall velocity from their model and estimated a magnetic field strength required to explain the slow infall velocity to be ∼2 mG. In addition to the disk and envelope, Bjerkeli et al. (2016) revealed disk wind from a radius range of 7–22 au from the disk in TMC-1A. Previous observations at a 8 au resolution revealed that optically thick dust hides the C18O and 13CO J = 2−1 lines in the central ± 40 au region (Harsono et al. 2018). The authors interpreted this high optical depth as a result of dust grains with millimeter size rather than a result of a massive disk because the high mass required to explain the high optical depth should cause gravitational instability, which is inconsistent with the smooth structure observed in the continuum emission.
This paper is structured as follows. We describe the settings of our SMA and ALMA observations in Section 2. Section 3 shows results of polarized 1.3 mm continuum emission observed with the SMA and ALMA, and Stokes I of the CO, 13CO, and C18O J = 2−1 lines observed with ALMA. We apply the Davis–Chandrasekhar–Fermi (DCF) method to the SMA result and analyze a non-axisymmetric component in the ALMA continuum image in Section 4. Possible origins of the observed polarization and the non-axisymmetric component are discussed in Section 5. We summarize our conclusions in Section 6.
2. SMA and ALMA Observations
2.1. SMA
We observed TMC-1A using the SMA for one track on 2018 January 3 with the full polarization mode. The total observing time is ∼525 minutes (8.75 hr) for TMC-1A including overhead. Seven antennas were used in the compact configuration. The minimum projected baseline length is 16 m. Any emission beyond 9'' (1300 au) was resolved out by ≳63% with the antenna configuration (Wilner & Welch 1994). Our SMA observations used two orthogonally polarized receivers, tuned to the same frequency range in the full polarization mode, and the SMA Wideband Astronomical ROACH2 Machine (SWARM, where ROACH2 is the second generation Reconfigurable Open Architecture Computing Hardware) correlator. The upper sideband (USB) and lower sideband (LSB) covered 213–221 and 229–237 GHz, respectively. Each sideband was divided into four chunks with a bandwidth of 2 GHz, and each chunk has a fixed channel width of 140 kHz.
The SMA data were calibrated with the with the Millimeter Interferometer Reduction (MIR) software package. 12 Instrumental polarization leakage was calibrated independently for USB and LSB using the Multi-channel Image Reconstruction, Image Analysis, and Display (MIRIAD) task gpcal and removed from the data. The calibrated visibility data in Stokes I, Q, and U were Fourier transformed and CLEANed with the natural weighting, using the MIRIAD package (Sault et al. 1995), by integrating channels without line emission. The polarized intensity, position angle, and polarization percentage were derived from the Stokes I, Q, and U maps using the MIRIAD task impol. The parameters of our SMA observations mentioned above and others are summarized in Table 1.
Table 1. Summary of the SMA Observational Parameters
| Date | 2018 Jan 3 |
| Projected baseline length | 16–77 m (12–58 kλ) |
| Primary beam | 54'' |
| Passband/polarization calibrator | 3C279 (7.2 Jy), 3C454.3 (12 Jy) |
| Flux calibrator | Neptune |
| Gain/polarization calibrator | 0510 + 180 (1.5 Jy), NRAO530 (1.5 Jy) |
| Coordinate center (J2000) | 04h39m35.20ˢ, 25° 41' 44.35'' |
| Frequency (GHz) | 224 |
| Bandwidth (GHz) | 8 |
| Beam (P.A.) | 2.8'' × 2.4'' (47°) |
| rms noise level (mJy beam−1) | 0.75 (Stokes I), 0.26 (Stokes Q/U) |
Download table as: ASCIITypeset image
2.2. ALMA
We also observed TMC-1A using ALMA in Cycle 6 on 2018 November 18 with the full polarization mode. The total observing time is ∼202 minutes (3.37 hr), while the on-source observing time for TMC-1A is ∼43 minutes. The number of antennas was 49. The array configuration was C43-5, whose minimum projected baseline length is 12 m. Any emission beyond 12'' (1700 au) was resolved out by ≳63% with the antenna configuration (Wilner & Welch 1994). Spectral windows for the 12CO, 13CO, and C18O (J = 2−1) lines have 1920, 960, and 960 channels covering 117, 59, and 59 MHz bandwidths at frequency resolutions of 61.0, 61.0, and 61.0 kHz, respectively. In making maps, channels are binned to produce the velocity resolution of 0.1 km s−1 for all three lines. Another spectral window covers 232–234 GHz, which was assigned to the continuum emission.
All of the imaging procedure was carried out with Common Astronomical Software Applications (CASA), version 5.6.2. The visibilities in Stokes I, Q, U, and V were Fourier transformed and CLEANed with Briggs weighting, a robust parameter of 0.5, and a threshold of 3σ. Emission of the three lines were detected only in Stokes I. The CLEAN process using the CASA task tclean adopted the auto-masking (auto-multithresh) with the parameters of sidelobethreshold = 3.0, noisethreshold = 3.0, lownoisethreshold = 1.5, and negativethreshold = 3.0. The polarized intensity and position angle were derived from the Stokes I, Q, and U maps using the CASA task immath.
We also performed self-calibration for Stokes I of the continuum data using tasks in CASA (clean, gaincal, and applycal). Only the phase was calibrated by decreasing the time bin from "inf", 90 s, and then 18 s. The self-calibration improved the rms noise level of the continuum maps by a factor of ∼120. The obtained calibration tables for the Stokes I continuum data were also applied to the other Stokes continuum data and the line data for consistency. The noise level of the line maps were measured in emission-free channels. The parameters of our ALMA observations mentioned above and others are summarized in Table 2.
Table 2. Summary of the ALMA Observational Parameters
| Date | 2018 Nov 21 | |||
| Projected baseline length | 12–1376 m (9.4–1070 kλ) | |||
| Primary beam | 27'' | |||
| Bandpass/flux calibrator | J0510+1800 | |||
| Polarization calibrator | J0522-3627 (1.0 Jy) | |||
| Check source | J0426+2952 | |||
| Phase calibrator | J0438+3004 (0.23 Jy) | |||
| Coordinate center (ICRS) | 04h39m35.20s, 25° 41' 44.23'' | |||
| Continuum | CO J = 2−1 | 13CO J = 2−1 | C18O J = 2−1 | |
| Frequency (GHz) | 234 | 230.538000 | 220.398684 | 219.560354 |
| Bandwidth/resolution | 2 GHz | 0.1 km s−1 | 0.1 km s−1 | 0.1 km s−1 |
| Beam (P.A.) | 0.37'' × 0.26'' (−2°) | 0.40'' × 0.28'' (−1°) | 0.42'' × 0.29'' (−1°) | 0.42'' × 0.29'' (−1°) |
| rms noise level | 25 μ Jy beam−1 | 2 mJy beam−1 | 2 mJy beam−1 | 2 mJy beam−1 |
Download table as: ASCIITypeset image
3. Results
3.1. SMA Polarized 1.3 mm Continuum
Figure 1 shows the polarized continuum emission at 1.3 mm observed with the SMA. The Stokes I map shows a compact component associated with TMC-1A and an extension to the east at the 3σ level, and slightly expands into the southwest. Gaussian fitting to the Stokes I emission provides a peak position of and a deconvolved size of 0.66'' ± 0.09'' × 0.50'' ± 0.11'' with a position angle of 66° ± 28°. This size corresponds to 92 × 70 au at the distance of TMC-1A, 140 au. The results of the Gaussian fitting is summarized in Table 3. The major axis of the emission is consistent with the major axis of the disk around TMC-1A and perpendicular to the associated outflow (Aso et al. 2015). The peak intensity and total flux density measured in our SMA observation are 0.171 Jy beam−1 and 0.182 Jy, respectively.
Figure 1. The continuum emission at 1.3 mm observed with the SMA. The contour map shows Stokes I with contour levels of 3, 6, 12, 24,... × σ, where 1σ corresponds to 0.75 mJy beam−1. The color map shows polarization fraction, not de-biased, in the region where Stokes I is above the 2σ level. The segments show (a) polarization angles and (b) those rotated by 90°, de-biased with the 2σ (0.52 mJy beam−1) cutoff. The diagonal lines denote the major (P.A. = 75°) and minor (165°) axes of the TMC-1A disk (Section 4.2), centered at the protostellar position. The filled ellipse denotes the SMA synthesized beam.
Download figure:
Standard image High-resolution imageTable 3. Results of Gaussian Fitting to the SMA and ALMA 1.3 mm Continuum Images
| Observations | Flux (mJy) | Center | Deconvolved FWHM | P.A. |
|---|---|---|---|---|
| SMA | 169.8 ± 0.9 | 04h39m35.202ˢ4ˢ ± 0.0005s | 0.66'' ± 0.09'' | 66° ± 28° |
| 0.50'' ± 0.10'' | ||||
| ALMA compact | 111.66 ± 0.03 | 04h39m35.199945ˢ ± 0.000003s | 0.2502'' ± 0.0002'' | 75.8° ± 0.1° |
| 0.1542'' ± 0.004'' | ||||
| ALMA extended | 66.8 ± 0.2 | 04h39m35.2017ˢ ± 0.0001s | 1.085'' ± 0.004'' | 73.4° ± 0.3° |
| 0.632'' ± 0.03'' | ||||
Note. The fitting to the ALMA image adopts a double-Gaussian function.
Download table as: ASCIITypeset image
The polarized fraction , where I, Q, and U are the Stokes parameters, is shown in the region where Stokes I is detected above the 2σ level. The orange segments have a uniform length and show the polarization angles in panel (a) and those rotated by 90° in panel (b) that are de-biased with the 2σ level. The polarization fraction is typically ∼10% in the north and east of TMC-1A, where the de-biased polarization is detected. In contrast, the fraction is ≲0.5%, i.e., depolarized in the northeast, center, and southwest. The polarization angle is ∼ −45° from the disk minor axis (Section 4.2) on the northern side of the depolarized layer, while being distributed around ∼+30° from the disk minor axis on the southern side of the depolarized layer. The angle is around the disk minor axis in the eastern extension.
The 90°-rotated segments (Figure 1(b)) are supposed to trace the direction of magnetic fields in the protostar on the 1000 au scale observed with the SMA. The 90° rotated segments have relative angles to the disk minor axis (P.A. ∼−15°; see Section 4.2), ranging from ∼20° to ∼50° in the northwest, while the relative angles range from ∼−80° to ∼−60° in the southeast. The inferred magnetic field morphology shows symmetry with respect to the depolarized layer. The inferred field appears to be drawn from the northeast to the southwest turning the direction at the depolarized layer. When the variation of the field is smaller than an observational beam size, the region appears to be depolarized. Hence, the drawn morphology of the magnetic fields may explain the observed depolarized layer. The depolarization due to such field variation is numerically simulated (Kataoka et al. 2012) and observed in other protostellar systems (e.g., Kwon et al. 2019).
3.2. ALMA Polarized 1.3 mm Continuum
Figure 2 shows the polarization continuum emission at 1.3 mm observed with ALMA. The spatial scale is five times smaller than the SMA figure, Figure 1. The Stokes I emission consists of a compact, strong component (≲50 au in radius or a signal-to-noise ratio of S/N ≳150σ) and an extended component having sizes in radius of ∼200 au in the direction of P.A. = 75° (the disk major axis in Section 4.2) and ∼120 au in the direction of P.A. = 165° (the disk minor axis in Section 4.2) at the 3σ level. The peak intensity and total flux density measured in our ALMA observation are 0.120 Jy beam−1 and 0.236 Jy, respectively. The direction of the major elongation is consistent with previous 1.3 mm observations at a spatial resolution of ∼8 au (Bjerkeli et al. 2016; Harsono et al. 2018). Because the Stokes I emission shows the compact and extended components, double-Gaussian fitting is more appropriate for this Stokes I emission than single-Gaussian fitting is. Double-Gaussian fitting provides a peak position of for the compact component, while for the extended component. We adopt the peak position of the compact component as the protostellar position of TMC-1A in this paper. The deconvolved sizes of the compact and extended components are 0.25'' × 0.15'' (P.A. = 76°) and 1.09'' × 0.63'' (P.A. = 73°), corresponding to 35 × 21 and 153 × 88 au, respectively.
Figure 2. The continuum emission at 1.3 mm observed with ALMA. The contour map shows Stokes I with contour levels of 3, 6, 12, 24,... × σ, where 1σ corresponds to 25 μ Jy beam−1. The color map shows polarization fraction, not de-biased, in the region where Stokes I is above the 3σ level. The segments show (a) polarization angles and (b) those rotated by 90°, de-biased with the 3σ (75 μ Jy beam−1) cutoff. The diagonal lines denote the major (P.A. = 75°) and minor (165°) axes of the TMC-1A disk (Section 4.2), centered at the protostellar position. The filled ellipse denotes the ALMA synthesized beam.
Download figure:
Standard image High-resolution imageThe polarized fraction is shown in the region where Stokes I is detected above the 3σ level. The polarization angles are de-biased with the 3σ level. The polarization fraction is typically ∼0.7% at the center, where the de-biased polarization is detected. This central polarized region is surrounded by a depolarized ring with a radius of ∼40–60 au showing a polarization fraction of ≲0.3%. The polarization angle in the central region is overall in the disk minor axis (Section 4.2), whereas it also has the azimuthal component particularly in the outer part of this region. The results of the Gaussian fitting is summarized in Table 3.
A similar depolarized ring is also reported in the disk around a massive protostar, GGD27 MM1 (Girart et al. 2018). In addition to the ring, the disk around GGD27 MM1 shows spatial distribution of polarization fraction similar to that of TMC-1A: the fraction is ∼1% in an inner part of the disk and >6% in an outer part of the disk. On the other hand, the inner polarization fraction in GGD27 MM1 is higher on the nearside of the disk, from which Girart et al. (2018) suggests that dust settling has not occurred yet in GGD27 MM1. In comparison, the inner polarization in TMC-1A shows symmetric distribution of the polarization fraction and thus could be interpreted as dust settling stronger than in GGD27 MM1. The outer polarization in GGD27 MM1 shows azimuthal directions, which the authors ascribe to self-scattering with optically thin continuum emission. In comparison, the outer polarization direction in TMC-1A is roughly radial, and thus the polarization mechanism in the outer part is unlikely the self-scattering.
In addition to the central polarized component, the de-biased polarization is also detected at ∼100 au north and south of the central protostar, where the polarization fraction is typically ∼10%. The segments in the northern and southern regions have relative angles to the disk minor axis (P.A. = −15°; see Section 4.2) ranging from ∼0° to ∼45° in the northern region, while the relative angles range from ∼0° to ∼35° in the southern region. In other words, the 90°-rotated segments are roughly in the azimuthal direction in the northern and southern regions, as shown in Figure 2(b). The polarization direction in the southern region is more consistent with the SMA result than that in the northern region, although it is difficult to directly compare the SMA and ALMA results because of the spatial scale difference by one order of magnitude. Unlike on the SMA scale, several mechanisms can cause polarization on the 100 au scale around protostars. Potential mechanisms will be discussed in Sections 5.1 and 5.2.
3.3. ALMA CO Isotopologue Lines
Figure 3 shows results of the CO, 13CO, and C18O J = 2−1 lines observed with ALMA. The spatial scale is the same as that of Figure 2. The blue- and redshifted emissions are integrated over the same velocity width, from the systemic velocity, and thus has the same noise level in each panel. The integrated range is divided at 2 km s−1, which roughly corresponds to the Keplerian velocity at the disk radius of TMC-1A, ∼100 au, with the central protostellar mass, ∼0.7 M☉, (Aso et al. 2015) and an inclination angle of 50°–60°. The high-velocity components of the C18O and 13CO emissions (Figure 3(b), (d)) are integrated until the highest velocity at which the emission is detected at the S/N = 3σ. The boundary of the high-velocity (Figure 3(f)) and very-high-velocity (Figure 3(g)) components of the CO emission is the highest velocity at which the blueshifted emission is detected at S/N = 3σ. In these integrated channel maps on the same scale as the continuum image, the entire emission is shown in Appendix A using the integrated intensity (moment 0) and mean velocity (moment 1) maps.
Figure 3. Integrated channel maps of the CO isotopologue lines observed with ALMA. The integrated velocity range relative to Vsys = 6.34 km s−1 (Section 4.3) is denoted in each panel. Blue and red contours show blue- and redshifted emissions, respectively. Contour levels are in 12σ, 24σ, and 36σ steps for C18O, 13CO, and CO, respectively, from 12σ, where 1σ corresponds to (a) 0.9, (b) 1.0, (c) 0.9, (d) 1.2, (e) 0.9, (f) 1.7, and (g) 1.5 mJy beam−1 km s−1. The diagonal lines denote the major (P.A. = 75°) and minor (165°) axes of the TMC-1A disk (Section 4.2), centered at the protostellar position. The filled ellipse at the bottom-left corner of each panel denotes the ALMA synthesized beam.
Download figure:
Standard image High-resolution imageThe C18O emission shows a velocity gradient mainly along the disk major axis (Section 4.2) in both the low- (Figure 3(a)) and high-velocity (Figure 3(b)) components. In addition to this main velocity gradient, the low-velocity component also shows blueshifted emission in the northwest and redshifted emission in the southeast at S/N ≲ 50σ, causing a different, diagonal velocity gradient. This diagonal velocity gradient is reported in Aso et al. (2015) in the low-velocity range <2 km s−1. The low-velocity component of the C18O emission shows double-peaked morphology on both the blue- and redshifted sides, whereas the high-velocity component shows compact, single-peaked morphology on both the blue- and redshifted sides. The double-peaked morphology in the low-velocity range is newly revealed with the higher angular resolution than in Aso et al. (2015).
The 13CO emission shows the same features as the C18O emission: the main velocity gradient along the disk major axis, another diagonal velocity gradient in the low-velocity component at S/N ≲ 120σ, and compact, single-peaked morphology in the high-velocity component. The emission peaks make the main velocity gradient along the disk major axis in both high- and low-velocity components, although the emission peaks are shifted to the north from the disk major axis in the low-velocity component. Emission at low S/N makes the diagonal velocity gradient shown in the low-velocity C18O emission above and that in Aso et al. (2015). The low-velocity emission decreases in the central ∼40 au, i.e., within one beam. This is consistent with the absorption in the 13CO J = 2−1 line due to strong continuum emission at the protostellar position, reported with the observation at an ∼8 au resolution (Harsono et al. 2018).
The CO emission shows more complicated structures than the C18O and 13CO emissions. The fainter, or absorbed, part in the low-velocity component is clearer in the CO line than in the 13CO line. The high-velocity component (Figure 3(f)) clearly traces the associated outflow going along the disk minor axis. Strong emission (S/N > 150σ) shows the main velocity gradient along the disk major axis, the same as the C18O and 13CO emissions. A part of the strong emission is also extended to the north tracing the outflow, as is also seen in the 13CO emission. Weak emission, S/N < 150σ, is extended to the southern side along the disk minor axis in both blue- and redshifted components in the high-velocity range (Figure 3(f)); these structures are not seen in the C18O or 13CO lines. The very-high-velocity component (Figure 3(g)) traces a part of the blueshifted outflow lobe, being more collimated than the high-velocity component (Figure 3(f)). This is consistent with the previous observation showing that emission in the blueshifted lobe is more collimated at higher velocities (Aso et al. 2015).
4. Analyses
4.1. DCF Method
TMC-1A has an infalling rotating envelope around the Keplerian disk. Aso et al. (2015) reported a radial infall velocity of ∼0.3 times the freefall velocity and suggested that a magnetic field of ∼2 mG in strength is required to reduce the infall velocity to the observed value. Our SMA observations enable us to test this suggestion by estimating the field strength. The DCF method (Davis 1951; Chandrasekhar & Fermi 1953) is the most widely used technique for inferring the magnetic field strength from polarization observations (e.g., Kwon et al. 2019). The method assumes that Alfvénic fluctuation dominates the magnetic and velocity fields, with the magnetic field strength Bpos in the plane-of-sky estimated from:
where 〈ρ〉, δ vlos, and δϕ are the mean density, dispersion of the line-of-sight velocity, and dispersion of the polarization angle, respectively. The correction factor ξ is usually taken to be ∼0.5 based on numerical simulations (Heitsch et al. 2001; Ostriker et al. 2001; Padoan et al. 2001).
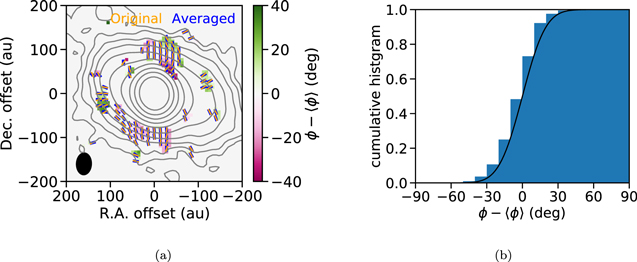
Measuring the angle dispersion δϕ requires an average angle at each position. We define the average angle 〈ϕ〉 by averaging the Stokes Q and U emissions over a 2D Gaussian function with an FWHM of 6''. This Gaussian function is larger than the SMA synthesized beam by a factor of ∼2. This size is selected because the polarized emission is detected over ∼4 beam area. Figure 4(a) shows the average angles as blue segments and the relative angle (ϕ − 〈ϕ〉) as a color map. The dispersion δϕ in Equation (1) is derived as the standard deviation of the relative angle, 21°. Figure 4(b) shows the cumulative histogram of the relative angle overlaid with the error function with a standard deviation of 21°. This histogram indicates that the standard deviation represents the distribution of the relative angle well.
Figure 4. (a) Deviation of polarization angles observed with the SMA from 2 beam averaged angles. The blue segments denote the 2 beam averaged angles 〈ϕ〉. The orange segments, the contour map, and the filled ellipse are the same as those in Figure 1. The coordinates are relative to the protostellar position. (b) Cumulative histogram of the relative polarization angle from the two beam averaged angle, ϕ − 〈ϕ〉. The black curve is the error function with a standard deviation of 21°.
Download figure:
Standard image High-resolution imageThe mean density 〈ρ〉 is derived from the total flux density and the size of the SMA continuum emission. The total flux density 0.182 Jy corresponds to ∼0.024 M☉ for a dust opacity coefficient, index, dust temperature, and gas-to-dust mass ratio of 0.035 cm2 g−1 at 850 μm (Andrews & Williams 2005), 1.46, 28 K (Chandler et al. 1998), and 100, respectively. The SMA continuum emission is detected over ∼500 au in radius at the 3σ level. Averaging the mass of 0.024 M☉ over a sphere of 500 au in radius, we obtain a mean density of ∼3 × 10−17 g cm−3, which is adopted as the mean density 〈ρ〉 in Equation (1).
The velocity dispersion is difficult to measure directly from the observations toward TMC-1A because this protostar is known to have ordered motions, such as rotation and/or radial infall, which are not included in the original DCF method. For this reason, the observed velocity dispersion provides an upper limit of δv in Equation (1). For example, the C18O emission observed in our ALMA observations has a velocity dispersion (standard deviation) of ∼1.0 km s−1 when the emission over the entire spatial area is included.
With the three quantities derived above, as well as the correction factor 0.5, Equation (1) yields Bpol ∼ 3 mG. This estimate is consistent with the prediction in Aso et al. (2015) for explaining the radial infall velocity of ∼0.3 times the freefall velocity in the TMC-1A envelope. We caution the reader that the estimate is very rough because each quantity has a large uncertainty. For example, if the average area for δϕ is changed from 1.5 to 4 beams, δ ϕ−1 would vary by ± 50%. If dust grains grow to such a large size that the dust opacity index is close to zero, would decrease by ∼40%. If the velocity dispersion due to Alfvénic motions is similar to the sound speed at 28 K (Chandler et al. 1998), ∼0.3 km s−1, δv would decrease by a factor of ∼3. When these uncertainties are taken into account, Blos is estimated to be within a range of 1–5 mG.
4.2. Axisymmetric Component Subtraction
The morphology of continuum emission helps us reveal the physical origin of the dust polarization. For this purpose, we investigate the morphology of the 1.3 mm continuum emission in our ALMA observations in this subsection. Specifically, we decompose the continuum emission into an axisymmetric component and a residual through model fitting.
Our axisymmetric model has a radial intensity profile, f(r), centered at (x0, y0). The central coordinates are free parameters, defined as offsets from the protostellar position derived from the double-Gaussian fitting in Section 3.2. This model is scaled along the minor axis direction at θ0 − 90° by a factor of and then convolved with the Gaussian beam with the same FWHM as the ALMA synthesized beam. The P.A. θ0 and the inclination angle i are free parameters. To produce an arbitrary radial profile, f(0 au), f(20 au), f(40 au), ..., f(300 au) are free parameters in this model fitting. The grid spacing of f(r), 20 au, is the half beam of the ALMA observations. Intensities at locations with 300 au but not on the grid radii are interpolated from the grid points, and those beyond 300 au are set to zero. The best-fit parameters are derived by minimizing in the image domain, where fobs, fmod, and σ are the observed intensity, model intensity, and rms noise level of the continuum observations, respectively. For this fitting, we adopt the Markov Chain Monte Carlo method using the open code ptemcee (Foreman-Mackey et al. 2013; Vousden et al. 2016), where the log-likelihood function is −χ2/2. The numbers of temperatures, walkers, and the number of steps are 2, 190, and 10,000, respectively. The first 5000 steps are burnt out. The uncertainties of the parameters are defined as the 10th and 90th percentiles of the parameter chain. The best-fit coordinates and angles, including their uncertainties, are , .
Figure 5 shows the best-fit model with the observation and the residual, and the observation minus the best-fit model. Although the best-fit model reproduces the overall shape of the observation, the residual interestingly shows positive and negative spiral-like patterns. Note that this residual is a relative structure from the axisymmetric component; in other words, a single one-armed spiral plus an axisymmetric component can provide such positive and negative patterns. The orientation angle θ0 = 75° is close to the disk major axis reported in previous works (Harsono et al. 2014; Aso et al. 2015; Bjerkeli et al. 2016), and thus we define this orientation angle as the disk major axis and the orthogonal direction as the disk minor axis of TMC-1A in this paper.
Figure 5. (a) Comparison of the ALMA 1.3 mm continuum and an axisymmetric model. (b) Residual, the observation minus the axisymmetric model, in the gray-scale and contour maps. The contour levels, diagonal lines, and the filled ellipse in both panels are the same as those in Figure 2.
Download figure:
Standard image High-resolution imageTo investigate the spiral-like residual in more detail, we determine the relation between the radius and azimuthal angle along the positive and negative patterns. The intensity-weighted mean position (radius) is derived along the radial direction at every 5°. This mean radius uses intensities above +3σ for the positive pattern and below −3σ for the negative pattern. The derived mean radii are plotted in Figure 6 on the residual map de-projected using the orientation and inclination angles, θ0 = 75° and i = 53°. The red and green points are the mean radii for the positive and negative patterns, respectively. Figure 6 shows that the derived points represent the spiral-like patterns well. The mean radii for the positive pattern (red points) are fitted with a simple logarithmic spiral, , on the de-projected plane, where r and θ are the polar coordinates, while r0 and α are free parameters. The best-fit model is obtained by minimizing on the angle grid, where robs and are the observed mean radii (red points in Figure 6) and the model fit, respectively. The best-fit parameters are r0 = 128 au and α = −0.195. This logarithmic spiral is consistent with the positive pattern as shown in Figure 6 (see the orange curve).
Figure 6. The de-projected residual along the disk minor axis, P.A. = 165° by a factor of . The filled ellipse is the de-projected beam, 0.38° × 0.34° (−17.2°). The diagonal lines are the same as those in Figure 2. The red points are the intensity-mean radius at every 5° of the positive residual, while the red line is an interpolated line. The green points and line are the contour parts for the negative residual. The orange curve is the logarithmic spiral fitted to the red points, , where r and θ are the radius and azimuthal angle in the de-projected plane, and θ is in the unit of radian.
Download figure:
Standard image High-resolution imageThe continuum residual also shows a correlation with the C18O emission. Figure 7 shows the residual map together with the C18O channel maps at a velocity resolution of 0.4 km s−1. One clear correlation can be seen at 4.35–5.15 km s−1 and 7.15–7.95 km s−1. From 2.35–4.35 km s−1, the emission peak moves outward from the protostellar position along the disk major axis. The emission peak arrives at the eastern edge of the positive residual at 4.35 km s−1 and is divided into two peaks in the disk minor axis direction from 4.75 km s−1, not going beyond the eastern edge of the positive residual. Similarly, from 10.35–8.35 km s−1, the emission peak moves outward from the protostellar position along the disk major axis. The emission peak arrives at the western edge of the positive residual at 7.95 km s−1 and is divided into two peaks in the disk minor axis direction from 7.55 km s−1. These results on the eastern and western sides suggest that the C18O emission is also concentrated inside the continuum residual, making the same asymmetry as the continuum residual. The high velocities V < 4.35 km s−1 and V > 8.35 km s−1 correspond to ∣V − Vsys∣ ≳ 2 km s−1. The fact that the emission peak is located along the disk major axis suggests that the C18O emission traces the Keplerian disk around TMC-1A at this velocity range. Furthermore, the emission peak is divided at the lower velocities. This change at ∣V − Vsys∣ ∼ 2 km s−1 suggests that the velocity channels at ∣V − Vsys∣ ∼ 2 km s−1 trace the C18O emission arising from the outer edge of the TMC-1A disk. In other words, the lowest rotational velocity in the TMC-1A disk (at the outer edge) is ∼2 km s−1. This is consistent with the disk radius, ∼100 au, and the central protostellar mass, ∼0.7 M☉, of TMC-1A previously reported by Aso et al. (2015).
Figure 7. Channel maps of the C18O line with contours overlaid on the gray-scale map of the continuum residual. The contour levels are in 10σ steps, where 1σ corresponds to 1 mJy beam−1. The diagonal lines are the same as those in Figure 2. The filled ellipse is the C18O synthesized beam. The velocity of each channel is denoted on the top-left corner of each panel.
Download figure:
Standard image High-resolution imageThe C18O intensity also implies another correlation with the continuum residual. Figure 8 shows the mean intensity of the C18O line on the positive (red in Figure 6) and negative (green in Figure 6) patterns at each velocity channel. The mean intensity on the positive pattern is significantly stronger than the negative one within ∣V − Vsys∣ < 2 km s−1. This suggests intensity enhancement in the C18O line at the same spiral as the intensity enhancement in the continuum emission, in this velocity range. On the other hand, the intensity on the positive pattern is stronger at blueshifted higher velocities (V − Vsys < − 2 km s−1), while the intensity on the negative pattern is stronger at redshifted higher velocities (V − Vsys > 2 km s−1). These differences at higher velocities are consistent with the Keplerian rotation as discussed in more detail in Section 4.3 using a Keplerian disk model; the solid lines without points in Figure 8 are from the model in Section 4.3.
Figure 8. Mean intensities of the C18O line along the positive and negative residuals of the continuum emission as each velocity channel. The vertical lines are Vsys − 2 km s−1, Vsys, and Vsys + 2 km s−1. The light color profiles show the mean intensities of the Keplerian disk model discussed in Section 4.3.
Download figure:
Standard image High-resolution image4.3. Keplerian Rotation and Infall Motion
The analysis in the previous subsection revealed correlations between the spatial distributions of the C18O emission and the continuum residual. In this subsection, the velocity structure of the C18O emission is modeled to help interpret the correlations. TMC-1A is known to have a Keplerian disk (Harsono et al. 2014; Aso et al. 2015; Bjerkeli et al. 2016). Hence, we model the Keplerian disk by fitting with a toy model. The main purpose of this fitting is not to constrain physical conditions of the disk but to derive the distribution of intensity arising from the disk in the position-position–velocity space. The velocity field in the toy model is the Keplerian rotation determined by the central protostellar mass M* and has a uniform line profile described as a Gaussian function with a standard deviation of cs . The systemic velocity is Vsys. The intensity in the model disk is a power-law function of radius up to an outer radius Rout, I100(r/100 au)−p , where r, I100, and p are the radius on the disk plane, a coefficient, and a power-law index, respectively. This intensity field is located on two parallel planes at ± H from the midplane, to mimic the scale height of the disk. The model disk is oriented by θ0 and inclined by i: the angles derived from the fitting to the continuum emission (Section 4.2). This model intensity is convolved with the Gaussian beam having the same FWHM as the C18O observation. In summary, the toy model has seven free parameters, M*, cs , Vsys, I100, p, Rout, and H. The best-fit parameters are derived by minimizing over the velocity range of 1.4–4.4 and 8.4–11.4 km s−1 in the image domain, where fobs. fmod, and σ are the observed C18O intensity, model intensity, and rms noise level of the C18O observation. The best-fit model has the parameters of (M*, cs , Vsys, I100, p, Rout, H) = (0.72 M☉, 0.38 km s−1, 6.34 km s−1, 1.5 mJy pixel−1, 0.48, 150 au, 14 au). The central protostellar mass is consistent with previous work (0.68 M☉; Aso et al. 2015). The best-fit model well reproduces the observed C18O channel maps in the fitted velocity range, as shown in Appendix B. This model also reproduces the mean intensities along the positive and negative residuals in the fitted velocity range, ∣V − Vsys∣ > 2.0 km s−1, as shown in Figure 8.
The Keplerian disk model can be used to inspect non-Keplerian components in the C18O data cube. In particular, it is worth comparing the velocity structure along the positive and negative residuals in the continuum emission with the Keplerian velocity field. For this purpose, Figures 9(a) and (b) show the PV diagrams of the observed C18O emission and the Keplerian disk model along the positive (red in Figure 6) and negative (green in Figure 6) residuals, where the abscissa coordinate is the position angle measured from the north to the east. These diagrams show that the overall velocity structure in the C18O line is the Keplerian rotation. A possible offset of the emission peak can be found in the positive-residual diagram around the minor axis (P.A. = 165°) as highlighted with an arrow in Figure 9(a): the observed velocity structure appears slightly redshifted with respect to the Keplerian disk model by 0.5–0.6 km s−1. This angle corresponds to a radius of 70–80 au on the de-projected plane (Figure 6). The Keplerian velocity at this radius is 2.8–3.0 km s−1 with M* = 0.72 km s−1. The ratio between the offset ∼0.5 km s−1 and the Keplerian velocity 2.8–3.0 km s−1 is consistent with the logarithmic spiral with α ∼ 0.2 derived in Section 4.2, suggesting a flowing motion along the positive residual with a radial infall velocity of ∼0.2 times the rotational velocity. The presence of the infalling component is consistent with the velocity gradient in the minor axis direction mentioned in Section 3.3.
Figure 9. PV diagrams along the positive (left) and negative (right) residuals of the continuum emission. The abscissa value is the position angle from the north to the east. The blue contours show a Keplerian disk model or a Keplerian+infall model. The contour levels are in 10σ steps. The white curve is the velocity field on the midplane. The vertical and horizontal dashed lines denote the disk minor axis and the systemic velocity, respectively. The arrows point to the main difference between the two models. Note that the positive residual prefers the Keplerian+infall model, while the negative residual is better fitted by the Keplerian-only model.
Download figure:
Standard image High-resolution imageFigure 9(c) shows comparison between the observed C18O emission (same as in Figure 9(a)) and an infalling rotating model that has the Keplerian rotation and a radial infall velocity of 0.2 times the Keplerian rotation. The emission peak of this Keplerian+infall model traces the observed peak better around the minor axis than that of the Keplerian disk model, while other parts are similar to each other. In contrast, the emission peak of the Keplerian disk model is more consistent with the observed peak in the negative-residual diagram than that of the Keplerian+infall model (Figure 9(b), (d)), in particular, around the minor axis (P.A. = −15°). This difference implies that only the positive residual has an inflow motion, supporting the possibility that a single one-armed spiral provides both positive and negative patterns as a relative structure with respect to the axisymmetric average component as mentioned in Section 4.2.
The radial infall velocity at r = 70–80 au revealed in this subsection corresponds to ∼14% of the freefall velocity, since the freefall velocity is times the Keplerian velocity. Although the radial infall velocity at outer radii cannot be evaluated from our results, a larger ratio of ∼30% is reported in Aso et al. (2015) at r = 100–200 au. This difference may suggest soft landing of the collapsing envelope material, through the one-armed spiral, onto the outer part of the disk.
5. Discussion
The origin of polarization is not as simple on the disk scale around protostars as on the envelope scale and larger. Polarization on the larger scales, such as that probed by our SMA observations, is generally thought to come from magnetic alignment. We discuss possible origins of the ALMA polarization, as well as that of the accretion flow, in this section.
5.1. Central Polarization
The ALMA polarization shows two components clearly divided by a depolarized ring: central (r ≲ 50 au) and a northern/southern component (Figure 2). The central component shows polarization E vectors along the disk minor axis near the axis and include an azimuthal component near the outer edge. These two morphological features suggest dust self-scattering occurring on the disk surface as the origin of the central polarization. Polarization due to self-scattering is detected in other Class 0 and I protostars (e.g., Lee et al. 2018). Theoretical simulations of self-scattering predict such polarization directions and polarization fractions ∼0.8% to ∼1.0% with inclination angles of 50°–60° (Yang et al. 2017), which is also consistent with the observed polarization fraction. Figure 10 shows the observed polarization fraction as a function of Stokes I. At the radii of the central component r ≲ 50 au, the polarization fraction is independent from Stokes I. This tendency prefers self-scattering to the magnetic alignment. The theoretical simulations suggest that self-scattering requires a high optical depth (τ ≳ 1) to produce a polarization fraction high enough (≳0.5%) to be observed. Previous observations toward TMC-1A indeed reported that the 1.3 mm dust continuum emission is optically thick in a central region with r ≲ 20–30 au (Harsono et al. 2018).
Figure 10. Polarization fraction as a function of Stokes I of the ALMA 1.3 mm continuum emission. The color denotes the radius of each point. The dashed line is the 3σ detection level for the polarization intensity. The data points with the larger point size correspond to the positions where de-biased polarization angles are derived in Figure 2.
Download figure:
Standard image High-resolution imageThe high optical depth in the TMC-1A disk was interpreted as a result of a high opacity due to dust grains with millimeter size (Harsono et al. 2018). Although a massive disk can also produce a high optical depth, such a disk should be gravitationally unstable and thus show some sign of instability on the disk (e.g., spiral arm or fragmentation). Previous observational studies did not show such a sign in the TMC-1A disk at the mm wavelength, preferring the millimeter grain scenario to the massive disk scenario. Millimeter grains are, however, not consistent with the self-scattering origin of polarization because self-scattering requires a maximum grain size of ∼80–300 μm to produce a polarization fraction of ≳1%, while millimeter-sized grains decrease the predicted polarization fraction to ∼0.01% (Kataoka et al. 2016). In addition to the self-scattering-induced polarization, we have revealed a spiral-like residual in the 1.3 mm continuum emission. This structure may hint at the gravitational instability; hence, the high optical depth in the TMC-1A disk could be due to a massive disk. For these reasons, we suggest that dust grains mainly have a size up to a few hundred microns in the TMC-1A disk.
5.2. Northern and Southern Polarization
The northern and southern components of the ALMA polarization are unlikely produced by scattering because of their high polarization fraction, location in the outer part of the disk along the minor axis, and relatively low optical depth. We consider three alternative possibilities. The first possibility is magnetic alignment by toroidal magnetic fields in the disk or outflow associated with TMC-1A. A toroidal field is described by an ellipse elongated along the disk major axis, which is broadly consistent with the 90°-rotated vectors detected with ALMA except for the central component. The polarization fraction in the north/south component is ∼10% and shows an anticorrelation with Stokes I (Figure 10). Such a high polarization fraction is possible with elongated dust particles aligned in a magnetic field, although boundary areas of a structure in interferometric observations can show a relatively high polarization fraction due to a larger filtering effect in Stokes I (Kwon et al. 2019). Kwon et al. (2019) also reported a negative power-law index, −0.4 to −1.0, between the two quantities on a few thousand astronomical unit scale in the protostellar system L1448 IRS 2, where polarization originates in the magnetic alignment. Because the TMC-1A system is inclined from the line of sight, the polarization near the minor axis is expected to be stronger than near the major axis because nonspherical grains rapidly spinning along their magnetically aligned short axis are effectively oblate spheres and such aligned oblate spheres are seen more edge-on near the minor axis and more face-on (and thus more circular with lower polarization) near the major axis (see the top panels of Figure 10 of Cho & Lazarian (2007) or the middle panels of Figure 3 of Yang et al. 2016). In addition, because of the disk inclination, the toroidal fields show a low (high) curvature near (far from) the outflow axis on the projected plane. When magnetic fields have a high curvature, observed polarization can have a low polarization fraction because signals with different polarization directions are summed in an observational beam and canceled out. These two effects could explain the fact that the polarized emission is detected with ALMA mainly in the north and south of the central protostar.
The second possibility is the mechanical alignment called the Gold mechanism by the associated outflow (Gold 1952). Dust grains in the outflow lobe are aligned in the outflow direction by the gas motion, as if each grain is a boat in a river. The aligned grains, then, produce the polarization direction parallel to the outflow direction as observed in our ALMA observations. The TMC-1A outflow shows a projected velocity faster than ∼10 km s−1, indicating that the velocity in this outflow is sufficiently high to provide supersonic gas flow that makes the Gold mechanism efficient (Lazarian 1994). However, because the disk material is expected to be much denser than the outflow material, most of dust emission must be coming from the disk. If the disk emission is not polarized, the intrinsic polarization from the outflow emission must be much higher than the observed 10%, which is unlikely. Furthermore, while the blueshifted outflow spatially coincides with the northern polarization component, there is no clearly detected redshifted outflow that spatially coincides with the southern polarization component. For these reasons, we regard the Gold mechanism as less likely. We should mention that another version of mechanical alignment was studied by Hoang et al. (2018), where the grains are expected to align their long axes perpendicular to the gas flow. It would predict polarization E vectors perpendicular to the minor axis, which are not observed in this component.
The third possibility is magnetic alignment by a magnetic field along the accretion flow suggested in Section 4.3. This possibility is motivated by the fact that the northern polarization is overlapped on the spiral-like residual and the 90° rotated vectors are also along the residual, as shown in Figure 11. This peculiar structure could explain the limited location of the detected polarization. This possibility cannot be applied to the southern polarization because the southern polarization is overlapped on the negative spiral outside the one-armed spiral.
Figure 11. ALMA polarization directions rotated by 90° overlaid on the spiral-like residual in the 1.3 mm Stokes I. The northern polarization shows the vectors (90° rotated) along the spiral-like residual.
Download figure:
Standard image High-resolution image5.3. Comparison of the DCF Method to the ALMA Polarization
The northern and southern components in the ALMA polarized 1.3 mm emission are likely to originate in toroidal magnetic fields in TMC-1A, as discussed in the previous subsection. Then, the DCF method allows us to roughly estimate the field strength, as it does for our SMA data (Section 4.1). The dispersion of the polarization angle is measured from the 2 beam averaged angles using a 2D Gaussian function with an FWHM of ∼0.6''. Note that the central polarization is masked by a threshold of polarization fraction <1% and not used for the average-angle calculation. Figure 12(a) shows the comparison of the original and average angles. The dispersion is calculated to be δϕ = 16° in this case. Figure 12(b) shows the cumulative histogram of the relative angle with the error function with a standard deviation of 16°. The northern and southern components have Stokes I ∼ 0.6 mJy beam−1. This corresponds to a mass column density of 0.12–0.33 g cm−2 on the same dust opacity, temperature, and gas-to-dust mass ratio as in Section 4.1. If this column density is distributed over the scale height of 14 au (Section 4.3), the mean density is 〈ρ〉 = 0.6–1.6 × 10−15 g cm−3. The velocity dispersion is also in the same range of 0.3–1.0 km s−1 as in Section 4.1. Consequently, from Equation (1), the field strength is calculated to be 5–25 mG.
Figure 12. (a) Deviation of polarization angles observed with ALMA from 2 beam averaged angles. The blue segments denote the 2 beam averaged angles 〈ϕ〉. The orange segments, the contour map, and the filled ellipse are the same as those in Figure 2. The coordinates are relative to the protostellar position. (b) Cumulative histogram of the relative polarization angle from the 2 beam averaged angle, ϕ − 〈ϕ〉. The black curve is the error function with a standard deviation of 16°.
Download figure:
Standard image High-resolution image5.4. Accretion Flow
The spiral-like residual suggests a one-armed accretion flow in the TMC-1A disk. A simple interpretation of this flow is occasional mass accretion from the associated envelope. The C18O emission also supports flowing motion along the spiral. Similar morphology is also identified in multiple protostellar systems. Tobin et al. (2016) show a one-armed spiral with a radius of ∼200 au in the triple protostellar system L1448 IRS3B observed in the 1.3 mm continuum emission. Their line observations in C18O J = 2−1 indicate a rotational motion perpendicular to an associated outflow. Takakuwa et al. (2014) show a one-armed spiral with a radius of ∼200 au in the protostellar binary L1551 NE observed in the 0.9 mm continuum emission. The authors reproduced the spiral structure and kinematics observed in the C18O J = 3−2 line using a hydrodynamic simulation. The similarity of the TMC-1A spiral with these multiple systems may hint at gravitational instability in the TMC-1A disk, although the instability may be weaker here so that the spiral can only be seen as the residual from the axisymmetric component.
An inner part of the spiral-like residual also appears to delineate a part of a ring with a radius of ∼50 au. Such a ring may result from the growth front (or the pebble production line; Lambrechts & Johansen 2014), where dust grains drastically grow from micron size to millimeter size. The growth front is estimated to be 50–60 au in radius with the typical age of Class I protostars, 0.1 Myr (Ohashi et al. 2021), which is consistent with the inner part of the spiral-like residual.
6. Conclusions
We have observed the linearly polarized dust continuum emission at 1.3 mm in the Class I protostellar system TMC-1A using the SMA and ALMA at angular resolutions of ∼3'' (400 au) and ∼0.3'' (40 au), respectively. The ALMA observations also included the CO, 13CO, and C18O J = 2−1 lines. The main results are summarized below.
- 1.The SMA polarization observations trace magnetic fields in the TMC-1A envelope on a 1000 au scale. The field directions are between the parallel and perpendicular directions to the outflow axis. We estimate the field strength to be 1–5 mG by applying the DCF method to the SMA polarization. The diagonal direction and mG-order strength of the magnetic field are consistent with the previous prediction by Aso et al. (2015) to explain the radial infall velocity at ∼30% of the freefall velocity.
- 2.We subtract an axisymmetric component from the ALMA continuum emission, Stokes I, and discover a spiral-like residual for the first time in TMC-1A. The de-projected spiral suggests an accretion flow with a radial infall velocity at 20% of the rotational velocity along the spiral-like residual. Comparison of the C18O emission and a Keplerian disk model also supports this ratio between the rotational and radial infall velocities.
- 3.The polarized emission observed with ALMA consist of a central component and a north/south component. The central component can be interpreted as a result of self-scattering because the polarization directions are mostly along the disk minor axis, but with an azimuthal component near the major axis, and the polarization fraction is ∼0.8% independent of the polarization intensity.
- 4.The north/south polarization component is located along the outflow direction (i.e., in the north and south of the protostellar position), and the polarization E vectors are also broadly parallel to the outflow direction. Three potential mechanisms are discussed for this polarization: (1) toroidal magnetic fields in the outflow or disk in this system, (2) mechanical grain alignment by the gaseous outflow, and (3) a magnetically channeled accretion flow as suggested by the spiral-like residual in Stokes I.
This paper makes use of the following ALMA data: ADS/JAO.ALMA#2018.1.00701.S. ALMA is a partnership of ESO (representing its member states), NSF (USA), and NINS (Japan), together with NRC (Canada), MOST and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO, and NAOJ. The Submillimeter Array is a joint project between the Smithsonian Astrophysical Observatory and the Academia Sinica Institute of Astronomy and Astrophysics and is funded by the Smithsonian Institution and the Academia Sinica. W.K. was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (NRF-2021R1F1A1061794). N.H. acknowledges a grant from the Ministry of Science and Technology (MoST) of Taiwan (MoST 109-2112-M-001-023, 110-2112-M-001-048). S.P.L. acknowledges grants from the Ministry of Science and Technology of Taiwan 109-2112-M-007-010-MY3. Z.Y.L. is supported in part by NASA 80NSSC18K1095 and NSF AST-1716259 and 1815784.
Facilities: ALMA - Atacama Large Millimeter Array, SMA. -
Software: APLpy (Robitaille & Bressert 2012), astropy (Astropy Collaboration et al. 2013, 2018), CASA (McMullin et al. 2007), MIR (https://github.com/qi-molecules/sma-mir), MIRIAD (Sault et al. 1995), ptemcee (Foreman-Mackey et al. 2013; Vousden et al. 2016).
Appendix A: Entire Moment Maps of the CO Isotopologue Lines
Figure 13 shows the CO isotopologue line emission in the J = 2−1 transition on the entire envelope scale. The contour maps show the integrated intensity (moment 0), while the color maps show the mean velocity (moment 1). The integrated velocity range is the same as in Figure 3. The spatial scale of the C18O and 13CO maps is four times larger than in Figure 3. These figures have angular resolutions three times higher than our previous observations toward TMC-1A reported in Aso et al. (2015). Overall velocity structures of the C18O envelope and those of the CO outflow are consistent with those in the lower-resolution observation in the same lines. Aso et al. (2015) did not observe the 13CO line, which traces the envelope and a part of the outflow. The higher angular resolution has revealed an excess in both moment 0 and moment 1 in a northern part in the C18O and 13CO maps (Figure 13(a), (c)). The CO emission, particularly in Figure 13(f), is stronger on the eastern, blueshifted side and on the western, redshifted side than the other side. This is consistent with another previous observation at an 8 au resolution (Bjerkeli et al. 2016).
Figure 13. Integrated intensity (moment 0) and mean velocity (moment 1) maps of the CO isotopologue lines observed with ALMA. The spatial scale is four times larger than in Figure 3. The integrated velocity range relative to Vsys = 6.34 km s−1 (Section 4.3) is denoted in each panel. Contour levels are in 12σ, 24σ, and 36σ steps for C18O, 13CO. and CO, respectively, from 12σ, where 1σ corresponds to (a) 1.3, (b) 1.4, (c) 1.3, (d) 1.7, (e) 1.3, (f) 2.4, and (g) 2.1 mJy beam−1 km s−1. The moment 1 maps are masked at the 6σ levels. The diagonal lines denote the major (P.A. = 75°) and minor (165°) axes of the TMC-1A disk (Section 4.2), centered at the protostellar position. The filled ellipse at the bottom-left corner of each panel denotes the ALMA synthesized beam.
Download figure:
Standard image High-resolution imageAppendix B: Comparison of the Keplerian Disk Model
Figure 14 shows comparison between the best-fit Keplerian disk model derived in Section 4.3 and the observed C18O channel maps. The best-fit model reproduces the overall distribution of the C18O emission observed with ALMA in the range of ∣V − Vsys∣ > 2.0 km s−1 (the channels with white backgrounds in Figure 14).
Figure 14. The best-fit Keplerian disk model in Section 4.3 (red) with the observed C18O channel maps (black). The contour levels are in 10σ steps, where 1σ corresponds to 2 mJy beam−1. The filled ellipse is the C18O synthesized beam. The velocity of each channel is denoted on the top-left corner of each panel. The diagonal lines are the same as those in Figure 2. The channels with gray backgrounds are excluded from the fitting for the Keplerian disk in Section 4.3.
Download figure:
Standard image High-resolution image