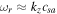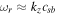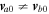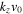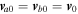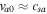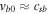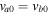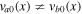Abstract
Theoretical models are presented to show that expansion of plasma in the radial direction from a denser solar surface to a rarefied upper atmosphere with short-scale inhomogeneous field-aligned flows and currents in the form of thin threads itself is an important source of electrostatic instabilities. Multifluid theory shows that the shear flow–driven purely growing electric fields appear in the transition region. On the other hand, plasma kinetic theory predicts that the short-scale current sheets (or filaments) produce current-driven electrostatic ion acoustic (CDEIA) waves in the hydrogen plasma of the transition region that damp out in the system through wave–particle interactions and increase the temperature. Similar processes take place in the solar corona and act positively for increasing the temperature further and maintaining it. The shear flow–driven instabilities and CDEIA waves have short perpendicular wavelengths of the order of 1 m and low frequencies of the order of 1 or several Hz when the ions' shear flow scale length is considered to be of the order of 1 km. It is pointed out that the purely growing fluid instabilities turn into oscillatory instabilities and the growth rates of kinetic CDEIA wave instabilities are reduced when the dynamics of 10% helium ions is taken into account along with 90% hydrogen ions. Therefore, the role of helium ions should not be ignored in the study of wave dynamics in solar plasma.
Export citation and abstract BibTeX RIS
1. Introduction
The solar corona (SC) contains hot rarefied plasma in which collisions are almost negligible. Low-frequency electrostatic waves, such as ion acoustic waves (IAWs) and ion cyclotron waves (ICWs), are damped in such plasmas due to ion Landau damping through wave–particle interactions (Goldstone & Rutherford 1995; Gurnett & Bhattacharjee 2005). This collisionless damping is useful for heating the plasma if, by some source of free energy, such waves can attain finite amplitudes. Therefore, it is interesting to investigate the possibilities of excitation of some low-frequency electrostatic waves in the SC that transfer their energy to charged particles through collisionless damping. On the other hand, it is also important to find out some mechanism for the excitation of electrostatic waves within the transition region (TR) where the temperature of the plasma rises drastically. Landau damping of waves can transfer wave energy to charged particles, which may cause a temperature increase. In addition to oscillatory instabilities, if purely growing electrostatic fields appear in both the TR and SC, they can accelerate charged particles to increase their kinetic energy, as was pointed out about a decade ago (Saleem et al. 2012). In that work, it was shown that the purely growing mode (D'Angelo 1965) appears in the corona, and drift dissipative instability can also occur.
An abrupt increase of the solar plasma temperature from about 6600 K at the surface to a million degrees Kelvin in the corona is still not a well-understood problem. This sudden jump in the magnitude of the temperature occurs when plasma enters from the chromosphere to the corona, passing through the thin TR of thickness of the order of 500 km. The temperature first decreases from 6600 K at the surface to 4400 K at a height of 500 km and starts increasing up to 104 K in the lower chromosphere. Then it increases from 104 K to 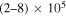 K in the TR and attains a value of
K in the TR and attains a value of 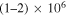 K in the lower corona (Priest 1982; Narain & Ulmschneider 1990; Klimchuk 2006; Slemzin et al. 2014; Tian 2017; Tian et al. 2018). Plasma is expanding in the radial direction adiabatically; therefore, it is counterintuitive that its temperature increases drastically in the outermost low-density region, the corona. It is commonly thought that the source of energy lies within the Sun itself, and energy is transferred from lower regions to the corona by physical mechanisms that are still to be explored and understood. If short-scale electrostatic fields appear in the TR and corona, they can accelerate charged particles to heat them continuously.
K in the lower corona (Priest 1982; Narain & Ulmschneider 1990; Klimchuk 2006; Slemzin et al. 2014; Tian 2017; Tian et al. 2018). Plasma is expanding in the radial direction adiabatically; therefore, it is counterintuitive that its temperature increases drastically in the outermost low-density region, the corona. It is commonly thought that the source of energy lies within the Sun itself, and energy is transferred from lower regions to the corona by physical mechanisms that are still to be explored and understood. If short-scale electrostatic fields appear in the TR and corona, they can accelerate charged particles to heat them continuously.
Kinetic theory shows that an electrostatic drift wave becomes unstable in a hot plasma, and a few authors have suggested that it contributes to the plasma heating in the SC in regions where the density gradient scale length is of the order of 1 km 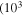 m) and wavelengths are of the order of 1 m (Vranjes & Poedts 2009a, 2009b). In these studies, the short-scale electric fields associated with drift waves have been investigated in the presence of a density gradient, and the magnitude of the electric field has been estimated to be
m) and wavelengths are of the order of 1 m (Vranjes & Poedts 2009a, 2009b). In these studies, the short-scale electric fields associated with drift waves have been investigated in the presence of a density gradient, and the magnitude of the electric field has been estimated to be 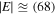 V m−1 assuming
V m−1 assuming 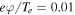 , where φ is the electrostatic potential perturbation, Te
is the electron temperature, and
, where φ is the electrostatic potential perturbation, Te
is the electron temperature, and 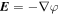 . The IAW is a fundamental low-frequency electrostatic mode of both unmagnetized and magnetized plasmas and can, in principle, appear in the TR and SC, provided that a source of free energy is available. If it is excited, then it will transfer energy to charged particles. Similarly, if the D'Angelo mode appears in the TR, then charged particles will be accelerated to increase the temperature rapidly. A detailed quantitative analysis of the contribution of these waves in the plasma heating in these regions should also be estimated and compared with other proposed models through simulations.
. The IAW is a fundamental low-frequency electrostatic mode of both unmagnetized and magnetized plasmas and can, in principle, appear in the TR and SC, provided that a source of free energy is available. If it is excited, then it will transfer energy to charged particles. Similarly, if the D'Angelo mode appears in the TR, then charged particles will be accelerated to increase the temperature rapidly. A detailed quantitative analysis of the contribution of these waves in the plasma heating in these regions should also be estimated and compared with other proposed models through simulations.
Here we focus our attention on the physical processes that can excite these waves in both the TR and SC. These physical processes naturally occur in solar plasma, where inhomogeneous flows of charged particles along field lines (radial expansion) excite IAWs and D'Angelo modes. The solar atmosphere is filled with jetlike structures (spicules), as well as curved magnetic tubes of hot plasma (loops) that emerge from the regions below the surface and reach heights of thousands of kilometers in the outer layers. Magnetohydrodynamics (MHD) is a good theoretical model to study large-scale phenomena. Therefore, incompressible Alfvén and compressible magnetosonic waves were investigated to explain their role in the heating of the solar outer atmosphere. Braginskii's small damping approximation was not very useful to study incompressible Alfvén waves; therefore, magnetosonic waves were chosen to investigate the heating of the corona by collisional damping of these waves (Porter et al. 1994). The Solar and Heliospheric Observatory (SOHO) and the Transition Region and Coronal Explorer (TRACE) observed waves in coronal plasma structures (Aschwanden et al. 1999; Berghmans & Clette 1999). These observations inspired researchers to study coronal heating by waves. The Japanese satellite Hinode observed Alfvén waves in the chromosphere, the layer between the surface and the corona (De Pontieu et al. 2007). Solar wind acceleration and solar coronal heating were discussed by simulation using Alfvén wave turbulence theory (Holst et al. 2014). The MHD simulations were performed to investigate the heating of loops by the transverse waves, mass ejection, and currents produced by spicules (Magyar & Doorsselaere 2016; De Pontieu et al. 2017; Sykora et al. 2018). Coronal loop heating and density profiles were investigated by analyzing data received from the Atmospheric Imaging Assembly (AIA) on board the Solar Dynamics Observatory (SDO) and Hi-C images (Aschwanden & Peter 2017; Goddard et al. 2017). Phase speed, amplitude, period of Alfvén waves, and seismological inversion of the magnetic field were investigated by 3D numerical simulations (Magyar & Doorsselaere 2018). Kink oscillations and a transverse density profile developed by a nonlinear Kelvin–Helmholtz instability (KHI) in coronal loops were also analyzed though computer simulations (Goddard et al. 2018). Wave heating of the coronal loops was numerically studied by considering the loops as bundles of individual strands (Guo et al. 2019), and a KHI induced by mixed transverse and torsional motions was investigated.
A recent Hi-C rocket detected that the magnetic fields in the loops are twisted and have complex structures (Klimchuk & DeForest 2020). Observations of Skylab, Yohkov, SOHO, and TRACE, through imaging in soft X-rays and the extreme ultraviolet (EUV), indicate that the corona is filled with closed and open magnetic field lines, and only a subset of these structures is loaded with hot plasma at a time (Hara et al. 1992; Litwin & Rosner 1993; Moses et al. 1997; Schrijver et al. 1999). Heating rates in active regions, the quiet Sun, and coronal holes have been estimated using observational data (Aschwanden 2001).
Plasma flows are ubiquitous in the solar atmosphere and have been observed in the quiet Sun (Brekke et al. 1997a), macrospicules (Pike & Harrison 1997), active region loops (Brekke et al. 1997b; Qiu et al. 1999; Schrijver et al. 1999; Zacharias et al. 2018; Johnston & Bradshaw 2019), and the TR (Chae et al. 1998; Brekke 1999; Peter & Judge 1999). Flows in coronal loops have also been investigated theoretically (Craig & McClymont 1986; Peres et al. 1992; Robb & Cally 1992).
Many theoretical models have been presented for coronal heating (Mandrini et al. 2000; Xie et al. 2017). Plasma heating by waves is considered to be one of the attractive mechanisms of temperature increase in the corona. Theories for coronal heating based on low-frequency electromagnetic Alfvén waves have been presented by several authors (Ionson 1983; Mok 1987; Poedts et al. 1989, 1990; Steinolfson & Davila 1993; Hollweg & Sterling 1994; Poedts et al. 1994; Ofman et al. 1995; Poedts & Goedbloed 1997).
About two decades ago (Aschwanden 2001), important conclusions were drawn about the problem of solar coronal heating from the observations of SOHO and TRACE by comparing the data with previous theoretical models. It was shown that the theoretical models that consider the coronal loops as homogeneous magnetized plasma tubes could not agree with observations because the heated denser plasma enters into the corona from the lower chromosphere and TR. Therefore, only those theoretical models that take into account the effects of inhomogeneities in flow, density, and temperatures of plasma species can be reasonable. The corona has filaments of different sizes (De Pontieu et al. 2007), and even the scale sizes of 1 km in the corona have been discussed (Woo 1996). Several theoretical models have been presented to explain the observed phenomenon of solar coronal heating, but it is still difficult to have a consensus on any one single model (Mandrini et al. 2000; Aschwanden 2001). However, a lot of progress has been made in this direction, and the wave heating mechanisms have attracted the attention of many researchers. Detailed analysis of the observations shows that the loop structures are not uniform but rather consist of threads and strands (Woo 1996; De Pontieu et al. 2007; Aschwanden & Peter 2017; Goddard et al. 2017; De Pontieu et al. 2017; Klimchuk & DeForest 2020). Since hydrogen and helium ions have high temperatures (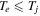 , where the subscript j denotes hydrogen or helium ions and e denotes electrons), a kinetic approach is also needed to consider wave–particle interaction.
, where the subscript j denotes hydrogen or helium ions and e denotes electrons), a kinetic approach is also needed to consider wave–particle interaction.
The short-scale currents and inhomogeneous parallel flows of plasma species can create unstable purely growing and oscillatory electric fields in the TR and corona, giving rise to an increase in temperatures. The CDEIA waves have already been investigated in pure oxygen (Gavrishchaka et al. 1998) and the oxygen hydrogen plasma of the upper ionosphere (Saleem et al. 2017; Saleem & Shan 2020). Shear in a field-aligned flow of ions relative to electron fluid produces a purely growing instability (D'Angelo 1965) in the usual single ion species plasma provided that the shear in the flow is along a positive x-axis if the ambient magnetic field has a direction along the z-axis 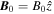 . On the other hand, if the shear in the flow is negative, i.e., along a negative x-axis, then the dispersion relation of IAWs is modified, and a nonresonant mode with zero real frequency does not occur. These modified IAWs are stable in a single ion species plasma. On the other hand, if the shear flow is positive and the plasma contains two kind of ions, then the purely growing instability may turn into a rapidly growing oscillatory instability. In magnetized plasma, IAWs propagate obliquely, making a small angle with the external magnetic field. The parallel wavelengths of the waves are much longer than the perpendicular wavelengths because
. On the other hand, if the shear in the flow is negative, i.e., along a negative x-axis, then the dispersion relation of IAWs is modified, and a nonresonant mode with zero real frequency does not occur. These modified IAWs are stable in a single ion species plasma. On the other hand, if the shear flow is positive and the plasma contains two kind of ions, then the purely growing instability may turn into a rapidly growing oscillatory instability. In magnetized plasma, IAWs propagate obliquely, making a small angle with the external magnetic field. The parallel wavelengths of the waves are much longer than the perpendicular wavelengths because 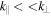 , where k∥ and k⊥ are the parallel and perpendicular components of the wavevector with respect to the external magnetic field
, where k∥ and k⊥ are the parallel and perpendicular components of the wavevector with respect to the external magnetic field 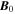 . If the perpendicular wavelength, say
. If the perpendicular wavelength, say 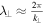 , is comparable to the ion Larmor radius
, is comparable to the ion Larmor radius 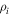 , then the IAW is heavily Landau damped in the plasma due to wave–particle interaction, which can be taken into account through plasma kinetic theory (Goldstone & Rutherford 1995; Gurnett & Bhattacharjee 2005). The dynamics of the electrons and ions can be defined with fluid equations if the ion Larmor radius is much smaller than the perpendicular wavelength, i.e.,
, then the IAW is heavily Landau damped in the plasma due to wave–particle interaction, which can be taken into account through plasma kinetic theory (Goldstone & Rutherford 1995; Gurnett & Bhattacharjee 2005). The dynamics of the electrons and ions can be defined with fluid equations if the ion Larmor radius is much smaller than the perpendicular wavelength, i.e., 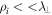 , because in this case, the wave–particle interaction effects are negligibly small. Fluid theory predicts that in a bi-ion plasma, the long-wavelength IAWs may become unstable if the shear in the field-aligned flow is in a positive x-direction (Saleem et al. 2017; Saleem & Shan 2020). On the other hand, kinetic theory shows that IAWs can become unstable if the electron current parallel to the external magnetic field is nonzero (Goldstone & Rutherford 1995) in a single ion species plasma.
, because in this case, the wave–particle interaction effects are negligibly small. Fluid theory predicts that in a bi-ion plasma, the long-wavelength IAWs may become unstable if the shear in the field-aligned flow is in a positive x-direction (Saleem et al. 2017; Saleem & Shan 2020). On the other hand, kinetic theory shows that IAWs can become unstable if the electron current parallel to the external magnetic field is nonzero (Goldstone & Rutherford 1995) in a single ion species plasma.
The Sun contains about 90% hydrogen and 10% helium, while the heavier elements are less than 0.1% (Priest 1982). In bi-ion plasma, the nonresonant mode may develop a small real frequency to become a rapidly growing oscillatory instability (Saleem et al. 2007a). Therefore, it is important to consider the role of helium ions 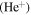 in the short-scale electrostatic instabilities. Using the multifluid plasma model for wavelengths much larger than the Larmor radius of the ions, it was shown that in the presence of a field-aligned shear flow and density gradient, the electrostatic drift waves can become unstable in spicules (Saleem et al. 2007b) and the SC (Saleem et al. 2012). In the plasma of electrons (e), hydrogen ions
in the short-scale electrostatic instabilities. Using the multifluid plasma model for wavelengths much larger than the Larmor radius of the ions, it was shown that in the presence of a field-aligned shear flow and density gradient, the electrostatic drift waves can become unstable in spicules (Saleem et al. 2007b) and the SC (Saleem et al. 2012). In the plasma of electrons (e), hydrogen ions  , and helium ions
, and helium ions 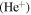 , rapidly growing electrostatic instabilities occur throughout the TR and corona.
, rapidly growing electrostatic instabilities occur throughout the TR and corona.
Two mechanisms are necessary to maintain the high temperature of the corona. One is the entry of heated plasma from lower regions into the corona, as mentioned above, and the second is the acceleration of charged particles by unstable electric fields arising in the corona itself. The first requires the excitation of electrostatic waves in the TR, and the second needs the excitation of such waves in the corona. Unstable electrostatic waves in both these regions of the Sun will be discussed using multifluid plasma theory and the plasma kinetic approach.
Our aim is twofold.
- I.It will be shown that the purely growing shear flow–driven instability turns into a rapidly growing oscillatory instability in the hydrogen–helium plasma of the solar atmosphere. The real frequencies of the unstable electrostatic waves are of the order of 1 Hz, and the perpendicular wavelengths are very short, of the order of 1 m, while the inhomogeneity scale length of the field-aligned shear flow is considered to be about 1 km. The parallel wavelengths are in the range of several kilometers. For this case, multifluid plasma theory is used.
- II.It will also be pointed out that when the electron parallel current is nonzero and the ions' shear flow is negative, current-driven electrostatic ion acoustic (CDEIA) waves appear in the hydrogen–helium plasma of both the TR and SC. For the CDEIA waves, plasma kinetic theory is used.
2. Physical Model
We consider local regions using Cartesian geometry with an external magnetic field 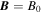
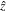 and a field-aligned shear flow of plasma species
and a field-aligned shear flow of plasma species 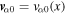
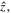 where subscript
where subscript  , and
, and 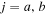 denotes electrons and ions, respectively. Here a is for hydrogen (H) and b is for helium (He) ions. Nonuniformity in the field-aligned flow can give rise to nonresonant and resonant electrostatic modes, which accelerate the charged particles randomly and convert flow energy into heat energy. An important point to note is that if only one kind of ion (
denotes electrons and ions, respectively. Here a is for hydrogen (H) and b is for helium (He) ions. Nonuniformity in the field-aligned flow can give rise to nonresonant and resonant electrostatic modes, which accelerate the charged particles randomly and convert flow energy into heat energy. An important point to note is that if only one kind of ion (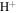 ) is considered, then the field-aligned shear flow does not produce oscillatory instabilities; rather, it generates only a purely growing electrostatic mode. In (H–He) plasma, instead of one purely growing mode (D'Angelo mode), we obtain two purely growing modes: one corresponding to hydrogen ions (
) is considered, then the field-aligned shear flow does not produce oscillatory instabilities; rather, it generates only a purely growing electrostatic mode. In (H–He) plasma, instead of one purely growing mode (D'Angelo mode), we obtain two purely growing modes: one corresponding to hydrogen ions (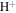 ) and the other to helium ions (He+).
) and the other to helium ions (He+).
The presence of helium ions is necessary to consider because their contribution is very important in the generation of unstable electrostatic oscillatory fluctuations in both the TR and corona when there is even a very small difference in the magnitudes of the 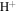 and He+ ion velocities, for example, if
and He+ ion velocities, for example, if 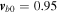
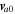 or
or 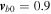
 . If the velocities are exactly equal, i.e.,
. If the velocities are exactly equal, i.e., 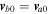 , then there appear only purely growing modes or stable IAWs modified by the presence of helium ions (He+).
, then there appear only purely growing modes or stable IAWs modified by the presence of helium ions (He+).
In the solar atmosphere, ions are hot, and the temperatures of both kinds of ions (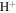 , He+) are equal to or larger than the electron temperature (
, He+) are equal to or larger than the electron temperature (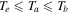 ); therefore, wave–particle interaction will not allow IAWs to grow according to kinetic theory. In hot ion plasmas, the IAW can become unstable by the parallel electron current, which is called the CDEIA wave. Assuming that the electrons move faster than the ions, we shall also discuss the CDEIA waves.
); therefore, wave–particle interaction will not allow IAWs to grow according to kinetic theory. In hot ion plasmas, the IAW can become unstable by the parallel electron current, which is called the CDEIA wave. Assuming that the electrons move faster than the ions, we shall also discuss the CDEIA waves.
In the present work, the excitation of IAWs is considered in the expanding plasma of the solar atmosphere using both fluid and kinetic theories. It is demonstrated using fluid theory that in the hydrogen–helium (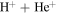 ) plasma of the solar atmosphere, a very small difference in the magnitudes of the field-aligned shear flows of
) plasma of the solar atmosphere, a very small difference in the magnitudes of the field-aligned shear flows of  and He+ ions generates short-scale electrostatic waves with frequencies closer to IAWs with large growth rates.
and He+ ions generates short-scale electrostatic waves with frequencies closer to IAWs with large growth rates.
The present theoretical model is an effort to investigate the following physical processes.
- 1.Generation of two purely growing low-frequency electrostatic modes in the TR and SC using multifluid theory.
- 2.Generation of oscillatory instabilities by the fluid model with real frequencies closer to IAW speeds corresponding to hydrogen and helium ions, i.e.,
 or
or  . Note that when
. Note that when  , the real frequency does not remain equal to
, the real frequency does not remain equal to  , which happens when
, which happens when  . If
. If  or
or  , then it is not possible to differentiate between IAWs and shear flow–driven unstable electrostatic waves.
, then it is not possible to differentiate between IAWs and shear flow–driven unstable electrostatic waves. - 3.Creation of CDEIA waves using kinetic theory in the TR and corona. In this treatment, the shear in the ions' flow is assumed to be negative to obtain analytical results by expanding the plasma dispersion functions. The phase speed of the IAWs shifts away from the region of heavy Landau damping (Gavrishchaka et al. 1998).
3. Fluid Approach
The equation for momentum conservation in collisionless plasma for the jth ion species is
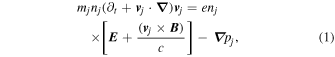
and for mass conservation, it is
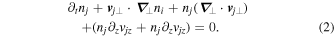
The perpendicular component of velocity 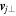 is obtained by the cross product of Equation (1) with the unit vector
is obtained by the cross product of Equation (1) with the unit vector  for the jth ions,
for the jth ions,
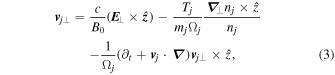
where 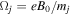 is the ion gyrofrequency. Using back-substitution for low-frequency perturbations, i.e.,
is the ion gyrofrequency. Using back-substitution for low-frequency perturbations, i.e., 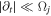 in homogeneous-density plasma, the above equation becomes
in homogeneous-density plasma, the above equation becomes
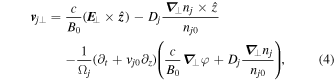
where 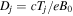 , and it yields
, and it yields

The parallel component of Equation (1) can be written as
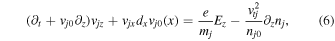
where 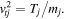
Using a Fourier transform, Equations (5) and (6) become, respectively,

and
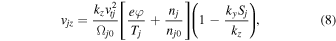
where 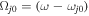 ,
, 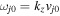 ,
, 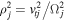 , and
, and  .
.
Then, the continuity equation yields
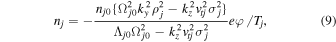
where 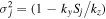 and
and 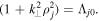
Electrons are considered to be inertialess in the low-frequency limit 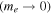 ; hence, they follow a Boltzmann density distribution,
; hence, they follow a Boltzmann density distribution,
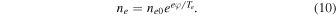
Helium ions can be singly or doubly charged; therefore, we use quasi-neutrality,
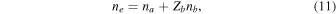
where  or
or  Using Equation (9) for ions a and b along with Equation (10) in Equation (11), we obtain the linear dispersion relation as
Using Equation (9) for ions a and b along with Equation (10) in Equation (11), we obtain the linear dispersion relation as
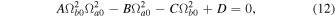
where
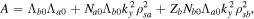
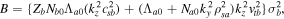
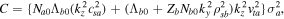
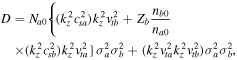
while 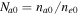 and
and 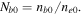 We consider long-wavelength perturbations
We consider long-wavelength perturbations 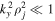 for the application of the fluid theory, which implies that
for the application of the fluid theory, which implies that 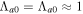 , and assume
, and assume 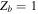 (for singly charged helium ions). In this case. Equation (12) reduces to
(for singly charged helium ions). In this case. Equation (12) reduces to
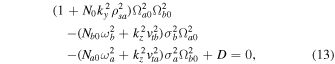
where  ,
, 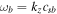 , and
, and 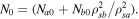 If we use the limit
If we use the limit 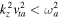 and
and  for
for 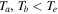 , then the factor D becomes smaller and can be ignored. In this case, Equation (13) becomes
, then the factor D becomes smaller and can be ignored. In this case, Equation (13) becomes

Note that Equation (14) can also be obtained using kinetic theory under certain conditions and will be solved for the case of negative shear in the ions' flow, i.e., 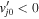 , in the next section.
, in the next section.
If only hydrogen plasma is considered for 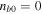 and
and 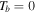 , then Equation (13) reduces to
, then Equation (13) reduces to
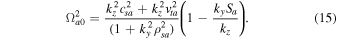
If
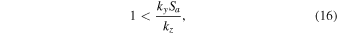
then the usual purely growing instability (D'Angelo 1965) takes place, and IAWs do not appear.
3.1. Fluid Instabilities for 
If both 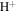 and He+ have exactly equal magnitudes of parallel velocities, i.e.,
and He+ have exactly equal magnitudes of parallel velocities, i.e., 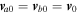 , then Equation (13) becomes
, then Equation (13) becomes
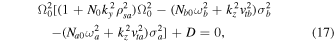
where 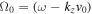 . If
. If 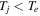 , then the factor D can be neglected, and we obtain
, then the factor D can be neglected, and we obtain
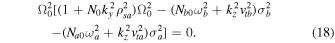
Two of the four roots are  , and the other two roots of Equation (18) are
, and the other two roots of Equation (18) are

Equation (18) is the modified linear dispersion relation of IAWs in bi-ion plasma having a parallel shear flow if
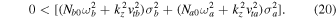
On the other hand, a purely growing instability occurs if
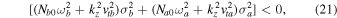
which is possible for 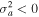 and
and 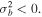 In a certain range of parameters, only
In a certain range of parameters, only 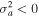 may be sufficient to satisfy Equation (21).
may be sufficient to satisfy Equation (21).
3.2. Effects of Velocity Difference 
In this case, 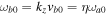 ,
, 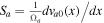 ,
, 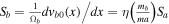 ,
, ![${\sigma }_{a}^{2}=\left[1-\tfrac{{k}_{y}}{{k}_{z}}{S}_{a}\right]$](https://content.cld.iop.org/journals/0004-637X/922/1/48/revision1/apjac05cbieqn84.gif) , and
, and ![${\sigma }_{b}^{2}=\left[1-\tfrac{{k}_{y}}{{k}_{z}}\eta \left(\tfrac{{m}_{b}}{{ma}}\right){S}_{a}\right]$](https://content.cld.iop.org/journals/0004-637X/922/1/48/revision1/apjac05cbieqn85.gif) . For a negative shear flow
. For a negative shear flow 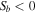 , we have
, we have 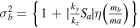 and
and 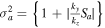 . The dispersion relation (Equation (14)) can be rewritten as
. The dispersion relation (Equation (14)) can be rewritten as
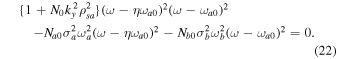
If  is assumed, then
is assumed, then 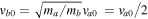 . Thus, we may choose
. Thus, we may choose 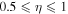 to investigate the effects of an equal and slightly different magnitude of the shear flow velocities of the two ion species, such as
to investigate the effects of an equal and slightly different magnitude of the shear flow velocities of the two ion species, such as  in local regions.
in local regions.
4. Kinetic Approach
Here we present a kinetic approach to investigating the low-frequency electrostatic perturbations in the hydrogen–helium plasma of the solar atmosphere having short-scale nonuniform velocities of ions and electrons. The Vlasov–Poisson system of equations for  yields the kinetic plasma dispersion relation,
yields the kinetic plasma dispersion relation,
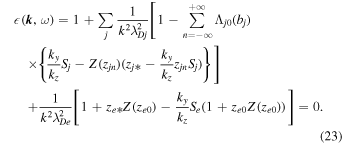
Here 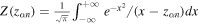 is defined as the plasma dispersion function,
is defined as the plasma dispersion function, 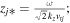
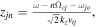
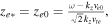
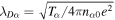 is the Debye radius,
is the Debye radius, 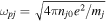 ion plasma frequency,
ion plasma frequency, 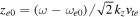 ,
, 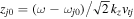 ,
, 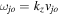 ,
, 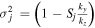 ,
, 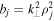 and
and 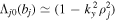 for
for 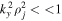 . For
. For 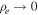 and
and 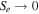 , the dielectric constant given in Equation (23) can be decomposed into real and imaginary parts as
, the dielectric constant given in Equation (23) can be decomposed into real and imaginary parts as
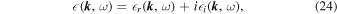
where 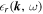 and
and 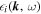 are given in the following:
are given in the following:
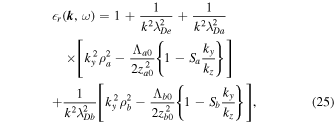
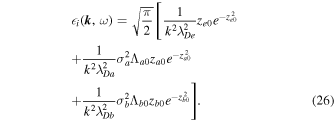
The plasma dispersion functions have been expanded for ions in the limit  and electrons in the limit
and electrons in the limit  to obtain Equations (25) and (26).
to obtain Equations (25) and (26).
The linear dispersion relation is obtained using  in the limit
in the limit  ; hence, it yields
; hence, it yields

This equation contains ion Larmor radius effects and reduces to the fluid Equation (14) for 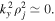
The general expression for the growth/damping rate ![${\gamma }_{{ab}}=-{\epsilon }_{i}({\boldsymbol{k}},\omega )/[\partial {\epsilon }_{r}({\boldsymbol{k}},\omega )/\partial \omega ]$](https://content.cld.iop.org/journals/0004-637X/922/1/48/revision1/apjac05cbieqn116.gif) becomes
becomes
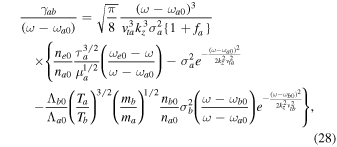
where 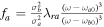 ,
, 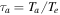 ,
, 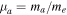 ,
, 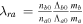 , and
, and 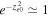 have been used.
have been used.
In this expression, we can obtain the case of pure hydrogen plasma by putting  . But in the solar atmosphere, we have
. But in the solar atmosphere, we have 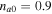 ne0 and
ne0 and 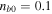 ne0.
ne0.
Let us consider a slab of thickness La in the x-direction, where the field-aligned flow varies linearly such that
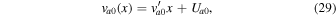
where  , and
, and  .
.
If both the 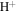 and He+ ions are assumed to flow with the same velocity along
and He+ ions are assumed to flow with the same velocity along 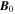 , i.e.,
, i.e., 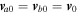 , then the linear dispersion relation (Equation (27)) and normalized growth rate
, then the linear dispersion relation (Equation (27)) and normalized growth rate 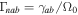 can be written, respectively, as
can be written, respectively, as

and
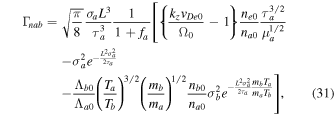
where  ,
, 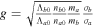 ,
, 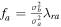 ,
, 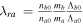 , and
, and  . Note that Equation (27) also has two other roots,
. Note that Equation (27) also has two other roots, 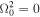 , which have been discarded.
, which have been discarded.
For the case of pure hydrogen plasma ( ), we obtain L = 1,
), we obtain L = 1, 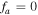 , and g = 0; then, for
, and g = 0; then, for 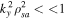 , Equation (30) becomes
, Equation (30) becomes
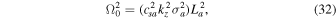
where 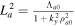 , and Equation (31) reduces to
, and Equation (31) reduces to
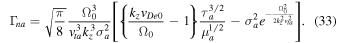
For a plasma without flow, Equation (33) becomes (Goldstone & Rutherford 1995)
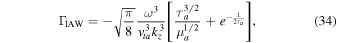
where 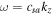 can be approximated to estimate the growth rate. The factor
can be approximated to estimate the growth rate. The factor  denotes the ion Landau damping factor of the IAW in a stationary H plasma. A purely growing instability is basically a fluid instability; therefore, to study the short-scale electrostatic instabilities in the TR and SC driven by shear flows of plasma species, we shall use multifluid plasma theory. On the other hand, CDEIA waves are produced when the electron parallel current contribution dominates over the ion Landau damping effect because the real frequency of the waves shifts away from the region of heavy Landau damping when
denotes the ion Landau damping factor of the IAW in a stationary H plasma. A purely growing instability is basically a fluid instability; therefore, to study the short-scale electrostatic instabilities in the TR and SC driven by shear flows of plasma species, we shall use multifluid plasma theory. On the other hand, CDEIA waves are produced when the electron parallel current contribution dominates over the ion Landau damping effect because the real frequency of the waves shifts away from the region of heavy Landau damping when 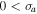 in single ion species plasma (Gavrishchaka et al. 1998). We shall investigate CDEIA waves in the bi-ion plasma of the solar atmosphere through the Vlasov–Poisson set of equations.
in single ion species plasma (Gavrishchaka et al. 1998). We shall investigate CDEIA waves in the bi-ion plasma of the solar atmosphere through the Vlasov–Poisson set of equations.
5. Plasma Scales and Theoretical Models
For realistic applications of the abovementioned theoretical models, the plasma parameters, used values of wavelengths, and chosen values of scale lengths of inhomogeneous flows should be clearly understood. Since temperatures and flows vary in different regions, the values of these parameters will be varied in our examples in Sections 6 and 7. To demonstrate the validity of our theoretical model to the solar atmosphere clearly, we write all of the plasma parameters in the TR and SC, along with the chosen values of the flow velocities and temporal and spatial scales that satisfy the approximations/assumptions used in deriving the analytical results. In the following subsections, we evaluate the plasma parameters for fixed values of Te , Ta , Tb , and va0, and in Sections 6 and 7, the values of these parameters will be varied in a small range around these values in different examples.
5.1. TR Plasma
Let us consider in the TR 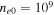 cm−3,
cm−3, 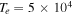 K, and
K, and 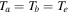 to estimate the plasma parameters. These values yield
to estimate the plasma parameters. These values yield 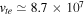 cm s−1,
cm s−1, 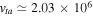 cm s−1,
cm s−1, 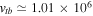 cm s−1,
cm s−1, 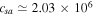 cm s−1,
cm s−1, 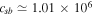 cm s−1,
cm s−1, 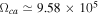 rad s−1,
rad s−1, 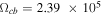 rad s−1,
rad s−1, 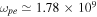 rad s−1,
rad s−1, 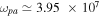 rad s−1 (
rad s−1 ( rad s−1 if
rad s−1 if 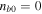 is assumed),
is assumed), 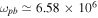 rad s−1,
rad s−1, 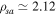 cm,
cm,  cm,
cm, 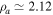 cm,
cm, 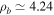 cm, and
cm, and 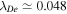 cm, whereas
cm, whereas 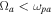 and
and 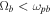 . Furthermore, in the TR, the higher-density
. Furthermore, in the TR, the higher-density 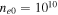 cm−3 can also be considered.
cm−3 can also be considered.
5.2. Solar Coronal Plasma
In the SC, the temperatures of the species are higher than in the TR, so we consider  K and
K and 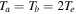 , whereas
, whereas 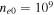 cm−3 and
cm−3 and 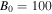 G. These values yield
G. These values yield 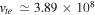 cm s−1,
cm s−1,  cm s−1,
cm s−1, 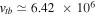 cm s−1,
cm s−1,  cm s−1,
cm s−1, 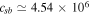 cm s−1,
cm s−1, 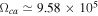 rad s−1,
rad s−1, 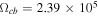 rad s−1,
rad s−1, 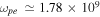 rad s−1,
rad s−1, 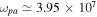 rad s−1 (
rad s−1 (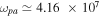 rad s−1 if
rad s−1 if 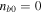 is assumed),
is assumed), 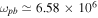 rad s−1,
rad s−1, 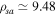 cm,
cm, 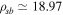 cm,
cm, 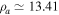 cm,
cm, 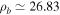 cm, and
cm, and 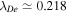 cm, whereas
cm, whereas  and
and 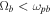 .
.
5.3. Validity of Assumptions and Approximations
Shear flow–driven instabilities are investigated using the fluid model, where the shear in the ions' flow is assumed to be in the positive x-direction, i.e., 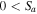 , and in this case, the purely growing D'Angelo instability (D'Angelo 1965) occurs for
, and in this case, the purely growing D'Angelo instability (D'Angelo 1965) occurs for 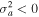 in a single ion species plasma. The validity of fluid theory demands
in a single ion species plasma. The validity of fluid theory demands 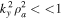 . We are studying the shear flow–driven instabilities in H and H–He plasma in the solar atmosphere; therefore, we require
. We are studying the shear flow–driven instabilities in H and H–He plasma in the solar atmosphere; therefore, we require 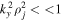 .
.
Current-driven electrostatic instabilities are studied through the Vlasov–Poisson system of equations assuming the shear in the ions' flow to be negative, i.e., 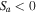 , which modifies the linear dispersion relation of IAWs. In 1998, the CDEIA waves were investigated using kinetic theory in the pure oxygen plasma of the upper ionosphere (Gavrishchaka et al. 1998). In that work, the shear in the flow was assumed to be negative, and
, which modifies the linear dispersion relation of IAWs. In 1998, the CDEIA waves were investigated using kinetic theory in the pure oxygen plasma of the upper ionosphere (Gavrishchaka et al. 1998). In that work, the shear in the flow was assumed to be negative, and  (where our a should denote oxygen plasma in that work); hence, the dispersion relation of the IAW was modified. In this case, D'Angelo instability does not take place. Two real roots of the modified IAW were obtained, and it was found that one of the roots becomes unstable due to a parallel electron flow for
(where our a should denote oxygen plasma in that work); hence, the dispersion relation of the IAW was modified. In this case, D'Angelo instability does not take place. Two real roots of the modified IAW were obtained, and it was found that one of the roots becomes unstable due to a parallel electron flow for 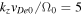 . This implies that the electron flow velocity was larger than the ion flow velocity. We study CDEIA waves in the bi-ion plasma of the solar atmosphere, which contains short-scale currents and flows. In the kinetic model, analytical expressions for the real dispersion relation (Equation (27)) and growth rate (Equation (28)) have been obtained for
. This implies that the electron flow velocity was larger than the ion flow velocity. We study CDEIA waves in the bi-ion plasma of the solar atmosphere, which contains short-scale currents and flows. In the kinetic model, analytical expressions for the real dispersion relation (Equation (27)) and growth rate (Equation (28)) have been obtained for  and
and  . The condition
. The condition 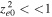 is generally valid for low-frequency waves, even for
is generally valid for low-frequency waves, even for 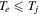 , but the condition
, but the condition 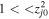 needs a careful choice of parameters. It is important to mention that we have assumed the factor
needs a careful choice of parameters. It is important to mention that we have assumed the factor 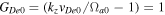 in our calculations for normalized growth rates, which implies
in our calculations for normalized growth rates, which implies
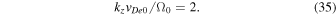
Using this equation, we can also estimate the magnitude of the electron velocity vDe0.
Local approximation must hold in both regions. We choose a fixed value of the dimensionless parameter 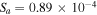 . For example, if the thickness of the slab of varying flow in the TR is assumed to be
. For example, if the thickness of the slab of varying flow in the TR is assumed to be 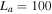 m,
m, 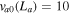 km s–1, and
km s–1, and 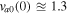 km s–1, it yields
km s–1, it yields 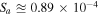 . Let us choose a perpendicular wavelength
. Let us choose a perpendicular wavelength 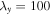 cm, which corresponds to
cm, which corresponds to 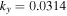 cm−1; hence, the local approximation
cm−1; hence, the local approximation  remains valid. The same value of Sa
is used in the SC assuming
remains valid. The same value of Sa
is used in the SC assuming 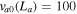 km s–1,
km s–1, 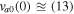 km s–1, and
km s–1, and 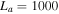 m. Thus, we can vary the magnitudes of the flow velocities in different regions assuming the same value of Sa
.
m. Thus, we can vary the magnitudes of the flow velocities in different regions assuming the same value of Sa
.
6. Application of Fluid Theory
Here the solutions of the dispersion relation (Equation (12)) are discussed in hot ion plasmas in both the TR and SC in the long-wavelength limit 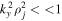 . These short-scale unstable electrostatic fields will accelerate the charged particles and damp in the system, causing an increase in temperature. The effects of wave–particle interactions and the electron parallel current will be taken into account through a kinetic approach in the next section.
. These short-scale unstable electrostatic fields will accelerate the charged particles and damp in the system, causing an increase in temperature. The effects of wave–particle interactions and the electron parallel current will be taken into account through a kinetic approach in the next section.
In a two-ion plasma, if the flow speeds of both ions are assumed to be the same, i.e., 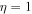 , then the purely growing instability condition is modified by the presence of the second kind of ion given by inequality (Equation (21)). However, if the flow speeds of both kinds of ion are different, i.e.,
, then the purely growing instability condition is modified by the presence of the second kind of ion given by inequality (Equation (21)). However, if the flow speeds of both kinds of ion are different, i.e.,  and
and  holds, then the purely growing instabilities develop real parts of frequencies as well. Generally, the real parts are smaller than or closer to imaginary frequencies. This indicates that the shear flow gives rise to rapidly growing electrostatic oscillatory instabilities. If the real parts of frequencies are closer to
holds, then the purely growing instabilities develop real parts of frequencies as well. Generally, the real parts are smaller than or closer to imaginary frequencies. This indicates that the shear flow gives rise to rapidly growing electrostatic oscillatory instabilities. If the real parts of frequencies are closer to 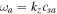 or
or 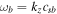 , which happens when
, which happens when  or
or 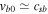 , then we cannot differentiate between shear flow–driven instabilities and IAWs. When the flow has a larger magnitude,
, then we cannot differentiate between shear flow–driven instabilities and IAWs. When the flow has a larger magnitude, 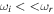 is obtained, where
is obtained, where 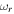 and
and  denote the real and imaginary parts of the perturbation frequency, respectively.
denote the real and imaginary parts of the perturbation frequency, respectively.
6.1. Fluid Instabilities in TR
Let us assume 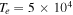 K and 0.5
K and 0.5  and choose
and choose 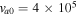 cm s−1 to estimate the Doppler-shifted frequency
cm s−1 to estimate the Doppler-shifted frequency 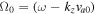 of the purely growing electrostatic modes of Equation (12) in the TR. For fixed
of the purely growing electrostatic modes of Equation (12) in the TR. For fixed 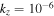 cm−1, we obtain
cm−1, we obtain 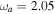 rad s−1,
rad s−1,  rad s−1,
rad s−1, 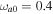 ,
, 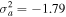 , and
, and 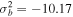 .
.
If the flow velocities of the 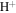 and He+ ions are exactly equal, i.e.,
and He+ ions are exactly equal, i.e., 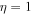 , then Equation (12) gives four complex conjugate roots in terms of
, then Equation (12) gives four complex conjugate roots in terms of 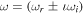 . Doppler-shifted frequencies
. Doppler-shifted frequencies 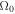 are purely imaginary in this case because the factor
are purely imaginary in this case because the factor 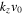 has the same value for all four roots. Note that in the bi-ion plasma, we get two purely growing electrostatic D'Angelo modes instead of one, contrary to the case of single ion species plasma. The real frequencies of both unstable modes are the same,
has the same value for all four roots. Note that in the bi-ion plasma, we get two purely growing electrostatic D'Angelo modes instead of one, contrary to the case of single ion species plasma. The real frequencies of both unstable modes are the same, 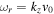 , as shown in Table 1. For
, as shown in Table 1. For 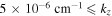 , two out of the four roots become real because in this case,
, two out of the four roots become real because in this case, 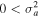 .
.
Table 1. Two Purely Growing Electrostatic Modes of Equation (12) in the TR for 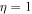 ,
, 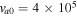 cm s−1,
cm s−1, 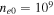 cm−3,
cm−3, 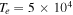 K, and
K, and 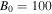 G.
G.

|
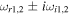
|
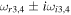
|
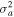
|
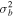
|
|---|---|---|---|---|
| 5 × 10−7 |

|

| −4.59 | −21.36 |
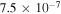
|
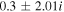
|
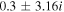
| −2.73 | −13.90 |
| 10−6 |
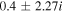
|
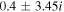
| −1.79 | −10.18 |
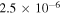
|
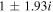
|
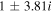
| −0.12 | −3.47 |
| 5 × 10−6 |
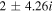
| −5.95, 9.95 | 0.44 | −1.23 |
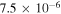
|
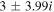
| −11.35, 17.35 | 0.63 | −0.49 |
| 10−5 |

| −16.57, 24.57 | 0.72 | −0.11 |
Note. Here 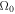 is imaginary and
is imaginary and 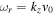 .
.
Download table as: ASCIITypeset image
If there is a difference in the magnitude of the field-aligned velocities of the hydrogen and helium ions, i.e.,  , then the real frequencies of the four modes do not remain the same. There appears to be a small difference in the magnitudes of the real frequencies and growth rates. This indicates that oscillatory instabilities appear with small differences in the real frequencies, as shown in Table 2. Let us consider a very small difference in the flow velocities of both kinds of ion that is
, then the real frequencies of the four modes do not remain the same. There appears to be a small difference in the magnitudes of the real frequencies and growth rates. This indicates that oscillatory instabilities appear with small differences in the real frequencies, as shown in Table 2. Let us consider a very small difference in the flow velocities of both kinds of ion that is 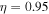 ; then we obtain four complex conjugate roots from Equation (12) corresponding to the same values of the parameters used in Table 1. For a larger kz
, the
; then we obtain four complex conjugate roots from Equation (12) corresponding to the same values of the parameters used in Table 1. For a larger kz
, the 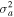 becomes positive; hence, one of the unstable roots disappears, as shown in Table 2.
becomes positive; hence, one of the unstable roots disappears, as shown in Table 2.
Table 2. Purely Growing Electrostatic Modes of Equation (12) in the TR Develop Small Real Frequencies for 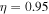 ,
, 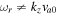 , and
, and  .
.
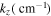
|
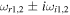
|
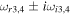
|
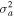
|
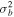
|
|---|---|---|---|---|
| 5 × 10−7 |
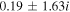
|
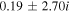
| −4.59 | −20.23 |
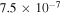
|

|

| −2.73 | −13.1593 |
| 10−6 |
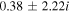
|
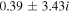
| −1.79 | −10.18 |
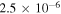
|
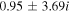
|
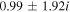
| −0.12 | −3.24 |
| 5 × 10−6 |
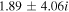
| −5.95, 9.96 | 0.44 | −1.12 |
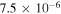
|
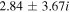
| −11.36, 17.36 | 0.63 | −0.41 |
| 10−5 |
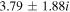
| −16.58, 24.58 | 0.72 | −0.11 |
Note. Here 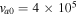 cm s−1,
cm s−1, 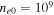 cm−3,
cm−3, 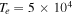 K, and
K, and 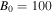 G.
G.
Download table as: ASCIITypeset image
For a larger flow velocity,  cm s–1, the complex conjugate roots of Equation (12) are mentioned in Table 3, where the real frequencies are sufficiently larger than the growth rates corresponding to larger values of kz
, i.e.,
cm s–1, the complex conjugate roots of Equation (12) are mentioned in Table 3, where the real frequencies are sufficiently larger than the growth rates corresponding to larger values of kz
, i.e., 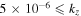 . This bi-ion plasma can support low-frequency, short-wavelength oscillatory electrostatic waves with real frequencies closer to the IAWs. Here
. This bi-ion plasma can support low-frequency, short-wavelength oscillatory electrostatic waves with real frequencies closer to the IAWs. Here 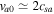 and hence
and hence 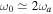 .
.
Table 3. Real Frequencies of the Purely Growing Electrostatic Modes of Equation (12) Increase for Larger Flow Velocities of H and He Ions in the TR.
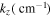
|

|
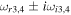
|
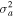
|
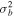
|
|---|---|---|---|---|
| 5 × 10−7 |
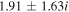
|

| −4.59 | −20.24 |
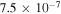
|
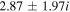
|
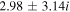
| −2.73 | −13.15 |
| 10−6 |
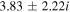
|
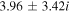
| −1.79 | −9.61 |
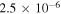
|
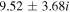
|
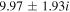
| −0.12 | −3.24 |
| 5 × 10−6 |

| 12.06, 27.97 | 0.44 | −1.12 |
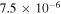
|
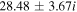
| 15.65, 44.37 | 0.63 | −0.41 |
| 10−5 |
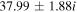
| 19.41, 60.58 | 0.72 | −0.11 |
Note. Here 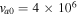 cm s−1, and the other parameters are the same as in Table 2.
cm s−1, and the other parameters are the same as in Table 2.
Download table as: ASCIITypeset image
In the TR, the electron temperature can be somewhat smaller, 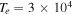 K. Let all other parameters and the perpendicular wavelength be the same as in Table 3. Then, for a larger difference in the field-aligned flow of H and He ions, i.e., for
K. Let all other parameters and the perpendicular wavelength be the same as in Table 3. Then, for a larger difference in the field-aligned flow of H and He ions, i.e., for 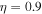 , we obtain four complex conjugate roots of Equation (12) in terms of the values of ω. Two of these roots are unstable. The real (
, we obtain four complex conjugate roots of Equation (12) in terms of the values of ω. Two of these roots are unstable. The real (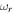 ) and imaginary (
) and imaginary (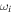 ) frequencies of these oscillatory instabilities are plotted versus kz
in Figures 1(a) and (b), respectively. These oscillatory instabilities are rapidly growing. For fixed
) frequencies of these oscillatory instabilities are plotted versus kz
in Figures 1(a) and (b), respectively. These oscillatory instabilities are rapidly growing. For fixed 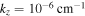 , we find
, we find 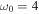 ,
,  , and hence
, and hence 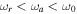 .
.
Figure 1. Two unstable roots of Equation (12) in the TR for  ,
, 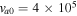 cm s−1,
cm s−1, 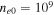 cm−3,
cm−3, 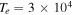 K, and
K, and 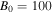 G. The real frequencies
G. The real frequencies 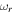 and imaginary frequencies
and imaginary frequencies 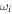 are plotted vs. kz
in Figures 1(a) and (b), respectively.
are plotted vs. kz
in Figures 1(a) and (b), respectively.
Download figure:
Standard image High-resolution imageCorresponding to the same values of the parameters but for different 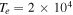 K and
K and 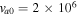 cm s−1, the real and imaginary frequencies of the two unstable roots of Equation (12) are plotted versus kz
in Figures 2(a) and (b), respectively, where we have again chosen
cm s−1, the real and imaginary frequencies of the two unstable roots of Equation (12) are plotted versus kz
in Figures 2(a) and (b), respectively, where we have again chosen 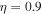 . In Figure 2, we have used
. In Figure 2, we have used  ; therefore, the real part of the frequency of the unstable mode becomes
; therefore, the real part of the frequency of the unstable mode becomes 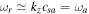 . Thus, it becomes difficult to differentiate between IAWs and the shear flow–driven mode. But it is clear that a rapidly growing unstable oscillatory mode appears.
. Thus, it becomes difficult to differentiate between IAWs and the shear flow–driven mode. But it is clear that a rapidly growing unstable oscillatory mode appears.
Figure 2. The unstable roots of Equation (12) are plotted in the TR choosing 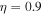 ,
,  cm s−1, and
cm s−1, and  K. Other parameters are the same as in Figure 1.
K. Other parameters are the same as in Figure 1.
Download figure:
Standard image High-resolution imageIn Figures 3(a) and (b), the real and imaginary frequencies obtained from Equation (12) are plotted versus kz
using a larger temperature 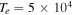 K and the same
K and the same 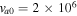 cm s−1 as in Figure 2.
cm s−1 as in Figure 2.
Figure 3. The unstable roots of Equation (12) are plotted in the TR choosing 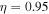 ,
,  cm s−1,
cm s−1,  cm−3, and
cm−3, and  K. Other parameters are the same as in Figure 1.
K. Other parameters are the same as in Figure 1.
Download figure:
Standard image High-resolution image6.2. Fluid Instabilities in the SC
The electron density and temperatures of charged species in this region are considered to be 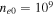 cm−3,
cm−3, 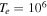 K, and
K, and  . If the flow velocities of both ions are considered to be exactly the same, i.e.,
. If the flow velocities of both ions are considered to be exactly the same, i.e., 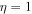 , then two purely growing D'Angelo modes are obtained. For
, then two purely growing D'Angelo modes are obtained. For 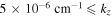 , we have positive
, we have positive 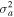 ; therefore, only one purely growing mode appears for smaller kz
, as shown in Table 4.
; therefore, only one purely growing mode appears for smaller kz
, as shown in Table 4.
Table 4. Two Purely Growing Electrostatic Modes of Equation (12) in the SC for 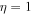 ,
, 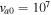 cm s−1,
cm s−1, 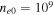 cm−3,
cm−3, 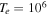 K, and
K, and  G.
G.

|

|
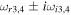
|
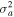
|
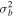
|
|---|---|---|---|---|
| 5 × 10−7 |

|
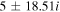
| −4.59 | −21.36 |
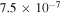
|
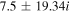
|

| −2.73 | −13.90 |
| 10−6 |
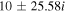
|
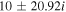
| −1.79 | −10.18 |
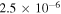
|
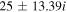
|
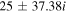
| −0.12 | −3.47 |
| 5 × 10−6 |
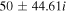
|
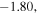 101.80 101.80 | 0.44 | −1.23 |
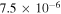
|
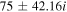
|
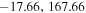
| 0.63 | −0.49 |
| 10−5 |
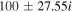
|
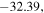 232.39 232.39 | 0.72 | −0.12 |
Note. Here 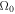 is imaginary and
is imaginary and 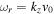 .
.
Download table as: ASCIITypeset image
The real part of the frequencies of the modes corresponding to H and He ions becomes different in the SC, as well as similar to the TR when 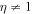 . The real and imaginary frequencies of four electrostatic modes in the SC are mentioned in Table 5, choosing
. The real and imaginary frequencies of four electrostatic modes in the SC are mentioned in Table 5, choosing 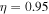 . Again, for larger values of kz
, i.e., for
. Again, for larger values of kz
, i.e., for 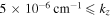 , two out of four modes become stable and have only real frequencies because
, two out of four modes become stable and have only real frequencies because 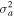 becomes positive (
becomes positive (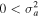 ). The real and imaginary frequencies of four complex roots of Equation (12) versus kz
are also plotted in Figures 4(a) and (b), respectively, for
). The real and imaginary frequencies of four complex roots of Equation (12) versus kz
are also plotted in Figures 4(a) and (b), respectively, for 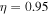 ,
, 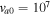 cm s−1, and fixed
cm s−1, and fixed  , which corresponds to
, which corresponds to 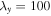 cm. In the case of a smaller flow velocity,
cm. In the case of a smaller flow velocity,  cm s−1, the real and imaginary frequencies of Equation (12) are plotted in Figures 5(a) and (b), respectively.
cm s−1, the real and imaginary frequencies of Equation (12) are plotted in Figures 5(a) and (b), respectively.
Figure 4. The unstable roots of Equation (12) are plotted in the corona, choosing 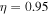 ,
,  cm s−1,
cm s−1,  ,
, 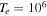 K, and
K, and 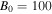 G.
G.
Download figure:
Standard image High-resolution imageFigure 5. The unstable roots of Equation (12) are plotted in the corona for 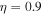 and
and  cm s−1. Other parameters are the same as in Figure 4.
cm s−1. Other parameters are the same as in Figure 4.
Download figure:
Standard image High-resolution imageTable 5. Two Purely Growing Electrostatic Modes of Equation (12) in the SC for 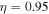 ,
, 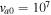 cm s−1,
cm s−1, 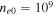 cm−3,
cm−3, 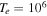 K, and
K, and 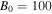 G.
G.
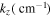
|
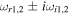
|
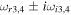
|
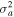
|
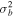
|
|---|---|---|---|---|
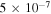
|
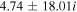
|
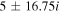
| −4.59 | −20.24 |
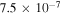
|
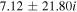
|
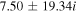
| −2.72 | −13.16 |
| 10−6 |
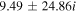
|
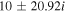
| −1.79 | −9.62 |
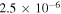
|
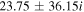
|
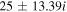
| −0.12 | −3.25 |
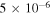
|
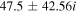
| −1.8, 102 | 0.44 | −1.12 |
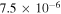
|
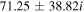
| −17.66, 167.66 | 0.63 | −0.41 |
| 10−5 |
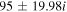
| −32.39, 232.38 | 0.72 | −0.06 |
Note. Here 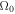 is imaginary and
is imaginary and 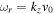 .
.
Download table as: ASCIITypeset image
7. Application of Kinetic Theory
In this section, we investigate the CDEIA waves in localized filamentary structures within the TR and SC. The real frequency of the IAW shifts away from the region of heavy ion Landau damping when 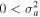 in a single ion species plasma. The waves become unstable when an electron parallel current overcomes the Landau damping effect. We investigate CDEIA waves in H–He plasma in both of these regions of the solar atmosphere.
in a single ion species plasma. The waves become unstable when an electron parallel current overcomes the Landau damping effect. We investigate CDEIA waves in H–He plasma in both of these regions of the solar atmosphere.
7.1. CDEIA Waves in the TR
Flow velocities in this region are assumed to be smaller than the corona. In H plasma, we choose 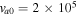 cm s−1, while
cm s−1, while 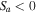 . The normalized growth rate
. The normalized growth rate 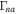 versus kz
is plotted in Figure 6 using Equation (33). For fixed
versus kz
is plotted in Figure 6 using Equation (33). For fixed 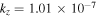 cm−1, we obtain
cm−1, we obtain 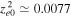 , and
, and 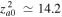 , Doppler-shifted frequency
, Doppler-shifted frequency 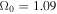 rad s−1 is obtained using Equation (32), and for growth rate, we use
rad s−1 is obtained using Equation (32), and for growth rate, we use  . The e-folding time turns out to be
. The e-folding time turns out to be  s.
s.
Figure 6. Using Equation (33), the normalized growth rate 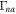 vs. kz
is plotted in the H plasma of the TR corresponding to the data mentioned in Section 7.1.
vs. kz
is plotted in the H plasma of the TR corresponding to the data mentioned in Section 7.1.
Download figure:
Standard image High-resolution imageIn the case of H–He plasma in the TR, using the same flow velocity as has been used in Figure 6 and assuming 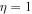 , we plot
, we plot 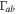 versus kz
in Figure 7 using
versus kz
in Figure 7 using 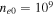 cm−3. For the same fixed value of
cm−3. For the same fixed value of  that has been used above, we obtain
that has been used above, we obtain 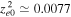 ,
, 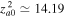 ,
,  , and
, and 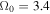 rad s−1. In Figure 7, we plot
rad s−1. In Figure 7, we plot 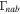 versus kz
. In this case, we obtain
versus kz
. In this case, we obtain 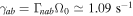 ,
, 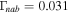 , and
, and 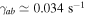 . Thus, the e-folding time is about 30 s. It is noted that whenever the electron number density is varied to
. Thus, the e-folding time is about 30 s. It is noted that whenever the electron number density is varied to 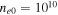 cm−3 in the case of the TR, the values of the plasma frequencies of the ions are modified; however, the growth rates of the instability remain the same.
cm−3 in the case of the TR, the values of the plasma frequencies of the ions are modified; however, the growth rates of the instability remain the same.
Figure 7. Using Equation (31), the normalized growth rate 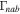 vs. kz
is plotted in the H–He plasma of the TR corresponding to the data given in Section 7.1.
vs. kz
is plotted in the H–He plasma of the TR corresponding to the data given in Section 7.1.
Download figure:
Standard image High-resolution image7.2. CDEIA Waves in the Corona
In the case of H plasma, we obtain a Doppler-shifted real frequency (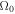 ) using Equation (32). The normalized growth rate
) using Equation (32). The normalized growth rate 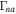 is plotted versus kz
in Figure 8 using Equation (33). To show that the approximations used,
is plotted versus kz
in Figure 8 using Equation (33). To show that the approximations used, 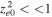 and
and 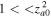 , are satisfied, let us choose a fixed value of kz
and evaluate these parameters. For fixed
, are satisfied, let us choose a fixed value of kz
and evaluate these parameters. For fixed 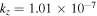 cm−1, we obtain
cm−1, we obtain 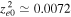 ,
, 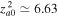 , a Doppler-shifted frequency
, a Doppler-shifted frequency  rad s−1, and a growth rate
rad s−1, and a growth rate 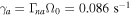 . Thus, the e-folding time becomes
. Thus, the e-folding time becomes 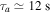 .
.
Figure 8. Plot of normalized growth rate  vs. kz
in the H plasma of the SC using Equation (33) corresponding to data given in Section 7.2. In this region,
vs. kz
in the H plasma of the SC using Equation (33) corresponding to data given in Section 7.2. In this region, 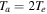 ; therefore, wave–particle interactions are significant. Hence, kz
has a very narrow window of permissible values for instability.
; therefore, wave–particle interactions are significant. Hence, kz
has a very narrow window of permissible values for instability.
Download figure:
Standard image High-resolution imageFor the case of H–He plasma, we assume that both species have the same parallel shear velocity (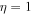 ). In this case, the Doppler-shifted real frequency
). In this case, the Doppler-shifted real frequency 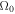 is obtained by using Equation (30), and the normalized growth rate of the CDEIA wave
is obtained by using Equation (30), and the normalized growth rate of the CDEIA wave 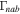 is found by using Equation (31). The normalized growth rate
is found by using Equation (31). The normalized growth rate 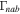 is plotted versus kz
in Figure 9. For the same fixed value of kz
that has been used above, we obtain
is plotted versus kz
in Figure 9. For the same fixed value of kz
that has been used above, we obtain 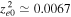 ,
, 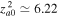 ,
, 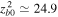 , and
, and 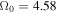 rad s−1. Then, corresponding to
rad s−1. Then, corresponding to 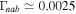 , we obtain
, we obtain  , which yields an e-folding time of
, which yields an e-folding time of 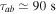 .
.
Figure 9. Using Equation (31), the normalized growth rate 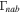 vs. kz
is plotted in the H–He plasma of the SC corresponding to the data mentioned in Section 7.2.
vs. kz
is plotted in the H–He plasma of the SC corresponding to the data mentioned in Section 7.2.
Download figure:
Standard image High-resolution image8. Discussion
Excitation of short-scale electrostatic fields in the presence of inhomogeneous flows, as well as currents in the solar atmosphere, has been investigated using both fluid and kinetic models. These electrostatic waves have low frequencies of the order of 1 or several Hz, perpendicular wavelengths of the order of 1 m, and parallel wavelengths of the order of several kilometers. It is found that radial expansion of the hydrogen–helium (H–He) plasma itself is a source for the generation of electrostatic instabilities in the TR and SC. Plasma enters into the less dense TR from a denser collisional surface with short-scale inhomogeneities in the form of strands and threads in the field-aligned flow and generates electrostatic fields. These short-scale fields seem to appear throughout the solar atmosphere and can accelerate charged particles, causing an increase in their thermal motions.
Plasma heating starts from the TR, and it is important to look for the generation of electrostatic waves in this region as well. Since the solar surface is collisional and contains neutrals, IAWs are less likely to be excited there. However, when the plasma having shear in a parallel flow enters into the rarefied TR, electrostatic instabilities should take place. Field-aligned shear flow can produce a purely growing D'Angelo instability in hydrogen plasma if the presence of helium ions is ignored. If the contribution of 10% helium ions is taken into account then instead of one mode, the two D'Angelo modes appear when the flow speeds of the H and He ions are exactly equal 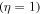 . On the other hand, a small difference
. On the other hand, a small difference  in the flow of H and He ions generates short-scale oscillatory electrostatic instabilities. The real frequencies are closer to the imaginary frequencies; hence, these are highly unstable waves produced by the plasma expansion. If the real frequency
in the flow of H and He ions generates short-scale oscillatory electrostatic instabilities. The real frequencies are closer to the imaginary frequencies; hence, these are highly unstable waves produced by the plasma expansion. If the real frequency 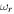 of an instability is not closer to
of an instability is not closer to 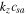 or
or 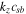 , then shear flow–driven electrostatic waves are produced. However, when the flow velocities of ions are comparable with csa
or csb
, then the waves excited by the plasma expansion seem to be the IAWs. Kinetic theory predicts that the IAW is damped in hot ion plasma through wave–particle interaction. We therefore consider long wavelengths, i.e.,
, then shear flow–driven electrostatic waves are produced. However, when the flow velocities of ions are comparable with csa
or csb
, then the waves excited by the plasma expansion seem to be the IAWs. Kinetic theory predicts that the IAW is damped in hot ion plasma through wave–particle interaction. We therefore consider long wavelengths, i.e., 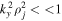 (where j denotes H and He ions), for the validity of the fluid approach.
(where j denotes H and He ions), for the validity of the fluid approach.
Wave–particle interaction effects remain obscure in fluid theory; therefore, we also investigate the excitation of IAWs in the framework of kinetic theory. More than two decades ago (Gavrishchaka et al. 1998), a theoretical model was presented to show that IAWs are excited in the upper ionosphere due to a parallel current in the presence of the field-aligned ions' shear flow. In this study, pure oxygen plasma was considered, and CDEIA waves were investigated. It was found that the phase velocity of the IAW increases due to the field-aligned shear flow of ions, and it shifts away from the region of heavy Landau damping. The parallel current causes instability of the IAW for 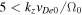 if Equation (33) is applied to the oxygen plasma of the ionosphere. This instability appears in the oxygen plasma even when the ion temperature is larger than the electron temperature, i.e.,
if Equation (33) is applied to the oxygen plasma of the ionosphere. This instability appears in the oxygen plasma even when the ion temperature is larger than the electron temperature, i.e., 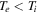 .
.
Since the solar atmosphere is also believed to have short-scale current sheets and filaments, the CDEIA waves have been investigated in both the TR and SC. In the TR, the CDEIA waves appear within current sheets. The normalized growth rate 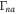 versus kz
is plotted in Figure 6 considering the pure hydrogen plasma of the TR. These waves are produced within the narrow range of
versus kz
is plotted in Figure 6 considering the pure hydrogen plasma of the TR. These waves are produced within the narrow range of 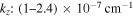 . When the dynamics of helium ions is also considered, the growth rate decreases, as can be seen in Figure 7. Corresponding to
. When the dynamics of helium ions is also considered, the growth rate decreases, as can be seen in Figure 7. Corresponding to 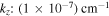 , we find
, we find 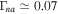 in pure H plasma in Figure 6 and
in pure H plasma in Figure 6 and 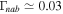 for H–He plasma in Figure 7. In the SC, the growth rate of CDEIA waves
for H–He plasma in Figure 7. In the SC, the growth rate of CDEIA waves 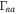 versus kz
is plotted in Figure 8 considering only hydrogen plasma, and
versus kz
is plotted in Figure 8 considering only hydrogen plasma, and 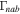 versus kz
is plotted in Figure 9 including the effects of helium ions. Corresponding to
versus kz
is plotted in Figure 9 including the effects of helium ions. Corresponding to 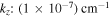 , we find
, we find 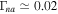 in pure H plasma in Figure 8 and
in pure H plasma in Figure 8 and 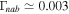 for H–He plasma in Figure 9. The normalized growth rate decreases about 10 times when the effects of helium ions are taken into account in the SC.
for H–He plasma in Figure 9. The normalized growth rate decreases about 10 times when the effects of helium ions are taken into account in the SC.
Researchers have studied the generation of short-scale electrostatic fields in the SC. Using 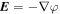 , we can estimate the magnitude of the electric fields in the TR and SC associated with shear flow–driven and CDEIA waves. In both cases, we have used the perpendicular wavelength
, we can estimate the magnitude of the electric fields in the TR and SC associated with shear flow–driven and CDEIA waves. In both cases, we have used the perpendicular wavelength 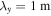 , which corresponds to
, which corresponds to 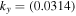 cm−1. The electrostatic drift waves have also been investigated in the SC (Vranjes & Poedts 2009a, 2009b). These authors pointed out that if initial perturbation is assumed to be
cm−1. The electrostatic drift waves have also been investigated in the SC (Vranjes & Poedts 2009a, 2009b). These authors pointed out that if initial perturbation is assumed to be 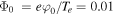 , then
, then 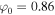 V, which exponentially grows due to linear instability because
V, which exponentially grows due to linear instability because 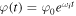 . They chose
. They chose 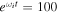 , and in this case, they obtained
, and in this case, they obtained 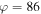 V in
V in 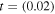 s because they had a large growth rate of drift instability,
s because they had a large growth rate of drift instability, 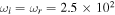 Hz. For CDEIA waves (oscillatory instabilities), we have
Hz. For CDEIA waves (oscillatory instabilities), we have 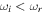 or
or 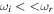 , which is more appropriate for the validity of linear theory. Therefore, if we also consider
, which is more appropriate for the validity of linear theory. Therefore, if we also consider 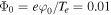 , then for
, then for 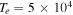 K in the TR, we obtain
K in the TR, we obtain 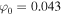 V, while in the SC, the potential turns out to be the same
V, while in the SC, the potential turns out to be the same 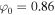 V for
V for 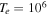 K. Since unstable waves have
K. Since unstable waves have 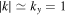 m, the initial electric field perturbation is of the order of
m, the initial electric field perturbation is of the order of 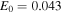 V m−1 in the TR and
V m−1 in the TR and 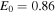 V m−1 in the SC. These initial amplitudes grow exponentially due to the instabilities
V m−1 in the SC. These initial amplitudes grow exponentially due to the instabilities 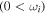 mentioned in the previous sections. Thus, our theoretical models based on multifluid plasma theory and the plasma kinetic approach predict that short-scale electrostatic waves are produced within thin threads and strands in the hydrogen–helium plasma of the TR and SC. It is important to note that the electric fields produced due to perturbations in the SC are stronger than in the TR because in this region, the electron temperature is larger and
mentioned in the previous sections. Thus, our theoretical models based on multifluid plasma theory and the plasma kinetic approach predict that short-scale electrostatic waves are produced within thin threads and strands in the hydrogen–helium plasma of the TR and SC. It is important to note that the electric fields produced due to perturbations in the SC are stronger than in the TR because in this region, the electron temperature is larger and 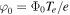 .
.
We have investigated the effects of helium ions on electrostatic instabilities using both fluid and kinetic theories. We conclude that as the (H–He) plasma leaves the denser surface and enters into the almost collisionless TR by expansion, the short-scale electrostatic fields appear at different low frequencies and longer wavelengths compared to ion gyroradii. Particles are accelerated in fluctuating fields, and the temperature of the plasma increases here. In the next step, when it enters into the corona again, CDEIA waves are generated to enhance and maintain the temperature in the corona. Helium ions transform purely growing instabilities into rapidly oscillating instabilities and reduce the growth rates of CDEIA waves. Therefore, it is stressed that the presence of a small number of helium ions should not be ignored in the study of wave dynamics in the TR and SC.
No observed data are available about such short-wavelength electrostatic waves in the solar atmosphere so far. It is expected that future solar missions will be able to detect such waves directly or indirectly. But it is very important to understand the possible mechanisms for the generation of short-scale electrostatic waves in the TR and SC, which must damp in the plasma due to wave–particle interactions and heat it. This work is also important for future observations and theoretical investigations in this direction.
The Solar Orbiter, a joint solar mission of the ESA and NASA launched on 2020 February 10, has detected a new phenomenon taking place throughout the corona named "campfires." These are the miniature solar flares about a million or billion times smaller than the usual flares (Antolin et al. 2021). We expect that the fluid and kinetic instabilities discussed in this work will be detected in future and may be coupled with short-wavelength Alfvén waves. The basic plasma theory clearly predicts the existence of these short-scale electrostatic waves in the TR and SC.
H.S. is grateful to the Higher Education Commission (HEC) of Pakistan for partial support under project NRPU 5841. H.S. is also grateful to Prof. Stefaan Poedts of K-Leuven University, Leuven, Belgium, for useful discussions.