Abstract
The synchrotron cooling of relativistic electrons is one of the most effective radiation mechanisms in astrophysics. It not only accompanies the process of particle acceleration, but also has feedback on the formation of the energy distribution of the parent electrons. The radiative cooling time of electrons decreases with energy as tSYN ∝ 1/E; correspondingly, the overall radiation efficiency increases with energy. However, this effect strictly limits the maximum energy of individual photons. Even in the so-called extreme accelerators, where the acceleration proceeds at the highest possible rate,  , allowed in an ideal magnetohydrodynamic plasma, the synchrotron radiation cannot extend well beyond the characteristic energy determined by the electron mass and the fine-structure constant:
, allowed in an ideal magnetohydrodynamic plasma, the synchrotron radiation cannot extend well beyond the characteristic energy determined by the electron mass and the fine-structure constant:  . In this paper, we propose a model in which the formation of synchrotron radiation takes place in compact magnetic blobs located inside the particle accelerator and develop a formalism for calculations of synchrotron radiation emerging from such systems. We demonstrate that for certain combinations of parameters characterizing the accelerator and the magnetic blobs, the synchrotron radiation can extend beyond this limit by a several orders of magnitude. This scenario requires a weak magnetization of the particle accelerator, and an efficient conversion of gas internal energy into magnetic energy in sufficiently small blobs. The required size of the blobs is constrained by the magnetic mirroring effect, which can prevent particle penetration into the regions of strong magnetic field under certain conditions.
. In this paper, we propose a model in which the formation of synchrotron radiation takes place in compact magnetic blobs located inside the particle accelerator and develop a formalism for calculations of synchrotron radiation emerging from such systems. We demonstrate that for certain combinations of parameters characterizing the accelerator and the magnetic blobs, the synchrotron radiation can extend beyond this limit by a several orders of magnitude. This scenario requires a weak magnetization of the particle accelerator, and an efficient conversion of gas internal energy into magnetic energy in sufficiently small blobs. The required size of the blobs is constrained by the magnetic mirroring effect, which can prevent particle penetration into the regions of strong magnetic field under certain conditions.
Export citation and abstract BibTeX RIS
1. Introduction
Acceleration of nonthermal particles in various astrophysical environments requires the presence of an electric field. If high energy particles are accelerated in a region with a typical magnetic field, B0, then the time required for the particle to gain energy E is t
ACC
= η
E/(eB0
c). Here, η is a dimensionless parameter, namely the ratio of the magnetic to the accelerating electric field,  . If the acceleration proceeds in a magnetohydrodynamic (MHD) flow, then
. If the acceleration proceeds in a magnetohydrodynamic (MHD) flow, then  and the acceleration efficiency is constrained by η > 1. The acceleration is efficient only in the energy range where the acceleration time is shorter than the cooling time. For the case where synchrotron losses dominate, the cooling time is
and the acceleration efficiency is constrained by η > 1. The acceleration is efficient only in the energy range where the acceleration time is shorter than the cooling time. For the case where synchrotron losses dominate, the cooling time is  ; (here, me, c, and σT are the electron mass, speed of light, and Thomson cross section, respectively). The electrons are subsequently accelerated up to a maximum energy
; (here, me, c, and σT are the electron mass, speed of light, and Thomson cross section, respectively). The electrons are subsequently accelerated up to a maximum energy  . Correspondingly, the electrons that achieve this energy produce synchrotron photons of energy
. Correspondingly, the electrons that achieve this energy produce synchrotron photons of energy  (Guilbert et al. 1983; here, α is the fine-structure constant). We note that this energy corresponds to the spectral maximum of synchrotron emission produced by an electron of energy
(Guilbert et al. 1983; here, α is the fine-structure constant). We note that this energy corresponds to the spectral maximum of synchrotron emission produced by an electron of energy  moving in a magnetic field B0 perpendicular to the velocity of the electron. Various factors can shift the exact position of the synchrotron maximum (for example, pitch angle, turbulent dispersion of magnetic field strength, energy distribution of emitting particles, etc.). However, the impact of these factors is expected to be small (see, e.g., Derishev & Aharonian 2019 for the comparison of the spectra averaged over pitch angle and turbulent distribution of magnetic field strength). A much more important factor is that this limit was obtained under the assumption of the perfect operation of the acceleration process, which is likely not achievable in real astrophysical accelerators. Thus, we adopt the above obtained energy as an energy that limits the extension of the synchrotron component (which is sometimes referred in literature as synchrotron burn-off limit; see, e.g., de Jager et al. 1996). Finally, we note that the maximum of the spectral energy distribution (SED) appears at higher energies, namely for the same underlying assumptions at ≈300η−1 MeV.
moving in a magnetic field B0 perpendicular to the velocity of the electron. Various factors can shift the exact position of the synchrotron maximum (for example, pitch angle, turbulent dispersion of magnetic field strength, energy distribution of emitting particles, etc.). However, the impact of these factors is expected to be small (see, e.g., Derishev & Aharonian 2019 for the comparison of the spectra averaged over pitch angle and turbulent distribution of magnetic field strength). A much more important factor is that this limit was obtained under the assumption of the perfect operation of the acceleration process, which is likely not achievable in real astrophysical accelerators. Thus, we adopt the above obtained energy as an energy that limits the extension of the synchrotron component (which is sometimes referred in literature as synchrotron burn-off limit; see, e.g., de Jager et al. 1996). Finally, we note that the maximum of the spectral energy distribution (SED) appears at higher energies, namely for the same underlying assumptions at ≈300η−1 MeV.
There are several ways to alleviate this constraint on the cut-off energy of the synchrotron component. Examples of a bypass are the inclusion of the relativistic motion of the production site, acceleration with efficiencies exceeding the ideal MHD threshold (η < 1), synchrotron emission of secondary electron positron pairs, synchrotron emission by particles heavier than electrons (muons and protons), and special regimes of emission (for example, in a small-scale turbulent magnetic field). We discuss these approaches in Section 2 in more detail. In this paper, we explore a new scenario for boosting the energy range of the synchrotron radiation utilizing the structure of the ambient magnetic field in the acceleration region. The principle behind our proposed scheme is the separation of the region of the electron acceleration and the region(s) of effective synchrotron radiation. More specifically, we consider a scenario in which the acceleration region contains a large number of compact magnetic field condensations (blobs), whose collective volume filling factor is small. Provided that the particle–blob collision time is long compared to the acceleration time, these blobs have only a minor impact on the acceleration process. That said, high energy particles that eventually collide with these blob regions give rise to a synchrotron radiation component that can extend well beyond 100 MeV. Throughout the discussion, we do not specify the acceleration mechanism, or the nature of the compact magnetic condensations, but focus on the propagation and radiation of the accelerated electrons colliding with the dense magnetic blobs. A high degree of inhomogeneity of magnetic plasma is favored by numerical simulations of shocks, magnetic reconnection, and turbulence. The general consideration of the suggested scenario is therefore potentially relevant for a number of astrophysical systems.
2. Magnetobremsstrahlung Feedback on the Particle Spectrum
The synchrotron burn-off turnover is caused by the feedback of synchrotron cooling on particle acceleration in an ideal MHD plasma and should be applied in the plasma co-moving reference frame. In the most simple set-up, where the magnetic field is homogeneous and perpendicular to the particle velocity, the cut off should appear at  , where m and
, where m and  are the mass of the emitting particle and the Doppler boosting factor, respectively. The Doppler boosting effect, which accounts for the relativistic motion of the production site, can be sufficient to explain, in a framework of an electron synchrotron scenario, bright Crab nebula GeV flares, whose SED peaks at a few hundred MeV,
are the mass of the emitting particle and the Doppler boosting factor, respectively. The Doppler boosting effect, which accounts for the relativistic motion of the production site, can be sufficient to explain, in a framework of an electron synchrotron scenario, bright Crab nebula GeV flares, whose SED peaks at a few hundred MeV,  . However, an extension of the synchrotron component to the very high energy (VHE) regime requires extremely high boosting factors
. However, an extension of the synchrotron component to the very high energy (VHE) regime requires extremely high boosting factors  . Such fast outflows are not expected in astrophysical objects unless one considers production of the emission in pulsar winds, whose bulk Lorentz factor can be very high,
. Such fast outflows are not expected in astrophysical objects unless one considers production of the emission in pulsar winds, whose bulk Lorentz factor can be very high,  . These winds originate in a very compact region, comparable in size to the pulsar magnetosphere, and almost unavoidably undergo strong adiabatic cooling due to their expansion. As a result, the temperature of the wind electrons (i.e., their energy in the co-moving frame) is expected to be very low, resulting in a strong suppression of the synchrotron emission. If some acceleration process, even with a modest efficiency, η < 103, operates in a pulsar wind, then the synchrotron emission produced there could be boosted into the VHE regime.
. These winds originate in a very compact region, comparable in size to the pulsar magnetosphere, and almost unavoidably undergo strong adiabatic cooling due to their expansion. As a result, the temperature of the wind electrons (i.e., their energy in the co-moving frame) is expected to be very low, resulting in a strong suppression of the synchrotron emission. If some acceleration process, even with a modest efficiency, η < 103, operates in a pulsar wind, then the synchrotron emission produced there could be boosted into the VHE regime.
Another obvious way to generate synchrotron emission in the VHE domain is to consider higher-mass particles. For example, protons, whose mass is ≈2000me, in an extreme accelerator, η ∼ 1, produce a synchrotron component that reaches the VHE domain. A modest Doppler boosting,  , can relax the requirement for acceleration efficiency or extend the spectrum to multi-TeV energies. The high cut-off energy of proton synchrotron emission comes at a price of very large energy of emitting particles. The energy of particles that reach the synchrotron cooling limit scales as m2, thus proton synchrotron scenarios require a very strong magnetic field of B ≥ 100 G to confine the ultra-high energy protons (Aharonian 2000).
, can relax the requirement for acceleration efficiency or extend the spectrum to multi-TeV energies. The high cut-off energy of proton synchrotron emission comes at a price of very large energy of emitting particles. The energy of particles that reach the synchrotron cooling limit scales as m2, thus proton synchrotron scenarios require a very strong magnetic field of B ≥ 100 G to confine the ultra-high energy protons (Aharonian 2000).
Variations in other underlining assumptions may also change the position of the burn-off limit. For example, if a particle is on a trajectory closely following a bent magnetic field line, then energy losses of the particle and its peak emitting frequency do not depend on the strength of the magnetic field but rather on its curvature radius. This emission mechanism is dubbed in the literature curvature radiation, and it is feasible that curvature radiation peaks above the synchrotron burn-off limit. Acceleration of particles for efficient emission via curvature radiation requires the presence of an electric field directed along the magnetic field. This implies a violation of the ideal MHD conditions, at least in certain regions of the source (in so-called gaps). Alternatively, one can consider the curvature radiation produced by secondary electrons, which are, for example, generated in a pulsar magnetosphere by photon magnetic absorption. In this case, the initial momentum of secondary particles is not necessary directed along the magnetic field, so the bulk of the particle energy is emitted via the synchrotron channel. The "100 MeV" limit does not concern the synchrotron radiation produced by secondary electrons independently on the specific mechanism of their generation. For example, under suitable conditions, the products of the interactions of primary protons with the surrounding gas or radiation fields can generate a synchrotron component that extends beyond the burn-off limit.
Models involving the synchrotron emission by secondary leptons represent an extreme realization of scenarios where the site of particle acceleration and emission are physically separated. Such scenarios do not necessary require violation of the ideal MHD conditions. If a considerable gradient of the magnetic field is present in the source, then particles accelerated in regions of weak magnetic field can travel up to regions with strong magnetic fields and eventually produce a synchrotron component extending beyond the burn-off limit. Some models invoke a conversion between the charged and uncharged state of the leading particle (e.g., via a cycle of pair production and inverse Compton scattering in the Klein–Nishina regime), which allows for the avoidance of synchrotron losses during the propagation to a strong B-field region.
The efficiency of the acceleration process influences the position of the cut off of the synchrotron spectrum. In the case of stochastic particle acceleration, the spectrum of electrons does not stop abruptly, but extends beyond  , although with a rather sharp cut-off shape, e.g., exponential or faster. Typically, the maximum of the SED, ν
Fν
, appears at the energy exceeding
, although with a rather sharp cut-off shape, e.g., exponential or faster. Typically, the maximum of the SED, ν
Fν
, appears at the energy exceeding  . However, for any realistic spectrum of electrons, the shift does not exceed a factor of a few. If one considers acceleration processes operating in nonideal MHD configurations, then one may expect high acceleration efficiencies, η < 1, and the synchrotron spectrum can extend considerably above the burn-off limit. Reconnection of magnetic field lines represents a nonideal MHD process that is believed to play an important role in particle acceleration in different astrophysical sources, including pulsar wind nebulae and jets from active galactic nuclei (AGNs). We note that there is a quite broad spectrum of processes that can get activated at magnetic reconnection and enhance particle acceleration. For example, this includes Fermi I acceleration in converging flows mediated by magnetic reconnection (Bosch-Ramon 2012), the transformation of a turbulent cascade with an important feedback on particle acceleration (Lazarian et al. 2020). Among other effects, the acceleration in the current sheet of an X-point is of special interest (Cerutti et al. 2013). In such regions, the reconnecting magnetic fields annihilate, leaving a guide magnetic field and an unscreened electric field
. However, for any realistic spectrum of electrons, the shift does not exceed a factor of a few. If one considers acceleration processes operating in nonideal MHD configurations, then one may expect high acceleration efficiencies, η < 1, and the synchrotron spectrum can extend considerably above the burn-off limit. Reconnection of magnetic field lines represents a nonideal MHD process that is believed to play an important role in particle acceleration in different astrophysical sources, including pulsar wind nebulae and jets from active galactic nuclei (AGNs). We note that there is a quite broad spectrum of processes that can get activated at magnetic reconnection and enhance particle acceleration. For example, this includes Fermi I acceleration in converging flows mediated by magnetic reconnection (Bosch-Ramon 2012), the transformation of a turbulent cascade with an important feedback on particle acceleration (Lazarian et al. 2020). Among other effects, the acceleration in the current sheet of an X-point is of special interest (Cerutti et al. 2013). In such regions, the reconnecting magnetic fields annihilate, leaving a guide magnetic field and an unscreened electric field  , where
, where  is the inflow speed. Although this configuration resembles the models with different accelerator and emitter magnetic fields discussed above, we note a principle difference between these two cases: the reconnection current sheet is not a region with an ideal MHD flow, so the burn-off limit is not applicable for that configuration.
is the inflow speed. Although this configuration resembles the models with different accelerator and emitter magnetic fields discussed above, we note a principle difference between these two cases: the reconnection current sheet is not a region with an ideal MHD flow, so the burn-off limit is not applicable for that configuration.
If the particle confinement time in the current sheet is long enough to accelerate particles beyond  , then these energetic particles should produce emission that peaks above the burn-off limit once they escape into the regions with magnetic field B0. It may seem that scenarios involving particle acceleration in current sheets alleviate completely the constraint imposed by synchrotron cooling. However, in any realistic configuration there are still important further limitations. First, to generate a synchrotron component that extends into VHE regime, the linear size of the accelerator should be sufficiently large,
, then these energetic particles should produce emission that peaks above the burn-off limit once they escape into the regions with magnetic field B0. It may seem that scenarios involving particle acceleration in current sheets alleviate completely the constraint imposed by synchrotron cooling. However, in any realistic configuration there are still important further limitations. First, to generate a synchrotron component that extends into VHE regime, the linear size of the accelerator should be sufficiently large,
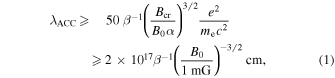
where Bcr is the Schwinger critical field strength. The existence of such an extended coherent reconnection site is questionable. Another important factor is the influence of the guide magnetic field, which should be present unless the reconnecting magnetic fields are perfectly antiparallel. Guide magnetic fields not only lead to synchrotron cooling, but also enhance the escape of high energy particles from the current sheet. These two factors are expected to suppress significantly the efficiency of the synchrotron process in the VHE regime.
Finally, the sharp decrease at the end of the synchrotron spectrum can be altered in a medium with inhomogeneous magnetic fields. For the case of highly turbulent magnetic fields whose correlation length crossing time, λB
/c, is small compared to the electron's inverse cyclotron frequency, 1/ωc
= me
c/eB0, the radiation proceeds in the so-called jitter regime. In this case, the peak in the radiation spectrum is shifted to higher frequencies by a factor of c/(ωc
λB
); (Kelner et al. 2013). Thus, for scenarios with extremely small-scale turbulence, one can formally expect radiation in the multi-GeV or higher energies. However, the plasma physics community has been quite pessimistic concerning the condition of λB
≪ c/ωc
, and correspondingly considers the realization of magnetobremsstrahlung in the jitter regime as a highly unlikely process. In principle, the presence of large-scale turbulence, λB
> c/ωc
, can also have an impact on the SED of synchrotron radiation. In particular, a broad power-law distribution of the magnetic field strength can result in a rather long power-law tail of radiation beyond  (Kelner et al. 2013). However, for more realistic magnetic field strength distributions, e.g., a Gaussian type distribution, the shift of the synchrotron peak is rather mild (Derishev & Aharonian 2019).
(Kelner et al. 2013). However, for more realistic magnetic field strength distributions, e.g., a Gaussian type distribution, the shift of the synchrotron peak is rather mild (Derishev & Aharonian 2019).
3. Toy Model: Mathematical Formulation
Although the postulation of magnetic field blobs inside the particle accelerator implies that we deal with a multizone scenario, mathematically one can describe the problem within a one-zone model. In this case, the description of the process is similar to the so-called leaky-box approximation which has been successfully applied to Galactic cosmic rays:
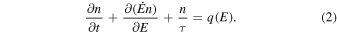
Here, τ is the particle–magnetic blob collision time, and  is the energy loss rate of electrons in the main (acceleration) zone, which depends on particle energy and magnetic field strength given by
is the energy loss rate of electrons in the main (acceleration) zone, which depends on particle energy and magnetic field strength given by
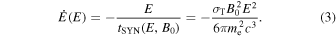
Within the standard treatment, these terms are responsible for the continuous and catastrophic losses of electrons, respectively. The function q(E) accounts for a phenomenological description of the acceleration process. Equation (2) is valid for particles with energy E > E*; the boundary energy is obtained from the solution of the equation:
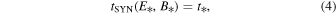
where B* is the magnetic field and t* is the electron confinement time in the blobs. The latter generally depends on the particle energy. See Appendix A for the justification of Equation (2). The relevant timescales are shown in Figure 1. We assume that in the absence of magnetic blobs, the injection spectrum contains a cut off at energy  , which is determined from the condition
, which is determined from the condition  . We define this timescale
. We define this timescale  . If the collision time is long compared to the acceleration time up to energy
. If the collision time is long compared to the acceleration time up to energy  , i.e.
, i.e.

then the impact of the magnetic blobs on the maximum energy of accelerated electrons can be ignored. Additionally, it is also helpful to define another timescale  . The spectral shape of electrons in the cut-off region depends on the specific acceleration process. Below, we assume that
. The spectral shape of electrons in the cut-off region depends on the specific acceleration process. Below, we assume that ![$q\propto {E}^{-\alpha }\exp \left[-{\left(E/{E}^{{\rm\small{MAX}}}\right)}^{\beta }\right]$](https://content.cld.iop.org/journals/0004-637X/914/2/76/1/apjabfcbfieqn27.gif) , where for simplicity, but without loss of generality, we adopt α = 2 and β = 1.
, where for simplicity, but without loss of generality, we adopt α = 2 and β = 1.
Figure 1. Characteristic timescales: the acceleration time in the main (acceleration) zone, t
ACC
(red line); the weak field synchrotron cooling time in the main zone, t
SYN
(E, B0); (blue dashed line); the strong field synchrotron cooling time in the blobs, t
SYN
(E, B*); (blue solid line); the confinement time of the electron in the blobs, t* (cyan line). Four characteristic collision times are considered: the purple curve for  , the green curve for
, the green curve for  , the light blue curve for
, the light blue curve for  , and the orange curve for
, and the orange curve for  . Note that the timescales
. Note that the timescales  and
and  are defined as
are defined as  and t
SYN
(E*, B0), respectively.
and t
SYN
(E*, B0), respectively.
Download figure:
Standard image High-resolution imageIn the fast cooling regime, when the injection and loss processes balance one another, the solution of Equation (2) is
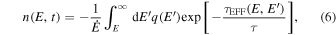
where the auxiliary function τ EFF is
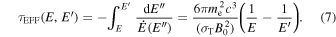
Two distinct components of synchrotron emission are produced in this scenario. In the main zone, the synchrotron radiation produced by electrons with an energy distribution given by Equation (6), takes a spectral shape of the form
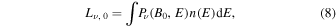
where Pν is the power per unit frequency emitted by an electron with energy E. The electrons that enter the blob, with its much stronger magnetic field, quickly emit their energy at a rate 1/τ. The time-averaged energy spectrum of their synchrotron radiation produced in the magnetic blobs is
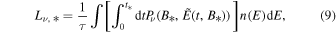
where  ; (see Appendix B).
; (see Appendix B).
As demonstrated in Figure 1, for the condition given by Equation (5) two different scenarios exist:  and
and  . In the first of these regimes, the presence of magnetic field blobs has only a minor impact on the particle spectrum, i.e., τ ≫ τ
EFF
. In the second regime the particle spectrum is deformed by interactions with the magnetic blobs, although the maximum energy of the particle spectrum remains unaffected.
. In the first of these regimes, the presence of magnetic field blobs has only a minor impact on the particle spectrum, i.e., τ ≫ τ
EFF
. In the second regime the particle spectrum is deformed by interactions with the magnetic blobs, although the maximum energy of the particle spectrum remains unaffected.
In Figures 2 and 3, we show the corresponding SEDs produced in four different collision timescale scenarios illustrated in Figure 1. In these figures two different strengths of the blob magnetic field, B* = 102
B0 and B* = 103
B0, are considered. These results show that for particular values of the collision time considered, the synchrotron radiation produced in the blobs indeed extends up to a factor B*/B0 beyond the limit  . However, for the case of
. However, for the case of  , the overall luminosity of this high energy emitted component is significantly less than that produced in the main zone. Only for the case of small collision timescales,
, the overall luminosity of this high energy emitted component is significantly less than that produced in the main zone. Only for the case of small collision timescales,  , is the SED dominated by the emission produced in the blobs. The dashed curves in these figures correspond to the emission in the accelerator's magnetic field B0 and the solid curves correspond to the emission in the blob's magnetic field B*. If particles enter the strong magnetic field region during the acceleration process, then the maximum attainable energy can be significantly affected, decreasing the energy of the SED maximum formed in the blobs (the case of τ4 in Figures 2 and 3).
, is the SED dominated by the emission produced in the blobs. The dashed curves in these figures correspond to the emission in the accelerator's magnetic field B0 and the solid curves correspond to the emission in the blob's magnetic field B*. If particles enter the strong magnetic field region during the acceleration process, then the maximum attainable energy can be significantly affected, decreasing the energy of the SED maximum formed in the blobs (the case of τ4 in Figures 2 and 3).
Figure 2. Characteristic spectral energy distributions for four example cases considered in Figure 1 (the same line colors for the cases considered in Figure 1 are used here also). The dashed lines indicate the emission from particles in the accelerator magnetic field (B0 = 0.1 G), and the solid lines indicate the emission from particles in the blobs of size R = 3 × 1013 cm having a magnetic field of B* = 102 B0.
Download figure:
Standard image High-resolution imageFigure 3. The same as Figure 2 but for B* = 103 B0.
Download figure:
Standard image High-resolution image4. Physical Justification of the Toy Model
The mathematical model introduced in Section 3 formally depends on a single parameter, τ. However, there are two hidden parameters, t* and B*, that determine the energy range where the leaky-box approximation used is actually valid. Furthermore, the main zone is characterized by two parameters: the size, R, and the magnetic field, B0. The question remains whether there exists a physically meaningful combination of these parameters that would allow the realization of the radiation scenario illustrated in Figure 2.
For the sake of simplicity, we assume that there exist  identical small-scale large field blobs of size r*. The interaction time of electrons with these blobs lasts a minimum duration of t* ≃ r*/c. This interaction time can be significantly longer if the electron is magnetically confined within the blob. To avoid this complication, we focus on sufficiently high electron energies (above E*) such that the electron lifetime is shorter than their minimal confinement time in the blobs ∼ r*/c.
identical small-scale large field blobs of size r*. The interaction time of electrons with these blobs lasts a minimum duration of t* ≃ r*/c. This interaction time can be significantly longer if the electron is magnetically confined within the blob. To avoid this complication, we focus on sufficiently high electron energies (above E*) such that the electron lifetime is shorter than their minimal confinement time in the blobs ∼ r*/c.
For the strong field of the blobs, the geometrical size of the blob dictates the collision time of the electrons with them,
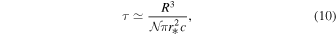
where we used R3 for the volume of the main zone. However, the magnetic field strength of the blob determines the electron energy above which the leaky-box treatment remains valid:
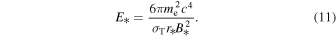
The scenario introduced in Section 3 is realized when the following three conditions are satisfied: (i)  , (ii)
, (ii)  , and (iii) B* ≫ B0. The former condition determines the range for
, and (iii) B* ≫ B0. The former condition determines the range for  , and can be fulfilled without interference with the two other conditions. We therefore need to check just one condition,
, and can be fulfilled without interference with the two other conditions. We therefore need to check just one condition,  , in the limit B* ≫ B0:
, in the limit B* ≫ B0:
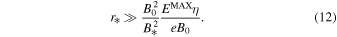
From the application of the maximum energy condition for a source (the "Hillas criterion")  , it follows that there should exist a range of r* such that
, it follows that there should exist a range of r* such that  and r* ≪ R. However, this requires a large ratio of magnetic fields: B* ≫ B0.
and r* ≪ R. However, this requires a large ratio of magnetic fields: B* ≫ B0.
Let us estimate the fraction of the magnetic energy in the blobs required for strong boosting of the radiation energy. It is determined by the condition  :
:
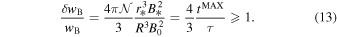
This implies that a significant transformation of the synchrotron spectrum beyond  is possible when the magnetic energy in the small blobs dominates over the energy in the main zone magnetic field. Note that this condition can be realized only in weakly magnetized environments, where the energy contained in the particles can provide an ample source for the formation of strong magnetic fluctuations (blobs). If the particle internal energy is transferred to the magnetic form in blobs, then the total pressure in the blobs should not exceed the external pressure, preventing such regions of strong magnetic field from instantly expanding.
is possible when the magnetic energy in the small blobs dominates over the energy in the main zone magnetic field. Note that this condition can be realized only in weakly magnetized environments, where the energy contained in the particles can provide an ample source for the formation of strong magnetic fluctuations (blobs). If the particle internal energy is transferred to the magnetic form in blobs, then the total pressure in the blobs should not exceed the external pressure, preventing such regions of strong magnetic field from instantly expanding.
We note that such conditions with weakly magnetized plasma are expected in several important gamma-ray sources. For example, while pulsar winds are believed to be weakly magnetized close to the termination shock, the overall conditions in pulsar wind nebulae favor the equipartition of gas and magnetic pressure. Thus, an initially weak magnetic field gets significantly amplified in the nebula. Another example could be gamma-ray burst afterglow emission. According to the standard framework, the afterglow emission is generated by particles that are accelerated at the GRB forward shock that propagates through the circumburst medium. If the circumburst medium magnetic field is ∼10μG, then the initial plasma magnetization is extremely small, say 10−10. The amplification of such a weak magnetic field to some "equipartition" strength may create conditions favorable for the formation of compact magnetic blobs.
5. Magnetic Mirroring
Another important aspect is the ability of particles to enter the regions of strong magnetic field. If the change of magnetic field is small, then particles move in a way such that the adiabatic invariant  is approximately conserved. In this case, the conservation of energy prevents particle penetration into a region with a significantly stronger magnetic field. To account for this effect, which is known as magnetic mirroring, and allow particle penetration from a region with magnetic field B0, the following condition should be fulfilled:
is approximately conserved. In this case, the conservation of energy prevents particle penetration into a region with a significantly stronger magnetic field. To account for this effect, which is known as magnetic mirroring, and allow particle penetration from a region with magnetic field B0, the following condition should be fulfilled:

where T ∼ 2π E/eB0 c and dB/dt ∼ cB*/r* are the particle gyro-rotation period and effective rate of the magnetic field change, respectively. Solving Equation (15) for particle energy, we obtain the minimum energy of particles that can penetrate into the blobs:
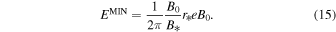
The realization of the discussed scenario requires that  , which can be written as a condition on the blob size:
, which can be written as a condition on the blob size:
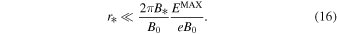
For B* ≫ B0, Equations (12) and (16) can be simultaneously fulfilled.
Equations (16) and (20) show that for the relevant range of magnetic blob sizes, the magnetic mirroring effect should not prevent penetration of particles into the regions of strong magnetic field. However, even if a particle penetrates to the blob, it does not necessarily mean that it could interact with the strongest field. For any realistic configuration of the field, there should exist a gradual increase from the main zone field strength, B0, to the blob field, B*. Motion of a particle in this boundary layer might be very complicated. Although the adiabatic invariant should not be conserved at a strong gradient of magnetic field, we may use it to estimate how deep a particle can penetrate into the blob. We assume that the strongest magnetic field strength, B(E), that a particle with energy E can reach, is determined by a relation similar to Equation (15):
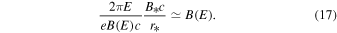
We note that this condition corresponds to the strongest magnetic mirroring. The level of the real effect might be significantly smaller. For example, observations of gamma-ray emission from the Sun (Linden et al. 2018) suggest that magnetic mirroring is not as efficient for reflecting high energy particles as it was naively expected (Seckel et al. 1991).
Solving Equation (17) for B(E), we obtain:
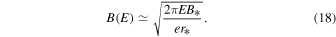
In addition one should take into account that the minimum and maximum magnetic field strength are B0 and B*, respectively.
To estimate the strongest possible impact of the magnetic mirroring, we compute the spectrum from the blob using the energy-dependent magnetic field strength, Equation (18):
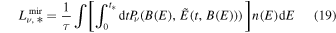
(compare to Equation (9)). In Figures 4 and 5 we show the corresponding SEDs for three different blob sizes: r* = 1013 cm, r* = 1012 cm, and r* = 1011 cm. As can be seen, in the case of strong magnetic mirroring, the spectra can become significantly suppressed at low energies. This is caused by the significant reflection of low-energy electrons. Higher energy particles may have difficulties reaching the strongest magnetic field, which results in spectrum suppression for large blobs, r* ≥ 1012 cm.
Figure 4. Characteristic spectral energy distributions from magnetized blobs showing the impact of strong magnetic mirroring for τ = τ3 and three different blob sizes: r* = 1013 cm, r* = 1012 cm, and r* = 1011 cm. The rest of the parameters are the same as in Figure 2.
Download figure:
Standard image High-resolution imageFigure 5. The same as Figure 4, but for τ = τ2 (left panel) and τ = τ4 (right panel).
Download figure:
Standard image High-resolution image6. Discussion
The synchrotron radiation of relativistic electrons is a unique process that proceeds with high efficiency in a wide variety of astrophysical environments and spans a broad energy range from the radio up to gamma rays. The typical short timescales characterizing the synchrotron cooling of electrons make this process the dominant radiation channel not only at radio wavelengths, but also in the relatively low (sub-GeV) energy gamma-ray band. This is the case, for example, of gamma-ray bursts (GRBs; Ajello et al. 2018), or the so-called Crab flares (Bühler & Blandford 2014). The characteristic spectral and temporal features of this mechanism seem very attractive for the interpretation of the fast and energetic phenomena in the very high energy gamma-ray band as well. One may recall, for example, the ultrafast VHE gamma-ray flares of blazars (Aharonian et al. 2007; Aleksić et al. 2014) or the extension of the gamma-ray spectra of late afterglows of GRBs (Abdalla et al. 2019). However, the self-regulated cut off in the synchrotron spectrum at ≤ 100 MeV has been thought to limit the applicability of the process for energies well above 100 MeV (in the frame of the source).
Synchrotron radiation can be significantly boosted in sources where the emission region moves relativistically,  . The Doppler boosting of the maximum of the synchrotron radiation can be naturally realized in relativistic outflows like the jets of AGNs and GRBs. Typically, in the AGN and late GRB afterglows, the jet's Doppler factors do not exceed 100. Thus the Doppler boosting alone cannot shift the synchrotron radiation to very high energies, especially given that in realistic conditions, e.g., with the inclusion of the presence of dissipative factors like adiabatic losses or plasma instabilities, the η-parameter may significantly exceed 1. The consideration of physically realistic values for η, therefore, exacerbates further the problem of accounting for emission at the
. The Doppler boosting of the maximum of the synchrotron radiation can be naturally realized in relativistic outflows like the jets of AGNs and GRBs. Typically, in the AGN and late GRB afterglows, the jet's Doppler factors do not exceed 100. Thus the Doppler boosting alone cannot shift the synchrotron radiation to very high energies, especially given that in realistic conditions, e.g., with the inclusion of the presence of dissipative factors like adiabatic losses or plasma instabilities, the η-parameter may significantly exceed 1. The consideration of physically realistic values for η, therefore, exacerbates further the problem of accounting for emission at the  scale as being synchrotron in origin.
scale as being synchrotron in origin.
In this paper, we propose a scenario for the formation of synchrotron radiation in compact magnetic blobs located inside the particle accelerator. The blobs do not participate in the acceleration process but serve as passive targets where the highest energy electrons accelerated in the main zone are instantly cooled via synchrotron losses, whose spectrum is effectively extended up to the VHE band. We have developed a simple mathematical formalism based on a "leaky-box" approach, for calculations of synchrotron radiation emerging from such systems. The results of numerical calculations confirm the qualitative estimates. They demonstrate that the synchrotron radiation of such systems can be effectively released in the very high energy regime, provided that the magnetic field in the blobs exceeds two or three orders of magnitude the magnetic field in the accelerator zone. Although the compact magnetic condensations occupy a rather small volume inside the accelerator, the total magnetic energy in these blobs should significantly exceed the electromagnetic energy contained in the acceleration zone. Remarkably, the MHD studies of magnetic amplification by a turbulent dynamo (Zhang et al. 2009) in relativistic outflows may result in such systems where the magnetic energy is predominantly contained in compact clumps. Moreover, this amplification of small-scale fields may be a general effect (Kazantsev 1968).
As shown in Section 4, the hierarchy of the characteristic timescales determining the feasibility of the scenario is such that the extension of the blob synchrotron component to the VHE regime is possible. Let us here outline some criteria for that regime. The toy model from Section 4 contains six parameters: R, B0, η, r*,  , and B*. It is convenient to replace parameter
, and B*. It is convenient to replace parameter  with filling factor, i.e.,
with filling factor, i.e.,  , as it allows us to eliminate the dependences on the size of the system, R. Thus, the radiation regime depends on only five parameters.
, as it allows us to eliminate the dependences on the size of the system, R. Thus, the radiation regime depends on only five parameters.
The extension of the synchrotron component allows one to define the strength of the blob magnetic field: B* ∼ 103
B0
η. This component has a significant luminosity if  , which translates into the condition
, which translates into the condition  . These two conditions further reduce the number of free parameters. Finally, two conditions,
. These two conditions further reduce the number of free parameters. Finally, two conditions,  and Equation (12), define the allowed range for r*:
and Equation (12), define the allowed range for r*:
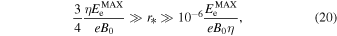
where  depends on B0 and η:
depends on B0 and η:
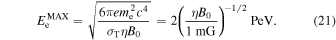
Normalizing the magnetic field to 1 mG, one obtains
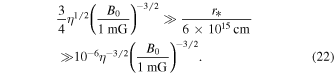
This multi-decade range shows that the requirements for the discussed scenario can be relatively easily met in astrophysical sources. We note here that Equation (16) provides a weaker constraint on the blob size compared to Equation (20). Furthermore, even for the extreme case of effective magnetic mirroring, this scenario can still be realized provided that the blobs have a sufficiently small size:
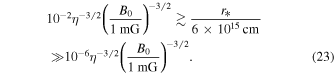
We thank the anonymous referee for useful comments that helped us to improve the manuscript. DK acknowledges support by JSPS KAKENHI Grant Numbers 18H03722, 18H05463, and 20H00153.
Appendix A: Leaky-box Approximation
Magnetic field fluctuations play a key role in both sink and source terms in the standard injection-cooling equation:
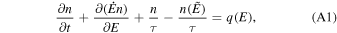
where q(E) is the injection term, n = dN/dE is the energy distribution function,  is energy losses in the main zone magnetic field, τ is the particle–fluctuation collision time, and
is energy losses in the main zone magnetic field, τ is the particle–fluctuation collision time, and  is the particle energy that cools down to E while interacting with the fluctuation. While the particle is interacting with the fluctuation, it loses energy via synchrotron emission in the strong magnetic field of strength B*. If the confinement time is t*, then the initial and final particle energies (
is the particle energy that cools down to E while interacting with the fluctuation. While the particle is interacting with the fluctuation, it loses energy via synchrotron emission in the strong magnetic field of strength B*. If the confinement time is t*, then the initial and final particle energies ( and E, respectively) are related as
and E, respectively) are related as
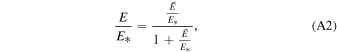
where  is the synchrotron cooling time in the magnetic field of strength B*, and E* is the solution of equation t* = t
SYN
(E*, B*). According to Equation (A2), for the energy range E > E*, there are no particles that cool down to E, and Equation (A1) takes a simple form
is the synchrotron cooling time in the magnetic field of strength B*, and E* is the solution of equation t* = t
SYN
(E*, B*). According to Equation (A2), for the energy range E > E*, there are no particles that cool down to E, and Equation (A1) takes a simple form
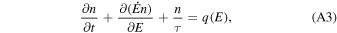
which is identical to the equation for the transport of cosmic rays under the leaky-box approximation. It allows a well-known analytical solution (Syrovatskii 1959):
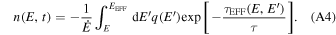
Here, the auxiliary parameters, E EFF and τ EFF , are
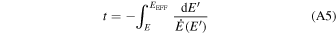
and
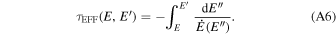
Since the dominant cooling mechanism is synchrotron losses, the above integral can be derived analytically.
Appendix B: Approximated Expression for the Synchrotron Spectrum
The total emission of a particle that enters a high magnetic field region needs to be computed accounting for the change of the particle energy. To be consistent with the standard textbooks, we operate with the total emitted energy per frequency:
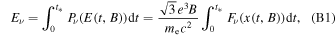
where
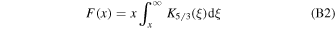
and
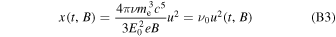
(here, u(t, B) = E0/E(t, B) and the above equation defines ν0). In Equation (B1) the particle energy, E(t), depends on the initial energy, E0, as

and
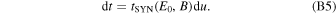
Although, formally, Equation (B1) is a four-parameter function, it is clear that
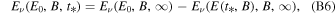
which allows one to reduce the dependence on t*, and in what follows we consider Equation (B1) in the limit t* → ∞.
Combining the above equations, one obtains
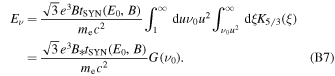
Changing the integral order allows one to derive one integral in the auxiliary function analytically:
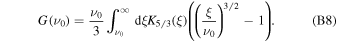
Using the approach introduced in Khangulyan et al. (2014), we approximate Equation (B8) with a simple analytic function:
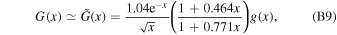
where
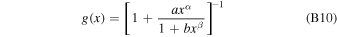
for a = 0.186, α = 0.57, b = 1.75, and β = 1.49. This approximation has an exact asymptotical behavior for x → 0 and ∞ . In the entire range it provides an accuracy of ≃0.2%, as shown in Figure 6.
Figure 6. Ratio of the exact and approximate functions that describe the synchrotron spectrum accounting for the change of the particle energy.
Download figure:
Standard image High-resolution image








