Abstract
Magnetorotational instability (MRI) in complex quantum plasma, which comprises electron, ion, and dust grains, is investigated. Electrons are considered to be degenerate while ions and dust grains are taken as nondegenerate. The general dispersion relation for MRI with the effect of spin magnetization is derived using local approximations. The instability criteria for spin quantum plasma are derived using low-frequency approximations. Due to the complex nature of the dispersion relation, MHD assumptions are used to define the instability criteria. The dust mass plays a significant role in both the dispersion and growth rate of the magnetorotational mode. The complex mass of dust modifies the instability criteria. Spin magnetization force arises due to electron Pauli spin matrices and has an important role in low-temperature and highly dense plasmas that are found mainly in white dwarfs, neutron stars, and in core-collapse supernovae. It is found that spin magnetization influences the criteria for instability and hence the properties of MHD waves in the degenerate plasma.
Export citation and abstract BibTeX RIS
1. Introduction
Many classical theories are presented exploring the dynamics of various rotating plasma instabilities, such as those of Vedenov et al. (1961) and Rosenbluth & Simon (1965). Initially studied by Velikov (1959), work in this area starts with the nondissipative Couette flow of an ideal conducting fluid between two differentially rotating cylinders. It is observed that the fluid is destabilized by applying an axial magnetic field. This work was confirmed by Chandrasekhar (1960). By now, research on magnetorotational instability (MRI) is well understood and reported in both experimentally (liquid metals; Rüdiger et al. 2003; Ji et al. 2004) and theoretically based studies of astrophysical plasmas (Blaes & Balbus 1994; Hawley et al. 1995; Quataert et al. 2002). In astrophysical environments, MRI is now believed to be the main factor deriving plasma turbulence and also to account for the accretion process that feeds stars and black holes (Kotake et al. 2004). After its discovery, MRI remained outside the general theory of plasma instabilities for almost four decades, and was revisited with its application to astrophysical objects by considering the anomalous viscosity problem in the accretion disks surrounding astrophysical compact objects; see Balbus & Hawley (1991). MRI is supposed to be a destructive factor for the hydrodynamical Rayleigh's stability criterion, making it magnetohydrodynamically unstable and leading directly to orbital angular momentum transport and disk turbulence (Hawley & Balbus 1991, 1992; Balbus & Hawley 1998). A two-fluid model for MRI in differentially rotating plasma was presented by Ren et al. (2011) to describe the dynamical behavior of ions and electrons in both low- and high-frequency regimes. They have demonstrated the instability criteria that differ significantly from the one derived in the single-fluid model (Balbus & Hawley 1991). Mikhailovskii et al. (2008a) studied MRI in dusty plasmas using a single-fluid MHD model. They derived a generalized relation by including the effect of dust particulates, and due to the induced electric field the rotation of equilibrium plasma was modified and gave rise to an instability called a dust-induced rotational instability. In their preceding work (Mikhailovskii et al. 2008b) with an immobile dust grain assumption, a comprehensive analysis was carried out for the collective phenomenon of instability which provides a more detailed theory about MRI. The MRI in differential rotating dusty plasmas with dissipative effects was investigated by using local linear analysis with effect of immobile dust grains (Ren et al. 2009).
Quantum plasma in recent times has attracted much attention due to its important and vital role in microelectronic devices (Mola et al. 1993; Manfredi & Feix 1996; Haas et al. 2000), resonant-tunneling diodes (Gardner 1994; Chen et al. 1995), nanostructured materials, quantum wires, and quantum wells (Manfredi & Hervieux 2006, 2007). In general, quantum effects become important when plasma is cooled down to an extremely low temperature such that the Fermi temperature becomes equal to or greater than the thermal temperature of the system. In such conditions the de Broglie wavelength of the charge carriers is comparable to the system dimension, where the ultracold plasma behaves like a Fermi gas and quantum mechanical effects dominantly play their role in the dynamics of charged particles. Recently, some theoretical and numerical investigations were carried out in quantum plasma in dense compact objects such as linear and nonlinear waves in dense magnetized plasma (Manfredi & Haas 2001; Opher et al. 2001; Chabrier et al. 2002; Marklund & Brodin 2007), electromagnetic waves in ultracold quantum plasma (Shukla & Stenflo 2006), quantum Weibel and filamentation instabilities (Haque & Saleem 2008; Haas & Lazar 2008; Haas 2008), and instabilities in quantum plasmas with spin and magnetization effects (Marklund et al. 2007; Brodin et al. 2008; Lundin et al. 2008).
The effect of the dust ingredients in plasmas are also of much interest and cannot be ignored, particularly in the physics of compact objects, accretion, and protoplanetary disks; see, for example, Pandey & Lakhina (1998) and Nomura & Nakagawa (2006). The dust grains are usually highly charged up to ∼104 e due to a variety of processes including plasma currents, photoelectric effects, and secondary emission. The grain size is estimated to be of the order of 10 nm–100 μm and massive up to the order of 108 mi (Jamil et al. 2015). In astrophysical conditions, the dust grains go through a formation process and are irregularly shaped aggregates. Due to their complex nature (porous/fluffy), aggregates acquire higher charge-to-mass ratios, which in turn may alter their subsequent dynamics (Ma et al. 2013). In most space environments, dust grains are exposed specifically to ultraviolet radiation and, consequently, collect electrostatic charges and respond to electromagnetic forces. Simultaneously, these unusual charged dust grains can alter the plasma environment as these particulates are significantly bigger in size and charged as compared to other plasma particles. Their presence can significantly influence the collective plasma properties and behavior by altering the dynamics of various wave modes and by triggering different types of instabilities.
Reach et al. (2005) have observed some evidence of degenerate dusty plasmas in astrophysical bodies. Their studies show that dust clouds (photospheric metals) are present around white dwarfs (WDs) and can contaminate their surfaces. Using the Spitzer Space Telescope they have computed the emission spectra of various materials (like amorphous carbon, crystalline enstatite, silicates, and forsterites) in WDs, supporting the idea of the presence of dust grains in dense objects. Another observation of dust particles (metal pollution) in WDs has been made by Petrovich & Muñoz (2017) by using a new mechanism. It is suggested therein that metal pollution comes from minor rocky bodies (e.g., asteroids) through tidal disruptions of dusty disks around WDs. The possibility is that these rocky bodies get close enough to a WD to be tidally disrupted (shattering the rocky bodies down to dust) and then accreted. A detailed observed explanation of photospheric metals and tidal disruptions are given in Dupuis et al. (1993), Zuckerman & Reid (1998), and Jura (2003). The high-metallicity materials that were observed in the atmosphere of the most polluted WDs consist of rock-forming materials, e.g., silicate materials (Zuckerman et al. 2007). These materials in the form of dust grains are the nucleosynthesis products in the form of aggregates with different shapes. These products (pollution) are modeled as dust particles present in the plasma environment, injected, and result in the rapid enrichment of the environment of the WDs. Dust may also be added to WDs when a star swells into a red giant and the interstellar clouds e.g., photospheric metals, moving around it are engulfed by it (Zuckerman et al. 2003). These objects are turned into dust grains due to the frictional forces and, after the supernova phase, a WD may appear with dust grains. Another existence of dust particulates in WDs was observed by Kuchner et al. (1998) and Houck et al. (2004) with the interpretation that a WD's interior is close to a dense solid with degenerate electrons surrounding an ion lattice and possibly other heavy particles. Similarly the existence of dust grains in neutron stars (NS) were recently observed: see, for example, Omand et al. (2019). It is found that the interior of NS resembles a giant atomic nucleus with a mixture of interacting nucleons, electrons, and possibly other heavy elementary particles and condensates. These unique states (extreme conditions) of matter occur due to a significant compression of the astrophysical medium which supports them against gravitational collapse. Dust can also be found in other strongly magnetized dense objects, besides NS, such as in supernovae, supernovae remnants, and young stellar objects (Okamoto et al. 2004). The current astrophysical interests of dust (Dunne et al. 2003) are focused on the nonlinear excitation of gravitational waves (Brodin et al. 2005) and infrared observations (Lau et al. 2015) to detect dust in old supernova remnants, and in quantum electrodynamic effects in supernovae shock propagation (Marklund et al. 2005).
In the present work we have proposed a dust model for the atmospheres of WDs. However, this model cannot reveal all the aspects of dusty plasmas at a complete quantum scale but rather some predicted correction terms on an assumed basis. It is directed toward the recent past predictions and observations of dust particles in the atmospheres of WDs. Unfortunately, some of the missing information, e.g., material, geometry, and size, provides constraints to understanding the physical applicability of the model. Also, the lack of precise predictions of relevant situations make it difficult to produce good theoretical results which describe the dust model of WD stars to the full extent. The observations and analysis carried out on WD stars mentioned above can at least partly provide a way to consider the system as dust-rich environment. Before proceeding further, we think that more concrete data of pollution in the atmospheres of WD stars needs to be acquired to put the model on firmer ground. To investigate and analyze the dynamics, we included the dust effect into the quantum hydrodynamics (QHD) equation in this model. A spin-force term is introduced and assumes electrons as degenerate-carrying quantum signatures. The ions and dust particles are considered as classical and have no quantum contributions because of the high mass that gives rise to an insignificant de Broglie wavelength. The dispersion relation (DR) is derived on the basis of local approximations that explain the different aspects of MRI in low-, high-, and intermediate-frequency regimes. Since the DR shows a complex nature, we only consider the low-frequency regime and discuss the instability criteria for MRI.
The rest of the manuscript is organized as follows. Section 2 describes the basic governing QHD equations including the spin-force term and the detailed assumptions are given. In Section 3, on the basis of QHD equations given in Section 2, the general DR for the local MRI is derived. Section 4 describes the detailed discussion devoted to the DR. Different modes and criteria for MRI are discussed in detail. Finally, Section 5 gives the conclusions.
2. Basic Mathematical Formulation
Consider a plasma composed of electrons, singly charged positive ions, and negatively charged dust grains in a cylindrical geometry with an external homogeneous magnetic field B0 directed along the z-axis that is assumed to rotate in an azimuthal direction with an angular frequency Ω = Ω(r). The quasi-neutrality condition can be written as ni = ne + Zd nd , where Zd is the number of negative charges residing on the dust particle and nj is the number density with j = i, e, d representing ion, electrons, and dust particles, respectively. The basic QHD equations of motion and continuity are, respectively, given as
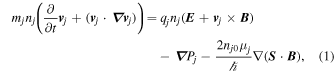
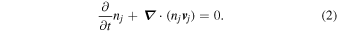
These two Equations (1) and (2) are coupled to Maxwell's equations in the form
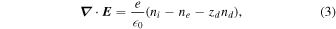

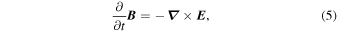
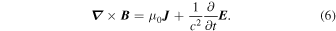
Here mj
,
v
j
, and Pj
are the mass, fluid velocity, and thermal pressure, respectively, qj
is the particle charge, E is the electric field, and B is the magnetic field. Ions and dust grains with the virtue of their high inertia are taken as nondegenerate, while electrons have low inertia and are treated as degenerate. For nondegenerate ions, the classical pressure is Pi
= γi
ni
kB
Ti
and for the degenerate electrons we define the Fermi pressure as 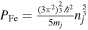 and
and 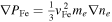 with
with  representing the Fermi velocity and ℏ being the reduced Planck's constant. The parameter J = ∑j=e,i
= qj
nj
vj
+ cJMe
is the current density with JMe
being the spin magnetization current density of electrons and c the speed of light in vacuum. The last term in Equation (1) corresponds to the spin correction term for electron dynamics only. The magnetic moment is represented by μj
(=q
ℏ/2mj
c) and for electrons it is defined as μe
= −μB, with
representing the Fermi velocity and ℏ being the reduced Planck's constant. The parameter J = ∑j=e,i
= qj
nj
vj
+ cJMe
is the current density with JMe
being the spin magnetization current density of electrons and c the speed of light in vacuum. The last term in Equation (1) corresponds to the spin correction term for electron dynamics only. The magnetic moment is represented by μj
(=q
ℏ/2mj
c) and for electrons it is defined as μe
= −μB, with 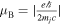 being the Bohr magneton. The spin evolution equation is given by Melrose & Mushtaq (2011):
being the Bohr magneton. The spin evolution equation is given by Melrose & Mushtaq (2011):
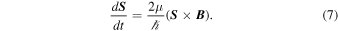
For the lowest-order spin analysis, Equation (7) leads to S × B = 0 and has the solution of the form
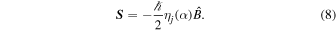
Here 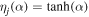 is the Langevin parameter that appears due to the magnetization of spin distribution in a thermodynamic equilibrium with an argument
is the Langevin parameter that appears due to the magnetization of spin distribution in a thermodynamic equilibrium with an argument 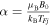 , where
, where  is the Fermi temperature of the degenerate jth particle. In order to eliminate the unperturbed current, i.e.,
J
0 = 0, the electrons and ions are supposed to have the same angular frequency and the equilibrium magnetic field is considered to be homogeneous. In the cylindrical coordinates system (r, θ, z), the equilibrium quantities are given as
v
0 = (0, rΩ, 0),
B
0 = (0, 0, B0),
E
0 = (E0, 0, 0), and Pj0 = Pj0(r).
is the Fermi temperature of the degenerate jth particle. In order to eliminate the unperturbed current, i.e.,
J
0 = 0, the electrons and ions are supposed to have the same angular frequency and the equilibrium magnetic field is considered to be homogeneous. In the cylindrical coordinates system (r, θ, z), the equilibrium quantities are given as
v
0 = (0, rΩ, 0),
B
0 = (0, 0, B0),
E
0 = (E0, 0, 0), and Pj0 = Pj0(r).
3. Dispersion Relation
In the standard cylindrical coordinates where plasma geometry is described by (r, θ, z) the radial, azimuthal, and longitudinal coordinates, the perturbed quantities such as magnetic field, electric field, and velocities are expressed as 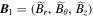 ,
, 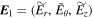 , and
, and 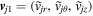 , respectively. Similarly the perturbed number density and pressure are given as
, respectively. Similarly the perturbed number density and pressure are given as 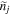 and
and 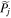 , respectively. All the perturbations are considered to be axisymmetrical and each perturbed profile is assumed to be in a sinusoidal form, i.e.,
, respectively. All the perturbations are considered to be axisymmetrical and each perturbed profile is assumed to be in a sinusoidal form, i.e., 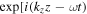 , where ω is the wave oscillation frequency and kz
is the wave projection along the z-direction. Plasma is assumed to be incompressible so that
, where ω is the wave oscillation frequency and kz
is the wave projection along the z-direction. Plasma is assumed to be incompressible so that 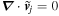 , and considering the homogeneous equilibrium state (unperturbed) nj0 = constant yields the perturbed number density as
, and considering the homogeneous equilibrium state (unperturbed) nj0 = constant yields the perturbed number density as  . The linearized momentum Equation (1) can be written as
. The linearized momentum Equation (1) can be written as
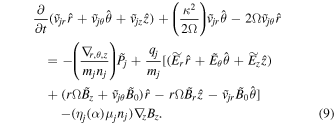
Here 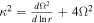 is the square of the epicyclic frequency or the Rayleigh's discriminant. In the Keplerian differential rotation system
is the square of the epicyclic frequency or the Rayleigh's discriminant. In the Keplerian differential rotation system  , κ = Ω. Equation (9) in three projections can be expressed as
, κ = Ω. Equation (9) in three projections can be expressed as
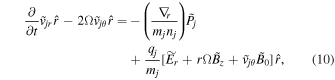
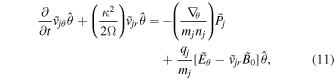
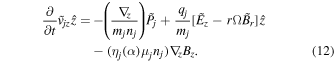
The perturbed Poisson's equation ∇ ·
E
1 = 0, resulting in 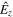 as
as
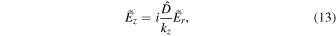
Here the operator 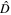 is defined as
is defined as 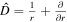 . The divergence-free property of the magnetic field is ∇ ·
B
1 = 0, which provides that
. The divergence-free property of the magnetic field is ∇ ·
B
1 = 0, which provides that
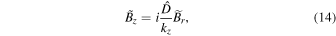
similarly assuming the fluid to be incompressible. From the incompressible condition 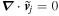 , we express
, we express
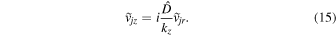
According to the perturbed Faraday's law in Equation (5), we obtain
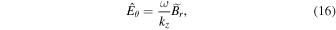
and
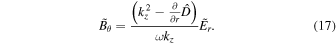
Solving Equation (12) for  in the form of other perturbations and using Equations (13)–(17) in Equations (10) and (11) we get the perturbed motion equations as
in the form of other perturbations and using Equations (13)–(17) in Equations (10) and (11) we get the perturbed motion equations as
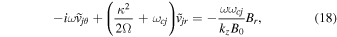
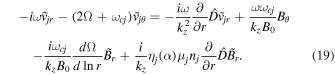
Here 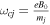 is the gyrofrequency of the jth particle. From Maxwell's Equation (6) the perturbed magnetic field is
is the gyrofrequency of the jth particle. From Maxwell's Equation (6) the perturbed magnetic field is
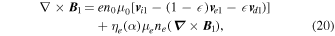
where  = Zd
nd0/ni0 represents the dust concentration ratio. Using the geometry of the problem the ion-perturbed velocities are yielded from Equation (20) as
= Zd
nd0/ni0 represents the dust concentration ratio. Using the geometry of the problem the ion-perturbed velocities are yielded from Equation (20) as
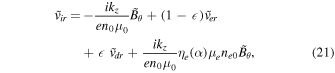
and
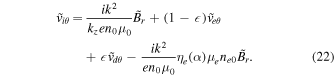
The above four Equations (18)–(19) and (21)–(22) describe eight variables in the form 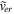 ,
, 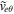 ,
, 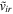 ,
,  ,
, 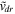 ,
, 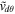 ,
, 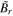 , and
, and  . From Equations (18) and (19), for electrons, the radial and azimuthal (r, θ) components of the perturbed magnetic fields are
. From Equations (18) and (19), for electrons, the radial and azimuthal (r, θ) components of the perturbed magnetic fields are
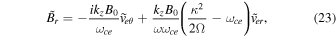
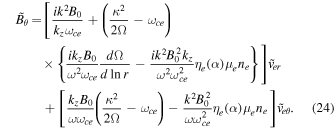
Here ωce
is the electron gyrofrequency. We adopted the local approximations by considering 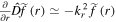 and kr
r ≫ 1 with kr
being the radial wavenumber, and
and kr
r ≫ 1 with kr
being the radial wavenumber, and 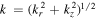 the total wavenumber. A local approach is applicable when there is no radial gradient of equilibrium plasma pressure. The rotation is sustained by the mutual compensation of the centrifugal effect and radial gravity. This approach is useful for the qualitative description of the instability. Writing Equations (18) and (19) for dust, and neglecting the contribution of spin magnetization, we derive the dust velocities as
the total wavenumber. A local approach is applicable when there is no radial gradient of equilibrium plasma pressure. The rotation is sustained by the mutual compensation of the centrifugal effect and radial gravity. This approach is useful for the qualitative description of the instability. Writing Equations (18) and (19) for dust, and neglecting the contribution of spin magnetization, we derive the dust velocities as
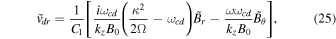
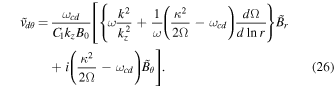
Here 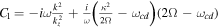 , and ωcd
= Zd
eB0/md
represents the dust gyrofrequency. Now we write Equations (18) and (19) for ions and insert the values of
, and ωcd
= Zd
eB0/md
represents the dust gyrofrequency. Now we write Equations (18) and (19) for ions and insert the values of 
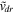 , and
, and  ; after some algebraic manipulation we arrive at the following coupled equations
; after some algebraic manipulation we arrive at the following coupled equations
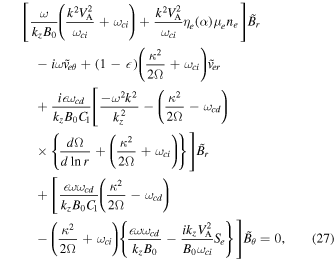
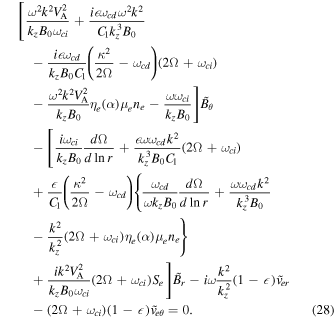
Here ωci
= eB0/mi
represents the ion cyclotron frequency, 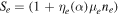 , and
, and 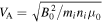 is the ion Alfvén speed. By inserting the values of perturbed magnetic fields
is the ion Alfvén speed. By inserting the values of perturbed magnetic fields 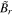 and
and 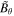 from Equations (23) and (24) into Equations (27) and (28), we obtain the following coupled equations
from Equations (23) and (24) into Equations (27) and (28), we obtain the following coupled equations
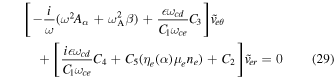
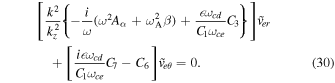
Here ωA = kz VA is the Alfvén frequency and
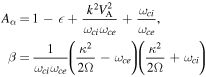
and C2, C3, C4, C5, C6, and C7 are given as
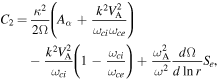
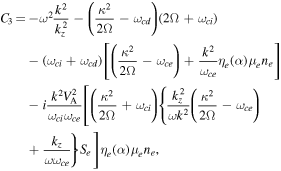
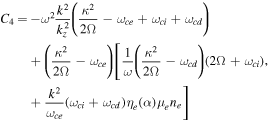
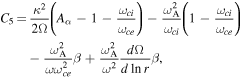


Eliminating the perturbations in the form of  and
and  from Equations (29) and (30), we obtain the following relation
from Equations (29) and (30), we obtain the following relation
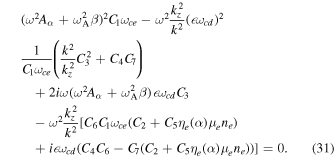
4. Results and Discussion
Equation (31) is the generalized DR of MRI in multicomponent plasma with the effect of dust particulates and the spin magnetization force. It gives information about MRI in all three regimes, low, high, and at intermediate frequencies. If we ignore the spin effect ηe
(α) = 0, the classical relation for MRI in dusty plasma can be recovered (Ren et al. 2009). By neglecting both the spin and dust effect ( = 0 , ηe
(α) = 0) we can get the result reported in Ren et al. (2011) for two-fluid electron–ion plasma.
= 0 , ηe
(α) = 0) we can get the result reported in Ren et al. (2011) for two-fluid electron–ion plasma.
Analytically the DR (31) is of a complex nature, therefore some assumptions and certain conditions are made to describe the criteria for MRI in multispecies plasma with the electron spin magnetization effect. The DR (31) under approximations Ω ≪ ωcd
, 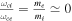 , and kVA ≪ ωcd
(the longer-wavelength approximation) can be written in the form of a biquadratic equation as
, and kVA ≪ ωcd
(the longer-wavelength approximation) can be written in the form of a biquadratic equation as
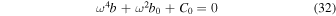
with
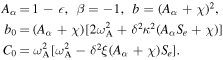
Here 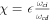 is the ratio of effective dust frequency
is the ratio of effective dust frequency  ωci
and ωcd
,
ωci
and ωcd
,  , and
, and 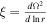 . Equation (32) has an unstable solution if either b0 < 0 or C0 < 0 that is
. Equation (32) has an unstable solution if either b0 < 0 or C0 < 0 that is
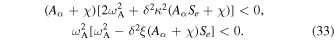
The second condition C0 < 0 represents the spin modified criterion of MRI in spin quantum dusty plasma, given as

The dust factor coupled to the spin magnetization weakens the stabilizing effect of the Alfvén wave. Ignoring the spin magnetization effect (ηe
(α) = 0), the criteria for MRI in classical dusty plasma dynamics can be obtained. The instability takes place when 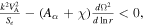 the dust effect χ plays a vital role if χ ≥ 1 and is neglected for χ ≪ 1. The term Se
coupled to the Alfvén velocity has a reducing effect on the dynamics of MHD waves. The general solution of Equation (32) can be written as
the dust effect χ plays a vital role if χ ≥ 1 and is neglected for χ ≪ 1. The term Se
coupled to the Alfvén velocity has a reducing effect on the dynamics of MHD waves. The general solution of Equation (32) can be written as
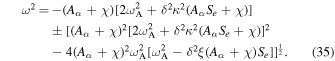
The solution of the second term describes the magnetorotational mode which can be unstable if the second condition in the above Equation (35) is satisfied. Taking the discriminant of the equation we have
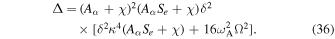
The growth rate 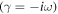 of the MRI can be determined by using the relation
of the MRI can be determined by using the relation
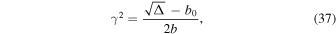
in which Δ is always positive. Hence we can see that for C0 = 0, ![$\mathrm{Re}\left[\gamma \right]=-1$](https://content.cld.iop.org/journals/0004-637X/911/1/50/revision2/apjabe94eieqn51.gif) and for C0 > 0,
and for C0 > 0, ![$\mathrm{Re}\left[\gamma \right]=-1$](https://content.cld.iop.org/journals/0004-637X/911/1/50/revision2/apjabe94eieqn52.gif) the system is stable. For C0 < 0, γ > 0 requires that C0 < b − b0 for
the system is stable. For C0 < 0, γ > 0 requires that C0 < b − b0 for 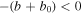 or C0 < 0 for
or C0 < 0 for 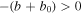 and the system becomes unstable.
and the system becomes unstable.
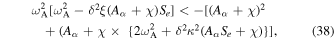
which implies
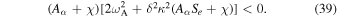
In our conclusion the instability criterion is defined that when 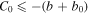 provided that
provided that
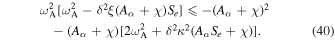
To study the effect of different plasma parameters on the growth rate of MRI, we numerically explore Equation (37) in the limit Ω ≪ ωcd
. For this, we have chosen some typical quantum plasma parameters relevant to dense astrophysical objects, e.g., NS and WDs (Manfredi & Haas 2001; Opher et al. 2001; Chabrier et al. 2002; Marklund et al. 2005; Marklund & Brodin 2007), where the strength of magnetic field is very high and reaches up to megatesla or sometimes to teratesla. The number densities and temperatures lie in the range 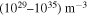 and
and 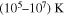 , respectively.
, respectively.
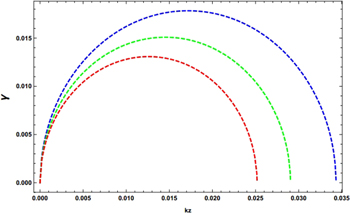
In this work, we have derived the criteria for MRI by taking into account the effect of a nonaxial magnetic field. The criteria obtained here in the form of an equation is analogous to the Solberg–Høiland criteria including the magnetic field B. As far as axisymmetric MRI is concerned, we identified different modes in the DR. We obtained a fourth-order DR describing four different magnetorotational modes. Different modes can certainly be unstable in some different conditions, but in this work we considered only one criterion that is purely unstable giving the growth rate of MRI expressed in Equation (37). We plotted the dependence of growth rate γ over the wavevector kz for the unstable magnetorotational mode in Figure 1. The growth rate of this mode is typically higher in the region of weak magnetic field B. The effect of strong magnetic field decreases the growth rate of the mode which is seen very clearly from the figure. Three different cases are plotted with red, blue, and green dotted lines, which correspond to B = 1 × 105 T, 1.1 × 105 T, and 1.2 × 105 T, respectively. When the value of magnetic filed B increases with the distance to the axis, the growth rate can become stable for some of the possible orientations of kz . Our calculations clearly show that only a strong magnetic field B can affect the stability properties of the system. In the presence of differential rotation, the main contribution to the total magnetic field strength would be from the toroidal magnetic field Bt , and the poloidal magnetic field component Bp would not be of much importance.
Figure 1. Normalized growth rate γ as a function of normalized wavevector kz for various values of magnetic field B0 such that B0 = 1.1 × 106 T (dotted blue curve), B0 = 1.3 × 106 T (dotted green curve), and B0 = 1.5 × 106 T (dotted red curve). Other physical parameters are chosen as ne0 = 1032 m−3, ni0 = 1.6 × 1032 m−3, md = 1.0 × 10−21 kg with Zd = 103, Ω = 102, and κ2 < 0.
Download figure:
Standard image High-resolution imageIn Figure 2 the growth rate γ (normalized by Ωd ) is plotted against the wavevector kz for different values of the equilibrium electron number density ne . It is clear from the figure, as expected, that the growth rate is reduced by enhancing the magnetic field and thus playing a role in confining the system. An important result that can be revealed from the figure is the increasing trend of the growth rate with the electron number density ne . An increase in the number density ne (the number density of ions is kept fixed) enhances the spin magnetization effect and consequently the instability of the system increases. This characteristic clearly emphasizes the diamagnetic behavior of a plasma medium. This instability can arise in different compact objects like WDs and NS, where the number density is of the order of 1029–1035 m−3 and results in core collapse even in the dense interior regions of the stars.
Figure 2. Normalized growth rate γ as a function of normalized wavevector kz for various values of electron number density neo such that ne0 = 1032 m−3 (dotted blue curve), ne0 = 1.5 × 1032 m−3 (dotted green curve), and ne0 = 2 × 1032 m−3 (dotted red curve). Other physical parameters are chosen as ni0 = 1.6 × 1032 m−3, B0 = 1.1 × 106 T, md = 1.0 × 10−21 kg with Zd = 103, Ω = 102, and κ2 < 0.
Download figure:
Standard image High-resolution imageFigure 3 shows the numerical plot of normalized growth rate γ against the wavevector kz corresponding to different values of the dust mass md . It is evident from the figure that higher values of the growth rate are achieved as the value of md increases. It is noted that the masses of the dust grain can vary between 1 × 10−15–1 × 10−21 kg. It can be concluded that enhancing the inertial contribution of the dust grains appears to provide free energy to the system and tries to destabilize it in the limit Ω << Ωd . Physically, there is a possibility that dust particles are of heavier mass so that they are neither perturbed nor rotated, since the typical instability is of the ion dynamic scale.
Figure 3. Normalized growth rate γ as a function of normalized wavevector kz for different values of masses of dust md such that md = 10−21 kg (dotted blue curve), md = 1.2 × 10−21 kg (dotted green curve), and md = 1.4 × 10−21 kg (dotted red curve). Other physical parameters are chosen as ne0 = 1032 m−3, ni0 = 1.6 × 1032 m−3, B0 = 1.1 × 106 T, Zd = 103, Ω = 102, and κ2 < 0.
Download figure:
Standard image High-resolution image4.1. MRI in MHD Modes
The dust is sufficiently massive as compared to electrons and ions. Making assumptions that the rotational frequency is much below the dust gyrofrequency that is Ω ≪ ωcd
, Ω ≪ ωci
, ωcd
≪ ωci
, and  ,
, 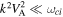 , Aα
= 1, and β = −1. The DR (31) can be written in the form
, Aα
= 1, and β = −1. The DR (31) can be written in the form
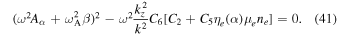
Equation (41) is the low-frequency reduced DR for MRI under the influence of the spin magnetization effect in dusty plasma. It has two branches: (i) the classical branch representing the linear phase of MRI in dusty plasma; (ii) the quantum branch with the electron spin magnetization effect via the Langevin factor ηe
(α), which is responsible for the magnetization energy and depends upon 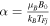 . Considering only the unstable term in Equation (41),
. Considering only the unstable term in Equation (41),
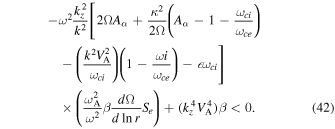
One can see the instability takes place under conditions where
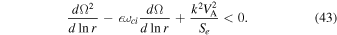
Equation (43) defines the criteria for MRI in multicomponent quantum plasma with the spin magnetization effect. The first term in Equation (43) is the Velikhov effect responsible for deriving the rotational velocity. The positive value of the Velikhov effect can drive an instability of an electromagnetic nature even in unmagnetized plasmas. In this case sufficiently longer-wavelength (low-frequency) perturbations are unstable. However, in the standard MHD regimes the positive value of the Velikhov effect 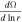 is necessary for instability to take place. The second term illustrates that when Ω increases outwardly the dust imposes a destabilizing effect, leading to the instability when
is necessary for instability to take place. The second term illustrates that when Ω increases outwardly the dust imposes a destabilizing effect, leading to the instability when  ωci
< 2Ω. In reverse, the dust grains give rise to a stabilizing effect when
ωci
< 2Ω. In reverse, the dust grains give rise to a stabilizing effect when  ωci
> 2Ω. The third term is the spin modified Alfvén velocity that can stabilize or destabilize the dynamics. In classical dynamics the Alfvén term is the stabilizing term to the instability. The spin contribution is important here as it depends on the value of the applied magnetic field and the direction of wave propagation. The pure Alfvén wave modes are independent of spin correction, due to the fact that spin will be aligned parallel to the background magnetic field B0 along the z-axis. In many cases it has a very low impact due to its negligible contribution to the total magnetic field. In magnetized plasma the term
ωci
> 2Ω. The third term is the spin modified Alfvén velocity that can stabilize or destabilize the dynamics. In classical dynamics the Alfvén term is the stabilizing term to the instability. The spin contribution is important here as it depends on the value of the applied magnetic field and the direction of wave propagation. The pure Alfvén wave modes are independent of spin correction, due to the fact that spin will be aligned parallel to the background magnetic field B0 along the z-axis. In many cases it has a very low impact due to its negligible contribution to the total magnetic field. In magnetized plasma the term 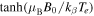 gives the net effect of the spin contribution. The spin effect vanishes when B0 = 0, due to coupling to the Alfvén term. When the factor μB
B0/kB
TFe ≪ 1 in the thermodynamic equilibrium, the spin has a negligible contribution and may be omitted under the approximation μ0
H0 ≈ B0. In the case of strongly magnetized plasma like that found in pulsars and magnetars, the spin contribution cannot be omitted and the factor μB
B0/kB
TFe ≫ 1 shows the strong magnetization effect. This reduces the Alfvénic speed and has an important contribution to the total magnetic field.
gives the net effect of the spin contribution. The spin effect vanishes when B0 = 0, due to coupling to the Alfvén term. When the factor μB
B0/kB
TFe ≪ 1 in the thermodynamic equilibrium, the spin has a negligible contribution and may be omitted under the approximation μ0
H0 ≈ B0. In the case of strongly magnetized plasma like that found in pulsars and magnetars, the spin contribution cannot be omitted and the factor μB
B0/kB
TFe ≫ 1 shows the strong magnetization effect. This reduces the Alfvénic speed and has an important contribution to the total magnetic field.
5. Conclusions
Using the QHD model MRI is investigated in multicomponent magnetized plasma. The plasma is considered to be degenerate and composed of negative inertia-less electrons, inertial ions, and dust-charged particles. A spin quantum force term is added to the dynamic equation and by applying the local approximations the DR is derived. The results agree with the classical one by omitting the spin-effect term. Due to the complex nature of the DR, MHD limitations are adopted to define the instability criteria. The reduced DR is obtained under the limitation Ω ≪ ωcd and the spin-magnetization-corrected dust-induced instability criteria is derived and given in Equation (34). The results about the MRI obtained from the MHD model are reliable only when the longer-wavelength approximation kVA ≪ ωci is satisfied. The condition for the MRI is only that the gradient in the angular velocity be negative. This condition is mainly satisfied in core-collapse supernovae environments. The instability growth rate in (37) is discussed with the variation of magnetic field B, number density of electrons ne , and mass of the dust grain md . The dust grains impose a destabilizing effect on the system and lead the system toward instability. In many astrophysical situations, e.g., supernovae, charged dust grains can affect the plasma dynamics in crucial ways. Dust grains grow in size by mutually sticking and moving sediment toward the midplane of compact disks. The stable region shrinks as the dust grains grow, therefore the protoplanetary compact disks can be magnetorotationally unstable even in their inner regions. The material must have been transported inward; if the material originates from the planetary system of the progenitor, then gravitational perturbations would occasionally send smaller bodies closer to the star. The smaller bodies lose mass by cometary sublimation, or break apart by thermal or gravitational stress, which will cause particles to spiral into the star and contaminate it. This flow could be supplied from the dust-rich interstellar clouds. In interstellar clouds, the dust mass is expected to be 106 mproton ∼ 10−21 kg. Enhancing the inertial contribution of the dust grains appears to provide free energy to the system to destabilize it. On the other hand, a magnetic field imposes a stabilizing effect by playing a role in confining the system. Electron number density also plays a vital role in defining whether the system is stabilizing or destabilizing. A high number density corresponding to instability results in core collapse in many stars. MRI criteria are discussed under MHD approximations and the instability criteria are derived with spin magnetization correction, which significantly differ from that reported in the classical regimes. The system remains unstable to MRI depending on the value of magnetic field. A low poloidal magnetic field can destabilize the rotation and lead the system to an accretion process that occurs on the boundaries where the spin force is not very important. The spin force, because of its coupling to the Alfvén velocity, provides valuable contributions to the dynamics, depending upon the direction of the magnetic field and wave propagation. The contribution of the spin effect vanishes due to the alignment of spin to the background magnetic field, or when the external magnetic field B0 = 0. Spin-force contribution is important in low-temperature and high-density plasma, like that found in WDs, NS, and in core-collapse supernovae. The spin magnetization can be minimized through the condition μB B0 ≪ kβ TFe, however it can even have an influence on the instability criteria and the properties of MHD waves in the degenerate plasma.
S.U. thanks the higher education commission of Pakistan for partial financial support under the international research support initiative program (IRSIP). The work was carried out at Lomonosov Moscow State University, Moscow, Russia. S.U. would like to thank Professor Pavel A. Andreev for many valuable discussions in the improvement of this manuscript.