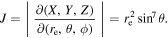Abstract
We have developed a collective plasma radio emission model for the radio pulsars based on the implications of the tangent model. The secondary pair (electron–positron) plasma particles get arranged into a phased array like an antenna due to plasma waves and radiate in phase. We have reproduced the polarization profiles by considering different viewing conditions in the pulsars having an oblique dipolar magnetic field. We find that when there is a resonance between the radio and the plasma waves, the flux of emitted radio waves gets enhanced. We numerically estimated the collective radio emission due to relativistic plasma. The model predicts the correlation between the sign reversal circular polarization and the polarization angle swing and the brightness temperature in the range ∼1031–1033 K.
Export citation and abstract BibTeX RIS
1. Introduction
Although almost 53 yr have passed since the pulsar discovery, their radio emission mechanism still remains unknown. This is one of the most challenging problems of modern astrophysics. Curvature radiation seems to be the most natural and practically unavoidable emission process in the pulsar magnetosphere. Pulsars emit radio waves in an intense, narrow beam that sweeps past the observer once per rotation period of the neutron star to produce the observed pulses (Hewish et al. 1968; Manchester & Taylor 1977; Lyne & Smith 2006). Pulsars are believed to produce radio waves in the open field line region of the polar cap. The shapes of average pulses are quite unique for any given pulsar, but the single pulses display erratic behavior on a timescale faster than the spin period. The pulse components' width, shape, and phase location in the pulsar average profiles are expected to reflect the emission region arrangement in the pulsar magnetosphere (Rankin 1983). The pulsar radiation is highly polarized in general, and the circular polarization is generally strongest in the central regions of profiles but is by no means confined to these regions (Han et al. 1998). The polarization angle (PA) swings like the "S"-shaped curve, explained by the rotating vector model (Radhakrishnan & Cooke 1969).
Gangadhara (2010) developed an incoherent curvature radiation model by including viewing geometry in the pulsar dipolar magnetosphere and thereby explained the polarization of pulsar radio emission and also showed that the correlation between PA swing and the sense reversal of circular polarization (Radhakrishnan & Rankin 1990) is a geometric property of the emission process. The incoherent curvature radiation model of Gangadhara (2010) was further developed by Kumar & Gangadhara (2012a, 2012b, 2013) and Wang et al. (2012) to include the perturbations, such as the aberration–retardation (A/R) effects and polar cap currents, and shown that they can change the pulse shapes and polarization.
Pulsars provide a clear case of coherent radio emission among celestial bodies. The very high brightness temperature 1024–1031 K (e.g., Cordes 1979) of radio pulsars implies that the emission is coherent. Since the radio emission is extremely bright, it requires a coherent emission mechanism because incoherent emission, in which each of the sources (plasma particles) radiates independently of the others, is inadequate (e.g., Sturrock 1971; Ruderman & Sutherland 1975; Totani 2013). The beamed radio emission from relativistic plasma particles, which are constrained to move along the curved trajectories, occurs in the direction of the velocity (e.g., Jackson 1999). The tangent model, which was developed and analyzed by Gangadhara (2004), is exact in the sense that the line of sight always remains tangent to the field line (Yuen & Melrose 2014).
The mechanism of coherent emission in pulsars is still an outstanding problem. By coherence, it is meant that the emitted radio waves are in phase, and mathematically speaking, coherent radiation can be represented by an almost perfect sine wave at a well-defined frequency. However, Katz (2018) showed that the coherent radiation need not be an almost perfect sine wave. In fact, in both pulsars and fast radio bursts (FRBs), it is usually fairly broadband (more so in pulsars than FRBs, where it may be confined to bands with Δν/ν ∼ 0.03). If there is a spatial clumpy radiating charge distribution, then it can produce the observed spectral structure; in that case, the characteristic curvature radiation frequency could be higher than the observed frequencies.
The collective plasma radiation process acts coherently on a timescale of nanoseconds and below in generating pulsar radio waves. Coherent curvature radiation has been considered as a natural emission mechanism for interpreting pulsar observations (Ruderman & Sutherland 1975). Based on the ideas of Sturrock (1971), they ascribed the radiation to coherence induced by a specific beam-plasma instability in the pulsar magnetosphere. The pulsar radio emission is believed to arise due to the growth of plasma instabilities in the relativistic secondary electron–positron plasma streaming out along the curved open dipolar magnetic field lines. Ruderman & Sutherland (1975) developed a magnetospheric model; however, the beam-plasma instability they envisioned does not grow rapidly enough to produce appreciable coherence (Buschauer & Benford 1976). The simplified expression for the radiation electric field (Equation (14.67) in Jackson 1999, used as Equation (17) by Tridb & Gangadhara 2019) is independent of acceleration; hence, the predictions of polarization are very approximate and cannot predict the correlation between PA swing and sense reversal of circular polarization. The models of coherent curvature radiation that have been developed in the literature consider a single arbitrary curved trajectory having almost no relevance to dipolar field geometry and do not consider the polarization of the emitted radiation. Hence, it is hard to make any polarization predictions that can be tested in pulsar observations.
The mystery of coherent radio emission from pulsars is worth solving, as it resolves one of the outstanding problems in pulsar astronomy. The pulsar magnetosphere consists of relativistic plasma, which can support plasma instabilities. The growth of instabilities due to wave–particle or wave–wave interactions can lead to large-amplitude plasma waves, which can impose correlations among particles. Further, if those particles are accelerated, they can radiate electromagnetic (EM) waves nearly in phase (e.g., Katz 2014; Ghisellini & Locatelli 2018). This condition is easily satisfied when the velocities are equal and aligned with the dipolar magnetic field line tangents. It is necessary to understand the general theoretical framework, including pulsar electrodynamics, the properties of the pulsar plasma that populates the relevant regions of a pulsar magnetosphere, and the properties of the wave modes excited (generated). So far, there has been no theory applied to the concept of coherence to broadband radiation with a wide and continuous range of frequencies and phases. In this regard, the initiation and progress made by Katz (2018) are essential. To date, there are no satisfactory explanations for the enigmatic behavior of pulsar radiation. It is of particular interest from the plasma physics viewpoint to understand how familiar plasma physics concepts and methods need to be modified and adapted to the extreme environment of the pulsar magnetosphere. Cordes (1979) reviewed the pulsar radio observations with a particular emphasis on the properties of radio emission relevant for understanding the emission mechanism.
In this paper, we consider a relativistic plasma moving along a curved trajectory with a radius of curvature ρ much longer than the wavelengths. We consider resonance as a phenomenon in which a small-amplitude driving force (charge density and current perturbations) could produce large-amplitude EM waves. These longitudinal electrostatic waves order the particles to phase up to emitting coherently. In Section 2, we develop the coherent curvature model and present the relevant analytical formulation. In Section 3, we simulate the pulse profiles of a typical pulsar and estimate the brightness temperature by considering different viewing geometries. Finally, we give the discussion and conclusion in Sections 4 and 5, respectively.
2. Radio Emission due to Collective Plasma Process
The rotationally induced electric field near the polar cap is believed to pull out electrons from the neutron star surface. They are called primary charged particles having a Lorentz factor γp ∼ 106 (Ruderman & Sutherland 1975). In the presence of the strong magnetic field, these particles radiate γ-rays via synchrotron and curvature emissions, which in turn decay into secondary pair (e+, e−) plasma, and the process continues until the secondary plasma Lorentz factor reaches γ ∼ 102–103. Some of the secondary electrons are expected to go back to the star surface to neutralize the neutron star from getting positively charged. The interaction of primary plasma with the secondary pair plasma can excite an instability such as the electrostatic-streaming instability in the secondary pair plasma (Buschauer & Benford 1976). The electrostatic instabilities make the (e+, e−) plasma into a phased array, which behaves like a radiating antenna (e.g., Lu & Kumar 2018) This proves to be much more efficient than the usual local picture of coherence, which extends only over one wavelength. The mathematical details related to the estimation of the radiation electric field due to the accelerated charged particles are given, for example, in Jackson (1999) and Gangadhara (2010). Here we extend them to the collective plasma emission.
2.1. Radiation Electric Field due to an Accelerated Plasma
For certain radiating systems, by choosing geometry involving symmetry, it is possible to find analytic/semianalytic solutions for the radiation fields and energy. The constrained (one-dimensional) motion of relativistic plasma along the superstrong magnetic field can be treated in analogy with the radiating current that flows in a finite conducting medium of simple geometry, such as in thin antennas of arbitrary length. Consider a Cartesian coordinate system XYZ, such that the Z-axis is parallel to the rotation axis  and the XZ-plane defines the fiducial plane. The line of sight can be chosen, without loss of generality, to lie in the XZ-plane,
and the XZ-plane defines the fiducial plane. The line of sight can be chosen, without loss of generality, to lie in the XZ-plane,
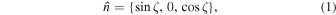
where ζ = α + ϱ, and α is the inclination angle of the magnetic axis  with respect to
with respect to  and ϱ is the line-of-sight impact angle with respect to
and ϱ is the line-of-sight impact angle with respect to  We shall treat the system XYZ as an inertial frame or a laboratory frame in which the neutron star spins (see Figure 1). Next, let us consider a coordinate system
We shall treat the system XYZ as an inertial frame or a laboratory frame in which the neutron star spins (see Figure 1). Next, let us consider a coordinate system  as the rest frame of the plasma and another coordinate system, xyz, which is the fixed frame embedded with the field lines. The axes of the frame xyz are chosen in such a way that the x-axis is parallel to the field line tangent
as the rest frame of the plasma and another coordinate system, xyz, which is the fixed frame embedded with the field lines. The axes of the frame xyz are chosen in such a way that the x-axis is parallel to the field line tangent  the z-axis is antiparallel to the field line curvature vector
the z-axis is antiparallel to the field line curvature vector  , and the y-axis is parallel to the binormal
, and the y-axis is parallel to the binormal  The primed frame
The primed frame  moves with velocity
v
in the x-direction with respect to the unprimed frame xyz. The reference frames coincide at
moves with velocity
v
in the x-direction with respect to the unprimed frame xyz. The reference frames coincide at  Consider a plasma that moves relativistically along the curved dipolar magnetic field lines above the pulsar polar cap. Then the charge density and current density perturbations excited due to the instability in the plasma rest frame
Consider a plasma that moves relativistically along the curved dipolar magnetic field lines above the pulsar polar cap. Then the charge density and current density perturbations excited due to the instability in the plasma rest frame  can be expressed as
can be expressed as
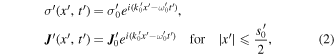
where  and
and  are the amplitudes,
are the amplitudes,  is the length of the plasma column, and
is the length of the plasma column, and  and
and  are the frequency and wavenumber of the longitudinal plasma wave, respectively. The phase velocity of the plasma wave is
are the frequency and wavenumber of the longitudinal plasma wave, respectively. The phase velocity of the plasma wave is  which is taken to be ∼0, for
which is taken to be ∼0, for  Then the Lorentz transformation of the four-current
Then the Lorentz transformation of the four-current  gives the charge and current densities in the frame xyz,
gives the charge and current densities in the frame xyz,
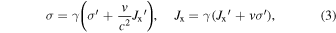
where  and c is the velocity of light. From the equation of continuity, we have
and c is the velocity of light. From the equation of continuity, we have  Since the phase of the plane wave is Lorentz invariant, the charge and current densities can be expressed as
Since the phase of the plane wave is Lorentz invariant, the charge and current densities can be expressed as
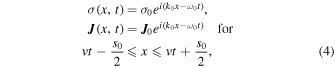
where
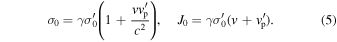
The radiation field due to an accelerated charge is given by (e.g., Jackson 1999)
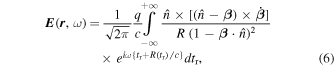
where tr = t − R(tr)/c is the retarded time; t is the observer time; q,
β
=
v
/c, and  are the charge, velocity, and acceleration of the particle, respectively; and R(tr) is the distance between the source and the observer. It can be approximated as
are the charge, velocity, and acceleration of the particle, respectively; and R(tr) is the distance between the source and the observer. It can be approximated as  , where
r
(tr) is the position vector of the emission point at the retarded time. Now, Equation (6) reduces to
, where
r
(tr) is the position vector of the emission point at the retarded time. Now, Equation (6) reduces to
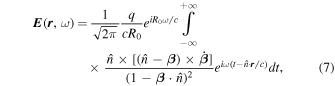
where the suffix "r" on the time variable has been omitted for brevity. To deduce the polarization state of the emitted radiation, we consider the equation of the radiation electric field, which includes acceleration (see Jackson 1999, Equation (14.65)), as it is consistent with the relativistic beaming; i.e., when  the intensity and linear polarization received by the observer go to maximum in the case of
the intensity and linear polarization received by the observer go to maximum in the case of 
Figure 1. Geometry for the estimation of collective plasma emission. The coordinate system XYZ is the pulsar frame (lab frame) chosen such that the spin axis  is parallel to Z, and the line of sight
is parallel to Z, and the line of sight  lies in the fiducial plane XZ. The magnetic axis
lies in the fiducial plane XZ. The magnetic axis  is inclined by angle α with
is inclined by angle α with  , and the curve C represents a typical open dipolar field line. The coordinate system xyz is embedded with the field line, and its axes are chosen in such a way that the x-axis is parallel to the field line tangent
, and the curve C represents a typical open dipolar field line. The coordinate system xyz is embedded with the field line, and its axes are chosen in such a way that the x-axis is parallel to the field line tangent  the y-axis is parallel to the binormal
the y-axis is parallel to the binormal  to the field line, and the z-axis is antiparallel to the curvature vector
to the field line, and the z-axis is antiparallel to the curvature vector  . The frame
. The frame  is the rest frame of the plasma, which moves relativistically with respect to the frame xyz. The
is the rest frame of the plasma, which moves relativistically with respect to the frame xyz. The  -axis is parallel to the field line tangent
-axis is parallel to the field line tangent  , which is in turn parallel to line of sight
, which is in turn parallel to line of sight  The position of the plasma packet is represented by the vector
r
, and the magnetic colatitude is represented by θ.
The position of the plasma packet is represented by the vector
r
, and the magnetic colatitude is represented by θ.
Download figure:
Standard image High-resolution imageWe make the following assumptions:
- 1.The relativistically beamed radio emission is received during the time tem ∼ 2ρ/(γ κ c), where ρ is the radius of curvature of the local trajectory of the plasma. The parameter κ specifies the speed of the plasma column as a fraction of c, and it is about 1.
- 2.The changes in the size and direction of the plasma packet's motion are minimal during the time tem.
- 3.The growth time of the instability is longer than tem.
- 4.The wave packet's phase variation relative to a pure harmonic wave is minimal over the packet's effective extent.
The position vector r of an arbitrary point on an inclined magnetic dipole field line in the Cartesian coordinate system XYZ is given by Gangadhara (2004),
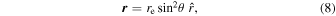
where the unit vector
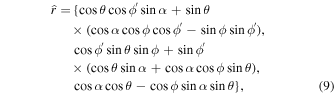
re
is the field line constant, and  is the rotation phase in the lab frame. The angles θ and ϕ are the magnetic colatitude and azimuth, respectively. The field line tangent is given by
b
= ∂
r
/∂θ. The velocity of the plasma in the frame xyz is given by
is the rotation phase in the lab frame. The angles θ and ϕ are the magnetic colatitude and azimuth, respectively. The field line tangent is given by
b
= ∂
r
/∂θ. The velocity of the plasma in the frame xyz is given by  where
where  The unit tangent vector
The unit tangent vector  , and
, and 
We can generalize Equation (7) for the collection of charges accelerated in the plasma column, which is constrained to move along dipolar field lines. In the limit of the continuum distribution of point charges, we can replace
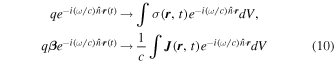
in Equation (7), where dV is the volume element. Then we have
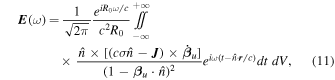
where
β
u =
u
/c and  are the normalized plasma velocity and acceleration in the lab frame.
are the normalized plasma velocity and acceleration in the lab frame.
Next, by substituting σ and J from Equation (4) into Equation (11), we obtain
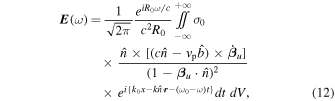
where k = ω/c is the wavenumber of radiation, and  is the phase velocity of the plasma wave in the frame xyz. We shall first evaluate the retarded time integral in Equation (12).
is the phase velocity of the plasma wave in the frame xyz. We shall first evaluate the retarded time integral in Equation (12).
2.2. Evaluation of Time Integration
The distance (arc length) covered by relativistic plasma in an incremental time dt is given by ds = κ cdt = ∣ b ∣d θ (Gangadhara 2010). We can integrate ds by choosing the initial condition that t = s = 0 at θ = 0 and obtain
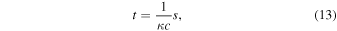
where s is the arc length of the magnetic field line (for derivation, see Appendix A) given by
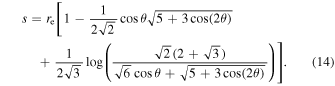
If we substitute s into Equation (13), we get the retarded time t as a function of θ for any given re. In Figure 2, we have shown the relativistically beamed emission cones centered on the field line tangent  at different colatitudes, θ1, θ0, and θ2 on a field line C, which lies in the fiducial plane (
at different colatitudes, θ1, θ0, and θ2 on a field line C, which lies in the fiducial plane ( -
- plane) at which the rotation phase
plane) at which the rotation phase  The observer receives radiation over the range θ1 ≤ θ ≤ θ2 with a maximum at θ = θ0 at which
The observer receives radiation over the range θ1 ≤ θ ≤ θ2 with a maximum at θ = θ0 at which  where η is the angle between
where η is the angle between  and
and  At θ1,2, we have η ∼ ∓ 1/γ, and at θ0, η = 0. For example, using the spin period P = 1 s, Lorentz factor γ = 400, α = 30°, ϱ = 2°, and re = 10rLC, where rLC = Pc/(2π) is the light cylinder radius, for any θ predicted by Equation (30), we can calculate s using Equation (14) and then t using Equation (13). In Table 1, we have tabulated the values of θ, s, and t at the three points.
At θ1,2, we have η ∼ ∓ 1/γ, and at θ0, η = 0. For example, using the spin period P = 1 s, Lorentz factor γ = 400, α = 30°, ϱ = 2°, and re = 10rLC, where rLC = Pc/(2π) is the light cylinder radius, for any θ predicted by Equation (30), we can calculate s using Equation (14) and then t using Equation (13). In Table 1, we have tabulated the values of θ, s, and t at the three points.
Figure 2. Relativistic beamed emission cones centered on the field line tangent  at different colatitudes θ1, θ0, and θ2 on a field line C. The observer receives radiation over the range θ1 ≤ θ ≤ θ2 with a maximum at θ = θ0 at which
at different colatitudes θ1, θ0, and θ2 on a field line C. The observer receives radiation over the range θ1 ≤ θ ≤ θ2 with a maximum at θ = θ0 at which 
Download figure:
Standard image High-resolution imageTable 1. Arc Length and Retarded Time at Different Points on a Magnetic Field Line
| Point | η (deg) | θ (deg) | s (km) | t (ms) |
|---|---|---|---|---|
| 1 | −0.14 | 1.24 | 222.81 | 0.74 |
| 2 | 0.00 | 1.33 | 258.51 | 0.86 |
| 3 | 0.14 | 1.43 | 296.85 | 0.99 |
Download table as: ASCIITypeset image
The component of
r
in the direction of  is given by
is given by
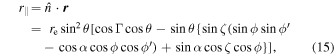
where ![${\rm{\Gamma }}=\arccos [\cos \alpha \cos \zeta +\sin \alpha \,\sin \zeta \,\cos \phi ^{\prime} ]$](https://content.cld.iop.org/journals/0004-637X/911/2/152/revision2/apjabe714ieqn54.gif) is the half-opening angle of the emission beam, i.e., the angle between
is the half-opening angle of the emission beam, i.e., the angle between  and
and  The coordinates of the emission point (θ = θ0, ϕ = ϕ0) at which
The coordinates of the emission point (θ = θ0, ϕ = ϕ0) at which  aligns with
aligns with  are deduced in the tangent model (Gangadhara 2004). The magnetic colatitude θ0 is given by
are deduced in the tangent model (Gangadhara 2004). The magnetic colatitude θ0 is given by
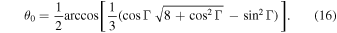
Since  and
and  the magnetic azimuth ϕ0 is given by
the magnetic azimuth ϕ0 is given by
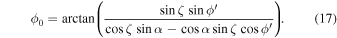
The magnetic colatitude of an arbitrary point on a magnetic field line is given by
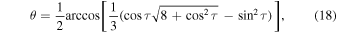
where τ is the angle between  and
and  and τ = Γ when
and τ = Γ when 
Since  we have k0
x ≈ k0
s over the emission receiving time tem. We change the variable of integration from t to θ using Equation (13) and keep the limits of integration at ±∞ for mathematical convenience, as the contributions to the integral vanish outside the range θ1 ≤ θ ≤ θ2 (see Figure 2). So, we have
we have k0
x ≈ k0
s over the emission receiving time tem. We change the variable of integration from t to θ using Equation (13) and keep the limits of integration at ±∞ for mathematical convenience, as the contributions to the integral vanish outside the range θ1 ≤ θ ≤ θ2 (see Figure 2). So, we have
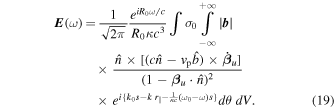
Let us define the argument of the integral as
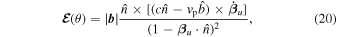
and power series expanding the components in powers of θ of about θ0. Then we obtain
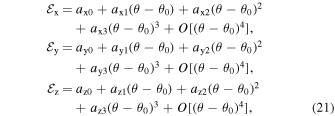
where axi , ayi , and azi ; i = 0, 1, 2, and 3 are the series expansion coefficients; and their expressions are given by Equations (B1)–(B12) in Appendix B. By expanding the (θ − θ0) terms and rewriting in powers of θ, we obtain
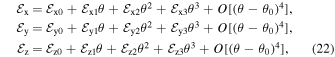
where
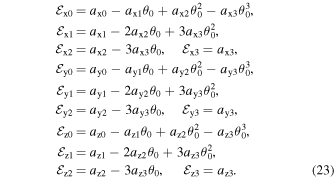
Similarly, the power series expansion of the argument of the exponential is given by
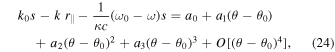
where ai ; i = 0, 1, 2, and 3 are the series expansion coefficients; and their expressions are given by Equations (B13)–(B16) in Appendix B. By expanding the (θ − θ0) terms and rewriting in powers of θ, we have
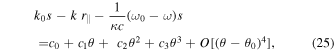
where
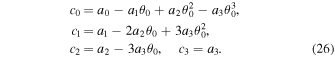
Therefore, the components of E in Equation (19) are
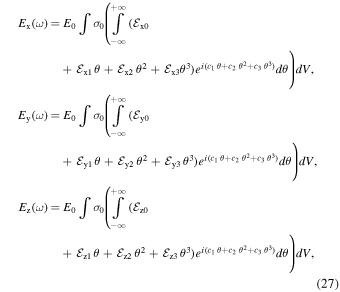
where

Now, by substituting the integral solutions S0 = I0, S1 = I1, S2 = I2, and S3 = I3, given in Appendix C, into Equation (27), we obtain
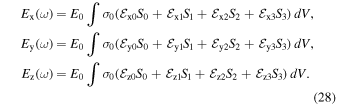
All of the information about the frequency behavior of E (t) is contained in E (ω). Having solved the time integral, we need to evaluate the volume integral.
2.3. Evaluation of Volume Integration
The field line constant re is constant for any given magnetic field line, but it does vary from field line to field line in such a way that it is larger at the magnetic axis and lower at the outer field lines. It is the equatorial distance from the magnetic axis to the field line, i.e., re = r at θ = π/2. Hence, its range is 0 ≤ re ≤ ∞, where re = ∞ for the magnetic axis. Since re varies across the field lines in the poloidal (θ) direction, we treat it as a variable while dealing with plasma motion encompassing many field lines. We consider a dipole field line coordinate system (re, θ, ϕ), which is defined in terms of the usual spherical polar coordinates (r, θ, ϕ), to solve the volume integral in Equation (28), since the plasma is constrained to move along the field lines. Since re gives the location of any arbitrary field line relative to the magnetic axis  the angle
the angle  becomes the half-opening angle of the emission beam when
becomes the half-opening angle of the emission beam when  Hence, we believe that the field line coordinate system allows for a deeper understanding of the geometry of the emission region. In Appendix D, we deduce the infinitesimal elements of area
Hence, we believe that the field line coordinate system allows for a deeper understanding of the geometry of the emission region. In Appendix D, we deduce the infinitesimal elements of area  (see Figure 3) and volume
(see Figure 3) and volume  (see Figure 4) for the plasma that streams out along the open dipolar magnetic field lines. So, the vectorial form of Equation (28) is given by
(see Figure 4) for the plasma that streams out along the open dipolar magnetic field lines. So, the vectorial form of Equation (28) is given by

Figure 3. Plasma moving between the field lines. The shaded region bounded by re1 ≤ re ≤ re2 and θ1 ≤ θ ≤ θ2 shows the area element in the ( )-plane, which lies in the XZ-plane at ϕ = 0. The position vector
r
intersects the field lines at the tangents
)-plane, which lies in the XZ-plane at ϕ = 0. The position vector
r
intersects the field lines at the tangents 
Download figure:
Standard image High-resolution imageFigure 4. Infinitesimal volume element of the plasma column moving along the dipolar field lines, which is bounded within re1 ≤ re ≤ re2, θ1 ≤ θ ≤ θ2, and ϕ1 ≤ ϕ ≤ ϕ2.
Download figure:
Standard image High-resolution imageThe secondary pair plasma cloud, which is constrained to move along the open dipolar magnetic field lines, can have arbitrary shapes and sizes depending upon its creation and evolution mechanism, which may be nonsteady. In the superstrong dipolar magnetic field, the plasma cloud density tends to fall with height as 1/r3 in the diverging field lines. At any given rotation phase, due to relativistic beaming, a distant observer tends to receive radiation from a specific region (beaming region) allowed by the viewing geometry. To find the net coherently radiated electric field of radiation, we need to know the integral limits in Equation (29) allowed by the relativistic beaming conditions.
2.3.1. The Beaming Region
Due to relativistic beaming, at any given rotation phase  a distant observer tends to receive the radiation from all of those field lines whose tangents lie within the angle ∼1/γ with respect to the sight line
a distant observer tends to receive the radiation from all of those field lines whose tangents lie within the angle ∼1/γ with respect to the sight line  (Gangadhara 2010). Let η be the angle between
(Gangadhara 2010). Let η be the angle between  and
and  then
then  and the maximum value of η is ∼1/γ. At any given ϕ0, we can solve
and the maximum value of η is ∼1/γ. At any given ϕ0, we can solve  for τ and find the allowed range (Γ − 1/γ) ≤ τ ≤ (Γ + 1/γ) of τ or −1/γ ≤ η ≤ 1/γ of η, which in turn allows us to find the range of θ with the help of Equation (18). So, at any given rotation phase
for τ and find the allowed range (Γ − 1/γ) ≤ τ ≤ (Γ + 1/γ) of τ or −1/γ ≤ η ≤ 1/γ of η, which in turn allows us to find the range of θ with the help of Equation (18). So, at any given rotation phase  for τ = Γ + η and η = ±1/γ, we can find the allowed range of θ using
for τ = Γ + η and η = ±1/γ, we can find the allowed range of θ using
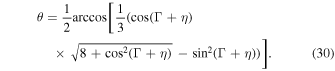
The range of η is nearly fixed at ∼±1/γ at all of the rotation phase. So, for mathematical convenience, we prefer to change the variable of integration from θ to η in Equation (29). At any given  we have
we have
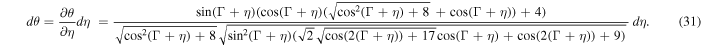
For any given η within its range, we find ϕ by solving  This gives (ϕ0 − δ
ϕ) ≤ ϕ ≤ (ϕ0 + δ
ϕ), where
This gives (ϕ0 − δ
ϕ) ≤ ϕ ≤ (ϕ0 + δ
ϕ), where
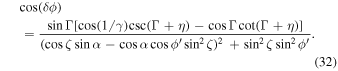
Next, using the characteristic frequency of curvature radiation, ν = 3γ3 c/(4π ρ) (Ruderman & Sutherland 1975), and the radius of curvature of the dipolar magnetic field line,
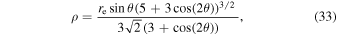
we can find the range of re . Substituting for ρ into the expression of ν and solving for re gives

If ν is the center frequency of observation with bandwidth δ
ν, then we will have a range of frequency between ν1 = ν + (δ
ν/2) and ν2 = ν − (δ
ν/2). At any given rotation phase  and Lorentz factor γ, we can find re1 by subsisting ν1 for ν in Equation (34). Similarly, we can find re2 from ν2.
and Lorentz factor γ, we can find re1 by subsisting ν1 for ν in Equation (34). Similarly, we can find re2 from ν2.
The density of electron–positron plasma near the pulsar is envisioned to be  cm−3 (Ruderman & Sutherland 1975; Benford & Buschauer 1977) in the frame xyz, which streams outward after it is created above a magnetospheric gap at the polar cap, and it evolves with altitude as
cm−3 (Ruderman & Sutherland 1975; Benford & Buschauer 1977) in the frame xyz, which streams outward after it is created above a magnetospheric gap at the polar cap, and it evolves with altitude as  in the diverging field lines, where rNS is the radius of the neutron star and
in the diverging field lines, where rNS is the radius of the neutron star and  is the altitude (emission height). Then the density of particles in the plasma rest frame
is the altitude (emission height). Then the density of particles in the plasma rest frame  becomes
becomes  , and the charge density
, and the charge density  Since
Since  , we have the charge density
, we have the charge density  in the frame xyz. The Lorentz transformation of wavenumber
in the frame xyz. The Lorentz transformation of wavenumber  is given by
is given by  For
For  , we have
, we have  and frequency ω0 = vp
k0, where vp ∼ u is the phase velocity of the plasma wave (ω0, k0).
and frequency ω0 = vp
k0, where vp ∼ u is the phase velocity of the plasma wave (ω0, k0).
2.3.2. Clumpy Plasma Distribution
In most cases, the pulsar average profiles show distinct emission components. Ruderman & Sutherland (1975) suggested that the entire polar cap does not radiate; only some selected regions radiate, which may be organized into a central core emission and coaxial conal emissions. This has overwhelming support from observations (e.g., Rankin 1990, 1993). Hence, the radiating region above the polar is believed to have a central column of emission (core) and a few coaxial conal regions of emission cones (e.g., Gil & Krawczyk 1997; Gangadhara & Gupta 2001; Gupta & Gangadhara 2003). The structure of pulsar emission beams are interpreted as nested cones around a core (Rankin 1993) or patchy based on detection of the number of components and their distribution in rotation phase (Lyne & Manchester 1988; Han & Manchester 2001). The emission components in pulsar average profiles are often identified by decomposing the average pulses into individual Gaussians by fitting one with each of the subpulse components (e.g., Kramer et al. 1994). Hence, the clumpy distributions of plasma such as bunches and columns are inevitable in the emission region. When the line of sight crosses the emission region during neutron star spin, it encounters a pattern in intensity. So we assume that in the emission region, the plasma density is Gaussian-modulated in the azimuthal direction. Hence, we define a modulation function f as
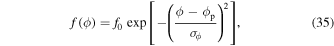
where ϕp is the peak location of the Gaussian function and f0 is the amplitude. If wϕ
is the FWHM, then  Therefore, the modulated charge density can be expressed as
Therefore, the modulated charge density can be expressed as

2.3.3. Net Radiation Electric Field from Beaming Region
Having defined the limits of volume integration, Equation (29) can be rewritten as
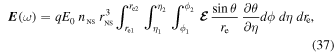
where the limits are η1 = −1/γ, η2 = 1/γ, ϕ1 = ϕ0 − δ ϕ, and ϕ2 = ϕ0 + δ ϕ, and the re limits are mentioned above. The expressions for θ and ∂θ/∂η are given by Equations (30) and (31), respectively. Since the argument of the integrals in Equation (37) is a very lengthy expression, it is challenging to find an analytic solution; therefore, we opt for numerical solutions. Hence, by incorporating all of the abovementioned substitutions, including the charge density σ0m, and taking into account the assumptions and limits of the beaming region, we numerically solve Equation (37) and estimate the radiation electric field.
To find the PA of the radiation field
E
(ω), we need to specify two reference directions perpendicular to the sight line  One could be the projected spin axis on the plane of the sky,
One could be the projected spin axis on the plane of the sky,  and then the other direction is specified by
and then the other direction is specified by  where
where  is a unit vector parallel to the Y-axis. Then the components of
E
(ω) in the directions
is a unit vector parallel to the Y-axis. Then the components of
E
(ω) in the directions  and
and  are given by
are given by

The Stokes parameters for the radiation electric field can be defined as
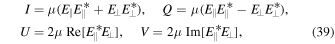
where μ = c/T is the proportionality factor. It is chosen in such a way that I is precisely the intensity or flux density of the pulse that repeats on an average timescale T.
3. Simulation of Pulse Profiles
Let us choose a typical normal pulsar having a spin period P = 1 s, α = 30°, ϱ = 2°, and T ∼ 5.5 ms. Consider a relativistic plasma with Gaussian distribution in charge density σ0m in the azimuthal direction and Lorentz factor γ = 400. Assume that an inertial observer situated at a distance R0 = 2 kpc receives the pulses at frequency ν = ω/2π = 600 MHz with a narrow bandwidth δ
ν ∼ 2 MHz. In the chosen geometry, the observer receives maximum emission at (θ0 = 1 33, ϕ0 = 0°) due to the accelerated plasma along the dipolar magnetic field lines. Using f0 = 1, σϕ
= 0.25, and ϕp = 0°, we have simulated the single component (core) polarization profiles due to coherently emitted radiation. In Figure 5, we have plotted the profiles in the two cases of frequency and wavenumber matching between the EM wave (ω, k) and plasma wave (ω0, k0). In Figures 5(a) and (c), we plot the intensity I with the black curve, linear polarization L with the dashed red curve, and circular polarization V with the green curve. The coherently emitted radiation is highly polarized; hence, I2 = L2 + V2, as in the case of 100% elliptically polarized radiation, where L2 = Q2 + U2. Since ∣V∣ < 20% and L > 94% within the pulse window
33, ϕ0 = 0°) due to the accelerated plasma along the dipolar magnetic field lines. Using f0 = 1, σϕ
= 0.25, and ϕp = 0°, we have simulated the single component (core) polarization profiles due to coherently emitted radiation. In Figure 5, we have plotted the profiles in the two cases of frequency and wavenumber matching between the EM wave (ω, k) and plasma wave (ω0, k0). In Figures 5(a) and (c), we plot the intensity I with the black curve, linear polarization L with the dashed red curve, and circular polarization V with the green curve. The coherently emitted radiation is highly polarized; hence, I2 = L2 + V2, as in the case of 100% elliptically polarized radiation, where L2 = Q2 + U2. Since ∣V∣ < 20% and L > 94% within the pulse window  the curves of I and L are superposed, as L dominates over V. The PA is plotted in Figures 5(b) and (d) and in close agreement with the rotating vector model (Radhakrishnan & Cooke 1969). The sense reversal of circular polarization is correlated with the swing (S-curve) of PA (Radhakrishnan & Rankin 1990; Gangadhara 2010). We observe that in the resonant case, i.e., when waves are resonantly coupled (ω, k) = (ω0, κ
k0), an efficient transfer of energy takes place from plasma to EM wave.
the curves of I and L are superposed, as L dominates over V. The PA is plotted in Figures 5(b) and (d) and in close agreement with the rotating vector model (Radhakrishnan & Cooke 1969). The sense reversal of circular polarization is correlated with the swing (S-curve) of PA (Radhakrishnan & Rankin 1990; Gangadhara 2010). We observe that in the resonant case, i.e., when waves are resonantly coupled (ω, k) = (ω0, κ
k0), an efficient transfer of energy takes place from plasma to EM wave.
Figure 5. Simulated polarization profiles. In the resonant case, ω = ω0, panel (a) shows the intensity I with a black curve, linear polarization L with a red dashed curve, and circular polarization V with a green curve. Panel (b) shows the plotted PA ψ. Similarly, we show the nonresonant case, ω = 2ω0, in panels (c) and (d) with f0 = 1, σϕ = 0.25, and ϕp = 0°.
Download figure:
Standard image High-resolution imageThe peak intensity  erg cm−2 s−1 Hz−1 in the resonant case (see Figure 5(a)) is nearly four times larger than that of the nonresonant case,
erg cm−2 s−1 Hz−1 in the resonant case (see Figure 5(a)) is nearly four times larger than that of the nonresonant case,  erg cm−2 s−1 Hz−1 (see Figure 5(c)). Hence, by knowing the peak values of emitted radiation flux density
erg cm−2 s−1 Hz−1 (see Figure 5(c)). Hence, by knowing the peak values of emitted radiation flux density  , we can estimate the brightness temperature Tb using the expression deduced by Cordes (1979) in the Rayleigh–Jeans regime,
, we can estimate the brightness temperature Tb using the expression deduced by Cordes (1979) in the Rayleigh–Jeans regime,
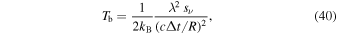
where kB is the Boltzmann constant, λ is the wavelength of the emitted radiation, and Δt is the timescale of sν variation. Using Δt ∼ T = 5.5 ms, λ = 50 cm, and the peak values of I in the two cases of Figures 5(a) and (c), we obtain Tb ≈ 1.15 × 1033 and 7.16 × 1031 K, respectively. They are in the ranges of brightness temperature estimated from the conventional radio pulsar observations.
Similarly, choosing α = 45° and ϱ = 5°, with the remaining parameters the same as in Figure 5, we have plotted the polarization profiles in Figure 6. The peak values of I in Figures 6(a) and (c) are  and
and  erg cm−2 s−1 Hz−1, respectively, and the respective values of Tb are ≈1.17 × 1033 and 7.31 × 1031 K.
erg cm−2 s−1 Hz−1, respectively, and the respective values of Tb are ≈1.17 × 1033 and 7.31 × 1031 K.
Figure 6. Same as Figure 5 but for α = 45° and ϱ = 5°.
Download figure:
Standard image High-resolution imageBy choosing α = 60° and ϱ = − 4°, we have reproduced a triple-component profile by considering three Gaussians, one centered at (θ0 = 2 66, ϕc
= 0°) and the other two at (θ0 = 3
66, ϕc
= 0°) and the other two at (θ0 = 3 54, ϕl = −40°) and (θ0 = 3
54, ϕl = −40°) and (θ0 = 3 54, ϕt = 40°) in Figure 7. For this simulation, we considered three Gaussians, one centered on the meridional plane and the other two located symmetrically on either side,
54, ϕt = 40°) in Figure 7. For this simulation, we considered three Gaussians, one centered on the meridional plane and the other two located symmetrically on either side,
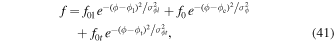
where chosen for the core (f0 = 1, σϕ
= 0.25), the leading component (f0l = 0.7, σϕ
l
= 0.2), and the trailing component (f0t = 0.7, σϕ
t
= 0.2). The peak intensities of the central component (core) in Figures 7(a) and (c) are  and
and  erg cm−2 s−1 Hz−1, respectively, and the respective values of Tb are ≈1.16 × 1033 and 7.28 × 1031 K. We observe that the circular polarization is more significant in the core emission than in the conal emissions.
erg cm−2 s−1 Hz−1, respectively, and the respective values of Tb are ≈1.16 × 1033 and 7.28 × 1031 K. We observe that the circular polarization is more significant in the core emission than in the conal emissions.
Figure 7. Simulated triple-component polarization profiles in the two cases in Figure 5 for α = 60° and ϱ = −4°. Chosen for the core (f0 = 1, σϕ = 0.25, ϕc = 0°), the leading component (f0l = 0.7, σϕ l = 0.2, ϕl = 40°), and the trailing component (f0t = 0.7, σϕ t = 0.2, ϕt = −40°).
Download figure:
Standard image High-resolution imageIf the beaming region emissions are incoherently emitted, then we have to add intensities, i.e., Stokes parameters, instead of radiation fields. Choosing α = 30° and ϱ = 4°, similar to Figure 7, simulated a triple-component profile due to incoherent curvature radiation; it is plotted in Figure 8. The profile shows a significantly unpolarized emission as I2 > L2 + V2. The profile at the central (core) and conal component peaks is nearly 56% linearly and 15% circularly polarized. The value of I at the core peak is  erg cm−2 s−1 Hz−1, and the corresponding brightness temperature is Tb ≈ 1.76 × 1017 K, which is far below the observed brightness temperature of pulsars.
erg cm−2 s−1 Hz−1, and the corresponding brightness temperature is Tb ≈ 1.76 × 1017 K, which is far below the observed brightness temperature of pulsars.
Figure 8. Simulated triple-component polarization profiles in the case of incoherent emission. We chose α = 30° and ϱ = 4°, and the other parameters are the same as in Figures 7(c) and (d).
Download figure:
Standard image High-resolution image4. Discussion
Coherent emission requires a large number of relativistic charges, which can be treated as continuous distribution, and the production of significant fields. Following Equations (4) and (11), it is clear that we treated the radiation mechanism as a hybrid of coherent plasma-curvature radiation, as suggested by Katz (2018). In Figures 5–7, we considered monochromatic waves, which are completely, or 100%, polarized, as the electric vector displays a simple, nonrandom directional behavior in time. The polarization signatures, including PA swing, are in agreement with the observations. The brightness temperature estimated from the model is in the range of ∼1031–1033 K and comparable with the observations. In practice, the radio receiver may not see a single monochromatic component but rather a superposition of many components emitted from different subsections of the beaming region, each with its own polarization state. However, if the amplitude and phase of the waves vary slowly over time, on short timescales of the order 1/ω, they look completely polarized with a definite state of polarization. But over much longer times, Δt ≫ 1/ω, characterizing the times over which amplitudes and phases change significantly, the polarization state can change substantially. Such a wave is no longer monochromatic; the frequency spread Δω can be estimated as Δω > 1/Δt, such that Δω ≪ ω. For this reason, the wave is called quasi-monochromatic. Then the frequency spread Δω becomes the bandwidth of the wave, and the time Δt can be taken as a coherence timescale. For a quasi-monochromatic wave, we have I2 ≥ Q2 + U2 + V2, as some portion of the intensity may not be polarized, as shown in Figure 8. An important property of the Stokes parameters is that they are additive for a superposition of independent waves.
Though coherence and resonance are required in the pulsar emission to account for the high brightness temperature, to some extent, coherence fluctuations and nonresonance (quasi-monochromatic) are also needed to explain the observed intensity variations. From single-pulse studies, we infer that magnetospheric pulsar plasma is highly variable and dynamic; hence, coherence fluctuates in time and space. The single pulses, which depict micropulses and subpulses, are, in some sense, incoherent ensembles of coherent emissions. The profiles presented in Figures 5–7 indicate 100% polarization, but in reality, there is some depolarized component as well. This component could arise due to an incoherent emission in some regions where the plasma conditions are not conducive for coherence. For example, the profile in Figure 5(a) is due to resonant and coherent emission where the plasma wave frequency matches that of an EM wave of 600 MHz, whereas in the nonresonant case in Figure 5(c), the plasma wave frequency does not match the EM wave of 600 MHz, and hence the intensity is lower. But it could be resonantly matched with an EM wave of 1200 MHz in some other region.
5. Conclusion
- 1.We have developed a coherent radio emission model for radio pulsars.
- 2.The collective behavior among the radiating plasma particles and the resonance coupling between the plasma wave and an EM wave are crucial for the enhanced emission.
- 3.The model explains the emission of coherent curvature radiation and its polarization state.
- 4.We confirm that the correlation between the PA swing and the sense reversal of circular polarization is a geometric effect.
- 5.The coherent curvature radiation is nearly 100% polarized in the case of a monochromatic wave.
- 6.The brightness temperatures, ∼1031–1033 K, predicted by the model are closely aligned with the observations.
R.T.G. is grateful to the CAS President's International Fellowship Initiative (PIFI) for supporting this work. J.L.H. is supported by National Natural Science Foundation of China (NSFC) grant No. 11988101. P.F.W. is supported by NSFC grant No. 11873058. We thank the anonymous referee for useful comments.
Appendix A: Arc Length of Magnetic Field Line
The incremental arc length of the field line (Gangadhara 2010) is given by
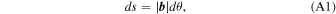
where  =
=  is the magnitude of the field line tangent. Next, by substituting for ∣
b
∣ in Equation (A1) and taking the integral on both sides, we have
is the magnitude of the field line tangent. Next, by substituting for ∣
b
∣ in Equation (A1) and taking the integral on both sides, we have
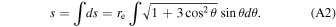
Let  ; then we have
; then we have  Therefore, Equation (A2) reduces to
Therefore, Equation (A2) reduces to
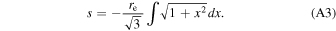
Next, by defining  and
and  we have
we have
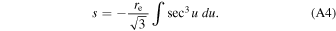
By taking  as the first function and
as the first function and  as the second function, we solve the integration by parts.
as the second function, we solve the integration by parts.
Consider
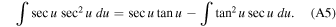
Using  we can express it as
we can express it as
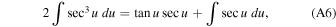
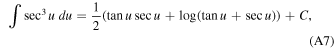
where C is the integration constant. Hence, Equation (A4) can be written as
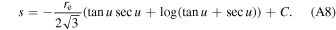
By substituting for  and
and  we get
we get

Next, by substituting back  and using the initial condition that s = 0 at the magnetic colatitude θ = 0°, we obtain
and using the initial condition that s = 0 at the magnetic colatitude θ = 0°, we obtain
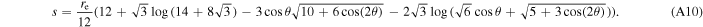
After combining the log terms and simplifying, we get Equation (14):
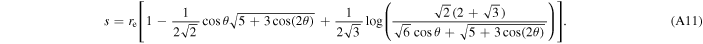
Appendix B: The Power Series Expansion Coefficients
The series coefficients appearing in Equation (21) are
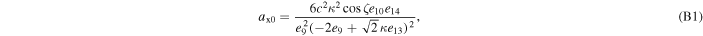
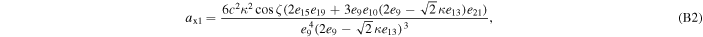
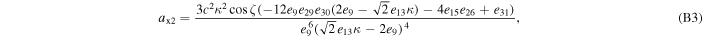
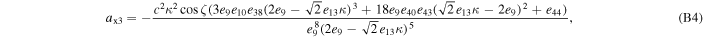
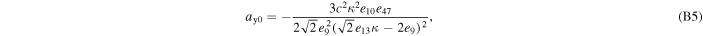

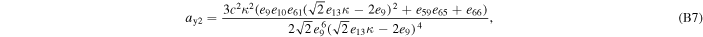
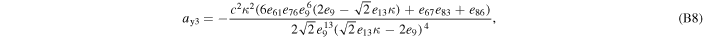
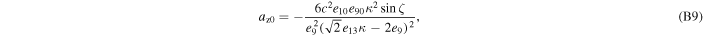
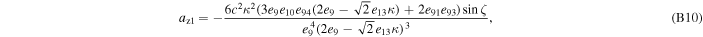
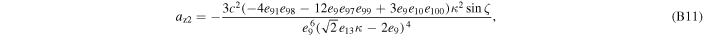
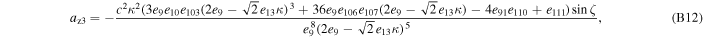
where
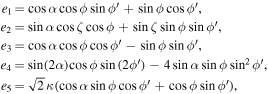
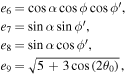
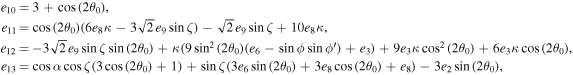
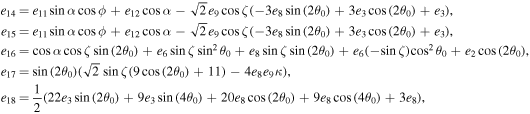
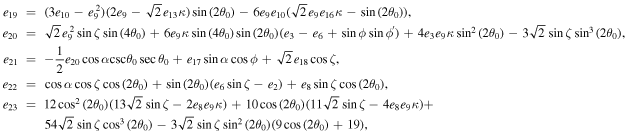
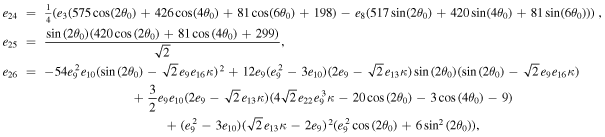
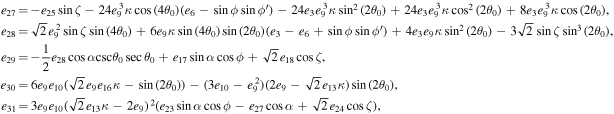
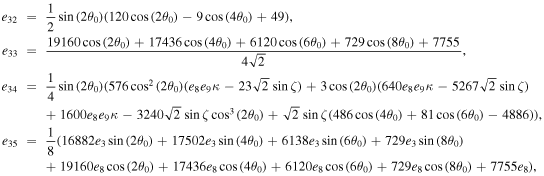
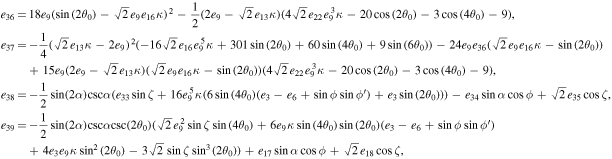
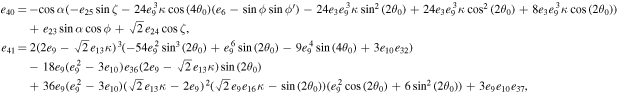
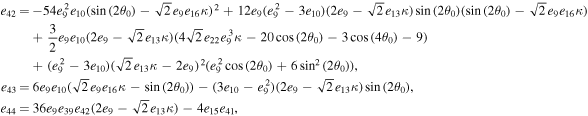
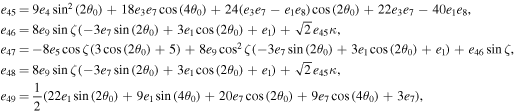
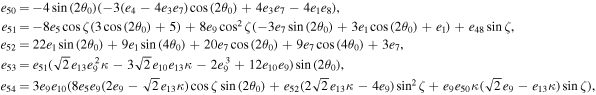
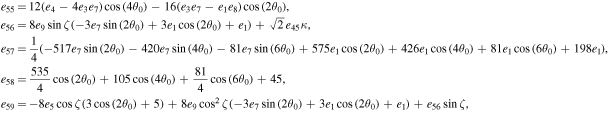
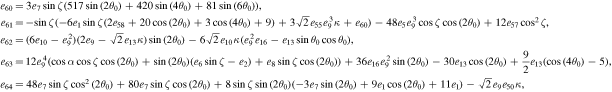

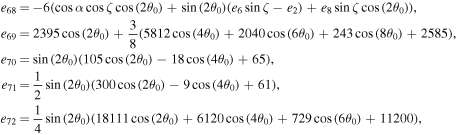


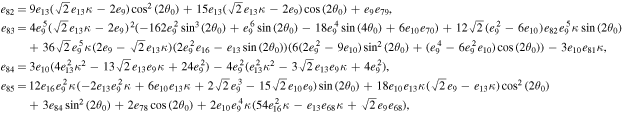

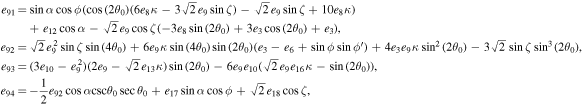


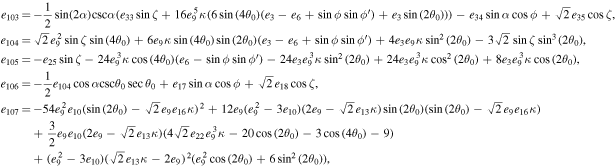
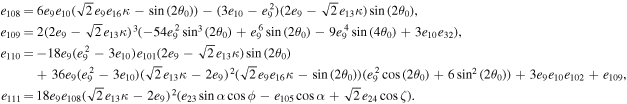
The series coefficients appearing in Equation (24) are
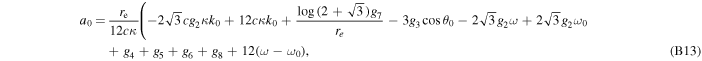
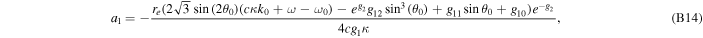
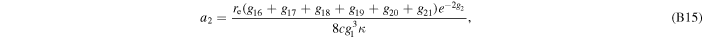
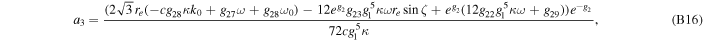
where

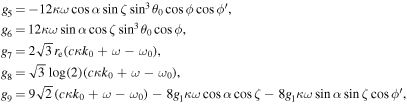
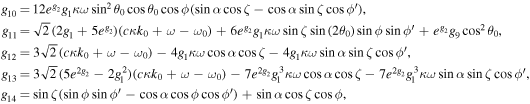

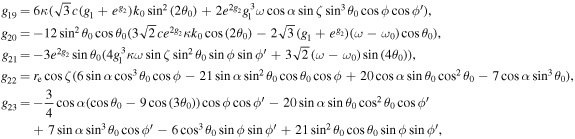
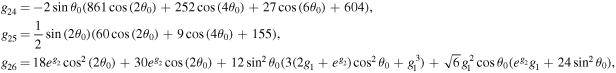
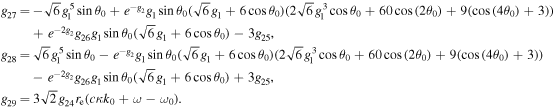
Appendix C: Solution to Fourier Integrals
Consider the integral appearing in Equation (27),
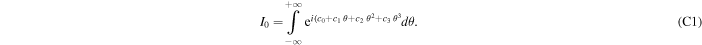
By changing the variable of integration θ = (x/l) + m and defining the constants ![$l=\sqrt[3]{{c}_{3}}$](https://content.cld.iop.org/journals/0004-637X/911/2/152/revision2/apjabe714ieqn122.gif) and m = − c2/(3c3), we obtain
and m = − c2/(3c3), we obtain

where
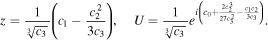
For  , we know
, we know
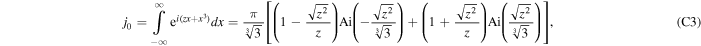
where Ai (z) is an entire Airy function of z with no branch cut discontinuities, and
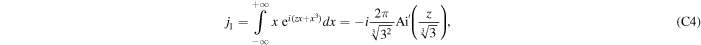
where Ai is the derivative of the Airy function Ai (z). Therefore, we have
is the derivative of the Airy function Ai (z). Therefore, we have
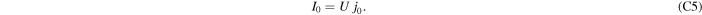
By differentiating Equation (C2) on both sides with respect to c1, we obtain
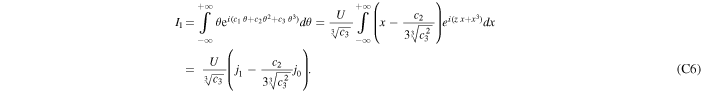
Differentiation of Equation (C2) on both sides with respect to c2 gives
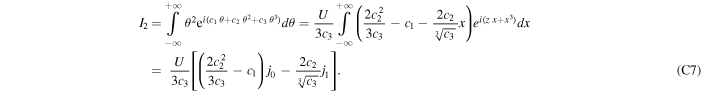
Next, by differentiating Equation (C2) on both sides with respect to c3, we get
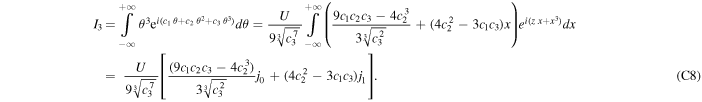
Appendix D: Volume Element of Plasma Moving along Dipolar Field Lines
By differentiating the position vector r presented in Equation (8) with respect to re , θ, and ϕ, we get

where we have chosen  The tangent to the field line is
The tangent to the field line is  , and the arc length
, and the arc length  Then the infinitesimal line element is given by
Then the infinitesimal line element is given by 
The infinitesimal area element, which is shown by the shaded region in the  -plane in Figure 2, is given by
-plane in Figure 2, is given by

Since  and
and  are nonorthogonal, we have
are nonorthogonal, we have
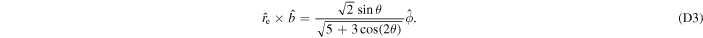
So, we get
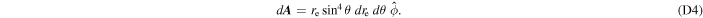
Therefore, the infinitesimal volume element, as shown in Figure 3, is given by
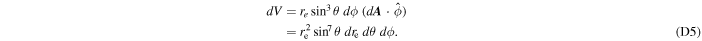
We can also obtain dV by estimating the Jacobian: