Abstract
In this paper, we develop a model to describe the generalized wave–particle instability in a quasi-neutral plasma. We analyze the quasi-linear diffusion equation for particles by expressing an arbitrary unstable and resonant wave mode as a Gaussian wave packet, allowing for an arbitrary direction of propagation with respect to the background magnetic field. We show that the localized energy density of the Gaussian wave packet determines the velocity-space range in which the dominant wave–particle instability and counteracting damping contributions are effective. Moreover, we derive a relation describing the diffusive trajectories of resonant particles in velocity space under the action of such an interplay between the wave–particle instability and damping. For the numerical computation of our theoretical model, we develop a mathematical approach based on the Crank–Nicolson scheme to solve the full quasi-linear diffusion equation. Our numerical analysis solves the time evolution of the velocity distribution function under the action of a dominant wave–particle instability and counteracting damping and shows a good agreement with our theoretical description. As an application, we use our model to study the oblique fast-magnetosonic/whistler instability, which is proposed as a scattering mechanism for strahl electrons in the solar wind. In addition, we numerically solve the full Fokker–Planck equation to compute the time evolution of the electron-strahl distribution function under the action of Coulomb collisions with core electrons and protons after the collisionless action of the oblique fast-magnetosonic/whistler instability.
Export citation and abstract BibTeX RIS
1. Introduction
Wave–particle resonances play an important role for the energy exchange between particles and waves in many space and astrophysical plasmas. For example, wave–particle resonances contribute to the acceleration and deceleration of particles in radiation belts (Ukhorskiy & Sitnov 2014), the deviation of the particle velocity distribution function (VDF) from a Maxwellian equilibrium in the solar wind (Marsch 2006), the thermodynamic state of the intracluster medium in galaxy clusters (Roberg-Clark et al. 2016), and the scattering and absorption of the surface radiation in neutron-star magnetospheres (Lyutikov & Gavriil 2006). Therefore, it is of great importance to study the mechanics of wave–particle resonances in order to advance our understanding of the physics of astrophysical plasmas throughout the universe.
According to kinetic theory, wave–particle resonances can occur in the form of Landau or cyclotron resonances, which contribute to wave instability or wave damping depending on the resonance's characteristics. The quasi-linear theory of magnetized plasma, first established by Yakimenko (1963) and Kennel & Engelmann (1966), provides a mathematical framework to predict the evolution of the particle VDF under the action of wave–particle resonances. Quasi-linear theory assumes that the spatially averaged VDF evolves slowly compared to the gyroperiod of the particles and the wave period. It furthermore assumes that the fluctuation amplitude is small and that the spatial average of the fluctuations vanishes. Based on this theory, numerous analytical studies have successfully explained the evolution of VDFs resulting from wave–particle resonances.
Resonant particles diffuse along specific trajectories in velocity space determined by the properties of the resonant wave (Kennel & Engelmann 1966; Gendrin 1968, 1981; Gendrin & Roux 1980; Stix 1992; Isenberg & Lee 1996; Summers et al. 1998, 2001). In these models, quasi-linear diffusion coefficients determine the diffusion rate of the resonant particles (Lyons et al. 1971; Lyons 1974; Albert 2004; Glauert & Horne 2005; Summers 2005; Isenberg & Vasquez 2011; Tang et al. 2020). Alternatively, quasi-linear diffusion models based on a bi-Maxwellian VDF, in which only its moments evolve in time, describe the effective evolution of particle VDFs under the action of microinstabilities (Seough & Yoon 2012; Yoon & Seough 2012; Yoon et al. 2015, 2017; Yoon 2017). Moreover, fully nonlinear simulations based on kinetic theory model the evolution of the particle VDF consistently with predictions from quasi-linear theory (Vocks & Mann 2003; Vocks et al. 2005; Gary et al. 2008; Saito et al. 2008, 2010; Saito & Peter Gary 2012). Observations from Helios revealed signatures in the proton VDFs consistent with ion cyclotron resonances as predicted by quasi-linear theory (Marsch & Tu 2001; Tu & Marsch 2002; Heuer & Marsch 2007; Marsch & Bourouaine 2011).
Realistic analytical models must describe the diffusive trajectory of resonant particles in velocity space, taking into account the localized (in wavevector space) energy density of the waves that resonate with these particles. These models must also account for non-Maxwellian features in the VDF evolution in order to advance our understanding of plasma observations and kinetic simulation results. A rigorous numerical analysis of the diffusion equation, including both the diagonal and off-diagonal diffusion terms, is necessary to support the theoretical description through the quantification of the diffusion rates.
By analyzing the quasi-linear diffusion equation, we propose a novel quasi-linear diffusion model for the time evolution of VDFs under the action of a dominant wave–particle instability and counteracting damping contributions in Section 2. Our model describes the creation and evolution of non-Maxwellian features in the particle VDF. We allow for an arbitrary type of the unstable and resonant wave mode with an arbitrary direction of propagation with respect to the background magnetic field. In our analysis, we express the electric field of this wave as a Gaussian wave packet in configuration space. The localization of such a wave packet in configuration space is the direct consequence of its generation through a linear instability, which is localized in wavevector space.
To investigate the stabilization of the VDF through quasi-linear diffusion, we apply our analysis of the quasi-linear diffusion equation to Boltzmann's H theorem. In this scheme, the localized energy density of the Gaussian wave packet in wavevector space defines the velocity-space range in which the dominant wave–particle instability and counteracting damping contributions are effective. In addition, we derive a relation to describe the diffusive trajectories of resonant particles in velocity space under the action of such an instability and damping. In this way, our model accounts for the diffusive behavior of resonant particles in different regions of velocity space.
For the numerical evaluation of our theoretical description, we develop a mathematical approach based on the Crank–Nicolson scheme (for numerical details, see Appendix A) that solves the full quasi-linear diffusion equation. Because of its reliable stability, the Crank–Nicolson scheme has been used previously to solve diffusion equations in a variety of fields (Khazanov et al. 2002; Albert 2004; Brügmann et al. 2004; Yang et al. 2009; Klein & Chandran 2016; Taran et al. 2019). However, most standard Crank–Nicolson schemes ignore the off-diagonal terms in the diffusion equation. In our case, these off-diagonal terms are important for the description of resonant pitch-angle scattering. We note that our mathematical approach is applicable to all general two-dimensional diffusion equations, including those with off-diagonal diffusion terms.
In Section 3, as an example, we apply our model to the scattering of the electron strahl, which is a field-aligned electron beam population in the solar wind (Pilipp et al. 1987; Štverák et al. 2009). Observations in the solar wind suggest that strahl electrons exchange energy with whistler waves, which ultimately leads to a scattering of strahl electrons into the halo population (Pagel et al. 2007; Lacombe et al. 2014; Graham et al. 2017). Our quasi-linear framework confirms that an instability of the fast-magnetosonic/whistler wave in oblique propagation with respect to the background magnetic field scatters the electron strahl into the electron halo, as predicted by linear theory (Vasko et al. 2019; Verscharen et al. 2019).
In Section 4, for a more realistic model of the strahl evolution after the collisionless action of the oblique fast-magnetosonic/whistler instability, we numerically solve the full Fokker–Planck equation for Coulomb collisions with our mathematical approach (for numerical details, see Appendix B). We model the time evolution of the electron-strahl VDF through the action of Coulomb collisions with core electrons and protons. This combined method allows us to compare the timescales for the strahl scattering and collisional relaxation.
In Section 5, we discuss the results of our model for the strahl scattering and electron-halo formation through the instability and Coulomb collisions. In Section 6, we summarize and conclude our treatment.
2. Quasi-linear Diffusion Model
In this section, we establish our general theoretical framework for the description of a resonant wave–particle instability in quasi-linear theory. Because our work focuses on nonrelativistic space plasma like the solar wind, we ignore relativistic effects throughout our study.
2.1. Analysis of the Quasi-linear Diffusion Equation
To investigate the time evolution of the particle VDF through wave–particle resonances, we study the quasi-linear diffusion equation, given by Stix (1992):
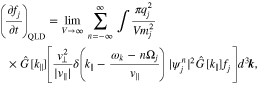
where
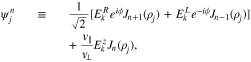
and
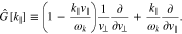
The integer n determines the order of the resonance, where n = 0 corresponds to the Landau resonance and 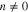 corresponds to cyclotron resonances. In our equations, we label contributions from a given resonance order with a superscript n. The subscript j indicates the particle species. The particle VDF of species j is denoted as
corresponds to cyclotron resonances. In our equations, we label contributions from a given resonance order with a superscript n. The subscript j indicates the particle species. The particle VDF of species j is denoted as 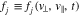 , which is spatially averaged and gyrotropic, qj and mj are the charge and mass of a particle of species j, and
, which is spatially averaged and gyrotropic, qj and mj are the charge and mass of a particle of species j, and 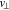 and v∥ are the velocity coordinates perpendicular and parallel with respect to the background magnetic field. We choose the coordinate system in which the proton bulk velocity is zero. We denote the nth-order Bessel function as
and v∥ are the velocity coordinates perpendicular and parallel with respect to the background magnetic field. We choose the coordinate system in which the proton bulk velocity is zero. We denote the nth-order Bessel function as 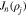 , where
, where 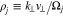 . The cyclotron frequency of species j is defined as
. The cyclotron frequency of species j is defined as 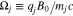 , B0 is the background magnetic field, c is the speed of light,
, B0 is the background magnetic field, c is the speed of light, 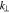 and k∥ are the perpendicular and parallel components of the wavevector k, and V is the volume in which the wave amplitude is effective so that the wave and particles undergo a significant interaction. We denote Dirac's δ function by δ and the azimuthal angle of wavevector k by ϕ. The frequency ω is a complex function of k, and we define
and k∥ are the perpendicular and parallel components of the wavevector k, and V is the volume in which the wave amplitude is effective so that the wave and particles undergo a significant interaction. We denote Dirac's δ function by δ and the azimuthal angle of wavevector k by ϕ. The frequency ω is a complex function of k, and we define 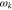 as its real part and
as its real part and 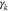 as its imaginary part (
as its imaginary part (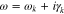 ). Without loss of generality, we set
). Without loss of generality, we set 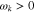 . Furthermore, we assume that
. Furthermore, we assume that 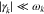 , i.e., the assumption of slow growth or damping that is central to quasi-linear theory.
, i.e., the assumption of slow growth or damping that is central to quasi-linear theory.
The spatially Fourier-transformed electric field has the form of 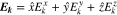 and is defined as (Gurnett & Bhattacharjee 2017)
and is defined as (Gurnett & Bhattacharjee 2017)
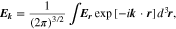
where 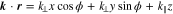 and r is the position vector. We take the constant background magnetic field as
and r is the position vector. We take the constant background magnetic field as 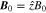 and define the right- and left-circularly polarized components of the electric field as
and define the right- and left-circularly polarized components of the electric field as 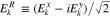 and
and 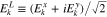 . The longitudinal component of the electric field is
. The longitudinal component of the electric field is 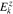 .
.
Linear instabilities typically create fluctuations across a finite range of wavevectors. The Fourier transformation of such a wave packet in wavevector space corresponds to a wave packet in configuration space. For the sake of simplicity, we model this finite wave packet by assuming that the electric field 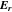 of the unstable and resonant waves has the shape of a gyrotropic Gaussian wave packet,
of the unstable and resonant waves has the shape of a gyrotropic Gaussian wave packet,
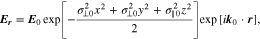
where 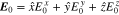 ,
, 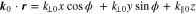 , and k0 is the wavevector of the Gaussian wave packet. We allow for an arbitrary angle θ0 between k0 and
, and k0 is the wavevector of the Gaussian wave packet. We allow for an arbitrary angle θ0 between k0 and  , which defines the orientation of the wavevector at maximum growth of the wave, and assume that
, which defines the orientation of the wavevector at maximum growth of the wave, and assume that  . The vector
. The vector 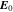 represents the peak amplitude of the electric field. The free parameters
represents the peak amplitude of the electric field. The free parameters  and
and 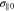 characterize the width of the Gaussian envelope. Quasi-linear theory requires that
characterize the width of the Gaussian envelope. Quasi-linear theory requires that 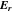 spatially averages to zero. Therefore, we assume that
spatially averages to zero. Therefore, we assume that 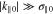 so that the spatial dimension of the Gaussian wave packet is large compared to the parallel wavelength
so that the spatial dimension of the Gaussian wave packet is large compared to the parallel wavelength 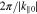 .
.
The spatial Fourier transformation of Equation (5) according to Equation (4) then leads to

We identify V with the volume of the Gaussian envelope, 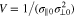 . Equation (6) describes the localization of the wave energy density in wavevector space. For the instability analysis through Equation (6), we define the unstable k spectrum as the finite wavevector range in which
. Equation (6) describes the localization of the wave energy density in wavevector space. For the instability analysis through Equation (6), we define the unstable k spectrum as the finite wavevector range in which 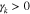 and argue that resonant waves exist only in this unstable k spectrum. We ignore any waves outside this k spectrum because they are damped.
and argue that resonant waves exist only in this unstable k spectrum. We ignore any waves outside this k spectrum because they are damped.
We define k∥0 as the value of k∥ at the center of the unstable k spectrum. We then obtain
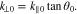
In the case of linear plasma instability, we identify 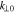 and k∥0 with the wavevector components at which the instability has its maximum growth rate as a reasonable approximation. To approximate the wave frequency of the unstable waves at the angle θ0 of maximum growth, we expand
and k∥0 with the wavevector components at which the instability has its maximum growth rate as a reasonable approximation. To approximate the wave frequency of the unstable waves at the angle θ0 of maximum growth, we expand 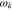 of the unstable and resonant waves around k∥0 as
of the unstable and resonant waves around k∥0 as
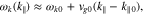
where
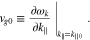
In Equations (8) and (9), 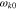 and vg0 are the wave frequency and parallel group velocity of the unstable and resonant waves, evaluated at
and vg0 are the wave frequency and parallel group velocity of the unstable and resonant waves, evaluated at 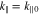 . We select the values of
. We select the values of  and
and 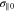 as the half widths of the perpendicular and parallel unstable k spectrum. In the case of linear plasma instability, the numerical values for
as the half widths of the perpendicular and parallel unstable k spectrum. In the case of linear plasma instability, the numerical values for 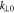 , k∥0,
, k∥0, 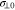 ,
, 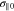 ,
, 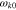 and vg0 can be found from the solutions of the hot-plasma dispersion relation, which thus closes our set of equations.
and vg0 can be found from the solutions of the hot-plasma dispersion relation, which thus closes our set of equations.
By using Equations (6) and (8), we rewrite Equation (1) as
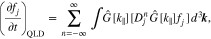
where
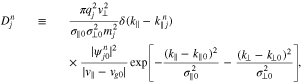
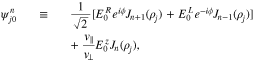
and
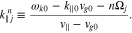
We set 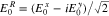 and
and 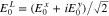 as constant, evaluated at
as constant, evaluated at 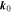 .
.
Equation (10) is the quasi-linear diffusion equation describing the action of the dominant wave–particle instability and coexisting damping contributions from other resonances in a Gaussian wave packet. We define the n resonance as the contribution to the summation in Equation (10) with only integer n. We note that any n resonance can contribute to wave instability or to wave damping depending on the resonance's characteristics.
2.2. Stabilization through a Resonant Wave–Particle Instability
We define stabilization as the process that creates the condition in which 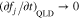 for all v⊥ and v∥. For our analysis of the stabilization of a VDF through a resonant wave–particle instability, including coexisting damping effects, we use Boltzmann's H theorem, in which the quantity H is defined as
for all v⊥ and v∥. For our analysis of the stabilization of a VDF through a resonant wave–particle instability, including coexisting damping effects, we use Boltzmann's H theorem, in which the quantity H is defined as
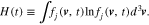
By using Equation (10), the time derivative of H is given by
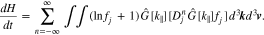
The integrand in Equation (15) is equivalent to
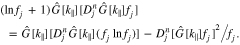
Upon substituting Equation (16) into Equation (15), the first term on the right-hand side in Equation (16) disappears after the integration over v. Then, by resolving the δ function in Djn through the k∥ integral, we obtain
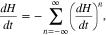
where
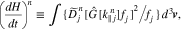
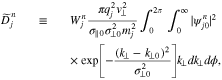
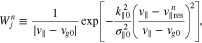
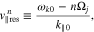
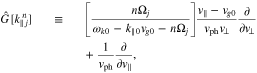
and
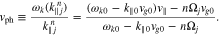
The function 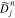 in Equation (19) plays the role of a diffusion coefficient for the n resonance. In
in Equation (19) plays the role of a diffusion coefficient for the n resonance. In 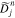 , the v∥ function Wjn defined in Equation (20) serves as a window function that determines the region in v∥ space in which the quasi-linear diffusion through the n resonance is effective. The window function Wjn is maximum at
, the v∥ function Wjn defined in Equation (20) serves as a window function that determines the region in v∥ space in which the quasi-linear diffusion through the n resonance is effective. The window function Wjn is maximum at 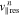 defined in Equation (21), which is the parallel velocity of the particles that resonate with the waves at
defined in Equation (21), which is the parallel velocity of the particles that resonate with the waves at 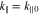 through the n resonance. Our window function Wjn is linked to Dirac's δ function in the limit
through the n resonance. Our window function Wjn is linked to Dirac's δ function in the limit
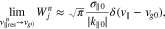
where 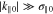 . Through this ordering between
. Through this ordering between 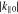 and
and 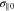 , we assume that Wjn restricts a finite region in v∥ space and that the Wjn for different resonances do not overlap with each other in v∥ space.
, we assume that Wjn restricts a finite region in v∥ space and that the Wjn for different resonances do not overlap with each other in v∥ space.
Only particles distributed within Wjn experience the n resonance and contribute to the quasi-linear diffusion, which is ultimately responsible for the stabilization. Because all terms in Equation (18) are positive semidefinite, all resonances independently stabilize fj through quasi-linear diffusion in the v∥ range defined by their respective Wjn, according to Equation (17). Therefore, H decreases and 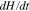 tends toward zero during the quasi-linear diffusion through all resonances while fj is in the process of stabilization. When fj reaches a state of full stabilization through all n resonances, the instability has saturated and its growth ends.
tends toward zero during the quasi-linear diffusion through all resonances while fj is in the process of stabilization. When fj reaches a state of full stabilization through all n resonances, the instability has saturated and its growth ends.
The v∥ function 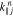 defined in Equation (13) is the resonant parallel wavenumber, fulfilling the condition that
defined in Equation (13) is the resonant parallel wavenumber, fulfilling the condition that 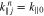 at
at 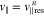 . It quantifies the k∥ component of the unstable k spectrum in the v∥ range defined by Wjn. Equation (23) defines the phase velocity at
. It quantifies the k∥ component of the unstable k spectrum in the v∥ range defined by Wjn. Equation (23) defines the phase velocity at 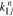 , which is only constant when
, which is only constant when 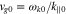 , in which case
, in which case 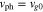 for all v∥. We discuss the diffusion operator
for all v∥. We discuss the diffusion operator ![$\hat{G}[{k}_{\parallel j}^{n}]$](https://content.cld.iop.org/journals/0004-637X/902/2/128/revision1/apjabb099ieqn60.gif) in Equation (22) in the next section.
in Equation (22) in the next section.
2.3. Nature of Quasi-linear Diffusion in Velocity Space
According to Equation (18), unless the wave amplitude is zero, the condition for achieving stabilization through the n resonance is
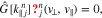
where 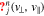 represents the stabilized VDF of species j through the n resonance. In Equation (25),
represents the stabilized VDF of species j through the n resonance. In Equation (25), ![$\hat{G}[{k}_{\parallel j}^{n}]$](https://content.cld.iop.org/journals/0004-637X/902/2/128/revision1/apjabb099ieqn62.gif) is a directional derivative along the isocontour of
is a directional derivative along the isocontour of 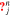 evaluated at a given velocity position. Considering the role of Wjn,
evaluated at a given velocity position. Considering the role of Wjn, ![$\hat{G}[{k}_{\parallel j}^{n}]$](https://content.cld.iop.org/journals/0004-637X/902/2/128/revision1/apjabb099ieqn64.gif) describes only the diffusion of resonant particles within Wjn along the isocontour of
describes only the diffusion of resonant particles within Wjn along the isocontour of 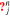 . Consequently, the particles experiencing the n resonance diffuse toward the stable state so that
. Consequently, the particles experiencing the n resonance diffuse toward the stable state so that 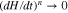 , while the isocontours of
, while the isocontours of 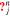 describe the diffusive velocity-space trajectories for the n resonance.
describe the diffusive velocity-space trajectories for the n resonance.
To find such a trajectory, we express an infinitesimal variation of 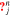 along an isocontour as
along an isocontour as
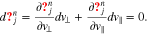
Equations (22) and (26) allow us to rewrite Equation (25) as
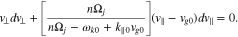
By integrating Equation (27), the diffusive trajectory for the n resonance is then given by
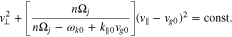
Kennel & Engelmann (1966) treat the two limiting cases in which 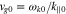 and
and 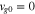 . Using their assumptions, our Equation (28) is equivalent to their Equation (4.8) if
. Using their assumptions, our Equation (28) is equivalent to their Equation (4.8) if  , and our Equation (28) is equivalent to their Equation (4.11) if
, and our Equation (28) is equivalent to their Equation (4.11) if 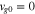 . Depending on the dispersion properties of the resonant waves, Equation (28) is either an elliptic or a hyperbolic equation when
. Depending on the dispersion properties of the resonant waves, Equation (28) is either an elliptic or a hyperbolic equation when 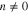 . In the case of electron resonances, it is safe to assume that
. In the case of electron resonances, it is safe to assume that
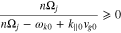
in Equation (28) if 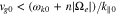 for all positive n and
for all positive n and 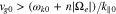 for all negative n. However, in the case of proton resonances, resonant waves are more likely to violate Equation (29) because
for all negative n. However, in the case of proton resonances, resonant waves are more likely to violate Equation (29) because 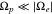 .
.
Figure 1 illustrates the diffusive flux of particles experiencing two arbitrary resonances: the n1 and n2 resonances for an unstable wave. The dark shaded areas represent isocontours of the VDFs of two particle populations in velocity space. The red and dark-blue solid curves represent the diffusive trajectories according to Equation (28) with 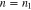 and
and  , assuming that the resonant wave fulfills Equation (29). The window functions
, assuming that the resonant wave fulfills Equation (29). The window functions 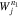 and
and 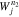 describe the v∥ ranges in which the n1 and n2 resonances are effective. The light-blue dashed semicircles correspond to contours of constant kinetic energy in the proton rest frame, for which
describe the v∥ ranges in which the n1 and n2 resonances are effective. The light-blue dashed semicircles correspond to contours of constant kinetic energy in the proton rest frame, for which
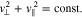
Figure 1. The diffusive flux of resonant particles in velocity space under the action of two arbitrary (n1 and n2) resonances. The dark shaded areas represent isocontours of the VDFs of two particle populations. The red and dark-blue solid curves show the diffusive trajectories, Equation (28) with 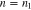 and
and 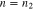 .
. 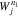 and
and 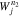 represent the window functions according to Equation (20), in which the n1 and n2 resonances are effective. The light-blue dashed semicircles correspond to constant-energy contours. The black solid line indicates
represent the window functions according to Equation (20), in which the n1 and n2 resonances are effective. The light-blue dashed semicircles correspond to constant-energy contours. The black solid line indicates 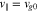 .
.
Download figure:
Standard image High-resolution imageIn general, the diffusive flux is always directed from higher to lower phase-space densities during the process of stabilization. At point A, resonant particles in 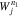 diffuse along the red solid curve toward smaller v∥. Considering the relative alignment between the diffusive flux and the constant-energy contour at point A, the diffusing particles lose kinetic energy. This energy is transferred to the resonant wave, which consequently grows in amplitude. Therefore, this situation corresponds to an instability of the resonant wave. At point B, particles do not diffuse along the red solid curve because this point lies outside
diffuse along the red solid curve toward smaller v∥. Considering the relative alignment between the diffusive flux and the constant-energy contour at point A, the diffusing particles lose kinetic energy. This energy is transferred to the resonant wave, which consequently grows in amplitude. Therefore, this situation corresponds to an instability of the resonant wave. At point B, particles do not diffuse along the red solid curve because this point lies outside 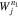 .
.
At point C, resonant particles in 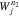 diffuse along the dark-blue solid curve toward greater v∥. Considering the relative alignment between the diffusive flux and the constant-energy contour at point C, the diffusing particles gain kinetic energy. This energy is taken from the resonant wave, which consequently shrinks in amplitude. Therefore, this situation corresponds to the damping of the resonant wave and counteracts the driving of the instability through the n1 resonance. Because the resonant wave is unstable, the n1 resonant instability must overcome the counteracting n2 resonant damping.
diffuse along the dark-blue solid curve toward greater v∥. Considering the relative alignment between the diffusive flux and the constant-energy contour at point C, the diffusing particles gain kinetic energy. This energy is taken from the resonant wave, which consequently shrinks in amplitude. Therefore, this situation corresponds to the damping of the resonant wave and counteracts the driving of the instability through the n1 resonance. Because the resonant wave is unstable, the n1 resonant instability must overcome the counteracting n2 resonant damping.
According to Equation (18), there are three factors that determine the diffusion rate for the action of an n resonance. The first factor is the particle density fj within Wjn. The second factor is 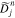 , whose magnitude is determined by the polarization properties of the resonant waves. The third factor is the quantity
, whose magnitude is determined by the polarization properties of the resonant waves. The third factor is the quantity ![$\hat{G}[{k}_{\parallel j}^{n}]{f}_{j}/{f}_{j}$](https://content.cld.iop.org/journals/0004-637X/902/2/128/revision1/apjabb099ieqn90.gif) , which defines the relative alignment between the isocontours of fi and the diffusive flux along the diffusion trajectory within Wjn. In Figure 1, the magnitude of
, which defines the relative alignment between the isocontours of fi and the diffusive flux along the diffusion trajectory within Wjn. In Figure 1, the magnitude of ![$| \hat{G}[{k}_{\parallel j}^{{n}_{1}}]{f}_{j}/{f}_{j}| $](https://content.cld.iop.org/journals/0004-637X/902/2/128/revision1/apjabb099ieqn91.gif) at point A is greater than the magnitude of
at point A is greater than the magnitude of ![$| \hat{G}[{k}_{\parallel j}^{{n}_{2}}]{f}_{j}/{f}_{j}| $](https://content.cld.iop.org/journals/0004-637X/902/2/128/revision1/apjabb099ieqn92.gif) at point C.
at point C.
Because the diffusive flux is directed from higher to lower values of fj, the quantity ![$\hat{G}[{k}_{\parallel j}^{n}]{f}_{j}/{f}_{j}$](https://content.cld.iop.org/journals/0004-637X/902/2/128/revision1/apjabb099ieqn93.gif) resolves the ambiguity in the directions of the trajectories for resonant particles. A careful analysis of
resolves the ambiguity in the directions of the trajectories for resonant particles. A careful analysis of ![$\hat{G}[{k}_{\parallel j}^{n}]$](https://content.cld.iop.org/journals/0004-637X/902/2/128/revision1/apjabb099ieqn94.gif) using Equation (29) shows that, if
using Equation (29) shows that, if ![$({k}_{\parallel }/| {k}_{\parallel }| )(\hat{G}[{k}_{\parallel j}^{n}]{f}_{j}/{f}_{j})\gt 0$](https://content.cld.iop.org/journals/0004-637X/902/2/128/revision1/apjabb099ieqn95.gif) at a given resonant velocity, resonant particles diffuse toward a smaller value of v∥ along the diffusive trajectory, while if
at a given resonant velocity, resonant particles diffuse toward a smaller value of v∥ along the diffusive trajectory, while if ![$({k}_{\parallel }/| {k}_{\parallel }| )(\hat{G}[{k}_{\parallel j}^{n}]{f}_{j}/{f}_{j})\lt 0$](https://content.cld.iop.org/journals/0004-637X/902/2/128/revision1/apjabb099ieqn96.gif) at a given resonant velocity, resonant particles diffuse toward a greater value of v∥.
at a given resonant velocity, resonant particles diffuse toward a greater value of v∥.
2.4. Numerical Analysis of the Quasi-linear Diffusion Equation
To simulate the VDF evolution and to compare the diffusion rates between resonances quantitatively, a rigorous numerical analysis of Equation (10) is necessary. For this purpose, we develop a mathematical approach based on the Crank–Nicolson scheme and present the mathematical details in Appendix A. Our approach is applicable to all two-dimensional diffusion equations with off-diagonal diffusion terms. Our numerical solution, given by Equation (A28), evolves the VDF under the action of multiple resonances in one time step. We tested our numerical solution by showing that the diffusive flux obeys the predicted diffusion properties discussed in Section 2.3.
3. Fast-magnetosonic/Whistler Wave and Electron-strahl Scattering
As an example, we apply our model developed in Section 2 to an electron resonant instability in the solar wind. The fast-magnetosonic/whistler (FM/W) wave propagating in the anti-sunward direction and with an angle of 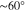 with respect to the background magnetic field scatters the electron strahl (Vasko et al. 2019; Verscharen et al. 2019). Because this prediction is based on linear theory, our quasi-linear framework is appropriate for demonstrating the action of this instability on the electron strahl.
with respect to the background magnetic field scatters the electron strahl (Vasko et al. 2019; Verscharen et al. 2019). Because this prediction is based on linear theory, our quasi-linear framework is appropriate for demonstrating the action of this instability on the electron strahl.
3.1. Linear Dispersion Relation
To find the characteristics of the unstable oblique FM/W wave, we numerically solve the hot-plasma dispersion relation with the NHDS code (Verscharen & Chandran 2018). We use the same plasma parameters as Verscharen et al. (2019), which are, notwithstanding the wide range of natural variation, representative for the average electron parameters in the solar wind (Wilson et al. 2019). We assume that the initial plasma consists of isotropic Maxwellian protons, core electrons, and strahl electrons. The subscripts p, e, c, and s indicate protons, electrons, electron core, and electron strahl, respectively.
We choose our coordinate system so that the anti-sunward and obliquely propagating FM/W waves have 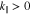 . We set
. We set 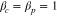 and
and 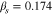 , where
, where 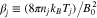 , nj and Tj are the density and temperature of species j, and kB is the Boltzmann constant. We set np = ne,
, nj and Tj are the density and temperature of species j, and kB is the Boltzmann constant. We set np = ne, 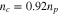 ,
, 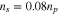 , Tc = Tp, and
, Tc = Tp, and 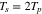 . In the proton rest frame, we set
. In the proton rest frame, we set 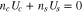 . We initialize the core and strahl bulk velocity with
. We initialize the core and strahl bulk velocity with 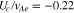 and
and 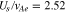 , where
, where 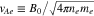 is the electron Alfvén speed. NHDS finds that, under these plasma parameters,
is the electron Alfvén speed. NHDS finds that, under these plasma parameters, 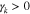 at angles between
at angles between 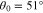 and
and 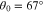 . Our strahl bulk velocity then provides a maximum growth rate of
. Our strahl bulk velocity then provides a maximum growth rate of 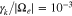 (Verscharen et al. 2019).
(Verscharen et al. 2019).
Figure 2 shows 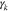 and
and 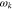 as functions of the k∥ component of the wavevector k for three different θ0. The oblique FM/W instability has its maximum growth rate at
as functions of the k∥ component of the wavevector k for three different θ0. The oblique FM/W instability has its maximum growth rate at 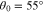 , while
, while 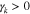 for
for 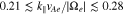 , which is the parallel unstable k spectrum. As defined in Section 2.1, we acquire
, which is the parallel unstable k spectrum. As defined in Section 2.1, we acquire 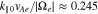 . This value with Equations (7)–(9) leads to
. This value with Equations (7)–(9) leads to 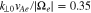 ,
, 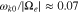 , and
, and 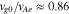 . We also acquire
. We also acquire 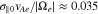 and
and 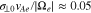 from the unstable k spectrum.
from the unstable k spectrum.
Figure 2. NHDS solutions provide 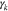 (dashed curves, axis on the left) and
(dashed curves, axis on the left) and 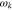 (solid curves, axis on the right) as functions of the k∥ component of the wavevector k. We show solutions for
(solid curves, axis on the right) as functions of the k∥ component of the wavevector k. We show solutions for 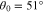 ,
, 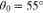 , and
, and 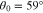 .
.
Download figure:
Standard image High-resolution image3.2. Theoretical Description of the Quasi-linear Diffusion in the FM/W Instability
Using the wave and plasma parameters from the previous section, we describe the electron strahl and core diffusion in velocity space. In our analysis, we only consider the n = +1, −1, and 0 resonances, ignoring higher-n resonances due to their negligible contributions.
Upon substituting our wave parameters into Equation (20), we quantify the dimensionless window functions  with n = +1, −1, and 0. In Figure 3, the red, dark-blue and orange lines represent
with n = +1, −1, and 0. In Figure 3, the red, dark-blue and orange lines represent 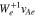 ,
, 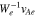 and
and 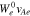 , which are maximum at
, which are maximum at 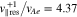 ,
, 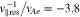 and
and 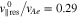 , respectively. We reiterate that the superscripts indicate the n resonance. The black line indicates
, respectively. We reiterate that the superscripts indicate the n resonance. The black line indicates 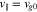 . Each
. Each 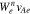 shows the v∥ range in which the quasi-linear diffusion through each resonance is effective. We note that the
shows the v∥ range in which the quasi-linear diffusion through each resonance is effective. We note that the 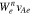 for the three resonances have different widths in v∥ space and maximum values due to the different magnitudes of
for the three resonances have different widths in v∥ space and maximum values due to the different magnitudes of 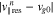 (see Equation (24)). By substituting our wave parameters into Equation (28), the diffusive trajectories for the n = +1, −1, and 0 resonances are given by
(see Equation (24)). By substituting our wave parameters into Equation (28), the diffusive trajectories for the n = +1, −1, and 0 resonances are given by
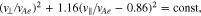
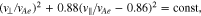
and
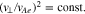
Equations (31) and (32) describe ellipses with their axes oriented along the v⊥ and v∥ directions. In Equation (33), the perpendicular velocity of resonant particles is constant.
Figure 3. The red, dark-blue, and orange curves illustrate 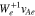 ,
, 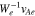 , and
, and 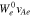 for the oblique FM/W wave. The black solid line represents
for the oblique FM/W wave. The black solid line represents 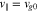 . Each
. Each 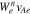 shows the v∥ range in which the corresponding resonance is effective. Each
shows the v∥ range in which the corresponding resonance is effective. Each 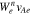 has a different width in v∥ space and maximum value due to a different magnitude of
has a different width in v∥ space and maximum value due to a different magnitude of 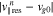 (see Equation (24)).
(see Equation (24)).
Download figure:
Standard image High-resolution imageFigure 4 illustrates the electron diffusion from these three resonances. We show the v∥ ranges in which the three resonances are effective according to 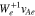 ,
,  , and
, and 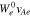 from Figure 3. The red, dark-blue, and orange solid curves represent the contours given by Equations (31)–(33), respectively. The light-blue dashed semicircles correspond to constant-energy contours in the proton rest frame (see Equation (30)). The black line indicates
from Figure 3. The red, dark-blue, and orange solid curves represent the contours given by Equations (31)–(33), respectively. The light-blue dashed semicircles correspond to constant-energy contours in the proton rest frame (see Equation (30)). The black line indicates 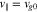 . For the initial strahl and core VDF, we apply the plasma parameters in Section 3.1 to the dimensionless Maxwellian distribution:
. For the initial strahl and core VDF, we apply the plasma parameters in Section 3.1 to the dimensionless Maxwellian distribution:
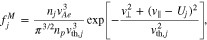
where 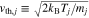 . The red and blue areas in Figure 4 represent fsM and fcM, which are normalized by the maximum value of fcM and plotted up to a value of 10−5. In this normalization, Figure 4 does not reflect the relative density ratio between both electron species.
. The red and blue areas in Figure 4 represent fsM and fcM, which are normalized by the maximum value of fcM and plotted up to a value of 10−5. In this normalization, Figure 4 does not reflect the relative density ratio between both electron species.
Figure 4. The red, dark-blue, and orange arrows illustrate the diffusive flux for the n = +1, −1, and 0 resonances in the oblique FM/W instability. The red and dark-blue filled semicircles represent isocontours of the strahl and core VDF. This figure does not reflect the relative densities of both electron species. The light-blue dashed semicircles correspond to constant-energy contours. The black solid line indicates 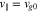 .
.
Download figure:
Standard image High-resolution imageDue to the v∥ profile of 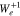 , the n = +1 resonance has a significant effect on fsM. As discussed in Section 2.3, because
, the n = +1 resonance has a significant effect on fsM. As discussed in Section 2.3, because ![$({k}_{\parallel }/| {k}_{\parallel }| )(\hat{G}[{k}_{\parallel e}^{+1}]{f}_{s}^{M}/{f}_{s}^{M})\gt 0$](https://content.cld.iop.org/journals/0004-637X/902/2/128/revision1/apjabb099ieqn154.gif) , this resonance leads to a diffusion of the resonant strahl electrons in
, this resonance leads to a diffusion of the resonant strahl electrons in 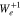 along trajectories represented by the red arrows. According to Equation (30), the phase-space trajectory of particles that diffuse without a change in kinetic energy is described by
along trajectories represented by the red arrows. According to Equation (30), the phase-space trajectory of particles that diffuse without a change in kinetic energy is described by
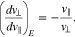
According to Equation (31), the phase-space trajectory of resonant particles fulfilling the n = +1 resonance, indicated by the superscript +1, is described by
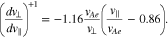
Comparing Equations (35) and (36) in 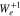 shows that
shows that 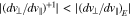 for the resonant electrons. Therefore, resolving the ambiguity in the directions of the trajectories, the distance of resonant strahl electrons from the origin of the coordinate system decreases. This decrease in
for the resonant electrons. Therefore, resolving the ambiguity in the directions of the trajectories, the distance of resonant strahl electrons from the origin of the coordinate system decreases. This decrease in 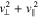 represents a loss of kinetic energy of the resonant strahl electrons. The n = +1 resonance, therefore, contributes to the driving of the FM/W instability.
represents a loss of kinetic energy of the resonant strahl electrons. The n = +1 resonance, therefore, contributes to the driving of the FM/W instability.
Due to the v∥ profile of 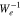 , the n = −1 resonance has a significant effect on fcM. Because
, the n = −1 resonance has a significant effect on fcM. Because ![$({k}_{\parallel }/| {k}_{\parallel }| )(\hat{G}[{k}_{\parallel e}^{-1}]{f}_{c}^{M}/{f}_{c}^{M})\lt 0$](https://content.cld.iop.org/journals/0004-637X/902/2/128/revision1/apjabb099ieqn160.gif) , this resonance leads to a diffusion of the resonant core electrons in
, this resonance leads to a diffusion of the resonant core electrons in 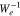 along trajectories represented by the dark-blue arrows. According to Equation (32), the phase-space trajectory of resonant particles fulfilling the n = −1 resonance, indicated by the superscript −1, is described by
along trajectories represented by the dark-blue arrows. According to Equation (32), the phase-space trajectory of resonant particles fulfilling the n = −1 resonance, indicated by the superscript −1, is described by
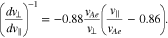
Comparing Equations (35) and (37) in 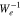 shows that
shows that 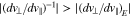 for the resonant electrons. Therefore, resolving the ambiguity in the directions of the trajectories, the distance of resonant core electrons from the origin of the coordinate system increases. This increase in
for the resonant electrons. Therefore, resolving the ambiguity in the directions of the trajectories, the distance of resonant core electrons from the origin of the coordinate system increases. This increase in 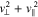 represents a gain of kinetic energy of the resonant core electrons. The n = −1 resonance, therefore, counteracts the FM/W instability through the n = +1 resonance.
represents a gain of kinetic energy of the resonant core electrons. The n = −1 resonance, therefore, counteracts the FM/W instability through the n = +1 resonance.
Due to the v∥ profile of We0, the n = 0 resonance has a significant effect on electrons in the v∥ range in which 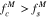 and
and 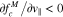 . Because
. Because ![$({k}_{\parallel }/| {k}_{\parallel }| )(\hat{G}[{k}_{\parallel e}^{0}]{f}_{c}^{M}/{f}_{c}^{M})\lt 0$](https://content.cld.iop.org/journals/0004-637X/902/2/128/revision1/apjabb099ieqn167.gif) , the resonant electrons in We0 diffuse along trajectories represented by the yellow arrows. Because the distance of these electrons from the origin of the coordinate system increases, these resonant electrons diffuse toward greater kinetic energies. This diffusion removes energy from the resonant FM/W waves and thus counteracts the driving of the FM/W instability through the n = +1 resonance.
, the resonant electrons in We0 diffuse along trajectories represented by the yellow arrows. Because the distance of these electrons from the origin of the coordinate system increases, these resonant electrons diffuse toward greater kinetic energies. This diffusion removes energy from the resonant FM/W waves and thus counteracts the driving of the FM/W instability through the n = +1 resonance.
Figure 4 only illustrates the nature of the quasi-linear diffusion through the n = +1, −1, and 0 resonances in velocity space. It does not give any information regarding the relative strengths of the diffusion rates between the three resonances. Because the FM/W wave is unstable according to linear theory, the n = +1 resonant instability must dominate over any counteracting contributions from the n = −1 and 0 resonances.
3.3. Numerical Description of the Quasi-linear Diffusion in the FM/W Instability
We use our numerical procedure from Equation (A28) to simulate the quasi-linear diffusion through the n = +1, −1, and 0 resonances, predicted in Section 3.2. According to the definitions in Appendix A, we select the discretization parameters Nv = 60 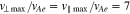 , and
, and 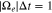 . For the computation of Equation (A28), we use the same parameters of resonant FM/W waves as those presented in Section 3.1 and quantify
. For the computation of Equation (A28), we use the same parameters of resonant FM/W waves as those presented in Section 3.1 and quantify 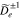 and
and 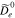 in Equation (19).
in Equation (19).
In 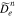 for each resonance, we only consider the J0 term in
for each resonance, we only consider the J0 term in 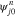 , ignoring higher-order Bessel functions due to their small contributions. Our NHDS solutions show that
, ignoring higher-order Bessel functions due to their small contributions. Our NHDS solutions show that 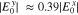 and
and 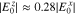 in the unstable k spectrum. Then, we set
in the unstable k spectrum. Then, we set 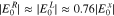 . Faraday's law yields
. Faraday's law yields ![${{E}}_{0}^{x}\,\approx [{\omega }_{k0}/({k}_{\parallel 0}c)]{{B}}_{0}^{y}$](https://content.cld.iop.org/journals/0004-637X/902/2/128/revision1/apjabb099ieqn177.gif) when ignoring the small contributions from any E0z terms. This allows us to express
when ignoring the small contributions from any E0z terms. This allows us to express 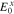 through
through 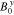 in
in 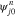 , where B0y represents the peak amplitude of the wave magnetic-field fluctuations. For simplicity, we assume that
, where B0y represents the peak amplitude of the wave magnetic-field fluctuations. For simplicity, we assume that 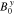 is constant in time during the quasi-linear diffusion. Under these assumptions, we acquire
is constant in time during the quasi-linear diffusion. Under these assumptions, we acquire
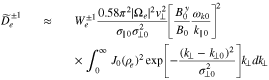
and
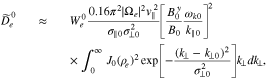
where the relative amplitude 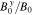 is a free parameter, and we set
is a free parameter, and we set 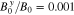 . Then, we apply Equations (38) and (39) to Equation (A28).
. Then, we apply Equations (38) and (39) to Equation (A28).
We initialize our numerical computation with the same fsM and fcM as defined in Section 3.2. Figure 5(a) represents the normalized 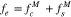 , plotted up to a value of 10−5. Figure 5(b) shows fe evolved through the n = +1, −1, and 0 resonances, resulting from our iterative calculation of Equation (A28). Considering the maximum value of the instability's growth rate,
, plotted up to a value of 10−5. Figure 5(b) shows fe evolved through the n = +1, −1, and 0 resonances, resulting from our iterative calculation of Equation (A28). Considering the maximum value of the instability's growth rate, 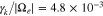 in Figure 2, we terminate the evaluation of our numerical computation at
in Figure 2, we terminate the evaluation of our numerical computation at 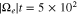 , which corresponds to
, which corresponds to 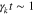 and thus a reasonable total growth of the unstable FM/W waves.
and thus a reasonable total growth of the unstable FM/W waves.
The strahl electrons at around 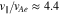 diffuse through the n = +1 resonance, as theoretically predicted in Figure 4. This diffusion increases the pitch angle of the resonant strahl electrons and generates a strong pitch-angle gradient at
diffuse through the n = +1 resonance, as theoretically predicted in Figure 4. This diffusion increases the pitch angle of the resonant strahl electrons and generates a strong pitch-angle gradient at 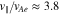 . During this process, the
. During this process, the 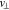 of the scattered strahl electrons increases while their v∥ decreases.
of the scattered strahl electrons increases while their v∥ decreases.
Because the longitudinal component of the electric-field fluctuations is weaker than their transverse components, the diffusion through the n = 0 resonance is only slightly noticeable over the modeled time interval. The diffusion through the n = −1 resonance is not noticeable even though 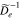 and
and 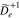 have similar magnitudes. This is because
have similar magnitudes. This is because ![$| \hat{G}[{k}_{\parallel e}^{-1}]{f}_{e}/{f}_{e}| $](https://content.cld.iop.org/journals/0004-637X/902/2/128/revision1/apjabb099ieqn193.gif) in
in 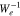 is much smaller than
is much smaller than ![$| \hat{G}[{k}_{\parallel e}^{+1}]{f}_{e}/{f}_{e}| $](https://content.cld.iop.org/journals/0004-637X/902/2/128/revision1/apjabb099ieqn195.gif) in
in 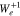 , as discussed in Section 2.3, and the number of core electrons in
, as discussed in Section 2.3, and the number of core electrons in 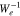 is very small (see Figures 4 and 5).
is very small (see Figures 4 and 5).
Figure 5. (a) The initial electron VDF; (b) the electron VDF evolved through the n = +1, −1, and 0 resonances. Compared to Figure 4, the effect of the n = +1 resonance dominates the evolution during the time 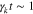 . It causes a significant pitch-angle gradient at
. It causes a significant pitch-angle gradient at 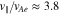 through the scattering of strahl electrons. An animation of this figure is available. The animation shows the time evolution of the distribution function from
through the scattering of strahl electrons. An animation of this figure is available. The animation shows the time evolution of the distribution function from 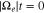 to
to 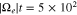 . During this evolution, the strahl scattering toward larger v⊥ is visible.
. During this evolution, the strahl scattering toward larger v⊥ is visible.
(An animation of this figure is available.)
Download figure:
Video Standard image High-resolution image4. The Secondary Effect of Coulomb Collisions
Because the collisionless action of resonant wave–particle instabilities often forms strong pitch-angle gradients (see, for example, Figure 5), collisions can be enhanced in the plasma. Therefore, a more realistic evolution of the total electron VDF must account for the action of Coulomb collisions of strahl electrons with core electrons and protons. For this purpose, we adopt the Fokker–Planck equation given by Ljepojevic et al. (1990) with Rosenbluth potentials (Rosenbluth et al. 1957) and normalize it in our dimensionless system of units as
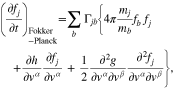
where
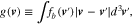
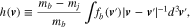
and
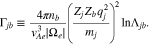
The subscript b indicates the species of background particles, with which the particles of species j Coulomb-collide. The quantity 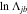 is the Coulomb logarithm and typically
is the Coulomb logarithm and typically 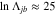 in space plasmas. The parameters Zj and Zb are the atomic masses of a particle of species j and b. The superscripts α and β indicate the component of the velocity in cylindrical coordinates and the summation convention holds.
in space plasmas. The parameters Zj and Zb are the atomic masses of a particle of species j and b. The superscripts α and β indicate the component of the velocity in cylindrical coordinates and the summation convention holds.
We assume that the timescale of Coulomb collisions is much longer than the timescale of the quasi-linear diffusion in the solar wind under our set of parameters. This assumption allows us to model the resonant wave–particle instability first and to use the resulting VDF as the input for the model of the subsequent, secondary effects of the collisions.
Based on our mathematical approach presented in Appendix A, we present our numerical scheme to solve the Fokker–Planck equation, Equation (40), in Appendix B. We tested our numerical solutions, Equation (B2), by showing that a set of arbitrary test VDFs diffuses toward fb with time.
For the computation of Equation (B2), we set isotropic Maxwellian electron-core and proton VDFs as background species, 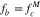 and
and 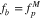 , for which we apply the plasma parameters presented in Section 3.1 to Equation (34). In this numerical computation, we select the discretization parameters Nv = 60,
, for which we apply the plasma parameters presented in Section 3.1 to Equation (34). In this numerical computation, we select the discretization parameters Nv = 60, 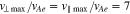 , and
, and 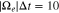 . Moreover, we set
. Moreover, we set 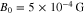 and
and 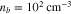 in Equation (43), which are representative for the conditions in the solar wind at a distance of 0.3 au from the Sun. We initialize fj with the electron-strahl VDF fs from our quasi-linear analysis of the oblique FM/W instability at time
in Equation (43), which are representative for the conditions in the solar wind at a distance of 0.3 au from the Sun. We initialize fj with the electron-strahl VDF fs from our quasi-linear analysis of the oblique FM/W instability at time 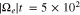 . In this setup, our initial electron VDF for the Coulomb collision analysis is the same as the electron VDF shown in Figure 5(b).
. In this setup, our initial electron VDF for the Coulomb collision analysis is the same as the electron VDF shown in Figure 5(b).
The iterative calculation of Equation (B2) results in the time evolution of the electron-strahl VDF under the action of Coulomb collisions with core electrons and protons. The result of this computation at the time 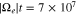 is shown in Figure 6. A detailed comparison of the distribution function before (Figure 6(a)) and after (Figure 6(b)) our calculation of the effect of Coulomb collisions reveals that Coulomb collisions relax the strong pitch-angle gradient at
is shown in Figure 6. A detailed comparison of the distribution function before (Figure 6(a)) and after (Figure 6(b)) our calculation of the effect of Coulomb collisions reveals that Coulomb collisions relax the strong pitch-angle gradient at 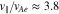 , which resulted from the action of the oblique FM/W instability. However, the Coulomb collisions are only capable of affecting strong pitch-angle gradients in the modified electron VDF under our plasma parameters. In addition, the required time for a noticeable collisional effect on this pitch-angle gradient is of order 105 times longer than the characteristic timescale of the quasi-linear diffusion.
, which resulted from the action of the oblique FM/W instability. However, the Coulomb collisions are only capable of affecting strong pitch-angle gradients in the modified electron VDF under our plasma parameters. In addition, the required time for a noticeable collisional effect on this pitch-angle gradient is of order 105 times longer than the characteristic timescale of the quasi-linear diffusion.
Figure 6. (a) The electron VDF as initial condition for our collision analysis; (b) the electron VDF evolved through Coulomb collisions of strahl electrons with core electrons and protons. The strong pitch-angle gradient at 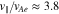 (shown in Figures 6(a) and 5(b)) is relaxed through Coulomb collisions. However, the required time for a noticeable collisional effect on that gradient is around 105 times longer than the timescale of the strahl scattering. An animation of this figure is available. The animation shows the time evolution of the distribution function from
(shown in Figures 6(a) and 5(b)) is relaxed through Coulomb collisions. However, the required time for a noticeable collisional effect on that gradient is around 105 times longer than the timescale of the strahl scattering. An animation of this figure is available. The animation shows the time evolution of the distribution function from 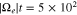 to
to 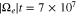 . During this evolution, the collisional smoothing of the pitch-angle gradients is visible.
. During this evolution, the collisional smoothing of the pitch-angle gradients is visible.
(An animation of this figure is available.)
Download figure:
Video Standard image High-resolution image5. Discussion of the Strahl Scattering
The numerical computation of Equation (17) shows that dH/dt is negative and asymptotically tends toward zero as the electron VDF evolves through the oblique FM/W instability and the counteracting damping effects until the time 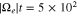 , which is presented in Figure 5. Therefore, our quasi-linear diffusion model reflects the stabilization of the particle VDF through the participating wave–particle resonances.
, which is presented in Figure 5. Therefore, our quasi-linear diffusion model reflects the stabilization of the particle VDF through the participating wave–particle resonances.
During the action of the oblique FM/W instability, the scattered strahl electrons reduce their collimation along the B0 direction and become more isotropic. Even though this instability does not cause significant strahl scattering, we argue that it contributes to the initial formation of the halo population. However, other mechanisms must be considered to account for the full strahl scattering, in agreement with observations (Gurgiolo et al. 2012; Gurgiolo & Goldstein 2016).
Alternative models describing Coulomb-collisional effects on the strahl VDF suggest that an anomalous-diffusion process must be considered in order to achieve an agreement with observations (Lemons & Feldman 1983; Horaites et al. 2018, 2019). We note that our analysis includes the subsequent action of Coulomb collisions after the action of collisionless wave–particle resonances assuming plasma parameters consistent with the solar wind at a distance of about 0.3 au from the Sun. Our collisional effects are similar to those proposed by Vocks et al. (2005). However, our model predicts that the collisional relaxation is so subtle that the strahl scattering through collisions is barely noticeable for the analyzed phase of the VDF evolution.
The clear separation of timescales between wave–particle effects and Coulomb-collisional effects complicates the description of the VDF evolution on heliospheric scales, because other processes act on comparable timescales. These additional processes, which our analysis ignores, include turbulence, shocks, plasma mixing, plasma expansion, and magnetic focusing (Feldman et al. 1983; Fitzenreiter et al. 2003; Ryu et al. 2007; Yoon et al. 2012; Tang et al. 2020). A complete model for the radial evolution of the VDF must quantify and account for these processes as well. In the context of our work, these processes can potentially push a VDF that has undergone stabilization as shown in Figure 5(b) into the unstable regime again. In this case, dH/dt in Equation (17) returns to a nonzero value, which signifies a new onset of wave–particle resonances and further scattering of resonant particles.
6. Conclusions
Wave–particle resonances are important plasma-physics processes in many astrophysical plasmas. Often, fully nonlinear simulations with codes solving the equations of kinetic plasma theory are used to model the evolution of the distribution function under the action of wave–particle resonances. However, quasi-linear theory augments this approach as it allows us to study the contributions of different processes to these resonances. Therefore, quasi-linear theory is a very helpful tool to improve our understanding of wave–particle resonances in astrophysical plasmas.
We propose a quasi-linear diffusion model for any generalized wave–particle instability. We analyze the quasi-linear diffusion equation by expressing the electric field of an arbitrary unstable and resonant wave mode as a Gaussian wave packet. From Boltzmann's H theorem in our quasi-linear analysis, we define a window function that determines the specific velocity-space range in which a dominant wave–particle instability and counteracting damping contributions are effective. This window function is the consequence of the localized energy density of our Gaussian wave packet both in configuration space and in wavevector space.
Moreover, we derive a relation describing the diffusive trajectories of the resonant particles for such an instability in velocity space. These trajectories evolve the particle VDF into a stable state in which no further quasi-linear diffusion occurs. Therefore, our theoretical model illustrates the diffusion and stabilization which resonant particles, depending on their location in velocity space, experience in wave–particle resonances.
For the computational quantification of our theoretical model, we introduce a mathematical approach based on the Crank–Nicolson scheme to numerically solve the full quasi-linear diffusion equation. We highlight that this mathematical approach applies to all general two-dimensional diffusion equations, including those with off-diagonal diffusion terms.
As an example, we apply our model to the oblique FM/W instability that scatters strahl electrons in the solar wind. Our model shows that the n = +1 resonant instability of FM/W waves propagating with an angle of  with respect to the background magnetic field scatters strahl electrons toward larger v⊥ and smaller v∥. The strahl scattering instability through the n = +1 resonance dominates over the counteracting damping contributions through the n = −1 and n = 0 resonances. This instability creates a strong pitch-angle gradient in the electron-strahl VDF.
with respect to the background magnetic field scatters strahl electrons toward larger v⊥ and smaller v∥. The strahl scattering instability through the n = +1 resonance dominates over the counteracting damping contributions through the n = −1 and n = 0 resonances. This instability creates a strong pitch-angle gradient in the electron-strahl VDF.
By numerically solving the Fokker–Planck equation, we show that Coulomb collisions of strahl electrons with core electrons and protons relax this strong pitch-angle gradient on a timescale about 105 times longer than the timescale of the collisionless strahl scattering. This finding suggests that collisional effects are negligible in the strahl-driven oblique FM/W instability, which is a representative example for a resonant wave–particle instability in the solar wind.
Our predicted evolution of the electron VDF is consistent with the observed formation of a proto-halo through strahl scattering (Gurgiolo et al. 2012). However, further observations are ambiguous regarding the exact source of the proto-halo (Gurgiolo & Goldstein 2016). Future high-resolution electron observations with Solar Orbiter and Parker Solar Probe at different distances from the Sun may help us resolve these ambiguities.
Our general quasi-linear diffusion model applies to all nonrelativistic collisionless plasmas, such as planetary magnetospheres (e.g., Mourenas et al. 2015). It also applies to other types of wave–particle instabilities in plasmas such as the resonant instabilities driven by temperature anisotropy or by relative drift. We especially note that our model is also capable of describing ion-driven instabilities.
We appreciate helpful discussions with Georgios Nicolaou, Konstantinos Horaites, and Jung Joon Seough. D.V. is supported by the STFC Ernest Rutherford Fellowship ST/P003826/1. D.V., R.T.W., and A.N.F. are supported by STFC Consolidated Grant ST/S000240/1.
Appendix A: Numerical Analysis of the Quasi-linear Diffusion Equation
Equation (10) is a second-order differential equation that includes cross-derivative operators such as 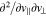 . In order to simultaneously evaluate the
. In order to simultaneously evaluate the 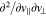 operators with the
operators with the 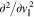 and
and 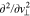 operators in Equation (10), we divide velocity space into
operators in Equation (10), we divide velocity space into 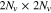 steps with equal step sizes of
steps with equal step sizes of 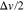 by defining the outer boundaries of velocity space as
by defining the outer boundaries of velocity space as 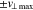 and
and 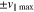 . The
. The 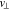 index M and the v∥ index N both step through 1, 3/2, 2, ..., Nv,
index M and the v∥ index N both step through 1, 3/2, 2, ..., Nv, 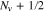 . We define the discrete velocity coordinates as
. We define the discrete velocity coordinates as 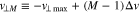 and
and 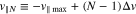 . We note that this definition introduces negative v⊥ values that, although they simplify our numerical analysis, we ignore in our computational results. We divide the time t with equal step sizes of
. We note that this definition introduces negative v⊥ values that, although they simplify our numerical analysis, we ignore in our computational results. We divide the time t with equal step sizes of 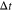 and the t-index T steps through
and the t-index T steps through 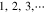 . We define the discrete time as
. We define the discrete time as 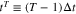 . We then define the discrete VDF as
. We then define the discrete VDF as 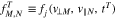 . For the discretization of the velocity derivatives, we adopt the two-point central difference operators (Gilat & Subramaniam 2011)
. For the discretization of the velocity derivatives, we adopt the two-point central difference operators (Gilat & Subramaniam 2011)
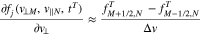
and
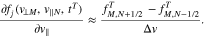
For the discretization of the time derivative, we adopt the forward difference operator
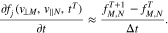
By using Equations (A1) and (A2), we discretize the right-hand side of Equation (10) and express it as
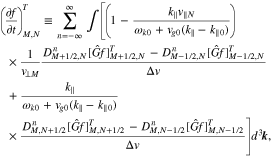
where
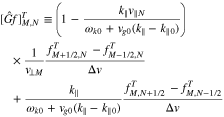
and
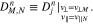
According to the Crank–Nicolson scheme (Iserles 2008), the full discretization of Equation (10) in its time and velocity derivatives is then given by
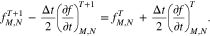
By using Equations (A4)–(A6) and resolving the δ functions in 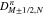 and
and 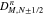 through the k∥ integral, we rewrite Equation (A7) as
through the k∥ integral, we rewrite Equation (A7) as
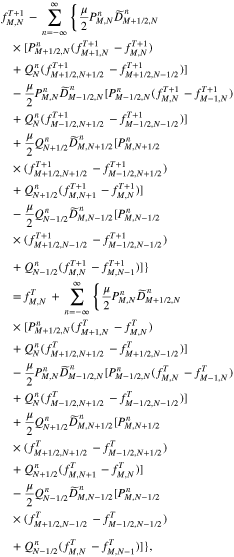
where
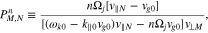
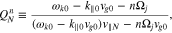
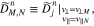
and 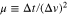 . Equation (A8) is a two-dimensional set of algebraic equations, the solution of which,
. Equation (A8) is a two-dimensional set of algebraic equations, the solution of which, 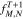 , for all
, for all 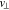 and
and 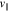 indexes describes the VDF at time
indexes describes the VDF at time 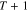 based on
based on 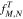 for all
for all  and
and 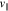 indexes.
indexes.
In order to transform Equation (A8) into a single matrix equation with a tridiagonal matrix, we introduce the concept of a double matrix. On both sides of Equation (A8), we group the terms by the same 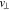 index in the VDF and rearrange these groups in increasing order in their
index in the VDF and rearrange these groups in increasing order in their 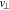 index. In each group, we then rearrange terms in increasing order in the v∥ index in the VDF. Then, we have
index. In each group, we then rearrange terms in increasing order in the v∥ index in the VDF. Then, we have
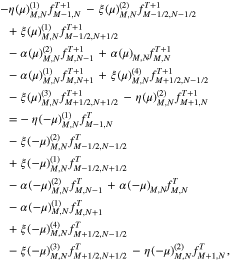
where
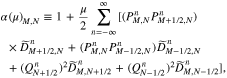
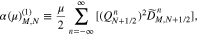
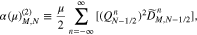
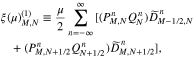

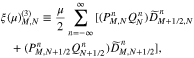

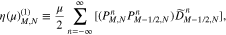
and
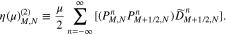
All terms on both sides of Equation (A12) with a constant v⊥ index account for variations in v∥ space only. Therefore, they can be grouped into a single system of one-dimensional algebraic equations.
We transform all terms with the v⊥ index M on both sides of Equation (A12) into the tridiagonal matrices ![$[A{\left(\mu \right)}_{M}][{F}_{M}^{T+1}]$](https://content.cld.iop.org/journals/0004-637X/902/2/128/revision1/apjabb099ieqn246.gif) and
and ![$[A{\left(-\mu \right)}_{M}][{F}_{M}^{T}]$](https://content.cld.iop.org/journals/0004-637X/902/2/128/revision1/apjabb099ieqn247.gif) , where
, where 
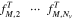
![${\left.{f}_{M,{N}_{v}+\tfrac{1}{2}}^{T}\right]}_{1\times 2{N}_{v}}^{{\boldsymbol{T}}}$](https://content.cld.iop.org/journals/0004-637X/902/2/128/revision1/apjabb099ieqn250.gif) (
(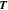 represents the transpose of a matrix), and
represents the transpose of a matrix), and
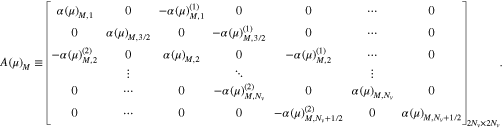
We transform all terms with the v⊥ index  on both sides of Equation (A12) into the tridiagonal matrices
on both sides of Equation (A12) into the tridiagonal matrices ![$[B{\left(\mu \right)}_{M}^{\left(1\right)}][{F}_{M-1/2}^{T+1}]$](https://content.cld.iop.org/journals/0004-637X/902/2/128/revision1/apjabb099ieqn253.gif) and
and ![$[B{\left(-\mu \right)}_{M}^{\left(1\right)}][{F}_{M-1/2}^{T}]$](https://content.cld.iop.org/journals/0004-637X/902/2/128/revision1/apjabb099ieqn254.gif) , where
, where
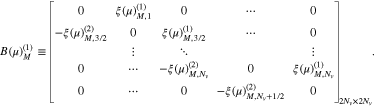
We transform all terms with the v⊥ index  on both sides of Equation (A12) into the tridiagonal matrices
on both sides of Equation (A12) into the tridiagonal matrices ![$[B{\left(\mu \right)}_{M}^{\left(2\right)}][{F}_{M+1/2}^{T+1}]$](https://content.cld.iop.org/journals/0004-637X/902/2/128/revision1/apjabb099ieqn256.gif) and
and ![$[B{\left(-\mu \right)}_{M}^{\left(2\right)}][{F}_{M+1/2}^{T}]$](https://content.cld.iop.org/journals/0004-637X/902/2/128/revision1/apjabb099ieqn257.gif) , where
, where

We transform all terms with the v⊥ index  on both sides of Equation (A12) into the tridiagonal matrices
on both sides of Equation (A12) into the tridiagonal matrices ![$[C{\left(\mu \right)}_{M}^{\left(1\right)}][{F}_{M-1}^{T+1}]$](https://content.cld.iop.org/journals/0004-637X/902/2/128/revision1/apjabb099ieqn259.gif) and
and ![$[C{\left(-\mu \right)}_{M}^{\left(1\right)}][{F}_{M-1}^{T}]$](https://content.cld.iop.org/journals/0004-637X/902/2/128/revision1/apjabb099ieqn260.gif) , where
, where
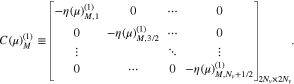
Lastly, we transform all terms with the v⊥ index 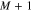 on both sides of Equation (A12) into the tridiagonal matrices
on both sides of Equation (A12) into the tridiagonal matrices ![$[C{\left(\mu \right)}_{M}^{\left(2\right)}][{F}_{M+1}^{T+1}]$](https://content.cld.iop.org/journals/0004-637X/902/2/128/revision1/apjabb099ieqn262.gif) and
and ![$[C{\left(-\mu \right)}_{M}^{\left(2\right)}][{F}_{M+1}^{T}]$](https://content.cld.iop.org/journals/0004-637X/902/2/128/revision1/apjabb099ieqn263.gif) , where
, where
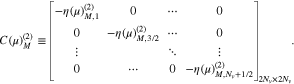
This strategy allows us to express Equation (A12) as a single system of one-dimensional algebraic equations:
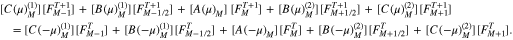
Equation (A27) only describes the VDF evolution in v⊥ space. However, each matrix term itself includes the VDF evolution in v∥ space. We transform Equation (A27) into a single tridiagonal matrix:
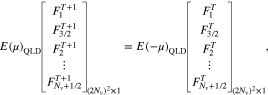
where
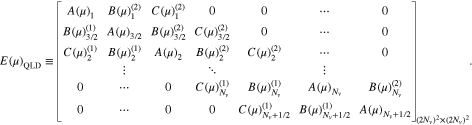
Equation (A28) is in the form of a double matrix, and 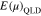 in Equation (A29) defines the evolution matrix. The inner matrices of
in Equation (A29) defines the evolution matrix. The inner matrices of 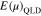 evolve
evolve 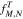 in v∥ space while the outer matrices of
in v∥ space while the outer matrices of 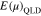 evolve
evolve 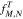 in v⊥ space during each time step. By multiplying Equation (A28) with the inverse of
in v⊥ space during each time step. By multiplying Equation (A28) with the inverse of 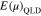 on both sides, Equation (A28) provides the time evolution of
on both sides, Equation (A28) provides the time evolution of 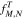 in one time step simultaneously in the v⊥ and v∥ spaces. Therefore, it represents the numerical solution of Equation (10), which describes the quasi-linear diffusion of a VDF through all resonances.
in one time step simultaneously in the v⊥ and v∥ spaces. Therefore, it represents the numerical solution of Equation (10), which describes the quasi-linear diffusion of a VDF through all resonances.
Appendix B: Numerical Analysis of the Fokker–Planck Equation
In this appendix, we present our numerical strategy to solve the Fokker–Planck equation for Coulomb collisions in Equation (40). Using the Crank–Nicolson scheme presented in Appendix A, we discretize Equation (40) as
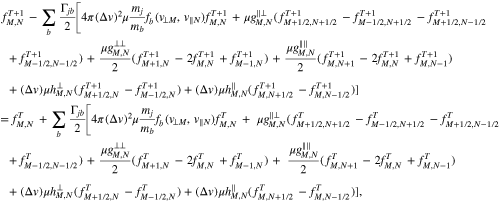
where 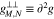 /
/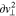 ,
, 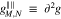 /
/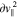 ,
, 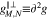 /
/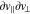 ,
, 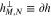 /
/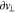 , and
, and 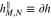 /
/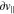 , estimated at
, estimated at 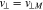 and
and 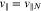 .
.
Equation (B1) represents a system of two-dimensional algebraic equations. Therefore, we transform Equation (B1) into a single tridiagonal matrix using the same strategy for a double matrix as presented in Appendix A.
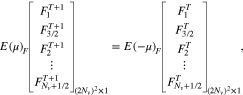
where
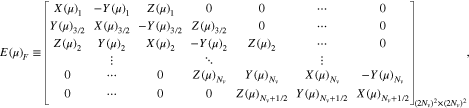
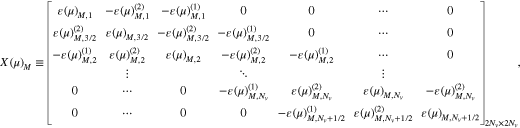
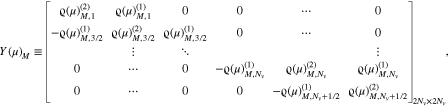
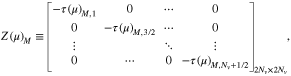
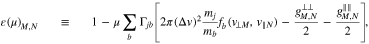
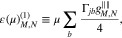
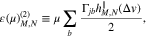
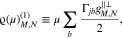
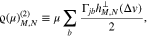
and
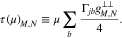
Like Equation (A28), Equation (B2) provides the time evolution of 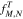 in one time step simultaneously in the v⊥ and v∥ spaces. Therefore, it represents the numerical solution of Equation (40), which describes the action of Coulomb collisions of particles in fj with particles in fb.
in one time step simultaneously in the v⊥ and v∥ spaces. Therefore, it represents the numerical solution of Equation (40), which describes the action of Coulomb collisions of particles in fj with particles in fb.







