Abstract
Radioactive isotopes produced in core-collapse supernovae (CCSNe) provide useful insights into the underlying processes driving the collapse mechanism and the origins of elemental abundances. Their study generates a confluence of major physics research, including experimental measurements of nuclear reaction rates, astrophysical modeling, and γ-ray observations. Here we identify the key nuclear reaction rates to the nucleosynthesis of observable radioactive isotopes in explosive silicon burning during CCSNe. Using the nuclear reaction network calculator SkyNet and current REACLIB reaction rates, we evolve temperature–density–time profiles of the innermost 0.45 M⊙ ejecta from the core collapse and explosion of a 12 M⊙ star. Individually varying 3403 reaction rates by factors of 100, we identify 141 reactions that cause significant differences in the isotopes of interest, namely, 43K, 47Ca, 44,47Sc, 44Ti, 48,51Cr, 48,49V, 52,53Mn, 55,59Fe, 56,57Co, and 56,57,59Ni. For each of these reactions, we present a novel method to extract the temperature range pertinent to the nucleosynthesis of the relevant isotope; the resulting temperatures lie within the range T = 0.47–6.15 GK. Limiting the variations to within 1σ of STARLIB reaction rate uncertainties further reduces the identified reactions to 48 key rates, which can be used to guide future experimental research. Complete results are presented in tabular form.
1. Motivation
Core-collapse supernovae (CCSNe) are important nucleosynthesis sites contributing to the origin of a broad range of elements (Woosley & Weaver 1995; Rauscher et al. 2002; Woosley et al. 2002; Nomoto et al. 2006; Chieffi & Limongi 2017; Curtis et al. 2019). At the extreme conditions during the explosion, many of the synthesized nuclei are produced as radioactive isotopes. Their ultimate contribution to nucleosynthesis is determined by the first stable isotope encountered along their β- or electron-capture decay chains. Most of these isotopes decay quickly, but a few have half-lives that are longer than the explosion timescale and are ejected into the interstellar medium prior to their decay. These longer-lived radioactive isotopes are of particular interest, as their signatures can provide information on isotopic abundances that are difficult to obtain from spectroscopic observations and can therefore serve as unique windows into a broad range of physics questions. These signatures include characteristic decay times of supernova light curves powered by radioactive decay, observation of characteristic γ-rays emitted in the nuclear decay by balloon- or satellite-based γ-ray observatories, isotopic anomalies in geological samples that incorporate supernova ejecta, or the direct detection of the ejected and subsequently accelerated radioactive isotopes as cosmic rays using space-based cosmic-ray observatories. Our goal here is to delineate the nuclear reactions that need to be understood to reliably predict the production of long-lived radioactive isotopes from CCSN models. This is essential for the interpretation of the observed signatures in terms of CCSN physics. We focus on isotopes produced in explosive oxygen and silicon burning, which is responsible for the synthesis of a broad range of long-lived radioactive isotopes. Explosive silicon burning is of particular interest, as it occurs in the deepest layers of the supernova and can therefore provide insights into mixing and ejection mechanisms and the delineation between ejecta and fallback onto the compact remnant, the so-called "mass cut" (The et al. 2006; Young et al. 2006; Grebenev et al. 2012; Grefenstette et al. 2014). Other long-lived isotopes in supernovae produced by neutron-capture processes in explosive carbon- or helium-burning layers, such as 41Ca or 60Fe, are not the subject of this study.
Nucleosynthesis during explosive silicon burning is governed by a typically α-rich freeze-out from a quasi-statistical equilibrium (Woosley & Hoffman 1992; Hix & Thielemann 1996; Meyer et al. 1998). During quasi-statistical equilibrium, groups of nuclei on the nuclear chart form equilibrium clusters, where fast nuclear reactions maintain equilibrium among the included nuclei. The resulting relative isotopic abundances within a cluster are therefore entirely determined by the thermodynamic properties of the nuclei and independent of the rates of the nuclear reactions (though the rates of the reactions determine the extent of the cluster). However, equilibrium clusters are connected by slow nuclear reactions that are critical in determining the overall abundance distribution among the clusters. As the material expands, more clusters form and more bottleneck reactions emerge.
Sensitivity studies are needed to identify the relatively few critical bottleneck reactions that affect the final composition. The et al. (1998) performed a sensitivity study using a simple parameterized α-rich freeze-out model. They identified a number of critical reactions that affect the synthesis of 44Ti by varying reactions individually by a factor of 100. A similar model was later used to identify nuclear reactions affecting the production of 59Ni, 57Co, 56Co, and 55Fe (Jordan et al. 2003). Hoffman et al. (1999) compared supernova nucleosynthesis in a full 1D explosion model of a 15 M⊙ and a 20 M⊙ star using two sets of reaction rates and identified the 40Ca(α,γ)44Ti reaction rate as critical in determining the 44Ti yield. Hoffman et al. (2010) used a set of parameterized expansion models to investigate the sensitivity of 44Ti production in explosive silicon burning to the 40Ca(α,γ)44Ti and 44Ti(α,p)47V reaction rates over a range of possible conditions. Tur et al. (2010) explored the sensitivity of 44Ti production to the 12C(α,γ)16O reaction in three 1D supernova models based on 15, 20, and 25 M⊙ progenitor stars. Magkotsios et al. (2010) carried out a full sensitivity study of the synthesis of 56Ni and 44Ti in explosive silicon burning using a combination of a broad set of parameterized trajectories that systematically cover the relevant parameter space and trajectories from three supernova models: a 1D Cas A–inspired model with a 16 M⊙ star, a 1D hypernova model, and a 2D rotating 15 M⊙ star model. They varied rates individually by factors of 100.
Here we present a much more comprehensive sensitivity study that considers all radioactive isotopes of potential interest and uses trajectories from a self-consistent supernova simulation instead of a parameterized approach. The CCSN explosion data we use, while 1D, include the effects of convection and turbulence, accurate energy-dependent neutrino transport, and approximate general relativity. In addition, we identify for the first time the temperature range over which the model is sensitive to the reaction rate. This information is critical to guide experiments.
We begin in Section 2 by laying out the background behind the detection of radioactive isotopes from CCSNe. Then, in Section 3 we describe the details of the CCSN simulation and our postprocessing calculations of nucleosynthesis using this simulation. In Section 4 we briefly summarize the results of the study and describe several points of interest. Next, we contextualize the results in Section 5 by evaluating the significance of reactions relative to the uncertainty of their reaction rates. We also compare to past work in terms of both the nucleosynthesis of the model and the most important reactions identified. Finally, we summarize the key differences in this work in Section 6 and conclude.
2. Background
We now discuss the relevant radioactive isotopes and their signatures in more detail. If the half-life of a radioactive isotope produced in a CCSN is long enough to allow mixing outward to a column depth where γ-radiation can escape, the decay γ-radiation can, in principle, be observed directly with balloon- or satellite-based γ-ray detectors (Vink 2005; Diehl 2017; Timmes et al. 2019). Such observations provide important isotopic abundance information. In addition, compared to visible light, UV, or X-rays, γ-rays are much less affected by attenuation in the surrounding gas or the interstellar medium. It is therefore much more straightforward to determine the total produced abundance, which can then be compared to CCSN model predictions. Due to the challenging instrument sensitivity requirements, only a small number of isotopes have so far been observed via their decay γ-radiation in supernova remnants. The γ-rays from the decay of 56Co (half-life T1/2 = 77.236 days; Tuli 2011) were observed from supernova 1987A 160 days after the explosion by balloon experiments (Cook et al. 1988; Mahoney et al. 1988; Sandie et al. 1988; Teegarden et al. 1989) and the Solar Maximum Mission (SMM) satellite (Matz et al. 1988; see also the review by Vink 2005). These observations occurred prior to the expected γ-ray transparency of the ejecta, indicating the importance of mixing processes during the explosion. Later, the observation of 57Co (T1/2 = 271.74 days; Tuli 2011) decay γ-rays from 1987A with the Compton Gamma Ray Observatory (CGRO) was reported by Kurfess et al. (1992). More recently, 44Ti (T1/2 = 60.0 yr; Tuli 2011) was detected in 1987A via γ-rays and hard X-rays by INTEGRAL (Grebenev et al. 2012) and NuSTAR (Boggs et al. 2015), with total inferred amounts of 44Ti of and M⊙, respectively. For 1987A, the produced amount of 44Ti can also be inferred from the late-time light curve (Jerkstrand et al. 2011; Seitenzahl et al. 2014).
The only other supernova remnant from which nuclear decay γ-rays have been unambiguously detected is Cas A, where 44Ti has been detected by CGRO/COMPTEL (Iyudin et al. 1994), BeppoSAX (Vink et al. 2001), INTEGRAL (Renaud et al. 2006), and NuSTAR (Grefenstette et al. 2014). The most recent analysis from INTEGRAL obtains a 44Ti mass of M⊙ (Siegert et al. 2015), while the result from NuSTAR is M⊙ (Grefenstette et al. 2014). These 44Ti abundances are at least a factor of 3 higher than standard 1D supernova model predictions, which provides constraints on CCSN physics such as homogeneity and the role of multidimensional effects such as bipolar explosions (The et al. 2006; Wheeler et al. 2008; Magkotsios et al. 2010; Chieffi & Limongi 2017). No other sources of 44Ti besides 1987A and Cas A have been identified with certainty, though a few candidates with insufficient significance to be considered detections have been reported, e.g., GRO J0852–4642 (Vela Junior) and G1.9+0.3 (see review by Diehl 2016). The et al. (2006) argued that the paucity of detectable 44Ti in the Galaxy is in conflict with simple assumptions about CCSNe, thus providing additional constraints on CCSN rates, star formation, and explosion physics. In contrast, Dufour & Kaspi (2013) found the number of supernova remnants with detectable 44Ti to be consistent with current models but posited that next-generation γ-ray telescopes (Timmes et al. 2019) can be expected to identify between eight and 21 supernova remnants based on their 44Ti decay flux.
Next-generation γ-ray telescopes are also expected to identify a larger number of longer-lived radioactive isotopes in addition to 44Ti. Timmes et al. (2019) estimated that with such an instrument, 48Cr, 48V, 52Mn, 56,57Co, and 56,57Ni may be detectable out to a distance of 1 Mpc and 43K, 44Ti, 44Sc, 47Sc, 47Ca, 51Cr, and 59Fe out to a distance of 50 kpc. Many of these isotopes have half-lives of just hours to days, thus requiring rapid mixing into outer layers where γ-rays can escape.
In addition to direct detection of γ-radiation, signatures of radioactive isotopes from CCSNe can be found in geological samples. The analysis of the composition of primitive meteorites provides information about the presence of radioactive isotopes in the early solar system. The main isotope of interest in the context of explosive silicon burning in CCSNe is 53Mn (T1/2 = 3.7 Myr; Tuli 2011). Analysis of isotopic anomalies created by the presence of the 53Cr decay daughter in meteorites has provided a fairly accurate value for the early solar system abundance of the 53Mn/55Mn ratio of (Tissot et al. 2017). Though CCSNe are considered the dominant source, Type Ia supernovae may also play a role (Wasserburg et al. 2006; Côté et al. 2019).
Isotopes with half-lives in excess of 0.1 Myr, such as 53Mn, accumulate in the interstellar medium, and their early solar system abundance provides a data point for this accumulation at the time and location of solar system formation. This provides unique constraints on chemical evolution probing the more recent Galactic chemical history, as opposed to stable isotopes that provide an integrated sample over the age of the Galaxy (Côté et al. 2019). The early solar system abundance of 53Mn also probes the circumstances and timescales of solar system formation (Lugaro et al. 2018), in particular the hypothesis of late-time injection by a supernova that potentially triggered the formation of the solar system (Meyer & Clayton 2000; Wasserburg et al. 2006). With this hypothesis, and using standard spherical CCSN models, there is an overproduction issue of about 3 orders of magnitude for 53Mn and 60Fe (Meyer & Clayton 2000; Wasserburg et al. 2006; Banerjee et al. 2016; Lugaro et al. 2018). This has been used to place constraints on the nature of the responsible supernova, e.g., on the layers ejected (Meyer & Clayton 2000), the nature of fallback (Takigawa et al. 2008), the mass of the progenitor (Banerjee et al. 2016), or the supernova explosion mechanism (Sawada & Maeda 2019). This underlines the importance of understanding the nuclear production processes.
Isotopic signatures of shorter-lived isotopes in supernova ejecta can also be incorporated in geological samples via presolar grains. These grains form as SiC dust in the supernova explosion and are then transported through space and incorporated into the solar system, where they can be found in primitive meteorites. Indeed, enhanced 44Ca from the decay of 44Ti has been found in SiC X-grains thought to originate from CCSNe (Hoppe et al. 1996; Nittler et al. 1996; Clayton 2011; see also the recent review by Nittler & Ciesla 2016). This provides constraints not only on the supernova but also on the grain formation process.
The CCSN signatures of long-lived radioactive isotopes that decay by electron capture can, in principle, also be identified in the composition of cosmic rays above Earth's atmosphere. After acceleration, the radioactive nuclei are fully stripped of electrons, which prevents electron-capture decay and leaves the typically very weak β+ decay branches as the only option for decay. As a result, the nuclei become sufficiently stable to propagate through the interstellar medium and be detected above Earth's atmosphere (DuVernois 1997; Wiedenbeck et al. 1999; Neronov & Meynet 2016; Benyamin & Shaviv 2018). The cosmic-ray source composition of radioactive isotopes inferred from such observations can therefore serve as a chronometer of the acceleration process. However, the observed composition has to be corrected for secondary production during propagation. Isotopes of interest are 44Ti, 49V, 51Cr, 55Fe, 57Co, and 59Ni (Benyamin & Shaviv 2018), as well as 53Mn (DuVernois 1997). The upper limit on the 59Ni source abundance obtained from observations with the CRIS instrument on board the Advanced Compton Explorer Spacecraft has placed constraints on cosmic-ray acceleration models (Israel et al. 2005). However, Neronov & Meynet (2016) recently pointed out the critical importance of understanding the production of 59Ni in explosive silicon burning for discriminating between fast and delayed cosmic-ray acceleration models. A signature of 44Ti in cosmic rays has been reported from CRIS (Scott 2005) and used to place constraints on 44Ti synthesis in CCSNe (Benyamin & Shaviv 2018). Finally, source limits on 53Mn have been obtained from data of the Ulysses High Energy Telescope (HET), but the uncertainties were too large to draw conclusions (DuVernois 1997). In addition to the detection of the above isotopes by cosmic rays, Leising (2001) estimated that the X-rays produced following electron capture are detectable by the current generation of X-ray spectrometers. While not as penetrating, these X-rays provide a useful complement to γ-rays, as in the detection of 44Ti in G1.9+0.3 (Borkowski et al. 2010) and the upper limit of 55Fe in 1987A (Leising 2006).
In summary, understanding the production of radioactive 43K, 47Ca, 44,47Sc, 44Ti, 48,51Cr, 48,49V, 52,53Mn, 55,59Fe, 56,57Co, and 56,57,59Ni in CCSNe is important for the interpretation of past and future observations in terms of a broad range of CCSN physics, chemical evolution, and cosmic-ray acceleration. The goal of the remainder of the paper is to identify the important nuclear reactions that need to be understood to make reliable predictions for the production of these isotopes during explosive silicon burning.
3. Methods
3.1. Supernova Model
We use thermodynamic trajectory data from a self-consistent Supernova Turbulence In Reduced-dimensionality (STIR) explosion model of Couch et al. (2020) for a 12 M⊙ progenitor star from Sukhbold et al. (2016). The STIR model includes energy-dependent, two-moment neutrino transport in the "M1" approximation (O'Connor 2015), a microphysical equation of state for dense matter (Steiner et al. 2013), and approximate general relativistic gravity (Marek et al. 2006). Total energy is approximately conserved within the STIR model when accounting for diffusive mixing of energy and composition due to turbulent convection, as discussed in Warren et al. (2019) and Couch et al. (2020). The 1D explosion is achieved by a novel model for including the effects of convection and turbulence based on a Reynolds decomposition of the hydrodynamic evolution equations that is then closed using the mixing-length theory (Couch et al. 2020). The explosion model we use here for a 12 M⊙ star results in a diagnostic explosion energy of 3.7 × 1050 erg and a final baryonic proto–neutron star mass (i.e., mass cut) of 1.48 M⊙. In STIR, both the explosion energy and proto–neutron star mass are predictions of the model, given a progenitor structure, and not set by hand.
The nucleosynthesis is calculated using a postprocessing approximation. Temperature (T), density (ρ), electron neutrino (νe ) flux, and electron antineutrino () flux as functions of time (referred to as trajectories) are taken from 100 equal-mass ( M⊙ each) zones. These zones subdivide a range in stellar radius from 1.486 to 1.935 M⊙ enclosed mass, comprising the silicon and oxygen shells of the progenitor, as shown in Figure 1. Figure 2 shows the thermodynamic characteristics of the trajectories using the following parameter definition for each trajectory: the peak temperature is the maximum temperature in GK; the total entropy is the entropy at peak temperature, which is nearly constant during the expansion; the peak radiation entropy is defined by Witti et al. (1994) as
where ρ5 = 10−5 × ρ g cm−3 with entropy in units of Boltzmann constant per baryon; and the peak density is the density at peak temperature in g cm−3. While the definition of peak radiation entropy assumes an ultrarelativistic electron–positron gas, the calculations in SkyNet assume the gas is arbitrarily relativistic and degenerate. Additionally, the innermost trajectory has a neutron excess η = 1–2Ye = −0.015, while all other trajectories are in the range 0.000 < η ≤ 0.002. Together, these trajectories span an α-rich freeze-out parameter space similar to recent studies (Hoffman et al. 2010; Magkotsios et al. 2010; Vance et al. 2020).
Figure 1. Initial composition of notable isotopes of the 12 M⊙ star before core collapse. Only the simulated region of enclosed mass is shown.
Download figure:
Standard image High-resolution imageFigure 2. Thermodynamic conditions for the simulated trajectories: peak temperature (top), peak total and radiation entropy (middle), and peak density (bottom). For some trajectories, peak radiation entropy is larger than peak total entropy; this is due to approximations used in the definition of peak radiation entropy.
Download figure:
Standard image High-resolution imageFigure 3. Final mass fractions of isotopes of interest by enclosed mass shell for evolution using standard REACLIB rates. Mass fractions include the short-lived parent isotopes in the mass chain (e.g., 56Co includes both 56Co and 56Ni). Only the simulated region of enclosed mass is shown.
Download figure:
Standard image High-resolution imageThe region we consider is located just above the mass cut. Material closer to the star is assumed to fall back onto the compact remnant, while material at larger distances does not undergo sufficient shock heating to produce the medium mass A = 40–60 nuclei of interest here. Since the supernova simulation ends at 1.93 s after bounce, the continuing evolution of the trajectories is modeled on a homologous expansion—the density scales as , and the temperature uses the self-heating evolution described in Lippuner & Roberts (2017). We end the trajectories at 140 s after bounce, at which time all zones have cooled below 0.01 GK and no further nucleosynthesis occurs.
3.2. Nuclear Reaction Network
For each of the 100 trajectories, the nucleosynthesis and final composition are calculated using the nuclear reaction network library SkyNet (Lippuner & Roberts 2017). The network used here includes 1683 nuclides with element numbers Z ≤ 50 and neutron numbers N ≤ 70 connected by 22,891 total reactions. Reactions considered include heavy ion fusion reactions; proton-, neutron-, and α-induced reactions and their inverse; and β-decays, electron capture, and free nucleon–neutrino interactions. As a baseline set of nuclear reaction rates, we use REACLIB v2.2 (Cyburt et al. 2010) and, where available, the weak reaction rates from Langanke & Martínez-Pinedo (2000), Oda et al. (1994), and Fuller et al. (1985) as compiled by Paxton et al. (2015). Free nucleon–neutrino interactions are included as described in Lippuner & Roberts (2017) and include weak magnetism and recoil corrections from Burrows et al. (2006), consistent with the rates used in the original CCSN simulation. The final composition of the simulated region by enclosed mass for the isotopes of interest is displayed in Figure 3.
The initial composition of a trajectory is taken from the same 12 M⊙ progenitor model used for the supernova simulation (Sukhbold et al. 2016; see Figure 1). The total ejected mass of an isotope of interest is determined by summing the contributions from all trajectories.
The sensitivity of the produced abundance of an isotope of interest to nuclear reaction rates is determined by changing individual reaction rates one by one and recalculating the nucleosynthesis for all trajectories (Iliadis et al. 2002). To reduce the number of reactions that need to be varied, we determined a subset of relevant reactions using the calculation with the baseline rates. Only reactions with a time-integrated reaction flow above 10−10 in any trajectory were added to the list of varied reactions. Smaller reaction flows are negligible even when varying a reaction rate by a factor as large as 100, as the smallest isotopic abundances of interest are ≈10−8. This approach results in a subset of 3403 relevant reactions. Each of these reactions was individually varied up and down by factors of 100. To explore the linearity of the resulting abundance changes, we perform additional calculations for the 141 rates that significantly affect the synthesis of an isotope of interest, using smaller variations of factors of 10 and 2. In total, 737,100 network evolutions were performed.
One goal of this work is to provide guidance for nuclear physics to improve the accuracy of nuclear reaction rates that affect the nucleosynthesis of the isotopes of interest. For both experimental and theoretical nuclear physics work, it is critical to understand the temperature range over which a particular reaction rate needs to be determined. We developed an approach to obtain this information for each reaction rate that was identified to affect a specific isotope i. We take advantage of the fact that reaction rates only matter during the cooling of a trajectory once nuclear statistical equilibrium (NSE) breaks down. At this late stage, in our model, the temperature is monotonically decreasing. Starting with the innermost and hottest trajectory, we sum together isotopic abundances from all trajectories with Tpeak ≥ T until we include all simulated trajectories. We can therefore uniquely determine at each temperature T the sum of the abundances of the mass chain of isotope i (Yi (T)) over all zones contributing ≥1% to the total final abundance of that mass chain and calculate the ratio of the abundances obtained with the varied reaction rate () to the baseline abundances,
Figure 4 presents an example for the specific effect of varying (α,p) by a factor of 0.01 on A = 44 production. The sharp increases in mass chain abundance at specific high temperatures are due to additional trajectories being included as the temperature drops. At high T > 6.5 GK, Ri (T) = 1, because abundances in NSE are insensitive to reaction rate changes. As the temperature drops, at some point, Ri starts deviating from 1 and transitions to the final value, Rf,i , at low temperatures when reactions freeze out completely. We determine the temperature range [Tmin, Tmax] for the reaction rate sensitivity as the highest temperature where and the lowest temperature where . We ignore high-temperature deviations of Ri from 1 so long as Ri returns to 1 for a sustained span of 0.05 GK.
Figure 4. The A = 44 abundance (orange dashed line) and ratio of A = 44 abundance to the baseline abundance when varying 44Ti(α,p)47V by a factor of 0.01 as a function of temperature (blue line). Dotted black vertical lines indicate the determined temperature range where the reaction affects 44Ti production.
Download figure:
Standard image High-resolution imageWe emphasize that this is an approximate approach that makes a number of assumptions that are reasonable for this particular scenario. Most importantly, we assume that temperature is dropping monotonically and reaction rates continually become slower. The approach would not be appropriate for a scenario where some intermediate abundance is built up at one temperature and then processed further at another temperature (our method would only identify the second temperature range). The use of ratios instead of absolute abundances ensures that we are sensitive to reactions that change the abundance of the entire relevant equilibrium cluster, even at times where the particular isotope of interest may not be fully populated within the cluster equilibrium. Also, this method primarily narrows down the relevant temperature range, excluding sensitivity for higher and lower temperatures. Sensitivity within the given temperature range may not be evenly distributed.
Then, [Tmin, Tmax] defines the temperature range over which the reaction rate has to be determined. This temperature range sensitively depends on the isotope of interest, even for the same reaction.
4. Results
Defining an impact factor
reaction rate variations that result in final abundance changes of Fi ≥ 1.1 (effectively a 10% difference) in an isotope of interest, i, are listed in Table 1. Reactions are sorted by the mass number of the produced isotope of interest and then in reverse order of impact, defined as the maximum of Fi for factors of 100 and 0.01 variations. Final abundances for the long-lived isotopes of interest, Yf,i , were calculated by adding the abundances of parent isotopes that had not fully decayed yet at the end of the calculation. Decays of the isotopes of interest are negligible within the 140 s of calculation time due to the much longer half-lives. For , , and , the parent isotopes are also long-lived isotopes of interest. In all three cases, these isotopes are predominantly produced by the decay of their parent isotope, with direct production being negligible at 0.1%, <0.01%, and 0.3%, respectively. The reaction rate sensitivity of the parent abundance is therefore the same as the sensitivity for the daughter abundance.
Table 1. Final Abundance Changes Resulting from Reaction Rate Variations
| Rf for Reaction Rate Multiplied by | T9 Range | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Isotope | Xi,rec | Reaction | 100 | 10 | 2 | 0.5 | 0.1 | 0.01 | T9,low | T9,high |
| 43K | 1.4e-08 | 24Mg(n,γ)25Mg | 0.139 | 0.196 | 0.571 | 1.61 | 3.12 | 4.01 | 1.39 | 2.38 |
| 42K(n,γ)43K | 3.97 | 2.93 | 1.54 | 0.622 | 0.239 | 0.139 | 1.39 | 2.38 | ||
| 25Mg(α,n)28Si | 6.94 | 4.47 | 1.62 | 0.697 | 0.484 | 0.443 | 2.15 | 2.4 | ||
| 25Mg(n,γ)26Mg | 0.166 | 0.333 | 0.764 | 1.2 | 1.47 | 1.55 | 1.41 | 2.38 | ||
| 43K(p,n)43Ca | 0.172 | 0.398 | 0.771 | 1.26 | 1.95 | 2.78 | 1.42 | 2.6 | ||
| 20Ne(n,γ)21Ne | 0.2 | 0.51 | 0.892 | 1.07 | 1.12 | 1.14 | 1.44 | 2.45 | ||
| 42K(p,n)42Ca | 0.203 | 0.47 | 0.828 | 1.16 | 1.39 | 1.49 | 1.44 | 2.45 | ||
| 25Mg(p,γ)26Al | 0.222 | 0.452 | 0.872 | 1.08 | 1.17 | 1.19 | 1.46 | 2.4 | ||
| 41K(n,γ)42K | 3.62 | 2.79 | 1.49 | 0.666 | 0.333 | 0.247 | 1.47 | 2.38 | ||
| 28Al(p,α)25Mg | 4.04 | 1.89 | 1.12 | 0.941 | 0.894 | 0.884 | 2.14 | 2.4 | ||
| 23Na(α,p)26Mg | 0.259 | 0.471 | 0.821 | 1.16 | 1.4 | 1.48 | 1.47 | 2.38 | ||
| 27Al(α,p)30Si | 0.294 | 0.523 | 0.857 | 1.12 | 1.27 | 1.32 | 2.06 | 2.4 | ||
| 20Ne(α,γ)24Mg | 0.3 | 0.525 | 0.855 | 1.12 | 1.26 | 1.31 | 2.1 | 2.6 | ||
| 41K(p,α)38Ar | 0.313 | 0.581 | 0.884 | 1.09 | 1.19 | 1.22 | 2.09 | 2.38 | ||
| 43K(n,γ)44K | 0.315 | 0.605 | 0.911 | 1.06 | 1.11 | 1.12 | 2.11 | 2.38 | ||
| 28Si(n,γ)29Si | 0.322 | 0.742 | 0.954 | 1.03 | 1.05 | 1.06 | 2.17 | 2.38 | ||
| 26Mg(α,n)29Si | 2.94 | 2.29 | 1.35 | 0.76 | 0.539 | 0.489 | 2.15 | 2.38 | ||
| 27Al(p,γ)28Si | 2.53 | 1.41 | 1.05 | 0.972 | 0.949 | 0.943 | 2.14 | 2.48 | ||
| 27Al(n,γ)28Al | 2.02 | 1.3 | 1.04 | 0.981 | 0.967 | 0.964 | 2.1 | 2.48 | ||
| 29Si(n,γ)30Si | 0.499 | 0.797 | 0.962 | 1.02 | 1.04 | 1.05 | 2.17 | 2.38 | ||
| 24Mg(α,γ)28Si | 1.93 | 1.14 | 1.02 | 0.991 | 0.985 | 0.984 | 2.09 | 2.48 | ||
| 23Na(p,α)20Ne | 1.09 | 1.08 | 1.04 | 0.935 | 0.721 | 0.53 | 2.15 | 2.38 | ||
| 30Si(p,γ)31P | 1.82 | 1.42 | 1.07 | 0.962 | 0.93 | 0.923 | 2.11 | 2.56 | ||
| 41K(p,γ)42Ca | 0.55 | 0.886 | 0.984 | 1.01 | 1.01 | 1.02 | 2.12 | 2.38 | ||
| 21Ne(α,n)24Mg | 1.07 | 1.06 | 1.03 | 0.95 | 0.764 | 0.582 | 2.24 | 2.38 | ||
| 27Al(p,α)24Mg | 0.762 | 0.796 | 0.904 | 1.13 | 1.44 | 1.67 | 2.14 | 2.48 | ||
| 29Si(p,γ)30P | 0.621 | 0.832 | 0.968 | 1.02 | 1.04 | 1.04 | 2.14 | 2.38 | ||
| 40Ar(p,γ)41K | 1.6 | 1.3 | 1.07 | 0.951 | 0.899 | 0.885 | 2.13 | 2.38 | ||
| 32S(n,α)29Si | 1.59 | 1.31 | 1.06 | 0.969 | 0.944 | 0.938 | 2.17 | 2.4 | ||
| 40K(n,γ)41K | 1.57 | 1.29 | 1.06 | 0.968 | 0.94 | 0.933 | 2.15 | 2.38 | ||
| 40Ca(n,γ)41Ca | 1.54 | 1.31 | 1.07 | 0.957 | 0.918 | 0.909 | 2.15 | 2.38 | ||
| 21Ne(p,γ)22Na | 0.71 | 0.925 | 0.992 | 1.0 | 1.01 | 1.01 | 2.22 | 2.38 | ||
| 41K(p,n)41Ca | 1.37 | 1.21 | 1.04 | 0.974 | 0.95 | 0.945 | 2.27 | 2.38 | ||
| 28Al(p,n)28Si | 1.04 | 1.03 | 1.02 | 0.973 | 0.869 | 0.747 | 2.14 | 2.38 | ||
| 41Ca(n,α)38Ar | 0.893 | 0.905 | 0.953 | 1.07 | 1.23 | 1.33 | 2.15 | 2.38 | ||
| 39Ar(n,γ)40Ar | 1.32 | 1.15 | 1.03 | 0.986 | 0.973 | 0.97 | 2.15 | 2.38 | ||
| 39K(n,γ)40K | 1.31 | 1.19 | 1.05 | 0.971 | 0.944 | 0.937 | 2.17 | 2.38 | ||
| 26Mg(p,γ)27Al | 1.14 | 1.29 | 1.11 | 0.909 | 0.797 | 0.763 | 2.06 | 2.38 | ||
| 37Cl(α,γ)41K | 1.3 | 1.03 | 1.0 | 0.998 | 0.997 | 0.997 | 2.17 | 2.38 | ||
| 16O(α,γ)20Ne | 1.07 | 1.05 | 1.02 | 0.96 | 0.905 | 0.803 | 2.02 | 2.6 | ||
| 27Al(α,n)30P | 0.803 | 0.957 | 0.994 | 1.0 | 1.01 | 1.01 | 2.11 | 2.38 | ||
| 16O(12C,p)27Al | 0.806 | 0.975 | 0.997 | 1.0 | 1.0 | 1.0 | 2.14 | 2.38 | ||
| 32S(n,γ)33S | 0.819 | 0.899 | 0.977 | 1.02 | 1.03 | 1.04 | 2.21 | 2.38 | ||
| 12C(12C,α)20Ne | 1.21 | 1.04 | 1.0 | 0.997 | 0.995 | 0.995 | 1.98 | 2.38 | ||
| 29Si(α,γ)33S | 0.841 | 0.976 | 0.997 | 1.0 | 1.0 | 1.0 | 2.15 | 2.38 | ||
| 38Ar(p,γ)39K | 1.18 | 1.07 | 1.01 | 0.992 | 0.985 | 0.983 | 2.15 | 2.38 | ||
| 42K(p,α)39Ar | 0.848 | 0.982 | 0.998 | 1.0 | 1.0 | 1.0 | 2.12 | 2.38 | ||
| 30Si(n,γ)31Si | 1.15 | 1.03 | 1.0 | 0.998 | 0.997 | 0.997 | 2.1 | 2.4 | ||
| 39Ar(p,γ)40K | 1.15 | 1.04 | 1.01 | 0.997 | 0.995 | 0.994 | 2.15 | 2.38 | ||
| 22Ne(α,n)25Mg | 1.02 | 1.02 | 1.01 | 0.981 | 0.916 | 0.874 | 2.17 | 2.38 | ||
| 28Al(n,γ)29Al | 0.878 | 0.978 | 0.997 | 1.0 | 1.0 | 1.0 | 2.21 | 2.38 | ||
| 23Na(α,γ)27Al | 0.885 | 0.986 | 0.998 | 1.0 | 1.0 | 1.0 | 2.17 | 2.38 | ||
| 21Ne(n,γ)22Ne | 0.893 | 0.987 | 0.998 | 1.0 | 1.0 | 1.0 | 2.24 | 2.38 | ||
| 26Al(n,p)26Mg | 0.922 | 0.933 | 0.97 | 1.03 | 1.1 | 1.12 | 2.15 | 2.38 | ||
| 43K(p,α)40Ar | 0.901 | 0.989 | 0.999 | 1.0 | 1.0 | 1.0 | 2.1 | 2.38 | ||
| 41Ca(n,γ)42Ca | 0.904 | 0.962 | 0.994 | 1.0 | 1.01 | 1.01 | 2.15 | 2.38 | ||
| 40K(n,α)37Cl | 0.907 | 0.924 | 0.971 | 1.03 | 1.06 | 1.07 | 2.15 | 2.38 | ||
| 23Na(n,γ)24Na | 0.908 | 0.97 | 0.996 | 1.0 | 1.0 | 1.0 | 2.05 | 2.38 | ||
| 38Ar(n,γ)39Ar | 1.1 | 1.06 | 1.01 | 0.991 | 0.983 | 0.981 | 2.12 | 2.38 | ||
| 44Ti | 3.01e-05 | 44Ti(α,p)47V | 0.209 | 0.385 | 0.74 | 1.35 | 2.61 | 5.74 | 0.88 | 3.94 |
| α(2α,γ)12C | 1.3 | 1.0 | 1.01 | 0.929 | 0.528 | 0.175 | 1.83 | 6.15 | ||
| 40Ca(α,γ)44Ti | 1.96 | 1.62 | 1.19 | 0.83 | 0.543 | 0.374 | 0.97 | 3.21 | ||
| 12C(α,γ)16O | 2.15 | 1.2 | 1.02 | 0.988 | 0.977 | 0.975 | 2.1 | 4.98 | ||
| 43Sc(p,γ)44Ti | 1.35 | 1.18 | 1.04 | 0.977 | 0.958 | 0.951 | 1.66 | 3.09 | ||
| 13N(α,p)16O | 1.29 | 1.05 | 1.01 | 0.994 | 0.992 | 1.01 | 2.08 | 4.98 | ||
| 43Sc(p,α)40Ca | 0.949 | 0.958 | 0.979 | 1.03 | 1.15 | 1.28 | 1.79 | 2.39 | ||
| 27Al(α,n)30P | 0.787 | 0.952 | 0.994 | 1.0 | 1.01 | 1.01 | 1.22 | 3.14 | ||
| 39K(p,α)36Ar | 1.02 | 1.01 | 1.01 | 0.991 | 0.941 | 0.849 | 1.35 | 2.64 | ||
| 42Ca(p,α)39K | 1.17 | 1.08 | 1.02 | 0.983 | 0.966 | 0.961 | 1.93 | 2.74 | ||
| 44Ti(p,γ)45V | 0.864 | 0.923 | 0.978 | 1.02 | 1.05 | 1.14 | 0.69 | 1.77 | ||
| 41Sc(p,γ)42Ti | 1.15 | 1.03 | 1.0 | 1.0 | 1.02 | 1.08 | 0.58 | 1.56 | ||
| 33S(n,α)30Si | 0.89 | 0.967 | 0.995 | 1.0 | 1.01 | 1.01 | 1.69 | 3.11 | ||
| 11B(α,n)14N | 0.9 | 0.969 | 0.997 | 1.0 | 1.01 | 1.0 | 2.13 | 3.19 | ||
| 45V(p,γ)46Cr | 0.902 | 0.906 | 0.956 | 1.04 | 1.09 | 1.11 | 0.93 | 2.39 | ||
| 47Sc | 6.12e-08 | 47Sc(n,γ)48Sc | 0.361 | 0.531 | 0.849 | 1.12 | 1.25 | 1.29 | 1.37 | 2.6 |
| 25Mg(α,n)28Si | 2.61 | 1.92 | 1.24 | 0.83 | 0.66 | 0.619 | 1.42 | 2.6 | ||
| 47Ti(n,p)47Sc | 0.408 | 0.546 | 0.813 | 1.24 | 1.85 | 2.23 | 1.38 | 2.71 | ||
| 24Mg(n,γ)25Mg | 0.462 | 0.537 | 0.811 | 1.21 | 1.65 | 1.91 | 1.39 | 2.65 | ||
| 30Si(p,γ)31P | 2.08 | 1.77 | 1.21 | 0.866 | 0.745 | 0.716 | 2.13 | 2.65 | ||
| 28Si(n,γ)29Si | 0.49 | 0.744 | 0.944 | 1.04 | 1.07 | 1.08 | 1.39 | 2.6 | ||
| 27Al(α,p)30Si | 0.495 | 0.631 | 0.867 | 1.13 | 1.35 | 1.44 | 1.39 | 2.65 | ||
| 27Al(p,γ)28Si | 2.01 | 1.43 | 1.07 | 0.964 | 0.934 | 0.926 | 2.16 | 2.65 | ||
| 20Ne(α,γ)24Mg | 0.503 | 0.693 | 0.898 | 1.1 | 1.31 | 1.41 | 1.41 | 2.65 | ||
| 25Mg(p,γ)26Al | 0.51 | 0.619 | 0.874 | 1.1 | 1.2 | 1.23 | 1.41 | 2.6 | ||
| 46Sc(n,γ)47Sc | 1.95 | 1.55 | 1.15 | 0.892 | 0.778 | 0.748 | 2.27 | 2.65 | ||
| 25Mg(n,γ)26Mg | 0.522 | 0.671 | 0.897 | 1.09 | 1.2 | 1.23 | 1.41 | 2.6 | ||
| 28Al(p,α)25Mg | 1.87 | 1.37 | 1.06 | 0.964 | 0.934 | 0.927 | 2.21 | 2.6 | ||
| 24Mg(α,γ)28Si | 1.8 | 1.27 | 1.04 | 0.981 | 0.966 | 0.963 | 2.18 | 2.65 | ||
| 46Sc(p,n)46Ti | 0.556 | 0.692 | 0.895 | 1.1 | 1.29 | 1.38 | 1.41 | 2.65 | ||
| 27Al(p,α)24Mg | 0.929 | 0.93 | 0.962 | 1.07 | 1.36 | 1.77 | 2.17 | 2.65 | ||
| 16O(α,γ)20Ne | 1.1 | 1.07 | 1.02 | 0.989 | 0.912 | 0.568 | 1.41 | 2.65 | ||
| 20Ne(n,γ)21Ne | 0.576 | 0.766 | 0.95 | 1.03 | 1.06 | 1.07 | 1.41 | 2.6 | ||
| 46Ca(n,γ)47Ca | 1.73 | 1.34 | 1.07 | 0.962 | 0.928 | 0.92 | 2.1 | 2.51 | ||
| 45Sc(n,γ)46Sc | 1.46 | 1.37 | 1.14 | 0.859 | 0.654 | 0.585 | 1.41 | 2.65 | ||
| 27Al(n,γ)28Al | 1.68 | 1.17 | 1.02 | 0.99 | 0.982 | 0.98 | 2.18 | 2.6 | ||
| 26Mg(α,n)29Si | 1.22 | 1.19 | 1.09 | 0.891 | 0.688 | 0.613 | 1.42 | 2.6 | ||
| 45Sc(p,γ)46Ti | 0.623 | 0.787 | 0.945 | 1.04 | 1.09 | 1.11 | 1.63 | 2.6 | ||
| 29Si(n,γ)30Si | 0.632 | 0.83 | 0.966 | 1.02 | 1.04 | 1.04 | 2.06 | 2.6 | ||
| 44Ca(p,γ)45Sc | 1.55 | 1.29 | 1.08 | 0.939 | 0.861 | 0.835 | 2.21 | 2.6 | ||
| 45Ca(n,γ)46Ca | 1.49 | 1.31 | 1.08 | 0.948 | 0.898 | 0.886 | 2.38 | 2.6 | ||
| 29Si(p,γ)30P | 0.672 | 0.777 | 0.938 | 1.04 | 1.09 | 1.1 | 2.12 | 2.6 | ||
| 42Ca(p,α)39K | 1.4 | 1.08 | 1.01 | 0.995 | 0.991 | 0.99 | 2.2 | 2.65 | ||
| 32S(n,α)29Si | 1.37 | 1.29 | 1.11 | 0.916 | 0.836 | 0.82 | 2.15 | 2.6 | ||
| 44Ca(n,γ)45Ca | 1.36 | 1.27 | 1.08 | 0.943 | 0.884 | 0.869 | 2.24 | 2.6 | ||
| 26Mg(p,γ)27Al | 0.734 | 0.871 | 0.983 | 0.999 | 0.974 | 0.96 | 2.45 | 2.6 | ||
| 41Ca(n,γ)42Ca | 1.36 | 1.15 | 1.02 | 0.987 | 0.976 | 0.973 | 2.21 | 2.6 | ||
| 23Na(α,p)26Mg | 0.736 | 0.875 | 0.979 | 1.01 | 1.0 | 0.997 | 2.14 | 2.66 | ||
| 46Sc(p,γ)47Ti | 0.755 | 0.948 | 0.993 | 1.0 | 1.01 | 1.01 | 2.16 | 2.6 | ||
| 29Si(α,γ)33S | 0.758 | 0.941 | 0.992 | 1.0 | 1.01 | 1.01 | 2.15 | 2.6 | ||
| 32S(n,γ)33S | 0.76 | 0.835 | 0.945 | 1.06 | 1.17 | 1.22 | 2.17 | 2.65 | ||
| 46Ca(p,γ)47Sc | 1.28 | 1.13 | 1.04 | 0.955 | 0.862 | 0.82 | 2.09 | 2.6 | ||
| 30Si(n,γ)31Si | 1.21 | 1.04 | 1.0 | 0.998 | 0.996 | 0.996 | 2.18 | 2.6 | ||
| 38Ar(α,γ)42Ca | 1.2 | 1.02 | 1.0 | 0.999 | 0.998 | 0.998 | 2.19 | 2.65 | ||
| 47Ca(p,n)47Sc | 0.95 | 0.96 | 0.982 | 1.03 | 1.11 | 1.19 | 2.19 | 2.6 | ||
| 21Ne(α,n)24Mg | 1.02 | 1.01 | 1.01 | 0.991 | 0.946 | 0.85 | 2.4 | 2.56 | ||
| 47Sc(p,γ)48Ti | 0.859 | 0.983 | 0.998 | 1.0 | 1.0 | 1.0 | 2.17 | 2.6 | ||
| 28Si(α,γ)32S | 0.861 | 0.962 | 0.993 | 1.0 | 1.01 | 1.01 | 2.21 | 2.6 | ||
| 31P(α,p)34S | 0.863 | 0.962 | 0.994 | 1.0 | 1.01 | 1.01 | 2.17 | 2.6 | ||
| 31P(p,α)28Si | 1.04 | 1.03 | 1.02 | 0.976 | 0.91 | 0.869 | 2.16 | 2.6 | ||
| 41Ca(n,α)38Ar | 0.964 | 0.968 | 0.984 | 1.02 | 1.1 | 1.15 | 2.2 | 2.6 | ||
| 27Al(α,n)30P | 0.878 | 0.973 | 0.997 | 1.0 | 1.0 | 1.0 | 2.17 | 2.65 | ||
| 42Ca(n,γ)43Ca | 1.14 | 1.11 | 1.04 | 0.961 | 0.91 | 0.895 | 2.17 | 2.6 | ||
| 27Al(α,γ)31P | 1.13 | 1.01 | 1.0 | 0.999 | 0.999 | 0.999 | 2.17 | 2.6 | ||
| 43Ca(n,γ)44Ca | 1.09 | 1.08 | 1.03 | 0.963 | 0.905 | 0.885 | 2.21 | 2.6 | ||
| 47Ca(n,γ)48Ca | 0.886 | 0.957 | 0.993 | 1.0 | 1.01 | 1.01 | 2.25 | 2.56 | ||
| 45Sc(p,α)42Ca | 0.887 | 0.983 | 0.998 | 1.0 | 1.0 | 1.0 | 2.17 | 2.6 | ||
| 46Sc(n,p)46Ca | 1.13 | 1.1 | 1.04 | 0.971 | 0.936 | 0.926 | 2.14 | 2.6 | ||
| 16O(12C,p)27Al | 0.891 | 0.979 | 0.997 | 1.0 | 1.0 | 1.0 | 2.15 | 2.6 | ||
| 28Al(p,n)28Si | 1.01 | 1.01 | 1.0 | 0.994 | 0.964 | 0.891 | 2.21 | 2.6 | ||
| 41K(p,γ)42Ca | 1.12 | 1.04 | 1.01 | 0.997 | 0.994 | 0.993 | 2.2 | 2.6 | ||
| 21Ne(p,γ)22Na | 0.895 | 0.973 | 0.997 | 1.0 | 1.0 | 1.0 | 2.29 | 2.6 | ||
| 41K(n,γ)42K | 1.1 | 1.07 | 1.02 | 0.985 | 0.97 | 0.966 | 2.2 | 2.6 | ||
| 30P(n,p)30Si | 0.985 | 0.988 | 0.994 | 1.01 | 1.04 | 1.1 | 2.21 | 2.6 | ||
| 48V () a | 9.24e-05 | 48Cr(α,p)51Mn | 0.395 | 0.572 | 0.834 | 1.2 | 1.84 | 3.13 | 1.83 | 3.57 |
| α(2α,γ)12C | 1.31 | 0.976 | 0.962 | 0.972 | 0.768 | 0.588 | 2.3 | 5.88 | ||
| 12C(α,γ)16O | 1.64 | 1.17 | 1.03 | 0.98 | 0.963 | 0.958 | 2.43 | 4.98 | ||
| 44Ti(α,p)47V | 1.2 | 1.16 | 1.06 | 0.932 | 0.766 | 0.629 | 1.1 | 4.33 | ||
| 40Ca(α,γ)44Ti | 1.15 | 1.12 | 1.05 | 0.941 | 0.793 | 0.664 | 2.16 | 2.84 | ||
| 13N(α,p)16O | 1.34 | 1.11 | 1.02 | 0.986 | 0.979 | 0.991 | 2.42 | 4.98 | ||
| 47V(p,γ)48Cr | 1.02 | 1.01 | 1.0 | 0.995 | 0.976 | 0.881 | 2.01 | 3.9 | ||
| 42Ca(α,γ)46Ti | 1.12 | 1.03 | 1.0 | 0.998 | 0.996 | 0.996 | 2.02 | 4.98 | ||
| 16O(12C,p)27Al | 0.907 | 0.937 | 0.977 | 1.02 | 1.04 | 1.05 | 2.4 | 5.77 | ||
| 49V | 6.08e-06 | 12C(α,γ)16O | 2.23 | 1.27 | 1.05 | 0.964 | 0.933 | 0.925 | 0.8 | 4.78 |
| 49Mn(p,γ)50Fe | 0.803 | 0.855 | 0.944 | 1.07 | 1.34 | 2.03 | 0.61 | 1.23 | ||
| 49V(p,γ)50Cr | 0.917 | 0.931 | 0.971 | 1.04 | 1.19 | 1.89 | 0.78 | 4.01 | ||
| 49Cr(n,p)49V | 0.705 | 0.797 | 0.933 | 1.07 | 1.25 | 1.49 | 0.7 | 3.9 | ||
| 13N(α,p)16O | 1.47 | 1.14 | 1.03 | 0.98 | 0.964 | 0.973 | 0.75 | 4.98 | ||
| 44Ti(α,p)47V | 1.02 | 0.994 | 0.991 | 1.02 | 1.12 | 1.44 | 0.8 | 4.1 | ||
| 42Ca(α,γ)46Ti | 1.3 | 1.07 | 1.01 | 0.995 | 0.99 | 0.989 | 0.74 | 4.49 | ||
| 49Cr(p,γ)50Mn | 0.813 | 0.875 | 0.958 | 1.04 | 1.12 | 1.17 | 0.62 | 1.21 | ||
| 48Cr(p,γ)49Mn | 1.15 | 1.12 | 1.04 | 0.955 | 0.87 | 0.82 | 0.58 | 1.03 | ||
| 49Cr(α,p)52Mn | 0.826 | 0.96 | 0.995 | 1.0 | 1.01 | 1.01 | 0.7 | 3.73 | ||
| 20Ne(α,γ)24Mg | 0.826 | 0.846 | 0.955 | 1.04 | 1.1 | 1.12 | 0.71 | 5.17 | ||
| α(2α,γ)12C | 1.1 | 0.93 | 0.95 | 1.01 | 0.932 | 0.833 | 0.58 | 6.13 | ||
| 48Cr(α,p)51Mn | 0.837 | 0.918 | 0.979 | 1.02 | 1.04 | 1.06 | 0.7 | 3.75 | ||
| 23Na(α,p)26Mg | 0.856 | 0.885 | 0.972 | 1.02 | 1.03 | 1.04 | 0.71 | 5.16 | ||
| 16O(12C,p)27Al | 0.861 | 0.901 | 0.967 | 1.02 | 1.05 | 1.06 | 0.71 | 4.98 | ||
| 23Na(p,γ)24Mg | 0.864 | 0.945 | 0.992 | 1.0 | 1.01 | 1.01 | 0.71 | 5.17 | ||
| 49Cr(n,γ)50Cr | 0.867 | 0.98 | 0.998 | 1.0 | 1.0 | 1.0 | 0.71 | 3.69 | ||
| 16O(12C,α)24Mg | 0.869 | 0.916 | 0.979 | 1.01 | 1.03 | 1.03 | 0.71 | 4.98 | ||
| 27Si(n,12C)16O | 0.891 | 0.956 | 0.993 | 1.0 | 1.01 | 1.01 | 0.71 | 4.98 | ||
| 26Al(n,α)23Na | 0.899 | 0.949 | 0.992 | 1.0 | 1.01 | 1.01 | 0.72 | 5.17 | ||
| 50Mn(n,p)50Cr | 0.906 | 0.985 | 0.998 | 1.0 | 1.0 | 1.0 | 0.71 | 3.72 | ||
| 51Cr | 1.85e-05 | 51Mn(p,γ)52Fe | 0.306 | 0.569 | 0.848 | 1.18 | 1.74 | 3.13 | 0.96 | 3.09 |
| 48Cr(α,p)51Mn | 0.969 | 0.965 | 0.982 | 1.03 | 1.16 | 1.69 | 1.1 | 1.49 | ||
| α(2α,γ)12C | 0.948 | 0.9 | 0.955 | 0.999 | 0.869 | 0.724 | 0.73 | 5.85 | ||
| 27Al(α,n)30P | 1.37 | 1.1 | 1.01 | 0.993 | 0.988 | 0.986 | 0.87 | 1.98 | ||
| 44Ti(α,p)47V | 1.06 | 1.02 | 0.999 | 1.01 | 1.07 | 1.28 | 0.89 | 4.19 | ||
| 12C(α,γ)16O | 1.28 | 1.11 | 1.02 | 0.971 | 0.963 | 0.961 | 0.85 | 4.98 | ||
| 42Ca(α,γ)46Ti | 1.27 | 1.07 | 1.01 | 0.994 | 0.988 | 0.987 | 0.86 | 4.33 | ||
| 55Co(p,γ)56Ni | 0.847 | 0.927 | 0.985 | 1.0 | 0.969 | 0.837 | 0.82 | 3.23 | ||
| 13N(α,p)16O | 1.17 | 1.06 | 1.02 | 0.986 | 0.976 | 0.988 | 0.84 | 5.17 | ||
| 33S(n,α)30Si | 1.15 | 1.05 | 1.01 | 0.997 | 0.995 | 0.994 | 0.85 | 1.93 | ||
| 53Fe(n,p)53Mn | 0.96 | 0.965 | 0.983 | 1.02 | 1.09 | 1.14 | 0.84 | 3.82 | ||
| 53Mn(p,α)50Cr | 0.878 | 0.97 | 0.996 | 1.0 | 1.0 | 1.0 | 0.82 | 3.71 | ||
| 20Ne(α,γ)24Mg | 0.879 | 0.897 | 0.964 | 1.03 | 1.08 | 1.1 | 0.82 | 5.17 | ||
| 51Cr(p,γ)52Mn | 0.987 | 0.989 | 0.996 | 1.01 | 1.03 | 1.12 | 0.84 | 3.81 | ||
| 50Cr(p,γ)51Mn | 1.08 | 1.06 | 1.02 | 0.981 | 0.939 | 0.896 | 0.64 | 2.72 | ||
| 49Mn(p,γ)50Fe | 1.02 | 1.01 | 1.0 | 0.998 | 1.03 | 1.12 | 0.8 | 1.38 | ||
| 45Sc(p,α)42Ca | 1.11 | 1.07 | 1.02 | 0.988 | 0.976 | 0.972 | 0.85 | 4.33 | ||
| 16O(12C,p)27Al | 0.899 | 0.932 | 0.974 | 1.01 | 1.03 | 1.03 | 0.82 | 4.98 | ||
| 48Cr(p,γ)49Mn | 1.02 | 1.02 | 1.01 | 0.987 | 0.949 | 0.903 | 0.69 | 1.16 | ||
| 54Fe(p,γ)55Co | 1.0 | 1.0 | 1.0 | 0.998 | 0.982 | 0.904 | 0.82 | 2.58 | ||
| 16O(12C,α)24Mg | 0.906 | 0.942 | 0.985 | 1.01 | 1.02 | 1.02 | 0.82 | 4.98 | ||
| 52Fe(α,p)55Co | 0.906 | 0.971 | 0.995 | 1.0 | 1.01 | 1.01 | 0.82 | 3.71 | ||
| 52Mn | 0.001 | 12C(α,γ)16O | 1.55 | 1.21 | 1.04 | 0.976 | 0.956 | 0.951 | 3.9 | 4.98 |
| 13N(α,p)16O | 1.39 | 1.15 | 1.03 | 0.979 | 0.953 | 0.941 | 3.9 | 4.98 | ||
| 52Fe(α,p)55Co | 0.732 | 0.871 | 0.962 | 1.04 | 1.15 | 1.27 | 2.72 | 3.63 | ||
| 44Ti(α,p)47V | 1.09 | 1.05 | 1.02 | 0.98 | 0.925 | 0.858 | 2.56 | 4.33 | ||
| α(2α,γ)12C | 1.11 | 0.856 | 0.917 | 0.993 | 0.918 | 0.863 | 2.27 | 5.98 | ||
| 53Fe(n,p)53Mn | 0.937 | 0.947 | 0.977 | 1.03 | 1.1 | 1.15 | 3.38 | 3.82 | ||
| 16O(12C,p)27Al | 0.886 | 0.925 | 0.972 | 1.02 | 1.05 | 1.06 | 3.85 | 5.15 | ||
| 16O(12C,α)24Mg | 0.897 | 0.935 | 0.981 | 1.01 | 1.03 | 1.03 | 3.85 | 4.98 | ||
| 53Mn(p,α)50Cr | 0.899 | 0.981 | 0.998 | 1.0 | 1.0 | 1.0 | 3.28 | 3.71 | ||
| 53Mn | 0.000107 | 53Fe(n,p)53Mn | 0.546 | 0.707 | 0.902 | 1.1 | 1.3 | 1.42 | 2.93 | 3.72 |
| 12C(α,γ)16O | 1.52 | 1.2 | 1.04 | 0.971 | 0.959 | 0.956 | 3.25 | 4.78 | ||
| 13N(α,p)16O | 1.36 | 1.14 | 1.03 | 0.975 | 0.943 | 0.931 | 3.21 | 4.78 | ||
| 52Fe(p,γ)53Co | 1.23 | 1.09 | 1.02 | 0.987 | 0.969 | 0.961 | 0.74 | 1.01 | ||
| 53Mn(p,γ)54Fe | 0.956 | 0.976 | 0.992 | 1.01 | 1.04 | 1.19 | 3.15 | 3.81 | ||
| 42Ca(α,γ)46Ti | 1.15 | 1.05 | 1.01 | 0.995 | 0.991 | 0.99 | 3.56 | 4.49 | ||
| 52Fe(α,p)55Co | 0.87 | 0.949 | 0.988 | 1.01 | 1.03 | 1.05 | 2.8 | 3.63 | ||
| 52Fe(n,p)52Mn | 1.08 | 1.06 | 1.02 | 0.975 | 0.916 | 0.873 | 3.06 | 3.56 | ||
| 16O(12C,p)27Al | 0.873 | 0.909 | 0.965 | 1.03 | 1.06 | 1.07 | 2.99 | 4.78 | ||
| 16O(12C,α)24Mg | 0.881 | 0.921 | 0.977 | 1.01 | 1.03 | 1.03 | 2.98 | 4.98 | ||
| 27Si(n,12C)16O | 0.9 | 0.954 | 0.993 | 1.0 | 1.01 | 1.01 | 2.99 | 4.78 | ||
| 52Mn(p,γ)53Fe | 1.0 | 1.0 | 1.0 | 0.997 | 0.983 | 0.906 | 3.06 | 3.62 | ||
| 53Fe(n,γ)54Fe | 0.907 | 0.989 | 0.999 | 1.0 | 1.0 | 1.0 | 3.05 | 3.56 | ||
| 55Fe | 0.000495 | 55Co(p,γ)56Ni | 0.605 | 0.761 | 0.921 | 1.09 | 1.32 | 1.8 | 2.21 | 3.13 |
| 12C(α,γ)16O | 1.53 | 1.23 | 1.05 | 0.96 | 0.939 | 0.932 | 3.81 | 5.17 | ||
| 13N(α,p)16O | 1.39 | 1.15 | 1.04 | 0.97 | 0.929 | 0.907 | 3.9 | 5.6 | ||
| 16O(12C,p)27Al | 0.858 | 0.893 | 0.957 | 1.03 | 1.06 | 1.07 | 3.57 | 5.15 | ||
| 16O(12C,α)24Mg | 0.864 | 0.907 | 0.972 | 1.02 | 1.03 | 1.04 | 3.58 | 4.49 | ||
| 42Ca(α,γ)46Ti | 1.15 | 1.05 | 1.01 | 0.995 | 0.99 | 0.989 | 3.56 | 4.49 | ||
| 12C(12C,α)20Ne | 1.14 | 1.09 | 1.02 | 0.984 | 0.967 | 0.963 | 3.19 | 5.17 | ||
| 12C(12C,p)23Na | 1.14 | 1.07 | 1.02 | 0.989 | 0.978 | 0.975 | 3.36 | 5.17 | ||
| 27Si(n,12C)16O | 0.886 | 0.946 | 0.992 | 1.0 | 1.01 | 1.01 | 3.65 | 4.49 | ||
| 23Na(α,p)26Mg | 0.887 | 0.894 | 0.965 | 1.02 | 1.04 | 1.04 | 3.54 | 5.16 | ||
| 54Fe(p,γ)55Co | 1.0 | 1.0 | 1.0 | 1.0 | 1.02 | 1.12 | 2.37 | 2.83 | ||
| 56Co () a | 0.0875 | α(2α,γ)12C | 1.24 | 1.14 | 1.05 | 0.944 | 0.847 | 0.803 | 3.22 | 5.77 |
| 12C(α,γ)16O | 1.11 | 1.04 | 1.01 | 0.996 | 0.993 | 0.992 | 3.99 | 4.98 | ||
| 57Co () a | 0.00256 | 57Ni(n,p)57Co | 0.727 | 0.809 | 0.934 | 1.07 | 1.24 | 1.38 | 2.04 | 3.48 |
| α(2α,γ)12C | 1.1 | 1.1 | 1.02 | 0.978 | 0.915 | 0.87 | 2.55 | 5.55 | ||
| 56Ni(p,γ)57Cu | 1.14 | 1.03 | 1.01 | 0.996 | 0.991 | 0.989 | 0.46 | 0.64 | ||
| 27Al(α,n)30P | 1.11 | 1.03 | 1.0 | 0.998 | 0.996 | 0.995 | 2.64 | 3.22 | ||
| 57Ni(n,γ)58Ni | 0.907 | 0.986 | 0.998 | 1.0 | 1.0 | 1.0 | 2.93 | 3.31 | ||
| 59Fe | 3.92e-05 | 59Fe(n,γ)60Fe | 0.687 | 0.843 | 0.967 | 1.02 | 1.04 | 1.04 | 1.32 | 2.34 |
| 58Fe(n,γ)59Fe | 1.31 | 1.15 | 1.04 | 0.964 | 0.903 | 0.871 | 1.32 | 2.34 | ||
| 24Mg(n,γ)25Mg | 0.825 | 0.859 | 0.946 | 1.05 | 1.12 | 1.14 | 1.32 | 2.34 | ||
| 25Mg(α,n)28Si | 1.21 | 1.15 | 1.05 | 0.966 | 0.93 | 0.921 | 1.34 | 2.34 | ||
| 20Ne(α,γ)24Mg | 0.832 | 0.879 | 0.962 | 1.03 | 1.07 | 1.08 | 1.32 | 2.34 | ||
| 20Ne(n,γ)21Ne | 0.844 | 0.918 | 0.983 | 1.01 | 1.02 | 1.02 | 1.32 | 2.34 | ||
| 16O(α,γ)20Ne | 1.07 | 1.06 | 1.03 | 0.965 | 0.891 | 0.849 | 1.32 | 2.34 | ||
| 25Mg(n,γ)26Mg | 0.853 | 0.905 | 0.974 | 1.02 | 1.04 | 1.05 | 1.32 | 2.34 | ||
| 59Fe(p,n)59Co | 0.858 | 0.96 | 0.994 | 1.0 | 1.01 | 1.01 | 1.32 | 2.34 | ||
| 25Mg(p,γ)26Al | 0.871 | 0.918 | 0.98 | 1.01 | 1.03 | 1.03 | 1.32 | 2.34 | ||
| 28Al(p,α)25Mg | 1.13 | 1.06 | 1.01 | 0.994 | 0.989 | 0.988 | 1.34 | 2.38 | ||
| 28Si(n,γ)29Si | 0.888 | 0.962 | 0.993 | 1.0 | 1.01 | 1.01 | 1.32 | 2.34 | ||
| 26Mg(α,n)29Si | 1.12 | 1.08 | 1.03 | 0.974 | 0.937 | 0.925 | 1.34 | 2.34 | ||
| 27Al(α,p)30Si | 0.907 | 0.951 | 0.988 | 1.01 | 1.02 | 1.02 | 1.32 | 2.34 | ||
| 58Fe(p,γ)59Co | 0.908 | 0.97 | 0.995 | 1.0 | 1.01 | 1.01 | 1.32 | 2.34 | ||
| 59Ni | 0.000162 | 59Cu(p,γ)60Zn | 0.274 | 0.464 | 0.775 | 1.29 | 2.12 | 2.77 | 1.37 | 2.39 |
| 57Cu(p,γ)58Zn | 1.68 | 1.17 | 1.02 | 0.989 | 0.982 | 0.974 | 0.78 | 1.07 | ||
| 59Cu(p,α)56Ni | 1.41 | 1.25 | 1.06 | 0.963 | 0.93 | 0.963 | 1.25 | 2.39 | ||
| 57Ni(n,p)57Co | 0.856 | 0.894 | 0.955 | 1.06 | 1.21 | 1.39 | 1.19 | 2.96 | ||
| α(2α,γ)12C | 0.739 | 0.893 | 0.964 | 1.01 | 0.924 | 0.847 | 1.08 | 5.72 | ||
| 20Ne(α,γ)24Mg | 0.937 | 0.948 | 0.98 | 1.03 | 1.13 | 1.31 | 1.73 | 2.04 | ||
| 57Ni(p,γ)58Cu | 1.01 | 1.01 | 1.0 | 0.989 | 0.926 | 0.788 | 1.21 | 1.6 | ||
| 27Al(α,n)30P | 1.25 | 1.06 | 1.01 | 0.995 | 0.994 | 1.0 | 1.19 | 1.54 | ||
| 48Cr(α,p)51Mn | 0.974 | 0.979 | 0.993 | 1.01 | 1.08 | 1.22 | 1.18 | 1.51 | ||
| 58Ni(p,γ)59Cu | 1.02 | 1.01 | 1.0 | 0.997 | 0.961 | 0.849 | 1.29 | 2.4 | ||
| 30Si(p,γ)31P | 0.981 | 0.978 | 0.992 | 1.01 | 1.08 | 1.14 | 1.37 | 2.6 | ||
| 33S(n,α)30Si | 1.14 | 1.04 | 1.0 | 1.0 | 0.999 | 1.0 | 1.27 | 1.96 | ||
| 58Cu(p,γ)59Zn | 1.0 | 1.0 | 1.0 | 1.01 | 0.972 | 0.882 | 1.24 | 1.63 | ||
| 26Al(n,α)23Na | 1.13 | 1.03 | 1.0 | 1.0 | 0.996 | 0.994 | 1.18 | 1.92 | ||
| 58Ni(α,γ)62Zn | 0.905 | 0.973 | 0.993 | 0.997 | 1.01 | 1.01 | 1.27 | 2.65 | ||
Note.
a The sensitivity of the long-lived parent isotope is the same.In total, we find 141 reaction rates with Fi ≥ 1.1 when varied by up to a factor of 100 for at least one isotope of interest i. The sensitivity of the final abundances to reaction rate variations varies widely. The lighter isotopes in the A = 43–49 mass range are affected by a larger number of reaction rates. The most sensitive isotope is the lightest and most neutron-rich isotope studied here, 43K. When varied by a factor of 100, 20 reaction rates have Fi ≥ 2, and 19 additional reaction rates have Fi ≥ 1.3. For the other interesting isotopes in this mass range, 47 reaction rates have Fi ≥ 1.3 for at least one isotope i. On the other hand, for each of the isotopes in the A = 52–57 mass range, there are no reaction rates with Fi ≥ 2 and only eight with Fi ≥ 1.3. The A = 52–57 isotopes are closer to the peak of the NSE abundance distribution at A = 56. Their synthesis is therefore more dominated by NSE, making them less susceptible to reaction rate variations.
The most impactful reactions generally fall into two categories: reactions involving the isotope of interest or its parent nuclei and rates that affect explosive nucleosynthesis more broadly. Reactions in the latter category are listed in Table 2. This group includes the strongest sensitivity identified in this study: the impact of the 24Mg(n,γ)25Mg reaction on 43K production. This reaction affects the production of all neutron-rich isotopes of interest. For the proton-rich isotopes, the reactions with the broadest impact are α(2α,γ)12C, 13N(α,p)16O, 16O(12C,p)27Al, and 12C(α,γ)16O, each of which significantly affects the production of seven or more of the 13 isotopes of interest. The reactions are bottlenecks in the buildup of heavy elements during NSE freeze-out.
Table 2. Reaction Rate Variations that Affect Three or More Isotopes of Interest
| Reaction | Number of Isotopes Affected |
|---|---|
| 12C(α,γ)16O | 8 |
| α(2α,γ)12C | 8 |
| 16O(12C,p)27Al | 8 |
| 13N(α,p)16O | 7 |
| 27Al(α,n)30P | 6 |
| 20Ne(α,γ)24Mg | 6 |
| 44Ti(α,p)47V | 5 |
| 42Ca(α,γ)46Ti | 5 |
| 16O(12C,α)24Mg | 5 |
| 48Cr(α,p)51Mn | 4 |
| 23Na(α,p)26Mg | 4 |
| 53Fe(n,p)53Mn | 3 |
| 52Fe(α,p)55Co | 3 |
| 33S(n,α)30Si | 3 |
| 30Si(p,γ)31P | 3 |
| 28Si(n,γ)29Si | 3 |
| 28Al(p,α)25Mg | 3 |
| 27Si(n,12C)16O | 3 |
| 27Al(α,p)30Si | 3 |
| 26Mg(α,n)29Si | 3 |
| 25Mg(p,γ)26Al | 3 |
| 25Mg(n,γ)26Mg | 3 |
| 25Mg(α,n)28Si | 3 |
| 24Mg(n,γ)25Mg | 3 |
| 20Ne(n,γ)21Ne | 3 |
| 16O(α,γ)20Ne | 3 |
Download table as: ASCIITypeset image
The other category of impactful reactions includes reactions that directly involve the isotope of interest or its parent nuclei. These include reactions like 42K(n,γ)43K, 47Sc(n,γ)48Sc, 49Mn(p,γ)50Fe, 51Mn(p,γ)52Fe, 52Fe(α,p)55Co, 53Fe(n,p)53Mn, 55Co(p,γ)56Ni, 57Ni(n,p)57Co, and 59Cu(p,γ)60Zn, which all are among the most impactful reactions for their respective isotopes and for these isotopes only. By nature, these reactions involve radioactive isotopes. Falling into both categories, 44Ti(α,p)47V and 48Cr(α,p)51Mn are somewhat of an exception. While they have the strongest impact on 44Ti and 51Cr production, respectively, they also impact a number of other isotopes of interest (see Table 2).
Table 1 also lists for each reaction rate variation the temperature range where the change in reaction rate produces the change in final abundance. This is the estimated temperature range over which the reaction rate needs to be known in order to reliably predict nucleosynthesis. These temperatures are mostly between 0.7 and 5.5 GK for all reactions. The α(2α,γ)12C reaction is an exception, often leading to changes at temperatures up to and above 6 GK. The typical temperature ranges depend strongly on the isotope of interest. For 43K, 47Sc, 59Fe, and 59Ni, the temperature range of interest is quite narrow (1.4–2.7 GK). The only outlier in that group is the 57Cu(p,γ)58Zn reaction affecting 59Ni at relatively low temperatures of 0.8–1.1 GK. For 44Ti, 48V, 49V, and 51Cr, the temperature range of interest is much broader (mostly 0.7–5 GK). For 52Mn, 53Mn, 55Fe, and 57Co, the temperature range is narrower but higher (2.0–5.5 GK), with two exceptions: the 52Fe(p,γ)53Co reaction affects 53Mn at 0.73–1 GK, and the 56Ni(p,γ)57Co reaction affects 57Co at very low temperatures of 0.47–0.65 GK.
5. Discussion
5.1. Nucleosynthesis
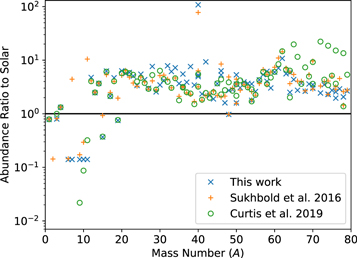
Figure 5 displays a comparison of the ejected masses of the mass chains of interest produced in the current model with two examples from previous work, Sukhbold et al. (2016) and Curtis et al. (2019). Figure 6 displays the ratios to solar abundances up to A = 80. All three use a 12 M⊙ progenitor. We take the progenitors evolved in Sukhbold et al. (2016), which are based on Woosley & Heger (2015), while Curtis et al. (2019) used Woosley & Heger (2007) progenitors. In terms of nuclear physics, Curtis et al. (2019) also used REACLIB reaction rates, while Sukhbold et al. (2016) used older rates as in Woosley & Heger (2007). The results from different models mostly agree within 40%, except for A = 48, where there is an 80% difference between our result and the result of Sukhbold et al. (2016). While differences with respect to Sukhbold et al. (2016) could be in part due to use of different reaction rates, there are clearly also astrophysical uncertainties in the prediction of nucleosynthesis from explosive Si burning.
Figure 5. Ratio of mass fraction of ejected isotopes in previous studies (Sukhbold et al. 2016; Curtis et al. 2019) to this work summed by mass number.
Download figure:
Standard image High-resolution imageFigure 6. Ratio of abundances of ejected isotopes to solar abundances summed by mass number.
Download figure:
Standard image High-resolution imageThe 44Ti yield in this work of M⊙ is about an order of magnitude lower than that inferred from observations of SN 1987a or Cas A, in line with previous 1D supernova model calculations (see Figure 5 and, for example, the summary in Chieffi & Limongi 2017).
5.2. Previous Sensitivity Studies
5.2.1. 44Ti
Given the importance of 44Ti for γ-ray observations, a number of previous studies have identified critical nuclear reactions affecting its production, in particular the studies of The et al. (1998) and Magkotsios et al. (2010). All studies, including this work, agree that 44Ti(α,p)47V, 40Ca(α,γ)44Ti, and α(2α,γ)12C are the most important reactions governing the production of 44Ti. There is also agreement that the 45V(p,γ)46Cr reaction plays a role, even though our model is much less sensitive to this reaction than both The et al. (1998) and Magkotsios et al. (2010), where this reaction ranks near the top. On the other hand, we do find a significant sensitivity to 44Ti(p,γ)45V, as did Magkotsios et al. (2010), indicating that in our model, the (p,γ)–(γ,p) equilibrium between 44Ti and 45V is not well established during 44Ti synthesis.
For the remaining reactions identified in this work, there are significant differences with The et al. (1998). Most of our sensitive reactions do not appear in their study, and we do not find the strong sensitivity to the 44Ti(α,γ)48Cr, 57Ni(p,γ)58Cu, and 57Co(p,n)57Ni reactions that they found. The et al. (1998) used a much narrower range of conditions and evolved a pure initial 28Si composition from NSE conditions at T = 5.5 GK and ρ = 107 g cm−3 through adiabatic expansion. In contrast, our model utilizes several initial compositions and thermodynamic trajectories, only the first ≈0.03 M⊙ of which achieve the NSE conditions of The et al. (1998). Our model therefore includes both complete and incomplete explosive burning. Even so, we do find a weak sensitivity on 44Ti(α,γ)48Cr of Fi ∼ 1.08 (when varied by a factor of 100), just below our threshold.
Overall, our results agree more closely with Magkotsios et al. (2010), who scanned a broad selection of peak temperatures and densities, indicating that more realistic models are needed to identify reaction rate sensitivities for 44Ti. There are only four out of 15 reactions in our list that do not appear in Magkotsios et al. (2010): 39K(p,α)36Ar, 27Al(α,n) 30P, 42Ca(p,α)39K, and 32S(n,α)30Si. However, 39K(p,α)36Ar does appear prominently in The et al. (1998). There are also three reactions that are ranked as "primary" in Magkotsios et al. (2010) that we do not find to have a strong sensitivity: 17F(α,p)20Ne, 21Na(α,p)24Mg, and again 57Ni(p,γ)58Cu. Here 57Ni(p,γ)58Cu has Fi ∼ 1.03, just below our threshold. They found the other two reactions to be significant only in regions of higher peak densities (ρ ∼ 109 g cm−3) than our conditions.
5.2.2. 55Fe, 57Co, and 59Ni
Reactions relevant for 55Fe, 57Co, and 59Ni production were identified in Jordan et al. (2003), who used a similar exponential expansion model as The et al. (1998). For 55Fe, we find only one of the four rates identified in Jordan et al. (2003), 55Co(p,γ)56Ni, to be significant. Of the three others, α(2α,γ)12C is found to cause an Fi ∼ 1.09 effect at a factor of 100 change, and both 59Cu(p,α)56Ni and 59Cu(p,γ)60Zn have only a minimal effect. As before, the simplified model and the more limited range of conditions explored in Jordan et al. (2003) are likely the reason for the discrepancy. Much of the 55Fe production in our model occurs in the trajectories that do not undergo complete burning and do not reach the temperatures or densities specified in Jordan et al. (2003). Because of this, we generate a higher mass fraction ( roughly 10 times more) of 55Fe than Jordan et al. (2003) and obtain a more complete picture of 55Fe production. For 57Co and 59Ni, our results agree with Jordan et al. (2003) on the most important reactions: 57Ni(n,p)57Co in the case of 57Co and 59Cu (p,γ)60Zn, 59Cu(p,α)56Ni, and α(2α,γ)12C in the case of 59Ni. For all three isotopes, we explore not only variations by a factor of 10, as in Jordan et al. (2003), but also variations by a factor of 100. Consequently, we identify a number of additional relevant reactions.
5.3. Rate Uncertainties
The main goal of this paper is to identify the nuclear reaction rates that determine long-lived radioisotope production in CCSNe. However, to provide guidance for nuclear physics on which of these reaction rates need improved accuracy, their current uncertainties must be considered. Such uncertainties are often difficult to estimate reliably, especially in the case of theoretical predictions. Nevertheless, to provide some approximate guidance, we used the uncertainty factors listed in the current STARLIB database (Sallaska et al. 2013) for the relevant temperature ranges that we identified in this work. While past studies (Fields et al. 2018) used Monte Carlo methods to sample STARLIB rates within the prescribed uncertainties, here we take a more simplified approach. We interpolated our sensitivities in Table 1 and determined the expected final abundance changes for rate variations within the STARLIB 1σ uncertainty (the impact factor). We considered both rate increases and rate decreases and used the larger sensitivity. Table 3 provides a list of reactions ordered by their impact factor, Fi , for Fi ≥ 1.1. Sixteen reactions have Fi ≥ 1.5. Reactions with large impact factors indicate the most important reaction rate uncertainties to be addressed for improved nucleosynthesis predictions.
Table 3. Reaction Rates with the Largest Impact Based on Their Current Estimated Uncertainties
| Reaction | Impact | Isotope Affected |
|---|---|---|
| 42K(n,γ)43K | 4.18 | |
| 44Ti(α,p)47V | 2.61, 1.31, 1.12 a | , , |
| 43K(p,n)43Ca | 2.51 | |
| 59Cu(p,γ)60Zn | 2.16 | |
| 42K(p,n)42Ca | 2.13 | |
| 23Na(α,p)26Mg | 2.12, 1.14, 1.13, 1.12 a | , , |
| 27Al(α,p)30Si | 1.91, 1.58 a | , |
| 28Al(p,α)25Mg | 1.89, 1.37 a | , |
| 47Sc(n,γ)48Sc | 1.88 | |
| 47Ti(n,p)47Sc | 1.85 | |
| 48Cr(α,p)51Mn | 1.84, 1.16 a | , |
| 51Mn(p,γ)52Fe | 1.76 | |
| 41K(p,α)38Ar | 1.72 | |
| 43K(n,γ)44K | 1.65 | |
| 46Sc(n,γ)47Sc | 1.55 | |
| 46Sc(p,n)46Ti | 1.45 | |
| 53Fe(n,p)53Mn | 1.41 | |
| 49Mn(p,γ)50Fe | 1.34 | |
| 55Co(p,γ)56Ni | 1.32 | |
| 45Ca(n,γ)46Ca | 1.31 | |
| 32S(n,α)29Si | 1.31, 1.29 a | , |
| 40Ar(p,γ)41K | 1.30 | |
| 44Ca(p,γ)45Sc | 1.29 | |
| 40K(n,γ)41K | 1.29 | |
| 45Sc(p,γ)46Ti | 1.27 | |
| 59Cu(p,α)56Ni | 1.25 | |
| 49Cr(n,p)49V | 1.25 | |
| 57Ni(n,p)57Co | 1.24, 1.21 a | , |
| 41Ca(n,α)38Ar | 1.23 | |
| 41K(p,n)41Ca | 1.21 | |
| 59Fe(n,γ)60Fe | 1.19 | |
| 49V(p,γ)50Cr | 1.19 | |
| 25Mg(α,n)28Si | 1.19, 1.11 a | , |
| 43Sc(p,γ)44Ti | 1.18 | |
| 57Cu(p,γ)58Zn | 1.17 | |
| 46Ca(p,γ)47Sc | 1.16 | |
| 52Fe(α,p)55Co | 1.15 | |
| 48Cr(p,γ)49Mn | 1.15 | |
| 43Sc(p,α)40Ca | 1.15 | |
| 41Ca(n,γ)42Ca | 1.15 | |
| 39Ar(n,γ)40Ar | 1.15 | |
| 28Al(p,n)28Si | 1.15 | |
| 13N(α,p)16O | 1.15, 1.15, 1.14, 1.14, 1.11 a | , , , , |
| 49Cr(p,γ)50Mn | 1.14 | |
| 40Ca(α,γ)44Ti | 1.14 | |
| 41K(p,γ)42Ca | 1.13 | |
| 47Ca(p,n)47Sc | 1.11 | |
| 45V(p,γ)46Cr | 1.10 |
Note.
a For reactions that impact multiple isotopes of interest, the impact numbers correspond to the isotopes listed, respectively.Download table as: ASCIITypeset image
We emphasize that the impact factors provide only some approximate guidance. In addition to astrophysical uncertainties and possible correlations between rate uncertainties, there are large uncertainties in the estimates of the reaction rate uncertainties. For example, the α(2α,γ)12C reaction does not appear in this list despite its importance, as its uncertainty in STARLIB is less than 35%. However, this rate needs to be known up to a temperature of around 5.8 GK. At such high temperatures, the role of resonances above the Hoyle state in 12C remains unclear, and uncertainties are likely underestimated considerably (Zimmerman et al. 2013). In addition, it has been pointed out that proton-induced scattering at sufficiently high densities and temperatures can lead to orders-of-magnitude increases in the α(2α,γ)12C reaction rate (Beard et al. 2017). The impact of these effects and their uncertainties needs to be investigated. The sensitivities provided in Table 1 can then be used to determine whether an improved reaction rate is needed for explosive Si-burning nucleosynthesis.
6. Conclusion
We determined the sensitivity of the production of long-lived radioactive isotopes in a model for explosive Si burning in a CCSN. We vary individual reaction rates to determine the local derivative of the final abundance of a given isotope with respect to a given reaction rate. This approach has been used in previous work (e.g., Iliadis et al. 2002) and enables the identification of critical reaction rates without making assumptions about their uncertainties. Compared to previous studies, we investigate the synthesis of a much broader range of 13 radioisotopes from 43K to 59Ni using a new model for 1D CCSN explosions that incorporates the crucial effects of convection and turbulence and does not resort to altering the microphysics to achieve explosions (Couch et al. 2020). We also develop a new method to identify the relevant temperature range for each reaction and find that these temperature ranges depend sensitively on the reaction and final isotope of interest. Our results can be used to determine the importance of a given reaction rate uncertainty (in the relevant temperature range provided by our work) for CCSN explosive nucleosynthesis predictions and provide guidance on which reactions require further study, both experimental and theoretical. This is of particular importance in light of new emerging capabilities in nuclear experiment and theory. To provide some initial guidance in this direction, we use the reaction rate uncertainties provided by the STARLIB database to produce a ranked list of the most important reaction rate uncertainties. We emphasize, however, that for a final decision on the importance of a reaction rate, a thorough analysis of the possible uncertainties is required, as well as considerations of the individual accuracy needs for the various long-lived radioactive isotopes.
The future reduction of nuclear physics uncertainties in explosive Si-burning nucleosynthesis models enabled by our work will be important to prepare the field for advances in X- and γ-ray observations (Timmes et al. 2019) and stardust analysis (Stephan et al. 2016) and for the potential observation of a Galactic supernova. Reduced and well-characterized nuclear physics uncertainties will enable quantitative comparisons of astrophysical models with observations. While our results for 44Ti are in overall reasonable agreement with the one previous study (Magkotsios et al. 2010) that explored a similar realistic range of conditions, there are some differences, especially for the weaker sensitivities. This may indicate that a broader range of sensitivity studies for different astrophysical models may be needed to identify the individual nuclear physics needs of each model.
We would like to thank Tuguldur Sukhbold for providing the full initial isotopic compositions used as the presupernova stellar model and Evan O'Connor for helpful discussions. This work was supported by the National Science Foundation under award Nos. PHY-1102511, PHY-1913554, and PHY-1430152 (JINA Center for the Evolution of the Elements) and in part through computational resources and services provided by the Institute for Cyber-Enabled Research at Michigan State University. S.M.C. is supported by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics, Early Career Research Program under Award Number DE-SC0015904. This material is based upon work supported by the U.S. Department of Energy, Office of Science, Office of Advanced Scientific Computing Research and Office of Nuclear Physics, Scientific Discovery through Advanced Computing (SciDAC) program under Award Number DE- SC0017955. This research was supported by the Exascale Computing Project (17-SC-20-SC), a collaborative effort of the U.S. Department of Energy Office of Science and the National Nuclear Security Administration. M.L.W. is supported by an NSF Astronomy and Astrophysics Postdoctoral Fellowship under award AST-1801844.
Software: matplotlib (Hunter 2007), NumPy (van der Walt et al. 2011), pandas (McKinney 2010; Reback et al. 2020), SkyNet (Lippuner & Roberts 2017).