Abstract
We have conducted an extensive X-ray spectral variability study of a sample of 20 Compton-thin type II galaxies using broadband spectra from XMM-Newton, Chandra, and Suzaku. The aim is to study the variability of the neutral intrinsic X-ray obscuration along the line of sight and investigate the properties and location of the dominant component of the X-ray-obscuring gas. The observations are sensitive to absorption columns of ∼ 1020.5–24 cm−2 of fully and partially covering neutral and/or lowly ionized gas on timescales spanning days to well over a decade. We detected variability in the column density of the full-covering absorber in 7/20 sources, on timescales of months to years, indicating a component of compact-scale X-ray-obscuring gas lying along the line of sight of each of these objects. Our results imply that torus models incorporating clouds or over-dense regions should account for line-of-sight column densities as low as ∼a few ×1021 cm−2. However, 13/20 sources yielded no detection of significant variability in the full-covering obscurer, with upper limits of ΔNH spanning 1021–23 cm−2. The dominant absorbing media in these systems could be distant, such as kiloparsec-scale dusty structures associated with the host galaxy, or a homogeneous medium along the line of sight. Thus, we find that overall, strong variability in full-covering obscurers is not highly prevalent in Compton-thin type IIs, at least for our sample, in contrast to previous results in the literature. Finally, 11/20 sources required a partial-covering, obscuring component in all or some of their observations, consistent with clumpy near-Compton-thick compact-scale gas.
1. Introduction
It is now generally agreed that the main source of energy of an active galactic nucleus (AGN) is the accretion of matter onto a supermassive black hole (SMBH). However, it is still unknown how gas located at kiloparsec scales in the host galaxy loses its angular momentum and falls into the gravitational potential well of the SMBH at sub-parsec scales and thereby powers the central engine. Galactic-scale bars, circumnuclear disks at scales of a few hundred parsecs, and circumnuclear gas structures at scales of parsecs, in the near vicinity of the SMBH, are each believed to play roles in transferring matter ultimately from large distances into the SMBH accretion disk.
The observed type 1/2 Seyfert dichotomy in the optical band led to orientation-dependent unification schemes: all AGNs function similarly, and the different spectral classifications of AGNs arise only due to the different lines of sight toward the central engine (Antonucci & Miller 1985). When we have a direct unobscured view of the central engine, then the optical-UV spectra exhibit broad as well as narrow emission lines, and the source is classified as a type 1–1.8 (collectively hereafter referred to as type I). On the other hand, if our line of sight to the central engine cuts across a dusty structure popularly known as a "torus," the central engine is no longer visible directly, and the optical-UV spectra we observe are characterized only by narrow emission lines. In such a case, the source is regarded as a type 1.9–2 (hereafter type II) AGN. Classically, the dusty torus was expected to extend to approximately parsec scales—larger than the broad-line region (BLR) but smaller than the narrow-line region (NLR; e.g., Krolik & Begelman 1988). The simplest configuration is an axisymmetric donut-shaped torus, but this notion was effectively a starting point for more complex models, and in recent decades the community has been probing the morphology, content, and radial extent of the circumnuclear gas (see, e.g., the reviews by Bianchi et al. 2012a; Ramos Almeida & Ricci 2017)
First, the community has been accumulating evidence for optical-reddening dust and X-ray-obscuring gas (which can potentially be dusty or non-dusty) to exist across multiple distance scales from the SMBH. Inside the dust sublimation radius, and commensurate with the BLR, temporary X-ray obscuration can occur due to individual clouds (possibly BLR clouds themselves) transiting the line of sight (e.g., Risaliti et al. 2009, 2011). In addition, observations of ratios of NH (as probed by X-rays) to V-band extinction AV are found to be much greater—sometimes a couple orders of magnitude—than the Galactic ratio (Maiolino et al. 2001). Farther out, optical/infrared (IR) reverberation monitoring indicates thermally emitting dust on scales of light-weeks to light-months (see, e.g., Suganuma et al. 2006). In addition, dusty gas on scales of a few parsecs to tens to hundreds of parsecs is revealed by IR interferometry (e.g., Kishimoto et al. 2009; Tristram et al. 2009); submillimeter observations also indicate dense molecular gas at these distance scales (e.g., Schinnerer et al. 2000; Boone et al. 2011; Gallimore et al. 2016; García-Burillo et al. 2016; Imanishi et al. 2016, 2018; Combes et al. 2019). These radial structures may potentially be connected; for example, Netzer & Laor (1993) and Elitzur (2007) posit that material spanning both the dusty torus and (non-dusty) BLR forms a radially continuous component (Toroidal Obscuring Region/BLR-Obscuring Region, or "TOR/BOR"). Henceforth, in this paper, for simplicity, we refer to the "torus" as a synonym for "compact-scale (<10 pc) X-ray-obscuring gas," with the exact morphology and extent to be determined. Specifically, we focus on all X-ray-obscuring gas along the line of sight both inside and outside the dust sublimation radius, regardless of morphology.
Second, some components of circumnuclear gas may contain discrete clumps or filaments, and/or over-densities embedded in a continuous, lower-density medium, as opposed to having a one-component continuous, homogeneous structure; clumpy-torus models positing extended distributions of clouds (e.g., Elitzur & Shlosman 2006; Risaliti et al. 2007; Nenkova et al. 2008; Hönig et al. 2013) are consequently finding observational support, particularly from X-ray spectral studies. For example, Risaliti et al. (2002) studied variability of line of sight, neutral, X-ray-obscuring column density NH in a sample of Compton-thin and moderately Compton-thick type IIs. They detected almost ubiquitous (22/25 objects) variability in NH on timescales of months to several years, with typical variations up to factors of ∼1.5–3. Their analysis combined multiple single-epoch observations across a range of different X-ray missions. For a subsample of 11 sources, the authors could detect relatively rapid variations (≤1 yr), with obscuring columns typically varying by 1022–1023 cm−2. More recently, the community has used more continuous X-ray monitoring data (e.g., from Rossi X-ray Timing Explorer; RXTE) or single-epoch X-ray long-looks (with, e.g., XMM-Newton or Suzaku) to track ingress/egress of individual clouds, finding support for clouds existing at radii spanning both inside and outside the dust sublimation radius (Lamer et al. 2003; Puccetti et al. 2007; Risaliti et al. 2009, 2011; Maiolino et al. 2010; Sanfrutos et al. 2013). Markowitz et al. (2014; hereafter MKN14) provided the first X-ray-based statistical support for the clumpy-torus model of Nenkova et al. (2008) by studying the obscuration variability of a sample of 55 type Is and Compton-thin type IIs using long-term RXTE monitoring. This variability database yielded a total of 12 full-covering eclipse events across eight objects. The event durations spanned hours to >1 yr, with clouds' column densities typically (4–26) × 1022 cm−2, i.e., no full-covering Compton-thick eclipse events were observed. In seven objects, the clouds were inferred to be located at radial distances commensurate with the outer BLR or the inner dusty torus. MKN14 also provided the first X-ray-based probability estimates for witnessing eclipses in type I/II objects. Finally, infrared studies probing the dusty part of the obscurer also support clumpy-torus models, via spectral energy distribution modeling (Ramos Almeida et al. 2011, 2014), the coexistence of relatively hotter and cooler dust components in nearby AGNs (Jaffe et al. 2004; Raban et al. 2009), and the range of 9.7 μm Si emission/absorption features spanned by type I and II Seyferts (Nikutta et al. 2009).
Both the dusty and non-dusty components of the torus are believed to play an active role in SMBH accretion, and hence, understanding the structure of the torus is essential for understanding both disk/SMBH fueling and orientation-dependent unification schemes. However, there are additional complications that simple orientation-dependent unification cannot easily explain. There is likely a dependence of the torus covering factor on luminosity or λEdd ≡ LBol/LEdd; relatively stronger radiation fields from the nucleus can clear out more obscuring material (Ricci et al. 2017b). In addition, there is support for the BLR to disappear toward low values of AGN bolometric luminosity, forming the "true type 2" objects (Elitzur & Ho 2009; Bianchi et al. 2012b). One might therefore refer to the "torus" or "TOR/BOR" component, but it is likely the case that its morphology and/or spatial extent do not remain the same from one object to the next. We reiterate that in this paper, we refer to the "torus" just to indicate compact-scale circumnuclear gas, with the precise morphology and spatial extent still to be determined by the community (e.g., a TOR/BOR is just one possibility), the content (smooth, clumpy, or mixed) also to be determined, and with the assumption that even if it is present in all AGNs, its morphology and extent are not guaranteed to be the same universally.
Yet another major complication for unification schemes is potential optical extinction and X-ray obscuration originating at length scales much greater than the compact torus, at hundreds of parsecs to 1 kpc, and due to dusty structures or lanes associated with the host galaxy. Optically selected samples of Seyferts tend to yield a systematic dearth of type Is in relatively more edge-on systems (Maiolino & Rieke 1995; Lagos et al. 2011). Edge-on systems also tend to exhibit relatively stronger optical extinction (Driver et al. 2007; Shao et al. 2007). The expansive Hubble Space Telescope (HST) snapshot survey of over 250 nearby Seyfert and starburst galaxies performed by Malkan et al. (1998; hereafter MGT98) revealed an array of fine-scale dusty structures in galaxies' centers. They (and others such as Prieto et al. 2014) concluded that type II Seyferts are intrinsically more likely to be hosted in galaxies with nuclear dust structures crossing the line of sight, potentially alleviating the requirement for a compact torus to explain the extinction of BLR lines (a fundamental component of orientation-dependent unification schemes).
X-ray studies yield a similar picture: in some high-spatial resolution X-ray images of nearby AGNs, we can resolve where dust lanes directly obscure soft X-ray diffuse emission (e.g., NGC 7582 and Cen A: Bianchi et al. 2007; Kraft et al. 2008). Moreover, Guainazzi et al. (2001, 2005) have compared X-ray obscuring columns with Balmer decrements or nuclear dust morphology in samples of Compton-thin and Compton-thick Seyferts. Their results support the notion (put forth by, e.g., Matt 2000) that Compton-thin type IIs tend to reside preferentially in galaxies with dusty nuclear environments on scales of >∼0.1 kpc. However, Compton-thick obscuration does not seem highly affected by nuclear dust content and is likely due to a compact torus instead.7 Host-galaxy characteristics—namely the chance of having or not having a dusty filament along the line of sight to the nucleus—can therefore potentially impact both optical spectral type and whether or not a source is perpetually Compton-thin obscured. Searching for time variability in X-ray obscuration can potentially provide clues to distinguish between obscuration due to a compact torus versus that from host-galaxy structures. Therefore, the main goal of the present paper is to test this simplified model with X-ray monitoring data, wherein the location of the X-ray-obscuring gas can be discerned by the extent of the variability in the X-ray obscurer. A detection of variability on timescales of years or shorter would point to a clumpy structure very likely associated with the torus. A lack of variability on timescales of years and longer in a given object supports the notion that the dominant obscuring gas is more likely associated with host-galaxy dusty structures.
The present paper is motivated in part by MKN14's results on a subsample of eight type IIs monitored with RXTE: these objects' X-ray column densities remained constant over timescales from 0.6 to 8.4 yr. However, RXTE's limited bandpass (no coverage <2 keV) meant that sensitivity in ΔNH in these objects was limited, with limits on variability spanning (0.6–9) × 1022 cm−2. In contrast, XMM-Newton, Suzaku, and Chandra observations of type II Seyferts can provide comparably stronger sensitivity in ΔNH, courtesy of their soft X-ray coverage.
In this paper, we investigate the variability of the X-ray obscuration column density of a sample of perpetually X-ray-obscured type II AGNs in the local universe to address the question, "What is the origin of perpetual Compton-thin X-ray obscuration in optical type IIs?" The rest of this paper is organized as follows: We present the sample and data reduction in Section 2, the spectral analysis in Section 3, the results for X-ray obscuration and its variability in Section 4, and we discuss physical interpretations in Section 5. Section 6 contains our main conclusions.
2. Sample Selection, Observations, and Data Reduction
2.1. The Sample Selection and Properties
2.1.1. Sample Selection
The sample of Compton-thin type II (X-ray classification) sources was selected from the existing literature, with the constraint that each source must have at least two observations for a given instrument with a minimum time separation of two days (observations executed within two days of each other are almost always part of the same proposal/long-look). The X-ray spectra for the sources in the sample are obtained from XMM-Newton, Chandra, and Suzaku observatories that are in the HEASARC public archives as of 2017 July 1. Only the Seyfert subtypes 1.9–2 (as listed in NED), referred to as Compton-thin type II, are considered in this work. We obtained a final list of 20 sources (see Table 1 for details). We focus on optical type II Seyferts because they are more likely to be perpetually obscured in X-rays compared to type Is, and we reviewed the literature to ensure that each source in our sample is indeed perpetually X-ray obscured. Our sample is not intended to be a complete sample (for instance, very roughly 10% of type IIs have values of NH below 1021 cm−2, e.g., Bassani et al. 1999), but it is an exploratory sample for expanding our knowledge on variability or lack thereof in the X-ray obscurers of type IIs. We focus on relatively X-ray bright objects (average observed 2–10 keV fluxes brighter than typically a few ×10−12 erg cm−2 s−1 to ensure adequate signal-to-noise within each observation). We exclude Compton-thick-obscured AGNs, as their X-ray spectra are best studied with bandpasses extending above 10 keV, such as NuSTAR. However, we are clearly sensitive to potentially detecting any Compton-thin to -thick transitions (or vice versa), though as we note below, none were observed.
Table 1. Source Properties
| Source | R.A. | Decl. | Redshift | MBH | Referencea | Methodb | Optical | |
|---|---|---|---|---|---|---|---|---|
| (J2000) | (J2000) | log(MBH/M⊙) | × 1020 cm−2 | Classificationc | ||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) |
| 1. Cen A | 13h25m27 6 6 |
−43d01m09s | 0.0018 | C09 | stellar | 8.09 | RG | |
| 2. Cyg A | 19h59m28 3 3 |
+40d44m02s | 0.0561 | T03 | gas | 2.72 | RG | |
| 3. Fairall 49 | 18h36m58 3 3 |
−59d24m09s | 0.0200 | 6.3 | I04 | X var | 6.47 | Sy |
| 4. IRAS F00521–7054 | 00h53m56 1 1 |
−70d38m04s | 0.0689 | ⋯ | 5.26 | Sy2 | ||
| 5. IRAS F05189−2524 | 05h21m45s | −25d21m45s | 0.0426 | 8.6 | X17 | stellar | 1.66 | Sy |
| 6. MCG–5-23-16 | 09h46m48 4 4 |
−33d36m13s | 0.0081 | 7.31 ± 1.00 | P12 | X var | 8.70 | Sy |
| 7. Mkn 348 | 00h48m47 1 1 |
+31d57m25s | 0.0150 | 7.21 | WU02 | stellar | 5.79 | Sy |
| 8. NGC 526A | 01h23m54 4 4 |
−35d03m56s | 0.0199 | 8.02 | W09 | K lum. | 2.31 | 1.9 |
| 9. NGC 1052 | 02h41m04 8 8 |
−08d15m21s | 0.0050 | 8.19 | WU02 | stellar | 2.83 | LINER |
| 10. NGC 2110 | 05h52m11s | −07d27m22s | 0.0077 | 8.3 ± 0.2 | M07 | stellar | 1.66 | Sy |
| 11. NGC 2992 | 09h45m42 0 0 |
−14d19m35s | 0.0077 | 7.72 | WU02 | stellar | 4.87 | Sy |
| 12. NGC 4258 | 12h18m57 5 5 |
+47d18m14s | 0.0015 | 7.59 ± 0.01 | H99 | maser | 1.60 | Sy2 |
| 13. NGC 4507 | 12h35m36 6 6 |
−39d54m33s | 0.0118 | 8.39 | W09 | K lum. | 7.04 | Sy |
| 14. NGC 5252 | 13h38m15 9 9 |
+04d32m33s | 0.0229 | 8.04 | WU02 | stellar | 2.14 | Sy2 |
| 15. NGC 5506 | 14h13m14 9 9 |
−03d12m27s | 0.0061 | 8 ± 1 | O99 | stellar | 4.08 | Sy |
| 16. NGC 6251 | 16h32m32s | +82d32m16s | 0.0247 | FF99 | gas | 5.57 | Sy2 | |
| 17. NGC 6300 | 17h16m59 5 5 |
−62d49m14s | 0.0037 | 6.7 | V10 | K lum. | 7.79 | Sy2 |
| 18. NGC 7172 | 22h02m01 9 9 |
−31d52m11s | 0.0087 | 8.31 | W09 | K lum. | 1.95 | Sy2 |
| 19. NGC 7314 | 22h35m46 2 2 |
−26d03m02s | 0.0048 | 7.84 | W09 | K lum. | 1.50 | Sy |
| 20. NGC 7582 | 23h18m23 5 5 |
−42d22m14s | 0.0053 | 8.31 | W09 | K lum. | 1.33 | Sy |
Notes. The Galactic column densities (column 8) are obtained from the LAB survey of Kalberla et al. (2005).
aReferences for MBH: C09 = Cappellari et al. (2009), FF99 = Ferrarese & Ford (1999), H99 = Herrnstein et al. (1999), I04 = Iwasawa et al. (2004), M07 = Moran et al. (2007), O99 = Oliva et al. (1999), P12 = Ponti et al. (2012), T03 = Tadhunter et al. (2003), V10 = Vasudevan et al. (2010), W09 = Winter et al. (2009), WU02 = Woo & Urry (2002), X17 = Xu et al. (2017). bMethods for black hole mass estimate: gas = gas dynamics; K lum. = estimated from K-band bulge stellar luminosity; maser = water masers; stellar = stellar velocity dispersion; X var. = from short-term X-ray variability amplitude. cOptical classification: to the left of the arrow is the optical classification from NED, while to the right are either: 1H, denoting that the source contains a type 1 hidden BLR observed in polarized optical emission, or 1I, denoting a type 1 hidden BLR identified via IR emission lines.Download table as: ASCIITypeset image
Table 2. List of X-Ray Observations of the Sources in the Sample
| Number | Source | Telescope | Observation | Observation | Exposure | Short Obsid |
|---|---|---|---|---|---|---|
| ID | Date | |||||
| 1. | CenA | XMM-Newton | 0093650201 | 2001 Feb 2 | 24 | X-1 |
| XMM-Newton | 0093650301 | 2002 Feb 6 | 15 | X-2 | ||
| XMM-Newton | 0724060501 | 2013 Jul 12 | 12 | X-3 | ||
| XMM-Newton | 0724060601 | 2013 Sep 7 | 12 | X-4 | ||
| XMM-Newton | 0724060701 | 2014 Jan 6 | 27 | X-5 | ||
| XMM-Newton | 0724060801 | 2014 Feb 9 | 23 | X-6 | ||
| Suzaku | 100005010 | 2005 Sep 19 | 65 | S-1 | ||
| Suzaku | 704018010 | 2009 Jul 20 | 62 | S-2 | ||
| Suzaku | 704018020 | 2009 Sep 5 | 51 | S-3 | ||
| Suzaku | 704018030 | 2009 Sep 14 | 56 | S-4 | ||
| Suzaku | 708036010 | 2013 Sep 15 | 11 | S-5 | ||
| Suzaku | 708036020 | 2014 Jan 6 | 7 | S-6 | ||
| 2. | Cyg Aa | XMM-Newton | 0302800101 | 2005 Oct 14 | 23 | X-1 |
| Suzaku | 803050010 | 2008 Nov 15 | 45 | S-1 | ||
| 3. | Fairall 49 | Chandra HETG | 3148 | 2002 Mar 20 | 57 | CH-1 |
| Chandra HETG | 3452 | 2002 Mar 23 | 51 | CH-2 | ||
| XMM-Newton | 0022940101 | 2001 Mar 5 | 75 | X-1 | ||
| XMM-Newton | 0724820101 | 2013 Sep 4 | 110 | X-2 | ||
| XMM-Newton | 0724820201 | 2013 Oct 15 | 107 | X-3 | ||
| Suzaku | 702118010 | 2007 Oct 26 | 78 | S-1 | ||
| 4. | IRAS F00521–7054 | XMM-Newton | 0301150101 | 2006 Mar 22 | 17 | X-1 |
| XMM-Newton | 0301151601 | 2006 Apr 22 | 14 | X-2 | ||
| Suzaku | 708005010 | 2013 May 19 | 103 | S-1 | ||
| 5. | IRAS F05189–2524 | Chandra ACIS-S | 2034 | 2001 Oct 30 | 20 | CA-1 |
| Chandra ACIS-S | 3432 | 2002 Jan 30 | 15 | CA-2 | ||
| XMM-Newton | 0085640101 | 2001 Mar 17 | 12 | X-1 | ||
| XMM-Newton | 0722610101 | 2013 Oct 2 | 38 | X-2 | ||
| Suzaku | 701097010 | 2006 Apr 10 | 78 | S-1 | ||
| 6. | MCG–5–23–16 | Chandra HETG | 2121 | 2000 Nov 14 | 76 | CH-1 |
| Chandra HETG | 6187 | 2005 Dec 8 | 30 | CH-2 | ||
| Chandra HETG | 7240 | 2005 Dec 9 | 20 | CH-3 | ||
| XMM-Newton | 0112830401 | 2001 Dec 1 | 25 | X-1 | ||
| XMM-Newton | 0302850201 | 2005 Dec 8 | 132 | X-2 | ||
| XMM-Newton | 0727960101 | 2013 Jun 24 | 138 | X-3 | ||
| XMM-Newton | 0727960201 | 2013 Jun 26 | 139 | X-4 | ||
| Suzaku | 700002010 | 2005 Dec 7 | 96 | S-1 | ||
| Suzaku | 708021010 | 2013 Jun 1 | 160 | S-2 | ||
| Suzaku | 708021020 | 2013 Jun 5 | 139 | S-3 | ||
| 7. | Mkn 348 | Chandra ACIS-S | 12809 | 2010 Oct 13 | 95 | CA-1 |
| XMM-Newton | 0067540201 | 2002 Jul 18 | 49 | X-1 | ||
| XMM-Newton | 0701180101 | 2013 Jan 4 | 13 | X-2 | ||
| Suzaku | 703029010 | 2008 Jun 28 | 87 | S-1 | ||
| 8. | NGC 526A | Chandra ACIS-S | 342 | 2000 Feb 7 | 9 | CA-1 |
| Chandra ACIS-S | 442 | 2000 Apr 23 | 5 | CA-2 | ||
| Chandra HETG | 4437 | 2003 Jun 21 | 29 | CH-1 | ||
| Chandra HETG | 4376 | 2003 Jun 21 | 29 | CH-2 | ||
| XMM-Newton | 0109130201 | 2002 Jun 30 | 12 | X-1 | ||
| XMM-Newton | 0150940101 | 2003 Jun 21 | 48 | X-2 | ||
| XMM-Newton | 0721730301 | 2013 Dec 21 | 56 | X-3 | ||
| XMM-Newton | 0721730401 | 2013 Dec 22 | 46 | X-4 | ||
| Suzaku | 705044010 | 2011 Jan 17 | 73 | S-1 | ||
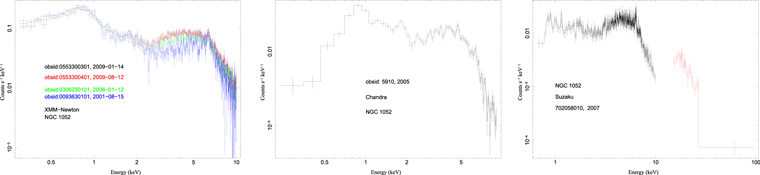
| 9. | NGC 1052 | Chandra ACIS-S | 5910 | 2005 Sep 18 | 60 | CA-1 |
| XMM-Newton | 0093630101 | 2001 Sep 15 | 16 | X-1 | ||
| XMM-Newton | 0306230101 | 2006 Jan 12 | 55 | X-2 | ||
| XMM-Newton | 0553300301 | 2009 Jan 14 | 52 | X-3 | ||
| XMM-Newton | 0553300401 | 2009 Sep 12 | 59 | X-4 | ||
| Suzaku | 702058010 | 2007 Jul 16 | 101 | S-1 | ||
| 10. | NGC 2110 | Chandra ACIS-S | 883 | 2000 Apr 22 | 50 | CA-1 |
| Chandra HETG | 3143 | 2001 Dec 19 | 34 | CH-1 | ||
| Chandra HETG | 3418 | 2001 Dec 20 | 76 | CH-2 | ||
| Chandra HETG | 3417 | 2001 Dec 22 | 33 | CH-3 | ||
| Chandra HETG | 4377 | 2003 Mar 5 | 96 | CH-4 | ||
| XMM-Newton | 0145670101 | 2003 Mar 5 | 60 | X-1 | ||
| Suzaku | 100024010 | 2005 Sep 16 | 102 | S-1 | ||
| Suzaku | 707034010 | 2012 Sep 31 | 103 | S-2 | ||
| Suzaku | 709011010 | 2015 Mar 20 | 46 | S-3 | ||
| 11. | NGC 2992 | Chandra HETG | 11858 | 2010 Feb 9 | 96 | CH-1 |
| XMM-Newton | 0147920301 | 2003 May 19 | 29 | X-1 | ||
| XMM-Newton | 0654910301 | 2010 May 6 | 59 | X-2 | ||
| XMM-Newton | 0654910401 | 2010 May 16 | 61 | X-3 | ||
| XMM-Newton | 0654910501 | 2010 May 26 | 56 | X-4 | ||
| XMM-Newton | 0654910601 | 2010 Jun 5 | 56 | X-5 | ||
| XMM-Newton | 0654910701 | 2010 Nov 8 | 56 | X-6 | ||
| XMM-Newton | 0654910801 | 2010 Nov 18 | 56 | X-7 | ||
| XMM-Newton | 0654910901 | 2010 Nov 28 | 56 | X-8 | ||
| XMM-Newton | 0654911001 | 2010 Dec 8 | 61 | X-9 | ||
| XMM-Newton | 0701780101 | 2013 May 11 | 13 | X-10 | ||
| Suzaku | 700005030 | 2005 Dec 13 | 47 | S-1 | ||
| Suzaku | 700005010 | 2005 Nov 6 | 38 | S-2 | ||
| Suzaku | 700005020 | 2005 Nov 19 | 37 | S-3 | ||
| 12. | NGC 4258 | Chandra ACIS-S | 350 | 2000 Apr 17 | 14 | CA-1 |
| Chandra ACIS-S | 1618 | 2001 May 28 | 21 | CA-2 | ||
| Chandra ACIS-S | 2340 | 2001 May 29 | 8 | CA-3 | ||
| Chandra HETG | 7879 | 2007 Oct 8 | 153 | CH-1 | ||
| Chandra HETG | 7880 | 2007 Oct 12 | 60 | CH-2 | ||
| Chandra HETG | 9750 | 2007 Oct 14 | 107 | CH-3 | ||
| XMM-Newton | 0110920101 | 2000 Dec 8 | 23 | X-1 | ||
| XMM-Newton | 0059140101 | 2001 May 6 | 13 | X-2 | ||
| XMM-Newton | 0059140201 | 2001 Jun 17 | 13 | X-3 | ||
| XMM-Newton | 0059140401 | 2001 Dec 17 | 15 | X-4 | ||
| XMM-Newton | 0059140901 | 2002 May 22 | 17 | X-5 | ||
| XMM-Newton | 0203270201 | 2004 Jun 1 | 49 | X-6 | ||
| XMM-Newton | 0400560301 | 2006 Nov 17 | 65 | X-7 | ||
| Suzaku | 701095010 | 2006 Jun 10 | 100 | S-1 | ||
| Suzaku | 705051010 | 2010 Nov 11 | 104 | S-2 | ||
| 13. | NGC 4507 | Chandra HETG | 2150 | 2001 Mar 15 | 140 | CH-1 |
| Chandra ACIS-S | 12292 | 2010 Dec 2 | 44 | CA-1 | ||
| XMM-Newton | 0006220201 | 2001 Jan 4 | 46 | X-1 | ||
| XMM-Newton | 0653870201 | 2010 Jun 24 | 20 | X-2 | ||
| XMM-Newton | 0653870301 | 2010 Jul 3 | 17 | X-3 | ||
| XMM-Newton | 0653870401 | 2010 Jul 13 | 17 | X-4 | ||
| XMM-Newton | 0653870501 | 2010 Jul 23 | 17 | X-5 | ||
| XMM-Newton | 0653870601 | 2010 Sep 3 | 22 | X-6 | ||
| Suzaku | 702048010 | 2007 Dec 20 | 104 | S-1 | ||
| 14. | NGC 5252 | Chandra ACIS-S | 4054 | 2003 Sep 11 | 63 | CA-1 |
| Chandra ACIS-S | 15618 | 2013 Mar 4 | 42 | CA-2 | ||
| Chandra ACIS-S | 15022 | 2013 Mar 7 | 71 | CA-3 | ||
| Chandra ACIS-S | 15621 | 2013 May 9 | 65 | CA-4 | ||
| XMM-Newton | 0152940101 | 2003 Jul 18 | 67 | X-1 | ||
| Suzaku | 707028010 | 2012 Dec 26 | 50 | S-1 | ||
| 15. | NGC 5506 | Chandra HETG | 1598 | 2000 Dec 31 | 90 | CH-1 |
| XMM-Newton | 0013140101 | 2001 Feb 2 | 20 | X-1 | ||
| XMM-Newton | 0013140201 | 2002 Jan 9 | 14 | X-2 | ||
| XMM-Newton | 0201830201 | 2004 Jul 11 | 22 | X-3 | ||
| XMM-Newton | 0201830301 | 2004 Jul 14 | 20 | X-4 | ||
| XMM-Newton | 0201830401 | 2004 Jul 22 | 22 | X-5 | ||
| XMM-Newton | 0201830501 | 2004 Sep 7 | 20 | X-6 | ||
| XMM-Newton | 0554170201 | 2008 Jul 27 | 91 | X-7 | ||
| XMM-Newton | 0554170101 | 2009 Jan 2 | 89 | X-8 | ||
| XMM-Newton | 0761220101 | 2015 Jul 7 | 132 | X-9 | ||
| Suzaku | 701030020 | 2016 May 27 | 53 | S-1 | ||
| Suzaku | 701030010 | 2016 May 27 | 48 | S-2 | ||
| Suzaku | 701030030 | 2016 May 28 | 57 | S-3 | ||
| 16. | NGC 6251 | Chandra ACIS-I | 847 | 2000 Sep 11 | 37 | CA-1 |
| Chandra ACIS-S | 4130 | 2003 Nov 11 | 49 | CA-2 | ||
| XMM-Newton | 0056340201 | 2002 Mar 26 | 50 | X-1 | ||
| Suzaku | 705039010 | 2010 Dec 2 | 87 | S-1 | ||
| Suzaku | 806015010 | 2011 Nov 20 | 100 | S-2 | ||
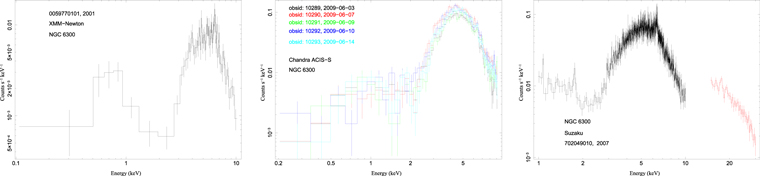
| 17. | NGC 6300 | Chandra ACIS-S | 10289 | 2009 Jun 3 | 10 | CA-1 |
| Chandra ACIS-S | 10290 | 2009 Jun 7 | 10 | CA-2 | ||
| Chandra ACIS-S | 10291 | 2009 Jun 9 | 10 | CA-3 | ||
| Chandra ACIS-S | 10292 | 2009 Jun 10 | 10 | CA-4 | ||
| Chandra ACIS-S | 10293 | 2009 Jun 14 | 10 | CA-5 | ||
| XMM-Newton | 0059770101 | 2001 Mar 2 | 47 | X-1 | ||
| Suzaku | 702049010 | 2007 Oct 17 | 83 | S-1 | ||
| 18. | NGC 7172 | Chandra ACIS-I | 905 | 2000 Jul 2 | 50 | CA-1 |
| XMM-Newton | 0147920601 | 2002 Nov 18 | 17 | X-1 | ||
| XMM-Newton | 0202860101 | 2004 Nov 11 | 59 | X-2 | ||
| XMM-Newton | 0414580101 | 2007 Apr 24 | 58 | X-3 | ||
| Suzaku | 703030010 | 2008 May 25 | 82 | S-1 | ||
| 19. | NGC 7314 | Chandra HETG | 3016 | 2002 Jul 19 | 29 | CH-1 |
| Chandra HETG | 3719 | 2002 Jul 20 | 68 | CH-2 | ||
| Chandra ACIS-S | 6976 | 2006 Sep 10 | 25 | CA-1 | ||
| Chandra ACIS-S | 7404 | 2006 Sep 15 | 15 | CA-2 | ||
| XMM-Newton | 0111790101 | 2001 May 2 | 45 | X-1 | ||
| XMM-Newton | 0311190101 | 2006 May 3 | 84 | X-2 | ||
| XMM-Newton | 0725200101 | 2013 May 17 | 140 | X-3 | ||
| XMM-Newton | 0725200301 | 2013 Nov 28 | 132 | X-4 | ||
| XMM-Newton | 0790650101 | 2016 May 14 | 65 | X-5 | ||
| Suzaku | 702015010 | 2007 Apr 25 | 109 | S-1 | ||
| Suzaku | 806013010 | 2011 Nov 13 | 101 | S-2 | ||
| 20. | NGC 7582 | Chandra ACIS-S | 436 | 2000 Oct 14 | 14 | CA-1 |
| Chandra ACIS-S | 2319 | 2000 Oct 15 | 6 | CA-2 | ||
| XMM-Newton | 0112310201 | 2001 May 25 | 23 | X-1 | ||
| XMM-Newton | 0204610101 | 2005 Apr 29 | 102 | X-2 | ||
| XMM-Newton | 0405380701 | 2007 Apr 30 | 45 | X-3 | ||
| XMM-Newton | 0782720301 | 2016 Apr 28 | 101 | X-4 | ||
| Suzaku | 702052010 | 2007 May 1 | 24 | S-1 | ||
| Suzaku | 702052020 | 2007 May 28 | 29 | S-2 | ||
| Suzaku | 702052040 | 2007 Nov 16 | 32 | S-3 | ||
| Suzaku | 702052030 | 2007 Nov 9 | 29 | S-4 | ||
Note.
aCyg A Chandra observations and the corresponding best-fit parameters are listed in Table B1.2.1.2. Activity Properties
Optical spectral classifications are listed in Table 1. Some of the sources are not Seyfert galaxies, such as Cen A or Cyg A, which host radio jets, or NGC 1052, which is an X-ray-obscured LINER exhibiting broad polarized lines. We note as a caveat that even if the torus exists in all objects, its morphology and spatial extent (scaled relative to MBH) may very well likely differ between different activity classes, e.g., radio-loud versus radio-quiet objects; a detailed discussion of the impact of the presence/lack of a jet on torus morphology is beyond the scope of the current paper. Ten sources have been confirmed to harbor hidden BLRs, five using scattered polarized emission (denoted by "1H" in Table 1) in which case a compact torus is likely to exist along the line of sight. The other five (denoted by "1I") have detections of broad recombination lines in the IR (e.g., Nagar et al. 2002); on that basis alone, it is not clear where the absorbing gas lies or how much of the total observed column is due to the host galaxy versus any putative torus; a potential observation of variability in NH could confirm the existence of the compact torus along the line of sight in such cases.
2.1.3. Host-galaxy Properties of the Sample
The objects in our sample are known to span a range of host-galaxy properties. The majority of our sample has been studied in the snapshot survey by Malkan et al. (1998): eight have dust lanes crossing the line of sight to the nucleus or just offset from it; four have filamentary/wispy or irregular dusty structures. Sixteen of our objects are hosted in spirals, with semimajor/minor axis ratios (as listed on NED) indicating disk inclinations spanning roughly 30°–75° from the plane of the sky. The other four are hosted in ellipticals (Cen A, Cyg A, NGC 1052, and NGC 6251).
2.2. Observations and Data Reduction
To effectively detect any Compton-thin variable obscuration in the X-rays, the best instruments to use are the EPIC cameras aboard XMM-Newton, the XIS detectors aboard Suzaku, and the ACIS detectors aboard Chandra, as they each provide a broadband spectral view in the energy range ∼0.5–10 keV, crucial for tracking the neutral absorption rollover. Table 2 lists the observations of the sources from these telescopes as on 2017 July. We describe below the methods employed to reprocess and clean the X-ray spectral data obtained from these telescopes.
2.2.1. XMM-Newton
The EPIC-pn data from XMM-Newton were reduced using the scientific analysis system (SAS) software (version 15) with the task epchain and using the latest calibration database available at the time we carried out the data reduction. We used EPIC-pn data because of its higher signal-to-noise ratio (S/N) as compared to MOS. We filtered the EPIC-pn data for particle background counts using a rate cutoff of <1 ct s−1 for photons >10 keV, and created time-averaged source and background spectra, as well as the response matrix function and auxiliary response function (ARF) for each observation using the xmmselect command in SAS. The source regions were selected with a circle radius of 40'' centered on the centroid of the source. The background regions were selected with a circle of 40'' located on the same CCD, but located a few arcminutes away from the source and avoiding X-ray-emitting point sources. Spectra were accumulated using pattern 0–4. We found that the sources NGC 4258 and Cyg A are extended in the EPIC-pn CCD image, possibly due to the resolved, diffuse stellar emission in the former, and due to diffuse X-ray emission from intercluster gas in the latter.
We checked for possible pileup in the sources using the command epatplot in SAS, and found that the spectra of the source Cen A are piled up. For Cen A we thus used an annular extraction region for the source, with an inner radius of 20'' and outer radius 40'' to minimize pileup. We did not detect significant pileup in the EPIC-pn spectra of the other sources.
2.2.2. Chandra
We considered Advanced CCD Imaging Spectrometer (ACIS-I and ACIS-S) data as well as zeroth-order High-Energy Transmission Grating Spectrometer (HETGS) data. All Chandra data were reprocessed using the command chandra_repro in the CIAO software (version 4.7.1) and using the latest calibration database. Source regions were selected using a circle of radius 4 0. The background regions were selected using a circle of radius 4
0. The background regions were selected using a circle of radius 4 0 on the same CCD as the source, but away from the source. We detected pileup (ranging from severe to mild) in the ACIS CCD spectra for the sources IRAS F05189−2524, NGC 1052, NGC 5252, NGC 5506, NGC 6251, NGC 6300, NGC 7172, NGC 7582, Mkn 348, NGC 4507, and MCG−5-23-16. Excluding a central circular region from the source image, as is typically done to exclude piled up data in XMM-Newton EPIC spectra, may lead to issues with the ARF in the Chandra spectra, and so that method was avoided. We instead use the pileup kernel in the spectral fitting codes to model the pileup. In those cases where the pileup is too severe to be modeled by such a kernel (such as in Cen A), we excluded those observations from our study.
0 on the same CCD as the source, but away from the source. We detected pileup (ranging from severe to mild) in the ACIS CCD spectra for the sources IRAS F05189−2524, NGC 1052, NGC 5252, NGC 5506, NGC 6251, NGC 6300, NGC 7172, NGC 7582, Mkn 348, NGC 4507, and MCG−5-23-16. Excluding a central circular region from the source image, as is typically done to exclude piled up data in XMM-Newton EPIC spectra, may lead to issues with the ARF in the Chandra spectra, and so that method was avoided. We instead use the pileup kernel in the spectral fitting codes to model the pileup. In those cases where the pileup is too severe to be modeled by such a kernel (such as in Cen A), we excluded those observations from our study.
2.2.3. Suzaku
The Suzaku observations were performed using the X-ray Imaging Spectrometer (XIS; Koyama et al. 2007) and Hard X-ray Detector (HXD; Takahashi et al. 2007). The XIS observations were obtained in both the 3 × 3 and 5 × 5 data modes. The aepipeline tool was used to reprocess and clean the unfiltered event files and to create the cleaned event files. In all observations, for both the XIS0 and XIS3 (front-illuminated CCD) and for XIS1 (back-illuminated CCD), we extracted the source spectra for each observation from the filtered event lists using a 120'' circular region centered at the source position. We also extracted the corresponding background spectral data using four circular regions of 120'' radii, a few arcminutes away from the source region and avoiding X-ray-emitting point sources. There are only a few cases of pileup in the Suzaku observations; we excluded those centrally located pixels for which pileup exceeded a threshold of 4%. During spectral fits, we did not co-add the front-illuminated XIS spectra, instead fitting them separately.
3. Spectral Analysis
We used Interactive Spectral Interpretation System (ISIS) software (Houck & Denicola 2000) for spectral fitting carried out in this work. The XMM-Newton spectra were grouped by a minimum of 20 counts per channel and a maximum of five resolution elements using the command Specgroup in SAS. The Chandra and Suzaku spectra were grouped by a minimum of 20 counts per channel in ISIS. As described below, we have carried out iterative steps to systematically fit all of the X-ray spectra and account for both soft- and hard-band components while obtaining precise estimates of the intrinsic neutral absorption column densities. In this section we first describe the models we used to fit the spectra and then elucidate stepwise the fitting procedure that we employed.
We started from a "baseline" model that follows (using ISIS notation):
tbabs(1) × (apec(1) + apec(2) + powerlaw(1) + ztbabs(1) × (powerlaw(2) + pexmon(1) + zgauss)).
If an additional partial-covering (PC) absorption component is required by the data, then our model became
tbabs(1) × (apec(1) + apec(2) + powerlaw(1) + ztbabs(1) × zpcfabs(1) × (powerlaw(2) + pexmon(1) + zgauss)).
The tbabs and ztbabs components model the Galactic and intrinsic fully covering neutral absorption column, respectively. zpcfabs models the PC absorption component, if significantly detected. The primary, hard power law (powerlaw(2)) models the Compton-upscattered emission from a hot optically thin corona in the central AGN. In addition we have tested for the possible presence of warm ionized absorbers (Blustin et al. 2005; Laha et al. 2014) using the warm abs model (Kallman & Bautista 2001) in ISIS, but did not detect any statistically significant warm absorption in any of the sources in the sample. The best-fit models and details of the analysis for every source have been reported in Appendix A.
The soft band may contain emission from thermal plasma, which could be due to star formation (e.g., Turner et al. 1997). Continuum emission due to scattering of the primary X-ray emission in Compton-thin circumnuclear gas out to ∼1 kpc (e.g., Cappi et al. 2006; Ueda et al. 2007; Awaki et al. 2008; Ricci et al. 2017a) is also expected. There also likely exist signatures of gas being photoionized and photoexcited, namely soft emission lines and radiative recombination continuum features, likely originating in the AGN-illuminated regions of the NLR (e.g., Bianchi et al. 2006; Guainazzi & Bianchi 2007). Indeed, 12 of our sources are contained in the CIELO-AGN sample of Guainazzi & Bianchi (2007); however, such features are typically identified by gratings observations and will be blurred at CCD resolution, so we do not explicitly model them here.
We use one (or two, if necessary) apec component(s) to model any thermal emission. powerlaw(1) denotes the secondary (soft) power law to model the scattered emission, with the expectation that the normalization of the soft power law will be of the order of ≲1% that of the hard power law, approximately. We first attempt to fit with the value of soft photon index ΓSX tied to that of the primary (hard) X-ray power law but only if a significant improvement in fit results from thawing ΓSX, then we do so. As mentioned earlier, the soft-band power law is expected to model scattered nuclear emission, and in the ideal case, the photon indices of the soft and hard power laws should match. However, there can be numerous potential reasons for a mismatch, including that the current value of the hard X-ray power-law photon index may be different from the long-term averaged photon index scattered off extended diffuse gas, or there may be blending with emission from other components, such as unresolved point sources (ULXs).
Although the baseline model gives a reasonable fit in most cases, it is definitely not the case that a common baseline model can be applied equally to all objects/observations. For a given instrument (e.g., XMM-Newton), some objects' spectra require only one apec component; others require two. Relativistically broad Fe K emission lines were detected only in two sources, MCG–5-23-16 and Fairall 49, and for simplicity we have used diskline to model them (see Appendix A for details of the fits).
In addition, for a given object, different instruments have different apertures, different responses/effective areas, etc., so some components (apec, narrow Fe K line) detected in one instrument for a given object are not detected in other instruments. As one example, the Chandra observations for the sources NGC 2992 and NGC 7314 did not require any apec components, but the XMM-Newton and Suzaku observations for the same sources required them. The goodness of fit upon adding a new model component has been tested both using a Δχ2 and F-test, requiring a >5σ improvement in statistics to consider the new model component as required in the fit.
Ideally, we would have liked to perform, for each object/instrument combination, joint fitting in which we can have certain parameters freed but tied across all spectral fits (power-law photon indices, apec temperatures, etc.), but for practical reasons that could not be done due to the huge computational power required (especially for those objects with multiple Suzaku data sets). We also note that not all objects in the sample adhere to a common "baseline" model, and not all objects follow the same spectral variability behavior in soft and hard X-ray bands. For example, given that soft-band emission likely originates in diffuse gas, we do not expect it to exhibit variability on timescales of ∼years and shorter. However, in several object/instrument cases, we did find strong evidence for soft-band variability; keeping soft-band parameters frozen resulted in poor fits in these cases: the XMM-Newton spectra of MCG–5-23-16, NGC 526a, NGC 2992, and NGC 7314, and the Chandra spectra of NGC 526a (see the spectral overplots in Appendix C, Figures C1–C20). For example, in the first XMM-Newton observation of NGC 2992 (denoted as X-1), the entire continuum (except for the narrow Fe line flux, which is ∼constant) is higher than for all subsequent XMM-Newton observations. There could be several possible reasons: a leaky, patchy absorber that obscures the AGN and that has changed its covering fraction, a sudden spurt in stellar emission, or flaring emission from a transient point source such as a ULX. A detailed study of the causes behind each of these soft-band spectral variations would require high-spatial resolution to separate out the AGN, stellar emission, other point sources, etc., and is therefore beyond the scope of this paper. At any rate, consequently, we adopt a two-step system: we first fit each observation separately, then for each object/instrument combination, we adopt the average values of all soft-band component parameters and freeze them during a second round of fits. While adopting this process, we note as caveats that (1) different spectra can have different statistical weights and (2) freezing some parameters may shrink some error bars on fitted values.
There is also the issue of the Compton reflection hump (hereafter CRH). The CRH is detected and mostly well constrained in individual Suzaku observations due to its broadband 0.3–40 keV coverage, but remains unconstrained for the XMM-Newton or Chandra observations—meaning that CRH reflection strength and hard X-ray power-law parameters (which can in turn impact modeling of NH) cannot be unambiguously and independently constrained in 80% of the observations involved in this work. We thus started our analysis for each object with Suzaku spectra and then applied that model to XMM-Newton and Chandra. We note here that for all 20 sources in our sample, we have at least one Suzaku observation, and hence we could use this approach for all of the sources.
We use pexmon to model the CRH and narrow Fe K emission line simultaneously. However, we need to understand how the CRH has varied with time for each object, in order to know which parameter values of the pexmon component to use for cases with multiple Suzaku observations. For simplicity, we consider two scenarios: (1) the CRH remains constant in absolute normalization with time, irrespective of the hard X-ray power-law Γ and flux, and (2) the CRH responds instantaneously to the hard X-ray power-law variations (relative normalization constant). There are eight sources for which there are multiple Suzaku observations and 12 sources with only one. For the 12 sources with only one Suzaku observation, we have used the best-fit pexmon values from that observation and assumed it to remain constant in absolute normalization in the XMM-Newton and Chandra observations, as there is no way to rule out or vindicate any of the above scenarios with the XMM-Newton or Chandra data. For the seven sources with multiple Suzaku observations (excluding Cen A, which lacks any CRH detected to date), we investigated potential CRH variability. After obtaining a broadband best fit to each Suzaku observation, we calculated the absolute normalization of the pexmon component (simply the product of the model normalization and the reflection fraction R). For the sources MCG–5-23-16, NGC 4258, NGC 7314, and NGC 7582, the absolute normalization is consistent with being constant in time. This is consistent with the notion that at least in these objects, the CRH arises from a distant medium and does not vary over the timescales of our observations. For NGC 2110, the absolute normalization tracks the hard X-ray power-law normalization, suggesting that CRH flux tracks that of the coronal power law closely. For the sources NGC 2992 and NGC 5506, insufficient S/N or lack of significant variability in the hard X-ray power law did not allow us to conclude the nature of CRH variability. Given the fact that a majority of these sources with multiple Suzaku observations are consistent with a constant-absolute normalization CRH, and since we lack information on the rest of the 12 objects, for simplicity and uniformity, we assumed a constant-absolute normalization CRH for all of the sources in our sample. In other words, we used the pexmon parameter values from the best fit to S-1 (for a given object) and held those frozen when fitting the XMM-Newton and Chandra data sets for each of these objects.
In addition, we note that we did not detect any significant variability in the narrow Fe Kα emission line (at ∼6.4 keV) flux in any of the objects. If we assume that the line arises from the same reprocessing medium as that responsible for the CRH, as is implicitly assumed when using pexmon, then this further supports the notion that reflected emission (CRH + Fe K line) is constant with time. We note however, that for the high-S/N XMM-Newton observations of MCG–5-23-16, we found that the narrow Fe K emission line and the CRH could not be simultaneously modeled by pexmon, implying, e.g., that they arise from different reprocessing media, or there is a non-solar Fe abundance. In fact, we had to thaw the Fe abundance relative to solar, ZFe, in pexmon to sub-solar values to obtain good fits: ZFe typically falls to ∼0.19 and χ2 drops by at least 200 in the X-2, X-3, and X-4 spectra.
The "second round" of fits are our best fits, listed in Tables 3 and 4. The error quoted on each parameter is the 90% confidence interval for one free parameter. Note that we have only reported the errors for the soft X-ray parameters in Table 4 when they are kept free in the second round of fits, that is, when the fit requires a different value of these parameters than those of the average values.
Table 3. Best-fit Parameters Obtained from X-Ray Spectral Fits
| Source | Obsid (year)a | fpc | ΓHard | PL-normb | 2–10 keV Fluxc | |||
|---|---|---|---|---|---|---|---|---|
| (1022 cm−2) | (1022 cm−2) | 10−11 erg cm−2 s−1 | ||||||
| 1. Cen A | X-1(01) | 11.9 ± 0.4 | ⋯ | ⋯ | 2.17 ± 0.07 | 0.167 ± 0.021 | 1612/1.14 | 33.10 |
| X-2(02) | 12.9 ± 0.6 | ⋯ | ⋯ | 2.18 ± 0.09 | 0.177 ± 0.032 | 865/0.95 | 32.31 | |
| X-3(13) | 10.9 ± 0.3 | ⋯ | ⋯ | 1.96 ± 0.05 | 0.292 ± 0.031 | 1402/1.05 | 83.12 | |
| X-4(13) | 11.1 ± 0.3 | ⋯ | ⋯ | 2.04 ± 0.05 | 0.309 ± 0.033 | 1319/0.998 | 70.71 | |
| X-5(14) | 12.0 ± 0.3 | ⋯ | ⋯ | 1.98 ± 0.05 | 0.125 ± 0.330 | 1418/1.003 | 55.31 | |
| X-6(14) | 10.8 ± 0.8 | 0.51 ± 0.08 | 2.44 ± 0.09 | 0.424 ± 0.156 | 1514/1.023 | 37.11 | ||
| S-1(05) | 10.76 ± 0.15 | 26 ± 8 | 0.157 ± 0.022 | 1.83 ± 0.02 | 0.132 ± 0.007 | 10388/1.05 | 63.11 | |
| S-2(09) | 10.86 ± 0.07 | ⋯ | ⋯ | 1.82 ± 0.01 | 0.169 ± 0.003 | 8226/1.09 | 58.81 | |
| S-3(09) | 10.93 ± 0.07 | ⋯ | ⋯ | 1.80 ± 0.01 | 0.175 ± 0.004 | 7851/1.04 | 70.77 | |
| S-4(09) | 11.03 ± 0.08 | ⋯ | ⋯ | 1.79 ± 0.01 | 0.149 ± 0.004 | 7775/1.06 | 63.12 | |
| S-5(13) | 9.98 ± 0.14 | ⋯ | ⋯ | 1.79 ± 0.02 | 0.143 ± 0.006 | 5305/0.99 | 51.22 | |
| S-6(14) | 10.59 ± 0.27 | ⋯ | ⋯ | 1.79 ± 0.04 | 0.095 ± 0.008 | 3256/0.98 | 72.42 | |
| 2. Cyg Ad | X-1(05) | 21.35 ± 1.12 | ⋯ | ⋯ | 1.7* | 0.0069 ± 0.0003 | 297/1.18 | 3.01 |
| S-1(08) | 22.52 ± 2.75 | ⋯ | ⋯ | 1.92 ± 0.02 | 0.0106 ± 0.0001 | 5936/1.05 | 5.91 | |
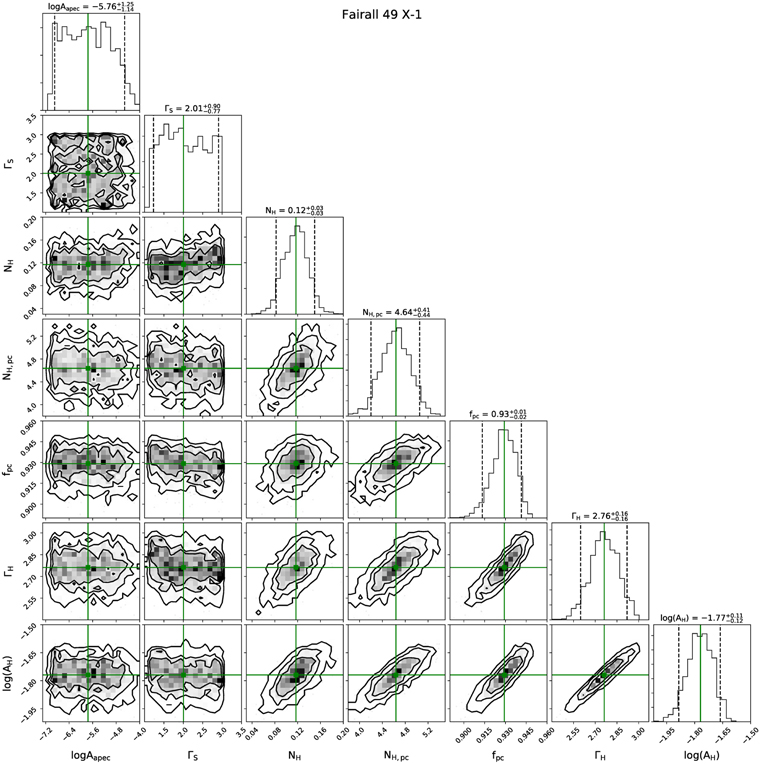
| 3. Fairall 49 | CH-1(02) | 0.81 ± 0.13 | 2.59 ± 0.68 | 0.68 ± 0.08 | 2.46 ± 0.02 | 0.016 ± 0.002 | 388/0.97 | 2.23 |
| CH-2(02) | 0.55 ± 0.40 | <50 | <0.95 | 1.96 ± 0.12 | 0.012 | 417/0.98 | 2.45 | |
| X-1(01) | 0.067 ± 0.017 | 3.98 ± 0.52 | 0.92 ± 0.01 | 2.60 ± 0.16 | 0.012 ± 0.004 | 226/1.45 | 1.07 | |
| X-2(13) | 0.75 ± 0.05 | 0.87 ± 0.08 | 0.62 ± 0.07 | 2.14 ± 0.02 | 0.0159 ± 0.0005 | 381/1.57 | 3.46 | |
| X-3(13) | 0.50 ± 0.06 | 0.71 ± 0.07 | 0.77 ± 0.05 | 2.07 ± 0.01 | 0.0099 ± 0.0003 | 462/1.90 | 2.45 | |
| S-1(07) | 1.09 ± 0.04 | 4.04 ± 0.89 | 0.29 ± 0.08 | 2.42 ± 0.01 | 0.021 ± 0.00012 | 6046/1.06 | 2.75 | |
| 4. IRAS F00521e | X-1(06) | 6.42 ± 1.65 | 12.90 ± 4.01 | 0.72 ± 0.16 | 2.5* | 0.0051 ± 0.0006 | 137/1.31 | 0.50 |
| X-2(06) | 7.21 ± 1.10 | 18.95* | 0.53* | 2.5* | 0.0041 ± 0.0008 | 154/1.31 | 0.35 | |
| S-1(13) | 7.26 ± 1.56 | 42.90 ± 3.09 | 0.51 ± 0.13 | 2.44 ± 0.03 | 0.0041 ± 0.0001 | 1533/1.06 | 0.87 | |
| 5. IRAS F05189e | X-1(01) | 6.29 ± 0.73 | ⋯ | ⋯ | 2.20 ± 0.15 | 0.0023 ± 0.0011 | 105/0.82 | 0.67 |
| X-2(13) | 5.50 ± 0.54 | 12.40 ± 4.35 | 0.61 ± 0.11 | 2.51 ± 0.20 | 0.0057 ± 0.0004 | 274/1.26 | 0.76 | |
| CA-1(01) | 6.08 ± 1.20 | ⋯ | ⋯ | 1.82 ± 0.24 | 0.0012 ± 0.0001 | 127/1.04 | 0.67 | |
| CA-2(02) | 5.20 ± 0.91 | ⋯ | ⋯ | 1.43 ± 0.22 | 0.00068 ± 0.00033 | 106/1.01 | 0.71 | |
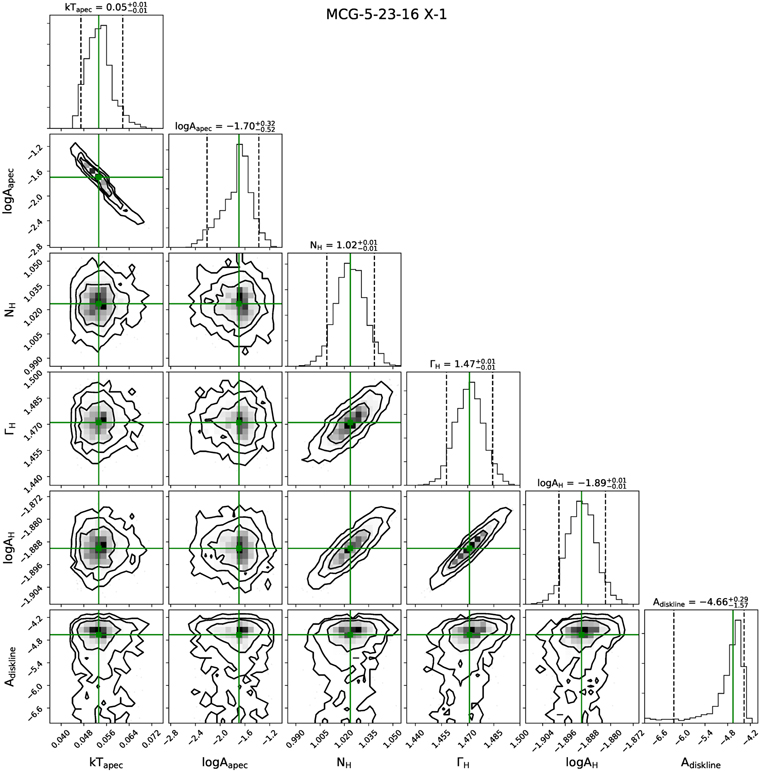
| 6. MCG–5–23–16 | CH-1(00) | 1.84 ± 0.20 | ⋯ | ⋯ | 1.66 ± 0.05 | 0.0129 ± 0.0003 | 471/1.05 | 2.51 |
| CH-2(05) | 1.44 ± 0.25 | ⋯ | ⋯ | 1.56 ± 0.03 | 0.0093 ± 0.0004 | 329/0.98 | 5.37 | |
| CH-3(05) | 1.29 ± 0.25 | ⋯ | ⋯ | 1.58 ± 0.03 | 0.011 ± 0.0004 | 232/0.97 | 4.26 | |
| X-1(01) | 1.02 ± 0.02 | ⋯ | ⋯ | 1.47 ± 0.01 | 0.012 ± 0.0001 | 307/1.15 | 7.76 | |
| X-2(05) | 1.24 ± 0.01 | ⋯ | ⋯ | 1.61 ± 0.01 | 0.0188 ± 0.0001 | 1148/4.3 | 9.33 | |
| X-3(13) | 1.26 ± 0.01 | ⋯ | ⋯ | 1.78 ± 0.02 | 0.0366 ± 0.0004 | 1356/5.10 | 13.4 | |
| X-4(13) | 1.25 ± 0.01 | ⋯ | ⋯ | 1.77 ± 0.01 | 0.0359 ± 0.0003 | 1383/5.21 | 13.4 | |
| S-1(05) | 1.44 ± 0.01 | ⋯ | ⋯ | 1.85 ± 0.01 | 0.0271 ± 0.0001 | 7764/1.08 | 9.33 | |
| S-2(13) | 1.34 ± 0.02 | ⋯ | ⋯ | 1.88 ± 0.01 | 0.0340 ± 0.0001 | 8995/1.17 | 10.91 | |
| S-3(13) | 1.36 ± 0.03 | ⋯ | ⋯ | 1.90 ± 0.01 | 0.0321 ± 0.0001 | 8574/1.13 | 12.22 | |
| 7. Mkn 348 | CA-1(10) | 8.49 ± 0.25 | ⋯ | ⋯ | 1.8* | 0.0095 ± 0.0005 | 528/1.01 | 1.99 |
| X-1(02) | 6.62 ± 2.01 | 8.93 ± 1.10 | 0.89 ± 0.05 | 1.58 ± 0.01 | 0.0107 ± 0.0001 | 320/1.35 | 5.12 | |
| X-2(13) | 10.02 ± 1.53 | 15* | 0.54 ± 0.20 | 1.80 ± 0.02 | 0.0041 ± 0.0008 | 176/1.10 | 1.51 | |
| S-1(08) | 5.42 ± 0.70 | 6.54 ± 2.11 | 0.72 ± 0.11 | 1.80 ± 0.01 | 0.0166 ± 0.0001 | 6007/1.02 | 6.45 | |
| 8. NGC 526A | X-1(02) | 1.00 ± 0.05 | ⋯ | ⋯ | 1.36 ± 0.02 | 0.0026 ± 0.0001 | 221/0.98 | 1.86 |
| X-2(03) | 1.03 ± 0.02 | ⋯ | ⋯ | 1.43 ± 0.03 | 0.0039 ± 0.0002 | 338/1.29 | 2.51 | |
| X-3(13) | 1.05 ± 0.02 | ⋯ | ⋯ | 1.42 ± 0.02 | 0.0043 ± 0.0007 | 359/1.37 | 2.81 | |
| X-4(13) | 1.06 ± 0.02 | ⋯ | ⋯ | 1.45 ± 0.04 | 0.005 ± 0.0003 | 377/1.45 | 3.38 | |
| CH-1(03) | 1.03 ± 0.31 | ⋯ | ⋯ | 1.22 ± 0.12 | 0.0046 ± 0.0022 | 63/0.98 | 9.92 | |
| CH-2(03) | 1.18 ± 0.09 | ⋯ | ⋯ | 1.57 ± 0.02 | 0.207 ± 0.0011 | 303/1.03 | 1.72 | |
| CA-1(00) | 1.58 ± 0.20 | ⋯ | ⋯ | 1.7* | 0.007 ± 0.002 | 240/1.07 | 3.64 | |
| CA-2(00) | 1.50 ± 0.22 | ⋯ | ⋯ | 1.7* | 0.0081 ± 0.0022 | 292/1.30 | 17.7 | |
| S-1(11) | 1.24 ± 0.09 | ⋯ | ⋯ | 1.70 ± 0.02 | 0.0112 ± 0.0001 | 6906/1.05 | 4.72 | |
| 9. NGC 1052 | X-1(01) | 4.84 ± 1.28 | 33.10 ± 8.20 | 0.87 ± 0.04 | 2.05 ± 0.01 | 0.0047 ± 0.0002 | 502/0.99 | 0.91 |
| X-2(06) | 4.65 ± 0.80 | 16.08 ± 5.21 | 0.69 ± 0.09 | 1.54 ± 0.16 | 0.00147 ± 0.0006 | 1341/0.94 | 0.74 | |
| X-3(09) | 4.22 ± 0.80 | 11.30 ± 3.20 | 0.75 ± 0.07 | 1.62 ± 0.14 | 0.00179 ± 0.0007 | 1343/0.92 | 0.83 | |
| X-4(09) | 3.76 ± 1.72 | 8.81 ± 3.31 | 0.84 ± 0.08 | 1.57 ± 0.12 | 0.00163 ± 0.0005 | 1475/0.96 | 0.83 | |
| CA-1(05) | 1.06 ± 0.32 | 11.65 ± 3.82 | 0.82 ± 0.05 | 1.37 ± 0.10 | 0.0012 ± 0.0005 | 336/1.08 | 0.93 | |
| S-1(07) | 3.57 ± 0.28 | 15.11 ± 4.44 | 0.76 ± 0.21 | 1.62 ± 0.01 | 0.0018 ± 0.0001 | 2660/1.02 | 0.95 | |
| 10. NGC 2110 | X-1(03) | 2.21 ± 0.11 | 5.98 ± 1.26 | 0.47 ± 0.03 | 1.82 ± 0.02 | 0.0092 ± 0.0001 | 477/1.01 | 3.46 |
| CA-1(01) | 1.96 ± 0.30 | 2.96 ± 1.01 | 0.67 ± 0.12 | 1.35 ± 0.10 | 0.0068 ± 0.0015 | 635/1.12 | 5.63 | |
| CH-1(01) | 2.30 ± 0.40 | ⋯ | ⋯ | 1.39 ± 0.05 | 0.0048 ± 0.0011 | 252/1.03 | 4.66 | |
| CH-2(01) | 2.85 ± 0.33 | ⋯ | ⋯ | 1.74* | 0.0078 ± 0.0008 | 297/1.26 | 18.6 | |
| CH-3(01) | 2.16 ± 0.26 | ⋯ | ⋯ | 1.31 ± 0.06 | 0.0054 ± 0.0007 | 442/0.98 | 9.45 | |
| CH-4(03) | 2.46 ± 0.25 | ⋯ | ⋯ | 1.34 ± 0.06 | 0.0047 ± 0.0005 | 543/1.09 | 7.25 | |
| S-1(05) | 2.37 ± 0.09 | 3.22 ± 0.88 | 0.65 ± 0.11 | 1.74 ± 0.01 | 0.036 ± 0.0001 | 8007/1.05 | 14.1 | |
| S-2(12) | 2.61 ± 0.12 | 4.03 ± 0.97 | 0.69 ± 0.08 | 1.79 ± 0.02 | 0.047 ± 0.0001 | 7965/1.05 | 16.8 | |
| S-3(15) | 2.54 ± 0.21 | 4.91 ± 1.12 | 0.75 ± 0.15 | 1.89 ± 0.03 | 0.028 ± 0.0001 | 6815/1.09 | 9.01 | |
| 11. NGC 2992 | CH-1(10) | 0.71 ± 0.18 | ⋯ | ⋯ | 1.71 ± 0.15 | 0.0004 ± 0.0001 | 300/1.38 | 0.275 |
| X-1(03) | 0.61 ± 0.01 | ⋯ | ⋯ | 1.76 ± 0.01 | 0.0271 ± 0.0005 | 1055/1.23 | 10.4 | |
| X-2(10) | 0.82 ± 0.03 | ⋯ | ⋯ | 1.64 ± 0.03 | 0.0011 ± 0.0001 | 316/1.29 | 0.62 | |
| X-3(10) | 0.79 ± 0.03 | ⋯ | ⋯ | 1.61 ± 0.03 | 0.0013 ± 0.0001 | 302/1.23 | 0.72 | |
| X-4(10) | 0.75 ± 0.02 | ⋯ | ⋯ | 1.56 ± 0.01 | 0.0025 ± 0.0001 | 336/1.32 | 1.41 | |
| X-5(10) | 0.77 ± 0.05 | ⋯ | ⋯ | 1.64 ± 0.04 | 0.0008 ± 0.0001 | 289/1.22 | 0.47 | |
| X-6(10) | 0.73 ± 0.04 | ⋯ | ⋯ | 1.63 ± 0.04 | 0.0008 ± 0.0001 | 245/1.03 | 0.48 | |
| X-7(10) | 0.71 ± 0.05 | ⋯ | ⋯ | 1.63 ± 0.04 | 0.00059 ± 0.00004 | 315/1.35 | 0.38 | |
| X-8(10) | 0.73 ± 0.05 | ⋯ | ⋯ | 1.77 ± 0.05 | 0.00029 ± 0.00005 | 323/1.42 | 0.17 | |
| X-9(10) | 0.83 ± 0.04 | ⋯ | ⋯ | 1.66 ± 0.04 | 0.001 ± 0.0001 | 282/1.17 | 0.58 | |
| X-10(13) | 0.71 ± 0.03 | ⋯ | ⋯ | 1.55 ± 0.03 | 0.003 ± 0.0002 | 194/0.85 | 1.73 | |
| S-1(05) | 0.98 ± 0.06 | ⋯ | ⋯ | 1.74 ± 0.02 | 0.0021 ± 0.0001 | 2987/1.08 | 1.12 | |
| S-2(05) | 1.06 ± 0.06 | ⋯ | ⋯ | 1.79 ± 0.01 | 0.0025 ± 0.0001 | 3770/1.15 | 0.95 | |
| S-3(05) | 0.89 ± 0.07 | ⋯ | ⋯ | 1.67 ± 0.01 | 0.0021 ± 0.0001 | 4066/1.05 | 1.09 | |
| 12. NGC 4258 | CH-1(07) | 7.56 ± 0.52 | ⋯ | ⋯ | 1.90* | 0.0044 ± 0.0003 | 146/1.05 | 1.17 |
| CH-2(07) | 6.64 ± 0.45 | ⋯ | ⋯ | 1.90* | 0.0031 ± 0.0002 | 217/1.28 | 1.90 | |
| CH-3(07) | 6.86 ± 0.43 | ⋯ | ⋯ | 1.90* | 0.0022 ± 0.0010 | 110/1.22 | 1.94 | |
| CA-1(00) | 8.14 ± 0.47 | ⋯ | ⋯ | 1.90* | 0.0026 ± 0.0005 | 365/1.05 | 1.65 | |
| CA-2(00) | 9.37 ± 0.66 | ⋯ | ⋯ | 1.90* | 0.0033 ± 0.0001 | 239/1.11 | 1.31 | |
| CA-3(01) | 8.85 ± 0.35 | ⋯ | ⋯ | 1.90* | 0.0033 ± 0.0004 | 316/0.99 | <1.01 | |
| X-1(00) | 9.40 ± 0.80 | ⋯ | ⋯ | 1.78 ± 0.16 | 0.0033 ± 0.0011 | 184/1.00 | 1.34 | |
| X-2(01) | 8.00 ± 0.79 | ⋯ | ⋯ | 1.67 ± 0.16 | 0.0023 ± 0.0011 | 189/1.03 | 1.23 | |
| X-3(01) | 7.95 ± 2.15 | ⋯ | ⋯ | 1.52 ± 0.35 | 0.0015 ± 0.0012 | 85/0.90 | 1.02 | |
| X-4(01) | 12.68 ± 1.62 | ⋯ | ⋯ | 1.46 ± 0.20 | 0.0013 ± 0.0007 | 157/0.95 | 0.85 | |
| X-5(02) | 7.47 ± 0.52 | ⋯ | ⋯ | 1.59 ± 0.11 | 0.0027 ± 0.0005 | 287/1.32 | 0.81 | |
| X-6(06) | 7.49 ± 0.51 | ⋯ | ⋯ | 1.64 ± 0.08 | 0.0012 ± 0.0002 | 390/1.65 | 0.60 | |
| S-1(06) | 10.35 ± 0.30 | ⋯ | ⋯ | 1.90 ± 0.01 | 0.0043 ± 0.0001 | 4298/1.04 | 1.28 | |
| S-2(10) | 12.19 ± 1.20 | ⋯ | ⋯ | 1.74 ± 0.02 | 0.0019 ± 0.0001 | 3376/1.07 | 0.76 | |
| 13. NGC 4507 | X-1(01) | 16.81 ± 9.21 | 31.46 ± 3.32 | >0.92 | 1.7* | 0.0118 ± 0.0006 | 404/1.67 | 5.88 |
| X-2(10) | 12.67 ± 2.21 | 60.05 ± 5.52 | >0.94 | 1.7* | 0.0101 ± 0.0011 | 294/1.48 | 6.60 | |
| X-3(10) | 11.56 ± 1.62 | 62.21 ± 5.62 | >0.94 | 1.7* | 0.0103 ± 0.0007 | 339/1.73 | 5.49 | |
| X-4(10) | 12.65 ± 1.55 | 59.48 ± 6.62 | >0.94 | 1.7* | 0.0109 ± 0.0008 | 255/1.30 | 8.12 | |
| X-5(10) | 11.03 ± 3.32 | 58.55 ± 7.21 | >0.94 | 1.7* | 0.0096 ± 0.0012 | 216/1.16 | 6.02 | |
| X-6(10) | 9.94 ± 1.21 | 48.33 ± 7.52 | >0.94 | 1.7* | 0.0067 ± 0.0007 | 241/1.27 | 8.91 | |
| CH-1(01) | 46.45 ± 11.22 | 187.24 ± 50.22 | >0.94 | 1.7* | 0.021 ± 0.001 | 250/1.42 | 3.39 | |
| CA-1(10) | 12.59 ± 6.56 | 47.42 ± 30.33 | >0.94 | 1.7* | 0.019 ± 0.003 | 406/1.23 | 9.57 | |
| S-1(07) | 12.35 ± 2.23 | 61.39 ± 21.29 | 0.91 ± 0.02 | 1.90 ± 0.02 | 0.008 ± 0.001 | 3660/1.34 | 4.84 | |
| 14. NGC 5252 | CA-1(03) | 2.84 ± 0.07 | ⋯ | ⋯ | 1.4* | 0.0025 ± 0.0003 | 506/1.01 | 7.02 |
| CA-2(13) | 4.51 ± 0.11 | ⋯ | ⋯ | # | 0.0028 ± 0.0002 | 593/1.12 | 1.31 | |
| CA-3(13) | 4.58 ± 0.16 | ⋯ | ⋯ | # | 0.00234 ± 0.0003 | 435/0.97 | 1.73 | |
| CA-4(13) | 3.51 ± 0.10 | ⋯ | ⋯ | # | 0.00247 ± 0.0006 | 505/0.99 | 2.78 | |
| X-1(03) | 2.26 ± 0.17 | 8.51 ± 2.01 | 0.47 ± 0.05 | 1.54 ± 0.08 | 0.0026 ± 0.0008 | 249/1.03 | 1.38 | |
| S-1(12) | 2.28 ± 0.31 | 4.47 ± 0.23 | 0.79 ± 0.12 | 1.59 ± 0.01 | 0.0027 ± 0.0003 | 2970/0.98 | 1.60 | |
| 15. NGC 5506 | X-1(01) | 2.77 ± 0.05 | ⋯ | ⋯ | 1.73 ± 0.02 | 0.0173 ± 0.0007 | 302/1.17 | 7.24 |
| X-2(02) | 2.80 ± 0.05 | ⋯ | ⋯ | 1.68 ± 0.02 | 0.0284 ± 0.0011 | 268/1.04 | 12.8 | |
| X-3(04) | 3.02 ± 0.05 | ⋯ | ⋯ | 1.81 ± 0.02 | 0.0233 ± 0.0011 | 339/1.31 | 8.70 | |
| X-4(04) | 3.03 ± 0.04 | ⋯ | ⋯ | 1.79 ± 0.03 | 0.0217 ± 0.0013 | 381/1.47 | 8.31 | |
| X-5(04) | 2.97 ± 0.05 | ⋯ | ⋯ | 1.84 ± 0.02 | 0.0212 ± 0.0010 | 286/1.11 | 7.58 | |
| X-6(04) | 2.92 ± 0.07 | ⋯ | ⋯ | 1.82 ± 0.04 | 0.0346 ± 0.0012 | 297/1.15 | 19.99 | |
| X-7(08) | 2.93 ± 0.05 | ⋯ | ⋯ | 1.81 ± 0.05 | 0.0331 ± 0.0010 | 433/1.66 | 12.30 | |
| X-8(09) | 2.95 ± 0.04 | ⋯ | ⋯ | 1.78 ± 0.05 | 0.0362 ± 0.0015 | 519/1.98 | 13.80 | |
| X-9(15) | 3.00 ± 0.01 | ⋯ | ⋯ | 1.72 ± 0.06 | 0.0201 ± 0.0021 | 602/1.64 | 7.45 | |
| CH-1(00) | 2.91 ± 0.08 | ⋯ | ⋯ | 1.65 ± 0.02 | 0.0100 ± 0.0011 | 334/0.96 | 1.69 | |
| S-1(16) | 3.12 ± 0.10 | ⋯ | ⋯ | 1.95 ± 0.01 | 0.0391 ± 0.0007 | 7533/1.09 | 12.30 | |
| S-2(16) | 3.15 ± 0.10 | ⋯ | ⋯ | 1.94 ± 0.01 | 0.0409 ± 0.0008 | 7426/1.05 | 11.40 | |
| S-3(16) | 3.16 ± 0.09 | ⋯ | ⋯ | 1.96 ± 0.01 | 0.0407 ± 0.0012 | 7658/1.09 | 11.70 | |
| 16. NGC 6251 | CA-1(00) | <0.476 | ⋯ | ⋯ | 1.41 ± 0.20 | 0.0005 ± 0.0002 | 66/0.99 | 0.35 |
| CA-2(03) | 0.058 ± 0.021 | ⋯ | ⋯ | 1.58 ± 0.08 | 0.0004 ± 0.0001 | 260/0.97 | 0.25 | |
| X-1(02) | 0.045 ± 0.010 | ⋯ | ⋯ | 1.93 ± 0.03 | 0.00128 ± 0.00005 | 260/1.24 | 0.37 | |
| S-1(10) | 0.75 ± 0.08 | ⋯ | ⋯ | 1.87 ± 0.01 | 0.00012 ± 0.0002 | 1504/1.07 | 0.19 | |
| 17. NGC 6300 | CA-1(09) | 19.83 ± 1.19 | ⋯ | ⋯ | 1.76* | 0.022 ± 0.008 | 199/1.32 | 7.84 |
| CA-2(09) | 19.29 ± 0.88 | ⋯ | ⋯ | 1.76* | 0.0118 ± 0.0051 | 160/0.99 | 4.98 | |
| CA-3(09) | 21.08 ± 1.07 | ⋯ | ⋯ | 1.76* | 0.028 ± 0.004 | 224/1.42 | 9.77 | |
| CA-4(09) | 19.28 ± 0.82 | ⋯ | ⋯ | 1.76* | 0.038 ± 0.011 | 167/0.93 | 15.80 | |
| CA-5(09) | 21.25 ± 0.85 | ⋯ | ⋯ | 1.76* | 0.036 ± 0.002 | 190/1.10 | 23.00 | |
| X-1(01) | 19.15 ± 2.51 | ⋯ | ⋯ | 1.45 ± 0.12 | 0.00017 ± 0.00011 | 53/0.84 | 0.114 | |
| S-1(07) | 21.76 ± 1.11 | ⋯ | ⋯ | 1.76 ± 0.01 | 0.0096 ± 0.00011 | 4721/1.09 | 3.62 | |
| 18. NGC 7172 | CA-1(00) | 9.95 ± 0.37 | ⋯ | ⋯ | 1.89* | 0.0092 ± 0.0003 | 807/1.83 | 5.91 |
| X-1(02) | 7.56 ± 0.61 | 6.81 ± 4.92 | 0.55 ± 0.35 | 1.66 ± 0.05 | 0.0080 ± 0.0004 | 221/1.02 | 4.16 | |
| X-2(04) | 8.14 ± 0.20 | ⋯ | ⋯ | 1.54 ± 0.04 | 0.0059 ± 0.0005 | 360/1.43 | 4.36 | |
| X-3(07) | 7.60 ± 0.20 | ⋯ | ⋯ | 1.57 ± 0.03 | 0.0133 ± 0.0010 | 348/1.39 | 7.58 | |
| S-1(08) | 9.57 ± 0.32 | ⋯ | ⋯ | 1.89 ± 0.02 | 0.0254 ± 0.0004 | 6515/1.05 | 7.65 | |
| 19. NGC 7314 | CH-1(02) | 0.74 ± 0.11 | ⋯ | ⋯ | 1.65 ± 0.10 | 0.0077 ± 0.0012 | 323/1.02 | 3.54 |
| CH-2(02) | 0.80 ± 0.12 | ⋯ | ⋯ | 1.75 ± 0.06 | 0.0099 ± 0.0011 | 543/1.08 | 2.45 | |
| CA-1(06) | 0.82 ± 0.10 | ⋯ | ⋯ | 1.66 ± 0.06 | 0.0197 ± 0.0008 | 512/1.19 | 8.51 | |
| CA-2(06) | 0.85 ± 0.08 | ⋯ | ⋯ | 1.79 ± 0.12 | 0.0198 ± 0.0016 | 437/1.16 | 8.31 | |
| X-1(01) | 0.73 ± 0.02 | ⋯ | ⋯ | 1.93 ± 0.01 | 0.0141 ± 0.0001 | 517/2.02 | 4.36 | |
| X-2(06) | 0.73 ± 0.03 | ⋯ | ⋯ | 1.77 ± 0.02 | 0.0043 ± 0.0002 | 355/1.40 | 1.65 | |
| X-3(13) | 0.80 ± 0.01 | ⋯ | ⋯ | 1.83 ± 0.03 | 0.0073 ± 0.0002 | 488/1.92 | 2.57 | |
| X-4(13) | 0.77 ± 0.01 | ⋯ | ⋯ | 1.78 ± 0.01 | 0.0057 ± 0.0001 | 392/1.54 | 2.13 | |
| X-5(16) | 0.75 ± 0.01 | ⋯ | ⋯ | 1.89 ± 0.02 | 0.0127 ± 0.0001 | 430/1.70 | 3.98 | |
| S-1(07) | 0.85 ± 0.05 | ⋯ | ⋯ | 1.79 ± 0.01 | 0.0022 ± 0.0002 | 4662/1.00 | 8.91 | |
| S-2(11) | 0.86 ± 0.07 | ⋯ | ⋯ | 2.04 ± 0.01 | 0.0065 ± 0.0003 | 6143/1.09 | 1.53 | |
| 20. NGC 7582 | CA-1(00) | 17.95 ± 2.11 | ⋯ | ⋯ | 1.84 ± 0.12 | 0.0087 ± 0.0012 | 160/1.10 | 1.38 |
| CA-2(00) | 19.90 ± 3.85 | ⋯ | ⋯ | 1.45* | 0.0047 ± 0.0011 | 65/1.16 | 1.41 | |
| X-1(01) | 15.50 ± 1.71 | 58.36± | 0.85± | 1.79 ± 0.01 | 0.0053 ± 0.0008 | 241/1.34 | 0.41 | |
| X-2(05) | 18.21 ± 4.71 | 78.43± | 0.89± | 2.01 ± 0.03 | 0.0051 ± 0.0007 | 360/1.65 | 0.23 | |
| X-3(07) | 28.79 ± 10.11 | ⋯ | ⋯ | 1.38 ± 0.01 | 0.0022 ± 0.0002 | 69/1.12 | 0.71 | |
| X-4(16) | 29.75 ± 0.56 | ⋯ | ⋯ | 1.41 ± 0.04 | 0.0036 ± 0.0003 | 518/2.14 | 0.93 | |
| S-1(07) | 31.71 ± 3.52 | ⋯ | ⋯ | 1.45 ± 0.05 | 0.0017 ± 0.0002 | 596/1.10 | 0.93 | |
| S-2(07) | 41.07 ± 5.52 | ⋯ | ⋯ | 1.33 ± 0.04 | 0.0014 ± 0.0001 | 645/1.31 | 0.93 | |
| S-3(07) | ⋯ | ⋯ | 1.33 ± 0.01 | 0.00058 ± 0.0001 | 466/1.15 | 255.1 | ||
| S-4(07) | ⋯ | ⋯ | 1.51 ± 0.01 | 0.00078 ± 0.0001 | 478/1.15 | 47.1 | ||
Notes. Quantities with a single * symbol are kept fixed during fitting, mostly due to limited spectral bandpass and/or due to low S/N. The errors on parameters quoted in the table are at the 90% confidence level.
⋯ denotes that these components were not required in the fit.
aX = XMM-Newton, S = Suzaku, CH = Chandra HETG, and CA = Chandra ACIS. bThe value of the power-law component at 1 keV in units of ph keV−1 cm−2 s−1. cThe 2–10 keV unabsorbed flux. dDue to the large number of observations, the entries for Cyg A's Chandra observations have been moved to Table B1. eIRAS F00521 = IRAS F00521–7054, IRAS F05189 = IRAS F05189–2524.Table 4. Best-fit Soft X-Ray and pexmon Parameters Obtained from X-Ray Spectral Fits
| Source | Obsid (year)a | apec1 kBT | apec1 Norm | apec2 kBT | apec2 Norm | SXPL Γ | SXPL Norm | pexmon(norm) | pexmon Γ | pexmon R | FeK Norm |
|---|---|---|---|---|---|---|---|---|---|---|---|
| (keV) | (10−4) | (keV) | (10−4) | (10−4) | (10−4) | ||||||
| 1. Cen A | X-1(01) | 0.84* | 4.01* | ⋯ | ⋯ | 0.73* | 13.86* | ⋯ | ⋯ | ⋯ | 3.62 ± 0.47 |
| X-2(02) | # | # | ⋯ | ⋯ | # | # | ⋯ | ⋯ | ⋯ | 4.74 ± 0.71 | |
| X-3(13) | # | # | ⋯ | ⋯ | # | # | ⋯ | ⋯ | ⋯ | 3.79 ± 1.06 | |
| X-4(13) | # | # | ⋯ | ⋯ | # | # | ⋯ | ⋯ | ⋯ | 5.86 ± 1.07 | |
| X-5(14) | # | # | ⋯ | ⋯ | # | # | ⋯ | ⋯ | ⋯ | 3.63 ± 0.67 | |
| X-6(14) | # | # | ⋯ | ⋯ | # | # | ⋯ | ⋯ | ⋯ | 4.25 ± 0.53 | |
| S-1(05) | 0.23* | 4.05 ± 0.33 | 0.79* | 2.67 ± 0.14 | 1.17* | 7.85 ± 0.15 | ⋯ | ⋯ | ⋯ | 3.30 ± 0.13 | |
| S-2(09) | # | 5.79 ± 0.70 | # | 3.39 ± 0.22 | # | 9.16 ± 0.21 | ⋯ | ⋯ | ⋯ | 3.91 ± 0.17 | |
| S-3(09) | # | 6.04 ± 0.19 | # | 3.44 ± 0.52 | # | 10.93 ± 0.24 | ⋯ | ⋯ | ⋯ | 4.16 ± 0.20 | |
| S-4(09) | # | 7.09 ± 0.83 | # | 3.51 ± 0.26 | # | 9.92 ± 0.24 | ⋯ | ⋯ | ⋯ | 4.40 ± 0.19 | |
| S-5(13) | # | 4.94 ± 1.20 | # | 2.92 ± 0.43 | # | 8.55 ± 0.43 | ⋯ | ⋯ | ⋯ | 2.94 ± 0.34 | |
| S-6(14) | # | 6.28 ± 1.82 | # | 3.54 ± 0.60 | # | 11.25 ± 0.58 | ⋯ | ⋯ | ⋯ | 7.87 ± 0.85 | |
| 2. Cyg Ab | S-1(08) | 0.23* | 6.01* | 4.17* | 130.11* | 1.89* | 49.00* | 0.0099d | 1.89d | 0.91± | 0.46 ± 0.11 |
| X-1(05) | 0.29* | 13.11* | 2.9* | 76.01* | 1.77* | 22.00* | # | # | # | 0.57 ± 0.11 | |
| 3. Fairall 49 | S-1(07) | 0.008* | 0.55* | ⋯ | ⋯ | 2.3* | 1.01* | 0.021d | 2.42d | 0.41 ± 0.11 | 0.26 ± 0.11 |
| CH-1(02) | 0.3* | 0.041* | ⋯ | ⋯ | 2.1* | 1.01* | # | # | # | ⋯ | |
| CH-2(02) | # | # | ⋯ | ⋯ | # | # | # | # | # | ⋯ | |
| X-1(01) | 0.3* | 0.10* | ⋯ | ⋯ | 2.3* | 1.01* | # | # | # | ⋯ | |
| X-2(13) | # | # | ⋯ | ⋯ | # | # | # | # | # | 0.42 ± 0.11 | |
| X-3(13) | # | # | ⋯ | ⋯ | # | # | # | # | # | 0.33 ± 0.11 | |
| 4. IRAS F00521c | S-1(13) | 0.25* | 0.11* | ⋯ | ⋯ | 2.44* | 0.15* | 0.0041d | 2.48d | 0.65 ± 0.21 | 0.028 ± 0.008 |
| X-1(06) | 0.25* | 0.11* | ⋯ | ⋯ | 2.51* | 0.10* | # | # | # | 0.057 ± 0.010 | |
| X-2(06) | # | # | ⋯ | ⋯ | # | # | # | # | # | 0.068 ± 0.010 | |
| 5. IRAS F05189c | X-1(01) | ⋯ | ⋯ | ⋯ | ⋯ | 3.31* | 0.39* | 0.0051* | 2.47* | 1.48* | 0.051 ± 0.011 |
| X-2(13) | ⋯ | ⋯ | ⋯ | ⋯ | # | # | # | # | # | 0.082 ± 0.012 | |
| CA-1(01) | ⋯ | ⋯ | ⋯ | ⋯ | 2.91* | 0.42 | # | # | # | 0.049 ± 0.025 | |
| CA-2(02) | ⋯ | ⋯ | ⋯ | ⋯ | # | # | # | # | # | 0.065 ± 0.042 | |
| 6. MCG–5–23–16 | CH-1(00) | 0.01* | 2.01* | ⋯ | ⋯ | 1.66* | 2.11* | 0.027* | 1.84* | 0.35* | 0.81 ± 0.41 |
| CH-2(05) | # | # | ⋯ | ⋯ | # | # | # | # | # | 0.98 ± 0.41 | |
| CH-3(05) | # | # | ⋯ | ⋯ | # | # | # | # | # | 0.86 ± 0.52 | |
| X-1(01) | 0.05 ± 0.01 | 180 ± 23 | ⋯ | ⋯ | 1.7* | 3.1 ± 0.12 | # | # | # | 0.53 ± 0.081 | |
| X-2(05) | 0.07 ± 0.01 | 20 ± 9 | ⋯ | ⋯ | 1.7* | 2.1 ± 0.22 | # | # | # | 0.72 ± 0.21 | |
| X-3(13) | 0.05 ± 0.02 | 160 ± 29 | ⋯ | ⋯ | 2.1* | 2.9* | # | # | # | 1.08 ± 0.11 | |
| X-4(13) | 0.06 ± 0.01 | 130 ± 12 | ⋯ | ⋯ | # | # | # | # | # | 1.10 ± 0.12 | |
| S-1(05) | 0.14* | 9 ± 4 | ⋯ | ⋯ | 1.85* | 0.76 ± 0.17 | 0.027d | 1.84d | 0.35 ± 0.12 | 0.98 ± 0.21 | |
| S-2(13) | # | 17 ± 6 | ⋯ | ⋯ | # | 0.40 ± 0.08 | 0.034d | 1.88d | 0.24 ± 0.08 | 0.95 ± 0.22 | |
| S-3(13) | # | 15 ± 6 | ⋯ | ⋯ | # | 0.66 ± 0.18 | 0.032d | 1.89d | 0.40 ± 0.05 | 0.92 ± 0.23 | |
| 7. Mkn 348 | S-1(08) | 0.008* | 2.0* | 0.92* | 0.11* | 1.81* | 0.25 | 0.0166d | 1.8d | 0.45 ± 0.08 | 0.34 ± 0.04 |
| CA-1(10) | 0.18* | 0.62* | 0.82* | 0.11* | 1.8* | 0.65* | # | # | # | 0.16 ± 0.12 | |
| X-1(02) | 0.18* | 0.43* | 0.95* | 0.11* | 1.42* | 0.33* | # | # | # | 0.21 ± 0.08 | |
| X-2(13) | # | # | # | # | # | # | # | # | # | 0.24 ± 0.07 | |
| 8. NGC 526A | X-1(02) | 0.90* | 0.20* | 0.19* | 0.46 ± 0.11 | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | 0.19 ± 0.12 |
| X-2(03) | # | # | # | 0.42 ± 0.12 | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | 0.17 ± 0.05 | |
| X-3(13) | # | # | # | 0.42 ± 0.12 | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | 0.23 ± 0.03 | |
| X-4(13) | # | # | # | 0.53 ± 0.16 | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | 0.25 ± 0.05 | |
| CH-1(03) | # | 0.39* | # | 0.74 ± 0.19 | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | 0.51 ± 0.01 | |
| CH-2(03) | # | # | # | 18.0* | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | 0.073 ± 0.002 | |
| CA-1(00) | # | # | # | # | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | 0.22 ± 0.05 | |
| CA-2(00) | # | # | # | # | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | 0.12 ± 0.02 | |
| S-1(11) | 0.90* | 0.0016* | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | 0.23 ± 0.01 | |
| 9. NGC 1052 | X-1(01) | 0.76* | 0.20* | ⋯ | ⋯ | 1.55* | 0.91* | 0.00189* | 1.62* | 0.29* | 0.17 ± 0.07 |
| X-2(06) | # | # | ⋯ | ⋯ | # | # | # | # | # | 0.12 ± 0.04 | |
| X-3(09) | # | # | ⋯ | ⋯ | # | # | # | # | # | 0.11 ± 0.03 | |
| X-4(09) | # | # | ⋯ | ⋯ | # | # | # | # | # | 0.12 ± 0.02 | |
| CA-1(05) | 0.80* | 0.32* | ⋯ | ⋯ | # | # | # | # | # | 0.14 ± 0.06 | |
| S-1(07) | 0.76* | 0.26* | ⋯ | ⋯ | # | # | 0.00189d | 1.62d | 0.29 ± 0.09 | 0.13 ± 0.06 | |
| 10. NGC 2110 | X-1(03) | 0.9* | 0.41* | ⋯ | ⋯ | 1.73* | 0.51* | 0.0365* | 1.74* | 0.268* | 0.61 ± 0.01 |
| CA-1(01) | 0.90* | 0.41* | ⋯ | ⋯ | 1.73* | 0.51* | 0.0365* | 1.74* | 0.268* | 0.82 ± 0.02 | |
| CH-1(01) | # | # | ⋯ | ⋯ | # | # | # | # | # | 0.67 ± 0.13 | |
| CH-2(01) | # | # | ⋯ | ⋯ | # | # | # | # | # | 0.39 ± 0.11 | |
| CH-3(01) | # | # | ⋯ | ⋯ | # | # | # | # | # | 0.81 ± 0.08 | |
| CH-4(03) | # | # | ⋯ | ⋯ | # | # | # | # | # | 0.95 ± 0.03 | |
| S-1(05) | 0.90* | 0.27* | ⋯ | ⋯ | 1.75* | 0.52* | 0.0365d | 1.74d | 0.268 ± 0.091 | 0.62 ± 0.08 | |
| S-2(12) | # | # | ⋯ | ⋯ | # | # | 0.047d | 1.79d | 0.295 ± 0.110 | 0.80 ± 0.06 | |
| S-3(15) | # | # | ⋯ | ⋯ | # | # | 0.028d | 1.89d | 0.588 ± 0.071 | 0.83 ± 0.12 | |
| 11. NGC 2992 | CH-1(10) | ⋯ | ⋯ | ⋯ | ⋯ | 1.51* | 0.86* | 0.0023* | 1.74* | 1.36* | 0.25 ± 0.04 |
| X-1(03) | 0.23 ± 0.03 | 1.61 ± 0.50 | ⋯ | ⋯ | 1.51* | 1.41* | # | # | # | 0.91 ± 0.11 | |
| X-2(10) | 0.78* | 0.21* | ⋯ | ⋯ | 1.51* | 1.41* | # | # | # | 0.21 ± 0.03 | |
| X-3(10) | # | # | ⋯ | ⋯ | # | # | # | # | # | 0.21 ± 0.02 | |
| X-4(10) | # | # | ⋯ | ⋯ | # | # | # | # | # | 0.28 ± 0.02 | |
| X-5(10) | # | # | ⋯ | ⋯ | # | # | # | # | # | 0.24 ± 0.02 | |
| X-6(10) | # | # | ⋯ | ⋯ | # | # | # | # | # | 0.25 ± 0.02 | |
| X-7(10) | # | # | ⋯ | ⋯ | # | # | # | # | # | 0.23 ± 0.02 | |
| X-8(10) | # | # | ⋯ | ⋯ | # | # | # | # | # | 0.19 ± 0.02 | |
| X-9(10) | # | # | ⋯ | ⋯ | # | # | # | # | # | 0.19 ± 0.02 | |
| X-10(13) | # | # | ⋯ | ⋯ | # | # | # | # | # | 0.35 ± 0.02 | |
| S-1(05) | 0.62* | 0.22* | ⋯ | ⋯ | 1.53* | 2.3* | 0.00211d | 1.74d | 1.36 ± 0.23 | 0.24 ± 0.02 | |
| S-2(05) | # | # | ⋯ | ⋯ | # | # | 0.0024d | 1.79d | 1.36 ± 0.21 | 0.23 ± 0.02 | |
| S-3(05) | # | # | ⋯ | ⋯ | # | # | 0.0021d | 1.67d | 0.98 ± 0.09 | 0.28 ± 0.02 | |
| 12. NGC 4258 | CH-1(07) | 0.10* | 0.01* | 0.45* | 0.10* | ⋯ | ⋯ | 0.0043* | 1.90* | 0.165* | <0.54 |
| CH-2(07) | # | # | # | # | ⋯ | ⋯ | # | # | # | <0.08 | |
| CH-3(07) | # | # | # | # | ⋯ | ⋯ | # | # | # | <0.03 | |
| CA-1(00) | # | # | 0.54 ± 0.08 | 0.28 ± 0.05 | ⋯ | ⋯ | # | # | # | ⋯ | |
| CA-2(00) | # | # | 1.01 ± 0.02 | 0.20 ± 0.06 | ⋯ | ⋯ | # | # | # | <0.01 | |
| CA-3(01) | # | # | 1.01 ± 0.03 | 0.21 ± 0.05 | ⋯ | ⋯ | # | # | # | ⋯ | |
| X-1(00) | 0.70* | 10.01* | 0.21* | 0.51* | 2.1* | 0.71* | # | # | # | 0.07 ± 0.004 | |
| X-2(01) | # | # | # | # | # | # | # | # | # | <0.05 | |
| X-3(01) | # | # | # | # | # | # | # | # | # | 0.05 ± 0.004 | |
| X-4(01) | # | # | # | # | # | # | # | # | # | <0.083 | |
| X-5(02) | # | # | # | # | # | # | # | # | # | 0.042 ± 0.003 | |
| X-6(06) | # | # | # | # | # | # | # | # | # | 0.027 ± 0.002 | |
| S-1(06) | 0.85* | 1.71* | 0.50* | 2.01* | 1.90* | 1.91* | 0.0043d | 1.90d | 0.165 ± 0.050 | 0.73 ± 0.03 | |
| S-2(10) | # | # | # | # | # | # | 0.0019d | 1.74d | 0.201 ± 0.091 | 0.047 ± 0.002 | |
| 13. NGC 4507 | X-1(01) | 0.18* | 0.71* | 0.78* | 0.35* | 1.70* | 1.01* | 0.0088* | 1.90* | 2.19* | 0.84 ± 0.09 |
| X-2(10) | # | # | # | # | # | # | # | # | # | 1.91 ± 0.30 | |
| X-3(10) | # | # | # | # | # | # | # | # | # | 1.61 ± 0.30 | |
| X-4(10) | # | # | # | # | # | # | # | # | # | 2.01 ± 0.60 | |
| X-5(10) | # | # | # | # | # | # | # | # | # | 2.31 ± 0.60 | |
| X-6(10) | # | # | # | # | # | # | # | # | # | 2.41 ± 1.10 | |
| CH-1(01) | # | # | # | # | # | # | # | # | # | 0.32 ± 0.19 | |
| CA-1(10) | # | # | # | # | # | # | # | # | # | 2.91 ± 1.12 | |
| S-1(07) | 0.78* | 0.45* | ⋯ | ⋯ | 1.90* | 1.51* | 0.0088d | 1.90d | 2.18 ± 0.167 | 2.92 ± 1.22 | |
| 14. NGC 5252 | CA-1(03) | 0.15* | 2.67 ± 0.87 | ⋯ | ⋯ | 1.32* | 0.450 ± 0.043 | ⋯ | ⋯ | ⋯ | 0.08 ± 0.06 |
| CA-2(13) | # | # | ⋯ | ⋯ | # | 0.965* | ⋯ | ⋯ | ⋯ | 0.16 ± 0.06 | |
| CA-3(13) | # | # | ⋯ | ⋯ | # | # | ⋯ | ⋯ | ⋯ | 0.19 ± 0.07 | |
| CA-4(13) | # | # | ⋯ | ⋯ | # | # | ⋯ | ⋯ | ⋯ | 0.15 ± 0.06 | |
| X-1(03) | # | 0.46 ± 0.04 | 0.90* | 0.085* | 2.48* | 0.35* | ⋯ | ⋯ | ⋯ | 0.09 ± 0.01 | |
| S-1(12) | # | 2.23 ± 0.12 | 0.82* | 0.21* | 1.53* | 0.46* | ⋯ | ⋯ | ⋯ | 0.13 ± 0.03 | |
| 15. NGC 5506 | X-1(01) | 0.94* | 0.41* | ⋯ | ⋯ | 1.80* | 4.01* | 0.0391* | 1.95* | 0.475* | 0.43 ± 0.12 |
| X-2(02) | # | # | ⋯ | ⋯ | # | # | # | # | # | 0.41 ± 0.14 | |
| X-3(04) | # | # | ⋯ | ⋯ | # | # | # | # | # | 0.48 ± 0.15 | |
| X-4(04) | # | # | ⋯ | ⋯ | # | # | # | # | # | 0.72 ± 0.12 | |
| X-5(04) | # | # | ⋯ | ⋯ | # | # | # | # | # | 0.67 ± 0.11 | |
| X-6(04) | # | # | ⋯ | ⋯ | # | # | # | # | # | 0.57 ± 0.11 | |
| X-7(08) | # | # | ⋯ | ⋯ | # | # | # | # | # | 0.56 ± 0.12 | |
| X-8(09) | # | # | ⋯ | ⋯ | # | # | # | # | # | 0.46 ± 0.11 | |
| X-9(15) | # | 21 ± 5e | ⋯ | ⋯ | ⋯ | ⋯ | # | # | # | 0.80 ± 0.13 | |
| CH-1(00) | 0.37* | 17.01* | ⋯ | ⋯ | 1.64* | 0.49* | # | # | # | 0.71 ± 0.11 | |
| S-1(16) | 0.68* | 0.77* | ⋯ | ⋯ | 1.95* | 4.5* | 0.0391d | 1.95d | 0.475 ± 0.081 | 0.35 ± 0.12 | |
| S-2(16) | # | # | ⋯ | ⋯ | # | # | 0.0409d | 1.94d | 0.447 ± 0.088 | 0.68 ± 0.12 | |
| S-3(16) | # | # | ⋯ | ⋯ | # | # | 0.0407d | 1.95d | 0.406 ± 0.091 | 0.39 ± 0.12 | |
| 16. NGC 6251 | CA-1(00) | 0.54 | 2.81 | ⋯ | ⋯ | ⋯ | ⋯ | 0.00012 | 1.87 | 0.59 | 0.25 ± 0.21 |
| CA-2(03) | 0.66 | # | ⋯ | ⋯ | ⋯ | ⋯ | # | # | # | 0.06 ± 0.02 | |
| X-1(02) | 0.56 | 0.37 | ⋯ | ⋯ | ⋯ | ⋯ | # | # | # | 0.07 ± 0.03 | |
| S-1(10) | 0.78 | 0.44 | ⋯ | ⋯ | 1.87 | 4.61 | 0.00012d | 1.87d | 0.59 ± 0.22 | 0.01 ± 0.01 | |
| 17. NGC 6300 | CA-1(09) | 0.69* | 0.05* | ⋯ | ⋯ | 1.86* | 0.51* | 0.0096* | 1.77* | 0.417* | 0.95 ± 0.55 |
| CA-2(09) | # | # | ⋯ | ⋯ | # | # | # | # | # | 0.22 ± 0.11 | |
| CA-3(09) | # | # | ⋯ | ⋯ | # | # | # | # | # | 0.68 ± 0.52 | |
| CA-4(09) | # | # | ⋯ | ⋯ | # | # | # | # | # | 0.80 ± 0.60 | |
| CA-5(09) | # | # | ⋯ | ⋯ | # | # | # | # | # | 0.72 ± 0.52 | |
| X-1(01) | 0.69* | 0.005* | ⋯ | ⋯ | 1.42* | 0.006* | # | # | # | 0.026 ± 0.011 | |
| S-1(07) | 0.99* | 0.059* | ⋯ | ⋯ | 1.77* | 0.81* | 0.0096d | 1.77d | 0.417 ± 0.12 | 0.34 ± 0.18 | |
| 18. NGC 7172 | CA-1(00) | 0.72* | 0.0016* | ⋯ | ⋯ | 1.70* | 0.081* | 0.0254* | 1.89* | 0.33* | 0.41 ± 0.14 |
| X-1(02) | 0.70* | 0.041* | ⋯ | ⋯ | 1.70* | 0.23* | # | # | # | 0.31 ± 0.09 | |
| X-2(04) | # | # | ⋯ | ⋯ | # | # | # | # | # | 0.27 ± 0.08 | |
| X-3(07) | # | # | ⋯ | ⋯ | # | # | # | # | # | 0.45 ± 0.09 | |
| S-1(08) | ⋯ | ⋯ | ⋯ | ⋯ | 1.89* | 0.17* | 0.0254d | 1.89d | 0.33 ± 0.08 | 0.42 ± 0.09 | |
| 19. NGC 7314 | CH-1(02) | ⋯ | ⋯ | ⋯ | ⋯ | 1.80* | 3.01* | 0.0022* | 1.79* | 0.67* | 0.23 ± 0.11 |
| CH-2(02) | ⋯ | ⋯ | ⋯ | ⋯ | # | # | # | # | # | 0.11 ± 0.06 | |
| CA-1(06) | ⋯ | ⋯ | ⋯ | ⋯ | # | # | # | # | # | 0.94 ± 0.11 | |
| CA-2(06) | ⋯ | ⋯ | ⋯ | ⋯ | # | # | # | # | # | 0.20 ± 0.10 | |
| X-1(01) | 0.29 ± 0.02 | 0.67 ± 0.07 | ⋯ | ⋯ | # | 1.3 ± 0.02 | # | # | # | 0.17 ± 0.04 | |
| X-2(06) | 0.19 ± 0.03 | 0.26 ± 0.11 | ⋯ | ⋯ | # | 0.61 ± 0.12 | # | # | # | 0.19 ± 0.03 | |
| X-3(13) | 0.34 ± 0.04 | 0.15 ± 0.01 | ⋯ | ⋯ | # | 1.45 ± 0.06 | # | # | # | 0.15 ± 0.03 | |
| X-4(13) | 0.27 ± 0.03 | 0.21 ± 0.04 | ⋯ | ⋯ | # | 1.15 ± 0.07 | # | # | # | 0.15 ± 0.03 | |
| X-5(16) | 0.27 ± 0.01 | 0.77 ± 0.08 | ⋯ | ⋯ | # | 0.89 ± 0.11 | # | # | # | 0.17 ± 0.03 | |
| S-1(07) | 0.45* | 0.0029* | ⋯ | ⋯ | 1.79* | 0.86* | 0.0022d | 1.79d | 0.67 ± 0.12 | 0.09 ± 0.05 | |
| S-2(11) | # | # | ⋯ | ⋯ | # | # | 0.0065d | 2.04d | 0.41 ± 0.11 | 0.08 ± 0.04 | |
| 20. NGC 7582 | CA-1(00) | 0.54* | 0.22* | 1.20 ± 0.24 | 0.39 ± 0.08 | 1.7* | 0.72* | 0.0017* | 1.43* | 1.59* | 0.53 ± 0.12 |
| CA-2(00) | 0.99* | 0.27* | <0.56 | 0.011 ± 0.008 | # | # | # | # | # | 0.77 ± 0.52 | |
| X-1(01) | 0.097* | 0.86* | 0.59* | 0.33* | 1.5* | 0.91* | # | # | # | 0.47 ± 0.12 | |
| X-2(05) | # | # | # | # | # | # | # | # | # | 0.77 ± 0.12 | |
| X-3(07) | # | # | # | # | # | # | # | # | # | 0.31 ± 0.08 | |
| X-4(16) | # | # | # | # | # | # | # | # | # | 0.82 ± 0.09 | |
| S-1(07) | 0.81* | 0.62 ± 0.08 | ⋯ | ⋯ | 1.43* | 0.89* | 0.0017d | 1.43d | 1.59 ± 0.12 | 0.37 ± 0.12 | |
| S-2(07) | # | 0.55 ± 0.04 | ⋯ | ⋯ | # | # | 0.0014d | 1.33d | 0.66 ± 0.23 | 0.35 ± 0.11 | |
| S-3(07) | # | 0.53 ± 0.09 | ⋯ | ⋯ | # | # | 0.0005d | 1.33d | 4.19 ± 0.72 | 0.42 ± 0.15 | |
| S-4(07) | # | 0.51 ± 0.12 | ⋯ | ⋯ | # | # | 0.00078d | 1.51d | 4.20 ± 0.63 | 0.39 ± 0.11 | |
Notes. The quantities in this table marked with * are kept fixed at an average value during fitting; hence, no errors are quoted. When the quantities are left free, as required by the data, the errors on the free parameters are quoted. Refer to Section 3 for details of the fitting.
# marked quantities are the same as the value just above it, which denotes that we have fixed it to an average value over all of the observations for a particular instrument.
⋯ denotes that these were not required in the fit.
aX = XMM-Newton, S = Suzaku, CH = Chandra HETG, and CA = Chandra ACIS. bCyg A Chandra observations and the corresponding best-fit parameters are listed in Table B1. cIRAS F00521 = IRAS F00521–7054, IRAS F05189 = IRAS F05189–2524. dThe pexmon normalization and the power-law slope (Γ) are tied to the hard X-ray power-law parameters for the respective Suzaku observation. eAbundance of apec component is low 0.0162 ± 0.0012 relative to solar, and hence the normalization is larger. See Appendix A for details.4. Results
Table 3 lists the best-fit parameters for the full-covering and PC line-of-sight absorbers, along with the 90% confidence uncertainties. We first discuss the characteristics of the full-covering absorbers. The column densities of the full-covering absorber in our sources have values spanning three orders of magnitude (NH ∼ 1020.5–23.5 cm−2). We note that the distribution of mean values of NH is roughly uniform, and does not show any clustering toward low or high values. We present light curves of NH for all sources, shown in Figure 1.
Download figure:
Standard image High-resolution imageDownload figure:
Standard image High-resolution imageDownload figure:
Standard image High-resolution imageFigure 1. The light curves of , Γ, and the 2–10 keV unabsorbed flux of the sources in the sample. The red circles, blue stars, and green triangles denote the data points obtained from XMM-Newton, Chandra, and Suzaku telescopes, respectively.
Download figure:
Standard image High-resolution imageFor a given source, we can search for variability in NH by examining a single instrument only (to eliminate cross-instrument systematic effects), and in parallel, across different missions. The latter, however, is subject to cross-instrument calibration issues, which are not straightforward to quantify and may depend on, e.g., intrinsic spectral shape, the effect of differing apertures, etc., so cross-instrument comparisons of a given parameter must be taken with a grain of salt, and are discussed further in Section 4.2. Nonetheless, we note first that none of the sources exhibits any Compton-thin to -thick (or vice versa) transitions, considering both single instruments and across missions. Furthermore, variations in best-fit values of NH are usually modest even over timescales of years: for any given object except Fairall 49, the maximum/minimum best-fit values of NH typically never vary in ratio by more than ∼1.5–1.8 (within one instrument) or more than ∼2–5 (across all instruments for a given source). Fairall 49 is the standout exception, displaying an order of magnitude increase in NH (this source is discussed further below).
As a caveat, we remind the reader that in this work we are limited by the relatively sparse time sampling of the data, and we are not exploring variability on timescales less than ∼1 day in this work. This lack of sustained sampling means we are not as sensitive compared to RXTE in detecting complete (ingress-to-egress) eclipse events as detected by, e.g., MKN14 and Risaliti et al. (2011). Nonetheless, we can probe up to timescales of nearly two decades, so we are probing a spatial extent similar to that of MKN14, although here we have greater sensitivity to smaller variations in NH, covering the range log(/cm−2) ∼ 20.5–23.5.
4.1. Candidates for Variability in NH Using Single Instruments
We select candidates for sources exhibiting variability in (henceforth "variable- sources"), but we first concentrate only on using single instruments for a given object. To be classified in this category, a given object/instrument combination must exhibit variability as follows:
- 1.As a first cut, values of NH between any two observations must differ by at least three times the 90% error in one parameter obtained from the ISIS spectral fit (adopting a conservative criterion).
- 2.A simple χ2 fit of the NH(t) light curve against a constant must satisfy χ2/dof > 5.
- 3.The X-ray spectra must be checked for possible model degeneracies that could influence NH values; as described below, we perform Bayesian analysis with MultiNest to vet candidate-variable objects.
The first criterion lead to eight object/instrument combinations as candidates (here, X, S, and CA denote XMM-Newton, Suzaku, and Chandra ACIS, respectively): Fairall 49/X, Cen A/S, MCG–5-23-16/X, MCG–5-23-16/S, NGC 2992/X, NGC 5252/CA, NGC 5506/X, and NGC 7582/X. We note that the XMM-Newton and Suzaku events of MCG–523-16 are different and not overlapping in time. All eight of the above events pass the second criterion, as testing against a constant yielded χ2/dof > 5. Two additional objects (NGC 4258/S and NGC 7582/X) pass this criterion but fail the first criterion (and partial coverers and/or low S/N may be at play), and hence we do not consider them further. Choosing a much less strict threshold for the first criterion, say two times the 90% errors, would have allowed only three more object/instrument combinations to pass this criterion. Similarly, choosing a lower threshold for χ2/dof would not have significantly increased the number of objects passing the second criterion; lowering the threshold to 2.5, for example, would have allowed only two more object/instrument combinations to pass this criterion. We are thus confident that these two criteria are each reasonable in terms of separating outlying variability from the bulk of the distribution in which variability is not detected. We then conducted Bayesian analysis to vet these candidates and verify that modest variations in NH are not the result of degeneracies with other spectral component parameters. Specifically, we use the MultiNest nested-sampling algorithm (Skilling 2004; Feroz et al. 2009) via the Bayesian X-ray Analysis (BXA) and PyMultiNest packages (Buchner et al. 2014)8 for XSPEC version 12.10.1f. Standard Markov Chain Monte Carlo (MCMC) algorithms form "chains" by comparing the likelihood of a test point against that of a new point randomly chosen from the prior distribution, and the test point moves to the new point with a probability determined by the likelihoods. However, there may be convergence issues, in that parameter subspaces with non-negligible probabilities can potentially be under-explored by such chains. Nested-sampling algorithms, including MultiNest, attempt to map out all of the most probable regions of parameter subspace: they maintain a set of parameter vectors of fixed length, and remove the least-likely point, replacing it with a point with a higher likelihood, and thus shrinking the volume of parameter space. We use MultiNest version 3.10 with default arguments (400 live points, sampling efficiency of 0.8) set in BXA version 3.31. We paid particular attention to potential degeneracies between NH and each of PC parameters, photon indices of the power laws, and apec component normalizations. For all candidates, pexmon and emission-line parameters were all kept frozen at best-fit values; additional details for individual objects' MultiNest runs are listed in Appendix D.
Given the 90% distribution of the posterior distributions on NH, we conclude that model degneracies do not significantly impact the measured values of NH and that the observed variations in NH are intrinsic to the objects. For brevity, we defer presentation of the confidence contours obtained from the MultiNest runs to Appendix D.
From Table 3, and taking into account the model degeneracies, we conclude that variations in NH are robust for the following objects; here, NH22 denotes NH/(1022 cm−2):
- 1.Cen A/Suzaku, S-3 to S-5: NH22 dropped from 11.03 ± 0.08 (S-3) to 9.98 ± 0.14 (S-5); the 90% confidence interval from the posterior distribution in MultiNest was 0.29.Considering the times and column densities of the other Suzaku observations as well, we infer that NH22 dropped from ∼10.9 in 2009 July–August (S-2–4) to 9.98 by 2013 August (S-5; ΔNH22 = −1.05 ± 0.29). (Unfortunately, there were no XMM-Newton or Suzaku observations during the two spikes in NH obtained from RXTE monitoring, in 2003–4 and 2010–1; Rivers et al. 2011; Rothschild et al. 2011; MKN14.)
- 2.Fairall 49, X-1 to X-2: NH22 increased from 0.067 ± 0.017 in 2001 to 0.75 ± 0.05 in 2013. We ran MultiNest for both X-1 and X-2 separately, given the large difference in measured columns, and the 90% confidence intervals from the posterior distribution spanned 0.03 and 0.05, respectively (we adopt ΔNH22 = +0.68 ± 0.04).
- 3.MCG–5-23-16/XMM-Newton, X-1 to X-2: NH22 decreased from in 2001 December to 1.366 ± 0.012 in 2005 December. The MultiNest 90% confidence interval on X-1's NH22 was 0.01; we adopt ΔNH22 = +0.35 ± 0.01.
- 4.MCG–5-23-16/Suzaku, S-1 to S-2: NH22 dropped from 1.44 ± 0.01 in 2005 December (S-1) to 1.34 ± 0.02 in 2013 June (S-2); the MultiNest 90% confidence interval was 0.02; we thus adopt ΔNH22 = −0.10 ± 0.02.
- 5.NGC 2992, X-1 to X-2: NH22 increased from 0.60 ± 0.01 to 0.82 ± 0.03 from 2003–2010. The MultiNest 90% uncertainty for X-1 was 0.01; Γsoft and kT1 are left free during the MultiNest runs (we adopt ΔNH22 = +0.22 ± 0.01). Curiously, X-1 corresponds to the highest flux state, both in the hard and soft X-ray bands. That is, the soft-band emission seems to track the decrease in hard power-law flux from 2003–2010.
- 6.NGC 5252/Chandra ACIS, CA-1 to CA-2, and CA-3 to CA-4: NH22 increased from 2.84 ± 0.07 in 2003 August (CA-1) to 4.51 ± 0.11 in 2013 March (CA-2). Values for CA-2 and CA-3 are consistent with each other; this is not surprising since the observations occurred only a few days apart. However, NH22 had dropped to 3.51 ± 0.10 by 2013 May. Given the MultiNest 90% confidence intervals, we adopt ΔNH22 = +1.67 ± 0.07 from 2003–2013 and ΔNH22 = −1.07 ± 0.10 from 2013 March to May.
- 7.NGC 5506, X-1, and X-2 to X-3: NH22 increased from 2.77 ± 0.05 and 2.80 ± 0.05 in 2001 and 2002, respectively, to 3.02 ± 0.05 in 2014; given the MultiNest uncertainty on X-1, we adopt ΔNH22 = +0.25 ± 0.07 over a period of 3.5 yr. In addition, as can be seen in Figure 2, the column densities increase from 2001–2004 but then remain consistently constant from 2004–2015
- 8.NGC 7582, X-1 to X-4: NH22 increased from 15.5 ± 1.7 to 29.8 ± 0.5 over Δt = 14.2 yr; ΔNH22 = +14.3, with a combined error from MultiNest runs of 2.7.
Figure 2. The overplot of the spectra of the sources listed in Table 2 and discussed in Section 4 whose full-covering values have varied between the observations. Here the spectra have been binned by a factor of four for plotting and visual purposes only. The source names, instruments, the observation identifiers (obsid), and dates of observations are written in the individual figures.
Download figure:
Standard image High-resolution imageAll of the above eight cases of variability, and the corresponding event durations are listed in Table 5. We present spectral overplots for these sources in Figure 2. For most of them, the variations in NH are modest enough that the change in spectral curvature is not always visually obvious, although the variation in Fairall 49's absorber is quite apparent.
Table 5. Summary of Measurements of Δ a
| Source | Instrumentb | Δ c | Δtd |
|---|---|---|---|
| (×1022 cm−2) | (yr) | ||
| Cen A | S | −1.05 ± 0.29 | 4.0 |
| Fairall 49 | X | +0.68 ± 0.04 | 12.5 |
| MCG–5-23-16 | X | +0.35 ± 0.01 | 4.0 |
| MCG–5-23-16 | S | −0.10 ± 0.02 | 7.5 |
| NGC 2992 | X | +0.22 ± 0.01 | 10.0 |
| NGC 5252 | CA | +1.67 ± 0.07 | 9.6 |
| CA | −1.07 ± 0.10 | 0.17 | |
| NGC 5506 | X | +0.25 ± 0.07 | 3.4 |
| NGC 7582 | X | +14.3 ± 2.7 | 14.2 |
Notes.
aSee Section 4.1 for details. bS, X, and CA denote Suzaku, XMM-Newton EPIC-pn, and Chandra ACIS, respectively. cThe positive and negative signs indicate increase and decrease in values, respectively. dΔt are the event durations. However, due to sparse sampling, these timescales can be regarded as lower limits on the actual event durations.Download table as: ASCIITypeset image
For the other objects in the sample, where there exist multiple observations per telescope, we can rule out variations in NH22 down to approximately
- 1.0.1 (NGC 7314/X), 0.2 (NGC 2992/X, excluding X-1; NGC 7314/CA),
- 2.0.25–0.40 (NGC 526A/CA; NGC 2110/S; NGC 2992/S; NGC 5506/S; NGC 7314/CH),
- 3.0.5–0.8 (Fairall 49/CA; NGC 526A/CH; NGC 6251/CA),
- 4.1.0–1.4 (MCG–5-23-16/CA; NGC 526A/X; NGC 2110/CH; NGC 7172/X),
- 5.1.9–2.3 (IRAS 05189/X; NGC 4258/CH),
- 6.2.7–4.2 (Cen A/X; IRAS 00521/X; IRAS 05189/CA; NGC 1052/X; NGC 4258/CA; NGC 4258/S; NGC 6300/CA),
- 7.7 (Mkn 348/X; NGC 4258/X), 10 (Cyg A/CA),
- 8.17 (NGC 4507/X), and
- 9.20 (NGC7582/S).
However, the reader is reminded that these limits are based on the statistical error on NH only and do not take into account potential model degeneracies with other parameters such as PC parameters. In addition, the various object/instrument combinations do not have equal numbers of points nor do they cover the same durations, so these limits cannot be considered to be uniformly derived in those senses. We present the overplots of the spectra of these sources ( not varied) in Appendix C Figures C1–C20.
4.2. Variability in NH across Multiple Instruments
Across the full sample, we would like to be able to, ideally, cross-calibrate values of full-covering column density between different instruments from different missions, and thus derive systematic differences in , which can enable us to not only create one combined NH light curve for each object, but to interpret it as well. However, doing so is particularly difficult for this sample of absorbed type IIs, for multiple reasons. Any offset value in we try to compute (e.g., (ACIS) − (XMM)) would likely have strong object-to-object and/or telescope-to-telescope variance due to: (1) differing soft-band spectra—even for the same object—as different extraction regions and effective areas/responses can lead to differing modeled contributions from extended thermal emission; (2) intrinsically variable hard X-ray power-law slope values from nonsimultaneous observations of the same object; and (3) in a few objects, PC components are detected only in a fraction of the observations. Finally, the location of the continuum rollover due to absorption will be quite different from one object to the next, given the wide range of column values and given how differences in response and effective area between any two telescopes evolve with energy; comparing systematic offsets between missions for objects with NH ∼ 1021 cm−2 to those obtained for ∼1023 cm−2 thus may not be highly fruitful. Consequently, a detailed analysis of the full range of potential systematic differences in NH (or other parameters) is beyond the scope of the current paper.
Nonetheless, we can still consider simultaneous observations of the same object as an initial exploration of such systematic differences, and derive approximate thresholds for detecting gross changes in full-covering NH. The only quasi-simultaneous observation of a source with all three missions is that of MCG–5-23-16 (observation IDs: CH-2, CH-3, X-2, and S-1), which occurred on 2005 December 7–10, and analyzed by Reeves et al. (2007); S-1, X-2, and CH-2 were in fact directly overlapping from 2005 December 8 ∼21 UTC until 2005 December 9 ∼2 UTC; S-1, X2, and CH-3 were directly overlapping from 2005 December 9 ∼21 UTC until 2005 December 10 ∼3 UTC. CH-2 and CH-3 did not yield any significant spectral variability, so we henceforth average the best-fit model parameters. We find NH22 (CH) − NH22 (X) = 0.00 ± 0.25, NH22 (S) − NH22 (CH) = 0.07 ± 0.25, and NH22 (S) − NH22 (X) = 0.07 ± 0.02 (CH, X, and S denote Chandra HETG, XMM-Newton, and Suzaku, respectively). That is, one can conclude that values of NH22 measured from Suzaku will be 0.07 ± 0.02 higher than those for XMM-Newton in the absence of intrinsic variability in column density. However, such a conclusion would only be reasonably applicable to those sources with a spectral shape very similar to that of MCG–5-23-16: full-covering NH ∼ 1.0–1.8 × 1022 cm−2, no PC component, and extremely low amounts of soft thermal emission and scattered power-law emission below 1 keV (see, e.g., Figure 4 of Reeves et al. 2007). In the Suzaku XIS spectrum, for instance, the value of spectral counts in counts s−1 keV−1 drops by well over an order of magnitude from ∼2 to ∼0.7 keV. Across our sample, only NGC 526A has a similar spectral shape. Considering observations taken two years apart, values of best-fit full-covering NH for NGC 526A's S-1 observation (in 2011) and X-3 (in 2013) yield NH22 (S) − NH22(X) = 0.19 ± 0.09, a bit higher than for the (simultaneous) observations of MCG–5-23-16. Similarly, offsets to NH22 (CH) are consistent with the upper limits derived for MCG–5-23-16. We conclude that the measured differences in NH between various missions for NGC 526A are consistent with inter-mission systematic offsets, and there is no evidence for variability in here.
Cen A also has a pair of simultaneous observations (X-5 and S-6) and a pair separated by eight days (X-4 and S-5). Assuming that the column does not vary on timescales shorter than eight days, these pairs of observations would imply that NH22 (X) is roughly 1.1–1.4 higher than NH22 (S) for objects with a spectral shape similar to that of Cen A. However, most of the other objects with columns similar to that of Cen A have very strong soft-band emission (NGC 4258) and/or partial coverers (e.g., Mkn 348 and NGC 4507), so a straightforward application is not possible.
Across the sample, excluding those sources where we have claimed variability in full-covering NH, we find that ratios of for the following instrument pairs typically span: NH(CA)/NH(X) ∼ 0.3–1.2, NH(CH)/NH(X) ∼ 1.0–1.7, NH(CH)/NH(CA) ∼ 0.8–2.3, and NH(S)/NH(X) ∼ 0.7–1.0. These ratios show that there is no general trend of any instrument consistently detecting higher/lower values of for the same source compared to other instruments. In addition, under the assumption that NH is intrinsically non-varying in these sources, these ratios demonstrate the approximate level of sensitivity required to claim variability in between different telescopes. While comparing the values of for a given object from different instruments, we conservatively consider differences in to be significant only if their ratio is greater than ∼2; to that effect, we do not find any object to display significant variability in full-covering up to this factor between different instruments.
At this point, it is worth noting a few important differences between the results found by Risaliti et al. (2002, hereafter REN02) and our work. Fifteen out of 20 sources in the sample by REN02 overlap with our sample. However, we do not detect variability with the same frequency as detected by REN02. Possible causes include: (1) REN02 considered variability in as obtained from different missions to be bona fide. However, relative flux and energy cross-instrument calibration issues likely play a role, different instruments had different apertures and/or energy bands, and in addition, model degeneracies play an important role in estimating the errors on the measured , which the authors have not considered. (2) The various sources were analyzed by different authors using different techniques and models, thus introducing an unknown amount of scatter in the errors derived on the measured parameters. (3) The data were obtained using missions that sometimes had a poorer energy resolution and/or narrower bandpass compared to our work. (4) The data quality did not allow REN02 to detect and constrain any PC absorption as we could do in our work.
4.3. Note on Partial-covering Absorbers
For four sources in our sample (Fairall 49, IRAS F00521–7054, NGC 1052, and NGC 4507), we consistently detected PC absorption components in all observations; in addition, in Mkn 348 we detected PC components in all but one observation. We have seven sources in which we detected PC absorption in some of their observations (Cen A, IRAS F05189–2524, Mkn 348, NGC 2110, NGC 5252, NGC 7172, and NGC 7582). Among these 11 sources (in total), PC column densities are typically cm−2 and with covering fractions fpc typically spanning ∼0.3–0.9. The detection of a partial coverer is independent of the value of the column density of the full coverer or the spectral index Γ, implying that the detection of the partial coverer is bona fide in these cases. In virtually all cases, the errors in both and/or fpc are large and impacted by some degree of model degeneracy, preventing us from making any statement about variability or constancy in these PC model parameters as a function of time, though the PC model component is statistically required in the fits in these cases. Future broadband (0.3–50 keV) high-S/N observations can distinguish between the following scenarios: (1) if the PC components are intrinsically variable in terms of crossing the line of sight, (2) or if they are not detected due to the complexity of the strongly absorbed spectrum and/or the lack of spectral coverage above 10 keV for XMM-Newton and Chandra, (3) or simply due to a lack of S/N.
5. Discussion
In this work, we have conducted a systematic study of variations in line-of-sight absorption column density NH across a sample of perpetually absorbed Compton-thin type II AGN. We have improved upon the RXTE-based study of MKN14 by using XMM-Newton, Chandra, and Suzaku, which yield comparatively greater sensitivity to smaller variations in ΔNH (by roughly an order of magnitude) as well as greater sensitivity to PC absorbers. We have classified the full-covering absorbers in each source into variable or non-variable (down to sensitivity levels of roughly 3%–10% when considering a single telescope, or factors of, very roughly, two when comparing inter-telescope data). We find evidence for variability in the full-covering obscuration components in seven sources (Cen A, Fairall 49, MCG–5-23-16, NGC 2992, NGC 5506, NGC 5252, and NGC 7582) to vary on timescales of 2 months to 14.5 yr, with values of spanning ∼0.1 to 1.9 × 1022 cm−2; in all cases, the variability is at the ≥3σ level. We also find that almost half the sources in our sample (9/20) require a PC absorber in all or almost all of their observations.
Below, we discuss the nature and location of the various absorbing components. In short, variable full-covering X-ray-obscuration components likely delineate compact-scale gas (less than ∼1–10 pc), which could be associated with the dusty or non-dusty components of the "torus." Meanwhile, non-variable columns could potentially indicate either distant material residing at scales of 0.1 kpc, to a few kpc such as dust lanes, or it could potentially indicate smooth (non-clumpy) homogeneous compact-scale gas Figure 3 shows a schematic representation of the three types of obscurers discussed in this work.
Figure 3. This image depicts the three types of probable neutral absorbers responsible for the absorption column density measured in the X-ray spectra of Compton-thin Type II AGN. The distance scales of the absorbers are highly uncertain.
Download figure:
Standard image High-resolution image5.1. The Full-covering X-Ray-obscuring Gas
5.1.1. Variable Full-covering NH, and Implications for Compact-scale Gas
As stated above, we detected eight occurrences of variable full-covering NH across seven sources. We discuss three physical models below, although the sparse sampling makes it impossible to fully distinguish between these models and thus discern the true nature of the variable-NH gas in each of the seven objects where variability in NH was detected. We did not, for example, detect any new complete eclipse events, with egress and ingress, for which sustained monitoring is usually necessary, e.g., as RXTE provided for variability on timescales of days to years, or as long-looks from XMM-Newton provided for timescales ≲1 day. Nonetheless, even establishing variability in full-covering NH is a rudimentary first step because it establishes the presence of relatively compact-scale gas contributing to the total observed value of NH.
Model A: All full-covering obscuration is due to discrete clumps only, e.g., in the torus, following Nenkova et al. (2008), and an observed increase (decrease) in NH indicates the number of clouds along the line of sight increasing from N to N + 1 (decreasing from N + 1 to N), where N cannot be zero for our perpetually absorbed sample. Ingress/egress of individual clouds should cause a step-like behavior in NH if the whole cloud enters the line of sight faster than the observation sampling. However, if a cloud ingress occurs very slowly relative to the observation sampling, then a slow increase/decrease in NH could be observed, depending on the cloud's transverse density profiles.
We do not have sufficient data to determine what the "average" value of NH corresponding to N clumps is for any source. We thus assume for simplicity that the lowest measured values of NH correspond to N clouds. We also use the simplifying assumption that all individual clouds have identical column densities. If the observed values of ΔNH correspond to ingress (egress) of one cloud into (out of) the line of sight, then, for example, the observed increases in NH in both NGC 2992 and NGC 5252 could each correspond to an increase from ∼3 to 4 clouds.
Model B: Full-covering obscuration is explained by the sum of a time-constant component (e.g., kiloparsec-scale dust structures, as discussed below) plus some number of compact-scale discrete clumps. Here, the extremely sparse sampling of our data precludes us from being able to cleanly separate the light curve into "eclipsed" versus "non-eclipsed" periods (in contrast to the sustained monitoring provided by RXTE).
We do not observe both ingress and egress for any variability event, so we would not be able to estimate radial distance to the occulting structure (e.g., following Risaliti et al. 2002, Equation (3), which assumes Keplerian motion) invoking assumptions on full eclipse duration and in particular cloud density.
Such constraints are necessary to obtain accurate distances and thus meaningful insights into the physical processes that create and sculpt clouds. For example, it would help to know if clouds are inside or outside the dust sublimation region, since the presence of dust can play a crucial role in the physical processes that form, shape, and drive compact structures, e.g., via radiation pressure on dust to drive winds (Czerny & Hryniewicz 2011; Dorodnitsyn & Kallman 2012; Baskin & Laor 2018).
In a third model, Model C, the variable component of the X-ray obscuration is due to a non-clumpy, volume-filling (contiguous), compact-scale medium, which contains inhomogeneities that transit the line of sight. MKN14 discuss a similar interpretation of the observed (t) light curve derived from RXTE monitoring of Cen A during 2010–2011. In addition to sharp increases in column density, interpreted as transits by discrete clumps, they detected a smooth decrease then increase by ≳10% over an 80 day span.9 In the current study, we observe an increase in in the XMM-Newton observations of NGC 5506 over a period of 3.5 yr, followed by remaining constant for an additional 11 yr. While we cannot completely rule out that this trend is due to ingress by a single cloud, it is unlikely unless the cloud has a rather contrived transverse density profile. Such smooth trends argue against the clumpy-torus model being able to explain all of the observed absorption in these two objects: ingress/egress of individual clouds would produce sharp step functions in the light curve, but the observed smooth trends (particularly in the RXTE data for Cen A) argue against such an interpretation. One possibility is that these variations are due to the line of sight's passing through a contiguous component of the torus (i.e., possibly an inter-cloud medium; Stalevski et al. 2012), and relative over- or under-dense regions transit the line of sight. That is, during 2001–2004, the line of sight in NGC 5506 was transited by a relatively under-dense region (by ≥8% relative to the long-term average), thus causing the observed "dip" in . Our observations thus provide constraints for column density ratios in such media for these cases.
5.1.2. Constant-NH Sources: Origin?
For 13 objects in our sample, the full-covering obscurer's column density is consistent with being constant in time, down to sensitivity levels of ΔNH ranging from ∼0.1 to 17 × 1022 cm−2. Could such obscuration be due to a single discrete cloud? At a distance of a few parsecs and beyond, typical velocities are of the order of hundreds of kilometers per second. To obscure for approximately a decade, its transverse diameter must be at least of the order of light-days. This is a very unrestrictive limit, not much larger than the inferred sizes of X-ray clumps so far. Furthermore, some models posit large-scale structures at tens of parsecs comprised of filaments of the order of a parsec thick (e.g., Wada 2012). However, a decade-long eclipse by a single cloud would require a near-uniform cloud density in the transverse direction, which is a somewhat contrived scenario. It is also highly unlikely that the bulk of the objects in our sample each have such a cloud along their lines of sight. For these objects, and/or to explain any potential non-variable component in the variable-NH objects, we therefore consider the following three interpretations:
(a) In the context of the clumpy-torus model of Nenkova et al. (2008), there could potentially exist a large number of clouds N along the line of sight, each with a very low value of NH, such that ingress/egress of individual clouds does not change N or the observed value of NH by perceptible amounts, giving us an impression of a non-varying column. For a fiducial total column of, say, 1022 cm−2, and limits on sensitivity of ΔNH ∼ 1021 cm−2, there would typically have to be at least ∼10 clouds with columns less than or equal to this limit in order to give us the impression of a non-varying . However, from theoretical considerations, Nenkova et al. (2008) posit that individual clouds each typically have visual optical depths of ∼30–100, corresponding to NH ∼ 8–20 × 1022 cm−2 for typical Galactic dust/gas ratios (e.g., Nowak et al. 2012), so a large number of clouds each with column ∼1021 cm−2 is unlikely.
(b) A smooth, contiguous, compact torus or inter-cloud medium: To model the IR emission of dusty tori, Stalevski et al. (2012) and Siebenmorgen et al. (2015) assumed the torus to exist in a two-phase medium, with high-density clouds and low-density gas filling the space between the cloud. In our study, the constant level of observed in X-rays may denote the inter-cloud medium, while the higher column density partial coverers and/or variable absorbers detected in X-rays denote the high-density clumps. In this case, the limits on column density between relative over- or under-dense regions must be ≲1021 cm−2 for the relatively less-absorbed sources in our sample.
(c) Host-galaxy dusty structures, e.g., lanes or filaments: A constant level of full-covering X-ray obscuration could also be attributed to dusty gas residing along the line of sight at scales ≳0.1 kpc to several kiloparsecs. As noted in the Introduction, there are multiple indications that the host galaxies of optical type II sources themselves may play a role in the observed X-ray obscuration and optical extinction.
Ideally, we would like to go through each source on a case-by-case basis, and compare the observed value of NH to values of NH estimated from both (1) AV from known sources of dust residing at kiloparsec scales and (2) AV from the dust residing in the parsec-scale torus at radial distances outside Rdust. If component (1) alone can fully account for NH, it would minimize the need to invoke a torus intersecting the line of sight (at least in that given object). If components (1) and (2) both exist and cannot account for , it would indicate a significant amount of non-dusty gas in a given object, likely residing inside Rdust. There are various known sources of dust extinction for many of our sources, as measured by Balmer decrements to narrow lines (e.g., several of our sources are contained in the samples of Maiolino et al. 2001 and Malkan et al. 2017), high-spatial resolution color–color maps (e.g., with HST; Mulchaey et al. 1994a; Schreier et al. 1996; Prieto et al. 2014), and NIR-MIR spectral fits (see, e.g., Burtscher et al. 2016). We could also consider 9.7 μm absorption as studied by Gallimore et al. (2010) using Spitzer: the Si-containing gas absorbs 9.7 μm continuum from warm dust, and must be due to gas more extended than that warm dust.
However, there are multiple obstacles to this goal:
(1) The above methods to determine AV cannot cleanly separate dust extinction along the total line of sight due to kiloparsec-scale dust lanes versus that due to a compact torus: one simply gets the total extinction along the line of sight.
(2) Certain methods (color–color maps, spectral fits) may lack the spatial resolution to guarantee that all optical extinction along the line of sight to the AGN is indeed accounted for; there might, potentially, be some compact giant molecular cloud lying along the line of sight that would be missed by the above methods, but would contribute to . It is even possible that NH along the line of sight could be overestimated if there exists a hole not picked up by the above methods.
(3) In those cases where individual kiloparsec-scale dust structures are resolved and noted to cross the line of sight to the nucleus ("DC" in Malkan et al. 1998), but where dust extinction maps (from color–color maps) have not yet been made, we could attempt to assign a "canonical" or "generic" value of AV to all dust lanes. For example, based on color–color maps made with HST for nearby Seyferts, AV is typically ∼0.5–2 mag (e.g., Mulchaey et al. 1994a), or AV ∼ 3–6 in the case of Cen A's famous dust lane (Schreier et al. 1996). Applying this to all galaxies, however, is dangerous: there is very strong dispersion from one dust lane to the next and from one line of sight to the next.
We found 45 total estimates of either V-band extinction or 9.7 μm Si line optical depth for our 20 sources from the literature, taken from the aforementioned references; see Figure 4. In estimating the corresponding values of NH, we assume the Galactic dust/gas conversion of Nowak et al. (2012): NH = AV × 2.7 × 1021 cm−2 mag−1. For the Si line optical depths in Gallimore et al. (2010), we multiply by 10 to obtain estimates of AV.
Figure 4. Mean values of full-covering column density for each object in our sample are plotted in ranked order. Superimposed are estimates of X-ray-absorbing column density based on various optical or IR extinction, assuming the standard Galactic dust/gas conversion: Balmer decrements for broad lines or narrow lines (Maiolino et al. 2001; Malkan et al. 2017, respectively), 9.7 μm Si line absorption (Gallimore et al. 2010), IR SED modeling (Burtscher et al. 2016), or color–color maps (Mulchaey et al. 1994a, 1994b; Schreier et al. 1996; Prieto et al. 2014). "ΔNH" denotes a detection of variability in the full-covering absorption component as measured in this paper. "PC" denotes those 11 sources wherein a PC component was detected in most or all of a given sources' observations. The top row denotes the nuclear dust morphology classification from Malkan et al. (1998), for those sources included in their sample; "DC," "D-[directional]," "DI," and "F/W" denote a dust lane directly crossing the line of sight to the nucleus, a dust lane just offset from the line of sight to one direction, irregular dust, and flocculent/wispy gas, respectively.
Download figure:
Standard image High-resolution imageThe median value (in linear space) of all of these estimates is NH = 0.84 × 1022 cm−2, and the 16th/84th percentiles are 0.40 and 2.1 × 1022 cm−2, respectively. There are some individual cases for which various measurements of AV in the literature imply values of NH that are roughly equal to or greater than our measured values, raising the possibility that all dusty gas (kiloparsec + parsec scale, in total) can indeed account for all X-ray obscuration, and that there is no need to invoke non-dusty gas inside Rdust. However, other measurements (sometimes for the same object) yield estimates of NH that fall short.
We can only make the very general conclusion that when NH is of the order of magnitude 1022 cm−2 or higher, there is a relatively increased likelihood that a component of non-dusty gas (likely inside Rdust and thus part of the innermost compact torus) exists. For smaller columns, there is a relatively increased likelihood that dust-containing structures intersecting the line of sight (sum of kiloparsec-scale and dusty parsec-scale structures) can explain NH. Our conclusions are generally consistent with those of several early and recent studies aiming to separate the contributions of galaxy-scale dust lanes and nuclear obscuration such as Matt (2000), Guainazzi et al. (2001), Guainazzi et al. (2005), and Buchner & Bauer (2017).
Although subject to very low number statistics, a Kolmogorv–Smirnov (K-S) test indicates that the distributions of values of NH in the -variable and the NH-non-variable subsamples are consistent with arising from the same parent population (the null hypothesis in the K-S test cannot be ruled out at a confidence of even merely 50%). See the right panel of Figure 5 for the two distributions. This finding would suggest that in Compton-thin obscured type IIs, neither the structures that comprise nonhomogeneous tori (and thus -variable) nor the structures comprising constant-NH media (be they due to host-galaxy structures or a homogeneous compact torus) have a preference for relatively high or low columns.
Figure 5. Left panel: the histogram plots for the values of the two sets of sources in our sample, the ones that have been detected with PC absorption (red solid line), and the ones that do not have partial absorbers (blue dashed–dotted line) Right panel: same as left panel, except that here we consider the sets of sources that have shown variability (pink bold line) and the ones that have not shown variability (black dashed–dotted line).
Download figure:
Standard image High-resolution image5.2. Sources with Partial-covering Absorption
As mentioned earlier, previous sample studies on X-ray absorption in Seyfert-2 galaxies, such as in Markowitz et al. (2014), used RXTE, which was not highly sensitive to PC and lower column density ( ≤ 1021 cm−2) absorbers. However, XMM-Newton, Chandra, and Suzaku are, and hence we can additionally constrain partial coverers apart from full coverers. Eleven out of 20 sources in the sample show signatures of PC absorption. Many similar PC absorption features have been identified in other observations of Seyfert galaxies such as NGC 1365 (Risaliti et al. 2009), Mkn 766 (Risaliti et al. 2011), and NGC 3227 (Turner et al. 2018), including previous observations of objects in our sample, e.g., NGC 7582 (Bianchi et al. 2009). However, our small sample spans a relatively small range in system parameters such as L2–10 keV and Lbol/LEdd, and thus extrapolation to determining the fraction of sources hosting sustained PC components across all Compton-thin and/or optically identified type IIs in the local universe is not straightforward. In our sample, we find the best-fit covering fractions spanning typically 30%–90% and column densities spanning 1–80 × 1022 cm−2 (assuming a neutral absorber in our model). We must note as a caveat that we do not have strong data constraints on PC model parameter values, given the CCD energy resolution and model complexity. We thus caution the reader not to interpret measured changes in PC and/or covering fraction too literally. There may exist multiple clouds residing and partially covering the line of sight, but we cannot discern ingress/egress of individual clouds; current data thus prevent us from confirming or rejecting this notion. Constraints on the sizes and the location of PC clouds from our data alone are not strong. If the clouds partially cover the corona, then the clouds must be smaller, so a corona size of say 10–30 Rg provides an upper limit on the size of the cloud. For example, for a 108M⊙ black hole, 30 Rg = 4.5 × 1014 cm. Such sizes are consistent with estimates using occultations by individual clouds (e.g., NGC 1365; Risaliti et al. 2009). Since we detected only neutral absorbers in our fits (and no ionized absorbers), we do not have a good handle on the ionization parameter of these clouds. For that matter, any value of the ionization parameter ξ that yields strong continuum curvature at ∼6 keV or below is plausible. Constraints based on ionization parameter generally thus only provide a rough lower limit to the radial distance of (order of magnitude) a light day in most cases.
The consistency of the PC components over a decade could indicate that there exists a population of clumps that are long-lived and orbiting mostly in Keplerian motion, with clouds either too dense to be tidally sheared by the SMBH, or else confined eternally by the ambient gas and pressure or a magnetic field (Rees 1987; Krolik & Begelman 1988). Another possibility is a mechanism that continuously produces clumps and deposits them along the line of sight, and that is both active and stable over timescales of at least one to two decades. Potential mechanisms include magnetohydrodynamic-driven winds (Blandford & Payne 1982; Contopoulos & Lovelace 1994; Konigl & Kartje 1994; Fukumura et al. 2010), or a turbulent dusty disk wind as proposed by Czerny & Hryniewicz (2011). The PC column density from our sample is mostly consistent with those derived by Fukumura et al. (2010). If the physical conditions in the disk remain stable over a timescale of years, then it is not hard to envision a persistent wind process.
Using a K-S test, we find that the distributions of the values of full-covering of sources with and without partial coverers are consistent (i.e., the null hypothesis in the K-S test cannot be ruled out at a confidence of even merely ∼60%, implying that these samples have been likely derived from the same parent sample), and suggest that the full and partial coverers are two independent components. See the left panel of Figure 5 for the two distributions.
6. Conclusions
We carried out an extensive X-ray spectral variability study of a sample of 20 Compton-thin Seyfert-2 galaxies to investigate the nature of the variability of the neutral intrinsic absorption in X-rays along the line of sight, and derive constraints on the location and properties of the X-ray obscurer. We are sensitive to an absorption column density of ∼ 1020.5–23.5 cm−2 of fully and partially covering, neutral and/or lowly ionized clouds transiting along the line of sight on timescales of days to decades. We list below the main conclusions from our study:
- 1.We detected variability in full-covering absorption column in X-ray spectra of seven out of 20 objects at ≥3× the 90% confidence level (obtained from spectral fits), implying compact-scale, nonhomogeneous gas along our line of sight in those objects. We detected variations as small as ∼1–2 × 1021 cm−2 in some objects (see Table 5). Models that explain torus geometry by invoking discrete clouds or other compact structures thus must include the possibility of structures with values of column density as small as these.
- 2.For most of these seven objects, due to their sparse sampling, we cannot distinguish between variability due to discrete clouds transiting the line of sight or a contiguous (volume-filling) inhomogeneous medium. An exception, though, is NGC 5506, in which we observe an increase in over 3.5 yr, followed by remaining constant for an additional 11 yr. Such a trend is qualitatively similar to the "dip" in in Cen A noted by MKN14. These trends are difficult to explain in the context of clumpy-torus models; one possible explanation is that the variable component of its column density originates in a nonhomogeneous contiguous medium. That is, we observed a relatively under-dense region (by ≥8% relative to the long-term average) transit the line of sight in NGC 5506 before 2004.
- 3.We do not detect any significant variability for 13/20 sources. Nuclear variability of Compton-thin type IIs is thus far less prevalent than previously reported in the literature. The X-ray obscurers in these sources may be associated with a contiguous, highly homogeneous (column density variations typically <∼1021 cm21) compact-scale medium. They could instead be associated with large-scale dusty structures or filaments intersecting the line of sight at distances of ≳0.1–1 kpc, consistent with previous studies.
- 4.We detected PC absorption in 11/20 sources over one to two decades, suggesting a long-lived population of clumpy clouds or a long-lived mechanism for producing such clouds. The distributions of the values of full-covering of sources with and without partial coverers are consistent, suggesting that the full and partial coverers are two independent components. There are six sources for which we detected PC absorption in some of their observations, but we refrain from commenting on the variability and/or the properties of the partial coverers due to a lack of signal-to-noise and lack of broad bandpass (0.3–50 keV) in 80% of our observations (XMM-Newton and Chandra). Future broadband (0.3–50 keV) high-S/N observations can distinguish between the following scenarios: (1) if the PC components are intrinsically variable in terms of crossing the line of sight, (2) or if they are not detected due to the complexity of the strongly absorbed spectrum and/or the lack of spectral coverage above 10 keV for XMM-Newton and Chandra, (3) or they not detected simply due to lack of S/N.
- 5.We do not observe any Compton-thin to -thick transitions, or vice versa, in our sample.
- 6.The distributions of average values of in the -variable and the -non-variable subsamples are consistent with arising from the same parent population, suggesting that in Compton-thin obscured type IIs, neither the structures that comprise nonhomogeneous tori (and thus -variable) nor the structures comprising constant- media (be they due to host-galaxy structures or a homogeneous compact torus) have a preference for relatively high or low columns. We are however limited to small number statistics (see Figure 5).
Future X-ray observations of larger samples of Compton-thin-obscured Seyferts can yield additional insight into compact-scale X-ray obscurers, the applicability of clumpy-torus models, and the potential presence of compact-scale non-clumpy gas such as an inter-cloud medium by further quantifying the fractions of sources with variable full-covering NH. Specifically, the community needs the combination of sustained multi-timescale monitoring (to probe spectral variability on timescales from days to years), as RXTE provided, plus soft X-ray coverage with at least CCD-quality resolution, as provided by XMM-Newton, Chandra, and Suzaku, to build a new database of NH variations, and distinguish among the various physical explanations for variations in .
S.L. and A.G.M. acknowledge financial support from NASA via NASA-ADAP Award NNX15AE64G. S.L. and A.G.M. thank Matt Malkan for insightful discussions. A.G.M. and T.S. both acknowledge partial funding from Narodowy Centrum Nauki (NCN) grant 2016/23/B/ST9/03123. M.K. acknowledges support from DLR grants 50OR1802 and 50OR1904. The authors thank Johannes Buchner for assistance in setting up and running BXA and MultiNest. This research has made use of data obtained from the Chandra, XMM-Newton, and Suzaku missions by NASA, ESA, and JAXA. This work has made use of HEASARC online services, supported by NASA/GSFC, and the NASA/IPAC Extragalactic Database, operated by JPL/California Institute of Technology under contract with NASA. S.L. is grateful to Jay Friedlander (NASA-GSFC) for making the cartoon figure of the absorbers.
Appendix A: Previous Studies and Details of Analysis of the Sources in the Sample
In this section we discuss the previous studies of the sources in the sample in the context of the analysis we have carried out and science goals in the paper. We also comment on a few important issues in the analysis for each of the sources and the best-fit baseline model used in each case. Here NH22 denotes /(1022 cm−2):
- 1.CenA: This is the nearest radio-loud galaxy. RXTE monitoring revealed two previous eclipse events by transiting clouds, each causing total line-of-sight NH to increase by 8 ± 1 × 1022 cm−2: one in ∼2003–2004 and one in 2010–20011, studied by Rothschild et al. (2011) and Rivers et al. (2011), respectively. MKN14 inferred these clouds to reside in the inner dusty torus. As described earlier, MKN14 also noted mild, smooth variations in the baseline level of NH, thanks to the combination of Cen A's X-ray brightness and sustained, regular monitoring (and to our knowledge, this is the only such case so far).Chandra data for the core of Cen A were not usable; the pileup was too severe to derive any reliable fluxes or spectral slopes (even with modeling the pileup during spectral fitting). Hence the Chandra observations were not used for this source.Following, e.g., Markowitz et al. (2007), we model the soft-band emission for the Suzaku data using two apec components plus a flat power law, the latter to model blended emission from point sources, jet components, and diffuse emission. For XMM-Newton data, using only one apec component sufficed; adding a second, lower-temperature component yielded no improvement to the fit and poor parameter constraints. No strong evidence for a Compton reflection component has been found so far. Various studies with RXTE, Suzaku, INTEGRAL, and NuSTAR have yielded upper limits to the pexrav reflection fraction R of, e.g., 0.28, 0.05, 0.05, 0.01, and 0.005 by Beckmann et al. (2011), Markowitz et al. (2007), Benlloch et al. (2001), Fürst et al. (2016), and Rivers et al. (2011), respectively; we thus freeze R at 0 in our fits.We find evidence for a PC component in observation S-1, consistent with Markowitz et al. (2007), and in X-6. We also modeled PC components for S-2, S-3, and S-4, following Fukazawa et al. (2011). However, for S-2, S-3, and S-4, the improvement in fit when the PC component is added is modest, the covering fractions are quite low, and moreover, values of NH,pc are poorly constrained in each case, usually falling to the same value as NH,full. We detected that NH22 dropped from 11.03 ± 0.08 (S-3) to 9.98 ± 0.14 (S-5) and hence consider this source as a variable source.
- 2.Cyg A: This is another powerful radio galaxy. Reynolds et al. (2015) observed the source with NuSTAR and measured a power law Γ = 1.7, a neutral absorption column of ∼ 1.6 × 1023 cm−2, a Compton hump at energies >10 keV with a reflection coefficient of R = 1.0, and a high-temperature thermal emission in the soft X-rays modeled by apec (kT ∼ 6.4 keV).Here, we describe the Chandra ACIS observations of Cyg A. The active nucleus is embedded in hot, X-ray emitting gas, and Chandra ACIS has been used to image both the active nucleus and the surrounding cluster gas (e.g., Snios et al. 2018, and references therein). The archive contains dozens of observations aimed at mapping the cluster emission, with the effect that the nucleus was not observed consistently, with many observations using different ACIS-I or ACIS-S chips and having different off-axis angles to the nucleus.We excluded those observations where the nucleus was located in a chip gap. Backgrounds were generated using the CIAO "blanksky" tool, as the cluster gas usually fills the majority of the ACIS chip field of view. Our model included a hard X-ray power law absorbed by a full-covering absorber; the photon index of the hard power law was always poorly constrained, and we froze it at 1.7. We also included two apec components and a soft power law whose photon index was also frozen at 1.7. The apec components typically had temperatures of 0.73 and 4.0 keV.We paid attention to those observations where the nucleus was within 16'' from the edge of a chip, as dithering could cause some fractions of photons to fall into the chip gap. However, we did not see any significant deviation in model parameters in these observations. We searched for, but did not detect, any correlation between NH and the off-axis angle of the nucleus, or between NH and the temperature of either thermal component; there was also no correlation with the ACIS chip used.We find a mean value (standard deviation) in NH,full of (25.6 ± 2.1) × 1022 cm−2. Given the variation in observations from one obsid to the next (e.g., different offset pointings, the nucleus falling on different chips), we conservatively avoid concluding that measured variations in NH,full from one obsid to the next are intrinsic to the source, although we can rule out the presence of strong systematic trends of the order of 1024 cm−2. See Table B1 for details of the best-fit parameters.The best-fit model used is tbabs∗(apec+apec(2)+powerlaw(1)+ztbabs∗(pexmon+powerlaw(2)+zgauss)). We do not detect significant variability in for this source.
- 3.Fairall 49: Also known as IRAS 18325-5926. The source was studied by Iwasawa et al. (2004) who found a relatively steep power-law slope Γ = 2.2, and a neutral absorption column of = 1.62 × 1022 cm−2. Kawamuro et al. (2016) detected a PC absorption with a covering fraction of fPC = 0.22 and column density of = 3.2 × 1022 cm−2, in addition to a full-covering absorption, with Suzaku observations. We detected partial covering in addition to full-covering absorption in all of the observations, except for CH-2, where the low S/N did not allow us to constrain of the partial absorber. We detected significant variability in for this source with XMM-Newton observations, with variations of by almost an order of magnitude. The best-fit model used is tbabs∗(apec(1)+powerlaw(1)+ztbabs∗zpcfabs∗(pexmon+powerlaw(2)+zgauss)).
- 4.IRAS F00521–7054: Ricci et al. (2014) modeled the X-ray spectrum by a steep power law of Γ = 2.2–2.3, obscured by a neutral column of ∼ 1022.9 cm−2, in addition to a blurred ionized disk reflection component with a reflection coefficient of R = 2.7. In our study, we too detected a steep power-law slope pegged at Γ = 2.5. The best-fit model is tbabs∗(apec+powerlaw(1)+ztbabs∗zpcfabs∗(pexmon+powerlaw(2)+zgauss)). We do not detect any significant variability in for the source, as was also concluded in a recent study by Walton et al. (2019) using NuSTAR observations.
- 5.IRAS F05189–2524: A detailed study of this source has been carried out by Teng et al. (2009), where the authors have found interesting variability in spectral shape and flux between different observations taken between 2001 and 2006 with Chandra, XMM-Newton, and Suzaku satellites. The source has shown an increase in obscuring column by a factor of 10 from 2002 (Chandra) to 2006 (Suzaku) observations, although the intrinsic unabsorbed 2–10 keV flux is constant over time. This source has been studied as a part of a sample of ULIRGs by Teng & Veilleux (2010) using Chandra observations. They found that for different observations, the hard X-ray power law varied from Γ = 1.4–2.3 (between 2001 and 2002 observations). They also detected a non-variable PC absorber of the source with ∼ 7 × 1022 cm−2 and a covering fraction of fpc ∼ 0.96. A more recent study by Teng et al. (2015) using NuSTAR data revealed a power law Γ = 2.5 and two PC absorbers of of 5.2 × 1022 cm−2 and 9.3 × 1022 cm−2 with covering fractions of 98% ± 0.2% and 74% ± 1.2%, respectively. Another study by Xu et al. (2017) using NuSTAR and XMM-Newton observations constrained the power-law slope Γ = 2.29 and Pexrav reflection component R = 1.48. In our study, we too required a partially covering neutral intrinsic absorber, but only for the observation X-2. The best-fit model used is tbabs∗(powerlaw(1)+apec+ztbabs∗zpcfabs∗(zgauss+pexmon+powerlaw(1)+zgauss(2))). We do not detect any significant variability in for the source.
- 6.MCG–5-23-16: Zoghbi et al. (2017) observed this source using NuSTAR for 0.5 Ms, with a focus on the relativistic reflection and primary coronal emission. The authors detected the presence of reflection features with a reflection coefficient of R = 0.84. Braito et al. (2007) carried out a time-resolved spectral study of this source and found that there is an absorption variability intrinsic to the source.In our study, we found that the X-ray spectra of this source are quite complex for all of the observations. In particular the high-S/N long exposure XMM-Newton observations X-2, X-3, and X-4 (∼130 ks each) exhibited several discrete spectral features that were visible after the "basline" model fit. We found that in the cases of X-2, X-3, and X-4, the FeKα emission line and the Compton reflection hump could not be modeled simultaneously, using the pexmon parameter values obtained from Suzaku observations. We therefore thawed the pexmon normalization, and this improved the fit by Δχ2 = 500. But the FeK emission line was not fully modeled, so we thawed the Fe abundance assuming that the reprocessing media for FeK emission and the Compton hump are different, which again improved the fit by Δχ2 = 300 and the best-fit Fe abundance ∼0.15–0.19 times solar abundance. We used a zgauss model to describe the higher ionization Fe emission lines. The best-fit model used is tbabs∗(apec+powerlaw(1)+ztbabs∗(pexmon+powerlaw(2)+zgauss)). We detect significant variability in for the source using XMM-Newton observations.
- 7.Mkn 348: Marchese et al. (2014) studied this Seyfert-2 galaxy with Suzaku and XMM-Newton. The authors detected variability in the X-ray spectral curvature, which they concluded could be due to changes in column density of neutral and ionized absorbers. They obtained a power-law photon index of Γ = 1.72, a neutral absorber column density of = 4.50 × 1022 cm−2, and a reflection coefficient of R = . In our analysis, we found that the spectra need a PC absorber in addition to a full-covering absorption in all but one observation (CA-1, possibly due to low S/N). The best-fit model used is tbabs∗(apec+apec(2)+powerlaw(1)+zpcfabs∗ztbabs∗(zgauss+pexmon+powerlaw(1))). We detected variability in between the 2008 observation with Suzaku and 2010 observation with Chandra. However, the variations are within the uncertainties of cross-instrument-calibration as discussed in Section 4.2, and so we have not considered this as one of the variable sources.
- 8.NGC 526A: This is a Seyfert-1.9 galaxy, studied by Landi et al. (2001) using the BeppoSAX X-ray telescope in the energy band 0.1–150 keV. The authors detected a relatively flat power-law slope of Γ = 1.6. Although the source flux varies strongly between the observations, the power-law slope remains constant over time. The reflection component detected is weak (R ∼ 0.7). In our study, we found that the best-fit baseline model for this source is tbabs × (apec(1) + apec(2) + powerlaw(1) + ztbabs × (powerlaw(2) + pexmon + zgauss)). The spectra did not require any soft X-ray power laws for any of the observations. We do not detect any significant variability in for the source.
- 9.NGC 1052: Identified as a low-ionization nuclear emission-line region (LINER) by Heckman (1980), the galaxy hosts a low-luminosity AGN (LLAGN) of a luminosity L1–100 GHz = 4.4 × 1040 erg s−1 (Wrobel 1984). The compact core of the AGN has a very flat X-ray power-law slope. The source is absorbed by an intrinsic neutral column of ∼ (0.6–0.8) × 1022 cm−2. In our analysis, we found that the Chandra observations are piled up. We used the best-fit model tbabs∗(apec+apec(2)+powerlaw(2)+ztbabs∗zpcfabs∗(zgauss+pexmon+powerlaw(1))). We detected variability in between the 2005 observation with Chandra and 2007 observation with Suzaku. However, due to uncertain cross-instrument-calibration, we have not considered this as one of the variable cases. This source was included in the spectral variability sample of Hernández-García et al. (2013).
- 10.NGC 2110: Marinucci et al. (2015) studied this Seyfert-2 galaxy using NuSTAR, XMM-Newton, Chandra, etc. No detectable contribution from Compton reflection has been found. The power-law slope Γ = 1.64, and the neutral absorption measured is = 4.3 × 1022 cm−2. In our study, the best-fit model used is tbabs × (apec(1) + powerlaw(1) + ztbabs × zpcfabs × (powerlaw(2) + pexmon + zgauss)). For the XMM-Newton observation, the frozen pexmon parameters (obtained from the Suzaku fits) were over-predicting the FeKα emission line, likely pointing toward a different origin of the emission line from that of the Compton hump. We thawed the Fe abundance in the pexmon fit and fitted the data. The fit improved by Δχ2 = 81, with a best-fit Fe abundance of the pexmon model Feabund = 0.55 ± 0.07 relative to solar. This has also been observed in MCG–5-23-16. The power-law slope Γ could not be constrained for the observation CH-2(01) and hence was frozen to 1.74 (the Γ estimated from S-1(05)). We do not detect any significant variability in for the source.
- 11.NGC 2992: Shu et al. (2010) studied the variability of the source in X-rays. This source is known to exhibit X-ray flaring on timescales of days to weeks. They measured a power law Γ = 1.83, neutral absorption column density =6.45 × 1021 cm−2, and reflection fraction R = 0.40.In our analysis, we detected large changes in flux (almost an order of magnitude) between the XMM-Newton observation in 2003 X-1 and the rest of them in 2010 (X-2 to X-10). The X-1 observation is in an unusually high flux state of the source with both the soft and the hard X-ray bands orders of magnitude higher than the other observations. The soft X-ray band in X-1 is dominated by the nuclear emission from the AGN. In our analysis, we therefore could not use averaged values for X-1. From X-1 to X-2, NH22 increased from 0.60 ± 0.01 to 0.82 ± 0.03 from 2003–2010, and hence we regard this source as an variable source. The best-fit model used is tbabs∗(apec+powerlaw(1)+ztbabs∗(zgauss+pexmon+powerlaw(2)++zgauss(3))). This source was included in the spectral variability sample of Hernández-García et al. (2017).
- 12.NGC 4258: Reynolds et al. (2009) have studied this low-luminosity AGN, also classified as a Seyfert-2, with XMM-Newton and Suzaku. The authors conclude that the circumnuclear environment of this AGN is very clean and lacks a Compton-thick obscuring torus. They obtained a best-fit power law Γ = 1.75, and an absorption column of = 9.2 × 1022 cm−2. In our analysis, we found that this source has spatially extended structures in soft X-ray emission as viewed with XMM EPIC-pn camera. The best-fit model we used is tbabs∗(apec+apec(2)+powerlaw(1)+ztbabs∗(zgauss+pexmon+powerlaw(2))). We do not detect any significant variability in for the source.
- 13.NGC 4507: The Chandra HETG and XMM-Newton data of this source has been studied by Matt et al. (2004) where they detect a Compton-thin absorption of column density of = 4 × 1023 cm−2. This source has also been studied as a part of a sample using Suzaku data by Kawamuro et al. (2016), and the authors found that the source required a Compton-thin absorber, a PC absorber, and a neutral reflection component of R = 0.43 ± 0.07. The power-law slope estimated by the authors is Γ = 1.79. In our study, the best-fit model used is tbabs∗(apec+apec(2)+powerlaw(1)+zgauss(2)+ztbabs∗zpcfabs∗(zgauss+pexmon+powerlaw(2))). We do not detect any significant variability in for the source. This source was included in the spectral variability sample of Hernández-García et al. (2015).
- 14.NGC 5252: Dadina et al. (2010) studied this source with Chandra. The intrinsic power-law slope and absorption column density obtained are Γ = 1.4–1.5 and = 1022 cm−2, respectively. No mention is made of a possible Compton hump.In our fits to the Chandra ACIS data, ΓHard is very poorly constrained, but we obtained best fits when it is frozen at 1.4 (i.e., forcing ΓHard to 1.66, as measured by Kawamuro et al. 2016 with Suzaku, yielded high values of ∼ 1.2). This value is consistent with previous fits to Chandra data done by Dadina et al. (2010), who measured Γ = 1.4–1.5. Traditionally, such flat values of ΓHard could be attributed to unmodeled Compton reflection hump emission, but we did not find any mention in the literature of a Compton hump, and our fits to the Suzaku data did not require one.In our study, the best-fit model used is tbabs∗(apec+apec(2)+powerlaw(1)+zpcfabs∗ztbabs∗(zgauss+pexmon+powerlaw(2))). We obtained good fits in the soft band by using a single apec component with a common temperature and normalization for all four spectra. ΓSoft was poorly constrained, but an average value of 1.32 allowed for good fits in all four spectra. However, the soft power-law normalization was found to vary. Satisfactory fits to CA-2, CA-3, and CA-4 were obtained with an average normalization of 9.65 × 10−5, but for CA-1, which occurred 10 years earlier, this value yielded a poor fit. CA-1 required a normalization of 4.50 ± 0.43 × 10−5 (and in the MultiNest runs, this parameter is left free in CA-1).Partial coverers were required in the XMM-Newton and Suzaku data only. We tried to insert partial coverers into the Chandra fits, but could not obtain reasonable constraints on those parameters. We note, though, that through using various values of photon index or requiring/lacking partial coverers, that the sequence of values in the ACIS data always consistently followed (CA-1) < (CA-2) ∼ (CA-3) > (CA-4), and (CA-1) < (CA-4).
- 15.NGC 5506: Matt et al. (2015) studied this source using NuSTAR observations. They found that the spectrum is well fitted by Γ = 1.9 intrinsically absorbed by = 3.10 × 1022 cm−2, and a distant reflection component and narrow Fe emission lines. Guainazzi et al. (2010) studied this source using XMM-Newton and measured a Γ = 1.9.In our study, we used the best-fit model tbabs∗(ztbabs(2)∗(apec+powerlaw(1))+zgauss(3)+ztbabs∗(pexmon+powerlaw(1)+zgauss+zgauss(2))). Note that we required two different full-covering absorbers. One that absorbs the central AGN and another that absorbs both the AGN and the outer parts of the galaxy (stellar emission) with a lower absorbing column density. The outer absorption column density is ∼ 1020 cm−2, and the inner absorption column ∼ 1022 cm−2. Most of the Chandra observations are piled up, and the pileup could not be modeled using the pileup kernel alone; hence, we have reported only one Chandra HETG observation that has lower pileup. We detect significant variability of in this source, with a gradual increase in column density from 2002–2004. The XMM-Newton observation of this source X-9, has a long exposure (∼132 ks) with a high S/N. The soft X-ray spectra (<1.3 keV) could be modeled by a single apec model component with a higher normalization but a lower abundance of elements, Z = 0.0162 ± 0.0012 relative to solar, as also detected in previous studies (Bianchi et al. 2003). We did not require any soft X-ray power law for this observation. The measured value of = (3.00 ± 0.01) × 1022 cm−2 for this observation is consistent with those detected for observations from 2004–2015 indicating a constant absorption for that period of time.
- 16.NGC 6251: This is a low excitation radio-loud galaxy. Evans et al. (2011) studied the Suzaku observation and detected a power law of Γ = 1.82 and two thermal plasma components, kT = 0.89 keV and kT = 2.63 keV, and no reflection component in the hard X-rays. The authors however could not rule out a Compton-thick obscuration. In our analysis, the best-fit model used is tbabs∗(apec+powerlaw(1)+ztbabs∗(pexmon+powerlaw(2)+zgauss)). The Chandra ACIS observation has no sufficient S/N to constrain the column density. We do not detect any significant variability in for the source.
- 17.NGC 6300: Matsumoto et al. (2004) studied the Seyfert-2 galaxy using XMM-Newton and obtained a power law Γ = 1.83 ± 0.08 and a Compton-thin absorber of column density = 2.2 × 1023 cm−2. The authors could model the soft emission using a power law. The relative reflection strength producing the Compton hump is estimated to be using the Pexrav model. In our study, the best-fit model used is tbabs∗(apec+powerlaw(1)+ztbabs∗(zgauss+pexmon+powerlaw(2))). We do not detect any significant variability in for the source. This source was included in the spectral variability sample of Hernández-García et al. (2015).
- 18.NGC 7172: Awaki et al. (2006) studied the variability of this source in a sample of Seyfert-2 galaxies, and measured a Γ = 1.55 ± 0.07, and an absorption column of = (8.3 ± 0.4) × 1022 cm−2. Akylas et al. (2001) have studied this source and detected a flatter slope of Γ = 1.64 and a neutral absorption of = 9.0 × 1022 cm−2. However, they could not rule out the possibility of an alternative scenario of a steeper slope of Γ = 1.78 and a reflection component of . In our work, we found that the Chandra observations are mostly piled up. The best-fit model we have used is tbabs∗(powerlaw(1) + apec(2) + ztbabs ∗ zpcfabs ∗ (zgauss+pexmon+powerlaw(2))). We do not detect any significant variability in for the source. This source was included in the spectral variability sample of Hernández-García et al. (2015).
- 19.NGC 7314: Ebrero et al. (2011) studied the source using XMM-Newton and Suzaku and found that the source shows rapid short-term variability. No Compton reflection was detected. A power-law slope of Γ = 2.14 was measured along with a neutral absorber column of = 2.9 × 1021 cm−2. Dewangan & Griffiths (2005) studied this source as a part of a small sample of obscured NLSy1 galaxies and found a reflection component of R = 2.83, Γ = 2.19, and no intrinsic absorption. In our study, the best-fit model used is tbabs∗(apec+powerlaw+ztbabs∗(zgauss+pexrav)). We do not detect any significant variability in for the source.
- 20.NGC 7582: This is a starburst-dominated galaxy with a Seyfert-2 nucleus at its center. Rivers et al. (2015) studied the source using NuSTAR and found that the source is variable with strong reflection features. The obscuring torus is patchy with a covering fraction of 80%–90% with a column density of 3.6 × 1024 cm−2. Another full-covering absorber was also needed with a column density of ∼3–12 × 1023 cm−2. The authors modeled the Compton hump with a Pexrav model with a best-fit reflection R = 4.3, which is much higher than expected. The authors suggest that the geometry of the reflecting material is not that of a flat disk. The power-law photon index they obtained is Γ = 1.78 ± 0.07. Bianchi et al. (2009) studied this source with Suzaku. The source is characterized by very rapid changes of the column density of an inner absorber, which makes the authors conclude the presence of complex absorbing system and not just a simple torus following from the unification model.In our study, the best-fit model used is tbabs∗(apec + apec(2) + apec(3) + powerlaw + zpcfabs ∗ ztbabs ∗ (zgauss + pexrav + zgauss(2) + zgauss(3) + zgauss(4))). We detected variability of in this source both using XMM-Newton and Suzaku observations. However, the Suzaku estimated values of are different with respect to each other at only 90% error margins obtained using ISIS, and do not qualify our "variability" criteria described in Section 4.1. Due to a high S/N in the XMM-Newton observations, we detected discrete emission lines at 2.5 keV (Sulphur K-α) and 6.4, 7.12, and 7.5 keV, indicative of FeKα and higher ionization of Fe emission lines. The observations X-1 and X-2 required PC absorption, while X-3 and X-4 did not require them. When we used a zpcfabs model for X-3 and X-4 and froze the parameter values to those obtained in X-1, we found that fit worsened by Δχ2 = 200. When left free, the value of went to zero with an improvement in statistics. We required three apec models for this source, possibly because this source is dominated by stellar emission from different regions in the galaxy (with different temperatures and emissivity) in the soft X-rays.
Appendix B: Cyg A Chandra Observations
In this section we list the best-fit parameters obtained from the fits to the Chandra observation of Cyg A (see Table B1).
Table B1. Chandra Observations of Cyg A and the Best-fit Absorption Column Densities, apec Temperatures, and Best-fit Statistic
| Chandra Obsid | Date of Obs | apec-KT | apec-KT | Fluxesa | ||
|---|---|---|---|---|---|---|
| (×1022 cm−2) | (keV) | (keV) | (×10−11 erg cm−2 s−1) | |||
| 359 | 2000 Mar 8 | 1.1 | 4.6 | 8.40 | 25.93/0.960 | |
| 360 | 2000 May 21 | 0.26 | 1.9 | 3.52 | 375.92/0.989 | |
| 1707 | 2000 May 26 | 0.28 | 2.0 | 7.28 | 170.69/0.938 | |
| 6225 | 2005 Feb 15 | 0.92 | 3.9 | 3.77 | 298.73/1.205 | |
| 5831 | 2005 Feb 16 | 0.78 | 3.3 | 4.22 | 448.74/1.039 | |
| 6226 | 2005 Feb 19 | 1.1 | 3.5 | 4.23 | 270.43/1.104 | |
| 6250 | 2005 Feb 21 | 0.43 | 3.3 | 4.57 | 80.97/0.976 | |
| 5830 | 2005 Feb 22 | 0.43 | 4.0 | 4.14 | 265.78/1.089 | |
| 6229 | 2005 Feb 23 | 0.69 | 4.1 | 4.26 | 228.11/0.939 | |
| 6228 | 2005 Feb 25 | 0.85 | 2.7 | 4.50 | 156.82/0.866 | |
| 6252 | 2005 Sep 7 | 0.93 | 4.0 | 5.33 | 350.30/1.052 | |
| 17505 | 2015 Jan 5 | 0.82 | 4.9 | 5.21 | 471.77/1.051 | |
| 17145 | 2015 Jan 10 | 0.97 | 5.1 | 5.66 | 420.56/0.960 | |
| 17530 | 2015 Apr 19 | 0.52 | 4.7 | 2.85 | 116.75/0.965 | |
| 17650 | 2015 Apr 22 | 1.06 | 7.0 | 2.75 | 161.40/1.121 | |
| 17144 | 2015 May 3 | 0.74 | 4.7 | 3.52 | 236.37/0.879 | |
| 17528 | 2015 Aug 30 | 0.88 | 3.7 | 3.37 | 390.46/1.004 | |
| 17143 | 2015 Sep 3 | 0.68 | 2.7 | 3.32 | 228.42/1.053 | |
| 17524 | 2015 Sep 8 | 0.66 | 2.6 | 2.87 | 196.28/1.175 | |
| 18441 | 2015 Sep 14 | 0.86 | 3.5 | 2.82 | 186.22/1.029 | |
| 17526 | 2015 Sep 20 | 0.35 | 3.3 | 3.34 | 397.67/1.063 | |
| 17527 | 2015 Oct 11 | 0.92 | 4.5 | 3.74 | 159.48/0.886 | |
| 18682 | 2015 Oct 14 | 0.79 | 7.2 | 3.32 | 142.93/0.928 | |
| 18641 | 2015 Oct 15 | 2.0 | 4.0 | 3.16 | 121.57/0.921 | |
| 18683 | 2015 Oct 18 | 0.69 | 4.3 | 2.67 | 98.54/1.263 | |
| 17508 | 2015 Oct 28 | 1.0 | 4.4 | 4.06 | 144.79/0.894 | |
| 18688 | 2015 Nov 1 | 0.54 | 1.3 | 4.96 | 344.60/0.999 | |
| 18871 | 2016 Jun 13 | 0.44 | 2.7 | 3.92 | 200.73/0.947 | |
| 17133 | 2016 Jun 18 | 0.85 | 3.5 | 3.39 | 298.38/1.033 | |
| 17510 | 2016 Jun 26 | 1.03 | 4.4 | 3.91 | 311.58/0.898 | |
| 17509 | 2016 Jul 10 | 0.70 | 3.6 | 3.74 | 414.29/0.989 | |
| 17518 | 2016 Jul 16 | 0.52 | 4.0 | 3.62 | 382.97/0.930 | |
| 17521 | 2016 Jul 20 | 0.43 | 2.0 | 3.78 | 297.22/1.126 | |
| 18886 | 2016 Jul 23 | 0.69 | 2.6 | 4.20 | 234.27/1.014 | |
| 17138 | 2016 Jul 25 | 0.89 | 2.9 | 3.97 | 320.98/1.180 | |
| 17513 | 2016 Aug 15 | 0.76 | 4.0 | 4.20 | 428.77/1.033 | |
| 17516 | 2016 Aug 18 | 0.67 | 3.2 | 3.82 | 418.26/1.023 | |
| 17523 | 2016 Aug 31 | 1.04 | 4.8 | 2.67 | 258.93/0.838 | |
| 17512 | 2016 Sep 15 | 0.82 | 3.8 | 3.73 | 445.67/0.975 | |
| 17139 | 2016 Sep 16 | 0.54 | 2.2 | 4.00 | 361.65/1.005 | |
| 17517 | 2016 Sep 17 | 1.11 | 4.1 | 3.65 | 253.62/0.998 | |
| 19888 | 2016 Oct 1 | 0.43 | 5.5 | 4.17 | 194.71/0.969 | |
| 17140 | 2016 Oct 2 | 0.44 | 2.2 | 4.22 | 304.83/0.929 | |
| 17507 | 2016 Nov 12 | 1.06 | 4.3 | 3.49 | 319.56/1.055 | |
| 17520 | 2016 Dec 6 | 0.74 | 10.9 | 3.58 | 209.14/0.890 | |
| 19956 | 2016 Dec 10 | 0.71 | 5.0 | 3.47 | 391.13/0.959 | |
| 17514 | 2016 Dec 13 | 0.72 | 2.8 | 3.54 | 407.98/0.990 | |
| 17529 | 2016 Dec 15 | 0.98 | 1.7 | 3.86 | 314.61/0.948 | |
| 17519 | 2016 Dec 19 | 0.17 | 4.3 | 3.86 | 7300.66/1.051 | |
| 17135 | 2017 Jan 20 | 0.70 | 3.8 | 4.15 | 182.04/0.910 | |
| 17136 | 2017 Jan 26 | 0.12 | 3.2 | 3.58 | 216.93/1.028 | |
| 19996 | 2017 Jan 28 | 0.54 | 4.4 | 3.32 | 282.59/1.075 | |
| 19989 | 2017 Feb 12 | 0.68 | 3.9 | 3.48 | 373.15/1.014 | |
| 17515 | 2017 Mar 21 | 0.7 | 4.2 | 3.23 | 295.30/0.937 | |
| 20043 | 2017 Mar 25 | 1.0 | 6.9 | 3.14 | 194.67/0.801 | |
| 20044 | 2017 Mar 26 | 0.12 | 2.4 | 3.47 | 140.45/1.025 | |
| 17137 | 2017 Mar 29 | 1.4 | 5.0 | 3.20 | 215.37/1.002 | |
| 17522 | 2017 Apr 8 | 0.72 | 5.9 | 3.49 | 336.64/0.879 | |
| 20059 | 2017 Apr 19 | 0.27 | 4.3 | 2.95 | 114.31/1.099 | |
| 17142 | 2017 Apr 20 | 0.54 | 5.0 | 2.88 | 174.94/1.346 | |
| 17525 | 2017 Apr 22 | 1.22 | 4.1 | 2.62 | 191.00/1.151 | |
| 20063 | 2017 Apr 22 | 0.88 | 6.3 | 3.18 | 193.57/1.030 | |
| 17511 | 2017 May 10 | 0.44 | 2.4 | 3.46 | 131.70/0.808 | |
| 20077 | 2017 May 13 | 0.21 | 4.2 | 3.25 | 272.28/1.072 | |
| 20048 | 2017 May 19 | 0.70 | 3.5 | 2.78 | 119.64/0.989 | |
| 17134 | 2017 May 20 | 1.1 | 4.3 | 3.46 | 270.15/0.986 | |
| 20079 | 2017 May 21 | 0.74 | 2.8 | 3.13 | 229.10/1.046 |
Notes. The power-law slope has been fixed at Γ = 1.7 in all cases.
aThe 2–10 keV unasborbed power-law fluxes.Appendix C: The Spectral Overplots
In Figures C1–C20, we plot the spectra of the sources from multiple observations.
Figure C1. The overplot of the spectra of Cen A. Here the spectra have been binned by a factor of four for plotting and visual purposes only.
Download figure:
Standard image High-resolution imageFigure C2. Same as Figure C1, except for the source, which is Cyg A.
Download figure:
Standard image High-resolution imageFigure C3. Same as Figure C1, except for the source, which is Fairall 49.
Download figure:
Standard image High-resolution imageFigure C4. Same as Figure C1, except for the source, which is IRASF00521.
Download figure:
Standard image High-resolution imageFigure C5. Same as Figure C1, except for the source, which is IRASF05189.
Download figure:
Standard image High-resolution imageFigure C6. Same as Figure C1, except for the source, which is MCG–5-23-16.
Download figure:
Standard image High-resolution imageFigure C7. Same as Figure C1, except for the source, which is MKN 348.
Download figure:
Standard image High-resolution imageFigure C8. Same as Figure C1, except for the source, which is NGC 526A.
Download figure:
Standard image High-resolution imageFigure C9. Same as Figure C1, except for the source, which is NGC 1052.
Download figure:
Standard image High-resolution imageFigure C10. Same as Figure C1, except for the source, which is NGC 2110.
Download figure:
Standard image High-resolution imageFigure C11. Same as Figure C1, except for the source, which is NGC 2992.
Download figure:
Standard image High-resolution imageFigure C12. Same as Figure C1, except for the source, which is NGC 4258.
Download figure:
Standard image High-resolution imageFigure C13. Same as Figure C1, except for the source, which is NGC 4507.
Download figure:
Standard image High-resolution imageFigure C14. Same as Figure C1, except for the source, which is NGC 5252.
Download figure:
Standard image High-resolution imageFigure C15. Same as Figure C1, except for the source, which is NGC 5506.
Download figure:
Standard image High-resolution imageFigure C16. Same as Figure C1, except for the source, which is NGC 6251.
Download figure:
Standard image High-resolution imageFigure C17. Same as Figure C1, except for the source, which is NGC 6300.
Download figure:
Standard image High-resolution imageFigure C18. Same as Figure C1, except for the source, which is NGC 7172.
Download figure:
Standard image High-resolution imageFigure C19. Same as Figure C1, except for the source, which is NGC 7314.
Download figure:
Standard image High-resolution imageFigure C20. Same as Figure C1, except for the source, which is NGC 7582.
Download figure:
Standard image High-resolution imageAppendix D: Bayesian X-Ray Analysis Simulations
As discussed in Section 4, we ran the MultiNest nested-sampling algorithm (Skilling 2004; Feroz et al. 2009) via the BXA and PyMultiNest packages (Buchner et al. 2014) for XSPEC version 12.10.1f to assess fit parameter distributions and explore potential model degeneracies between and other model parameters. Due to the long computational times required, it was not feasible to run MultiNest on all observations for a given source/instrument combination. Instead we ran MultiNest on select cases of interest to make sure that deviating parameter values for a particular observation were not the result of, e.g., a low exposure time in that observation (as we had initially suspected, but then ruled out, for Cen A S-5).
We caution the reader, however, about the limitations of such simulations, as they are intended for exploring fit parameter distributions for an assumed model. They are not intended for determining the goodness of fit of that model to the observed data. In addition, a couple assumptions implicit in these simulations are worth noting. When we specify a model as input for these simulations, we implicitly assume that the input model is accurate in terms of containing the proper components (we assume we are not missing spectral components that are intrinsically present in the source, nor adding components to our model that are intrinsically lacking in the source). We also assume that each spectral component intrinsically present in the real data follows the equation-based model components we use (e.g., we assume that the real data's primary continuum indeed follows a strict power law). If the real data has, for example, some very mild continuum curvature such that our modeling cannot significantly reject a strict power law, then best-fit parameters could differ slightly between the observed/modeled spectrum and the simulated spectra.
We display the resulting parameter posterior contour plots in Figures D1 through D12.
Figure D1. Parameter posterior distributions for the MultiNest run of Cen A, observation S-5. The green solid lines denote the median posterior value, and the dashed black lines denote the 5th and 95th percentile values. The solid black contours denote the 68%, 90%, and 99% confidence levels. Here, Aapec1,2 denote apec normalizations, AS,H denote the 1 keV normalization of the soft- and hard-band power laws, and AHXD refers to the HXD-PIN/XIS0 cross-instrument constant.
Download figure:
Standard image High-resolution imageFigure D2. Same as Figure D1, but for Fairall 49, X-1. Here, NH,pc and fpc denote PC absorber parameters.
Download figure:
Standard image High-resolution imageFigure D3. Same as Figure D1, but for Fairall 49, X2.
Download figure:
Standard image High-resolution imageFigure D4. Same as Figure D1, but for MCG–5-23-16, S-1.
Download figure:
Standard image High-resolution imageFigure D5. Same as Figure D1, but for MCG–5-23-16, X-1.
Download figure:
Standard image High-resolution imageFigure D6. Same as Figure D1, but for NGC 2992, X-1.
Download figure:
Standard image High-resolution imageFigure D7. Same as Figure D1, but for NGC 5252, CA-1.
Download figure:
Standard image High-resolution imageFigure D8. Same as Figure D1, but for NGC 5252, CA-4.
Download figure:
Standard image High-resolution imageFigure D9. Same as Figure D1, but for NGC 5506, X-1. Here, NH,1 refers to the component absorbing the soft-band emission components, as discussed in Appendix A; NH,2 refers to the variable full-covering absorber that is absorbing the hard-band components.
Download figure:
Standard image High-resolution imageFigure D10. Same as Figure D9, but for NGC 5506 X-3.
Download figure:
Standard image High-resolution imageFigure D11. Same as Figure D1, but for NGC 7582, X-1.
Download figure:
Standard image High-resolution imageFigure D12. Same as Figure D1, but for NGC 7582 X-4, and which lacks a PC component.
Download figure:
Standard image High-resolution imageFootnotes
- 7
On the other hand, Goulding et al. (2012) find evidence from mid-IR spectroscopy of nearby Compton-thick AGNs that in at least some of these sources, the dominant dust extinction is associated with the host galaxy instead.
- 8
- 9
We should note that since Cen A is a radio galaxy and no BLR has been confirmed yet, it may not represent a standard Seyfert galaxy; nonetheless, searches for such non-clumpy, contiguous components of the torus are important for testing the applicability of clumpy-torus models across AGNs.