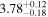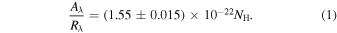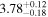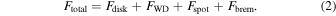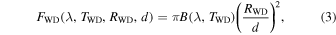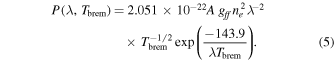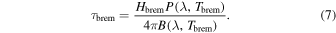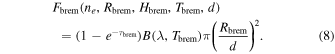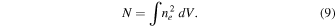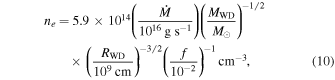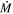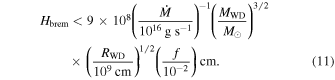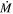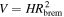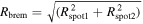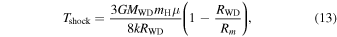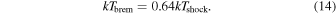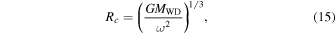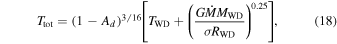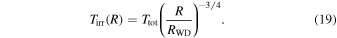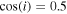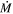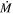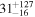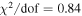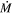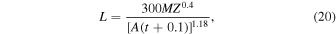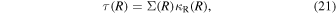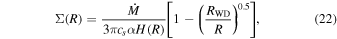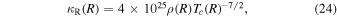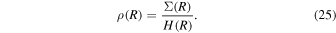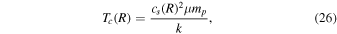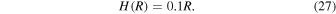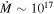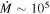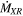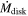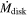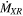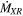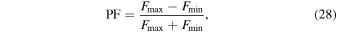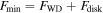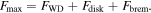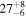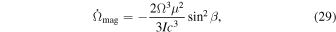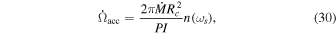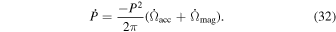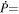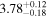Abstract
The quiescent emission of the anomalous X-ray pulsar (AXP) 4U 0142+61 extends over a broad range of energy, from radio up to hard X-rays. In particular, this object is unique among soft gamma-ray repeaters (SGRs) and AXPs in presenting simultaneously mid-infrared emission and pulsed optical emission. In spite of the many propositions to explain this wide range of emission, it still lacks one that reproduces all of the observations. Filling this gap, we present a model to reproduce the quiescent spectral energy distribution of 4U 0142+61 from mid-infrared up to hard X-rays using plausible physical components and parameters. We propose that the persistent emission comes from a magnetic accreting white dwarf (WD) surrounded by a debris disk. This model assumes that (i) the hard X-rays are due to the bremsstrahlung emission from the postshock region of the accretion column, (ii) the soft X-rays are originated by hot spots on the WD surface, and (iii) the optical and infrared emissions are caused by an optically thick dusty disk, the WD photosphere, and the tail of the postshock region emission. In this scenario, the fitted model parameters indicate that 4U 0142+61 harbors a fast-rotator magnetic near-Chandrasekhar WD, which is very hot and hence young. Such a WD can be the recent outcome of a merger of two less massive WDs. In this case, 4U 0142+61 can evolve into a supernova Ia and hence give hints of the origin of these important astrophysical events. Additionally, we also present a new estimate of 4U 0142+61's distance, kpc, based on the measured hydrogen column density and new interstellar extinction 3D maps.
1. Introduction
Anomalous X-ray pulsars (AXPs) present spin periods of a few seconds, quiescent soft X-ray emission with a blackbody temperature of approximately 0.4 keV, and a luminosity of about 1033 erg s−1 (e.g., Olausen & Kaspi 2014). Initially, AXPs were considered X-ray binaries. However, due to the lack of a companion and a smaller soft X-ray temperature compared to X-ray binaries, they were classified as a whole new group. Meanwhile, soft gamma-ray repeaters (SGRs) are associated with energetic outburst events. Presently, AXPs/SGRs are considered as the same class of objects, which are observationally characterized by a quiescent soft X-ray (2–10 keV) luminosity in the range 1030–1035 erg s−1, period of 2–12 s, and spin-down of 10−15–10−10 s s−1 (see Olausen & Kaspi 2014, and references therein). In outburst, the energy can reach 1043 erg (see, e.g., Coti Zelati et al. 2018). Some AXPs/SGRs also present hard X-ray emission, as well as soft gamma-ray flare events. For comprehensive reviews of observations of AXP/SGRs, see Mereghetti (2008), Turolla et al. (2015), and Kaspi & Beloborodov (2017).
The emission nature of AXPs/SGRs is still up for debate. There are several proposed scenarios to explain their observed spectra and properties. The most accepted scenario is the magnetar model, which was first proposed by Duncan & Thompson (1992) and Thompson & Duncan (1995) and later developed by several other authors, such as Beloborodov & Thompson (2007), Rea et al. (2012b), and Beloborodov (2013). In this model, the AXPs/SGRs present a huge magnetic field (B) in the range 1013–1015 G. Their persistent X-ray luminosity, as well as the bursts and flares typical of these sources (Mazets et al. 1979; Hurley et al. 1999a, 1999b), are believed to be powered by the decay of their ultrastrong magnetic fields. However, some limitations of the model, such as the discovery of the low-B (<4.4 × 1013 G) sources—SGR 0418+5729, Swift J1822.3–1606, and 3XMM J185246.6+003317 (Rea et al. 2010, 2012a, 2013; Livingstone et al. 2011; Zhou et al. 2014)—have increased the interest in alternative scenarios. Some examples are the neutron star (NS) accreting scenario, raised by van Paradijs et al. (1995) and Alpar (2001), and the white dwarf (WD) pulsar model (Paczynski 1990; Malheiro et al. 2012; Coelho & Malheiro 2014; Lobato et al. 2016).
The AXP 4U 0142+61 was reported for the first time in the UHURU catalog (Bradt & McClintock 1983). This object presents quiescent emission in a broad range of energy, from radio (Malofeev et al. 2010) to hard X-rays (Kuiper et al. 2006). Its period is 8.68 s, and the spin-down is around 2.0 × 10−12 s s−1 (Olausen & Kaspi 2014). The luminosities in soft and hard X-rays are estimated as 2.8 × 1035 and 0.68 × 1035 erg s−1, respectively, considering a distance of 3.6 kpc (Enoto et al. 2011). This source is unique among AXPs/SGRs, since it presents mid-infrared (IR) emission and pulsed optical emission, which even separately are rare features in the class. The outbursts and glitches in 4U 0142+61 are less energetic compared to the bulk of SGR/AXP bursts (Göğüş et al. 2017). No flare has been observed in 4U 0142+61 so far (Olausen & Kaspi 2014).
In the magnetar paradigm, the IR emission of 4U 0142+61 is interpreted as a passive fallback disk (Wang et al. 2006), and the hard and soft X-ray emissions were fitted by Hascoët et al. (2014) using a model based on large magnetic loops that was proposed by Beloborodov (2013). Specifically, the hard X-ray emission is caused by the production of e−–e+ pairs close to the NS surface. The soft X-ray emission requires a combination of two modified blackbodies from the NS photosphere and a hot spot (see Hascoët et al. 2014, for details). The optical emission is reproduced by a power-law function proposed to be of magnetospheric origin (Wang et al. 2006).
In the accreting NS model, a debris disk is responsible for the IR and optical emissions (Ertan et al. 2007) and acts as a reservoir of matter for the accretion. The hard X-rays are caused by the accreting structure and the soft X-rays by a polar cap in the NS surface (Trümper et al. 2013; Zezas et al. 2015).
In a third proposed scenario, that of a WD pulsar, the optical/IR data are explained by the WD photosphere and a disk (Rueda et al. 2013), and the X-ray emission is caused by a pulsar-like emission (Malheiro et al. 2012; Coelho & Malheiro 2014; Lobato et al. 2016). However, no attempt to fit the X-ray emission 4U 0142+61 in this model was presented up to now.
In this paper, we present a new scenario to explain the spectral energy distribution (SED) of 4U 0142+61 from mid-IR up to hard X-rays. We propose that the persistent emission comes from an accreting isolated magnetic WD surrounded by a debris disk having gas and dusty regions. This scenario is inspired by the periodic flux modulation and the presence of mid-IR emission, which is rare for NSs. In fact, only three isolated NSs have detected mid-IR: the radio pulsars Crab, Vela, and Geminga (Sandberg & Sollerman 2009; Danilenko et al. 2011). Only two AXPs/SGRs have mid-IR emission: 1E 2259+586 (Kaplan et al. 2009) and 4U 0142+61 (Wang et al. 2006). Thus, mid-IR appears in about 0.3% of all isolated NSs. On the other hand, the presence of mid-IR in WDs is quite common. Debes et al. (2011) found that about 7% of WDs present an excess of mid-IR.
The presence of a dusty disk in 4U 0142+61 is corroborated by a possible emission feature around 9 μm, probably due to silicate (Wang et al. 2008). The presence of disks around isolated NSs is still a question for debate. A protoplanetary disk is one possible origin of the planetary system around PSR B1257+12 (Wolszczan & Frail 1992; Miller & Hamilton 2001). Fallback disks are also raised to explain the observed braking index smaller than 3 in some NSs (Menou et al. 2001). However, no isolated NSs have confirmed debris disks. On the other hand, at least 27% of the WDs present traces of high elements that could only be explained by the accretion of material from planetary disks (Koester et al. 2014). All of these arguments reinforce a WD nature for 4U 0142+61.
This paper presents a study of 4U 0142+61 emission in the context of a WD nature. It is organized as follows. In Section 2, we introduce the 4U 0142+61 observations that are used to test the proposed scenario. In Section 3, we estimate a new distance for 4U 0142+61 based on the 3D reddening map of Green et al. (2018, 2019) and compare it with previous estimates. In Section 4, we present an overview of the model and its parameters. In Section 5, we show the spectral fit of 4U 0142+61 and discuss the derived parameters. In Section 6, we derive the magnetic field of 4U 0142+61 from its spin-down. In Section 7, we discuss the probable origin and evolution of the object in our scenario. In Section 8, we discuss possible mechanisms for the glitches, bursts, and radio emission of 4U 0142+61 in our model. Finally, in Section 9, we summarize our findings.
2. The SED of 4U 0142+61
In quiescence, 4U 0142+61 emits in the X-ray, optical, mid/near-IR, and radio. In this section, we describe these data and the SED used in the modeling.
The 4U 0142+61 soft X-ray spectrum was observed using several telescopes in recent decades, e.g., ASCA (White et al. 1996) and Chandra (Juett et al. 2002). In our fit, we used the data from Suzaku (Enoto et al. 2010),4 which are deconvolved from the instrumental response. The hard X-ray emission was discovered by INTEGRAL (20–300 keV; Kuiper et al. 2006) and also observed by other telescopes, such as NuSTAR in 0.5–79 keV (Tendulkar et al. 2015) and Suzaku in 15–60 keV (Enoto et al. 2017). In our fit, we used the INTEGRAL data, whose reduction is presented in Section 2.1
The optical emission of 4U 0142+61 was discovered by Hulleman et al. (2000). Complementary photometry was performed by Hulleman et al. (2004), Dhillon et al. (2005), and Muñoz-Darias et al. (2016), who also presented the first optical spectrum of 4U 0142+61. We used the Gran Telescopio Canarias (GTC) optical data from Muñoz-Darias et al. (2016; see Table 1). This quasi-simultaneous data set has been homogeneously reduced, and a careful differential photometric calibration was performed. This data set is consistent with previous measurements.
Table 1. Optical and Near-IR Data and Reddening Used in the 4U 0142+61 Modeling
| Band | Aλ | Observed Mag. | Date | Reference |
|---|---|---|---|---|
| g | 3.67 | 27.37 ± 0.25(0.58) | 2013 Aug 9 | 1 |
| r | 2.67 | 25.79 ± 0.07(0.26) | 2013 Aug 9 | 1 |
| i | 2.01 | 24.55 ± 0.05(0.22) | 2013 Aug 9 | 1 |
| z | 1.44 | 23.76 ± 0.07(0.28) | 2013 Aug 9 | 1 |
| J | 0.87 | 21.97 ± 0.16 | 2004 Nov 2 | 2 |
| H | 0.59 | 20.69 ± 0.12 | 2004 Nov 2 | 2 |
| Ks | 0.36 | 19.96 ± 0.07 | 2004 Nov 2 | 2 |
Note. The errors in parentheses represent the zero-point error and were also considered in the fitting procedure.
References. (1) Muñoz-Darias et al. (2016); (2) Durant & van Kerkwijk (2006a).
Download table as: ASCIITypeset image
The near-IR K-band flux was measured for the first time in 1999 using the Keck telescope by Hulleman et al. (2004). After that, several near-IR observations were performed. Even though most of them are in the K band, data in the J and H bands have been taken using CFHT, Subaru, and Gemini (Durant & van Kerkwijk 2006a). For the near-IR, we selected the Gemini J, H, and Ks observations from Durant & van Kerkwijk (2006a; see Table 1) because they provide a smoother SED when combined with the GTC optical data and the mid-IR Spitzer in 4.5 and 8.0 μm data from Wang et al. (2006), which are also used to model the 4U 0142+61 SED (Section 5.1).
The emission of 4U 0142+61 is strongly affected by interstellar absorption and extinction; hence, the data must be corrected by this effect. We adopted an interstellar hydrogen column density, NH, of 6.4 × 1021 cm−2. This value was obtained using individual absorption edges of metals in the X-ray spectrum (Durant & van Kerkwijk 2006b). The X-ray absorption cross sections are from Morrison & McCammon (1983), who presented an approximate analytic expression. To calculate the optical and near-IR extinction, we considered the ratio of total to selective extinction RV = 3.1 and the relation between NH and the extinction Aλ from Zhu et al. (2017). Hence, we obtained
We used the extinction law Rλ from Cardelli et al. (1989). The obtained values of extinction for 4U 0142+61 in each band are shown in Table 1.
The dereddened and deabsorbed 4U 0142+61 SED adopted to fit our model is shown in Figure 1. This figure also displays the optical points from Hulleman et al. (2000, 2004) and the upper limit for gamma-ray fluxes from CGRO COMPTEL (den Hartog et al. 2008). The 4U 0142+61 radio emission at 111 MHz is 30 ± 20 mJy (Malofeev et al. 2010), which we did not attempt to fit in this paper.
Figure 1. Dereddened and deabsorbed SED of 4U 10142+61, along with the best fit. The solid black curve is the complete fit, the long-dashed curve is the disk component, the dotted–dashed curve is the WD photosphere, the two dotted curves are the hot-spot components, and the short-dashed curve is the bremsstrahlung component. The black crosses are from Spitzer (mid-IR; Wang et al. 2006), Gemini (near-IR; Durant & van Kerkwijk 2006a), and GTC (optical; Muñoz-Darias et al. 2016). Green crosses represent the soft X-ray data from Suzaku (Enoto et al. 2010), the blue crosses are the INTEGRAL data (see Section 2.1), and the orange upper limits in gamma-rays are from COMPTEL (den Hartog et al. 2008). Top panel: entire spectral range, from mid-IR up to gamma-rays. Bottom left panel: zoom at the high-energy end. Bottom right panel: optical and IR region. The red points represent the measurements from Hulleman et al. (2000, 2004).
Download figure:
Standard image High-resolution image2.1. INTEGRAL Data Reduction
In our 4U 0142+61 modeling, we used the 2007 data available in the INTEGRAL database and presented in Table 2. These data were first presented by den Hartog et al. (2008). We searched for data within a 14 5 wide field of view and a minimum exposure time () of 100 s. To reduce and obtain the spectrum, we used the OSA 10.2 software and the recipes of the IBIS/ISGRI telescope (Lebrun et al. 2003; Ubertini et al. 2003). In each task, default parameter values were used. The data in the entire revolution group were used to obtain one spectrum. To deconvolve this spectrum from instrumental effects, we fitted it in the 20–200 keV energy range with a power-law component in order to obtain the unfolded spectrum. This fit was performed using the XSPEC software (Arnaud 1996). The resulting unfolded spectrum is used in our model fitting.
5 wide field of view and a minimum exposure time () of 100 s. To reduce and obtain the spectrum, we used the OSA 10.2 software and the recipes of the IBIS/ISGRI telescope (Lebrun et al. 2003; Ubertini et al. 2003). In each task, default parameter values were used. The data in the entire revolution group were used to obtain one spectrum. To deconvolve this spectrum from instrumental effects, we fitted it in the 20–200 keV energy range with a power-law component in order to obtain the unfolded spectrum. This fit was performed using the XSPEC software (Arnaud 1996). The resulting unfolded spectrum is used in our model fitting.
Table 2. INTEGRAL Observations
| Revolutions | MJD | Time Span | ScWs | teff (ks) |
|---|---|---|---|---|
| 528 ToO | 54,139.7661–54,142.0288 | 2007 Feb 8–2007 Feb 11 | 50 | 114 |
Note. ScWs is the number of science windows used to obtain the spectra, and teff is the effective observation time.
Download table as: ASCIITypeset image
3. Distance of 4U 0142+61
Our aim is to present a model that fits not only the shape of the 4U 0142+61 SED but also the level of the observed emission from mid-IR to X-rays. Hence, we refined the 4U 0142+61 distance as presented below.
Durant & van Kerkwijk (2006c) estimated the distance of 4U 0142+61 using the following methodology. They selected the red clump stars, helium-core-burning giants, from the Two Micron All Sky Survey (2MASS) catalog along the line of sight of 4U 0142+61 and derived the variation of extinction according to the distance. Thus, they estimated a distance of 3.6 ± 0.4 kpc using NH = 6.4 × 1021 cm−2 and the relation NH/AV = (1.79 ± 0.03) × 1021 cm−2 mag−1 (see Predehl & Schmitt 1995). This method presents some limitations, such as the small amount of red clump stars and the contamination by other types of stars, once the identification of red clump giants was done solely by their position in the color–magnitude diagram.
In an attempt to get a more accurate distance, we used the updated relation of NH/AV = (2.08 ± 0.02) × 1021 cm−2 mag−1 from Zhu et al. (2017). The resulting difference in the value of AV, and hence E(B – V), is approximately 15%. Moreover, we used the online version5 of the Galactic reddening 3D map from Green et al. (2018, 2019), which associates the distance with E(B − V) = AV/RV, to get a new estimate of the distance for 4U 0142+61. Using the relation from Zhu et al. (2017) and RV = 2.742 (see Green et al. 2018, 2019 and Table 6 of Schlafly & Finkbeiner 2011), we found E(B − V) = 1.12 ± 0.04 mag. Thus, our distance estimate for 4U 0142+61 is kpc, which is used throughout this paper.
4. A Magnetic WD Accretion Model
In this section, we describe the proposed scenario and the quantitative model for the emission of 4U 0142+61 as an isolated WD. We propose that the persistent emission comes from the WD photosphere, a disk, and a magnetic accretion column. This scenario is inspired by (i) the periodic flux modulation, which could be explained by an accretion column, and (ii) the detected IR emission and silicate line emission, which indicate the presence of a disk. The disk has a gaseous inner region and an outer portion made up of dust and gas. In spite of also having gas, we call the external portion a dusty disk. Even though only the dusty disk is observed in most WDs, the presence of the gaseous region has already been confirmed for some objects (Gänsicke et al. 2006, 2007, 2008; Melis et al. 2012).
The dusty disk is optically thick and its emission can be represented by a combination of blackbodies of different temperatures. The temperature of its inner radius is the grain sublimation temperature, which is about 1500 K for silicates. Conversely, the gaseous disk is optically thin, and its emission can be neglected (see Section 5.2.4). The inner radius of the gaseous disk is equal to the magnetosphere radius. For that point on, the matter flows into the WD surface following the magnetic field lines, and the debris disk ceases to exist.
Close to the WD photosphere, the infalling flow of matter suffers a collisional shock, forming an extremely hot region, the so-called postshock region, that emits bremsstrahlung (see, e.g., Mukai 2017). About half of that energy reaches the WD surface, where it is absorbed and reemitted in lower energies, forming hot spots. Once the high-energy emission of 4U 0142+61 is pulsed, with two peaks per phase, it is plausible that we see the emission from two different accreting regions.
To sum up, the emitted flux of 4U 0142+61 can be expressed by
The next sections are devoted to explaining each term of the equation above, expanding all of them in their parameters. First, we discuss the blackbody flux emitted by the photosphere of the WD (FWD) and the hot spot (Fspot). Then, we comment on the emission from the accretion column (Fbrem). At last, we describe the emission from the disk (Fdisk).
4.1. WD Photosphere and Hot Spots
We assumed that the WD photosphere emission can be represented by a blackbody, in which the intensity for a given wavelength λ and temperature T is the Planck function, B(λ, T). Therefore, the photosphere flux (FWD) is
where TWD is the effective temperature of the photosphere, RWD is the radius of the WD, and FWD is fitted simultaneously with Fdisk and after the accretion column and hot spots (see Section 5.1). Hence, TWD is a free parameter, but RWD is a fixed parameter in the optical and IR fitting, because it was previously estimated by the hard X-ray fitting.
The flux for each hot spot on the WD surface is also assumed as a blackbody and given by
where Tspot is the temperature of the spot, Rspot is the radius of the spot, and Fspot is the main emission mechanism in the soft X-ray. In the 4U 0142+61 fit, we considered two spots, whose parameters are discriminated by indexes 1 and 2.
4.2. Postshock Region
We assumed that the postshock region emits by thermal bremsstrahlung. According to Mewe et al. (1986), the bremsstrahlung-emitted power is
The parameters ne, Tbrem, and gff are the electron number density, temperature of the bremsstrahlung emission, and Gaunt factor, respectively. For the range of temperatures found in postshock regions of WDs, it is necessary to apply the relativistic correction, A, found in Rybicki & Lightman (1979):
For temperatures below ∼100 keV, we can consider a nonrelativistic gff (Karzas & Latter 1961; Sutherland 1998). However, for higher temperatures, which is the case for our fit, as we show later, we must take into account the relativistic gff. Thus, we adopted the gff from Nozawa et al. (1998), Itoh et al. (2000), and van Hoof et al. (2015). To estimate gff, it is also necessary to evaluate the ion charge of the infalling matter, which depends on its chemical composition. Hence, it was necessary to define the disk material. In the WD accreting model, 4U 0142+61 is probably the product of the merger of two CO WDs (see Section 7). Therefore, we adopted a disk composition of carbon (Lorén-Aguilar et al. 2009).
Assuming that the region is cylindrical, with a height Hbrem, the optical depth of the bremsstrahlung emission, τbrem, is
Assuming that the radius is Rbrem, the flux of the bremsstrahlung emission can be written as
It is useful to define a normalization factor, N, related to the total squared number density of emitting particles in the region:
The value of ne, in cm−3, of the postshock region can be calculated as (see Frank et al. 2002)
which depends on MWD, RWD, the accretion rate , and the fraction f of the WD photosphere area covered by the footprint of the accretion column.
The upper limit of Hbrem is given by (Frank et al. 2002)
We adopted the following estimate for :
where G is the gravitational constant and Lbrem is the accretion luminosity of the model and is related to the bremsstrahlung flux (Equation (8)). The emission from the postshock region is optically thin in the X-ray range, so it is proportional to the volume of the emitting region, . We artificially considered to guarantee that the accretion column and hot spots have similar areas.
An analytic formula for the postshock temperature of a WD (Tshock) was first derived by Aizu (1973). Since then, improvements on this formula have been presented by several authors. In this paper, we used the expression from Suleimanov et al. (2016),
where mH is the mass of the hydrogen atom, k is the Boltzmann constant, Rm is the magnetospheric radius, and μ is the mean molecular weight of the infalling gas, which we considered to be 1.714 for a carbon disk.
We adopted the following relation between Tbrem and Tshock (also from Suleimanov et al. 2016):
To estimate Tshock and Tbrem, we should adopt a value for the magnetospheric radius Rm. We considered Rm equal to the corotational radius, Rc,
where ω = 2π/T is the angular speed, T being the WD rotation period. In Section 6, we discuss the relation between Rm and Rc and confirm the validity of this assumption.
To sum up, Fbrem can be represented by
Therefore, the hard X-ray fit can be performed considering only N and Tbrem. All other parameters (MWD, RWD, , Lbrem, ne, Hbrem, Rbrem, f) are derived from N, Tbrem, Rspot1, and Rspot2.
4.3. Multitemperature Disk
Disks around WDs are common for both young and old populations (Koester et al. 2014). For instance, several old, cool, metal-rich WDs have small disks around them, supposedly caused by tidal disruption of small bodies (Jura 2003). These disks are optically thick and geometrically thin (Metzger et al. 2012) and usually emit from mid-IR to optical wavelengths. The inner and outer radii range from a fraction of to a few R⊙. In contrast, young hot WDs, such as those of the Helix planetary nebula, have large disks, which are probably created by the collision of Kuiper Belt–like objects (Chu et al. 2011). Those disks emit in the far to mid-IR, and the radii are approximately a few au (Chu et al. 2011). In both cases, the WD accretes matter from the disk.
As 4U 0142+61 emits from the mid-IR to optical, we fitted the data adopting the disk flux relation proposed by Chiang & Goldreich (1997) for disks around T Tauri stars. They are passive disks, which absorb the emission from the star and the accretion column and reemit the absorbed energy in mid-IR. Hence, the dominant heating mechanism is irradiation. This same model was used by Jura (2003) to fit the disk of the cold WD G29-38 and Rueda et al. (2013) to fit the IR emission of 4U 0142+61 in the WD pulsar scenario. According to Chiang & Goldreich (1997) and Jura (2003), the emitted flux from the debris disk in a given frequency ν can be expressed by
where i is the inclination of the disk, h is the Planck constant, c is the speed of light, x = hν/kTirr(R), and Tirr(R) is the debris disk temperature, which ranges from Tout to Tin. Here Ttot quantifies the disk heating by the two heating sources in the system, namely the WD and the accretion column, and is given by (Chiang & Goldreich 1997)
where σ is the Stefan–Boltzmann constant and Ad is the albedo. It is important to include the effect of the albedo because part of the incident flux on the disk is reflected and does not contribute to the heating.
It is assumed that the temperature decays as R−3/4 (see Equation (19)). Thus, each Tirr(R) value has an associated radius, R, in such a way that a given value of Tin (Tout) corresponds to a value of Rin (Rout):
For radii between Rm and Rin, the disk is gaseous and does not emit (see Section 5.2.4). In addition, we considered an average value for the cosine, i.e., .
The Fdisk is fitted simultaneously with FWD. We used the estimated values of RWD, MWD, and from the hard X-ray fitting. Here TWD, Tin, and Tout are free parameters in the fit of the IR and optical SED.
5. An Accreting WD Model for 4U 0142+61
In this section, we describe the fit procedure of the dereddened and deabsorbed 4U 0142+61 SED (Section 2). We assumed the model presented in Section 4, which is based on a magnetic accreting WD model for 4U 0142+61. We also discuss the consequences of the derived parameters for a WD scenario.
5.1. Fitting the 4U 0142+61 SED
As the model parameters for each spectral region are not the same, we opted to fit the spectral regions separately. Doing this, we could also constrain some parameters in a simpler way than doing an overall fitting. First, we fitted the hard X-rays independently of other parts of the SED. After that, we fitted the soft X-rays by considering the contribution of hard X-ray bremsstrahlung in this energy range. Finally, we fitted the optical/IR emission by taking all of the previously fitted components and parameters into account. The distance to 4U 0142+61 is considered equal to 3.78 kpc (see Section 3 in all calculations.
We used the Markov Chain Monte Carlo (MCMC) method (Goodman & Weare 2010) to estimate the parameters and their uncertainties. The adopted figure of merit is the ratio between χ2 and the degrees of freedom (dof). The parameters of the fit and the resulting SED are shown in Table 3 and Figure 1.
Table 3. Parameters of the Fitting of 4U 0142+61 in the Accreting WD Model
| Parameter | Description | Value |
|---|---|---|
| X-Rays | ||
| Fixed parameters | ||
| d | Distance of 4U 0142+61 | 3.78 kpc |
| NH | Columnar density of hydrogen | 6.4 1021 cm−2 |
| Tbrem | Temperature of the emission for the accretion column | 674.5 keV |
| MWD | WD's mass | 1.41 M⊙ |
| RWD | WD's radius | 1021 105 cm |
| Fitted parameters | ||
| N | Normalization parameter | 3.30 ± 1.09 1056 cm−3 |
| χbrem2/dof | Reduced χ2 for the hard X-rays | 0.85 |
| Tspot1 | Temperature of spot 1 | 0.632 ± 0.033 keV |
| Rspot1 | Radius of spot 1 | 2.35 ± 0.45 105 cm |
| Tspot2 | Temperature of spot 2 | 0.337 ± 0.012 keV |
| Rspot2 | Radius of spot 2 | 13.83 ± 0.73 105 cm |
| χ2/dof | Reduced χ2 for the soft X-rays | 1.06 |
| Derived parameters | ||
| Tshock | Temperature of the shock front | 1053.9 keV |
| Lbrem | Bolometric luminosity due to bremsstrahlung | 6.29 1035 erg s−1 |
| Accretion rate | 3.43 1017 g s−1 | |
| Rbrem | Radius of the hard X-ray emission | 14.03 105 cm |
| Hbrem | Height of the accretion column | 1.27 105 cm |
| ne | Electron number density | 2.05 1019 cm−3 |
| Optical/IR | ||
| Fitted parameters | ||
| TWD | WD's effective temperature | 9.4 ± 7.3 104 K |
| Tin | Inner temperature of the debris disk | 1991 ± 16 K |
| Tout | Outer temperature of the debris disk | 285 ± 200 K |
| Ad | Albedo of the disk | 0.985 ± 0.003 |
| χ2/dofa | Reduced χ2 for the optical/IR range | 2.45 |
| Derived parameters | ||
| Rin | Inner radius of the debris disk | 2.35 ± 0.03 R⊙ |
| Rout | Outer radius of the debris disk | R⊙ |
Notes. The fixed parameters were derived before the fit by independent methods. For the IR/optical fit, all X-ray parameters are considered fixed; therefore, RWD is not a fitted parameter for this range of energy.
aThe estimate of χ2/dof in the optical/IR range did not take into account the Ks band, since it presents a distinct trend and would disturb the fit of the other bands.Download table as: ASCIITypeset image
The fit quality of the hard X-rays increases with the bremsstrahlung temperature, but there is a limit imposed by the maximum mass a WD can have, since the temperature is related to the WD mass by Equations (13) and (14). The highest temperature we can reach for the limiting mass of 1.41 M⊙ and radius of 1021 km (Carvalho et al. 2018) is 674.5 keV, which results in a for the hard X-ray emission. If we use a smaller mass, for instance, 1.36 M⊙, we obtain ∼250 keV, which gives χ2/dof = 1.04. We fit the hard X-ray data using Equation (16). The only free parameter is N (see Equation (9)), since Tbrem is fixed at 674.5 keV (see the above paragraph).
After modeling the hard X-rays, we performed the fit of the soft X-rays. The bremsstrahlung component was also included in the fit. To increase the quality of the fit, we used two blackbody components, which can have different temperatures and radii. The flux for each hot spot is given by Equation (4), in which Tspot1, Rspot1, Tspot2, and Rspot2 are free parameters and d is fixed. In Table 3, we present the parameters for hard and soft X-ray fits, and Figure 1 shows the fitted model. Two spots with different temperatures are necessary to represent the multitemperature characteristic of the soft X-ray emission; if we use only one blackbody, the soft X-rays are not well fit. The two-spot approximation can be a mathematical simplification for a single spot with a temperature gradient, which is consistent with the smooth soft X-ray emission—in opposition to a double-peaked soft X-ray emission. On the other hand, the two-spot model can reflect the presence of two accretion columns, which would imply two bremsstrahlung components in hard X-rays. However, due to the similar power-law behavior of the bremsstrahlung emission for T < 100 keV, two components with slightly different temperatures are indistinguishable. Therefore, we could not differentiate between one or two postshock regions using the observed SED in hard X-rays.
Using the parameters obtained in X-ray fits, we can derive some important quantities of the system. First, we estimated Lbrem, which is the accretion column luminosity, by integrating Fbrem in all energies. Using the estimated Lbrem, we calculated (see Equation (12)). We considered the area of the column equal to the soft X-ray emitting area, which gives an average radius for Rbrem of 14.02 km. Thus, we were able to estimate ne using Equations (9) and (10). Knowing N, ne, and Rbrem, we have the value of Hbrem. The downward bremsstrahlung photons illuminate not only an area equal to the footprint of the accretion column but also a surrounding circular ring. In other words, we should have Rbrem of the same order as, but still smaller than, . Nonetheless, we can have higher Hbrem and, consequently, smaller Rbrem, since Hbrem is only 48% of the upper limit given by Equation (11).
To fit the optical and IR emission, we used the WD photosphere blackbody and the debris disk, whose fluxes are given by Equations (3) and (17), respectively. We used the same values of RWD derived from the bremsstrahlung fit. Moreover, we included the tail of the bremsstrahlung component in the fit. We did not consider the presence of hot spots in the fit of the optical/IR data because their emission is negligible in this energy range. The best fit for the optical and IR is presented in Table 3 and Figure 1. Hulleman et al.'s (2000, 2004) data follow a different slope compared with mid- and near-IR data (Durant & van Kerkwijk 2006a; Wang et al. 2006), whereas the recent optical data from Muñoz-Darias et al. (2016) fit more smoothly with the IR emission. Due to those differences, we perform the optical fit considering only the data from Muñoz-Darias et al. (2016) but present both data in Figure 1(b), in order to show that the fit is consistent with both optical ensembles.
Figure 1 also shows the upper limits of gamma-ray emission from 4U 0142+61 obtained using the CGRO COMPTEL instrument (den Hartog et al. 2008). Hence, the proposed model is able to consistently fit all observational data of 4U 0142+61.
5.2. Discussion of the Resulting Parameters of 4U 0142+61
5.2.1. Postshock Region
Wang et al. (2014) tried for the first time to fit the hard X-rays of 4U 0142+61 with a bremsstrahlung component and found a poor fit. However, they used XSPEC 12.6.0q, which uses a nonrelativistic Gaunt factor derived from Karzas & Latter (1961) and Kellogg et al. (1975). Conversely, we used the relativistic Gaunt factor from Nozawa et al. (1998), which, depending on the energy range, can differ from the nonrelativistic prescription by orders of magnitude. Moreover, we used a composition of carbon opposed to 92.2% hydrogen and 7.8% helium and applied the relativistic correction for high temperatures. All of those differences in the methodology allow us to fit the data with a bremsstrahlung component that has a natural cutoff at high energies, in agreement with the observed data (see Figure 1).
The absence of Hα emission in the optical spectrum of 4U 0142+61 was interpreted by Muñoz-Darias et al. (2016) as evidence against accretion. However, the carbon composition of the accreted mass naturally explains the absence of Hα emission.
To fit the data, we need a value for the temperature of the accretion structure of around 670 keV. Such a high temperature is not observed for any known cataclysmic variable (CV). However, high values are theoretically possible for a massive WD (see Equation (13)). In addition, infalling matter composed of carbon and oxygen increases the mean molecular weight, which also increases the temperature. Also, D. Belloni (2020, private communication) has implemented a shock solution for accreting WDs. Their results show that shock temperatures as high as 1000 keV can be found for massive WDs accreting C-O material, which corroborates the temperature of our fitting
5.2.2. WD Temperature and Age
The temperature of the WD photosphere for our model for 4U 0142+61 is high (TWD = 9.4 × 104 K). Werner & Rauch (2015) presented two extremely hot WDs, H1504+65 (TWD = 2.0 × 105 K and M = 0.83 M⊙) and RX J0439.8–6709 (TWD = 2.5 × 105 K and M = 0.86 M⊙). Both of them are hotter than our models. Hence, our findings are consistent with the temperatures that we do see in WDs.
From the effective temperature, we can estimate the WD age. The Mestel cooling law (Mestel 1952) was the first attempt at such an estimate. Hurley & Shara (2003) presented an improved version of that cooling law, which for ages <9000 Myr is
where L is the WD luminosity in solar units, M is the WD mass in solar units, A denotes the average atomic number, t is the age in Myr, and Z is the metallicity. We consider a core composition of 60% carbon and 40% oxygen, and Z = 0.001 (Rueda et al. 2013), which results in a cooling age of 5.5 Myr.
5.2.3. Debris Disk
The inner temperature of the debris disk is 1991 K (see Table 3), larger than the silicate sublimation temperature (Ts) of about 1300–1500 K (Lodders 2003). However, this Ts is based on the solar abundance and mainly used to model protoplanetary disks of young stars. Rafikov & Garmilla (2012) argued that those values of Ts are underestimates of Tin for disks around WDs, once the composition and evolution of these disks are distinct from those around young stars. In fact, some WDs have Tin larger than 1500 K, such as HE 1349−2305 (Girven et al. 2012) and GD 56 (Farihi et al. 2009), both with Tin = 1700 K. Moreover, according to Rafikov & Garmilla (2012), Tin is larger for WDs with higher accretion rates and TWD, which agrees with the larger Tin of 4U 0142+61 compared to the Tin of other isolated WDs.
Once we consider the debris disk opaque, we can estimate the minimum mass of the dusty disk using the approach from Jura (2003). The surface area of the dusty region can vary from A ∼ 1025 to 1027 cm2. Rafikov & Garmilla (2012) stated that the particle sizes in debris disks around WDs vary from 0.03 to 30 cm. Thus, if we consider 10 cm diameter particles, the opacity is 0.05 g−1 cm2 at 15 μm (Ossenkopf et al. 1992), resulting in a minimum dust mass around 1026–1028 g.
Once the disk is formed by gas and dust, we should also estimate the mass in gaseous form. Ansdell et al. (2016) suggested that protoplanetary disks can have a gas-to-dust mass ratio from 100 up to 103. Assuming the maximum value, the total mass of the disk would be around 1029–1031 g. The above value does not consider the mass in the internal gas disk. In view of all approximations and uncertainties, this value should be regarded as a crude estimate of the minimum disk mass. As we will discuss in Section 7, the expected total mass of a disk resulting from the merger of two CO WDs is about 1032 g.
5.2.4. Gaseous Disk
Our fit is based on the assumption that the gaseous disk is optically thin and does not contribute to the optical and IR emission of the system. In this section, we demonstrate that it is a valid assumption. We adopted the thin disk model proposed by Frank et al. (2002), with some adaptations to fit our needs. Below, we present the main equations, which are not dependent on any assumption on the optical depth. Considering a geometrically thin steady disk, the optical depth τ is
where κR is the Rosseland mean opacity and Σ(R) is the disk surface density. Assuming that the viscosity parameter α follows the Shakura & Sunyaev (1973) prescription and that the disk is geometrically thin, we can write Σ(R) as (Frank et al. 2002):
where cs is the sound speed and H(R) is the height of the disk in the radius R. We must point out that there are some discussions about the validity of the α-parameterization for the outcome disk of a merger of WDs (Becerra et al. 2018). Its use is justified by the lack of other applicable theories and the widespread use of such prescriptions in disks surrounding isolated WDs and pre-main-sequence stars.
Moreover, we can estimate cs from the height H(R) and R using (Frank et al. 2002)
Following the methodology from Frank et al. (2002), we use Kramer's law to estimate κR(R). However, we consider a carbon (or entirely metallic) composition instead of the solar one, which gives (Hansen et al. 2004)
where Tc(R) is the central temperature and ρ(R) is the volumetric density, given by (Frank et al. 2002)
In contrast to Frank et al. (2002), we calculated Tc(R) considering that the radiation pressure is negligible, i.e., the pressure has only the gas component. Doing this, we obtain
where mp is the proton mass.
It is not possible to estimate the optical depth solely by the equations above, since there are more parameters than equations. The missing equation in the model of Frank et al. (2002) correlates Tc(R) with τ(R). However, this equation is based on the assumption of an optically thick disk. Since we aim to verify whether the disk is optically thin or not, we cannot consider an equation for an optically thick disk. Thus, we propose a new equation for the system to be solvable.
We assumed H(R)/R ∼ 0.1, following the simulations of Raskin et al. (2012) for a disk around a WD produced in a merger. This hypothesis is corroborated by the fitting of the SED of FU Ori, which also resulted in H/R ∼ 0.1 (Kenyon & Hartmann 1991). This result was later used by Hartmann et al. (1993) to estimate the optical depth of Herbig Ae star disks, which could be optically thin for accretion rates of ∼10−9 M⊙ yr−1. Thus, supported by results related to merger simulations and pre-main-sequence disks, we fixed the relation between R and H with Equation (27). Hence, we can calculate the optical depth of the gaseous disk:
We arbitrated that the disk is optically thick if the optical depth is larger than 1. Using the above equations, we obtained τ ≤ 1 for α ≥ 0.15, which is consistent with α = 0.1–0.4 for accretion disks (King et al. 2007). Hence, the gaseous disk of our model is optically thin.
5.2.5. Accretion Rate
Our model predicts an accretion rate of g s−1, which is much higher than the –1011 g s−1 for isolated WDs (Koester et al. 2014; Farihi et al. 2018). Conversely, our is similar to that of pre-main-sequence stars, such as T Tauri and Herbig Ae/Be objects (Vorobyov & Basu 2008; Mendigutía et al. 2011). This is consistent with our hypothesis that the 4U 0142+61 disk is similar to protoplanetary disks (see Section 4.3).
Analyzing the population of T Tauri objects, Vorobyov & Basu (2008) proposed a correlation between the disk mass and accretion rate of those objects given by . Hence, expanding this behavior for isolated WDs, the high difference between the accretion rate of 4U 0142+61 and isolated WDs can be qualitatively explained by the huge difference between their disk masses (see Table 4).
Table 4. Comparison between for 4U 0142+61 and WD G29-38 and the Estimated Value Based on the Relation between the Disk Mass and the Accretion Rate, which Is Denoted by
| Object | Mdust | Mdisk | ||
|---|---|---|---|---|
| 4U 0142+61 | ∼1029a | ∼1032 | 2 × 1017 | 3.4 × 1017a |
| WD G29-38 | ∼1023b | ∼1026 | 6 × 1010 | 7 × 1010c |
Notes. We consider the same dust-to-gas ratio from Section 5.2.3.
aOur work. bJura (2003). cFarihi et al. (2018).Download table as: ASCIITypeset image
Table 4 compares the accretion rates for WD G29-38 (an isolated WD) and 4U 0142+61 obtained from X-ray emission, , with the estimated accretion rate calculated using Mdisk. Interestingly, both values are very close, giving some plausibility for the proposed relation.
5.3. Optical Pulsed Fraction
The main goal of this paper is to propose a plausible model of the quiescent spectrum of 4U 0142+61 in a WD scenario. However, our model is also consistent with the 4U 0142+61 flux modulation, as we show below.
Object 4U 0142+61 has periodic variability in the X-ray and optical wavelengths (den Hartog et al. 2008; Kern & Martin 2002). The X-ray pulsed emission could be explained by the change of the observer view of the magnetic accretion structure and the hot spots on the WD surface along the WD rotation. Regarding the optical pulsation, the accreting magnetic WD model has cyclotron emission as a common explanation. However, we did not include this radiative process in our model. The nonnegligible bremsstrahlung contribution, which is still optically thin in optical wavelengths (see Figure 1), can also qualitatively explain the flux modulation in the optical regime.
Below, we show that the optical pulsed fraction (PF) is also quantitatively consistent with the proposed scenario. We adopt the PF definition of Kern & Martin (2002),
in which Fmax and Fmin are, respectively, the maximum and minimum fluxes during a rotation.
In our model, the maximum possible optical PF occurs if the postshock region is completed self-eclipsed by the WD. In this case, we can write
and
Thus, the maximum PF in the I band is 28%, which is very close to the observational PF of % (Kern & Martin 2002).
5.4. Comparison with Previous Models
For the magnetar model, the X-ray SED of 4U 0142+61 was successfully modeled by Hascoët et al. (2014) using the phenomenology proposed by Beloborodov (2013). In this scenario, the IR emission is attributed to a passive irradiated disk (Wang et al. 2006). The optical emission is supposed to be of magnetospheric origin (Wang et al. 2006); however, it lacks a quantitative explanation for such emission.
Similar to the magnetar model, the accreting NS model can reproduce the X-ray emission (Zezas et al. 2015). But, for this model, there are some attempts to fit the optical and IR data using a fallback disk. Hulleman et al. (2000) and Perna et al. (2000) were unable to fit 4U 0142+61 optical data using a fallback disk with T αR−3/7. Using a model in which T αR−1/2 and F αν−1, Ertan & Çalışkan (2006) and Ertan et al. (2007) were able to fit the optical/IR data.
The X-rays of 4U 0142+61 in the WD pulsar model are due to a pulsar-like emission. However, we are not aware of any attempt to fit the 4U 0142+61 X-ray SED in this model. Recently, Cáceres et al. (2017) inferred the structure parameters, magnetic field, rotation period, and spin-down rates of a WD pulsar death line. They showed that WDs above the death line emit blackbody radiation in the soft X-ray band via magnetic polar cap heating by backflowing pair-created particle bombardment. Moreover, the WD pulsar model has been used to explain the emission of other objects, such as AR Scorpii (Geng et al. 2016).
The optical/IR modeling of 4U 0142+61 in the WD pulsar model uses the same components of our model: a debris disk modeled by Equation (17) and a photosphere emitting as a blackbody (Rueda et al. 2013). For this model, RWD = 4.2 × 108 cm, MWD = 1.1 M⊙, and TWD = 1.31 × 105 K. In comparison, our estimates are more extreme. We obtained smaller RWD, higher MWD, and roughly similar TWD. Apart from the different data set, we used the derived RWD from the hard X-rays in order to build a model that is consistent in all wavelengths, whereas Rueda et al. (2013) used the optical/IR data alone to derive the WD parameters, which results in more standard parameters. Thus, even though the fits have distinct RWD and TWD, 4U 0142+61 is thought to be a young WD in both cases.
The nature of the optical pulsed emission is challenging for all previous models. For an NS scenario, Kern & Martin (2002) pointed out that the observed fraction is higher than expected by a disk irradiated by X-rays. Thus, Kern & Martin (2002) proposed that such pulsation could be magnetospheric in the magnetar model. However, no component of the Hascoët et al. (2014) model extends up to the optical range. The NS accreting model does not present estimates for the expected optical PF, even though Ertan & Cheng (2004) stated that the PF could be caused by outer gaps in the pulsar magnetosphere operating with an internal disk. To our knowledge, there has been no attempt to explain the optical pulsation in the context of the WD pulsar model.
6. Spin-down, Propeller Regime, and the Magnetic Field
Object 4U 0142+61 is slowing down. Thus, in this section, we infer the magnetic field of 4U 0142+61 to reproduce the spin-down in an accreting regime.
The corotational radius, Rc (Equation (15)), is the disk position in which the particle's rotational velocity is equal to stellar rotation. According to Ekşi et al. (2005), Rc must be larger than both RWD and Rm for the system to be in the accreting regime. Moreover, Rm must be larger than RWD for the accretion to be magnetic and create spots.
If we consider only the effect of matter falling onto the WD, we will have spin-up. However, the WD can spin down in the accretor regime if other spin-down mechanisms compensate for the increase due to accretion, such as the coupling between the magnetic field and the disk or the misalignment between the magnetic field and rotation axes (Wang 1987; García-Berro et al. 2012).
García-Berro et al. (2012) argued that the alignment of the dipole magnetic field with the spin axis can be the main cause of the spin-down for merger remnants. That spin-down effect is more prominent on WDs that are the product of a merger of two WDs with different masses, once the misalignment between the magnetic field and the spin axes is larger in that case (see García-Berro et al. 2012, for details). This spin-down can be estimated by
where μ (G cm3) is the magnetic moment, I (g cm2) is the moment of inertia, and β represents the angle between the magnetic field and rotation axes.
The accretion and coupling spin change can be calculated by (Wang 1987)
where n(ωs) can be obtained in Wang (1987), for ωs = Rm/Rc. In this case, the equation accounts for both of the components: the coupling between the magnetic field and the disk and the accretion onto the central remnant. In this model, the WD can spin down if the ratio between the magnetosphere radius and the corotational radius is in the range of 0.971 to 1.0 (Wang 1987). To estimate Rm, we adopted (Ferrario et al. 1989)
where B is the dipolar magnetic field.
The total spin-down is given by
For our model to be feasible, 4U 0142+61 must have Rc > Rm > RWD and a spin-down around 10−12 s s−1. Moreover, the inferred value of the magnetic field to reproduce the spin-down must be consistent with a bremsstrahlung scenario. Depending on the nature of the WD and its accretion structure, different types of cooling could be predominant (Lamb & Masters 1979; Kylafis & Lamb 1982). A condition for the bremsstrahlung emission dominates over cyclotron emission is that the magnetic field has to be smaller than 6 × 106 (Lf/1036 erg s−1)2/5, where Lf is Lbrem divided by f. Considering Rbrem and RWD, we have f ∼ 1.88 × 10−4, which gives an upper limit for B of 2.03 × 108 G.
Adopting a moment of inertia equal to 1048 g cm2 and considering that the pulsar magnetic dipole moment is misaligned with the spin axis by an angle β = 90°, we obtain of 5.3 × 10−15 s s−1, which is much smaller than the observed spin-down of 4U 0142+61. Therefore, the contribution from the misalignment of the magnetic field and rotation axes is not able to reproduce the spin-down and can be neglected. Thus, we need to reproduce the spin-down solely by the coupling disk magnetic field (see Equation (30)), which imposes 0.971 < Rm/Rc < 1. Therefore, if this proof is successful, we will also prove the assumption that Rc ∼ Rm, which was used in the estimate Tshock by Equation (13). For β = 90°, we must have B = 2.82 × 107 G to reach 2 × 10−12 s s−1. Conversely, if we consider β = 0°, we must have B = 5.63 × 107 G. Thus, we obtain 2.82 × 107 G < B < 5.63 × 107 G. Those values are consistent with the upper limit imposed by the bremsstrahlung emission. Moreover, this spin-down requires Rm/Rc = 0.994, which is extremely close but still consistent with the condition to be in the accreting regime.
We can compare the above values of magnetic fields with those observed in magnetic WDs. In magnetic CVs of the polar class, the observed WD magnetic fields vary from 7 MG (V2301 Oph) up to 240 MG (AR UMa), whereas intermediate polars have magnetic fields of ∼4–30 MG, with the highest value of ∼32 MG for V405 Aur (Ferrario et al. 2015). Isolated WDs have magnetic fields in the range from 103 to ∼109 G. There are several examples of isolated WDs that have B around 107 G. We cite some: WD 0806+376, with a field of 3.97 × 107 G, and WD 1017–367, with B = 6.5 × 107 G (see Ferrario et al. 2015, for other examples of magnetic WDs). Thus, our estimate of the magnetic field is consistent with the observed values in magnetic CVs.
7. Possible Origin and Evolution of the Object
In this accreting WD scenario, 4U 0142+61 is a fast-spinning, isolated, magnetic, hot, and extremely massive WD. Even though those characteristics are very uncommon for a WD, sources with similar characteristics have already been observed. For example, RE J0317–853 is in a binary system without any interaction with the secondary. This object has a period of 725.4 s, an estimated mass of 1.35 M⊙, an effective temperature of ∼50,000 K, and a magnetic field of ∼340 MG (Barstow et al. 1995). The most plausible origin for that source is the merger of two less massive CO WDs (Ferrario et al. 1997), which is the same origin proposed for 4U 0142+61 in the WD pulsar model (Rueda et al. 2013).
There are some arguments in favor of a merger origin for massive and magnetic WDs. For instance, merger is one of the most plausible scenarios to explain why magnetic isolated WDs are usually more massive than nonmagnetic ones (García-Berro et al. 2012). In fact, all four isolated WDs with M⊙ > 1.3 have B > 106 G (Należyty & Madej 2004). Recent Gaia observations in the solar neighborhood (d ≲ 100 pc) show the presence of a substantial number of massive WDs and a bifurcation in the color–magnitude diagram that are consistent with a merger formation (Kilic et al. 2018). Toonen et al. (2017) analyzed the sample of WDs within 20 pc and showed that the number of WDs in double WD systems (∼25%) is smaller than the percentage of solar-type main-sequence stars in double systems (∼50%). They concluded that this discrepancy is consistent with about 10%–30% of all isolated WDs being the result of a merger.
The merger of WDs with different core compositions leads to several final results (Dan et al. 2014). The merger of two CO WD progenitors results in a near-Chandrasekhar mass product. The remnant consists of a cold core formed by the primary, a hot envelope made by a fraction of the secondary mass, and a disk containing the remnant of the secondary. A small amount of mass, about 10−3 M⊙, is ejected and leaves the system (Lorén-Aguilar et al. 2009). The exact percentage of the secondary mass in the disk varies according to the mass of the progenitors. According to previous simulations, a good estimate for this percentage is ∼50% of the less massive progenitor (Becerra et al. 2018), which gives an initial mass for the disk of the order of 10−1 M⊙.
This newborn WD is also expected to have a fast rotation right after the coalescence. Becerra et al. (2018) stated that the remnant (cold core and envelope) spins as a rigid body. In contrast, Yoon et al. (2007) argued that the cold core rotates as a rigid body and the envelope spins differentially, leading the photosphere to present a quasi-Keplerian angular velocity. This differential rotation, however, vanishes quickly, and the remnant eventually starts to rotate uniformly. There is also an expected enhancement of the magnetic field during the coalescence (Ji et al. 2013; Zhu et al. 2015) and in the early years after the merger (García-Berro et al. 2012). All of those previous properties—presence of the disk, fast spin, and huge magnetic field—are consistent with the observations of 4U 0142+61. Thus, if the accreting WD model for 4U 0142+61 is correct, this object probably is a young product of a merger of two less massive CO WDs.
Moreover, the remnant is expected to accrete matter from the disk during its early years, which is also consistent with the proposed model. However, how the disk and the accretion rate evolve is still a question for debate. Külebi et al. (2013) argued that the disk is viscous-supported and can be described by the α-formalism of Shakura & Sunyaev (1973). In this model, the accretion rate would be about 10−1 M⊙ s−1 in the first second, rapidly decreasing (Becerra et al. 2018). For those high accretion rates and a rigid-body rotation, the massive WD would spin up in the first years and probably break (Külebi et al. 2013). Therefore, we do not take into account this evolutionary hypothesis. On the other hand, Yoon et al. (2007) argued that the disk is more likely to be thermal pressure–supported, and the early accretion rate is of the order of 10−7 M⊙ yr−1 (Becerra et al. 2018). Considering a initial spin period of about 2.5 s (Becerra et al. 2018) and an accretion rate smaller than the Eddington limit, we have Rm > Rc in the early years. Thus, the remnant would initially pass through a propeller phase. This propeller phase spins down the remnant, protecting it from breaking. As a consequence of the spin-down, the period and, consequently, the corotational radius increase, thus enabling the WD to accrete matter from the disk.
How this very massive WD would evolve after the start of the accretion is hard to foresee, as neither the evolution of the postmerger product nor the fate of very massive accreting WDs are well understood. In either case, 4U 0142+61 would be a probable candidate to become a supernova (SN) Ia or an NS by collapse. It is also possible that 4U 0142+61 survives as an extremely massive WD, such as RE J0317–853.
Several astrophysical objects have been proposed as SN Ia progenitors, as discussed in the review of Maoz et al. (2014). The AXPs/SGRs as high-mass WDs are cited as good candidates for the SN Ia "spin-up/spin-down" scenario. In this case, a rapidly rotating high-mass WD, which is rotation-supported against ignition, can eventually explode after a period of spin-down (Maoz et al. 2014). This outcome is possible for 4U 0142+61, since we predict a fast spinning-down Chandrasekhar WD.
Nonetheless, the accretion rate can also disturb the stability of isolated high-mass WDs. For an accretion rate in the range of 10−5–10−6 M⊙ yr−1, Saio & Nomoto (2004) argued that a WD formed by the merger of two CO WDs would not explode as an SN Ia because it would inevitably become an O–Ne–Mg WD. In this case, the accretion could lead the WD to exceed the limiting mass and become an NS by carbon deflagration collapse (Nomoto & Kondo 1991).
Conversely, Yoon et al. (2007) considered accretion rates smaller than 10−6 M⊙ yr−1, which are consistent with our accretion rate estimates for 4U 0142+61. They found that the remnant of two CO WDs can lead to an SN Ia after ∼105 yr. Thus, if the accreting WD model is correct, 4U 0142+61 is a good candidate to explode as an SN Ia in a small amount of time. On the other hand, if the fate of 4U 0142+61 is collapse into an NS or a very massive WD, 4U 0142+61 is a priceless object, since it can give clues as to how the merger of two CO WDs evolves.
8. Thoughts about Bursts, Glitches, and Radio Emission
This paper focuses on the quiescent emission of 4U 0142+61. However, 4U 0142+61 has bursts and glitches (Gavriil et al. 2011; Dib & Kaspi 2014; Archibald et al. 2017), which are nonetheless less energetic compared to the bulk of magnetar bursts (Göğüş et al. 2017). Rotational instabilities in very fast-spinning WDs can explain these events. This mechanism is particularly appealing for 4U 0142+61, which has a period of 8.68 s, not far from the breaking frequency of a WD (Malheiro et al. 2012).
The increase of luminosity in bursts can be generated by thermonuclear runways of carbon (Gasques et al. 2005). In fact, thermonuclear reactions are seen in some classes of accreting objects, such as NS X-ray bursts (Ayasli & Joss 1982; Lewin et al. 1993) and WD recurrent novae (Webbink et al. 1987; Warner 2003).
The glitches in SGRs/AXPs are a decrease in the spin and spin-down. They can be accompanied by an increase in the luminosity (Dib & Kaspi 2014). Those glitches can have the same phenomenology proposed by Usov (1994) and Malheiro et al. (2012) for the WD pulsar model. In this case, a near-Chandrasekhar WD can present sudden changes in the spin, thereby decreasing the centrifugal forces of the core. Thus, gravity would make the WD less oblate, which would lead to a change in the gravitational energy and consequent release of energy.
Some clues about the origin of the 4U 0142+61 radio emission (see Section 2) can be traced. Radio emission is observed in some accreting WDs. According to Barrett et al. (2017), 21 out of 121 magnetic CVs have detected radio emission. The most plausible interpretations are gyrosynchrotron for the weakly polarized radio emitters and electron–cyclotron maser emission for the highly polarized sources. Since we do not know the polarization of the radio emission of 4U 0142+61, both interpretations are possible.
9. Conclusions
We have used observational data of 4U 0142+61 from the mid-IR to the hard X-ray to investigate the scenario of an accreting magnetic WD with a debris disk. It is essential to mention that we do not claim that this scenario is valid for all SGRs/AXPs.
We obtain a good fit for the entire SED of 4U 0142+61 using plausible components and parameters. The bremsstrahlung emission from the postshock region of 4U 0142+61 reproduces the hard X-rays. A fraction of this emission is reprocessed by the WD photosphere, originating hot spots, which respond by the soft X-rays. The bremsstrahlung emission extends to the optical range, in which the disk and the WD photosphere also contribute. The disk dominates the emission in the IR range.
The emission from the hard X-ray bremsstrahlung implies a near-Chandrasekhar WD, for which we assume a mass of 1.41 M⊙ and a radius of 1021 km. From the fit of the optical/IR emission, we obtain a WD effective temperature of 9.4 × 104 K. Those WD characteristics point to a young WD having an estimated age of a few Myr. The disk has inner and outer temperatures of 1991 and 285 K, respectively. Those temperatures are consistent with disks seen around WDs.
From the spin-down rate, we can estimate a magnetic field of ∼107 G, which is consistent with the estimated values in magnetic WDs.
This way, we were able to present a model that explains all of the quiescent emission of 4U 0142+61, as well as the observed spin-down. Such a WD can be understood as the result of a recent merger of two less massive WDs. In this scenario, 4U 0142+61 is a good candidate to become an SN Ia.
We also estimated a new value for the 4U 0142+61 distance, kpc, based on the 3D reddening map of Green et al. (2018, 2019).
We thank the anonymous referees for comments that helped us to improve the manuscript. We acknowledge T. Enoto for kindly providing us with Suzaku soft X-ray data of 4U 0142+61.
The authors are thankful for grant No. 2013/26258-4, Thematic Project of São Paulo Research Foundation (FAPESP). S.V.B. acknowledges Coordenadoria de Aperfeiçoamento de Pessoal de Nível Superior (CAPES). C.V.R. acknowledges CNPq (Proc. 303444/2018-5). J.G.C. is likewise grateful to grant No. 2013/15088-0, São Paulo Research Foundation (FAPESP), and CNPq (Proc. 421265/2018-3 and 305369/2018-0). M.C. acknowledges financial support under grant No. 2015/25972-0 from the São Paulo Research Foundation (FAPESP). M.M. acknowledges financial support from CAPES and CNPq.
Facility: INTEGRAL. -
Software: XSPEC (Arnaud 1996), INTEGRAL Off-line Scientific Analysis package.
Footnotes
- 4
Observations taken on 2007 August 13 04:04:13 (seq. number 402013010). Kindly provided by the authors.
- 5