Abstract
The slowly pulsating B star HD 50230, which is in fact a hybrid B-type pulsator, has been observed by CoRoT for at least 137 days. Nearly equidistant period spacing patterns are found among eight modes that are extracted from the oscillation spectrum with more than 500 frequencies. However, it is thought to be most likely accidental by Szewczuk et al. In the present work, we analyze the eight modes in depth with the χ2-matching method. Based on the best-fitting model (model MA), we find that they can be well explained as sequences of consecutive dipolar (l, m) = (1, 0). The period discrepancies between observations and the best-fitting model are within 100 s except for the outlier, which is up to 300 s. Based on the calculated χ2-minimization models, we find that, for pure g-mode oscillations, the buoyancy radius, Λ0, can be precisely measured with the χ2-matching method between observations and calculations. It represents the "propagation time" of the g-mode from the stellar surface to the center. It is of Λ0 = 245.78 ± 0.59 μHz with a precision of 0.24%. In addition, we also find that HD 50230 is a metal-rich (Zinit = 0.034–0.043) star with a mass of M = 6.15–6.27 M⊙. It is still located in the hydrogen-burning phase with central hydrogen of XC = 0.298–0.316 (or  ); therefore, it has a convective core with a radius of Rcc = 0.525–0.536 R⊙ (or
); therefore, it has a convective core with a radius of Rcc = 0.525–0.536 R⊙ (or  ). In order to interpret the structure of the observed period spacing pattern well, the convective core overshooting (fov = 0.0175–0.0200) and the extra diffusion mixing (
). In order to interpret the structure of the observed period spacing pattern well, the convective core overshooting (fov = 0.0175–0.0200) and the extra diffusion mixing ( ) should be taken into account in theoretical models.
) should be taken into account in theoretical models.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Slowly pulsating B stars (hereafter, SPB stars) are the upper main-sequence stars of intermediate masses (2.5 ∼ 8 M⊙; for more descriptions, see, e.g., Aerts et al. 2010). Their effective temperatures range from about 11,000 to 22,000 K with spectral types between B3 and B9. Their pulsation pattern represents the characteristic of nonradial, high-order, low-degree, multiperiodic g-mode oscillations with a period of about 0.5–3 days (Aerts et al. 2010). The oscillations of SPB stars are thought to be excited by the κ-mechanism, i.e., the opacity is enhanced due to the ionization of iron-group elements, also called the Z-bump, at a temperature of about 200,000 K ( ; see, e.g., Aerts et al. 2010; Moravveji et al. 2016).
; see, e.g., Aerts et al. 2010; Moravveji et al. 2016).
Recently, more and more SPB stars have been observed and abundant seismological data have been collected (e.g., Degroote et al. 2010, 2012; Pápics et al. 2012, 2014, 2015, 2017; Moravveji et al. 2015, 2016; Triana et al. 2015; Briquet et al. 2016; Bowman et al. 2018; Buysschaert et al. 2018; Zhang et al. 2018; Pedersen et al. 2019) via ground- and space-based missions, such as CoRoT (e.g., Baglin et al. 2006), Kepler (e.g., Borucki et al. 2010; Gilliland et al. 2010; Koch et al. 2010), K2 (e.g., Haas et al. 2014; Howell et al. 2014), and the Transiting Exoplanet Survey Satellite (TESS; e.g., Ricker et al. 2015). Some SPB stars have extremely slow rotations, such as KIC 10526294 with a rotational period of Prot ∼ 188 days (e.g., Pápics et al. 2014; Moravveji et al. 2015); some of them are moderate or faster rotators, such as KIC 7760680 with a rotational frequency of frot ∼ 0.48 day−1 (Moravveji et al. 2016) and KIC 3459297, KIC 6352430A, KIC 4930889 (A?), KIC 9020774, and KIC 11971405 with rotational frequencies of frot ∼ 0.63, 0.64, 0.74, 1.06, and 1.62 day−1, respectively (see Pápics et al. 2017, refer to Table 14). In addition, some SPB stars have both rotation and magnetic field—for instance, ζ Cassiopeiae has a moderate rotation period of Prot = 5.370447 ± 0.000078 days and a weak magnetic field whose intensity is about 100–150 G (see Briquet et al. 2016); HD 43317 has a lower rotation period of Prot =0.897673 days and a magnetic field of Bp = 1312 ± 332 G (see Buysschaert et al. 2018).
Recently, Moravveji et al. (2015) made detailed model analyses for the ultra-slow rotating SPB star KIC 10526294. Finally, they found that the profile of elements, i.e., the shape of the buoyancy frequency (N) beyond and near the convective core can be constrained by comparing theoretical models with the observed 19 dipole prograde  g-modes through period spacing pattern (i.e., period spacing versus period). In the process, they also found that the exponentially decaying diffusion in convective core overshooting (fov =0.017–0.018) is better than the corresponding step function formulation; in addition, an extra diffusion mixing (
g-modes through period spacing pattern (i.e., period spacing versus period). In the process, they also found that the exponentially decaying diffusion in convective core overshooting (fov =0.017–0.018) is better than the corresponding step function formulation; in addition, an extra diffusion mixing ( ) is necessary to explain the sine-like structure in the observed period spacing pattern in this target.
) is necessary to explain the sine-like structure in the observed period spacing pattern in this target.
Moravveji et al. (2016) analyzed 37 clearly identified dipole prograde (l, m) = (1, +1) g-modes in KIC 7760680. Similar to Moravveji et al. (2015) in KIC 10526294, they also found that the exponentially decaying diffusion in convective core overshooting is better than the corresponding step function formulation. In addition, they found that the convective core overshooting (fov ≈ 0.024 ± 0.001) can coexist with moderate rotation (frot ∼ 0.48 day−1). In order to interpret the sine-like structure of period spacing pattern, the extra diffusion mixing is also necessary in theoretical models. But they found that the optimal extra diffusion mixing coefficient of  is notably smaller than that of KIC 10526294 (
is notably smaller than that of KIC 10526294 ( ), in that KIC 7760680 rotates faster and also has an older age compared to KIC 10526294.
), in that KIC 7760680 rotates faster and also has an older age compared to KIC 10526294.
Buysschaert et al. (2018) modeled HD 43317 via 16 identified modes that are retrograde modes with (l, m) =(1, −1) and (2, −1) and one distinct prograde (2, 2) mode and constrained the surface strength of the magnetic field (Bp = 1312 ± 332 G), except for precisely determining its fundamental parameters. On the other hand, they found that the magnetic field caused a suppression of near-core mixing in this star and that it has a lower convective core overshooting parameter ( ).
).
These previous works (Moravveji et al. 2015, 2016; Buysschaert et al. 2018) give us so many new insights into seismically modeled SPB stars and help us understand the interior structure of SPB stars on a higher level, such as the connection among the extra diffusive mixing, the shape of the buoyancy frequency (N) and the structure of the period spacing pattern, as well as the relationship and/or interaction among convective core overshooting, rotation, and the magnetic field.
However, there are still significant discrepancies between observed periods and model calculated ones. The maximum period discrepancy is up to about 500 s for both KIC 10526294 (see Figure 4 of Moravveji et al. 2015) and KIC 7760680 (see Figure 8 of Moravveji et al. 2016). For HD 43317, the period discrepancy between observations and the best-fitting model is up to thousands of seconds (see Buysschaert et al. 2018, Table 3). So, what factors cause such large period discrepancy between the observations and the best-fitting models? Up until now, the question has remained unanswered.
In the present work, we make detailed seismic analyses of a unique SPB star, HD 50230, in order to probe its interior structures. HD 50230 has a larger mass (7–8 M⊙; Degroote et al. 2010), which is close to the upper limit of the mass range of SPB stars (2.5–8 M⊙) and is larger than that of the other analyzed SPB stars (refer to, e.g., Moravveji et al. 2015, 2016; Buysschaert et al. 2018). It also has a higher metallicity ( ) and stays in a binary system (for a more detailed introduction about HD 50230, see Section 2).
) and stays in a binary system (for a more detailed introduction about HD 50230, see Section 2).
2. HD 50230
HD 50230 is a metal-rich ( ; Z⊙ = 0.02) young massive star with a spectral type of B3V and a visual magnitude of 8.95 (e.g., Degroote et al. 2010, 2012; Szewczuk et al. 2014). It is the primary component of a binary system with a rotational velocity (
; Z⊙ = 0.02) young massive star with a spectral type of B3V and a visual magnitude of 8.95 (e.g., Degroote et al. 2010, 2012; Szewczuk et al. 2014). It is the primary component of a binary system with a rotational velocity ( ) of 6.9 ± 1.5 km s−1. The effective temperature is of Teff = 18,000 ± 1500 K, and surface gravity to be of
) of 6.9 ± 1.5 km s−1. The effective temperature is of Teff = 18,000 ± 1500 K, and surface gravity to be of  (c.g.s. units; refer to Degroote et al. 2012). For the effective temperature of the secondary component, Degroote et al. (2012) give an upper limit of
(c.g.s. units; refer to Degroote et al. 2012). For the effective temperature of the secondary component, Degroote et al. (2012) give an upper limit of  when assuming surface gravity
when assuming surface gravity  (c.g.s. units).
(c.g.s. units).
Based on CoRoT observations of ∼137 days, Degroote et al. (2010) extracted eight peaks, which are listed in Table 1, from the oscillation power spectra. These peaks are almost uniformly spaced in period with the mean spacing of 9418 s and a deviation of about 200 s. Degroote et al. (2010) interpreted them as consecutive radial orders, n, with the same spherical harmonic degree, l, and azimuthal order, m. Based on the assumption of l = 1 and m = 0, Degroote et al. (2010) found the mass of HD 50230 to be of 7–8 M⊙ with an overshooting extension of  (HP pressure scale height) by the step overshooting description in the radiative regions adjacent to the convective core (see Szewczuk et al. 2014 for an overview). In addition, Degroote et al. (2010) suggested that the HD 50230 stays in the middle of the main sequence, and about 60% of the initial hydrogen in its center has already been consumed.
(HP pressure scale height) by the step overshooting description in the radiative regions adjacent to the convective core (see Szewczuk et al. 2014 for an overview). In addition, Degroote et al. (2010) suggested that the HD 50230 stays in the middle of the main sequence, and about 60% of the initial hydrogen in its center has already been consumed.
Table 1. Summary of Observations for HD 50230
| Fre. ID | ng |
 a
a
|
 a
a
|
 a
a
|
|---|---|---|---|---|
| (10−3day−1) | (s) | (s) | ||
| f028 | −6 | 1236.85 ± 0.04 | 69854.873 ± 6.777 | 9241.379 ± 20.692 |
| f101 | −7 | 1092.34 ± 0.09 | 79096.252 ± 19.551 | 9640.178 ± 20.301 |
| f006 | −8 | 973.67 ± 0.02 | 88736.430 ± 5.468 | 9522.432 ± 8.652 |
| f005 | −9 | 879.31 ± 0.02 | 98258.862 ± 6.705 | 9186.452 ± 10.451 |
| f011 | −10 | 804.13 ± 0.02 | 107445.314 ± 8.017 | 9562.853 ± 12.436 |
| f016 | −11 | 738.41 ± 0.02 | 117008.166 ± 9.508 | 9233.798 ± 14.590 |
| f001 | −12 | 684.40 ± 0.02 | 126241.964 ± 11.067 | 9430.037 ± 33.819 |
| f052 | −13 | 636.83 ± 0.05 | 135672.000 ± 31.956 | ⋯ |
Notes. Observations include frequencies νi, associated periods (Pi) and period spacings (ΔPi), and the corresponding observational uncertainties  ,
,  , and
, and  , respectively. The radial order (ng) is decided from the best-fitting model.
, respectively. The radial order (ng) is decided from the best-fitting model.
 ) come from Degroote et al. (2012, Table A.2). Periods (Pi) and period spacings (ΔPi) are derived from the frequencies (νi). Similar to Table 1 of Degroote et al. (2012), the uncertainties of periods and period spacings (
) come from Degroote et al. (2012, Table A.2). Periods (Pi) and period spacings (ΔPi) are derived from the frequencies (νi). Similar to Table 1 of Degroote et al. (2012), the uncertainties of periods and period spacings ( and
and  ) correspond to
) correspond to  in the table.
in the table.
Download table as: ASCIITypeset image
Motivated by the detection of period spacings, Degroote et al. (2012) reanalyzed the observations. They extracted 566 frequencies from the oscillation power spectra, including high- and low-order g-mode and low-order p-mode. Most of them are not clearly identified. Based on those extracted frequencies, they obtained a rotational splitting of p-mode to be of Δfobs = 0.044 ± 0.007 day−1 via the analysis of the autocorrelation of the periodogram between 10 and 15 day−1. Finally, Degroote et al. (2012) suggested that the rotational effects should be taken into account in modeling when interpreting the small deviations from the uniform period spacings despite the fact that the surface rotational velocity has merely an order of magnitude of 10 km s−1.
Recently, Szewczuk et al. (2014) reanalyzed the light curves of HD 50230 and extracted 515 frequencies to try to interpret the oscillation spectra in depth and to reidentify the detected frequencies. They found three series modes nearly uniformly spaced in periods from these extracted frequencies. But they have some common modes. The largest series has 11 frequencies and includes 8 frequencies that Degroote et al. (2010, 2012) determined (see Figure 1 of Szewczuk et al. 2014). But, finally, the 11 frequencies are thought to have different degrees l and azimuthal orders m.
Assuming the equatorial velocity to have an order of magnitude of Veq ∼ 10 km s−1 (Szewczuk et al. 2014), and assuming the radius be of R ∼ 5 R⊙, the corresponding rotational frequency is about Ωrot ≡ Veq/R ∼ 0.040 day−1, which is far smaller than the oscillation frequencies ν ∼ 1 day−1 (see Table 1), i.e., Ωrot ≪ ν. This indicates that the perturbation theory of rotational splitting for low-degree, high-order modes is available for the slow rotating star HD 50230.
Based on the rotational splitting of p-mode  , and the first-order approximation of rotational splitting of low-degree, high-order modes (Dziembowski & Goode 1992; Christensen-Dalsgaard 2003; Aerts et al. 2010):
, and the first-order approximation of rotational splitting of low-degree, high-order modes (Dziembowski & Goode 1992; Christensen-Dalsgaard 2003; Aerts et al. 2010):

where L = l(l + 1), the corresponding rotational splitting of g-mode is about  for dipolar modes. Correspondingly, the second-order approximation term of the low-degree, high-order mode is about
for dipolar modes. Correspondingly, the second-order approximation term of the low-degree, high-order mode is about  (the second-order approximation term
(the second-order approximation term  is derived from Dziembowski & Goode 1992). The second-order approximation term can be ignored compared to the first-order approximation term
is derived from Dziembowski & Goode 1992). The second-order approximation term can be ignored compared to the first-order approximation term  for target HD 50230. In addition, combining the rotational splitting of p-mode and Equation (1), we obtain the rotational frequency of HD 50230 to be of
for target HD 50230. In addition, combining the rotational splitting of p-mode and Equation (1), we obtain the rotational frequency of HD 50230 to be of  .
.
3. Physical Inputs and Modeling
3.1. Physical Inputs
In the present work, our theoretical models were computed by the Modules of Experiments in Stellar Astrophysics (MESA), which was developed by Paxton et al. (2011). It can be used to calculate both the stellar evolutionary models and their corresponding oscillation information (Paxton et al. 2013, 2015). We adopt the package "pulse" of version "v6208" to make our calculations for both stellar evolutions and oscillations (for more detailed descriptions refer to Paxton et al. 2011, 2013, 2015, 2016, 2018). The package "pulse" is a test suite example of MESA in the directory of '$MESA_DIR/star/test_suite/pulse." The module of the pulsation calculation is based on the ADIPLS code, which was developed by Christensen-Dalsgaard (2008) and added into MESA by the MESA team (for more information, refer to Paxton et al. 2011, 2013, 2015, 2016, 2018).
Based on the default parameters, we adopt the OPAL opacity table GS98 (Grevesse & Sauval 1998) series. We choose the Eddington gray-atmosphere T–τ relation as the stellar atmosphere model, and treat the convection zone by the standard mixing-length theory (MLT) of Cox & Giuli (1968) with mixing-length parameter αMLT = 2.0.
In the previous asteroseismic modeling of SPB stars, Moravveji et al. (2015, 2016) reported that the exponentially decaying diffusive description is better than a step function formulation for treating the convective core overshooting. Here, we also adopt the theory of Herwig (2000) to treat the convective overshooting in the core. The overshooting mixing diffusion coefficient Dov exponentially decreases with distance, which extends from the outer boundary of the convective core with the Schwarzschild criterion:
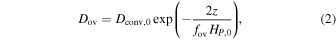
where  and
and  are the MLT derived diffusion coefficient near the Schwarzschild boundary and the corresponding pressure scale height at that location, respectively. z is the distance in the radiative layer away from that location. fov is an adjustable parameter (for more detailed descriptions, refer to Herwig 2000; Paxton et al. 2011).
are the MLT derived diffusion coefficient near the Schwarzschild boundary and the corresponding pressure scale height at that location, respectively. z is the distance in the radiative layer away from that location. fov is an adjustable parameter (for more detailed descriptions, refer to Herwig 2000; Paxton et al. 2011).
In addition, the element diffusion, semiconvection, thermohaline mixing, and the mass-loss were not included in the theoretical models.
The previous works (Degroote et al. 2010; Moravveji et al. 2015, 2016) suggested that extra diffusion mixing (Dmix) is necessary in theoretical models for interpreting the deviations of period spacings. In the present work, we also take it into account in the theoretical models.
Similar to the works of Moravveji et al. (2015, 2016), we also set the initial hydrogen mass fraction Xinit = 0.71 which takes from the Galactic B-star standard (Nieva & Przybilla 2012). Therefore, the adjustable parameter of element compositions reduce to one, initial metal mass fraction Zinit or helium mass fraction Yinit. They follow the relation: Xinit + Yinit + Zinit = 1.
3.2. Modeling and Finding the Best-fitting Model
According to the works described above, there are four initial input parameters, stellar mass (M), initial metal mass fraction (Zinit), overshooting parameter in convective core (fov), and extra diffusion mixing ( ) in theoretical models. The ranges and corresponding steps of the initial input parameters are listed in Table 2. According to the study of Degroote et al. (2010, 2012) and Szewczuk et al. (2014), we preliminarily set stellar mass
) in theoretical models. The ranges and corresponding steps of the initial input parameters are listed in Table 2. According to the study of Degroote et al. (2010, 2012) and Szewczuk et al. (2014), we preliminarily set stellar mass ![$M\in [6.6,8.2]\,{M}_{\odot }$](https://content.cld.iop.org/journals/0004-637X/881/1/86/revision1/apjab2ad8ieqn36.gif) with a step of 0.2 M⊙, initial metal mass fraction Zinit ∈ [0.010, 0.040] with a step of 0.005, overshooting parameter fov ∈ [0.010, 0.035] with a step of 0.005, and the extra diffusion mixing coefficient
with a step of 0.2 M⊙, initial metal mass fraction Zinit ∈ [0.010, 0.040] with a step of 0.005, overshooting parameter fov ∈ [0.010, 0.035] with a step of 0.005, and the extra diffusion mixing coefficient ![$\mathrm{log}\,{D}_{\mathrm{mix}}\in [2.0,4.5]$](https://content.cld.iop.org/journals/0004-637X/881/1/86/revision1/apjab2ad8ieqn37.gif) with a step of 0.5, respectively (Grid A hereafter).
with a step of 0.5, respectively (Grid A hereafter).
Table 2. Model Calculation Grids
| Variables | Parameter Ranges | Steps |
|---|---|---|
| Grid A | ||
| Mass (M/M⊙) | 6.6–8.2 | 0.2 |
| Initial metal abundance (Zinit) | 0.010–0.040 | 0.005 |
| Overshooting parameter (fov) | 0.010–0.035 | 0.005 |
Extra mixing ( ) ) |
2.0–4.5 | 0.5 |
| Grid B | ||
| Mass (M/M⊙) | 6.0–7.2 | 0.1 |
| 6.10–6.30 | 0.05 | |
| Initial metal abundance (Zinit) | 0.0300–0.0425 | 0.0025 |
| Overshooting parameter (fov) | 0.0150–0.0250 | 0.0025 |
Extra mixing ( ) ) |
3.2–4.4 | 0.2 |
| 3.4–4.2 | 0.1 | |
| Grid C | ||
| Mass (M/M⊙) | 6.1500–6.3000 | 0.0125 |
| Initial metal abundance (Zinit) | 0.03500–0.04375 | 0.00125 |
| Overshooting parameter (fov) | 0.0150–0.0225 | 0.0025 |
| 0.01750–0.02000 | 0.00125 | |
Extra mixing ( ) ) |
3.6–4.2 | 0.1 |
Download table as: ASCIITypeset image
Based on the above initial input parameters, we use MESA to calculate the corresponding stellar models and oscillation frequencies. Similar to the work of Wu & Li (2016, 2017a, 2017b), we will use a χ2-matching method to compare the observations and models to search the best-fitting model. In the process, we also merely use the asteroseismic information (periods and/or period spacings) to constrain the theoretical models. First, we decide on the χ2-minimization model (CMM hereafter) from every evolutionary track, as shown in Figure 1. Finally, we determine the best-fitting model from the selected CMMs. The χ2 is defined as

where N = 8, the superscripts "obs" and "mod" represent observations and theoretical calculations, respectively. Pi and ΔPi ( ) are the oscillation period and period spacing, respectively.
) are the oscillation period and period spacing, respectively.  and
and  denote their corresponding observational errors, which are listed in Table 1.
denote their corresponding observational errors, which are listed in Table 1.
Figure 1. χ2,  , and
, and  as a function of central hydrogen mass fraction (central hydrogen hereafter) XC for the evolution of stellar mass M = 6.20 M⊙, initial metal mass fraction Zinit = 0.040, initial hydrogen mass fraction Xinit =0.71, overshooting parameter fov = 0.020, and extra mixing coefficient
as a function of central hydrogen mass fraction (central hydrogen hereafter) XC for the evolution of stellar mass M = 6.20 M⊙, initial metal mass fraction Zinit = 0.040, initial hydrogen mass fraction Xinit =0.71, overshooting parameter fov = 0.020, and extra mixing coefficient  .
.
Download figure:
Standard image High-resolution imageIn order to obtain the real best-fitting model, the ranges and the steps of the initial input parameter spaces are adjusted step by step during the model calculations. As shown in Table 2, from Grid A to Grid B to final Grid C, the model grids become denser and denser. Correspondingly, as shown in Figure 2 the minimum value of  becomes smaller and smaller. Finally, more than 8000 evolutionary tracks are calculated, i.e., more than 8000 CMMs are determined.
becomes smaller and smaller. Finally, more than 8000 evolutionary tracks are calculated, i.e., more than 8000 CMMs are determined.
Figure 2.
 as a function of the initial inputs: stellar mass (M; panel (a)), initial metal mass fraction (Zinit; panel (b)), overshooting parameter (fov; panel (c)), and extra mixing coefficient (
as a function of the initial inputs: stellar mass (M; panel (a)), initial metal mass fraction (Zinit; panel (b)), overshooting parameter (fov; panel (c)), and extra mixing coefficient ( panel (d)), respectively. The corresponding smaller panels are their zooms, which are marked with boxes in those panels.
panel (d)), respectively. The corresponding smaller panels are their zooms, which are marked with boxes in those panels.
Download figure:
Standard image High-resolution imageIt can be seen from Equation (3) and Figure 1 that there are three methods used to determine the CMMs. The corresponding best-fitting models are noted as models MA—χ2, MP— , and MDP—
, and MDP— , respectively. Their fundamental parameters are listed in Table 3. For a given evolutionary track, the CMMs decided by different methods might be different, especially for that of
, respectively. Their fundamental parameters are listed in Table 3. For a given evolutionary track, the CMMs decided by different methods might be different, especially for that of  , as shown in Figure 1. While they are almost consistent overall for constraining the optimal parameter ranges of the target HD 50230 from those calculated models. In the present work, we will mainly analyze the combination term, i.e., χ2.
, as shown in Figure 1. While they are almost consistent overall for constraining the optimal parameter ranges of the target HD 50230 from those calculated models. In the present work, we will mainly analyze the combination term, i.e., χ2.
Table 3. The Parameters of the Best-fitting Models
| Variables | Values | ||
|---|---|---|---|
| MAa | MPa | MDPa | |
| Initial Inputs | |||
| Mass M (M⊙) | 6.2125 | 6.1625 | 6.2125 |
| Initial metal abundance Zinit | 0.04125 | 0.040 | 0.040 |
| Overshooting parameter fov | 0.0175 | 0.020 | 0.01875 |
Extra mixing 
|
3.8 | 3.7 | 3.7 |
| Fundamental Parameters | |||
| Age (Myr) | 61.6 | 63.6 | 62.0 |
| Central hydrogen XC | 0.306 | 0.306 | 0.297 |
| Effective temperature Teff (K) | 14923 | 14907 | 14931 |
| Luminosity L (L⊙) | 1440 | 1443 | 1477 |
| Radius R (R⊙) | 5.68 | 5.70 | 5.75 |
Surface gravity  (c.g.s. unit) (c.g.s. unit) |
3.722 | 3.716 | 3.712 |
| Mass of convective core Mcc (M⊙) | 1.028 | 1.025 | 1.021 |
Radius of convective core  (R⊙) (R⊙) |
0.531 | 0.529 | 0.529 |
| Period spacing ΔΠl = 1 (s) | 9051.6 | 9031.1 | 9032.4 |
χ2,  , ,  b
b
|
58.5 | 64.7 | 36.3 |
Notes.
aMA, MP, and MDP represent the best-fitting models which are decided by χ2, , and
, and  , respectively.
bχ2,
, respectively.
bχ2,  , and
, and  correspond to MA, MP, and MDP.
correspond to MA, MP, and MDP.
Download table as: ASCIITypeset image
4. Results
The determined CMMs are shown in Figure 2 for matching goodness  against different initial inputs: stellar mass (M)—panel (a), initial metal mass fraction (Zinit)—panel (b), overshooting parameter (fov)—panel (c), and extra diffusion mixing coefficient (
against different initial inputs: stellar mass (M)—panel (a), initial metal mass fraction (Zinit)—panel (b), overshooting parameter (fov)—panel (c), and extra diffusion mixing coefficient ( )—panel (d), respectively. In addition,
)—panel (d), respectively. In addition,  against period spacing
against period spacing  and the other fundamental parameters, such as central hydrogen XC, stellar age tage, and radius R, are shown in Figures 3–5.
and the other fundamental parameters, such as central hydrogen XC, stellar age tage, and radius R, are shown in Figures 3–5.
Figure 3.
 as a function of period spacing ΔΠ1 (right) and of buoyancy radius Λ0 (left) for all of the calculated CMMs. The smaller panels are zoomed-in images of the box in the larger panels. The depth of color represents stellar mass (M⊙). The green lines in the zoomed panels represent
as a function of period spacing ΔΠ1 (right) and of buoyancy radius Λ0 (left) for all of the calculated CMMs. The smaller panels are zoomed-in images of the box in the larger panels. The depth of color represents stellar mass (M⊙). The green lines in the zoomed panels represent  .
.
Download figure:
Standard image High-resolution imageFigure 4. Similar to Figures 3,  as a function of stellar fundamental parameters, central hydrogen (XC), age (tage), radius (R), effective temperature (Teff), luminosity (L), surface gravity (
as a function of stellar fundamental parameters, central hydrogen (XC), age (tage), radius (R), effective temperature (Teff), luminosity (L), surface gravity ( ), mass, and radius of convective core (Mcc and Rcc), respectively, for all of the calculated CMMs of Xinit = 0.71. The horizontal dashed lines represent
), mass, and radius of convective core (Mcc and Rcc), respectively, for all of the calculated CMMs of Xinit = 0.71. The horizontal dashed lines represent  and 75, respectively. The zoomed panels are shown in Figure 5.
and 75, respectively. The zoomed panels are shown in Figure 5.
Download figure:
Standard image High-resolution imageFigure 5. Zoomed-in images of Figure 4 for those CMMs whose  are smaller than 120. Horizontal dished lines represent
are smaller than 120. Horizontal dished lines represent  . The 65 selected better candidates are shown in figures with filled points.
. The 65 selected better candidates are shown in figures with filled points.
Download figure:
Standard image High-resolution image4.1. Buoyancy Radius 
The work of Wu & Li (2016) suggested that the acoustic radius τ0 is the only global parameter that can be accurately measured by the  -matching method between observed frequencies and theoretical model calculating ones for pure p-mode. This means that the pure p-mode mainly carries information about the acoustic size of the p-mode propagation cavity in stars.
-matching method between observed frequencies and theoretical model calculating ones for pure p-mode. This means that the pure p-mode mainly carries information about the acoustic size of the p-mode propagation cavity in stars.
Similarly, as shown in Figure 3, the CMMs converge into one point (or a narrow range) on the period spacing  and/or buoyancy radius Λ0, which characterizes the buoyancy size of the g-mode propagation cavity (for more descriptions, see Appendix A) except for those outliers whose
and/or buoyancy radius Λ0, which characterizes the buoyancy size of the g-mode propagation cavity (for more descriptions, see Appendix A) except for those outliers whose  are larger than 3 × 104.
are larger than 3 × 104.
However, these CMMs distribute into a very large range of other fundamental parameters, as shown in Figure 4, such as the central hydrogen XC, radius R, surface gravity  , and the mass of convective core Mcc. The distribution of CMMs on the radius of convective core Rcc has similar behaviors with that of period spacing
, and the mass of convective core Mcc. The distribution of CMMs on the radius of convective core Rcc has similar behaviors with that of period spacing  and/or buoyancy radius Λ0, but it has a slightly larger range (about Rcc ∼ 0.52–0.54 R⊙).
and/or buoyancy radius Λ0, but it has a slightly larger range (about Rcc ∼ 0.52–0.54 R⊙).
As shown in Figure 3, the distribution of CMMs on period spacing  and/or buoyancy radius Λ0 resemble a flying bird with a pair of asymmetrical wings. Those CMMs can be roughly divided into two parts by a horizontal dashed line of
and/or buoyancy radius Λ0 resemble a flying bird with a pair of asymmetrical wings. Those CMMs can be roughly divided into two parts by a horizontal dashed line of  . The normal part, which has smaller
. The normal part, which has smaller  (<3 × 104), constructs the "body" of the bird, while the outliers, which have larger
(<3 × 104), constructs the "body" of the bird, while the outliers, which have larger  (≥3 × 104), have larger or smaller period spacings ΔΠ1 compared with the normal part and make up the asymmetrical "wings."
(≥3 × 104), have larger or smaller period spacings ΔΠ1 compared with the normal part and make up the asymmetrical "wings."
It can be seen from Figure 2 that the centers of the optimal initial inputs are about 6.2 on M, 0.041 on Zinit, 0.01785 on fov, and 3.8 on  , respectively. Figure 6 intuitively illustrates the influence of extreme inputs for the value of
, respectively. Figure 6 intuitively illustrates the influence of extreme inputs for the value of  . In the figure, point size is proportional to
. In the figure, point size is proportional to  , i.e., the larger point denotes larger discrepancy from the center value of 3.8 for the initial input
, i.e., the larger point denotes larger discrepancy from the center value of 3.8 for the initial input  . The light or deep colors represent the discrepancy of fov from the optimal center value of 0.01875. It can be easily found from Figures 2, 3, and 6 that those outliers possess extreme input parameters in stellar mass Minit, initial metal mass fraction Zinit, overshooting parameter fov, and extra diffusion coefficient
. The light or deep colors represent the discrepancy of fov from the optimal center value of 0.01875. It can be easily found from Figures 2, 3, and 6 that those outliers possess extreme input parameters in stellar mass Minit, initial metal mass fraction Zinit, overshooting parameter fov, and extra diffusion coefficient  .
.
Figure 6.
 as a function of Zinit and M. The light and deep colors of points are related to
as a function of Zinit and M. The light and deep colors of points are related to  . The size of points is inversely proportional to
. The size of points is inversely proportional to  .
.
Download figure:
Standard image High-resolution imageIt can be found from Figures 3 and 6 that both ΔΠ1 and  are seriously affected by the extreme initial inputs. The above analysis indicates that the farther initial inputs are far away from the center (or proper) values; the larger the values of
are seriously affected by the extreme initial inputs. The above analysis indicates that the farther initial inputs are far away from the center (or proper) values; the larger the values of  are, the larger or smaller the period spacing
are, the larger or smaller the period spacing  and/or buoyancy radius Λ0 of the CMMs will be.
and/or buoyancy radius Λ0 of the CMMs will be.
As shown in Figure 3 the period spacing ΔΠ1 of HD 50230 can be accurately determined from the χ2-matching method. It is ΔΠ1 = 9038.4 ± 21.8 s, i.e., ΔΠ1 = 9016.6 – 9060.2 s, which is decided from those 65 selected better candidates whose  are smaller than 75 as shown in the smaller panel of Figure 3. Its relative precision is about 0.24%. Correspondingly, the buoyancy radius is Λ0 = 245.78 ± 0.59 μHz, i.e., those selected better candidates distribute in the range of 245.19–246.37 μHz on buoyancy radius Λ0 as shown in the right panel of Figure 3.
are smaller than 75 as shown in the smaller panel of Figure 3. Its relative precision is about 0.24%. Correspondingly, the buoyancy radius is Λ0 = 245.78 ± 0.59 μHz, i.e., those selected better candidates distribute in the range of 245.19–246.37 μHz on buoyancy radius Λ0 as shown in the right panel of Figure 3.
What the buoyancy radius Λ0 is to g-mode oscillations, the acoustic radius τ0 is to p-mode ones (for more information, see Appendix A). Both of them represent the "Propagation Time" of oscillation waves of g- and p-modes, respectively, from stellar surface to center, i.e., the "size" of oscillating cavities. The distribution of CMMs on Λ0 and initial inputs indicates that proper inputs correspond with suitable oscillating cavities.
4.2. Fundamental Parameters
It can be seen from Figure 4 that the distribution of CMMs on other fundamental parameters (i.e.,  against the other fundamental parameters) seems disordered compared to
against the other fundamental parameters) seems disordered compared to  versus ΔΠ1 (Figure 3). Therefore, it is very difficult to directly determine the optimal range of the other fundamental parameters from Figure 4, such as deciding period spacing ΔΠl = 1 and buoyancy radius Λ0 from Figure 3. However, the zoomed-in figure (i.e., Figure 5) illustrates that those CMMs whose
versus ΔΠ1 (Figure 3). Therefore, it is very difficult to directly determine the optimal range of the other fundamental parameters from Figure 4, such as deciding period spacing ΔΠl = 1 and buoyancy radius Λ0 from Figure 3. However, the zoomed-in figure (i.e., Figure 5) illustrates that those CMMs whose  are smaller than 120 also converge into a certain relatively narrow region on these fundamental parameters, including central hydrogen (XC), stellar age (tage), radius (R), effective temperature (Teff), luminosity (L), surface gravity (
are smaller than 120 also converge into a certain relatively narrow region on these fundamental parameters, including central hydrogen (XC), stellar age (tage), radius (R), effective temperature (Teff), luminosity (L), surface gravity ( ), and mass and radius of the convective core (Mcc, Rcc). In Figure 5, filled points represent the 65 selected better candidates whose
), and mass and radius of the convective core (Mcc, Rcc). In Figure 5, filled points represent the 65 selected better candidates whose  are smaller than 75. Based on those better candidates, as shown in Figure 5, we obtain the optimal ranges of the fundamental parameters, which are listed in Table 4.
are smaller than 75. Based on those better candidates, as shown in Figure 5, we obtain the optimal ranges of the fundamental parameters, which are listed in Table 4.
Table 4. The Optimal Variable Range of the Fundamental Parameters of HD 50230
| Ranges | ||
|---|---|---|
| Variables |
 a
a
|
68.3% Probability |
| Stellar mass M (M⊙) | 6.15–6.27 (6.21 ± 0.06) | 6.187 ± 0.025b |
| Initial metal abundance Zinit |

|
0.0408 ± 0.0009b |
| Overshooting parameter in core fov | 0.0175–0.0200 | 0.0180 ± 0.0014b |
Extra mixing parameter 
|
3.7–3.9 (3.8 ± 0.1) | 3.800 ± 0.045b |
| Period spacing ΔΠ1 (s) | 9016.6–9060.2 (9038.4 ± 21.8) |

|
| Buoyancy radius Λ0 (μHz) | 245.19–246.37 (245.78 ± 0.59) |

|
| Age (Myr) |

|

|
Central hydrogen 
|

|

|
| Effective temperature Teff (K) |

|

|
Luminosity  (L⊙) (L⊙) |

|

|
| Radius R (R⊙) |

|

|
Surface gravity  (c.g.s. unit) (c.g.s. unit) |

|

|
| Mass of convective core Mcc (M⊙) |

|

|
| Radius of convective core Rcc (R⊙) |

|

|
Notes.
aThe range x1 − x2 represents the minimization and maximization of the parameters for the CMMs whose . For the form of
. For the form of  , x corresponds to the value of the best-fitting model (MA) as shown in Table 3. Correspondingly, +dx and −dx express the discrepancy between the x and x1, x2, respectively.
bFitting the probability distribution density with Gaussian function and adopting 1σ. The fitting results are shown in Figure 8.
, x corresponds to the value of the best-fitting model (MA) as shown in Table 3. Correspondingly, +dx and −dx express the discrepancy between the x and x1, x2, respectively.
bFitting the probability distribution density with Gaussian function and adopting 1σ. The fitting results are shown in Figure 8.
Download table as: ASCIITypeset image
As shown in Figure 7 and Table 4 the central hydrogen XC of HD 50230 is about 0.298–0.316. This indicates that about 55%–58% of the initial hydrogen has been exhausted in the stellar center. This is slightly smaller than the result of Degroote et al. (2010, 60%).
Figure 7. Distribution of CMMs on  vs. Teff. The solid and dashed thin lines represent the observations and their observational uncertainties:
vs. Teff. The solid and dashed thin lines represent the observations and their observational uncertainties:  ,
,  ,
,  , and
, and  , respectively. They are marked with solid lines with arrows in the figure. The gray thick solid box presents the optimal ranges of Teff and
, respectively. They are marked with solid lines with arrows in the figure. The gray thick solid box presents the optimal ranges of Teff and  which is listed in Table 4. The asterisk symbols model MA.
which is listed in Table 4. The asterisk symbols model MA.
Download figure:
Standard image High-resolution imageAccording to the radius of the best-fitting model MA (R = 5.68 R⊙; see Table 3) and the optimal range of radius (R =5.50–5.81 R⊙; see Table 4), we express the radius of HD 50230 as  . According to Equation (1) and the observation of rotational splitting of the p-mode
. According to Equation (1) and the observation of rotational splitting of the p-mode  (Degroote et al. 2012), the rotational velocity is
(Degroote et al. 2012), the rotational velocity is  . It is consistent with the spectroscopic observation of
. It is consistent with the spectroscopic observation of  (Degroote et al. 2012) on the same order of magnitude. Based on these, we can obtain the inclination angle i of the rotating axis to be of
(Degroote et al. 2012) on the same order of magnitude. Based on these, we can obtain the inclination angle i of the rotating axis to be of  , which is consistent with the prediction of Degroote et al. (2012, i to be i > 20°).
, which is consistent with the prediction of Degroote et al. (2012, i to be i > 20°).
As shown in Figure 7 and Table 3 the surface gravity of HD 50230 is  (for model MA), which is in good agreement with the spectroscopic observation of
(for model MA), which is in good agreement with the spectroscopic observation of  (Degroote et al. 2012). The effective temperature is about
(Degroote et al. 2012). The effective temperature is about  ), which is consistent with the spectroscopic observation of Teff = 18,000 ± 1500 K (Degroote et al. 2012) with
), which is consistent with the spectroscopic observation of Teff = 18,000 ± 1500 K (Degroote et al. 2012) with  .
.
Degroote et al. (2010, 2012) and Szewczuk et al. (2014) suggested that SPB star HD 50230 is a metal-rich ( ; Z⊙ = 0.02) star, i.e., Z ≃ 0.04. In the present work, the optimal range of better candidates in metallicity (Zinit) is of 0.034–0.043 (or
; Z⊙ = 0.02) star, i.e., Z ≃ 0.04. In the present work, the optimal range of better candidates in metallicity (Zinit) is of 0.034–0.043 (or  ), which is consistent with that of the literature.
), which is consistent with that of the literature.
In addition, the calculations indicate that HD 50230 has a convective core. Its radius (Rcc) and mass (Mcc) are 0.525–0.536 R⊙ (or  ) and 1.004–1.063 M⊙ (or
) and 1.004–1.063 M⊙ (or  ), respectively.
), respectively.
4.2.1. Statistical Analysis: Probability Distribution of Fundamental Parameters
Similar to the work of Giammichele et al. (2016), Gai et al. (2018), and Tang et al. (2018), we calculate the likelihood function in 5D parameter space

from the merit function, χ2(x1, x2, x3, x4, x5). For the five independent variables, four of them are the initial input parameters, i.e., stellar mass (M), initial metal mass fraction (Zinit), convective overshooting parameter (fov) in the center, and the extra diffusion coefficient ( ). The other one represents the evolutionary status of the star, such as stellar age (tage), radius (R), and center hydrogen mass fraction (XC). For a chosen parameter, such as x1, the density of the probability function can be defined from the following integration over the full parameter range
). The other one represents the evolutionary status of the star, such as stellar age (tage), radius (R), and center hydrogen mass fraction (XC). For a chosen parameter, such as x1, the density of the probability function can be defined from the following integration over the full parameter range

Then, normalizing the density of the probability function, i.e., assuming that the integration of p(x1)dx1 over the allowed parameter range ![$[{x}_{1,\min },{x}_{1,\max }]$](https://content.cld.iop.org/journals/0004-637X/881/1/86/revision1/apjab2ad8ieqn146.gif) is equal to 1, to decide the normalization factor,
is equal to 1, to decide the normalization factor,

Based on such a statistical analysis method, the distributions of the density of the probability function for initial input parameters and the other stellar fundamental parameters are determined and shown in Figures 8 and 9, respectively.
Figure 8. Density of probability as a function of the initial inputs: stellar mass (M), initial metal mass fraction (Zinit), overshooting parameter (fov), and extra mixing coefficient ( ), respectively. In the bottom four panels, thick green lines represent the Gaussian fit of the density of probability.
), respectively. In the bottom four panels, thick green lines represent the Gaussian fit of the density of probability.
Download figure:
Standard image High-resolution imageFigure 9. Distribution of the density of probability (black) and probability (red) of stellar fundamental parameters: XC, tage, R, Teff, L,  , Mcc, Rcc, and ΔΠ1. The three horizontal lines represent 15.85% (blue), 50% (green), and 84.15% (blue), respectively.
, Mcc, Rcc, and ΔΠ1. The three horizontal lines represent 15.85% (blue), 50% (green), and 84.15% (blue), respectively.
Download figure:
Standard image High-resolution imageAs shown in Figure 8 the profile of the density of the probability function is similar to a δ-like function. The probability centers on a narrow range. In order to determine their optimal values and the corresponding uncertainties, we adopt a Gaussian function to fit the density of probability for the four initial input parameters: M, Zinit, fov, and  , because the parameter space of (M, Zinnit, fov,
, because the parameter space of (M, Zinnit, fov,  ) has lower resolution. However, as shown in Figure 9, we integrate the density of probability to determine them for other parameters. The final decided optimal values are listed in Table 4.
) has lower resolution. However, as shown in Figure 9, we integrate the density of probability to determine them for other parameters. The final decided optimal values are listed in Table 4.
It can be seen from Table 4 and Figures 8 and 9 that compared to these values, which are decided by CMMs whose  are smaller than 75, the statistical analyses have lower uncertainties. In the present work, we adopt the former method to determine the optimal range of the fundamental parameters.
are smaller than 75, the statistical analyses have lower uncertainties. In the present work, we adopt the former method to determine the optimal range of the fundamental parameters.
4.3. Asteroseismic Analysis
The period spacings (ΔP) of the observations and the best-fitting models and the differences of periods between them (Pobs − Pmod) are shown in Figure 10.
Figure 10. Period spacings ΔP as a function of periods P (upper panel); the differences of periods between observations and the best-fitting models Pobs − Pmod as a function of periods Pobs (bottom panel). MA, MP, and MDP represent different best-fitting models, which are listed in Table 3. The radial orders ng are shown by the text in the figure.
Download figure:
Standard image High-resolution imageIt can be found from the upper panel of Figure 10 that the period spacings  of the best-fitting models are almost consistent with those of observations, except for the last one (g13). As shown in the bottom panel of Figure 10 the observed periods are larger than those of model MDP, which is decided by matching period spacing ΔPi between observations and models except for the first mode (g6). For model MA, which is decided by matching both period Pi and period spacing ΔPi, and MP, which is decided by matching period Pi, their periods are consistent with observations within about 100 s except for the last one (g13) whose period is smaller than the observed one to be about 300 s.
of the best-fitting models are almost consistent with those of observations, except for the last one (g13). As shown in the bottom panel of Figure 10 the observed periods are larger than those of model MDP, which is decided by matching period spacing ΔPi between observations and models except for the first mode (g6). For model MA, which is decided by matching both period Pi and period spacing ΔPi, and MP, which is decided by matching period Pi, their periods are consistent with observations within about 100 s except for the last one (g13) whose period is smaller than the observed one to be about 300 s.
It can be found from the upper panel of Figure 10 that the observed period spacings and the model calculated ones have different tendencies at the end of the larger period. The period spacing decreases with the increase of period for models when P ≳ 1.3 days. Based on those best-fitting models, the last observed period (g13) seems to be an outlier for the sequence of (l = 1, m = 0).
The period difference δP ∼ 300 s in the last mode ( ) corresponds to about δf ∼ −0.0014 day−1 (or −0.016 μHz) in frequency. As shown in Figure 11 the rotational splitting parameters βnl are around 0.5 for all of these modes. As a matter of fact, for all of the calculated CMMs, βnl are around 0.5. They are pure g-mode. For the "outlier" corresponding mode (g13), its rotational parameter βnl is about 0.4934. Therefore, the frequency difference of δf ∼ −0.0014 day−1 might be explained as a rotation splitting of
) corresponds to about δf ∼ −0.0014 day−1 (or −0.016 μHz) in frequency. As shown in Figure 11 the rotational splitting parameters βnl are around 0.5 for all of these modes. As a matter of fact, for all of the calculated CMMs, βnl are around 0.5. They are pure g-mode. For the "outlier" corresponding mode (g13), its rotational parameter βnl is about 0.4934. Therefore, the frequency difference of δf ∼ −0.0014 day−1 might be explained as a rotation splitting of  , which corresponds to a rotational frequency of
, which corresponds to a rotational frequency of  . Surely such rotational frequency is far smaller than that of observation
. Surely such rotational frequency is far smaller than that of observation  (=0.509 μHz, see Section 2), which is calculated from the rotational splitting of p-mode. Therefore, it is not suitable that the period difference of last mode (g13) between observations and best-fitting models is explained as rotational splitting.
(=0.509 μHz, see Section 2), which is calculated from the rotational splitting of p-mode. Therefore, it is not suitable that the period difference of last mode (g13) between observations and best-fitting models is explained as rotational splitting.
Figure 11. Rotational splitting parameter βnl as a function of period P for the three best-fitting models: MA, MP, and MDP.
Download figure:
Standard image High-resolution imageAs shown in Figure 12 most of the oscillation energy is trapped in the μ-gradient region, which is nearby the convective core, for the best-fitting model: model MA. The residual oscillation energy distributes into the outer region of the μ-gradient region but within r/R ≲ 0.85 for low-order modes. For high-order modes (see the bottom panel of Figure 12), the oscillation energy partly extends to stellar surface. According to the theory of stellar oscillations, therefore, as shown in Figure 10, the period spacings ΔP will decrease with the increase of period P for high-order g-mode since they have larger propagation cavity compared with the low-order modes.
Figure 12. Right and left axes represent buoyancy frequency N/2π and  of model MA, which presents the distribution of oscillation energy, respectively. g5, g6, ..., and g17 correspond to the radial orders
of model MA, which presents the distribution of oscillation energy, respectively. g5, g6, ..., and g17 correspond to the radial orders  , which are shown in Figure 11.
, which are shown in Figure 11.
Download figure:
Standard image High-resolution imageFor the period discrepancy of the last mode (g13), based on the calculated theoretical models in the present work, there are two possibilities that might explain it. The first is that it is really an outlier, and it might not belong to the prograde mode sequence of (l = 1, m = 0). The second is that it is caused by certain possible physical mechanisms that can partly decrease the frequency of the last mode to make it consistent with the observation, such as the mode trapping. But it is not properly considered in the present theoretical models.
It can be seen from Figure 10 that there is a sine-like signal on the period discrepancy between the observations and the best-fitting models. Similar phenomena also appear in previous works, such as Moravveji et al. (2015, Figures 4, 6, A.1, and A.2), Moravveji et al. (2016, Figure 8), and Buysschaert et al. (2018, Table 3). Such sine-like signals might be caused by a thin layer in the stellar interior (see, e.g., Gough & Thompson 1990; Christensen-Dalsgaard 2003), which is not considered or improperly expressed in the present theoretical models. For the best-fitting model of HD 50230, the strength of mode trapping in the μ-gradient region beyond the convective core might be a possible factor. On the other hand, perhaps, the present best-fitting model needs an extra mode trapping cavity to slightly revise the periods. We will investigate this question in depth in the future.
4.4. The Influences: Outlier, Initial Hydrogen, and Observational Uncertainties
In the above sections, we used all of the eight modes to constrain theoretical models, which are calculated with a fixed initial hydrogen Xinit. In the process, we adopt the observational uncertainties as weight factors. In this section, we will discuss the influences of different initial hydrogen, observational uncertainties, and the last mode for constraining the theoretical models and deciding the final best-fitting models.
First, our method here is similar to the above section, but we only use the former seven modes (i.e., g6, g7, ..., and g12) to constrain theoretical models. The last mode (g13) is not considered. The corresponding best-fitting models are noted as models MA7, MP7, and MDP7, respectively. The period spacings and period differences between observations are shown in Figure 13. It can be seen from Figures 10 and 13 that the final results are almost entirely the same with or without the last mode (g13) in observations. This indicates that eliminating the last mode from observations only partly decreases the value of  of the best-fitting model from 58.5 (model MA) to 53.5 (model MA7). In fact, model MA and model MA7 are the same model. This means that the last mode (g13; "outlier") does not effectively work for constraining the theoretical models in the present work.
of the best-fitting model from 58.5 (model MA) to 53.5 (model MA7). In fact, model MA and model MA7 are the same model. This means that the last mode (g13; "outlier") does not effectively work for constraining the theoretical models in the present work.
Figure 13. Similar to Figure 10, but for a normal case. Here, the outlier (mode g13) is not considered when constraining the theoretical models. We only use the former seven periods to constrain theoretical models. The corresponding best-fitting models are noted as models MA7, MP7, and MDP7, respectively.
Download figure:
Standard image High-resolution imageSecond, we change the initial hydrogen Xinit from the fixed value 0.71 to 0.69, 0.70, and 0.72 and calculate the corresponding theoretical models to determine the best-fitting model. For the added calculations, their parameter resolutions are the same as the above calculations (see Table 2). Finally, more than 5500 evolutionary tracks are calculated for the added initial hydrogen Xinit = 0.69, 0.70, and 0.72. Similar to the best-fitting model of model MA, we note the corresponding best-fitting models as models MAX0.69, MAX0.70, and MAX0.72, respectively. Their  are about 62.0, 65.8, and 60.0, respectively. They are larger than that of model MA (58.5).
are about 62.0, 65.8, and 60.0, respectively. They are larger than that of model MA (58.5).
It can be seen from Figure 14 that the best-fitting model does not obviously become better or worse when slightly changing (increase or decrease) the initial hydrogen Xinit. The periods of the best-fitting models almost overlap each other. On the other hand, their  are on the same level. They are close to about 60.
are on the same level. They are close to about 60.
Figure 14. Similar to Figures 10 and 13, but for the best-fitting models of initial hydrogen Xinit = 0.69, 0.70, 0.71, and 0.72, respectively. They are noted as models MAX0.69, MAX0.70, MA, and MAX0.72, respectively, compared to the best-fitting model: model MA, whose initial hydrogen is 0.71.
Download figure:
Standard image High-resolution imageIt can be seen from Table 1 (the observations) that the observational uncertainties of periods range from 5.5 s (g8) to about 32 s (g13). The ratio between them is about 5.8. Correspondingly, in Equation (3), their weight ratio is up to about 34 for calculating the value of χ2 between the two modes.
In order to analyze the influence of the observational uncertainties for the final best-fitting model, we change the χ2-matching formulas (i.e., Equation (3)) as:

to constrain theoretical models. Here, ΔP,  , and Δall represent the means of differences between observations and theoretical models for period P, period spacing ΔP, and both of them, respectively. Correspondingly, the Δall-minimum model denotes model MAabs whose Δall is about 84.9 s. For model MA, the corresponding Δall is about 91.1 s. The difference of Δall between the two models is mainly contributed by the last period and the last period spacing since they have lower weight compared with the other modes. The period discrepancies with observations of mode g13 decrease from about 326 s for model MA to about 235 s for model MAabs as shown in Figure 15.
, and Δall represent the means of differences between observations and theoretical models for period P, period spacing ΔP, and both of them, respectively. Correspondingly, the Δall-minimum model denotes model MAabs whose Δall is about 84.9 s. For model MA, the corresponding Δall is about 91.1 s. The difference of Δall between the two models is mainly contributed by the last period and the last period spacing since they have lower weight compared with the other modes. The period discrepancies with observations of mode g13 decrease from about 326 s for model MA to about 235 s for model MAabs as shown in Figure 15.
Figure 15. Similar to Figures 10, 13, and 14, but for the best-fitting models of model MA and model MAabs.
Download figure:
Standard image High-resolution imageThe initial parameters of model MA and model MAabs are the same, except MAabs has a slightly higher initial metal abundance (Zinit = 0.04375). In addition, their fundamental parameters are almost consistent with each other. As shown in Figure 15 the periods and period spacings for the best-fitting model (model MAabs) are not changed significantly. This indicates that the final results are not seriously changed whether using the observational uncertainties as a weight or not for determining the best-fitting model.
In addition, similarly, we eliminate the last mode (g13) from the observations and adopt Equation (7) to determine the best-fitting model, which is named model MA7abs, similar to model MA7. The Δall of model MA7abs is 53.3 s. Correspondingly, that of model MA7 is about 56.0 s. Models MA7 and MA7abs are located on a common evolutionary track, i.e., their initial parameters are the same. In addition, they are two adjacent models, i.e., their fundamental parameters are merely different.
As shown in the upper panel of Figure 16 the period spacings overlap with that of model MA7. For period differences δP = Pobs − Pmod, model MA7abs is slightly larger than model MA7 overall. However, the mean values of  are 43.8 and 48.5 s for models MA7abs and MA7, respectively.
are 43.8 and 48.5 s for models MA7abs and MA7, respectively.
Figure 16. Similar to Figures 10, 13–15, but for the best-fitting models of model MA7 and model MA7abs.
Download figure:
Standard image High-resolution imageIt can be found from Figures 13, 15, and 16 that the final results are almost not affected whether using the observational uncertainties and the last mode (g13) to constrain theoretical models or not for the present calculated models.
5. Summary
SPB star HD 50230 is the primary component of a binary system. It has observed about 137 days with the CoRoT satellite and more than 560 frequencies are extracted. There are eight modes identified as likely low-order g-modes with l = 1 and m = 0 among the extracted modes due to almost uniform period spacings among them. In addition, the period spacings periodically vary with periods. In the present work, we make model calculations and analyze the eight modes with high-precision asteroseismology. Finally, the investigation can be briefly concluded as follows:
- Similar to pure p-mode oscillations, the oscillation frequencies mainly carry the information of the size of oscillation wave propagation cavity and the acoustic radius τ0 is the only global parameter that can be precisely measured by the χ2-matching method between observed frequencies and model calculations (Wu & Li 2016), the buoyancy radius Λ0 also can be easily and precisely measured with a similar method for pure g-mode oscillations (m = 0), as shown in Figure 3, compared to the other parameters, such as stellar age, effective temperature, and radius, which are shown in Figure 4. This is because the distribution of CMM on buoyancy radius is not sensitive for initial input parameters compared to the other fundamental parameters. Both acoustic radius and buoyancy radius represent the "propagation time" of oscillation waves from stellar surface to center for pure p- and g-modes, respectively.
- Based on the calculated models, we find that the value of
 and the distribution of CMMs on buoyancy radius Λ0 can be slightly affected by some extreme initial inputs. Finally, we obtain that the buoyancy radius of HD 50230 is of Λ0 = 245.78 ± 0.59 μHz with a higher relative precision of 0.24%. Correspondingly, the period spacing of HD 50230 is
and the distribution of CMMs on buoyancy radius Λ0 can be slightly affected by some extreme initial inputs. Finally, we obtain that the buoyancy radius of HD 50230 is of Λ0 = 245.78 ± 0.59 μHz with a higher relative precision of 0.24%. Correspondingly, the period spacing of HD 50230 is  .
. - HD 50230 is a metal-rich (
 ) moderate massive star with a mass of M = 6.21 ± 0.06 M⊙ and located on the middle phase of the main-sequence branch with an age of
) moderate massive star with a mass of M = 6.21 ± 0.06 M⊙ and located on the middle phase of the main-sequence branch with an age of  Myr. About 57% of the initial hydrogen is exhausted in its center (
Myr. About 57% of the initial hydrogen is exhausted in its center ( ), which is close to Degroote et al.'s (2010) estimated (60%). In addition, HD 50230 has a convective core with a radius of
), which is close to Degroote et al.'s (2010) estimated (60%). In addition, HD 50230 has a convective core with a radius of  . The corresponding convective core mass is
. The corresponding convective core mass is  .
. - Based on the optimal range of stellar radius R = 5.50–5.81 R⊙, we obtain that the rotational velocity of
 km s−1 with an inclination angle of
km s−1 with an inclination angle of  .
. - In order to interpret the structure in the observed period spacing pattern of HD 50230, the exponentially decaying diffusive core overshooting (fov = 0.0175–0.0200) and the extra diffusive mixing (
 ) should be taken into account in theoretical models.
) should be taken into account in theoretical models. - The theoretical models indicate that, for the eight modes, at least seven modes can be well explained as dipole g-modes of (l, m) = (1, 0). Their period discrepancies between the observations and the best-fitting models are within 100 s. For the last mode (g13), it is almost up to 300 s. In the present work, we still do not find a suitable interpretation for such large discrepancy, but we exclude the possibility that the discrepancy is caused by rotational splitting, i.e., it is not the mode of (l, m) = (1, −1).
In the present work, the rotational effects are not taken into account in theoretical models. Degroote et al. (2012) predicted that the rotational effects should be considered when interpreting the structure in the observed period spacing pattern, since they will slightly change the period of the g-mode (Aerts & Dupret 2012). Perhaps, they could be helpful in explaining the larger period discrepancy between observation and best-fitting model. We will consider this in the next work.
This work is cosponsored by the NSFC of China (grant Nos. 11333006, 11503076, 11503079, 11773064, 11873084, and 11521303), and by Yunnan Applied Basic Research Projects (grant No. 2017B008). The authors gratefully acknowledge the computing time granted by the Yunnan Observatories, and provided on the facilities at the Yunnan Observatories Supercomputing Platform. The authors also express their sincere thanks to Pro. Guo, J.H., Dr. Zhang, Q.S., Dr. Su, J., and Dr. Chen, X.H. for their productive advice. Finally, the authors are cordially grateful to an anonymous referee for instructive advice and productive suggestions to improve this paper overall.
Appendix A: Propagation Velocity of g-mode and Buoyancy Radius
The propagation velocity of p-mode (i.e., adiabatic sound speed c) and the corresponding acoustic radius (τ0) are shown in the works of Unno et al. (1989), Christensen-Dalsgaard (2003), and Aerts et al. (2010) in detail. Here, we inspect it briefly as the background of those of g-mode as follows.
For high radial order oscillations, the oscillation equation can be approximately expressed as follows in the Cowling approximation (Christensen-Dalsgaard 2003, Equation (5.17) on page 76),
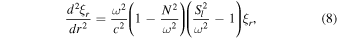
or

where

Sl is the characteristic acoustic frequency

N is buoyancy frequency and also called Brunt–Väisälä frequency. It is expressed as

where, ∇ad, ∇, and ∇μ are the adiabatic temperature gradient, the temperature gradient, and μ-gradient, respectively.
For high-order p-modes, typically ω2 ≫ N2, then K can be approximately expressed as (Christensen-Dalsgaard 2003, Equation (5.29) on page 80)
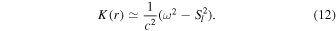
The length of the wave vector  can be expressed as the sum of a radial component and a horizontal component, i.e.,
can be expressed as the sum of a radial component and a horizontal component, i.e.,

The radial component kr
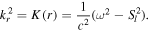
The horizontal component kh (Christensen-Dalsgaard 2003, Equation (4.51) on page 64)

Therefore, substituting Sl, kr, and kh into Equation (13) and obtaining the dispersion relation of p-mode oscillations (Christensen-Dalsgaard 2003, Equation (3.55) on page 52)

According to the definition of phase velocity (for more description, refer to Unno et al. 1989, Equation (15.16) of page 116):

the propagation velocity of p-mode is  , i.e., p-mode propagates with sound speed in stars.
, i.e., p-mode propagates with sound speed in stars.
The definition of acoustic depth (Aerts et al. 2010, Equation (3.228) on page 219)
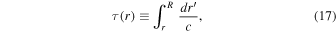
presents the propagation time of the oscillating wave (p-mode) from stellar surface to stellar inner position r' = r. Correspondingly, the propagation time from stellar surface to center is called the acoustic radius

This represents the "size" (i.e., acoustic size) of the p-mode propagation cavity.
For high-order g-mode, typically  and thus K can be approximately expressed as (Christensen-Dalsgaard 2003, Equation (5.33) on page 81)
and thus K can be approximately expressed as (Christensen-Dalsgaard 2003, Equation (5.33) on page 81)
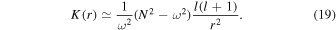
Similarly, for g-mode, the length of the wave vector can be expressed as

i.e.,
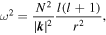
which is the dispersion relation of g-mode oscillations (a more detailed description refers to Unno et al. 1989, Equation (33.18) on page 286). Correspondingly, the propagation velocity of g-mode ( ) is
) is

This shows that the propagation velocity is directly proportional to the oscillation frequency ω2 and inversely proportional to the degree  . Similarly to the definition of acoustic depth τ(r)—Equation (17)—the buoyancy depth can be defined as
. Similarly to the definition of acoustic depth τ(r)—Equation (17)—the buoyancy depth can be defined as

which also represents the propagation time of the oscillation wave, but for g-mode oscillations. Correspondingly, the buoyancy radius, which presents the time of a g-mode oscillating wave propagating from stellar surface to center, is defined as
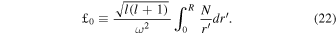
Compared with acoustic depth (or radius; Equations (17) and (18)), the buoyancy depth (or radius; Equations (21) and (22)) is not only related to the stellar structure (N and r) but also related to the oscillation frequencies ω and their degrees l. Therefore, we adopt the quantities of
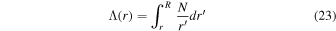
and
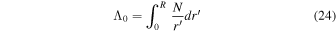
to replace  and £0 to characterize the buoyancy size (buoyancy depth and radius) of stars. Similar to τ(r) and τ0, Λ(r) and Λ0 are merely dependent on stellar structure and independence of the oscillations. Correspondingly, the dimensions of the improved buoyancy depth and radius are transformed to ones of angular frequency (radian per second) from ones of time. Correspondingly, the buoyancy radius Λ0 can be expressed with period spacing ΔΠl as follows:
and £0 to characterize the buoyancy size (buoyancy depth and radius) of stars. Similar to τ(r) and τ0, Λ(r) and Λ0 are merely dependent on stellar structure and independence of the oscillations. Correspondingly, the dimensions of the improved buoyancy depth and radius are transformed to ones of angular frequency (radian per second) from ones of time. Correspondingly, the buoyancy radius Λ0 can be expressed with period spacing ΔΠl as follows:
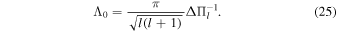
Appendix B: Inlist File of Pulse in MESA (V6208)
| &star_job ! HD49385 |
| create_pre_main_sequence_model = .true. |
| kappa_file_prefix = 'gs98' |
| change_initial_net = .true. |
| new_net_name = 'o18_and_ne22.net' |
| / ! end of star_job namelist |
| &controls |
| initial_mass = 0.60875000D+01 |
| initial_z = 0.43750000D-01 |
| initial_y = 0.26625000D+00 |
| overshoot_f_above_burn_h = 0.20000000D-01 |
| min_D_mix = 0.50118723D+04 |
| do_element_diffusion = .false. ! .true. |
| calculate_Brunt_N2 = .true. |
| !use_brunt_dlnRho_form = .true. |
| use_brunt_gradmuX_form = .true. |
| which_atm_option = 'Eddington_grey' |
| max_years_for_timestep = 0.1d6 |
| varcontrol_target = 1d-4 ! for main-sequence stars (5d-4 for pre_main_sequence) |
| dH_hard_limit = 1d-3 |
| mesh_delta_coeff = 0.4 |
| max_allowed_nz = 30000 ! maximum number of grid points allowed |
| max_model_number = 70000 ! negative means no maximum |
| xa_central_lower_limit_species(1) = 'h1' |
| xa_central_lower_limit(1) = 0.05 |
| mixing_length_alpha = 2. |
| set_min_D_mix = .true. |
| min_center_Ye_for_min_D_mix = 0.4 ! min_D_mix is only used when center Ye >= this |
| dH_div_H_limit_min_H = 2d-1 |
| dH_div_H_limit = 0.0005d0 |
| dH_div_H_hard_limit = 1d-2 |
| / ! end of controls namelist |
Download table as: ASCIITypeset image






























