Abstract
The Parker Solar Probe (PSP) will eventually reach and cross the Alfvén point or surface as it provides us with direct in situ measurements of the solar atmosphere. The Alfvén surface is the location at which the large-scale bulk solar wind speed  and the Alfvén speed
and the Alfvén speed  A are equal, and thus it separates sub-Aflvénic coronal flow
A are equal, and thus it separates sub-Aflvénic coronal flow  from super-Alfvénic solar wind flow
from super-Alfvénic solar wind flow  . The nature of turbulence at the Alfvén surface is not fully understood, and the PSP measurements at the Alfvén surface will be revealing. We investigate turbulence at the Alfvén surface from a theoretical perspective by using the 2012 and 2017 Zank et al. turbulence transport model equations. The 2012 Zank et al. description is applicable to a large plasma beta βp ≫ 1 regime, whereas the 2017 Zank et al. model applies to a plasma beta regime of order of βp ∼ 1 or ≪1. The distinction in the βp ≫ 1 and βp ≪ 1 or ∼1 turbulence description is in a sense geometric, in that the βp ≫ 1 description yields a fully 3D description of magnetohydrodynamic turbulence whereas βp ≪ 1 or ∼1 describes predominantly quasi-2D (with respect to the large-scale or mean magnetic field) turbulence and a minority slab turbulence component. Our analyses suggest that turbulence at the Alfvén surface (i) turns off if the higher order plasma beta turbulence transport model equations are used and (ii) does not turn off if the lower order plasma beta, nearly incompressible turbulence transport model equations are used.
. The nature of turbulence at the Alfvén surface is not fully understood, and the PSP measurements at the Alfvén surface will be revealing. We investigate turbulence at the Alfvén surface from a theoretical perspective by using the 2012 and 2017 Zank et al. turbulence transport model equations. The 2012 Zank et al. description is applicable to a large plasma beta βp ≫ 1 regime, whereas the 2017 Zank et al. model applies to a plasma beta regime of order of βp ∼ 1 or ≪1. The distinction in the βp ≫ 1 and βp ≪ 1 or ∼1 turbulence description is in a sense geometric, in that the βp ≫ 1 description yields a fully 3D description of magnetohydrodynamic turbulence whereas βp ≪ 1 or ∼1 describes predominantly quasi-2D (with respect to the large-scale or mean magnetic field) turbulence and a minority slab turbulence component. Our analyses suggest that turbulence at the Alfvén surface (i) turns off if the higher order plasma beta turbulence transport model equations are used and (ii) does not turn off if the lower order plasma beta, nearly incompressible turbulence transport model equations are used.
Export citation and abstract BibTeX RIS
1. Introduction
With the launch of the Parker Solar Probe (PSP) and Solar Orbiter (expected to occur in 2019), the nature of turbulence in the sub-Alfvénic coronal flow is attracting the attention of the science community. The PSP provides us with an opportunity to study in situ how (i) the solar corona is heated and (ii) the solar wind is accelerated within a few solar radii of the solar surface. Over the past decade, various models that describe the dissipation of waves and turbulence in the sub-Alfvénic coronal flow have been proposed, in which coronal heating is due to the transfer of magnetic energy to plasma at both large and small scales. Two leading candidates for heating the solar corona, ion cyclotron heating and the turbulence cascade, both rely on the presence of upwardly propagating Alfvénic or magnetized fluctuations. The conversion of magnetic energy due to photospheric-driven motion of the magnetic carpet or even the higher canopy of the magnetic field via either direct heating (some form of reconnection) or the launching of waves is generally thought to be the origin of the energy needed to heat the corona. Ion cyclotron heating and the turbulent cascade models exploit the notion that low-frequency shear Alfvén waves excited in the chromosphere will survive into the lower corona. The transition of these fluctuations from the coronal base to the super-Alfvénic solar wind has been investigated (i) from a linear wave perspective (Heinemann 1980; Heinemann & Olbert 1980; Leer et al. 1982), (ii) on the basis of nonlinear waves and wave steepening (Hollweg et al. 1982; Hollweg 1987), (iii) using phenomenological wave/turbulence (W/T) models (Matthaeus et al. 1999a; Viñas et al. 2000; Dmitruk et al. 2001, 2002; Oughton et al. 2001; Suzuki & Inutsuka 2005; Cranmer et al. 2007, 2013; Chandran & Hollweg 2009; Chandran et al. 2010; Verdini et al. 2010; Woolsey & Cranmer 2014), and (iv) using a recently developed nearly incompressible (NI) turbulence transport model (Zank et al. 2017, 2018a). Ion cyclotron resonant heating, one of the most widely accepted mechanisms for coronal heating, results from the energization of particles interacting resonantly with Alfvén waves, thus heating the solar corona (Isenberg 2001; Isenberg et al. 2001; Isenberg 2004). The turbulent cascade, the alternative to ion cyclotron heating, exploits the possibility that upwardly propagating low-frequency Alfvén waves are partially reflected, thereby driving a turbulent cascade through coupling to zero-frequency modes (Matthaeus et al. 1999a; Oughton et al. 2001; Cranmer et al. 2007, 2013; Cranmer & van Ballegooijen 2010). The cascade is expected to be quasi-perpendicular, and the dissipation of energy at high wavenumber may therefore lead to quasi-perpendicular heating of the corona. More recently, the turbulent cascade model has been modified to argue that nonpropagating quasi-2D low-frequency magnetohydrodynamic (MHD) turbulence is responsible primarily for the transfer of turbulent energy to the coronal plasma and that Alfvén waves entered as slab turbulence as a minority component (Zank et al. 2017, 2018a). Which of these approaches is valid requires the detailed observations that will soon be made by the PSP.
In propagating from sub- to super-Alfvénic flow regions, the fluctuations must eventually encounter the Alfvén critical point or surface (located at RA, the position where the large-scale solar wind speed  and the Alfvén speed
and the Alfvén speed  A are equal, i.e.,
A are equal, i.e.,  =
=  A). The nature and characteristics of turbulence at the Alfvén point/surface are not understood, and indeed there is debate about whether turbulence survives or dies at RA. The answer to this interesting question will hopefully be addressed by the PSP because it will travel through the Alfvén surface. Here, we investigate solar wind turbulence at the Alfvén surface from a theoretical perspective by using the Zank et al. (2012, 2017) turbulence transport models and a model developed for the solar corona and its associated heating by the dissipation of quasi-2D turbulence (Zank et al. 2018a). The Zank et al. (2012, 2017) models have been validated observationally. The numerical solutions of these models in the supersonic solar wind have been compared successfully with those measured by Helios 2, Ulysses, and Voyager 2 from 0.3 to 75 au (see Adhikari et al. 2015b, 2017; Zank et al. 2017). Zank et al. (2018a) used the quasi-2D and slab turbulence transport equations of Zank et al. (2017) to investigate turbulence in the solar atmosphere between 1R⊙ and 15R⊙. The dissipation of turbulence in the Zank et al. (2018a) model yields coronal temperatures > 106 K within two to three solar radii, which is consistent with earlier heating models (Matthaeus et al. 1999a; Viñas et al. 2000; Dmitruk et al. 2001, 2002; Oughton et al. 2001; Suzuki & Inutsuka 2005; Cranmer et al. 2007, 2013; Chandran & Hollweg 2009; Chandran et al. 2010; Verdini et al. 2010; Woolsey & Cranmer 2014). This suggests that turbulence transport models might be reasonable candidates to explain coronal heating, and hence the implications of the model should be explored with a view to PSP observations. In this paper, we use the same solar wind speed, solar wind density, and magnetic field background profiles as in Zank et al. (2018a).
A). The nature and characteristics of turbulence at the Alfvén point/surface are not understood, and indeed there is debate about whether turbulence survives or dies at RA. The answer to this interesting question will hopefully be addressed by the PSP because it will travel through the Alfvén surface. Here, we investigate solar wind turbulence at the Alfvén surface from a theoretical perspective by using the Zank et al. (2012, 2017) turbulence transport models and a model developed for the solar corona and its associated heating by the dissipation of quasi-2D turbulence (Zank et al. 2018a). The Zank et al. (2012, 2017) models have been validated observationally. The numerical solutions of these models in the supersonic solar wind have been compared successfully with those measured by Helios 2, Ulysses, and Voyager 2 from 0.3 to 75 au (see Adhikari et al. 2015b, 2017; Zank et al. 2017). Zank et al. (2018a) used the quasi-2D and slab turbulence transport equations of Zank et al. (2017) to investigate turbulence in the solar atmosphere between 1R⊙ and 15R⊙. The dissipation of turbulence in the Zank et al. (2018a) model yields coronal temperatures > 106 K within two to three solar radii, which is consistent with earlier heating models (Matthaeus et al. 1999a; Viñas et al. 2000; Dmitruk et al. 2001, 2002; Oughton et al. 2001; Suzuki & Inutsuka 2005; Cranmer et al. 2007, 2013; Chandran & Hollweg 2009; Chandran et al. 2010; Verdini et al. 2010; Woolsey & Cranmer 2014). This suggests that turbulence transport models might be reasonable candidates to explain coronal heating, and hence the implications of the model should be explored with a view to PSP observations. In this paper, we use the same solar wind speed, solar wind density, and magnetic field background profiles as in Zank et al. (2018a).
The supersonic and subsonic solar winds are observed to be primarily in the plasma beta regime βp ∼ 1 or βp ≪ 1, respectively (see Bruno & Carbone 2013; Adhikari et al. 2017),  , where n is the solar wind density, kB is the Boltzmann constant, T is the solar wind temperature, B is the large-scale magnetic field, and μ0 is the magnetic permeability. The regime βp ≫ 1 is therefore not appropriate to the solar wind unless possibly in the neighborhood of the heliospheric current sheet. In the 1990s, Zank & Matthaeus (1992b, 1993) considered three different plasma beta regimes, βp ≫ 1, βp ∼ 1, and βp ≪ 1, to derive distinct descriptions of the solar wind turbulence for the three plasma beta cases. Of particular interest was that Zank & Matthaeus (1992b, 1993) found that the dimensionality of the underlying MHD description was related to the plasma beta. The leading-order incompressible description was found to collapse from 3D to 2D in the regimes βp ∼ 1 and βp ≪ 1 (Zank & Matthaeus 1992b, 1993), a result that carries over to an inhomogeneous magnetized plasma (Hunana & Zank 2010), except that the collapse in dimensionality for the βp ∼ 1 case is quasi-2D. In the βp ≫ 1 regime, the leading-order incompressible MHD description is fully 3D, whereas in the βp ∼ 1 and βp ≪ 1 regimes, the leading-order description reduces to 2D in a plane perpendicular to the magnetic field. Similarly, higher order incompressible fluctuations in the βp ∼ 1 and βp ≪ 1 regimes propagate parallel to the magnetic field (Zank et al. 2017). NI MHD in the βp ∼ 1 and βp ≪ 1 regimes predicts that solar wind turbulence is a superposition of majority quasi-2D and minority slab turbulence (Zank & Matthaeus 1992b, 1993; Zank et al. 2017).
, where n is the solar wind density, kB is the Boltzmann constant, T is the solar wind temperature, B is the large-scale magnetic field, and μ0 is the magnetic permeability. The regime βp ≫ 1 is therefore not appropriate to the solar wind unless possibly in the neighborhood of the heliospheric current sheet. In the 1990s, Zank & Matthaeus (1992b, 1993) considered three different plasma beta regimes, βp ≫ 1, βp ∼ 1, and βp ≪ 1, to derive distinct descriptions of the solar wind turbulence for the three plasma beta cases. Of particular interest was that Zank & Matthaeus (1992b, 1993) found that the dimensionality of the underlying MHD description was related to the plasma beta. The leading-order incompressible description was found to collapse from 3D to 2D in the regimes βp ∼ 1 and βp ≪ 1 (Zank & Matthaeus 1992b, 1993), a result that carries over to an inhomogeneous magnetized plasma (Hunana & Zank 2010), except that the collapse in dimensionality for the βp ∼ 1 case is quasi-2D. In the βp ≫ 1 regime, the leading-order incompressible MHD description is fully 3D, whereas in the βp ∼ 1 and βp ≪ 1 regimes, the leading-order description reduces to 2D in a plane perpendicular to the magnetic field. Similarly, higher order incompressible fluctuations in the βp ∼ 1 and βp ≪ 1 regimes propagate parallel to the magnetic field (Zank et al. 2017). NI MHD in the βp ∼ 1 and βp ≪ 1 regimes predicts that solar wind turbulence is a superposition of majority quasi-2D and minority slab turbulence (Zank & Matthaeus 1992b, 1993; Zank et al. 2017).
The original W/T models are based on a 3D incompressible MHD description that emerges in the higher order plasma beta βp ≫ 1 regime (Zank & Matthaeus 1992a, 1992b, 1993). Similarly, several turbulence transport models (e.g., Matthaeus et al. 1994, 1999a; Zank et al. 1996, 2012; Smith et al. 2001; Breech et al. 2008; Usmanov et al. 2011; Kryukov et al. 2012; Adhikari et al. 2014, 2015b; Shiota et al. 2017) developed from the standard 3D incompressible MHD equations are applicable only to the βp ≫ 1 plasma. In our study, we employ two turbulence transport models, Zank et al. (2012, hereafter Z2012) and Zank et al. (2017, hereafter Z2017), to investigate turbulence at the Alfvén point or surface. Both Z2012 and Z2017 turbulence transport model equations are derived using a moment hierarchy (Matthaeus et al. 1994; Zank et al. 1996; Matthaeus et al. 2004; Breech et al. 2005, 2008) of scale-separated equations of incompressible and nearly incompressibe MHD equations in an inhomogeneous flow, respectively (Marsch & Tu 1989, 1990a, 1990b; Zhou & Matthaeus 1990a, 1990b; Hunana & Zank 2010). Therefore, both the Z2012 and Z2017 models capture the spatial and temporal inhomogeneity of the background fields. However, these turbulence model equations, as with other turbulence models, do not contain viscosity and magnetic diffusivity. Because the coronal/solar wind plasma is collisionless, the form of the viscosity and magnetic diffusivity is not known. Nonetheless, in deriving energy-containing turbulence models, the implicit assumption is that the inertial range of the turbulence spectrum is self-similar to the energy input rate in the inertial range, which balances the dissipation rate, indicating that the rate of energy transfer in the turbulence model is determined by the nonlinear term. This, therefore, determines the heating of the solar wind plasma. The key point is that although turbulence transport models represent a theory for the energy-containing fluctuations, the attenuation of these fluctuations is controlled by invoking the Kolmogorov/Iroshnikov–Kraichnan (IK) phenomenology. The turbulence transport model therefore calculates the rate at which energy enters (and dissipates) in the inertial range, and we assume the fully developed turbulence Kolmogorov/IK form of the inertial range. Several observational studies show that fluctuations of the magnetic field exhibit either Kolmogorov or IK power laws (Podesta et al. 2007; Horbury et al. 2008; Wicks et al. 2010; Bruno & Telloni 2015).
The Z2012 model equations are applicable in the higher order plasma beta βp ≫ 1 regime, while the Z2017 model equations are appropriate to the order βp ∼ 1 or ≪1 regimes. Besides the plasma beta regime, the Z2012 model includes the large-scale Alfvén velocity in the turbulence transport equations, whereas the quasi-2D turbulence transport equations of Z2017 do not include  A, unlike the minority slab turbulence transport equations of Z2017 in which the Alfvén velocity
A, unlike the minority slab turbulence transport equations of Z2017 in which the Alfvén velocity  A enters. Therefore, the Z2012 model equations exhibit a singular point at the Alfvén point RA, while the quasi-2D turbulence transport equations of Z2017 do not, although the minority slab turbulence equations do exhibit a singular point at the Alfvén point. Note that the singularity
A enters. Therefore, the Z2012 model equations exhibit a singular point at the Alfvén point RA, while the quasi-2D turbulence transport equations of Z2017 do not, although the minority slab turbulence equations do exhibit a singular point at the Alfvén point. Note that the singularity  is present in the full incompressible MHD equations, and the turbulence transport equations simply reflect this. The purpose of this study is to investigate solar wind turbulence at these singular points by using a critical point analysis. We present detailed analyses of the Z2012 and Z2017 models in Appendices A and B, respectively.
is present in the full incompressible MHD equations, and the turbulence transport equations simply reflect this. The purpose of this study is to investigate solar wind turbulence at these singular points by using a critical point analysis. We present detailed analyses of the Z2012 and Z2017 models in Appendices A and B, respectively.
The nonlinear terms in the turbulence transport models of Z2012 and Z2017 describe the attenuation of turbulence energy, indicating energy transfer from large to small scales. The nonlinear term can be modeled using a Kolmogorov phenomenology. The nonlinear term determines the rate of dissipation for the heating of the coronal and solar wind plasma. Due to plasma heating mediated by the nonlinear term, the radial profile of the solar wind temperature decreases more slowly than the adiabatic profile r−4/3, where r is the heliocentric distance (see Adhikari et al. 2015b, 2017; Zank et al. 2018a). Because the cascading of energy to small scales results in the heating of the coronal or solar wind plasma, a zero nonlinear term indicates no heating of the plasma. This approach to plasma heating of the solar wind has been validated observationally for nearly two decades, beginning with Matthaeus et al. (1999b) to most recently Adhikari et al. (2017).
The outline of this paper is as follows. We present an analysis of the large plasma beta βp ≫ 1 turbulence transport equations (Z2012) in Section 2. In Section 3, we re-examine the plasma beta βp ∼ 1 or ≪1 NI turbulence transport model equations (Z2017). Finally, we present our discussion and conclusions in Section 4.
2.
 Turbulence Model
Turbulence Model
The evolution and transport of magnetic field and velocity fluctuations in the solar wind can be described in terms of the Elsässer variable formulation of the incompressible MHD equations. Based on the fully 3D equations of incompressible MHD, the transport equations for the Elsässer variables  can be expressed as (Marsch & Tu 1989; Zhou & Matthaeus 1990a, 1990b)
can be expressed as (Marsch & Tu 1989; Zhou & Matthaeus 1990a, 1990b)
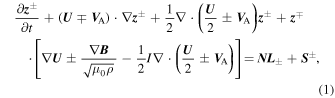
where  (
( and
and  are the velocity and magnetic field fluctuations, and ρ is the solar wind density) are the backward/forward propagating modes with respect to the outward interplanetary magnetic field field orientation, I is the identity matrix, and
are the velocity and magnetic field fluctuations, and ρ is the solar wind density) are the backward/forward propagating modes with respect to the outward interplanetary magnetic field field orientation, I is the identity matrix, and  are nonlinear terms. The parameters
are nonlinear terms. The parameters  are sources of turbulence. The derivation of the transport Equation (1) was based explicitly on an expansion of the 3D incompressible MHD equations. It indicates a vital restriction from the perspective of the theory of NI MHD, which argues that such a formalism is suitable only in the limit of a large plasma beta (Zank & Matthaeus 1992a, 1992b, 1993; Hunana & Zank 2010). Equation (1) evidently incorporates Alfvén propagation effects and introduces a singular point at the Alfvén critical point RA. Z2012 derived six coupled turbulence transport equations by taking moments of Equation (1). The six coupled turbulence transport equations describe the evolution of energy in backward/forward propagating modes
are sources of turbulence. The derivation of the transport Equation (1) was based explicitly on an expansion of the 3D incompressible MHD equations. It indicates a vital restriction from the perspective of the theory of NI MHD, which argues that such a formalism is suitable only in the limit of a large plasma beta (Zank & Matthaeus 1992a, 1992b, 1993; Hunana & Zank 2010). Equation (1) evidently incorporates Alfvén propagation effects and introduces a singular point at the Alfvén critical point RA. Z2012 derived six coupled turbulence transport equations by taking moments of Equation (1). The six coupled turbulence transport equations describe the evolution of energy in backward/forward propagating modes  and the corresponding correlation lengths λ±, and the residual energy ED and the corresponding correlation length λD (see Appendix A). Adhikari et al. (2015a, 2015b) and Shiota et al. (2017) applied the Z2012 model equations to investigate turbulence in super-Alfvénic solar wind flow, i.e.,
and the corresponding correlation lengths λ±, and the residual energy ED and the corresponding correlation length λD (see Appendix A). Adhikari et al. (2015a, 2015b) and Shiota et al. (2017) applied the Z2012 model equations to investigate turbulence in super-Alfvénic solar wind flow, i.e.,  ≫
≫  A. Related studies have been presented by Usmanov et al. (2011) although using a somewhat simpler description for the transport of MHD turbulence (Breech et al. 2008). In addition, Adhikari et al. (2016a, 2016b) employed the Z2012 model to explore the interaction of turbulence with interplanetary shocks at 1 au. A similar analysis of the interaction of turbulence with termination shock using majority quasi-2D and minority slab turbulence model equations can be found in Zank et al. (2018b).
A. Related studies have been presented by Usmanov et al. (2011) although using a somewhat simpler description for the transport of MHD turbulence (Breech et al. 2008). In addition, Adhikari et al. (2016a, 2016b) employed the Z2012 model to explore the interaction of turbulence with interplanetary shocks at 1 au. A similar analysis of the interaction of turbulence with termination shock using majority quasi-2D and minority slab turbulence model equations can be found in Zank et al. (2018b).
The nonlinear terms  ± in the Z2012 model equations are obtained using the systematic and constructive approach employed in Matthaeus et al. (1994) and Zank et al. (1996), which is an extended form of the von Karman–Howarth–Batchelor one-point closure for hydrodynamic turbulence (von Karman & Howarth 1938; Batchelor 1953). The nonlinear terms due to spectral transfer can be expressed as (Zank et al. 2012)
± in the Z2012 model equations are obtained using the systematic and constructive approach employed in Matthaeus et al. (1994) and Zank et al. (1996), which is an extended form of the von Karman–Howarth–Batchelor one-point closure for hydrodynamic turbulence (von Karman & Howarth 1938; Batchelor 1953). The nonlinear terms due to spectral transfer can be expressed as (Zank et al. 2012)
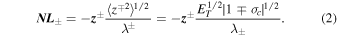
Here,  is used, where
is used, where  is the total turbulent energy and
is the total turbulent energy and  is the normalized cross-helicity. By taking moments of Equations (1) and (2), Z2012 derive the transport equations, including the dissipation terms, for the energy in backward/forward propagating modes
is the normalized cross-helicity. By taking moments of Equations (1) and (2), Z2012 derive the transport equations, including the dissipation terms, for the energy in backward/forward propagating modes  and the residual energy ED. The total dissipation term for the Z2012 model may be defined as
and the residual energy ED. The total dissipation term for the Z2012 model may be defined as
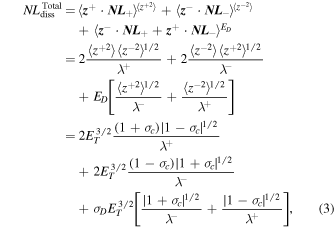
where  is the normalized residual energy. In Equation (3),
is the normalized residual energy. In Equation (3),  , and
, and  denote the dissipation terms for the transport equations of the backward and forward propagating modes, and the residual energy, respectively. Equation (2) (and also Equation (3)) describes the transfer of energy through the inertial range. If the right-hand sides (rhs) of Equations (2) and (3) are zero, the nonlinear terms (and thus the total dissipative term) vanish, suggesting no transfer of energy through the inertial range. In this case, turbulence "dies." Therefore, Equations (2) and (3) allow us to investigate whether or not turbulence turns off at the Alfvén critical point. Because there is no cascade of energy from large to small scales, as a result of the nonlinear term being zero, there is no heating of the coronal/solar wind plasma by turbulence. By examining the critical points in the Z2012 turbulence transport model equations (see Appendix A), we determine the ET, σc, and σD at RA, from which Equations (2) and (3) are used to determine whether the nonlinear terms (and thus the total dissipative term) become zero or not. We first write the Z2012 model equations, assuming a 1D steady state, in a spherical coordinate system r using the background profiles of the solar wind velocity, solar wind density, and the magnetic field given in Equation (15). We rewrite the 1D steady-state equations as an autonomous differential set, and then solve for the critical point (see Appendix A). From Appendix A, we find that
denote the dissipation terms for the transport equations of the backward and forward propagating modes, and the residual energy, respectively. Equation (2) (and also Equation (3)) describes the transfer of energy through the inertial range. If the right-hand sides (rhs) of Equations (2) and (3) are zero, the nonlinear terms (and thus the total dissipative term) vanish, suggesting no transfer of energy through the inertial range. In this case, turbulence "dies." Therefore, Equations (2) and (3) allow us to investigate whether or not turbulence turns off at the Alfvén critical point. Because there is no cascade of energy from large to small scales, as a result of the nonlinear term being zero, there is no heating of the coronal/solar wind plasma by turbulence. By examining the critical points in the Z2012 turbulence transport model equations (see Appendix A), we determine the ET, σc, and σD at RA, from which Equations (2) and (3) are used to determine whether the nonlinear terms (and thus the total dissipative term) become zero or not. We first write the Z2012 model equations, assuming a 1D steady state, in a spherical coordinate system r using the background profiles of the solar wind velocity, solar wind density, and the magnetic field given in Equation (15). We rewrite the 1D steady-state equations as an autonomous differential set, and then solve for the critical point (see Appendix A). From Appendix A, we find that

at the Alfvén point. Because σc = −1, only outward modes exist at the Alfvén point, i.e.,  and
and  . It also implies that
. It also implies that  , which suggests that the velocity and magnetic field fluctuations are perfectly aligned. In this case, the correlation lengths of the velocity and magnetic fluctuations, lu and lb, respectively, also become equal,
, which suggests that the velocity and magnetic field fluctuations are perfectly aligned. In this case, the correlation lengths of the velocity and magnetic fluctuations, lu and lb, respectively, also become equal,  (Zank et al. 2017). As discussed above, the incompressible MHD turbulence transport equations of Z2012 reflect the inhomogeneity of the background fields (see Appendix A). Although the gradient of the background field in the turbulence model can produce backward modes, Equation (4) shows that the backward mode corresponding to the larger plasma beta turbulence transport equations (Z2012) is zero at the Alfvén surface. Although compressive effects may produce backward modes, our analysis is restricted to an incompressible framework, like most studies of MHD turbulence (Matthaeus et al. 1999a; Viñas et al. 2000; Dmitruk et al. 2001, 2002; Oughton et al. 2001; Suzuki & Inutsuka 2005; Cranmer et al. 2007, 2013; Chandran & Hollweg 2009; Chandran et al. 2010; Verdini et al. 2010; Woolsey & Cranmer 2014). Using Equation (4) in Equations (2) and (3), we immediately find that
(Zank et al. 2017). As discussed above, the incompressible MHD turbulence transport equations of Z2012 reflect the inhomogeneity of the background fields (see Appendix A). Although the gradient of the background field in the turbulence model can produce backward modes, Equation (4) shows that the backward mode corresponding to the larger plasma beta turbulence transport equations (Z2012) is zero at the Alfvén surface. Although compressive effects may produce backward modes, our analysis is restricted to an incompressible framework, like most studies of MHD turbulence (Matthaeus et al. 1999a; Viñas et al. 2000; Dmitruk et al. 2001, 2002; Oughton et al. 2001; Suzuki & Inutsuka 2005; Cranmer et al. 2007, 2013; Chandran & Hollweg 2009; Chandran et al. 2010; Verdini et al. 2010; Woolsey & Cranmer 2014). Using Equation (4) in Equations (2) and (3), we immediately find that
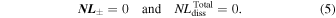
Equation (5) clearly indicates that the nonlinear and total dissipative terms become zero at the Alfvén surface, and suggests that the turbulence turns off at the Alfvén point (RA). Notice that this result is obtained from the higher order plasma beta (βp ≫ 1) Z2012 turbulence transport model equations. In the next section, we analyze the turbulence at RA by using the βp ≪ 1 or ∼1 NI turbulence transport model equations.
3.
 and βp ∼ 1 Turbulence Model
and βp ∼ 1 Turbulence Model
Z2017 used the NI MHD equations of Hunana & Zank (2010) to derive transport equations for the majority quasi-2D  and minority slab
and minority slab  Elsässer variables. The transport equations for the majority quasi-2D Elsässer variables
Elsässer variables. The transport equations for the majority quasi-2D Elsässer variables  are (Zank et al. 2017)
are (Zank et al. 2017)
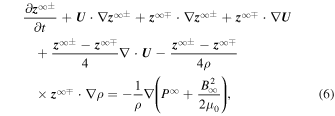
where " " refers to quasi-2D turbulence. Here,
" refers to quasi-2D turbulence. Here,  and
and  denote the velocity and magnetic fluctuations of quasi-2D turbulence, respectively. An important distinction between Equations (6) and (1) is that the quasi-2D Elsässer variables are advected by the large-scale plasma flow, and Equation (6) does not include the Alfvén velocity. Quasi-2D turbulence does not contain Alfvén propagation effects, and hence does not exhibit a singular point at the Alfvén critical point RA as does Equation (1). Using a similar approach to the derivation of Equation (2), the nonlinear terms in Equation (6) can be constructed as (Zank et al. 2017)
denote the velocity and magnetic fluctuations of quasi-2D turbulence, respectively. An important distinction between Equations (6) and (1) is that the quasi-2D Elsässer variables are advected by the large-scale plasma flow, and Equation (6) does not include the Alfvén velocity. Quasi-2D turbulence does not contain Alfvén propagation effects, and hence does not exhibit a singular point at the Alfvén critical point RA as does Equation (1). Using a similar approach to the derivation of Equation (2), the nonlinear terms in Equation (6) can be constructed as (Zank et al. 2017)
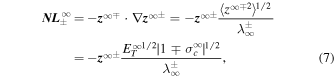
where  are the quasi-2D energies in backward/forward propagating modes and
are the quasi-2D energies in backward/forward propagating modes and  are the corresponding correlation lengths.
are the corresponding correlation lengths.  is the total turbulent energy and
is the total turbulent energy and  is the normalized cross-helicity of quasi-2D turbulence. Similarly, the turbulence transport equations for the higher order NI Elsässer variables
is the normalized cross-helicity of quasi-2D turbulence. Similarly, the turbulence transport equations for the higher order NI Elsässer variables  are (Zank et al. 2017)
are (Zank et al. 2017)
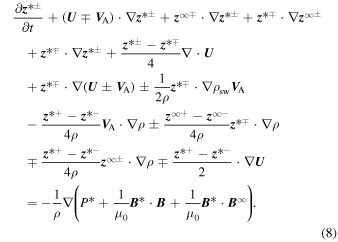
Equation (8) shows that the  are coupled to leading-order core Elsässer variables
are coupled to leading-order core Elsässer variables  in a passive scalar sense, so that the primary dissipation of
in a passive scalar sense, so that the primary dissipation of  is due to mixing rather than nonlinearity. The nonlinear interaction between counterpropagating Alfvén waves can also be responsible for the decay of slab turbulence, although the dominant contribution is due to mixing with quasi-2D turbulence (see the discussion about critical balance in Zank et al. 2017). Unlike the quasi-2D case, the Alfvén velocity
is due to mixing rather than nonlinearity. The nonlinear interaction between counterpropagating Alfvén waves can also be responsible for the decay of slab turbulence, although the dominant contribution is due to mixing with quasi-2D turbulence (see the discussion about critical balance in Zank et al. 2017). Unlike the quasi-2D case, the Alfvén velocity  A now enters the transport equation for
A now enters the transport equation for  , and slab turbulence therefore exhibits an Alfvén critical point RA. The nonlinear terms for slab turbulence can be modeled as (Zank et al. 2017)
, and slab turbulence therefore exhibits an Alfvén critical point RA. The nonlinear terms for slab turbulence can be modeled as (Zank et al. 2017)
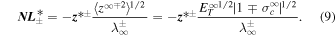
Equation (9) is different from Equations (2) and (7) in that the leading-order nonlinear terms are due to mixing with quasi-2D turbulence. We may define the total (quasi-2D and slab) nonlinear term as
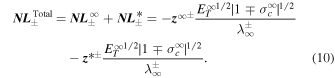
Z2017 derived the dissipation terms for the forward and backward propagating modes, and the residual energy. Similarly, the total (quasi-2D + slab) nonlinear dissipation term, corresponding to forward and backward propagating modes and the residual energy, can be expressed as (Zank et al. 2017, 2018a)

We note that Equations (10) and (11) are the total nonlinear and dissipative terms for the βp ∼ 1 and βp ≪ 1 regime for the NI quasi-2D and slab turbulence transport equations of Z2017. Similar to the β ≫ 1 turbulence transport model, the rhs of Equation (11) acts as a dissipative source for the heating of the coronal and solar wind plasma (Adhikari et al. 2017; Zank et al. 2018a). If the rhs term is zero, there is no heating of the coronal and solar wind plasma by turbulence. Again, by checking whether or not these terms vanish at RA, we can determine whether or not turbulence turns off at the Alfvén point. For this we employ the 1D steady-state turbulence transport model equations of Zank et al. (2018a; see Equations (29)–(38) in Appendix B), which are derived from Z2017 by using the background profiles (Equation (15)). As in the case of Z2012, we rewrite the 1D steady-state coupled turbulence transport Equations (29)–(38) as an autonomous differential system, and then apply a critical point analysis. The detailed analysis is presented in Appendix B. From Appendix B, we find the following possible critical point values at the Alfvén surface,

As in the large βp ≫ 1 plasma beta regime, Equation (12) shows that only one mode is possible at the Alfvén point for slab turbulence. Moreover, the slab velocity and magnetic field fluctuations are perfectly correlated, which shows that the corresponding correlation lengths are also equal  (Zank et al. 2017). In contrast, such a correlation between velocity and magnetic field fluctuations and the existence of only one mode is not possible for quasi-2D turbulence. Counterpropagating quasi-2D modes therefore exist at the Alfvén point. Using Equation (12) in Equation (10), we immediately find that
(Zank et al. 2017). In contrast, such a correlation between velocity and magnetic field fluctuations and the existence of only one mode is not possible for quasi-2D turbulence. Counterpropagating quasi-2D modes therefore exist at the Alfvén point. Using Equation (12) in Equation (10), we immediately find that
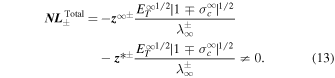
Equation (13) indicates that the nonlinear terms at the Alfvén surface corresponding to NI turbulence transport model equations are not zero. Note that the first and second terms on the rhs of Equation (13) are nonlinear terms for quasi-2D and slab turbulence, respectively. The first terms do not vanish because  or
or  . Interestingly, the second terms also do not vanish for values of
. Interestingly, the second terms also do not vanish for values of  , unlike in the higher order plasma beta βp ≫ 1 case (see Equation (5)). In the large plasma beta βp ≫ 1 case, the nonlinear terms or spectral transfer terms are due to counterpropagating modes, i.e.,
, unlike in the higher order plasma beta βp ≫ 1 case (see Equation (5)). In the large plasma beta βp ≫ 1 case, the nonlinear terms or spectral transfer terms are due to counterpropagating modes, i.e.,  , which vanish in either the (i)
, which vanish in either the (i)  and
and  , or (ii)
, or (ii)  and
and  case. However, the nonlinear terms for the NI slab turbulence model equations are due to mixing with quasi-2D turbulence, i.e.,
case. However, the nonlinear terms for the NI slab turbulence model equations are due to mixing with quasi-2D turbulence, i.e.,  . It is obvious that
. It is obvious that  does not vanish for
does not vanish for  and
and  (i.e.,
(i.e.,  ) and
) and  does not vanish for
does not vanish for  and
and  (i.e.,
(i.e.,  ). Similarly, the total dissipation term for the NI quasi-2D and slab turbulence transport model equations becomes
). Similarly, the total dissipation term for the NI quasi-2D and slab turbulence transport model equations becomes
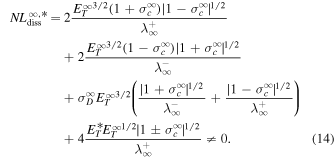
Equations (13) and (14) show clearly that the total nonlinear and dissipation terms derived from the NI turbulence transport model equations, having plasma beta of the order of βp ∼ 1 or less, do not become zero at the Alfvén point. Therefore, turbulence does not turn off at the Alfvén point in the βp ∼ 1 or ≪1 regime for the NI turbulence transport model equations.
4. Discussion and Conclusions
We employed the Z2012 and Z2017 turbulence transport model equations to investigate turbulence at the Alfvén critical point or surface. The Alfvén point is the location at which the solar wind speed and the Alfvén speed are equal, i.e.,  =
=  A. The Alfvén surface separates the sub- and super-Alfvénic solar wind flow regions. Between two models, the Z2012 model is appropriate in the higher order plasma beta βp ≫ 1 regime and the Z2017 model is applicable to a plasma beta βp ∼ 1 or ≪1 regime. The Z2017 model equations are therefore more appropriate for solar wind plasma conditions. Our analysis is directly related to the PSP because it will cross the Alfvén surface in the near future.
A. The Alfvén surface separates the sub- and super-Alfvénic solar wind flow regions. Between two models, the Z2012 model is appropriate in the higher order plasma beta βp ≫ 1 regime and the Z2017 model is applicable to a plasma beta βp ∼ 1 or ≪1 regime. The Z2017 model equations are therefore more appropriate for solar wind plasma conditions. Our analysis is directly related to the PSP because it will cross the Alfvén surface in the near future.
Both models (Z2012 and Z2017) describe the transport of energy in forward and backward propagating modes, the residual energy, and the corresponding correlation lengths. However, the latter model describes the superposition of majority quasi-2D and minority slab turbulence components, while the former describes isotropic turbulence with no preferred orientation. The Z2012 model includes the large-scale Alfvén velocity and exhibits a singular point at the Alfvén surface. In the Z2017 model, the quasi-2D turbulence transport equations do not exhibit an Alfvén critical point, whereas the slab turbulence component admits an Alfvén critical point. Quasi-2D turbulence, being 2D in a plane perpendicular to the large-scale magnetic field, is advected by the large-scale bulk flow through the Alfvén point. Because the Z2012 equations and the slab turbulence transport equations of Z2017 possess singular points at the Alfvén surface, we employed critical point analysis to determine the turbulence quantities at the Alfvén surface.
The analysis of the two different plasma beta regime turbulence transport models yields two quite different results for the existence of turbulence at the Alfvén surface. Our findings in the case of the Z2012 βp ≫ 1 turbulence transport equations are as follows:
- (i)only one propagating (outward) mode exists at the Alfvén critical surface;
- (ii)the velocity and magnetic field fluctuations are perfectly correlated at the Alfvén surface, and hence the correlation lengths of the velocity and magnetic field fluctuations are also equal at the Alfvén surface; and
- (iii)the total nonlinear and dissipation terms are zero at the Alfvén point. As these terms describe the transfer of large-scale energy into small-scale energy through the inertial range, the zero nonlinear/dissipation terms indicate that no transfer of energy occurs in the inertial range. Therefore, the higher order plasma beta turbulence transport model equations suggest that turbulence turns off at the Alfvén surface.
In the case of the Z2017 NI turbulence transport model equations for βp ∼ 1 or ≪1, our findings are as follows:
- (i)there is no critical point at the Alfvén surface for the majority quasi-2D component, but a critical point at the Alfvén point does exist for the minority slab turbulence component;
- (ii)the higher order slab turbulence transport equations show that only one propagating mode (outward) exists at the Alfvén surface;
- (iii)the velocity and magnetic field fluctuations in the slab turbulence are perfectly aligned at the Alfvén point, and therefore the correlation lengths of the velocity and magnetic fluctuations of slab turbulence are also equal;
- (iv)although only one mode exists for slab turbulence at the Alfvén surface, the nonlinear dissipation does not turn off as in the Z2012 model because the dissipation of slab turbulence is due mainly to mixing with quasi-2D turbulence;
- (v)the leading-order quasi-2D turbulence shows that both outward and inward nonpropagating modes exist at the Alfvén point. Similarly, the majority quasi-2D velocity and magnetic field fluctuations are not perfectly correlated at the Alfvén point as in the slab turbulence; and
- (vi)the total nonlinear/dissipation terms are nonzero at the Alfvén surface, which indicates that energy is transferred through the inertial range. Therefore, the NI turbulence model equations for the plasma beta βp ≪ 1 or ∼1 regime predicts that turbulence does not turn off at the Alfvén critical surface.
Because the PSP will eventually reach and cross the Alfvén surface, it will provide us with direct in situ measurements of the solar atmosphere, and confirm what happens to solar wind turbulence at the Alfvén surface.
We acknowledge the partial support of NASA grants NNX 08AJ33G, subaward 37102-2, NNX14AC08G, NNX14AJ53G, A99132BT, RR185-447/4944336, and NNX12AB30G, and an NSF-DOE grant PHY-1707247. G.P.Z. acknowledges the generosity of the International Space Science Institute (ISSI) in supporting him through the 2017 Johannes Geiss Fellowship. This work is also partly supported by the International Space Science Institute (ISSI) in the framework of International Team 504 entitled Current Sheets, Turbulence, Structures and Particle Acceleration in the Heliosphere.
Appendix A: Z2012
We introduce a simple model for the large-scale solar wind velocity, solar wind density, and the magnetic field in the solar corona (Adhikari 2015; Zank et al. 2018a):
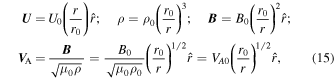
where U0 = 30 kms−1, VA0 = 1200 kms−1, ρ0, and B0 are the solar wind velocity, Alfvén velocity, solar wind density, and the magnetic field at r0 (= being a solar radius), respectively. These values of the solar wind velocity and the Alfvén velocity at the base of the solar surface yield an Alfvén surface at
being a solar radius), respectively. These values of the solar wind velocity and the Alfvén velocity at the base of the solar surface yield an Alfvén surface at  . Since the solar wind velocity is linearly increasing, Equation (15) is not applicable at large distances beyond the Alfvén point. With the background profiles (Equation (15)), the 1D steady-state turbulence transport equations of Z2012, ignoring mixing and source terms, and assuming a = 1/2 and b = 0, can be written as
. Since the solar wind velocity is linearly increasing, Equation (15) is not applicable at large distances beyond the Alfvén point. With the background profiles (Equation (15)), the 1D steady-state turbulence transport equations of Z2012, ignoring mixing and source terms, and assuming a = 1/2 and b = 0, can be written as
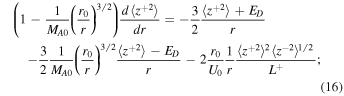
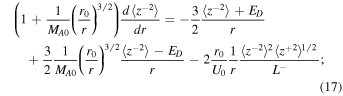
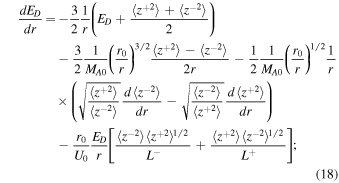
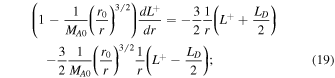
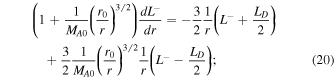
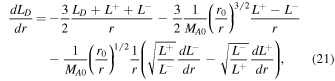
where  are the energy in backward/forward propagating modes, ED is the residual energy,
are the energy in backward/forward propagating modes, ED is the residual energy,  are the correlation functions of
are the correlation functions of  , and
, and  is the correlation function corresponding to ED.
is the correlation function corresponding to ED.  is the Alfvén Mach number. The third terms on the rhs of Equations (16) and (17) are the nonlinear dissipative terms for the energy in forward and backward propagating modes. Similarly, the fourth term on the rhs of Equation (18) is the nonlinear dissipative term for the residual energy. These nonlinear dissipative terms are formulated by taking moments of the nonlinear terms
is the Alfvén Mach number. The third terms on the rhs of Equations (16) and (17) are the nonlinear dissipative terms for the energy in forward and backward propagating modes. Similarly, the fourth term on the rhs of Equation (18) is the nonlinear dissipative term for the residual energy. These nonlinear dissipative terms are formulated by taking moments of the nonlinear terms  ±, i.e.,
±, i.e.,  , and
, and  (Zank et al. 2012), where
(Zank et al. 2012), where  indicates an ensemble average. The 1D steady-state turbulence transport Equations (16)–(21) are appropriate to the large β ≫ 1 plasma beta regime. Because β < 1 or ≪1 in the solar corona, it is inappropriate to use Equations (16)–(21), but the equations do allow one to consider sub-Alfvénic flows. Hence, we use these equations to study turbulence in the solar atmosphere. Notice that the turbulence Equations (16)–(21) do not contain any sources of turbulence, such as stream shear, for example, which is important within ∼5 au, or pickup ions, which are important beyond ∼5 au. It is unclear whether in situ sources of turbulence exist in the quiet solar corona other than the generation of turbulence in the photosphere, as discussed in Zank et al. (2018). Currently, in situ coronal sources of turbulence are not considered typically and turbulence is prescribed at the coronal base (see, Matthaeus et al. 1999a; Viñas et al. 2000; Dmitruk et al. 2001, 2002; Oughton et al. 2001; Suzuki & Inutsuka 2005; Cranmer et al. 2007; Chandran & Hollweg 2009; Chandran et al. 2010; Cranmer et al. 2013; Verdini et al. 2010; Woolsey & Cranmer 2014; Zank et al. 2018a). These models predict typical coronal temperatures >106 K, which suggest the possibility that this can drive the solar wind. In regions from which the slow solar wind may originate, the situation is undoubtedly more complicated. The PSP will tell us more about sources of turbulence near the Sun, and will be important for understanding turbulence in the solar atmosphere.
indicates an ensemble average. The 1D steady-state turbulence transport Equations (16)–(21) are appropriate to the large β ≫ 1 plasma beta regime. Because β < 1 or ≪1 in the solar corona, it is inappropriate to use Equations (16)–(21), but the equations do allow one to consider sub-Alfvénic flows. Hence, we use these equations to study turbulence in the solar atmosphere. Notice that the turbulence Equations (16)–(21) do not contain any sources of turbulence, such as stream shear, for example, which is important within ∼5 au, or pickup ions, which are important beyond ∼5 au. It is unclear whether in situ sources of turbulence exist in the quiet solar corona other than the generation of turbulence in the photosphere, as discussed in Zank et al. (2018). Currently, in situ coronal sources of turbulence are not considered typically and turbulence is prescribed at the coronal base (see, Matthaeus et al. 1999a; Viñas et al. 2000; Dmitruk et al. 2001, 2002; Oughton et al. 2001; Suzuki & Inutsuka 2005; Cranmer et al. 2007; Chandran & Hollweg 2009; Chandran et al. 2010; Cranmer et al. 2013; Verdini et al. 2010; Woolsey & Cranmer 2014; Zank et al. 2018a). These models predict typical coronal temperatures >106 K, which suggest the possibility that this can drive the solar wind. In regions from which the slow solar wind may originate, the situation is undoubtedly more complicated. The PSP will tell us more about sources of turbulence near the Sun, and will be important for understanding turbulence in the solar atmosphere.
To explore the physics of turbulence at the Alfvén critical point, we first transform the 1D steady-state Equations (16)–(18) into 1D steady-state equations for the total turbulent energy  , the normalized cross-helicity σc = EC/ET (
, the normalized cross-helicity σc = EC/ET ( is the cross-helicity), and the normalized residual energy σD = ED/ET. We then rewrite the equations as an autonomous system by using the chain rule,
is the cross-helicity), and the normalized residual energy σD = ED/ET. We then rewrite the equations as an autonomous system by using the chain rule,
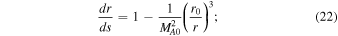
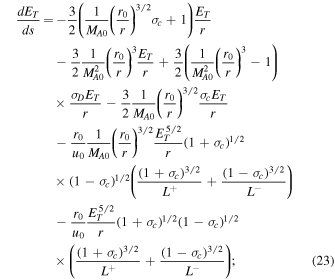
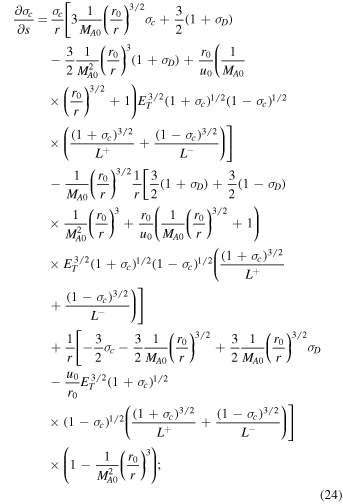
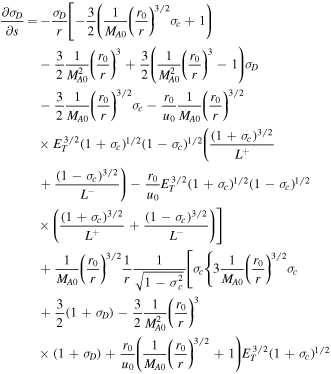
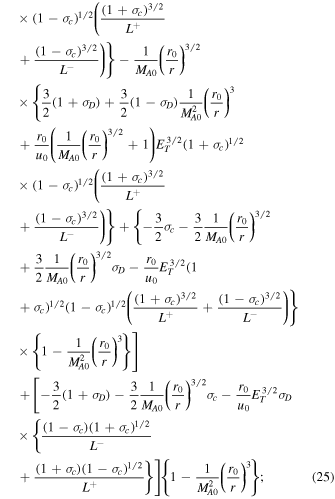
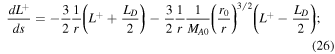
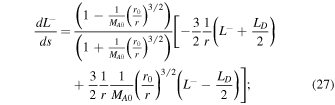
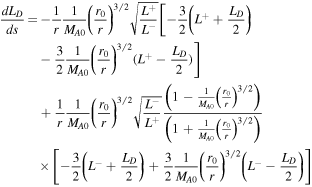
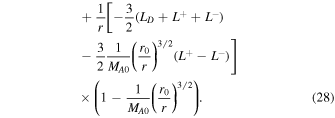
Equations (22)–(28) are an autonomous system of differential equations because the rhs are independent of s. To identify the critical point, we solve  ,
,  ,
,  , and dLD/ds = 0.
, and dLD/ds = 0.
- dr/ds = 0 yields

-
 yields
yields
-
 yields
yields
-
 yields
yields
-
 yields L+ = 0.
yields L+ = 0. -
 and
and  yield L− and LD arbitrary.
yield L− and LD arbitrary.
Appendix B: Z2017
On using the large-scale background profiles of the solar wind velocity, solar wind density, and the magnetic field described by Equation (15), the majority quasi-2D turbulence transport equations can be written in 1D steady-state form as (Zank et al. 2018a)
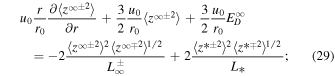
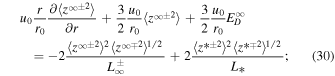
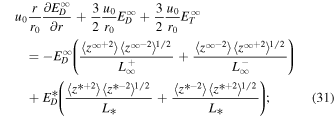

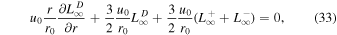
where " " refers to quasi-2D turbulence, and "*" denotes slab turbulence. The
" refers to quasi-2D turbulence, and "*" denotes slab turbulence. The  are the quasi-2D/slab energy in backward/forward propagating modes,
are the quasi-2D/slab energy in backward/forward propagating modes,  is the quasi-2D/slab residual energy,
is the quasi-2D/slab residual energy,  are the 2D correlation functions corresponding to
are the 2D correlation functions corresponding to  , and
, and  is the correlation function corresponding to
is the correlation function corresponding to  . Similarly, the 1D steady-state minority slab turbulence equations can be written as (Zank et al. 2018a)
. Similarly, the 1D steady-state minority slab turbulence equations can be written as (Zank et al. 2018a)
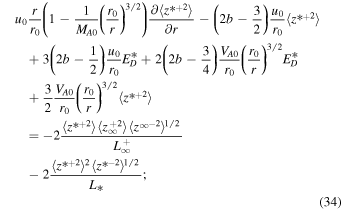
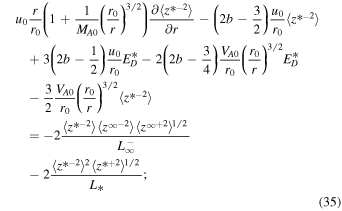
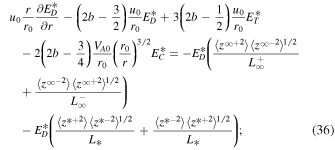
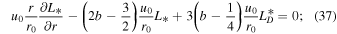
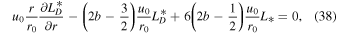
where  is assumed for the slab turbulence. With this assumption, the Alfvén velocity terms in the transport equations for the correlation functions are eliminated. The 1D steady-state turbulence transport Equations (29)–(38) are appropriate for the small or order β ∼ 1 plasma beta regime. Similar to Equations (16)–(21), these quasi-2D and slab turbulence transport model equations do not contain any turbulent sources. Zank et al. (2018a) used the NI turbulence transport model Equations (29)–(38) with a heating model to investigate coronal heating in the solar atmosphere. Zank et al. (2018a) obtained coronal temperatures within a few solar radii of >106 K, which is consistent with earlier heating models and the inferred coronal temperature. The system of autonomous differential equations for quasi-2D turbulence can be written as
is assumed for the slab turbulence. With this assumption, the Alfvén velocity terms in the transport equations for the correlation functions are eliminated. The 1D steady-state turbulence transport Equations (29)–(38) are appropriate for the small or order β ∼ 1 plasma beta regime. Similar to Equations (16)–(21), these quasi-2D and slab turbulence transport model equations do not contain any turbulent sources. Zank et al. (2018a) used the NI turbulence transport model Equations (29)–(38) with a heating model to investigate coronal heating in the solar atmosphere. Zank et al. (2018a) obtained coronal temperatures within a few solar radii of >106 K, which is consistent with earlier heating models and the inferred coronal temperature. The system of autonomous differential equations for quasi-2D turbulence can be written as
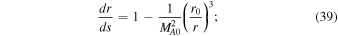
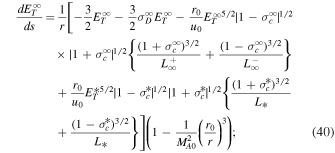
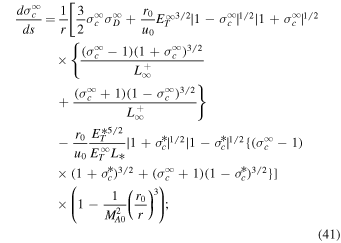
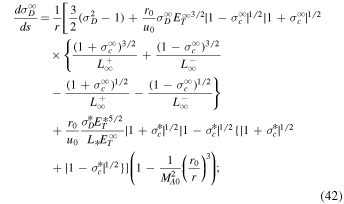
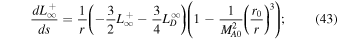
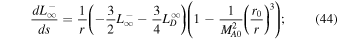
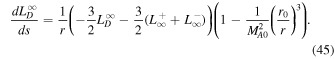
Similarly, the system of autonomous differential equations for slab turbulence is
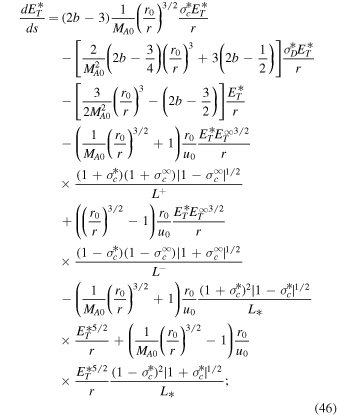
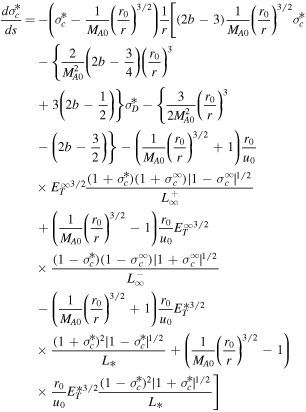
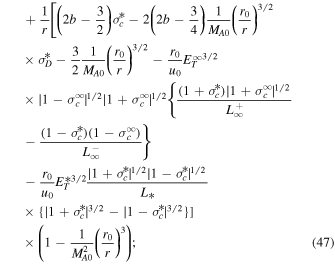
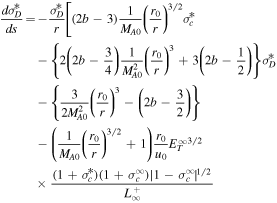
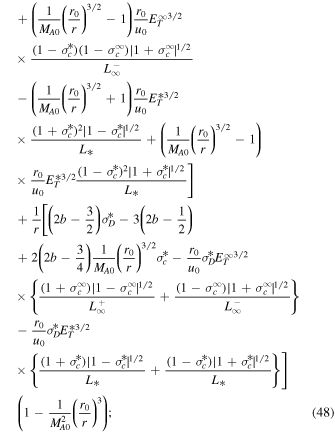
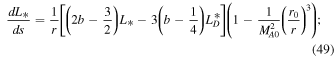
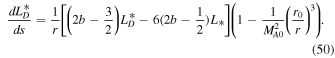
Here,  are the quasi-2D/slab total turbulent energy,
are the quasi-2D/slab total turbulent energy,  are the quasi-2D/slab normalized cross-helicity, and
are the quasi-2D/slab normalized cross-helicity, and  are the quasi-2D/slab normalized residual energy. Because the Alfvén critical point is absent in the quasi-2D turbulence transport model equations, we need only determine the critical point for the slab turbulence transport model equations. We find that
are the quasi-2D/slab normalized residual energy. Because the Alfvén critical point is absent in the quasi-2D turbulence transport model equations, we need only determine the critical point for the slab turbulence transport model equations. We find that
- dr/ds = 0 yields

-
 /
/ gives
gives
-
 yields
yields
-
 yields
yields
-
 yields L* arbitrary.
yields L* arbitrary. -
 yields
yields  arbitrary.
arbitrary.
Because there is no critical point for the quasi-2D turbulence transport models, we do not find particular quasi-2D turbulence values of  , and
, and  at the Alfvén surface as in the slab turbulence transport model equations. The quasi-2D turbulence, being 2D in a plane perpendicular to the large-scale magnetic field, is advected by the large-scale bulk flow through the Alfvén point without disturbance.
at the Alfvén surface as in the slab turbulence transport model equations. The quasi-2D turbulence, being 2D in a plane perpendicular to the large-scale magnetic field, is advected by the large-scale bulk flow through the Alfvén point without disturbance.


























