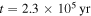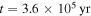Abstract
We construct an analytical model of gravitationally unstable protoplanetary disks consisting of three regions: the inner region where the internal dissipation dominates the heating, the intermediate region where the central protostar irradiation dominates, and the outer region where background irradiation dominates. We use this analytical model and an evolutionary numerical model of protoplanetary disks to calculate the cooling time and find out the location of the isothermal region. We investigate the effects of the isothermal region on the disk instability model for giant planet formation. We find that the fragmentation region found in previous studies is contained in the isothermal region of a disk. In this case, the cooling time criterion is not applicable for fragmentation. Therefore, the constraint on the disk instability model caused by the cooling time criterion should be relieved. The viability of the disk instability model is improved. When the isothermal region is considered, the inner boundary of the fragmentation region is extended inward to ∼20 au. We also show that if the contribution of the protostar irradiation to the disk surface temperature can be included in the cooling rate, the fragmentation region defined by the cooling time criterion can be extended inward to ∼26 au. We find that a disk tends to be isothermal in the region where the cooling time criterion is satisfied. We also find that at the later stage of disk instability, the inner boundary of the fragmentation region is determined by the inner boundary of the gravitationally unstable region.
Export citation and abstract BibTeX RIS
1. Introduction
There are two main theories for giant planet formation: the disk instability model and core accretion model. For a review of both models, see D'Angelo et al. (2010). In this paper, we focus on the disk instability model. According to the disk instability model, a disk that is gravitationally unstable fragments into self-gravitating dense clumps. Then, they contract to become gas giant planets. The formation of planets by the disk instability is constrained by disk fragmentation. The critical issue that might determine viability of the disk instability model is whether a disk can fragment or under what condition a disk can fragment. Extensive studies have been done on finding conditions that might lead to the fragmentation. For a review on this issue, see, e.g., D'Angelo et al. (2010). It is well known that in order for a disk to be gravitationally unstable, the Toomre parameter (Toomre 1964), Q, must satisfy the following condition:
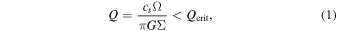
where cs is the local sound speed, Ω is the angular velocity, G is the gravitational constant, and Σ is the surface density. This particular form is for a Keplerian disk. Qcrit is the critical value, which ranges from 1 to 2 (e.g., Armitage 2010). Here we take Qcrit = 1.4.
In order for a disk to fragment, not only must a disk be gravitationally unstable, but also it must cool fast enough. Gammie (2001) studied the nonlinear outcome of gravitational instability in cooling disks by using local, numerical models. In his simulation, cooling is described with a constant cooling time. He considered heating due to dissipation of turbulence. He found that the disk fragments, possibly forming planets, if
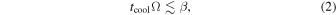
where tcool is the cooling time of the disk and β ∼ 3. Rice et al. (2003) tested whether Gammie's local results are valid globally. They found that for T Tauri disk masses, the fragmentation boundary still appears around 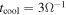 . A similar description of the fragmentation boundary has been found in other simulations (e.g., Rice et al. 2005; Clarke et al. 2007).
. A similar description of the fragmentation boundary has been found in other simulations (e.g., Rice et al. 2005; Clarke et al. 2007).
Along this direction, extensive work has been done on the critical cooling timescales, namely, the value of β in Equation (2) with consideration of mechanical heating. Gammie (2001) found that β ∼ 3 for 2D disks. Rice et al. (2005) investigated the cooling criterion in 3D disks and found that β ∼ 6 when the specific heat ratio γ = 5/3 and β ∼ 12 when γ = 7/5. It is also suggested that the critical cooling timescales may depend on the temperature dependence of the cooling law (Cossins et al. 2010) and the thermal history of disks (Clarke et al. 2007). Meru & Bate (2011) found that the cooling time criterion is not converged with increasing resolution in smoothed particle hydrodynamics simulations. Meru & Bate (2012) suggested that these nonconvergent results are related to artificial viscosity.
Rafikov (2005) critically examined the viability of the disk instability model by using two fragmentation conditions (Equations (1) and (2)). He suggested that these two conditions put strict constraints on the properties of disks that are able to fragment. He found that observational properties of such disks are unusual. His argument puts severe constraints on the disk instability model. Rafikov (2007) also considered convective cooling and demonstrated that fragmentation is unlikely to happen within several tens of au. This is similar to the conclusion of Rafikov (2005).
The simulation of Gammie (2001) is a local one, which shows the conditions under which a disk can fragment but does not tell where the fragmentation conditions can be satisfied and where a disk can fragment. In those global simulations, initial conditions of disks are chosen artificially. The location of the fragmentation region is related to the initial conditions. Extensive work has been done on where fragmentation can happen in the disk by using the criteria of Equations (1) and (2). Rafikov (2009) investigated the properties of gravitationally unstable disks by using a description of the effective viscosity due to gravitational torques. He constructed an analytical model of steady-state disks. He adopted the fragmentation criterion from the local simulation of Gammie (2001) to estimate where the fragmentation criterion can be satisfied in gravitationally unstable disks and where a disk can fragment. His calculation of the cooling time is based on the assumption that the cooling rate equals the dissipation rate of turbulence. The estimate by Rafikov (2009) with β ∼ 1 showed that giant planet formation by disk instability in steady-state disks can occur only at a radius ≳120 au. Clarke (2009) constructed an analytic model for self-gravitating disks with realistic cooling. She also used the Gammie (2001) fragmentation criterion to estimate the fragmentation region and assumed that the cooling rate equals the rate of internal dissipation. The estimate by Clarke (2009) with β ∼ 6 demonstrated that fragmentation can occur at a radius ≳70 au for solar-mass stars when the accretion rate from the progenitor core is less than 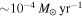 . In their review, Chabrier et al. (2014) suggested that fragmentation of an optically thick disk is unavoidable beyond 60–100 au around a solar-mass star but cannot happen interior to this region. Despite the differences in details of calculations, from numerical and analytical studies, it is generally thought that fragmentation is unlikely in the inner part of a disk, where the cooling time is long. Formation of self-gravitating objects is possible beyond 50–100 au from the star.
. In their review, Chabrier et al. (2014) suggested that fragmentation of an optically thick disk is unavoidable beyond 60–100 au around a solar-mass star but cannot happen interior to this region. Despite the differences in details of calculations, from numerical and analytical studies, it is generally thought that fragmentation is unlikely in the inner part of a disk, where the cooling time is long. Formation of self-gravitating objects is possible beyond 50–100 au from the star.
However, Johnson & Gammie (2003) extended the Gammie (2001) local model with more realistic cooling. They also considered the limit of strong external irradiation. They suggested that when the external irradiation dominates the heating of the disk, it is isothermal. Therefore, they investigated gravitational instability in an isothermal disk. For isothermal disks, instead of fragmentation criterion based on the cooling time, their calculations show that disks fragment if
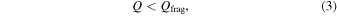
where Qfrag ∼ 1.4.
Extensive work has been done on hydrodynamics simulations of locally isothermal, gravitationally unstable protoplanetary disks. Boss (2000) constructed 3D, hydrodynamical disk models. He assumed the disk to be locally isothermal with 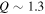 . By "locally isothermal," he means that the radial temperature profile is kept unchanged during the simulations. He found that Jupiter-mass clumps can be formed by disk instability in a disk with the mass in the inferred range for the solar nebula. Nelson et al. (1998) carried out a large set of hydrodynamic simulations of disks around protostars. The disks were assumed to be locally isothermal. Nelson et al. (1998) suggested that the isothermal assumption implies that the central protostar irradiation dominates the heating. They found that disks with
. By "locally isothermal," he means that the radial temperature profile is kept unchanged during the simulations. He found that Jupiter-mass clumps can be formed by disk instability in a disk with the mass in the inferred range for the solar nebula. Nelson et al. (1998) carried out a large set of hydrodynamic simulations of disks around protostars. The disks were assumed to be locally isothermal. Nelson et al. (1998) suggested that the isothermal assumption implies that the central protostar irradiation dominates the heating. They found that disks with  fragment into protobinary or protoplanetary clumps. Mayer et al. (2004) also presented a series of high-resolution, smoothed particle hydrodynamics simulations of gravitational instability in protoplanetary disks. They considered locally isothermal disks. They found that disks evolved isothermally fragment for
fragment into protobinary or protoplanetary clumps. Mayer et al. (2004) also presented a series of high-resolution, smoothed particle hydrodynamics simulations of gravitational instability in protoplanetary disks. They considered locally isothermal disks. They found that disks evolved isothermally fragment for  .
.
Rafikov (2009) and Clarke (2009) did not consider the fragmentation criterion for locally isothermal disks found by Johnson & Gammie (2003) and other authors. In this paper, we extend the work of Rafikov (2009) and Clarke (2009) in the following ways. (1) In addition to Gammie's (2001) fragmentation criterion, Johnson & Gammie's (2003) criterion is also considered. (2) For our analytical disk model, we consider a more realistic protostar irradiation and the background irradiation. (3) In calculating the cooling rate, we also consider the possible effects of contributions of protostar irradiation and background irradiation to the disk surface temperature. (4) In addition to the analytical disk model, we also use an evolutionary numerical model of protoplanetary disks to investigate where and when a disk can fragment.
In this paper, we show that most of the fragmentation region is isothermal. In particular, the fragmentation region found in previous studies is contained in the isothermal region of a disk. Therefore, the fragmentation criterion (Equation (3)), instead of the cooling time criterion (Equation (2)), is applicable. The constraint on the disk instability model caused by the cooling time criterion should be relieved. This improves the viability of the disk instability model. When the isothermal region is considered, by using Equation (3), the inner boundary of the fragmentation region is extended inward to ∼20 au. We also show that a disk tends to be isothermal in the region where the cooling time criterion is satisfied. We also consider the contributions of external irradiation (protostar irradiation and background irradiation) to the disk surface temperature in addition to the internal dissipation. The disk surface temperature is enhanced. If these contributions can be included in the cooling rate, the cooling rate is enhanced. In this way, the fragmentation region defined by Equations (1) and (2) can also be extended inward to ∼26 au.
In Section 2, we construct an analytical model of gravitationally unstable protoplanetary disks consisting of three regions: the inner region where the internal dissipation dominates the heating, the intermediate region where the central protostar irradiation dominates, and the outer region where the background irradiation dominates. We use this analytical model to calculate the cooling time and find out the location and the size of the isothermal region. Thus, we can show our points analytically. To illustrate our points with numerical calculations, we use the evolutionary disk model, which is an improved version of Jin & Sui (2010) and Jin & Li (2014). In Section 3, we review the basic ingredients of the Jin and Sui disk model and describe our improvements to the model. In Section 4, we present our numerical results and show our points numerically. Discussions and conclusions are presented in Section 5.
2. An Analytical Model of Gravitationally Unstable Protoplanetary Disks and Its Application to the Disk Instability Model for Giant Planet Formation
In this section, we discuss analytically the structure of a gravitationally unstable protoplanetary disk consisting of three regions: the inner region where the internal dissipation dominates the heating, the intermediate region where the central protostar irradiation dominates, and the outer region where the background irradiation dominates. By investigating the structure of an unstable disk, we can find out the location and the size of the isothermal region. Particularly, we want to calculate the radius at which the transition from the internal dissipation region to the protostar irradiation region occurs. This radius determines the location and the size of the isothermal region. Then, we can show that the isothermal region of a disk contains the region where the cooling time criterion is satisfied. In particular, we demonstrate that the fragmentation region found in previous studies is contained in the isothermal region of a disk. We also show that the outer part of a disk becomes isothermal owing to the irradiation from the central protostar, rather than being optically thin.
The evolution of self-gravitating disks has been investigated extensively (e.g., Rice et al. 2003; Lodato & Rice 2004; Mejía et al. 2005; Durisen et al. 2007), and it is thought that such disks settle into a state with constant Q near Qcrit, in which the cooling and heating balance. A disk develops spiral structure when 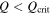 . The spiral structure produces disk torques that transport angular momentum and mass and provides a heat source in the unstable region. Therefore, spiral arms can stabilize the disk by raising the sound speed and spreading mass. If Q increases significantly above Qcrit, the spiral structure shuts off, the disk cools, and the spiral structure develops again. Thus, the disk reaches a state of self-regulation where Q maintains a constant near Qcrit.
. The spiral structure produces disk torques that transport angular momentum and mass and provides a heat source in the unstable region. Therefore, spiral arms can stabilize the disk by raising the sound speed and spreading mass. If Q increases significantly above Qcrit, the spiral structure shuts off, the disk cools, and the spiral structure develops again. Thus, the disk reaches a state of self-regulation where Q maintains a constant near Qcrit.
In addition to the above argument from previous studies (e.g., Clarke 2009; Armitage 2010; Helled et al. 2014), we wish to mention the following. According to Kratter et al. (2008), the effective gravitational viscosity, αGI, is a sensitive function of Q in the gravitationally unstable region. A slight decrease in Q results in a significant increase in αGI and a decrease in Σ. This leads to the increase in Q. This self-regulating process can maintain a constant Q. In particular, this process might operate to maintain a constant Q in the external-irradiation-dominated region, where the sound speed is controlled by the irradiation.
Several authors (e.g., Clarke 2009; Rafikov 2009; Rice et al. 2010) have studied the properties of self-gravitating disks with constant Q. They assumed that a disk is irradiated by external irradiation at a constant temperature. Here we specify the central protostar irradiation and the background irradiation. By doing that, we can clarify some issues that have not been clarified and get a definite picture of the disk structure. This disk structure can be compared with our numerical model. We use this disk model to establish our points analytically.
For a gravitationally unstable disk in which Q is a constant, Q0, from Equation (1), Σ can be expressed as

where we have used
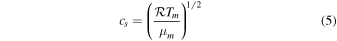
and
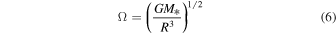
for a Keplerian disk, where 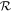 is the gas constant, Tm is the midplane temperature,
is the gas constant, Tm is the midplane temperature, 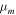 is the mean molecular weight, M* is the central protostar mass, and R is the cylindrical radius of the disk. We adopt
is the mean molecular weight, M* is the central protostar mass, and R is the cylindrical radius of the disk. We adopt 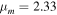 .
.
The internal dissipation rate per unit area is
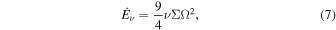
where ν is the kinematic viscosity. We can express the irradiation from the protostar by an effective temperature (Ruden & Pollack 1991),
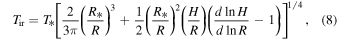
where R* is the protostar radius, T* is its effective temperature, and H is the half-thickness of the disk. We adopt 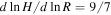 (Chiang & Goldreich 1997; Hueso & Guillot 2005). In the region where the protostar irradiation dominates,
(Chiang & Goldreich 1997; Hueso & Guillot 2005). In the region where the protostar irradiation dominates, 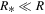 , and the first term in the above equation can be neglected. By using
, and the first term in the above equation can be neglected. By using 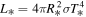 , where L* is the total luminosity of the protostar and σ is the Stefan–Boltzmann constant, Equation (8) can be manipulated into
, where L* is the total luminosity of the protostar and σ is the Stefan–Boltzmann constant, Equation (8) can be manipulated into

We employ Equation (5) of Zhu et al. (2010),
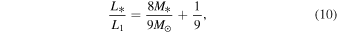
to express L* as a function of the protostar mass, M*, where L1 is the protostar luminosity with M* = 1 M☉. We use 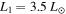 (e.g., Kenyon & Hartmann 1995) as the fiducial value. The background irradiation can be written as
(e.g., Kenyon & Hartmann 1995) as the fiducial value. The background irradiation can be written as 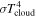 , where Tcloud is the cloud temperature.
, where Tcloud is the cloud temperature.
Assuming the balance of heating and cooling and using the radiative diffusion approximation, we have the midplane temperature,
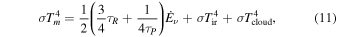
for both optically thin and thick cases (e.g., Nakamoto & Nakagawa 1994), where 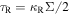 and
and 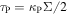 are the Rosseland and the Planck mean optical depths to the disk midplane, respectively, where
are the Rosseland and the Planck mean optical depths to the disk midplane, respectively, where 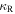 and
and 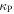 are the Rosseland and Planck mean opacities, respectively.
are the Rosseland and Planck mean opacities, respectively.
2.1. The Outer Region Heated by the Background Irradiation
Because both the internal dissipation and the central protostar irradiation decrease with radius, the background irradiation from the molecular cloud can dominate heating if a disk can extend to the large radius. The internal dissipation is strong at small radius and declines with radius more steeply than the protostar irradiation (see solutions below). Equation (11) allows us to distinguish the three regions. In the outer region where the background irradiation dominates,
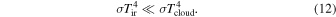
The disk temperature is determined by the background cloud temperature (e.g., Nakamoto & Nakagawa 1994; Jin & Sui 2010). In this case, the disk midplane temperature, Tm, is Tcloud. From Equation (4), we get
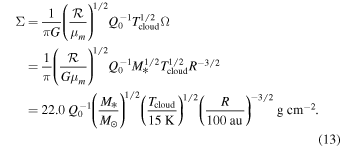
By using  (Pringle 1981), we obtain
(Pringle 1981), we obtain

2.2. The Intermediate Region Heated by the Central Protostar Irradiation
In the intermediate region where the central protostar irradiation dominates, the protostar irradiation controls the midplane temperature and the inequalities,
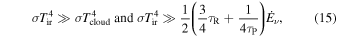
are satisfied. In this case, Tm equals  . From Equations (9) and (10), we get
. From Equations (9) and (10), we get
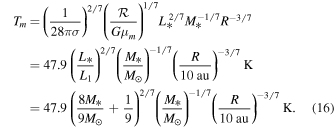
From Equation (4), we find
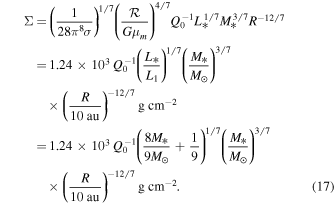
In this region, H/R can be expressed as
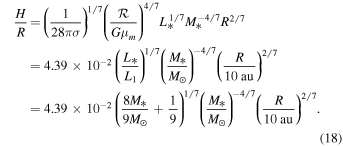
From Equation (9), we know that 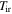 is a decreasing function of radius. The radius, Rio, at which the transition from the intermediate region to the outer region occurs can be obtained by equating Tcloud to Tm given by Equation (16). The transition radius is
is a decreasing function of radius. The radius, Rio, at which the transition from the intermediate region to the outer region occurs can be obtained by equating Tcloud to Tm given by Equation (16). The transition radius is
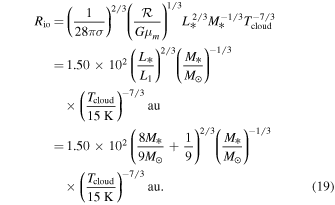
Taking the fiducial values, 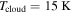 and M* = 1 M☉, we get
and M* = 1 M☉, we get 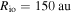 .
.
2.3. The Inner Region Heated by the Internal Dissipation
In the inner region where internal dissipation dominates, the inequality,
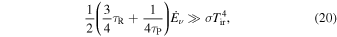
is satisfied and the internal dissipation controls the midplane temperature. We have
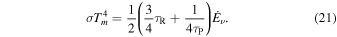
This region is optically thick. We will confirm this after we get the solution. Therefore, Equation (21) becomes
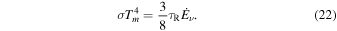
With the aid of Equation (7), we find
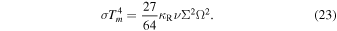
In a steady-state disk, the accretion rate, 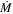 , is a constant and (Pringle 1981)
, is a constant and (Pringle 1981)
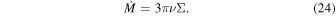
If 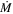 changes with radius slowly, the above equation can be used as an approximation. For our analytical estimate, we assume that this equation is valid. As long as
changes with radius slowly, the above equation can be used as an approximation. For our analytical estimate, we assume that this equation is valid. As long as 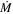 is known, Σ can be determined. Using Equation (24), Equation (23) can be written as
is known, Σ can be determined. Using Equation (24), Equation (23) can be written as

In this paper, we are interested in the transition radius between the inner region and the intermediate region because this radius determines the boundary of the isothermal region. Near this radius, the temperature is low. At 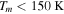 , the opacity can be expressed as
, the opacity can be expressed as
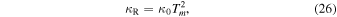
where 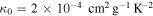 (Bell & Lin 1994; Semenov et al. 2003). Inserting this
(Bell & Lin 1994; Semenov et al. 2003). Inserting this 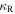 into Equation (25), we have
into Equation (25), we have
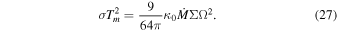
Combining Equations (4) and (27), we obtain
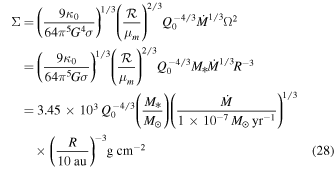
and

We can also get
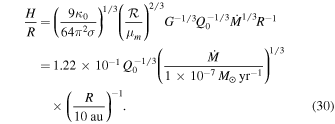
2.4. The Location of the Isothermal Region of a Disk
The radius, Rii, at which the transition from the inner region to the intermediate region occurs can be obtained by equating Tm given by Equations (16) and (29). The transition radius is
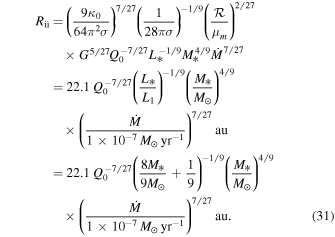
A disk becomes isothermal at 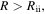 since the protostar irradiation dominates the heating at
since the protostar irradiation dominates the heating at 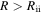 . Taking the fiducial values, Q0 = 1, M* = 1 M☉, and
. Taking the fiducial values, Q0 = 1, M* = 1 M☉, and 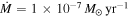 , we find
, we find 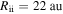 . This analytical estimate suggests that a disk becomes isothermal owing to the protostar irradiation at R ≳ 20 au, approximately. The isothermal region of a disk is large.
. This analytical estimate suggests that a disk becomes isothermal owing to the protostar irradiation at R ≳ 20 au, approximately. The isothermal region of a disk is large.
From Equation (29), the midplane temperature at Rii can be written as
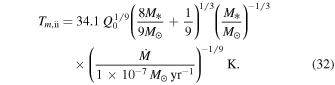
Taking Q0 = 1, M* = 1 M☉, and 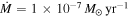 , we get
, we get 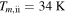 . The temperature is below
. The temperature is below 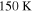 . This justifies the usage of
. This justifies the usage of 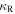 in Equation (26) near the transition radius, Rii.
in Equation (26) near the transition radius, Rii.
Combining Equations (26), (28), and (29), the optical depth in the inner region can be calculated as

Using Equation (31), the optical depth at the transition radius, Rii, can be expressed as
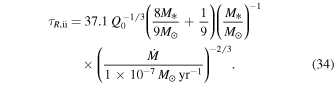
Taking the fiducial values, Q0 = 1, M* = 1 M☉, and 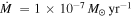 , we find
, we find 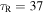 at Rii. Since
at Rii. Since 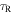 decreases with R, this estimate confirms our early assumption that the disk is optically thick in the inner region.
decreases with R, this estimate confirms our early assumption that the disk is optically thick in the inner region.
Combining Equations (26), (16), and (17), the optical depth in the intermediate region can be written as
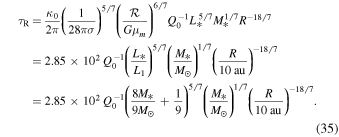
The radius, Rτ, at which the transition from the optically thick region to thin region occurs can be obtained by setting τR = 1. We find
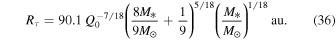
Taking the fiducial values, Q0 = 1, M* = 1 M☉, and 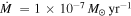 , we get Rτ = 90 au. By comparing this radius with Rii in Equation (31), we find that the outer part of a disk becomes isothermal owing to the irradiation from the central protostar, rather than being optically thin. We also note that the fiducial value of Rτ is less than the fiducial value of Rio (see Equation (19)). This means that the transition from the optically thick region to thin region occurs in the intermediate region.
, we get Rτ = 90 au. By comparing this radius with Rii in Equation (31), we find that the outer part of a disk becomes isothermal owing to the irradiation from the central protostar, rather than being optically thin. We also note that the fiducial value of Rτ is less than the fiducial value of Rio (see Equation (19)). This means that the transition from the optically thick region to thin region occurs in the intermediate region.
2.5. The Cooling Time Criterion
In the isothermal region, namely, at 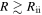 , only the criterion of Equation (3) needs to be satisfied for fragmentation to occur. Therefore, we need to consider the cooling time criterion only in the inner region where the internal dissipation dominates. The cooling time can be expressed as
, only the criterion of Equation (3) needs to be satisfied for fragmentation to occur. Therefore, we need to consider the cooling time criterion only in the inner region where the internal dissipation dominates. The cooling time can be expressed as

where Λ is the cooling function and U is the internal energy per unit area. The internal energy can be written as
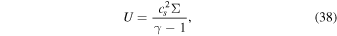
where γ is the adiabatic index, where γ = 5/3 is used. When the internal dissipation dominates, the cooling function can be calculated as (e.g., Armitage 2010)
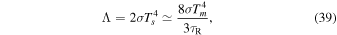
where Ts is the disk surface temperature. Using 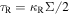 and combining Equations (5), (26), (37), (38), and (39), we get
and combining Equations (5), (26), (37), (38), and (39), we get
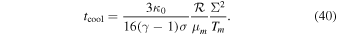
Using Equation (4), we find
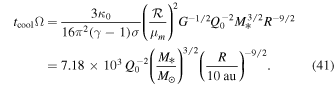
At R = Rii, tcoolΩ is
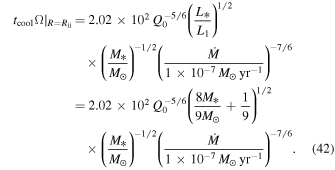
Taking the fiducial values, Q0 = 1, M* = 1 M☉, and 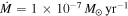 , tcoolΩ at Rii is ∼200. Therefore, the criterion, Equation (2), is not satisfied at R = Rii. Since tcoolΩ decreases with radius (see Equation (41)), the cooling time criterion can be satisfied at a radius that is greater than Rii. This estimate indicates that a disk already becomes isothermal in the region where the cooling time criterion is satisfied. Alternatively, this can be explained as follows. We define a radius, Rcooling, at which
, tcoolΩ at Rii is ∼200. Therefore, the criterion, Equation (2), is not satisfied at R = Rii. Since tcoolΩ decreases with radius (see Equation (41)), the cooling time criterion can be satisfied at a radius that is greater than Rii. This estimate indicates that a disk already becomes isothermal in the region where the cooling time criterion is satisfied. Alternatively, this can be explained as follows. We define a radius, Rcooling, at which 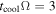 . Namely, the cooling time criterion, Equation (2), can be satisfied at
. Namely, the cooling time criterion, Equation (2), can be satisfied at 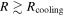 . If we assume that the internal dissipation region extends to Rcooling (this assumption has been used in previous studies), we find
. If we assume that the internal dissipation region extends to Rcooling (this assumption has been used in previous studies), we find
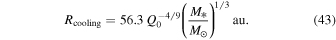
Taking the fiducial values, Q0 = 1 and M* = 1 M☉, the cooling time criterion can be satisfied at R ≳ 56 au. This radius is greater than Rii. This suggests that the region where the cooling time criterion is satisfied is contained in the isothermal region.
2.6. The Location of the Self-gravitating Region of a Disk
If we employ the alpha prescription of the viscosity (Shakura & Sunyaev 1973), ν can be written as (Pringle 1981)
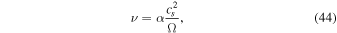
where α is a dimensionless parameter. Previous studies (Levin 2007; Armitage 2011) have suggested that the α value that parameterizes viscous dissipation due to self-gravity in the internal dissipation region can be expressed as
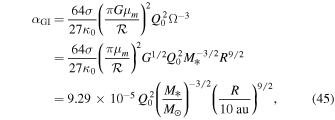
with κ described in Equation (26). This αGI decreases as R decreases. Armitage (2011) suggested that the value of αGI is low at small radii and transport by other mechanisms will render the disk stable against self-gravity. The radius at which other mechanisms generate the same stresses as αGI can be considered as the inner boundary of the self-gravitating region. From Equation (45), the radius of the inner boundary, RQ, is given by
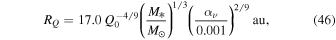
where αν is the viscosity due to the other mechanisms. A disk is gravitationally unstable at 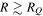 . These other mechanisms could be magnetorotational instability or some hydrodynamic effects. The magnetorotational instability might not be efficient at this radius. We take
. These other mechanisms could be magnetorotational instability or some hydrodynamic effects. The magnetorotational instability might not be efficient at this radius. We take  as the fiducial value. We find RQ = 17 au with Q0 = 1 and M* = 1 M☉.
as the fiducial value. We find RQ = 17 au with Q0 = 1 and M* = 1 M☉.
If we use Equations (1) and (2) as the fragmentation criterion, the fragmentation region where both Equations (1) and (2) are satisfied is located at 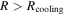 . Since
. Since  and the disk becomes isothermal at
and the disk becomes isothermal at 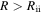 , the fragmentation region defined by Equations (1) and (2) is in the isothermal region. We also note that the radii of the inner boundary of the fragmentation region found in previous studies (see Section 1) are comparable to Rcooling and are greater than Rii. Therefore, the fragmentation region found in previous studies is in the isothermal region of a disk. In this case, fragmentation criterion (Equation (3)), instead of the cooling time criterion (Equation (2)), is applicable. The constraint on the disk instability model caused by the cooling time criterion should be relieved. By using Equation (3), the fragmentation region is located at
, the fragmentation region defined by Equations (1) and (2) is in the isothermal region. We also note that the radii of the inner boundary of the fragmentation region found in previous studies (see Section 1) are comparable to Rcooling and are greater than Rii. Therefore, the fragmentation region found in previous studies is in the isothermal region of a disk. In this case, fragmentation criterion (Equation (3)), instead of the cooling time criterion (Equation (2)), is applicable. The constraint on the disk instability model caused by the cooling time criterion should be relieved. By using Equation (3), the fragmentation region is located at 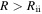 . The fragmentation region is extended from Rcooling to Rii when the isothermal region is considered.
. The fragmentation region is extended from Rcooling to Rii when the isothermal region is considered.
3. Numerical Model of Protoplanetary Disks
To illustrate our points with numerical calculations, we use the disk model, which is an improved version of Jin & Sui (2010) and Jin & Li (2014). Here we review the basic ingredients of the Jin and Sui model and describe our improvements to the model. According to the star formation theory, a star forms from the gravitational collapse of a molecular cloud core. Observations have shown us that a core rotates slowly and almost rigidly with an angular velocity ω (Goodman et al. 1993; Caselli et al. 2002). Due to the conservation of the angular momentum, a protostar+disk system forms. The mass accretion rate from the core to the protostar+disk system is (Shu 1977)
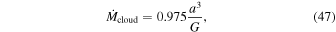
where a is the isothermal sound speed in the core. Following Cassen & Moosman (1981), Nakamoto & Nakagawa (1994) derived the mass influx onto the disk surface, 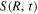 , as a function of R and time t. We use the mass influx of Nakamoto & Nakagawa (1994), which is
, as a function of R and time t. We use the mass influx of Nakamoto & Nakagawa (1994), which is
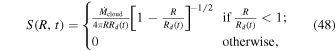
where Rd(t) is the centrifugal radius given by
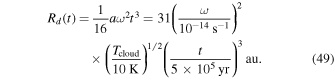
The beginning of the collapse of the cloud core is taken to be t = 0. The properties of a cloud core can be described by the temperature Tcloud, the core mass 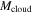 , and the angular velocity ω (e.g., Shu 1977). Observationally, Tcloud ranges from 7 to
, and the angular velocity ω (e.g., Shu 1977). Observationally, Tcloud ranges from 7 to 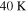 , with
, with 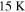 as the median (Jijina et al. 1999), and ω ranges from
as the median (Jijina et al. 1999), and ω ranges from 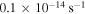 to
to 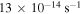 , with
, with 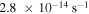 as the median (Goodman et al. 1993; Caselli et al. 2002). The core mass is correlated with the host star mass. The host star mass ranges from 0.1 to 3 M☉, with 1 M☉ as the median.
as the median (Goodman et al. 1993; Caselli et al. 2002). The core mass is correlated with the host star mass. The host star mass ranges from 0.1 to 3 M☉, with 1 M☉ as the median.
The disk model is a time evolution model of surface density with inclusion of the mass influx onto the disk from the collapse. Both the protostar and the disk start with zero mass. The protostar gains mass from both the collapse and the accretion from the disk. The surface density evolution of a disk is described by (Jin & Sui 2010)
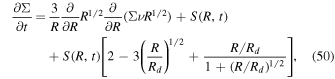
where the third term on the right-hand side is due to the difference in the specific angular momentum between the material in the disk and the infall material.
To solve Equation (50), we use the viscosity expression of Equation (44). When calculating viscosity, we consider the effects of gravitational instability and magnetorotational instability, and α is given by
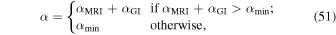
where αMRI is the viscosity due to the magnetorotational instability, αGI is the effective viscosity of gravitational instability, and αmin is the minimum of the viscosity value in the region where 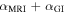 is very low. αmin could be due to some hydrodynamic effects. Here we use
is very low. αmin could be due to some hydrodynamic effects. Here we use 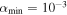 . For αMRI, we use the numerical results of Fleming & Stone (2003). One of the improvements to the disk model of Jin & Sui (2010) is that we adopt αGI of Kratter et al. (2008), which is given by
. For αMRI, we use the numerical results of Fleming & Stone (2003). One of the improvements to the disk model of Jin & Sui (2010) is that we adopt αGI of Kratter et al. (2008), which is given by
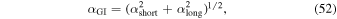
where
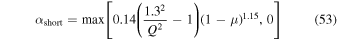
and
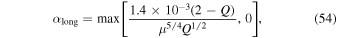
where μ is the ratio of the total disk mass to the total mass of the protostar+disk system. When calculating αGI, 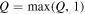 according to Kratter et al. (2008).
according to Kratter et al. (2008).
In our numerical disk model, the temperature is calculated by using Equation (11). In the calculation of 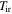 , Jin & Sui (2010) used a constant protostar luminosity. Another improvement to the disk model of Jin & Sui (2010) is that we consider the protostar luminosity as a function of the protostar mass since the protostar mass changes during the disk evolution. Namely, we use Equation (10). In the next section, we use this disk model to confirm numerically our results that we find in Section 2 analytically.
, Jin & Sui (2010) used a constant protostar luminosity. Another improvement to the disk model of Jin & Sui (2010) is that we consider the protostar luminosity as a function of the protostar mass since the protostar mass changes during the disk evolution. Namely, we use Equation (10). In the next section, we use this disk model to confirm numerically our results that we find in Section 2 analytically.
4. Numerical Results
We consider the prototype: the structure of a protoplanetary disk with 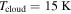 ,
,  , and
, and 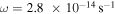 at
at  . Contributions of internal dissipation, protostar irradiation, and background irradiation to
. Contributions of internal dissipation, protostar irradiation, and background irradiation to  as a function of radius (see Equation (11)) are plotted in Figure 1. The internal dissipation declines with radius more steeply than the protostar irradiation. From Figure 1, we find Rii = 20 au and Rio = 145 au. Namely, at R > 20 au, the protostar irradiation dominates the internal dissipation and the disk becomes isothermal. We mention that the pattern of the contributions to
as a function of radius (see Equation (11)) are plotted in Figure 1. The internal dissipation declines with radius more steeply than the protostar irradiation. From Figure 1, we find Rii = 20 au and Rio = 145 au. Namely, at R > 20 au, the protostar irradiation dominates the internal dissipation and the disk becomes isothermal. We mention that the pattern of the contributions to 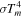 at different times is similar to Figure 1.
at different times is similar to Figure 1.
Figure 1. Contributions of internal dissipation, protostar irradiation, and background irradiation to 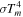 as a function of radius (see Equation (11)) in a protoplanetary disk with
as a function of radius (see Equation (11)) in a protoplanetary disk with  ,
, 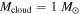 , and
, and 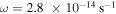 at
at 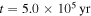 . The solid, dashed, and dotted lines represent the contributions of internal dissipation, protostar irradiation, and background irradiation to
. The solid, dashed, and dotted lines represent the contributions of internal dissipation, protostar irradiation, and background irradiation to 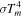 , respectively. The beginning of the collapse of the cloud core is taken to be t = 0.
, respectively. The beginning of the collapse of the cloud core is taken to be t = 0.
Download figure:
Standard image High-resolution imageThe radial dependences of Q, tcoolΩ, 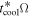 , and
, and 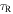 are shown in Figure 2. They are all dimensionless. tcoolΩ is calculated by using Equation (41) in Section 2. From Figure 2, we find Rcooling = 44 au. We note that the radii of the inner boundary of the fragmentation region found in previous studies (see Section 1) are comparable to Rcooling and the calculations of these radii are similar to the calculation of Rcooling. For comparison, we use Rcooling as a representative of previous calculations. The calculation of the cooling time,
are shown in Figure 2. They are all dimensionless. tcoolΩ is calculated by using Equation (41) in Section 2. From Figure 2, we find Rcooling = 44 au. We note that the radii of the inner boundary of the fragmentation region found in previous studies (see Section 1) are comparable to Rcooling and the calculations of these radii are similar to the calculation of Rcooling. For comparison, we use Rcooling as a representative of previous calculations. The calculation of the cooling time, 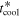 , is different from Equation (41). For
, is different from Equation (41). For 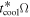 , in calculating the cooling rate,
, in calculating the cooling rate, 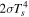 , we include contributions of protostar irradiation and background irradiation to the disk surface temperature in addition to the internal dissipation. If the heating is balanced by radiative losses from both surfaces of the disk,
, we include contributions of protostar irradiation and background irradiation to the disk surface temperature in addition to the internal dissipation. If the heating is balanced by radiative losses from both surfaces of the disk, 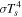 can be written as (Nakamoto & Nakagawa 1994; Hueso & Guillot 2005; Jin & Sui 2010)
can be written as (Nakamoto & Nakagawa 1994; Hueso & Guillot 2005; Jin & Sui 2010)
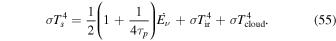
The first, second, and third terms on the right-hand side represent the contributions of internal dissipation, protostar irradiation, and background irradiation and dominate in the inner, intermediate, and outer regions, respectively. Particularly, in the intermediate region where protostar irradiation dominates, the disk surface temperature and the cooling rate are enhanced by including the protostar irradiation. In the inner region, this enhancement is negligible. We can also define a radius, 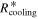 , at which
, at which 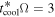 . If we use
. If we use 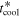 as the cooling time, the cooling time criterion, Equation (2), can be satisfied at
as the cooling time, the cooling time criterion, Equation (2), can be satisfied at 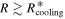 . From Figure 2, we find
. From Figure 2, we find 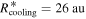 . Due to the enhancement of the cooling rate mentioned above,
. Due to the enhancement of the cooling rate mentioned above, 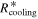 found from Figure 2 is less than Rcooling. By including the contributions of the external irradiation to the disk surface temperature, the region where the cooling time criterion can be satisfied is extended inward from 44 to 26 au. This extension is mainly due to the protostar irradiation because the protostar irradiation is stronger than the background irradiation in the intermediate region. We note that
found from Figure 2 is less than Rcooling. By including the contributions of the external irradiation to the disk surface temperature, the region where the cooling time criterion can be satisfied is extended inward from 44 to 26 au. This extension is mainly due to the protostar irradiation because the protostar irradiation is stronger than the background irradiation in the intermediate region. We note that 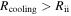 and
and 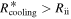 . Hence, we confirm the conclusion in Section 2 that the region where the cooling time criterion is satisfied is contained in the isothermal region.
. Hence, we confirm the conclusion in Section 2 that the region where the cooling time criterion is satisfied is contained in the isothermal region.
Figure 2. Radial dependences of Q, tcoolΩ, 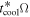 , and
, and 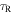 in a protoplanetary disk with
in a protoplanetary disk with 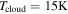 ,
, 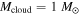 , and
, and  at
at  . The solid, dashed, dot-dashed, and dotted lines represent Q, tcoolΩ,
. The solid, dashed, dot-dashed, and dotted lines represent Q, tcoolΩ, 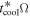 , and
, and 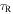 , respectively. For the definition of
, respectively. For the definition of 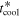 , see text.
, see text.
Download figure:
Standard image High-resolution imageFrom Figure 2, we find Rτ = 68 au. Namely, at R > 68 au, τR is less than 1 and the disk becomes optically thin. Comparing Rτ with Rii, we confirm the conclusion in Section 2 that the outer part of a disk becomes isothermal owing to the irradiation from the central protostar, rather than being optically thin. We note that Rτ is less than Rio. This confirms the result in Section 2 that the transition from the optically thick region to thin region occurs in the intermediate region.
From Figure 2, we find RQ = 16 au. We confirm the conclusion of previous studies (e.g., Rice et al. 2003; Lodato & Rice 2004; Mejía et al. 2005; Durisen et al. 2007) that Q is nearly a constant in the gravitationally unstable region. We wish to mention that there is also an outer boundary of the gravitationally unstable region, Rout. This is explained as follows. By considering only viscous heating and constant α, Ruden & Lin (1986) showed that 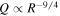 . This suggests that Q decreases with R at
. This suggests that Q decreases with R at 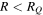 , where the viscous heating dominates. But in the outer part of a disk, where either the protostar irradiation or the background irradiation dominates the heating, Tm decreases slowly with R and also Σ decreases more steeply than in the inner region (e.g., Kratter et al. 2010; Jin & Li 2014), so that Q will increase with R (see Equation (1)). Therefore, there is a radius, Rout, beyond which Q is greater than Qcrit. For Figure 2, Rout = 90 au.
, where the viscous heating dominates. But in the outer part of a disk, where either the protostar irradiation or the background irradiation dominates the heating, Tm decreases slowly with R and also Σ decreases more steeply than in the inner region (e.g., Kratter et al. 2010; Jin & Li 2014), so that Q will increase with R (see Equation (1)). Therefore, there is a radius, Rout, beyond which Q is greater than Qcrit. For Figure 2, Rout = 90 au.
If we use Equations (1) and (2) as the fragmentation criterion and tcool as the cooling time, the fragmentation region is located between Rcooling = 44 au and Rout = 90 au. Since 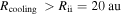 and the disk becomes isothermal at
and the disk becomes isothermal at 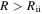 , the fragmentation region defined by Equations (1) and (2) is in the isothermal region. This is one of the results that we find in Section 2. From previous studies (see Section 1), the radius of the inner boundary of the fragmentation region is >50 au. This radius is comparable to Rcooling and greater than Rii. We numerically confirm one of the results of Section 2 that the fragmentation region found in previous studies is in the isothermal region of a disk. In this case, the fragmentation criterion (Equation (3)), instead of the cooling time criterion (Equation (2)), is applicable. Therefore, the constraint on the disk instability model caused by the cooling time criterion should be relieved. By using Equation (3), the fragmentation region is located between
, the fragmentation region defined by Equations (1) and (2) is in the isothermal region. This is one of the results that we find in Section 2. From previous studies (see Section 1), the radius of the inner boundary of the fragmentation region is >50 au. This radius is comparable to Rcooling and greater than Rii. We numerically confirm one of the results of Section 2 that the fragmentation region found in previous studies is in the isothermal region of a disk. In this case, the fragmentation criterion (Equation (3)), instead of the cooling time criterion (Equation (2)), is applicable. Therefore, the constraint on the disk instability model caused by the cooling time criterion should be relieved. By using Equation (3), the fragmentation region is located between 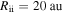 and
and 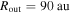 . The inner boundary of the fragmentation region is extended inward to
. The inner boundary of the fragmentation region is extended inward to 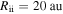 when the isothermal region is considered.
when the isothermal region is considered.
We plot time evolution of RQ, Rout, Rii, Rcooling, and 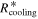 in a protoplanetary disk with
in a protoplanetary disk with 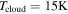 ,
, 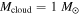 , and
, and  in Figure 3. We also plot a line of 50 au, which represents the minimum radius of the inner boundary of the fragmentation region found in the previous studies. For comparison, we use Rcooling and 50 au as representative radii of the inner boundary from previous studies. Because of the inside-out collapse of a cloud core (Shu 1977), the inner part of the disk forms first and then the disk expands outward (e.g., Jin & Li 2014). Before the mass influx from the collapse stops, both the disk mass and Σ increase because of the existence of the mass supply from the cloud core. Hence, Q decreases (see Equation (1)). The gravitationally unstable region (between RQ and Rout) expands (the disk gains enough mass to be unstable at
in Figure 3. We also plot a line of 50 au, which represents the minimum radius of the inner boundary of the fragmentation region found in the previous studies. For comparison, we use Rcooling and 50 au as representative radii of the inner boundary from previous studies. Because of the inside-out collapse of a cloud core (Shu 1977), the inner part of the disk forms first and then the disk expands outward (e.g., Jin & Li 2014). Before the mass influx from the collapse stops, both the disk mass and Σ increase because of the existence of the mass supply from the cloud core. Hence, Q decreases (see Equation (1)). The gravitationally unstable region (between RQ and Rout) expands (the disk gains enough mass to be unstable at 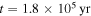 ). Namely, Rout increases and RQ decreases. During this time, Rout is limited by the disk edge. Rout reaches its maximum at the time when the mass influx stops (
). Namely, Rout increases and RQ decreases. During this time, Rout is limited by the disk edge. Rout reaches its maximum at the time when the mass influx stops (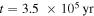 ). After
). After 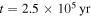 , the inner disk is in steady state because the mass supply offsets the loss due to the accretion onto the protostar and provides mass for the disk expansion (e.g., Jin & Li 2014). Therefore, RQ is roughly a constant. After the mass influx stops, Σ decreases owing to the mass accretion onto the protostar and the mass spreading in the disk by viscosity, so Q increases. The gravitationally unstable region shrinks until it disappears. Namely, Rout decreases and RQ increases. The disk becomes stable at
, the inner disk is in steady state because the mass supply offsets the loss due to the accretion onto the protostar and provides mass for the disk expansion (e.g., Jin & Li 2014). Therefore, RQ is roughly a constant. After the mass influx stops, Σ decreases owing to the mass accretion onto the protostar and the mass spreading in the disk by viscosity, so Q increases. The gravitationally unstable region shrinks until it disappears. Namely, Rout decreases and RQ increases. The disk becomes stable at 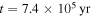 .
.
Figure 3. Time evolution of RQ, Rout, Rii, Rcooling, and 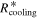 in a protoplanetary disk with
in a protoplanetary disk with 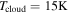 ,
, 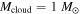 , and
, and 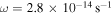 . The solid, dotted-dashed, long-dashed, short-dashed, and dotted lines represent RQ, Rout, Rii, Rcooling, and
. The solid, dotted-dashed, long-dashed, short-dashed, and dotted lines represent RQ, Rout, Rii, Rcooling, and 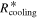 , respectively. The horizontal dotted line represents 50 au, the minimum radius of the inner boundary of the fragmentation region found in the previous studies.
, respectively. The horizontal dotted line represents 50 au, the minimum radius of the inner boundary of the fragmentation region found in the previous studies.
Download figure:
Standard image High-resolution imageAs explained above, the disk expands outward before the mass influx stops. Rii and 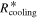 increase with the disk expansion and reach their maxima at the time when the influx stops. After the influx stops, Σ decreases. As mentioned in Section 2, αGI is a sensitive function of Q, and a small decrease in Σ results in a significant decrease in αGI in the gravitationally unstable region. As Σ decreases, the disk adjusts to the decrease in αGI. Σ in the unstable region decreases slowly. Also, Tm and Ts change slowly in the region where the protostar irradiation dominates the heating. Therefore, the cooling time,
increase with the disk expansion and reach their maxima at the time when the influx stops. After the influx stops, Σ decreases. As mentioned in Section 2, αGI is a sensitive function of Q, and a small decrease in Σ results in a significant decrease in αGI in the gravitationally unstable region. As Σ decreases, the disk adjusts to the decrease in αGI. Σ in the unstable region decreases slowly. Also, Tm and Ts change slowly in the region where the protostar irradiation dominates the heating. Therefore, the cooling time, 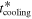 , changes slowly, and
, changes slowly, and 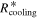 is almost a constant. The internal dissipation is a function of α, Σ, and Tm. Since α decreases significantly, the internal dissipation decreases significantly. Hence, Rii decreases. We also note that Rcooling increases as M* increases (Equation (43)).
is almost a constant. The internal dissipation is a function of α, Σ, and Tm. Since α decreases significantly, the internal dissipation decreases significantly. Hence, Rii decreases. We also note that Rcooling increases as M* increases (Equation (43)).
From Figure 3, we find that 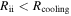 ,
, 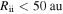 ,
, 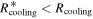 , and
, and 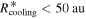 during the disk evolution. The following conclusions are valid throughout the disk evolution: (1) The fragmentation region found in previous studies is in the isothermal region of a disk. (2) When the isothermal region is considered, by using Equation (3), the inner boundary of the fragmentation region is extended inward to ∼20 au. (3) If the contribution of the protostar irradiation to the disk surface temperature can be included in the cooling rate, the region where the cooling time criterion can be satisfied is extended inward to ∼26 au. Note that the gravitationally unstable region is between RQ and Rout. Therefore, the fragmentation region defined by Equations (1) and (2) is extended inward to ∼26 au. (4) A disk tends to be isothermal in the region where the cooling time criterion is satisfied. If we use tcool as the cooling time,
during the disk evolution. The following conclusions are valid throughout the disk evolution: (1) The fragmentation region found in previous studies is in the isothermal region of a disk. (2) When the isothermal region is considered, by using Equation (3), the inner boundary of the fragmentation region is extended inward to ∼20 au. (3) If the contribution of the protostar irradiation to the disk surface temperature can be included in the cooling rate, the region where the cooling time criterion can be satisfied is extended inward to ∼26 au. Note that the gravitationally unstable region is between RQ and Rout. Therefore, the fragmentation region defined by Equations (1) and (2) is extended inward to ∼26 au. (4) A disk tends to be isothermal in the region where the cooling time criterion is satisfied. If we use tcool as the cooling time, 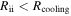 and the region where the cooling time criterion is satisfied is contained in the isothermal region. In our numerical calculations, we consider the contributions of the external irradiation to the disk surface temperature. Even in this case, most of the time
and the region where the cooling time criterion is satisfied is contained in the isothermal region. In our numerical calculations, we consider the contributions of the external irradiation to the disk surface temperature. Even in this case, most of the time 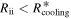 and the isothermal region contains the region where the cooling time criterion is satisfied. During the short period between
and the isothermal region contains the region where the cooling time criterion is satisfied. During the short period between 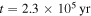 and
and 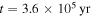 in Figure 3,
in Figure 3, 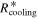 is slightly less than Rii (the maximum difference is about 3 au) and most of the region where the cooling time criterion is satisfied is still in the isothermal region of a disk.
is slightly less than Rii (the maximum difference is about 3 au) and most of the region where the cooling time criterion is satisfied is still in the isothermal region of a disk.
From Figure 3, the disk gains enough mass to be unstable at 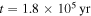 . From
. From  to
to  , the fragmentation region is between Rii and Rout. From
, the fragmentation region is between Rii and Rout. From 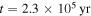 to
to 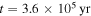 , the fragmentation region is between
, the fragmentation region is between  and Rout if the contributions of the external irradiation to the disk surface temperature are included. From
and Rout if the contributions of the external irradiation to the disk surface temperature are included. From 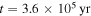 to
to 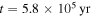 , the fragmentation region is between Rii and Rout. After the mass influx stops, the gravitationally unstable region shrinks and RQ increases. After
, the fragmentation region is between Rii and Rout. After the mass influx stops, the gravitationally unstable region shrinks and RQ increases. After 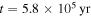 , RQ becomes greater than Rii. From
, RQ becomes greater than Rii. From 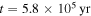 to
to 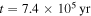 (the ending time of gravitational instability), the fragmentation region is between RQ and Rout and is the gravitationally unstable region of the disk. In previous studies, Rcooling has been used as the inner boundary of the fragmentation region. Differently, from Figure 3, we find that Rii, RQ, or
(the ending time of gravitational instability), the fragmentation region is between RQ and Rout and is the gravitationally unstable region of the disk. In previous studies, Rcooling has been used as the inner boundary of the fragmentation region. Differently, from Figure 3, we find that Rii, RQ, or 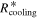 is the inner boundary at different times. We also mention that Rout is the outer boundary of the fragmentation region.
is the inner boundary at different times. We also mention that Rout is the outer boundary of the fragmentation region.
From Figure 3, even if the contributions of the external irradiation to the disk surface temperature are included, the fragmentation region defined by Equations (1) and (2) (between 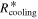 and Rout) is in the isothermal region of the disk most of the time. During the short period between
and Rout) is in the isothermal region of the disk most of the time. During the short period between 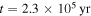 and
and 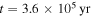 , most of the fragmentation region is still in the isothermal region of the disk.
, most of the fragmentation region is still in the isothermal region of the disk.
In the calculations of Figure 3, the disk is going through the earliest stage of its evolution. This stage includes the mass infall phase when there is mass influx onto the disk from the collapse of the cloud core and a period of about 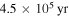 after the infall phase. The time evolution of the protostar and disk masses corresponding to Figure 3 is plotted in Figure 4. The beginning of the collapse of the cloud core is taken to be t = 0. Both the protostar and the disk have zero mass at t = 0. The protostar gains mass from both the collapse and the accretion from the disk so that the protostar mass increases with time. The mass influx from the collapse stops at
after the infall phase. The time evolution of the protostar and disk masses corresponding to Figure 3 is plotted in Figure 4. The beginning of the collapse of the cloud core is taken to be t = 0. Both the protostar and the disk have zero mass at t = 0. The protostar gains mass from both the collapse and the accretion from the disk so that the protostar mass increases with time. The mass influx from the collapse stops at 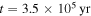 . Before the influx stops, the disk gains mass from the influx and its mass increases. After the influx stops, the disk mass decreases owing to the accretion onto the protostar. The protostar and disk masses in Figure 2 (
. Before the influx stops, the disk gains mass from the influx and its mass increases. After the influx stops, the disk mass decreases owing to the accretion onto the protostar. The protostar and disk masses in Figure 2 (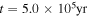 ) are 0.68 and 0.32 M☉, respectively. At
) are 0.68 and 0.32 M☉, respectively. At 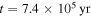 , the disk becomes gravitationally stable. The disk mass decreases to 0.28 M☉, and the protostar mass is 0.72 M☉.
, the disk becomes gravitationally stable. The disk mass decreases to 0.28 M☉, and the protostar mass is 0.72 M☉.
Figure 4. Time evolution of the protostar and disk masses corresponding to Figure 3. The dashed and solid lines represent the protostar mass and disk mass, Mdisk, respectively.
Download figure:
Standard image High-resolution imageNote that in our disk model, we do not assume any artificial initial conditions. Both the protostar and the disk start with zero mass. The disk gains mass from the mass influx from the collapse of its progenitor cloud core. Our disk model includes disk formation and early evolution. The initial conditions of the protostar+disk system are determined by the properties of the progenitor cloud core, namely, Tcloud, 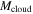 , and ω.
, and ω.  and
and 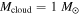 are typical values. Observed ω ranges from
are typical values. Observed ω ranges from 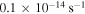 to
to 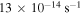 (Goodman et al. 1993; Caselli et al. 2002). To see the dependence of the results on ω, we plot time evolution of RQ, Rout, Rii, Rcooling, and
(Goodman et al. 1993; Caselli et al. 2002). To see the dependence of the results on ω, we plot time evolution of RQ, Rout, Rii, Rcooling, and 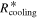 in a protoplanetary disk with
in a protoplanetary disk with 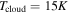 ,
, 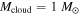 , and
, and 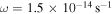 in Figure 5 and the time evolution of the protostar and disk masses in Figure 6. The general trend of the time evolution in Figures 5 and 6 is similar to that in Figures 3 and 4, respectively. The main difference is that the protostar+disk system with
in Figure 5 and the time evolution of the protostar and disk masses in Figure 6. The general trend of the time evolution in Figures 5 and 6 is similar to that in Figures 3 and 4, respectively. The main difference is that the protostar+disk system with 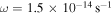 has less angular momentum and less material spreading out than that with
has less angular momentum and less material spreading out than that with 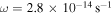 . Therefore, the protostar with
. Therefore, the protostar with 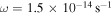 has more mass. Compared to the disk with
has more mass. Compared to the disk with 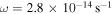 , the disk with
, the disk with 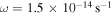 has less mass (see Figures 4 and 6) and smaller size. The gravitationally unstable region becomes smaller (RQ increases and Rout decreases), and the duration of the instability becomes shorter. Significantly, Rout for disk with
has less mass (see Figures 4 and 6) and smaller size. The gravitationally unstable region becomes smaller (RQ increases and Rout decreases), and the duration of the instability becomes shorter. Significantly, Rout for disk with 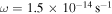 is much smaller than that with
is much smaller than that with 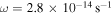 . Rcooling hardly changes because it is an insensitive function of Q0 and M* (see Equation (43)) and both Q0 and M* do not change significantly. Compared to Figure 3, Rii and
. Rcooling hardly changes because it is an insensitive function of Q0 and M* (see Equation (43)) and both Q0 and M* do not change significantly. Compared to Figure 3, Rii and 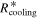 in Figure 5 do not change much. This can be explained as follows. In the intermediate region, the disk temperature (both Tm and Ts) is determined by the protostar irradiation, which is an insensitive function of M*, and M* changes slightly (see Figure 4 and 6). Therefore, the disk temperature in the intermediate region does not change much. As mentioned in Section 2, Q maintains a constant near Qcrit in the unstable region. From Equation (1), Σ also does not change much. Therefore, Rii and
in Figure 5 do not change much. This can be explained as follows. In the intermediate region, the disk temperature (both Tm and Ts) is determined by the protostar irradiation, which is an insensitive function of M*, and M* changes slightly (see Figure 4 and 6). Therefore, the disk temperature in the intermediate region does not change much. As mentioned in Section 2, Q maintains a constant near Qcrit in the unstable region. From Equation (1), Σ also does not change much. Therefore, Rii and 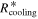 calculated from Σ, Tm, and Ts do not change much. We mention that for the extreme case of ω = 0 the system is spherically symmetric, all material falls directly onto the protostar, and the disk has zero mass.
calculated from Σ, Tm, and Ts do not change much. We mention that for the extreme case of ω = 0 the system is spherically symmetric, all material falls directly onto the protostar, and the disk has zero mass.
Figure 5. Time evolution of RQ, Rout, Rii, Rcooling, and 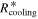 in a protoplanetary disk with
in a protoplanetary disk with 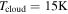 ,
, 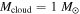 , and
, and 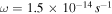 . The solid, dotted-dashed, long-dashed, short-dashed, and dotted lines represent RQ, Rout, Rii, Rcooling, and
. The solid, dotted-dashed, long-dashed, short-dashed, and dotted lines represent RQ, Rout, Rii, Rcooling, and  , respectively. The horizontal dotted line represents 50 au, the minimum radius of the inner boundary of the fragmentation region found in the previous studies.
, respectively. The horizontal dotted line represents 50 au, the minimum radius of the inner boundary of the fragmentation region found in the previous studies.
Download figure:
Standard image High-resolution imageFigure 6. Time evolution of the protostar and disk masses corresponding to Figure 5. The dashed and solid lines represent the protostar mass and disk mass, Mdisk, respectively.
Download figure:
Standard image High-resolution image5. Discussions and Conclusions
For Figure 3, we find that the maximum radius of the outer boundary of the fragmentation region is 145 au and the minimum radius of the inner boundary is 18 au. The period of time when fragmentation conditions are satisfied between 25 and 60 au is relatively long. Therefore, the probability of fragmentation between 25 and 60 au is relatively high.
Previous studies suggested that disk instability is expected to occur during the infall phase of disk evolution (e.g., D'Angelo et al. 2010). In our calculations of Figure 3, with an evolutionary disk model, we find that fragmentation can happen from 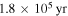 to
to 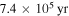 . Namely, fragmentation can happen during the infall phase and during the period of about
. Namely, fragmentation can happen during the infall phase and during the period of about  after the end of the infall phase. Our numerical calculations quantitatively confirm the previous suggestion.
after the end of the infall phase. Our numerical calculations quantitatively confirm the previous suggestion.
Rafikov (2009) adopted the fragmentation criterion from Gammie's (2001) local simulation and assumed that the cooling rate equals the dissipation rate of turbulence. His estimate with β ∼ 1 showed that fragmentation can occur only at a radius ≳120 au. Similarly, Clarke's (2009) estimate with β ∼ 6 demonstrated that fragmentation can occur at a radius ≳70 au. Compared to Rafikov (2009) and Clarke (2009), the fragmentation region in our model extends inward to ∼20 au when the isothermal region is considered, and the fragmentation region extends inward to ∼26 au when the contribution of the protostar irradiation to the disk surface temperature is considered in the calculation of the cooling rate.
According to the disk instability model, a gravitationally unstable disk fragments into self-gravitating dense clumps. Then, they contract to become gas giant planets. Disk fragmentation is a prerequisite for planet formation by the disk instability. One of the critical issues that might determine the viability of the disk instability model is whether a disk can fragment or under what condition a disk can fragment. In this paper, we use the fragmentation conditions found in previous studies to investigate where and when a disk can become gravitationally unstable and fragment. We only deal with the fragmentation, which is one of the issues related to the giant planet formation by disk instability. But the fragmentation of a disk does not guarantee that a giant planet can form. The limitation of our approach is that we do not consider other processes related to the giant planet formation. There are other factors that might also affect the planet formation. For example, if clumps do not cool quickly, they might be tidally disrupted (e.g., Vorobyov 2011; Zhu et al. 2012; Forgan et al. 2017). Also, the protoplanets may disappear owing to the migration toward the protostar (e.g., Vorobyov & Basu 2010; Machida et al. 2011). Even if the fragmentation can happen and clumps collapse into protoplanets, subsequent accretion may result in the formation of brown dwarfs (e.g., Zhu et al. 2012).
In this paper, we construct an analytical model of gravitationally unstable protoplanetary disks consisting of three regions: the inner region where the internal dissipation dominates the heating, the intermediate region where the central protostar irradiation dominates, and the outer region where the background irradiation dominates. We use this analytical model and an evolutionary numerical model of protoplanetary disks to calculate the cooling time and the radius at which the transition from the internal dissipation region to the protostar irradiation region occurs. This radius determines the location of the isothermal region. We investigate the effects of the isothermal region on the disk instability model for giant planet formation. We also calculate the cooling rate by including the contributions of the external irradiation to the disk surface temperature and discuss the effects of such a rate on the region where the cooling time criterion is satisfied. We also investigate the evolution of the gravitationally unstable region in a disk. The main conclusions are as follows:
- 1.The fragmentation region found in previous studies is contained in the isothermal region of a disk. Therefore, the fragmentation criterion (Equation (3)), instead of the cooling time criterion (Equation (2)), is applicable. The constraint on the disk instability model caused by the cooling time criterion should be relieved. This improves the viability of the disk instability model.
- 2.When the isothermal region is considered, by using Equation (3), the inner boundary of the fragmentation region is extended inward to ∼20 au.
- 3.If the contribution of the protostar irradiation to the disk surface temperature can be included in the cooling rate, the region where the cooling time criterion can be satisfied is extended inward to ∼26 au. Therefore, the fragmentation region defined by Equations (1) and (2) is extended inward to ∼26 au.
- 4.A disk tends to be isothermal in the region where the cooling time criterion is satisfied.
- 5.Even if the contributions of the external irradiation to the disk surface temperature are included, the fragmentation region defined by Equations (1) and (2) is in the isothermal region of the disk most of the time. During a short period of time (between
 and
and  in Figure 3), most of this fragmentation region is still in the isothermal region of the disk.
in Figure 3), most of this fragmentation region is still in the isothermal region of the disk. - 6.In previous studies, Rcooling has been used as the inner boundary of the fragmentation region. Differently, we find that Rii, RQ, or
 is the inner boundary at different times. In particular, at the later stage of disk instability, the inner boundary of the fragmentation region is determined by the inner boundary of the gravitationally unstable region of a disk. We also find that Rout is the outer boundary of the fragmentation region.
is the inner boundary at different times. In particular, at the later stage of disk instability, the inner boundary of the fragmentation region is determined by the inner boundary of the gravitationally unstable region of a disk. We also find that Rout is the outer boundary of the fragmentation region. - 7.The transition from the optically thick region to thin region occurs in the intermediate region where the central protostar irradiation dominates the heating.
- 8.The outer part of a disk becomes isothermal owing to the irradiation from the central protostar, rather than being optically thin.
We thank the referee for very helpful comments. This research has been supported in part by the National Natural Science Foundation of China (NSFC) grants 11373019 and 11073009.