Investigating the Relation between Sunspots and Umbral Dots

Umbral dots (UDs) are small, bright features observed in sunspot umbrae and pores. They cover only 3%–10% of the umbral area and contribute 10%–20% of its brightness (Sobotka et al. 1993; Watanabe et al. 2012). It has been suggested that UDs, light bridges, etc., play a vital role in the energy balance of sunspots (Solanki 2003). While the strong magnetic field in the umbra suppresses energy transport by convection, some form of energy transport must be required to explain the observed umbral brightness.

The nature of UDs has been described in a number of models. The cluster model of Parker (1979) proposes that the umbral magnetic field is gappy, allowing field-free plasma to transport heat. A UD would represent the tip of such a field-free intrusion. The monolithic flux tube model of Weiss (2002) considers a sunspot as a collection of uniform vertically thin columns, and UDs as a natural result of the overstable oscillatory convection, which is the preferred mode just below the photosphere. Simulations by Schüssler & Vögler (2006) show that UDs are the result of narrow, upflowing, convective plumes with adjacent downflows.

Based on their location, UDs are classified as central UDs (CUDs) and peripheral UDs (PUDs; Grossmann-Doerth et al. 1986). CUDs appear in the inner regions of the umbra, whereas PUDs are located near the umbra–penumbra boundary. The size of UDs ranges from 180 to 300 km, and their intensity ranges from about 0.2 to 0.7 times the quiet-Sun (QS) intensity at visible wavelengths (Sobotka et al. 1997; Kitai et al. 2007; Louis et al. 2012a). The distribution of UDs in the umbra is not uniform. Sobotka et al. (1997) reported that larger, long-lived UDs are seen in regions of enhanced umbral background intensity. Watanabe et al. (2009) also reported that UDs are likely to appear in regions where the magnetic field is weaker and inclined, whereas they tend to disappear in locations where the field is stronger and vertical. In addition, their study shows that the lifetimes and sizes of UDs are almost constant, regardless of the magnetic field strength.

The physical properties of UDs have been extensively studied by several authors (Sobotka et al. 1997; Riethmüller et al. 2008; Hamedivafa 2011; Louis et al. 2012a; Watanabe et al. 2012), but they are primarily confined to time-sequence observations of single spots or spots in a single active region (AR). Watanabe (2014) investigated the spatial distribution of UDs in several sunspots using Hinode observations. The results showed that UDs became more clustered in the latter phase of sunspots. If UDs are driven by small-scale magnetoconvection in umbrae, then the subphotospheric convective flows could influence the properties of UDs observed at the photosphere. The motivation of this article is to investigate whether the macroproperties of sunspots, namely, area, umbral fill fraction, decay rate, and phase, have any bearing on the physical characteristics of UDs, specifically intensity and size. To that extent, we combine observations from Hinode and and Solar Dynamics Observatory (SDO)/Helioseismic and Magnetic Imager (HMI) to determine the properties of UDs and their host sunspots. The article is organized in the following manner. The observations and data analysis are described in Section 2. The algorithm used for the identification of UDs is discussed in Section 3. In Section 4, we present our results. The discussion and conclusions are presented in Sections 5 and 6, respectively.

In order to study the physical properties of UDs in different sunspots, we employed high-resolution G-band images acquired by the Broadband Filter Imager (BFI) of the Solar Optical Telescope (SOT; Tsuneta et al. 2008) on board Hinode (Kosugi et al. 2007). The primary criterion for selecting the data was the proximity of sunspots to disk center to reduce the projection effects on the physical properties of UDs. Sunspots with heliocentric angles Θ ≤ 25° (μ ≥ 0.9) were chosen for the study. We carefully examined the G-band images of fully evolved sunspots with well-developed penumbrae from Hinode observations that were acquired between 2013 January and 2014 December. During these 2 years, we found 42 sunspots that met our selection criterion. This period coincides with the maximum phase of solar cycle 24. Out of 42 sunspots, 18 were located in the northern hemisphere (Figure 1). The details of the chosen sunspots are listed in Table 1.⁴ All selected Hinode images were corrected for dark current, flat-field, and bad pixels using routines available in the Hinode SolarSoft package. The spatial sampling for a majority of the Hinode G-band images was 022 pixel^–1 and 011 pixel^–1 for six cases (Table 1).

Zoom In Zoom Out Reset image size

Table 1.  Details of the ARs Analyzed in the Study

Spot	NOAA	Date	Time	xpos	ypos	Dumb	Iumb
No.	(AR #)	(yy mm dd)	(UT)	(arcsec)	(arcsec)	(arcsec)
1a	11692	2013 Jan 14	04:17:42	−87	211	12.7	0.16
2b	11765	2013 Jun 07	07:31:31	9	115	10.8	0.18
3b	11785	2013 Jul 07	21:21:30	−4	−260	16.3	0.11
4a	11809	2013 Aug 06	04:39:06	−3	59	8.8	0.17
${5}_{{\rm{a}}}^{{\rm{L}}}$	11861	2013 Oct 12	18:10:02	45	−234	16.6	0.12
${6}_{{\rm{a}}}^{{\rm{F}}}$	11861	2013 Oct 12	18:10:02	−55	−248	14.5	0.14
7a	11884	2013 Nov 07	17:32:10	−254	−274	19.5	0.09
8b	11890	2013 Nov 19	10:43:02	181	30	34.3	0.08
${9}_{{\rm{a}}}^{{\rm{L}}}$	11921	2013 Dec 15	17:41:38	−10	85	19.7	0.10
${10}_{{\rm{a}}}^{{\rm{F}}}$	11921	2013 Dec 15	17:41:38	−10	85	14.1	0.11
11b	11934	2013 Dec 26	10:28:02	58	−273	13.3	0.14
${12}_{{\rm{a}}}^{{\rm{L}}}$	11944	2014 Jan 07	08:44:58	−74	−65	40.0	0.09
${13}_{{\rm{a}}}^{{\rm{F}}}$	11944	2014 Jan 07	08:44:58	−180	−65	20.0	0.14
14a	11959	2014 Jan 23	10:48:31	−179	−214	18.8	0.14
15a	11960	2014 Jan 24	14:49:02	10	−332	16.2	0.12
${16}_{{\rm{a}}}^{{\rm{L}}}$	11967	2014 Feb 03	06:08:14	15	−147	37.9	0.10
${17}_{{\rm{a}}}^{{\rm{F}}}$	11967	2014 Feb 03	06:08:14	15	−147	30.6	0.11
18b	11974	2014 Feb 10	23:16:36	−210	−110	13.1	0.14
19a	11990	2014 Mar 03	01:45:03	50	−138	14.7	0.13
20a	11991	2014 Mar 03	06:55:01	−108	−251	9.1	0.16
21a	12002	2014 Mar 12	13:56:04	−254	−225	14.7	0.15
22a	12005	2014 Mar 18	00:35:00	−95	285	18.7	0.12
23a	12014	2014 Mar 26	11:29:57	166	−134	15.0	0.12
24a	12027	2014 Apr 06	04:16:59	−43	282	16.3	0.12
25a	12032	2014 Apr 13	16:14:59	−61	282	15.6	0.11
${26}_{{\rm{a}}}^{{\rm{L}}}$	12056	2014 May 11	18:50:57	−35	103	12.4	0.14
${27}_{{\rm{a}}}^{{\rm{F}}}$	12056	2014 May 11	18:50:57	−125	168	13.0	0.13
28a	12080	2014 Jun 08	03:08:58	−54	−243	13.1	0.11
29a	12096	2014 Jun 28	18:11:58	127	33	8.7	0.17
30	12104	2014 Jul 04	20:25:26	−13	−270	12.1	0.15
31	12104	2014 Jul 04	20:25:26	−31	−220	10.0	0.15
32a	12121	2014 Jul 27	21:25:29	−114	−42	13.6	0.14
33a	12135	2014 Aug 11	02:52:00	−93	69	14.3	0.14
34a	12146	2014 Aug 22	18:28:41	−26	−9	14.6	0.12
35a	12151	2014 Aug 30	08:07:49	165	−287	14.2	0.13
36a	12158	2014 Sep 11	10:46:00	66	83	23.2	0.12
${37}_{{\rm{a}}}^{{\rm{L}}}$	12172	2014 Sep 26	07:32:08	−24	−290	18.7	0.10
${38}_{{\rm{a}}}^{{\rm{F}}}$	12172	2014 Sep 26	07:32:08	−190	−276	18.1	0.14
39a	12178	2014 Oct 03	07:55:27	−38	−173	14.4	0.12
40a	12205	2014 Nov 10	08:26:58	−10	162	12.6	0.13
41a	12216	2014 Nov 26	06:00:58	10	−287	17.3	0.11
42b	12227	2014 Dec 09	14:04:35	171	−108	13.3	0.15

Note. The effective umbral diameter (D_umb) and the normalized mean umbral intensity (I_umb) are given in the seventh and eighth columns, respectively. In the first column, superscript L indicates a leading spot, superscript F indicates a following spot, subscript a indicates spatial sampling of 022 pixel^–1, and subscript b indicates spatial sampling of 011 pixel^–1.

Download table as:  ASCIITypeset image

Full-disk, limb-darkening-removed, continuum images from HMI (Scherrer et al. 2012) on board the SDO (Pesnell et al. 2012) were employed to estimate the epoch, growth, and decay rate of the selected spots. The HMI images are 4096 × 4096 pixels in size, with a spatial sampling of around 05 pixel^–1 and a time cadence of 6 hr.⁵

2.1. Instrumental Stray-light Correction

Space-based observations are free from seeing effects, but the optical quality of an instrument degrades over a period of time, resulting in decreased sensitivity and image contrast (Mathew et al. 2007). Instrumental scattered light can greatly influence the physical properties of sunspot fine structure (Louis et al. 2012a). All G-band images were corrected for instrumental stray light using the point-spread function (PSF) derived by Mathew et al. (2009). They determined the PSF of the broadband images of the SOT by analyzing the transit of Mercury observed on 2006 November 6. The PSF was modeled as a combination of four Gaussians with different widths and weights (Table 1 of Mathew et al. 2009). Restoration of the images was carried out by performing a deconvolution using the maximum likelihood approach (Richardson 1972; Lucy 1974) available in the IDL Astrolib package. This method iteratively updates the current estimate of the image by the product of the previous deconvolution and the correlation between the re-convolution of the subsequent image and the PSF. The G-band images were normalized to the average QS intensity (I_QS) over a 100 × 100 pixel area far away from the spot. Bright points in this patch exceeding 1.6I_QS were ignored while computing the mean intensity.

Figure 2 shows the improvement in image contrast after stray-light correction for a sunspot in NOAA AR 12227, observed on 2014 December 9 by Hinode/SOT. The mean minimum umbral intensity in selected sunspots decreases from 0.096I_QS to 0.044I_QS, and the mean contrast in the umbra increases from 0.4 to 0.51, after removal of stray light. Hereafter, the uncorrected and stray-light-corrected G-band images will be referred to as UC and SC images, respectively.

Zoom In Zoom Out Reset image size

2.2. Sunspot Epoch, Decay, and Growth Rate

Full-disk HMI continuum images were used to determine the macroproperties of the sunspots. Prior to estimating the sunspot area, the images were corrected for geometric foreshortening in the following manner. The position of each pixel on the solar disk was defined in terms of the position angle ${\theta }_{i}={\tan }^{-1}({x}_{i}/{y}_{i})$ and the radial distance ${\rho }_{i}=\sqrt{{x}_{i}^{2}+{y}_{i}^{2}}$, where x_i and y_i represent the position of the ith pixel on the surface of the Sun measured from disk center. The heliographic coordinates (B and L) were calculated from the following equations:

$$\begin{eqnarray}&&B={\sin }^{-1}\{\sin {B}_{0}\cos \rho +\cos {B}_{0}\sin \rho \cos (P-{\theta }_{i})\}\end{eqnarray} \tag{ 1 }$$

$$\begin{eqnarray}&&L={\sin }^{-1}\left\{\displaystyle \frac{\sin {\rho }_{i}\cos (P-{\theta }_{i})}{\cos B}\right\}+{L}_{0}\end{eqnarray} \tag{ 2 }$$

$$\begin{eqnarray}&&\rho ={\sin }^{-1}\left\{\displaystyle \frac{{\rho }_{i}}{S}\right\}-{\rho }_{i},\end{eqnarray} \tag{ 3 }$$

where S is the radius of the Sun in arcsec and P is the equatorial horizontal parallax angle. Once the heliographic coordinates for each pixel were known, they were transferred to a 2D image defined by latitude and longitude. This process was carried out on all HMI continuum images for the selected sunspots. The HMI filtergrams were normalized with the QS intensity at disk center.

Before calculating the sunspot area, the intensity corresponding to the umbra–penumbra boundary and the penumbra–QS boundary was determined using the cumulative intensity histogram method (Pettauer & Brandt 1997). The intensity thresholds for the umbra–penumbra and penumbra–QS boundaries were estimated to be 0.5I_QS and 0.9I_QS, respectively. The variation of the spot area with time was used to determine the decay or growth rate using a linear fit (Chapman et al. 2003). The area change of a sunspot as a function of time can be expressed as A(T) = m × (T − T₀) +  A₀, where m yields the decay or growth rate and A₀ is the maximum area of a decaying spot (minimum in the case of a growing spot). From the above expression, the time when the area of a decaying spot reduces to zero works out to be T_n = A₀/m, where T₀ is the time when the area of a decaying sunspot is maximum (minimum in the case of a growing spot) on the solar disk. In order to relate the macroproperties of a sunspot to the physical characteristics of UDs, we determined the epoch of a decaying spot as the ratio of the Hinode observing time (T_H) to the time when the spot area reduces to zero (T_n), whereas for the growing spot it is defined as the ratio of the Hinode observing time (T_H) to the time when the spot area is maximum. As an example, the decay rate of a sunspot in NOAA AR 11974 is shown in Figure 3. The area rate of change and epoch of the spots are described in the sixth and seventh columns of Table 2, respectively.

Zoom In Zoom Out Reset image size

Table 2.  Physical Properties of UDs Determined from the Hinode Stray-light-corrected Images

Spot	Imean/IQS	Imax/IQS	Deff	UD	ff	Area Change	Epoch
No.			(arcsec)	No.	(%)	106 × Km2 day–1
1	0.23 (0.09)	0.26 (0.11)	0.64 (0.14)	24	6.3	10.63 (2.35)a	0.054
2	0.27 (0.07)	0.30 (0.09)	0.35 (0.07)	52	5.5	113.06 (26.57)a	0.188
3	0.30 (0.18)	0.36 (0.25)	0.51 (0.14)	33	3.4	110.04 (23.06)a	0.262
4	0.21 (0.07)	0.24 (0.09)	0.57 (0.11)	15	6.5	36.44 (3.55)a	0.383
5	0.17 (0.09)	0.20 (0.11)	0.69 (0.16)	33	6.0	68.07 (19.90)b	0.507
6	0.22 (0.15)	0.26 (0.19)	0.64 (0.15)	27	5.6	47.78 (4.06)a	0.087
7	0.18 (0.14)	0.21 (0.18)	0.68 (0.17)	37	4.8	53.80 (10.97)a	0.097
8	0.21 (0.13)	0.25 (0.15)	0.55 (0.17)	128	3.5	9.34 (4.66)b	0.073
9	0.18 (0.06)	0.21 (0.07)	0.47 (0.15)	77	4.5	57.99 (9.07)a	0.244
10	0.16 (0.06)	0.19 (0.08)	0.49 (0.17)	49	6.2	95.77 (14.42)b	0.521
11	0.24 (0.12)	0.28 (0.15)	0.46 (0.08)	49	6.0	29.82 (3.22)a	0.225
12	0.18 (0.09)	0.22 (0.12)	0.83 (0.32)	114	5.3	42.58 (3.19)a	0.101
13	0.20 (0.06)	0.24 (0.08)	0.69 (0.21)	47	6.0	54.65 (10.42)a	0.046
14	0.22 (0.11)	0.25 (0.14)	0.50 (0.12)	82	6.1	11.02 (1.80)a	0.039
15	0.22 (0.13)	0.26 (0.16)	0.66 (0.14)	21	3.7	31.47 (2.64)a	0.132
16	0.22 (0.13)	0.26 (0.16)	0.74 (0.23)	98	4.1	153.73 (49.73)a	0.034
17	0.22 (0.14)	0.26 (0.18)	0.70 (0.19)	59	3.4	223.40 (28.32)b	0.681
18	0.25 (0.14)	0.29 (0.18)	0.54 (0.14)	23	4.1	17.14 (1.61)a	0.099
19	0.21 (0.10)	0.24 (0.14)	0.66 (0.15)	24	5.1	61.01 (6.17)a	0.116
20	0.22 (0.10)	0.24 (0.11)	0.62 (0.18)	10	5.1	69.52 (22.10)a	0.151
21	0.22 (0.15)	0.25 (0.19)	0.58 (0.13)	27	4.4	92.84 (4.66)a	0.049
22	0.19 (0.14)	0.22 (0.17)	0.64 (0.22)	41	5.3	31.56 (2.16)a	0.125
23	0.17 (0.11)	0.19 (0.13)	0.66 (0.16)	28	5.7	37.49 (2.90)b	0.572
24	0.15 (0.07)	0.17 (0.10)	0.70 (0.11)	27	5.2	33.12 (2.45)a	0.122
25	0.14 (0.07)	0.16 (0.09)	0.70 (0.16)	23	4.8	12.71 (1.87)a	0.048
26	0.19 (0.08)	0.22 (0.09)	0.57 (0.13)	32	7.0	37.13 (2.35)a	0.170
27	0.14 (0.07)	0.16 (0.07)	0.68 (0.22)	10	3.0	25.14 (1.70)a	0.123
28	0.17 (0.11)	0.20 (0.14)	0.69 (0.18)	11	3.2	23.31 (2.3)b	0.233
29	0.28 (0.09)	0.32 (0.12)	0.66 (0.24)	8	5.1	55.84 (5.04)a	0.466
30	0.20 (0.08)	0.22 (0.09)	0.67 (0.16)	22	7.2	73.44 (6.00)a	0.225
31	0.17 (0.08)	0.19 (0.09)	0.58 (0.15)	13	4.5	86.37 (5.26)a	0.310
32	0.20 (0.09)	0.22 (0.10)	0.65(0.13)	25	5.9	29.72 (2.76)a	0.135
33	0.16 (0.06)	0.18 (0.08)	0.72 (0.14)	21	5.5	11.96 (1.34)a	0.056
34	0.16 (0.07)	0.19 (0.09)	0.70 (0.17)	23	5.6	44.36 (7.44)b	0.635
35	0.17 (0.10)	0.19 (0.12)	0.75 (0.11)	20	5.8	26.69 (2.24)a	0.132
36	0.19 (0.07)	0.21 (0.08)	0.66 (0.15)	65	5.6	130.75 (23.23)a	0.302
37	0.11 (0.06)	0.12 (0.07)	0.61 (0.15)	44	4.9	252.80 (38.66)a	0.023
38	0.20 (0.10)	0.22 (0.12)	0.65 (0.16)	45	6.2	38.07 (5.59)a	0.061
39	0.29 (0.21)	0.36 (0.28)	0.84 (0.14)	13	4.5	13.30 (7.51)a	0.042
40	0.21 (0.10)	0.23 (0.12)	0.65 (0.16)	21	5.9	44.47 (12.48)a	0.243
41	0.15 (0.09)	0.16 (0.10)	0.67 (0.15)	22	3.5	137.53 (23.02)a	0.299
42	0.25 (0.16)	0.28 (0.19)	0.38 (0.10)	68	5.8	15.40 (1.49)a	0.098

Notes. The second through sixth columns correspond to the mean intensity (I_mean/I_QS), maximum intensity (I_max/I_QS), mean effective diameter (D_eff), total number of UDs (UD No.), and the filling factor (ff), respectively. The seventh and eighth columns represent the area change in the selected sunspots and epoch, respectively, which were estimated from HMI/SDO continuum images. The values in the parentheses represent the rms value.

^aDecaying spot. ^bGrowing spot.

Download table as:  ASCIITypeset image

The first step in identifying UDs from the Hinode G-band images was to extract the umbral region. The SC images, corresponding to a spatial sampling of 011 pixel⁻¹, were smoothed by a 15 pixel × 15 pixel boxcar (a 7.5 pixel × 7.5 pixel boxcar was used for spots with a coarser spatial sampling), and the umbra was extracted using the cumulative histogram method employed earlier for the HMI images. This yielded a value of 0.35I_QS corresponding to the umbra–penumbra boundary in the Hinode G-band images. The identification of UDs was carried out using a 2D multilevel tracking (MLT; Bovelet & Wiehr 2001) algorithm that has been implemented by Riethmüller et al. (2008) and Louis et al. (2012a). This algorithm works in the following manner. The intensity range in the umbra is binned into several levels chosen by the user, and the algorithm identifies UDs at each intensity level, moving from the highest to the lowest. All UDs corresponding to the maximum intensity in the umbra are tagged uniquely. Then, the intensity threshold is reduced to the next lower level and the UDs are identified once again, with the previously identified structures retaining their tagged number. This process continues until the last intensity level is reached. The number of UDs detected increases with the number of intensity levels defined in the MLT algorithm.

In order to optimize the MLT algorithm for our data set, the number of intensity levels was varied between 10 and 45 in steps of 5, and the corresponding values of the physical parameters were noted. We observed that although the number of UDs detected increased by a factor of about 1.5 when the number of intensity levels changed from 25 to 45, the average value of the physical parameters remained unchanged, and the overall variation for different-sized sunspots was nearly similar at and above 25 intensity levels. Furthermore, a visual inspection was carried out to verify whether the algorithm identified all discernible UDs for a given number of levels. With 10 intensity levels obvious UDs go undetected, while with 45 levels the algorithm primarily detects smaller and diffuse structures, whose inclusion does not alter the final statistical results. A final test was performed, with a smaller sample of sunspots, spanning 10''–40'' in diameter, and it was found that the final results were unaffected. This test was also carried out for a different number of intensity levels, and the outcome was similar to the one described above. These tests allowed us to finally select 25 intensity levels for the MLT routine.

Once the UDs are identified by the MLT routine, the boundary of each UD is defined by a contour that corresponds to 50% of its maximum and background intensity, i.e., (I_max + I_bg)/2. The background umbral image is determined by smoothing the original image with a 7 pixel × 7 pixel boxcar window. Figure 4 shows the extraction of an umbra from a sunspot and the location of UDs identified using the MLT algorithm.

Zoom In Zoom Out Reset image size

For each UD, we determine its peak intensity and mean intensity over all pixels enclosed by the UD boundary. We assume that the shape of each UD is circular, although they can be elliptical (Kilcik et al. 2012). The effective diameter for each identified UD was calculated as ${D}_{\mathrm{eff}}=\sqrt{4A/\pi }$, where A represents the total number of pixels in a UD. Those structures that had an area of greater than 2 pixels were considered for the analysis. We also checked whether selecting UDs on the basis of their proximity to the umbra–penumbra boundary had any discernible effect on the final results, and we found that neither an ingress of the umbra–penumbra boundary, moving from 2 to 8 pixels inward, nor excluding conspicuous bright peripheral features altered the average value of the physical parameters chosen for our study.

For each sunspot, the mean of the following quantities pertaining to the UDs was determined: maximum intensity, mean intensity, and effective diameter. Hereafter, the term "intensity" will be used to refer to the average of both the mean and maximum intensity of UDs, unless explicitly mentioned.

In this section, we present the physical properties of UDs observed in the umbra of 42 different sunspots, which are summarized in Table 2.

4.1. Umbral Size, Intensity, and Number of UDs

The umbrae (D_umb) from the 42 selected sunspots in the Hinode data set varied from 8'' to 40'' in diameter (see Table 1). However, the majority of sunspots had a diameter between 10'' and 20'', and only four sunspots had a diameter between 30'' and 40''.

Panel (a) of Figure 5 shows the relation between the mean intensity in the umbra and umbral diameter for the SC data set. A nonlinear relation between the two quantities is clearly evident. The mean intensity in the umbra for all spots varies between 0.08I_QS and 0.19I_QS. However, in smaller umbrae (D_umb < 20'') the intensity decreases much faster than in larger umbrae. For D_umb > 20'' the intensity decreases slowly and linearly. In order to understand this behavior, the observed distribution is fitted with linear and power-law functions. However, we noticed that a power-law fit describes this distribution better than a linear fit. The power law describing the nonlinear trend is indicated by a solid line, and the corresponding parameters are included in Table 3. It is also observed that smaller umbrae are brighter than the bigger ones by a factor of 1.7. In order to verify that the observed trend between the mean umbral intensity and the umbral diameter is not an artifact from the PSF deconvolution, we plot the same for the uncorrected data set as well, which is shown in panel (b) of Figure 5. The nonlinear trend is clearly visible, although the intensities are much higher, ranging from 0.12I_QS to 0.24I_QS, which would be expected from the uncorrected data set. The plots also show that the slopes for the SC and UC data sets only differ by 10%.

Zoom In Zoom Out Reset image size

Table 3.  Fit Parameters for the Power Law (y = A × x^B; Figures 5(a) and (b)) and Linear (y = A + Bx; Figures 5(c) and (f), Figures 6–9) Functions

Figure	x	y	A	B	CC
5(a)†	Dumb	Iumb	0.38 (0.48)	−0.40 (0.45)	−0.69
5(b)‡	Dumb	Iumb	0.46 (0.58)	−0.36 (0.45)	−0.78
5(c)†	Dumb	NUD	−9.2 (15.70)	3.44 (0.65)	0.83
5(d)‡	Dumb	NUD	−11.52 (14.41)	3.02 (0.60)	0.81
5(e)†	Dumb	ff	5.77 (1.03)	−0.06 (0.046)	−0.30
5(f)‡	Dumb	ff	5.30 (0.80)	−0.05 (0.04)	−0.24
6†	Iumb	ff	3.02 (0.71)	17.15 (5.06)	0.46
7(a)†	Dumb	IUD	0.23 (0.02)	−2.01 (1.14) × 10−4	−0.028
7(b)†	Dumb	Deff	0.55 (0.04)	4.44 (2.21) × 10−3	0.30
8(a)†	ff	IUD	0.25 (0.04)	−3.5 (7.6) × 10−3	−0.073
8(b)†	ff	Deff	0.70 (0.08)	−0.013 (0.015)	−0.138
9†	Iumb	IUD	0.14 (0.04)	0.70 (0.33)	0.31
10(a)†	dA/ dt	${{\rm{I}}}_{\mathrm{UD}}^{\max }$	0.24 (0.02)	−1.2 (1.4) × 10−4	−0.131
10(b)†	Epoch	${{\rm{I}}}_{\mathrm{UD}}^{\max }$	0.23 (0.01)	−1.8 (4.6) × 10−4	−0.063
10(c)†	dA/ dt	Deff	0.63 (0.02)	−6.13 (3.0) × 10−5	−0.032
10(d)†	Epoch	Deff	0.63 (0.02)	−1.9 (9.3) × 10−4	−0.032

Note. Abbreviations "ff," "I_umb," and "I_UD" correspond to the filling factor, QS-normalized mean umbral intensity, and maximum UD intensity, respectively. In the sixth column "cc" refers to the linear Pearson correlation coefficient between parameters. The numbers in parentheses denote 1σ errors. The parameters retrieved from SC and UC images are indicated by superscripts "†" and "‡," respectively. The rate of area change is denoted by dA/dt.

Download table as:  ASCIITypeset image

Panel (c) of Figure 5 demonstrates the relation between the number of UDs (NUD) and the umbral diameter for the SC images, and it is seen that the NUD increases with the umbral diameter. To first order, this scatter can be expressed with a linear fit between the two quantities. The same is observed with the UC images (panel (d)), although the NUD is marginally smaller than that in the SC images, specifically for spots with umbral diameters larger than 30''. We obtained a strong positive correlation of 0.83 and 0.81 between the two quantities for the SC and UC images, respectively. For spots with umbral diameters less than 15'', the NUD is less than 50, with a scatter amounting to about 20.

We also determined the fill fraction of UDs as the ratio of the total area occupied by UDs to the umbral area. The fill fraction ranges from 3% to 7.2% (bottom panels of Figure 5) for all sunspot umbrae. A weak negative correlation coefficient of −0.3 and −0.24 was observed in the SC and UC images, respectively. Smaller umbrae exhibit a higher fill fraction compared to larger umbrae. In order to see the overall trend, the average fill fraction was determined for umbral diameters within 8'' bins, and the solid line in the figure represents the best linear fit to the average values. The slope of the fit indicates that the fill fraction is nearly independent of the umbral diameter.

A scatter plot in Figure 6 illustrates the relation between the mean umbral intensity and the filling factor. We observe that the filling factor shows a weak positive correlation with the mean umbral intensity. The filling factor increases by a factor of about 1.4 over the range of the mean umbral intensities. We also note that if the number of levels in the MLT routine is increased to 45, the newly detected UDs only reflect an increase in the fill fraction of 1% as compared to the case when 25 levels are used in the detection scheme.

Zoom In Zoom Out Reset image size

4.2. Intensity and Size of UDs

Figure 7(b) shows that the maximum intensity of UDs in the data set ranges from 0.12I_QS to 0.36I_QS, while the mean intensity of UDs varies from 0.11I_QS to 0.3I_QS. The mean and maximum UD intensities are mainly confined between 0.15I_QS and 0.3I_QS. The brightest UD in the smallest umbra exceeds that in the biggest umbra by a factor of 1.5. Unlike the power-law relation between the size and intensity of the sunspot umbra (Figure 5(a)), neither the maximum nor mean intensity of UDs exhibits a correlation with the umbral size as seen in the top panel of Figure 7. Figure 7(b) shows that the effective diameter of UDs primarily lies between 04 and 07, with minimum and maximum values of 035 and 084, respectively. A linear fit to the scatter suggests that UDs dwelling in smaller umbrae are smaller than those found in larger umbrae, with a modest correlation coefficient of about 0.3.

Zoom In Zoom Out Reset image size

We also do not observe any dependence of the intensity and effective diameter of UDs on the fill fraction (Figure 8). The bottom panel of Figure 8 indicates that the effective diameter of UDs is negatively correlated with the fill fraction, due to the large scatter in the data. The linear fit (Table 3) indicates that for a fill fraction of 10% the effective diameter of UDs would be around 057.

Zoom In Zoom Out Reset image size

The mean umbral intensity exhibits a modest correlation with intensity of UDs (Figure 9). We see that the maximum intensity of UDs exceeds the mean umbral intensity by about 10% with a slope of around 0.7.

Zoom In Zoom Out Reset image size

4.3. UD Parameters versus the Area Change and Epoch of Sunspots

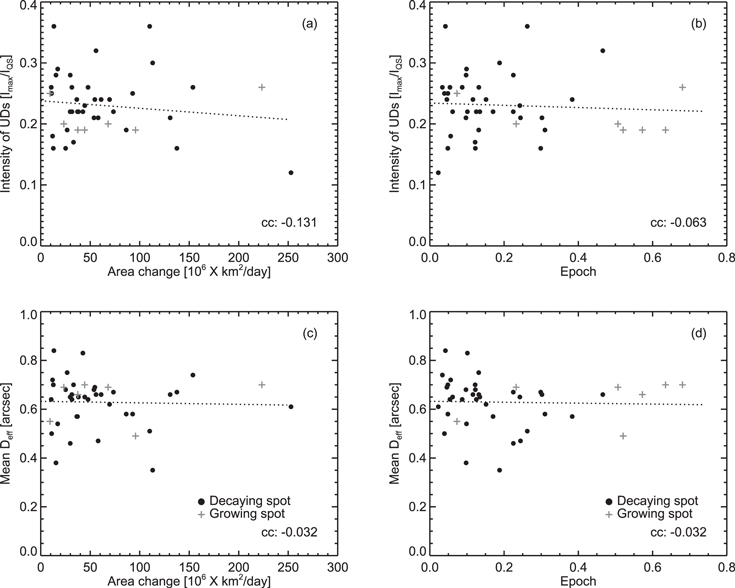
Figure 10 (bottom panels) shows the relation of the effective diameter of UDs (D_eff) with the decay/growth rate and epoch of sunspots. It is observed that the effective diameter of UDs (D_eff) is insignificantly related to both the decay/growth rate and epoch for the 42 sunspots studied here. The bottom left panel of Figure 10 indicates that a majority of the UDs are associated with sunspots having a slow rate of area change (<50 M km²). Similarly, the bottom right panel of Figure 10 illustrates that the effective diameter of UDs is also independent of the epoch of sunspots.

Zoom In Zoom Out Reset image size

Similar to the effective diameter of UDs, the top panels of Figure 10 demonstrate that the maximum intensity of UDs does not exhibit any trend with the rate of area change and the epoch of sunspots. Even though UDs tend to be brighter when sunspots decay slowly, this variation is less than 5%. The same is valid for the sunspot epoch, where the UDs are only a fraction brighter during the early phase of sunspots.

UDs are manifestations of small-scale magnetoconvection in sunspots. Our study shows that there is a dependence of the mean umbral brightness on the spot size, which is in agreement with Mathew et al. (2007), where smaller spots are brighter than larger ones. This would imply that darker spots comprise stronger magnetic fields that suppress magnetoconvection as suggested by Maltby (1977), Kopp & Rabin (1992), and Livingston (2002). Thus, if UDs are manifestations of small-scale magnetoconvection, then one would expect that their physical properties have a bearing on the macroproperties of a sunspot. In the context of Parker's "jelly-fish" model (Parker 1979), the energy transport in umbrae ought to be more vigorous during the late phase of sunspots as they approach fragmentation, and the reduced magnetic pressure would be insufficient to overcome the resulting gas pressure. This should be seen as brighter and/or larger UDs, which could then be used as a proxy for several large-scale properties of sunspots, namely, their area, rate of decay, and evolutionary phase. With this motivation in mind, we have selected a large set of sunspots and tracked them during their transition across the solar disk. By employing high-resolution G-band filtergrams from Hinode, close to disk center, the physical properties of UDs were estimated and related to the above-mentioned sunspot properties. We have taken care of instrumental stray light in the Hinode filtergrams, which is known to affect the geometrical and photometric properties of UDs (Louis et al. 2012a), and our analysis primarily focuses on the intensity and effective diameter.

We find that a strong linear relationship exists between the number of UDs and umbral diameter, which would suggest that in bigger spots there are larger spaces for convection to occur within the umbra. However, the fill fraction of UDs is nearly independent of the umbral diameter and accounts for less than 10% of the umbral area, which is in agreement with Sobotka et al. (1993) and Sobotka & Hanslmeier (2005). This stems from the fact that the diameter of UDs does not show any variation with the spot size. In addition, both the mean and maximum intensity and diameter of UDs do not show any visible trend with the area decay rate or the spot epoch, exhibiting very weak, negative correlations. We find that although UDs tend to be brighter during the late phase of sunspots, this variation is less than 5%. We also observed a similar behavior with the rate of area change. We also see that UDs tend to be smaller for spots that either are in an advanced stage of evolution or decay faster. This is reflected in a negative, although very weak, correlation coefficient. Our results show that the maximum intensity of UDs is about 10% brighter than the mean umbral intensity. We interpret this as a combined effect of the small fill fraction of less than 10% and the weak dependence between the diameter of UDs and the host umbra. This would indicate that the dependence of umbral intensity on the spot size originates primarily from the background regions of the umbra and for a very small fraction from UDs. The lack of a relationship between the properties of UDs and the macroproperties of the parent spots is discussed below.

In addition to UDs, light bridges represent large-scale, convective intrusions in the umbrae of sunspots and pores (Muller 1979; Sobotka 1994; Lites et al. 2004; Louis et al. 2009, 2008). The association between these two phenomena has been established in several works (Garcia de La Rosa 1987; Hirzberger et al. 2002; Rimmele 2008). Katsukawa et al. (2007) studied the formation of sunspot light bridges using Hinode observations. They found that the formation was preceded by an inward motion of UDs that appeared well within the umbra and not the penumbra. They interpreted this observation as a sign of the weakening of the magnetic field by the hot rising plasma, which then allowed several UDs from the leading edges of penumbral filaments to intrude further into the umbra, forming a light bridge out of a collection of UDs. The formation of a light bridge is associated with a rapid increase of intensity, from umbral to penumbral values in about 4 hr, which is accompanied by a large reduction in the field strength (Louis et al. 2012b). In light of the above, the lack of trend between the UD size and the spot area suggests that the interaction of the magnetic field and convection, within the umbra, occurs over a set of distinct, interchangeable spatial scales. Thus, depending on the underlying conditions of the magnetic and gas pressure, UDs would coalesce to form light bridges during late stages of spot decay, and light bridges would disintegrate into UDs during the spot's maturity (see, e.g., Figure 2 of Schlichenmaier et al. 2010). Since the contribution of light bridges to the intensity of UDs was excluded in our analysis, it would be necessary to determine how these structures influence the size and intensity of the latter.

Another possibility of the lack of any discernible relation between the intensity and diameter of UDs with the spot size could be attributed to the shallow depth to which these structures extend. MHD simulations of magnetoconvection in the umbra by Schüssler & Vögler (2006) show that UDs correspond to vertically rising convective plumes from a depth of around 2 Mm, while light bridges extend a little deeper to around 6–7 Mm (Cheung et al. 2010). Even with this simulation depth, the photospheric properties of light bridges are in good agreement with those typically seen in observations. These depths only represent a small fraction of the solar convection zone that is strongly stratified by 6 orders of magnitude over a depth of 200 Mm (Christensen-Dalsgaard et al. 1991). This poses an enormous computational challenge, and as such numerical models focus either on the deep convection zone, leaving out the uppermost 10–20 Mm, or on the uppermost 10 Mm, including the solar photosphere.

According to Schüssler & Rempel (2005), during the final phase of the ascent of a rising flux loop toward the surface, the upper part of the loop develops a buoyant upflow of plasma. The combination of the pressure buildup by the upflow and the cooling of the upper layers of an emerged flux tube by radiative losses at the surface leads to a progressive weakening of the magnetic field at depths of several megameters, which can lead to a dynamic disconnection of the bipolar structure from its magnetic roots. The disconnection depth extends to a few tens of megameters as shown by Švanda et al. (2009), but it is associated with only one-third of the sample analyzed. Similar values of the disconnection depth have been reported by Maurya & Ambastha (2010), who find a linear relation of the above to the remaining lifetime of ARs. This would suggest that UDs and light bridges are strongly influenced by near-surface convective flows, rather than those that are associated with the severing of sunspots from their roots, which occur much deeper.

The study of UDs with high-resolution data is crucial for understanding small-scale magnetoconvection in sunspot umbrae, which can constrain existing sunspot models in a more robust manner. In this article, we have attempted to relate the physical properties of UDs with the large-scale properties of sunspots, in order to determine whether the underlying physical processes that influence the evolution and stability of the latter are indeed scale invariant. We do not find any significant relationship between the effective diameter of UDs and the sunspot area, epoch, and decay rate. The same is observed with the mean and maximum intensity of the UDs. We conclude that the above could be due to either the distinct transition of spatial scales associated with overturning convection in the umbra, where UDs can coalesce to form light bridges, or the shallow depth associated with UDs, which makes them impervious to the deeper, large-scale, convective flows that affect the anchoring of sunspots, or both. We intend to investigate whether this lack of trend is extended to sunspots over an entire solar cycle and with spots that have an umbral radius greater than 25''. Facilities such as the 1.5 m GREGOR solar telescope (Schmidt et al. 2012) and the 4 m Daniel K. Inoyue Solar Telescope (DKIST, formerly ATST; Keil et al. 2003) will be extremely important in these investigations, as spatially resolved UDs would allow improved statistics by providing evidence of magnetoconvection at the smallest spatial scales.

Hinode is a Japanese mission developed and launched by ISAS/JAXA, collaborating with NAOJ as a domestic partner, NASA and STFC (UK) as international partners. Scientific operation of the Hinode mission is conducted by the Hinode science team organized at ISAS/JAXA. This team mainly consists of scientists from institutes in the partner countries. Support for the post-launch operation is provided by JAXA and NAOJ (Japan), STFC (UK), NASA, ESA, and NSC (Norway). The HMI data used here are courtesy of NASA/SDO and the HMI science team. The Center of Excellence in Space Sciences India is funded by the Ministry of Human Resource Development, Government of India. R.E.L. is grateful for the financial assistance from SOLARNET–the European Commission's FP7 Capacities Programme under grant agreement no. 312495. This work was also supported by grants AYA2014-60476-P and SP2014-56169-C6-2-R at the Instituto de Astrofísica de Canarias, Tenerife, Spain. We thank the referee for reviewing our article and for providing insightful comments.