Nonlocal Ohms Law, Plasma Resistivity, and Reconnection During Collisions of Magnetic Flux Ropes

Flux ropes are magnetic structures with helical magnetic fields and currents. They are ubiquitous as they occur on the Sun, throughout space, in the plasma surrounding the Earth, and in astrophysical plasmas (Russell et al. 1990). Flux ropes routinely occur within the Earth's magnetopause boundary layer, and also within the Earth's magnetotail (Slavin et al. 2003). The Pioneer Venus Orbiter was the first to observe magnetic flux ropes near Venus in the late 1970s (Russell & Elphic 1979). The smoothly rotating field of magnetic clouds (Klein & Burlaga 1982) is the result of the spiraling currents associated with a flux rope (Burlaga 1988). When viewed in ultra violet or X-ray emissions the surface of the Sun is blanketed in arched filaments, which are believed to be flux ropes. A single flux rope can writhe and twist about itself, and, if the current in it is large enough, form a kink. When two or more flux ropes are close to one another they interact. The ${\boldsymbol{J}}\times {\boldsymbol{B}}$ forces (the magnetic field of one interacting with the current of the other) will cause the ropes to twist about one another. It is common in nature for flux ropes to have one or more companions. Multiple arched ropes emanating from the surface of the Sun interact in complex ways. On the Sun, flux ropes can be forced to collide when their footprints (which are anchored to the solar surface) are dragged about by flows. During a collision, component reconnection can occur, which is between the anti-parallel magnetic fields of the ropes. During the reconnection process, field line topology rapidly changes as magnetic energy is converted to kinetic energy, thermal energy, and particle acceleration. When the process is two-dimensional a magnetic null can exist with field lines piling into it and reconnecting. This can happen in the magnetotail (Henderson et al. 2006) and has been observed in numerous laboratory experiments (Gekelman et al. 1982; Stenzel et al. 1982, 1983; Gekelman & Stenzel 1984; Yamada et al. 1997; Yamada 2001). Generally, in nature there is no location where the magnetic field is zero; the magnetic fields are fully three-dimensional. Reconnection happens nevertheless (Priest & Démoulin 1955). Arched magnetic flux ropes with helical fields have been studied in the laboratory (Tripathi & Gekelman 2013) but here we consider a simpler geometry with two, side-by side flux ropes. The ropes are kink unstable and periodically smash into one another, resulting in periodic reconnection (Gekelman et al. 2016a). When reconnection occurs, there are changes in the local electric field, electron temperature, and other quantities, such as the plasma resistivity. Ohm's law links the local plasma resistivity to the total electric field and current. All the plasma parameters necessary to calculate every term in Ohms law, save the resistivity, were measured in this experiment. We demonstrate that when flux ropes collide the application of Ohm's law may not be useful and alternative approaches, such as evaluation of the Kubo resistivity, are more meaningful.

The flux rope experiments were done in the Large Plasma Device (LaPD) at UCLA (Gekelman et al. 2016c). The ambient plasma is produced by a DC discharge between a barium oxide-coated cathode (Leneman et al. 2006) and mesh anode. The bulk of the plasma carries no net current and is therefore quiescent. The background plasma parameters are

$$\begin{eqnarray*}&&\displaystyle \frac{\delta n}{n}\approx 3 \% ,\ {T}_{e}=5\,\mathrm{eV},n\simeq 2\times {10}^{12}\,{\mathrm{cm}}^{-3},{T}_{i}\approx 1\,\mathrm{eV}.\end{eqnarray*}$$

The background plasma is pulsed at 1 Hz with a typical plasma duration of 15 ms. The LAPD can run continuously for approximately four months before the cathode has to be cleaned and recoated. A schematic of the machine indicating how the background plasma and flux ropes are generated is shown in Figure 1.

Zoom In Zoom Out Reset image size

The background plasma is generated by an oxide-coated cathode schematically shown on the right of Figure 1(b). A transistor switch capable of switch 25 kA currents (Pribyl & Gekelman 2004) in series with a 4 Farad capacitor bank is used to pulse a voltage between the negatively biased cathode and a molybdenum anode located 50 cm away. The background plasma is 18 m in length and 60 cm in diameter. A second, high emissivity lanthanum hexaboride cathode (LaB₆; Cooper et al. 2010) is inserted in the machine. The LaB₆ cathode is masked with a carbon plate with two holes 3.5 in radius and 1 cm apart edge-to-edge. The current forced the unmasked areas to form the flux ropes.

When the ropes are pulsed on there is additional ionization and the plasma density in the ropes doubles and the electron temperature rises to over 12 eV in the helium discharge. At this point the plasma in the ropes is highly ionized. The electrical systems, which generate the ropes, and background plasma are independent of one another. A second transistor switch, capacitor bank and charging supply is used for the ropes.

Ohm's law has long been used to estimate the plasma resistivity in the analysis of spacecraft data, interpretation of laboratory experiments and in various types of computer simulations (fluid, kinetic, and hybrid). Often one or more terms are dropped using symmetry arguments or assumptions on the relative size of terms. The justification for this is often questionable. It is a fluid description and therefore suffers from the neglect of kinetic effects or non-Maxwellian distribution functions, which are often found in space and in the laboratory.

The generalized Ohm's law in SI units is

$$\begin{eqnarray}\displaystyle \frac{{m}_{e}}{{{ne}}^{2}}\displaystyle \frac{\partial {\boldsymbol{J}}}{\partial t} & = & {\boldsymbol{E}}+{\boldsymbol{u}}\times {\boldsymbol{B}}+\displaystyle \frac{1}{{ne}}{\rm{\nabla }}\cdot \overleftrightarrow{P}-\displaystyle \frac{1}{{ne}}{\boldsymbol{J}}\\ & & \times {\boldsymbol{B}}-{\eta }_{\parallel }{{\boldsymbol{J}}}_{\parallel }-{\eta }_{\perp }{{\boldsymbol{J}}}_{\perp }.\end{eqnarray} \tag{ 1 }$$

Here $\overleftrightarrow{P}$ is the pressure tensor, n the plasma density, ${{\boldsymbol{J}}}_{\parallel }$ the current (in this experiment it is carried by the electrons), e is the absolute value of the electron charge and ${\boldsymbol{B}}$ is the total magnetic field. The resistivity, η, is different along and across the magnetic field. In the steady state and when there is no magnetic field or pressure, Ohm's law reduces to the familiar ${\boldsymbol{E}}=\eta {\boldsymbol{J}}$. For the first time, to our knowledge all the terms in this equation, apart from the resistivity were measured as a function of space and time in a flux rope experiment. The goal was to derive the resistivity from the data. This work presents measurements of all the terms and considerably expands what was recently published in a short letter (Gekelman et al. 2017).

Before presenting the Ohm's law result and an alternate approach, we discuss how all the terms in (1) were measured and present their spatial patterns and relative sizes.

The magnetic field was measured using a three-axis differentially wound magnetic pickup probe. Probes of this type have been in use for decades (Loveberg 1965) and a similar one is described in Everson et al. (2009). The three-axis probes were wound on a 3 mm cube, which was encased in a ceramic bulb. Identical probes were used for the reference and movable detectors. The oppositely wound 10-turn loops for each axis were subtracted with differential amplifiers with a frequency response up to 3 MHz. The movable probe was mounted on a 2D probe drive and recorded data at 2810 locations at each of 15 planes transverse to the background magnetic field. The flux ropes rotate about each other in addition to being kink unstable. Because the rope rotation starts at a slightly different time for each experimental shot, a conditional averaging technique (Gekelman et al. 2016b) was used to define the experimental start time, which differs from the time the rope currents are switched on by approximately ±100 μs. Briefly, the technique consists of correlating the temporal sequence of one component (B_x) of the reference probe (fixed at δx = 5 cm, δy = 0, δz = 966 cm) to determine the lag time between motion of the rope past the fixed probe and the rope passing the movable probe. The fixed probe was used for conditional triggers in acquisition of plasma flow, electric field, density, and temperature. Magnetic field lines are shown in Figure 2 along with the Quasi-Separatrix-Layer or QSL (Lawrence & Gekelman 2009; Gekelman et al. 2012).

The magnetic field was measured at 42,200 spatial locations and time series digitized at 7000 time steps (δt = 0.33 μs). First of all, the magnetic vector potential was evaluated from the magnetic field data (Gekelman et al. 2014). The data was "divergence cleaned" to generate a second B field that satisfied ${\rm{\nabla }}\,\bullet \,{\boldsymbol{B}}=0$. Visually, the data sets were almost indistinguishable. To obtain the magnetic field at any location in the volume, 3D spline coefficients of the vector potential, ${\boldsymbol{A}}$, were calculated at every time step over the entire volume. The splined data are then used to evaluate B at arbitrary locations. The resulting magnetic field lines writhe about themselves and twist about one another as previously observed (Intrator et al. 2009; Gekelman et al. 2012). When the kink mode drives the ropes into one another there are bursts of reconnection and at that time a Quasi Separatrix Layer (Priest & Démoulin 1955) forms. QSL's are regions in which the magnetic field connectivity changes rapidly but continuously across a narrow spatial region. Two field lines, which are very close to one another entering a QSL wind up spatially far apart when they emerge. The presence of a QSL is indicative that magnetic field line reconnection is taking place. Reconnection also results in the conversion of magnetic field energy into other forms such as particle heating, wave generation or flows. Reconnection results in an induced electric field (as a result of Faraday's law) which, in principle, can drive reverse currents in the plasma. If the waves it produces are turbulent, there can be an enhanced resistivity. Although reconnection is obviously present, it turns out to be a minor player as will be shown. Finally, contours of the axial component of the vector potential, A_z, are often used as a surrogate for field lines in a plane. This is an excellent approximation if the magnetic field is invariant along z. Figure 2 suggests this is not the case and this is shown in Figure 3.

Zoom In Zoom Out Reset image size

The perpendicular magnetic field can be as large as 30 Gauss, about 1/10 of the background field, ${B}_{0z}=330$ G. This is consistent with the 375 A current in each flux rope.

The three-dimensional plasma currents are evaluated from the magnetic field using ${\rm{\nabla }}\times {\boldsymbol{B}}={\mu }_{0}{\boldsymbol{J}}$, as Maxwell's contribution to Ampere's law is negligibly small due to the low frequency motion of the ropes (${E}_{\parallel }\lt 2\,{\rm{V}}\,{{\rm{m}}}^{-1}$, f = 5 kHz, ${\varepsilon }_{0}{{fE}}_{\parallel }\simeq {10}^{-7}{J}_{\parallel }$). The perpendicular and parallel currents, carried by electrons, are shown in Figure 4, as well as the temporal behavior of J_z at one location. At 3.0 A cm⁻², the parallel electron drift velocity in the current, in a rope center is 7 × 10⁶ cm s⁻¹. The ion drift velocity is 3% of the electron drift; therefore, the ion contribution to the current is negligible in this experiment. Figure 4(c) shows the axial component of the current at a fixed location in the x–y plane. It is always negative since electrons flow toward the current source (in the –z direction). The triangular appearance of the waveform is due to the motion of the ropes and is not a nonlinear effect.

Zoom In Zoom Out Reset image size

The plasma density was measured everywhere in the volume by collection of ion saturation current to the six faces of a Mach probe (Hudis & Lidsky 1970). The ion saturation current, I_sat, to a probe is proportional to ${I}_{\mathrm{sat}}\propto n\sqrt{{T}_{e}}$. To extract the density, the electron temperature must be known. The electron temperature was determined by sweeping the I–V characteristic of a Langmuir probe at hundreds of spatial locations and at several times on three x–y planes. The contours of electron temperature calculated from the Langmuir probe swept in 50 μs, closely matched contours of constant current on these planes at the times the probe was swept. Figure 5 illustrates that the current density closely matches contours of the electron temperature. The same holds true for the plasma density. The background electron temperature, where there was no current, was 4 eV. Figure 6 is a 3D map of the electron temperature shown at one instant of time.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

The flow, which corresponds to the ion motion, was measured with a three-axis Mach probe, which had six faces. Each face was approximately 2 square mm and much smaller than the ion gyroradii ($0.6\leqslant {R}_{{ci}}\leqslant 1.5\,\mathrm{cm}$) in the background plasma or ropes. It was determined that the Mach number could be obtained from

$$\begin{eqnarray}&&M=\displaystyle \frac{v}{{c}_{s}}=\displaystyle \frac{{I}_{1}-{I}_{2}}{{I}_{1}+{I}_{2}},\end{eqnarray} \tag{ 2 }$$

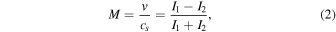
where c_s is the ion sound speed and I₁ and I₂ are the ion saturation current to faces 1 and 2 respectively. This is the limit in which the probe size is much less than the ion gyroradius. The flow was always subsonic, rarely exceeding M = 0.5. Three components of the flow at a position on the x–z plane are shown as a function of time in the insert in Figure 7. At any position, the Mach number oscillates at the flux rope rotation frequency of 5 kHz. This is also the case for all other quantities in Ohm's law. The axial component of the Mach number grows in the z direction, which is aligned with the background magnetic field.

Zoom In Zoom Out Reset image size

Figure 8 shows the scalar plasma pressure, $P=n({\boldsymbol{r}},t){{KT}}_{e}({\boldsymbol{r}},t)$ at one time (t = 5.5865 ms) after the ropes are switched on. In the first few meters, the isosurface of constant pressure P = 5 J m⁻³ mirrors that of the rope magnetic field. Isosurfaces of lower pressure fill more of the volume. The contours of constant pressure closely resemble the current density. Inside the ropes, the plasma is fully ionized as a result of the enhanced temperature. The larger pressure near the origin of the ropes causes plasma flow toward the other end of the device as seen in Figure 7. The proper term in Ohm's law is the divergence of the pressure tensor. This was not possible to acquire in the experiment, as a complete measurement of the tensor pressure requires the measurement of the 3D electron distribution function. This is routinely done with velocity analyzers in space where the Debye length is meters or more and the electron gyroradius is much larger than the spacecraft. In this experiment the Debye length is several microns and the electron gyroradius, 250 μm. Building such an instrument would require a large project in micromachining. However, in the experiment, the electron–electron collisional relaxation rate is 5 MHz or about one thousand times faster than timescales associated with the flux rope motion. The plasma is not collisionless and collisions isotropise the pressure tensor. We therefore assume ${T}_{e\parallel }={T}_{e\perp }$. A typical mean-free path for collisions between 10 eV electrons is 21 cm, far smaller than the length of the ropes. Finally, the large guide field in comparison to the transverse flux rope fields suppresses meandering orbits of electrons in the transverse plane, which lead to tensor pressures.

Zoom In Zoom Out Reset image size

The electric field has two components, ${\boldsymbol{E}}=-{\rm{\nabla }}\phi -\tfrac{\partial {\boldsymbol{A}}}{\partial t}$. The first component, which is due to space charge is often neglected by arguing that any space charge parallel to the magnetic field is immediately neutralized by electrons flowing along the field lines. This is not the case and in fact the space charge term is larger than the induced electric field throughout the volume. The potential is measured using an emissive probe. Since the density in this experiment is relatively high, a hot tungsten wire cannot be used because it melts before the proper electron emission current is obtained and the probe "floats" to within T_e of the plasma potential, V_p. To achieve the required emission, a specialized probe (Martin et al. 2015) was constructed using a material CeB₆, which is similar to LaB₆ in emission properties. Before acquiring data, the probe was heated to emission temperature (1800°C) and the I–V characteristic curve was swept and determined to be symmetric to ensure that it was performing correctly. The IV sweep circuit was then removed and the emissive probe electrically "floats." The probe impedance with respect to the ground is 500 kΩ, it draws very little current (microamperes) and therefore measured the potential at one point in space. The plasma potential at each spatial location and time (the same grid was utilized for all quantities) was derived by a correction using the local electron temperature (Chen 1965). The gradient of the plasma potential was used to determine the space charge contribution to the electric field. This component of the electric field is shown in Figure 9.

Zoom In Zoom Out Reset image size

The space charge electric field clearly shows that the flux ropes are negatively charged as the electric field points inward toward their centers. This is most evident at z = 64 cm, where the ropes are vertically positioned. At further axial locations, the ropes tilt sideways and merge. The perpendicular electric field is largest near the origin of the ropes. The axial component E_z, is several percent of the perpendicular component. This will be discussed in greater detail later on. The next component of the electric field is the inductive part $-\tfrac{\partial {\boldsymbol{A}}}{\partial t}$. The perpendicular components of the induced electric field are of the order of 1% of the perpendicular electric field from space charge and when added to $-{\rm{\nabla }}{V}_{p}$ make no discernable difference to the data shown in Figure 9. The axial component of the induced field is important in discussions of reconnection. It is generally much smaller than the space charge field as shown in Figure 10, where they are compared.

Zoom In Zoom Out Reset image size

Although there are some locations where $-\tfrac{\partial {\boldsymbol{A}}}{\partial t}$ is as high as 0.5 V m⁻¹ it is always smaller than the space charge electric field. It is also evident that they have different spatial morphologies. The role of the inductive field in reconnection will be discussed later on.

The total electric field may be used to derive the drift velocity ${{\boldsymbol{v}}}_{{EB}}=\tfrac{{\boldsymbol{E}}\times {\boldsymbol{B}}}{{B}^{2}}$. The drift velocity is a function of space and time and is shown in Figure 11. Also shown in Figure 11 is the measured flow speed. Both are normalized by dividing the drift velocity by the ion sound speed based on the local electron temperature (also see Figure 7). The flow patterns are similar; however, the largest measured flow velocity is 1/4 v_EB. If all the terms in Equation (1) except ${\boldsymbol{E}},{\boldsymbol{B}}$ and ${\boldsymbol{u}}$ were zero, one would expect that the velocities in Figures 11(a) and (b) would be the same. The existence of pressure gradients, for example, modifies the flow and the drift is not due to ${\boldsymbol{E}}\times {\boldsymbol{B}}$ alone.

Zoom In Zoom Out Reset image size

All the terms in Ohm's law (Equation (1)) have units of Volts/meter and arise when there are plasma flow, pressure gradients, and ${\boldsymbol{J}}\times {\boldsymbol{B}}$. They are displayed in a transverse plane, δz = 320 cm and at a given time, t = 5.3760 ms in Figure 12. This is at a location at which the ropes have tilted but not merged. The transverse patterns differ at every z location and change in time but the overall trend is the same. The ${\boldsymbol{J}}\times {\boldsymbol{B}}$ and ${\rm{\nabla }}P$ terms nearly cancel and if there were no flow or space charge field, they would balance one another. The flow term, ${\boldsymbol{u}}\times {\boldsymbol{B}}$, is the smallest in Ohm's law but is not entirely negligible. When the terms are summed, the resulting transverse field is large, of the order of 0.5 kV m⁻¹and the largest contribution comes from space charge. The axial electric field is much smaller, about 1% of the transverse field. The only term not shown is $\tfrac{{m}_{e}}{{{ne}}^{2}}\tfrac{\partial {\boldsymbol{J}}}{\partial t}$, which is negligibly small (this term is on the order of mV m⁻¹ or ${10}^{-3}$ of the terms on the right-hand side of Equation (1)). All quantities oscillate at a frequency of 5 kHz as the kink unstable flux ropes bounce against one another and a QSL is formed repeatebly.¹⁰ Using this frequency, the average plasma density, and the largest current oscillation in the data set, this term is at most 10 mV m⁻¹ and is ignored in the analysis.

Zoom In Zoom Out Reset image size

The parallel resistivity is calculated using Ohm's law (Equation (1)), which in the parallel direction may be written as

$$\begin{eqnarray}&&{\boldsymbol{E}}\,\bullet \,\hat{b}+\displaystyle \frac{1}{{ne}}{{\rm{\nabla }}}_{\parallel }P\,\bullet \,\hat{b}={\eta }_{\parallel }{J}_{\parallel },\end{eqnarray} \tag{ 3 }$$

where $\hat{b}=\tfrac{{\boldsymbol{B}}}{| {\boldsymbol{B}}| }$ is a unit vector along the local direction of the magnetic field due to the DC solenoidal magnets and plasma current and P is the scalar pressure gradient. The time-varying current term is again negligible. There are second-order terms in Ohm's law, which were not included in Equation (1) because they are very small. For example, the electric field due to thermal gradients $0.71{n}_{e}{\rm{\nabla }}{T}_{e\parallel }$ is several percent of the other terms in Equation (3). Figures 13(a)–(c) show the instantaneous parallel resistivity (δt = t.552 ms) calculated by this method on three planes, each a different distance from the origin of the ropes. The pattern changes continuously over the 15 planes data was acquired on. Figure 13(d) shows the resistivity on the same plane as in Figure 13(a) but averaged over one cycle of the flux rope oscillation. This was done to discount any contribution from the reactive part of the resistivity. As the derivation of ${\eta }_{\parallel }$ from Equation (3) involved division by the local current, the resistivity could "blow up" in regions when it was very small. When the local current density dropped below 0.5 Amp cm⁻², less than one-tenth of its maximum value, the resistivity was set to its classical value.

Zoom In Zoom Out Reset image size

The negative resistivity was largest on the planes closest to the current source and near the end anode, where the current was collected. The resistivity averaged over the entire volume is, however, always positive and several times classical. Instead of evaluating it plane-by-plane, an average ${\eta }_{\parallel }$ was calculated using

$$\begin{eqnarray}&&\langle {\eta }_{\parallel }\rangle =\displaystyle \frac{{\int }_{{fl}}{\boldsymbol{E}}\,\bullet \,d{\boldsymbol{l}}}{{\int }_{{fl}}{\boldsymbol{J}}\,\bullet \,d{\boldsymbol{l}}},\end{eqnarray} \tag{ 4 }$$

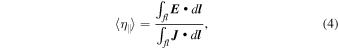
where fl indicates that the integral was taken along magnetic field lines. Here ${\boldsymbol{E}}$ contains all the terms in Ohm's law. The results of this calculation at two times on a plane are shown in Figure 14.

Zoom In Zoom Out Reset image size

The resistivity is largest in the current gradients, which is also seen in Figure 13. Here ${\langle {\eta }_{\parallel }\rangle }_{{fl}}$ is positive everywhere at t = 5.2880 ms but has small negative regions at an earlier time (t = 5.2122 ms). The temporal appearance of negative resistivity has nothing to do with reconnection and is not observed at the QSL location. The resistivity given by Equation (4) was also averaged over a flux rope oscillation and exhibited negative regions as in Figure 14.

Any region of negative resistivity is either unphysical or implies the existence of some sort of dynamo. Reverse currents have been seen in past experiments on reconnection. They could be generated by the induced electric field but are generally not coincident with it. In Figure 10(a), the induced field, $-\tfrac{\partial {\boldsymbol{A}}}{\partial t}$, in the direction opposite to that which drives the currents is largest in the center of the current system and not in the regions of reverse ${J}_{| | }$. There are axial pressure gradients that can drive reverse currents, but all of these are measured and were included in the Ohm's law evaluation. Assuming there is no dynamo, one may question if Ohm's law can be used at all in these circumstances. It is possible that the Ohm's law that should be used is nonlocal. This occurs when fields and pressure gradients in a region along a field line all contribute to the resistivity at a point. What does nonlocal resistivity mean? Consider a magnetic field line, which rapidly changes shape or moves around. In the Ohm's law picture, there should be an electric field, ${E}_{| | }$, along the field line. Ohm's law requires a point-by-point balance between momentum gain from the electric field and loss due to scattering. But in this experiment or in past experiments with magnetic shear, currents have been observed with no associated electric field or one of the wrong sign. Jacobson & Moses (1984) discovered that this loss and gain may be in global balance but not locally. The criterion for this is governed by a parameter α:

$$\begin{eqnarray}&&\alpha =\langle {({\rm{\Delta }}x)}^{2}\rangle {\left[\displaystyle \frac{1}{{E}_{\parallel }}{{\rm{\nabla }}}_{\perp }{E}_{\parallel }\right]}^{2}.\end{eqnarray} \tag{ 5 }$$

Here ${{\boldsymbol{E}}}_{\parallel }$ is the local electric field parallel to a magnetic field line. The first factor, $\langle {({\rm{\Delta }}x)}^{2}\rangle$, is the mean-square cross-field excursion for an electron that scatters 90° traversing L. The second is the inverse of the characteristic length for variation of ${E}_{| | }$.

The first term is discussed by Rechester & Rosenbluth (1977), and may be written

$$\begin{eqnarray}&&\langle {({\rm{\Delta }}x)}^{2}\rangle =2{{LD}}_{{rr}},\ {D}_{{rr}}={l}_{c}{\left(\displaystyle \frac{\delta B}{B}\right)}^{2}.\end{eqnarray} \tag{ 6 }$$

Here δB is the fluctuating rope field and l_c is the length of the field fluctuation. Alpha may be rewritten as

$$\begin{eqnarray}&&\alpha =2{{Ll}}_{c}{\left(\displaystyle \frac{\delta B}{B}\right)}^{2}{\left[\displaystyle \frac{1}{{E}_{\parallel }}{{\rm{\nabla }}}_{\perp }{E}_{\parallel }\right]}^{2}.\end{eqnarray} \tag{ 7 }$$

When α ≪ 1, the local version of Ohm's law is correct. In our analysis, we took the smallest length possible for L, the electron mean-free path in the center of the flux rope (L = 30 cm). The second length is less clear and we consider two cases. In the first l_c = L, the smallest possible value. We may also take l_c to be the field line length derived from a correlation function. The correlation of B_x(z, t) as well as B_y(z, t) was calculated with signals for a probe fixed in the center of one of the flux ropes at (x, y, z) = (−4.8, −1.8, 448.) cm. The signals are 80% correlated over a distance of 5 m. As the quantities in Equation (5) vary in time, α was averaged over one rope oscillation (from 5.104 ms < t < 5.321 ms). Isosurfaces of α in a portion of the plasma volume is shown in Figure 16, when L = l_c = 1/3 m. Alpha is as high as 35 and the average over the total plasma volume $\langle \alpha \rangle =1.52$. If l_c is taken to be 5 m, then all of the quantities displayed in Figure 15 must be multiplied by a factor of 15. In either case, α is greater than one when averaged over the plasma volume and can be much larger than one within the volume. Ohm's law is thus shown to be nonlocal.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Figure 15 indicates that the non-locality condition is satisfied and Ohm's law as expressed in Equation (2) cannot be used to evaluate the parallel resistivity. It is still possible to calculate the resistivity using another method. We next examine the resistivity due to the fluctuating currents in the ropes using the fluctuation dissipation theorem.

Since it was determined that Ohm's law cannot be used, we use another method to determine the global resistivity, which is based on the fluctuation dissipation theorem (Onsager 1931). The AC plasma conductivity tensor was derived by Kubo (1966) and is given by

$$\begin{eqnarray}&&{\sigma }_{\mu \nu }(\omega )=\displaystyle \frac{{{ne}}^{2}}{{{mv}}_{\mathrm{th}}^{2}}\iint {e}^{-i\omega t}{v}_{\nu }(t){v}_{\mu }(t+\tau ){dtd}\tau .\end{eqnarray} \tag{ 8 }$$

Here, n is the plasma density and v_the is the electron thermal velocity of the bulk plasma. This is a correlation function in which the index ν pertains to the velocity at a point chosen to lie on a field line in the center of the average current of one of the ropes. The other index μ is that of the velocity field at all locations in the x–y plane for a given z location. The velocity in the integral is the electron drift, which can be obtained from the current density ${\boldsymbol{J}}={ne}{\boldsymbol{v}}$, which is also known throughout the volume. This is an approximation. We have assumed that the current is from a drifting symmetric distribution function, which we have measured, on average, to be a Kappa distribution $(\kappa =2.46)$. The integral is a velocity correlation function and yields an effective collision term. The tensor conductivity, both the real and imaginary parts, was evaluated at 5 kHz, the rope oscillation frequency. Note that all relevant quantities, for example, those shown in Figure 16 oscillate at this frequency as well. The entire Kubo tensor, $| \sigma (\omega ^{\prime} )|$, where $\omega ^{\prime} =2\pi {f}_{\mathrm{rope}}$, is shown in Figure 16. Here the reference location is at x = 24.02 cm, y = 29.19 cm on a plane 3.20 m from the start of the ropes.

The largest conductivity in Figure 16 is σ_zz = 15,212 and corresponds to a resistivity of η = 6.6 × 10⁻⁵ Ohm m, which is three times the mean classical resistivity at that location. (As the flux ropes move, the Spitzer resistivity oscillates in time along with the density and temperature.) The diagram is insensitive to the position of the reference field line as long as it is the region where the currents are large. Three different reference field lines were tried and the result is virtually identical to that shown in Figure 16. The conductivity is smaller between the currents on this plane. The Kubo resistivity on four planes is shown in Figure 17. In Figure 17, the two current channels are positioned at the upper right and lower left in the right-hand side panel (δz = 1.28 m). The resistivity is also large in regions where the current is small, for example, the edges of the plane in Figure 17. The spatial dependence of the σ_zz tensor component of the Kubo conductivity is shown in Figure 18.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

The largest Kubo conductivity occurs in the gradient region surrounding the plasma currents. This is clearly visible on planes far from the origin of the flux ropes, for example, at δz = 7.68 m. The conductivity is lower between the currents where the QSL is to be found.

Let us focus in the central region where current is appreciable and reconnection occurs and examine the parallel Kubo resistivity, ${\eta }_{{zz}}=\tfrac{1}{{\sigma }_{{zz}}}$ in the reconnection region. The reconnection is thought to be greatest in the first four meters of the interaction region. This is the volume in which the rope collision occurs. This is reflected in the larger resistivity in the center of Figures 18(a) and (b). In Figure 20(b), η' peaks inside the current channels, which have nearly merged. Enhanced or anomalous resistivity is thought to be caused by enhanced fluctuations, which scatter current-carrying electrons. We have not identified these instabilities but in all likelihood they are different in the current channels and the reconnection region. Note that the resistivity shown in Figure 18 is not instantaneous but is the average at 5 kHz over the lifetime of the ropes.

The Kubo resistivity is shown as isosurfaces of constant η_zz in Figure 19. This is a companion to Figure 18. The lowest part of the figure drawn as a plane is δz = 0.64 m from the origin of the ropes. The data volume is highly compressed as it is 5 m in length but only tens of centimeters across in each transverse direction. The largest resistivity is 80 times classical, however, the mean η_zz over the volume is η_zz = 6.9 η_classical. The QSL (Q = 100) is drawn in magenta and magnetic field lines inside the QSL are visible. The central region of higher resistivity is very close to the QSL and may be associated with reconnection processes. We note that the QSL is drawn at one time (τ = 5.472 ms) but the Kubo resistivity is a 5 kHz average; therefore, Q is shown to guide the eye. The two outer regions of high resistivity are in the average location of the flux rope currents (which also move about in time).

Zoom In Zoom Out Reset image size

It is instructive to show that the frequency spectra as wave fields can be the cause of enhanced resistivity. The high and low electric and magnetic field spectra are shown in Figure 20. Figure 20(a) shows the magnetic spectrum up to 50 kHz; the largest peak at 5 kHz is the rope kink frequency. The experimental frequency cutoff for the low frequency magnetic field probe was 3 MHz. A 3-axis electric dipole probe was constructed for high frequency (30 kHz–625 MHz) oscillations. We estimate that the electric field at the flux rope frequency is at least two orders of magnitude higher than the signal above 1 MHz. The lower hybrid frequency is approximately 11 MHz and the spectrum in Figure 20 suggests the presence of whistler waves. Figure 20(c) shows the spatial location of the electric field signal at 970 kHz and is representative of the spatial structure of the electric field signals. Figure 20(d) shows the location of the average of the three magnetic field components at 5 kHz magnetic field. The flux ropes at 5 kHz are resolved.

Zoom In Zoom Out Reset image size

There is little magnetic signal above 100 kHz, whereas the electric field has fluctuations up to 100 MHz. The ion cyclotron frequency is 126 kHz. The ion plasma frequency is above 100 MHz. These low amplitude waves could, in principle, contribute to the resistivity, but the data indicate they are largest in the center of the ropes, where the current is largest.

Measurement of the plasma resistivity in current-carrying plasmas is a difficult task considering all the terms in Equation (1). Traditional approaches such as the use of the ratio of the external voltage to the current and neglecting sheaths cannot be employed (DeSilva & Rakhel 2009). It is a simple matter to measure the current but the external voltage has no relation to the internal electric field due to non-neutral sheaths, which always develop on the boundaries. Sheaths are extremely narrow, they are tens of Debye lengths across (${\lambda }_{D}\simeq 30\,\mu$) and probing them is exceedingly difficult. Experiments have tried to correct for the boundary effects (Roehling 1963) but one cannot be sure the corrections are valid without corroborating sheath measurements. Other earlier experiments have used Ohm's law with various assumptions and neglected terms to estimate the resistivity (Baum et al. 1978; Zarnstorff et al. 1988; Kuritsyn et al. 2006). There is no way of knowing if the results stand. The closest experimental configuration to this one was reported by Intrator et al. (2009). In that experiment, the flux ropes were produced by two plasma guns at the end of a vacuum vessel, with an axial magnetic field and no background plasma. Because the experimental repetition rate was low, a probe array which measured B_x, B_y in a single experimental shot was employed on several planes transverse to the background magnetic field. The electrostatic potential was measured at one or more axial locations using a swept Langmuir probe (which has poor temporal resolution) and was considered constant across the transverse planes. It was smaller than the induced electric field, which is not the case here. The perpendicular flow velocity was not directly measured but deduced from ${E}_{z}\times {B}_{\perp }$ although the authors' state that the their approach "fails to estimate the substantial E_z that must exist in the laboratory frame." The axial pressure gradient (Equation (3)) was not included. Although the value of the resistivity is not called out by Intrator et al., one can estimate from Figure 4(a) that it is of the order of 1.3 larger than a classical global estimation. The key result of that experiment was that the magnetic flux pile-up outside the central diffusion region slowed up the reconnection rate through ${\boldsymbol{J}}\times {\boldsymbol{B}}$ forces.

In this experiment, all the terms in Ohm's law have been evaluated using the most comprehensive data set acquired to date. Negative, non-physical, resistivities were deduced when Ohm's law was evaluated point-by-point or by integrating the electric field and plasma current along field lines. This was also the case when Equation (4) was averaged over a flux rope collision. We then examined the possibility that Ohm's law was nonlocal. This turned out to be the case and therefore Ohm's law could not be used to evaluate η.

The AC Kubo conductivity was derived from the data and the parallel resistivity evaluated using Equation (7). The resistivity evaluated at the flux rope kink frequency is enhanced in the regions where the flux rope currents are large. It is just as big in the region between the current channels at a location where the QSL is large. The currents inside the QSL do not directly emanate from electrons drifting from the cathode to the anode 11 m away (see Figure 4(b)). These secondary currents with their own large resistivity are induced by electric fields and possibly electrostatic fields generated by magnetic reconnection. What is the cause of anomalous resistivity (anything larger than classical Coulomb scattering)? Turbulence associated with scattering of the electrons by waves is often invoked as the cause. These waves must have strong enough electric fields to do the job of scattering electrons; candidates are ion acoustic and Langmuir waves. The electron drift speed in the rope current is of the order of eight times the ion sound speed ${c}_{s}=\sqrt{\tfrac{{{KT}}_{e}}{{M}_{i}}}$, and T_e > T_i. Under these conditions, one might expect ion acoustic turbulence to grow. The spectrum in Figure 20(b) has power below 100 MHz. At 50 MHz, the wavelength of an ion acoustic wave is of the order of 200 μm, much smaller than the size of the electric field probe. The wave fields are averaged over the length of the 5 mm legs of the electric dipole, which may result in a far smaller measured field. To get a sense of the wave amplitude, a microprobe (Stillman et al. 2009; Lefebvre et al. 2010) must be employed. This may be done in the future. Finally, is the cause of enhanced resistivity in the rope currents the same as in the reconnection region? This should be the subject of future experiments.

W.G. would like to thank George Morales for interesting discussions. We also would like to thank Zoltan Lucky, Marvin Drandell, and Tai Ly for their expert technical support. The work was funded in part by a Grant from the University of California, Office of the President (12-LR-237124). It was performed at the Basic Plasma Science Facility, which is funded by DOE (DE-FC02-07ER54918) and the National Science Foundation (NSF-PHY 1036140).