Abstract
The Transiting Exoplanet Survey Satellite (TESS) recently observed 18 transits of the hot Jupiter WASP-4b. The sequence of transits occurred 81.6 ± 11.7 s earlier than had been predicted, based on data stretching back to 2007. This is unlikely to be the result of a clock error, because TESS observations of other hot Jupiters (WASP-6b, 18b, and 46b) are compatible with a constant period, ruling out an 81.6 s offset at the 6.4σ level. The 1.3 day orbital period of WASP-4b appears to be decreasing at a rate of 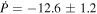 ms per year. The apparent period change might be caused by tidal orbital decay or apsidal precession, although both interpretations have shortcomings. The gravitational influence of a third body is another possibility, though at present there is minimal evidence for such a body. Further observations are needed to confirm and understand the timing variation.
ms per year. The apparent period change might be caused by tidal orbital decay or apsidal precession, although both interpretations have shortcomings. The gravitational influence of a third body is another possibility, though at present there is minimal evidence for such a body. Further observations are needed to confirm and understand the timing variation.
Export citation and abstract BibTeX RIS
1. Introduction
Although the Transiting Exoplanet Survey Satellite (TESS; Ricker et al. 2015) is designed to detect new planets, it is also precisely monitoring most of the planets that have been discovered by ground-based transit surveys over the last two decades. One application of the new TESS data is to search for timing anomalies in previously known hot Jupiter systems. Long-term monitoring of hot Jupiter transit and occultation times should eventually reveal variations caused by three different phenomena.
First, the orbits of most hot Jupiters should shrink because of tidal orbital decay (Counselman 1973; Hut 1980; Levrard et al. 2009; Matsumura et al. 2010). Directly measuring the rate of decay might lead to an improved understanding of how friction dissipates the energy of tidal disturbances (a problem reviewed by Mazeh 2008 and Ogilvie 2014). Second, if hot Jupiter orbits are appreciably eccentric, then long-term timing studies should reveal rotation of the orbital ellipse within the orbital plane ("apsidal precession"). If this effect were observed, it could yield a measure of the planet's Love number, which would constrain the planet's interior structure (Ragozzine & Wolf 2009). The most convincing direct evidence yet found for either orbital decay or apsidal precession of a hot Jupiter is the case of WASP-12b, which has a transit period that has decreased by about 30 ms per year over the last decade (Maciejewski et al. 2016; Patra et al. 2017).
The final effect of interest that can produce period changes in hot Jupiter systems is gravitational acceleration caused by massive outer companions (e.g., Agol et al. 2005, Section 4). Prototypes include WASP-53 and WASP-81, systems in which the inner hot Jupiters are periodically perturbed by eccentric brown dwarf companions with semimajor axes of a few astronomical units (Triaud et al. 2017).
Here, we present evidence for a timing anomaly in the WASP-4 system. The hot Jupiter WASP-4b orbits a G7V star every 1.34 days, corresponding to an orbital distance of 5.5 stellar radii (Wilson et al. 2008; Huitson et al. 2017). It is a good target to search for departures from a constant period, because transits have been observed since 2007. The orbital eccentricity is less than 0.018 (2σ), based on the work of Knutson et al. (2014), who combined the available transit times, occultation times, and Doppler data. The sky projection of the stellar obliquity is also compatible with zero, within about 10° (Triaud et al. 2010; Sanchis-Ojeda et al. 2011).
In what follows, Section 2 presents the new TESS observations, and Section 3 describes our timing analysis. We tried fitting the data with three models: a constant period; a steadily shrinking period; and a slightly eccentric, precessing orbit. A constant period can be ruled out. We cannot distinguish between the possibilities of a decaying orbit, a precessing orbit, and the unmodeled possibility of an orbit being gravitationally perturbed by an outer companion. Any of the three scenarios would have interesting implications (Section 4), and more data are required for a definitive ruling (Section 5). The appendix considers the possibility that the WASP-4 timing anomaly is due to an error in time stamps in the TESS data products. We found this possibility to be unlikely because none of the other hot Jupiters we examined show a timing offset with the same amplitude as was seen for WASP-4.
2. New Transits and System Parameters
2.1. Observations
WASP-4 was observed by TESS with Camera 2 from 2018 August 23 to September 20, within the second "sector" of science operations. The star is designated as TIC 402026209 in the TESS Input Catalog (Stassun et al. 2018). The pixel data for an 11 × 11 array surrounding WASP-4 were averaged into 2 min stacks by the onboard computer. The data were downlinked via the Deep Space Network,14 and the spacecraft time stamps were calibrated against the ground-station clocks. The spacecraft clock times were then transformed by the Payload Operations Center into the Temps Dynamique Barycentrique (TDB) reference system. The images were then reduced to light curves by the Science Processing Operations Center (SPOC) at NASA Ames (Jenkins et al. 2016). During this processing, the SPOC used the known spacecraft trajectory to compute the barycentric time corrections on a target-by-target basis and expressed the time stamps as Barycentric TESS Julian Dates (BTJD), which is simply the Barycentric Julian Date minus 2,457,000. Light curves that were flagged by the SPOC pipeline as crossing a transit detection threshold were then vetted and released by the MIT TESS Science Office to the Mikulski Archive for Space Telescopes on 2018 November 29 (Ricker & Vanderspek 2018).
We began our analysis with the Presearch Data Conditioning (PDC) light curve, which has had nonastrophysical variability removed through the methods discussed by Smith et al. (2017a, 2017b). We then processed the light curve as follows. First, we removed all points with nonzero quality flags. This removed data that might have been adversely affected by "momentum dumps," the firing of thrusters and resetting of reaction wheels15 that took place every 2.5 days during sector 2. The data during these events were assigned quality flags corresponding to "Reaction Wheel Desaturation Event" and "Manual Exclude" (Tenenbaum & Jenkins 2018, Table 28). For WASP-4, these flags were simultaneously set for 54 distinct cadences, and there were 10 momentum dumps, averaging about 10 min of flagged data per dump. Out of caution, we clipped out an additional 10 min before and after every momentum dump. We also removed the data within the first and last hours of both orbits, because of correlated red noise that appears during those time ranges.
All told, we removed 8% of the original data points and were left with 18,165 measurements of the relative flux of WASP-4. We normalized the data by dividing out the median flux, yielding the measurements shown in Figure 1. We converted the time stamps from BTJDTDB into BJDTDB by adding the appropriate 2,457,000 day offset (Tenenbaum & Jenkins 2018). Many of these and subsequent processing steps were performed using astrobase (Bhatti et al. 2018). We did not "flatten" the light curves, as is often done with splines, polynomials, or Gaussian processes. Instead, we modeled the out-of-transit flux variations simultaneously with the transit parameters, as described below.
2.2. Measuring the Transit Times
Using the cleaned PDC light curve, we applied the Box Least Squares algorithm (Kovács et al. 2002) to estimate the orbital period, transit duration, and a reference epoch using the TESS data alone. Based on the results, we isolated the data within four transit durations of each transit midpoint. To find the transit parameters that best fit the data, we first fitted a line to the out-of-transit flux measurements surrounding each transit and divided it out. We then created a phase-folded light curve from all 18 transits and fitted a standard transit model using the analytic formulae given by Mandel & Agol (2002) and implemented by Kreidberg (2015, BATMAN). We assumed the orbit to be circular, consistent with the limits from radial velocities and occultation timing (Beerer et al. 2011; Knutson et al. 2014; Bonomo et al. 2017). The free parameters were the reference epoch, the planet-to-star radius ratio Rp/R⋆, the orbital distance to stellar radius ratio a/R⋆, the inclination i, two quadratic limb-darkening coefficients  , and the orbital period P.
, and the orbital period P.
We sampled the posterior probability distribution for all of the parameters using the algorithm proposed by Goodman & Weare (2010) and implemented by Foreman-Mackey et al. (2013, emcee). Table 1 gives the results, which are in reasonable agreement with the parameters reported by, for example, Southworth et al. (2009) and Huitson et al. (2017). Figure 2 shows the phase-folded light curve.
Table 1. Selected System Parameters of WASP-4b
| Parameter | Value | 68% Confidence Interval | Comment |
|---|---|---|---|
| Transit/RV parameters: | |||
| Rp/R⋆ | 0.15201 |
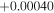 , −0.00033 , −0.00033 |
A |
| i (deg) | 89.06 | +0.65, −0.84 | A |
| a/R⋆ | 5.451 | +0.023, −0.052 | A |
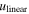
|
0.382 | ⋯ | A |
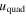
|
0.210 | ⋯ | A |
| K (m s−1) | 241.1 | +2.8, −3.1 | B |
| Stellar parameters: | |||
 (K) (K) |
5400 | ±90 | C |
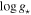 (cgs) (cgs) |
4.47 | ±0.11 | C |
![$[\mathrm{Fe}/{\rm{H}}]$](https://content.cld.iop.org/journals/1538-3881/157/6/217/revision1/ajab189fieqn8.gif)
|
−0.07 | ±0.19 | C |
 (erg cm−2 s−1) (erg cm−2 s−1) |
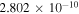
|
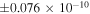
|
D |
| AV (mag) | 0.03 | +0.02, −0.01 | D |
| π (mas) | 3.7145 | 0.0517 | F |
| R⋆ (R⊙) | 0.893 | ±0.034 | E |
 (g cm−3) (g cm−3) |
1.711 |
 , −0.048 , −0.048 |
E |
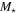 (M⊙) (M⊙) |
0.864 |
 , −0.090 , −0.090 |
E |
| T magnitude | 11.778 | ±0.018 | G |
| Planetary parameters: | |||
| a (au) | 0.0226 |
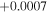 , −0.0008 , −0.0008 |
E |
| Mp (MJup) | 1.186 |
 , −0.098 , −0.098 |
E |
| Rp (RJup) | 1.321 | ±0.039 | E |
Note. (A) From phase-folded TESS light curve (Section 2.2). Orbital periods are in Table 4. The limb-darkening parameters were allowed to float around the Claret (2017) prediction, but were unconstrained. (B) Triaud et al. (2010). (C) From HARPS spectra (Doyle et al. 2013). (D) Stassun et al. (2017). (E) This work, see Section 2.3. (F) Gaia Collaboration et al. (2018). (G) Stassun et al. (2018).
Download table as: ASCIITypeset image
To measure the transit times, we returned to the "cleaned" PDC time series and fitted the data within four transit durations of each transit separately. We used four free parameters, the time of midtransit ttra, the planet-to-star radius ratio, and the slope and intercept of a linear trend, to account for any slow variations unrelated to the transit. We fixed the remaining parameters at the values that had been determined from the phase-folded TESS light curve. The uncertainty in each photometric data point was set equal to the rms level of the out-of-transit data.
To verify that the measured uncertainties are estimated accurately, we computed the χ2 value for a linear ephemeris fit to the measured TESS midtransit times. We found that  , with n = 16 degrees of freedom. The variance of the χ2 distribution is 2n, so we would expect χ2 = 16 ± 5.7. Visually inspecting the residuals showed that the error variance had been overestimated, so we multiplied the measured TESS errors by a factor f = 0.76, forcing a reduced χ2 of unity. This lowered the mean uncertainty of the transit midtimes from 29.8 to 22.6 s. We verified that omitting this step did not appreciably alter any of our conclusions.
, with n = 16 degrees of freedom. The variance of the χ2 distribution is 2n, so we would expect χ2 = 16 ± 5.7. Visually inspecting the residuals showed that the error variance had been overestimated, so we multiplied the measured TESS errors by a factor f = 0.76, forcing a reduced χ2 of unity. This lowered the mean uncertainty of the transit midtimes from 29.8 to 22.6 s. We verified that omitting this step did not appreciably alter any of our conclusions.
Figure 1 shows the light curve of each individual transit, the best-fit models, and the residuals. Table 2 reports the midtransit times and their uncertainties. After binning the residuals to 1 hr windows, the light curves have an rms scatter of 586 ppm. The prelaunch TESS noise model16 (Winn 2013; Sullivan et al. 2015, Section 6.4) would have predicted an error budget consisting of the following terms added in quadrature: 410 ppm from photon-counting noise, 202 ppm from detector read noise, and 673 ppm from the zodiacal background light. The level of background light appears to have been overestimated in the model.
Figure 1. TESS observations of WASP-4b. On the left, black points are TESS flux measurements, with a vertical offset applied. Blue curves are best-fit models. The numbers printed next to each light curve are the approximate transit times expressed in BJD minus 2,457,000. The right side shows the residuals.
Download figure:
Standard image High-resolution imageFigure 2. Phase-folded light curve of WASP-4b. Gray points are TESS flux measurements, with median 1σ uncertainty shown in the lower right. Yellow points are binned measurements. The bottom panel shows the residuals. The fit to the phase-folded transit (blue line) is used when measuring midtransit times of individual transits (see Section 2.2).
Download figure:
Standard image High-resolution imageTable 2. WASP-4b Transit Times, Uncertainties, and References
| ttra (BJDTDB) |
 (days) (days) |
Epoch | H13? | References |
|---|---|---|---|---|
| 2454368.59279 | 0.00033 | −1073 | 1 | Wilson et al. (2008) |
| 2454396.69576 | 0.00012 | −1052 | 1 | Gillon et al. (2009b) |
| 2454697.79817 | 0.00009 | −827 | 1 | Winn et al. (2009) |
| 2454701.81303 | 0.00018 | −824 | 1 | Hoyer et al. (2013) |
| 2454701.81280 | 0.00022 | −824 | 1 | Hoyer et al. (2013) |
| 2454705.82715 | 0.00029 | −821 | 1 | Hoyer et al. (2013) |
| 2454728.57767 | 0.00042 | −804 | 1 | Hoyer et al. (2013) |
| 2454732.59197 | 0.00050 | −801 | 1 | Hoyer et al. (2013) |
| 2454740.62125 | 0.00035 | −795 | 1 | Hoyer et al. (2013) |
| 2454748.65111 | 0.00007 | −789 | 1 | Winn et al. (2009) |
| 2454752.66576 | 0.00069 | −786 | 1 | Dragomir et al. (2011) |
| 2455041.72377 | 0.00018 | −570 | 1 | Hoyer et al. (2013) |
| 2455045.73853 | 0.00008 | −567 | 1 | Sanchis-Ojeda et al. (2011) |
| 2455049.75325 | 0.00007 | −564 | 1 | Sanchis-Ojeda et al. (2011) |
| 2455053.76774 | 0.00009 | −561 | 1 | Sanchis-Ojeda et al. (2011) |
| 2455069.82661 | 0.00029 | −549 | 1 | Nikolov et al. (2012) |
| 2455069.82617 | 0.00038 | −549 | 1 | Nikolov et al. (2012) |
| 2455069.82670 | 0.00028 | −549 | 1 | Nikolov et al. (2012) |
| 2455069.82676 | 0.00031 | −549 | 1 | Nikolov et al. (2012) |
| 2455073.84108 | 0.00029 | −546 | 1 | Nikolov et al. (2012) |
| 2455073.84128 | 0.00026 | −546 | 1 | Nikolov et al. (2012) |
| 2455073.84111 | 0.00023 | −546 | 1 | Nikolov et al. (2012) |
| 2455073.84114 | 0.00018 | −546 | 1 | Nikolov et al. (2012) |
| 2455085.88418 | 0.00086 | −537 | 1 | Dragomir et al. (2011) |
| 2455096.59148 | 0.00022 | −529 | 1 | Hoyer et al. (2013) |
| 2455100.60595 | 0.00012 | −526 | 1 | Sanchis-Ojeda et al. (2011) |
| 2455112.64986 | 0.00039 | −517 | 1 | Nikolov et al. (2012) |
| 2455112.65009 | 0.00033 | −517 | 1 | Nikolov et al. (2012) |
| 2455112.65005 | 0.00031 | −517 | 1 | Nikolov et al. (2012) |
| 2455112.65005 | 0.00049 | −517 | 1 | Nikolov et al. (2012) |
| 2455132.72310 | 0.00041 | −502 | 1 | Hoyer et al. (2013) |
| 2455468.61943 | 0.00046 | −251 | 1 | Hoyer et al. (2013) |
| 2455526.16356 | 0.00008 | −208 | 0 | Ranjan et al. (2014) |
| 2455828.60375 | 0.00041 | 18 | 1 | Hoyer et al. (2013) |
| 2455832.61815 | 0.00041 | 21 | 1 | Hoyer et al. (2013) |
| 2455844.66287 | 0.00009 | 30 | 0 | Huitson et al. (2017) |
| 2456216.69123 | 0.00006 | 308 | 0 | Huitson et al. (2017) |
| 2456288.95622 | 0.00015 | 362 | 0 | C. Baxter et al. (2019, in preparation) |
| 2456292.97025 | 0.00019 | 365 | 0 | C. Baxter et al. (2019, in preparation) |
| 2456576.67556 | 0.00005 | 577 | 0 | Huitson et al. (2017) |
| 2456924.61561 | 0.00006 | 837 | 0 | Huitson et al. (2017) |
| 2458355.18490 | 0.00025 | 1906 | 0 | This work |
| 2458356.52251 | 0.00027 | 1907 | 0 | This work |
| 2458357.86105 | 0.00026 | 1908 | 0 | This work |
| 2458359.19946 | 0.00026 | 1909 | 0 | This work |
| 2458360.53707 | 0.00028 | 1910 | 0 | This work |
| 2458361.87538 | 0.00025 | 1911 | 0 | This work |
| 2458363.21411 | 0.00027 | 1912 | 0 | This work |
| 2458364.55193 | 0.00025 | 1913 | 0 | This work |
| 2458365.89057 | 0.00026 | 1914 | 0 | This work |
| 2458369.90506 | 0.00028 | 1917 | 0 | This work |
| 2458371.24298 | 0.00026 | 1918 | 0 | This work |
| 2458372.58124 | 0.00026 | 1919 | 0 | This work |
| 2458373.91981 | 0.00028 | 1920 | 0 | This work |
| 2458375.25792 | 0.00025 | 1921 | 0 | This work |
| 2458376.59623 | 0.00024 | 1922 | 0 | This work |
| 2458377.93434 | 0.00026 | 1923 | 0 | This work |
| 2458379.27319 | 0.00025 | 1924 | 0 | This work |
| 2458380.61098 | 0.00028 | 1925 | 0 | This work |
Note. ttra is the measured transit midtime, and  is its 1σ uncertainty.
is its 1σ uncertainty.  was evaluated from the sampled posteriors by taking the maximum of the difference between the 84th percentile minus the median, and the median minus the 16th percentile. The resulting error variances then appeared to have been overestimated, so we lowered the uncertainties as described in Section 2.2. The "Reference" column refers to the work describing the original observations. The "H13?" column is 1 if the midtime value was taken from Hoyer et al. (2013). Otherwise, the midtime came from the column listed in "Reference." The Hoyer et al. (2013) BJDTT times are equal to BJDTDB for our purposes (Urban & Seidelmann 2012). We omitted the timing measurements from Southworth et al. (2009) because there were technical problems with the computer clock at the time of observation (Nikolov et al. 2012). The two C. Baxter et al. (2019, in preparation) times were obtained from Spitzer/IRAC transit light curves in the 3.6 and 4.5 μm channels.
was evaluated from the sampled posteriors by taking the maximum of the difference between the 84th percentile minus the median, and the median minus the 16th percentile. The resulting error variances then appeared to have been overestimated, so we lowered the uncertainties as described in Section 2.2. The "Reference" column refers to the work describing the original observations. The "H13?" column is 1 if the midtime value was taken from Hoyer et al. (2013). Otherwise, the midtime came from the column listed in "Reference." The Hoyer et al. (2013) BJDTT times are equal to BJDTDB for our purposes (Urban & Seidelmann 2012). We omitted the timing measurements from Southworth et al. (2009) because there were technical problems with the computer clock at the time of observation (Nikolov et al. 2012). The two C. Baxter et al. (2019, in preparation) times were obtained from Spitzer/IRAC transit light curves in the 3.6 and 4.5 μm channels.
2.3. Star and Planet Parameters
We calculated the stellar and planetary parameters in the following way. We computed the star's spectral energy distribution based on the Gaia DR2 parallax (after making the small correction advocated by Stassun & Torres 2018) and the broadband magnitudes from the available all-sky catalogs: G from Gaia DR2, BT and VT from Tycho-2, BVgri from APASS, JHKS from 2MASS, and the WISE 1–4 passbands, thus spanning the wavelength range 0.4–22 μm. We adopted the effective temperature from the work by Doyle et al. (2013), who determined the spectroscopic parameters of WASP-4 using high signal-to-noise ratio observations with the High Accuracy Radial-velocity Planet Searcher (HARPS). Then, we determined the stellar radius through the combination of the bolometric luminosity and the effective temperature, using the Stefan–Boltzmann law. To determine the stellar mass, we first computed the mean stellar density based on the value of a/R⋆ that gave the best fit to the phase-folded TESS light curve (for the relevant equation, see Seager & Mallén-Ornelas 2003 or Winn 2010). The mass was calculated from the radius and density, and the orbital distance was also calculated from the radius and a/R⋆. The planetary radius was calculated as the product of R⋆ and Rp/R⋆. Finally, the planet mass was calculated based on the stellar mass, the radial-velocity amplitude observed by Triaud et al. (2010), and the orbital inclination.
Table 1 gives the resulting parameters, which we adopted for the remaining analysis. The uncertainties in our derived stellar and planetary parameters are propagated according to standard analytic formulae, under the assumption that the variables are uncorrelated and normally distributed. Our system parameters are in agreement with those of previous investigators, but have the benefit of incorporating the Gaia parallax (Wilson et al. 2008; Gillon et al. 2009a; Winn et al. 2009; Southworth 2011; Petrucci et al. 2013; Huitson et al. 2017). By comparing the star's luminosity and spectroscopic parameters with the outputs of the Yonsei–Yale stellar-evolutionary models, we found that WASP-4 is a main-sequence star with an age of approximately 7 Gyr (Demarque et al. 2004).
3. Timing Analysis
3.1. Pre-TESS Timing Measurements
Table 2 gives the transit times we used in our analysis. We included data from peer-reviewed literature for which the analysis was based on observations of a single transit, and for which the midpoint was allowed to be a free parameter. We also required that the time system be clearly documented. Many of the times were previously compiled by Hoyer et al. (2013). We confirmed that the times in that paper were in agreement with the original sources and that barycentric corrections had been performed when needed.
The earliest epoch is from EulerCam on the 1.2 m Euler telescope (Wilson et al. 2008). The second epoch is based on z-band photometry acquired by Gillon et al. (2009b) at the VLT 8.2 m with FORS2. Subsequent observations were performed by Winn et al. (2009), Dragomir et al. (2011), Sanchis-Ojeda et al. (2011), Nikolov et al. (2012), Hoyer et al. (2013), and Ranjan et al. (2014). Finally, Huitson et al. (2017) acquired optical transit spectra with the 8.1 m Gemini South telescope between 2011 and 2014, one transit per season. The per-point standard deviation of their light curves was a few hundred parts per million. The average precision in their reported transit times was 5.6 s. Since these data points carry significant weight in the analysis, we corresponded with the authors to confirm that the time stamps in their data represent midexposure times, that the barycentric correction was performed correctly, and that the time system of the final results was BJDTDB. These same authors also used the same instrument and method to analyze other hot Jupiters, none of which showed a departure from a constant-period model. Finally, these authors also measured two transit midpoints using Spitzer (C. Baxter et al. 2019, in preparation); these times agree with the Gemini South results.
We also compiled the available occultation times, which are given in Table 3. The tabulated values have been corrected for the light travel time across the diameter of the orbit by subtracting 2a/c = 22.8 s from the observed time. Beerer et al. (2011) observed two occultations of WASP-4b using warm Spitzer in the 3.6 and 4.5 μm bands. Cáceres et al. (2011) detected an occultation from the ground in the KS band and gave a time in HJD, without specifying the time standard. We assumed the standard was UTC, and we performed the appropriate corrections to convert to BJDTDB. We verified that none of our conclusions would be changed if this assumption was mistaken. Finally, Zhou et al. (2015) observed an occultation with the Anglo-Australian Telescope. They did not report the observed midpoint, but they did report a result for  based upon the observed midpoint. We calculated the implied midpoint using the formula (e.g., Winn 2010)
based upon the observed midpoint. We calculated the implied midpoint using the formula (e.g., Winn 2010)

for E the transit number, t0 the reference epoch, e the eccentricity, and ω the argument of pericenter. In total, there are four available occultation times.
Table 3. WASP-4b Occultation Times, Uncertainties, and References
 (BJDTDB) (BJDTDB) |
 (days) (days) |
Epoch | References |
|---|---|---|---|
| 2455102.61210 | 0.00074 | −511 | Cáceres et al. (2011)a |
| 2455172.20159 | 0.00130 | −459 | Beerer et al. (2011) |
| 2455174.87780 | 0.00087 | −457 | Beerer et al. (2011) |
| 2456907.88714 | 0.00290 | 838 | Zhou et al. (2015)b |
Notes.  is the measured occultation midtime, minus the 2a/c = 22.8 s light travel time;
is the measured occultation midtime, minus the 2a/c = 22.8 s light travel time;  is the 1σ uncertainty on the occultation time.
is the 1σ uncertainty on the occultation time.
 and converted to
and converted to  for the tabulated time.
bZhou et al. (2015) fixed the epoch and let
for the tabulated time.
bZhou et al. (2015) fixed the epoch and let 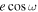 float. Using the reported dates of observation, we converted their
float. Using the reported dates of observation, we converted their 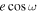 values into an occultation time using Equation (1) of the text.
values into an occultation time using Equation (1) of the text.
Download table as: ASCIITypeset image
3.2. Analysis
First, we performed a weighted least-squares fit of a constant-period model (a "linear ephemeris") to the pre-TESS data, and we used it to extrapolate to the epochs of the TESS observations. The residuals of the best-fitting model are shown in Figure 3. The transits observed by TESS occurred earlier than expected. Because the TESS mission is still in an early stage, we were concerned about a possible offset in the TESS time stamps due to an error with the TESS clock or the data processing pipeline. The appendix describes some tests that convinced us that a simple offset is unlikely. Assuming that the observed timing variation is astrophysical, we proceeded by exploring three models for the timing data in a manner identical to the study by Patra et al. (2017).
Figure 3. TESS saw WASP-4b transit earlier than expected. Both plots show the deviations between observed and calculated transit times, where the calculation is based only on pre-TESS data and assumes a constant period. The blue bands depict the ±1σ credible interval of the predicted times. Top: The full timing data set spans 11 yr. The darkest points correspond to the most precise data. The binned TESS point is the weighted average of 18 TESS transits. Bottom: close-up of the TESS observations. The red band shows the average deviation of the TESS transits (±1σ), which arrived  earlier than predicted.
earlier than predicted.
Download figure:
Standard image High-resolution imageThe first model assumes a constant orbital period on a circular orbit:


where E is the epoch number. We defined the epoch numbers such that E = 0 is near the weighted average of the observed times. This helps to reduce the covariance between t0 and P.
The second model assumes the period is changing at a steady rate:


The three free parameters are the reference epoch t0, the period at the reference epoch, and the period derivative,  .
.
The third model assumes the planet has a slightly eccentric orbit and that the line of apsides is rotating (Giménez & Bastero 1995):


where Ps is the sidereal period, e is the eccentricity,  is the anomalistic period, and ω is the argument of pericenter. In this model, the angular velocity of the line of apsides
is the anomalistic period, and ω is the argument of pericenter. In this model, the angular velocity of the line of apsides  is constant,
is constant,

and the sidereal and anomalistic periods are connected through the equation

The sidereal period is the duration required to return to the same orientation with respect to the stars; the slightly longer anomalistic period is the duration required to reach a fixed longitude with respect to the rotating line of apsides. The five free parameters of this model are  , denoting the reference epoch, the sidereal period, the eccentricity, the argument of pericenter at the reference epoch, and the angular velocity of the line of apsides.
, denoting the reference epoch, the sidereal period, the eccentricity, the argument of pericenter at the reference epoch, and the angular velocity of the line of apsides.
We fitted each model by assuming a Gaussian likelihood and sampling over the posterior probability distributions. The prior for the quadratic model allowed the period derivative to have any sign. We considered two possible priors for the precession model: the first is a wide prior that allows nonphysical values of the planetary Love number (Equation (18)). The second prior requires that the planetary Love number is less than that of a sphere of constant density.
Figure 4 shows the residuals with respect to the constant-period model. The best-fitting constant-period model has χ2 = 174 and 61 degrees of freedom. The best-fitting quadratic model has χ2 = 62.6 and 60 degrees of freedom. The best-fitting precession model under the wide prior has χ2 = 64.3 and 58 degrees of freedom. Under the physical prior, the best fit is slightly worse, with χ2 = 64.8. The precession and quadratic models both provide much better fits than the constant-period model. The difference in χ2 between the linear and quadratic models corresponds to  .
.
Figure 4. Timing residuals and best-fit models for WASP-4b. The vertical axis shows the observed times minus the calculated times assuming a constant period for transits (top) and occultations (bottom). In the upper panel, darker points correspond to more precise data. The constant-period model (gray line) is a poor description of the data. Models with a decreasing period (blue) or an eccentric, precessing orbit (orange) provide better fits. The binned TESS point (red square) is the weighted average of 18 TESS transits and is for display purposes only. The models were fitted to all of the individual transit times.
Download figure:
Standard image High-resolution imageThe quadratic model provides a marginally better fit to the data than the precession model. It is favored by Δχ2 = 1.7 and has two fewer free parameters. A useful heuristic for model comparison is the Bayesian information criterion,

where k is the number of free parameters, and n is the number of data points. In this case, n = 62. The difference in the BIC between the precession and decay models is  , assuming a wide prior for the precession model. This corresponds to a Bayes factor of
, assuming a wide prior for the precession model. This corresponds to a Bayes factor of  . Likewise, the Akaike information criterion favors the constant-period-derivative model by ΔAIC = 5.8. Differences of this magnitude are traditionally deemed "strong evidence" that one model is a better description of the data than the other (Kass & Raftery 1995), although we prefer to reserve judgment until more data can be obtained.
. Likewise, the Akaike information criterion favors the constant-period-derivative model by ΔAIC = 5.8. Differences of this magnitude are traditionally deemed "strong evidence" that one model is a better description of the data than the other (Kass & Raftery 1995), although we prefer to reserve judgment until more data can be obtained.
In the quadratic model, the period derivative is
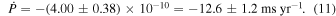
For comparison, the best-fitting period derivative of WASP-12b is  (Maciejewski et al. 2016; Patra et al. 2017). If both planets are truly falling onto their stars, then WASP-4b is falling at about half the rate of WASP-12b.
(Maciejewski et al. 2016; Patra et al. 2017). If both planets are truly falling onto their stars, then WASP-4b is falling at about half the rate of WASP-12b.
In the precession model, the best-fit eccentricity is

The longitude of periastron advances by  , and the precession period is
, and the precession period is  yr. All of the best-fitting parameters (the medians of the posterior distributions) and the 68% credible intervals are reported in Table 4.
yr. All of the best-fitting parameters (the medians of the posterior distributions) and the 68% credible intervals are reported in Table 4.
Table 4. Best-fit Transit Timing Model Parameters
| Parameter | Median Value (Unc.)a |
|---|---|
| Constant period | |
t0 (
|
2455804.515752(+19)(−19) |
| P (days) | 1.338231466(+23)(−22) |
| Constant period derivative | |
t0 (
|
2455804.515918(+24)(−24) |
| P (days) | 1.338231679(+31)(−31) |
| dP/dt |

|
| Apsidal precession (wide prior) | |
t0 (
|
2455804.51530(+25)(−31) |
| Ps (days) | 1.33823127(+20)(−48) |
| e |

|
 (rad) (rad) |
2.40(+38)(−34) |
 (rad epoch−1) (rad epoch−1) |

|
Note.
aThe numbers in parentheses give the 68% confidence interval for the final two digits, where appropriate.Download table as: ASCIITypeset image
3.3. Possible Systematic Errors
To assess the overall robustness of our results, we considered a few possible systematic effects in the timing data set.
Suspect pre-TESS light curves—Some of the pre-TESS light curves have incomplete phase coverage: a handful of the transit times in Table 2 are from light curves with gaps. A separate issue is the effect of spot-crossing anomalies on transit timings. To address these concerns, we repeated the model fitting described above, but omitted epochs −827, −804, −537, and −208 because of gaps in their coverage. We also omitted epochs −526 and −561 because of visible spot anomalies during the transits. (All epoch numbers are as in Table 2.) The resulting best-fit transit timing model parameters were all within 1σ of the values quoted in Table 4. The uncertainties, goodness-of-fit statistics, and model comparison statistics did not appreciably change.
Spot-crossing events in TESS data—To explore the effect of possible spot-crossing events on the TESS transit time measurements, we performed a separate test. We injected triangular spot anomalies with amplitude 0.03% and duration 30 min at random phases into each transit. The amplitude was chosen to be larger than the spot-crossing anomalies observed by Southworth et al. (2009) and Sanchis-Ojeda et al. (2011), and the duration was chosen to be comparable to those of previously observed events. Spots of these amplitudes resemble the possible anomalies present in transits "1360.54" and "1372.58" of Figure 1.
With spots injected, we repeated our measurement of the transit times. On average, the measured transit times did not change after injecting spots, because the flux deviations are equally likely to occur in the first and second halves of the transit. For individual transits, there were no cases for which the timing deviation was larger than one minute. The largest shifts occur when the spot anomaly occurs during transit ingress or egress, in which case the measured midtime is shifted either late or early by between 30 and 50 s.
The TESS observations could therefore be skewed early if there were spot-crossing events during every egress. Two arguments rule out this possibility. (1) The light-curve residuals do not show evidence for these events. (2) The stellar rotation period is between 20 and 40 days, and the sky-projected stellar obliquity is less than 10° (Triaud et al. 2010; Sanchis-Ojeda et al. 2011; Hoyer et al. 2013). Since the planet orbits every 1.3 days, requiring that spot anomalies always occur during egress would be equivalent to requiring a stellar spot distribution that is exquisitely (and thus implausibly) distributed to match the planet egress times.
Detrending choices in pre-TESS data—There is a final concern that is difficult to address. We collected the midtransit time values derived by different authors, who used heterogeneous methods to fit and detrend their light curves. We have also assumed that these authors have correctly documented the time systems in which the data are reported. Further, though many choices in transit fitting (e.g., parameterization of limb darkening and eccentricity) do not affect transit midtime measurements, different detrending approaches can asymmetrically warp transits and shift midtransit times. The magnitude of this systematic effect is hard to quantify, but the situation is fairly clear from Figure 4. Many independent authors provided transit measurements shortly after WASP-4b's discovery, and the data are consistent with each other. Huitson et al. (2017) provided the most important data from epochs 0 to 1000. If their data were systematically affected by detrending choices or time-system confusion at the level of several times their reported uncertainties, then it is possible that the orbital period is constant despite the evidence in the TESS data. For this reason, we paid careful attention to the Huitson et al. (2017) data set, and we corresponded with the authors to confirm that their results are not affected by systematic effects of the required amplitude.
None of the concerns mentioned in this subsection seem likely to explain the observed timing variations. We proceed by considering possible astrophysical explanations.
4. Interpretation
4.1. Orbital Decay
If the timing variation is caused entirely by orbital decay, then the best-fit model parameters yield a characteristic decay timescale of

For comparison, the corresponding time for WASP-12b is 3.2 Myr (Patra et al. 2017).
If WASP-4 really is undergoing rapid orbital decay, then how many of the other known hot Jupiters should have orbits that are decaying at detectable (or nearly detectable) rates? Figure 5 compares some key properties of WASP-4 with those of a larger ensemble of hot Jupiters. The middle panel displays two parameters that strongly affect the expected orbital-decay timescale,  and a/R⋆. WASP-4 has one of the shortest theoretical timescales for orbital decay. Figure 5 shows about 20 hot Jupiters (including WASP-12) for which the theoretical timescale is shorter. In almost all of those cases, though, the planet was discovered more recently than WASP-4, and a decade-long baseline of observations is not yet available. A separate consideration not shown in Figure 5 is that the hot Jupiter host stars have a variety of different structures, from being fully convective to nearly fully radiative, which may lead to widely divergent tidal dissipation timescales.
and a/R⋆. WASP-4 has one of the shortest theoretical timescales for orbital decay. Figure 5 shows about 20 hot Jupiters (including WASP-12) for which the theoretical timescale is shorter. In almost all of those cases, though, the planet was discovered more recently than WASP-4, and a decade-long baseline of observations is not yet available. A separate consideration not shown in Figure 5 is that the hot Jupiter host stars have a variety of different structures, from being fully convective to nearly fully radiative, which may lead to widely divergent tidal dissipation timescales.
Figure 5. WASP-4b in the context of other hot Jupiters. Most of the data in these plots are from Bonomo et al. (2017), who measured the eccentricities using radial velocities. The colored symbols highlight WASP-4, WASP-12 (which also shows evidence for a decreasing period), and the hot Jupiters analyzed in the appendix. Top: key parameters relevant to eccentricity damping. Solid squares represent planets with a securely detected nonzero eccentricity. Circles represent planets whose orbits are consistent with circular. Lines of constant damping timescale are drawn based on Equation (14) and assuming  . WASP-4b has one of the shortest eccentricity damping times. Middle: key parameters relevant to orbital decay. Lines of constant decay timescale are drawn based on Equation (15), assuming
. WASP-4b has one of the shortest eccentricity damping times. Middle: key parameters relevant to orbital decay. Lines of constant decay timescale are drawn based on Equation (15), assuming  . WASP-4b has a relatively short orbital-decay timescale, although it is not as extreme a case in this regard as it is for eccentricity damping. Bottom: a Hertzsprung–Russell diagram for hot Jupiter hosts. WASP-4 appears to be on the main sequence.
. WASP-4b has a relatively short orbital-decay timescale, although it is not as extreme a case in this regard as it is for eccentricity damping. Bottom: a Hertzsprung–Russell diagram for hot Jupiter hosts. WASP-4 appears to be on the main sequence.
Download figure:
Standard image High-resolution imageIn the simple "constant phase lag" model for tidal interaction (Zahn 1977), the rate of dissipation can be parameterized by a modified17
quality factor,  . Here, Q⋆ is the ratio between the energy stored in the equilibrium deformation of the star and the energy lost to heat per tidal period (e.g., Goldreich & Soter 1966). A larger Q⋆ implies less efficient tidal dissipation. The dimensionless number k⋆ is the stellar Love number, which is smaller when the star's density distribution is more centrally concentrated. In this model, once the planet's spin and orbit are synchronized, then the semimajor axis and eccentricity evolve as (Appendix B of Metzger et al. 2012)
. Here, Q⋆ is the ratio between the energy stored in the equilibrium deformation of the star and the energy lost to heat per tidal period (e.g., Goldreich & Soter 1966). A larger Q⋆ implies less efficient tidal dissipation. The dimensionless number k⋆ is the stellar Love number, which is smaller when the star's density distribution is more centrally concentrated. In this model, once the planet's spin and orbit are synchronized, then the semimajor axis and eccentricity evolve as (Appendix B of Metzger et al. 2012)
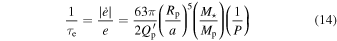
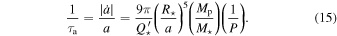
The orbital period evolves as

The modified quality factor of WASP-4 corresponding to the observed value of  is
is

This is about an order of magnitude lower than the value that was inferred for WASP-12b. It is also smaller than most theoreticians would have expected. The  value of Jupiter is estimated to be ≈
value of Jupiter is estimated to be ≈ , based on the observed motions of the Galilean moons (Lainey et al. 2009). For stars, studies of the binary eccentricity distribution have been interpreted with tidal models, giving
, based on the observed motions of the Galilean moons (Lainey et al. 2009). For stars, studies of the binary eccentricity distribution have been interpreted with tidal models, giving  (e.g., Meibom & Mathieu 2005; Belczynski et al. 2008; Geller et al. 2013; Milliman et al. 2014). Population studies of hot Jupiter systems have also been undertaken, generally finding
(e.g., Meibom & Mathieu 2005; Belczynski et al. 2008; Geller et al. 2013; Milliman et al. 2014). Population studies of hot Jupiter systems have also been undertaken, generally finding  using different models (Jackson et al. 2009; Hansen 2010; Penev et al. 2012, 2018; Collier Cameron & Jardine 2018). For instance, motivated by the rapid rotation of some hot Jupiter hosts (Pont 2009; Ciceri et al. 2016a; Penev et al. 2016), Penev et al. (2018) modeled the evolution of hot Jupiter systems under the influence of a magnetized wind and a constant phase-lag tide. For WASP-4, their method gave
using different models (Jackson et al. 2009; Hansen 2010; Penev et al. 2012, 2018; Collier Cameron & Jardine 2018). For instance, motivated by the rapid rotation of some hot Jupiter hosts (Pont 2009; Ciceri et al. 2016a; Penev et al. 2016), Penev et al. (2018) modeled the evolution of hot Jupiter systems under the influence of a magnetized wind and a constant phase-lag tide. For WASP-4, their method gave  , which would correspond to
, which would correspond to 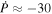 μs per year. This strongly disagrees with the period change that we have observed.
μs per year. This strongly disagrees with the period change that we have observed.
Essick & Weinberg (2016) studied the problem of the orbital decay of hot Jupiters using a theory in which gravity modes are excited at the base of the stellar convective zone, propagate inward through the radiative core, and break near the stellar core, leading to energy dissipation. They predicted the stellar quality factors in hot Jupiter systems to vary in  . From their Equation (26), the prediction for WASP-4 is
. From their Equation (26), the prediction for WASP-4 is 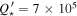 , which is an order of magnitude larger than implied by the observed period change.
, which is an order of magnitude larger than implied by the observed period change.
The applicability of the Essick & Weinberg (2016) model depends on the evolutionary state of the star. Weinberg et al. (2017) showed that more rapid dissipation—enough to account for the period change of WASP-12b—could exist in stars that have begun evolving into red giants. The bottom panel of Figure 5 shows a Hertzsprung–Russell diagram of hot Jupiter hosts, including WASP-4. On the y axis is  , for g the apparent Gaia-band magnitude and μ the distance modulus reported by Gaia Collaboration et al. (2018). The x axis is the effective temperature from Bonomo et al. (2017), which for WASP-4 agrees within 1σ of that from Table 1. Inspecting the HR diagram, we see WASP-4 shows little evidence of being evolved, in agreement with our analysis from Section 2.3.
, for g the apparent Gaia-band magnitude and μ the distance modulus reported by Gaia Collaboration et al. (2018). The x axis is the effective temperature from Bonomo et al. (2017), which for WASP-4 agrees within 1σ of that from Table 1. Inspecting the HR diagram, we see WASP-4 shows little evidence of being evolved, in agreement with our analysis from Section 2.3.
To summarize, if the observed period change is caused entirely by tidal orbital decay, then the constant-phase-lag tidal model implies a stellar tidal dissipation rate that is higher than expected by at least an order of magnitude. It might be possible that we are observing at a special time, shortly after the planet's inward migration, or when the planet is near resonance with a stellar oscillation mode. Tidal dissipation rates might also be increased if the star is just turning off the main sequence. Another hypothesis, recently advanced by Millholland & Laughlin (2018) for the case of WASP-12b, is that an exterior planet could be trapping WASP-4b's spin vector in a high-obliquity state, leading to rapid dissipation through planetary obliquity tides.
4.2. Apsidal Precession
If instead the observed timing variation is just a small portion of an apsidal precession cycle, then the orbital eccentricity is a few times 10−3, and the full precession period is about 27 yr. Ragozzine & Wolf (2009) calculated apsidal precession periods for hot Jupiters, finding them to range between about 10 and 100 yr. They highlighted that for many hot Jupiters, including WASP-4b, the theoretical precession rate is dominated by the non-Keplerian force that is due to the planet's tidal bulge. Precession from general relativity, the planet's rotational bulge, and the star's rotational and tidal bulges contribute at the 10% level at most. Thus, a measurement of the precession rate can be used to determine the planet's Love number. From their Equation (14), the implied Love number for WASP-4b is


where the uncertainties in the semimajor axis and planet radius have been propagated through our Markov chains, and  denotes the uniform distribution. For comparison, the Love number of Jupiter is about 0.55 (Wahl et al. 2016; Ni 2018), and a uniform-density sphere has
denotes the uniform distribution. For comparison, the Love number of Jupiter is about 0.55 (Wahl et al. 2016; Ni 2018), and a uniform-density sphere has  . The uncertainty in
. The uncertainty in  for WASP-4b is large because the eccentricity, reference time, and
for WASP-4b is large because the eccentricity, reference time, and 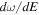 have strongly correlated errors, and the four available occultation times only weakly constrain these parameters (Figure 7).
have strongly correlated errors, and the four available occultation times only weakly constrain these parameters (Figure 7).
The results under both priors are larger than the Love number of Jupiter, at weak statistical significance. Imposing the physically motivated prior truncates the allowed values of  and drives the precession period toward larger values. Different priors therefore change the predicted evolution of the orbit. While the precession model matches the orbital decay model for the next two decades in transits (Figure 7), in occultations the precession model can deviate from the orbital decay model, particularly if one requires the planetary Love number to be smaller. This suggests that promptly obtaining occultation time measurements for the system could help rule out the apsidal precession model. For the time being, the data are insufficient to make a stronger judgment.
and drives the precession period toward larger values. Different priors therefore change the predicted evolution of the orbit. While the precession model matches the orbital decay model for the next two decades in transits (Figure 7), in occultations the precession model can deviate from the orbital decay model, particularly if one requires the planetary Love number to be smaller. This suggests that promptly obtaining occultation time measurements for the system could help rule out the apsidal precession model. For the time being, the data are insufficient to make a stronger judgment.
Regardless of the detailed model assumptions, the main physical problem with the apsidal precession hypothesis is explaining why the eccentricity would be as large as ∼10−3 despite rapid tidal circularization. For WASP-4, Equation (14) gives  . The star is several billion years old, so unless the planet arrived very recently, any initial eccentricity should have been lowered well below ∼10−3. The top panel of Figure 5 compares the expected eccentricity damping time of WASP-4b with that of other transiting giant planets. WASP-4b has one of the shortest known eccentricity damping times.
. The star is several billion years old, so unless the planet arrived very recently, any initial eccentricity should have been lowered well below ∼10−3. The top panel of Figure 5 compares the expected eccentricity damping time of WASP-4b with that of other transiting giant planets. WASP-4b has one of the shortest known eccentricity damping times.
Neighboring companion—One way to maintain a significant eccentricity is through the gravitational perturbations from another planet. Mardling (2007) considered the long-term tidal evolution of hot Jupiters with companions. The companion in their model is coplanar and can have a mass down to an Earth mass; the main requirement is that both the hot Jupiter and the outer companion start on eccentric orbits. They found that although the early phases of the two-planet eccentricity evolution occur quickly, the final phase of the joint eccentricity evolution toward circularity would occur on timescales several orders of magnitude longer than the circularization time of an isolated hot Jupiter (see their Figures 4 and 5).
A separate way a neighboring companion could excite the hot Jupiter's eccentricity is through the Kozai–Lidov mechanism (Kozai 1962; Lidov 1962). In this case, the orbital plane of the outer companion, "c," would need to be inclined relative to that of the hot Jupiter, "b," by at least 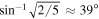 . For the Kozai–Lidov mechanism to operate at maximum efficiency, we need (Bailey & Goodman 2019, Equation (20))
. For the Kozai–Lidov mechanism to operate at maximum efficiency, we need (Bailey & Goodman 2019, Equation (20))

where  is the semimajor axis of WASP-4b,
is the semimajor axis of WASP-4b,  is the mass of the hypothetical WASP-4c, and
is the mass of the hypothetical WASP-4c, and  is WASP-4c's semimajor axis. Owing to our imprecise measurement, in Equation (20) we have assumed WASP-4b's Love number is
is WASP-4c's semimajor axis. Owing to our imprecise measurement, in Equation (20) we have assumed WASP-4b's Love number is  , similar to Jupiter. For the radial velocity (RV) signal of the companion to remain undetected, it would need to be in the residual
, similar to Jupiter. For the radial velocity (RV) signal of the companion to remain undetected, it would need to be in the residual 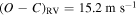 reported by Triaud et al. (2010). Again following Bailey & Goodman (2019), this implies
reported by Triaud et al. (2010). Again following Bailey & Goodman (2019), this implies

for  , a geometric prefactor that depends on the argument of periastron
, a geometric prefactor that depends on the argument of periastron 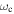 and inclination
and inclination  of the exterior companion (Bailey & Goodman 2019, Equation (23)). Since WASP-4b is transiting, f can be arbitrarily small, and both of the preceding limits can be satisfied.
of the exterior companion (Bailey & Goodman 2019, Equation (23)). Since WASP-4b is transiting, f can be arbitrarily small, and both of the preceding limits can be satisfied.
Fluctuations in the gravitational potential from convection—An independent mechanism to pump the eccentricity invokes the gravitational fluctuations from stellar convection (Phinney 1992, Section 7). From Equation (7.33) of that work, the mean-squared eccentricity of the orbit is

where L is the stellar luminosity,  and
and  are the width and mass of the convective region, μ is the reduced mass, n is the orbital frequency, and a is the semimajor axis. For the luminosity, reduced mass, and semimajor axis, we used values from Table 1, combined with the Stefan–Boltzmann law and standard definitions. To estimate the width and mass of the convective region, we ran the MESA code for a star with mass and metallicity matched to WASP-4 and the input physics detailed in the MIST isochrones project (Paxton et al. 2011, 2013, 2015; Choi et al. 2016; Dotter 2016). We identified the tachocline boundary using the mixing types specified in the resulting radial profiles and found
are the width and mass of the convective region, μ is the reduced mass, n is the orbital frequency, and a is the semimajor axis. For the luminosity, reduced mass, and semimajor axis, we used values from Table 1, combined with the Stefan–Boltzmann law and standard definitions. To estimate the width and mass of the convective region, we ran the MESA code for a star with mass and metallicity matched to WASP-4 and the input physics detailed in the MIST isochrones project (Paxton et al. 2011, 2013, 2015; Choi et al. 2016; Dotter 2016). We identified the tachocline boundary using the mixing types specified in the resulting radial profiles and found  and
and  . For WASP-4, this implies
. For WASP-4, this implies  . Hence, this mechanism does not seem capable of producing the required eccentricity of ∼10−3.
. Hence, this mechanism does not seem capable of producing the required eccentricity of ∼10−3.
4.3. Timing Variation Due to Line-of-sight Acceleration
An acceleration of the center of mass of the system toward our line of sight could cause a decrease in the apparent orbital period. The period derivative would be

where 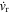 is the time derivative of the radial velocity.
is the time derivative of the radial velocity.
Knutson et al. (2014), combining radial-velocity data from their own program with those of Wilson et al. (2008), Pont et al. (2011), and Husnoo et al. (2012), found evidence for a long-term trend in WASP-4, with low statistical significance:

This acceleration translates to an expected  . The period decrease from the observed RV trend is an order of magnitude smaller than the observed
. The period decrease from the observed RV trend is an order of magnitude smaller than the observed  from transit times,
from transit times,  (Table 4).
(Table 4).
Nonetheless, it is intriguing that the host star shows a weakly significant acceleration, and with the correct sign needed to explain the transit timing variations. Given the potential importance of the radial velocities for interpreting this system, we performed an independent analysis, as follows.
First, we collected the usable RV measurements from CORALIE, HARPS, and HIRES. We included the CORALIE measurements from Wilson et al. (2008) and Triaud et al. (2010), using the homogeneous radial velocities calculated by the latter authors. We included the HARPS values reported by Pont et al. (2011), which are identical to those from Husnoo et al. (2012). We omitted the HARPS data points taken over three nights by Triaud et al. (2010) for Rossiter–McLaughlin observations because they were calculated using a different pipeline than the longer-baseline Pont et al. HARPS measurements, and necessary inclusion of an extra offset term would nullify their statistical value. Finally, we included the five HIRES measurements taken over many years by Knutson et al.(2014).
We then fitted a single Keplerian orbit, plus instrument offsets, jitters, and a long-term trend (Fulton et al. 2018, radvel). We set Gaussian priors on the period and time of inferior conjunction using the values from Table 4, and we fixed the eccentricity to zero, consistent with results from Beerer et al. (2011), Knutson et al. (2014), and Bonomo et al. (2017). The remaining free parameters were the velocity semiamplitude, the instrument zero points, the instrument jitters (an additive white noise term for each instrument), and linear ( ) and optionally second-order (
) and optionally second-order ( ) acceleration terms.
) acceleration terms.
We found that the best-fitting model with both linear and quadratic radial velocity terms was marginally preferred (by  ) over the best-fitting model with only a linear term. Regardless, for consistency with Knutson et al. (2014), who fixed the quadratic component of the long-term trend to zero, in Figure 6 we show best-fitting models for the linear-trend case. The best-fit value for the line-of-sight acceleration,
) over the best-fitting model with only a linear term. Regardless, for consistency with Knutson et al. (2014), who fixed the quadratic component of the long-term trend to zero, in Figure 6 we show best-fitting models for the linear-trend case. The best-fit value for the line-of-sight acceleration,

is within 1σ of the value reported by Knutson et al. (2014). (Note that the CORALIE data used in our and their analyses differ, as we included additional measurements reported by Triaud et al. 2010.) The implied period derivative is still therefore about an order of magnitude smaller than our observed  from transit timing.
from transit timing.
Figure 6. Radial velocities of WASP-4 (top), and residuals from the best-fit Keplerian model (bottom). The lower panel shows the best-fit linear trend inferred from the RV data (black line, 1σ errors in gray), and the trend that would be needed to produce the period decrease seen in transits (purple dotted line). Since both the RV and transit timing data sets are sparse after 2013, a distant, massive companion on an eccentric orbit might still explain the observations.
Download figure:
Standard image High-resolution imageTo summarize, only about one-tenth of the observed period decrease can be explained through a constant acceleration of the WASP-4 system's center of mass. However, given the limited amount and uneven time coverage of the existing radial-velocity data (Figure 6), it remains possible that the center of mass has a more complex motion, perhaps due to a companion on an eccentric orbit (e.g., WASP-53 or WASP-81, Triaud et al. 2017). It would be useful to gather more radial-velocity data to confirm or refute this possibility.
4.4. Applegate Effect
A separate candidate explanation for the timing deviations is the Applegate (1992) effect. Some eclipsing binaries exhibit period modulations with amplitudes of ≲0.05 day over timescales of decades (e.g., Söderhjelm 1980; Hall 1989). The Applegate mechanism explains these modulations by positing that the internal structure of a magnetically active star changes shape via cyclic exchange of angular momentum between the inner and outer zones of the star. This model could also apply to a hot Jupiter orbiting a star with a convective zone. The changing gravitational quadrupole of the star would cause the orbit of the planet to precess on the timescale of the stellar activity cycle. An essential difference between this process and apsidal precession is that Applegate timing variations need not be strictly periodic (e.g., Söderhjelm 1980, Figure 12). This mechanism would also produce transit and occultation timing deviations of the same sign, while for apsidal precession they would have opposite signs. For WASP-4, Watson & Marsh (2010) estimated that the Applegate effect could produce timing deviations of up to 15 s, depending on the modulation period of the stellar dynamo. If this analysis is accurate, then the Applegate mechanism cannot explain the majority of our observed 82 s variation.
4.5. Other Possible Explanations
There are two other small effects worth noting. The first is the Shklovskii (1970) effect, due to the star's proper motion, which leads to an apparent period change of  , which is only 6 × 10−13 for the case of WASP-4. The second effect, described by Rafikov (2009), comes from the star's on-sky motion altering our viewing angle and leads to an observed apsidal precession. The corresponding period change is
, which is only 6 × 10−13 for the case of WASP-4. The second effect, described by Rafikov (2009), comes from the star's on-sky motion altering our viewing angle and leads to an observed apsidal precession. The corresponding period change is 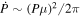 , which is on the order of 10−21 for WASP-4, too small to be of any consequence.
, which is on the order of 10−21 for WASP-4, too small to be of any consequence.
5. Call for Additional Observations
A primary purpose of this work has been to call attention to the timing anomaly of WASP-4 that has been sighted by TESS, and alert observers to the need for follow-up transit timing, occultation timing, and radial-velocity monitoring. There is no unique interpretation of the current data, and two of the possibilities—orbital decay and apsidal precession—would be of great interest to confirm. Detection of orbital decay would lead to an unusually direct determination of a stellar dissipation rate. Detection of apsidal precession would give a rare constraint on the interior density distribution of an exoplanet. The third possibility—a massive outer companion—would be the least exotic option, but nonetheless a valuable discovery.
If TESS is extended beyond its primary mission, it will likely observe additional transits of WASP-4b in the early 2020s. High-precision transit observations with larger telescopes would also be useful. In order to decide between orbital decay and apsidal precession, occultation measurements in both the near term and also in the mid-2020s will be needed (Figure 7). More radial-velocity data would help in the search for additional bodies that could be causing dynamical perturbations or an overall acceleration of the host star. The transit duration variations are expected to be of order 10 s (Pál & Kocsis 2008) and so may remain out of reach.
Figure 7. Further observations are needed to confirm and understand the timing variations of WASP-4b. Symbols are as in Figure 4. Lines are 100 random draws from the posteriors of the apsidal precession model (orange) and the orbital decay model (blue). The prior for the precession model assumes ![${k}_{2,{\rm{p}}}\sim { \mathcal U }[0.015,1.5];$](https://content.cld.iop.org/journals/1538-3881/157/6/217/revision1/ajab189fieqn96.gif) dashed orange lines emphasize samples with planetary Love numbers below 0.75.
dashed orange lines emphasize samples with planetary Love numbers below 0.75.
Download figure:
Standard image High-resolution imageTESS will also be monitoring the other known hot Jupiters, which will reveal whether the timing anomalies seen in WASP-12 and now WASP-4 are commonplace, and may shed some light on the circumstances in which they arise. Other wide-field photometric surveys, such as the Next Generation Transit Survey (Wheatley et al. 2018), HATPI (hatpi.org), and PLATO (Rauer et al. 2014), will also extend the time baseline of transit timing for a large number of systems.
L.G.B. and J.N.W. gladly acknowledge helpful discussions with A. Bailey, J. Goodman, K. Patra, D. Ragozzine, and V. Van Eylen and are grateful to the people who have turned TESS from an idea into reality. L.G.B. thanks A. Bixel and E. May for clarifying details concerning the available IMACS light curves. WASP-4 was included on the "short-cadence" target list thanks to the Guest Investigator programs of J. Southworth and S. Kane (G011112 and G011183, respectively). J.N.W. thanks the TESS project and the Heising-Simons Foundation for supporting this work. T.D. acknowledges support from MIT's Kavli Institute as a Kavli postdoctoral fellow. J.M.D. acknowledges funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement No. 679633; Exo-Atmos), and support from the NWO TOP Grant Module 2 (Project No. 614.001.601). J.E.R. was supported by the Harvard Future Faculty Leaders Postdoctoral Fellowship. This paper includes data collected by the TESS mission, which are publicly available from the Mikulski Archive for Space Telescopes (MAST). Funding for the TESS mission is provided by NASA's Science Mission directorate. This research has made use of the NASA Exoplanet Archive, which is operated by the California Institute of Technology, under contract with the National Aeronautics and Space Administration under the Exoplanet Exploration Program. This work made use of NASA's Astrophysics Data System Bibliographic Services. This research has made use of the VizieR catalog access tool, CDS, Strasbourg, France. The original description of the VizieR service was published in A&AS 143, 23. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement.
Facilities: TESS (Ricker et al. 2015), Gaia (Gaia Collaboration et al. 2016, 2018), Tycho-2 (Høg et al. 2000), 2MASS (Skrutskie et al. 2006), APASS (Henden et al. 2012), WISE (Wright et al. 2010).
Software: astrobase (Bhatti et al. 2018), astropy (The Astropy Collaboration et al. 2018), astroquery (Ginsburg et al. 2018), BATMAN (Kreidberg 2015), corner (Foreman-Mackey 2016), emcee (Foreman-Mackey et al. 2013), IPython (Pérez & Granger 2007), matplotlib (Hunter 2007), MESA (Paxton et al. 2011, 2013, 2015) numpy (Walt et al. 2011), pandas (McKinney 2010), radvel (Fulton et al. 2018), scikit-learn (Pedregosa et al. 2011), scipy (Jones et al. 2001).
Appendix: Verifying the TESS Time Stamps Using Other Hot Jupiters
An obvious concern that one might have about the WASP-4b timing anomaly is that there might be a systematic offset between the TESS time system and the time system in which the previous observations have been reported. There is a precedent for this type of error: data from the Kepler mission was afflicted by a systematic timing error that was corrected only late in the mission (Thompson et al. 2013, Section 3.4).
If the observed timing delay in WASP-4b were caused by a systematic global offset between the TESS time system and the BJD TDB reference, we would expect that it would be apparent in other hot Jupiter systems, too. It would also be apparent in eclipsing binary observations and any other periodic phenomena that have been observed over a long time baseline. Here we examine only hot Jupiters because of our greater familiarity with the data.
We repeated all the data reduction and analysis steps described in this paper for other hot Jupiters observed by TESS for which timing data exists spanning many years. First, we checked which hot Jupiters were observed over the first three TESS sectors using a combination of tessmaps18 and TEPCat (Southworth 2011). We recalculated the barycentric corrections using the Eastman et al. (2010) code and found values that agreed with the light-curve headers to within about 1 s. We then selected hot Jupiters for which there were at least five distinct epochs reported in the peer-reviewed literature. We required that each observation be of a single transit, that the midpoint be fit as a free parameter, and that the time system be clearly documented. Our final hot Jupiter sample included WASP-4b, 5b, 6b, 18b, and 46b. The collected and measured times are given in Tables 5–8 for each.
Table 5. WASP-5b Transit Times, Uncertainties, and References
| ttra (BJDTDB) |
 (days) (days) |
Epoch | Reference |
|---|---|---|---|
| 2454383.76750 | 0.00040 | −885 | Anderson et al. (2008) |
| 2454387.02275 | 0.00100 | −883 | Anderson et al. (2008) |
| 2454636.17459 | 0.00082 | −730 | Fukui et al. (2011) |
| 2454699.68303 | 0.00041 | −691 | Hoyer et al. (2012) |
| 2454707.82465 | 0.00052 | −686 | Hoyer et al. (2012) |
| 2454707.82523 | 0.00025 | −686 | Southworth et al. (2009) |
| 2454730.62243 | 0.00031 | −672 | Southworth et al. (2009) |
| 2454730.62301 | 0.00076 | −672 | Hoyer et al. (2012) |
| 2454761.56356 | 0.00047 | −653 | Hoyer et al. (2012) |
| 2454772.96212 | 0.00075 | −646 | Fukui et al. (2011) |
| 2454774.59093 | 0.00030 | −645 | Hoyer et al. (2012) |
| 2454787.61792 | 0.00069 | −637 | Hoyer et al. (2012) |
| 2455005.82714 | 0.00036 | −503 | Hoyer et al. (2012) |
| 2455049.79540 | 0.00080 | −476 | Hoyer et al. (2012) |
| 2455075.84947 | 0.00056 | −460 | Dragomir et al. (2011) |
| 2455079.10830 | 0.00079 | −458 | Fukui et al. (2011) |
| 2455110.04607 | 0.00089 | −439 | Fukui et al. (2011) |
| 2455123.07611 | 0.00079 | −431 | Fukui et al. (2011) |
| 2455129.58759 | 0.00043 | −427 | Hoyer et al. (2012) |
| 2455364.08150 | 0.00110 | −283 | Fukui et al. (2011) |
| 2455377.10955 | 0.00093 | −275 | Fukui et al. (2011) |
| 2455448.75927 | 0.00110 | −231 | Dragomir et al. (2011) |
| 2456150.61479 | 0.00056 | 200 | Moyano et al. (2017) |
| 2456150.61396 | 0.00057 | 200 | Moyano et al. (2017) |
| 2458355.50829 | 0.00083 | 1554 | This work |
| 2458357.13741 | 0.00071 | 1555 | This work |
| 2458358.76412 | 0.00068 | 1556 | This work |
| 2458360.39377 | 0.00070 | 1557 | This work |
| 2458362.02273 | 0.00073 | 1558 | This work |
| 2458363.64908 | 0.00090 | 1559 | This work |
| 2458365.27827 | 0.00071 | 1560 | This work |
| 2458366.90627 | 0.00075 | 1561 | This work |
| 2458370.16411 | 0.00076 | 1563 | This work |
| 2458371.79126 | 0.00071 | 1564 | This work |
| 2458373.42123 | 0.00075 | 1565 | This work |
| 2458375.04910 | 0.00069 | 1566 | This work |
| 2458376.67856 | 0.00074 | 1567 | This work |
| 2458378.30530 | 0.00087 | 1568 | This work |
| 2458379.93419 | 0.00082 | 1569 | This work |
Note. ttra is the measured transit midtime, and  is its 1σ uncertainty. The "Reference" column refers to the work describing the original observations. All of the literature times except for the two Moyano et al. (2017) times are from the homogeneous Hoyer et al. (2012) analysis.
is its 1σ uncertainty. The "Reference" column refers to the work describing the original observations. All of the literature times except for the two Moyano et al. (2017) times are from the homogeneous Hoyer et al. (2012) analysis.
Download table as: ASCIITypeset image
Table 6. WASP-6b Transit Times, Uncertainties, and References
| ttra (BJDTDB) |
 (days) (days) |
Epoch | References |
|---|---|---|---|
| 2454425.02167 | 0.00022 | −398 | Gillon et al. (2009a) |
| 2455009.83622 | 0.00021 | −224 | Tregloan-Reed et al. (2015) |
| 2455046.80720 | 0.00015 | −213 | Tregloan-Reed et al. (2015) |
| 2455073.69529 | 0.00013 | −205 | Tregloan-Reed et al. (2015) |
| 2455409.79541 | 0.00010 | −105 | Tregloan-Reed et al. (2015) |
| 2455446.76621 | 0.00058 | −94 | Dragomir et al. (2011) |
| 2455473.65439 | 0.00097 | −86 | Jordán et al. (2013) |
| 2455846.72540 | 0.00045 | 25 | Sada et al. (2012) |
| 2456088.71801 | 0.00013 | 97 | Nikolov et al. (2015) |
| 2456095.43974 | 0.00017 | 99 | Nikolov et al. (2015) |
| 2456132.41082 | 0.00017 | 110 | Nikolov et al. (2015) |
| 2458357.39410 | 0.00033 | 772 | This work |
| 2458360.75573 | 0.00033 | 773 | This work |
| 2458364.11691 | 0.00032 | 774 | This work |
| 2458370.83872 | 0.00033 | 776 | This work |
| 2458374.19952 | 0.00031 | 777 | This work |
| 2458377.56026 | 0.00033 | 778 | This work |
| 2458380.92185 | 0.00038 | 779 | This work |
Note. ttra is the measured transit midtime, and  is its 1σ uncertainty. The "Reference" column refers to the work describing the original observations.
is its 1σ uncertainty. The "Reference" column refers to the work describing the original observations.
Download table as: ASCIITypeset image
Table 7. WASP-18b Transit Times, Uncertainties, and References
| ttra (BJDTDB) |
 (days) (days) |
Epoch | References |
|---|---|---|---|
| 2454221.48163 | 0.00038 | −4037 | Hellier et al. (2009) |
| 2455221.30420 | 0.00010 | −2975 | Maxted et al. (2013) |
| 2455432.18970 | 0.00010 | −2751 | Maxted et al. (2013) |
| 2455470.78850 | 0.00040 | −2710 | Maxted et al. (2013) |
| 2455473.61440 | 0.00090 | −2707 | Maxted et al. (2013) |
| 2455554.57860 | 0.00050 | −2621 | Maxted et al. (2013) |
| 2455570.58400 | 0.00048 | −2604 | Maxted et al. (2013) |
| 2455876.55590 | 0.00130 | −2279 | Maxted et al. (2013) |
| 2456896.14780 | 0.00080 | −1196 | Wilkins et al. (2017) |
| 2457255.78320 | 0.00030 | −814 | Wilkins et al. (2017) |
| 2457319.80100 | 0.00039 | −746 | Wilkins et al. (2017) |
| 2458354.45782 | 0.00016 | 353 | This work |
| 2458355.39933 | 0.00015 | 354 | This work |
| 2458356.34070 | 0.00018 | 355 | This work |
| 2458357.28229 | 0.00018 | 356 | This work |
| 2458358.22348 | 0.00018 | 357 | This work |
| 2458359.16523 | 0.00020 | 358 | This work |
| 2458360.10661 | 0.00017 | 359 | This work |
| 2458361.04810 | 0.00017 | 360 | This work |
| 2458361.98968 | 0.00016 | 361 | This work |
| 2458362.93130 | 0.00018 | 362 | This work |
| 2458363.87267 | 0.00018 | 363 | This work |
| 2458364.81374 | 0.00017 | 364 | This work |
| 2458365.75525 | 0.00019 | 365 | This work |
| 2458366.69709 | 0.00018 | 366 | This work |
| 2458369.52128 | 0.00017 | 369 | This work |
| 2458370.46281 | 0.00017 | 370 | This work |
| 2458371.40407 | 0.00017 | 371 | This work |
| 2458372.34537 | 0.00018 | 372 | This work |
| 2458373.28728 | 0.00018 | 373 | This work |
| 2458374.22818 | 0.00016 | 374 | This work |
| 2458375.16977 | 0.00017 | 375 | This work |
| 2458376.11132 | 0.00018 | 376 | This work |
| 2458377.05267 | 0.00017 | 377 | This work |
| 2458377.99444 | 0.00018 | 378 | This work |
| 2458378.93573 | 0.00016 | 379 | This work |
| 2458379.87722 | 0.00017 | 380 | This work |
| 2458380.81889 | 0.00018 | 381 | This work |
| 2458386.46729 | 0.00016 | 387 | This work |
| 2458387.40888 | 0.00017 | 388 | This work |
| 2458388.35021 | 0.00016 | 389 | This work |
| 2458389.29161 | 0.00015 | 390 | This work |
| 2458390.23334 | 0.00016 | 391 | This work |
| 2458391.17452 | 0.00016 | 392 | This work |
| 2458392.11593 | 0.00016 | 393 | This work |
| 2458393.05748 | 0.00015 | 394 | This work |
| 2458393.99898 | 0.00016 | 395 | This work |
| 2458394.94024 | 0.00017 | 396 | This work |
| 2458396.82309 | 0.00015 | 398 | This work |
| 2458397.76450 | 0.00015 | 399 | This work |
| 2458398.70656 | 0.00016 | 400 | This work |
| 2458399.64748 | 0.00015 | 401 | This work |
| 2458399.64748 | 0.00015 | 401 | This work |
| 2458400.58898 | 0.00017 | 402 | This work |
| 2458401.53083 | 0.00016 | 403 | This work |
| 2458402.47209 | 0.00017 | 404 | This work |
| 2458403.41360 | 0.00016 | 405 | This work |
| 2458404.35492 | 0.00017 | 406 | This work |
Note. ttra is the measured transit midtime, and  is its 1σ uncertainty. The "Reference" column refers to the work describing the original observations. All of the literature times are from the homogeneous Wilkins et al. (2017) analysis.
is its 1σ uncertainty. The "Reference" column refers to the work describing the original observations. All of the literature times are from the homogeneous Wilkins et al. (2017) analysis.
Download table as: ASCIITypeset image
Table 8. WASP-46b Transit Times, Uncertainties, and References
| ttra (BJDTDB) |
 (days) (days) |
Epoch | References |
|---|---|---|---|
| 2455396.60785 | 0.00062 | −673 | Anderson et al. (2012) |
| 2455449.53082 | 0.00026 | −636 | Anderson et al. (2012) |
| 2455722.73178 | 0.00023 | −445 | Ciceri et al. (2016b) |
| 2455757.06195 | 0.00094 | −421 | Petrucci et al. (2018) |
| 2455858.61833 | 0.00009 | −350 | Ciceri et al. (2016b) |
| 2456108.92771 | 0.00094 | −175 | Petrucci et al. (2018) |
| 2456111.79422 | 0.00016 | −173 | Ciceri et al. (2016b) |
| 2456111.79413 | 0.00012 | −173 | Ciceri et al. (2016b) |
| 2456111.79424 | 0.00015 | −173 | Ciceri et al. (2016b) |
| 2456130.38895 | 0.00042 | −160 | Petrucci et al. (2018) |
| 2456131.81456 | 0.00112 | −159 | Petrucci et al. (2018) |
| 2456194.75916 | 0.00027 | −115 | Ciceri et al. (2016b) |
| 2456217.64127 | 0.00015 | −99 | Ciceri et al. (2016b) |
| 2456217.64156 | 0.00013 | −99 | Ciceri et al. (2016b) |
| 2456227.65574 | 0.00060 | −92 | Petrucci et al. (2018) |
| 2456407.88096 | 0.00015 | 34 | Ciceri et al. (2016b) |
| 2456407.88085 | 0.00018 | 34 | Ciceri et al. (2016b) |
| 2456407.88148 | 0.00028 | 34 | Ciceri et al. (2016b) |
| 2456407.88159 | 0.00043 | 34 | Ciceri et al. (2016b) |
| 2456460.80526 | 0.00017 | 71 | Ciceri et al. (2016b) |
| 2456460.80450 | 0.00024 | 71 | Ciceri et al. (2016b) |
| 2456460.80547 | 0.00064 | 71 | Ciceri et al. (2016b) |
| 2456510.86818 | 0.00060 | 106 | Petrucci et al. (2018) |
| 2456510.86699 | 0.00015 | 106 | Petrucci et al. (2018) |
| 2456516.58667 | 0.00119 | 110 | Petrucci et al. (2018) |
| 2456520.88012 | 0.00064 | 113 | Petrucci et al. (2018) |
| 2456533.75260 | 0.00071 | 122 | Ciceri et al. (2016b) |
| 2456533.75480 | 0.00015 | 122 | Ciceri et al. (2016b) |
| 2456576.66289 | 0.00109 | 152 | Petrucci et al. (2018) |
| 2456589.54197 | 0.00090 | 161 | Petrucci et al. (2018) |
| 2456609.56653 | 0.00043 | 175 | Petrucci et al. (2018) |
| 2456839.85440 | 0.00123 | 336 | Petrucci et al. (2018) |
| 2456862.74085 | 0.00048 | 352 | Petrucci et al. (2018) |
| 2456882.76566 | 0.00073 | 366 | Petrucci et al. (2018) |
| 2456885.62429 | 0.00053 | 368 | Petrucci et al. (2018) |
| 2456915.66040 | 0.00123 | 389 | Petrucci et al. (2018) |
| 2456942.83880 | 0.00078 | 408 | Petrucci et al. (2018) |
| 2456948.56384 | 0.00074 | 412 | Petrucci et al. (2018) |
| 2457274.68458 | 0.00184 | 640 | Petrucci et al. (2018) |
| 2457294.70886 | 0.00140 | 654 | Petrucci et al. (2018) |
| 2457550.74797 | 0.00031 | 833 | Petrucci et al. (2018) |
| 2457593.65692 | 0.00024 | 863 | Petrucci et al. (2018) |
| 2457600.80985 | 0.00039 | 868 | Petrucci et al. (2018) |
| 2457610.82286 | 0.00020 | 875 | Petrucci et al. (2018) |
| 2458326.00972 | 0.00091 | 1375 | This work |
| 2458327.43899 | 0.00093 | 1376 | This work |
| 2458328.86970 | 0.00094 | 1377 | This work |
| 2458330.29965 | 0.00105 | 1378 | This work |
| 2458331.73234 | 0.00105 | 1379 | This work |
| 2458333.15977 | 0.00086 | 1380 | This work |
| 2458334.59230 | 0.00095 | 1381 | This work |
| 2458336.02222 | 0.00082 | 1382 | This work |
| 2458337.45111 | 0.00099 | 1383 | This work |
| 2458340.31143 | 0.00093 | 1385 | This work |
| 2458341.74347 | 0.00093 | 1386 | This work |
| 2458343.17362 | 0.00093 | 1387 | This work |
| 2458344.60303 | 0.00110 | 1388 | This work |
| 2458346.03436 | 0.00091 | 1389 | This work |
| 2458347.46335 | 0.00168 | 1390 | This work |
| 2458348.89621 | 0.00086 | 1391 | This work |
| 2458350.32672 | 0.00101 | 1392 | This work |
| 2458351.75486 | 0.00103 | 1393 | This work |
Note. ttra is the measured transit midtime, and  is its 1σ uncertainty. The "Reference" column refers to the work describing the original observations. All of the literature times are from the homogeneous Petrucci et al. (2018) analysis. Fourteen of the light curves were acquired by ETD observers (see Petrucci et al. 2018).
is its 1σ uncertainty. The "Reference" column refers to the work describing the original observations. All of the literature times are from the homogeneous Petrucci et al. (2018) analysis. Fourteen of the light curves were acquired by ETD observers (see Petrucci et al. 2018).
Download table as: ASCIITypeset image
We determined the best-fitting constant-period ephemeris based on the pre-TESS data. Then we used the parameters and uncertainties in the best-fitting model to calculate the predicted transit times during the TESS observation period, as well as the uncertainty in the predicted times. The uncertainties are 11, 94, 18, 42, and 59 s for WASP-4b, 5b, 6b, 18b, and 46b, respectively. By comparing the observed and predicted times, Figure 8 shows that WASP-4b is the only hot Jupiter that transited significantly earlier than expected.
Figure 8. There is no evidence for a systematic offset between TESS times and the barycentric reference. While the WASP-4b transits fell about 82 s earlier than expected, other well-observed hot Jupiters, in particular WASP-6b and WASP-18b, arrived on time. Ticks are observed TESS transit midtimes; the orange distribution is a Gaussian centered on zero with standard deviation ( ) calculated from the pre-TESS transit times. The blue distribution is a Gaussian centered on the weighted average of the TESS times, with width equal to the uncertainty in the mean, that is, the standard deviation of the TESS residual times divided by
) calculated from the pre-TESS transit times. The blue distribution is a Gaussian centered on the weighted average of the TESS times, with width equal to the uncertainty in the mean, that is, the standard deviation of the TESS residual times divided by  , with N the number of transits.
, with N the number of transits.
Download figure:
Standard image High-resolution imageTo use these results to place a quantitative limit on any global clock offset, for each hot Jupiter we considered the model

for toffset a systematic constant offset between the reported time stamps and the true  reference. Our priors were
reference. Our priors were



where  and
and  denote a normal and uniform distribution,
denote a normal and uniform distribution,  are the best-fit reference time and period using only the pre-TESS transit times, and
are the best-fit reference time and period using only the pre-TESS transit times, and 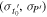 are the corresponding uncertainties.
are the corresponding uncertainties.
For each planet, we asked: what fraction of the posterior for  is consistent with an offset worse than 81.6 s? For WASP-4b, the answer is unsurprisingly 50%. For WASP-6b, the most constraining object, about 1 sample in 2 million is consistent with such a timing offset (4.9σ). For WASP-18b, 1 in 103 samples would be consistent with this timing offset (2.3σ), and in WASP-46b, the limit is 1 in 49 samples (2.0σ). For WASP-5b, the predicted time is too imprecise to rule out timing offsets at the necessary amplitude. Multiplying the three independent probabilities for WASP-6b, 18b, and 46b, we can rule out
is consistent with an offset worse than 81.6 s? For WASP-4b, the answer is unsurprisingly 50%. For WASP-6b, the most constraining object, about 1 sample in 2 million is consistent with such a timing offset (4.9σ). For WASP-18b, 1 in 103 samples would be consistent with this timing offset (2.3σ), and in WASP-46b, the limit is 1 in 49 samples (2.0σ). For WASP-5b, the predicted time is too imprecise to rule out timing offsets at the necessary amplitude. Multiplying the three independent probabilities for WASP-6b, 18b, and 46b, we can rule out  at 6.4σ, or about 1 part in 11 billion.
at 6.4σ, or about 1 part in 11 billion.
Footnotes
- 14
- 15
The spacecraft pointing and momentum dumps are described in the sector 2 data release notes, available at archive.stsci.edu/tess/tess_drn.html.
- 16
github.com/lgbouma/tnm, commit be06f09.
- 17
For stars,
 , so it is important to explicitly distinguish
, so it is important to explicitly distinguish  from Q⋆ (e.g., Schwarzschild 1958).
from Q⋆ (e.g., Schwarzschild 1958). - 18
github.com/lgbouma/tessmaps, commit 569bbc2.