ABSTRACT
The interaction between a small twist and a horizontal chromospheric shocktube is investigated. The magnetic flux tube is modeled using 1.5-D magnetohydrodynamics. The presence of a supersonic yet sub-Alfvénic flow along the flux tube allows the Alfvénic pulse driven at the photospheric boundary to become trapped and amplified between the stationary shock front and photosphere. The amplification of the twist leads to the formation of slow and fast shocks. The pre-existing stationary shock is destabilized and pushed forward as it merges with the slow shock. The propagating fast shock extracts the kinetic energy of the flow and launches rapid twists of 10–15 km s−1 upon each reflection. A cavity is formed between the slow and fast shocks where the flux tube becomes globally twisted within less than an hour. The resultant highly twisted magnetic flux tube is similar to those prone to kink instabilities, which may be responsible for solar eruptions. The generated torsional flux is calculated.
Export citation and abstract BibTeX RIS
1. INTRODUCTION
Magnetic flux tubes are ubiquitous within the solar atmosphere. They are known as the building blocks that may form small or large scale structures. Flux tubes on different scales often exhibit mass flow. Examples include siphon flows in coronal loops (Orlando et al. 1995a, 1995b), counterstreaming (Lin et al. 2003), and field-aligned flows within filament channels (Lin et al. 2005), spicules (Hollweg et al. 1982; De Pontieu et al. 2004; Zaqarashvili & Erdélyi 2009; Scullion et al. 2011), Evershed flows within sunspots (Montesinos & Thomas 1997; Plaza et al. 1997). In addition, non-thermal broadenings have been observed within the chromosphere (Beckers 1968, 1972; Pishkalo 1994; Jess et al. 2009, 2015). These non-thermal broadenings are usually interpreted as Alfvén waves and have been considered as a possible mechanism responsible for Type-I spicule formation (Hollweg et al. 1982; Sterling & Hollweg 1988; Hollweg 1992; Kudoh & Shibata 1999; James et al. 2003; Erdélyi & James 2004) though it is possible that other mechanisms such as leakage of p-mode oscillations along inclined field lines are responsible (De Pontieu et al. 2004). For a review, see Sterling (2000).
Using Hinode De Pontieu et al. (2007) proposed the existence of Type-II spicules, which are more explosive than the classical, Type-I variety. De Pontieu et al. (2012) used the Swedish 1 m Solar Telescope to establish and quantify three types of motions within Type-II spicules: (i) field aligned flows of 50–100 km s−1 (ii) swaying back and forth with speeds of 15–20 km s−1 and (iii) torsional motions between 25 and 30 km s−1. Type-II spicules are often associated with regions of rapid blueshift and redshift. The launch of IRIS (Interface Region Imaging Spectrograph) has led to observations of small-scale twists that propagate along these structures. The typical amplitudes are 10–30 km s−1 and the duration is less than a minute (De Pontieu et al. 2014).
Recently, high-resolution observations from Crisp Imaging Spectro-Polarimeter (Wedemeyer-Böhm et al. 2012) detected a number of small-scale chromospheric swirls. It was also shown numerically by (non)convection simulations (Fedun et al. 2011; Wedemeyer-Böhm et al. 2012) that granular-driven magnetic vortices in the photosphere (Brandt et al. 1988; Bonet et al. 2008, 2010) are capable of driving such motions up to the transition region and further into the lower corona, which provides an alternative method for transmitting energy.
Li et al. (2012) witness flow channels within a solar tornado that rise and fall along curved trajectories and suggest that the motions are along helical magnetic field lines. They also claim that flows and density waves may propagate along the magnetic field lines within the solar tornado. In intergranular lanes, similar motions have been seen in the form of magnetic whirlpools of downflowing plasma (Bonet et al. 2008, 2010). However, it is also worth mentioning that Panasenco et al. (2014) show rapid swirling motions and solar tornadoes may be an illusion caused by 2D projection effects at the solar limb.
Work by Vranjes (2014) has shown that partial ionization of the chromosphere can lead to Alfvén waves being severely damped between the photosphere and corona. Studies by James et al. (2003) and Erdélyi & James (2004) have shown that partial ionization of the atmosphere may aid Alfvén waves with the heating and formation of chromospheric structures such as spicules.
Magnetohydrodynamics (MHD) instabilities in the solar atmosphere play an important role in the amplification of perturbations, which may drastically alter the system. Taroyan (2008) discovered the possibility of a new MHD instability which is based on the interaction between an incompressible Alfvénic perturbation and a compressible plasma flow. The perturbations amplify due to over-reflection—a concept first investigated by Acheson (1976) in regards to the Kelvin–Helmholtz instability.
The Alfvén instability was investigated for siphon flows within asymmetric coronal loops and found that linear torsional perturbations driven at the footpoints are exponentially amplified (Taroyan 2009). Taroyan (2011) considered the Alfvén instability for smooth plasma flow within open and expanding flux tubes in the presence of gravity. The analysis was extended by Taroyan (2015) to include non-isothermal flows, a body force term in the momentum equation, and a full energy equation.
The study of shock waves can be dated back to the 17th century with Sir Isaac Newton's Principia in 1687. Poisson's memoirs in 1808 laid the foundations for the first shock wave theory and later work by De Laplace (1816) and subsequently Rankine (1859) improved Newton's theory by assuming that sound is an adiabatic process. In Hugoniot's (1889) memoirs, the equation which relates the internal energy to the kinetic energy of a thermodynamic system is introduced. Fast forward a couple of centuries and shocks are a topical study in astrophysics and the Sun. Orlando et al. (1995b) investigate the physical conditions within coronal loops that allow the formation of isothermal and adiabatic shocks for shocked critical solutions and shocked supersonic solutions when a siphon flow is present. Shocks appear in abundance in the solar system with shock waves in the solar atmosphere (Hollweg 1992; Ryutova & Tarbell 2003; Centeno et al. 2009), CMEs (Magdalenić et al. 2014; Fainshtein & Egorov 2015; Lugaz et al. 2015), interplanetary shocks within the solar wind (Grygorov et al. 2014) and at the solar wind termination shock (Baranov et al. 1996).
High resolution observations have shown that the Evershed flow is mainly concentrated into the dark penumbral filaments where the magnetic field is nearly horizontal (Title et al. 1992). The flow speed can reach up to 20 km s−1 or more in individual filaments. In some filaments the flow is observed to slow abruptly at a location of enhanced emission, which is strongly suggestive of a standing shock in supersonic siphon flow (Maltby 1975; Georgakilas et al. 2003; Borrero et al. 2005). However, none of these studies have focused on the interaction between a standing shock and an Alfvén wave, until now.
The present paper is the first, pure numerical study that confirms the existence of the Alfvén instability. The study extends the investigation of the phenomenon to the nonlinear regime. The interaction of a small Alfvénic twist with a classical gas-dynamic shock; the amplification of the twist and consequences of nonlinearity; and the role the Alfvén wave plays in energy transfer are analyzed.
In the next section the model set-up is presented. This includes the geometry used, choice of boundary conditions, replication of an Alfvén wave, setting up a stationary shock, and normalization. In Section 3, the conditions required for the Alfvén instability and thus the amplification of an Alfvén wave are discussed. The model results are presented in Section 4 and discussed in Sections 5 and 6.
2. NUMERICAL MODEL
The model presented in this paper is a 1.5-D axisymmetric magnetic shocktube, which was introduced by Hollweg et al. (1982) and subsequently employed by Sterling & Hollweg (1988), Kudoh & Shibata (1999), Matsumoto & Shibata (2010), and others. It is discussed by Hollweg (1981) that a single field-line is modeled which resides close to but not on the axis of symmetry, such that for typical cylindrical coordinates,  at any point. The equations used in these models may describe torsional and shear Alfvén waves in the nonlinear regime depending on whether the chosen geometry is cylindrical or Cartesian (Priest 2014, Section 4.3).
at any point. The equations used in these models may describe torsional and shear Alfvén waves in the nonlinear regime depending on whether the chosen geometry is cylindrical or Cartesian (Priest 2014, Section 4.3).
A uniform background magnetic field in the longitudinal direction, Bz which does not vary in space or time is defined. The magnetic field is highly inclined such that the field-line is virtually horizontal.
In the forthcoming analysis, θ denotes the azimuthal direction and as it is assumed that none of the quantities vary in the azimuthal direction, it follows that  . The model is generated using the MHD equations in VAC (Versatile Advection Code; see, e.g., Tóth 1997). The numerical scheme used to resolve the system is CD4 (4th order central differencing) with a TVDLF (Total Variance Diminishing Lax–Friedrich) predictor step and minmod limiter. The shocktube geometry can be seen in Figure 1.
. The model is generated using the MHD equations in VAC (Versatile Advection Code; see, e.g., Tóth 1997). The numerical scheme used to resolve the system is CD4 (4th order central differencing) with a TVDLF (Total Variance Diminishing Lax–Friedrich) predictor step and minmod limiter. The shocktube geometry can be seen in Figure 1.
Figure 1. A schematic of the magnetic field above a sunspot region. A flow emanates from within a sunspot (red arrows) and propagates along the field lines (black lines). The encircled portion of the flux tube represents the region modeled in this study. In this region, the flow becomes supersonic and propagates from left to right along the magnetic field line, Bz. A stationary shock is situated in the center of the modeled shocktube with subscripts 1 and 2 denoting the system variables upstream (yellow region) and downstream (red region) of the shock. The region either side of the shock are described by the Rankine–Hugoniot jump conditions (9)–(12) and result in the following inequalities:  and e1 < e2. A driven boundary is implemented for ρvθ at the left boundary and is denoted by the torsional arrows. All other boundary conditions are set to continuous for this study.
and e1 < e2. A driven boundary is implemented for ρvθ at the left boundary and is denoted by the torsional arrows. All other boundary conditions are set to continuous for this study.
Download figure:
Standard image High-resolution image2.1. Normalization
Distance z is normalized with respect to the length L of the tube section under consideration. All other quantities are normalized with respect to the corresponding initial values in the upstream region which is denoted by the index, 1 (Figure 1). An initial plasma density, ρ1 = 5.26 × 10−8 kg m−3 and sound speed, cS1 = 10 km s−1 are assumed. A background flow speed of vz1 = 30 km s−1, sonic Mach speed of Mc1 = 3, and initial Alfvén speed of cA1 = 38.9 km s−1 are employed. These Alfvén speed and density values yield a constant magnetic field of Bz = 100 G. The specific heats ratio γ is taken as γ = 1.2 to represent the photosphere and low chromosphere where the shocktube is embedded (see Aschwanden 2005). In order to satisfy Equation (14) the thermal pressure is taken as p1 = 43.8 dyn cm−2, which is consistent with the lower chromosphere. The numerical domain contains 1000 grid points with a uniform spacing of 10 km for a total length L = 10,000 km. Physical time is normalized as L/cS1, giving a unit time t of 1000 s.
2.2. Model Equations
For the 1.5-D problem, the MHD equations implemented in VAC that describe the model are shown below:
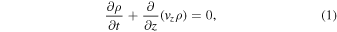
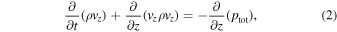
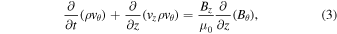
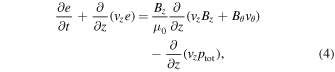
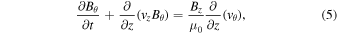
where
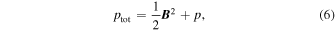
and
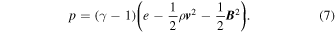
For brevity,  , and
, and  . The plasma density is denoted by ρ, whereas the longitudinal and transverse velocities are presented as vz and vθ. The internal energy is denoted by e, while the thermal, and total pressures are p and ptot. Bz and Bθ are the longitudinal and transverse magnetic field components. In this first study, the gravitational force is not included in the momentum equation, which implies a highly inclined longitudinal magnetic field. Such magnetic field configurations are observed in the photosphere and in the chromosphere. Examples include sunspot penumbrae and plage regions in the chromosphere.
. The plasma density is denoted by ρ, whereas the longitudinal and transverse velocities are presented as vz and vθ. The internal energy is denoted by e, while the thermal, and total pressures are p and ptot. Bz and Bθ are the longitudinal and transverse magnetic field components. In this first study, the gravitational force is not included in the momentum equation, which implies a highly inclined longitudinal magnetic field. Such magnetic field configurations are observed in the photosphere and in the chromosphere. Examples include sunspot penumbrae and plage regions in the chromosphere.
The last terms of Equations (2) and (4) describe the nonlinear coupling between the z and θ variables. Due to the small initial twist the perturbation of the magnetic field and corresponding derivatives remain small. Therefore, the initial system behavior is linear. With amplification of the perturbations, the ptot terms become more significant and lead to nonlinear behavior by producing momentum perturbations in the z components.
The expression for energy conservation, which is of the same form as that used by Hollweg (1992) is obtained through combining Equations (4), (6), and (7):
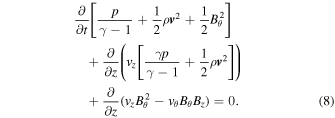
The terms within the temporal derivative of Equation (8) give the thermal, kinetic, and magnetic energy densities. The two terms within the first spatial derivative give the convection of enthalpy and kinetic energy whereas the two terms in the second spatial derivative give the Poynting flux in the inertial frame.
2.3. Shock Equilibrium
In order to set up the required stationary gas-dynamic shock in the center of the shocktube, a longitudinal background flow, which is supersonic yet sub-Alfvénic, is introduced. The plasma either side of the gas-dynamic shock is described by the Rankine–Hugoniot jump conditions (9)–(12). Subsequently, the background flow becomes subsonic once it passes through the shock interface whereas the density, pressure, and temperature of the plasma increase:
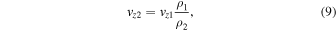
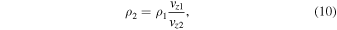
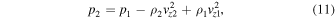
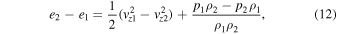
where
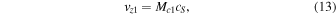
and

Subscript 1 denotes the plasma upstream of the shock and subscript 2 denotes the post-shock plasma. Mc1 and cS are the sonic Mach number of the plasma flow, and sound speed in region 1. R is the molar gas constant, T is the plasma temperature, and ξ is the molar mass. From Priest (2014), Equations (9)–(11) can be expressed in terms of the sonic Mach number of region 1:
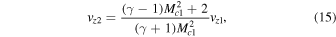
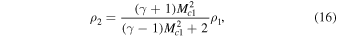

Analytically, the shock location is represented by a sharp discontinuity in the density, pressure, and velocity variables. The computational modeling of such a structure is difficult due to numerical instabilities appearing at the shock region. This difficulty in replicating an analytical shock is true regardless of the number of grid-points incorporated as there will always be an associated error. These errors lead to the Gibbs phenomenon at the shock with a trailing wake of oscillations downstream of the discontinuity. In order to eliminate this and introduce stability throughout the simulation, smoothing is introduced using a smooth cubic function. The smooth profile adjusts itself into a stable, static shock, where the Rankine–Hugoniot jump conditions are completely satisfied either side of this region (Figure 2). The resulting profile is then taken as the initial equilibrium from which the study begins.
Figure 2. Plots show the intitial (blue) and final (black) shock interface configuration for a smooth cubic function. The final state shown here is the initial condition for subsequent simulations. The analytical (red), sharp discontinuity is provided for comparison.
Download figure:
Standard image High-resolution image2.4. Boundary Conditions
There are different approaches as far as photosphere boundary conditions are concerned. In studies of thin flux tubes it is customary to introduce a driven boundary at the photospheric level. For example, a driven photospheric boundary was introduced by Hollweg (1981) to study loop resonances and by Hollweg (1986), Van Ballegooijen et al. (2011) to study Alfvén wave turbulence via nonlinear interactions. On the other hand, in their study of wave propagation and conversion in 30–40 Mm wide sunspot slabs, Khomenko et al. (2009) adopted a model which extends from 10 Mm below the photosphere to the low chromosphere and has a gradual decrease in the density.
Two different types of wave excitation were implemented for the simulation. First, consider a single sine-squared driver, F which is implemented as a source term in Equation (3) with the following form:
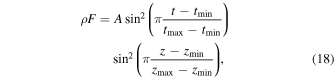
and in Equation (4) as ρF · vθ. Note that, tmin < t < tmax, and zmin < z < zmax. The start time for the simulation is denoted as tmin and is chosen for any time after the equilibrium stabilizes. The source term is active until time,  . A is the amplitude of the driver and zmin, zmax denote the region in which the driver is active.
. A is the amplitude of the driver and zmin, zmax denote the region in which the driver is active.
It is assumed that the ghost cells for ρ, ρvz, e, Bz, and Bθ are all set as symmetric (reflects from close-by mesh cells). This corresponds to a zero derivative boundary condition, i.e., a Neumann boundary condition. This means that the reflected quantity is "squashed" by the dense photosphere until the photosphere "pushes" that quantity back into the atmosphere due to Newton's 3rd law of motion.
The boundary type for ρvθ is set as asymmetric, which is the same as symmetric with the addition that the reflection is multiplied by −1. The multiplication by −1 means that the twist velocity changes sign and direction as the pulse interacts with the boundary. This corresponds to a Dirichlet boundary and allows the twist to reflect back into the direction it has just propagated from rather than allowing the twist to "skip" off the surface and twist in the same direction continually. This choice of driver and boundary conditions generates a smooth Alfvénic pulse, which upon backward propagation reflects at the photospheric boundary.
Second, a driven boundary for ρvθ was tested to drive the Alfvénic perturbations from the photosphere. The driven boundary is prescribed as:
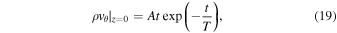
where the decay time of the wave is T = 1/1000 L/cS1 and t > tmin. The remaining quantities are set to continuous at the left boundary. Additionally, it is worth mentioning that we also tested a driven boundary for  when driving the
when driving the  boundary. However, no discernible difference could be made between this incorporation and solely driving the
boundary. However, no discernible difference could be made between this incorporation and solely driving the  boundary.
boundary.
Convection in general is a complex compressible fluid motion with the energy spectrum corresponding to the turbulence. Cranmer & Van Ballegooijen (2005) took the power spectrum of transverse magnetic bright point motions in the photosphere as the lower boundary condition for their model of Alfvénic fluctuations. Here, we are interested in the basic physics of the twist evolution. In order to have a clear picture of the process, a single, decaying pulse of the form (19) is introduced at the footpoint. As the results are largely similar, the principle of Occam's razor may be applied in that the boundary condition (19) with fewest assumptions is best.
That is, the ghost cells at the base of the magnetic shocktube are set as continuous for all variables, except ρvθ, which is driven through Equation (19) to excite Alfvén waves at the photospheric level. This is an inhomogeneous Dirichlet-like boundary condition for ρvθ, which results in the boundary becoming reflective. At the other side of the shocktube, the boundary type for the ghost cells is set to continuous. This allows the propagation of waves and flows to pass through the end of the simulated region without any reflections.
3. THE INSTABILITY CRITERION
Alfvénic pulses generated in region 1 will become over-reflected and amplified at the shock interface if
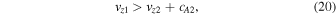
where cA denotes the Alfvén speed in the corresponding regions (Taroyan 2008) and is described by
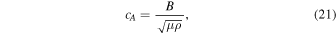
where μ is the permeability of free space.
In the case of a sub-Alfvénic flow, vz1 < cA1 which also satisfies condition (20), the shock tube is unstable with respect to Alfvénic perturbations as they bounce back and forth between the shock interface and the photospheric driver upstream of the shock. The shock front reflects and transmits Alfvénic perturbations upstream and downstream with amplified amplitudes. It acts as an amplifier leading to the Alfvén instability. The flow velocity jump across the shock interface is expressed through the Rankine–Hugoniot relation (15).
Condition (20) contains equilibrium quantities both upstream and downstream of the shock that are dependent. Using the Rankine–Hugoniot relation for velocity (15) it is possible to rewrite the over-reflection condition (20) in terms of the independent sonic and Alfvénic Mach numbers in the upstream region 1. First, note that the Alfvén speeds on either side of the shock are related through the equation:
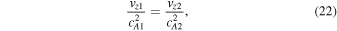
which is a consequence of the continuity condition (10). Substituting the expressions (15) and (22) into the over-reflection condition (20) yields
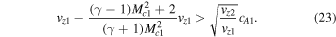
Using the Rankine–Hugoniot relation (15) and the inequality (23), the following Alfvén instability criterion is derived in terms of the sonic Mach number, Mc1, and the Alfvénic Mach number, MA1 = vz1/cA1:
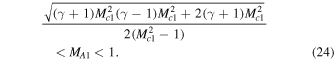
This condition (24) shows that the Alfvén instability is not present when MA1 ≳ 1 because the flow becomes super-Alfvénic. For γ ≳ 1 the instability condition (24) is reduced to
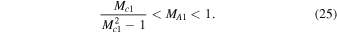
The above derived inequality (25) shows that the range of flow speeds for which the system is unstable becomes broader with increasing sonic Mach numbers.
4. NUMERICAL RESULTS
The implemented driver (19), which mimics the torsional component of the photospheric motions, such as granular buffeting, generates a small-amplitude torsional Alfvén wave. This twist propagates along the shocktube at a constant speed of  until it interacts with the gas-dynamic shock.
until it interacts with the gas-dynamic shock.
At this point, if the flow is too low to satisfy the instability criterion (20), the pulse is partially reflected and transmitted with damped amplitudes. The reflected wave propagates against the supersonic plasma flow at a constant speed of  until it reaches the photosphere. The wave bounces back and forth between the dense photosphere and static shock until the pulse vanishes after a few iterations of this process.
until it reaches the photosphere. The wave bounces back and forth between the dense photosphere and static shock until the pulse vanishes after a few iterations of this process.
However, if the Alfvén instability is present, the Alfvén wave is amplified through over-reflection and transmission at the shock position. The pulse propagates backwards until it returns to the photosphere where it is reflected, and the process repeats (Supplementary Movie 1).
The amplification of the Alfvénic perturbation leads to the formation of secondary waves (Figures 3 and 4). This occurs due to nonlinear coupling of the transverse variables with the longitudinal variables in Equations (2) and (5). The variable ptot (6) translates twists in the magnetic field to form perturbations in the longitudinal variables. Initially, the Alfvénic perturbation is small, so the effects of this nonlinear coupling between the two directions is negligible—i.e., this corresponds to the linear stage of the amplification process. The secondary waves generated by the initial twist correspond to fast- and slow-magnetoacoustic waves propagating along the magnetic field lines with phase speeds of cA and cS in the flow reference frame. This is discussed in detail in the book by Priest (2014).
Download figure:
Video Standard image High-resolution imageFigure 3. (a) Time–distance plot for normalized density, ρ. The density upstream of the gas-dynamic shock increases and propagating shocks are seen here, as with Figure 4. (b) The amplitude increase for the propagating secondary waves/shocks can be seen as a consequence of the Alfvén instability at z = 0.3. Panel (c) shows the downstream density at z = 0.99.
Download figure:
Video Standard image High-resolution imageFigure 4. (a) Time–distance plot of the normalized longitudinal velocity, vz. It can be seen that the gas-dynamic shock remains stationary until propagating fast shocks form. Here, the shock is impelled along the z-direction by each shock that "hits" the gas-dynamic shock. (b) The flow speed upstream of the shock (z = 0.3) decreases as it is converted into twisting motions. Panel (c) shows the flow speed at z = 0.99.
(An animation of this figure is available.)
Download figure:
Video Standard image High-resolution imageDuring the growth of the Alfvén wave via over-reflection, the nonlinear coupling becomes more important, as the magnetoacoustic waves form into propagating shocks. These are described by Hollweg (1992) as an increase in  across the shock for a fast shock and a decrease in
across the shock for a fast shock and a decrease in  across the shock for a slow one. The fast-shock corresponds to the leading edge of the Alfvénic pulse and travels at
across the shock for a slow one. The fast-shock corresponds to the leading edge of the Alfvénic pulse and travels at  upon forward propagation, and
upon forward propagation, and  on backward propagation. The slow-shock travels at the
on backward propagation. The slow-shock travels at the  on forward propagation and corresponds to the trailing edge of the Alfvénic pulse.
on forward propagation and corresponds to the trailing edge of the Alfvénic pulse.
However, unlike the fast-shock, the reflected slow-shock does not propagate against the plasma flow once it reaches the gas-dynamic shock, nor does it propagate through the shock interface and out of the low-chromosphere. Instead, it remains at the gas-dynamic shock location as it is too slow to propagate against the upcoming flow, yet too fast for the post-shock flow to overcome its backward propagation.
Note that unlike previous studies (Hollweg et al. 1982; Hollweg 1992; and others), the formation of slow and fast shocks does not require the presence of gravity. Instead, the formation of these shocks is caused by the instability mechanism.
Each subsequent slow-shock that is generated by the photospheric reflection of the Alfvénic pulse is trapped in the same manner, with each one merging with the gas-dynamic shock and contributing to the formation of a standing shock in vθ and Bθ. This evolution of the slow-mode waves with the gas-dynamic shock can be seen in Figures 5 and 6 and Supplementary Movie (1) as initially there is no discernible difference between the pre-shock and post-shock values—and later it is clear that a standing shock is created in the transverse variables. For details on the confluence of shocks, see Whitham (1975; pp. 52–53 and 110–112).
Figure 5. (a) Time–distance plot of normalized vθ. The velocity is negative upon forward propagation and positive on backward propagation of the Alfvén wave. The signal is amplified at the shock location upon each reflection, with a portion of the signal being transmitted. A standing slow shock forms at the gas-dynamic shock location and can be seen as a faint, white line after t = 2 at z = 0.5. Panel (b) shows the trapped portion of the Alfvén wave at z = 0.3. The transmitted portion is shown in panel (c) for z = 0.99.
(An animation of this figure is available.)
Download figure:
Video Standard image High-resolution imageFigure 6. (a) Normalized Bθ time–distance plot. The magnetic field initially exhibits a series of small twists that correspond to the Alfvén wave. These gradually amplify and form a standing shock, as is the case with vθ. The twist is continual in the same direction and the time taken for the twists to travel from the shock to the photopshere and back to the shock decreases upon each reflection. Panel (b) shows that amplification and direction of the magnetic twist more clearly at z = 0.3. Panel (c) highlights that the twist is not confined to the region between the shock and photosphere as a large amount of twisting occurs before the shock passes through z = 0.99. Once the shock propagates beyond the low-chromosphere, the magnetic flux tube remains permanently twisted.
(An animation of this figure is available.)
Download figure:
Video Standard image High-resolution imageIn addition to the generation of shocks, the nonlinear coupling also affects the sound speed (Figure 7), and Alfvén speed (Figure 8) of the shocktube plasma. It is clear that a change in sound speed also means a change in the plasma temperature (see Equation (14)). Therefore the system evolves into a configuration of ever-increasing complexity until the Alfvénic pulse ceases to amplify and twist the shocktube due to the propagation of the gas-dynamic shock. Figure 8 also shows that as the damping time of the driver becomes long, the amplification process and the nonlinear evolution occurs over a shorter period of time. However, qualitatively the response of the system to the twist remains similar.
Figure 7. (a) Normalized sound speed time–distance plot shows that as the nonlinear effects take place, the sound speed, and from Equation (14) temperature, increase upstream of the shock. Panel (b) shows the sound speed variation for z = 0.3 and panel (c) provides the variations for z = 0.99.
(An animation of this figure is available.)
Download figure:
Video Standard image High-resolution imageFigure 8. Plots showing the maximum values of  , Bθ, and the Alfvén speed as functions of time. The sharp, thin dips seen in
, Bθ, and the Alfvén speed as functions of time. The sharp, thin dips seen in  correspond to a change in direction for the pulse, i.e., the velocity is changing from positive to negative or negative to positive—the velocity value decreases, passes through zero, and increases to the correct size. A comparison where the decay period, T, of Equation (19) is changed to 10 T is provided (red lines).
correspond to a change in direction for the pulse, i.e., the velocity is changing from positive to negative or negative to positive—the velocity value decreases, passes through zero, and increases to the correct size. A comparison where the decay period, T, of Equation (19) is changed to 10 T is provided (red lines).
Download figure:
Standard image High-resolution imageOnce the gas-dynamic shock propagates out of the modeled magnetic flux tube, the Alfvén wave disappears, and a new equilibrium is formed. The resulting equilibrium is shown in Figure 8 and Supplementary Movies (1) and (2) after t = 4.5 L/cS1. The magnetic field has become highly twisted from the entrapment and amplification of the Alfvén wave between the gas-dynamic shock and photosphere. The highly twisted magnetic field leads to the Alfvén speed doubling when the nonlinear coupling is at its strongest, and remains raised thereafter (Figure 8). The plasma flow remains supersonic, though its speed has been reduced by the Alfvén wave amplification through over-reflection at the shock interface. The density and pressure have been raised to ρ = 1.14ρ1 and p = 1.33p1. This is a consequence of the nonlinear coupling, which has altered the plasma properties, i.e., heating of the flux tube, increased magnetic field strength, Alfvén and sound speeds increasing and a decrease in flow speed upstream of the shock.
4.1. Gas-dynamic Shock Propagation
Here, the physical behavior of the region which is related to the gas-dynamic shock is considered. Initially, the momentum either side of the shock is balanced due to the Rankine–Hugoniot jump conditions (9)–(12). The advection term in the longitudinal momentum Equation (2) is balanced by the pressure gradient on the right-hand side. When the propagating shock-waves are reflected by the gas-dynamic shock, a standing shock is formed. This leads to an extra nonlinear magnetic pressure force in the momentum equation, which is positive due to the negative gradient in Bθ. The total pressure force becomes positive and the shock front gains momentum in the positive direction. This imbalance persists until the magnetic pressure force declines and is no longer able to push the shock-front forward.
At first, the shock returns to its initial location as the movement of the gas-dynamic shock is small (this can be seen in all the time–distance plots and Supplementary Movies 1 and 2). The nonlinear magnetic pressure force vanishes due to the vanishing gradient in Bθ. The negative thermal pressure force takes over and the shock-front is "pulled" back due to the total pressure force becoming negative on the right-hand side of the momentum Equation (2). Once the trailing edge clears the immediate downstream of the shock, the Rankine–Hugoniot jump conditions are virtually restored and the shock becomes quasi-static.
Upon each reflection of the Alfvénic pulse at the interface, the width of the signal increases in addition to the amplitude being amplified. It is this broadening of the signal which is responsible for the eventual propagation of the gas-dynamic shock. Again, consider the same situation as before, but with an Alfvénic pulse with large amplitude. Once the leading edge of the Alfvénic pulse and fast-shock pass through the shock-front, the slow shock and with it the magnetic pressure gradient increase in amplitude. The separation between the fast- and slow-shock has now become sufficiently large so the time from when the initial pulse reaches the shock-front until all the Alfvénic perturbations have propagated beyond the immediate downstream of the interface has increased significantly. This means it takes longer for the Rankine–Hugoniot conditions to be restored and the shock to become stationary again.
Once the signal is sufficiently amplified and broadened however, this restoration ceases to occur. The Alfvénic pulse that was previously reflected from the gas-dynamic shock has travelled to the photosphere, reflected, and propagated back to the reference frame before the trailing edge has cleared the immediate downstream of the gas-dynamic shock. This increases the imbalance further, and causes the gas-dynamic shock to continue to propagate along the shocktube before the Rankine–Hugoniot conditions can be restored. This key juncture in the balance of forces at the gas-dynamic shock location occurs between t = 4.0–4.5 L/cS1.
The propagation of the gas-dynamic shock can be interpreted by looking at the nonlinear term of Equation (2). As is mentioned previously, the slow propagating shock becomes trapped at the gas-dynamic shock upon reflection as it cannot propagate against the upflow of plasma, but is too fast for the plasma downstream of the gas-dynamic shock to carry it forwards. This means Bθ decreases across the slow shock in the direction of the plasma flow. This leads to a negative derivative, and as there is a minus sign in-front of the term in Equation (2), the term becomes positive. Thus, as the slow shock grows in amplitude at the gas-dynamic shock position, it leads to the torsional magnetic twists being converted into z-momentum.
4.2. The Conversion of Energy and Generation of a Global Twist
In the nonlinear regime, the slow shock becomes important in the over-reflection process. As the fast shock propagates back and forth between the photosphere and gas-dynamic shock, the slow shock becomes trapped upon reflection and forms a stationary shock, which is separate to the gas-dynamic shock. The slow shock grows in amplitude upon each successive reflection of the Alfvénic pulse. This prevents the fast shock amplitude from decreasing, as it provides a cavity in which the flux tube may continually twist.
Downstream of the gas-dynamic shock, the fast shock only ever propagates forwards. This means that the derivative of ptot is always negative, giving an increase to the longitudinal momentum from Equation (2). Thus, downstream of the gas-dynamic shock, the Alfvén wave converts magnetic energy into kinetic energy. This behavior means the Alfvén signal acts as a means of energy transport between the two regions either side of the gas-dynamic shock.
The nonlinear term also allows the Alfvén wave to convert kinetic energy of the plasma flow into magnetic energy when the Alfvén instability is present. Once the wave has been reflected by the gas-dynamic shock, the backward propagating pulse generates an increase in the derivative of Bθ in the direction of the flow. This causes a decrease in vz at the location of the pulse. As the pulse amplifies and broadens, the tail end of the pulse occupies the entirety of the plasma upstream of the gas-dynamic shock. Now, the pulse continually converts kinetic energy from the entire region into magnetic twists, and the flow does not get a chance to restore to its initial velocity.
While the nonlinear term in Equation (2) is responsible for creating the slow shock in the z-momentum and allowing the over-reflection process to evolve, it is also responsible for its demise. The generation of Bθ perturbations leads to an increased Alfvén speed for the plasma (Figure 8). This increase in Alfvén speed changes the minimum flow speed required for the Alfvén instability to occur from 2.25 cS1 to 2.95 cS1 by t = 4 L/cS1. The flow at this time has decreased to vz = 2.853 cS1. Thus, the amplification of the Alfvén wave no longer occurs as the Alfvén instability is not present. The nonlinear coupling continues to convert the kinetic energy of the flow into magnetic twists, further decreasing the flow speed, and the Alfvénic signal dampens and then ceases.
4.3. Energy Flux and Energy Density
Following Hollweg (1992), Equation (8) can be split into longitudinal and transverse components to yield the energy fluxes for z and θ:
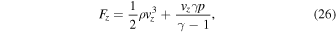
and
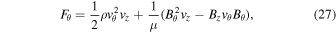
where μ is the permeability of free space.
It is worth noting that the integral of the internal energy may be expressed as
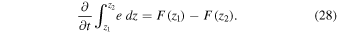
This shows that the difference in the energy flux between two spatial locations is equal to the temporal derivative of the energy content in the region between those two locations. The energy content in a region increases when the right-hand side of the above equation is positive. Conversely, a negative flux difference corresponds to a decrease in the energy content.
Figure 10 shows that during the linear stage of the evolution the torsional flux upstream and downstream of the gas-dynamic shock are approximately equal and there is no change in the energy content. However, as the system becomes nonlinear, the θ-flux downstream of the gas-dynamic shock does not amplify as much as the flux upstream of the gas-dynamic shock (Figure 10). The explanation for this is related to the propagation of the fast shock. That is, the nonlinear coupling term in Equation (2) translates the magnetic perturbations into z-momentum. Thus, some of the θ-flux generated by the Alfvénic perturbations at z = 0.3 L is not seen by the time the perturbations reach z = 0.99 L. The decrease in the θ-flux from left to right is represented by the difference between the black and blue curves in Figure 8. According to Equation (28) this leads to an increase in the corresponding energy content, namely, the magnetic energy and the θ component of the kinetic energy. Indeed, Figure 9 shows an increasing trend for the θ components of the energy density. Similarly, the increase in the z-flux from left to right represented by the difference between green and red curves in Figure 8. According to Equation (9), the result is a decrease in the corresponding energy content represented by the thermal energy and the z-component of the kinetic energy. Again, this is evidenced by Figure 9. The slight increase in the kinetic energy density at z = 0.99 L is explained above. These results indicate that the instability mechanism extracts the z components of energy and largely converts those into θ components.
Figure 9. The internal energy of the shocktube plasma is split into its constituents—thermal, z-kinetic, θ-kinetic, and θ-magnetic energies for z = 0.3 (brown) and z = 0.99 (purple).
Download figure:
Standard image High-resolution imageFigure 10. Top: z-energy flux density, bottom: θ-energy flux density of the shocktube plasma. Each plot shows their respective quantities for all time at positions z = 0.3 and z = 0.99.
Download figure:
Standard image High-resolution image4.4. The Effect of Flow Speed on the System Evolution
The effect the initial flow speed vz has on the evolution with respect to the Alfvénic instability discussed in Section 3 is also investigated. For an initial Alfvén speed of 3.89 cS1, the range for the flow-speed that will yield the Alfvénic instability is 2.25 cS1 ≤ vz1 ≤ cA1. All parameters are kept constant, with the same values as used before, but with vz1 varying from 2.25 cS1 to 3.75 cS1 in increments of 0.25 cS1. Figure 11 shows that as the initial flow-speed approaches the initial Alfvén speed, the time required for the Alfvénic pulse to amplify and "push" the gas-dynamic shock out of the low-chromosphere decreases. The speed of this process more than doubles when vz1 = 3.75 cS1 compared to when the initial speed is taken as the lower velocity limit, vz1 = 2.25 cS1. It can also be seen in Figure 11 that not only does the time required for this process to occur decrease but the amplitude of the Alfvénic perturbations increase with increasing flow-speed. These results are interesting as one could initially assume that as the flow-speed approaches the Alfvén speed, it may inhibit the backward propagation of the reflected waves/shocks due to  approaching 0. When the initial flow-speed approaches the Alfvén speed, the strength of the over-reflection of the pulse at the gas-dynamic location must sufficiently increase the Alfvén speed upon reflection so that the backward propagation is not inhibited. It may be trivial to mention, but it is worth remembering that the fast- and slow-shock forward propagation will only increase as the flow-speed increases, which is another contributing factor into the decreasing timespan for the instability to amplify the Alfvén waves and "push" the gas-dynamic shock out of the shocktube.
approaching 0. When the initial flow-speed approaches the Alfvén speed, the strength of the over-reflection of the pulse at the gas-dynamic location must sufficiently increase the Alfvén speed upon reflection so that the backward propagation is not inhibited. It may be trivial to mention, but it is worth remembering that the fast- and slow-shock forward propagation will only increase as the flow-speed increases, which is another contributing factor into the decreasing timespan for the instability to amplify the Alfvén waves and "push" the gas-dynamic shock out of the shocktube.
Figure 11. Plots show the effect varying the flow speed, vz has on the evolution of vθ. Each plot is shifted by a value of 2.175, which is the maximum amplitude of vθ seen in any of the simulations. The increase in vz shows that the duration for the amplification to occur and "push" the gas-dynamic shock beyond the low-chromosphere reduces and the maximum amplitudes of the wave increases. An initial flow speed of vz1 = 2.25 cS1 is the lower limit for the instability to occur with the chosen Alfvén and sound speeds.
Download figure:
Standard image High-resolution image5. DISCUSSION
It has been shown that a small twist may amplify through over-reflection at a gas-dynamic shock. This occurs for a supersonic yet sub-Alfvénic flow. The Alfvén wave amplifies through harnessing kinetic energy of the supersonic flow upon reflection at the shock location and converts it into magnetic twists. Due to this strong reflection at the shock, and the inability for perturbations to propagate into the photosphere, the Alfvénic pulse becomes trapped between the photosphere and gas-dynamic shock. Here, it continually amplifies and broadens until a nonlinear system evolves due to the instability. The magnetic twists reach a maximum velocity of vθ = 15.4 km s−1 with the magnetic field eventually reaching a global twist of Bθ = 1.04 Bz. During the linear stage of the evolution, the twists propagate downstream quasi-periodically with each pulse lasting for about 10 s. However, as the amplitudes increase and nonlinearity sets in, the periodicity deteriorates and the pulses last longer. The propagating nonlinear twists are a signature of fast shocks accompanied by fluctuations in density, temperature and flow speed. The entire process of evolution from an undisturbed shocktube to a globally twisted tube takes about 50 minutes. This is within the lifetimes of Evershed flows (Rimmele 1994).
The nonlinear coupling means that the Alfvén pulse converts the kinetic energy of the plasma flow into magnetic energy upstream of the stationary shock. Downstream of the shock, these twists are somewhat converted back into the flow as kinetic energy. The Alfvén pulse thus acts as a means of energy transport from the upstream to the downstream plasma.
The conversion of kinetic energy from the background flow to magnetic energy in the upstream plasma leads to an imbalance in the total pressure gradient as a slow shock is set-up. At first, the gas-dynamic shock remains quasi-stationary as the Rankine–Hugoniot jump conditions are disturbed then restored. However, as the over-reflection of the Alfvénic pulse continues, the time taken for the jump conditions to restore increases until eventually they cannot be restored before the leading edge of the pulse has returned to the gas-dynamic shock. At this point, the gas-dynamic shock continually propagates until it exits the flux tube.
Before the shock is lost, the Alfvénic perturbations have sufficiently converted kinetic energy of the supersonic flow into magnetic twists such that the Alfvén instability is lost. The perturbations are now damped upon reflection and eventually cease all together.
The magnetic field, unlike the torsional velocity, continually twists in the same direction during this study. This is regardless of the propagation direction of the torsional perturbations. Similar twisting motions have been seen as magnetic swirls in solar tornadoes (Li et al. 2012; Su et al. 2014). Wedemeyer-Böhm & Steiner (2014) showed numerically that such spiral motions are caused by the rotation of magnetic field structures, which are driven by photospheric vortices. However, previous work by Shelyag et al. (2013) demonstrates that these motions are due to torsional Alfvén waves.
The twisting motions are not only confined to the region between the photosphere and gas-dynamic shock. It is seen in Figure 6 that the portion of the Alfvénic pulse, which is transmitted through the gas-dynamic shock, induces a global magnetic twist. This means that the mechanism could permanently twist a larger flux tube without the gas-dynamic shock propagating along the entirety of the flux tube. The final state of the shocktube presented is similar to the equilibrium assumed by Zaqarashvili et al. (2010) and Díaz et al. (2011). They consider a magnetic flux tube with a helical magnetic field and mass flow along the z-axis. This means the magnetic field structure is "pulled" along the flux tube without any deformation. These twisted flux tubes are prone to the kink instability, which may lead to explosive events such as solar flares and CMEs.
The amplification of the Alfvén wave results in velocities ≈10–15 km s−1, which is within the lower limits of the ranges observed in the chromosphere (De Pontieu et al. 2007, 2014). The observed twists last for less than a minute and propagate at the local Alfvén speed. However, the torsional amplitude of the waves presented in this model is somewhat lower than the reported values in Type-II spicules, which have torsional velocities of 25–30 km s−1 (De Pontieu et al. 2012). That said, the field-aligned flow of Type-II spicules observed by De Pontieu et al. (2012) is between 50 and 100 km s−1, which is 2–3 times the initial background flow employed in this study. Also, the amplitudes are expected to increase with increasing altitude when gravitational stratification is taken into account.
The θ-energy flux density observed during this study is 4–5x larger than that seen in spicular studies (Hollweg et al. 1982; Kudoh & Shibata 1999; Matsumoto & Shibata 2010). However, this is not necessarily a negative attribute as these studies either meet the lower end of the energy requirement to heat the quiet corona (Kudoh & Shibata 1999) or fail to meet even these minimum requirements for coronal heating (Hollweg 1992). This increased flux density is due to the background flow, the energy of which is extracted and transferred downstream by amplified twists. That said, the values employed are all consistent with the lower chromosphere.
Incorporating gravity and a magnetic flux tube that expands as a function of height, such that rBz ≈ constant, where r is the flux tube radius, leads to increased torsional velocities as an Alfvén wave propagates forwards (Hollweg 1992; James et al. 2003; Erdélyi & James 2004). These additions to the model will only serve to further increase the amplitude of the torsional motions seen, and possibly strengthen the effects of the Alfvénic instability along the shocktube.
6. CONCLUSION
Using the 1.5-D approximation for a magnetic shocktube, it has been shown that a gas-dynamic shock traps and amplifies a twist when the flow is supersonic and sub-Alfvénic. Propagating fast shocks are produced due to the nonlinear coupling in Equations (2) and (4) once the Alfvén wave is sufficiently amplified. The amplification and broadening of the Alfvénic pulse leads to magnetic twisting motions that are always in the same direction, much like the swirls seen in solar tornadoes (Li et al. 2012). This continuous twisting in the same direction leads to a global twist along the flux tube where Bθ becomes, and remains, comparable to Bz.
The amplification strengthens the nonlinear effects and destabilizes the gas-dynamic shock. Initially, the shock sways back and forth as the total pressure balance is repeatedly disturbed by the impelling signals.
Eventually, the pressure balance can no longer be restored and the gas-dynamic shock propagates indefinitely. The twisting motions cease to amplify at this point as the Alfvénic pulse becomes damped in the absence of the Alfvén instability. The end result is a highly twisted magnetic flux tube with a sub-Alfvénic mass flow which pulls the magnetic field structure along the z-axis. This is much like the flux tubes used as a starting point for kink instability studies by Zaqarashvili et al. (2010) and Díaz et al. (2011).
The torsional energy flux generated by this mechanism is comparable to spicular models that provide sufficient energy to heat the corona (Kudoh & Shibata 1999; Matsumoto & Shibata 2010). However, adding gravitational stratification, losses and expansion of the flux tube will affect the Alfvén instability and torsional flux generated by the model and will be addressed in a future study.
The authors would like to thank the referee for their helpful comments and T.W. would also like to thank the STFC for their financial support.









