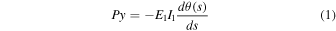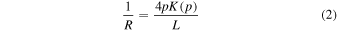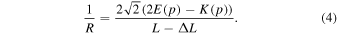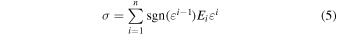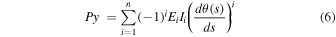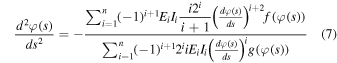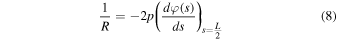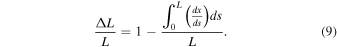Experimental and theoretical analyses of curvature and surface strain in bent polymer films

Flexible electronics, representing technology that builds electronic/optoelectronic devices on flexible substrates, is one of the important trends of modern electronics because of its excellent compatibility with Internet of things (IoT), smartphones, mobile data connections, and so on. ^1–4) Thanks to the rapid progress of research & development (R&D) in this area, various flexible electronic devices, such as flexible displays, ^5–7) wearable devices, ^8,9) electronic skins (E-skins), ^10,11) electronic papers (E-papers), ^12,13) organic transistors, ^4,14,15) and batteries ^16,17) have been reported. These devices must possess bending durability to maintain their performance even when they largely bend. ^1,18,19) The durability correlates with polymer films used as substrates, because large bending of the substrates damages the fragile electronic/optoelectronic devices. Therefore, understanding bending behavior of the polymer films is extremely important for R&D of flexible electronic devices.

Although several methods evaluating bending behavior of polymer films have been proposed, ^1,20–27) curvature [Fig. 1(a) right] perhaps is the most appropriate criterion to evaluate bending characteristic of a polymer film in design of flexible electronic devices. ¹⁸⁾ We previously reported bending behaviors of elastomer films focused on bending surface strain. ^28–31) These works made us recognize that curvature explains the bending of films as curvature is proportional to the bending surface strain. However, the factor that controls curvature of largely bent polymer films remains unclear, and naturally, such discussion has never been reported. This issue hinders the further progress of R&D for flexible electronics.

Zoom In Zoom Out Reset image size

To address the abovementioned issue, here, we report a comprehensive, experimental and theoretical study on the curvature of bent polymer films. We measured curvature of bent polymer films with our laboratory-made equipment [Fig. 1(a)] and then revealed that curvature depended on not only chemical structure of polymer films but also film thickness. Such experimental results cannot be explained by the conventional beam theory allowing large bending analysis. However, we found that the inherent non-linearity of a film between stress and strain significantly affects curvature of the bent film. The theoretical model of a bent polymer film, which was constructed by taking into account that stress depended on strain with a measured stress–strain (S–S) curve, demonstrated well the experimental results.

With our laboratory-made bending equipment, curvature at the center of a bent film was evaluated from the shape profile of the film captured by a charge-coupled device (CCD) camera. In detail, the bent shape was fitted by a sixth-order function to obtain the curvature. The film was precisely bent by the applied strain (∆L/L), which was defined as the ratio of a change in the distance between both ends of the film (∆L) to the film length (L) as shown in Fig. 1(b). ²⁷⁾ Unless otherwise stated, to precisely determine curvatures, all measurements were performed at least thrice and more.

Figure 2(a) shows the curvature of bent polycarbonate (PC; Eupiron FE-2000, Mitsubishi Gas Chemical) films with thicknesses of 100, 300, and 500 μm which were cut into rectangular-shaped (40 mm length × 30 mm width) prior to the measurements. All the films showed increase in curvature as applied strain increased from 0% to 75%; curvatures of the films with thicknesses of 100, 300, and 500 μm reached 0.24 mm⁻¹, 0.26 mm⁻¹, and 0.32 mm⁻¹, respectively. The curvatures of the films were identical below applied strain of approximately 15% but became different at applied strains of more than 15%; larger curvatures were obtained in thicker films.

Zoom In Zoom Out Reset image size

Such experimental trends in curvature might be due to non-linear-elastic deformation of a PC film, which was predicted by comparison of the experimental results and the Elastica theory ^32,33) allowing the bending analysis of a linear-elastic material (the material holds that stress is proportional to strain). On the Elastica theory, a film is modelled as a beam of length (L), width (w), and thickness (h). The film is subjected to axial compression with a certain load (P), and then the distance between both ends of the film is denoted as L–∆L [Fig. 2(b)]. At an arbitrary point x, the length along the film is expressed by s, and the angle between the line tangent to the bent film and the x-axis is expressed by θ(s). The differential equation for the deflection curve, then, is given by

$$\begin{eqnarray}&&Py=-{E}_{1}{I}_{1}\displaystyle \frac{d\theta \left(s\right)}{ds}\end{eqnarray} \tag{ 1 }$$

where E₁ and I₁ (=wh³ /12) are the elastic modulus and the moment of inertia of area, respectively. Let θ(0) be β, and the solution of Eq. (1) yields curvature at the center of the film (1/R, where R denotes radius of curvature) under the following two boundary conditions. The first condition that the bent film surface is not in contact with the film holders [namely 0 ≤ β < π/2, see Fig. 2(b) top] gives 1/R and ∆L/L as follows: ^32,33)

$$\begin{eqnarray}&&\displaystyle \frac{1}{R}=\displaystyle \frac{4pK\left(p\right)}{L}\end{eqnarray} \tag{ 2 }$$

$$\begin{eqnarray}&&\displaystyle \frac{{\rm{\Delta }}L}{L}=2\left(1-\displaystyle \frac{E\left(p\right)}{K\left(p\right)}\right)\end{eqnarray} \tag{ 3 }$$

where K(p) and E(p) denote the complete elliptic integrals of the first and second kind, respectively. The symbol p denotes sin(β/2). The other condition that the bent film surface is in contact with the film holders [namely β = π/2, see Fig. 2(b) bottom] gives 1/R, which is a function of ∆L, as follows: ³³⁾

$$\begin{eqnarray}&&\displaystyle \frac{1}{R}=\displaystyle \frac{2\sqrt{2}\left(2E\left(p\right)-K\left(p\right)\right)}{L-{\rm{\Delta }}L}.\end{eqnarray} \tag{ 4 }$$

The Elastica theory agreed well with the experimental curvatures of the 100 μm thick film [Fig. 2(a)]. In contrast, the curvatures of the 300 μm thick and the 500 μm thick films became larger compared with the Elastica theory. These results suggest that the 100 μm thick PC film keeps its elasticity during bending (<75% applied strain), whereas the 300 μm thick and the 500 μm thick PC films cause plastic deformation.

The disagreement between the experimental and theoretical (the Elastica theory) curvatures was clearly elucidated by the calculation of bending surface strain (ε_s ) from ε_s = h/2R ^{1,18,19,28,31)} [Fig. 3(a)]. The surface strain of all the films increased as the applied strain increased to 75%; surface strains with the thicknesses of 100 μm, 300 μm, and 500 μm increased to 1.2%, 4.2%, and 8.2%, respectively. The surface strain of the 300 μm thick and the 500 μm thick films calculated from the experimental curvatures were larger than those calculated from the Elastica theory at surface strain of 1.5% and higher, respectively. However, the surface strain of the 100 μm thick film calculated from the experimental curvatures agreed well with that calculated from the theory, which was less than 1.5%. We investigated tensile strain from a S–S curve of a PC film cut into rectangular-shaped (100 mm length × 2 mm width) measured at a strain rate of 0.1 min⁻¹ [Fig. 3(b)]. We found that the film kept elasticity below 1.5% strain but became plastic with strain of more than 1.5%. As a result, the 100 μm thick PC film remains elastic when bent, because the surface strain is approximately 1.5% or less [see Fig. 3(a) and 3(b)]. In contrast, the bending surface strains of the 300 μm thick and 500 μm thick PC films indicate that the films become plastic, as shown in the non-linear regime of the S–S curve. Consequently, the curvature and the bending surface strain deviated from the Elastica theory in a PC film might be explained by the non-linearity of stress and strain.

Zoom In Zoom Out Reset image size

On the basis of the hypothesis, we proposed the modified Elastica theory which takes into account non-linearity of stress as apparent in a S–S curve, unlike the Elastica theory which considers only the linear regime. First, to formulate a S–S curve including the linear to the non-linear regime, we approximated the S–S curve with a polynomial function of degree six by the following equation:

$$\begin{eqnarray}&&\sigma =\displaystyle \sum _{i=1}^{n}{\rm{sgn}}\left({\varepsilon }^{i-1}\right){E}_{i}{\varepsilon }^{i}\end{eqnarray} \tag{ 5 }$$

where σ, ε, and E_i denote stress, strain, and polynomial coefficients. Subsequently, a film was modeled as the beam again. Then, the differential equation of the deflection curve is obtained as:

$$\begin{eqnarray}&&Py\,=\displaystyle \sum _{i=1}^{n}{\left(-1\right)}^{i}{E}_{i}{I}_{i}{\left(\displaystyle \frac{d\theta \left(s\right)}{ds}\right)}^{i}\end{eqnarray} \tag{ 6 }$$

where I_i is calculated from 2w(h/2)ⁱ⁺²/(i + 2). The differential and integral of Eq. (6) yield

$$\begin{eqnarray}&&\displaystyle \frac{{d}^{2}\varphi \left(s\right)}{d{s}^{2}}=-\displaystyle \frac{\displaystyle {\sum }_{i=1}^{n}{\left(-1\right)}^{i+1}{E}_{i}{I}_{i}\displaystyle \frac{i{2}^{i}}{i+1}{\left(\tfrac{d\varphi \left(s\right)}{ds}\right)}^{i+2}f\left(\varphi \left(s\right)\right)}{\displaystyle {\sum }_{i=1}^{n}{\left(-1\right)}^{i+1}{2}^{i}i{E}_{i}{I}_{i}{\left(\tfrac{d\varphi \left(s\right)}{ds}\right)}^{i}g\left(\varphi \left(s\right)\right)}\end{eqnarray} \tag{ 7 }$$

where φ(s), f[φ(s)], and g[φ(s)] denote arcsin(θ(s)/p), p^i–1sinφ(s)cos^i–2 φ(s)[1–p²sin² φ(s)]^–(i+1)/2[(1 – i + (i + 1)p²cos² φ(s)[1 – p²sin² φ(s)]^–1], and p^i–1cos^i–1 φ(s) [1 – p²sin² φ(s)]^-(i+1)/2, respectively. Finally, 1/R (at the center of a film) and ∆L/L satisfy the following equations:

$$\begin{eqnarray}&&\displaystyle \frac{1}{R}=-2p{\left(\displaystyle \frac{d\varphi \left(s\right)}{ds}\right)}_{s=\displaystyle \frac{L}{2}}\end{eqnarray} \tag{ 8 }$$

$$\begin{eqnarray}&&\displaystyle \frac{{\rm{\Delta }}L}{L}=1-\displaystyle \frac{\displaystyle {\int }_{0}^{L}\left(\tfrac{dx}{ds}\right)ds}{L}.\end{eqnarray} \tag{ 9 }$$

Assuming that tensile and compressive stresses in a film are the same during bending, the obtained Eq. (5) by approximating a measured S–S curve with a polynomial function of degree six (Fig. S1 is available online at stacks.iop.org/APEX/13/056502/mmedia) allows us to numerically calculate 1/R and ∆L/L. These values were calculated under the same two boundary conditions as the Elastica theory (one is 0 ≤ β < π/2, and the other is β = π/2). In the first condition [0 ≤ β < π/2, see Fig. 2(b) top], the value (dφ(s)/ds)_s = L/2 was numerically calculated from Eq. (7), yielding 1/R and ∆L/L simultaneously. In the other condition [β = π/2, see Fig. 2(b) bottom], let l be the length of the bent film where is not in contact with the holders (0 < l ≤ L). We then numerically calculated 1/R and ∆L/L in the similar manner as the first condition except that L was replaced with l in all the calculations. The obtained theoretical values of the PC films with thicknesses of 100, 300, and 500 μm are shown in Fig. 4(a). All the theoretical curvatures agreed very well with the experimental ones. Not surprisingly, all the surface strains calculated from these theoretical curvatures also agreed very well with those calculated from the experimental ones, respectively [Fig. 4(b)]. As a result, the modified Elastica theory, which we constructed, successfully elucidated the non-linearity between stress and strain affects the curvature of largely bent PC films.

The curvature of various polymer films also changes due to their inherent non-linearity. We first measured curvatures of a 300 μm thick polyethylene terephthalate (PET; Lumirror H10, TORAY) film and a 300 μm thick polyurethane (PU; Higress DUS605-CER, Sheedom) film during bending as shown in Fig. 5(a). Both curvatures became identical up to 0.1 mm⁻¹ which corresponds to applied strain of approximately 35% but became different above the value; the largely bent PET film showed larger curvature compared with the PU film. Subsequently, S–S curves of PET and PU films were measured and then were normalized by dividing by the respective elastic moduli [Fig. 5(b)]. Both curves agreed well with Hooke's law only below strain of 1.5%, and non-linearity of the S–S curve of the PET film became higher than that of the PU film. The strain of 1.5% was the boundary between the linear and non-linear regimes in the S–S curves, and also the bending surface strain of 1.5% corresponding to curvature of 0.1 mm⁻¹ was the boundary that curvature significantly changed. Curvature of a film is therefore related to the S–S curve of the film. Finally, we repeated the numerical calculation of curvatures of the PET and the PU films from the respective S–S curves (Fig. S1). The theoretical curvatures of the PET and the PU films [see lines in Fig. 5(a)] agreed very well with the experimental ones, respectively. Thus, these results clearly indicate that the curvature of a largely bent polymer film is predicted by the modified Elastica theory and an experimental S–S curve of the film, especially including the non-linearity.

Zoom In Zoom Out Reset image size

To summarize the work presented here, we focused on the curvature of a bent polymer film to elucidate bending behavior for R&D of flexible materials and devices. Curvature of the PC films measured by a CCD camera showed different values depending on the film thickness, even though the Elastica theory assuming a linear regime in a S–S curve gives a single curvature independent of the film thickness and chemical structure of polymer. Then we constructed the modified Elastica theory by considering non-linearity of S–S curve, which gave the significant changes in curvature of bent films, depending on polymer structure and film thickness. The modified Elastica theory enables us to predict the curvature of various polymer films for flexible electronic materials and devices only with the measured S–S curve of the films. Appropriate design of polymer materials with the modified Elastica theory might serve for R&D of flexible electronic devices.

Zoom In Zoom Out Reset image size

Acknowledgments