Abstract
This review is devoted to one of the most relevant areas of modern condensed matter physics, the anomalous Josephson effect (AJE), which consists of the appearance of a phase shift in a hybrid structure, leading to a finite superconducting current at zero phase difference. AJE reflects the joint manifestation of superconductivity, spin-orbit interaction, and magnetism, and the study of such structures allows progress in understanding their mutual influence, while also opening up promising applications in superconducting spintronics. This review describes the physics of the φ0 junction, the control of the magnetic properties of the barrier by means of a superconducting current, and, in turn, the effect of the magnetic moment of the barrier on the Josephson current. A discussion of new effective methods of magnetic moment reversal in the φ0 junction, in particular, by a superconducting current pulse, as well as studies of the quantum properties of Josephson nanostructures with magnetic and topologically nontrivial barriers for the creation of new superconducting spintronic devices, is presented. The experimental realization of the φ0 junction, which has recently been demonstrated in a number of studies by direct measurement of the current-phase relation, allows the magnitude of the spin-orbit coupling to be measured and opens up new possibilities for the phase control of Josephson devices. This research helps in understanding fundamental spin-dependent phenomena and developing applications for computer technology. In particular, control of the magnetic state by superconductivity opens up new possibilities for the development of ultrafast cryogenic memory. This review presents the results of studying the magnetic dynamics along the current–voltage characteristic of the φ0 junction and analysis of the spin dynamics in this junction. The question of the possibility of controlling the magnetic precession by the appearance of higher harmonics in the current–phase relation, as well as the DC component of the current, which significantly increase near ferromagnetic resonance, is considered. Interesting phenomena in the φ0 junction occur under the influence of external electromagnetic radiation. Thus, the review presents an analysis of the main theoretical and experimental work devoted to AJE, gives examples of the manifestation of AJE in various systems, indicates the prospects for research in this area, and discusses unsolved problems.
Export citation and abstract BibTeX RIS
1. Introduction
Superconducting spintronics is one of the most intensively developing areas of condensed matter physics. An important place in this area occupy the study of Josephson junctions (JJs) associated with magnetic systems [1, 2]. The ability to control magnetic properties using the Josephson current as well as the influence on the superconducting current by the precession of the magnetic moment have attracted particular attention [3–5]. Spin-orbit (SO) interaction plays a central role in these phenomena. In Josephson superconductor/ferromagnet/superconductor (SFS) structures, spin-orbit interaction in a ferromagnet without inversion symmetry provides a direct (linear) coupling mechanism between the magnetic moment and superconducting current. In these junctions with broken symmetry with respect to time reversal, the current–phase relation (CPR) is defined as I = Ic sin (φ – φ0) (Ic is the critical current), where the phase shift φ0 is proportional to the magnetic moment perpendicular to the gradient of the asymmetric spin-orbit potential [6]. Josephson junctions with such a CPR are called φ0 junctions and demonstrate a number of unique properties that are important for superconducting spintronics and modern information technologies, in particular, control of the internal magnetic moment using the Josephson current [6, 7]. In the φ0 junction, the magnetization is related to the intensity of the spin-orbit interaction; therefore, in the case of magnetization oscillations, the opposite phenomenon should be expected. Namely, the Josephson current can pump the φ0 phase shift, which is fed by magnetization precession and spin-orbit interaction. This leads to the appearance of a constant component of the superconducting current, which plays an important role in the transformation of the current–voltage characteristic (CVC) in the resonant region.
The Josephson φ0 junction is ideal for studying quantum tunneling of the magnetic moment [8]. It is expected that magnetic tunneling will manifest itself in AC voltage across the junction, and it can be controlled by an applied bias current. The anomalous Josephson effect in various hybrid heterostructures reflects the interplay of superconductivity, spin-orbit interaction, and magnetism [9–24]. The study of such heterostructures, which combine superconducting and ferromagnetic properties, reveals the problem of the mutual influence of superconductivity and ferromagnetism, makes it possible to realize exotic superconducting states, such as the Larkin–Ovchinnikov–Fulde–Ferrell state and triplet ordering, and opens up new prospects for using the spin degree of freedom [15]. It is assumed that the anomalous Josephson effect can be realized in junctions where the normal region is a heterostructure formed by alternating ferromagnetic layers with spin-orbit interaction. In the experiments proposed, one can observe a significant dependence of the critical current on the direction [10].
The theory of the anomalous Zeeman effect and the spin-galvanic effect in φ0 junctions was discussed in [25, 26]. The mutual influence of Rashba and Zeeman interactions in a one-dimensional quantum wire leads to an anomalous phase shift in the CPR [11]. Resonance effects, which are important for the transport properties of weakly interacting electrons in symmetric contacts, are preserved in the presence of a strong Rashba interaction only for special conditions at the normal metal/superconductor interface [11]. In Ref. [12], the authors consider a ballistic JJ, where the interlayer between the superconducting electrodes is a two-dimensional electron gas with Rashba's spin-orbit interaction. When included in the circuit, the JJ superconductor/quantum dot/superconductor (S/QD/S) acts as a spin filter. It is shown that, in an external magnetic field lying in the plane of the 2D junction, an anomalous superconducting current occurs even at zero phase difference between the superconducting electrodes. In addition, the external field causes a large asymmetry of the critical current depending on its direction, which leads to rectification effects of the superconducting current.
Interesting features arise if the surface of the JJ is taken into account. In particular, it was demonstrated in Ref. [17] that the ground state of a superconductor/ferromagnet/superconductor JJ corresponds to a phase difference of π/2 with a critical current density that has a random sign along the junction's surface. Inhomogeneous Josephson structures in the presence of an external magnetic field demonstrate an unusual phase dependence of the current, which depends on the flux [22]. In such JJs, a ground state arises with a phase shift, the magnitude of which is determined by the external magnetic flux. Tunable ±φ junctions and hybrid systems of φ and φ0 junctions were studied in Refs [19–21].
In Josephson structures consisting of two semiconductor nanowires with Rashba spin-orbit interaction and proximitized superconductivity [24], the junction reflects the geometrically induced anomalous Josephson effect [24].
An experimental observation of a φ0 junction based on a nanowire quantum dot controlled by an electrostatic gate was reported by Szombati et al. [27]. Also, the presence of an anomalous φ0 phase shift was experimentally observed directly through the measurement of the CPR in a superconductor/normal metal/superconductor hybrid JJ fabricated on the basis of Bi2Se3 (which is a topological insulator with strong spin-orbit coupling) in a magnetic field [28]. This experiment allows direct measurement of the spin-orbit coupling and opens up new possibilities for phase-dependent Josephson devices based on materials with strong spin-orbit coupling. An important step in the study of the anomalous Josephson effect was made on the basis of the experiments of Mayer et al. [29], which demonstrated a gate-controlled anomalous phase shift in an Al/InAs-based JJ, as well as the recently published work on the first experimental implementation of a phase battery in hybrid superconducting circuit [30]. However, the magnetic dynamics in Josephson SFS structures remains experimentally unstudied [31–33].
The DC-superconducting current arising in the SFS φ0 junction leads to a strong orientational effect on the magnetic moment [34]. Applying a constant voltage to the φ0 junction causes the current to oscillate and hence magnetic precession. They can be controlled by the appearance of higher harmonics in the CPR, as well as by the presence of a DC component of the superconducting current, which increases significantly near the ferromagnetic resonance [7]. The authors emphasized that the magnetic dynamics of the SFS φ0 junction can be quite complex and strongly anharmonic. However, it was shown in [35] that the precession of the magnetic moment in some current intervals along the CVC can be quite simple. It is expected that the external radiation will lead to a number of new phenomena, in particular, to the appearance of half-integer Shapiro steps (in addition to the usual integer ones) and the generation of an additional magnetic precession with the frequency of the external radiation [7]. However, this important problem associated with the mutual influence of the Josephson current and magnetization at different values of the bias current along the CVC has not yet been experimentally investigated.
AJE has been predicted in a wide class of Josephson structures, in particular, in SFS structures based on ordinary superconductors and ferromagnets with spin-orbit interaction [6, 9, 12, 26, 36–40], in nontraditional superconductors [41–45], and in topologically nontrivial superconductors [46]. In the presence of a magnetic flux penetrating the normal intermediate layer, superconducting currents are generated due to the proximity effect, which leads to a phase shift in the CPR [22, 47].
Interesting systems in which AJE is also implemented [48] are SFS junctions with an inhomogeneous magnetization texture [15, 49–55]. In such systems, the current is a function of the magnetization distribution I = I (φ, M). In the presence of symmetry with respect to time reversal, as well as the symmetry of magnetization inversion, I (φ, M) = –I(– φ, M), AJE is not observed. To create a φ0 state, one can break the symmetry I (φ, M) = I(φ,– M). To implement AJE in S/F/F/F/S ballistic structures, a noncoplanar magnetic structure is required that breaks the inversion symmetry [51–53]. The anomalous current obtained in these studies demonstrates rapid oscillations depending on the thickness of the ferromagnet, which is the result of the Fabry–Perot interference of electron waves reflected at the S/F and F/F interfaces.
In diffuse SFS structures used in experiments [56–61], a scattering by impurities makes the directions of electron propagation random and, therefore, suppression of the rapidly oscillating anomalous current can be expected. Semiclassical studies of diffuse JJs with various noncoplanar structures, including helical structures [62], magnetic vortices [63], and skyrmions [64], did not show the occurrence of AJE. On the contrary, in studies devoted to diffuse systems with half-metallic elements [15, 50] and junctions between magnetic superconductors with spin filters [54, 55], a finite anomalous current is predicted.
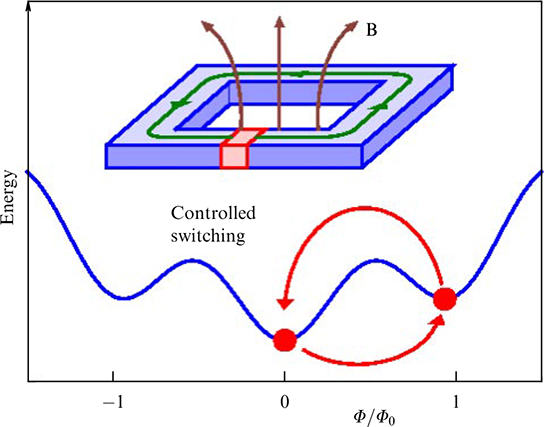
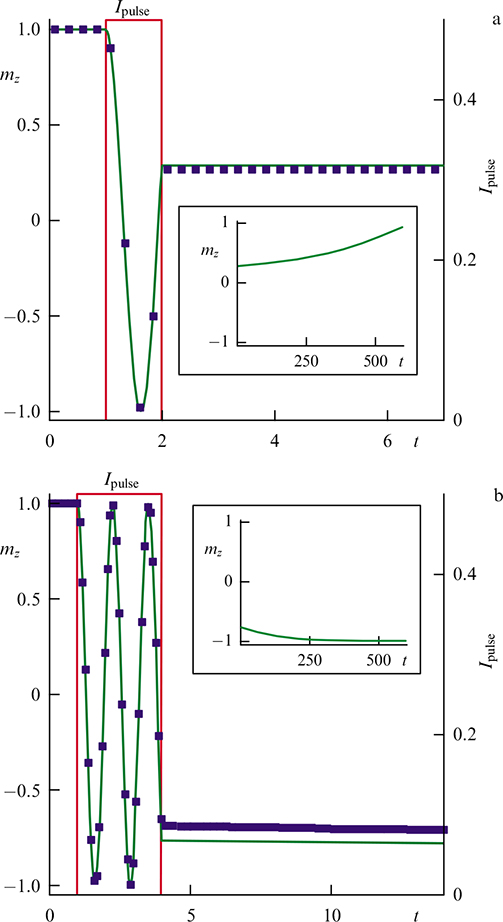
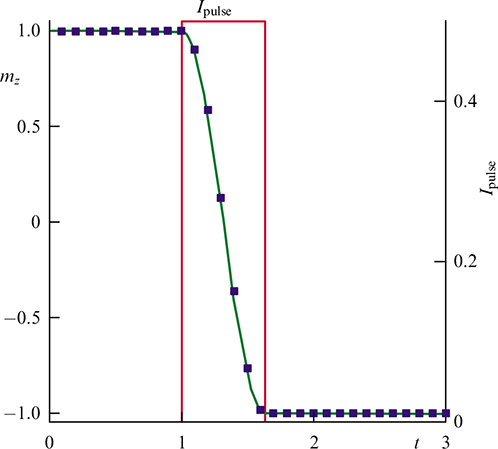
One of the important results presented in this review is the relatively short time for switching the direction of the magnetic moment of a ferromagnet in the φ0 junction (magnetization reversal interval) obtained by applying a current pulse to the junction. As follows from the results (see Fig. 39a and Fig. 40, where the time is normalized to the inverse ferromagnetic frequency), the remagnetization time is ωF t ≃ 100, which corresponds to the switching time of 10−8 s for typical ferromagnetic frequency ωF ≃ 10 GHz. The optimization of the parameters of the current pulse and the φ0 junction carried out in [65] (and demonstrated in Fig. 44) leads to a magnetization reversal time of t ≃ 0.6 × 10−10 s, which is 2 orders of magnitude less than the above estimate. In order to determine the optimal operating temperature of the proposed memory element, in Ref. [66], the effect of noise on the average stationary magnetization was studied, taking into account thermal fluctuations that affect both the Josephson phase and the dynamics of the magnetic moment. In this case, the estimate of the switching time, taking into account thermal fluctuations, also amounted to a close value, namely, t ≃ 10−9 s was obtained.
Figure 1. Geometry of a Josephson junction with a metal with broken inversion symmetry as a weak link. Exchange field is directed along the z-axis, and the gradient of the asymmetric potential is directed along the y-axis. Total length of the weak link is 2L. (From [6].)
Download figure:
Standard imageFigure 2. Geometry of the considered φ0 junction. Ferromagnetic easy axis is directed along the z-axis, which is also the direction of the spin-orbit potential gradient. Magnetization of the My component is related to the Josephson current through the phase shift φ0 ∝ n (M × ∇Ψ), where Ψ is the superconducting order parameter (∇ Ψ is directed along the x-axis). (From [7].)
Download figure:
Standard imageFigure 3. (a) Manifestation of ferromagnetic resonance in the CVC of the φ0 junction. (b) Dependence of the average value of the superconducting current on the bias current. Inset shows the dependence of maximum amplitude 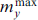 on the average voltage at which the resonant peak is observed. (From [87].)
on the average voltage at which the resonant peak is observed. (From [87].)
Download figure:
Standard imageFigure 4. Manifestation of ferromagnetic resonance in the current–voltage characteristic. Shown are the CVC of the φ0 junction for G = 0.1, α = 0.1, ωF = 0.5 at different values of spin-orbit interaction parameter r. (From [87].)
Download figure:
Standard imageFigure 5. (a) Dependence of maximum amplitude  on the voltage at different values of spin-orbit interaction parameter r. (b) The same without the term r dmy
/dt. (c) Comparison of the results of panels a and b at r = 0.3. (From [87].)
on the voltage at different values of spin-orbit interaction parameter r. (b) The same without the term r dmy
/dt. (c) Comparison of the results of panels a and b at r = 0.3. (From [87].)
Download figure:
Standard imageFigure 6. (a) Dependence of maximum amplitude 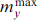 on voltage, calculated on the basis of system of equations (13), and analytical dependence my
(ωJ), according to formula (18). (b) Voltage dependence of superconducting current Is, calculated on the basis of system of equations (13), and analytical dependence I0(ωJ), according to formula (21). In the normalization used, ωJ = V. (From [87].)
on voltage, calculated on the basis of system of equations (13), and analytical dependence my
(ωJ), according to formula (18). (b) Voltage dependence of superconducting current Is, calculated on the basis of system of equations (13), and analytical dependence I0(ωJ), according to formula (21). In the normalization used, ωJ = V. (From [87].)
Download figure:
Standard imageFigure 7. Transformation of the ferromagnetic resonance region with a change in the value of parameter r indicated in the figures. Notation Ri with the corresponding arrows indicates regions of the CVC in which magnetization trajectories were studied, shown in Fig. 8. (From [35].)
Download figure:
Standard imageFigure 8. (Color online.) Trajectories of magnetization in planes my – mx , mz – mx , and mz – my in regular regions Ri . (From [35].)
Download figure:
Standard imageFigure 9. (a) Dynamics of mz at ωJ = 5, G = 500π, r = 0.1, α = 0.1. Inset shows the character of the time dependence at the beginning of the time interval. (b) Same as in Fig. a for my . (From [34].) (c) Influence of parameter G at r = 0.5. Numbers indicate the magnitude of n in G = nπ. (From [96].)
Download figure:
Standard imageFigure 10. (Color online.) (a) Superconducting electrodes forming a Josephson junction are placed on top of a ferromagnetic strip. Position of the domain wall on the strip can be controlled by normal current jn. (b) Simplified model of the Josephson junction region. Néel-type domain wall is present in the intermediate layer. Josephson superconducting current flows in the F-region in the direction x. (From [101].)
Download figure:
Standard imageFigure 11. CVC of the SFS junction with the domain wall at rest (blue curve 1) and in motion (red curve 2) at β = 1, α = 0.1, eKdw/(π jc) = 5, td = 40tJ, where tJ = 1/2eRIc. Top inset shows Shapiro steps at I(t) = I + 0.3Ic cos (ωt), 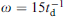 . Bottom inset shows equivalent junction circuit. (From [101].)
. Bottom inset shows equivalent junction circuit. (From [101].)
Download figure:
Standard imageFigure 12. (Color online.) S/AF/S junction, orientation (110). Unit cell of an antiferromagnet containing two neighboring atoms belonging to different sublattices is shown by a black rectangle. Basis vectors ex, z are shown along with unit vectors a and b along the crystal axes. (From [102].)
Download figure:
Standard imageFigure 13. φ0 as a function m for two values VR at dF = 21. Stable (metastable) branches φ0 are shown by solid (dashed) lines. (From [102].)
Download figure:
Standard imageFigure 14. φ0 as a function of the mz -component of magnetization at node A at dF = 21, m = 0.9, and VR = 0.28. (From [102].)
Download figure:
Standard imageFigure 15. (Color online.) Model of a Josephson junction with a two-channel nanowire in an external magnetic field. (From [109].)
Download figure:
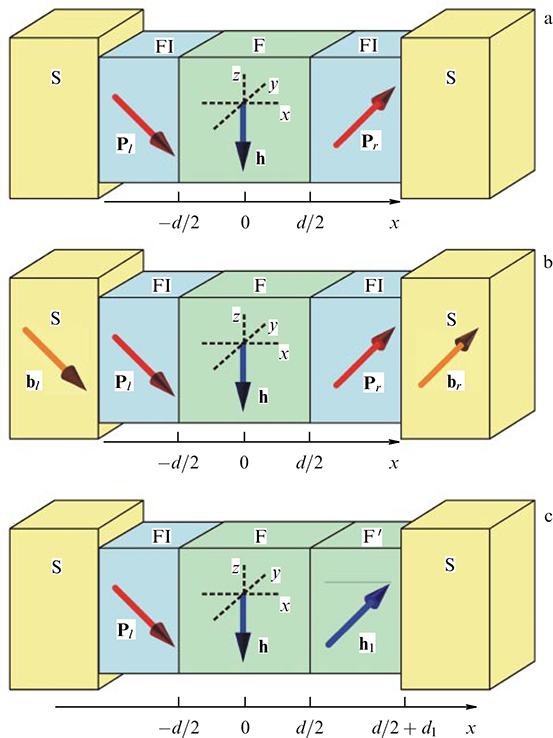
Standard imageFigure 16. Typical noncoplanar three-layer SFS systems. (a) Noncollinear spin filter barriers (FI) with polarization Pr, l , and a metallic ferromagnetic layer (F) with exchange field h. (b) Same configuration as in the case of Fig. a, and Zeeman fields br, l , in superconducting electrodes. (c) Spin-filtering barrier with polarization P and two layers of a metallic ferromagnet with noncollinear magnetizations h (F) and h1 (F'). (From [48].)
Download figure:
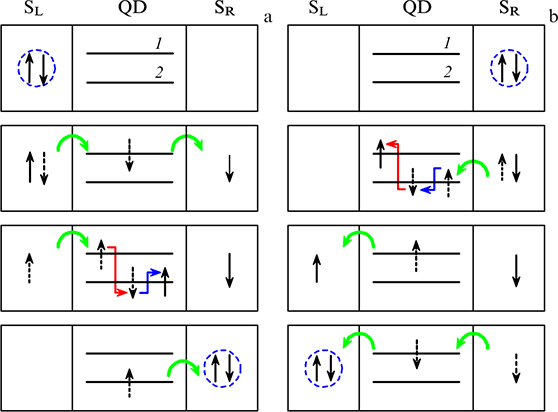
Standard imageFigure 17. (Color online.) Schematic of Cooper pair transfer through a two-level quantum dot (QD). (a) Contribution to tL → R leading to anomalous superconducting current. (b) Reverse process, contribution to tR → L. Top and bottom panels represent initial and final states, respectively, which are connected by a sequence of intermediate virtual states. Solid arrows indicate transitions due to tunneling (green, connecting the banks and the quantum dot), spin-orbit (red, connecting different levels of the quantum dot), and Zeeman interaction (blue). (From [36].)
Download figure:
Standard imageFigure 18. (a) Schematic representation of the model. Pair potential is induced in the nanowire due to the proximity effect. Δ(x) = Δ0 exp (iφL) at x < 0 and Δ0 exp (iφR) at L < x, while Δ (x) = 0 at 0 < x < L. There are several impurities in the nanowire. Spin-orbit interaction and the Zeeman effect are taken into account only in the normal region. (b) Tight binding model leads to a scattering matrix 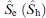 for electrons (holes) that relates incident ae and scattered be electrons (holes ah, bh). At x = 0 and L, electron be is reflected as hole ah due to Andreev reflection, while hole bh is reflected as electron ae. (From [9].)
for electrons (holes) that relates incident ae and scattered be electrons (holes ah, bh). At x = 0 and L, electron be is reflected as hole ah due to Andreev reflection, while hole bh is reflected as electron ae. (From [9].)
Download figure:
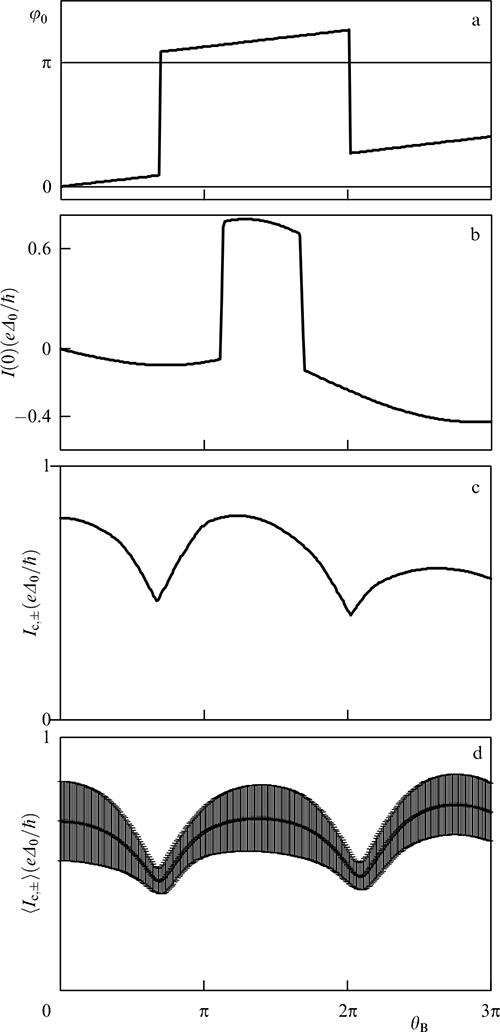
Standard imageFigure 19. Calculation results for N = 1 and l0/L = 1. Spin-orbit interaction is kα /kF = 0.15. Magnetic field is applied in the y direction. (a) Phase difference φ0 at ground state energy minimum as a function of magnetic field θB . (b) Anomalous Josephson current I (φ = 0). (c) Critical current Ic, ±. Current in the positive direction Ic, ± is the same as the current in the negative direction Ic, –. (d) Average critical current 〈Ic, ±〉 with average deviation (〈[ΔIc, ±]2〉)1/2 as an error bar, where ΔIc, ± ≡ Ic, ± – 〈Ic, ±〉. Random average is taken for 400 samples. (From [9].)
Download figure:
Standard imageFigure 20. (Color online.) Sketch of a superconducting loop containing a ψ Josephson junction that allows switching between states with different numbers of vortices by periodically exciting Josephson phase ψ of the ground state of the junction. (From [136].)
Download figure:
Standard imageFigure 21. (Color online.) (a) Sketch of a ψ Josephson junction, where the weak link consists of a half-metallic layer between two ferromagnets. Phase of ground state ψ coincides with the angle between projections of the magnetic moments on the plane perpendicular to the spin quantization axis of the half-metal. (b) Sketch of a possible experimental setup in which circularly polarized electromagnetic radiation rotates the magnetic moment in layer F2 and leads to a change in Josephson phase ψ. (From [136].)
Download figure:
Standard imageFigure 22. Dynamics of the Josephson phase corresponding to a controlled transition from state n = 0 to state n = 1 and back. Drive frequency values are indicated at the top of the figure. Dashed lines indicate the moments of excitation on and off. (From [136].)
Download figure:
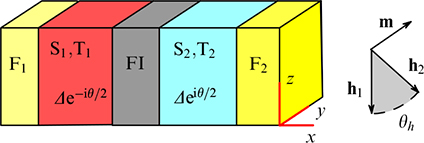
Standard imageFigure 23. Sketch of the FS/FI/SF system under thermal displacement with superconducting electrodes S1, 2 at different temperatures T1, 2. Exchange fields h1 and h2 in ferromagnetic electrodes F1 and F2 form a noncoplanar system with spin polarization m of the ferromagnetic barrier (FI). (From [137].)
Download figure:
Standard imageFigure 24. Phase shift in CPR φ0 = φ0(T) and in thermal CPR θ0 = θ0(T) at (a) P = 0.8 and (b) P = 0.9999. Exchange splitting h = 0.5 Δ0 and spin-orbital relaxation (Tc0 τSO)−1 = 1. Magnetic configuration corresponds to h1, 2 ⊥ m and θh = π/2. (From [137].)
Download figure:
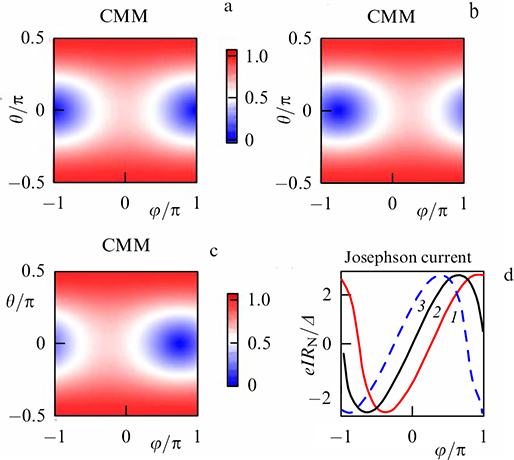
Standard imageFigure 25. (Color online.) Contour diagram of the energy level of chiral Majorana mode EJ (CMM) as a function of θ and φ for (a) mx = 0; (b) mx = 0.4mz ; (c) mx = –0.4mz . (d) Resultant Josephson current in S/FI/S junctions: 1 — mx /mz = 1, 2 — mx /mz = 0.4, 3 — mx /mz = –0.4. In all figures, mzd/νF = 1, μ/mz = 1, and my /mz = 0. T = 0.05Tc, where Tc is the critical temperature. (From [155].)
Download figure:
Standard imageFigure 26. Anomalous Josephson effect in short (L = 0.1ξ, Figs a and b) and long (L = 10ξ, Figs c and d) S/QSHI/S junctions. Figures a and c show the phase dependence of the current at temperature T/Δ0 = 10−3 for various values of applied magnetic field h. Figures b and d show the anomalous Josephson current at φ0 = 0 as a function of h. (From [25].)
Download figure:
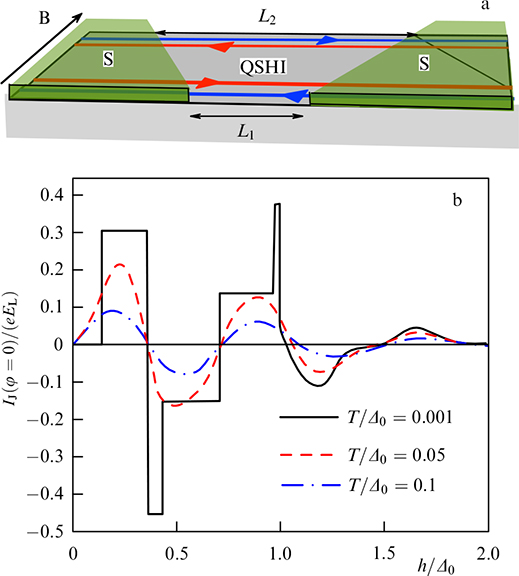
Standard imageFigure 27. (a) Proposed setup for detecting φ0 in a hybrid S/QSHI/S system: magnetic field B is applied in the junction plane. Edge states on both sides of the sample contribute to the Josephson current. Scheme of the anomalous Josephson effect is preserved if the junctions are not of the same length, L1 ≠ L2. (b) Anomalous Josephson current in the φ0 junction as a function of h = μB geff |B|/2 for L2 = 10ξ and L1 = L2/3 at various temperatures. (From [25].)
Download figure:
Standard imageFigure 28. Scheme of a Josephson junction with a topological insulator for creating a φ0 junction by injection of quasiparticles. (From [40].)
Download figure:
Standard imageFigure 29. Scheme of the described S/(F/TI)/S system. (From [162].)
Download figure:
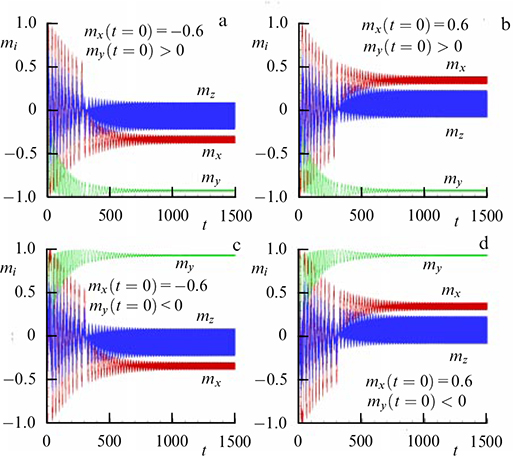
Standard imageFigure 30. (Color online.) Dynamics of magnetization under various initial conditions indicated in the figure, showing transitions to stable states under the influence of noise. Four parts of the figure show the transition to the four possible stable states for large t. Γ = 1.57, r = 0.5,  , α = 0.01, ΩF/ΩJ = 0.2, time is measured in units of inverse Josephson frequency
, α = 0.01, ΩF/ΩJ = 0.2, time is measured in units of inverse Josephson frequency 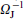 . (From [162].)
. (From [162].)
Download figure:
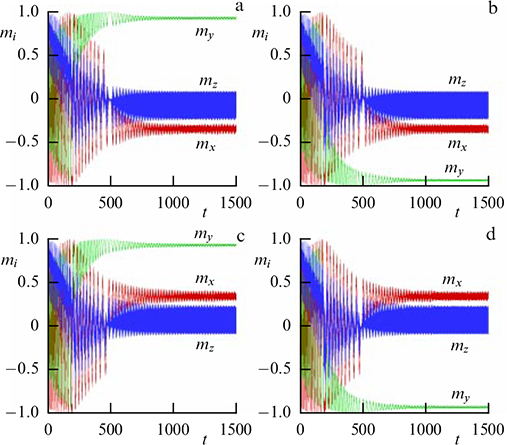
Standard imageFigure 31. (Color online.) Dynamics of magnetization starting from the unstable state mx = my = 0 and mz = 1 with noise taken into account. Four parts of the figure show the transition to the four possible stable states for large t. Parameters are the same as in Fig. 30. (From [162].)
Download figure:
Standard imageFigure 32. Illustration of the system under consideration with an equivalent electrical circuit. Nanomagnet is located at distance a from the weak coupling center of the Josephson junction. (From [169].)
Download figure:
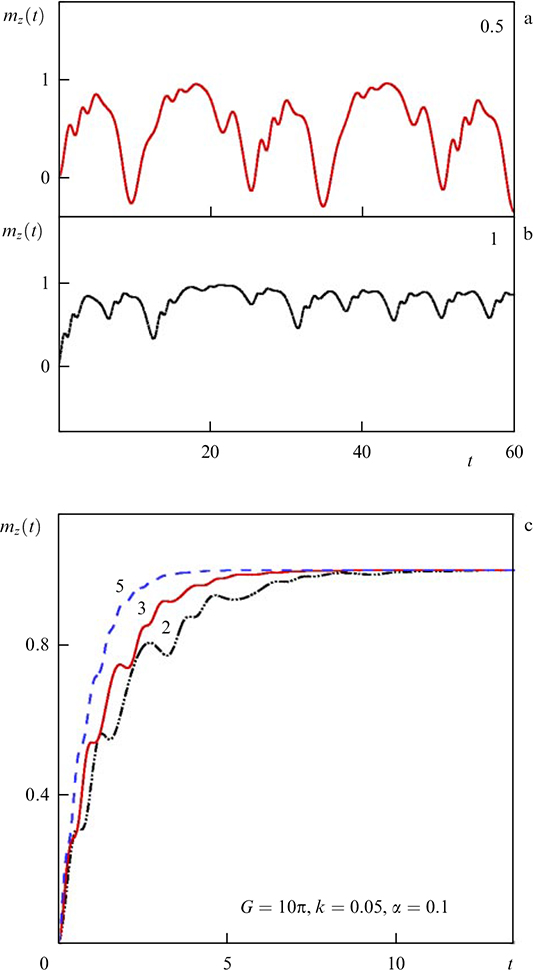
Standard imageFigure 33. (a) Manifestation of FMR on dependence 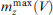 . Numbers indicate the amount of Gilbert parameter α. (b) Effect of the ratio of the Josephson energy to the nanomagnet energy G on the FMR width. Numbers indicate the G value. (From [169].)
. Numbers indicate the amount of Gilbert parameter α. (b) Effect of the ratio of the Josephson energy to the nanomagnet energy G on the FMR width. Numbers indicate the G value. (From [169].)
Download figure:
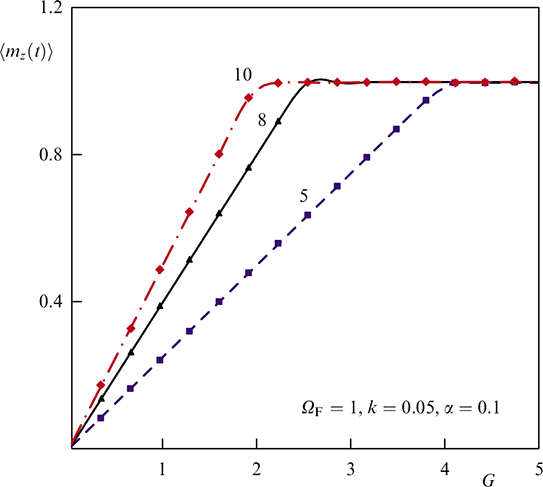
Standard imageFigure 34. Dynamics of component mz depending on the value of parameter G at k = 0.05 and α = 0.1. (From [169].)
Download figure:
Standard imageFigure 35. (a) Dynamics of component mz at ΩJ = 0.5. (b) Same for ΩJ = 1. (c) Same for ΩJ = 2, 3, and 5. (From [169].)
Download figure:
Standard imageFigure 36. Dependence of average value mz on the ratio of the Josephson energy to the magnetic energy (G). Numbers indicate the value of the Josephson frequency. (From [169].)
Download figure:
Standard imageFigure 37. CVC of a JJ with a nanomagnet (solid line, CVC) and without it (dashed line) together with the dependence of maximum mz on voltage. (From [169].)
Download figure:
Standard imageFigure 38. Josephson SFS junction controlled by a rectangular current pulse Ibias with amplitude Imax. The z-component of the magnetization Mz is an observable. It is used to determine logical states 0 and 1. (From [66].)
Download figure:
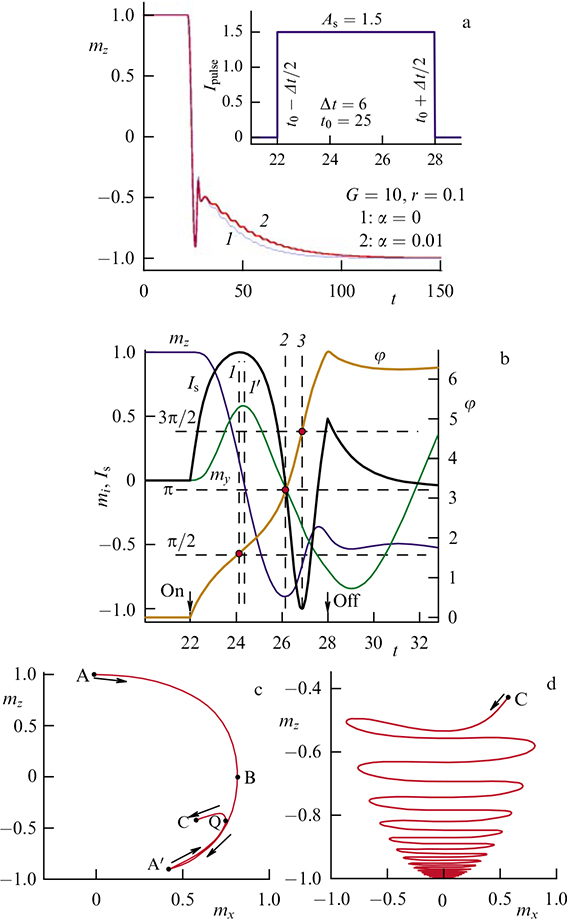
Standard imageFigure 39. (a) Transient dynamics of magnetization component mz for a system with a rectangular current pulse shown in the inset. (b) Dynamics of the magnetization components together with phase difference φ and superconducting current Is. Arrows indicate the beginning and end of the electric current pulse. Vertical dashed lines indicate characteristic moments of time, and the horizontal ones indicate corresponding values of the phase difference. (c, d) Magnetization trajectories of components in planes mx – mz in the transition region: (c) during the action of an electric pulse (between points A and C), (d) after the pulse is turned off. (From [34].)
Download figure:
Standard imageFigure 40. Demonstration of transient dynamics mz for a Gaussian electric current pulse (shown in inset). (From [34].)
Download figure:
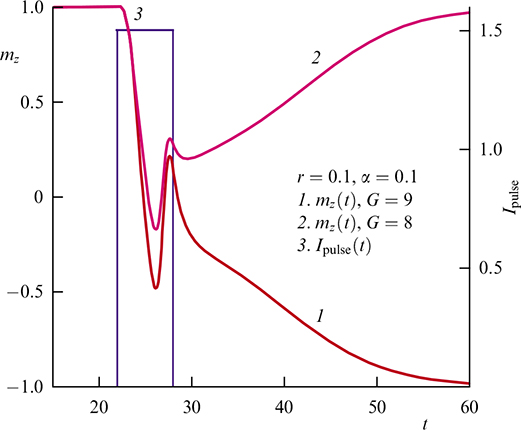
Standard imageFigure 41. Demonstration of the influence of the Josephson to magnetic ratio parameter (G) on the reversal of the magnetic moment. Calculations were carried out with spin-orbit coupling r = 0.1, dissipation parameter α = 0.1, and pulse amplitude As = 1.5. (From [181].)
Download figure:
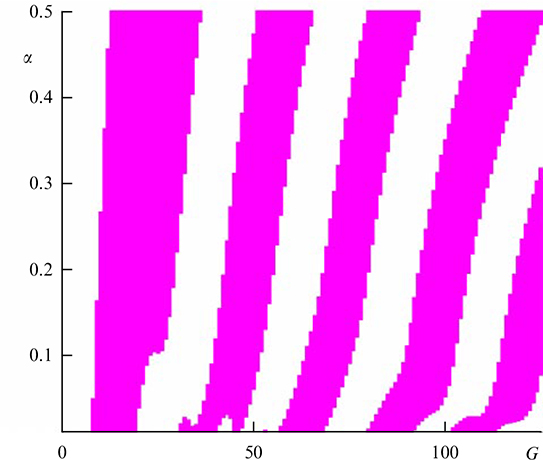
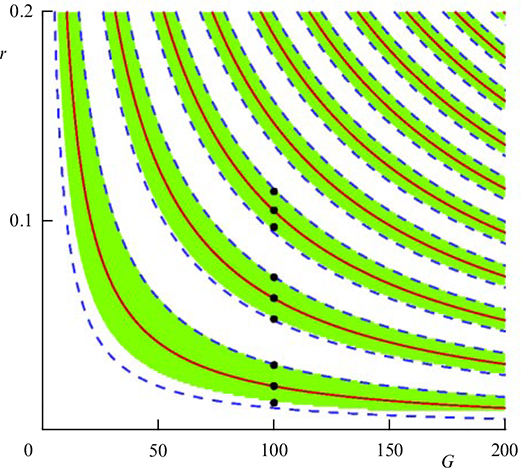
Standard imageFigure 42. Demonstration of the periodicity of reversal intervals in the plane (G,α). Results obtained in increments of ΔG = 1 and Δα = 0.001 at As = 1.5, r = 0.1, t0 = 25, Δt = 6. (From [181].)
Download figure:
Standard imageFigure 43. (Color online.) Dynamics of mz based on numerical solution of (13) and (72) (blue squares) and analytics (76) (green line) at various pulse widths. Current pulse is shown in red. Calculation parameters G = 100, r=0.1, α = 0.005, w = 0.01, t0 = 1. (a) As = 0.5, δt = 1, (b) As = 0.5, δt = 3. (From [65].)
Download figure:
Standard imageFigure 44. (Color online.) Demonstration of the fastest magnetization reversal at pulse width δteff = 0.628 according to (80). Green line corresponds to the analytical solution, and blue squares, to the numerical one. Current pulse is shown as a red line. (From [65].)
Download figure:
Standard imageThis review presents the results of the above theoretical and experimental studies, as well as a number of other investigations devoted to the anomalous Josephson effect, gives examples of its manifestation in various systems, and indicates the prospects for their applications.
2. Anomalous Josephson effect. Main properties
In this section, we consider the realization of a direct coupling between the magnetic moment and the superconducting current in the φ0 Josephson junction in the Buzdin model. The control of the magnetic moment of a ferromagnet with the help of a superconducting current is discussed, and a description of some phenomena that manifest themselves in the φ0 junction is presented. Namely, we will consider the manifestation of the properties of the Kapitza pendulum, the renormalization of tunneling splitting by the interaction between the magnetic moment and the superconducting order parameter in the φ0 junction, the possibility of detecting quantum tunneling and quantum oscillations of the magnetic moment based on the φ0 junction by measuring the voltage across the junction, and the control of the speed of magnetic tunneling through the junction by superconducting current.
2.1. Realization of a direct coupling between the magnetic moment and superconducting current in the φ0 Josephson junction
In conventional superconductor/insulator/superconductor JJs, the current–phase dependence near the critical temperature is sinusoidal, I(φ) = Ic sin φ; however, with decreasing temperature, the contribution of higher harmonics ∼ In sin (nφ) can be observed, but the current–phase dependence remains antisymmetric, I(–φ) = –I(φ) [4]. When symmetry is broken with respect to time reversal, a more general dependence I(φ) = I0sin (φ + φ0) arises, as pointed out in Josephson's paper [67]. Such a general dependence is also predicted in JJ with unconventional superconductors [41, 43, 44].
Buzdin [6], using the phenomenological Ginzburg–Landau (GL) equations, showed that a JJ with a magnetic normal metal as a weak coupling with a Rashba-type spin-orbit interaction has a specific nonsinusoidal current–phase dependence. The ground state of such a junction is characterized by a finite phase difference φ0, which is proportional to the magnitude of the spin-orbit interaction and the exchange energy in the magnetic metal. As a result, a direct coupling is realized between the magnetic moment and the Josephson current, and the corresponding JJs are called φ0 junctions. The thickness of the metal layer in such a junction determines the magnitude of the phase shift, which may be of interest for superconducting spintronics. It should be noted that there is a difference with the case of a JJ with a dominant second harmonic, where there is also a phase shift through the junction at a negative shift of the second harmonic, but there is no coupling between the magnetic exchange field and the superconducting phase. The anomalous properties of the φ0 junction are associated with the features of the superconducting proximity effect in a magnetic metal with broken inversion symmetry.
The special nature of the electronic spectrum in materials with broken inversion symmetry arises due to Rashba-type spin-orbit coupling [68, 69] α (σ × p)n, where n is the unit vector along the gradient of the asymmetric potential, and the parameter α describes its value. This type of interaction, taking into account the exchange field h acting on the electron spin, leads to the following GL free energy density [70, 71]:
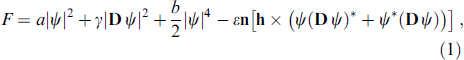
where ψ is the superconducting order parameter, Di
= –i∂i
– 2eAi
, a and b are the GL coefficients, and γ is the gyromagnetic ratio. The special nature of superconductivity in a material with broken inversion symmetry is described by the last term in (1) with the coefficient  ∼ α.
∼ α.
Neglecting the orbital effect in geometry, where the n and h vectors are mutually perpendicular and perpendicular to the current direction (the x-axis, see Fig. 1), and also neglecting the nonlinear terms, the GL equation is reduced to the form [6]
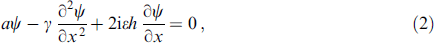
whose solution has the form
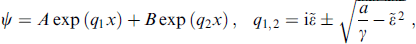
where  . The expression for the superconducting current in the limit of a long junction
. The expression for the superconducting current in the limit of a long junction  is written as
is written as
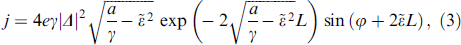
i.e., 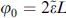 .
.
A similar dependence can be obtained up to |Δ|2 at temperatures close to the critical one Tc if we use the expression for the superconducting current in terms of the anomalous Green's functions fij (v, r):
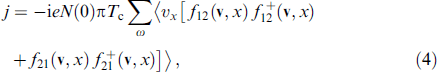
where N(0) is the density of states at the Fermi level. Anomalous Green's functions fij (v, r) are determined from the Eilenberger equations [72]. Under the condition L > ν/h, the main contribution to (4) comes from directions with |νx | ≲ ν and the formula for the current takes the simple form
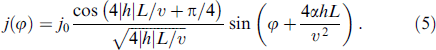
Here,
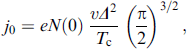
and, in the absence of spin-orbit interaction (α = 0), this expression coincides with the corresponding expression for the 2D SFS junction obtained in [7]. Comparing (5) with the formula for j(φ) derived from the Ginzburg–Landau theory (3), we can see that the phase shift φ0 = 4αhL/ν2 in both cases is proportional to the spin-orbit interaction and the product hL. On the other hand, the critical current in (5) oscillates with L, changing its sign. This is typical for SFS junctions with a strong exchange field h ≫ Tc [3]. Such oscillations are absent in the GL approximation (3), since it is valid for h ≲ Tc; otherwise, the gradient terms in (1) change signs and it becomes necessary to take higher derivatives into account. Such a modified GL functional indeed qualitatively describes the oscillations of the superconducting order parameter under the proximity effect in the S/F structure [3].
As shown in [6], in the 1D weak coupling model (single-channel approximation), the current–phase dependence is obtained similarly to (5):

Above are the results in the pure limit (ballistic mode). In diffusion mode, a convenient approach is provided by the Usadel equations [73] for Green's functions integrated over the Fermi surface: Fij (r) = 〈fij (v, r)〉. The superconducting current in this case can also be represented as j (φ) = j0sin (φ + φ0). Consequently, φ0 junction formation based on materials with broken inversion symmetry is a fairly common phenomenon that can be observed in both 'clean' and 'dirty' limits.
2.2. Controlling the magnetic moment of a ferromagnet using the superconducting current
In the φ0 Josephson junction, the phase shift is proportional to the magnetic moment perpendicular to the gradient of the asymmetric spin-orbit potential [6], which makes it possible to control the internal magnetic moment of the ferromagnetic layer using the superconducting phase difference, that is, the Josephson current. The spin dynamics of the SFS junction has been intensively studied recently, demonstrating a number of unique properties. We note the pioneering research [74], in which the narrowing of the ferromagnetic resonance below the superconducting transition temperature in Nb/Ni80Fe20 was observed. The dynamics of a single spin in the Josephson junction was studied theoretically in papers [75–78], the dynamically induced triplet proximity effect in the SFS was demonstrated in [79, 80], and the properties of junctions with several ferromagnetic layers with different magnetizations were discussed in [31, 32].
Investigations of the SFS φ0 junction in the low frequency regime ℏωJ ≪ Tc (where ωJ = 2eV/ℏ is the Josephson frequency) [7] using a quasi-static approach to the superconducting subsystem, in contrast to the case analyzed in [79, 80], led to the conclusion that the superconducting current can produce a strong orientational effect on the magnetic moment of the ferromagnetic layer. More interestingly, an alternating Josephson current, when there is DC voltage V at the φ0 junction, causes magnetic precession, which can be controlled by the appearance of higher harmonics in the CPR, as well as DC components in the superconducting current. In certain regimes, a complete magnetization reversal can be observed, and in the case of a strong coupling between the magnetic and superconducting subsystems, complex nonlinear dynamic regimes arise [7].
To demonstrate the unusual properties of the φ0 junction, the authors in Ref. [7] consider the case of magnetic anisotropy of an easy-axis ferromagnet (Fig. 2). Both the easy axis and the gradient of the asymmetric spin-orbit potential n are directed along the z-axis. It was assumed that suitable materials for the intermediate layer F could be MnSi or FeGe. In these systems, the absence of an inversion center is associated with the crystal structure, but the origin of symmetry with broken inversion can be due to external factors, as in the case near the surface of a thin F film. We note that study [7] did not take into account the magnetic induction, which in the xy plane is negligibly small for a thin layer F, while the demagnetization coefficient cancels internal induction along the z-axis (N = 1). The coupling between the subsystems F and S, due to the orbital effect, was studied in Ref. [81] and, as it turned out, is very weak and quadratic in the magnetic moment M when the flow M through the layer F is small compared to the flux quantum Φ0 = h/2e.
For I < Ic, the total energy of the φ0 junction is given by [82]
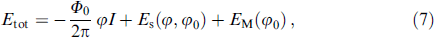
where the superconducting part is

In the ballistic limit, an estimate of the characteristic Josephson energy EJ = Φ0
Ic/2π leads to Φ0
Ic/S∼  with ℓ = 4hL/ℏνF, where S, L, and h are the section, length, and exchange field in layer F, respectively [3]. The phase shift is defined as
with ℓ = 4hL/ℏνF, where S, L, and h are the section, length, and exchange field in layer F, respectively [3]. The phase shift is defined as

where the parameter νSO/νF characterizes the relative intensity of the spin-orbit interaction [6]. It is assumed, that νSO/νF ∼ 0.1.
The contribution of the magnetic energy is reduced to the anisotropy energy

where K is the anisotropy constant and  is the volume of the F-layer.
is the volume of the F-layer.
Naturally, one can expect that the most interesting situation corresponds to the case when the magnetic anisotropy energy does not greatly exceed the Josephson energy. Measurements [83] on permalloy with very weak anisotropy imply K ∼ 4 × 10−5 K Å −3. On the other hand, the typical value of L in an SFS junction is L ∼ 10 and sin ℓ/ℓ ∼ 1. Then, the ratio of the Josephson energy to the magnetic energy will be EJ/EM ∼ 100 at Tc ∼ 10 K. Naturally, in a more realistic case of stronger anisotropy, this ratio will be smaller, but one can expect a wide variety of regimes from EJ/EM ⪡ 1 to EJ/EM ⪢ 1.
The shift of the superconducting phase difference φ and the precession of the magnetic moment My = M0 sin θ (where θ is the angle between the z-axis and the M direction) are determined from the minimum energy condition ∂φ Etot = ∂φ0 Etot = 0, which results in
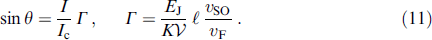
This means that the superconducting current forces the rotation of the magnetic moment My in the plane yz. Therefore, for small angles, the dependence θ (I) is linear. In principle, the Γ parameter can be greater than one. In this case, if the condition I/Ic ⩾ 1/Γ is satisfied, the magnetic moment will be oriented along the y-axis. Therefore, the application of DC superconducting current changes the direction of magnetization, while applying an AC superconducting current to a φ0 junction can generate magnetic moment precession.
It was noted in [7] that, when the spin-orbit potential gradient is directed along y (perpendicular to the easy axis z), then φ0 = ℓ (νSO/νF) cos θ. The total energy (7) has two minima θ = (0, π), and the degeneracy between them is lifted when a current is applied. However, an energy barrier exists for a transition from one minimum to another. This barrier can disappear if Γ > 1 and the current is large enough, I > Ic/Γ. In this mode, the superconducting current will cause the magnetization to switch between one stable configuration, θ = 0, and another, θ = π. This corresponds to switching between the +φ0 and –φ0 states. Reading the state of the φ0 junction can be easily done if it is part of some SQUID-like circuit (φ0 junction causes the diffraction pattern to shift by φ0) [7].
The JJ in the given voltage mode and, accordingly, the AC Josephson effect provide an ideal tool for studying magnetic dynamics in the φ0 junction. In this case, the superconducting phase changes with time as φ (t) = ωJ t. With ℏ ωJ ⪡ Tc, you can use a static value for JJ energy (7), considering φ (t) to be an external potential. In Josephson junctions with a thin ferromagnetic layer, the superconducting phase difference and the F-layer magnetization are two coupled dynamic variables. The system of equations describing the dynamics of these variables is formed from the Landau–Lifshitz–Gilbert (LLG) [84] equation and the Josephson relations for the phase difference and current. In particular, the dynamics of the magnetization of the system is described by the LLG equation with an effective field depending on the phase difference:
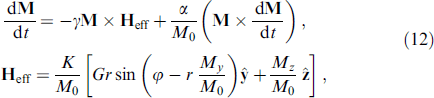
where γ is the gyromagnetic ratio, α is the phenomenological dissipation parameter, φ is the phase difference between superconductors along the junction, M0 = |M|, 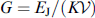 , K is the anisotropy constant,
, K is the anisotropy constant,  is the volume of the F-layer, r = lνSO/νF is the spin-orbit interaction parameter, νSO/νF characterizes the intensity of spin-orbit interaction, νF is the Fermi velocity, l = 4hL/(ℏ νF), L is the length of the F layer, and h denotes the exchange field in the ferromagnetic layer. The complete system of equations used in numerical calculations, in normalized units, takes the form
is the volume of the F-layer, r = lνSO/νF is the spin-orbit interaction parameter, νSO/νF characterizes the intensity of spin-orbit interaction, νF is the Fermi velocity, l = 4hL/(ℏ νF), L is the length of the F layer, and h denotes the exchange field in the ferromagnetic layer. The complete system of equations used in numerical calculations, in normalized units, takes the form
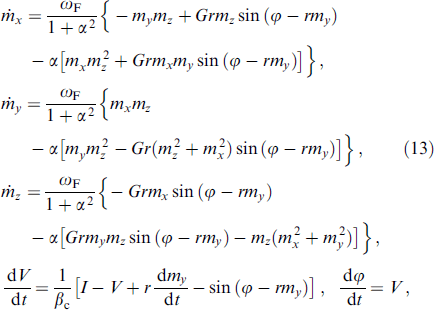
where βc = 2eIc
CR2/ℏ is the McCumber parameter, mi
= Mi
/M0 for i = x,y,z, and ωF = ωF/ωc with ferromagnetic resonance frequency ωF = γK/M0 and characteristic frequency ωc = 2eRIc/ℏ. Here, time is normalized to 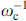 , external current I is normalized to Ic, and voltage V, to Vc = Ic
R.
, external current I is normalized to Ic, and voltage V, to Vc = Ic
R.
Usually, this system of equations is solved numerically by the Runge–Kutta or Gauss–Legendre methods, as a result of which mi (t), V(t), and φ (t) are determined as functions of time and external current I. After the averaging procedure [85, 86], the CVC is calculated for fixed system parameters [35]. Below are a number of results of modeling the properties of the φ0 junction based on system of equations (13).
2.3. Manifestation of ferromagnetic resonance in the current–voltage characteristic of the φ0 junction
Ferromagnetic resonance (FMR) is one of the main phenomena that occurs in the SFS structure when the Josephson frequency approaches that of the ferromagnet eigenmode. To demonstrate the manifestation of FMR in the φ0 junction along the CVC, in Refs [35, 87] the maximum and minimum values of the magnetization components were determined, in particular, 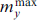 and
and 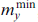 , calculated at each value of the bias current. FMR also appears in the dependence of the average superconducting current as a function of bias current. The manifestation of FMR is shown in Fig. 3, which shows the CVC of the φ0 Josephson junction, which demonstrates specific behavior in the vicinity where the Josephson frequency coincides with the ferromagnetic one, i.e., in the region of FMR [87]. The dependence of the average value of the superconducting current on the value of the bias current also demonstrates a manifestation of FMR in the form of a maximum at I = 0.6 (see Fig. 3b). FMR manifests itself clearly in the dependence of the maximum value of the oscillation amplitude my
on voltage, which is shown in the inset to Fig. 3b. The above dependences reflect the mutual influence of the Josephson current and magnetization precession in the ferromagnetic layer in the φ0 junction.
, calculated at each value of the bias current. FMR also appears in the dependence of the average superconducting current as a function of bias current. The manifestation of FMR is shown in Fig. 3, which shows the CVC of the φ0 Josephson junction, which demonstrates specific behavior in the vicinity where the Josephson frequency coincides with the ferromagnetic one, i.e., in the region of FMR [87]. The dependence of the average value of the superconducting current on the value of the bias current also demonstrates a manifestation of FMR in the form of a maximum at I = 0.6 (see Fig. 3b). FMR manifests itself clearly in the dependence of the maximum value of the oscillation amplitude my
on voltage, which is shown in the inset to Fig. 3b. The above dependences reflect the mutual influence of the Josephson current and magnetization precession in the ferromagnetic layer in the φ0 junction.
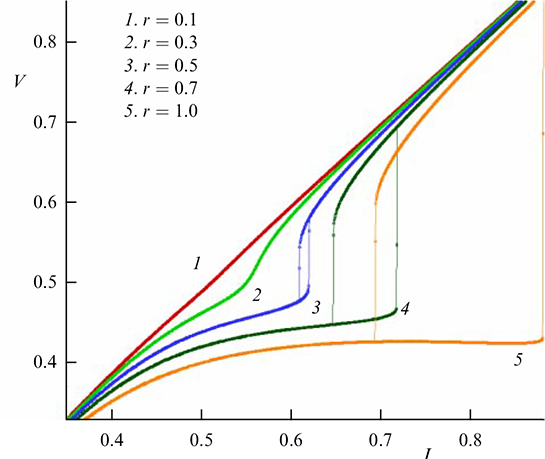
Depending on the magnitude of the spin-orbit coupling, the manifestation of FMR in the CVC can be quite significant, as shown in Fig. 4, which shows parts of the CVC of the φ0 junction for G = 0.1, α = 0.1, ωF = 0.5 for different values of the spin-orbit interaction parameter.
Based on the presented results, it can be noted that a change in the parameters of the Josephson junction and the ferromagnetic layer in a system with damping can lead to a fairly strong coupling between the superconducting current and magnetization. The contribution of the superconducting DC current manifests itself here as a deviation of the CVC from a linear dependence in the resonant region. Note that the observed feature in the CVC in the resonance region actually reflects the appearance of a resonant branch, which is emphasized by the appearance of the corresponding hysteresis at r = 0.7 and 1. With an increase in the spin-orbit coupling parameter, the rate of increase in the amplitude of the magnetic moment increases, and, accordingly, the length of the resonant branch in the CVC increases. The mechanism of the appearance of this branch is similar to the mechanism in shunted Josephson junctions at parallel resonance [88, 89], as well as the appearance of a resonant branch in the CVC of a two-terminal SQUID [90].
The influence of the spin-orbit interaction on the resonant character of the dependence of 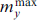 on voltage, shown in Fig. 5 for various values of the spin-orbit interaction parameter, can serve as a theoretical justification for developing an experimental method to determine the intensity of spin-orbit coupling in noncentrosymmetric materials.
on voltage, shown in Fig. 5 for various values of the spin-orbit interaction parameter, can serve as a theoretical justification for developing an experimental method to determine the intensity of spin-orbit coupling in noncentrosymmetric materials.
Note that, in the equation of the RCSJ (Resistively Capacitance Shunted Junction) model (the fourth equation in system (13)), which describes the dynamics of the φ0 junction, the phase difference φ is replaced by φ –rφ0 to preserve the gauge invariance. Taking it into account leads to an additional term r dmy
/dt in the equation of the RCSJ model, which was neglected in [7, 35]. Figure 5b shows the results without this term. As can be seen, its contribution does not change the qualitative picture of the described phenomenon for small values of the spin-orbit coupling parameter r. Up to values of the order of r = 0.5, the dependences of  on V practically coincide in both cases. Figure 5c compares the results for r = 0.3.
on V practically coincide in both cases. Figure 5c compares the results for r = 0.3.
The dynamics of the system can be studied analytically in the ℏ ωJ ⪡ Tc approximation, i.e., when the energy of the Josephson junction and the magnitude of the superconducting current are determined by a fixed Josephson frequency ωJ [7, 87], also neglecting the displacement current. In this case, the Josephson phase φ can be replaced by ωJ t, which means the choice of one point on the CVC of the junction. At a fixed voltage in the case without dissipation (α = 0) in the 'weak coupling' mode G ⪡ 1 (i.e., the Josephson energy EJ is small compared to the magnetic energy EM), the last two equations in (13) lead to a linear time dependence of the phase difference φ = Vt (Josephson junction with voltage). At the chosen normalization V = ωJ, so φ = ωJ t. If the other components satisfy the conditions mx , my ⪡ 1, then equations (13) can be linearized:
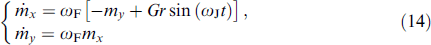
and the corresponding solutions are
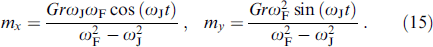
Thus, the magnetic moment precesses around the z-axis. The precessing magnetic moment affects the φ0 junction current:
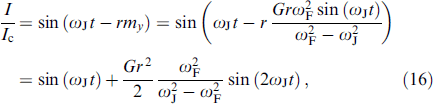
where it is taken into account that  . Thus, in addition to the oscillations of the first harmonic, the current contains contributions from higher harmonics. The amplitude of the harmonics increases near resonance and changes sign when ωJ = ωF. Thus, monitoring the second harmonic of the current oscillations will make it possible to monitor the dynamics of the magnetic system.
. Thus, in addition to the oscillations of the first harmonic, the current contains contributions from higher harmonics. The amplitude of the harmonics increases near resonance and changes sign when ωJ = ωF. Thus, monitoring the second harmonic of the current oscillations will make it possible to monitor the dynamics of the magnetic system.
An important role in the dynamics of the system under consideration is played by dissipation, the inclusion of which leads to a constant contribution to the Josephson current. Near the resonance ωJ ≈ ωF, the linearization conditions leading to equations (15) are violated, and allowance for dissipation becomes necessary. In this case [7], the linearization of the LLG equation in system (13), taking into account mz ≈ 1 and neglecting the quadratic terms mx and my , leads to
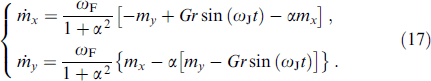
The corresponding expression for my in the presence of dissipation takes the form
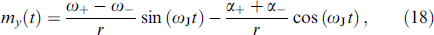
where
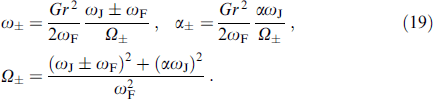
Thus, my exhibits resonance with dissipation when the Josephson frequency is tuned to the ferromagnetic frequency (ωJ → ωF). In addition, dissipation results in phase oscillations my (t) (term proportional to cos (ωJ t) in equation (18)). As a result, the superconducting current
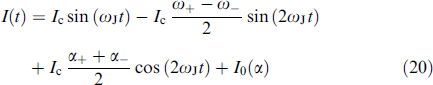
contains a time independent (DC) component:
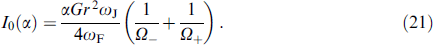
The presence of this DC contribution shows that the Gilbert damping plays an important role in the dynamics of the φ0 junction. This contribution depends on the value of the spin-orbit interaction r and the ratio of the Josephson energy to the magnetic one G, and is absent at α = 0.
On the other hand, the presence of a given constant Josephson current at a constant voltage V applied to the junction means the presence of a dissipative regime, which can be easily detected experimentally. The appearance of a direct current peak near resonance resembles the appearance of a Shapiro step in the Josephson junctions in an external electromagnetic field. Note that the presence of the second harmonic in I(t) in Eqn (20) should also lead to half-integer Shapiro steps on the CVC of φ0 junctions [7, 91].
Figure 6 shows the dependence of the maximum amplitude 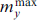 on voltage, calculated on the basis of system of equations (13) and the analytical dependence my
(ωJ) according to formula (18), in addition to the dependence of the superconducting current Is on voltage, calculated on the basis of system of equations (13) and the analytical dependence I0(ωJ) according to formula (21). As can be seen, the numerical and analytical results are in good agreement with each other. We emphasize that numerical calculations do not use any approximations, as opposed to analytical ones (where the weak coupling mode is used and the case mx
, my
⪡ 1 is considered). This manifests itself in characteristic features at V ≈0.25 and V ≈0.16 in the numerically simulated dependence
on voltage, calculated on the basis of system of equations (13) and the analytical dependence my
(ωJ) according to formula (18), in addition to the dependence of the superconducting current Is on voltage, calculated on the basis of system of equations (13) and the analytical dependence I0(ωJ) according to formula (21). As can be seen, the numerical and analytical results are in good agreement with each other. We emphasize that numerical calculations do not use any approximations, as opposed to analytical ones (where the weak coupling mode is used and the case mx
, my
⪡ 1 is considered). This manifests itself in characteristic features at V ≈0.25 and V ≈0.16 in the numerically simulated dependence 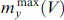 , which reflects the occurrence of ferromagnetic resonance harmonics at ωJ = ωF/2 and ωJ = ωF/3.
, which reflects the occurrence of ferromagnetic resonance harmonics at ωJ = ωF/2 and ωJ = ωF/3.
It is expected that the impact of external microwave radiation with frequency ωR on the φ0 junction will lead to a number of new interesting phenomena. It was noted in [7] that, in addition to integer Shapiro steps at ωJ = nωR, half-integer steps will appear in the CVC. Second, the microwave magnetic field can also generate an additional magnetic precession with a frequency of ωR. Depending on the parameters of the φ0 junction and the microwave radiation amplitude, the main precession mechanism can be associated either with the Josephson current or with microwave radiation. In the latter case, the spin-orbit coupling can significantly affect the width of the Shapiro steps. Therefore, one can expect its sharp increase at frequencies near the ferromagnetic resonance. In the event that the influence of radiation and Josephson current on the precession of the magnetic moment are comparable, a rather complex regime can be observed. In the case of a ferromagnet with weak in-plane anisotropy, the detailed dynamics of the magnetic precession can change dramatically. Note that a detailed study of these phenomena has not yet been carried out.
Of interest is the 'strong coupling' limit Γ ⪢ 1 (but r ⪡ 1), which can also be considered analytically [7]. In this case, my ≈ 0, and the solution of the LLG equations leads to
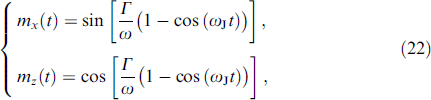
which are magnetization reversal equations; a complete flip occurs at Γ/ω > π/2. Strictly speaking, these solutions are not exact oscillatory functions in the sense that mz (t) rotates counterclockwise around the center of the sphere, and then rotates and returns to the position mz (t = 0) = 1 clockwise like a pendulum in a spherical potential.
2.4. Dynamics of magnetization along the current–voltage characteristic of the φ0 junction
One of the interesting results of numerical simulations of the ferromagnet magnetic moment dynamics along the CVC of the φ0 junction is the discovery of a rather simple precession of the magnetic moment in some current intervals, leading to specific trajectories in the my
– mx
, mz
– mx
, and mz
– my
planes [35]. In this case, the spin-orbit interaction exerts a strong influence on the appearance of such intervals. The transformation of the dependence  in the region of ferromagnetic resonance with a change in the spin-orbit interaction parameter is shown in Fig. 7.
in the region of ferromagnetic resonance with a change in the spin-orbit interaction parameter is shown in Fig. 7.
With an increase in parameter r, along with the appearance of chaotic dynamics of the magnetization, regular regions appear in the dependence  , denoted as Ri
in Fig. 7d. These regions are characterized by specific trajectories, such as an apple (b), sickle (d), mushroom (e), fish (g), and moon (h) in the my
– mx
, mz
– mx
, and mz
– my
planes shown in Fig. 8 at different values of the bias current.
, denoted as Ri
in Fig. 7d. These regions are characterized by specific trajectories, such as an apple (b), sickle (d), mushroom (e), fish (g), and moon (h) in the my
– mx
, mz
– mx
, and mz
– my
planes shown in Fig. 8 at different values of the bias current.
The transformation of trajectories with a change in the bias current is extremely interesting, and its experimental detection would contribute to the discovery of a new direction in the study of the properties of the φ0 junction. As already noted, external electromagnetic radiation leads to a number of new effects; for example, it can fix the type of structure in the current range corresponding to the Shapiro step, and a change in the radiation amplitude can cause certain transformations of the magnetic precession, in particular, the transformation of a left mushroom into a right one [35].
2.5. Reorientation of the easy axis of a ferromagnet in the φ0 junction
A particle moving simultaneously in a constant field and in a field oscillating at a high frequency exhibits unusual behavior [92, 93]. In particular, in a pendulum with a vibrating suspension point, an external sinusoidal force can invert the stability position of the pendulum. Kapitza gave an analytical explanation of the causes of stability by introducing fast and slow motion variables. By averaging the classical equations of motion over fast oscillations, Kapitza found that the upper position of the pendulum becomes stable at sufficiently large perturbation amplitudes, while the lower one turns out to be unstable. This pioneering study marked the beginning of the field of vibrational mechanics, while the Kapitza method is used to describe periodic processes in various physical systems (see [94, 95] and references therein). In nonlinear control theory, the Kapitza pendulum is used as an example of a parametric oscillator that demonstrates the concept of dynamic stabilization.
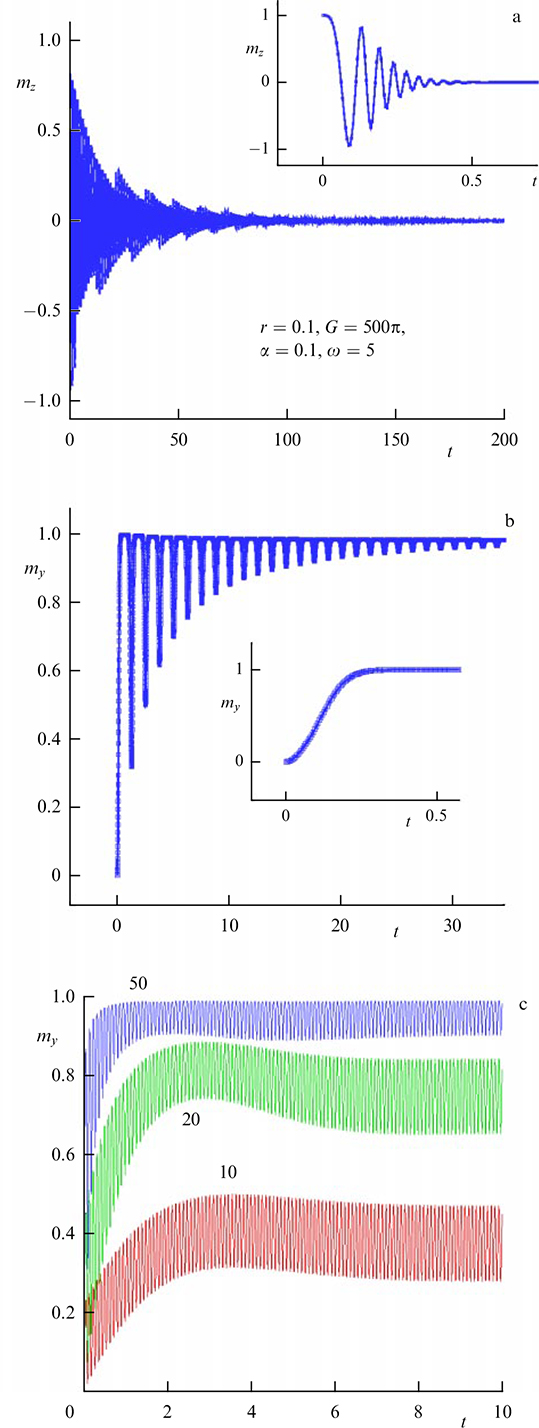
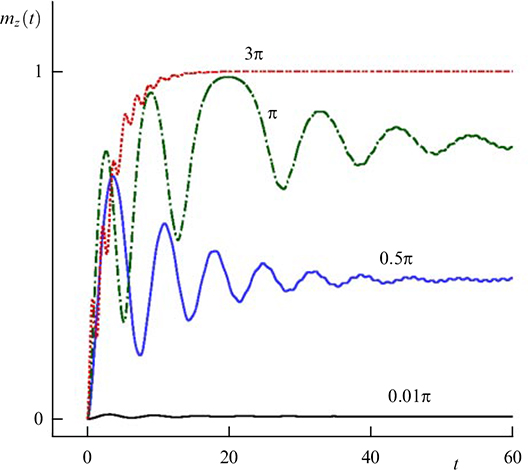
The properties of a mechanical pendulum with an oscillating suspension point, in particular, the inversion of the stability position of the pendulum, the stabilization of new equilibrium positions [92], manifest themselves in the φ0 Josephson junction, in which the reorientation of the easy axis of the ferromagnet occurs by changing the critical current of the Josephson junction and the spin-orbit interaction in the ferromagnet [96]. An example of such behavior is presented in Fig. 9, where it is shown that the magnetization component mz in the φ0 junction, which is an easy axis, with the corresponding values of the parameters indicated in the figure, vanishes, while my becomes equal to one. The influence of parameter G, which determines the ratio of the Josephson energy to the magnetic one in the φ0 junction, is shown in Fig. 9c. As the value of G increases, the mean value of my , relative to which oscillations of a given magnetization component occur, approaches unity.
Since the magnitude of the magnetization depends on the magnitude of the spin-orbit interaction, the results obtained may contribute to the development of new methods for determining the magnitude of the spin-orbit interaction in ferromagnetic metals.
2.6. Quantum tunneling of the magnetic moment in the superconductor/ferromagnet/superconductor φ0 junction
The use of the φ0 Josephson junction can make it possible to detect macroscopic quantum tunneling and quantum oscillations of the magnetic moment by measuring the alternating voltage at the junction, and the rate of magnetic tunneling in the φ0 junction can be controlled by a superconducting current [8]. Below, following [8, 97], we discuss the main results leading to this conclusion.
At I = 0, the equilibrium state of the φ0 junction corresponds to two opposite orientations M (for example, along the y-axis) with an energy barrier between them equal to U0 = (1/2)K∥ V. A decrease in the barrier value to zero under the action of a current can lead to switching between these states [6, 7]. Of interest is quantum switching M at a finite barrier.
The equations of motion for φ and M in this case have the form
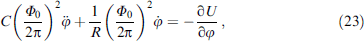
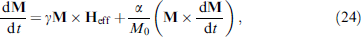
where C and R are the capacitance and resistance of the junction, respectively, and

is the effective field acting on the magnetic moment. To implement quantum tunneling, the junction must be sufficiently small; therefore, the capacitance can be neglected.
Quantum tunneling M is implemented as an instanton solution of equations (23) and (24), which at I = 0 for M = M0(sin θ cos ϕ,sin θ sin ϕ,cos θ) has the form [97–99]
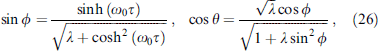
where ω0 = [ω∥ (ω∥ + ω⊥)]1/2, λ = ω∥/ω⊥, ω∥, ⊥ = 2γ K∥,⊥/(M0
V). The instanton switches magnetization 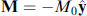 at τ = –∞ to
at τ = –∞ to 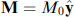 at τ = +∞.
at τ = +∞.
The interaction of the magnetic moment with the superconducting order parameter renormalizes the level splitting upon tunneling,
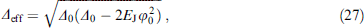
where Δ0 is the splitting at I = 0, and the decoherence rate provided by the finite junction resistance R is given by

At 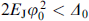 in the state M with orientation along the y-axis, oscillations My
and φ occur:
in the state M with orientation along the y-axis, oscillations My
and φ occur:
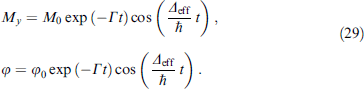
Allowance for damping leads to a decrease in the intensity of quantum voltage oscillations at the φ0 junction with the corresponding quality factor

For φ0 ∼ 0.1, the estimates give Q ∼ 0.1R(Ω), which is a fairly high value for a dielectric ferromagnetic layer.
Oscillations φ lead to voltage oscillations at the junction:
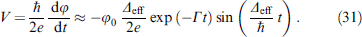
At φ0 ∼ 0.1 and Δeff ∼ 0.1 K, the initial (t = 0) amplitude of the alternating voltage will be of the order of 1 μV, and the frequency of Δeff/(2πℏ) will be of the order of 1 GHz.
With a strong enough interaction,

tunneling is frozen: Δeff = 0.
Thus, the following main conclusions can be drawn [8]. First, the interaction between the magnetic moment and the superconducting order parameter in the φ0 junction renormalizes the tunneling splitting in a way that can be accurately calculated and measured. The second point is that the φ0 Josephson junction makes it possible to detect quantum tunneling and quantum oscillations of the magnetic moment by measuring the voltage across the junction. The third point is that the φ0 junction allows us to control the rate of magnetic tunneling of the superconducting current through the junction. Note that the exact form of the spin-orbit interaction (Rashba, Dresselhaus, or others) is important for the specific dependence φ0(M); the rest is determined by the symmetry of the magnetic anisotropy (crystal field).
The foregoing suggests an alternative approach to detecting coherent quantum spin oscillations compared to probing Rabi oscillations using the electron spin resonance method [80]. Such experiments are rather difficult, as they are carried out with small samples at low temperatures in order to freeze the superparamagnetic behavior. However, magnetic tunneling in a nanoparticle was studied on the basis of JJ at millikelvin temperatures [100]. In the φ0 junction, the coupling of the magnetic moment to the Josephson dynamics is strong enough that it provides an interesting new tool for studying magnetic tunneling.
3. Manifestations of the anomalous Josephson effect in various structures
3.1. φ0 junction in the presence of moving domain walls
Another type of anomalous phase shift occurs in a superconductor/ferromagnet/superconductor JJ (Fig. 10) in the presence of moving domain walls [101]. Such systems, in the presence of magnetization dynamics, become dissipative in nature and, in principle, cannot support a superconducting current of any magnitude due to the voltage generated by the magnetization precession. The situation is analogous to type II superconductors, in which the mixed state is resistive, since, at an arbitrarily small value of the electric current, vortex motion occurs, which generates an electric field, leading to resistance and ohmic losses. The precession of magnetization in the SFS structure, created by supercurrent, necessarily generates an electric field and ohmic losses, similar to the motion of Abrikosov vortices (flux-flow regime). The difference is that, in the case of a magnetic system, the dynamics of the magnetic order parameter is responsible for the emerging electric field and ohmic losses in the superconducting state due to Gilbert dissipation.
In [101], the SFS junction was considered, in which the coupled dynamics of the magnetization M and the Josephson phase difference φ are determined by the system of equations
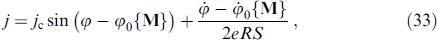
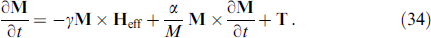
Equation (33) represents a generalized RSJ (Resistively Shunted Junction) model with a nonequilibrium current–phase relation with an anomalous phase shift φ0 M determined by the spin-orbit interaction and magnetic texture. The LLG equation (34) contains the spin torque T = (γ/M)(Js∇) M + (2γ/M)(M × Bj ) Js, j due to the current, where the first term is due to the spin current Js and the second term is due to the spin-orbit interaction determined by the spin vector Bj = (Bxj ,Byj ,Bzj ) corresponding to the jth spatial component of the spin-orbit interaction tensor Bi j .
The anomalous phase shift φ0 M is expressed as
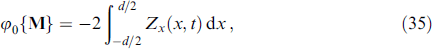
where Z = Zm + ZSO.
The term 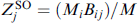 is due to the spin-orbit interaction, with Bij
describing a linear spin-orbit coupling of the general form
is due to the spin-orbit interaction, with Bij
describing a linear spin-orbit coupling of the general form 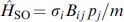 . It is assumed that
. It is assumed that 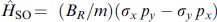 . Zm is nonzero only for a noncoplanar magnetic structure, and, in the case under consideration, Zm = 0.
. Zm is nonzero only for a noncoplanar magnetic structure, and, in the case under consideration, Zm = 0.
Equation (33) is quite general and is applicable to a wide class of Josephson systems that exhibit an anomalous phase shift. In the case of a Néel domain wall and Rashba spin-orbit interaction, 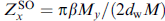 , and the anomalous phase shift is determined by the expression
, and the anomalous phase shift is determined by the expression

The results obtained are valid for |d/2 ± x0| ⪢ dw, i.e., when the domain wall is separated from the interface between the superconductor and the ferromagnet.
Figure 11 shows the CVC at rest and stationary moving domain wall. In fact, V(t) was determined by the derivative of  .
.
3.2. Anomalous effect in a Josephson junction with an antiferromagnetic layer
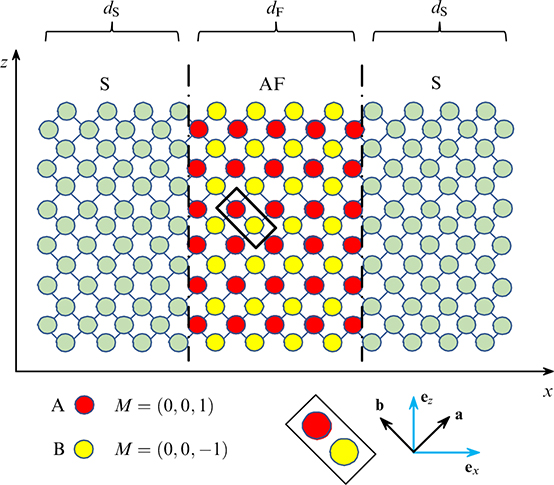
The anomalous Josephson effect can arise in S/AF/S structures with an antiferromagnet in the presence of Rashba spin-orbit interaction [102]. A diagram of such a system is shown in Fig. 12.
In [102], junctions were considered both with an uncompensated magnetic moment (in the figure, the AA junction, in which there are A-type atoms at both interfaces with the superconductor) and with a fully compensated moment, the AB junction. It was shown that the presence of an uncompensated magnetic moment at the S/AF boundary leads to an anomalous phase shift, which strongly depends on the magnitude of the spin-orbit coupling. One of the most interesting results is the strong dependence of the anomalous phase shift on the orientation of the Néel vector with respect to the S/AF interface. The uncompensated magnetic moment at the interface does not require the expenditure of antiferromagnetic exchange energy, in contrast to the uncompensated moment in the bulk of the antiferromagnet. In this regard, by analogy with ferromagnetic systems [101], the presence of an anomalous phase shift in Josephson systems makes it possible to detect electrically and to control the dynamics of the Néel vector by a superconducting current.
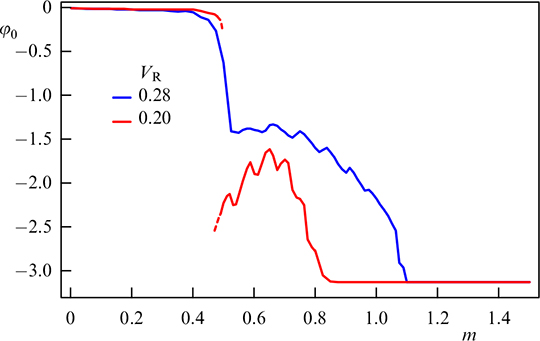
The dependence of the anomalous phase shift on the magnitude of the local magnetization m, presented in Fig. 13, shows that, as m increases, the system transitions from state 0 to state π, and the transition occurs through a wide region of intermediate states φ0. It can also be seen that φ0 is a strongly nonlinear function of m, which contrasts sharply with the available theoretical and experimental results on the anomalous phase shift in Josephson junctions with low-dimensional ferromagnetic layers or in an in-plane magnetic field in the presence of Rashba spin-orbit interaction [6, 26, 28, 29]. This is also a direct consequence of the fact that, for antiferromagnets, the manifestation of the magnetoelectric effect is determined not by the magnitude of the sublattice magnetization m but by the uncompensated magnetic moment, which is rather small and can lead to large values of the anomalous phase only when the system is close to the 0 – π transition. Here, we also see the ambiguous behavior of the anomalous phase shift with stable and metastable branches.
The anomalous phase shift exhibits a strong dependence on the angle α between the magnetization of the A-site m and the boundary. Figure 14 shows the phase shift φ0 as a function of the mz
-component of the magnetization at site A. The Néel vector rotates in the plane x,z. When the Néel vector component along the boundary vanishes, φ0 = 0. The nature of the dependence of the anomalous phase shift on the orientation of the Néel vector is dictated by the Lifshitz-type term: the symmetry of the tensor 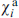 is determined by the symmetry underlying the spin-orbit coupling. In the considered case of Rashba spin-orbit interaction, the only nonzero elements of
is determined by the symmetry underlying the spin-orbit coupling. In the considered case of Rashba spin-orbit interaction, the only nonzero elements of  are
are  . As a result, the anomalous phase shift, which is the phase difference along the x-axis, can only be associated with mz
, i.e., the anomalous phase shift is proportional to mz
, at least for small mz
, when the linear approximation is performed. In principle, this dependence of the anomalous phase shift on the orientation of the Néel vector opens up a new direction for studying the prospects for controlling the Néel vector using a superconducting current.
. As a result, the anomalous phase shift, which is the phase difference along the x-axis, can only be associated with mz
, i.e., the anomalous phase shift is proportional to mz
, at least for small mz
, when the linear approximation is performed. In principle, this dependence of the anomalous phase shift on the orientation of the Néel vector opens up a new direction for studying the prospects for controlling the Néel vector using a superconducting current.
3.3. φ0 junction in multichannel transport systems
Systems with multiple conducting channels provide a unique opportunity to design devices with tunable transport properties on the quantum length scale. One of the promising implementations of such devices is based on localized electronic states arising, for example, on the surface of a topological insulator [103] or at the edges of graphene nanoribbons [104] and various types of nanowires [105–107]. The physics of charge transfer through these states seems to be extremely rich due to the strong spin-orbit coupling, the large anisotropic g factor, and a number of other properties. The physics of edge states associated with bulk superconducting banks [104, 105] makes it possible to create a new type of Josephson devices with controlled current-phase dependences [3, 6]. Here, favorable conditions arise for observing Majorana fermions [108].
In [109], the appearance of a one-dimensional φ0 junction was shown in the framework of the Bogoliubov–de Gennes formalism for the case of a nonquadratic electronic spectrum (it is sufficient to take into account nonquadratic corrections to the spectrum near the bottom of the band). The authors studied magnetotransport phenomena in a Josephson system containing several conducting channels simulating edge states localized, for example, on the surface of a single nanowire, taking into account strong spin-orbit and Zeeman interactions. This model, illustrated in Fig. 15, allows us to describe both the orbital and spin mechanisms of the influence of the magnetic field, as well as the nontrivial ground state of the Josephson junction with a nonzero superconducting phase difference. The Zeeman interaction creates spatial oscillations of the wave function of the Cooper pair on the scale ℏνF/gμB H (similar to those observed in superconductor/ferromagnet structures [3]), which lead to magnetic oscillations of the critical current with a characteristic period ℏνF/gμB L, where L is the channel length. The orbital effect causes a standard phase enhancement of ∼ 2πHS/Φ0 (Φ0 = πℏc/|e| is the flux quantum) in the electron wave function, similar to that arising in the Aharonov–Bohm effect. Here, S is the area bounded by a pair of interfering trajectories projected onto a plane perpendicular to the magnetic field. In this case, the interfering quantum-mechanical amplitudes cause magnetic oscillations in the total transfer amplitude with a period of 2Φ0/S. Andreev reflection at the boundaries of superconductors can double the effective charge in the oscillation period [110]. The authors of [109] showed that, in the general case, the resulting critical current oscillates with competing periods of 2Φ0/S and Φ0/S. This physical picture is modified in the presence of the spin-orbit coupling, which is responsible for the dependence of the Fermi velocity on the spin projection and momentum direction. Such a specific dependence creates a spontaneous Josephson phase difference [6, 11, 12] and can cause a significant renormalization of the indicated oscillation periods.
The current–phase dependence was determined on the basis of the following equation [111]:
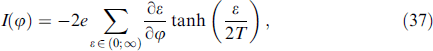
where, to calculate the energy of quasiparticle excitations ε, the Bogoliubov–de Gennes equation
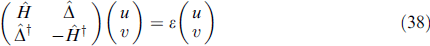
was solved with the Hamiltonian of an insulated wire, which in the absence of a magnetic field had the form
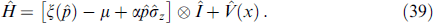
Here, 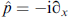 is the x projection of the momentum, ξ(p) is the energy of an electron in an insulated wire, and μ is the chemical potential. The term
is the x projection of the momentum, ξ(p) is the energy of an electron in an insulated wire, and μ is the chemical potential. The term  describes the Rashba spin-orbit interaction arising due to inversion symmetry breaking in the y direction [68], the operator
describes the Rashba spin-orbit interaction arising due to inversion symmetry breaking in the y direction [68], the operator 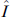 is the 2 × 2 identity matrix in the channel subspace, and the potential
is the 2 × 2 identity matrix in the channel subspace, and the potential 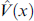 describes the scattering at the superconductor-nanowire interface. The magnetic field is taken into account by the Zeeman term
describes the scattering at the superconductor-nanowire interface. The magnetic field is taken into account by the Zeeman term 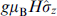 in (39) and by replacing
in (39) and by replacing 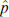 with
with 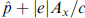 with gauge Ax
(y) = –Hy.
with gauge Ax
(y) = –Hy.
For a short junction 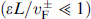 , only the intragap Andreev states contribute to the Josephson current, which leads to four positive intragap energy levels:
, only the intragap Andreev states contribute to the Josephson current, which leads to four positive intragap energy levels:
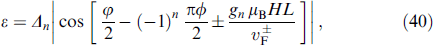
where n numbers the channels. As a result, the current-phase dependence (37) at T ⪢ Δn takes the form
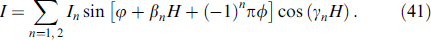
Here, 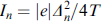 is the critical current of the nth channel at H = 0, the magnetic flux ϕ creates squid-like oscillations Ic, the term cos (γnH
), which depends on the constants
is the critical current of the nth channel at H = 0, the magnetic flux ϕ creates squid-like oscillations Ic, the term cos (γnH
), which depends on the constants 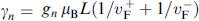 , describes the oscillatory dependence Ic due to the Zeeman interaction, similar to the dependence in the SFS structure [3]. The term
, describes the oscillatory dependence Ic due to the Zeeman interaction, similar to the dependence in the SFS structure [3]. The term 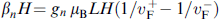 describes the formation of the φ0 junction due to the spin-orbit interaction [6].
describes the formation of the φ0 junction due to the spin-orbit interaction [6].
3.4. Anomalous Josephson effect in a diffuse ferromagnetic junction
In [48], the possibility of realizing AJE in diffuse superconductor/ferromagnet/superconductor junctions was studied. It was shown that the conditions for observing this effect are a noncoplanar distribution of the magnetization and violation of the invariance of the superconducting current upon inversion of the magnetization. This symmetry is inherent in the widely used semiclassical approximation, and taking it into account leads to the absence of an anomalous superconducting current. In diffuse systems, it can be eliminated if the spin-dependent boundary conditions for the semiclassical equations at the superconductor/ferromagnet interface are taken into account. Using this procedure, the authors determined the ideal experimental conditions for increasing the anomalous Josephson current.
The anomalous current obtained in [48] demonstrates fast oscillations, depending on the thickness of the ferromagnet. These oscillations are the result of Fabry–Perot interference of electron waves reflected at S/F and F/F interfaces.
In diffuse SFS structures used in experiments [56–59, 61, 112], scattering by impurities makes the directions of electron propagation random; therefore, suppression of a rapidly oscillating anomalous current can be expected. Semiclassical studies of diffuse Josephson junctions with various noncoplanar structures, including helical [62], magnetic vortices [63], and skyrmions [64], have not shown AJE. On the contrary, in studies devoted to diffuse systems with half-metallic elements [15, 50] and junctions between magnetic superconductors with spin filters [54, 55], a finite anomalous current is predicted.
It was shown in [48] that AJE can appear in any diffuse SFS system with a noncoplanar magnetization texture under fairly general conditions. Figure 16 shows typical non-coplanar three-layer SFS systems leading to AJE. The reason why anomalous currents were not detected in previous studies on diffuse SFS systems is related to the additional symmetry of the magnetization inversion I(φ, M) = I(φ, –M), which was taken into account in the semiclassical approximation [72, 73] with respect to the original Hamiltonian [48].
3.5. φ0 junction based on superconducting structures with quantum dots
The Josephson effect provides a fundamental feature of phase-coherent transport through mesoscopic samples with time reversal symmetry [4].
In Ref. [113], the authors calculated the equilibrium Josephson current through a multilevel quantum dot with Rashba or Dresselhaus spin-orbit coupling. The critical current can change radically with a change in the spin-orbit coupling parameter, which, in an external magnetic field, leads to oscillatory dependences on the Datta–Dass-type coupling parameter.
A new impetus to the study of mesoscopic and nanoscale Josephson junctions was given by the experimental demonstration of a gate-tunable Josephson current through junctions with several electronic levels (quantum dots) in various systems, in particular, in InAs-nanowires [114–116], carbon nanotubes [117], and 2D electron gas in semiconductors [118, 119].
Mesoscopic systems based on ordinary s-wave superconductors form a new class of systems with spontaneously broken symmetry with respect to time reversal and, therefore, exhibit anomalous supercurrents. In [11], a long ballistic one-dimensional Rashba quantum wire was studied, where Ia ≠ 0 was determined by the Zeeman effect and the difference between the velocities of electrons moving to the right and to the left. The obtained value α and the value Ia ∝ α4 turned out to be very small, practically unrealizable for the experiment. The anomalous Josephson effect was investigated by numerical simulation for a multichannel spin-polarized quantum point contact [12]. In Ref. [36], the authors calculated the Josephson current through a typical phase-coherent mesoscopic system (arbitrary multilevel quantum dot). Figure 17 shows the transfer of a Cooper pair through a two-level quantum dot and indicates the contributions to the matrix element during the forward and reverse tunneling processes. It was found that the necessary conditions for Ia ≠ 0 are the presence of a spin-orbit coupling and a suitably oriented Zeeman field. In addition, the quantum dot must be a chiral conductor.
3.6. Anomalous Josephson effect in semiconductor nanowires
The presence of a strong spin-orbit interaction in narrow-gap InSb and InAs semiconductors [120–122], which makes it possible to electrically control the spin, makes them natural materials for the realization of the anomalous Josephson effect [123].
For conduction electrons in direct-gap semiconductors, the spin-orbit interaction is expressed as

where V (r) is the external potential and σ indicates the electron spin s = σ/2. For an external electric field  , the replacement V(r) = e
, the replacement V(r) = e z in expression (42) leads to the Rashba interaction:
z in expression (42) leads to the Rashba interaction:

Here, the coupling constant α = e λ is tunable by an electric field or gate voltage.
λ is tunable by an electric field or gate voltage.
The diagram of the Josephson junction and a brief description of the model used in [9] are shown in Fig. 18, and the results in the case of one impurity, in Fig. 19.
In [9], the anomalous Josephson effect was studied numerically using the tight coupling model for a nanowire in the case of a short junction in the presence of a magnetic field. The energy levels En of the Andreev bound states were calculated numerically as functions of the phase difference φ between the superconductors; the DC Josephson current was estimated from the Andreev levels. I(–φ) = –I(φ) ratio violation has been demonstrated. It was also shown that the anomalous Josephson current and the direction dependence of the critical current are qualitatively the same as in the single scatterer model, and that the spin-dependent mixing channel plays an important role in the presence of spin-orbit interaction.
3.7. Change in the magnetic flux in a superconducting loop containing a ψ Josephson junction
It is well known that the magnetic flux Φ through a superconducting loop placed in an external magnetic field is quantized, i.e., is equal to an integer number of flux quanta Φ = nΦ0. The possibility of transitions between states with different vortex structures (different n) makes it possible to implement multiply connected superconducting systems, such as flux qubits [124, 125], ultrasensitive magnetic field detectors [126], and Josephson generators of a sequence of sharp uniformly distributed voltage pulses [127]. Flow quantization also naturally implies the use of a superconducting loop as a topologically protected memory cell in fast single-quantum logic devices (RSFQ) [128].
However, as the loop size R decreases at a fixed value of the magnetic flux, the field value increases as R−2, which becomes a serious obstacle to the miniaturization of flux devices. Switching without the use of an external magnetic field can be implemented in a superconducting loop containing a Josephson junction with built-in magnetic order and/or broken inversion symmetry [1, 3, 4, 129]. Unlike conventional Josephson systems, such junctions maintain a nonzero phase difference in the ground state. The φ0 junctions included in the superconducting circuit play the role of a phase battery in the creation of a spontaneous electric current, which corresponds to the magnetic flux Φ = (φ0/2π)Φ0 through the circuit [58, 130, 131]. It can be expected that control of the phase of the ground state of the φ0 junction, for example, by voltage or radiation, should effectively rearrange the magnetic flux and switch the system between states with a different number of vortices without applying an external magnetic field.
However, in most existing φ0 junctions, the phase change is limited (δφ0 <2 π) and the corresponding flow Φ < Φ0 cannot change the number of vortices n through the superconducting circuit. Indeed, Josephson junctions with a ferromagnetic layer between superconducting banks support only π-states with φ0 = π [56, 57, 132], which allow the design of environmentally decoupled qubits [58], but are not suitable for changing the loop vorticity. A variable F-layer thickness (see, for example, [133] and references therein), as well as the presence of an Abrikosov vortex or a pair of current injectors in one of the superconductors [134, 135], can lead to a second-order phase transition with a spontaneous phase φ0 varying from zero to π (so δ φ0 < π). The situation looks more promising for SFS compounds with broken inversion symmetry, where the spin-orbit interaction creates an arbitrary spontaneous phase φ0 ∝ ν sin θ (θ is the angle between the exchange field in the ferromagnet and the direction of the broken inversion symmetry), while the constant ν characterizes the intensity of the spin-orbit interaction and exchange field [6, 12, 27, 36, 50]. However, the ν parameter is usually small, which limits the φ0 variation.
It was shown in [136] that a ψ Josephson junction with a half-metallic weak link integrated into a superconducting circuit (Fig. 20) makes it possible to pump a magnetic flux penetrating the loop.
In such a compound, the phase of the ground state ψ is determined by the mutual orientation of the magnetic moments in two ferromagnets (Fig. 21) surrounding the half-metal. The precession of the magnetic moment in one of the ferromagnets, controlled, for example, by microwave radiation, leads to the accumulation of phase ψ and subsequent switching between states with different numbers of vortices. The proposed flux pumping mechanism does not require the application of voltage or an external magnetic field, which makes it possible to design electrically decoupled memory cells for superconducting spintronics.
Appropriate selection of the driving frequency Ω makes it possible to realize controlled switching between different stable states φn , an example of which between states n = 0 and n = 1 is shown in Fig. 22.
3.8. Thermal analogue of the anomalous Josephson effect
In Ref. [137], a thermal analogue of the anomalous Josephson effect in an SFS structure with a noncoplanar magnetic texture is predicted. It is shown that the thermal current through the junction has a phase-sensitive interference component proportional to cos (θ – θ0), where θ is the Josephson phase difference and θ0 is the texture-dependent phase shift.
In a three-layer magnetic structure with a tunnel barrier with a spin filter, the value of θ0 is determined by the spin chirality of the magnetic configuration and can be considered a direct manifestation of energy transfer involving spin-triplet Cooper pairs. In the case of an ideal spin filter, it is shown that the phase shift is resistant to spin relaxation caused by spin-orbit scattering. Possible applications of the relation between heat flux and magnetic precession are discussed.
As mentioned above, in recent years, much attention has been paid to phase-coherent caloritronics in hybrid superconducting structures [138]. The mechanism of phase-sensitive heat transfer is based on the thermal analog of the Josephson effect [139–141], which occurs in a system consisting of two superconductors S1 and S2 separated by a weak link and at temperatures T1 and T2, respectively. A nonzero temperature shift (for definiteness, it is assumed that T1 > T2) generates a constant heat flux from S1 and S2, which is expressed in terms of thermal CPR:
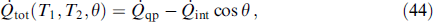
where θ is the phase difference between the superconducting electrodes. Here, the first term on the right-hand side is the usual quasi-particle thermal current, and the second one describes the contribution of energy transfer involving Cooper pairs. In accordance with the Onsager symmetry, the thermal current is invariant under time reversal, since the phase-coherent term in equation (44) does not change with phase inversion:  .
.
The mutual influence of heat transfer and the Josephson effect have been experimentally studied starting from observations of thermoelectric effects in superconductor/normal metal/superconductor junctions [142]. Recently, the presence of coherent thermal currents (44) was confirmed in experiments using Josephson thermal interferometry in tunnel junctions [138, 143]. Subsequently, a number of applications have been proposed, including thermal interferometers [138, 143, 144], transistors [145], phase-sensitive ferromagnetic Josephson valves [146], and topological Andreev coupled state probes [147].
The  direction in equation (44) can be controlled experimentally, providing the implementation of the 0 – π thermal Josephson junction [148].
direction in equation (44) can be controlled experimentally, providing the implementation of the 0 – π thermal Josephson junction [148].
Paper [137] reported on the possibility of obtaining a generalized thermal CPR in the form
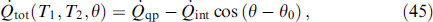
where, in contrast to equation (44), there is an arbitrary phase shift θ0.
This effect takes place in systems with broken time reversal symmetry and chiral symmetry, such as SFS junctions with noncoplanar magnetic texture or spin-orbit interaction. It can be considered a thermal analogue of the anomalous Josephson effect characterized by the generalized CPR:

Here, Ic is the critical current, and φ0 is an arbitrary phase shift, which in the general case differs from the phase shift in the generalized thermal CPR: θ0 ≠ φ0.
Paper [137] demonstrates a thermal CPR with a phase shift (45) using the example of a Josephson spin valve [149], which contains three noncoplanar magnetic vectors (Fig. 23). It consists of two ferromagnetic layers with exchange fields h1, 2 interacting with superconducting electrodes separated by a spin filter barrier with magnetic polarization directed along m. Figure 24 shows the phase shifts in the CPR with φ0 and θ0 for two barrier spin filter efficiencies P. Recently, the spin filter effect was demonstrated in SF structures based on ferromagnetic insulators of europium chalcogenides [150, 151] and GdN tunnel barriers [152]. The role of external contacts F1, 2 is to induce effective exchange fields in superconducting electrodes. In the case of metallic ferromagnets, this can be achieved on the basis of the inverse proximity effect [153, 154]. Alternatively, F1, 2 can be ferromagnetic insulators and induce an effective exchange field in S1, 2 as a result of spin-mixing scattering of conduction electrons [129].
4. Anomalous Josephson effect in structures with a topological insulator
At present, a number of Josephson structures are known in which AJE is realized due to the properties of topological materials. In this section, we consider the possibility of controlling the anomalous Josephson current by means of the Majorana mode. We describe the junction formed by the contact of two superconductors through the helical edge states of a quantum spin-Hall insulator. The relationship between electric charge and spin polarization is discussed for equilibrium and nonequilibrium electric transport through a two-dimensional Josephson junction containing disordered surface channels of a three-dimensional topological insulator (3D TI). The splitting of the easy axis of a ferromagnet in the φ0 Josephson junction on a 3D TI surface is also demonstrated.
4.1. Control of anomalous Josephson current by means of the Majorana mode
A distinctive feature of a topological insulator is edge or surface states. In the two-dimensional case, helical modes appear at the edge of the sample, i.e., a pair of one-dimensional modes coupled by time reversal symmetry and propagating in opposite directions for opposite pseudospins. A 2D chiral Dirac fermion on the surface of a strong TI (an odd number of chiral Dirac fermions on the surface) is protected by the topology and the presence of a volume bandgap. Such systems are interesting objects for the search for 2D phonon or exciton superconductivity (see references in [155]). Fu and Kane [156] predicted the appearance of chiral Majorana fermions as bound Andreev states at the interface of an insulator (FI) and an ordinary superconductor (S) having dispersion along the interface.
The charge transfer phenomena in normal metal/ferromagnetic insulator/superconductor structures and S/FI/S with a chiral Majorana mode on a 3D surface of TI were studied by Tanaka et al. [155]. Emergence of the chiral Majorana mode can be controlled with high sensitivity by the direction of the magnetization m in FI. The phase shift can be continuously tuned with the component m perpendicular to the interface. Control of the Andreev reflection and the Josephson current by means of the Majorana mode opens unique opportunities for superconducting spintronics.
Figure 25 shows a contour diagram of the energy level of the chiral Majorana mode EJ (CMM) as a function of θ and φ for mx = 0, 0.4mz , and –0.4mz and the resulting Josephson current in junctions, showing the change in CPR with the direction of magnetization in a ferromagnetic insulator.
The calculation of the Josephson current, taking into account the chiral Majorana mode and magnetization in FI, carried out in [155], leads to the expression
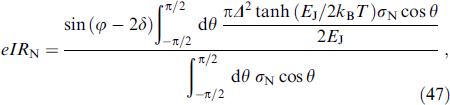
where RN is the resistance in the normal state, δ = mxd/νF is the phase shift, T is the temperature, and σN is the junction transparency in the normal state.
The Josephson current is practically independent of my , because its contribution to I is compensated by Majorana modes with opposite chiralities. On the other hand, mx significantly affects the value I as an effective vector potential, which directly enters the Josephson phase φ. The absence of a small factor e/c, which reduces the connection with the magnetic field, greatly facilitates the restructuring of the CPR. It is remarkable that, in this model, the anomalous CPR arises by changing the magnetization vector only, without using unconventional pairing mechanisms.
4.2. φ0 junctions in superconductor structures with quantum spin-Hall insulators
One of the variants of the φ0 Josephson junction based on the topology of the barrier is the junction formed by the contact of two superconductors through the spiral edge states of a quantum spin-Hall insulator (QSHI) [25]. The influence of an external magnetic field on the CPR of such a junction leads to the fact that, as a result of the Zeeman effect, along the axis of spin quantization of the edges of the helix AJE arises. The phase shift φ0 is associated with so-called helical superconductivity, which is the result of the mutual influence of the Zeeman effect and spin-orbit coupling.
Helical superconductivity due to edge states leads to current
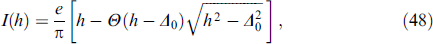
where Θ is the Heaviside function and h is the applied magnetic field. The current I (φ = 0) flows in a short JJ, L ⪡ ξ with ξ = νF/Δ0, at zero phase difference. Thus, proximitized superconductivity brings the system into an excited state, which leads to the anomalous Josephson effect. The anomalous current increases in proportion to the applied magnetic field h at h < Δ0, and then decreases as 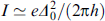 at h ⪢ Δ0. Note the fact that Δ0 is an induced gap, which also implies the validity of the condition h > Δ0 as long as the gap Δ0 is sufficiently small compared to the intrinsic gap of the superconductors forming the junction.
at h ⪢ Δ0. Note the fact that Δ0 is an induced gap, which also implies the validity of the condition h > Δ0 as long as the gap Δ0 is sufficiently small compared to the intrinsic gap of the superconductors forming the junction.
Figure 26 shows the phase dependence of the current for various values of the applied magnetic field h, as well as the anomalous Josephson current at φ = 0 as a function of h.
The spatial separation of the two spirals is important. AJE occurs only if the connections at the edges are of unequal length, as shown schematically in Fig. 27a, where the Josephson current is carried by edge states. The anisotropy of the gyromagnetic tensor should make it possible to observe the effect with a magnetic field in the plane. The effect is stable with respect to a small shift between the applied field and the spin quantization axis. The dependence of the anomalous Josephson current on the magnetic field h at φ0 = 0 for various temperatures is shown in Fig. 27b. We note an additional phase shift between the two edges due to the orbital effect of the field [157–159].
Thus, the basis of the anomalous Josephson effect in S/QSHI/S systems is the helical nature of edge states QSHI exposed to a magnetic field. The resulting anomalous superconducting current flowing at zero phase difference between the two superconducting terminals is rebuilt by the magnetic field. The fields in the superconductor and in the contact region, which contribute to the superconducting current, feel the helical nature of the edge states in the corresponding parts of the system. Analyzing the contributions of both edges, the required direction of the magnetic field, and the stability of the effect with respect to the final chemical potential and the misorientation of the magnetic field and the spin quantization axis, Dolcini et al. [25] proposed methods for experimental observation of the effect using hybrid structures based on available implementations. The CPR was determined as a function of the external magnetic field and the contact length. It is expected that AJE will be pronounced in junctions based on nanowires with strong spin-orbit interaction [160, 161] in the topological regime.
4.3. φ0 junction controlled by quasiparticle injection
The connection between the electric charge and spin polarization during equilibrium and nonequilibrium electric transport through a two-dimensional Josephson junction containing disordered surface channels of a three-dimensional topological insulator can serve as the basis for the appearance of AJE [40]. In this case, the Edelstein effect is more pronounced in equilibrium than in a conventional material with spin-orbit coupling.
Using the semiclassical technique of Keldysh, Bobkova et al. [40] demonstrated the formation of a φ0 junction resulting from the modulation of quasiparticle injection into the junction, the scheme of which is shown in Fig. 28. The ground state of the system corresponds to zero superconducting current, realized at a nonzero phase difference φ = φ0 = –4dIh/α. The anomalous phase shift is proportional to the voltage difference V between the superconductors and the normal injection electrode, which determines the injection rate of quasiparticles, making it possible to switch the φ0-state of the JJ on and off experimentally by controlling the injection of the quasiparticle flow.
4.4. Splitting of the easy axis of a ferromagnet in a superconductor/ferromagnet/superconductor φ0 Josephson junction on the surface of a three-dimensional topological insulator
The strong dependence of the Josephson energy on the orientation of the magnetization in Josephson junctions with ferromagnetic interlayers and spin-orbit coupling opens up new possibilities for controlling the magnetization of a ferromagnet by a superconducting current (Josephson phase). Such a dependence arises in Josephson SFS junctions on the surface of a three-dimensional topological insulator containing Dirac quasiparticles.
Dirac quasiparticles exhibit complete spin-momentum locking: the electron spin always forms a right angle with its own momentum, which leads to a pronounced dependence of the CPR on the magnetization direction [16, 155, 163]. At present, great progress has been made in the experimental implementation of hybrid structures F/TI. In particular, alloying with transition metal elements, such as Cr or V, has been used to introduce a ferromagnetic order into TI. Another way to introduce a ferromagnetic order into TI, which has been successfully implemented experimentally, is based on the coupling of a nonmagnetic TI with a magnetic insulator with a high Tc to create a strong exchange interaction in surface states through the proximity effect. Such a structure was studied by Nashaat et al. [162], and it was shown that the phase shift of the anomalous ground state of the φ0 junction on the surface of a 3D TI is proportional to the magnetization component in the plane perpendicular to the direction of the superconducting current [16, 163]. An anomalous phase shift causes precession of the magnetization, similarly to the case of a system with spin-orbit coupling. However, for the system under consideration, the absolute value of the critical current highly depends on the orientation of the magnetization, namely, on the magnetization component in the plane along the current direction. This dependence in the regime with a given voltage can lead to splitting of the easy axis of the ferromagnet and stabilization of the fourfold degenerate ferromagnetic state, which contrasts sharply with the usual twofold degenerate ferromagnetic state of the easy axis.
Figure 29 shows a diagram of the described system, in which two ordinary s-wave superconductors and a ferromagnet deposited on a 3D TI surface form a JJ. The calculation procedure consists of calculating the CPR based on the formalism of semiclassical Green's functions. For the case with a given voltage, the electric current through the junction comprises two parts: the Josephson current js and the normal jn. The Josephson current is associated with the presence of nonzero anomalous Green's functions in the interlayer and manifests itself in equilibrium. In the low applied voltage mode eV/(kB Tc)⪡ 1, the deviation of the distribution function from equilibrium is small and can be ignored in the calculation of the Josephson current. The result is the following final expression for the Josephson current:

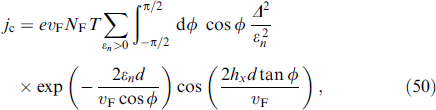

where εn = πT(2n + 1). At high temperatures, T ≈ Tc ⪢ Δ, the lowest Matsubara frequency makes the main contribution to the current, and expression (50) is simplified:
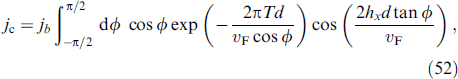
where jb = eνF NF Δ2/(π2T ). A similar expression was obtained for Dirac materials by Linder et al. [164]. The normal current is due to the deviation of the distribution function from equilibrium. However, for the system under consideration, assuming that the ferromagnet is metallic, practically the entire normal current flows through the ferromagnet, since in real experimental setups the TI resistance must be much larger than the resistance of the ferromagnet. As for the Josephson current, it is greatly suppressed inside the ferromagnetic layer, since the exchange field there is usually much larger than the induced exchange field heff in the TI surface layer. Therefore, the current flows through the TI surface states.
The dynamics of the magnetization of a ferromagnet is described in terms of the LLG equation. The electric current flowing through the TI surface states induces a spin-orbital torque [165–168] due to the presence of a strong coupling between the quasi-particle spin and the momentum. In principle, if ferromagnetism and spin-orbit coupling coexist spatially, then this torque is determined by the total electric current flowing through the system. However, in the case under consideration, only the superconducting current flows through the TI surface states, where spin-momentum synchronization takes place. Therefore, only this superconducting current creates a torque acting on the magnetization. A normal current flows through a homogeneous ferromagnet in which there is no spin-orbit coupling.
The torque caused by the superconducting current can be taken into account as an additional contribution to the effective field, which has the form
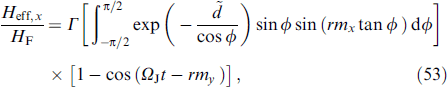
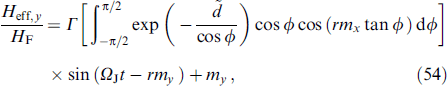

where m = M/Ms, 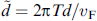 is the length of the JJ, Γ = φ0
jbSr/2πKVF is proportional to the ratio of the Josephson and magnetic energy, r = 2dheff/νF, ΩJ = 2eV is the Josephson frequency, and HF = ΩF/γ = K/Ms.
is the length of the JJ, Γ = φ0
jbSr/2πKVF is proportional to the ratio of the Josephson and magnetic energy, r = 2dheff/νF, ΩJ = 2eV is the Josephson frequency, and HF = ΩF/γ = K/Ms.
Figure 30 shows the evolution of the magnetization m obtained from the numerical solution of the LLG equation. It can be seen that, under different initial conditions, the system goes into four different stable states: two with a positive component my and ±mx (shown in panels a and c) and two with ±mx and a negative component my (panels b and d).
The system can switch to these states spontaneously under the influence of noise acting on states with ± mz . The results are presented in Fig. 31 showing all four possible end states.
A similar approach to studying the dynamics of magnetization in voltage-shifted junctions has already been applied to systems with spin-orbit coupling in the intermediate layer [7, 96]. The qualitative difference between the system based on TI surface states and these investigations is that, in the case under consideration, the critical current demonstrates a strong dependence on the x component of the magnetization. Previously, it was considered independent of the direction of magnetization. This dependency results in a nonzero value of Heff, x ∼ mx for small values of mx , which means that the easy axis y can become unstable in a junction in a state with voltage or bias current, while this axis is always stable if the critical current does not depend on the direction of magnetization. Moreover, for the system, there is no difference between the ±mx -components of the magnetization. This leads to the remarkable fact that, in a controlled system, the easy axis does not reorient itself, retaining two stable directions of magnetization, as was already obtained earlier, but splits, demonstrating four stable directions of magnetization.
5. Anomalous Josephson effect in the Josephson junction/nanomagnet system
The φ0 junction can also occur in the Josephson junction/nanomagnet (JJ/NM) system shown in Fig. 32 due to the purely electromagnetic interaction between a tunneling junction current and the magnetic moment of a nanomagnet located in close proximity to each other [100]. In this case, the magnetic field of the nanomagnet changes the tunneling current through the junction, while the magnetic field generated in the JJ affects the magnetic moment of the nanomagnet.
The peculiarity of the system manifests itself in the choice of the structure geometry, the nature of the interaction, and the final junction resistance in the normal state, which is taken into account within the RSJ model [82]. The attractiveness of a model with purely electromagnetic interaction lies in the absence of unknown parameters, which should be essential for its experimental study.
5.1. Properties of the Josephson junction/nanomagnet system
Within the framework of this structure, it is assumed that a number of characteristic phenomena will be observed [100], in particular, the appearance of Shapiro-like steps in the CVC of the JJ, created by the NM precession, the reversal of the magnetic moment when a time-varying voltage is applied to the JJ, and Rabi oscillations of the quantum spin induced by applied constant voltage. The intensity of the interaction between the NM and the JJ is determined by the parameter  = EJ/EB, which describes the ratio of the Josephson energy to the magnetic one, which is, in order of magnitude, the ratio of the magnetic field generated by the tunneling current to the effective field Beff acting on the magnetic moment due to the magnetic anisotropy and the applied external field. Estimates show that the possibility of observing the first Shapiro step at
= EJ/EB, which describes the ratio of the Josephson energy to the magnetic one, which is, in order of magnitude, the ratio of the magnetic field generated by the tunneling current to the effective field Beff acting on the magnetic moment due to the magnetic anisotropy and the applied external field. Estimates show that the possibility of observing the first Shapiro step at  (as well as the peak at V0 = 0.5 due to nonlinearity) looks quite realistic [100]. In this case, the width of the first step decreases linearly with decreasing
(as well as the peak at V0 = 0.5 due to nonlinearity) looks quite realistic [100]. In this case, the width of the first step decreases linearly with decreasing  , the width of the second harmonic
, the width of the second harmonic  is proportional to
is proportional to  2, and so on.
2, and so on.
A remarkable property of the system is that, despite the weakness of the field generated by the tunneling current, for a certain time dependence of the applied voltage, an effective pumping of spin excitations into a nanomagnet and a reversal of its magnetic moment can occur. The reversal is realized under the condition  > α, while the realistic value of the damping parameter is α = 0.01 [170]. Parameter
> α, while the realistic value of the damping parameter is α = 0.01 [170]. Parameter  determines the number of cycles in the precession of the magnetic moment leading to a reversal, which is proportional to 1/
determines the number of cycles in the precession of the magnetic moment leading to a reversal, which is proportional to 1/ . For
. For  = 0.05, the required time to reversal is close to
= 0.05, the required time to reversal is close to 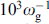 , which for ωg ∼ 1011 s−1 is ∼ 10 ns. Smaller
, which for ωg ∼ 1011 s−1 is ∼ 10 ns. Smaller  would require a slower voltage V0 versus time, which is not a problem for such an experiment [100]. However, a smaller
would require a slower voltage V0 versus time, which is not a problem for such an experiment [100]. However, a smaller  will require less dissipation due to the
will require less dissipation due to the  > α condition. In addition, the smaller
> α condition. In addition, the smaller  is, the more sensitive the time evolution of the magnetic moment to the time dependence of the voltage. A small change in this dependence is sufficient to return to the original state after the reversal. Below is an example of studying the reversal of the magnetic moment in this system.
is, the more sensitive the time evolution of the magnetic moment to the time dependence of the voltage. A small change in this dependence is sufficient to return to the original state after the reversal. Below is an example of studying the reversal of the magnetic moment in this system.
Rabi oscillations of the quantum spin in the JJ/NM system, induced by an applied constant voltage, are determined not by parameter  but by the ratio of the Zeeman interaction of the spin with the tunnel current field and tunnel splitting Δ [100]. They strongly depend on the applied voltage. The greatest effect occurs when V0 satisfies one of the resonant conditions eV0 = (m/n) Δ, where m and n are integers. With such a resonant behavior, the probability of finding a spin in the 'up' or 'down' state is very different from the nonresonant case, which indicates the fundamental possibility of electromagnetic control of the JJ/NM qubit by means of an applied voltage.
but by the ratio of the Zeeman interaction of the spin with the tunnel current field and tunnel splitting Δ [100]. They strongly depend on the applied voltage. The greatest effect occurs when V0 satisfies one of the resonant conditions eV0 = (m/n) Δ, where m and n are integers. With such a resonant behavior, the probability of finding a spin in the 'up' or 'down' state is very different from the nonresonant case, which indicates the fundamental possibility of electromagnetic control of the JJ/NM qubit by means of an applied voltage.
The JJ/NM model was considered in [100]. The phase difference φ = φ0 + φA is determined by the applied voltage V0(t) (dφ0/dt = 2eV0(t)/ℏ) and the voltage VA = (ℏ/2e) × (dφA /dt), which is the electromotive force induced in the junction by the time dependent magnetic field generated by the rotating magnetic moment of the nanomagnet. The vector potential is determined by the sum A = AB + AM of the vector potential of the external field AB = 1/2(B × r) and the vector potential AM = (μ0/4π)(M × r)/r3 created by the magnetic field of the nanomagnet. The derivative dφ/dt is proportional to the total voltage drop across the junction:
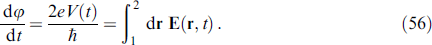
Here, E is the electric field, and integration is carried out from one end of the weak link to the other.
Thus, in the JJ/NM system, the phase shift in the expression for the superconducting current

arises due to taking into account the magnetic field created by the rotating magnetic moment of the nanomagnet.
The dynamics of the magnetic moment is determined by the LLG equation:
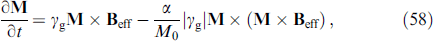
where Γg is the gyromagnetic ratio for M, α is the Gilbert damping, and
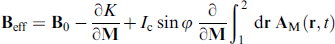
is the effective field acting on M. The last term in this expression is equal to the magnetic field BJ, created by the tunnel current I = Ic sin φ at the location of the nanomagnet.
In normalized units, the LLG equation takes the form
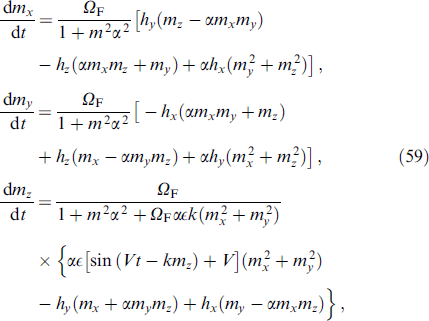
where mi = Mi /Ms are the normalized components of the magnetic moment, Ms is the saturation magnetic moment, ΩF = ωF/ωc is the normalized ferromagnetic resonance frequency, ωc = 2eRIc/ℏ, Ic is the critical current,
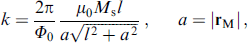
Φ0 is the magnetic flux quantum, m is the absolute value of magnetic moment, and α is the Gilbert damping parameter. Here, time t is normalized to  , voltage V is normalized to ℏωc/(2e). The components of the effective magnetic field hi
in normalized values are determined by the expressions [100]
, voltage V is normalized to ℏωc/(2e). The components of the effective magnetic field hi
in normalized values are determined by the expressions [100]
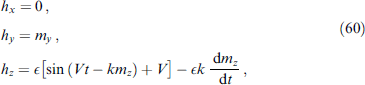
where  = G k, G =
= G k, G =  J/Kan
ν, ν is the volume of the nanomagnet, and Kan is the magnetic anisotropy constant. The components of the effective magnetic field are normalized to HF = ωF/γg. Equations (59), (60), together with the equations of the RSJ model, form the basis for studying the dynamics and current–voltage characteristics of the JJ/NM system.
J/Kan
ν, ν is the volume of the nanomagnet, and Kan is the magnetic anisotropy constant. The components of the effective magnetic field are normalized to HF = ωF/γg. Equations (59), (60), together with the equations of the RSJ model, form the basis for studying the dynamics and current–voltage characteristics of the JJ/NM system.
5.2. Ferromagnetic resonance in the Josephson junction/nanomagnet system
Josephson oscillations in the junction excite the precession of the magnetic moment of the nanomagnet, which leads to FMR when the precession frequency becomes equal to the natural frequency of the magnetic system ΩF. In [169], to describe the resonance, system of equations (59) was solved by the Gauss–Legendre method, as a result of which the time dependences of the magnetic moment components were determined, and the maximum amplitude of oscillations of the magnetic moment components in the time domain was calculated for each given voltage value.
Figure 33a shows the results of calculations of the maximal amplitude of oscillations 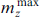 as a function of voltage V on the JJ at ΩF = 0.5 and two values of the damping parameter α = 0.001 and 0.3. In the chosen normalization, V = ΩJ; therefore, at a voltage corresponding to the frequency of Josephson oscillations ΩJ = 0.5, an FMR peak is observed. For
as a function of voltage V on the JJ at ΩF = 0.5 and two values of the damping parameter α = 0.001 and 0.3. In the chosen normalization, V = ΩJ; therefore, at a voltage corresponding to the frequency of Josephson oscillations ΩJ = 0.5, an FMR peak is observed. For 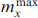 , the result is qualitatively the same. An increase in damping leads to an increase in the width of the resonance and its shift towards lower frequencies, which is shown in Fig. 33a at α = 0.3. The positions of the peaks at low damping are in good agreement with the frequency values following from the analytical formulas obtained from the linearization of the LLG equations [169]. In particular, if the deviation of the magnetic moment from the equilibrium direction due to interaction with the Josephson current is small, i.e., G < 1 and
, the result is qualitatively the same. An increase in damping leads to an increase in the width of the resonance and its shift towards lower frequencies, which is shown in Fig. 33a at α = 0.3. The positions of the peaks at low damping are in good agreement with the frequency values following from the analytical formulas obtained from the linearization of the LLG equations [169]. In particular, if the deviation of the magnetic moment from the equilibrium direction due to interaction with the Josephson current is small, i.e., G < 1 and 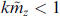 , then the resonant frequency is given by
, then the resonant frequency is given by
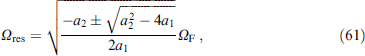
where
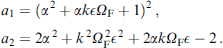
So, at G = 0.3, k = 0.01, and ΩF = 0.5, for α = 0.001, the resonant frequency is Ωres ≈ 0.5, and, for α = 0.3, Ωres ≈ 0.45, which is quite close to the values obtained numerically (Fig. 33a).
The width of the resonance depends on the Gilbert damping parameter α, the ratio of the Josephson energy to the energy of the nanomagnet G, and coupling parameter k. Figure 33b demonstrates the influence of parameter G on the properties of ferromagnetic resonance. As G increases, a decrease in the resonant frequency and asymmetry of the resonant peak with respect to ΩJ = ΩF are observed. Analytic expressions in this case give Ωres ≈0.492 at α = 0.1, G = 0.1, k = 0.01, and ΩF = 0.5. However, at G = 3π, analytical calculations lead to overestimated values, which means that higher order terms must be taken into account at G ⪢ 1. Thus, the deviation mz in resonance at certain values of G, k, and α can be quite strong and manifest itself under experimental conditions [169].
5.3. Manifestation of Kapitza's pendulum features in the Josephson junction/nanomagnet system
Another interesting result that manifests itself in the JJ/NM system is the demonstration of the reorientation of the easy axis of the nanomagnet with an increase in the ratio of the Josephson energy to the magnetic one, i.e., a peculiar manifestation of the properties of the Kapitza pendulum in the Josephson junction/nanomagnet system [169]. Figure 34 shows the dynamics of the magnetic moment component mz (t) for different values of parameter G. We emphasize that at the initial moment of time the magnetic moment is directed along the easy axis (the y-axis, see Fig. 32). We see that for small values of G the time dependence of the mz (t) component reaches a certain constant value. As G increases, this dependence changes significantly, and at G = 3π, mz (t) oscillating, tends to unity, i.e., my goes to zero. Thus, the easy axis of the nanomagnet is reoriented. In intermediate states, the magnetic moment of the nanomagnet is oriented between the axes y and z, and the reorientation time decreases with increasing G.
The dynamics of mz at various values of the Josephson frequency ΩJ is shown in Fig. 35. For small ΩJ, the mz component precesses near a certain fixed value, while for large ΩJ, oscillating, it goes to unity [169].
It is known that the position of stable equilibrium of a pendulum changes if its suspension point oscillates with a high frequency [93]. The ratio of the Josephson energy to the magnetic energy (G) corresponds to the amplitude of the variable force in the problem of the Kapitza pendulum, which should contribute to the reorientation of the easy axis of the ferromagnet. The nature of the increase in the average value of mz depending on the ratio of the Josephson energy to the magnetic one is shown in Fig. 36, which also demonstrates an analogy with Kapitza's pendulum. A similar behavior is observed with increasing coupling parameter k of the Josephson and magnetic subsystems.
5.4. Shapiro-like steps in the current–voltage characteristic of the Josephson junction/nanomagnet system
Until now, we have considered the effect of Josephson oscillations on the dynamics of the magnetic moment of a nanomagnet. Let us now briefly describe the reverse effect, i.e., the influence of the dynamics of the magnetic moment on the CVC of the Josephson junction [5]. The calculation of the CVC is carried out for the junction in the biased current case. In this case, within the framework of the RCSJ model [82], the system of equations has the following form:
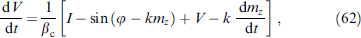

where φ is the phase difference in the Josephson junction, and βc is the McCumber parameter. In addition, to calculate the CVC in system of equations (59), in the expression for the effective field (60), it is necessary to replace Vt with φ.
Figure 37 shows the results of calculating the CVC of a JJ with and without a nanomagnet (CVC of the SIS junction) together with the dependence of the maximum component mz on voltage [169]. The CVC of a JJ with a nanomagnet demonstrates the feature indicated by the arrow, which is absent in the case of a JJ without a nanomagnet. The voltage position of this feature corresponds to the position of the mz resonant peak. Thus, the nanomagnet precession manifests itself in the CVC of the JJ, which can serve as a method for controlling its dynamics. Note that justification for the parameter values used and their correspondence to the experimental conditions is given in [100, 171], which implies the possibility of an experimental study of the observed effects.
As unexplored properties of the JJ/NM system, the appearance of chaotic states under periodic action on the system should be noted [172]. Chaos in the JJ under external electromagnetic radiation, which is modeled by adding the term A sin (ωt) to the bias current (ω is the frequency, A is the radiation amplitude), was considered in detail in [173]. It is assumed that, in the system under study, the precession of the magnetic moment under superconducting oscillations in the JJ can also lead to the appearance of chaotic states. Research in this area has not yet been carried out, but undoubtedly it is important for the practical applications of these systems.
6. Reversal of the magnetic moment in the φ0 junction
Superconducting electronics plays an important role in the development of computers with ultralow power consumption [66, 128, 174–176]. One of the key problems in achieving this goal is the creation of a reliable and scalable cryogenic memory architecture, for which Josephson SFS junctions are promising structures. Indeed, the mutual influence of the intrinsic exchange field and induced superconductivity in a ferromagnet leads to a π junction [56, 57]. Vertical ferromagnetic multilayer structures are used as Josephson magnetic memory. The two logical states of these memory elements usually correspond to states with different relative orientations of the magnetic layers, which in turn determines whether the junction is in the 0- or π-state. Readout schemes are generally based on the difference between resistive and nonresistive states.
This review considers an alternative cryogenic memory element based on the φ0 junction [6], the ground state of which corresponds to the final phase shift in its CPR. Such an anomalous phase was recently discovered experimentally in hybrid Josephson junctions, in particular, fabricated using a topological insulator Bi2Se3 [28] and based on Al/InAs heterostructures [29, 177]. Both materials have a strong spin-orbit coupling, and in these experiments time reversal is broken by an external magnetic field that acts as a Zeeman field. The considered memory element is a Josephson junction with a ferromagnetic interlayer, so the spin-orbit interaction is violated by the exchange field. In these compounds, the magnetization of a ferromagnet can be controlled by electric current [7, 31, 33, 34, 178, 179]. In [66], it was proposed to use such a junction as a memory element with information encoded in the direction of the magnetization of the ferromagnetic layer.
6.1. Reversal of the magnetic moment by a current pulse
The possibility of magnetization reversal in the φ0 Josephson junction by a current pulse was demonstrated in [34]. It was shown that the reversal of the magnetic moment is extremely sensitive to the values of the system parameters. In view of the sufficient complexity of the system under consideration, the question of the possibility of predicting a complete reversal for given parameters of the system and the current pulse remained open until recently. Below, we discuss an analytical criterion for reversal, which makes it possible to do this for certain parameters of the φ0 junction and the current pulse.
The scheme of the considered φ0 junction is shown in Fig. 38. The easy axis of the ferromagnetic layer is directed along the z-axis, which also coincides with the direction of the spin-orbit potential gradient. The magnetic moment component my is related to the Josephson current directed along the x-axis.
The dynamics of the magnetic moment of the system under consideration is described by the LLG equation [34], for which the effective field Heff depends on the Josephson phase difference φ:
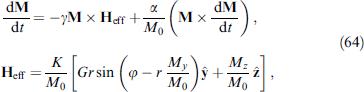
where γ is the gyromagnetic ratio, α is the Gilbert dissipation, M0 = |M|,  is the ratio of Josephson energy to magnetic anisotropy energy, K is the anisotropy constant,
is the ratio of Josephson energy to magnetic anisotropy energy, K is the anisotropy constant, 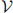 is the ferromagnetic layer volume, and r is the spin-orbit interaction parameter.
is the ferromagnetic layer volume, and r is the spin-orbit interaction parameter.
In dimensionless quantities, the system of equations is written as
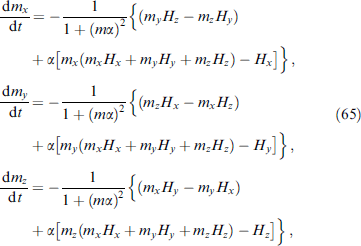
where the magnetic moment components mi are normalized to M0, i = x, y, z, and Hi are the effective field components normalized to K/M0, which are determined by the expressions
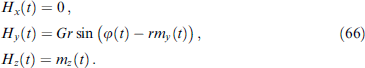
In system of equations (65), the time is normalized to 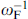 (where ωF = γK/M0 is the ferromagnetic resonance frequency). The equation for the phase difference is written in the framework of the resistive model [82], where, for simplicity, a JJ with a small capacitance C (R2
C/LJ ⪡ 1, LJ is the inductance of the Josephson junction, R is its resistance in the normal state), i.e., displacement current, is not taken into account. In this case, the expression for the electric current I through the Josephson junction, normalized to the critical current Ic, is written as
(where ωF = γK/M0 is the ferromagnetic resonance frequency). The equation for the phase difference is written in the framework of the resistive model [82], where, for simplicity, a JJ with a small capacitance C (R2
C/LJ ⪡ 1, LJ is the inductance of the Josephson junction, R is its resistance in the normal state), i.e., displacement current, is not taken into account. In this case, the expression for the electric current I through the Josephson junction, normalized to the critical current Ic, is written as
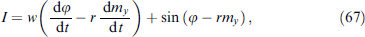
where w = VF/(IcR ) = ωF/ωR , VF = ℏωF/(2e), and ωR = 2eIcR /ℏ. It should be noted that the results in [7, 34] were obtained under the assumption that the term r(dmy /dt) is small. It is shown below that taking it into account does not really lead to qualitative changes, but it is necessary to maintain the gauge invariance of the equations used [178].
In (67), a rectangular current pulse with amplitude As and duration Δt,
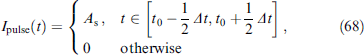
and with initial conditions
was used.
The calculations were carried out using an implicit scheme based on the two-step Gauss–Legendre method [180]. This approach provided higher accuracy (fourth order O(h4) ≈ 10−8) and stability than the Runge–Kutta method. System of equations (65) was solved numerically together with Eqn (67) using (68) with initial conditions (69). In all calculations, w = 1 was assumed; the values of the remaining parameters are indicated in the captions to the corresponding figures.
An example of transient dynamics for a reversal mz with residual oscillations is shown in Fig. 39a, and the dynamics of the components of the magnetic moment, phase difference, and superconducting current are shown in Fig. 39b. As can be seen, in the transition region, the phase difference changes from 0 to 2π and, accordingly, the superconducting current changes its direction twice. This is followed by an interval with damping of the oscillations of the superconducting current.
In Fig. 39b, the characteristic moments of time are indicated by vertical dashed lines. Line 1 corresponds to the phase difference π/2 and indicates the maximum superconducting current Is. Line 1 ', which corresponds to the maximum of my and mz = 0, has a slight offset from line 1. This fact demonstrates that, in general, the time dependence features of mx and my do not coincide with the features on Is (t), i.e., there is a delay in the response of the magnetic moment to changes in the superconducting current. Another characteristic point corresponds to φ = π. At this point in time, line 2 crosses points Is = 0, my = 0 and the minimum of mz . At the time when φ = 3π/2, line 3 crosses the minimum of Is. When the pulse is turned off, a superconducting current flows through the resistance, exhibiting damped oscillations and causing residual oscillations in the magnetic moment components. Note also that the end time of the pulse (t = 28) does not actually appear immediately in the dynamics of my (and mx not shown here). They demonstrate a continuous transition to damped oscillating behavior.
The data of Fig. 39b indicate a direct way to determine the magnitude of the spin-orbit coupling in the junction by means of the estimate r. For this, we note that  can be determined up to an initial time-independent constant φ00 as the voltage V(t) across the junction changes. In addition, maxima and minima of Is occur at times tmax and tmin (Fig. 39b), for which
can be determined up to an initial time-independent constant φ00 as the voltage V(t) across the junction changes. In addition, maxima and minima of Is occur at times tmax and tmin (Fig. 39b), for which
Determining φ00 from these equations, one can obtain
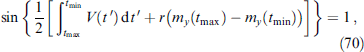
which makes it possible in principle to determine r from magnetization my at the maximum and minimum supercurrent and voltage V at the junction. We emphasize that, for the experimental implementation of the proposed method, it is necessary to distinguish between the magnetization values at times of the order of 10−10 – 10−9 s. At present, studying the dynamics of magnetization with such time resolution is a rather difficult task. To experimentally determine the spin-orbit coupling constant r, it is more convenient to vary the parameters of the current pulse I (t) and study the switching threshold of the magnetic moment.
The dynamics of the system in the form of magnetization trajectories in the my – mx and mz – mx planes during the transition time interval for the same momentum and JJ parameters at α = 0 is shown in Fig. 39. It can be seen that the magnetic moment performs a spiral rotation, approaching the state with mz = –1 after turning off the electric current pulse. The figures clearly show the features of the dynamics near the points B, A', and Q and the damped oscillations of the magnetization components (Fig. 39b, d). Point B in Fig. 39c corresponds to the transition from an increase in the absolute value mx to its decrease and back at point A'. The behavior of the magnetic system turns out to be quite sensitive to the parameters of the electric current pulse and the JJ. Paper [34] shows different magnetization reversal protocols when changing the parameters As, G, and r.
It is interesting to compare the effect of a rectangular pulse with a Gaussian one of the form
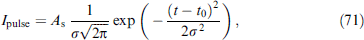
where σ denotes the full width at half maximum of the pulse, and A is its maximum amplitude at t = t0. An example of the reversal of the magnetic moment in this case is shown in Fig. 40, which displays the dynamics of mz at r = 0.1, G = 10, As = 5, σ = 2 at low dissipation α = 0.01 .
In this case, the magnetization reversal occurs more smoothly than in the case of a rectangular pulse.
6.2. Periodicity in the occurrence of magnetic moment reversal intervals with a change in the parameters of the Josephson junction and the current pulse
The study of the magnetization dynamics of the φ0 junction led to the discovery of a periodicity in the occurrence of intervals of reversal of the magnetic moment with a change in the parameters of the JJ and the current pulse. Figure 41 shows examples of the dynamics of the magnetic moment mz for two values of the ratio of the Josephson energy to the magnetic one: G = 9 (curve 1) and G = 8 (curve 2), as well as the applied current pulse Ipulse (curve 3). In the first case (G = 9), a reversal of the magnetic moment is observed, while in the second (G = 8), it is absent, which reflects the dependence of the implementation of the reversal on the chosen values of the system parameters. The influence of the model parameters and the current pulse on the reversal of the magnetic moment in the φ0 Josephson junction was discussed in Refs [34, 179]. However, the study of the possibility of predicting the reversal and determining the intervals of parameters at which the reversal of the magnetic moment occurs have not been carried out until recently.
To determine the intervals of G in which the reversal occurs, the time dependence of the magnetic moment was calculated in [181] for values of G from 1 to 130 with step ΔG = 1 for values of α from 0.01 to 0.5 with step Δα = 0.001. The value of the spin-orbit coupling parameter was assumed to be r = 0.1. For each pair of values (α, G), systems of equations (65), (67), and (68) were solved by the Gauss–Legendre method with step h = 0.01 in the interval t ∈ [0,Tmax], Tmax = 200. For t = Tmax, the inequality |mz + 1| ⩽ 0.0001 was checked in order to fix the realization of the reversal of the magnetic moment. In the case of its implementation, the corresponding values of α and G were selected and stored. These data, presented in Fig. 42, indicate a periodic dependence in the implementation of the reversal of the magnetic moment with increasing G. Let us emphasize some features in the manifestation of this dependence, in particular, the absence of a reversal at small G and the shift of intervals along G with increasing α. In this case, an increase in the width of these intervals along the G-axis is observed.
Paper [181] also presents the results of calculating the implementation of the reversal of the magnetic moment on the plane (G, r), where a periodicity appears in the occurrence of reversal intervals with a change in G. An increase in the spin-orbit coupling parameter r leads to a shift of the domain with a reversal to the region of small G with a simultaneous decrease in its width.
As mentioned above, the easy axis of a ferromagnet is directed along the z-axis and has two stable states, mz = ±1. The current pulse causes the magnetic moment to oscillate. The critical value for the reversal is its value at the end of the pulse, which is determined by the parameters of the φ0 junction and the parameters of the pulse. Paper [181] presents the time dependences of the magnetic moment component mz for different values of the spin-orbit coupling parameter r, the Gilbert damping parameter α, and the ratio of the Josephson to the magnetic energy G for the first and second bands. If the value of mz turns out to be close to zero or negative, then the presence of Gilbert damping ensures that mz tends to –1. The periodicity in the occurrence of reversal intervals can be explained by assuming a periodic dependence of the mz component on the parameters of the model used. Section 6.3 presents analytical studies of the magnetic moment reversal in Josephson structures with an anomalous phase shift.
6.3. Analytical criteria for magnetization reversal in the φ0 junction
As already noted, one of the main problems in superconducting electronics is the creation of a memory element [174, 175, 182] with low energy dissipation. Various versions of such devices have been considered, including those based on φ0 Josephson junctions [66, 182–184].
The DC component of the superconducting current applied to the SFS φ0 junction can have a strong orientational effect on the ferromagnetic magnetic moment in the layer [34]. Guarcello and Bergeret in [66] indicated the possibility of using the SFS φ0 junction as an element of cryogenic memory based on the pulse switching proposed in [34]. In such a scheme, a bit of information is associated with the direction of the magnetic moment along or against the direction of the easy axis of the ferromagnetic layer. The recording is carried out as an inversion of the magnetic moment by a current pulse, and the readout is carried out by detecting the magnetic flux by a SQUID inductively coupled to the φ0 junction. The stability of the current-induced magnetization reversal to thermal fluctuations was also studied, and a method was proposed for breaking the coupling between the Josephson phase and the magnetization dynamics by tuning the intensity of the Rashba spin-orbit interaction by the gate voltage. We emphasize that, in all the studies mentioned above, magnetization reversal was studied only numerically.
As noted above, the physics of switching in the φ0 junction is determined by the LLG equation (65) and the model equation of RSJ (67). An interesting feature of this system in the case of strong dissipation is the decoupling of the equations, i.e., equation (67) for Φ = φ – φ0 = φ – rmy turns out to be unrelated to the LLG equation (65). This makes it possible to find an analytical solution for Φ and construct a theory of magnetization reversal for certain values of the junction and current pulse parameters.
Thus, at the period of the current pulse action t0 ⩽ t ⩽ t0 + δt, the equation for Φ has the form
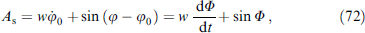
with the initial condition Φ (t = t0) = 0. At As < 1, this gives
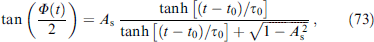
where 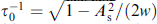 defines the time scale of approaching a constant value Φ. Formula (73) allows finding sin Φ during the current pulse t0 ⩽ t ⩽ t0 + δt. In the second time interval t ⩾ t0 + δt, when the impulse is disabled (Ip(t) = 0),
defines the time scale of approaching a constant value Φ. Formula (73) allows finding sin Φ during the current pulse t0 ⩽ t ⩽ t0 + δt. In the second time interval t ⩾ t0 + δt, when the impulse is disabled (Ip(t) = 0),
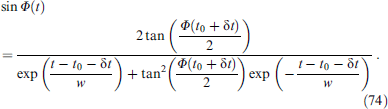
This expression exhibits an exponential decay towards zero with a τ1 ∼ w time scale. Here, tan [Φ (t0 + δt)/2] is determined by equation (73).
The theory is based on the following basic assumptions: (1) for small w and for momenta with As ≠ 1, the wdΦ/dt term in equation (72) can be neglected, which implies the relation Ip(t) = sin Φ; (2) the condition Gr ⪢ 1, which does not imply G ⪡ 1 for w ⪡ 1 (see [7]), so that G can vary over a wide range, from G ⪡ 1 to G ∼ 100 ⪢ 1; (3) the smallness of the Gilbert damping α ⪡ 1 [185–187]. Under these conditions, the LLG equation during the period of the current pulse can be written in the form
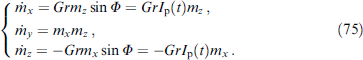
The tight coupling limit Gr ⪢ 1 (but r ⪡ 1) can be considered analytically [7]. In this case, my
(t) ≈ 0, and for the applicability of the method, we must put GrIp(t) ⪢ 1. Then, in polar coordinates ρ and ϕ, we get mx
= ρ sin ϕ, mz
= ρ cos ϕ, and 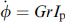 . Thus:
. Thus:

As can be seen from (73), after the current pulse is turned off, sin Φ quickly drops to 0 due to the condition w ⪡ 1. In this time interval, the magnetization dynamics is determined only by magnetic anisotropy and Gilbert damping, which causes the magnetization to align along the easy axis [96].
As follows from (76), magnetization reversal occurs at
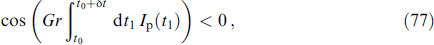
where δt is the pulse duration.
The results of analytical calculations, together with the results of the numerical solution of the complete system of equations, are shown in Fig. 43 for rectangular pulse Ip(t) = As[θ (t – t0) – θ (t – t0 – δt)] with As = 0.5 for δt1 = 1 and δt2 = 3.
In the case of δt = 1, criterion (77) gives cos (GrAs δt1) = 0.28 > 0, so there is no reversal, while, for δt2 = 3, it turns out to be cos (GrAs δt1) = –0.76 < 0 and remagnetization is observed. It can be seen that numerical solution (76) represented by the blue squares coincides with the analytical solution represented by the green solid curve. When the pulse is disabled, damping prevents any deviation from the easy mz = ±1 axis. This is shown in the insets to Fig. 43. It should be noted that the magnetization reversal is affected not by the shape of the current pulse but only by the integral over the pulse duration [65].
6.4. Periodicity of reversal intervals in the plane r – G
According to (77), the magnetization reversal in plane r – G under the current pulse action Ip(t) = As[θ (t – t0) – θ (t – t0 – δt)] leads to hyperbolic regions at
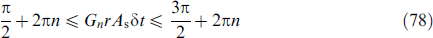
for n = 0, ±1,..., while the most efficient reversal occurs when condition

is satisfied, i.e., at GrAs δt = π + 2πn.
In the case of a rectangular current pulse in the weak damping regime and small w, Eqn (78) gives hyperbolic curves for different n. From a physical point of view, they are curves of constant amplitude for the force in the LLG equation (64). In such a situation, the magnetic moment aligns in the mz = –1 direction immediately after the pulse is turned off, and the appropriate time scale is determined only by the pulse duration and not by the Gilbert damping. This helps to optimize the pulse width to achieve a fast reversal. It can be seen from (79) that the minimum time for the reversal is realized at n = 0, i.e.,

The described situation is shown in Fig. 44 for G = 100, r = 0.1, α = 0.005, w = 0.01, As = 0.5, and δteff = 0.628, resulting in a remagnetization time of δtrev ≈0.6 × 10−10 s for typical ωF ∼ 10 GHz. This time is two orders of magnitude shorter than that calculated in [34].
Figure 45 compares the numerical results with the analytical ones obtained on the basis of equations (78) and (79). The almost perfect agreement between numerical and analytical calculations emphasizes the validity of the theory for the selected system parameters. Comparing both results, we can conclude that, in fact, term  (72), which makes the equations gauge-invariant, only slightly shifts the remagnetization regions. But, on the other hand, the gauge-invariant form of the equations makes it possible to consider Eqn (72) analytically.
(72), which makes the equations gauge-invariant, only slightly shifts the remagnetization regions. But, on the other hand, the gauge-invariant form of the equations makes it possible to consider Eqn (72) analytically.
Figure 45. (Color online.) Periodicity in the occurrence of magnetization reversal in plane r – G. Realization of the magnetization reversal is shown by green stripes, the boundaries of the regions (78) are blue dashed lines, and the solid curves of the most efficient reversal (79) are red. Calculations are performed in increments of ΔG = 0.5 and Δr = 0.001. Other parameters: α = 0.005, w = 0.01, As/Ic = 0.7, δt = 3. Solid lines correspond to formula (78) with n = 0,1,2,...,9. Black dots indicate points where the dynamics of mz (t) was studied in detail in [65]. (From [65].)
Download figure:
Standard image7. Experimental implementation of the anomalous Josephson effect and prospects for its application
If the chiral and time reversal symmetry are violated simultaneously during the tunneling of Cooper pairs through a junction, the Josephson current is nonzero at zero phase difference, which corresponds to a phase shift in the ground state. Recently, various methods have been proposed for implementing the violation of these symmetries, in particular, based on the use of noncentrosymmetric and multilayer ferromagnets [6, 51], point contacts [12], topological insulators [25, 155], diffuse systems [22, 39], nanowires [9, 188] and quantum dots [36, 37, 113], and a parallel combination of 0 and π junctions [19, 189].
7.1. φ0 Josephson junction based on a nanowire quantum dot
In quantum dots, the breaking of both symmetries can be achieved by a combination of an external magnetic field and spin-orbit interaction [36, 37, 113]. The finite Zeeman splitting for spin 'up' and spin 'down' electrons breaks symmetry under time reversal. On the other hand, chiral symmetry breaking arises under the mutual influence of the spin-orbit interaction and the magnetic field, when the orbital inside the quantum dot changes during tunneling. Szombati et al. [27] report the first experimental implementation of the φ0 junction based on a nanowire quantum dot, where it was demonstrated that the phase shift φ0 can be controlled using an electrostatic gate. The tunneling of an electron through a quantum dot with two orbitals that mix during the spin-orbit interaction was considered. When the orbital does not change, the contributions from both processes cancel each other out. When the orbital changes during tunneling, due to the mutual influence of the spin-orbit interaction and the magnetic field, compensation does not occur. In this case, an additional phase factor is acquired, which depends on the tunneling direction and is different for the left and right tunneling processes. As a consequence, the two processes cannot cancel each other, and this results in chiral symmetry breaking. The magnitude of the phase shift φ0 depends on the intensity of the spin-orbit interaction and the magnitude of the magnetic field in the plane. The results of observing a continuous phase change in the φ0 Josephson junction in a magnetic field in the plane were presented. In contrast to the case Bin-plane = 0, the phase shift of the voltage oscillations in the flow is tuned using the gate voltage.
7.2. Anomalous phase shift in a Josephson junction based on Bi2 Se3 due to spin-orbit interaction
An anomalous phase shift φ0 can be obtained in systems with both a Zeeman field and the Rashba spin-orbit coupling term HR = (α/ℏ)(p × ez )σ in the Hamiltonian [6, 39], where α is the Rashba coefficient, ez is the direction of the Rashba electric field, and σ is the vector of Pauli matrices describing the spin. Physically, these terms lead to spin-induced dephasing of the superconducting wave function.
The anomalous phase shift is associated with the inverse Edelstein effect observed in metals or semiconductors with a strong spin-orbit coupling. While the Edelstein effect generates a spin polarization in response to an electric field [190], the inverse Edelstein effect [191], also called the spin-galvanic effect, generates a charge current by nonequilibrium spin polarization. These two magnetoelectric effects also arise in superconductors as a consequence of a Lifshitz-type term in the free energy [26, 192]. Thus, in a superconductor with a strong Rashba coupling, the Zeeman field induces an additional term in the supercurrent. In Josephson junctions, this term leads to an anomalous phase shift in the CPR [39].
An anomalous phase shift φ0 can be detected experimentally in a Josephson interferometer (JI) by measuring the CPR. Anomalous phase shifts have recently been identified in a JI created from a parallel combination of a normal 0 and π junction [27], which breaks the parity symmetry.
Due to the large values of the g factor (g = 19.5) [193] and the Rashba coefficient, Bi2Se3 is a promising candidate for observing the anomalous Josephson effect due to the mutual influence of the Zeeman field and the spin-orbit interaction.
As described in detail in [26, 39], the amplitude of the anomalous phase depends on the amplitude of the Rashba coefficient α, the transparency of interfaces, spin relaxation terms such as the Dyakonov–Perel coefficient, and whether the junction is in the ballistic or diffusion mode. It is predicted that for small values of α the anomalous phase is proportional to α3; for large values, it should be proportional to α.
In the ballistic regime [6] and for large α, the anomalous phase shift is given as φ0 = 4EZ αL/(ℏνF)2 for a magnetic field of magnitude B perpendicular to the Rashba electric field, where EZ = (1/2)gμB B is the Zeeman energy, L is the distance between the superconductors, and νF is the Fermi velocity of the barrier material. For the spin-split Rashba conduction band with α = 0.4 eV Å, νF = 3.2 × 105 m s−1, and junction length L = 150 nm, the magnetic field B = 100 mT generates an anomalous phase φ0 ≃ 0.01 π, while for the Dirac states with νF = 4.5 × 105 m s−1 the value φ0 ≃ 0.005π [28].
In the diffusion regime, the expected anomalous phase shift was calculated in [39]. For weak α with highly transparent interfaces and ignoring spin relaxation, the anomalous phase shift is determined by the relation

where τ = 0.13 ps is the elastic scattering time,  is the diffusion constant, and m* = 0.25me is the effective electron mass [194].
is the diffusion constant, and m* = 0.25me is the effective electron mass [194].
To test these theoretical predictions, a JJ and a Josephson interferometer were prepared from Bi2Se3 in [28]. According to measurements of the relative phase shift between two JIs with different orientations of the JJs relative to the magnetic field in the plane, an anomalous phase shift was determined corresponding to formula (81). The results are presented in Figs 46 and 47 and in the table.
Figure 46. (Color online.) Anomalous phase shift measurement. (a) Sketch of a setup consisting of two Josephson interferometers (JIs) fabricated on a single chip. Reference and anomalous JIs have the same area, Sref and S, respectively, where S ≃ Sref ≃ 20.6 μm2. Aluminum electrodes are 20 nm thick. (b) Voltage map showing oscillations of the critical current of two devices as a function of magnetic field B. (c) Oscillation frequency can be changed by mechanically tilting the sample, i.e., by changing angle θ between the plane containing the superconducting loop and magnetic field B. Colored arrows serve as a guide for the eyes to help visualize the phase shift increase in the anomalous device. (From [28].)
Download figure:
Standard imageFigure 47. (Color online.) Comparison of JI frequencies as functions of angle θ. (a) Critical current shown as a function of the magnetic field. Red and blue curves correspond to the reference and anomalous device, respectively. Since the critical current of a large JI decreases with the magnetic field, this results in a decrease in the background set for both devices, shown in solid lines. (b) Critical current as a function of the magnetic field, at which the background indicated by solid lines in panel a is subtracted. Anomalous device shows a higher oscillation frequency than the control device. Colored dots help visualize the increased frequency of the anomalous device (blue dots) compared to the reference device (red dots). The two JIs are in-phase in a weak magnetic field and out of phase in a strong magnetic field, with an anomalous phase shift of up to φ0 ≃ π for B ≃ 100 mT. Periods are compared one by one, and the average of the ratios for one period gives the value ω/ωref. (c) Ratio of the oscillation frequencies is plotted as a function of angle θ. Without generating an anomalous phase shift, this ratio should be constant and equal to the surface ratio S/Sref ≃ 1. This ratio diverges as 1/θ for small θ as shown by equation (82). Fitting the curve with equation (82) makes it possible to determine spin-orbit coupling coefficient α. (From [28].)
Download figure:
Standard imageIn the absence of disorder, the anomalous phase shift induced by Rashba spin-orbit coupling can only be generated by an in-plane magnetic field By . The stress map shown in Fig. 46b shows the oscillations of the critical current of the two devices as a function of the magnetic field B. The critical current of both devices oscillates due to the perpendicular component of the magnetic field Bz = B sin θ. The oscillation frequency can be changed by mechanically tilting the sample, i.e., by changing the angle θ between the plane containing the superconducting loop and the magnetic field. Due to the anomalous phase shift, the frequency of the anomalous device is greater than the reference.
Figure 47 compares the JI frequencies as functions of the angle θ. Since the critical current of a large JI decreases with increasing magnetic field, this leads to a decrease in the background set for both devices, shown in the figure with solid lines. As can be seen, the anomalous device is characterized by a higher frequency of oscillations than the control one. The two JIs are in-phase in a weak magnetic field and out of phase in a strong magnetic field, with the anomalous phase shift reaching φ0 ≃ π for B ≃ 100 mT. In Figure 47c, the ratio of the oscillation frequencies is shown as a function of the angle θ. Without generating an anomalous phase shift, this ratio should be constant and equal to the surface ratio S/Sref ≃ 1. It was found that this ratio diverges as 1/θ for small θ in accordance with the equation
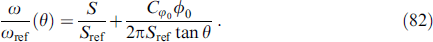
Curve fitting equation (82) determines the spin-orbit coupling coefficient α.
Table. Anomalous phase shifts obtained at B ≃ 100 mT and comparison with theory.
| θ = 0.1° | θ = 0.22° | θ = 0.46° | Ballistic regime | Dirac state | Diffusion regime | |
|---|---|---|---|---|---|---|
| φ0 | 0.88π | 1.01π | 0.85π | 0.01π | 0.005π | 0.94π |
The table shows the anomalous phase shifts obtained at B ≃ 100 mT, as well as theoretical values. The first three columns show the anomalous phase shifts extracted from the last nodes of the critical current oscillations shown in Fig. 47 for three curves taken at different angles θ. The last three columns show the calculated anomalous phase shifts in the ballistic mode for Rashba splitting conduction states, Dirac states, and in the diffusion mode for Rashba splitting conduction states. In theoretical calculations, the values α = 0.4 eV Å were used for conduction states with Rashba splitting and α = 3 eV Å for Dirac states.
7.3. Gate-controlled anomalous phase shift in the Josephson junction based on Al/InAs
As noted, AJE has been demonstrated in JJs with InSb nanowires in the quantum dot geometry [27] and more recently in JJs using Bi2Se3 [28]. In a JJ with a quantum dot, the phase shift can be changed by the gate voltage, but is limited by the geometry and supports only a few modes; therefore, small critical currents are realized in the JJ. Based on the topological insulator Bi2Se3, it is possible to implement a planar φ0 junction, but in this case the phase shift cannot be tuned by the gate voltage [29, 177]. Heterostructures formed by InAs and epitaxial superconducting Al [195] are promising not only for mesoscopic superconductivity [196] but also for the realization of topological superconductivity and Majorana fermions [197]. This is due to the fact that the induced superconducting gap Δind in InAs can be as large as in Al [198], and InAs has a large g-factor and spin-orbit coupling. As a consequence, a JJ fabricated on this platform can have a high critical current and high transparency [177, 199]. In addition, it is possible to control the magnitude of the spin-orbit coupling by changing the InAs density through an external gate [200].
The possibility of changing the magnitude of the anomalous phase shift in a JJ formed on the basis of InAs and Al is due to the possibility of varying the intensity of the spin-orbit coupling through an external gate [29]. The observation of a finite phase shift φ0 indicates a relationship among the phase difference of superconductors, electric current, and spin in these heterostructures. The phase shift for different in-plane magnetic fields and gate voltages is shown in Fig. 48, and the evolution of the phase shift is shown in Fig. 49.
Figure 48. (Color online.) Device resistance as a function of phase shift applied to the SQUID and current at three different in-plane fields By
and three different gate voltages  . In all cases,
. In all cases,  has a value of –2 V. Dotted orange line indicates the position of the maximum oscillation at
has a value of –2 V. Dotted orange line indicates the position of the maximum oscillation at  V. Orange stars indicate position of the maximum at each value of the magnetic field. (From [29].)
V. Orange stars indicate position of the maximum at each value of the magnetic field. (From [29].)
Download figure:
Standard imageFigure 49. Evolution of the phase shift in the Josephson junction of a SQUID as a function of gate voltage  (a) and the applied magnetic field (b). Phase shift Δφ0 is measured between the oscillation at the set value
(a) and the applied magnetic field (b). Phase shift Δφ0 is measured between the oscillation at the set value  and the oscillation at –4 V used as a reference. In panel b, solid lines correspond to linear fits to measured phase shifts. (From [29].)
and the oscillation at –4 V used as a reference. In panel b, solid lines correspond to linear fits to measured phase shifts. (From [29].)
Download figure:
Standard imageThe value of φ0 is proportional to the Zeeman energy and turns out to be much larger than the given theoretical estimates. Most likely, this is due to the fact that such scaling is valid for a long junction with several channels, which is not directly related to the system under study.
The implementation of large values of the phase shift φ0 and its tuning are very important for applications in superconducting spintronics, where large spin gradients can be used to create a phase battery [1]. This opens up the possibility of generating spin gradients in a controlled manner via Josephson currents or phase shift. The possibility of achieving a large value φ0 in heterostructures InAs/Al and the fact that it strongly depends on the InAs density are directly related to efforts to realize topological superconducting states [201, 202].
7.4. Josephson phase batteries
A phase battery is a quantum device that provides a continuous (constant) phase shift for the wave function of a quantum circuit and is a key element for quantum technologies based on quantum coherence. In [30], the first experimental implementation of a phase battery in a hybrid superconducting circuit is reported. It consists of an n-doped InAs nanowire with unpaired spin surface states proximitized by aluminum superconducting contacts. The ferromagnetic polarization of unpaired spin states is effectively converted into a constant phase shift φ0 along the wire, which leads to the anomalous Josephson effect [6, 39]. By applying an external magnetic field in the plane, a continuous change in φ0 is achieved, which allows the battery to be charged and discharged. The joint action of the spin-orbit coupling and the exchange interaction breaks the phase rigidity of the system, causing a strong coupling among the charge, spin, and phase. This relationship opens up broad prospects for topological quantum technologies [1].
Side hybrid JJs made from materials with strong spin-orbit interaction [27] or topological insulators [28] are ideal options for creating φ0 junctions. The lateral arrangement breaks the symmetry of the inversion and provides a natural polar axis 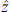 that is perpendicular to the current direction. Moreover, the spin polarization of electrons s, induced either by a Zeeman field or by the exchange interaction with ordered magnetic impurities, breaks the time reversal symmetry. As a result, the structure acquires a toroidal symmetry described by the anapole moment
that is perpendicular to the current direction. Moreover, the spin polarization of electrons s, induced either by a Zeeman field or by the exchange interaction with ordered magnetic impurities, breaks the time reversal symmetry. As a result, the structure acquires a toroidal symmetry described by the anapole moment 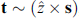 , retaining the magnetoelectric effects in the presence of the spin-orbit interaction. In this case, the anomalous shifts φ0 are controlled by a Lifshitz-type invariant in the free energy (FL), which can be composed from the product of the anapole moment and the superfluid velocity [39]:
, retaining the magnetoelectric effects in the presence of the spin-orbit interaction. In this case, the anomalous shifts φ0 are controlled by a Lifshitz-type invariant in the free energy (FL), which can be composed from the product of the anapole moment and the superfluid velocity [39]:

where f (α, h) is the odd intensity function of the Rashba spin-orbit interaction α, h is the exchange or Zeeman field, nh is the unit vector pointing in the direction of the latter, and vs is the superfluid velocity of Cooper pairs flowing in the JJ. The scalar triple product defines vector symmetries φ0, while the magnitude of the shift depends on specific microscopic details of the sample, as well as macroscopic quantities such as temperature.
As shown in Fig. 50, the phase battery consists of a JJ made on the basis of an InAs nanowire enclosed between two Al superconducting poles. The supercurrent and, hence, vs flow along the nanowire (x-direction) orthogonally to the Rashba spin-orbit interaction vector indicating the plane of the substrate (z-direction). In the same nanowire, surface oxides or defects generate unpaired spins that behave like magnetic impurities (indicated by yellow arrows in Fig. 50) that can be polarized along the y-direction to provide an exchange interaction h in this direction. This leads to the final triple product in equation (83) and, hence, to an anomalous phase shift φ0. Due to the ferromagnetic order of the unpaired spins, the phase shift persists even in the absence of an applied magnetic field. The phase battery converts the ferromagnetic order into a quantum phase shift. It was shown in [30] that the shift φ0 can also be controlled by the Zeeman interaction with an external magnetic field B. By scanning the shifts φ0 in all directions of the plane magnetic field, the authors showed the geometric origin of the anomalous phase described by Eqn (83).
Figure 50. (Color online.) Josephson phase battery. (a) Conceptual diagram of a Josephson phase battery consisting of an InAs nanowire (red) embedded between two superconducting poles (blue) that converts the spin polarization of the surface unpaired spins (yellow) into phase shift φ0. (b) Schematic illustration of a hybrid (InAs nanowire–Al) SQUID interferometer used to quantify the phase shift φ0 produced by two JJs (red). Ring lies in the x – y plane with the nanowire parallel to the x-axis. Magnetic field Bz penetrating the ring is used to modulate the critical current of the SQUID (IS) as measured by a four-wire setup. I is current flowing through the interferometer, ΔV is the resulting voltage drop across the device. (c) Scanning electron microscope image of the active region of the phase battery, consisting of two φ0 junctions, not in corresponding colors. By is the magnetic field in the plane orthogonal to the nanowire. (d) Temperature dependence R(T) of the interferometer resistance in the normal state, showing the Kondo rise at low temperatures, which is consistent with the background of magnetic impurities. From the fit (yellow curve), a spin density of ∼ 4 ppm is estimated. (e) Voltage drop ΔV measured across the SQUID versus bias current I and magnetic flux Φ. Green line is the best fit for SQUID critical current IS(Φ) defined by the interface between nondissipative (red) and dissipative (colored) modes. (f) Recording ΔV(Φ) from (e) for two selected bias currents (below and above 2 Ic), which exhibits φ0-periodicity in both nondissipative and dissipative modes. Data in (e) and (f) were recorded at a bath temperature of 80 mK. (From [30].)
Download figure:
Standard image7.5. Cryogenic memory element based on the anomalous Josephson effect
An important problem for the memory element is effects due to inevitable thermal fluctuations. In [66], an exhaustive analysis of the noise in the φ0 junction dynamics was presented, taking into account the influence of stochastic thermal fluctuations. The current-induced magnetic bistability makes it possible to determine two well-distinguishable logical states and to investigate the stability of such a memory against noise effects. A sensing scheme based on a current controlled SQUID (Fig. 51) has been proposed in which no additional magnetic flux is required to set the optimum operating point. In addition, the intriguing possibility of effective screening of the memory state by voltage gating in a device formed by a ferromagnetic layer with a linear momentum term of the Dresselhaus spin-orbit coupling was discussed.
Figure 51. Reading out states based on the SQUID and demonstrating the value of the SQUID critical current (points on the curves) in the case of both positive and negative orientation of the magnetic moment along the z-axis (panels a and b, respectively). (From [66].)
Download figure:
Standard imageIn Ref. [66], a nonvolatile memory element based on a lateral ferromagnetic Josephson junction with spin-orbit coupling and out-of-plane magnetization is proposed. The interaction between the magnetic moment and the exchange field of a ferromagnet leads to a magnetoelectric effect, which couples the electric current through the junction and magnetization, which makes it possible to switch the direction of the magnetic moment in the ferromagnet by a current pulse. The two memory states are encoded in the direction of out-of-plane magnetization. In order to determine the optimal operating temperature for a memory element, the influence of noise on the average stationary magnetization was studied, taking into account thermal fluctuations that affect both the Josephson phase and the dynamics of the magnetic moment. The switching process is studied depending on the parameters of the ferromagnet, such as the Gilbert damping and the spin-orbit coupling intensity, and a non-destructive readout scheme based on the DC SQUID is proposed. In addition, in [66], a method was analyzed for protecting the memory state from external disturbances by voltage gating in systems with Rashba and Dresselhaus type linear spin-orbit coupling in the momentum.
8. Conclusions
This review attempts to highlight the main studies of the anomalous Josephson effect, which is one of the most topical areas of superconducting spintronics. The above results testify to the variety of physical phenomena that arise in φ0 junctions of various types, due to the relationship between the Josephson phase and the magnetization of the ferromagnet. In the review, much attention is directed to a description of the Buzdin model, within the framework of which was demonstrated the implementation of a direct relationship between the quantities characterizing superconductivity and magnetism, as well as the possibility of controlling magnetic properties by means of a superconducting current and, in turn, the influence of the magnetic characteristics of the barrier in the φ0 junction on its superconducting properties. Investigations of ferromagnetic resonance and variations in the magnetic dynamics along the CVC of the φ0 junction have led to a number of unique results that have not been touched upon by experimenters to date. The possibility of reorienting the easy axis of a ferromagnet by a Josephson current, which is analogous to the Kapitza pendulum in mechanical systems, will undoubtedly be developed in superconducting spintronics. The manifestation of the anomalous Josephson effect in various structures presents a wide field for both theoretical and experimental studies.
Important are the results of detailed studies of the DC component of the superconducting current, which arises in the junction due to the precession of the magnetic moment, as well as the influence of external electromagnetic radiation on the properties of the φ0 junction. The ability to realize large phase shifts φ0 and to tune them is also important for various applications in spintronics, where large spin gradients can be used to create a phase battery [1]. This opens up the possibility of generating spin gradients in a controlled manner via Josephson currents or a phase shift. Achieving a large value of φ0 and its rearrangement can find key applications in various quantum schemes and are directly related to efforts to realize topological superconducting states [201, 202].
The experimental realization of the φ0 junction makes it possible to measure the magnitude of the spin-orbit coupling and opens up new possibilities for the phase control of Josephson devices. These studies help in understanding fundamental spin-dependent phenomena, as well as developing applications for computer technology. In particular, control of the magnetic state due to superconductivity stimulates the development of ultrafast cryogenic memory. The development of effective methods to reverse the magnetic moment in the φ0 junction, in particular, by a superconducting current pulse, as well as the study of the quantum properties of Josephson nanostructures with magnetic and topologically nontrivial barriers for the creation of new superconducting spintronic devices, are the most important tasks of modern science.
Research on the anomalous Josephson effect is being intensively developed. Thus, a number of new interesting results have recently been obtained. The spin-orbit coupling in two-dimensional systems is usually a Rashba or Dresselhaus spin-orbit coupling linear in the wave vector. However, the class of materials that support the dominant cubic structure of the spin-orbit interaction along the wave vector is currently expanding. In [203], Josephson junctions were considered in a Zeeman field with superconductors separated by a normal region with spin-orbit interaction. A strongly anharmonic current–phase relation and a complex spin structure were found. Experimental tuning of the spin-orbit interaction will make it possible to tune both the anomalous phase shift and the supercurrent that flows at zero phase difference in the junction. The spin-orbit interaction in Josephson junctions results in spin-triplet f-correlations of superconductivity, which are important for superconducting spintronics and support Majorana bound states. Collective excitations of the magnetic moment and the Josephson phase in ψ junctions are demonstrated in Ref. [204]. This leads to a shift in the ferromagnetic resonance frequency, anomalies in CVCs, and the appearance of additional magnetic anisotropy in F-layers. In contrast to the previously studied SFS junctions, the coupling between the magnetic and plasma modes also arises in the long-wavelength limit. It is shown that such a coupling provides controlled magnetization reversal in the F-layer, controlled by a direct current pulse, which makes it possible to efficiently control the magnetic moment in superconducting spintronic devices. In Ref. [205], the magnetization reversal effect was studied as a function of the internal parameters of a ferromagnet, such as Gilbert damping and spin-orbit coupling intensity. The optimal values of the parameters for fast switching and the conditions that make the system more resistant to noise have been found. A review of the current state and prospects of superconducting spintronics is presented in [206].
It should be noted that this review does not cover all studies devoted to the anomalous Josephson effect, not all theoretical and experimental results are described in sufficient detail, and a number of applications of the φ0 junction, which are worthy of discussion but are not included due to the limitation of the scope of the review, have not been described.
Acknowledgments
The author is grateful to A Buzdin, A Melnikov, V Krasnov, I Bobkova, A Bobkov, S Mironov, M Silaev, I Rahmonov, A Mazanik, K Kulikov, M Nashaat, and A E Bota for their helpful discussions of certain issues in this review. This study was supported by the Russian Foundation for Basic Research within the framework of scientific project no. 19-12-50211, Expansion. A number of results of numerical calculations given in Sections 2, 4, 5, and 6 were obtained within the framework of project 18-71-10095 of the Russian Science Foundation.