Abstract
A large class of Laboratory, Space, and Astrophysical plasmas is nearly collisionless. When a localized energy or particle sink, for example, in the form of a radiative cooling spot or a black hole, is introduced into such a plasma, it can trigger a plasma thermal collapse, also known as a thermal quench in tokamak fusion. Here we show that the electron thermal conduction in such a nearly collisionless plasma follows the convective energy transport scaling in itself or in its spatial gradient, due to the constraint of ambipolar transport. As a result, a robust cooling flow aggregates mass toward the cooling spot and the thermal collapse of the surrounding plasma takes the form of four propagating fronts that originate from the radiative cooling spot, along the magnetic field line in a magnetized plasma. The slowest one, which is responsible for deep cooling, is a shock front.
Export citation and abstract BibTeX RIS

Published by the EPLA under the terms of the Creative Commons Attribution 4.0 International License (CC-BY). Further distribution of this work must maintain attribution to the author(s) and the published article's title, journal citation, and DOI.
Introduction
A signature property of a large class of magnetized and unmagnetized plasmas in the Laboratory, Space, and Astrophysical systems is the extremely low collisionality that can be due to high plasma temperature Te
or low plasma density ne
, or a combination of the two [1]. For example, a fusion-grade plasma in a tokamak reactor has 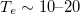 kiloelectronvolts (keV) and
kiloelectronvolts (keV) and  per cubic meter, which results in a mean free path
per cubic meter, which results in a mean free path 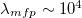 meters (m), while the toroidal length of the confinement chamber is merely 20–30 m [2–4]. In the Earth's radiation belt, the electron λmfp
can be as long as 1011 m or higher with huge variations in electron energy and density [5–8]. At the even greater scale of clusters of galaxies, the intracluster hot gas has
meters (m), while the toroidal length of the confinement chamber is merely 20–30 m [2–4]. In the Earth's radiation belt, the electron λmfp
can be as long as 1011 m or higher with huge variations in electron energy and density [5–8]. At the even greater scale of clusters of galaxies, the intracluster hot gas has 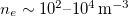 and
and 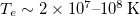 [9–13], so λmfp
is in the order of tens of kiloparsec to megaparsec.
[9–13], so λmfp
is in the order of tens of kiloparsec to megaparsec.
A whole class of problems arises if a localized cooling spot is introduced into such a nearly collisionless plasma. This could be structure formation in a galaxy cluster where a radiative cooling spot is driven by increased particle density [9] or an event horizon of a black hole that provides an absorbing boundary for plasmas [14]. A satellite traversing the Earth's radiation belt can be a sink for plasma energy and particles [15,16]. In a tokamak reactor, solid pellets that are injected into the fusion plasma for fueling and disruption mitigation [17–20], provide localized cooling due to a combination of energy spent on phase transition and ionization of the solid materials, and the radiative cooling that is especially strong when high-Z impurities are embedded in the frozen pellet. Even in the absence of pellet injection, large-scale magnetohydrodynamic instabilities can turn nested flux surfaces into globally stochastic field lines that connect fusion core plasma directly onto the divertor/first wall [21–24], causing a thermal collapse via fast parallel transport along the field lines within a short period of time that can range from micro-seconds to milliseconds [25]. Notice that the high-Z impurities originated from the divertor region can migrate to the core region and cool the plasma in both regions via radiations, e.g., see ref. [26]. An outstanding physics question is how a thermal collapse of the surrounding plasma, commonly known as a thermal quench in tokamak fusion, would come about in such a diverse range of applications.
The most obvious route for the thermal collapse is via electron thermal conduction along the magnetic field line that intercepts the cooling spot, for which the Braginskii formula [27] would produce an enormous heat flux [9,11] if there is a sizeable temperature difference 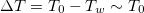 between the cooling spot (Tw
) and surrounding plasmas (T0),
between the cooling spot (Tw
) and surrounding plasmas (T0),

Here 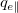 is the parallel electron conduction heat flux,
is the parallel electron conduction heat flux, 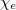 the thermal conductivity,
the thermal conductivity, 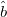 the unit vector in the magnetic field direction,
the unit vector in the magnetic field direction, 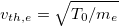 the electron thermal speed, and LT
the distance or field line length over which ΔT is established. For a nearly collisionless plasma, the temperature collapse necessarily starts with Knudsen number
the electron thermal speed, and LT
the distance or field line length over which ΔT is established. For a nearly collisionless plasma, the temperature collapse necessarily starts with Knudsen number 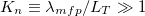 , a regime in which the free-streaming limit [28] of
, a regime in which the free-streaming limit [28] of

is supposed to apply in lieu of Braginskii, with 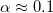 [29].
[29].
The pressure-gradient–driven plasma flow 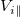 along the magnetic field line is limited by the ion sound speed cs
, so the convective electron energy flux is bounded by ne
cs
T0. Equation (2) suggests that the electron energy flux would be dominated by conduction as normally
along the magnetic field line is limited by the ion sound speed cs
, so the convective electron energy flux is bounded by ne
cs
T0. Equation (2) suggests that the electron energy flux would be dominated by conduction as normally  in a plasma of comparable electron and ion temperatures. In such a conduction-dominated situation, the much colder but denser cooling spot would be rapidly heated up by the electron thermal conduction from the surrounding hot plasma, and as a result, it can become over-pressured and the original cooling spot, say an ablated pellet in a tokamak, tends to expand into the surrounding plasma, yielding an outflow.
in a plasma of comparable electron and ion temperatures. In such a conduction-dominated situation, the much colder but denser cooling spot would be rapidly heated up by the electron thermal conduction from the surrounding hot plasma, and as a result, it can become over-pressured and the original cooling spot, say an ablated pellet in a tokamak, tends to expand into the surrounding plasma, yielding an outflow.
In the aforementioned problem of clusters of galaxies, one has instead observed robust cooling flows into the radiative cooling spot that aggregate mass onto the cooling spot [9], although more recent observations reveal a more modest mass-accreting cooling flow that indicates the role of various additional heating mechanisms to balance the cooling [11–13]. This is inconsistent with the conduction-dominated scenario mentioned above [9,11,30,31]. Extensive efforts have been made to find ways to inhibit the electron thermal conduction in the nearly collisionless plasma, for example, by tangled magnetic fields [32,33] or plasma instabilities [34–36], in order to reach the convection-dominated scenario, which would naturally yield the cooling flow regime of a plasma thermal quench.
In this letter, we show that in a nearly collisionless plasma, even along the magnetic field lines, like in the case of pellet injection into a tokamak, ambipolar transport will naturally constrain the electron parallel thermal conduction in such a way that the plasma thermal collapse comes with a cooling flow toward the radiative cooling spot. The necessary constraint is on the spatial gradient of electron parallel conduction flux, which can be seen from the energy equation for the electrons along the magnetic field,

Here x is the distance along the magnetic field line,  are the density, parallel temperature, and parallel flow of the electrons, and
are the density, parallel temperature, and parallel flow of the electrons, and  is a component of the parallel heat flux. Let the cooling flow span a length LT
, one can see the convective energy transport terms follow the scaling of
is a component of the parallel heat flux. Let the cooling flow span a length LT
, one can see the convective energy transport terms follow the scaling of 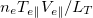 . Ambipolar transport constrains
. Ambipolar transport constrains 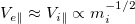 , so the free-streaming scaling of qen
in eq. (2) would predict
, so the free-streaming scaling of qen
in eq. (2) would predict 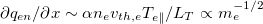 , which would overwhelm the convective energy transport
, which would overwhelm the convective energy transport 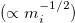 to force a
to force a 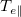 collapse and remove the pressure gradient drive that sustains the cooling flow. The condition for accessing the cooling flow regime of plasma thermal quench is thus
collapse and remove the pressure gradient drive that sustains the cooling flow. The condition for accessing the cooling flow regime of plasma thermal quench is thus

and it is violated by both eq. (1) and eq. (2), two most commonly used heat flux closures in fluid codes. We report in this letter that the condition of eq. (4) is indeed realized by ambipolar constraint in a nearly collisionless plasma, a constraint that has found important implications in fusion plasmas (e.g., see [37–41]). In the case that the cooling spot is a perfect particle and energy sink (e.g., a black hole), which can be modeled by an absorbing boundary, qen
itself obtains the convective energy transport scaling, 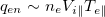 . With a radiative cooling mass, which can be modeled as a thermobath, the boundary of which recycles all particles across the boundary but clamps the temperature to a low value
. With a radiative cooling mass, which can be modeled as a thermobath, the boundary of which recycles all particles across the boundary but clamps the temperature to a low value 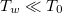 , the cold electrons thus produced can restore the free-stream scaling for
, the cold electrons thus produced can restore the free-stream scaling for 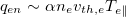 but its spatial gradient over the cooling flow region retains the convective energy transport scaling of eq. (4). As a result, a robust cooling flow appears to aggregate mass towards the cooling spot.
but its spatial gradient over the cooling flow region retains the convective energy transport scaling of eq. (4). As a result, a robust cooling flow appears to aggregate mass towards the cooling spot.
Methods
We deployed fully kinetic simulations using the VPIC [42] code to investigate the thermal collapse of a nearly collisionless plasma in the presence of a cooling spot, where the parallel transport physics will dominate. The simplest problem setup to decipher the parallel cooling physics is to unwind the open field lines into a one-dimensional slab with length Lx
, where a cooling spot is introduced at the left boundary and the right boundary is effectively at infinity. The cooling spot is implemented as either a thermobath (for a radiative cooling spot) or an absorbing boundary (for a sink of both energy and particles), where the former conserves particles by re-injecting electron-ion pairs (equal to the ions across the boundary) with a clamped temperature 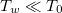 . The boundary simply reflects the particles so it does not change the plasma particle number nor the plasma energy. In such a semi-infinite collisionless plasma, there is no characteristic length except for the Debye length λD
that must be resolved in VPIC simulations. Therefore, we choose the resolution of the grid as dx = 0.1λD
with 5000 markers per cell. This simulated "infinity" right boundary would not affect the plasma cooling dynamics as long as the electron precooling front (defined later) has not reached the simulation boundary on the right side.
. The boundary simply reflects the particles so it does not change the plasma particle number nor the plasma energy. In such a semi-infinite collisionless plasma, there is no characteristic length except for the Debye length λD
that must be resolved in VPIC simulations. Therefore, we choose the resolution of the grid as dx = 0.1λD
with 5000 markers per cell. This simulated "infinity" right boundary would not affect the plasma cooling dynamics as long as the electron precooling front (defined later) has not reached the simulation boundary on the right side.
Results
Most interestingly, in such a cooling flow regime, the plasma thermal collapse comes in the form of propagating fronts that originate from the cooling spot with characteristic speeds. There are in total four (three) propagating fronts for the thermobath (absorbing) boundary: two of them propagate at speeds that scale with vth,e
, so are named electron fronts, while the other two are ion fronts that propagate at speeds that scale with the local ion sound speed cs
(the last ion front disappears for the absorbing boundary). Figure 1 illustrates the structure of the four fronts that propagate into a hot plasma (T0) for the thermal collapse with a thermobath boundary 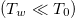 . We notice that the results from collisionless plasma simulation with
. We notice that the results from collisionless plasma simulation with 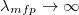 are similar to those in nearly collisionless plasma with
are similar to those in nearly collisionless plasma with 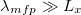 so only the former are used in the letter. It is important to note that cooling of a nearly collisionless plasma produces a strong temperature anisotropy, so one must examine the collapse of
so only the former are used in the letter. It is important to note that cooling of a nearly collisionless plasma produces a strong temperature anisotropy, so one must examine the collapse of 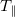 and
and 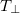 separately.
separately.
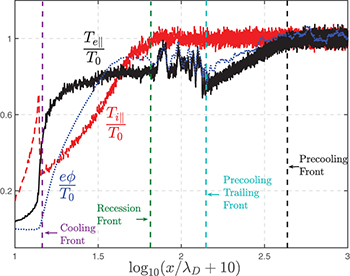
Fig. 1: Normalized parallel electron and ion temperature, and electrostatic potential at ωpe
t = 176 for Tw
= 0.01T0 from first-principle VPIC simulations. Different right-going fronts are labeled, where a uniform plasma with constant temperature T0 and density n0 initially fills the whole domain ![$x\in [0,1500 \lambda_D]$](https://content.cld.iop.org/journals/0295-5075/141/5/54002/revision3/epl22100926ieqn31.gif) with λD
the Debye length. The simulation uses a reduced ion mass of mi
= 100me
, δx = 0.1λD
, and 5000 markers per cell. The boundary conditions are explained in the text. Notice that the electrostatic potential plotted here is directly integrated from the instantaneous electric field that contains large amplitude Langmuir waves, which thus is only used as a guide for the qualitative behavior of the quiescent ambipolar potential.
with λD
the Debye length. The simulation uses a reduced ion mass of mi
= 100me
, δx = 0.1λD
, and 5000 markers per cell. The boundary conditions are explained in the text. Notice that the electrostatic potential plotted here is directly integrated from the instantaneous electric field that contains large amplitude Langmuir waves, which thus is only used as a guide for the qualitative behavior of the quiescent ambipolar potential.
Download figure:
Standard image
Electron fronts. Cooling of 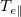 in a nearly collisionless plasma is primarily through free-streaming loss of suprathermal electrons satisfying
in a nearly collisionless plasma is primarily through free-streaming loss of suprathermal electrons satisfying  into the radiative cooling spot. Here (ΔΦ)max
is the maximum reflective potential in the plasma with
into the radiative cooling spot. Here (ΔΦ)max
is the maximum reflective potential in the plasma with 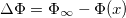 and the constant
and the constant 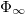 the far upstream plasma potential. The precooling zone bounded by the precooling front (PF) and the precooling trailing front (PTF) has
the far upstream plasma potential. The precooling zone bounded by the precooling front (PF) and the precooling trailing front (PTF) has 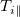 unchanged and
unchanged and  , but a lowered
, but a lowered 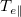 , which is due to the depletion of fast electrons satisfying
, which is due to the depletion of fast electrons satisfying ![$v_\parallel > v_c = \sqrt{2 e \left[\left(\Delta\Phi\right)_{max} - \Delta\Phi\right]/m_e}$](https://content.cld.iop.org/journals/0295-5075/141/5/54002/revision3/epl22100926ieqn39.gif) , yielding a truncated Maxwellian
, yielding a truncated Maxwellian

with 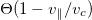 the Heaviside step function that vanishes for
the Heaviside step function that vanishes for 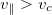 , and δ(x) the Dirac delta function. The ambipolar electric field can draw some low-energy electrons to compensate for the loss of high-energy electrons and thus maintain quasi-neutrality. This in-falling cold electron population is modeled in eq. (5) as a cold beam that due to ambipolar electric field acceleration has the speed vc
(see appendix). Between the PF and PTF, the electron beam can be ignored, so
, and δ(x) the Dirac delta function. The ambipolar electric field can draw some low-energy electrons to compensate for the loss of high-energy electrons and thus maintain quasi-neutrality. This in-falling cold electron population is modeled in eq. (5) as a cold beam that due to ambipolar electric field acceleration has the speed vc
(see appendix). Between the PF and PTF, the electron beam can be ignored, so

where 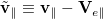 .
.
Equation (6) predicts a detectable decrease in 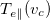 from T0 for
from T0 for 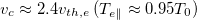 considering the PIC noise, suggesting an electron PF propagating at
considering the PIC noise, suggesting an electron PF propagating at

This corresponds to fast electrons with  traveling from the left boundary into the plasma, leaving behind a distribution at the PF with a void in
traveling from the left boundary into the plasma, leaving behind a distribution at the PF with a void in 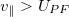 . The PTF comes about due to the reflecting potential
. The PTF comes about due to the reflecting potential 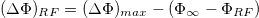 with ΦRF
the ambipolar potential at the ion recession front (RF), which sets a lower cutoff speed vc
at
with ΦRF
the ambipolar potential at the ion recession front (RF), which sets a lower cutoff speed vc
at

The deeper void now gives rise to a further reduced 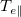 ,
,

The PTF rides these electrons that are reflected by the reflecting potential, and propagates at UPTF
(< UPF
). Since the ambipolar reflecting potential must satisfy 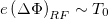 in a nearly collisionless plasma,
in a nearly collisionless plasma, 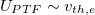 and
and 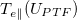 is only mildly cooler than T0. Furthermore,
is only mildly cooler than T0. Furthermore, 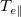 and Φ vary little between the RF and PTF, since the cutoff velocity remains the same at UPTF
.
and Φ vary little between the RF and PTF, since the cutoff velocity remains the same at UPTF
.
The ion flow remains vanishingly small ahead of the RF, so the electron cooling between the RF and PF is the result of electron conduction, which for the model fe in eq. (5) with vc > vth,e takes the form

Between PTF and PF, 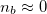 and
and 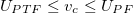 so qen
does scale as the free-streaming limit of eq. (2), but with α modulating in space as a function of vc
. In fact, for
so qen
does scale as the free-streaming limit of eq. (2), but with α modulating in space as a function of vc
. In fact, for  , one finds
, one finds

so the solution of the energy equation, 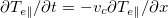 , reveals that vc
is the recession speed of
, reveals that vc
is the recession speed of 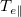 , re-affirming the particle picture noted earlier that the momentum space void in fe
propagates upstream with a speed of vc
. This large qen
drives fast propagating electron fronts (PF and PTF) but produces modest amount of
, re-affirming the particle picture noted earlier that the momentum space void in fe
propagates upstream with a speed of vc
. This large qen
drives fast propagating electron fronts (PF and PTF) but produces modest amount of 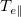 cooling for the large cutoff speed vc
= UPTF
.
cooling for the large cutoff speed vc
= UPTF
.
Ion fronts. Much more aggressive cooling would need to occur as the plasma approaches the radiative cooling spot that is clamped at 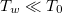 . These are facilitated by the ion fronts that provide the reflecting potential (ΔΦ)RF
. The RF is where
. These are facilitated by the ion fronts that provide the reflecting potential (ΔΦ)RF
. The RF is where 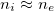 starts to drop, and behind which plasma pressure gradient drives a cooling flow toward the radiative cooling spot. The main reflection potential, which is tied to the electron pressure gradient, is also behind the ion RF. An ion recession layer bounded by the RF and the cooling front (CF) is similar to the rarefaction wave formed in the cold plasma interaction with a solid surface [43,44], where the plasma parameters recede steadily with the local sound speed. What is different for the thermal quench of a nearly collisionless plasma is the large plasma temperature and pressure gradient and the nature of the heat flux. The electron flow associated with fe
of eq. (5) within the recession layer is
starts to drop, and behind which plasma pressure gradient drives a cooling flow toward the radiative cooling spot. The main reflection potential, which is tied to the electron pressure gradient, is also behind the ion RF. An ion recession layer bounded by the RF and the cooling front (CF) is similar to the rarefaction wave formed in the cold plasma interaction with a solid surface [43,44], where the plasma parameters recede steadily with the local sound speed. What is different for the thermal quench of a nearly collisionless plasma is the large plasma temperature and pressure gradient and the nature of the heat flux. The electron flow associated with fe
of eq. (5) within the recession layer is

where ![$n_e(v_c) = \left[1+{\rm Erf}\left(v_c/\sqrt{2}v_{th,e}\right)\right] n_m/2 + n_b$](https://content.cld.iop.org/journals/0295-5075/141/5/54002/revision3/epl22100926ieqn61.gif) with Erf(x) being the error function. For an absorbing boundary (nb
= 0), a cutoff speed around
with Erf(x) being the error function. For an absorbing boundary (nb
= 0), a cutoff speed around 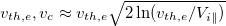 is sufficient to produce a
is sufficient to produce a 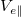 that matches onto the increasing ion flow,
that matches onto the increasing ion flow, 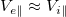 , for ambipolar transport through the recession layer. The in-falling cold electron beam reduces vc
and hence produces a lower reflecting potential across the recession layer as elucidated in eq. (12).
, for ambipolar transport through the recession layer. The in-falling cold electron beam reduces vc
and hence produces a lower reflecting potential across the recession layer as elucidated in eq. (12).
The physics of qen in the recession layer can be elucidated by rewriting eq. (10) as

For an absorbing wall, nb
= 0, and one finds qen
itself has a convective energy transport scaling: 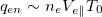 . The condition for the cooling flow regime, eq. (4), is obviously satisfied. In the case of a radiative cooling spot that produces a copious amount of cold electrons, the leading order of
. The condition for the cooling flow regime, eq. (4), is obviously satisfied. In the case of a radiative cooling spot that produces a copious amount of cold electrons, the leading order of 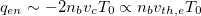 follows the free-streaming limit of eq. (2). Remarkably the plasma thermal quench still produces a cooling flow, in which case eq. (4) is satisfied due to the collisionless cold beam in the ambipolar electric field follows flux conservation nb
vc
= const, so
follows the free-streaming limit of eq. (2). Remarkably the plasma thermal quench still produces a cooling flow, in which case eq. (4) is satisfied due to the collisionless cold beam in the ambipolar electric field follows flux conservation nb
vc
= const, so 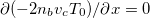 and the remaining terms in qen
have convective energy transport scaling. The VPIC [42] kinetic simulations shown in fig. 2 confirm that convective scaling of eq. (4) holds in the recession layer. In other words, electron cooling in a nearly collisionless plasma is modified by ambipolarity in such a way that large
and the remaining terms in qen
have convective energy transport scaling. The VPIC [42] kinetic simulations shown in fig. 2 confirm that convective scaling of eq. (4) holds in the recession layer. In other words, electron cooling in a nearly collisionless plasma is modified by ambipolarity in such a way that large 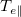 gradient can be supported in the recession layer to drive a cooling flow.
gradient can be supported in the recession layer to drive a cooling flow.
Fig. 2: Electron heat flux qen
for different mi
/me
and boundary conditions at ωpi
t = 13.6. The superscripts Ab and Th denote the absorbing and thermobath boundaries at x = 0, respectively, while the subscripts 100 and 1600 label mi
/me
= 100 and 1600. For the absorbing boundary, qen
behind the recession front (RF) follows the convective scaling by itself, which can be seen by comparing 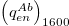 and
and 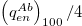 (notice that their small difference, as seen from eq. (13) for nb
= 0, comes from the dependence of
(notice that their small difference, as seen from eq. (13) for nb
= 0, comes from the dependence of 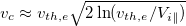 on mi
). For the thermobath boundary, qen
recovers the free-streaming formula, but its spatial gradient within the cooling flow region, which is between the cooling front (CF) and the RF, follows the convective scaling, as illustrated by the same slope of the curve as that for the absorbing boundary when mi
/me
is fixed.
on mi
). For the thermobath boundary, qen
recovers the free-streaming formula, but its spatial gradient within the cooling flow region, which is between the cooling front (CF) and the RF, follows the convective scaling, as illustrated by the same slope of the curve as that for the absorbing boundary when mi
/me
is fixed.
Download figure:
Standard imageThe propagation speed of the RF can be understood by examining the ion dynamics in the recession layer [45–48],



where we invoked the electron force balance 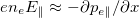 and quasi-neutrality ne
= Zni
with Z the ion charge, and
and quasi-neutrality ne
= Zni
with Z the ion charge, and 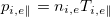 . Introducing a parameterization of
. Introducing a parameterization of 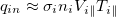 , which is known from [49], and
, which is known from [49], and 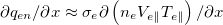 from eq. (4), where
from eq. (4), where 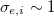 are analogous to the energy transmission coefficients, we obtain an universal length scale for
are analogous to the energy transmission coefficients, we obtain an universal length scale for 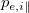 ,
,

where ![$\mu = (3+\sigma_e)/(3+\sigma_i) \times [-U+(1+\sigma_i)V_{i\parallel}]/[-U+(1+\sigma_e)V_{i\parallel}]$](https://content.cld.iop.org/journals/0295-5075/141/5/54002/revision3/epl22100926ieqn78.gif) . It is interesting to note that U > 0 and
. It is interesting to note that U > 0 and 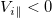 have opposite sign in the recession layer where a cooling flow resides. As a result, eqs. (14)–(16) have self-similar solutions with similarity variable
have opposite sign in the recession layer where a cooling flow resides. As a result, eqs. (14)–(16) have self-similar solutions with similarity variable 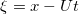 with U being the local recession speed. We find
with U being the local recession speed. We find

where 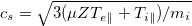 is the local sound speed of a nearly collisionless plasma with anisotropic temperatures. At the ion recession front,
is the local sound speed of a nearly collisionless plasma with anisotropic temperatures. At the ion recession front, 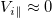 , so the speed of the ion recession front is
, so the speed of the ion recession front is

For Z = 1, σi
= 1, μ = 1 and 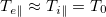 at the recession front, we have
at the recession front, we have 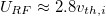 with
with 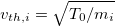 the ion thermal speed, which agrees well with the simulation result. It is worth noting that the self-similar solution of eq. (18) also recovers a known constraint [50] on the plasma exit flow at an absorbing boundary where a non-neutral sheath forms. The sheath entrance cannot propagate further upstream in this case so U = 0, by which eq. (18) predicts an ion exit flow speed
the ion thermal speed, which agrees well with the simulation result. It is worth noting that the self-similar solution of eq. (18) also recovers a known constraint [50] on the plasma exit flow at an absorbing boundary where a non-neutral sheath forms. The sheath entrance cannot propagate further upstream in this case so U = 0, by which eq. (18) predicts an ion exit flow speed

with

and  . This is consistent with the Bohm criterion for plasma in steady state (d/dt = 0) when including the heat flux in the transport model [50].
. This is consistent with the Bohm criterion for plasma in steady state (d/dt = 0) when including the heat flux in the transport model [50].
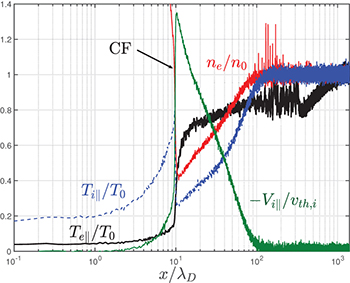
In the absence of an absorbing boundary, the mass aggregated by the cooling flow will pile up, and the resulting back-pressure can now drive a second ion front (cooling front, CF). Behind the CF, 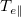 equilibrates with Tw
as shown in fig. 3. Such a deep cooling of
equilibrates with Tw
as shown in fig. 3. Such a deep cooling of 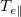 is through thermal conduction as indicated in fig. 2. When the cooling flow runs into this nearly static plasma, the ion flow energy, which is substantial in the cooling flow, is converted into ion thermal energy via a plasma shock as shown in fig. 3. Matching the conserved quantities across the shock while ignoring the heat flux, we find that the speed of the shock, which propagates upstream into the plasma, is simply the upstream sound speed at the shock front. The CF is the shock front, so its speed is
is through thermal conduction as indicated in fig. 2. When the cooling flow runs into this nearly static plasma, the ion flow energy, which is substantial in the cooling flow, is converted into ion thermal energy via a plasma shock as shown in fig. 3. Matching the conserved quantities across the shock while ignoring the heat flux, we find that the speed of the shock, which propagates upstream into the plasma, is simply the upstream sound speed at the shock front. The CF is the shock front, so its speed is

Since the plasma temperature at the CF is considerably lower than that at the RF, we have UCF
< URF
. Generally, the colder Tw
, the smaller UCF
. The presence of the CF and the cooling zone behind it is of fundamental importance to 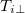 and
and 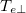 cooling as the cold particles provide dilutional cooling. It is also the source of cold electrons that are accelerated by the ambipolar electric field into the recession layer and beyond, cooling down
cooling as the cold particles provide dilutional cooling. It is also the source of cold electrons that are accelerated by the ambipolar electric field into the recession layer and beyond, cooling down 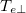 further upstream.
further upstream.
Fig. 3: Plasma profiles corresponding to fig. 1. The jumps near the cooling front (CF) are illustrated, where the huge plasma density near the radiative cooling boundary ne > n0 is cut out off the figure.
Download figure:
Standard imageDiscussions
In summary, the thermal collapse of a nearly collisionless plasma due to its interaction with a localized particle or energy sink is associated with a cooling flow toward the cooling spot. This applies to unmagnetized plasmas, for example, in astrophysical systems, and magnetized plasmas, for example, in Earth's magnetosphere or a tokamak fusion plasma. It is the fundamental constraint of ambipolar transport, along the field line in a magnetized plasma, that limits the spatial gradient of electron (parallel) heat flux to the much weaker convective 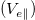 scaling as opposed to the free-streaming (vth,e
) scaling. Such weaker scaling is essential to sustain a temperature and hence pressure gradient for driving the cooling flow toward the cooling spot over the ion recession layer. The cooling flow eventually terminates against the cooling spot via a plasma shock that converts the ion flow energy into ion thermal energy. This shock or cooling front propagates away from the cooling spot at upstream ion sound speed, and it has the most profound role in the deep cooling of the surrounding hot plasmas, especially the ions. Unlike the ions, the electrons can be cooled ahead of the recession front due to an electron heat flux that follows the free-streaming limit
scaling as opposed to the free-streaming (vth,e
) scaling. Such weaker scaling is essential to sustain a temperature and hence pressure gradient for driving the cooling flow toward the cooling spot over the ion recession layer. The cooling flow eventually terminates against the cooling spot via a plasma shock that converts the ion flow energy into ion thermal energy. This shock or cooling front propagates away from the cooling spot at upstream ion sound speed, and it has the most profound role in the deep cooling of the surrounding hot plasmas, especially the ions. Unlike the ions, the electrons can be cooled ahead of the recession front due to an electron heat flux that follows the free-streaming limit 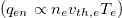 . Interestingly this large heat flux does not imply significant cooling of
. Interestingly this large heat flux does not imply significant cooling of 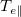 in a nearly collisionless plasma ahead of the recession front, but induces a very limited amount of
in a nearly collisionless plasma ahead of the recession front, but induces a very limited amount of 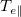 drop over a very large volume, because the precooling and precooling trailing fronts have propagation speeds that scale with electron thermal speed.
drop over a very large volume, because the precooling and precooling trailing fronts have propagation speeds that scale with electron thermal speed.
Acknowledgments
We thank the U.S. Department of Energy Office of Fusion Energy Sciences and Office of Advanced Scientific Computing Research for support under the Tokamak Disruption Simulation (TDS) Scientific Discovery through Advanced Computing (SciDAC) project, and the Base Theory Program, both at Los Alamos National Laboratory (LANL) under contract No. 89233218CNA000001. YZ was supported under a Director's Postdoctoral Fellowship at LANL. This research used resources of the National Energy Research Scientific Computing Center (NERSC), a U.S. Department of Energy Office of Science User Facility operated under Contract No. DE-AC02-05CH11231 and the Los Alamos National Laboratory Institutional Computing Program, which is supported by the U.S. Department of Energy National Nuclear Security Administration under Contract No. 89233218CNA000001.
Data availability statement: All data that support the findings of this study are included within the article (and any supplementary files).
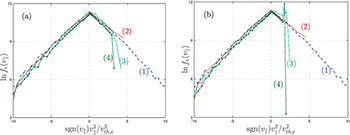
: Appendix
The electron distributions in 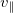 at different locations from the first-principle VPIC kinetic simulations as shown in fig. 4. In contrast to the absorbing boundary, there is a cold electron beam in fe
at the trap-passing boundary up to the precooling trailing front for the thermobath boundary, which causes a smaller cutoff velocity. This observation motivates the choice of eq. (5) in the paper as a model electron distribution to understand the electron transport physics underlying the thermal collapse of a nearly collisionless plasma.
at different locations from the first-principle VPIC kinetic simulations as shown in fig. 4. In contrast to the absorbing boundary, there is a cold electron beam in fe
at the trap-passing boundary up to the precooling trailing front for the thermobath boundary, which causes a smaller cutoff velocity. This observation motivates the choice of eq. (5) in the paper as a model electron distribution to understand the electron transport physics underlying the thermal collapse of a nearly collisionless plasma.
Fig. 4: Electron distributions at different locations. (a) is for the absorbing boundary and (b) is for the thermobath boundary. The positions are ahead of precooling front (1), between precooling and precooling trailing fronts (2), between recession and precooling trailing fronts (3) and within the recession layer (4). The parameters for the simulation with the thermobath boundary are the same as fig. 1 in the paper.
Download figure:
Standard image