Abstract
Materials with near-zero refractive index have attracted much attention over the past decade due to the fascinating phenomena they enabled, such as energy squeezing in thin waveguides, engineering of wavefronts, and "photonic doping". These materials are not directly available in nature, but can be realized in periodic artificial structures. Among near-zero refractive index materials, double-zero-index materials are a special type with both constitutive parameters vanishing simultaneously, leading to intriguing applications including arbitrarily shaped high-transmission waveguides, cloaking of inclusions, nonlinear enhancement, and directional emissions. This perspective focuses on the recent developments on double-zero-index materials, including their fundamental physics, design principles, experimental realizations, and potential applications.
Export citation and abstract BibTeX RIS

Published by the EPLA under the terms of the Creative Commons Attribution 4.0 International License (CC-BY). Further distribution of this work must maintain attribution to the author(s) and the published article's title, journal citation, and DOI.
Introduction
Metamaterials, artificial materials with unusual effective parameters attributed to their delicate structures in wavelength or subwavelength scales, can control classical wave propagation as wish [1–5]. As one special type of metamaterials, zero-index media (ZIM), with one or more constitutive parameters vanishing, have attracted broad interest in the past decade due to their intriguing wave manipulation properties [6–16], such as directive emission [6–8], wave tunneling [9–12], and wave front engineering [13–16].
As illustrated in fig. 1(a), based on the number of zero constitutive parameters, electromagnetic ZIM can be divided into two categories: single-zero-index medium (SZIM), with only one constitutive parameter approaching zero; and double-zero-index medium (DZIM), with both constitutive parameters vanishing. Although both SZIM and DZIM possess zero refractive index, they support drastically different properties. For instance, electromagnetic waves can tunnel through a two-dimensional (2D) thin channel filled with an epsilon-near-zero (ENZ) medium with nearly unity transmittance [17]. As shown in fig. 1(b), both the magnetic field and the power flow are compressed and tunnel through the channel. The "energy squeezing" effect is originated from near-zero cross-sectional area of channel, enforcing zero circulation of the electric field over the ENZ medium and leading to total transmission irrespective of any bend of the channel (see fig. 1(c)) [17,18]. Another typical feature associated with SZIM is the so-called "photonic doping" [19–22], i.e., the response of a 2D ENZ medium is determined by its embedded impurities. Figure 1(d) is a conceptual sketch of photonic doping. When several impurities are embedded in an irregular-shaped ENZ medium, the response of the ENZ can be described by effective relative permeability and permittivity [19],

where 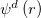 is the magnetic field distribution within the impurities, A and Ad
are the cross-sectional area of the ENZ medium and the d-th impurities, respectively.
is the magnetic field distribution within the impurities, A and Ad
are the cross-sectional area of the ENZ medium and the d-th impurities, respectively.
Fig. 1: Typical properties of SZIM and DZIM. (a) Electromagnetic parameter space. ENZ medium, μ-near-zero medium and DZIM are marked by green, blue, and red, respectively. (b) Top: magnetic field distribution; bottom: Poynting vector distribution when a plane wave tunnels through a channel filled with ENZ medium [11]. (c) Magnetic field distribution when a plane wave tunnels through a channel with sharp bends and corners filled with ENZ medium [18]. (d) Conceptual sketch of photonic doping [19]. (e) Electric field distribution (top) and magnetic field distribution (bottom) when an electromagnetic wave totally passes through a DZIM with PMC inclusion [25]. (f) Magnetic field distribution (top) and electric field distribution (bottom) when an electromagnetic wave is totally reflected by 2D DZIM with some inclusions [23].
Download figure:
Standard imageThe mismatch between the effective impedance of an SZIM and most natural materials is significant. A simply connected 2D DZIM, i.e., a 2D DZIM without any impurities inside, may overcome this issue and efficiently couple with normal incident plane waves because both constitutive parameters are vanishingly small [23–35]. Another feature of a DZIM can be derived from Maxwell's equations, i.e.,

From eq. (2), one can derive that for TM (transverse magnetic) waves, where the electric field is along the z-direction perpendicular to the 2D plane, the electric field in a 2D DZIM is a constant while the curl of magnetic field is zero. When there are impurities in 2D DZIM, the response of a 2D DZIM to normal incident plane waves is determined by the integral of electromagnetic fields along the boundaries of impurities [23–27]. As shown in fig. 1(e), an electromagnetic wave with Ez polarization can pass through a DZIM filled waveguide without any distortion even if there is a big heart-shaped PMC inside the DZIM [25], while perfect reflection is observed for the same system when the inclusion is changed into a small PEC object [26]. For dielectric inclusions, the transmission spectra depend on their material and geometric properties. In this review, we limit the discussions to the DZIM.
Artificial 2D DZIM
Despite the intriguing features of 2D DZIM, they do not naturally exist. Their realization had been a longstanding challenge, until a practical solution, i.e., metamaterials with a Dirac-like conical dispersion [28–37], was proposed in 2011 [28]. Figure 2(a) shows the band structure of such a photonic crystal (PC), exhibiting a threefold accidental degeneracy of a monopolar state and two dipolar states at the center of the Brillouin zone. Such dispersion is called Dirac-like because it possesses zero Berry phase and cannot be casted into Dirac equations [29]. To distinguish it from the Dirac points, we call it a Dirac-like point. Figure 2(b) shows the effective permittivity and the effective permeability of the PC calculated from a dynamic effective medium theory [30]. Both parameters cross zero simultaneously at the frequency of Dirac-like point 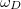 , indicating the PC is a 2D DZIM at
, indicating the PC is a 2D DZIM at 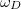 . The strategy of using linear dispersion to achieve DZIM was successfully extended to phononic crystals [32,33], semiconductors [34], and even photonic quasicrystals [35–37]. From a degenerate perturbation theory, the presence or absence of Dirac-like points can be predicted by the spatial symmetry of the degeneracy states [38].
. The strategy of using linear dispersion to achieve DZIM was successfully extended to phononic crystals [32,33], semiconductors [34], and even photonic quasicrystals [35–37]. From a degenerate perturbation theory, the presence or absence of Dirac-like points can be predicted by the spatial symmetry of the degeneracy states [38].
Fig. 2: Realization of 2D DZIM. (a) Left: the band structure of a PC consisting of a square lattice of dielectric rods in air. Right: the electric field distributions of eigenstates at the Dirac-like point [28]. (b) The effective relative permittivity and relative permeability of the PC in (a) [28]. (c) An experimentally realized out-of-plane DZIM in a PC [40]. (d) Left: the unit cell of an experimentally realized in-plane DZIM in a SOI wafer. Right: directional emission of such a DZIM [41]. (e) The scanning electron microscopy image of a zero-index concave lens [39]. (f) A design of zero-index BIC by utilizing accidental degeneracy of quadrupolar states and a hexapolar state in a PC slab [46]. (g) A design of zero-index BIC by designing the height of PC [48].
Download figure:
Standard imageRealization of on-chip DZIM in the optical regime is of practical importance due to its potential to be integrated. There are two categories of such on-chip DZIM: out-of-plane DZIM and in-plane DZIM [38–45]. Figure 2(c) shows an example of out-of-plane DZIM, consisting of a stack of silicon rods embedded in silicon oxide [40]. Light propagates in the direction perpendicular to the substrate. For the in-plane case, as double-zero property leads to constant electromagnetic field in 2D DZIM, PC can efficiently engineer the wavefront of outgoing waves. Figure 2(d) is an example of in-plane DZIM in a silicon on insulator (SOI) wafer. The PC has Dirac-like conical dispersion at the center of the Brillouin zone [40]. The wave comes from a silicon waveguide, and shines on a triangular-shaped PC. The refraction angle equals zero when the working wavelength is 1570 nm, implying effectively zero-refractive index. Figure 2(e) illustrates an optical zero-index lens based on silicon nanopillars [41]. At the working wavelength 1490 nm, plane wave passes through the zero-index concave lens and focuses on its focal point.
In the realization of in-plane DZIM, one important task is to reduce the radiation loss. A realistic approach is to sandwich PC with a pair of metallic layers, reducing out-of-plane radiation and enforcing the electric field in the PC perpendicular to the metallic layers [41]. Another common approach is zero-index photonic modes which do not radiate into the environment, i.e., zero-index bound states in the continuum (BIC), attributed to different underlying physics [46–48]. Figure 2(f) is a proposal of zero-index BIC, consisting of a hexagonal lattice of air holes [46]. An accidental degeneracy between twofold quadrupolar states and a hexapolar state induces a Dirac-like cone at the center of the Brillouin zone, where the symmetries of all states prevent them from coupling to external plane waves, thus the quality factors diverge. Such a zero-index BIC is protected by the symmetries of eigenstates at Dirac-like point, independent of the thickness of PC, thus can be denoted as symmetry-protected zero-index BIC. Figure 2(g) demonstrates another realization of zero-index BIC with monopolar state and dipolar states in a PC composed by silicon pillars in silica background [48]. In this PC, the eigenstates at Dirac-like point can couple with external plane waves. With coupled mode theory, the height of pillars is designed to mimic the radiation loss. BIC occur at the intersection of the resonance conditions of eigenstates. Such a zero-index BIC can be denoted as resonance-protected BIC [48].
Non-Hermitian DZIM
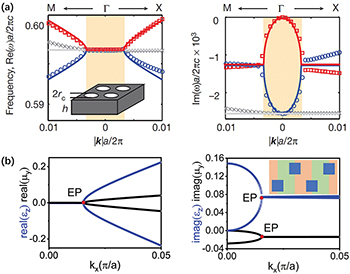
When the effective parameters of a DZIM are vanishing, small perturbations, such as non-Hermiticity and/or anisotropy, will greatly change the properties of the DZIM [49–57]. Figure 3(a) shows the real and imaginary parts of the eigenfrequencies of a photonic crystal slab with finite thickness. The open boundaries of the slab cause radiation loss, corresponding to non-Hermitian perturbations in the Hamiltonian [50],

with complex eigenvalues

γ represents the radiation loss of the dipolar states, which deforms a Dirac-like cone into a two-dimensional flat band enclosed by a ring of exceptional points (EPs) [52–54]. The trajectory of EPs, 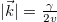 , divides the Brillouin zone into two parts: the real parts of eigenvalues are dispersionless and degenerate at
, divides the Brillouin zone into two parts: the real parts of eigenvalues are dispersionless and degenerate at  , the imaginary parts of eigenvalues are dispersionless and degenerate at
, the imaginary parts of eigenvalues are dispersionless and degenerate at  . Differently from Hermitian systems, the band dispersion in such a PC is in the complex space. The eigenfrequencies and effective parameters are also complex valued [53]. Figure 3(b) shows the effective permittivity and permeability of a 2D PC, with alternatively distributed gain and loss in the background [52]. At the EP along kx
, both the real parts of effective permittivity
. Differently from Hermitian systems, the band dispersion in such a PC is in the complex space. The eigenfrequencies and effective parameters are also complex valued [53]. Figure 3(b) shows the effective permittivity and permeability of a 2D PC, with alternatively distributed gain and loss in the background [52]. At the EP along kx
, both the real parts of effective permittivity 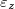 and effective permeability
and effective permeability 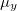 are vanishingly small, the PC behaves like a complex conjugate medium because effective refractive index
are vanishingly small, the PC behaves like a complex conjugate medium because effective refractive index 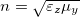 is real. In PT-exact phase, both the eigenfrequencies and wave vectors are real, the effective permittivity and permeability are complex numbers with opposite phases. In PT-broken phase, the eigenfrequencies are complex, the effective permittivity and permeability are complex numbers with non-cancelling phases. This PC enables fascinating phenomena, such as angular sensing, coherent perfect absorption, and lasing effect [51,52].
is real. In PT-exact phase, both the eigenfrequencies and wave vectors are real, the effective permittivity and permeability are complex numbers with opposite phases. In PT-broken phase, the eigenfrequencies are complex, the effective permittivity and permeability are complex numbers with non-cancelling phases. This PC enables fascinating phenomena, such as angular sensing, coherent perfect absorption, and lasing effect [51,52].
Fig. 3: Non-Hermitian DZIM. (a) The real and imaginary parts of the band diagrams of a PC slab [50]. (b) The real and imaginary parts of the effective permittivity (blue) and the effective permeability (black) of a 2D PC. Inset: the unit cell of the PC, composed by silicon blocks (blue,  ) in silica with gain (light orange,
) in silica with gain (light orange,  ) and loss (light green,
) and loss (light green, 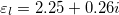 ) [52].
) [52].
Download figure:
Standard imageAnisotropic DZIM
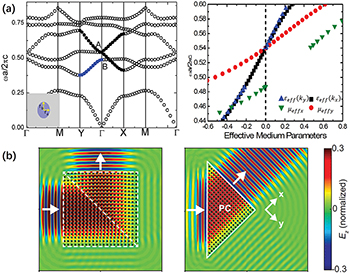
When anisotropy is considered, the effective parameters are direction dependent. Figure 4(a) shows the band structure of a 2D PC composed by a square array of elliptical cylinders with permittivity  embedded in air [55]. An accidental degeneracy of a monopolar state and a dipolar-x state results in a semi-Dirac point, i.e., twofold degenerate point with linear dispersion along kx
and quadradic dispersion along ky
, at Γ point. At the frequency of the semi-Dirac point, the PC can be regarded as a DZIM along the x-direction and an ENZ along the y-direction. Figure 4(b) exhibits a beam-bending effect in such an anisotropic ZIM. In both cases, the wave is incident to the PC and propagates along the direction of DZIM. Such kind of directional propagation implies the potential of PC with semi-Dirac point to work as filters of incident angle. The working frequency of the filter can be extended to a narrow range around the frequency of the semi-Dirac point, and depends on the range of linear dispersions.
embedded in air [55]. An accidental degeneracy of a monopolar state and a dipolar-x state results in a semi-Dirac point, i.e., twofold degenerate point with linear dispersion along kx
and quadradic dispersion along ky
, at Γ point. At the frequency of the semi-Dirac point, the PC can be regarded as a DZIM along the x-direction and an ENZ along the y-direction. Figure 4(b) exhibits a beam-bending effect in such an anisotropic ZIM. In both cases, the wave is incident to the PC and propagates along the direction of DZIM. Such kind of directional propagation implies the potential of PC with semi-Dirac point to work as filters of incident angle. The working frequency of the filter can be extended to a narrow range around the frequency of the semi-Dirac point, and depends on the range of linear dispersions.
Fig. 4: Anisotropic DZIM. (a) Left: the band structure for Ez polarization in a 2D PC exhibits a semi-Dirac point at Γ point. Right: the effective parameters of the PC along kx and ky directions near the frequency of semi-Dirac point [55]. (b) Electric field distributions of a beam-bending effect in a PC with a semi-Dirac point in band structure [56]. Left: the PC at the bottom left (upper right) is effectively a DZIM along the horizontal direction (vertical direction). Right: the PC is effectively a DZIM along the x-direction.
Download figure:
Standard imageThree-dimensional (3D) electromagnetic DZIM
The increase of dimensionality brings interesting physics. For example, 3D and 2D electromagnetic waves are inherently different as the latter obey scalar wave equations while the former follow vector wave equations. Thus, 3D DZIM naturally offers distinctive functionalities inaccessible to its 2D counterparts [58–64]. Figure 5(a) is a schematic of "antidoping" effect, which exclusively belongs to the 3D electromagnetic DZIM. The 3D electromagnetic DZIM is filled in a transverse electromagnetic waveguide made of PEC walls (colored yellow) and PMC walls (colored blue). Some impurities are embedded in the DZIM. When the electric field of incident plane wave is perpendicular to the PEC walls, the transmission can be obtained as [62]

where 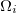 denotes the i-th impurity, dx
(dy
) is the width of the DZIM in the y(z)-direction, ω is the angular frequency,
denotes the i-th impurity, dx
(dy
) is the width of the DZIM in the y(z)-direction, ω is the angular frequency,  and k0 are the permittivity and wave vector in air, respectively, H0 is the amplitude of magnetic field of the incident wave. If surfaces A1 and A2 are simply connected, which means they do not intersect with any impurity, the integrations in eq. (5) are vanishing because of zero integration paths. This leads to total transmission irrespective of the quantity, material, shape, and filling ratio of the impurities. It is drastically different from any 2D DZIM, where the transmission depends on the impurities as discussed earlier in the first section. Figure 5(b) shows the simulation results of total (zero) transmission with (without) the pair of simply connected surfaces when some dielectric cylinders are randomly placed inside the DZIM.
and k0 are the permittivity and wave vector in air, respectively, H0 is the amplitude of magnetic field of the incident wave. If surfaces A1 and A2 are simply connected, which means they do not intersect with any impurity, the integrations in eq. (5) are vanishing because of zero integration paths. This leads to total transmission irrespective of the quantity, material, shape, and filling ratio of the impurities. It is drastically different from any 2D DZIM, where the transmission depends on the impurities as discussed earlier in the first section. Figure 5(b) shows the simulation results of total (zero) transmission with (without) the pair of simply connected surfaces when some dielectric cylinders are randomly placed inside the DZIM.
Fig. 5: 3D electromagnetic DZIM. (a) Schematic of the "antidoping" effect [59]. (b) Left: simulated electric-field distribution, showing total transmission when there is a pair of simply connected surfaces A1 and A2 in DZIM. Right: simulated electric-field distribution, showing zero transmission when there are no simply connected surfaces in DZIM [59]. (c) A design of 3D DZIM in a 3D PC consisting of a simple cubic lattice of core-shell spheres. A sixfold Dirac-like point exists at the Γ point, where the PC is effectively an electromagnetic DZIM [60]. (d) The unit cell (left) and band structure (right) of a PC with sixfold Dirac-like point [62]. (e) Experimental setup to illustrate the "antidoping" effect [62].
Download figure:
Standard imageThe first theoretical design of 3D electromagnetic DZIM is a 3D PC consisting of a simple cubic lattice of core-shell spheres in air background [60]. The core is a PEC sphere and the shell is dielectric with  and
and  . Figure 5(c) is the band structure of the PC. The accidental degeneracy of electric and magnetic dipolar states results in a sixfold degenerate Dirac-like point at the Γ point, at which the effective permittivity and permeability of the PC cross zero simultaneously. However, the design is very sensitive to the radius of PEC core and dielectric shell, the fabrication of isotropic core-shell spheres suspended in air is quite complex, and absorption in subwavelength metallic inclusions is inevitable. Figure 5(d) demonstrates a realization of 3D electromagnetic DZIM by using all-dielectric PC, which is composed of dielectric meshes. Dirac-like dispersions with four linear bands intersecting with two flat bands are observed [62]. Figure 5(e) shows the picture of the experimental setup. The electromagnetic wave emits from a horn, passes through a perforated sponge and the PC, and is measured by a probe. Many applications, such as the "antidoping" effect, outer-boundary–controlled switching, and 3D perfect wave steering, are realized [62].
. Figure 5(c) is the band structure of the PC. The accidental degeneracy of electric and magnetic dipolar states results in a sixfold degenerate Dirac-like point at the Γ point, at which the effective permittivity and permeability of the PC cross zero simultaneously. However, the design is very sensitive to the radius of PEC core and dielectric shell, the fabrication of isotropic core-shell spheres suspended in air is quite complex, and absorption in subwavelength metallic inclusions is inevitable. Figure 5(d) demonstrates a realization of 3D electromagnetic DZIM by using all-dielectric PC, which is composed of dielectric meshes. Dirac-like dispersions with four linear bands intersecting with two flat bands are observed [62]. Figure 5(e) shows the picture of the experimental setup. The electromagnetic wave emits from a horn, passes through a perforated sponge and the PC, and is measured by a probe. Many applications, such as the "antidoping" effect, outer-boundary–controlled switching, and 3D perfect wave steering, are realized [62].
Acoustic DZIM
While electromagnetic DZIM has seen great success, its acoustic counterpart, i.e., acoustic DZIM, also has received much attention. In 2D systems, the acoustic wave equation is mathematically equivalent to that of electromagnetic waves [29]. Therefore, the design principle can be used for the acoustic waves [65–67]. For example, in ref. [32], a phononic crystal consisting of a square lattice of rubber cylinders in water was proposed. The dispersion relation of this phononic crystal possesses a Dirac-like point at the center of the Brillouin zone, where both effective mass density and compressibility become zero simultaneously. The realization of DZIM for airborne sound is a bit challenging, as the speed of sound in air is generally much lower than the speed of sound in solid or liquid materials, in stark contrast to the electromagnetic or waterborne sound cases, where the wave speed in the scatterer is lower compared to that in the environment. To tackle this problem, in fig. 6(a), the first-order waveguide mode is utilized to effectively introduce an acoustic DZIM [45]. The DZIM collimates the emission from a point source to a plane wave. With an acoustic DZIM, intriguing properties, such as energy squeezing and tunnelling [12], high efficiency unidirectional transmission [65,67], acoustic cloaking [66], are demonstrated. In 3D systems, the acoustic wave equation is different from the electromagnetic wave equation. Nevertheless, we can still extend the strategy of using accidental degeneracy to find the DZIM. In fig. 6(b), by judiciously incorporating the glide symmetry and accidental degeneracy, we proposed the first realistic design of 3D acoustic DZIM, in which three groups of aluminum rods are used to construct the unit cell of the phononic crystal [58]. We take the ease of fabrication, the accidental degeneracy of monopolar state and dipolar states, and the validation of effective medium theory into the design of the phononic crystal. Its dispersion relation shows a Dirac-like cone, with two linear bands intersecting with two flat bands. Although the design of 3D acoustic DZIM has different symmetries compared with the design of 3D electromagnetic DZIM, it still has isotropic effective parameters. At the Dirac-like frequency, both effective mass density and compressibility equal zero. Based on this structure, we designed an acoustic periscope in a sound-hard waveguide with two 90° bends [58]. Such a "periscope" demonstrates flexibly control over normal incident plane waves in 3D space.
Fig. 6: Acoustic DZIM. (a) Left: top and side views of the unit cell of a phononic crystal with a Dirac-like point in its band structure. Middle: acoustic pressure fields of the first-order waveguide mode, showing degenerate monopolar and dipolar modes at the Dirac-like point. Right: measured acoustic pressure field at the frequency of Dirac-like point, radiated by acoustic point source embedded in the phononic crystal [45]. (b) Left: the unit cell of a 3D phononic crystal. Middle: the band structure of the phononic crystal exhibits a Dirac-like point at the center of the Brillouin zone. Right: acoustic pressure field distribution when a plane wave with the frequency of Dirac-like point is normally incident to the PC in a 3D waveguide with two 90° bends [58].
Download figure:
Standard imageSummary and outlook
In this perspective, we reviewed the development of ZIM over the past decade, from theoretical proposals to realistic structures, from Hermitian to non-Hermitian systems, from isotropic to anisotropic systems, from 2D to 3D systems, and from electromagnetic to acoustic systems.
Looking into the future, we believe DZIM will continue to advance the field. Considering complex parameters and anisotropy in DZIM offers new possibilities to control waves [68–71]. For example, the double-zero-index property boosts the effect of non-Hermitian perturbations, thus small loss can lead to large absorption. Some people combine the concept of BIC with ZIM to realize low-loss DZIM, while others utilize loss in ZIM to realize interesting phenomena such as collimation, enhancement of transmission, and coherent perfect absorption [68–70]. Recently, zero-index was introduced to a bianisotropic material, extending the concept of ZIM to topology [71]. Very recently, incorporating ZIM into other systems has brought new perspectives. A geometry-independent antenna was realized when some ports were opened at a PEC-enclosed cavity which was filled with doped ENZ medium [72]. An inviscid, incompressible, and irrotational ideal electromagnetic fluid was experimentally realized with doped ENZ medium in a complex-shaped waveguid [73]. Another celebrated effect is the realization of bianisotropic DZIM in a metamaterial, accompanied by an anomalous electromagnetic tunneling [74]. These contributions manifest how active this field is. There still exist abundant opportunities. For example, taking time, one of the most fundamental physical variables, into account, one can design time-varying (or time-Floquet) ZIM, which may give rise to fascinating properties [75–77]. Overall, ZIM, especially DZIM, are promising platforms to connect materials science with optics and to advance both theoretical and applied fields.
Acknowledgments
This work is supported by the King Abdullah University of Science and Technology (KAUST) Office of Sponsored Research (OSR) under Award No. OSR-CRG2020-4374 and the KAUST Baseline Research Fund under No. BAS/1/1626-01-01.
Data availability statement: No new data were created or analysed in this study.