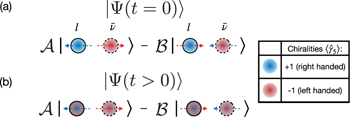Abstract
The solutions of the Dirac equation are given in terms of bispinors, four-component objects which include both spin and chirality as internal degrees of freedom. For massive particles, the Dirac equation couples components of the bispinor with different chiralities, yielding chiral oscillations. This phenomenon can be particularly relevant for recent proposals aimed at measuring non-relativistic cosmic neutrinos, and can find analogies in Dirac-like systems, such as graphene. In this paper, a concise review of chiral oscillations is presented, including their description with the Dirac's equation dynamics and the underlying group structure. Two paradigmatic cases of chiral oscillations in physical systems are shown: the effects on lepton-antineutrino spin quantum correlations, and neutrino flavor oscillations. Finally, extensions of recent theoretical investigations as well as future research developments are discussed.
Export citation and abstract BibTeX RIS
Introduction
The solutions of the Dirac equation, called Dirac bispinors, are pivotal in the description of fermionic particles [1–3] and in the physics of low-energy systems with relativistic-like behaviour, such as graphene [4]. One of the biggest successes of the Dirac equation in relativistic quantum mechanics, was the inclusion of the spin as a degree of freedom (DoF) intrinsic to the bispinor structure. In addition, due to the group structure underlying the Dirac equation [5], bispinors include the chirality (or intrinsic parity) as a discrete DoF [6]. The latter is associated with the parity symmetry, which connects two-component spinors of different chiralities. Such composition of two-component objects into a four-component bispinor is required when describing massive particles. In Dirac-like systems, such composite structure arises from the relevant symmetries in the system. For instance, in bilayer graphene, the honeycomb lattice structure and the relative configuration of the layers determines the form of the Dirac-like Hamiltonian describing the system excitations [4]. In this particular case one identifies two DoFs analogous to spin and chirality: lattice and layer [7].
The concept of chirality is especially important in weak interaction processes. Due to the violation of parity symmetry, weak processes describing, e.g., the creation of a fermion, project the state into a definite chirality state [3,8]. The mass term of the Dirac equation couples left- and right-handed components of the bispinor, inducing chiral oscillations [9–11]. For example, a state created by a weak process initially in a left-handed state has a finite probability to be in a right-handed state during its free evolution. One example is the neutrino: the particle is created only via weak-interaction processes, thus with a definite chirality [9]. The amplitude of such oscillations depends on the ratio between mass and energy, and is therefore negligible for relativistic particles.
Recent advancements in the measurement of cosmic particles have aimed at probing relic neutrinos, particles akin to the photons of the cosmic microwave background [12,13]. Experiments such as PTOLEMY [14] are expected to measure such cosmic neutrinos whose root mean square momentum can be estimated as  [14–16], putting them in the non-relativistic regime. Chiral oscillation effects and their implication in such upcoming experiments include corrections to the neutrino flavor oscillation formula for both Dirac and Majorana neutrinos [17], and a depletion of the expected measured flux of cosmic neutrinos by
[14–16], putting them in the non-relativistic regime. Chiral oscillation effects and their implication in such upcoming experiments include corrections to the neutrino flavor oscillation formula for both Dirac and Majorana neutrinos [17], and a depletion of the expected measured flux of cosmic neutrinos by 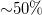 [17,18]. Likewise, in low-energy Dirac-like systems, analogous effects of chiral oscillations can be identified. Such Dirac-like systems include graphene [4,7,19,20], trapped ions [21,22], photonic [23,24] and optomechanical [25] systems. In particular, graphene systems have already been considered as a platform for probing the Zitterbewegung effect [19,20] (the free jittering motion due to the free Dirac dynamics), which has an intrinsic connection to chiral oscillations [26].
[17,18]. Likewise, in low-energy Dirac-like systems, analogous effects of chiral oscillations can be identified. Such Dirac-like systems include graphene [4,7,19,20], trapped ions [21,22], photonic [23,24] and optomechanical [25] systems. In particular, graphene systems have already been considered as a platform for probing the Zitterbewegung effect [19,20] (the free jittering motion due to the free Dirac dynamics), which has an intrinsic connection to chiral oscillations [26].
In this perspective review, chiral oscillations are described in the context of the Dirac equation. A brief overview of the theoretical formulation of chiral oscillation is presented, including the relation to the group structure underlying the Dirac equation. Two paradigmatic examples of chiral oscillation effects are discussed: the modification of spin correlations encoded between spins of a lepton-antineutrino pair, and the effects on non-relativistic neutrino flavor oscillations. Generalizations of the formulation as well as novel research directions are presented. For conciseness, some explicit formulas that were omitted in the main text are presented in the Supplementary Material Supplementarymaterial.pdf (SM).
Dirac equation and chiral oscillations
Let us consider the Dirac equation in its Hamiltonian form [1,2,9]

where 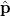 is the momentum operator and m is the particle's mass. The
is the momentum operator and m is the particle's mass. The  Dirac matrices are denoted by
Dirac matrices are denoted by 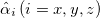 and
and 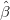 , and satisfy the anti-commutation relations:
, and satisfy the anti-commutation relations: 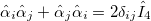 ,
, 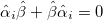 , and
, and  . We adopt the chiral representation of the Dirac matrices [27] in which the chiral matrix is diagonal
. We adopt the chiral representation of the Dirac matrices [27] in which the chiral matrix is diagonal 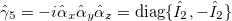 . The positive- and negative-energy plane-wave solutions of (1)
. The positive- and negative-energy plane-wave solutions of (1) 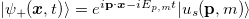 , and
, and  are given in terms of the eigenspinors of the Dirac equation with s denoting the spin polarization (see the SM for their explicit formula in the chiral representation) and where
are given in terms of the eigenspinors of the Dirac equation with s denoting the spin polarization (see the SM for their explicit formula in the chiral representation) and where 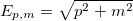 . In what follows, we present results for plane-wave solutions. Generalizations to wave-packets and Majorana particles are discussed below.
. In what follows, we present results for plane-wave solutions. Generalizations to wave-packets and Majorana particles are discussed below.
Group structure and bispinors
The Dirac equation is the dynamical equation for the irreducible representations (irreps) of the complete Lorentz group, which includes the proper Lorentz group and parity transformations [5]. To understand the intrinsic structure of the bispinors, one first considers the irreps of the proper Lorentz group. Those are labeled by 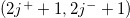 , and the spinor representations
, and the spinor representations 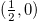 and
and 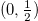 , isomorphic to the SU(2), are composed by 2 component objects called, respectively, right- and left-handed Weyl spinors. The two spinor representations of the proper Lorentz group are disconnected: no element of the group transforms a right-handed Weyl spinor into a left-handed Weyl spinor. In fact, massless particles have fixed chirality and, in particular, massless fermions are described by Weyl spinors with dynamics given by the Weyl equation
, isomorphic to the SU(2), are composed by 2 component objects called, respectively, right- and left-handed Weyl spinors. The two spinor representations of the proper Lorentz group are disconnected: no element of the group transforms a right-handed Weyl spinor into a left-handed Weyl spinor. In fact, massless particles have fixed chirality and, in particular, massless fermions are described by Weyl spinors with dynamics given by the Weyl equation  , with
, with  valid for right (left)-handed spinors. Such spinors carry one discrete DoF, the spin.
valid for right (left)-handed spinors. Such spinors carry one discrete DoF, the spin.
Parity connects the two disjoint spinor representations of the proper Lorentz group. In fact, under parity 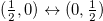 , and to construct the irreps of the complete Lorentz group, one has to combine left and right-handed Weyl spinors in a single object: a bispinor. Such irreps are then isomorphic to
, and to construct the irreps of the complete Lorentz group, one has to combine left and right-handed Weyl spinors in a single object: a bispinor. Such irreps are then isomorphic to 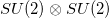 , and therefore the bispinors carry not only the spin but another discrete DoF: chirality (or intrinsic parity). In general, spin and chirality DoFs can become entangled under external potentials [28]. Analogous effects in Dirac-like systems include lattice-layer entanglement in bilayer graphene systems [7]. Such intrinsic spin-chirality structure of bispinors is highlighted in the chiral representation of the Dirac matrices, in which an arbitrary bispinor is written as
, and therefore the bispinors carry not only the spin but another discrete DoF: chirality (or intrinsic parity). In general, spin and chirality DoFs can become entangled under external potentials [28]. Analogous effects in Dirac-like systems include lattice-layer entanglement in bilayer graphene systems [7]. Such intrinsic spin-chirality structure of bispinors is highlighted in the chiral representation of the Dirac matrices, in which an arbitrary bispinor is written as ![$|{\xi}\rangle = [|{\xi_R}\rangle, |{\xi_L}\rangle]^T$](https://content.cld.iop.org/journals/0295-5075/139/4/44002/revision2/epl22100457ieqn21.gif) , where
, where 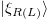 is the right (left)-handed components of the bispinor. Accordingly, a bispinor with definite chirality can be obtained via chiral projections,
is the right (left)-handed components of the bispinor. Accordingly, a bispinor with definite chirality can be obtained via chiral projections, 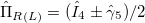 .
.
Free-particle dynamics and chiral oscillations
In the chiral representation of the Dirac matrices, eq. (1) yields a system of coupled equations for the left- and right-handed spinor components

where it is evident that the mass term is responsible for the coupling between left and right-handed components of a given bispinor. Thus, a bispinor with definite chirality at t = 0 will undergo chiral oscillations as a consequence of (2). In fact, since ![$[\hat{H}_D, \hat{\gamma}_5] = 2 m \hat{\beta} \hat{\gamma}_5$](https://content.cld.iop.org/journals/0295-5075/139/4/44002/revision2/epl22100457ieqn24.gif) , chirality is not a constant of motion under the Dirac equation dynamics. A massive particle has no definite chirality [29], even though chirality itself is invariant under Lorentz transformations [1]. This is in contrast to helicity, the projection of spin in the momentum direction, which is constant under free Dirac dynamics but is not Lorentz invariant for massive particles. In the massless case, the system (2) decouples, and chirality is conserved and coincides with the helicity, e.g., left-handed massless particles always have negative helicity.
, chirality is not a constant of motion under the Dirac equation dynamics. A massive particle has no definite chirality [29], even though chirality itself is invariant under Lorentz transformations [1]. This is in contrast to helicity, the projection of spin in the momentum direction, which is constant under free Dirac dynamics but is not Lorentz invariant for massive particles. In the massless case, the system (2) decouples, and chirality is conserved and coincides with the helicity, e.g., left-handed massless particles always have negative helicity.
To illustrate chiral oscillations, we consider plane-wave helicity eigenstates. Those correspond to fixing the polarization of the bispinors such that 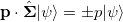 , which can be set along the
, which can be set along the 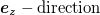 . Furthermore, we define
. Furthermore, we define

which can be taken as the starting point for describing states created via weak interaction processes, which involve projections into definite chirality states.
The time-evolved bispinor state, in general, is a superposition of both positive- and negative-energy solutions of the Dirac equation [1,2]. In particular, for a plane-wave bispinor state such that 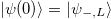 (initially left-handed and negative helicity), the temporal evolution in terms of (3) reads
(initially left-handed and negative helicity), the temporal evolution in terms of (3) reads

The probability that the state, initially left handed, is in a right-handed state is therefore given by

This chiral quantum oscillations have a period 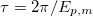 and amplitude
and amplitude 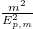 . For relativistic particles, with a small mass to energy ratio, chiral oscillations are negligible. Nevertheless, in the non-relativistic regime, chiral oscillations occur with maximum amplitude. This is the case of, for example, relic neutrinos. In fact, as
. For relativistic particles, with a small mass to energy ratio, chiral oscillations are negligible. Nevertheless, in the non-relativistic regime, chiral oscillations occur with maximum amplitude. This is the case of, for example, relic neutrinos. In fact, as 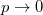 , the amplitude of chiral oscillations is maximized, driving full oscillations between left- and right-handed components of the bispinor. The chiral oscillation frequency corresponds, for a free particle, to an oscillation length that can be estimated as
, the amplitude of chiral oscillations is maximized, driving full oscillations between left- and right-handed components of the bispinor. The chiral oscillation frequency corresponds, for a free particle, to an oscillation length that can be estimated as 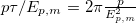 , which depends on the momentum-to-energy ratio. Typically, chiral oscillations happen at a fast rate which justifies averaging this effect over other relevant periods of oscillations, such as flavor oscillations for neutrinos (see below). The average chirality of (4) is given by
, which depends on the momentum-to-energy ratio. Typically, chiral oscillations happen at a fast rate which justifies averaging this effect over other relevant periods of oscillations, such as flavor oscillations for neutrinos (see below). The average chirality of (4) is given by

We stress that the results presented here are for Dirac particles and plane-wave solutions of the Dirac equation. The inclusion of wave-packets and extension to Majorana particles in the context of bispinors is discussed below. Next, two examples of chiral oscillations in the dynamics of non-relativistic particles are presented: entanglement in a lepton-antineutrino pair, and neutrino flavor oscillations.
Chiral oscillations and quantum entanglement in lepton-antineutrino pairs
Weak interactions lead pions to decay into lepton-antineutrino pairs. In general, due to conservation of angular momentum, the pair is created in a spin superposition [3] which is entangled. Furthermore, weak interactions violate parity and create states in which each particle has a definite chirality: the electron is left handed while the antineutrino is right handed. We can then describe such a state in terms of parity projected bispinors starting with the joint lepton-antineutrino state

were 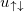 and
and 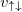 bispinors with spins polarized parallel
bispinors with spins polarized parallel 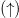 and atiparallel
and atiparallel 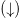 to
to  . To describe the intrinsic handedness of weak interactions, the initial state is obtained by projecting (7) into definite chiralities for the lepton and the antineutrino parts, such that at t = 0
. To describe the intrinsic handedness of weak interactions, the initial state is obtained by projecting (7) into definite chiralities for the lepton and the antineutrino parts, such that at t = 0

where the indexes 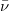 and l denote antineutrino and lepton, respectively, and
and l denote antineutrino and lepton, respectively, and 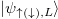 and
and 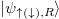 are defined similarly to (3). The factors
are defined similarly to (3). The factors 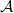 and
and 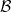 depend on the momentum and on the masses (expressions given in the SM). For small antineutrino mass,
depend on the momentum and on the masses (expressions given in the SM). For small antineutrino mass, 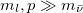 , and therefore
, and therefore 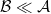 , the antineutrino state approaches a definite helicity state. The framework is schematized in fig. 1. The time evolution of (8) can be obtained by decomposing the state in terms of the Dirac eigenspinors and then, time-evolving each component, the complete expression for
, the antineutrino state approaches a definite helicity state. The framework is schematized in fig. 1. The time evolution of (8) can be obtained by decomposing the state in terms of the Dirac eigenspinors and then, time-evolving each component, the complete expression for 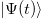 is given in [30]. The average chirality of the lepton
is given in [30]. The average chirality of the lepton 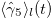 is given by (6), while for the antineutrino
is given by (6), while for the antineutrino 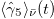 is given by (6) multiplied by –1 and with
is given by (6) multiplied by –1 and with 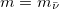 .
.
Fig. 1: (a) Lepton-antineutrino state obtained after a parity projection describing the intrinsic handedness of the chiral oscillations. (c) The free evolution of the particles induces chiral oscillations due to the mass term of the Dirac equation, which in turn affects the entanglement initially encoded only in the spins.
Download figure:
Standard imageThe lepton-antineutrino bispinor state has four discrete DoFs: the spin and chirality of the lepton and the spin and chirality of the antineutrino. Since each DoF is dichotomic, the state can be interpreted as a four-qubit state. Furthermore, the spins in (8) are entangled: it is not possible to write this state as a tensor product 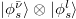 , altough at t = 0, the chiralities are not correlated with the spins. As the particles freely propagate, both lepton and antineutrino undergo chiral oscillations, and chirality becomes entangled with the spin. Consequently, the correlations that were solely encoded in the spins are redistributed into different partitions of the system and the overall effect is an oscillation of the spin entanglement due to chiral oscillations. The entanglement between the spins can be quantified in terms of the spin-spin negativity as
, altough at t = 0, the chiralities are not correlated with the spins. As the particles freely propagate, both lepton and antineutrino undergo chiral oscillations, and chirality becomes entangled with the spin. Consequently, the correlations that were solely encoded in the spins are redistributed into different partitions of the system and the overall effect is an oscillation of the spin entanglement due to chiral oscillations. The entanglement between the spins can be quantified in terms of the spin-spin negativity as

where 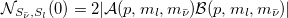 is the spin-spin entanglement encoded in the initial state, which in turn depends on the ratio between the masses and the momentum p. The factor
is the spin-spin entanglement encoded in the initial state, which in turn depends on the ratio between the masses and the momentum p. The factor 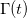 is given in terms of the average chiralities as
is given in terms of the average chiralities as

The entanglement shared between chiralities and spins is given by

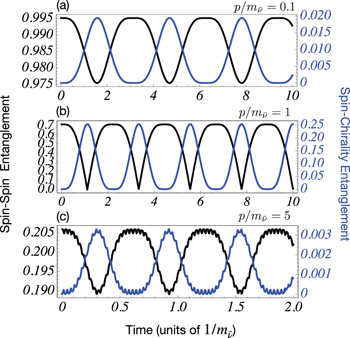
which is maximized at times where the spin-spin entanglement is minimum. Chiral oscillations effects on such quantum correlations are more evident in the dynamical regime  , when the momentum is of the same order of the antineutrino mass, as depicted in fig. 2, where both
, when the momentum is of the same order of the antineutrino mass, as depicted in fig. 2, where both 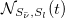 and
and 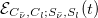 are shown. The amplitude of the oscillations exhibits a resonance-like effect for
are shown. The amplitude of the oscillations exhibits a resonance-like effect for 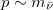 , even though the amount of spin-spin correlations is larger for
, even though the amount of spin-spin correlations is larger for 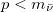 . The plots in fig. 2 show the redistribution of the spin-spin entanglement into chirality-spin entanglement due to chiral oscillations. As the ratio
. The plots in fig. 2 show the redistribution of the spin-spin entanglement into chirality-spin entanglement due to chiral oscillations. As the ratio 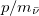 increases, the state becomes less entangled and chiral oscillations have a weaker effect. Another oscillation frequency which is related to the chiral oscillations of the lepton appears in fig. 2(c).
increases, the state becomes less entangled and chiral oscillations have a weaker effect. Another oscillation frequency which is related to the chiral oscillations of the lepton appears in fig. 2(c).
Fig. 2: Chiral oscillation effects on correlations encoded in a lepton-antineutrino pair: spin-spin entanglement and spin-chirality entanglement as a function of time for sample value of the ratio 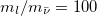 and for (a)
and for (a)  , (b)
, (b) 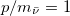 and (c)
and (c) 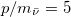 .
.
Download figure:
Standard imageAlternatively, chiral oscillations also have an imprint in spin correlations evaluated via Bell-like spin observables. Those quantify non-local correlations and have similar dynamical features to those of the spin-spin entanglement. While the latter requires a full reconstruction of the joint lepton-antineutrino state, a Bell-like measurement can be evaluated with repeated spin correlation measurements with, e.g., Stern-Gerlach apparatuses.
Chiral and flavor neutrino oscillations
Chiral oscillations also have an effect on the dynamics of neutrino states under flavor mixing. Since neutrinos are created with definite chirality, the surivival probability of a neutrino state has to take into account not only the flavor in which the state was originally created, but also its chirality. This framework is described by considering the state of a neutrino created with a definite flavor α at t = 0. Such flavor state is a superposition of mass eigenstates, each described as a massive bispinor evolving according with the Dirac equation. Furthermore, given the intrinsic parity violation of weak interactions, such state can be described by a left-handed projection of the mass superposition. In this case the state reads

where 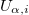 are the elements of the mixing matrix transforming mass eigenstates into flavor eigenstates. The temporal evolution of the state is given by
are the elements of the mixing matrix transforming mass eigenstates into flavor eigenstates. The temporal evolution of the state is given by

with 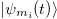 given by (4).
given by (4).
With the time evolved state, the probability that the state is left handed is given by 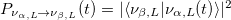 and the probability that the state is right handed
and the probability that the state is right handed 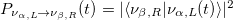 , where
, where

The complete formulas for the oscillation probabilities for N-flavors mixing are given in the SM. The survival probability of the state is given by 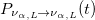 . The oscillation probability to right-handed states is a sum of terms that are all proportional to mass-to-energy ratios, and are suppressed for relativistic neutrinos
. The oscillation probability to right-handed states is a sum of terms that are all proportional to mass-to-energy ratios, and are suppressed for relativistic neutrinos 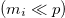 . In this regime, the oscillation probability to left-handed states tends to the usual neutrino flavor oscillation probability formula obtained via the standard description of mass eigenstates with plane-wave solutions of the Schrödinger equation [12,31,32]. Unlike the standard neutrino oscillation probability formula,
. In this regime, the oscillation probability to left-handed states tends to the usual neutrino flavor oscillation probability formula obtained via the standard description of mass eigenstates with plane-wave solutions of the Schrödinger equation [12,31,32]. Unlike the standard neutrino oscillation probability formula, 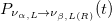 depends on both the energy difference
depends on both the energy difference  and the energy sum
and the energy sum 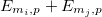 . The latter is a consequence of the superposition involving both positive- and negative-energy solutions of the Dirac equation required to construct the temporal evolution of an initially left-handed state. The survival probability has the form
. The latter is a consequence of the superposition involving both positive- and negative-energy solutions of the Dirac equation required to construct the temporal evolution of an initially left-handed state. The survival probability has the form

which is composed by the standard survival probability 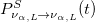 , the term that accounts for chiral oscillations
, the term that accounts for chiral oscillations 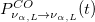 , and a term oscillating with the energy sum
, and a term oscillating with the energy sum 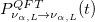 . The latter is also obtained in a quantum field theory of neutrino flavor mixing [33–35].
. The latter is also obtained in a quantum field theory of neutrino flavor mixing [33–35].
While flavor oscillations have a period 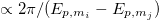 , the period of chiral oscillations is
, the period of chiral oscillations is 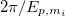 , which is typically much shorter compared with the former. To evaluate how the fast chiral oscillations affect the neutrino oscillation probabilities, one defines the time-averaged oscillation probability as
, which is typically much shorter compared with the former. To evaluate how the fast chiral oscillations affect the neutrino oscillation probabilities, one defines the time-averaged oscillation probability as

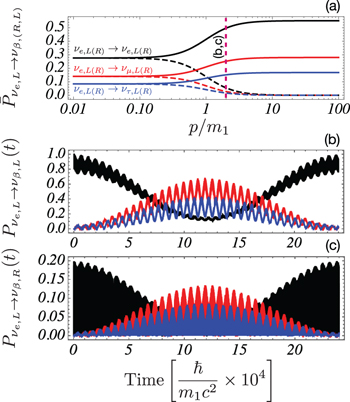
where τ is the longest among the oscillation periods. In fig. 3(a) the averaged oscillation probabilities for three flavors is depicted as a function of the ratio between momentum and the lightest mass. In the non-relativistic regime, the average oscillation probabilities to right-handed states are comparable to those to left-handed states, which could yield a depletion on the measured flux of relic neutrinos (see the discussion section). Correspondingly, in fig. 3(b) and (c) the oscillation probabilities to left- and right-handed states are shown as a function of time for 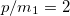 . Chiral oscillations appear as fast oscillations and as a finite probability of oscillation to a right-handed state.
. Chiral oscillations appear as fast oscillations and as a finite probability of oscillation to a right-handed state.
Fig. 3: Chiral oscillation effects on non-relativistic neutrino flavor oscillations for 3-flavor mixing and normal mass hierarchy. (a) Time-averaged oscillation probabilities for an electron neutrino to left- and right-handed states as a function of the momentum in units of the lightest mass m1. (b) Oscillation probability to left-handed states as a function of time for 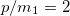 . (c) Oscillation probability to right-handed states as a function of time for
. (c) Oscillation probability to right-handed states as a function of time for 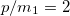 . Parameters:
. Parameters: 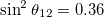 ,
, 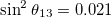 ,
, 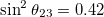 ,
, 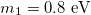 ,
, 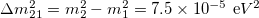 ,
, 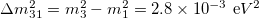 .
.
Download figure:
Standard imageGeneralizations
The analysis presented in the above section has focused on a simple framework for the description of chiral oscillations and their effects in the dynamics of non-relativistic neutrinos. In this treatment, only plane-wave solutions were considered and the results focused on Dirac neutrinos and flavor mixing do not differentiate between left- and right-handed states. We now briefly discuss some potential generalizations.
Wave-packet dynamics
While the description of chiral oscillations in terms of plane waves is useful for understanding the underlying physics of the phenomenon, particles are created with a momentum distribution and a more thorough evaluation of chiral oscillations requires the description of particle states by means of wave-packets. This can be done by using the completeness relations for the bispinors, and considering that the initial state has a momentum distribution 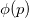 . The time evolution of an arbitrary bispinor is given in terms of the Fourier transform of the momentum distribution [36], from which all the properties discussed here can be derived. For example, for
. The time evolution of an arbitrary bispinor is given in terms of the Fourier transform of the momentum distribution [36], from which all the properties discussed here can be derived. For example, for 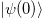 as in (4), the probability that the state is in a right-handed configuration is given by
as in (4), the probability that the state is in a right-handed configuration is given by

The integral needed to evaluate such probability (and the average chirality) has, in general, no analytical expression. For relativistic states, approximations can be done depending on the momentum distribution  , e.g., for a Gaussian centred around
, e.g., for a Gaussian centred around 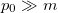 one can consider a first order approximation in
one can consider a first order approximation in 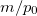 [36,37].
[36,37].
The momentum distribution of mass eigenstates yields further modifications to flavor oscillations, since the initial coherence of the superposition can be destroyed due to free evolution and the spatial separation of the wave packets, which propagate at different group velocities, affecting, for example, the correlation content of flavor neutrino states [38]. Since chiral oscillations are intrinsic to the dynamics of mass eigenstates, they would still persist even after the separation of the mass eigenstate wave packets, but an interplay between wave-packet dynamics and chiral oscillation effects on flavor correlations is expected.
Chiral oscillations and Majorana bispinors
For Majorana particles, the mass term in (1) depends on the charge conjugated bispinor 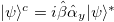

For a bispinor that satisfies the Majorana condition, 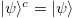 , the above equation is identical to the Dirac equation (1). In contrast, Dirac bispinors are unconstrained objects. The mathematical structure of Majorana bispinors and the formulation of relativistic quantum mechanics for such particles are different than the one for Dirac bispinors [39], but some conclusions about chiral oscillations for Majorana partices can be drawn as follows.
, the above equation is identical to the Dirac equation (1). In contrast, Dirac bispinors are unconstrained objects. The mathematical structure of Majorana bispinors and the formulation of relativistic quantum mechanics for such particles are different than the one for Dirac bispinors [39], but some conclusions about chiral oscillations for Majorana partices can be drawn as follows.
Since charge conjugation inverts both chirality and helicity, the constraint imposed by the Majorana condition implies that a Majorana bispinor always has both left and right-handed chirality components [29]. Thus, any bispinor that is its own charge conjugated always has zero chirality, and therefore does not undergo chiral oscillations [17]. Otherwise, a state initially with a definite chirality (which does not satisfy the Majorana condition) but whose temporal evolution is given by (18), undergoes chiral oscillations with conversion formula equal to the one obtained for Dirac particles [17]. Another framework corresponds to consider a mixed Dirac-Majorana mass terms, for which chiral oscillations formulas can be obtained as outlined in [17], and can exhibit substantial differences from the usual Dirac or Majorana cases. Likewise, in a field theoretical treatment, the dynamics of the lepton number carried by Majorana neutrinos has also been recently considered [40].
CP violation phases
The neutrino flavor mixing matrix appearing in (12) can include complex phases associated with CP violation. The number of phases for N-flavor mixing depends on whether the particle is Dirac or Majorana: for Dirac neutrinos a maximum of 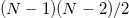 phases are allowed, while in the Majorana case the maximum number of phases are
phases are allowed, while in the Majorana case the maximum number of phases are  [41]. For three flavors, the Majorana mixing matrix is given by
[41]. For three flavors, the Majorana mixing matrix is given by ![$U^M = U \Phi= U {\rm{diag}}[1, e^{i \phi_2 /2}, e^{i \phi_3 /2}]$](https://content.cld.iop.org/journals/0295-5075/139/4/44002/revision2/epl22100457ieqn93.gif) , where U is the mixing matrix for the Dirac case. The oscillation formulas are the same as for the Dirac case and do not depend on the extra phases, since the oscillation probabilities depend on terms of the form
, where U is the mixing matrix for the Dirac case. The oscillation formulas are the same as for the Dirac case and do not depend on the extra phases, since the oscillation probabilities depend on terms of the form 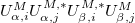 , in which the dependence of the extra CP violation phases is cancelled.
, in which the dependence of the extra CP violation phases is cancelled.
Alternatively, in the case of mixing that distinguishes left- and right-handed components of the bispinor, the oscillation probability formula will depend on a left-right phase difference. In this case, the relation between flavor and mass basis is given by left (right) state as

For a neutrino state initially left handed, the only difference in the oscillation formulas is for  . The additional Majorana phases are therefore included in the corresponding mixing matrices such that
. The additional Majorana phases are therefore included in the corresponding mixing matrices such that  , where
, where 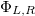 are diagonal matrices which include two complex phases each. As in the previously discussed case, UL(R) are the mixing matrix for the Dirac case. The oscillation probability to a right-handed state in this case depends on the difference between left- and right-handed phases (for the full formula, see the SM). The two-flavor case was recently investigated in [42].
are diagonal matrices which include two complex phases each. As in the previously discussed case, UL(R) are the mixing matrix for the Dirac case. The oscillation probability to a right-handed state in this case depends on the difference between left- and right-handed phases (for the full formula, see the SM). The two-flavor case was recently investigated in [42].
Discussions and perspectives
Chiral oscillations are intrinsic to the dynamics of bispinors and, as discussed in this review, they exhibit large amplitude in the non-relativistic dynamical regime, with frequencies that are typically higher than other relevant frequencies in the systems of interest. This is the case for neutrino oscillations, where chiral oscillations deplete the average transition probabilities to left-handed states. Neutrino detection is based on weak interaction processes, which are only sensitive to left-handed (or right-handed for antineutrinos) components of the state. Taking into account the time-average prescription presented here [17], one notices that chiral oscillations can deplete the survival probability of left-handed neutrino states to almost 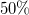 of the value obtained in the standard treatment for neutrino flavor oscillations, which can be particularly relevant for the measurement of relic neutrinos. In fact, the flux of measured neutrinos via tritium capture can exhibit a substantial depletion due to chiral oscillations, as discussed in [18]. Such depletion in the neutrino capture rate due to chiral oscillations does not distinguish between Dirac and Majorana neutrinos [17,18], even though the absorption of Majorana neutrinos is approximately two times that of Dirac neutrinos, due to the presence of right-handed and positive helicity states for the former.
of the value obtained in the standard treatment for neutrino flavor oscillations, which can be particularly relevant for the measurement of relic neutrinos. In fact, the flux of measured neutrinos via tritium capture can exhibit a substantial depletion due to chiral oscillations, as discussed in [18]. Such depletion in the neutrino capture rate due to chiral oscillations does not distinguish between Dirac and Majorana neutrinos [17,18], even though the absorption of Majorana neutrinos is approximately two times that of Dirac neutrinos, due to the presence of right-handed and positive helicity states for the former.
A distinction between Dirac and Majorana neutrinos via chiral oscillations is possible, in principle, if flavor mixing differentiates between left- and right-handed components of the state, also affected by the presence of additional Majorana CP violation phases. The transition probability depends on the phase difference, which modifies the time average oscillation probabilities. A different approach suggests to evaluate the quantum entanglement encoded in flavor neutrino states, which exhibit non-trivial dynamical features [38,43,44]. The inclusion of chirality in such framework can yield a distinction between Dirac and Majorana neutrinos. Finally, chiral oscillations behave differently in the presence of an external magnetic field [45,46], which also might affect flavor oscillation predictions.
Chiral oscillations also have analogous in low-energy systems. A paradigmatic example is given by the bilayer graphene [4], whose excitation can be effectively described with a Dirac Hamiltonian including external fields [7]. In this case, it has been shown that the internal spin-chirality bispinor structure is emulated by lattice and layer DoFs, which are in general entangled. In such a context, graphene systems were also proposed as platforms to probe the Zitterbewegung effect [19,20], the fast jittering motion of free particles. The latter has an intrinsic connection to chiral oscillations [26], and a potential prospect is to investigate effects analogous to flavor-chiral oscillations in the non-relativistic regime in such low-energy tunable systems. Other potential Dirac-like systems in which non-relativistic chiral oscillations could be emulated include photonic systems [24] and trapped ions [21,22].
Finally, a field theory treatment of chiral oscillations could also reveal novel features and establish chiral oscillations in a formalism compatible with those used for describing flavor oscillations [33–35].
Conclusions
Chiral oscillations are a consequence of the intrinsic structure of the bispinors. In this review, the general framework was presented in the context of the Dirac equation. The phenomenon is prominent in the non-relativistic regime, which could be particularly relevant in upcoming experiments probing the cosmic neutrino background. Also, chiral oscillations affect neutrino flavor oscillations and quantum correlations encoded in a lepton-antineutrino pair. Novel research frameworks include the study of chiral oscillation in Dirac-like systems, such as graphene, and the extension of the formalism in a fully field theoretical approach. This can further refine the present models potentially yielding novel scenarios in which Dirac and Majorana neutrinos can be distinguished.
Acknowledgments
VASVB acknowledges financial support from the Max Planck Society through a Max Planck independent research group. The work of AEB. is supported by the Brazilian Agencies FAPESP (Grant No. 2018/03960-9) and CNPq (Grant No. 301000/2019-0).
Data availability statement: All data that support the findings of this study are included within the article (and any supplementary files).