Abstract
Nano-patterned substrates offer possibilities for controlling the motion of fluids without external energy supply in novel technologies in microfluidics, coatings, etc. Here, we report on the rugotaxial motion of droplets on wrinkled substrates with gradient in the wavelength of the wrinkles by exploring a broad range of parameters, such as amplitude of the wrinkles, substrate wettability, droplet size and wavelength gradient. Adopting a theoretical and molecular dynamics approach, we determine the Cassie-Baxter and Wenzel states of the droplets, investigate the efficiency of rugotaxis as a function of different parameters, and discuss additional effects, such as pinning. We find that shallow wrinkles characterised by small wavelength gradients, and moderate adhesion of the droplet to the substrate favour the rugotaxis motion with growing droplet size, when pinning is avoided. We also find that the driving force in rugotaxis is the gain in interfacial energy between the droplet and the substrate as the droplet enters regions of denser wrinkles (smaller wavelengths of the wrinkles).
Export citation and abstract BibTeX RIS
The development of various technologies in microfluidics, microfabrication, coatings, and biology require the motion of fluids along predetermined trajectories [1–8]. A possibility of realising such motion is by using gradient substrates, namely substrates with gradually changing properties in a certain direction along the substrate [9–12]. For example, by exploiting differences in tissue stiffness, cells are able to move from softer to stiffer regions, a phenomenon known as durotaxis [13,14]. Durotaxis is particularly appealing for nanotechnology applications, because fluid motion is sustainable without providing external energy from a source [15–18]. In contrast, motion caused, for example, by a temperature gradient (thermotaxis) would require external energy supply into the system to maintain the gradient that is responsible for the fluid motion [19]. In this regard, characteristic cases of droplet motion caused by external energy supply are chemically driven droplets [20,21], and droplets on vibrated substrates [22–24] or wettability ratchets [25–27].
Hiltl and Böker have recently demonstrated in their experiments the possibility of causing the motion of a water droplet onto a sinusoidal wrinkle-patterned, solid substrate without using an external energy source, a phenomenon known as rugotaxis [28]. In this case, the wavelength characterising the wavy shape of the wrinkles decays as a function of the position, namely, there is a wavelength gradient characterising the wrinkles [28]. Hiltl and Böker have found that the droplet moves toward smaller wrinkle dimensions (wrinkles described by smaller wavelength). By investigating wrinkled substrates with wavelengths between 230 and 1200nm, and amplitudes ranging from 7 to 230nm, they attributed this phenomenon to the imbalance of the receding and advancing contact angles. In particular, contact angles correlate with the wavelength of the wrinkles, that is, larger contact angles for larger wavelengths, which naturally corresponds to differences of the substrate density along the direction of the wavelength gradient and the rugotaxial motion. The imbalance between the advancing and the receding contact angles as the driving force for droplet motion has been theoretically discussed in detail by Brochard [29] in the context of chemical or thermal gradients. Recently, an asymptotic theory has been developed to match the advancing and the receding angles to respective solutions of the problem at the microscale, using the velocity as a small parameter of an asymptotic expansion, which determines droplet shape and velocity as a function of the wettability gradient [31].
While wrinkled substrates without gradients [32–39] and substrates of similar geometries [40–46] have been studied in different contexts, rugotaxis has remained unexplored. Inspired by the work of Hiltl and Böker [28], we employ theoretical [47,48] and molecular dynamics (MD) [17] modelling to investigate the self-propelled motion of nanodroplets on wrinkled, solid substrates with wavelength gradient characterising the wrinkles. We show that the efficiency depends on the particular choice of parameters for the substrate, which leads to specific scenarios, when rugotaxis is possible. We also find that the driving force of the rugotaxis phenomenon is the gain in the interfacial energy between the droplet and the substrate as the droplet reaches areas of denser wrinkles. Toward studying rugotaxis, we have also explored the transition between Cassie-Baxter [49] (CB, a state where the liquid droplet does not fully penetrate the grooves on rough surfaces and leaves air gaps between the droplet and the substrate) and Wenzel [50] (W, a state where the droplet fully penetrates the grooves) states in substrates without gradient and compared our results with theoretical predictions [39] in order to set the stage for a better understanding of rugotaxis.
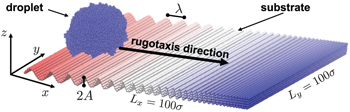
Figure 1 illustrates an initial configuration of our in silico experiments for a particular case. A liquid droplet is placed on a sinusoidal substrate with wavelength gradient of the wrinkles in the x-direction. This requires that the x and z coordinates of the beads be associated with the relation 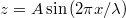 , where A is the amplitude and λ is the wavelength characterising the wrinkles. To implement a gradient in the wavelength of the wrinkles, one needs to multiply the wavelength with a coefficient that depends linearly on the position x of the bead on the substrate. Such substrate design is able to cause the rugotaxial motion of the droplet in the x-direction along the wavelength gradient. Rugotaxial motion will take place for a particular set of parameters characterising the substrate design, such as the amplitude of the wrinkles, A, as well as the initial wavelength,
, where A is the amplitude and λ is the wavelength characterising the wrinkles. To implement a gradient in the wavelength of the wrinkles, one needs to multiply the wavelength with a coefficient that depends linearly on the position x of the bead on the substrate. Such substrate design is able to cause the rugotaxial motion of the droplet in the x-direction along the wavelength gradient. Rugotaxial motion will take place for a particular set of parameters characterising the substrate design, such as the amplitude of the wrinkles, A, as well as the initial wavelength,  at the one end of the substrate and the final wavelength at the other end,
at the one end of the substrate and the final wavelength at the other end, 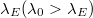 . The latter wavelengths determine the wavelength gradient of the wrinkles, expressed as
. The latter wavelengths determine the wavelength gradient of the wrinkles, expressed as  (Lx
is the linear dimension of the substrate in the x-direction). The adhesion of the droplet to the substrate is controlled through the
(Lx
is the linear dimension of the substrate in the x-direction). The adhesion of the droplet to the substrate is controlled through the 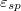 parameter of the Lennard-Jones potential. The details of our MD model are the same as in ref. [17] (see, also, the Supplementary Material Supplementarymaterial.pdf (SM)). In order to suppress droplet evaporation, we consider polymer melt droplets made of sufficiently long linear macromolecules of length N = 10 monomers each. This choice ensures the absence of evaporation effects, which might have otherwise affected the outcome of our in silico experiments [17]. In our study, different droplet sizes were considered, namely
parameter of the Lennard-Jones potential. The details of our MD model are the same as in ref. [17] (see, also, the Supplementary Material Supplementarymaterial.pdf (SM)). In order to suppress droplet evaporation, we consider polymer melt droplets made of sufficiently long linear macromolecules of length N = 10 monomers each. This choice ensures the absence of evaporation effects, which might have otherwise affected the outcome of our in silico experiments [17]. In our study, different droplet sizes were considered, namely 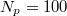 , 600, and 4800, where Np
is the total number of polymer chains comprising the droplet.
, 600, and 4800, where Np
is the total number of polymer chains comprising the droplet.
Fig. 1: A typical snapshot of an initial configuration for the rugotaxis study with a droplet on a wrinkled substrate with gradient in the wavelength, λ, characterising the sinusoidal shape of the wrinkles. The dimensions of the substrate in the x and y directions are 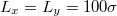 . The amplitude of the wrinkles is
. The amplitude of the wrinkles is 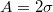 , the initial wavelength at the very left side of the substrate is
, the initial wavelength at the very left side of the substrate is 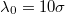 and that at the right side of the substrate is
and that at the right side of the substrate is 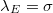 . Given the linear decrease of the wavelength in the x-direction, the wavelength gradient is constant and equal to
. Given the linear decrease of the wavelength in the x-direction, the wavelength gradient is constant and equal to 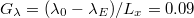 , in this case. The rugotaxial motion of the droplet takes place in the x-direction, along the wavelength gradient, as indicated by an arrow. Snapshots have been produced using the VMD software [30].
, in this case. The rugotaxial motion of the droplet takes place in the x-direction, along the wavelength gradient, as indicated by an arrow. Snapshots have been produced using the VMD software [30].
Download figure:
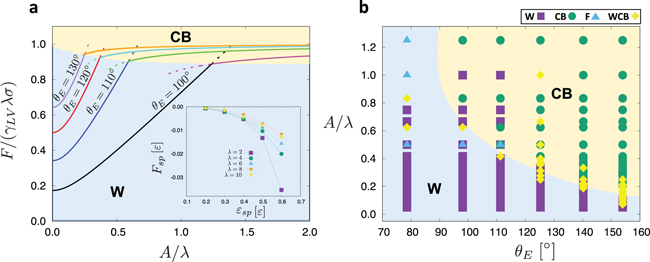
Standard imageBy investigating a range of amplitudes (A = 0.5–2.5σ), wavelengths (λ = 1–10σ) and strengths of attraction  –0.7ε) between the droplet and the substrate, we have initially determined the state (e.g., Wenzel (W), Cassie-Baxter (CB)) of the droplet on substrates without gradient by using MD simulation. Our results are presented in the form of state diagrams in fig. 2 for two cases, namely
–0.7ε) between the droplet and the substrate, we have initially determined the state (e.g., Wenzel (W), Cassie-Baxter (CB)) of the droplet on substrates without gradient by using MD simulation. Our results are presented in the form of state diagrams in fig. 2 for two cases, namely 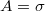 and
and 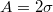 . The cases
. The cases 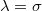 are not shown in the figure, because they represent flat substrates and a discussion about W and CB states would be irrelevant. Also, cases where the attraction strength
are not shown in the figure, because they represent flat substrates and a discussion about W and CB states would be irrelevant. Also, cases where the attraction strength 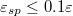 were omitted, because the droplet would detach from the substrate due to its thermal fluctuations. The results of fig. 2 are in agreement with theoretical predictions [39], which suggest that the CB state gradually appears in our diagrams in place of the W state as the amplitude of the wrinkles increases, which translates into the increase of the substrate roughness
were omitted, because the droplet would detach from the substrate due to its thermal fluctuations. The results of fig. 2 are in agreement with theoretical predictions [39], which suggest that the CB state gradually appears in our diagrams in place of the W state as the amplitude of the wrinkles increases, which translates into the increase of the substrate roughness 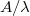 for each λ. Moreover, an increasing strength of attraction between the droplet and the substrate favours the W state, in agreement with the theory [39]. While for very small amplitude
for each λ. Moreover, an increasing strength of attraction between the droplet and the substrate favours the W state, in agreement with the theory [39]. While for very small amplitude 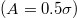 the W state appears even for very small strength of attraction between the substrate and the droplet and the CB state is only partially present during the simulations, for
the W state appears even for very small strength of attraction between the substrate and the droplet and the CB state is only partially present during the simulations, for 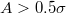 , the CB state becomes stable and appears in a larger number of cases as the roughness
, the CB state becomes stable and appears in a larger number of cases as the roughness  increases. However, the MD results also indicate the existence of a metastable state (WCB; fig. 2), where the droplet is either in the W or the CB state during the simulation. In addition, we observe that the WCB regime is generally narrow and, also, absent in particular cases as
increases. However, the MD results also indicate the existence of a metastable state (WCB; fig. 2), where the droplet is either in the W or the CB state during the simulation. In addition, we observe that the WCB regime is generally narrow and, also, absent in particular cases as  increases. Our results can be summarised as follows: the formation of the W state is favoured by a small amplitude, A, a large wavelength, λ, and a large attraction between the droplet and the substrate,
increases. Our results can be summarised as follows: the formation of the W state is favoured by a small amplitude, A, a large wavelength, λ, and a large attraction between the droplet and the substrate, 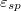 . Our results are in agreement with the theoretical predictions and further comparisons with theory will be discussed in the following [39].
. Our results are in agreement with the theoretical predictions and further comparisons with theory will be discussed in the following [39].
Fig. 2: State diagrams for droplets on wrinkled substrates without gradient as a function of the wavelength, λ, and the substrate-droplet attraction strength, 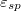 , for different substrate amplitudes, as indicated. Symbols are as follows: W, Wenzel state; CB, Cassie-Baxter state; WCB, droplet is in the W or the CB states at different instances in time during the simulation due to the thermal fluctuations; and F, film (droplet spreading due to the strong attraction between the droplet and the substrate as the density of the wrinkles increases). Here,
, for different substrate amplitudes, as indicated. Symbols are as follows: W, Wenzel state; CB, Cassie-Baxter state; WCB, droplet is in the W or the CB states at different instances in time during the simulation due to the thermal fluctuations; and F, film (droplet spreading due to the strong attraction between the droplet and the substrate as the density of the wrinkles increases). Here, 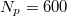 .
.
Download figure:
Standard imageThe equilibrium contact angle [51–54], 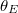 , provides the means of theoretically computing the free energies of Wenzel (W) and Cassie-Baxter (CB) states as a function of the substrate roughness
, provides the means of theoretically computing the free energies of Wenzel (W) and Cassie-Baxter (CB) states as a function of the substrate roughness 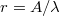 [39]. These results are presented in fig. 3(a) for four representative values of
[39]. These results are presented in fig. 3(a) for four representative values of 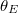 . The free energies are given in dimensionless form,
. The free energies are given in dimensionless form, 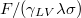 , where
, where  is the surface tension of the liquidvapour boundary, and σ is the monomer diameter. As expected (fig. 2(a)), with increasing roughness, the W state becomes metastable, while the CB state becomes stable. For each value of
is the surface tension of the liquidvapour boundary, and σ is the monomer diameter. As expected (fig. 2(a)), with increasing roughness, the W state becomes metastable, while the CB state becomes stable. For each value of  , this transition occurs at a particular critical roughness,
, this transition occurs at a particular critical roughness, 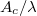 . Above the line, the CB states are stable, while below the line the W states are stable. Following this analysis, the results obtained from the simulation are presented in fig. 3(b), which are in very good agreement with the theoretical predictions (see fig. S1 and discussion in the SM). In particular, for
. Above the line, the CB states are stable, while below the line the W states are stable. Following this analysis, the results obtained from the simulation are presented in fig. 3(b), which are in very good agreement with the theoretical predictions (see fig. S1 and discussion in the SM). In particular, for  , only W states are possible. In addition, as
, only W states are possible. In addition, as  approaches 180°, even a small degree of roughness can induce the transition from W to CB states. The simulation results indicate that the boundary between the W and CB becomes sharper for larger values of
approaches 180°, even a small degree of roughness can induce the transition from W to CB states. The simulation results indicate that the boundary between the W and CB becomes sharper for larger values of 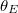 . Finally, the CB state is absent for
. Finally, the CB state is absent for  , in agreement with the theoretical calculations [39] (fig. 3(a)). We have also analysed the different contributions to the free energy on the basis of a hybrid MD-DFT approach [47,48] (see the SM for more details on the method and references therein). In particular, we have identified the attractive term between the droplet and the substrate, Fsp
, as the main factor that determines the state of the droplet (W or CB). Interestingly, the dependence of Fsp
on the attraction strength,
, in agreement with the theoretical calculations [39] (fig. 3(a)). We have also analysed the different contributions to the free energy on the basis of a hybrid MD-DFT approach [47,48] (see the SM for more details on the method and references therein). In particular, we have identified the attractive term between the droplet and the substrate, Fsp
, as the main factor that determines the state of the droplet (W or CB). Interestingly, the dependence of Fsp
on the attraction strength, 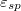 , shows a faster than linear decrease as
, shows a faster than linear decrease as 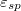 increases, that is, when the adhesion of the droplet to the substrate is stronger. This is due to the increase of the substrate density as the wrinkles become denser for smaller wavelengths, λ (inset of fig. 3(a)). Moreover, differences in Fsp
are small, at least for weaker adhesion, when the droplet is in "loose" contact with the substrate.
increases, that is, when the adhesion of the droplet to the substrate is stronger. This is due to the increase of the substrate density as the wrinkles become denser for smaller wavelengths, λ (inset of fig. 3(a)). Moreover, differences in Fsp
are small, at least for weaker adhesion, when the droplet is in "loose" contact with the substrate.
Fig. 3: (a) Free energies of Wenzel (W) and Cassie-Baxter (CB) states of a droplet with 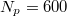 as a function of substrate roughness,
as a function of substrate roughness, 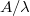 , for four values of the contact angle
, for four values of the contact angle 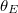 , as indicated. Solid lines correspond to stable states while dashed lines correspond to the metastable states. The inset presents the free energy component of the interaction between the droplet and the substrate as a function of the interaction parameter
, as indicated. Solid lines correspond to stable states while dashed lines correspond to the metastable states. The inset presents the free energy component of the interaction between the droplet and the substrate as a function of the interaction parameter 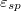 for a substrate with
for a substrate with 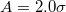 . (b) Diagram of different states (W, CB, WCB, F) as a function of the roughness,
. (b) Diagram of different states (W, CB, WCB, F) as a function of the roughness,  , and the contact angle,
, and the contact angle, 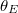 (cf. fig. S1 of the SM showing the theoretical prediction [39]).
(cf. fig. S1 of the SM showing the theoretical prediction [39]).
Download figure:
Standard imageWe have analysed the rugotaxial motion for a wide and relevant range of parameters. From our results, we have determined that each case is distinct. For example, two substrates with the same gradient,  , but different sets of
, but different sets of 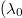 ,
, 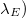 can show completely different behaviour regarding their ability to cause rugotaxial motion. Apart from these obvious differences, certain parameter combinations can cause the droplet to be in the W or CB states, the formation of a film, pinning, and others. In a recent molecular dynamics study [55], it has been found that even the slightest heterogeneity on the substrate can hinder the motion of a droplet on a substrate (pinning). Overcoming such a pinning barrier (i.e., depinning) can take place by increasing the interfacial energy between droplet and substrate due to changes of the substrate properties along the direction of motion. Thus, the difference in wettability on both sides of the pinning barrier has been exploited [55], while in our study the droplet steps over the barrier due to the decrease of the wavelength, which in turn results in an increase of the interfacial energy between droplet and substrate. This further highlights that successful and efficient rugotaxis requires an appropriate design, which takes into account all these effects.
can show completely different behaviour regarding their ability to cause rugotaxial motion. Apart from these obvious differences, certain parameter combinations can cause the droplet to be in the W or CB states, the formation of a film, pinning, and others. In a recent molecular dynamics study [55], it has been found that even the slightest heterogeneity on the substrate can hinder the motion of a droplet on a substrate (pinning). Overcoming such a pinning barrier (i.e., depinning) can take place by increasing the interfacial energy between droplet and substrate due to changes of the substrate properties along the direction of motion. Thus, the difference in wettability on both sides of the pinning barrier has been exploited [55], while in our study the droplet steps over the barrier due to the decrease of the wavelength, which in turn results in an increase of the interfacial energy between droplet and substrate. This further highlights that successful and efficient rugotaxis requires an appropriate design, which takes into account all these effects.
Based on our previous experience with investigations on the durotaxis phenomenon [17] and the experience gained by the current study, we have determined that the average rugotaxial velocity, V, of the droplet is an appropriate measure to assess the overall efficiency of the rugotaxis motion in successful cases, that is cases that can uninterruptedly translocate throughout the substrate in the direction of the wavelength gradient. In this case,  , where L is the distance covered by the centre of mass of the droplet during its translocation from the very left part of the substrate to the very right part of the substrate in the x-direction (fig. 1), and t is the time required to complete the rugotaxis motion. Then, fig. 4 presents various characteristic examples that illustrate the dependence of the velocity for different droplet size and different scenarios of successful rugotaxis cases. In general, larger droplets are able to easier overcome the pinning barriers [55], with the latter becoming more pronounced as the droplet is in the Wenzel state (fig. 2), which otherwise favour the rugotaxial motion. Still, one can observe the difference in the behaviour of large droplets
, where L is the distance covered by the centre of mass of the droplet during its translocation from the very left part of the substrate to the very right part of the substrate in the x-direction (fig. 1), and t is the time required to complete the rugotaxis motion. Then, fig. 4 presents various characteristic examples that illustrate the dependence of the velocity for different droplet size and different scenarios of successful rugotaxis cases. In general, larger droplets are able to easier overcome the pinning barriers [55], with the latter becoming more pronounced as the droplet is in the Wenzel state (fig. 2), which otherwise favour the rugotaxial motion. Still, one can observe the difference in the behaviour of large droplets 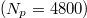 between substrates with
between substrates with 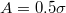 and
and 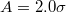 , where the increase of
, where the increase of 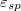 leads to different behaviour in the rugotaxis efficiency. Moreover, we have found that
leads to different behaviour in the rugotaxis efficiency. Moreover, we have found that 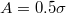 leads to the most efficient rugotaxis, particularly for smaller droplets.
leads to the most efficient rugotaxis, particularly for smaller droplets.
Fig. 4: The dependence of the average rugotaxis velocity, V, on the attraction strength, 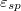 , for different cases of
, for different cases of 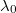 ,
, 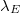 , Np
and A, as indicated.
, Np
and A, as indicated.
Download figure:
Standard imageWe take a closer look at the rugotaxis efficiency and inspect the different scenarios in our in silico experiments, providing, also, further insight into the parameters determining rugotaxis' performance (fig. 4). We have identified a clear distinction between substrates with small 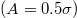 and larger amplitudes
and larger amplitudes 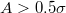 . In particular, in the case of shallow wrinkles,
. In particular, in the case of shallow wrinkles, 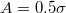 , we observe two different scenarios. In the first scenario, the droplets attain their highest velocity V for small
, we observe two different scenarios. In the first scenario, the droplets attain their highest velocity V for small 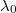 , namely
, namely 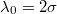 and
and  , albeit V tends to decrease with growing adhesion
, albeit V tends to decrease with growing adhesion 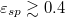 . In particular, the motion of small droplets
. In particular, the motion of small droplets 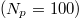 is significantly hampered as the adhesion strength,
is significantly hampered as the adhesion strength, 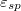 , grows.
, grows.
In contrast (cf. fig. 4(a)), larger gradients (e.g., 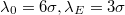 ), generally lower the mean velocity, V, which is found, however, to grow then steadily with increasing adhesion
), generally lower the mean velocity, V, which is found, however, to grow then steadily with increasing adhesion 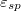 . Moreover, the larger gradient
. Moreover, the larger gradient 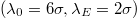 nearly doubles V with respect to
nearly doubles V with respect to 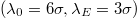 whereby for
whereby for 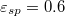 the speed of the largest drop attains that from the first scenario. For deeper wrinkles,
the speed of the largest drop attains that from the first scenario. For deeper wrinkles, 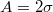 (fig. 4(b)), the same trend is observed although pinning effects occur more frequently so that for the case,
(fig. 4(b)), the same trend is observed although pinning effects occur more frequently so that for the case, 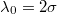 ,
,  (not shown here), no rugotaxis whatsoever takes place. Apart from the smallest droplets,
(not shown here), no rugotaxis whatsoever takes place. Apart from the smallest droplets,  , an increase in the gradient
, an increase in the gradient 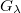 leads similarly to faster motion, which becomes more efficient with growing drop size. However, further increase of the gradient or
leads similarly to faster motion, which becomes more efficient with growing drop size. However, further increase of the gradient or 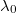 will hinder the motion of the droplets, independently of the droplet size. Moreover values of
will hinder the motion of the droplets, independently of the droplet size. Moreover values of 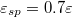 (strong adhesion of the droplet to the substrate) will always prevent the motion of the droplet or lead to complete droplet spreading (e.g., for
(strong adhesion of the droplet to the substrate) will always prevent the motion of the droplet or lead to complete droplet spreading (e.g., for 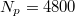 ). Still, we have observed that larger droplets overcome more easily the pinning barriers, which is in agreement with recent simulation results [55].
). Still, we have observed that larger droplets overcome more easily the pinning barriers, which is in agreement with recent simulation results [55].
As in the case of durotaxial motion [17], we have identified the change in the interfacial energy between the droplet and the substrate as the main driving force of rugotaxis, also determining its efficiency (fig. 5). In our case, the interfacial energy is simply the total pair interaction between the droplet and the substrate beads. Crucially, for a certain droplet size this depends on the particular parameters, A,  ,
, 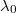 , and
, and 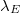 . We have also identified cases when the droplet exhibits pinning during rugotaxis but is also able to overcome the associated energy barrier caused by the pinning and eventually complete the rugotaxial motion. While in such cases, rugotaxis is successful and eventually the droplet reaches the very right end of the substrate (fig. 5), in many other cases considered in our study as unsuccessful rugotaxis cases, the droplet failed to overcome the associated energy barrier. Typically, such pinning events occur at the transition from W to CB state as the drop partially climbs out of the substrate troughs whereby the interfacial energy Esp
rises before the whole droplet attains a new CB state where droplet beads cannot enter into the narrowed wrinkles [55].
. We have also identified cases when the droplet exhibits pinning during rugotaxis but is also able to overcome the associated energy barrier caused by the pinning and eventually complete the rugotaxial motion. While in such cases, rugotaxis is successful and eventually the droplet reaches the very right end of the substrate (fig. 5), in many other cases considered in our study as unsuccessful rugotaxis cases, the droplet failed to overcome the associated energy barrier. Typically, such pinning events occur at the transition from W to CB state as the drop partially climbs out of the substrate troughs whereby the interfacial energy Esp
rises before the whole droplet attains a new CB state where droplet beads cannot enter into the narrowed wrinkles [55].
Fig. 5: Interfacial energy, Esp
, and position of the mass centre of the droplet, xcom
, as a function of time, as indicated. Hence, the distance covered by the droplet refers to its centre of mass and droplets of different size will move a different distance in each in silico expriment. Arrows indicate the time when pinning occurs for different cases of Np
as indicated. We also indicate the unpinning of the droplet with an arrow in the case of 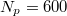 . For
. For 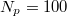 , the droplet remains pinned throughout the simulation. For
, the droplet remains pinned throughout the simulation. For 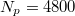 , there is no pinning. Here,
, there is no pinning. Here, 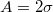 ,
, 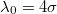 ,
, 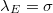 ,
, 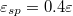 .
. 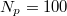 , 600 and 4800, as indicated.
, 600 and 4800, as indicated.
Download figure:
Standard imageFigure 5 contains plots of the position of the centre of mass of the droplet, xcom
, and the interfacial energy, Esp
, as a function of the elapsed time from the beginning until the end of the rugotaxial motion. For 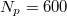 , we find that the droplet tranlocates efficiently until pinning occurs. An important point here is that the energy, Esp
, continues to decrease just after the pinning, which allows the droplet to move to the right, where the underlying density (and wettability) of the substrate increases with the wavelength gradient.
, we find that the droplet tranlocates efficiently until pinning occurs. An important point here is that the energy, Esp
, continues to decrease just after the pinning, which allows the droplet to move to the right, where the underlying density (and wettability) of the substrate increases with the wavelength gradient.
In summary, we have investigated solid, wrinkled substrates with and without wavelength gradient in one direction, in an attempt to explore the rugotaxial motion of droplets. To achieve our goal we have mainly employed MD simulation based on coarse-grained force fields, as we have done previously in the case of durotaxis. [17] We have also provided relevant theoretical background and, also, performed numerical calculations based on a hybrid MD-DFT approach [47,48,56].
We have constructed the diagram of W and CB states for a range of parameters. For small wrinkle amplitudes, the W state prevails for a range of droplet-substrate adhesion strength and wrinkle wavelengths. As the amplitude increases, the CB state sets in initially at small adhesion strengths and wrinkle wavelengths. As the amplitude further increases, the CB state appears for a larger range of wavelengths and adhesion strengths. Theory [39] predicts the boundary between W and CB states, which is in agreement with the simulation results. Based on a hybrid MD-DFT approach, we have identified the interfacial energy term to be mainly responsible for the different behaviour (W or CB).
In the case of the rugotaxis MD in silico experiments, we find a range of optimal choices of the parameters that govern rugotaxis. In the case of shallow wrinkles with 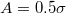 , we observe the most efficient rugotaxial motion for
, we observe the most efficient rugotaxial motion for 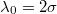 , which corresponds to a small wavelength gradient. For larger amplitudes, increased wavelength gradients lead to more efficient rugotaxis up to some moderate adhesion strength. As a result, our results indicate that an appropriate substrate design will determine the efficiency of the rugotaxial motion.
, which corresponds to a small wavelength gradient. For larger amplitudes, increased wavelength gradients lead to more efficient rugotaxis up to some moderate adhesion strength. As a result, our results indicate that an appropriate substrate design will determine the efficiency of the rugotaxial motion.
Based on our analysis, we have identified that changes of the interfacial energy between the substrate and the droplet constitute the driving force of rugotaxial motion, as has been also found previously in the case of durotaxis [17]. Hence, the two phenomena share characteristics, but, in the case of rugotaxis, this crucially depends on a larger number of parameters that can lead to different scenarios, with pinning playing a crucial role. We anticipate that our study elucidates important aspects of the rugotaxis phenomenon and suggests design principles for nano-fabricated wirnkle-patterned substrates that can increase the efficiency of rugotaxial motion.
Acknowledgments
This research has been supported by the National Science Centre, Poland, under grant No. 2019/35/B/ST3/03426. AM acknowledges support by COST (European Cooperation in Science and Technology (see http://www.cost.eu and https://www.fni.bg) and its Bulgarian partner FNI/MON under KOST-11). This research was supported in part by PLGrid Infrastructure.
Data availabilty statement: All data that support the findings of this study are included within the article (and any supplementary files).