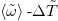Abstract
The low-temperature-differential (LTD) Stirling heat engine technology constitutes one of the important sustainable energy technologies. The basic question of how the rotational motion of the LTD Stirling heat engine is maintained or lost based on the temperature difference is thus a practically and physically important problem that needs to be clearly understood. Here, we approach this problem by proposing and investigating a minimal nonlinear dynamic model of an LTD kinematic Stirling heat engine. Our model is described as a driven nonlinear pendulum where the motive force is the temperature difference. The rotational state and the stationary state of the engine are described as a stable limit cycle and a stable fixed point of the dynamical equations, respectively. These two states coexist under a sufficient temperature difference, whereas the stable limit cycle does not exist under a temperature difference that is too small. Using a nonlinear bifurcation analysis, we show that the disappearance of the stable limit cycle occurs via a homoclinic bifurcation, with the temperature difference being the bifurcation parameter.
Export citation and abstract BibTeX RIS

Published by the EPLA under the terms of the Creative Commons Attribution 3.0 License (CC-BY). Further distribution of this work must maintain attribution to the author(s) and the published article's title, journal citation, and DOI.
Introduction
Technology that can use thermal energy as a resource is one of the most important technologies needed to develop a sustainable society. The Stirling heat engine, which was invented in the early 19th century, has received renewed attention over the past several years for its potential application in sustainable energy technology [1,2]. Owing to technological innovations during the past few decades, some types of the Stirling heat engine that can operate under very low temperature differences have been developed [3], and make the use of thermal energy in our daily life possible. The demonstration of a low-temperature-differential (LTD) Stirling heat engine operating in the palm of the hand under the difference between the body temperature and room temperature is remarkable [3], and serves as useful material for both teaching and learning thermodynamics.
From a fundamental physics perspective, it is important to understand how the rotational motion of the LTD Stirling heat engine is maintained or lost based on the temperature difference. In contrast to the ideal Stirling thermodynamic cycle with an external operation [1,2], actual Stirling heat engines run autonomously in a self-sustained manner under a sufficient temperature difference. This is accomplished with the aid of a crank-piston mechanism [1,2]. Mathematical modeling of the Stirling heat engine thus involves solving coupled equations that describe both the dynamics of a working fluid and that of the mechanical degrees of freedom of the engine [4]. While a simple theoretical model of an LTD Stirling heat engine that reproduces the rotational motion of the engine has been proposed [5], how this motion is lost with decreasing temperature difference remains to be clarified.
In this study, we provide an answer to this question by proposing and investigating a minimal model of an LTD Stirling heat engine based on nonlinear dynamics. To be more specific, we model a kinematic Stirling heat engine that has been adopted to implement actual LTD Stirling heat engines [2]. Our model is the simplest in the sense that dynamical equations with the fewest degrees of freedom and a stable limit-cycle solution interpreted as the rotational motion of the engine are involved. We then analyze a bifurcation of the stable limit-cycle solution, with the temperature difference being the bifurcation parameter.
Kinematic Stirling heat engine
The kinematic Stirling heat engine is a gamma-configuration (cylinder-split) Stirling heat engine [1,2]. In fig. 1, we illustrate a kinematic Stirling heat engine designed for an LTD operation (a prototype of this LTD kinematic engine is the N-92 type designed and built by Senft [3]): The working substance, a gas, is confined into a cylinder with total volume V. The cylinder consists of a large cylinder with volume Vd and a small cylinder with volume Vp, where  . The small cylinder with a power piston on its top is placed on the large cylinder. The power piston is connected to a crank with a small radius via a connecting rod. The reciprocating motion of the power piston is converted to a rotational motion by the crank. The cylinder is separated into upper and lower regions by a reciprocating displacer piston in the large cylinder. The displacer piston is connected to the other crank with the same radius as the former via a connecting rod. The two cranks, along with a flywheel with a large moment of inertia, are combined to rotate as a single synchronized unit with the same crankshaft centered at the cranks. The phase angle
. The small cylinder with a power piston on its top is placed on the large cylinder. The power piston is connected to a crank with a small radius via a connecting rod. The reciprocating motion of the power piston is converted to a rotational motion by the crank. The cylinder is separated into upper and lower regions by a reciprocating displacer piston in the large cylinder. The displacer piston is connected to the other crank with the same radius as the former via a connecting rod. The two cranks, along with a flywheel with a large moment of inertia, are combined to rotate as a single synchronized unit with the same crankshaft centered at the cranks. The phase angle  (
( ) of the crank connected to the displacer piston is arranged such that it leads the phase angle θ (
) of the crank connected to the displacer piston is arranged such that it leads the phase angle θ ( ) of the crank connected to the power piston by
) of the crank connected to the power piston by  as
as  [2], where
[2], where  and θ increase clockwise from the origin corresponding to the lowest point of each piston. This unit, which is supported by a pillar, is fixed above the cylinder. There is a small space of negligible volume between the displacer piston and the wall of the large cylinder. The gas is transferred back and forth through the space between the upper and the lower regions of the cylinder because of the reciprocating motion of the displacer piston. The volume Vd of the large cylinder that agrees with the swept volume of the displacer piston remains constant, while that of the small cylinder Vp changes with θ. At the bottom of the large cylinder, the engine contacts a heat reservoir (e.g., a warm palm or cold ice) at temperature Tb. The surrounding air with temperature
and θ increase clockwise from the origin corresponding to the lowest point of each piston. This unit, which is supported by a pillar, is fixed above the cylinder. There is a small space of negligible volume between the displacer piston and the wall of the large cylinder. The gas is transferred back and forth through the space between the upper and the lower regions of the cylinder because of the reciprocating motion of the displacer piston. The volume Vd of the large cylinder that agrees with the swept volume of the displacer piston remains constant, while that of the small cylinder Vp changes with θ. At the bottom of the large cylinder, the engine contacts a heat reservoir (e.g., a warm palm or cold ice) at temperature Tb. The surrounding air with temperature  serves as the other heat reservoir and the atmospheric pressure
serves as the other heat reservoir and the atmospheric pressure  acts on the power piston. As shown in fig. 1, an LTD Stirling heat engine has some characteristics in its geometry that include the following [2,3]: the compression ratio of the engine is small; the diameter of the large cylinder and the displacer piston is large; the displacer piston is short, and its stroke is small; the top and bottom surfaces of the large cylinder for thermal conduction are large.
acts on the power piston. As shown in fig. 1, an LTD Stirling heat engine has some characteristics in its geometry that include the following [2,3]: the compression ratio of the engine is small; the diameter of the large cylinder and the displacer piston is large; the displacer piston is short, and its stroke is small; the top and bottom surfaces of the large cylinder for thermal conduction are large.
Fig. 1: Schematic illustration of the low-temperature-differential (LTD) kinematic Stirling heat engine: Front view (left), side view (right top), and oblique view (right bottom).
Download figure:
Standard imageFor  , the kinematic Stirling heat engine runs clockwise. Initially, the phase angle of the crank is located at
, the kinematic Stirling heat engine runs clockwise. Initially, the phase angle of the crank is located at  (
( ) with a positive angular velocity. The points
) with a positive angular velocity. The points  and
and  where the volume of the cylinder reaches its minimum and maximum are called the top dead center (TDC) and the bottom dead center (BDC), respectively [2,6]; a torque force transmitted from the power piston to the crank vanishes at these points. The engine then undergoes the following cyclic process (fig. 2) [1,2]: (i) → (ii) transfer stroke: the crank rotates clockwise and overcomes
where the volume of the cylinder reaches its minimum and maximum are called the top dead center (TDC) and the bottom dead center (BDC), respectively [2,6]; a torque force transmitted from the power piston to the crank vanishes at these points. The engine then undergoes the following cyclic process (fig. 2) [1,2]: (i) → (ii) transfer stroke: the crank rotates clockwise and overcomes  (TDC) with the aid of the moment of inertia of the flywheel even against a frictional torque, and the gas expands from the minimum volume
(TDC) with the aid of the moment of inertia of the flywheel even against a frictional torque, and the gas expands from the minimum volume  at
at  to push the power piston against the atmospheric pressure. Meanwhile, the displacer piston transfers most of the gas to the lower region of the cylinder. The more gas that gathers in the lower region, the more it is heated up by the hot heat reservoir (warm palm) with Tb at the bottom surface of the large cylinder. (ii) → (iii) Expansion stroke: the gas temperature becomes close to Tb at
to push the power piston against the atmospheric pressure. Meanwhile, the displacer piston transfers most of the gas to the lower region of the cylinder. The more gas that gathers in the lower region, the more it is heated up by the hot heat reservoir (warm palm) with Tb at the bottom surface of the large cylinder. (ii) → (iii) Expansion stroke: the gas temperature becomes close to Tb at  (
( ) where the gas is completely separated from the cold heat reservoir (surrounding air) at the top surface of the large cylinder. The gas continues to expand and pushes the power piston until the volume reaches the maximum
) where the gas is completely separated from the cold heat reservoir (surrounding air) at the top surface of the large cylinder. The gas continues to expand and pushes the power piston until the volume reaches the maximum  at
at  (
( ). (iii) → (iv) Transfer stroke: with the aid of the moment of inertia of the flywheel, the crank keeps rotating, overcoming
). (iii) → (iv) Transfer stroke: with the aid of the moment of inertia of the flywheel, the crank keeps rotating, overcoming  (BDC), and the power piston starts to compress the gas against the gas pressure. Meanwhile, the displacer piston transfers the gas to the upper region of the large cylinder. The more gas that gathers in the upper region, the more it is cooled down by the cold heat reservoir with
(BDC), and the power piston starts to compress the gas against the gas pressure. Meanwhile, the displacer piston transfers the gas to the upper region of the large cylinder. The more gas that gathers in the upper region, the more it is cooled down by the cold heat reservoir with  at the top surface of the large cylinder. (iv) → (i) Compression stroke: the gas temperature becomes close to
at the top surface of the large cylinder. (iv) → (i) Compression stroke: the gas temperature becomes close to  at
at  (
( ) where the gas is completely separated from the hot heat reservoir at the bottom surface of the large cylinder. The power piston continues to compress the gas until the volume reaches the minimum
) where the gas is completely separated from the hot heat reservoir at the bottom surface of the large cylinder. The power piston continues to compress the gas until the volume reaches the minimum  at
at  (
( ) and the engine returns to the initial state. In this cyclic process, the displacer piston serves as an automatic controller that realizes the alternate attachment and detachment of the heat reservoirs with the gas, depending on its location. In contrast, the power piston is a motive part that converts the thermal energy into the rotational motion of the engine via the crank.
) and the engine returns to the initial state. In this cyclic process, the displacer piston serves as an automatic controller that realizes the alternate attachment and detachment of the heat reservoirs with the gas, depending on its location. In contrast, the power piston is a motive part that converts the thermal energy into the rotational motion of the engine via the crank.
Fig. 2: Schematic illustration of the cycle process of the LTD kinematic Stirling heat engine for  (clockwise rotation): (i) → (ii) transfer stroke, (ii) → (iii) expansion stroke, (iii) → (iv) transfer stroke, and (iv) → (i) compression stroke.
(clockwise rotation): (i) → (ii) transfer stroke, (ii) → (iii) expansion stroke, (iii) → (iv) transfer stroke, and (iv) → (i) compression stroke.
Download figure:
Standard imageThis engine runs counterclockwise for  [3]. The engine starts from
[3]. The engine starts from  at
at  with a negative angular velocity and follows the following sequence: (i) → (ii) transfer stroke, (ii) → (iii) expansion stroke, (iii) → (iv) transfer stroke, and (iv) → (i) compression stroke, and this sequence is the same as the clockwise case with
with a negative angular velocity and follows the following sequence: (i) → (ii) transfer stroke, (ii) → (iii) expansion stroke, (iii) → (iv) transfer stroke, and (iv) → (i) compression stroke, and this sequence is the same as the clockwise case with  in fig. 2. One difference is that the gas is transferred to the upper region of the cylinder at the first transfer stroke and is heated up by the surrounding air (which acts as the hot heat reservoir) while it is transferred to the lower region of the cylinder at the second transfer stroke and is cooled down by, e.g., cold ice acting as the cold heat reservoir.
in fig. 2. One difference is that the gas is transferred to the upper region of the cylinder at the first transfer stroke and is heated up by the surrounding air (which acts as the hot heat reservoir) while it is transferred to the lower region of the cylinder at the second transfer stroke and is cooled down by, e.g., cold ice acting as the cold heat reservoir.
Nonlinear dynamic model
We propose a minimal nonlinear dynamic model that captures the above features of the LTD kinematic Stirling heat engine. We assume that the gas, the working substance, can be approximated as an ideal gas. We also assume that the gas has spatially uniform temperature T and density over the entire cylinder with total volume V.
Our model is a coupled system with mechanical and thermodynamic degrees of freedom [4,5]. The mechanical degree of freedom is the phase angle θ of the crank, which has a radius r. We assume that the equation of motion of the crank is given by

where  . Here, I is the moment of inertia of the crank with the flywheel attached,
. Here, I is the moment of inertia of the crank with the flywheel attached,  and
and  are the volume of the small cylinder and that of the large cylinder, respectively, with
are the volume of the small cylinder and that of the large cylinder, respectively, with  and
and  being the bottom areas of these cylinders. The total volume
being the bottom areas of these cylinders. The total volume  of the cylinder is given by
of the cylinder is given by

where  at
at  and
and  at
at  . F is a net force acting on the power piston created by the pressure difference between the internal gas and the surrounding air. The gas pressure is given by the equation of state for the ideal gas
. F is a net force acting on the power piston created by the pressure difference between the internal gas and the surrounding air. The gas pressure is given by the equation of state for the ideal gas  with n and R being the number of moles of the gas and the molar gas constant, respectively. Γ is a coefficient of the frictional torque, and the mass of the displacer piston, mass of the connecting rods, and gravity are negligible for simplicity. We can derive eq. (1) from the standard setup of a crank-piston mechanism [6] by imposing conditions
with n and R being the number of moles of the gas and the molar gas constant, respectively. Γ is a coefficient of the frictional torque, and the mass of the displacer piston, mass of the connecting rods, and gravity are negligible for simplicity. We can derive eq. (1) from the standard setup of a crank-piston mechanism [6] by imposing conditions  and
and  , where l and mp are the length of the connecting rod and the mass of the power piston with negligible friction, respectively. Under the condition
, where l and mp are the length of the connecting rod and the mass of the power piston with negligible friction, respectively. Under the condition  , the net force F acting on the power piston is transmitted to the crank via the connecting rod in a nearly parallel fashion [4]. This allows us to interpret the part
, the net force F acting on the power piston is transmitted to the crank via the connecting rod in a nearly parallel fashion [4]. This allows us to interpret the part  on the r.h.s. of eq. (1) as the tangential component of the force applied to the crank and hence
on the r.h.s. of eq. (1) as the tangential component of the force applied to the crank and hence  as the rotational torque, which vanishes at
as the rotational torque, which vanishes at  (TDC) and
(TDC) and  (BDC).
(BDC).
The thermodynamic degree of freedom in our model is the gas temperature T. The time-evolution equation of T is given by the first law of thermodynamics (the law of energy conservation) for the ideal gas [7]:

where  is the total number of spatial and internal degrees of freedom per molecule and
is the total number of spatial and internal degrees of freedom per molecule and  . We assume that the heat flows from the two heat reservoirs according to the Fourier law and flows only through the top and the bottom surface of the large cylinder into the gas.
. We assume that the heat flows from the two heat reservoirs according to the Fourier law and flows only through the top and the bottom surface of the large cylinder into the gas.  (
( ) in eq. (3) is a state-dependent thermal conductance defined by
) in eq. (3) is a state-dependent thermal conductance defined by

Here G is a usual thermal conductance and

is a function expressing a degree of coupling between the gas and the heat reservoir on each side of the large cylinder separated by the displacer piston, where

are the separated volumes of the large cylinder by the displacer piston. According to eq. (5), the amount of heat flowing into one side of the large cylinder increases owing to the increase in volume on this side, while the amount of heat flowing into the other side of the large cylinder reduces with the decrease in volume on that side. The degree-of-coupling function eq. (5) models the role of the displacer piston as shown in the transfer strokes in (i) → (ii) and (iii) → (iv) in fig. 2, where the reciprocating motion of the displacer piston alternately transfers the gas into one side of the large cylinder, making the gas thermally isolated from the heat reservoir on the other side of the large cylinder ( and
and  correspond to (ii) in fig. 2 and
correspond to (ii) in fig. 2 and  and
and  correspond to (iv) in fig. 2).
correspond to (iv) in fig. 2).
To clarify the role of the displacer piston from another perspective, it is convenient to rewrite the heat flow term in eq. (3) as

where we used eqs. (4)–(6), and

is an effective temperature. While this engine runs autonomously, we may interpret eq. (7) as if one heat reservoir with  is tactically attached to the engine by an external agent as in the case of a usual thermodynamic cycle. We can also rewrite eq. (8) as a function of V by using eq. (2) as
is tactically attached to the engine by an external agent as in the case of a usual thermodynamic cycle. We can also rewrite eq. (8) as a function of V by using eq. (2) as

where the plus (minus) sign applies for  (
( ) (the solid curve in fig. 3). This is comparable to the
) (the solid curve in fig. 3). This is comparable to the  diagram of the ideal Stirling thermodynamic cycle [1,2] (the dashed line in fig. 3). An important difference is that the ideal cycle has a square shape with a clear distinction between the temperature-changing process and the volume-changing process whose temperature modulation is a periodic square-shaped function of θ. However, the
diagram of the ideal Stirling thermodynamic cycle [1,2] (the dashed line in fig. 3). An important difference is that the ideal cycle has a square shape with a clear distinction between the temperature-changing process and the volume-changing process whose temperature modulation is a periodic square-shaped function of θ. However, the  diagram of the present kinematic engine has a circular shape, as in eq. (9), whose temperature modulation is the sinusoidal-shaped function of θ as in eq. (8), which loosely approximates the ideal cycle and is better suited for a practical engine. We note that essentially the same idea of a state-dependent thermal contact of this kind was adopted in earlier studies on different autonomous heat engines [8–10].
diagram of the present kinematic engine has a circular shape, as in eq. (9), whose temperature modulation is the sinusoidal-shaped function of θ as in eq. (8), which loosely approximates the ideal cycle and is better suited for a practical engine. We note that essentially the same idea of a state-dependent thermal contact of this kind was adopted in earlier studies on different autonomous heat engines [8–10].
Fig. 3:  diagram of the kinematic Stirling heat engine in eq. (9) (solid curve), where
diagram of the kinematic Stirling heat engine in eq. (9) (solid curve), where  for
for  (
( ) and
) and  (
( ) for
) for  (
( ). The dashed line indicates the
). The dashed line indicates the  diagram of the ideal Stirling thermodynamic cycle consisting of (i') → (ii') constant-volume heating process
diagram of the ideal Stirling thermodynamic cycle consisting of (i') → (ii') constant-volume heating process  at
at  , (ii') → (iii') isothermal expansion process
, (ii') → (iii') isothermal expansion process  at
at  , (iii') → (iv') constant-volume cooling process (
, (iii') → (iv') constant-volume cooling process ( at
at  ), and (iv') → (i') isothermal compression process
), and (iv') → (i') isothermal compression process  at
at  .
.
Download figure:
Standard imageFor convenience, we nondimensionalize our coupled equations (1) and (3). We define the following nondimensionalized quantities as  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , and
, and  is a nondimensionalized temperature difference between the heat reservoirs that will serve as a bifurcation parameter. By defining
is a nondimensionalized temperature difference between the heat reservoirs that will serve as a bifurcation parameter. By defining  as a nondimensionalized quantity of the angular velocity
as a nondimensionalized quantity of the angular velocity  , we can obtain the nondimensionalized dynamical equations corresponding to eqs. (1) and (3) as
, we can obtain the nondimensionalized dynamical equations corresponding to eqs. (1) and (3) as



where  and
and  .
.
For simplicity, we make the assumption of a time-scale separation between θ and  as slow variables and
as slow variables and  as a fast variable. Under this assumption,
as a fast variable. Under this assumption,  in eq. (12) starting from an initial value at an initial time quickly relaxes to an adiabatic solution
in eq. (12) starting from an initial value at an initial time quickly relaxes to an adiabatic solution  determined by the slow variables, which is obtained by solving
determined by the slow variables, which is obtained by solving  in eq. (12):
in eq. (12):

By substituting eq. (13) into eq. (11), we can eliminate  from eq. (11) (adiabatic elimination [11]) and obtain the simple dynamical equations closed by the slow variables instead of eqs. (10)–(12) as follows:
from eq. (11) (adiabatic elimination [11]) and obtain the simple dynamical equations closed by the slow variables instead of eqs. (10)–(12) as follows:


where

With eqs. (14) and (15), we can consider the dynamics of our engine on the phase plane  as a dynamical system. This model with eqs. (14) and (15) may be regarded as a certain type of a driven nonlinear pendulum [12] that is motive-powered by a temperature difference.
as a dynamical system. This model with eqs. (14) and (15) may be regarded as a certain type of a driven nonlinear pendulum [12] that is motive-powered by a temperature difference.
Numerical calculations
We perform numerical calculations of eqs. (10)–(12) and eqs. (14) and (15). We choose the parameters in the equations by assuming actual palm-sized LTD Stirling heat engines, some of which have been determined by referring to [3,5]: we set f = 3,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , and
, and  . These parameters yield the nondimensionalized parameters in the equations as
. These parameters yield the nondimensionalized parameters in the equations as  ,
,  ,
,  , and
, and  . Because an estimation of Γ is difficult, here we simply choose
. Because an estimation of Γ is difficult, here we simply choose  as an adjusted value that makes the rotational speed of the engine to be approximately dozens to hundreds of revolutions per minute (rpm) on average, as observed in actual LTD Stirling heat engines [3]. We use the 4th Runge-Kutta method with time interval
as an adjusted value that makes the rotational speed of the engine to be approximately dozens to hundreds of revolutions per minute (rpm) on average, as observed in actual LTD Stirling heat engines [3]. We use the 4th Runge-Kutta method with time interval  in the numerical calculations. Hereafter, we denote by a quantity with
in the numerical calculations. Hereafter, we denote by a quantity with  a long-time averaged one.
a long-time averaged one.
In fig. 4, we show the dynamics of  obtained as the solution of eqs. (10)–(12) before the adiabatic elimination for
obtained as the solution of eqs. (10)–(12) before the adiabatic elimination for  with the initial condition
with the initial condition  at
at  . We also show
. We also show  in eq. (13) calculated using the solution of eqs. (14) and (15) after the adiabatic elimination with the initial condition
in eq. (13) calculated using the solution of eqs. (14) and (15) after the adiabatic elimination with the initial condition  at
at  . We can see that
. We can see that  quickly relaxes to the adiabatic solution eq. (13) as expected, validating our approximation to use eqs. (14) and (15) instead of eqs. (10)–(12).
quickly relaxes to the adiabatic solution eq. (13) as expected, validating our approximation to use eqs. (14) and (15) instead of eqs. (10)–(12).
Fig. 4: Comparison between the dynamics of  obtained as the solution of eqs. (10)–(12) before the adiabatic elimination and
obtained as the solution of eqs. (10)–(12) before the adiabatic elimination and  in eq. (13) calculated using the solution of eqs. (14) and (15) after the adiabatic elimination for
in eq. (13) calculated using the solution of eqs. (14) and (15) after the adiabatic elimination for  . The initial conditions at
. The initial conditions at  are
are  and
and  , respectively, and
, respectively, and  .
.
Download figure:
Standard imageIn fig. 5, we show  obtained by solving eqs. (14) and (15) as a function of the bifurcation parameter
obtained by solving eqs. (14) and (15) as a function of the bifurcation parameter  . The two attractors —the stable limit cycle and the stable fixed point— correspond to the rotational state with
. The two attractors —the stable limit cycle and the stable fixed point— correspond to the rotational state with  and the stationary state with
and the stationary state with  , respectively. These states coexist for the sufficiently large
, respectively. These states coexist for the sufficiently large  , while for the too-small
, while for the too-small  , the rotational state does not exist. The two bifurcation points where the stable limit cycle disappears are
, the rotational state does not exist. The two bifurcation points where the stable limit cycle disappears are  and
and  . The diagram is not symmetric as
. The diagram is not symmetric as  because eqs. (14) and (15) are not invariant under the transformation
because eqs. (14) and (15) are not invariant under the transformation  ,
,  and
and  . For
. For  , the engine rotates clockwise while for
, the engine rotates clockwise while for  , it rotates counterclockwise, reproducing the actual feature of the engine [3]. While the basin structure yielding the stable limit cycle may be complicated, the initial angular velocities with the sufficiently large magnitude in the expected rotational direction of the engine depending on the sign of
, it rotates counterclockwise, reproducing the actual feature of the engine [3]. While the basin structure yielding the stable limit cycle may be complicated, the initial angular velocities with the sufficiently large magnitude in the expected rotational direction of the engine depending on the sign of  always lead to the rotational states without reaching the stationary states.
always lead to the rotational states without reaching the stationary states.
Download figure:
Standard imageFixed-point analysis
As a preparation to explain the bifurcations in fig. 5, we investigate fixed points  of eqs. (14) and (15). There are four total fixed points at most.
of eqs. (14) and (15). There are four total fixed points at most.
The first two fixed points are the stationary solutions  and
and  obtained from
obtained from  in eq. (15), where
in eq. (15), where  's are TDC and BDC. From the linearized equation around
's are TDC and BDC. From the linearized equation around  , we obtain the eigenvalue
, we obtain the eigenvalue  in a form using the determinant
in a form using the determinant  and the trace
and the trace  of the linearized matrix [12], which are given by
of the linearized matrix [12], which are given by


We note that  and
and  always exist for any parameter.
always exist for any parameter.
The other two fixed points represent the stationary solutions  and
and  obtained from the pressure equilibrium
obtained from the pressure equilibrium  in eq. (15). These solutions may not exist depending on the parameters. Because it is difficult to obtain
in eq. (15). These solutions may not exist depending on the parameters. Because it is difficult to obtain  and
and  analytically, we obtain their
analytically, we obtain their  dependence numerically with the other parameters being fixed in fig. 6. The determinant and the trace of the linearized matrix around
dependence numerically with the other parameters being fixed in fig. 6. The determinant and the trace of the linearized matrix around  (
( ) are given by
) are given by


respectively. By using the data of  obtained in fig. 6, we can determine the
obtained in fig. 6, we can determine the  dependence of
dependence of  and
and  (data not shown). We can then classify the type of
(data not shown). We can then classify the type of  and
and  together with that of
together with that of  and
and  as follows (see also fig. 6) [12]. For
as follows (see also fig. 6) [12]. For  ,
,  and
and  do not exist because there does not exist any solution satisfying the pressure equilibrium, while
do not exist because there does not exist any solution satisfying the pressure equilibrium, while  and
and  are a stable spiral point and a saddle point, respectively, as confirmed from
are a stable spiral point and a saddle point, respectively, as confirmed from  ,
,  and
and  for
for  and
and  for
for  . As
. As  increases,
increases,  and
and  appear via a saddle node bifurcation at
appear via a saddle node bifurcation at  (
( ) ((SN) in fig. 6).
) ((SN) in fig. 6).  , the stable node, immediately changes to the stable spiral point at
, the stable node, immediately changes to the stable spiral point at  satisfying
satisfying  . As
. As  further increases,
further increases,  , the stable spiral point, changes to the stable node at
, the stable spiral point, changes to the stable node at  obtained from
obtained from  . At
. At  obtained from
obtained from  ,
,  agrees with 0 (TDC, identified with
agrees with 0 (TDC, identified with  ) and
) and  and
and  change to the stable node and the saddle point, respectively, switching their stabilities via a transcritical bifurcation
change to the stable node and the saddle point, respectively, switching their stabilities via a transcritical bifurcation  ((T1) in fig. 6). As
((T1) in fig. 6). As  increases from this point,
increases from this point,  immediately changes from the stable node to the stable spiral point. As
immediately changes from the stable node to the stable spiral point. As  further increases,
further increases,  changes from the stable spiral point to the stable node once again before achieving the condition
changes from the stable spiral point to the stable node once again before achieving the condition  obtained from
obtained from  . At this
. At this  ,
,  agrees with π (BDC) and
agrees with π (BDC) and  and
and  change to the saddle point and the stable node, respectively, switching their stabilities via a transcritical bifurcation
change to the saddle point and the stable node, respectively, switching their stabilities via a transcritical bifurcation  ((T2) in fig. 6).
((T2) in fig. 6).
Fig. 6:  -dependence of
-dependence of  obtained as solutions of the pressure equilibrium
obtained as solutions of the pressure equilibrium  in eq. (15) shown together with
in eq. (15) shown together with  . The solid (dashed) lines and curves indicate that
. The solid (dashed) lines and curves indicate that  is stable (unstable).
is stable (unstable).
Download figure:
Standard imageAs understood from this analysis, at least one stable fixed point always exists, which explains the stationary state with  in fig. 5.
in fig. 5.
Homoclinic bifurcation
We show that the disappearance of the stable limit cycle at  and
and  in fig. 5 occurs via a homoclinic bifurcation as a global bifurcation [12,13], where the saddle point
in fig. 5 occurs via a homoclinic bifurcation as a global bifurcation [12,13], where the saddle point  plays an essential role in this bifurcation.
plays an essential role in this bifurcation.
In fig. 7(a) and (b), the stable spiral point  and saddle point
and saddle point  are shown on the phase plane for
are shown on the phase plane for  and
and  before and after the bifurcation at
before and after the bifurcation at  in fig. 5.
in fig. 5.  and
and  do not exist in these
do not exist in these  's as seen from fig. 6. The stable and the unstable manifolds
's as seen from fig. 6. The stable and the unstable manifolds  and
and  of
of  and the stable limit-cycle orbit with
and the stable limit-cycle orbit with  are also shown on the phase plane. Here,
are also shown on the phase plane. Here,  (
( ) of
) of  is defined as the set of initial values of
is defined as the set of initial values of  satisfying
satisfying  (
( ) [12]. The bifurcation scenario is then described as follows [12]. In fig. 7(a), we can see that the branch of
) [12]. The bifurcation scenario is then described as follows [12]. In fig. 7(a), we can see that the branch of  labeled U (the dashed curve) converges to the stable limit-cycle orbit (the bold curve) as
labeled U (the dashed curve) converges to the stable limit-cycle orbit (the bold curve) as  . As
. As  decreases, these two orbits come close to each other. Finally, at
decreases, these two orbits come close to each other. Finally, at  , the limit-cycle orbit touches the saddle point
, the limit-cycle orbit touches the saddle point  , forming a homoclinic orbit connecting
, forming a homoclinic orbit connecting  to itself in an infinite period. At the same time, the limit-cycle orbit disappears. As
to itself in an infinite period. At the same time, the limit-cycle orbit disappears. As  further decreases, U becomes a heteroclinic orbit connecting
further decreases, U becomes a heteroclinic orbit connecting  and
and  . The same scenario applies for the disappearance of the stable limit-cycle orbit with
. The same scenario applies for the disappearance of the stable limit-cycle orbit with  at
at  in fig. 5. Compare the behavior of U for
in fig. 5. Compare the behavior of U for  and
and  before and after the bifurcation in fig. 7(c) and (d).
before and after the bifurcation in fig. 7(c) and (d).
Fig. 7: The stable spiral point  , the saddle point
, the saddle point  , the stable and the unstable manifolds
, the stable and the unstable manifolds  and
and  of
of  , and the stable limit-cycle orbit shown on the phase plane for (a)
, and the stable limit-cycle orbit shown on the phase plane for (a)  , (b)
, (b)  , (c)
, (c)  , and (d)
, and (d)  .
.
Download figure:
Standard imageThis bifurcation is physically understood as follows [12]. As  decreases, it becomes increasingly difficult for the crank to sustain the rotational motion by overcoming BDC against the frictional torque even with the aid of the moment of inertia. At the critical value, the crank with vanishingly small speed at BDC takes an infinitely long time to pass and then return to it, which corresponds to the formation of the homoclinic orbit. The crank can no longer sustain the rotational motion for the smaller
decreases, it becomes increasingly difficult for the crank to sustain the rotational motion by overcoming BDC against the frictional torque even with the aid of the moment of inertia. At the critical value, the crank with vanishingly small speed at BDC takes an infinitely long time to pass and then return to it, which corresponds to the formation of the homoclinic orbit. The crank can no longer sustain the rotational motion for the smaller  .
.
Discussion
Our model captures the qualitative features of actual LTD kinematic Stirling heat engines and predicts the homoclinic bifurcation. Accordingly, a comparison with experiments must be important to confirm the validity of the model. The bifurcation points  and
and  in fig. 5 correspond to
in fig. 5 correspond to  and
and  in the original parameters. These values less than
in the original parameters. These values less than  may be comparable to measured values at which the actual engines including the N-92 type begin rotating [3]. The model thus reproduces the actual engine behavior quantitatively to some extent, as well as qualitatively. However, it seems that experiments that aim to investigate a type of a bifurcation in LTD kinematic engines have not yet been conducted. Because our bifurcation scenario is a mathematically natural consequence of the physically sound model, it is important to verify this scenario experimentally. Besides, experimental evaluations of the extent to which this minimal model oversimplifies actual engines will also be important, especially for an appropriate extension of the model.
may be comparable to measured values at which the actual engines including the N-92 type begin rotating [3]. The model thus reproduces the actual engine behavior quantitatively to some extent, as well as qualitatively. However, it seems that experiments that aim to investigate a type of a bifurcation in LTD kinematic engines have not yet been conducted. Because our bifurcation scenario is a mathematically natural consequence of the physically sound model, it is important to verify this scenario experimentally. Besides, experimental evaluations of the extent to which this minimal model oversimplifies actual engines will also be important, especially for an appropriate extension of the model.
Conclusion
We proposed a minimal nonlinear dynamic model of the LTD kinematic Stirling heat engine. By replacing the role of the displacer piston with the state-dependent thermal conductance and eliminating the thermodynamic degree of freedom adiabatically, we derived our dynamical equations that describe the engine as the driven nonlinear pendulum. Our model reproduced the rotational motion of the engine with the expected direction as the stable limit cycle and the stationary state of the engine as the stable fixed point, respectively. We clarified that the stable limit cycle disappears via the homoclinic bifurcations, with the temperature difference being the bifurcation parameter. Some of the topics that we could not discuss in this study, such as an analysis of the performance of the engine, will be reported elsewhere. Although we have considered the simplest case of the kinematic Stirling heat engine, it is of great interest to investigate a bifurcation scenario of a Ringbom engine [5,14] as the other LTD Stirling heat engine [2] based on nonlinear dynamics. Moreover, we may even invent completely new types of LTD heat engines by using nonlinear dynamics as a powerful design and analytical tool. We expect that the present work will contribute to deepening the understanding of the physics of the Stirling heat engine and facilitate the use of Stirling heat engines for the development of sustainable societies.
Acknowledgments
The author is grateful to H. Kori for helpful discussions. This work was supported by JSPS KAKENHI Grant Number 16K17765.