Abstract
Mechanical-energy harvesters based on coiled carbon nanotube yarns are promising materials for sustainable energy generation. In this work, we present a novel mechanism to harvest energy from mechanical fluctuations by using coiled carbon nanotube yarns coated with polyelectrolyte gel. We developed a theory to explain how this new kind of energy harvesting is possible. The gel fills up all space between the coils and expands when the yarn is stretched. This translates into a change in electrical double-layer configuration, hence into a change in electrical potential. This makes it possible to electrochemically convert tensile or torsional mechanical energy into electrical energy. The influence of the yarn surface charge, polyelectrolyte charge density and salt concentration is analyzed, giving directions for optimum process design. We show calculation results for the generated power of a system consisting of two yarns coated with positive and negative polyelectrolyte gel.
Export citation and abstract BibTeX RIS
Corrections were made to this article on 14 March 2018. The year of online publication was amended to 2018.
Introduction
Present-day research to harvest energy by exploiting small amplitude oscillations shows great potential for sustainable generation and recovery of energy [1–3]. Mechanical vibration sources are ubiquitous since every step and action of a living being results in a release of kinetic energy that is partially dissipated. Converting this vibrational energy into electric energy may provide an alternative to batteries or chargers in portable electronic devices [1,4,5]. This conversion can be used for self-powered wireless sensors, structural and human-health monitoring systems, extraction of energy from ocean waves [3] and from wind [6]. Different systems based on induction or piezo-electricity have been proposed in the past years in order to recover this mechanical energy but the generated power is still too low [7]. Furthermore, interesting nanogenerators were also introduced to harvest human energy from walking, breathing, typing and more, utilizing piezo-electricity and triboelectricity [8,9]. Recently, a promising alternative, based on carbon nanotube (CNT) yarns, was developed to convert mechanical energy into electrical energy from both torsional and tensile motion [3]. Kim et al. [3] in their mechanical-energy harvester employed CNT yarns that are so highly twisted that they completely coil. The yarns they tested are dipped in a liquid electrolyte bath or coated with a gel made of 10 wt% polyvinyl alcohol in 0.1 M HCl.
In our work, we propose an alternative version where the coiled CNT yarn is coated with charged polyelectrolyte (PE) gel. The gel fills up all space between the coils and at the gel-yarn surface it expands when the yarn is stretched, translating into a change in electrical double-layer (EDL) configuration. This change brings about a change in electrical potential. Hence, the external mechanical energy input is exploited to create a change in EDL configuration that translates into a different electric potential profile. It has been demonstrated that polymer brushes can reversibly bend cantilevers due to conformational changes of the brush in response to changes in environmental conditions [10,11], while polyelectrolyte gels were recently used to convert chemical into electrical energy [12], and into mechanical energy [13]. Inspired by these promising recent studies, we theoretically investigated the possibility to use polymer gels to convert external mechanical oscillations into electrical energy. For a more complete and clear picture of our system, it is useful first to describe the model of the PE gel, coated on the coiled twisted yarn (fig. 1). We can think of the PE gel as a charged polymer network with positive or negative charges fixed on its chains, and free counterions (and co-ions) localized in the network. PE gels are able to absorb a significant amount (up to ∼2000 times the polymer weight) of water within its network structure [14], but do not dissolve in water [15]. A PE gel is characterized by a molar concentration of fixed charges, that we define as X. The yarn surface charge as well as the gel fixed charge density are responsible for the salt ions distribution in the EDL, hence for the profile in the dimensionless potential, that we call y, see fig. 1. As depicted in fig. 1, it is possible that the potential, y (relative to bulk solution) can flip sign. For a positively charged gel, we can then have an excess of cations at the yarn surface, even though in the gel bulk phase we mainly have free anions. One may think that, because the gel volume will remain constant during stretching, the fixed charge concentration X will not change. This is indeed correct in the bulk of the gel (away from any surface). However, it is likely that directly at any (yarn) surface, stretching a gel can lead to a lowering of X, because the polymer chains are at some points connected to the yarn, and because the gel has to follow the contours of the yarn. Thus, even though a gel bulk may not be diluted upon stretching, near the surface, the polymer fixed charge X can be expected to go down.
Fig. 1: (Colour online) The carbon yarn is coated with a positively charged polyelectrolyte gel which holds free ions. The carbon yarn surface and the gel fixed charge density are responsible for the free ions distribution in the EDL, hence for the profile of the dimensionless potential, y, from the gel-yarn interface into the gel bulk. In this case it is possible that while the gel bulk mainly holds anions, right near the surface there is an excess of cations.
Download figure:
Standard imageTheory
In this section, we explain EDL theory of a charged surface coated with a polyelectrolyte gel. In a later section the model of energy harvesting from a system containing two electrodes made of carbon nanotube yarns in a coiled configuration is presented. We start the derivation describing the equilibrium EDL profile for potential and ion concentration near a charged surface covered with a polyelectrolyte charged gel. Since the EDL around the yarn is thin, we can use the one-dimensional planar form of the Poisson equation

where Ψ is the electric potential, x is the direction perpendicular to the gel-yarn interface, ε is the absolute permittivity, and  is the local electric charge density. We define the dimensionless potential, y, as
is the local electric charge density. We define the dimensionless potential, y, as

where F is Faraday's constant, R is the gas constant and T is the temperature. At chemical equilibrium, for the EDL in a charged gel, the local electric charge density is given by

where ω is the sign of the fixed membrane charge (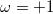 for positive charges and
for positive charges and 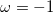 for negative ones). Equation (2) was obtained for a monovalent salt, with bulk concentration (outside the gel)
for negative ones). Equation (2) was obtained for a monovalent salt, with bulk concentration (outside the gel)  , in mol/m3.
, in mol/m3.
Combining eqs. (1)–(3), we obtain the modified Poisson-Boltzmann equation,

Multiplying each side of eq. (4) by 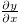 , we obtain
, we obtain

which, with boundary conditions 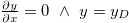 for
for  ,
, 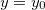 for x = 0, can be integrated to the modified Gouy-Chapman equation
for x = 0, can be integrated to the modified Gouy-Chapman equation

where 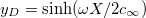 is the Donnan potential, which is the potential in the gel far from the EDL at the yarn surface relative to that in free electrolyte outside the gel [16,17]. Equation (6) is also given in ref. [18] but the boundary condition far away from the surface is given as
is the Donnan potential, which is the potential in the gel far from the EDL at the yarn surface relative to that in free electrolyte outside the gel [16,17]. Equation (6) is also given in ref. [18] but the boundary condition far away from the surface is given as 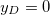 . Equation (6) is similar to eq. (13) in ref. [19], which assumes the presence of only counterions, an equation which was earlier presented in ref. [20]. Note that this equation for the counterions-only case cannot predict the change in sign in potential as depicted in fig. 1, but our equation (6) can. We also define y0 as the dimensionless potential at the start of the diffuse layer. For X = 0, eq. (6) simplifies to the classical Gouy-Chapman equation for a charged surface in contact with an electrolyte.
. Equation (6) is similar to eq. (13) in ref. [19], which assumes the presence of only counterions, an equation which was earlier presented in ref. [20]. Note that this equation for the counterions-only case cannot predict the change in sign in potential as depicted in fig. 1, but our equation (6) can. We also define y0 as the dimensionless potential at the start of the diffuse layer. For X = 0, eq. (6) simplifies to the classical Gouy-Chapman equation for a charged surface in contact with an electrolyte.
Making use of Gauss' law

where Σ is the yarn surface charge in C/m2, it is possible to obtain

which we rewrite as

where 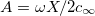 ,
, 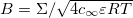 and
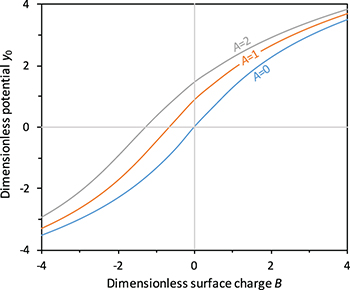
and  . We can think of A as a dimensionless gel fixed charge density and B as a dimensionless yarn surface charge. These parameters will be shown to have a significant influence on system performance. Furthermore, by looking at fig. 2 it is possible to understand what are the effects of the two parameters A and B on the dimensionless potential at the yarn surface. Increasing the yarn surface charge, represented by B, leads to an increase in surface potential. For A = 0, hence for a gel with no fixed charges, the surface potential equals the potential in the salt solution bulk (hence it is zero) when B = 0. Increasing the value of A, the value of B at which the surface potential is zero, shifts towards negative values. Starting from that point, the potential at the surface is positive for higher values of B and negative for lower values of B. Hence, A and B signs and values are of fundamental importance to describe the structure of the EDL near a PE-coated yarn.
. We can think of A as a dimensionless gel fixed charge density and B as a dimensionless yarn surface charge. These parameters will be shown to have a significant influence on system performance. Furthermore, by looking at fig. 2 it is possible to understand what are the effects of the two parameters A and B on the dimensionless potential at the yarn surface. Increasing the yarn surface charge, represented by B, leads to an increase in surface potential. For A = 0, hence for a gel with no fixed charges, the surface potential equals the potential in the salt solution bulk (hence it is zero) when B = 0. Increasing the value of A, the value of B at which the surface potential is zero, shifts towards negative values. Starting from that point, the potential at the surface is positive for higher values of B and negative for lower values of B. Hence, A and B signs and values are of fundamental importance to describe the structure of the EDL near a PE-coated yarn.
Fig. 2: (Colour online) Dimensionless potential at the yarn surface, y0, as a function of the dimensionless yarn surface charge, B, for different values of the dimensionless gel fixed charge density, A.
Download figure:
Standard imageIt is also interesting for our purpose to define a novel parameter γ, which is a measure of the change of electrical energy upon expanding the gel, while the surface charge B is constant, given by

The parameter γ allows us to identify, for a given value of A, the optimal value of B. Taking the derivative of eq. (9) with respect to the variable A,

our γ can be easily obtained as

To better understand the influence of A and B on γ, it useful to consider the iso-lines for γ (fig. 3). These iso-lines were obtained by numerically solving eq. (9) for a chosen range of A and B, and then using the output values, y0 and yD, to calculate γ using eq. (12).
Fig. 3: (Colour online) Iso-lines of the dimensionless sensitivity, γ, as a function of the dimensionless gel fixed charge density, A, and the dimensionless yarn surface charge, B.
Download figure:
Standard imageFigure 3 is used in the next section, in order to identify the optimal values of fixed gel charge density, salt concentration and yarn surface charge. Given that A cannot be increased indefinitely (in our case study we use a value of A = 50 which we think could not easily be made higher in practice), it is possible to observe that the highest value of γ can be achieved for a certain optimal value of B. Notice that γ is dimensionless, and must be multiplied by 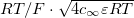 to obtain an energy sensitivity with unit J/m2.
to obtain an energy sensitivity with unit J/m2.
Results and discussion
It is possible to build a system in which two coated coiled yarns, one with positive fixed charges and one with negative charges, are dipped in a salt solution of given concentration 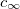 , to produce energy, see fig. 4(a). In order to reach this objective an external load is placed into the system (fig. 4(b)). The external load, REXT, is taken as a free parameter in our calculations in fig. 5 and fig. 6, while in fig. 7 results are shown as a function of REXT. The value of REXT gives some information about the external device that captures the energy, e.g., a battery or other storage system, or direct use in an appliance. Furthermore, an external capacitor is also placed in the circuit in order to charge the yarn surface, similar to the external battery used in the dynamic circuit for harvesting energy from water salinity differences [21]. During a working cycle, we assume that each coiled yarn is stretched with the same frequency, that we define as β. For this reason the polymer fixed charge density X oscillates with the same frequency β, which we describe by
, to produce energy, see fig. 4(a). In order to reach this objective an external load is placed into the system (fig. 4(b)). The external load, REXT, is taken as a free parameter in our calculations in fig. 5 and fig. 6, while in fig. 7 results are shown as a function of REXT. The value of REXT gives some information about the external device that captures the energy, e.g., a battery or other storage system, or direct use in an appliance. Furthermore, an external capacitor is also placed in the circuit in order to charge the yarn surface, similar to the external battery used in the dynamic circuit for harvesting energy from water salinity differences [21]. During a working cycle, we assume that each coiled yarn is stretched with the same frequency, that we define as β. For this reason the polymer fixed charge density X oscillates with the same frequency β, which we describe by

where X0 is the fixed charge density of both gels at t = 0, when the yarn is in its equilibrium position, while 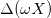 is the maximum variation in gel charge density during the cycle.
is the maximum variation in gel charge density during the cycle.
Fig. 4: (Colour online) (a) Schematic picture of an electrochemical cell consisting of two yarns coated with positive and negative polyelectrolyte gel. (b) Electrical circuit diagram of the same system, indicating also the salt solution with resistance RINT in which the two yarns are dipped, the load to harvest energy, and the external capacitor.
Download figure:
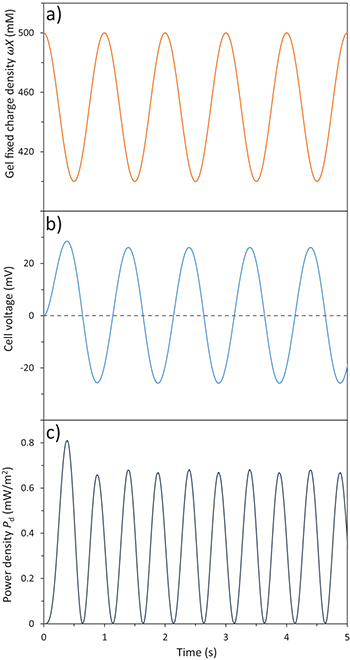
Standard imageFig. 5: (Colour online) (a) Gel fixed charge density  (mM), (b) cell voltage, Vcell (mV), and (c) power density Pd (mW/m2) as a function of time (s) for our case study.
(mM), (b) cell voltage, Vcell (mV), and (c) power density Pd (mW/m2) as a function of time (s) for our case study.
Download figure:
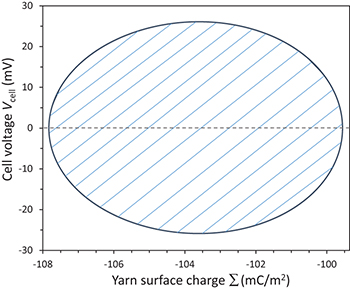
Standard imageFig. 6: (Colour online) Cell voltage, Vcell, in mV, as a function of the yarn surface charge Σ (mC/m2) during the limit cycle for our case study. The area enclosed in the diagram equals the energy harvested in one cycle.
Download figure:
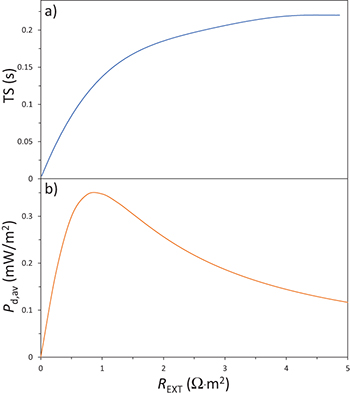
Standard imageFig. 7: (Colour online) (a) Time shift, TS, and (b) average power density, Pd,av, vs. external resistance, REXT, for our case study.
Download figure:
Standard imageFor the system described above, it is possible to write Kirchhoff's voltage law as

where 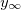 (assumed as reference, hence zero) is the dimensionless potential in the solution bulk, while Vcell, VEC and VINT are the cell voltage, the voltage across the external capacitor and across the ionic solution. Equation (14) is based on two perfectly symmetric gel electrodes (with only the fixed charge density of opposite sign), and y0 used in eq. (14) is evaluated in one of the electrodes. Assuming Ohmic behavior for the external load, and for the ionic transport in the gel and solution, we have
(assumed as reference, hence zero) is the dimensionless potential in the solution bulk, while Vcell, VEC and VINT are the cell voltage, the voltage across the external capacitor and across the ionic solution. Equation (14) is based on two perfectly symmetric gel electrodes (with only the fixed charge density of opposite sign), and y0 used in eq. (14) is evaluated in one of the electrodes. Assuming Ohmic behavior for the external load, and for the ionic transport in the gel and solution, we have

where I is the current density (A/m2), while REXT and RINT are respectively the external load, and the internal resistance in the gel and solution, in 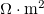 .
.
The current density, I, relates to the surface charge, Σ, by

Combining the above equations, it is possible to obtain the unknown variables of our system. Thus, it is possible to calculate the electrical power generated per unit area, Pd, by

Now we can proceed with the analysis of a cycle in which the two coiled NC yarns are stretched with a certain frequency β in order to produce energy. Before starting, some parameters values characterizing our system must be given: 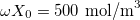 ,
, 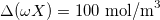 ,
, 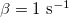 ,
, 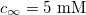 ,
, 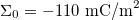 ,
,  ,
, 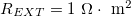 where
where 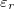 is the medium's relative permittivity. In our case study, we set RINT to zero. At time zero, for the given value of A, reading from the graph (fig. 3) and maximizing γ, the B value, hence the initial surface charge density,
is the medium's relative permittivity. In our case study, we set RINT to zero. At time zero, for the given value of A, reading from the graph (fig. 3) and maximizing γ, the B value, hence the initial surface charge density,  , was obtained. A value for VEC by using eq. (14), with the condition I = 0 at t = 0, was then calculated (
, was obtained. A value for VEC by using eq. (14), with the condition I = 0 at t = 0, was then calculated ( ). Optimal conditions for γ, as can be identified in fig. 3, are obtained when A is positive and B is negative. This situation is represented in fig. 1, where we observe a flip in the sign of the potential, y, from yD > 0 far away from the yarn surface to y0 < 0 at that surface. In particular, we can distinguish two regions, one near the yarn surface rich in cations and one away from the surface that is rich in anions. The optimum sensitivity is found when B and A have opposite sign.
). Optimal conditions for γ, as can be identified in fig. 3, are obtained when A is positive and B is negative. This situation is represented in fig. 1, where we observe a flip in the sign of the potential, y, from yD > 0 far away from the yarn surface to y0 < 0 at that surface. In particular, we can distinguish two regions, one near the yarn surface rich in cations and one away from the surface that is rich in anions. The optimum sensitivity is found when B and A have opposite sign.
In fig. 5(a), we show the trend of 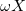 vs. time. One notices that every minimum in
vs. time. One notices that every minimum in 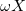 corresponds to the instant in which the maximum stretch of the gel, that we defined as
corresponds to the instant in which the maximum stretch of the gel, that we defined as 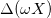 , is reached. It is possible to notice that a similar oscillating trend with respect to time is present in the cell voltage, Vcell, and generated power, Pd, see fig. 5(b) and fig. 5(c). Instead of plotting voltage Vcell vs. time, we can also plot cell voltage vs. charge Σ, as shown in fig. 6. The area enclosed by the ellipse shown represents the energy density in μJ/m2 obtained during a cycle.
, is reached. It is possible to notice that a similar oscillating trend with respect to time is present in the cell voltage, Vcell, and generated power, Pd, see fig. 5(b) and fig. 5(c). Instead of plotting voltage Vcell vs. time, we can also plot cell voltage vs. charge Σ, as shown in fig. 6. The area enclosed by the ellipse shown represents the energy density in μJ/m2 obtained during a cycle.
Finally, we show result as a function of the external load, REXT, and present in fig. 7 results for the average generated power Pd,av and the time shift, TS. Indeed, if we compare fig. 5(b) and fig. 5(c) with fig. 5(a), we can observe that the moments when 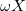 is not changing, do not coincide with the moments when the cell voltage and power density are zero. Instead, a time shift occurs and its value depends on the value of REXT as shown in fig. 7(a).
is not changing, do not coincide with the moments when the cell voltage and power density are zero. Instead, a time shift occurs and its value depends on the value of REXT as shown in fig. 7(a).
With increasing REXT, the time shift, TS, increases until a value of 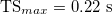 is reached, where it is possible to notice a plateau. The trend of cycle-averaged power density, Pd,av, with respect to the external resistance REXT is shown in fig. 7(b). We observe that a maximum for Pd,av is obtained for
is reached, where it is possible to notice a plateau. The trend of cycle-averaged power density, Pd,av, with respect to the external resistance REXT is shown in fig. 7(b). We observe that a maximum for Pd,av is obtained for 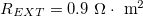 . This represents the optimal condition for power generation.
. This represents the optimal condition for power generation.
If we assume a yarn having a 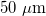 diameter, constituted of 5.0 nm diameter close-packed nanotubes with 24 kg/m3 of bulk density [22], we obtain a yarn surface area of 4.4 m2/g. Hence, we can calculate the achievable average power, that amounts to ∼770 mW/kg of yarn. This value is similar to the values obtained by Kim et al. in their experiments where yarns are stretched by ocean waves [3].
diameter, constituted of 5.0 nm diameter close-packed nanotubes with 24 kg/m3 of bulk density [22], we obtain a yarn surface area of 4.4 m2/g. Hence, we can calculate the achievable average power, that amounts to ∼770 mW/kg of yarn. This value is similar to the values obtained by Kim et al. in their experiments where yarns are stretched by ocean waves [3].
Conclusions
Motivated by recent experimental work on energy harvesting using coiled nanocarbon twisted yarns [3], we have reported a novel mechanism to harvest energy from mechanical oscillations by using coiled carbon nanotube yarns coated with polyelectrolyte gel. We have developed a model for the change in the electrical double-layer structure when a gel, coated on a charged surface, is stretched. Our approach is mathematically simple while it is able to explain the scientific basis behind a hypothetical mechanical-energy harvester made of coiled yarn coated with polyelectrolyte gel. The effects of gel fixed charge density, yarn surface charge, and salt concentration were studied. These results represent a helpful guide for future process improvement and development. The analyzed case study and the calculations performed show the achievable power in a system made of two yarns, where one is coated with a positive polyelectrolyte gel, and the other is coated with a negative gel layer.
Acknowledgments
This work was performed in the cooperation framework of Wetsus, European Centre of Excellence for Sustainable Water Technology (www.wetsus.eu). Wetsus is co-funded by the Dutch Ministry of Economic Affairs and Ministry of Infrastructure and Environment, the Province of Fryslân, and the Northern Netherlands Provinces. The authors would like to thank the participants of the research theme Concentrates for fruitful discussions and financial support.