Abstract
In this paper, we investigate the optical forces exerted on a graphene-coated dielectric particle by the Gaussian beam transmitted through the prism setup systematically. It is shown that the optical force spectra exhibit significant Fano resonance under the excitation of a Gaussian evanescent wave. The magnitude and morphology of Fano resonance can be modulated effectively by the graphene coating. Also, the modification on the threshold of the Fermi energy of graphene could help to regulate the trapping behavior efficiently. The proposed work may provide a new avenue in the specific optical tweezers and nano-optics.
Export citation and abstract BibTeX RIS
Introduction
Optical tweezers have already been an indispensable tool in manipulating microscopic particles since the pioneering work of Ashkin [1]. This non-contact technique is now a useful tool in a variety of applications in physics, biochemistry and medicine etc. Single-beam optical tweezers have been used to trap and manipulate dielectric particles [2], metal nanoparticles [3], nanostructures [4], and even some submicron objects such as viruses [5]. Guiding particles using near-field and evanescent field is also an effective way which allows simultaneous optical manipulation of large numbers of particles [6] Several configurations have been used such as total internal reflection by prism or waveguide [6,7], near-field optical trapping [8] and surface plasmon polariton (SPP) excitation [9]. Also, comprehensive theoretical works for calculating the optical forces exerted on particles immersed in evanescent field have been made [10–13].
Currently, graphene and the two-dimensional Dirac fermions are at the center of a significant research effort [14]. Due to its exceptional optical properties [15,16], graphene has been widely applied in the photonic and optoelectronic fields such as nanoantennas [17], photodetectors [18], optical modulators [19,20] and surface plasmons [21]. Recently, the experimental fabrication of curved and spherical graphene sheets is demonstrated [22,23], which allows its potential applications in the optical tweezers.
Here in this paper, we apply graphene to the conventional optical tweezers by coating the dielectric nanoparticles with graphene layers. Based on our previous work [24], we systematically investigate the optical forces exerted on the graphene-coated particles by a Gaussian evanescent wave. We find that the scattering optical force spectra exhibit significant Fano resonance, whose characteristics are strongly dependent on the properties of graphene coating.
Theoretical description
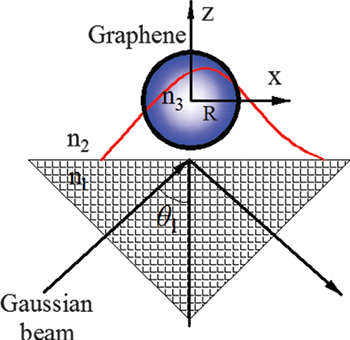
The geometric system we study is illustrated in fig. 1. The origin of the coordinate system coincides with the center of a graphene-coated polystyrene spherical particle with refractive index 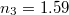 and radius R situated on the interface (the particle touches the interface). The refractive indices of the mediums below and above the interface are
and radius R situated on the interface (the particle touches the interface). The refractive indices of the mediums below and above the interface are  and
and 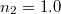 , representing the glass-air interface.
, representing the glass-air interface. 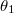 is the incident angle. The red line in the figure is a profile of the evanescent wave through the interface when
is the incident angle. The red line in the figure is a profile of the evanescent wave through the interface when 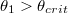 . The center of the Gaussian beam is located at (xc, yc, zc) with waist radius
. The center of the Gaussian beam is located at (xc, yc, zc) with waist radius 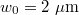 and input power
and input power 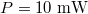 . We take the x-z plane as the incident plane.
. We take the x-z plane as the incident plane.
Fig. 1: (Colour online) A focused Gaussian beam is incident from below with incident angle 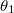 . A graphene-coated polystyrene spherical particle with radius R is situated on the glass-air interface. The red line in the figure is a profile of the evanescent wave through the interface when
. A graphene-coated polystyrene spherical particle with radius R is situated on the glass-air interface. The red line in the figure is a profile of the evanescent wave through the interface when 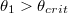 .
.
Download figure:
Standard imageThe theoretical analysis of the optical force exerted on a spherical nanoparticle is done in the framework of the Mie theory and arbitrary beam theory (ABT) [25,26]. The radial part of the electromagnetic fields incident upon a spherical particle can be expanded in the spherical coordinate as follows [25]:
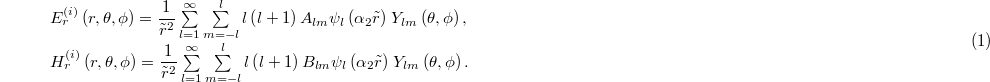
The expansion coefficients Alm and Blm that characterize the incident electric and magnetic fields are

where 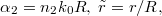 the wave vector
the wave vector 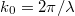 , λ is the incident wavelength, θ and
, λ is the incident wavelength, θ and 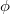 are the polar angle and azimuthal angle, respectively.
are the polar angle and azimuthal angle, respectively. 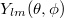 is the spherical harmonics,
is the spherical harmonics, 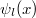 is the Riccati-Bessel function of the first kind.
is the Riccati-Bessel function of the first kind.
The radiation force exerted on a spherical particle illuminated by the electromagnetic wave can be determined through the surface integral of Maxwell's stress tensor enclosing the particle. It is obtained as a series over coefficients Alm, Blm, alm and blm [26], where  and bl are the expansion coefficients for the scattered electromagnetic field by the particle.
and bl are the expansion coefficients for the scattered electromagnetic field by the particle.
Then we derive the expansion coefficients Alm and Blm of the Gaussian evanescent wave in ABT. Using the angular spectrum representation [10], the vector potential A of a perpendicularly polarized Gaussian beam can be expressed as

where the polarization is along the y direction, and the x-z plane is the incident plane  is the Fourier spectrum for the Gaussian beam:
is the Fourier spectrum for the Gaussian beam:

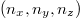 denote the dimensionless projections of the wave vector k along the Cartesian coordinate axes, the phase
denote the dimensionless projections of the wave vector k along the Cartesian coordinate axes, the phase ![$f_{i}({x,y,z})=k_{1} [n_{x}({x-x_{c}})+n_{y} ({y-y_{c}})-n_{z} ({z-z_{c}})],C$](https://content.cld.iop.org/journals/0295-5075/116/2/24006/revision1/epl18220ieqn18.gif) is a normalization factor and the integration is over the domain of
is a normalization factor and the integration is over the domain of 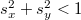 and nz > 0.
and nz > 0. 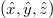 are unit vectors.
are unit vectors.
The electromagnetic fields E and H can be derived from the vector potential A through Maxwell's equations:

here we use the Lorentz gauge condition in the Gaussian system of units. Substituting eqs. (3) and (4) into eq. (5), the electromagnetic fields of the incident Gaussian beam are obtained as


where  and
and 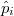 and are the vectors that are perpendicular and parallel to the plane of incidence, respectively. They are defined as
and are the vectors that are perpendicular and parallel to the plane of incidence, respectively. They are defined as

The Fresnel amplitude coefficients of the transmitted wave through the interface for p polarization and s polarization are:

Here ![$\xi =[{1-({{n_{1}}/ {n_{2}}})^{2} (n_{x}^{2}+n_{y}^{2}})]^{1/2}$](https://content.cld.iop.org/journals/0295-5075/116/2/24006/revision1/epl18220ieqn23.gif) . The integral domain is
. The integral domain is 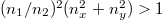 for generating the evanescent wave. Under the paraxial condition, we have
for generating the evanescent wave. Under the paraxial condition, we have 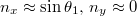 . If
. If 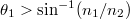 , the parameter ξ will be an imaginary number, the Gaussian evanescent wave is generated above the interface. As a result, the transmitted electromagnetic fields are written as
, the parameter ξ will be an imaginary number, the Gaussian evanescent wave is generated above the interface. As a result, the transmitted electromagnetic fields are written as


where


d is the distance between the particle center and the interface. By substituting the radial transmitted field components 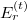 and
and 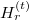 into eq. (2), finishing the integrals about θ and ϕ, the characteristic coefficients Alm and Blm for the Gaussian evanescent field are obtained as
into eq. (2), finishing the integrals about θ and ϕ, the characteristic coefficients Alm and Blm for the Gaussian evanescent field are obtained as


where Ac and Bc are constants:


the functions 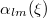 and
and 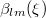 are defined as
are defined as


Then we investigate the scattering of the electromagnetic wave by a graphene-coated dielectric particle. The graphene coating can be considered as a surface current around the spherical dielectric particle. Using the continuous boundary conditions of the particle, the expansion coefficients of the scattered electromagnetic field by the graphene-coated particle are obtained as [24]:


where  . The expansion coefficients of the interior electromagnetic field inside the particle are
. The expansion coefficients of the interior electromagnetic field inside the particle are


The optical conductivity of the graphene layer 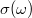 can be derived from the Kubo formula [27–29]. For simplicity, we only consider the low-temperature conditions where the absolute value of the Fermi level Ef of graphene is much larger than kBT. kB is the Boltzmann constant and T is the absolute temperature. Then the optical conductivity
can be derived from the Kubo formula [27–29]. For simplicity, we only consider the low-temperature conditions where the absolute value of the Fermi level Ef of graphene is much larger than kBT. kB is the Boltzmann constant and T is the absolute temperature. Then the optical conductivity 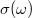 is expressed over the intraband
is expressed over the intraband  and interband
and interband 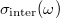 transition contributions:
transition contributions:

where the Drude conductivity describes the intraband processes:

and the interband optical conductivity is

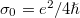 is called the universal conductivity of graphene, e is the electronic charge, ℏ is the reduced Planck constant and
is called the universal conductivity of graphene, e is the electronic charge, ℏ is the reduced Planck constant and 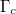 is the damping constant. The optical conductivity is the function of the incident wave frequency, the Fermi level Ef and damping constant
is the damping constant. The optical conductivity is the function of the incident wave frequency, the Fermi level Ef and damping constant 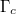 of graphene. The dimensionless surface conductivity
of graphene. The dimensionless surface conductivity  of the particle can be tuned by changing the optical conductivity of graphene
of the particle can be tuned by changing the optical conductivity of graphene 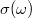 , which has the relationship
, which has the relationship  , where
, where 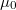 and
and 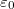 are the permeability and permittivity in vacuum, respectively.
are the permeability and permittivity in vacuum, respectively.
Numerical results
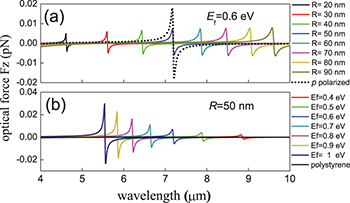
Figure 2 depicts the vertical optical force Fz exerted on a graphene-coated polystyrene particle by a Gaussian evanescent wave as a function of the wavelength: (a) with different particle radius R (Fermi energy is fixed as 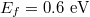 ); (b) with different Fermi energy Ef of the graphene layer (particle radius is fixed as
); (b) with different Fermi energy Ef of the graphene layer (particle radius is fixed as 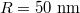 ). It is shown in fig. 2(a) that with the increase of particle size, the corresponding wavelength to Fano resonance increases gradually. For the p-polarized incident wave, whose polarization is in the x-z plane, the vector potential A of Gaussian beam is
). It is shown in fig. 2(a) that with the increase of particle size, the corresponding wavelength to Fano resonance increases gradually. For the p-polarized incident wave, whose polarization is in the x-z plane, the vector potential A of Gaussian beam is

Its corresponding optical force spectra (dotted line) also exhibits significant Fano resonance, the resonant position coincides with that of s polarization, but the magnitude becomes larger. In fig. 2(b), with the Fermi energy Ef increasing (this can be quantified through chemical doping on different level), the corresponding wavelength to Fano resonance decreases subsequently. Furthermore, the magnitude of the Fano resonant optical force is significantly enhanced.
Fig. 2: (Colour online) Vertical optical force spectra Fz of the graphene-coated polystyrene particle exerted by a Gaussian evanescent wave as a function of the wavelength: (a) with different particle size, (b) with different Fermi energy of graphene.
Download figure:
Standard imageThe analysis demonstrates that the intensity of Fano resonance and the excitation wavelength can be modulated to a large extent by tuning the Fermi energy of the graphene coating, which is determined by the chemical doping or the gate voltage. This specific Fano resonance in the scattering force spectra is originated from the excitation of the inhomogeneously distributed evanescent wave. The interference between the individual plasmonic modes of the graphene-coated dielectric particle excited by the evanescent wave generates the significant Fano resonance [30]. Here for the relatively small size particle, the Fano resonance is mainly contributed by the strong interference between the dipolar and quadrupolar modes. The black line in fig. 2(b) illustrates the optical force on a bare polystyrene particle of radius 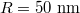 . It shows that no Fano-shaped resonance exists in the infrared wave band, which indicates that the plasmonic behavior is generated by the mutual interaction of polystyrene particle and graphene coating.
. It shows that no Fano-shaped resonance exists in the infrared wave band, which indicates that the plasmonic behavior is generated by the mutual interaction of polystyrene particle and graphene coating.
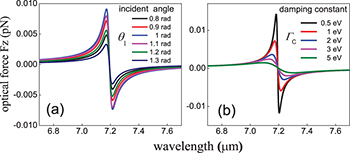
Figure 3 shows the variation of the Fano-shaped optical force spectra Fz with different: (a) incident angle  (larger than the critical angle
(larger than the critical angle 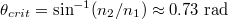 , here
, here 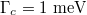 ); (b) damping constant
); (b) damping constant 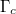 of graphene coating
of graphene coating 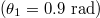 , respectively. Particle size
, respectively. Particle size 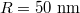 , Fermi energy
, Fermi energy 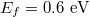 . It is observed in fig. 3(a) that the incident angle plays a limited role on the morphology of the Fano resonance, where the magnitude of Fano resonant optical forces varies slightly with increasing incident angle. While in fig. 3(b) the morphology of the Fano resonance is modulated in a wide range by tuning the damping constant of graphene coating. When the damping constant
. It is observed in fig. 3(a) that the incident angle plays a limited role on the morphology of the Fano resonance, where the magnitude of Fano resonant optical forces varies slightly with increasing incident angle. While in fig. 3(b) the morphology of the Fano resonance is modulated in a wide range by tuning the damping constant of graphene coating. When the damping constant  decreases, the magnitude of Fano resonant optical forces is greatly enhanced. Moreover, the width at half-maximum of the resonant peak is reduced, the shape of the Fano resonance becomes sharper.
decreases, the magnitude of Fano resonant optical forces is greatly enhanced. Moreover, the width at half-maximum of the resonant peak is reduced, the shape of the Fano resonance becomes sharper.
Fig. 3: (Colour online) Vertical optical force spectra Fz of the graphene-coated polystyrene particle exerted by a Gaussian evanescent wave with different: (a) incident angle, (b) damping constant of graphene. 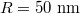 ,
, 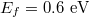 .
.
Download figure:
Standard imageAs we know, the damping constant  characterizes the transport properties of the graphene layer, which is inversely proportional to the momentum relaxation time [29,31]. This means the smaller damping constant, the longer the carrier relaxation time, the lower scattering rate and the higher mobility in graphene. Moreover, the amplitude of the plasmonic resonance would be increased for higher electron mobility, so the enhanced interference excites the sharper Fano resonance.
characterizes the transport properties of the graphene layer, which is inversely proportional to the momentum relaxation time [29,31]. This means the smaller damping constant, the longer the carrier relaxation time, the lower scattering rate and the higher mobility in graphene. Moreover, the amplitude of the plasmonic resonance would be increased for higher electron mobility, so the enhanced interference excites the sharper Fano resonance.
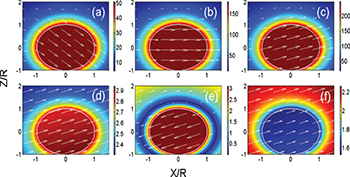
In order to get a deep physical insight into the morphological variations of Fano optical force spectra, we investigate the interactions between the graphene-coated polystyrene particle and the Gaussian evanescent wave. The electric field distributions 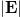 around the particle are shown in fig. 4. Since the dipole mode
around the particle are shown in fig. 4. Since the dipole mode 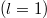 dominates the plasmonic resonance, here we only show the electric field patterns of the dipole mode. The particle radius is 50 nm that corresponds to the resonant wavelength of 7.17 μm. The white arrows denote the Poynting vectors of the energy flow. The unit of the electric field magnitude is statvolt/cm and
dominates the plasmonic resonance, here we only show the electric field patterns of the dipole mode. The particle radius is 50 nm that corresponds to the resonant wavelength of 7.17 μm. The white arrows denote the Poynting vectors of the energy flow. The unit of the electric field magnitude is statvolt/cm and 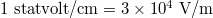 .
.
Fig. 4: (Colour online) Electric field patterns of the dipole mode of the graphene-coated polystyrene particle with different graphene layer properties: (a)–(c) 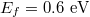 , while (a)
, while (a) 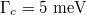 , (b)
, (b) 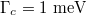 , (c)
, (c) 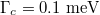 ; (d), (e)
; (d), (e) 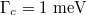 , while (d)
, while (d)  , (e)
, (e) 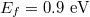 ; (f) bare polystyrene particle.
; (f) bare polystyrene particle. 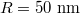 .
.
Download figure:
Standard imageFigures 4(a)–(c) are the electric field patterns at Fano resonance with Fermi energy 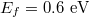 . Here we investigate three damping constant: (a)
. Here we investigate three damping constant: (a) 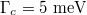 , (b)
, (b) 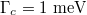 , (c)
, (c) 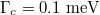 , which correspond to the optical force spectra in fig. 3(b), respectively. It is noticeable that at resonant condition, most energy of the incident evanescent wave is coupled into the particle. The internal field intensity is greatly enhanced that leads to sharp Fano resonant optical force spectrum. Furthermore, when the damping constant
, which correspond to the optical force spectra in fig. 3(b), respectively. It is noticeable that at resonant condition, most energy of the incident evanescent wave is coupled into the particle. The internal field intensity is greatly enhanced that leads to sharp Fano resonant optical force spectrum. Furthermore, when the damping constant 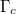 decreases, the internal field intensity increases gradually and the corresponding Fano optical force spectrum becomes sharper, as shown in fig. 3(b). Interestingly, the propagating direction of the evanescent wave around the particle switches upward gradually with
decreases, the internal field intensity increases gradually and the corresponding Fano optical force spectrum becomes sharper, as shown in fig. 3(b). Interestingly, the propagating direction of the evanescent wave around the particle switches upward gradually with 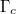 increasing.
increasing.
The electric field distributions in figs. 4(d) and (e) correspond to two off-resonant Fermi energies (d) 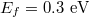 , (e)
, (e) 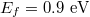 , respectively. Damping constant
, respectively. Damping constant 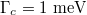 for both cases. It is shown that off the Fano resonance, the intensity of the internal field decays rapidly and the corresponding optical forces decrease accordingly, as already shown in fig. 2(b). Notice that in fig. 4(e) with large Fermi energy
for both cases. It is shown that off the Fano resonance, the intensity of the internal field decays rapidly and the corresponding optical forces decrease accordingly, as already shown in fig. 2(b). Notice that in fig. 4(e) with large Fermi energy 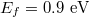 , the arrows of Poynting vectors inside the particle are opposite to the outside ones. The large Fermi energy corresponds to the heavy doping level, which results in a high carrier density and strong interactions of the graphene-coated particle and the evanescent wave [32]. This exhibits a mutual competitive relationship of the internal and external field of the particle. Figure 4(f) is the field distribution of a same-sized bare polystyrene particle for comparison. As we can see, without the graphene coating, little of the evanescent wave couples into the particle, nor the resonance on the optical force spectra occurs.
, the arrows of Poynting vectors inside the particle are opposite to the outside ones. The large Fermi energy corresponds to the heavy doping level, which results in a high carrier density and strong interactions of the graphene-coated particle and the evanescent wave [32]. This exhibits a mutual competitive relationship of the internal and external field of the particle. Figure 4(f) is the field distribution of a same-sized bare polystyrene particle for comparison. As we can see, without the graphene coating, little of the evanescent wave couples into the particle, nor the resonance on the optical force spectra occurs.
Next we investigate the trapping behavior of the graphene-coated dielectric particle, whose optical forces as a function of x-axis displacements along the prism interface with different Fermi energy are: (a) the vertical force Fz, (b) the horizontal force Fx and (c) the transformation of the horizontal force Fx. Particle radius 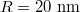 . The incident laser is the helium-neon laser with wavelength
. The incident laser is the helium-neon laser with wavelength 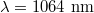 . Firstly in fig. 5(a), the value of the vertical force Fz is negative, this means that the particle experiences a pulling force toward the interface. Fz reaches the maximum around the center of the beam waist, and it always shows a Lorentz shape with the variation of the Fermi energy. Interestingly in fig. 5(b), the trend of the horizontal force Fx with the variation of Fermi energy is not monotonous. It exhibits a bidirectional shape above the specific Fermi energy of about 0.6 eV, while less than this threshold, the horizontal force show a Lorentz shape.
. Firstly in fig. 5(a), the value of the vertical force Fz is negative, this means that the particle experiences a pulling force toward the interface. Fz reaches the maximum around the center of the beam waist, and it always shows a Lorentz shape with the variation of the Fermi energy. Interestingly in fig. 5(b), the trend of the horizontal force Fx with the variation of Fermi energy is not monotonous. It exhibits a bidirectional shape above the specific Fermi energy of about 0.6 eV, while less than this threshold, the horizontal force show a Lorentz shape.
Fig. 5: (Colour online) Optical forces as a function of the x-axis displacements along the interface with different Fermi energy: (a) vertical force Fz, (b) horizontal force Fx and (c) transformation of Fx. 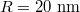 ,
,  .
.
Download figure:
Standard imageThe detailed transformation of the horizontal force is shown in fig. 5(c). As we can see, the transformation arises within a small interval of the Fermi energy, the threshold of the Fermi energy is about 0.584 eV. Below the threshold, the horizontal force shows a Lorentz shape. Then with the Fermi energy increasing, the optical force on the positive x-axis declines gradually, forming the bidirectional distribution eventually. So when the Fermi energy exceeds this threshold, the bidirectional optical force traps the particle at the center of the evanescent wave along the interface. While below this threshold, the particle is always pushed along the way that the evanescent wave propagates.
This interesting phenomenon is induced by the competition of interband and intraband contributions in the optical conductivity of graphene. As illustrated in eqs. (24)–(26), the interband and intraband terms in the optical conductivity vary drastically with the Fermi energy and incident wavelength. At low frequencies, the intraband term (Drude conductivity) significantly exceeds the interband term, while in the high-frequency range the interband term dominates [31,33]. The threshold of the Fermi energy is 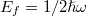 ; for wavelength
; for wavelength  , the threshold is
, the threshold is 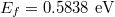 , which is exactly equal to the transformation value in fig. 5(c). As a result, the distinct optical forces on both directions can be modulated effectively by the Fermi energy of graphene coating which is determined by the chemical doping or gate voltage. The investigations may provide a new idea about the oriented manipulation of microscopic particles.
, which is exactly equal to the transformation value in fig. 5(c). As a result, the distinct optical forces on both directions can be modulated effectively by the Fermi energy of graphene coating which is determined by the chemical doping or gate voltage. The investigations may provide a new idea about the oriented manipulation of microscopic particles.
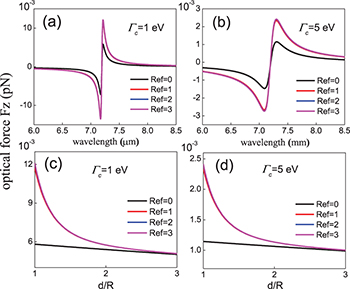
Finally, we investigate the impacts of the multiple scattering of the Gaussian evanescent wave between the graphene-coated polystyrene particle and the interface on the Fano resonant optical forces [34,35]. The calculation results are shown in fig. 6 with damping constant: (a)  , (b)
, (b) 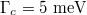 , respectively. Other parameters:
, respectively. Other parameters: 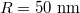 ;
; 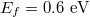 . The black line denotes the optical force without reflection, while the red, blue and magenta lines represent the evanescent wave reflected between the particle and the interface for once, twice and three times, respectively. As we can see, experiencing the multiple reflections, the optical forces could be enhanced over 50% in the center of Fano resonant peaks. Furthermore, the multiple scattering effects are different on the two distinct Fano resonant peaks, which is more significant in the entire region of smoother resonant peak with large damping constant in fig. 6(b). This is because most photons of the evanescent wave are gathered in the resonant regions where the optical force is stronger and the absorptions and dissipations from the reflections between the particle and the interface are more significant in these regions. Overall, after experiencing 3 times the reflections of the evanescent wave, the optical forces converge ultimately. However, the multiple scattering effects fundamentally would not change the dominant characteristics of the Fano resonant optical force spectra.
. The black line denotes the optical force without reflection, while the red, blue and magenta lines represent the evanescent wave reflected between the particle and the interface for once, twice and three times, respectively. As we can see, experiencing the multiple reflections, the optical forces could be enhanced over 50% in the center of Fano resonant peaks. Furthermore, the multiple scattering effects are different on the two distinct Fano resonant peaks, which is more significant in the entire region of smoother resonant peak with large damping constant in fig. 6(b). This is because most photons of the evanescent wave are gathered in the resonant regions where the optical force is stronger and the absorptions and dissipations from the reflections between the particle and the interface are more significant in these regions. Overall, after experiencing 3 times the reflections of the evanescent wave, the optical forces converge ultimately. However, the multiple scattering effects fundamentally would not change the dominant characteristics of the Fano resonant optical force spectra.
Fig. 6: (Colour online) Effects of the multiple scattering of the evanescent wave between the graphene-coated dielectric particle and the interface on the Fano resonant optical force spectra. Damping constant: ((a), (c)) 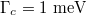 ; ((b), (d))
; ((b), (d)) 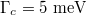 , respectively. (c) and (d) show the variation of the gap distance between the particle and the interface.
, respectively. (c) and (d) show the variation of the gap distance between the particle and the interface. 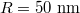 .
. 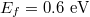 .
.
Download figure:
Standard imageIn figs. 6(c) and (d) we investigate the influence of the gap distance between the particle and the interface on the multiple scattering. Here the wavelength corresponds to the resonance peak in figs. 6(a) and (b), respectively. It is clearly visible that the effects of multiple scattering on the optical force decrease drastically when the gap distance increases. When the gap distance is about 2 particle radius  , the multiple scattering effect basically disappears.
, the multiple scattering effect basically disappears.
Conclusions
In summary, we investigate the optical forces exerted on the graphene-coated dielectric particles by a Gaussian wave through the prism setup systematically. The scattering optical force spectra exhibit strong Fano resonance under the excitation of the evanescent wave. The magnitude and excitation wavelength of the Fano resonance can be tuned by modulating the Fermi energy of graphene coating. The morphology of the Fano resonance can be modified effectively by tuning the damping constant of graphene. Moreover, the threshold of the Fermi energy plays an important role in the particle manipulations. These investigations can find rich potential applications in the optical tweezers and nano-optics.
Acknowledgments
This work was supported by the International S&T Cooperation Program of China (Nos. 2014DFA52000), National Natural Science Foundation of China (Nos. 11574021, 51172009).