Abstract
This letter deals with the transport of particles through granular assemblies and, specifically, with the intermittent formation of blockages originated from collective and purely mechanical clogging of constrictions. We perform numerical experiments with a micro-hydromechanical model that is able to reproduce the complex interplay between the carrier fluid, the transported particles and the granular assembly. The probability distribution functions (PDFs) of the duration of blockages and displacements give the time scale on which the effect of blockages is erased and the advection-dispersion paradigm is valid. Our experiments show that these PDFs fit exponential laws, reinforcing the idea that the formation and destruction of blockages are homogeneous Poisson processes.
Export citation and abstract BibTeX RIS
Introduction
The transport of passive particles in porous media is a widely studied problem with applications in many different contexts [1]. Particle transport is determined by the interaction of particles with each other and with porous medium surfaces. This letter focuses on the transport of solid particles of diameter larger than 5 · 10−5 m which are moderately large in comparison with the constrictions and which interact exclusively via excluded volume repulsion. Other forces, such as those acting between colloidal particles in suspensions, are not considered. These conditions are met, for instance, during the internal erosion of silty or sandy soils. Even when the porous medium and initial boundary conditions (for both the fluid flow and the particle transport) are supposed to be macroscopically homogeneous, the experience has confirmed the presence of preferential fluid and particle flows [2,3]. The reasons behind them not only have to do with local variations in the permeability of the clean porous medium but also with the relocation of transported particles itself. Indeed, in some cases, particles can be temporarily immobilized, adding complexity to their transport. For example, particles may get trapped because they stick at surfaces, crevices, caverns, etc. [4], or because they clog constrictions (individually or collectively).
Anomalous transport processes [5,6] are referred to those cases in which the advection-Fickian dispersion paradigm fails to reproduce the evolution of the concentration of particles in space and time. The complexity of natural porous media [7] may involve multiscale heterogeneities, which are known to be a reason for anomalous transport [8–12], but even in quite homogeneous systems, preferential flow paths may lead to anomalous transport [13,14]. For instance, in random fractured networks subtle features of the steady flow-field distribution through the network are behind time-dependent anomalies [15].
Our objective is to investigate the role played by the intermittent formation of blockages in the constrictions of the porous medium (fig. 1). We want to understand the length and time scales affected by these events and their consequences for particle transport. We focus on purely mechanical clogging: one or several inert particles form an arch in a constriction via mechanical forces that locally block particle flows. The probability of forming an arch in these conditions depends on the size and shape of constrictions and particles, on the friction, and on the number of them passing simultaneously through the constriction. Indeed, sometimes the size of the crowd is known to be more significant than the driving force to explain the ability of a constriction to clog [16], but this ability decreases with the square root of the kinetic energy [17]. Once an arch is formed, other particles can be retained upstream, increasing the blockage. Dynamically changing fuid flows or collisions from other particles can break up the blockage and cause the collapse of the clogging arch. Whether or not these events have implications for particle transport is something strongly related with the statistics of their duration and frequency. Exponential and power laws have been found in other cases of intermittent flow to explain, for example, avalanche sizes during silo discharge [18], burst sizes in escape panic experiments [19], clogging duration in the discharge of granular hoppers under external vibration of low amplitude [20] or time lapses between the passage of consecutive particles through a bottleneck [21]. In our case, if the statistical distributions of waiting and traveling times have finite second moments, on a time scale much longer than the time scale of blockages, the classical advection-dispersion paradigm will be valid to explain the evolution of the concentration of particles. Similarly, on a time scale comparable to that of blockages, the distinction between retained and transported particles together with appropriate mass transfer laws, is required to properly model particle transport. These laws have been often proposed either phenomenologically or after micromechanical approaches (e.g., [4,22–24] for colloids). In contrast to these approaches, we deduce them for the specific case of mechanical clogging due to physical crowding, after a statistical analysis of the frequency and duration of blockages.
Fig. 1: (Colour online) Numerical experiments on particle transport performed with a micro-hydromechanical model. (a) Intermittent formation of blockages in the constrictions (the inset represents the arch formed by three fine frictionless particles that originates a blockage). (b) Sample of time series of particle positions in the main flow direction. Horizontal intervals represent periods during which particles were trapped.
Download figure:
Standard imageIn particular, we study the transport of passive particles in macroscopically homogeneous media. We consider unchangeable granular assemblies and viscous and incompressible fluids that flow through the assemblies due to stationary hydraulic pressure gradients  . Gravity is not included. The fluid flow can be described at the scale of the interstitial space by the Stokes equations (valid at small Reynolds number). For a given flow field the hydraulic tortuosity
. Gravity is not included. The fluid flow can be described at the scale of the interstitial space by the Stokes equations (valid at small Reynolds number). For a given flow field the hydraulic tortuosity  accounts for the effective elongation of fluid paths. Equivalently, on the scale of the granular sample, Darcy's law can be applied to obtain the average fluid flux
accounts for the effective elongation of fluid paths. Equivalently, on the scale of the granular sample, Darcy's law can be applied to obtain the average fluid flux  (discharge per unit area) as
(discharge per unit area) as  , where μ is the dynamic viscosity and κ is the permeability tensor. κ depends on the pores structure, the porosity ϕ (the fraction of the volume of the voids over the total volume) and the constriction size distribution CSD [25]. The fluid velocity in a clean porous medium of permeability
, where μ is the dynamic viscosity and κ is the permeability tensor. κ depends on the pores structure, the porosity ϕ (the fraction of the volume of the voids over the total volume) and the constriction size distribution CSD [25]. The fluid velocity in a clean porous medium of permeability  is
is 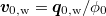 .
.
The introduction of fine particles in the voids of the structure results in a new granular assembly of longer and thinner tortuous passages of varying cross-sections. The permeability is reduced since 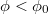 and the constrictions are smaller, too. If fine particles are not attached to the granular assembly, the Stokes flow is able to convey them through the porous medium via pressure and viscous forces. When transported particles are of size comparable to that of pores, the relative motion between them and the carrier fluid is very significant. Moreover, the average tortuosity of particle paths
and the constrictions are smaller, too. If fine particles are not attached to the granular assembly, the Stokes flow is able to convey them through the porous medium via pressure and viscous forces. When transported particles are of size comparable to that of pores, the relative motion between them and the carrier fluid is very significant. Moreover, the average tortuosity of particle paths  is different from
is different from 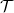 because fine particles do not follow closely the streamlines. As particles move they change the domain for the fluid flow.
because fine particles do not follow closely the streamlines. As particles move they change the domain for the fluid flow.
If  is the concentration of transported particles (being
is the concentration of transported particles (being  the volume of the transported particles and V the total volume of an element), the advection-dispersion equation ADE, based on the macroscopic conservation of particles, reads
the volume of the transported particles and V the total volume of an element), the advection-dispersion equation ADE, based on the macroscopic conservation of particles, reads

where  is the advective velocity of the particles and D is the hydrodynamic dispersion tensor. Although the ADE is a continuum balance law, it can be also derived from grain level considerations. In effect, the advective flux of particles
is the advective velocity of the particles and D is the hydrodynamic dispersion tensor. Although the ADE is a continuum balance law, it can be also derived from grain level considerations. In effect, the advective flux of particles  accounts for the fact that particles tend to follow, on average, the prevailing directions marked by the fluid flow. Then
accounts for the fact that particles tend to follow, on average, the prevailing directions marked by the fluid flow. Then  is parallel to
is parallel to  and
and  is always higher, and often much higher, than
is always higher, and often much higher, than  . For a given porous medium,
. For a given porous medium, 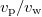 depends on the size of the particles with respect to that of pores, their shape, the interparticle friction and the value of C, as has been shown in interparticle percolation by gravity [26–29]. The dispersion mechanism is exhibited in a frame of reference that moves with the center of mass of the cloud of particles. Dispersion is random in nature. Fick's law
depends on the size of the particles with respect to that of pores, their shape, the interparticle friction and the value of C, as has been shown in interparticle percolation by gravity [26–29]. The dispersion mechanism is exhibited in a frame of reference that moves with the center of mass of the cloud of particles. Dispersion is random in nature. Fick's law  takes up the idea that dispersion occurs from high- to low-C regions. The dispersion tensor depends on
takes up the idea that dispersion occurs from high- to low-C regions. The dispersion tensor depends on 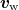 (e.g., as expressed for isotropic media in [30]).
(e.g., as expressed for isotropic media in [30]).
Normal dispersive transport can be conceived as the macroscopic manifestation of an underlying microscopic uncorrelated and Gaussian stochastic process. Normal and anomalous transport can be identified by tracking particles. In effect, having an ensemble of trajectories over large times and distances, the mean displacement gives the advective velocity 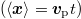 while the growth of the centered mean square displacement
while the growth of the centered mean square displacement 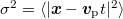 with time unveils the kind of transport.
with time unveils the kind of transport. 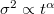 with
with  is normal dispersion while anomalous dispersion means that
is normal dispersion while anomalous dispersion means that  (superdispersion) or
(superdispersion) or 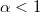 (subdispersion).
(subdispersion).
Anomalous transport occurs when the assumptions made to explain the Fickian law do not hold. This is the case of very short time or length scales, when the motion involves correlations (e.g., typically below the free path or the pore size lengths). On large time scales, memory effects are sometimes facilitated by the complexity of porous media. Although homogeneous media do not foster any hierarchy of pipes, the effect of trapping events on the motion deserves investigation.
To study the effects of non-Gaussian statistics, the simplest model of Brownian random walk (with always the same walk lengths and times) is not enough. Deviations from normal dispersion can be interpreted in terms of a stochastic continuous time random walks model CTRW [31,32]. In a CTRW the length  and duration of walks
and duration of walks 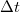 , as well as the times elapsed between consecutive walks, are drawn from a probability distribution function
, as well as the times elapsed between consecutive walks, are drawn from a probability distribution function  [5]. Walk lengths and/or pauses drawn from PDFs with no finite second moment lead to anomalous transport processes. In these cases, the behavior of particles is dominated by the largest displacements and/or the longest pauses, because the system memory about such rare events is never erased. What is a large displacement or a long pause depends on the observation scale.
[5]. Walk lengths and/or pauses drawn from PDFs with no finite second moment lead to anomalous transport processes. In these cases, the behavior of particles is dominated by the largest displacements and/or the longest pauses, because the system memory about such rare events is never erased. What is a large displacement or a long pause depends on the observation scale.
We carry out numerical experiments (fig. 1) to check the aspect of the PDFs of pause and walking times in cases in which blockages are possible. An originality of our approach is that we simulate on a microscopic level the interplay between fluid, transported particles and porous media. Our experiments capture events like drag forces, interparticle collisions, bouncing and rolling, formation and destruction of clogging arches and blockages.
Micro-hydromechanical model
We use a micro-hydromechanical numerical method, the DEM-PFV [33,34] implemented in YADE [35] to model particle transport. This method applies for Stokes flows of incompressible and Newtonian fluids. The DEM-PFV couples the discrete element method [36] with a pore-scale finite-volume formulation that solves the flow problem.
In the PFV framework, finite volumes are defined from a weighted Delaunay tessellation of the granular assembly. Therefore, at a given time, the geometry of the packing defines an open network of connected voids: finite volumes are tetrahedra whose apexes coincide with particle centers (fig. 2). Each finite volume represents a pore and deforms as the solid particles move. In our case, not only the coarse particles of the granular assembly but also the transported ones define the network of connected voids and hence this network changes dynamically with particle transport.
Fig. 2: (Colour online) Schematic of the finite-volume formulation used in the DEM-PFV method. (a) Tetrahedral element of the finite-volume decomposition, (b) network of connected voids and (c) definition of facet-spheres intersections in 3D (after [33]).
Download figure:
Standard imageThe deformation of a tetrahedron leads, in general, to a change in its volume that must be balanced by the fluid fluxes through its four faces, so the continuity equation applied to the fluid phase in each pore reads [34]

where  is the volumetric strain rate of pore i deduced from the particle velocities at the four apexes of the tetrahedron i, and qij is the flux between the pore i and one of its four adjacent pores j. As explained in eq. (2), inter-pore fluxes qij are related to the hydraulic pressure gradients between the corresponding pores. pi, pj is the hydraulic pressure in pore i, j, respectively, and lij is the distance between i and j. A Stokes flow leads to linear relationships between fluid fluxes and pressure gradients that are characterized by the hydraulic conductivities gij. For a given fluid dynamic viscosity, gij only depends on the hydraulic radius and the cross-section areas of constrictions [33].
is the volumetric strain rate of pore i deduced from the particle velocities at the four apexes of the tetrahedron i, and qij is the flux between the pore i and one of its four adjacent pores j. As explained in eq. (2), inter-pore fluxes qij are related to the hydraulic pressure gradients between the corresponding pores. pi, pj is the hydraulic pressure in pore i, j, respectively, and lij is the distance between i and j. A Stokes flow leads to linear relationships between fluid fluxes and pressure gradients that are characterized by the hydraulic conductivities gij. For a given fluid dynamic viscosity, gij only depends on the hydraulic radius and the cross-section areas of constrictions [33].
For a full coupling, the forces applied by the fluid on solid particles have to be taken into account in the DEM in addition to inter-particle contact forces. The fluid forces result from the integration of fluid pressure and viscous stresses over the surface of each solid particle. The development of these surface integrals shows that the pressure force  and the viscous force
and the viscous force  acting on a particle k due to a fluid flow between pores i and j are proportional to the product between the pressure drop
acting on a particle k due to a fluid flow between pores i and j are proportional to the product between the pressure drop  and the surface areas
and the surface areas  ,
, 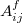 and
and 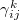 (fig. 2) that describe the geometrical features of the interface plane and the constriction between two tetrahedra:
(fig. 2) that describe the geometrical features of the interface plane and the constriction between two tetrahedra:

with  the unit vector pointing from pores i to j.
the unit vector pointing from pores i to j. 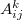 ,
, 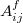 and
and  are relatively easily computed for spheres.
are relatively easily computed for spheres.
Numerical experiments
We use granular assemblies of monodispersed spheres of size  as porous media. We report results from random, quasi-crystalline and perfect crystalline structures included in parallelepiped periodic simulation boxes. Quasi-crystalline structures (face-centered cubic (FCC*) and simple cubic (SC*)) are generated from the corresponding crystalline ones, by enlarging unit cells and slightly displacing particles from crystalline positions.
as porous media. We report results from random, quasi-crystalline and perfect crystalline structures included in parallelepiped periodic simulation boxes. Quasi-crystalline structures (face-centered cubic (FCC*) and simple cubic (SC*)) are generated from the corresponding crystalline ones, by enlarging unit cells and slightly displacing particles from crystalline positions.  and
and  are slightly higher than in perfect crystals but the tortuosities are almost the same. However, as the CSD is modified, blockages are only possible in some of the constrictions. On the contrary, in crystalline structures (face-centered cubic (FCC),
are slightly higher than in perfect crystals but the tortuosities are almost the same. However, as the CSD is modified, blockages are only possible in some of the constrictions. On the contrary, in crystalline structures (face-centered cubic (FCC), 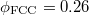 ) the formation of blockages is not conditioned by the porous structure since identical constrictions are found all over the medium.
) the formation of blockages is not conditioned by the porous structure since identical constrictions are found all over the medium.
Fine particles of size 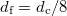 are randomly and uniformly introduced in the voids of the assembly up to an average concentration C. Hookean contact is used to model interactions between solid particles and all the particles are frictionless.
are randomly and uniformly introduced in the voids of the assembly up to an average concentration C. Hookean contact is used to model interactions between solid particles and all the particles are frictionless. 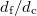 is below the maximum value that a frictionless particle can have in order to pass through the smallest possible constriction found in FCC media
is below the maximum value that a frictionless particle can have in order to pass through the smallest possible constriction found in FCC media 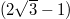 . Therefore, fine particles cannot get trapped alone. However, they can form a collective clogging arch when they locate in a constriction as shown in the inset of fig. 1(a). Obviously for a given CSD, blockages are more likely at high concentrations since clogging is basically a matter of the probability of the presence of particles [37,38]. We have checked this by changing the total amount of fine particles (i.e., the average C). We report exclusively the longitudinal velocity and dispersion (in the direction of
. Therefore, fine particles cannot get trapped alone. However, they can form a collective clogging arch when they locate in a constriction as shown in the inset of fig. 1(a). Obviously for a given CSD, blockages are more likely at high concentrations since clogging is basically a matter of the probability of the presence of particles [37,38]. We have checked this by changing the total amount of fine particles (i.e., the average C). We report exclusively the longitudinal velocity and dispersion (in the direction of  ). In normal dispersion,
). In normal dispersion,  and the Péclet number
and the Péclet number 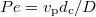 gives an idea of the importance of advective with respect to dispersive transport. We use
gives an idea of the importance of advective with respect to dispersive transport. We use  as a reference for velocities and
as a reference for velocities and  for time.
for time.
Results and discussion
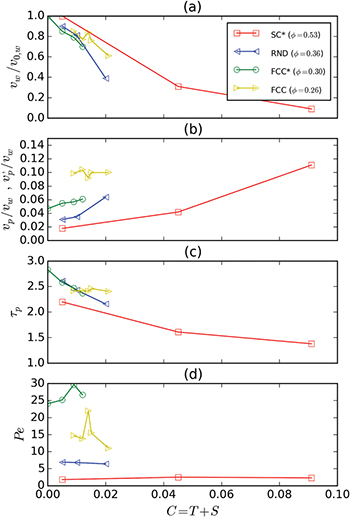
In SC* media, fine particles cannot form blockages and after some time the displacements of particles are uncorrelated because of collisions. Then we observe that the transport is normal,  (fig. 4(a)). In fig. 3 we show how
(fig. 4(a)). In fig. 3 we show how  decreases with C, whereas
decreases with C, whereas 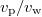 grows because a higher number of transported particles in the voids increases
grows because a higher number of transported particles in the voids increases  and reduces
and reduces 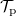 . These results are similar to those of particle percolation by gravity [27–29].
. These results are similar to those of particle percolation by gravity [27–29].
Fig. 3: (Colour online) Effect of C on (a) the fluid velocity  , (b) the advective velocity (
, (b) the advective velocity (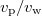 or
or 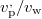 , (c) the tortuosity of particle paths and (d) the Péclet number
, (c) the tortuosity of particle paths and (d) the Péclet number 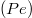 in SC*, RND, FCC* and FCC structures.
in SC*, RND, FCC* and FCC structures.
Download figure:
Standard imageIn FCC* and RND media at low C, blockages are very unlikely but they may last a long time. Sometimes this time is much longer than that of observation, so that we find that some particles never move, while the remaining ones are normally transported. In effect, the data shown in figs. 3 and 4 correspond exclusively to transported particles. Regarding the growth of  with t (fig. 4(b), (c)), if the whole sample of fine particles is considered and a few of them are trapped, the center of mass moves more slowly than that of transported particles. Therefore, the contribution of the dispersion to
with t (fig. 4(b), (c)), if the whole sample of fine particles is considered and a few of them are trapped, the center of mass moves more slowly than that of transported particles. Therefore, the contribution of the dispersion to  is hidden by a "ballistic" effect
is hidden by a "ballistic" effect 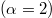 . In effect, if a fraction r of particles is transported as the ADE states (with
. In effect, if a fraction r of particles is transported as the ADE states (with 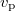 and D) while the others are stopped, after a time t, we find that
and D) while the others are stopped, after a time t, we find that  and
and  . When
. When  then
then 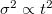 . If the trapped particles are discarded, then only the advection and dispersion mechanisms are observed. In summary, in this case the transport is normal but we cannot forget that particles have a small chance of being trapped and that if they do, they will rest for a long time.
. If the trapped particles are discarded, then only the advection and dispersion mechanisms are observed. In summary, in this case the transport is normal but we cannot forget that particles have a small chance of being trapped and that if they do, they will rest for a long time.
Fig. 4: (Colour online) The centered mean square displacement of particles as a function of time obtained in different media for different C. Solid markers represent, rightward, the time in which particles have traveled, on average, a distance of 1, 10 and 100 times  .
.
Download figure:
Standard imageIn FCC media there are many traps so that the probability for blockage formation grows very quickly with C but, conversely, blockages are easily destroyed, too, since there are many particles in the voids and the fluid flow changes very quickly. As a result, on the time scale of observation we find that blockages appear and disappear and the growth of 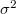 with time is not that of normal dispersion, as shown in fig. 4(d). In the framework of CTRW this motion can be seen as a succession of walks (displacements between consecutive blockages) and pauses (times that particles remain in a blockage). During walks particles move on average at an effective velocity (fig. 3)
with time is not that of normal dispersion, as shown in fig. 4(d). In the framework of CTRW this motion can be seen as a succession of walks (displacements between consecutive blockages) and pauses (times that particles remain in a blockage). During walks particles move on average at an effective velocity (fig. 3)  (since
(since  implicitly includes the pauses) and disperse according to the normal transport paradigm.
implicitly includes the pauses) and disperse according to the normal transport paradigm.
Then the kind of transport on a longer time scale depends on whether or not the PDFs of pause and walking times have finite second moment. Some examples of power laws with non-finite second moment have been found in other situations [39], but in this case there is a reason to consider exponential decays, i.e., 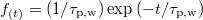 being
being  the time scale factors of pauses and walks, respectively. In effect, if particles pass through all the constrictions in similar conditions (number of neighbors, velocities, constant probability of finding other particles blocking the constriction, etc.) and trapping events occur independently of each other, this corresponds to a homogeneous Poisson process, and the time between each pair of consecutive events follows an exponential distribution. Similar assumptions have been made in silo discharge problems, where a constant probability of clogging during the whole avalanche duration is assumed [40]. Regarding blockage destructions, an exponential decay also means a constant probability of blockage failure and non-dependence between consecutive events.
the time scale factors of pauses and walks, respectively. In effect, if particles pass through all the constrictions in similar conditions (number of neighbors, velocities, constant probability of finding other particles blocking the constriction, etc.) and trapping events occur independently of each other, this corresponds to a homogeneous Poisson process, and the time between each pair of consecutive events follows an exponential distribution. Similar assumptions have been made in silo discharge problems, where a constant probability of clogging during the whole avalanche duration is assumed [40]. Regarding blockage destructions, an exponential decay also means a constant probability of blockage failure and non-dependence between consecutive events.
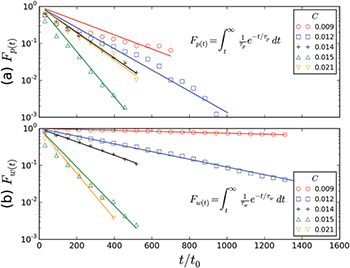
The PDFs of walking and pause times computed from our experiments fit quite well with exponential decays (except for the pause time of FCC  , probably as a consequence of the insufficient size of the statistical sample). In fig. 5 we plot a cumulative distribution function
, probably as a consequence of the insufficient size of the statistical sample). In fig. 5 we plot a cumulative distribution function  since this helps to identify power law and exponential decays [39]. For the latter we expect
since this helps to identify power law and exponential decays [39]. For the latter we expect  . The corresponding least squares approximation is also shown in fig. 5. Exponential PDFs lead to normal transport at time
. The corresponding least squares approximation is also shown in fig. 5. Exponential PDFs lead to normal transport at time  . Therefore,
. Therefore, 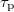 and
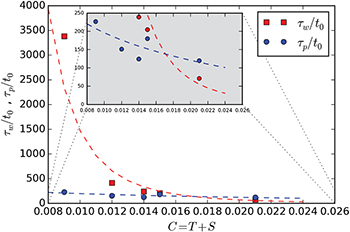
and 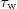 establish the time scales on which the memory effect of blockages formation is erased. These scales are, in the end, determined by the number of traps in the medium and the probability of finding several particles in the same pore (i.e., on C). We have found (fig. 6) that the higher C, the shorter
establish the time scales on which the memory effect of blockages formation is erased. These scales are, in the end, determined by the number of traps in the medium and the probability of finding several particles in the same pore (i.e., on C). We have found (fig. 6) that the higher C, the shorter 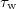 , with
, with 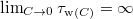 and
and  .
. 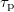 decreases slowly with C but this relationship deserves further investigation. At high C, the local changes of fluid flows are presumably more frequent and intense, but with more particles in the blockages, those that are very embedded may need more time to be released. For
decreases slowly with C but this relationship deserves further investigation. At high C, the local changes of fluid flows are presumably more frequent and intense, but with more particles in the blockages, those that are very embedded may need more time to be released. For 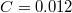 , and especially for
, and especially for  , the time scale is much longer than our observation time, and this anticipates that media having wider CSDs blockages (i.e., fewer traps) lead to higher
, the time scale is much longer than our observation time, and this anticipates that media having wider CSDs blockages (i.e., fewer traps) lead to higher  , indicating how to approach FCC* cases.
, indicating how to approach FCC* cases.
Fig. 5: (Colour online) Cumulative distribution functions of pause (a) and walking times (b). The markers show the results of numerical experiments and the dotted lines are the least squares approximations to an exponential decay.
Download figure:
Standard imageFig. 6: (Colour online) Variation of  and
and  with C in FCC media. These series have been respectively fitted (dotted lines) with a potential and a logarithmic curve.
with C in FCC media. These series have been respectively fitted (dotted lines) with a potential and a logarithmic curve.
Download figure:
Standard imageWith these results in mind, some already known transport models can be used to study particle transport when mechanical clogging of constrictions is expected.
In particular, a continuum transport model with 1st-order kinetic mass transfer laws can be used. This needs the inclusion on the right-hand side of eq. (1) of laws of type 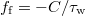 and
and 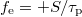 , being
, being 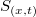 the concentration of trapped particles, and
the concentration of trapped particles, and 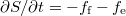 . We have compared the predictions of this model to the results of DEM-PFV simulations (fig. 7(a)). A steady-state solution of the corresponding 1D problem with periodic boundary conditions is
. We have compared the predictions of this model to the results of DEM-PFV simulations (fig. 7(a)). A steady-state solution of the corresponding 1D problem with periodic boundary conditions is 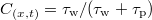 which is in the end the expected value of the average fraction of traveling particles
which is in the end the expected value of the average fraction of traveling particles 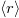 .
.  , directly measured in the simulations, is compared to
, directly measured in the simulations, is compared to 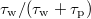 in fig. 8 (where
in fig. 8 (where  come from the statistical fitting). Furthermore,
come from the statistical fitting). Furthermore,  , also shown in fig. 8 should be equal to
, also shown in fig. 8 should be equal to  , since, on average, particles are expected to move at
, since, on average, particles are expected to move at  for a fraction of time
for a fraction of time 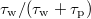 .
.
Fig. 7: (Colour online) Transport models used to reproduce some DEM-PFV simulations. (a) An ADE with sinks and sources reproduces the distribution of particles with respect to their original position in a FCC structure with  . (b) A CTRW fitted for FCC at
. (b) A CTRW fitted for FCC at  . Solid lines are the least squares approximations. On the short time scale,
. Solid lines are the least squares approximations. On the short time scale, 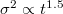 .
.
Download figure:
Standard imageFig. 8: (Colour online) Effect of C on the fraction of traveling particles: values directly measured from DEM-PFV simulations 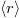 , values computed after fitting walk and pause times to exponential distributions
, values computed after fitting walk and pause times to exponential distributions  and ratio of the effective to the actual velocity of the particles.
and ratio of the effective to the actual velocity of the particles.
Download figure:
Standard imageOn the other hand, CTRW models can also be used. We have also compared the DEM-PFV simulations to a CTRW model (fig. 7(b)) in which we consider that at a given time, each particle is either traveling or trapped. In the first case, as the motion of particles between consecutive blockages is supposed to be normal, its path can be described (until the end of the corresponding traveling period) as a succession of advective 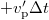 and random steps
and random steps  that occur at fixed
that occur at fixed  . During a trapping period, the particle does not move. The duration of traveling and waiting periods (i.e., the number of steps that particles move or do not move) is drawn from exponential laws of the parameters
. During a trapping period, the particle does not move. The duration of traveling and waiting periods (i.e., the number of steps that particles move or do not move) is drawn from exponential laws of the parameters 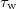 and
and 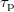 , respectively. The inclusion of these pauses is what makes the difference with respect to an usual random walk model, and this explains the behavior of the ensemble of particles on the short time scale. Moreover, the time scale for normal transport (i.e.,
, respectively. The inclusion of these pauses is what makes the difference with respect to an usual random walk model, and this explains the behavior of the ensemble of particles on the short time scale. Moreover, the time scale for normal transport (i.e.,  ) and the effective transport parameters can be obtained in turn from this model.
) and the effective transport parameters can be obtained in turn from this model.
Conclusion
Thanks to the DEM-PFV numerical method, "ab initio" simulations of particle transport in dense granular assemblies have been performed. Fluid-solid interactions were considered on a particle scale (including transported particles). We find reasonably good fits with exponential decays for the duration of trapping events and of displacements between consecutive trapping events. This establishes the scale for normal transport. On shorter scales we show that an ADE with 1st-order kinetic mass transfer laws (a model originally introduced for other systems) is valid to account for the intermittent formation of blockages during the transport of moderately large, passive, solid particles that interact only mechanically with both the fluid and the porous medium. We also show, how, for some porous structures, exponential factors and transport parameters depend on the concentration.
Acknowledgments
This work has been partially supported by the LabEx Tec 21 (Investissements d'Avenir - grant agreement nANR-11-LABX-0030).