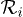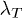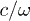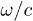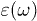Abstract
We theoretically study heat transfer between two anisotropic nanoparticles in vacuum, and derive closed expressions in terms of the anisotropic dipole polarizabilities. We show that transfer between two small spheroids can be many times as large as the one for two spheres of same volumes. Such increase with anisotropy is also found for the heat emission of an isolated small spheroid. Furthermore, we observe a strong dependence of transfer on the relative orientation, yielding the interpretation as a heat transfer switch. The switch quality, given as the ratio of transfer in the "on" and "off" positions, is observed to be as large as 103 in the near field and even larger in the far field.
Export citation and abstract BibTeX RIS
The phenomenon of radiative heat transfer is of amplified interest due to recent experimental observations [1–5] of its strong increase for distances below the micron range. In this regime, transfer is enhanced by the so-called near-field effects attributed to evanescent waves [6]. On the theoretical side, two frameworks underlie thermal radiation and transfer, both of which are fundamental concepts. First, the theory of quantum thermal fluctuations that goes back all the way to the beginning of quantum mechanics, i.e., Planck's law of black-body radiation [7]. Second, the scattering of light by objects that are small compared to the wavelength, which is by itself a modern field of both experimental and theoretical study [8,9].
Radiative energy exchange between objects at different temperatures is on the macro scale well understood in terms of the laws by Planck and Stefan-Boltzmann and inclusion of view factors and gray factors [10] to account for non-planar geometries and non-black bodies, respectively. However, such heat transfer is distinctly different, if the size of the objects or the distance between them is small or comparable to the thermal wavelength, which is roughly 8 microns at room temperature. On these scales, also nontrivial dependences on the shape of the objects have been observed, as e.g. for sharp tips [11]. Many recent works computed the exact heat transfer between non-planar objects including two spheres [12,13] or a sphere [11,14,15] or cone [11] in front of a planar surface, periodic structures [16], or even more abstract geometries [17,18]. Formalisms for treating fluctuation electrodynamics for arbitrary objects at different temperatures have been recently presented [14,17,19,20].
Due to theoretical simplicity, a large influence on understanding was provided by the study of nanoparticles, i.e., particles much smaller than the wavelength [21–23], including many-body effects [24,25]. Such particles are accesibble experimentally. A recent work studies transfer between an anisotropic nanoparticle (a spheroid) and a planar surface [26] (and the related Casimir interactions between small ellipsoids are analyzed in ref. [27]).
In this letter, we study radiative heat transfer between two anisotropic particles, as for example spheroids. We show that the transfer between two spheroids as well as the heat emission of an isolated one can be many times as large as the corresponding value for spheres of equal volume. We also demonstrate that the transfer between parallel spheroids can be many times as large as compared to the perpendicular configuration, an effect which is due to the narrow peaks of the polarizabilities of nanoparticles as a function of frequency. We analyze means of tuning the extent of this effect by changing the shape or materials of the two objects. While the described dependences on shapes and orientations may be directly measurable by use of (shaped) AFM tips [2], they might also be stimulating for the larger field of nano plasmonics, where interference effects of nearby objects are of increased interest (see, e.g., ref. [28]).
Consider two arbitrary objects at temperatures T1 and T2 in vacuum, whose classical scattering properties in isolation are given in terms of the scattering matrices 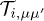 [23,29] (with
[23,29] (with  labeling the objects) relating the amplitude of an incoming wave with index
labeling the objects) relating the amplitude of an incoming wave with index 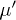 to the scattered wave with index μ. The transfer between the two objects is then computed as an integral in frequency ω and the trace of a matrix product [23],
to the scattered wave with index μ. The transfer between the two objects is then computed as an integral in frequency ω and the trace of a matrix product [23],
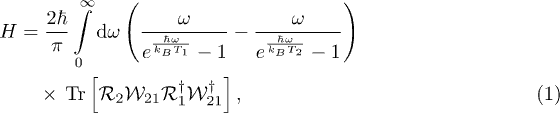
where  are the emission or absorption matrices. Furthermore, multiple scattering of waves between the objects is accounted for by the matrix
are the emission or absorption matrices. Furthermore, multiple scattering of waves between the objects is accounted for by the matrix 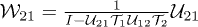 , including the matrix
, including the matrix 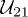 . The latter translates the vector waves from the coordinate system of object 1 to the one of object 2. ℏ and kB are Planck's and Boltzmann's constant, respectively, and the superscript †denotes the adjoined of an operator, e.g.
. The latter translates the vector waves from the coordinate system of object 1 to the one of object 2. ℏ and kB are Planck's and Boltzmann's constant, respectively, and the superscript †denotes the adjoined of an operator, e.g. 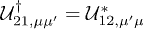 .
.
Equation (1) is exact but can often not easily be evaluated analytically. However simplifications are possible for nano-particles. If the sizes of the objects, Ri (loosely defined as the largest dimension of the anisotropic objects), is much smaller than the distance d between their centers, 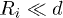 , a one reflection approximation, amounting to setting
, a one reflection approximation, amounting to setting 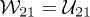 in eq. (1), becomes asymptotically exact.
in eq. (1), becomes asymptotically exact.
Additional simplification is possible for objects that are sufficiently small such that their scattering properties are described by their (electric) dipole polarizabilities. While for dielectric objects, this limit is typically fulfilled if Ri is small compared to the thermal wavelength 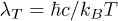 , care has to be taken for metallic objects, where the skin depth is small, and even for Ri of a few nanometer, the description in terms of the dipole polarizabilities is inaccurate [23]. Assuming small enough objects, we start by considering the anisotropic dipole polarizability tensors
, care has to be taken for metallic objects, where the skin depth is small, and even for Ri of a few nanometer, the description in terms of the dipole polarizabilities is inaccurate [23]. Assuming small enough objects, we start by considering the anisotropic dipole polarizability tensors 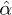 of the two objects, which, in properly chosen coordinate systems, can be assumed diagonal. For simplicity, we furthermore restrict to objects with an axis of rotational symmetry, for which the objects polarizabilities are characterized by the two components
of the two objects, which, in properly chosen coordinate systems, can be assumed diagonal. For simplicity, we furthermore restrict to objects with an axis of rotational symmetry, for which the objects polarizabilities are characterized by the two components
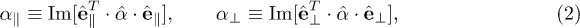
where 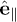 and
and 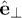 are unit vectors pointing along the axis of rotational symmetry and perpendicular to it, respectively. Our results will depend only on the imaginary part of the polarizability, and the definition in eq. (2) allows for a compact notation below. The respective orientations of the axes of symmetry of the two objects are then determined by two angles, with respect to the line connecting their centers, and a line perpendicular to it, see fig. 1. Technically, the objects' polarizabilities
are unit vectors pointing along the axis of rotational symmetry and perpendicular to it, respectively. Our results will depend only on the imaginary part of the polarizability, and the definition in eq. (2) allows for a compact notation below. The respective orientations of the axes of symmetry of the two objects are then determined by two angles, with respect to the line connecting their centers, and a line perpendicular to it, see fig. 1. Technically, the objects' polarizabilities 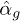 measured in the frame shown in fig. 1 are obtained by rotations of
measured in the frame shown in fig. 1 are obtained by rotations of 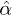 . We then expand eq. (1) to lowest order in the size of the objects, where the elements of the
. We then expand eq. (1) to lowest order in the size of the objects, where the elements of the 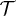 matrix, measured in the global frame, are straight forwardly obtained from
matrix, measured in the global frame, are straight forwardly obtained from 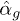 . The relevant combination
. The relevant combination 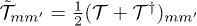 of elements for electric polarization and multipole indices l = 1 and
of elements for electric polarization and multipole indices l = 1 and 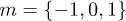 (dipoles) are given by
(dipoles) are given by
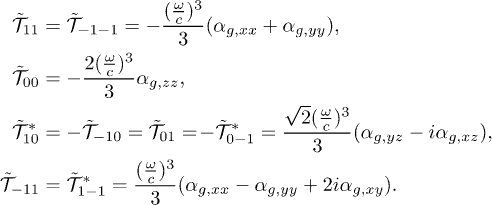
In contrast to a homogeneous sphere, the 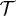 matrix is not diagonal for anisotropic particles. Equation (3) shows the result for the transfer between sufficiently small nano-particles1
(setting
matrix is not diagonal for anisotropic particles. Equation (3) shows the result for the transfer between sufficiently small nano-particles1
(setting 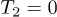 for brevity),
for brevity),
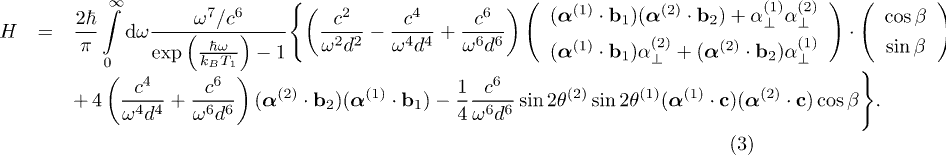
where  , and we have introduced a vector containing
, and we have introduced a vector containing 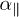 and
and 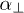 ,
, 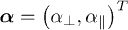 . The azimuthal angles enter eq. (3) only through their difference, denoted
. The azimuthal angles enter eq. (3) only through their difference, denoted 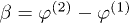 , and finally
, and finally 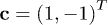 . Equation (3) can be rationalized by comparison to classical radiation [30]; for example, for all angles being zero, we have the far-field
. Equation (3) can be rationalized by comparison to classical radiation [30]; for example, for all angles being zero, we have the far-field 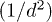 term being proportional to
term being proportional to 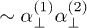 , a form which can be anticipated from the radiation field of a dipole [30]. A special case of eq. (3), evaluated in the figures below, considers the two axes of symmetry in the plane perpendicular to the center-to-center vector (
, a form which can be anticipated from the radiation field of a dipole [30]. A special case of eq. (3), evaluated in the figures below, considers the two axes of symmetry in the plane perpendicular to the center-to-center vector (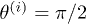 , see fig. 2), for which eq. (3) simplifies,
, see fig. 2), for which eq. (3) simplifies,
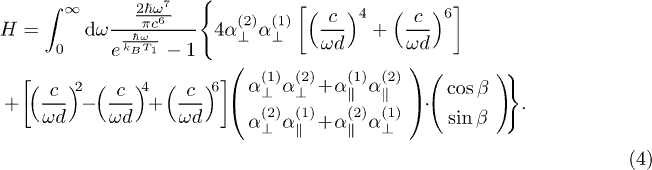
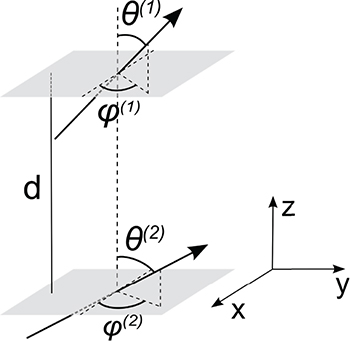
Fig. 1: Sketch of the two objects under study, their center-to-center distance d and orientations (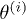 and
and 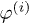 ) with respect to the global frame
) with respect to the global frame 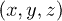 . The objects are mimicked by arrows, which point to the direction of their respective axes of rotational symmetry, thereby completely specifying the objects' orientations. Note that the resulting transfer will only depend on the difference
. The objects are mimicked by arrows, which point to the direction of their respective axes of rotational symmetry, thereby completely specifying the objects' orientations. Note that the resulting transfer will only depend on the difference 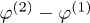 , denoted β below.
, denoted β below.
Download figure:
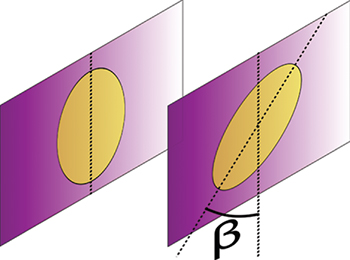
Standard imageFig. 2: (Colour on-line) Illustration of the situation considered in eq. (4) using the example of spheroids.
Download figure:
Standard imageAn interesting example scenario is given by spheroids, i.e., ellipsoids with an axis of rotational symmetry. We denote 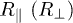 the radius parallel (perpendicular) to this axis. The corresponding polarizabilities are given by [8,29,31] (recall that
the radius parallel (perpendicular) to this axis. The corresponding polarizabilities are given by [8,29,31] (recall that 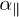 and
and  denote the imaginary part),
denote the imaginary part),
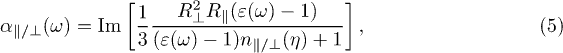
with the depolarizing factors 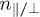 ,
,

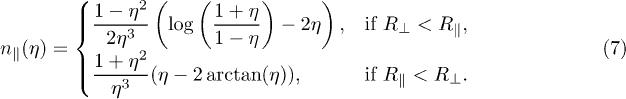
η is the angular eccentricity of the spheroid, 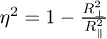 for a prolate
for a prolate 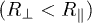 and
and 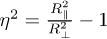 for an oblate spheroid
for an oblate spheroid  , and
, and 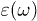 is the dielectric permittivity2
.
is the dielectric permittivity2
.
The following figures use temperatures 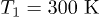 and
and 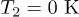 and a typical dielectric material, SiC, with optical properties given by [32]
and a typical dielectric material, SiC, with optical properties given by [32]
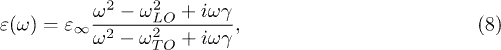
where 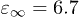 , and
, and 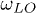 ,
, 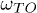 and γ take values of 0.12, 0.098 and
and γ take values of 0.12, 0.098 and 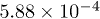 , all in eV. SiC supports surface resonances, so called surface phonon polaritons, and is hence a good candidate for radiative near-field heat transfer [33,34].
, all in eV. SiC supports surface resonances, so called surface phonon polaritons, and is hence a good candidate for radiative near-field heat transfer [33,34].
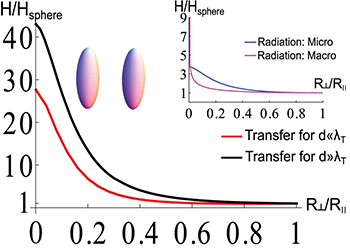
Figure 3 shows the transfer between two identical parallel spheroids (i.e. 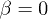 in eq. (4), see also the sketch in the figure) as a function of the ratio
in eq. (4), see also the sketch in the figure) as a function of the ratio 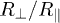 (keeping the volumes fixed), normalized by the value for two spheres of same center-to-center distance and volumes. In other words, the curves approach unity for
(keeping the volumes fixed), normalized by the value for two spheres of same center-to-center distance and volumes. In other words, the curves approach unity for 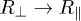 , where the polarizabilities in eq. (5) approach the polarizability of a sphere,
, where the polarizabilities in eq. (5) approach the polarizability of a sphere,
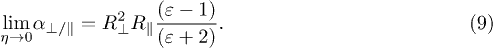
The figure shows both the far-field regime, 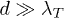 , where the
, where the 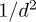 -term in eq. (4) dominates, as well as the near-field regime, where the
-term in eq. (4) dominates, as well as the near-field regime, where the 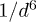 -term is largest. In these limits, the distance dependence cancels in the shown ratio, since these limiting power laws are the same for any shape. Because of this, the normalized curves in fig. 3 are similar for
-term is largest. In these limits, the distance dependence cancels in the shown ratio, since these limiting power laws are the same for any shape. Because of this, the normalized curves in fig. 3 are similar for 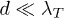 and
and 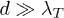 , despite the fact that the absolute transfer can differ by several orders of magnitude in these two limits. We note that the transfer in both regimes can be many times (30−40) as large as the transfer between two spheres, showing the strong tunability of transfer by changing the objects' shapes.
, despite the fact that the absolute transfer can differ by several orders of magnitude in these two limits. We note that the transfer in both regimes can be many times (30−40) as large as the transfer between two spheres, showing the strong tunability of transfer by changing the objects' shapes.
Fig. 3: (Colour on-line) Heat transfer between two identical parallel spheroids (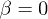 in eq. (4)) with
in eq. (4)) with 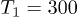 and
and 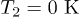 , of fixed volumes as a function of
, of fixed volumes as a function of 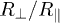 in the limit of small (red curve) and large (black curve) distance. In these limits, the curves are independent of distance, see main text. Inset: dashed blue and magenta lines represent the heat radiation of an isolated micro-spheroid (eq. (10)) and a macroscopic spheroid (computed by the Stefan-Boltzmann law), respectively. All curves in the figure are normalized by the value for spheres with volumes equal to the spheroid volumes.
in the limit of small (red curve) and large (black curve) distance. In these limits, the curves are independent of distance, see main text. Inset: dashed blue and magenta lines represent the heat radiation of an isolated micro-spheroid (eq. (10)) and a macroscopic spheroid (computed by the Stefan-Boltzmann law), respectively. All curves in the figure are normalized by the value for spheres with volumes equal to the spheroid volumes.
Download figure:
Standard imageThe inset presents the heat emission of an isolated spheroid which can be either micro- or macroscopic. The latter case describes the situation where the spheroid is large compared to the thermal wavelength 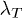 . For the microscopic case the emission is given in terms of the trace of the polarizability,
. For the microscopic case the emission is given in terms of the trace of the polarizability,
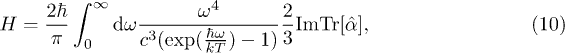
which, due to the cyclic property of the trace, is independent of orientation. It also increases with decreasing 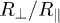 , yet not as strongly as expected from the transfer curves; Naively, we expect the transfer to be the product of the emissivities, i.e., the blue curve in the inset to be roughly the square root of the red or black curves in the main graph. This estimate, which neglects orientation effects, appears however too rough. We labelled the result of eq. (10) by "Micro" as it holds for small anisotropic particles (e.g. spheroids). In contrast, the second curve in the inset of fig. 3 gives the emissivity of a macroscopic spheroid as a function of its eccentricity. Macroscopic bodies emit proportional to their surface area [10] according to the Stefan-Boltzmann law, almost independent of shape. The curve labelled "Macro" thus shows the surface area of the spheroid for fixed volume. It is below the curve for the micro-spheroid, however diverges for
, yet not as strongly as expected from the transfer curves; Naively, we expect the transfer to be the product of the emissivities, i.e., the blue curve in the inset to be roughly the square root of the red or black curves in the main graph. This estimate, which neglects orientation effects, appears however too rough. We labelled the result of eq. (10) by "Micro" as it holds for small anisotropic particles (e.g. spheroids). In contrast, the second curve in the inset of fig. 3 gives the emissivity of a macroscopic spheroid as a function of its eccentricity. Macroscopic bodies emit proportional to their surface area [10] according to the Stefan-Boltzmann law, almost independent of shape. The curve labelled "Macro" thus shows the surface area of the spheroid for fixed volume. It is below the curve for the micro-spheroid, however diverges for 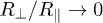 as
as 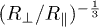 .
.
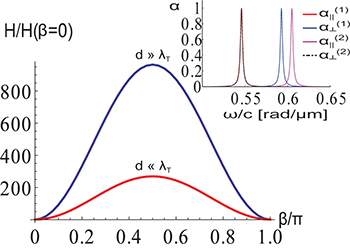
The inset of fig. 4 shows the transfer for two identical spheroids (still considering 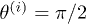 ), as a function of their relative angle β (see eq. (4) and the sketch in the figure). The curves, drawn for moderately stretched objects with
), as a function of their relative angle β (see eq. (4) and the sketch in the figure). The curves, drawn for moderately stretched objects with 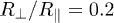 , show the characteristics of a switch, the transfer in the parallel ("on") position being more than thousand times as large as in the perpendicular ("off") position3
. The main figure shows the switch quality, i.e., the ratio of maximal and minimal values of the transfer in the inset (i.e., the value for
, show the characteristics of a switch, the transfer in the parallel ("on") position being more than thousand times as large as in the perpendicular ("off") position3
. The main figure shows the switch quality, i.e., the ratio of maximal and minimal values of the transfer in the inset (i.e., the value for 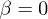 ), as a function of eccentricity. Making the spheroids thinner increases the quality, which can, for very stretched objects, reach values of ten thousands. The strong dependence on β shown in the inset can be understood by noticing that
), as a function of eccentricity. Making the spheroids thinner increases the quality, which can, for very stretched objects, reach values of ten thousands. The strong dependence on β shown in the inset can be understood by noticing that 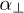 and
and 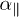 show distinct resonances at different frequencies (compare also the inset of fig. 5 below). Regarding
show distinct resonances at different frequencies (compare also the inset of fig. 5 below). Regarding 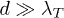 , the integrand is
, the integrand is 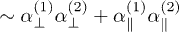 in the "on" position, while it is
in the "on" position, while it is 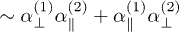 in the "off" position. The overlap of
in the "off" position. The overlap of 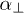 and
and 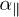 is small, reducing the relative transfer in the "off" position. This can be seen from eq. (5) because the position of their respective resonances as functions of ω (related to the minima of the denominators) are different, the more so the larger the eccentricity η. The shown behavior thus follows from a correlation of shape and material related properties. For
is small, reducing the relative transfer in the "off" position. This can be seen from eq. (5) because the position of their respective resonances as functions of ω (related to the minima of the denominators) are different, the more so the larger the eccentricity η. The shown behavior thus follows from a correlation of shape and material related properties. For 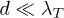 , eq. (4) shows a β-independent term that causes the switch quality to be lower by almost a factor of a hundred.
, eq. (4) shows a β-independent term that causes the switch quality to be lower by almost a factor of a hundred.
Fig. 4: (Colour on-line) Heat transfer between two identical spheroids with 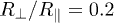 , as a function of the angle β (see inset). The main graph gives the quality of the transfer switch as a function of
, as a function of the angle β (see inset). The main graph gives the quality of the transfer switch as a function of 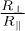 (see main text). In the shown limits for d, the transfer assumes simple power laws, such that the given ratios are d-independent.
(see main text). In the shown limits for d, the transfer assumes simple power laws, such that the given ratios are d-independent.
Download figure:
Standard imageFig. 5: (Colour on-line) Heat transfer between slightly different spheroids, i.e., 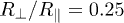 (0.2) and
(0.2) and 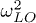 in eq. (8) multiplied by 1.05 (1.1) for object 1 (object 2), as a function of angle β. Insert: Imaginary part of the polarizabilities (normalized to unity), demonstrating the desired overlaps.
in eq. (8) multiplied by 1.05 (1.1) for object 1 (object 2), as a function of angle β. Insert: Imaginary part of the polarizabilities (normalized to unity), demonstrating the desired overlaps.
Download figure:
Standard imageThis angle-independent term can be suppressed by e.g. using two spheroids that have distinct shape and/or material composition. Figure 5 shows the case of two spheroids with slightly detuned material resonances of 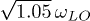 and
and 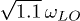 , respectively. As seen in the upper inset, this reduces the overlap of the polarizabilities
, respectively. As seen in the upper inset, this reduces the overlap of the polarizabilities 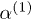 and
and 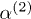 , thereby suppressing the angle-independent term in eq. (4). Furthermore we also chose the anisotropy of the two spheroids slightly different, with
, thereby suppressing the angle-independent term in eq. (4). Furthermore we also chose the anisotropy of the two spheroids slightly different, with 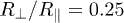 and 0.2. This restores the desired overlap of
and 0.2. This restores the desired overlap of 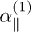 with
with 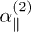 (see inset). These manipulations lead to a switch quality of
(see inset). These manipulations lead to a switch quality of 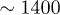 in the near field, for moderately stretched objects.
in the near field, for moderately stretched objects.
The angle-independent term can as well be suppressed by considering transfer between a prolate and an oblate spheroid, as shown in fig. 6. The inset shows again the different polarizabilities, where we note that the desired overlaps have been achieved for identical 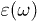 , i.e., the two spheroids have identical materials. The main panel demonstrates the strong orientation dependence, where now the transfer is maximal for
, i.e., the two spheroids have identical materials. The main panel demonstrates the strong orientation dependence, where now the transfer is maximal for 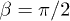 . The quality is
. The quality is 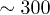 in the near field, which is still an unexpectedly large value, given that the prolate spheroid is not very much stretched
in the near field, which is still an unexpectedly large value, given that the prolate spheroid is not very much stretched 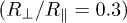 .
.
Fig. 6: (Colour on-line) Heat transfer between a prolate 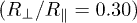 and an oblate
and an oblate 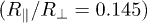 spheroid with identical dielectric permittivities. The insert shows the imaginary part of the polarizability of the two objects (normalized to unity), demonstrating the desired overlaps.
spheroid with identical dielectric permittivities. The insert shows the imaginary part of the polarizability of the two objects (normalized to unity), demonstrating the desired overlaps.
Download figure:
Standard imageHeat transfer between anisotropic nanoparticles allows for a large freedom of tunability. For a typical dielectric material, the transfer between parallel spheroids can be 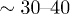 times as large as for two spheres of equal volumes and distance. The strong dependence on the relative angle of two spheroids, which can also be tuned, can increase or reduce the transfer by factors up to 103 or 104 by a simple twist of one of the objects, thereby providing the interpretation of a transfer switch.
times as large as for two spheres of equal volumes and distance. The strong dependence on the relative angle of two spheroids, which can also be tuned, can increase or reduce the transfer by factors up to 103 or 104 by a simple twist of one of the objects, thereby providing the interpretation of a transfer switch.
Future work may investigate the effect shown in fig. 3 for metallic particles. The overall magnitude of the radiation and transfer is expected to be much smaller in this case, however it might even stronger depend on the particles' shapes than depicted in fig. 3 for SiC. Indeed, an initial scaling analysis, motivated by the findings for the equilibrium Casimir force between metallic spheroids [27], shows intriguing laws for sufficiently large 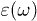 and small
and small 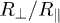 . There exist a regime where from eq. (5),
. There exist a regime where from eq. (5), 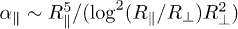 , and hence the quantity shown in fig. 3 scales as
, and hence the quantity shown in fig. 3 scales as 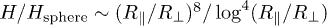 hence strongly increasing for decreasing
hence strongly increasing for decreasing 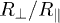 . At even smaller
. At even smaller 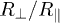 , this divergence is however cut off and saturates (depending on
, this divergence is however cut off and saturates (depending on 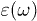 ). We note that the switch effect may not be present for metallic particles due to the absence of sharp resonances.
). We note that the switch effect may not be present for metallic particles due to the absence of sharp resonances.
Acknowledgments
We thank G. Bimonte, R. L. Jaffe, M. Kardar, A. W. Rodriguez and M. T. H. Reid for useful discussions. This research was supported by DFG grant No. KR 3844/2-1.
Footnotes
- 1
As mentioned above, eq. (3) is valid if
 is small compared to d, the material skin depth and the thermal wavelength
is small compared to d, the material skin depth and the thermal wavelength  .
. - 2
In the scattering properties of the spheroid, the wavelength
 is compared to geometric scales (e.g. object size) and material scales (e.g., resonance wavelengths). Equations (5)–(7) are valid to lowest order for small
is compared to geometric scales (e.g. object size) and material scales (e.g., resonance wavelengths). Equations (5)–(7) are valid to lowest order for small  with respect to geometric scales and to arbitrary order in material scales, i.e.,
with respect to geometric scales and to arbitrary order in material scales, i.e.,  is not expanded in ω.
is not expanded in ω. - 3
Ref. [35] considers a related phenomenon for two gratings.