Abstract
Exocytosis from dense core vesicles is an important ubiquitous process by which neurotransmitters are released from many cells. This has stimulated strong efforts to monitor and understand vesicular release events in order to infer their biological and physicochemical mechanisms. Though much has been achieved so far, many experimental observations remain unexplained, even puzzling, essentially because they envision that the vesicle matrixes consist of a homogeneous polyelectrolytic condensed phase encapsulated by the vesicles membranes. This work discloses a new model of dense core matrixes based on the physics of polyelectrolytes involving long chains of anionic moieties (here, chromogranins) condensed by a mixture of bulky monocations and small dications (here, catecholamines and calcium ions). It follows that matrixes cannot be homogeneous but necessarily consist of a dispersion of tightly compacted nano-grains immersed in a less condensed phase involving loosely folded chromogranin strands in which catecholamine cations may diffuse at significant rates. Even if such pomegranate-like description has to remain essentially theoretical up to when direct experimental means of testing is available, it leads to a whole set of predictions that are fully coherent with all experimental observations based on amperometric monitoring of vesicular exocytosis including some recent extremely puzzling ones.
Export citation and abstract BibTeX RIS

This is an open access article distributed under the terms of the Creative Commons Attribution Non-Commercial No Derivatives 4.0 License (CC BY-NC-ND, http://creativecommons.org/licenses/by-nc-nd/4.0/), which permits non-commercial reuse, distribution, and reproduction in any medium, provided the original work is not changed in any way and is properly cited. For permission for commercial reuse, please email: oa@electrochem.org.
Over the two past decades, amperometric measurements of vesicular exocytosis based on the "artificial synapse" method have proven extremely useful for investigating its mechanisms.1–5 The principle of the method is to mimic what occurs in a real synapse by placing the electroactive surface of a microelectrode (generally a carbon fiber disk) at sub-micrometric distance from the cytoplasmic membrane of an investigated cell. Under such conditions, the microelectrode acts as a receiving neuron would do in a real synapse and collects all neurotransmitters released in the artificial synaptic cleft. Neurotransmitters cations are detected electrochemically through their two-electron-two-proton oxidation (n = 2).3 Since diffusion across the ca. 100 to 200 nm artificial synaptic cleft is extremely fast (< 0.1 ms), the oxidation current i(t) directly transcribes, without any filtering or distortion,4 the temporal variations of brief individual exocytotic released fluxes, i.e., i(t) = −nF(dq/dt), where F is the Faraday (96,485 A.s.mol-1) and q(t) the quantity of moles of neurotransmitter present inside the vesicle at any time t.
There is a considerable continuous interest from neurobiologists and medical doctors about the fine details of intracellular vesicular transport and extracellular delivery of neurotransmitters owing to their vital role in allowing many cells functions.6–9 This high importance is evidenced, for example, by the award of two recent Nobel prizes in physiology and medicine bearing on these issues, the latest one being awarded in 2013 to James E. Rothman, Randy W. Schekman, and Thomas C. Südhof.8,10–12 However, it must be recognized that despite strong efforts of physiologists the very final acts of this process, viz., those controlling extracellular release are still poorly understood. Indeed, experimental methods prone to investigate these decisive steps are scarce due to their very small duration (millisecond range), the fact that they involve minute amounts of molecules (thousands to millions at most) and that they rely on transient dynamic nanometric biological structures.
Patch-clamp methods are sufficiently sensitive and fast to observe initial fusion pores formation and dynamics (Figure 1)13–17 but their performance cannot be straightforwardly extended to examine "full fusion" stages though this is when most of the neurotransmitter vesicular contents are released, at least in endocrine cells if not in neurons.16 Indeed, deconvoluting patch-clamp impedance data requires independent calibrations which are not available except for the initial fusion pore stage.17,18 On the other hand, if fluorescence microscopy (TIRFF) is certainly useful for validating experimentally the very concept of vesicular exocytosis,20 it lacks two important characteristics to be fully adequate for quantitative investigations of the very act of release at the required precision level. One stems from the still too low spatial resolution that does not allow precise scrutiny of fast dynamic structures of nanoscale dimensions. The other, may be more important even if not pointed out, is that TIRFF conclusions rely on the observation of a few specific events whose frequency of occurrence is not reported. It is thus difficult to infer statistically significant data from them. Indeed, each vesicular exocytotic event is a single event with its own characteristics, no matter that thousands to millions of molecules are released during each one. Amperometric measurements have clearly established that these characteristics vary substantially around median values, i.e., with large relative variances.2 Hence, whatever is the intrinsic value of the information brought by TIRFF experiments, up to now, it cannot be considered as statistically representative but should be rather viewed as reporting only on those maybe rare events whose characteristics fit the requirements of the method to be discernable and analyzed.
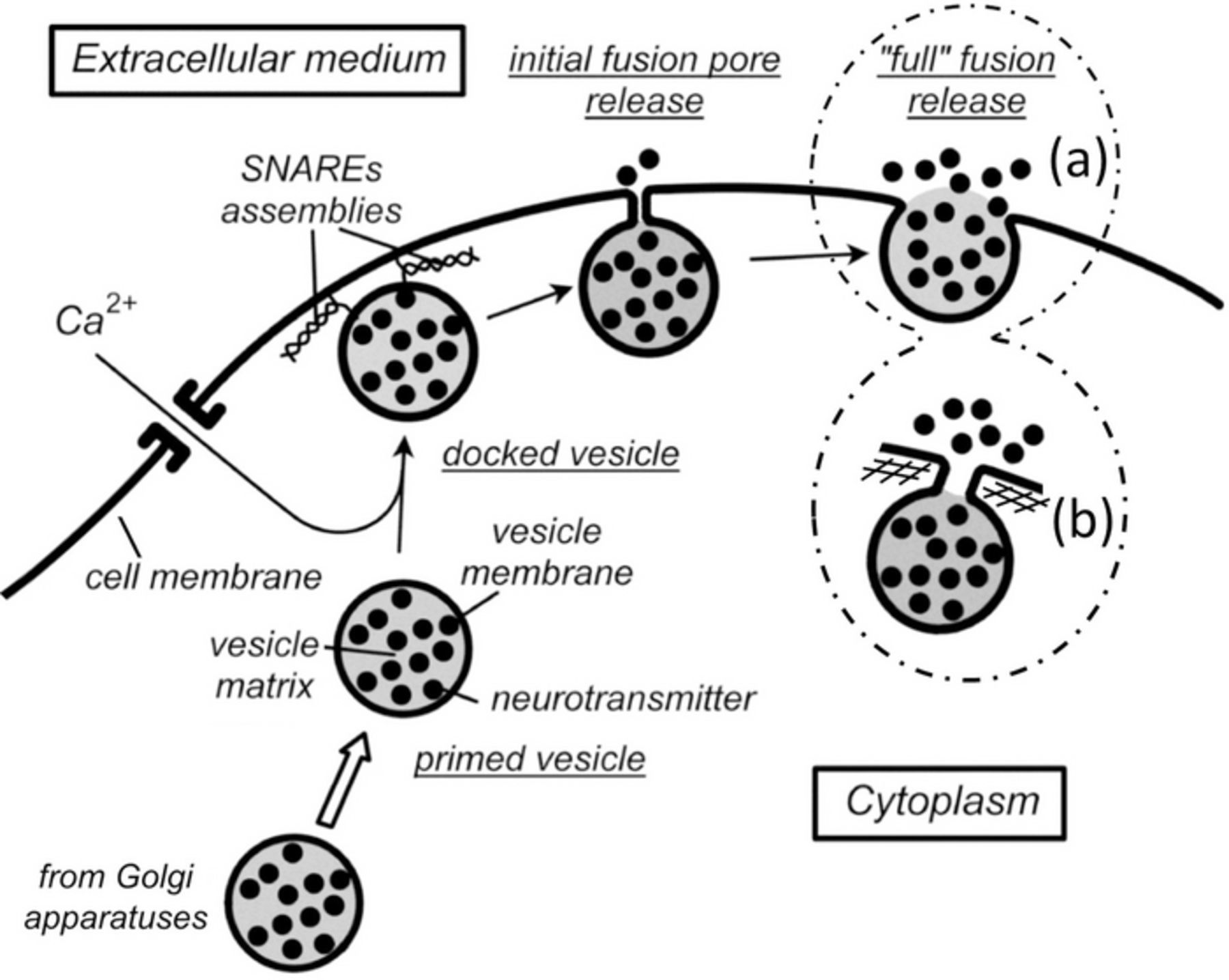
Figure 1. Schematic representation of the "life" of an exocytotic vesicle. Each cartoon enclosed by dashed lines displays one of the two current views of the "full fusion" topology: in (a) is shown the classical one given in neurobiological textbooks or inferred from TIRFF experiments, i.e., involving a large proportion of the former vesicle membrane being mechanically integrated into that of the cell; in (b) is shown a recent view based on recent works from Ewing's group and ours in which the fusion pore has drastically enlarged vs. its initial size but has still a small dimension compared to the vesicle radius. SNAREs assemblies are shown only in the "docking" stage and omitted elsewhere for clarity; the same is true for the inner and sub-membrane cytoskeletons, except in (b) where the sub-membrane cytoskeleton mesh is sketched to illustrate one possible mean of constraining the fusion pore expansion.
To the best of our knowledge, the third method widely used nowadays is the "artificial synapse" amperometry that was briefly alluded to above.1–5,19,21–25 It possesses all the sensitivity, the selectivity and the precision required for monitoring of exocytotic vesicular fluxes including those which lead to releasing only a few thousands molecule over a few milliseconds range. It also allows measurements of thousands of single events contained in a single amperometric trace enabling statistically meaningful information to be obtained at the single cell level. These powerful advantages and the fact that it is easily implemented using low cost and common instrumentation explain its high popularity and its dissemination beyond the electrochemical community in neurobiological laboratories.
However, as with patch-clamp, deconvoluting amperometric currents for extracting precise quantitative data about the fusion pore topology, energy and dynamics for each single event monitored requires a proper theory, hence a proper model.22–25 We proposed recently such theory to deconvolute diffusional components (diffusion of the neurotransmitter cation inside the vesicle matrix on its way out) from current-time measurements to extract dynamic and topological data relative to fusion pores as well as their relative energy distribution.24–25 In the hands of Ewing's group and ours,24–27 this has allowed establishing that, in contradiction with the admitted knowledge summarized in neurobiology textbooks, fusion pores do not expand sufficiently to lead to a "full fusion" of such amplitude that the former vesicle membrane is almost fully integrated mechanically into the cytoplasmic one.20 In fact, Ewing's data and ours, though obtained independently on different endocrine cell models (PC12 for Ewing's group, chromaffins for ours) established that at its maximum expansion the fusion pore surface area reaches barely one or two hundredth of that of the vesicle membrane. This is considerable when compared to the ca. one hundred times smaller surface area of the initial nanometric pore but is still very small compared to vesicles sizes. This evidences that the few reported TIRFF observations of total "full fusion" events ought to be rare ones spotted precisely because they are the only ones with the adequate characteristics to be observable by TIRFF. Most of vesicles remain connected to the extracellular medium through a nanometric pore (or a nanotube in Ref. 28). Note that even if Nature is not necessarily parsimonious in managing its own energetics, this seems to be a more energy-efficient mechanism than the assumed "full fusion" one. Indeed, the vesicle can then readily close its nanopore and be recycled without implying long and energetically and entropically costing endocytotic mechanisms.
Nevertheless, one must be well aware that despite their importance all these data rest on an assumption introduced by Wightman and one of us when the first quantitative kinetic model describing such amperometric responses was reported.22 Indeed, in this seminal work and all following models transport of neurotransmitter cations inside vesicles is supposed to involve only diffusion or diffusion-equivalent processes such as hopping between chromogranins chelating sites.29–33 In other words, although this occurs within a dense anionic polyelectrolyte matrix, migration and matrix-swelling effects are neglected. Migration can safely be neglected owing to the high ionic content of matrixes that rapidly screens strong electrostatic interactions (see below).34 However, the effect of osmotic pressure,35 i.e., of swelling of matrix granules has to be seriously considered as several authors did.36–37 Indeed, according to thermodynamics, swelling of these granules is expected as a consequence of the exchange of neurotransmitter cations by hydrated monovalent ions that necessarily enter inside it to maintain electroneutrality during release.36–37 However, this expected swelling may not contribute kinetically to transport during release under three circumstances. Swelling may be extremely fast so that diffusion would be the slow step. Conversely, diffusion may be faster than swelling so that it would be unseen in measurements of release rates by amperometry. Finally, swelling may not occur at all at any significant level. We wish to establish in the following that the second or third situations are theoretically favored when release occurs under normal physiological conditions, i.e., when the matrix remains wrapped by its intact membrane during the whole release process. This in turn will lead us to propose a new model for the internal matrixes structures. This model considers that dense cores are not homogeneous but consists of compact nano-grains dispersed in a less compacted polyelectrolyte structure. This view fully complies with fundamental physical laws established by de Gennes and his school to describe the structure and properties of condensed polyelectrolytes at nanoscale levels.38,39 Though theoretical, hence, to the best of our knowledge, difficult to validate directly under physiological conditions with the present means of investigation, this model will be shown to be fully coherent with all amperometric data published up to now, and furthermore predicts many reported recent puzzling observations that had to remain unexplained up to now.
Results and Discussion
Figure 1 summarizes the sequence of steps followed by an exocytotic vesicle after it has been tailored in the Golgi apparatuses and arrived near the releasing site.6–12 Molecular motors transport the vesicle along the actin cytoskeleton up to near the releasing hotspots where it reaches a vesicle pool and becomes primed. When calcium ions enter nearby through specific opening of calcium channels, the vesicle docks at its release site through a calcium-promoted assembling of SNAREs complexes.40–42 This provokes a drastic increase in the curvatures of the vesicle and cell nanometric membrane patches entrapped between the SNAREs pillars. That and the mutual strong electrical fields generated onto each other by the membrane patches closely facing at angströmic distances are expected to spontaneously provoke the easy electroporation of both bilayers and their fusing to relieve the high membranes electrostatic and mechanical tensions.43 Several physicochemically realistic mechanisms have been proposed to model these fundamental steps44,45 yet, for our purpose here, it is sufficient to consider that this very fast process leads to the sudden opening of a well-characterized nanometric initial fusion pore (ca. 1.2 nm radius as deduced from patch-clamp measurements)17 through which the vesicular matrix content is exposed to the extracellular medium.
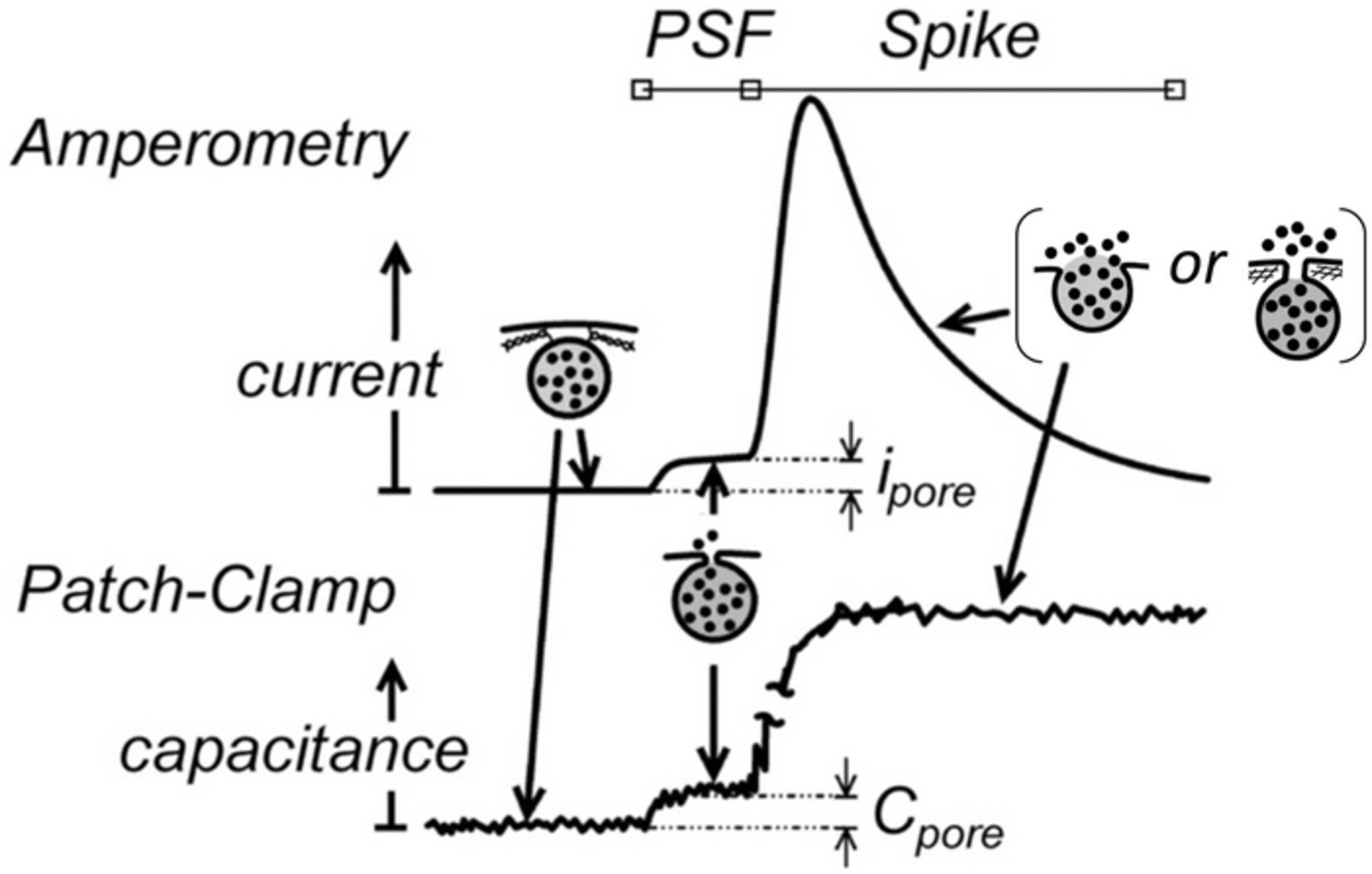
In amperometric measurements (see Figure 2), the initial fusion pore lasts generally a few milliseconds at most, and can be observed in ca. 30% of the events as a small current plateau, ipore, named PSF (pre-spike feature) or "foot".25–27,46,47 After this initial phase, the SNAREs architecture is supposed to unlock so the fusion pore may rapidly expand to release the tension due to the locally high membrane curvatures. Indeed, bilipidic bilayer membranes are borne to reach a flat topology to minimize their curvatures. Thus, in absence of any other effect the fusion pore should expand by mechanical transfer of the vesicle membrane into the cell one. This would lead to a complete "full fusion" as sketched in inset (a) of Figure 1. There is no doubt that this may occur based on a few TIRFF reports.20 These showed that all fluorescent-tagged bilipids dispersed within vesicle membranes were transferred into the cell membrane within a few milliseconds. This is much faster than diffusion or flip-flop mechanisms would allow, thus supporting the occurrence of a literal "mechanical streaming" of the vesicle membrane into the cell one. However, a considerable body of statistically significant quantitative amperometric evidences questions the generality of this process and led to the progressive emergence of a new view of the "full fusion" stage. According to it, the expansion of the fusion pore stops after its surface area reaches at most ca. a few hundredths of that of the vesicle membrane.25–27 This is depicted in inset (b) of Figure 1. In this cartoon, for simplicity, the pore expansion is assumed to be stopped by the sub-membrane cytoskeleton (ca. 20–25 nm mesh size).48 However, several other intracellular proteins may be responsible for refraining the fusion pore expansion and may conceivably cooperate.26,27 Whatever the biological constraint involved, the pore may then stay stable up to the end of release or, for a small proportion of observable events, even undergo a closing phase before release ends.49
However, although firmly based on quantitative grounds and simulations, this new concept rests on models that consider that the transport of the neurotransmitter cations within the vesicle matrix occurs exclusively by diffusion.23–25 In other words, this assumes that the vesicle matrix swelling plays no kinetic role during the release stage, a fact that needs to be discussed and validated hereafter in more detail than was done in our previous work.
Diffusion vs. matrix swelling in controlling rates of release
At first glance, thermodynamics might appear to require swelling of condensed polyelectrolyte matrixes when they release. Indeed, to account for electroneutrality the outward flux of neurotransmitter cations is necessarily compensated by an equal influx of monocations associated to an inflow of water molecules (probably hydrated Na+ and H3O+ ions owing to their prevalence in the extracellular fluid) and possibly by inward ATPases-driven proton fluxes across the vesicle membrane. These hydrated monocations cannot create a dense hydrogen-bonds network with the polyanionic matrix peptidic groups as catecholamine cations do. This enforces dipole-dipole repulsions between chromogranins carboxylate moieties that must then mutually fend off to allow sufficient screening of the local dipole-dipole electrostatic repulsions. Hence, an isolated vesicle matrix should not retain its initial compacted stage during release and should swell concomitantly. This has been validated in vitro by experiments performed on isolated giant mast cells granules from beige mice whose membranes had been stripped off.37,50–52 The same was observed during exocytosis of "naked" cortical granules from Lytechinus pictus eggs,53 and may even be observed in electron microscopy (EM) micrographs in which a considerable fraction of the former matrix is literally extruded through large fusion pores.54 However, there are several indications that under physiological conditions, i.e., when the vesicles membranes are left intact, swelling is kinetically delayed. For example, the same authors as in Reference 53 reported that under in vivo conditions giant mast cells granules from beige mice exhibited fusion pore expansions before the granules could swell to any observable extent.55 This indicates that observations performed in vitro on "naked" vesicular granules cannot be readily generalized to physiological in vivo conditions.
Tanaka and Fillmore established theoretically that the swelling rates of spherical gels submitted to a positive osmotic pressure π0 is given by Equation 1:35
![Equation ([1])](https://content.cld.iop.org/journals/1945-7111/163/4/H3014/revision1/d0001.gif)
where Rt = 0gel is the initial gel radius, Rt → ∞gel = Rgelt = 0/[1 − π0/(3K)] the final one achieved when expansion stops because the initially applied osmotic pressure π0 has been fully relaxed, and K the bulk modulus of the polymeric network. This prediction was fully validated by the same authors through measurements performed on a series of millimetric-sized spherical polyacrylamide gels. Interestingly, the swelling time constant τswell scales with the square of the final particle radius:
![Equation ([2])](https://content.cld.iop.org/journals/1945-7111/163/4/H3014/revision1/d0002.gif)
where μ is the shear modulus of the gel and f the friction coefficient between the gel network and the fluid medium which penetrates into it during swelling. Note that Dswell = (K + 4μ/3)/f has the dimension of a diffusion coefficient and is called the "diffusion coefficient of the gel" for this reason35 though this may be misleading outside of this context. Hence, τswell = (Rt → ∞gel)2/Dswell is formally identical to the time constant of diffusional leakage from a spherical body of identical radius when its entire outer surface is fully permeable to the diffusing particles. In fact, this formal mathematical analogy is total as evidenced by the long time limit of Equation 1 which is achieved as soon as t > τswell:
![Equation ([3])](https://content.cld.iop.org/journals/1945-7111/163/4/H3014/revision1/d0003.gif)
Indeed, introducing qgel(t) = ω[Rt → ∞gel − Rgel(t)], where ω is a suitable constant quantity with the units of moles/length (yet, see later an important caveat about such formal definition), Equation 3 results strictly identical to that giving the quantity, q(t):
![Equation ([4])](https://content.cld.iop.org/journals/1945-7111/163/4/H3014/revision1/d0004.gif)
of molecules or ions remaining at time t inside a fully exposed spherical body of radius Rves initially filled with a quantity qt = 0 = ω(Rt → ∞gel − Rgelt = 0) of ions or molecules that diffuse out of it with a constant diffusion coefficient Dves, as soon as t > τdiff = (Rves)2/Dves. Note that this formal identity is true at any time even if we insist here only on the long time limits for simplicity in comparing Equations 3 and 4. However, this mathematical analogy between swelling and releasing rates is wrong and misleading because it rests on the introduction of an ad-hoc quantity, ω, that has no physical sense. Hence, any such formal identity between a swelling radius and a diffusing quantity has no physical meaning at all as is established immediately hereafter, though this has misled previous authors.36
It is important to remark that under the conditions where Equation 3 applies, the local swelling "wave" performs under quasi-steady state across the whole gel,35 i.e., the swelling intensity along one gel diameter becomes independent of time when normalized to that of Rgel(t) (note that the same is true for concentration profiles when Equation 4 applies). Therefore, when a swelling gel may release material only through swelling (i.e., upon assuming no diffusion limitation but that ions and molecules are released infinitely fast to only cope with the local amount of swelling), the quantity of material, qswell(t), still contained inside the spherical gel at any time t > τswell is given by (see Appendix):
![Equation ([5])](https://content.cld.iop.org/journals/1945-7111/163/4/H3014/revision1/d0005.gif)
where Rgel(t) is given by Equation 1 or Equation 3 according to the time scale relative to τswell. This readily follows through remarking that the total number of unit cells, viz., filled and empty, in the gel matrix remains constant (as would chromogranin anionic moieties during exocytosis) while their local volumes expand with time due to the partial local exchange between catecholamine cations by hydrated monocations. Since Equation 3 shows that Rgel(t) approaches its limiting value Rt → ∞gel in a strict single-exponential mode, its involvement to the cubic power in Equation 5 implies that qswell(t) time-variations cannot follow a single-exponential mode. More precisely, qswell(t) time-variations are given by a linear combination of three exponentials with perfectly related time constants: τswell, τswell/2 and τswell/3. This is then also to be the case for, φswell, the released flux of material since φswell = −dqswell/dt. This cannot be reconciled with the single-exponential decay predicted for release by diffusion from a homogeneous matrix (Equation 4). Furthermore, this is in clear contradiction with most amperometric measurements that establish that descending branches of amperometric spikes (see Figure 2) follow a strict single-exponential mode decay or, as recently reported by Ewing and coll., may display a two-exponential one involving two unrelated time constants (see below). This clearly shows that swelling and diffusion cannot be simultaneous active during vesicular release. Either swelling occurs rapidly compared to diffusion or, if swelling actually occurs, this happens only after release fluxes have reached too low amplitudes to be observed by amperometry.
This conclusion, is made even stronger when remarking that the above analysis considered the most favorable situation for swelling. Indeed, Equations 1 and 3 are only valid for a "naked" matrix although in the case of vesicular exocytosis matrixes are still, at least in part, wrapped by their membranes. Tanaka and Fillmore rate law thus overestimate vesicular matrixes swelling rates through neglecting the Laplace tension-induced pressure, πsurf, exerted by the membrane onto the matrix over most part of its surface and that increases with time as detailed below. This ought to compensate the osmotic pressure π0 driving force thus reducing the swelling trend. For small fusion pores, π0 needs to be replaced by (π0 − πsurf) since the membrane almost covers the whole matrix. Conversely, for large fusion pores, (π0 − πsurf) applies only where the matrix is still covered by its membrane, so that whenever a large pore may be formed, π0 may induce swelling over the membrane-free pore area. This may possibly lead to an extrusion of the swelling matrix section through large fusion pores as observable in some EM micrographs.54
It is thus understood that the presence of the membrane affects swelling vs. the case of a gel as investigated by Tanaka et al. because of the role of πsurf. So, let us precisely examine the role of πsurf in limiting swelling. For this purpose we assume that at a given time swelling provokes an increase ΔRves of the vesicle radius Rves(t). To account for this increased radius the surface area of the membrane vesicle needs to increase by 8πRvesΔRves if the radius of the fusion pore Rpore is constant (if not, e.g., at the very beginning of release, the membrane surface area increase is 2π(4RvesΔRves − RporeΔRpore) where ΔRpore is the simultaneous increment of the pore radius). The duration of exocytotic release, being in a few milliseconds range, is too short to allow any biological mechanism to incorporate intracellular bilipids inside the vesicle membrane bilayer to compensate for such rapid surface increase. Since there is not any observation establishing that some of the cell membrane could slip by the pore area to compensate for this increase (in fact the rare TIRFF observations evidencing membrane flows show exactly the opposite20), any ΔRves would increase the membrane surface tension energy by 8πγRvesΔRves, where γ is the membrane surface tension coefficient. Thus, unless the vesicle membrane structure is totally ruptured or forms a high number of pores due to the surface tension building up56 the osmotic driving pressure is rapidly counteracted by the Laplace tension pressure exerted by the vesicle membrane. Therefore, the impeded swelling accumulates a positive energy inside the matrix core while release occurs. According to Laplace law, the surface tension coefficient, γ, of the vesicle membrane increases with time proportionally to the pressure difference, ΔP(t), building between the vesicle inside due to the impeded swelling and that, ca., 1 atm, prevailing in the cytoplasm: γ(t) = RvesΔP(t)/2. This evidences that even if a small amount of initial swelling occurs initially and provokes the rapid fusion pore expansion, it is rapidly contained by the membrane surface tension.
A second consequence of the membrane-refrained swelling is coherent with the fact that under normal physiological conditions exocytotic events appear to release significantly less than their total initial content in catecholamine.21 Considering that release occurs from a matrix not allowed to swell to any significant degree implies that the content of catecholamine cations inside the matrix cannot drop to too low values. Indeed, the presence of catecholamine cations stabilizes the condensed structure of the matrix (see below). Conversely, when the vesicle membrane is stripped off, swelling may occur and its whole initial content may be released.21,36
The above established that if swelling seems a priori favored based on simple thermodynamic considerations it must be kinetically and thermodynamically hampered by the vesicle membrane while it contains the whole granule. This is certainly an important conclusion since it is predictable that changes of the membrane bilipid composition in different vesicles or over longer time scales may result in a modulation of release rates and quantities through controlling swelling upon increasing or decreasing πsurf.
The situation results entirely different for diffusion. Indeed, we established previously that fast diffusional release may easily occur even when the pore surface area is much smaller than that of the vesicle.24,25 The fact that diffusion out of the matrix then occurs through a small fusion pore of radius Rpore = ρRves only results in a moderate apparent decrease of the outward-diffusion rate, i.e., from kdiff = (Dves/R2ves) for a fully exposed matrix to kdiffρ = Λρ(Dves/R2ves), where Dves is the cation diffusion coefficient inside the polyelectrolyte matrix and Λρ is a factor that varies linearly with ρ = Rpore/Rves when this is small.24 Indeed, Λρ ≈ Arcsin(ρ)/π2 up to ρ ≈ 0.85, i.e., Λρ ≈ ρ/π2 for ρ < 0.4, a range that amply covers that of the maximal fusion pore extensions.25 The descending branch of the amperometric current is then readily given by:
![Equation ([6])](https://content.cld.iop.org/journals/1945-7111/163/4/H3014/revision1/d0006.gif)
in full agreement with quantitative analyses of most experimental spikes24,25,57 (sed vide infra). In other words, in drastic contrast with its huge effect on swelling, the presence of a membrane still covering most of the matrix during release just slightly slows down the rate of diffusional release.
Do vesicles contain homogeneously compacted core matrixes?
The fact that diffusion dominates over swelling creates a delicate problem. Indeed, amperometric data for chromaffin or PC12 cells evidence that the diffusion rate Dves/R2ves of catecholamine cations inside the matrix must be in the order of 420 s−1,24,25 which corresponds to Dves values in the range of 10−7 cm2s−1 for vesicles with radii Rves ranging between 100 and 150 nm. This is essential to account for the large measured release fluxes. However, diffusion coefficients of bulky ions such as catecholamine cations prone to create a dense network of hydrogen-bonds in a condensed polyelectrolyte such as exocytotic granules are expected to be rather small. More precisely, a high concentration (0.3 to 0.6 M) of catecholamine cations confined inside a spherical domain of radius, Rves ≈ 100 − 150 nm, corresponds to a few millions of molecules.2,21 Hence, assuming a homogeneous, viz., an isotropic distribution of catecholamine cations within the matrix points out that each cation-anion pair would occupy an average volume of 2–3 nm3. This is similar to what is expected for the global size of one peptidic anionic moiety and one catecholamine cation, i.e., should leave almost no significant free space to allow sufficiently fast diffusion. However, this difficulty does not hold if the matrix structure is not homogeneous, viz., if it contains domains with different compaction levels. This seems to contradict the general experimental knowledge based on the fact that EM investigations of prepared cell slices suggest that matrixes are rather homogeneous.54
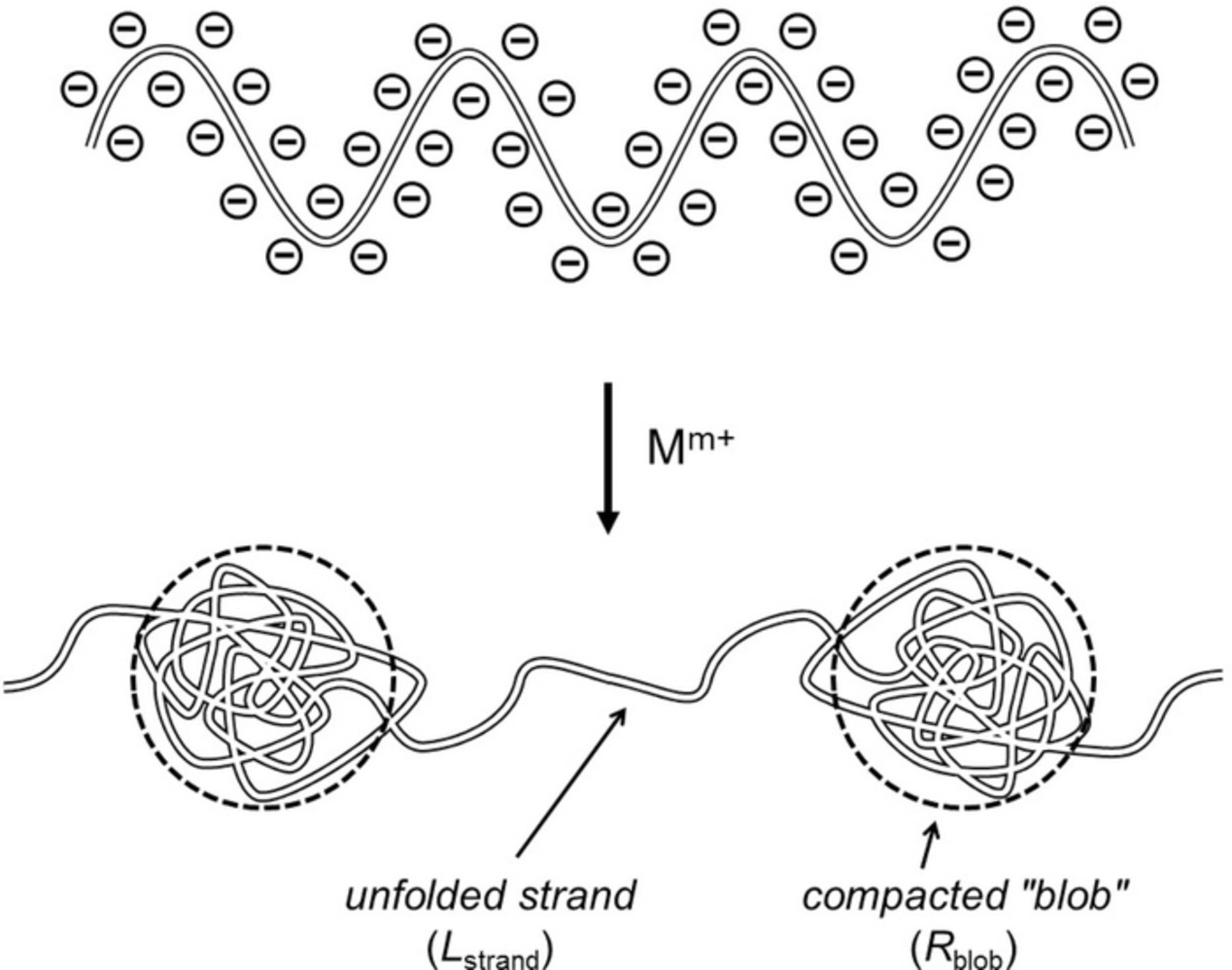
The homogeneous condensation of chromogranins is unlikely to prevail under in vivo conditions based on the physics of polyelectrolytes. de Gennes and coll., established the physical laws that govern the condensation of long polyanionic polymer chains such as chromogranins depends drastically on the counter-cations charges.38,39 Briefly, the too small electrostatic energies provided by monocations is rapidly overran by the increasing negative entropy due to the dense folding of the polyanionic chain when the size of the compacted nodules increases. To relax this entropic load the polyanion-monocations ensemble adopts a pearl necklace type structure as occurs for long DNA single strands, in which small highly compacted nanodomains are separated by polyanionic strands around which monocations are less tightly bound (Figure 3). Dications lead to a similar structure except that the dense nodules size result larger due to the increase in electrostatic interactions and to the possibility of locking electrostatically topologically distant negative moieties into hairpin configurations. Conversely, trications provide sufficiently high electrostatic energies to allow a high compaction over macroscopic distances. Note that this may be the reason for the apparent homogeneity of dense core matrixes as revealed by EM since most cell slices preparations involve the use of lanthanides trications for providing a high density contrast between the matrix (hence the common name of "dense core matrixes") and the surrounding cytoplasmic components.54 In fact, molecular dynamic simulations of chromogranins folded structures58,59 agree with the above prediction based on the nowadays classical de Gennes' "blob" theory since they evidence a coexistence of two types of nanoscale domains with different compaction as predicted here.
Figure 3. Schematic representation of the condensation of polyanionic polymeric chains such as chromogranins by cations Mm+ according to de Gennes and coll. When the cation charge 'm+' increases the radius Rblob of the compacted "blobs" increases while the length Lstrand of the near unfolded domains between blobs decreases (see text). For simplicity only one free chain is represented. When this is extrapolated to a 3-dimension volume such as a vesicle matrix, it is presumable that this leads to compact nodules (the 'blobs' here) dispersed in a less compact structure (formed by weak association of the much less folded strands) such as that depicted in Figure 4A.
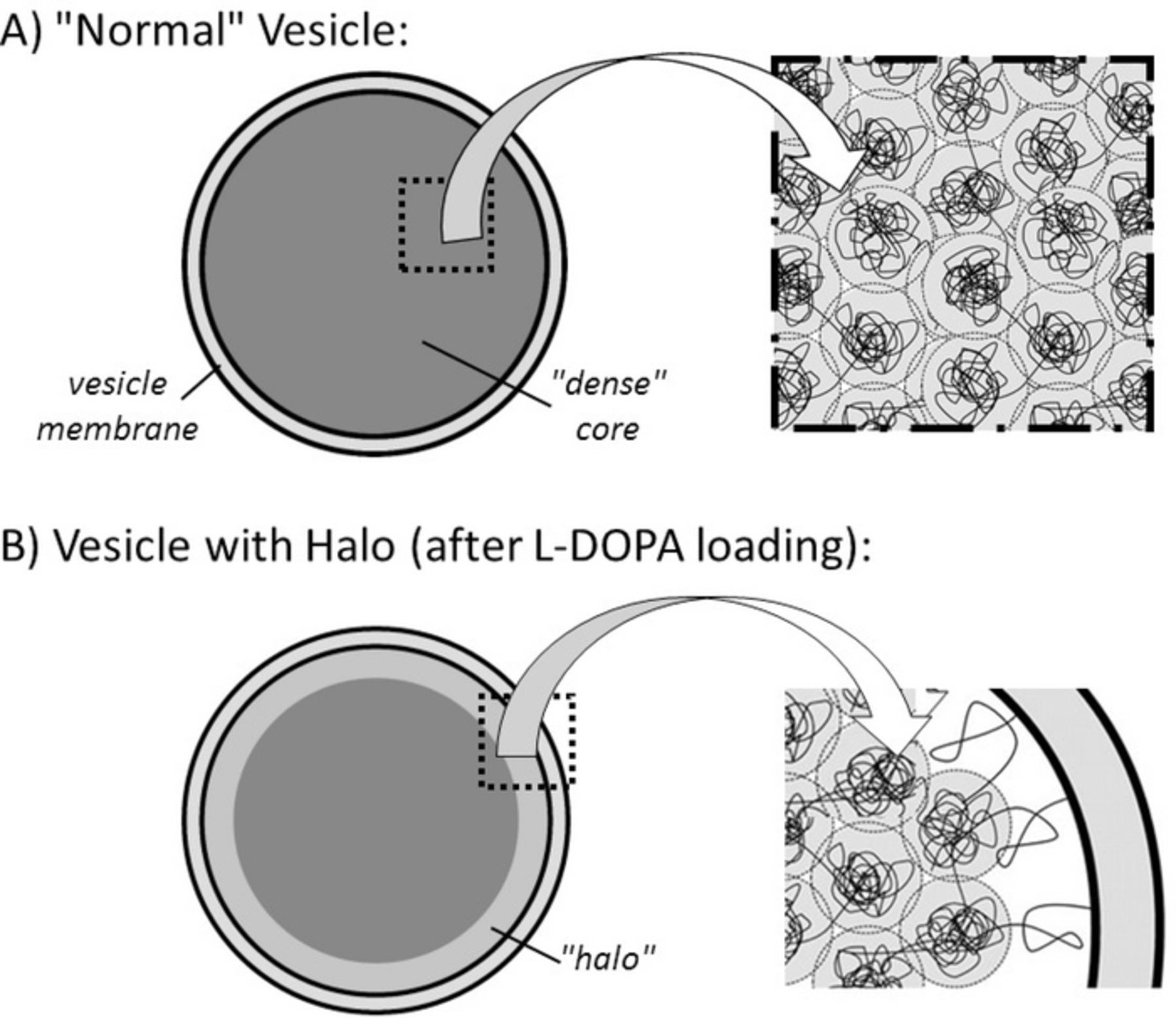
Catecholamine cations (Cat+) carry a single charge but their phenolic OH groups and ammonium N-H ones are prone to form a dense network of hydrogen-bonds with peptidic groups along the chain. This provides additional energy vs. simple 1:1 local electrostatic interactions. It is then presumable that they enforce a stronger compaction than that expected from hydrated monocations (e.g., Na+,n H2O; H3O+,n H2O) though weaker than that enforced by dications such as Ca2+ and far less than trivalent counter-cations do.60 In this respect, it is worth recalling that in addition to a high concentration of catecholamine cations, vesicle matrixes contain also non-negligible concentrations of strongly chelated calcium ions (ca. 40 mM)61 whose long term permanence inside vesicles is maintained by specific calcium channel pumps.61–64 Though the relative amount of Ca2+ vs Cat+ is small, it is noted that calcium ions have a high affinity for hydroxyl groups. Besides the effect of Ca2+ dications per se (see above) they may chelate up to 3–6 Cat+ per Ca2+. If so within the matrix, this will form highly charged aggregates, CanCAnx(2+x)n where x ≤ 6, contributing both to a higher level of compaction than Ca2+ alone would do and to firmly sequestrate up to a few tens percents of catecholamine cations within these highly compacted nodules. The remaining Cat+ should then be contained in the less tight environments formed by the less folded chromogranin chain sections.58,59 Not only these latter are less bound to the matrix backbone than those in the dense nodules, but they should also be able to diffuse much faster across the matrix through the interconnected less compact domains (Figure 4A) than they would if the matrix structure was homogeneously compacted.
Figure 4. (A) Schematic depiction of the nano-components internal structure proposed here for dense core vesicle matrixes. The black filaments represent the chromogranin backbones, while the gray areas feature the less compacted areas containing less tightly bound catecholamine cations and serving of fast releasing reservoirs. (B) Creation of a halo after loading with L-DOPA (see text) through slow swelling of the outer layers of the structure shown in A.
Evidently, this model has to remain theoretical in essence up to when more physiologically compatible means of investigation at the subnanometric scale become available. However, it is firmly rooted on established fundamental physical laws of polyelectrolytes condensation. So, presently, its validity can be established only by reference to the de Gennes' theory38,39 and through the validity of the predictions that it allows in view of the body of amperometric data present in the literature. So, let us examine what predictions can be derived from this model.
A first evident conclusion is that the existence of a highly compact polyelectrolyte nano-reservoirs allows increasing the free space around the less-bound Cat+ cations stored in the less compacted polyelectrolyte. Though this is not readily quantifiable presently, this is expected to allow significant diffusion rates compared to what would occur in a homogeneously compacted matrix as already perfectly observable in the outcome of molecular dynamic simulations.58,59
A second direct consequence of this two-reservoir model is that the strongly bound Cat+ ions contained in the tight nodules should not be easily available to release unless there is some non-negligible kinetic exchange between the two types of reservoirs during release or if the whole matrix may partially swell before the membrane reaches a critical tension and blocks swelling. The consequences of possible kinetic exchange between the two types of reservoirs during release will be examined in a next section, so let us focus here on the second possibility. As established above, whenever the matrix membrane is removed completely or at least over a large section of the matrix surface area, swelling is not anymore impeded so that the swollen dense nodules may release their content so the whole content of the matrix may be discharged. Conversely, under physiological conditions, i.e., when release occurs through a small fusion pore connecting the vesicle inside to the extracellular medium, swelling of the dense nodule should not occur to any significant extent as established above. Hence, amperometric measurements of the vesicles load must result less by a few tens percents than the overall content present in vesicles (sed vide infra if a kinetic exchange between the two types of reservoirs happens at a sufficient rate during release). Interestingly, this is exactly what Ewing's group has observed.21 In a series of seminal experiments they convincingly demonstrated that under in vivo physiological conditions PC12 cells vesicles release stops (i.e., gives rise to amperometric currents, if any, that become indistinguishable from the background current) while the vesicles still contain in average between ca. 40 to 60% of their initial catecholamine content. Oppositely, release from the same PC12 vesicles was total after their membranes were stripped off.
Consequence of the two-reservoir nanostructure on release kinetics
Cat+ cations stored in each of the two types of nanoreservoirs differ by the strength of their attachment to the chromogranins backbone (i.e., different partition coefficients vs. the extracellular fluid) and by their mobility within their local environments (i.e., different diffusion rates). Both factors affect the rates of release into the extracellular environment. To be released, the strongly bound Cat+ cations need to exchange with the less bound ones, while the latter ones diffuse at significant rates along tortuous paths around the highly compacted domains (Figure 4A). As a first approximation, this duality may be represented by the following mechanism:
![Equation ([7])](https://content.cld.iop.org/journals/1945-7111/163/4/H3014/revision1/d0007.gif)
where qslow and qfast represent the time dependent quantities (moles) stored in the highly and less compacted reservoirs respectively and qout that which has been already released in the extracellular fluid, hence been detected electrochemically. With these definitions, qslow + qfast + qout = qt = 0total where qt = 0total = qslowt = 0 + qt = 0fast is the initial vesicle load at t = 0. k1, k2 and kdiffρ = Λρ(Dves/R2ves) are kinetic parameters globally equivalent to classical rate constants though they combine chemical and physicochemical components. In fact, they should be more appropriately viewed as reciprocals of the time constants featuring each of the three phenomena represented in Equation 7. Note that k1/k2 = qt = 0fast/qt = 0slow if the matrixes were in thermodynamic equilibrium before release started. Note that considering Ewing's reports that between ca. 40 and 60% of the catecholamine cations remain trapped within the matrix at the end of release,21 k1/k2 values are then expected to range between 2/3 and 1.5. Within this framework, the amperometric current is then simply expressed as:
![Equation ([8])](https://content.cld.iop.org/journals/1945-7111/163/4/H3014/revision1/d0008.gif)
In the following, we assume for simplification that the fusion pore suddenly opens at its maximal aperture Rpore = ρRves × Θ(t) where Θ(t) is the Heaviside step function. In other words, the following analysis considers only the descending branches of amperometric spikes. Indeed, these are the spikes currents components that essentially report about the diffusion-controlled kinetics of release. To produce full simulated current spikes the following results need to be convoluted with specific pore opening time functions, Rpore(t), as previously reported in detail.24,25 This only alters the short-time currents, i.e., before and shortly after the spike maximum, so for the sake of simplicity and generality we do not consider this issue here.
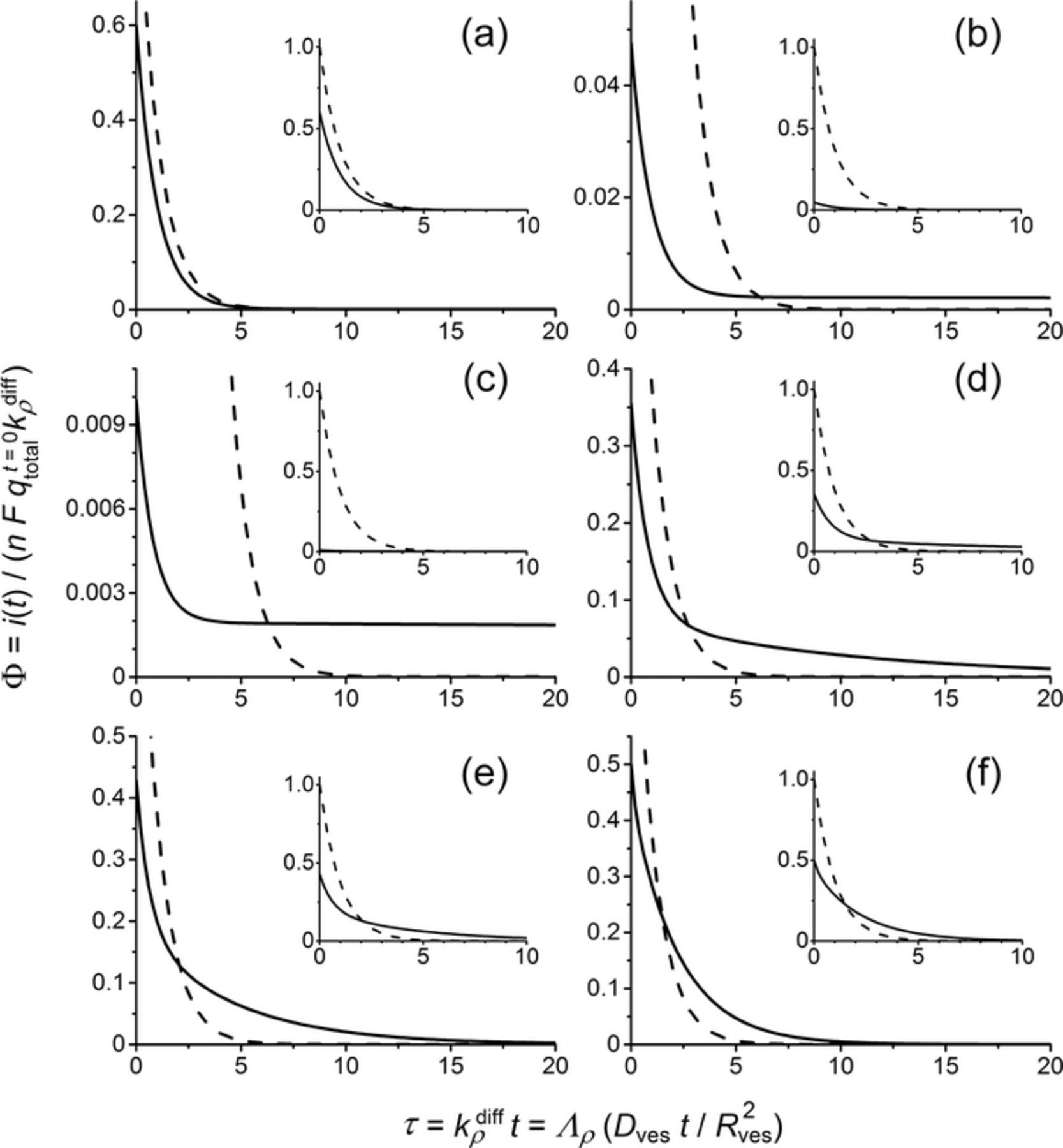
The system in Equations 7 and 8 can readily be solved analytically or numerically to afford different spikes shapes as a function of the relative values of k1, k2 and kdiffρ as illustrated in Figure 5 for a selected choice of χ = k1/kρdiff and κ = k1/k2 values (note that the current and time scales are shown in dimensionless format to account for any possible values of the initial vesicle load qt = 0total or of the apparent diffusion rate kdiffρ).
Figure 5. Effect of the relative values of χ = k1/kρdiff and κ = k1/k2 on the shape and magnitude of amperometric spikes descending branches. χ = 2.5 10− 3 (a,b,c), 0.10 (d), 0.36 (e) and 2.5 (f); κ = 1.5 (a), 0.05 (b), 0.01 (c), 0.5 (d), 0.75 (e) and 1.0 (f). (a): classical single-exponential decay and Qspike = 0.6nFqt = 0total. (b-e): different shapes of the two-exponential decay modes and Qspike = nFqt = 0total (note that Qspike = 0.33nFqt = 0total (b) and Qspike = 0.09nFqt = 0total (c) when the near constant current sections are excluded out). (f): totally mixed behavior (see text) and Qspike = nFqt = 0total. The dashed curve shown as a reference in each panel corresponds to the current predicted for total release (Qspike = nFqt = 0total) from a homogeneous matrix (viz., qt = 0fast = qtotalt = 0 and qt = 0slow = 0) for the same kρdiff value.
In fact, three main limiting situations may be observed. A first one corresponds to k1 and k2 being larger than kdiffρ so that at each moment the content of the two types of nano-reservoirs rapidly equilibrate, i.e., qfast(t) = (k1/k2)qslow(t), so that their global content is released in phase through the action of kdiffρ. Solving the kinetic system in Equation 7 then shows that the current is given by:
![Equation ([9])](https://content.cld.iop.org/journals/1945-7111/163/4/H3014/revision1/d0009.gif)
so that the total electrical charge, 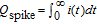 , of the amperometric spike is:
, of the amperometric spike is:
![Equation ([10])](https://content.cld.iop.org/journals/1945-7111/163/4/H3014/revision1/d0010.gif)
Hence, the whole vesicle initial content is released through a spike displaying a classical single-exponential decay branch. However, this occurs with a slower rate than predicted for release from a homogeneously loaded matrix for the same kdiffρ value due to the process of equilibration between the two types of nano-reservoirs. Unless kdiffρ may be known independently, the current variations in Equation 9 cannot be distinguished experimentally from those predicted for a fully homogeneous matrix since (kdiffρ)app = kρdiff/(1 + k2/k1). Would such behavior be observed experimentally it would then be easily mistaken for a normal one and would lead to the determination of a smaller maximal opening of the fusion pore than the actual one: (Rmaxpore)app ≈ Rporemax/(1 + k2/k1) = Rmaxpore/(1 + qt = 0slow/qt = 0fast). Considering the above evaluation of qt = 0slow/qfastt = 0 based on Ewing's experimental results,21 the real maximal opening of the fusion pore would be between ca. 5/3 and 2.5 larger than that determined through a straight application of Equation 6. This would evidently lead to some ambiguity onto the precise determination of Rmaxpore value. Though, this uncertainty is not large enough to obliterate our former conclusions that at their maximal expansion fusion pores radii are much smaller than those of their vesicles.25 Yet, as will be made clear in the following this situation is not likely to be observed in amperometric traces.
The exactly opposite situation is met with when k1 and k2 are much smaller than kdiffρ. This prevents any kinetic exchange between the slow and fast nano-reservoirs over the duration of an amperometric spike. Then only the fast one contributes, i.e., qslow = qt = 0slow at any time. The current again decays through a single-exponential mode, but its amplitude is smaller than expected for the total vesicle load since now release is restricted to the initial content of the fast nano-reservoir, the content of the slow one remaining trapped inside the matrix when the amperometric current returns to the baseline:
![Equation ([11])](https://content.cld.iop.org/journals/1945-7111/163/4/H3014/revision1/d0011.gif)
and:
![Equation ([12])](https://content.cld.iop.org/journals/1945-7111/163/4/H3014/revision1/d0012.gif)
Again, this situation (shown in Figure 5a) may be easily confused with that predicted by Equation 6. Indeed, unless qt = 0total is known independently, the identity between Equations 12 and 6 is total. Interestingly, this seems to exactly correspond to what Ewing and coll. reported in their recent works, i.e., that mean vesicles loads determined from the charge of amperometric spikes were statistically lower than the actual average values measured for the same vesicles when they had their membrane totally stripped off and could release their full neurotransmitter loads.21 Would these measurements correspond to this situation, it is inferred that qt = 0fast ≈ ηqtotalt = 0 was determined by amperometry (with 0.4 ⩽ η ⩽ 0.6 according to Ewing's results) while qt = 0total was measured for membrane-free vesicles. Hence, Ewing's results suggest that the situation described by Equation 12 is extremely frequent.
Finally, a third limiting situation of extreme interest is observed when k1, though small vs. kdiffρ is large enough for its effect not being anymore negligible during a spike duration. The fast nano-reservoirs then deplete rapidly as before but may now be slowly refilled by the slow ones. In other words, the fast nano-reservoirs empty quickly giving rise to the usual single-exponential behavior with a time constant 1/kdiffρ, though this adds onto a slower second single-exponential release with a time constant 1/k1 featuring the slow but continuous kinetic refill from the slow nano-reservoirs. This is leading to a two-exponential formulation of the amperometric current:
![Equation ([13])](https://content.cld.iop.org/journals/1945-7111/163/4/H3014/revision1/d0013.gif)
where:
![Equation ([14])](https://content.cld.iop.org/journals/1945-7111/163/4/H3014/revision1/d0014.gif)
so that:
![Equation ([15])](https://content.cld.iop.org/journals/1945-7111/163/4/H3014/revision1/d0015.gif)
whatever is the value of Γ. This situation corresponds to the cases (b-e) shown in Figure 5. The two-exponential components are clearly visible in panels (d,e), however in (b,c) the second exponential is so slow relative to the first one that it seems to give rise to a near constant current. Its single-exponential nature would show up if the time scale had been extended up to t ≫ 1/k1. However, in real amperometric traces, the time gap between two successive spikes is generally not sufficiently wide to allow such long monitoring of a single spike, so that spikes behaving as in (b,c) may appear as regular spikes superimposed to a constant current onto which the next spike would add. This is often observed in amperometric traces, but up to now such spikes were generally eliminated from quantitative analysis because they were thought to be normal spikes corrupted by a baseline drift. Furthermore, it is noted that the quantity released during the exponential fraction of the current is rather modest (Qspike = 0.09nFqt = 0total for Figure 5c) so that, under experimental circumstances, such spikes would anyway be ascribed to small vesicles (compare to the small relative sizes of the corresponding current intensities compared to a normal spike shown in dashed line). Conversely, when χ = k1/kρdiff is closer to unity (Figures 5d,5e) spikes exhibit a clear two-exponential mode. Although this seems a rather frequent occurrence, i.e., concerns more than half of the spikes in an amperometric trace based on a recent systematic analysis from Ewing's group,26 they were also generally eliminated from quantitative kinetic analyses. Indeed, before the present theory could justify such observations, these spikes were though to result from the accidental superimposition of two spikes, viz., a large sharp one overlaid over a small sluggish one.
The last situation shown in Figure 5f represents a totally mixed behavior in which the spike descending branch cannot be properly resolved into its two single-exponential components but Qspike = nFqt = 0total. This occurs when k1 and k2 have values only slightly higher than that of kdiffρ. It should be noted that even if the present model predicts the possible occurrence of such situations, they seem to be extremely rare based on our own analyses of amperometric traces (chromaffin cells).2 In fact, the above cited systematic quantitative analysis by Ewing and coll. (PC12 cells) evidenced that the large majority of experimental spikes displayed descending current branches that could be described either by a clear single-exponential mode or by a clear two-exponential one exception taken of those eliminated because they were considered to be corrupted by a baseline drift (see above and Figures 5b,5c). This shows a fortiori that the probability of observing release events in which k1 and k2 have values higher than those of kdiffρ is extremely low.
As a consequence, the first limiting situation giving rise to Equations 9 and 10, though theoretically possible, seems very improbable. This suggests that in an amperometric trace, most of the spikes will belong to one of the three following categories: (i) single-exponential descending branch described by Equation 11 and Qspike = nFqt = 0fast < nFqt = 0total, i.e., when k1 and k2 are negligible compared to kdiffρ (Figure 5a); (ii) single-exponential descending branch superimposed to a near constant current plateau (Figures 5b,5c) with Qexpalspike = nFqfastt = 0 < nFqt = 0total, viz., following the limit of Equation 13 when k1 is small but not totally negligible compared to kdiffρ; (iii) two single-exponential descending branch according to Equation 13 and Qspike = nFqt = 0total (Figures 5d,5e). To the best of our knowledge these three categories encompass integrally all the different spike shapes and properties that have been observable in our laboratory or have been reported in the literature. Furthermore, since in most quantitative analyses of release kinetics categories (ii) and (iii) have been generally excluded since they are thought to be corrupted by some accidental superimposition of different spikes (iii) or by some drift of the baseline (ii) it is probable that most quantitative analyses relied exclusively on spikes of category (i). This is important to note that they then correspond only to a partial release of the initial quantity of catecholamine cations stored in the vesicle before release. This is entirely coherent with Ewing's observations that at the end of release between ca. 40 and 60% of the neurotransmitter remains trapped within the vesicle.
Application to the presence of "halos" in PC12 vesicles
A significant proportion of PC12 vesicles exhibit a "halo" around their dense core matrixes. These vesicles are morphologically distinct from dense core vesicles in mast and chromaffin cells, a fact that maybe related to the ability of PC12 to continuously reload their vesicles.65–67 Beyond the very origin of this important morphological difference, it must be noted that the observation of these halos in EM micrographs provides a strong support for the co-existence of different compaction domains of chromogranins-catecholamine cations inside of vesicles.
The formation of such halos is fully consistent with the physical laws giving rise to the present description of dense core vesicles structure.38,39 Indeed, when vesicles are detached from the Golgi apparatuses their initial content in chromogranins is not expected to change. Conversely, when cells are equipped with mechanisms allowing the continuous loading of their exocytotic vesicles with catecholamines, mechanisms which concomitantly tailor their vesicle membranes are also active as evidenced by the larger size of vesicles equipped with halos. This is expected to adjust to the larger surface areas demanded by larger granule sizes without increasing the membranes tension (see above). Hence, in contradiction with cells such as chromaffins whose vesicles cannot be loaded with catecholamines, the slow loading processes should occur while keeping the Laplace tensions more or less constant irrespective of the enlarged vesicle size.
Would these matrixes be homogeneous before loading one would expect that the Cat+ excess is rapidly distributed over the whole matrix. Indeed, such homogeneous-matrixes view imposes that Cat+ mobilities are large enough inside the whole matrix. Would that not be the case, amperometric current intensities of significant magnitude could not be detected when these vesicles release. However, fast mobilities during release is tantamount to saying that equilibration of the extra catecholamine cations all across the matrixes should a fortiori occur during the comparatively long incubation times. It is then deduced that the matrixes will remain homogeneous while loading, hence, halos should not be observable.
Conversely, the formation of kinetically stable halos is a natural consequence of the present model. Indeed, an increase of the [Cat+]/[Ca2+] ratio while keeping the quantity of calcium ions constant61 necessarily leads to an increase of the volume of the less-bound areas through swelling within the present view of dense core vesicle structure. Based on Tanaka and Fillmore's swelling mechanism in Equations 1 and 3,35 the external areas of the initial matrixes must swell faster than the zones closer to their centers where swelling is necessarily delayed kinetically by the increasingly stronger shear forces. Hence, during long incubation times, some vesicles may achieve uniform swelling over their whole volume, while others may not have yet reached this equilibration stage. These latter ones should then display what will appear as a halo around a denser core in EM micrographs (Figure 4B). Conversely, those in which swelling had time to equilibrate all over the matrix volume should appear as large dense ones in EM microphotographs. Finally, those that were not appreciably loaded have to remain small and dense as in normal cells. Interestingly these three categories are observable in EM microphotographs of cell slices after L-DOPA loading, in full coherence with the present model. Note however that when a halo is present, the model has to include an additional rather disorganized reservoir (Figure 4B), in addition to the two previous ones considered above.
For those vesicles in which a halo is formed, the mechanism in Equation 7 should then be modified to account for this fact:
![Equation ([16])](https://content.cld.iop.org/journals/1945-7111/163/4/H3014/revision1/d0016.gif)
where qhalo represents the time dependent quantity (moles) of catecholamine cations stored in the halo. The halo is by definition supposed to be less condensed than the fast releasing reservoir (Figure 4B) and is directly exposed to the fusion pore entrance. It is thus legitimate to assume that release is now mostly occurring through the halo, this being constantly supplied by exchange from the fast reservoir. Furthermore, for a same ρ value, (kdiffρ)halo ought to be larger than kdiffρ considered in the above section owing to the largely disorganized structure of the halo. Finally, for the same reason one may assume for simplification that the quantities stored in the halo and in the fast reservoir are in rapid equilibrium at any time: qhalo = (k3/k4)qfast. Though exchange with the slow-releasing reservoirs can be accounted analytically, for simplification we consider here that this does not occur. Following the same lines as for the derivation of Equation 9, one obtains:
![Equation ([17])](https://content.cld.iop.org/journals/1945-7111/163/4/H3014/revision1/d0017.gif)
and:
![Equation ([18])](https://content.cld.iop.org/journals/1945-7111/163/4/H3014/revision1/d0018.gif)
where qt = 0halo + fast represents the quantity stored jointly in the halo and the fast reservoir, i.e., the total quantity stored in the vesicle diminished by what is poised in the slow-releasing nano-grains. These results need to be contrasted with those given above in Equations 11 and 12. It immediately follows that the overall released quantity (Equation 18 vs. Equation 12) is increased by the presence of the halo, in full agreement with the experimental observations. The relative magnitude of current intensities is more delicate to predict ex nihilo. Indeed, they depend on the global ratio:
![Equation ([19])](https://content.cld.iop.org/journals/1945-7111/163/4/H3014/revision1/d0019.gif)
in which the first two terms are larger than unity but their effect is modulated by the value of (1 + k4/k3) that is unknown a priori.
However, this problem may be solved experimentally. Indeed, another interesting observation from Ewing's group and ours is relative to the changes incurred by vesicles of PC12 cells supplemented with a L-DOPA enriched diet. Under such conditions, the natural vesicles "refilling" mechanisms and "membrane-tailoring" slowly allows incorporating a large excess of catecholamine cations inside doped vesicles. This has two experimentally observable effects. One is the formation of larger vesicles with much larger "halos" than in controls.65–67 The second is that amperometric currents intensities increase by ca. 250% and that the total charge of amperometric spikes also increases by ca. 250%.65–66 However, despite these extremely important changes, the time constants of the current spikes descending branches do not vary significantly for L-DOPA-loaded vesicles compared to controls. This suggests that even if (kdiffρ)halo/kdiffρ is larger than unity, this gain is more or less compensated by the decrease associated to the presence of the factor 1/(1 + k4/k3) in the time constant in Equation 17. Hence, [(kdiffρ)halo/kdiffρ]/(1 + k4/k3) has to be close from unity. This suggests that the increase in current magnitude (Equation 19) has to track approximately that of the released quantity (Equation 18). Although this conclusion is only based on a comparison of time-constants between L-DOPA-loaded vesicles compared to controls it is fully coherent with experimental amperometric observations on PC12 cells since both the current intensity and the released charged increased by ca 250% upon incubation of the cells with L-DOPA.
Finally, if the catecholamine cation kinetics of exchange between the slow and fast reservoirs is sufficient to contribute to slowly refill the fast reservoir while this one empties, Equation 17 should be modified to account for this slow release component. Hence, the current is predicted to obey a composite equation similar to that in Equation 13 and must display as well a two-exponential decay mode. Since no experimental data have been yet reported about such double-exponential behavior for L-DOPA loaded vesicles we did not wish to elaborate further on this possibility. However, it is most certainly highly probable since in vesicles with halos k1 values in Equation 16 should be at least of the same order as in controls (Equation 7) or possibly faster owing to the partial disorganization induced by the partial swelling leading to halo formation.
Conclusions
This work proposed a new conceptual view of the structure of dense core vesicle matrixes. In opposition with the classical opinion that all catecholamine cations stored into vesicular granules are more or less equivalent, viz., experience similar environments, the present model considers the co-existence of two different types of nanometric stores of neurotransmitters. Within this framework, a significant fraction of neurotransmitters cations are tightly bound, possibly together with calcium ions, into highly condensed "blobs" of tightly folded chromogranin sections. The other fraction is less strongly bound and prone to rapidly diffuse within the less compact areas of the matrix that surround the highly compacted nodules.
Such dual nano-reservoirs structure is certainly almost impossible to test presently owing to the lack of experimental method allowing investigations with the proper scale-resolution under physiological conditions. However, the very concept on which this model relies is a normal consequence of the nowadays classical physical laws elaborated by de Gennes and his school to describe the condensation of polyanionic polymers by cations. This theory has been validated under many circumstances including biological ones (e.g., folding of DNA single long strands), so there is no fundamental reason for not considering that it does not apply to chromogranins and catecholamine cations contained in exocytotic vesicles. Basically, it amounts to consider that any long polymeric chain carrying a high density of anionic charges cannot be condensed uniformly by monocations such as catecholamine ones but acquires a structure in which some of its sections are highly condensed and form compact nodules that are immersed into a less condensed domain. The main fundamental reason that lead to such structure rather than a homogeneously compacted one is very reminiscent of that which leads to the splitting of the electrochemical double-layer into a compact one and a diffuse one. Increasing the size of the strongly collapsed cores would amount to increase the negative folding entropy beyond what can be compensated by the decreasing interactions between monocations and anionic sites of the folded chromogranins due to the increasing electrostatic screening. Hence, beyond a threshold size of the highly compacted nodules the polyanionic chain cannot be tightly folded anymore and adopts a loosen structure up to when it may closely fold again to create another nodule, etc. The situation is drastically changed when long polyanionic chains such as chromogranins are condensed by trivalent cations such as those used in preparing cell slices for EM when one wishes to increase the density contrast between vesicle matrixes and the other cellular components in the microphotographs. In this respect, one must be extremely careful about not over-interpreting the outcome of such preparations.
It is noteworthy that this new concept allowed theoretical predictions that were all found to be fully coherent with the whole panel of experimental data relative to vesicular exocytosis as investigated by amperometry. In particular, it explained how catecholamine cations may diffuse across an overall highly compacted matrix with a constant diffusion coefficient whose value is large enough to sustain the high diffusion rates (Dves/R2ves > 400 s− 1) required to produce measurable amperometric current intensities. Furthermore, this model offered plausible physicochemical rationales for several puzzling observations that remained unexplained up to now due to the lack of proper theoretical justifications.
A second outcome of this work has been to establish that whenever exocytotic vesicles release under normal in vivo conditions their matrixes swelling is refrained by their membranes. Indeed, the Laplace pressure due to the increasing membrane surface tension opposes the osmotic pressure that would otherwise lead to swelling. This ought to be the case while the fusion pores radii remain small vs. that of the vesicles, i.e., during the whole phase in which release gives rise to measurable amperometric currents. Swelling may occur after release provided that the fusion pore does not close before, but cannot be contributing to amperometric measurements. This impeded swelling may be responsible for the apparent sequestration of a significant fraction of the catecholamine cations inside the slow reservoirs of exocytotic vesicles after a current spike has returned almost to baseline levels. Yet, if the rate of Cat+ transfer from the slow nano-reservoirs into the fast one is fast enough compared to the diffusion rate, the total quantity stored initially into the vesicle may be released leading to the observation of amperometric spike with descending branches following a double-exponential decay mode. Both predictions are in full agreement with recent experimental observations.
As a final comment, we hope that this new view of dense core vesicular matrixes will prove a useful paradigm to the community of neuroscientists as a whole. Indeed, it should be clear that the presence of a pomegranate-like nanostructuration of vesicle granules leading to the storage of neurotransmitters in two reservoirs is a direct, though overlooked, consequence of basic fundamental laws of polyelectrolytes condensation. We have shown that the natural tailoring of granules at this nanoscale level brings many potential properties to vesicles in performing their releasing functions through controlling the rate and intensities of release while allowing closure of the fusion pore after some duration. This model and its consequences have been validated based on quantitative treatments reported in the literature pertaining to two different endocrine cells (chromaffin and PC12) but it is evident due to the prevalence of physical laws governing polyelectrolyte condensation that this new paradigm applies to most endocrine cells. It application to mammalian neurons is more delicate to predict since this depends on the presence or not inside their vesicles of long polyanionic peptidic moieties used to store electrostatically the charged catecholamines molecules that are released in synapses. Also, the much smaller volume of neuron vesicles (by ca. 500 to 1,000 times) compared to chromaffin and PC12 cells may be compatible with a homogeneous condensation of such polyelectrolytes if they are present. In fact, there are hints that the storage of neurotransmitters cations in synaptic vesicles also involves long polyanionic peptidic moieties though, to the best of our knowledge, this has not been detected in cell slices EM. For example, on the one hand, the level of storage is similar in concentration to what is observed in endocrine vesicles; on the other hand, if catecholamine diffusivities in neuron vesicles are found a bit larger than in endocrine cells they still remain 50 to 100 times smaller than in physiological medium.19 Both facts suggest the presence of a condensing polyanionic system that plays an equivalent role to chromogranins in endocrine cells, maybe as occurs in the halos forming in this latter cells.
Acknowledgments
In Paris, this work was supported by CNRS UMR 8640 PASTEUR (CNRS, ENS, and UPMC) and the French Ministry of Research and Higher Education as well as by the CNRS International Laboratory (LIA) NanoBioCatEchem. In Xiamen, it was supported by the MOST of China (2013CB933703) the NSFC (21303146) and by the LIA NanoBioCatEchem. CA wishes to thank strongly Prof. Jean-François Joanny (Institut Curie and ESPCI-ParisTech, France), a former Pierre-Gilles de Gennes collaborator on the "blob theory" for stimulating discussions, as well as Professor Andrew G. Ewing (Goteborg and Chalmers Universities, Sweden) for extensive discussions about his most recent results.
This work is dedicated to Prof. Allen J. Bard at the occasion of his birthday for his gentleness and great wisdom that have constantly been providing luminous inspiration and intelligent guidelines to our scientific pathways.
: Appendix
In the following we establish Equation 5 that provides the relationship between the swelling rate as proposed by Tanaka and Fillmore and the corresponding release rate if exocytosis occurs by swelling only, i.e. if neurotransmitters cations are immediately released as soon as local swelling occurs within a homogeneous matrix.
Let us consider that the matrix consists of a network of N0 infinitely small unit cells, whose volume depend on their degree of swelling. We assume for simplicity that these cells may have only two statuses, viz., may be filled with the neurotransmitter when un-swollen or empty when they have already swollen. This is perfectly consistent with the model of Tanaka and Fillmore and allows a direct coupling between release and swelling rates.
It follows that at any given time the overall volume of the matrix is:
![Equation ([A1])](https://content.cld.iop.org/journals/1945-7111/163/4/H3014/revision1/d0020.gif)
where  and
and  are the volume of one elementary unit cell according to its state and Rgel(t) is the overall gel radius at the same time. Initially no cell has yet swollen so that Nfilled(t = 0) = N0. Conversely, at infinite time all cells are swollen so that Nempty(t → ∞) = N0. This allows relating
are the volume of one elementary unit cell according to its state and Rgel(t) is the overall gel radius at the same time. Initially no cell has yet swollen so that Nfilled(t = 0) = N0. Conversely, at infinite time all cells are swollen so that Nempty(t → ∞) = N0. This allows relating  and
and  to Rt → ∞gel and Rt = 0gel values involved in Tanaka and Fillmore's model (Equations 1 and 3 in the main text):
to Rt → ∞gel and Rt = 0gel values involved in Tanaka and Fillmore's model (Equations 1 and 3 in the main text):
![Equation ([A2])](https://content.cld.iop.org/journals/1945-7111/163/4/H3014/revision1/d0021.gif)
![Equation ([A3])](https://content.cld.iop.org/journals/1945-7111/163/4/H3014/revision1/d0022.gif)
so that Equation A1 may be rewritten as:
![Equation ([A4])](https://content.cld.iop.org/journals/1945-7111/163/4/H3014/revision1/d0023.gif)
We have not specified the number N0 of unit cells nor their dimension or initial content in catecholamine cation. Hence, unit cells may be viewed as individual sites within the homogeneous vesicle matrix containing initially one or more catecholamine cation according to the microscopic chemical structure of the condensed polyelectrolyte. Furthermore, within the context of exocytosis, the volume difference between  and
and  simply reflect that incurred at the microscopic level when a catecholamine cation is replaced by a hydrated monocation as allowed by the local swelling. This shows that the above dichotomic view, viz., 'filled vs. empty' status, does not limit the present analysis while it greatly simplifies it.
simply reflect that incurred at the microscopic level when a catecholamine cation is replaced by a hydrated monocation as allowed by the local swelling. This shows that the above dichotomic view, viz., 'filled vs. empty' status, does not limit the present analysis while it greatly simplifies it.
It immediately follows that the quantity qswell(t) of neurotransmitters still contained inside the vesicle at the same time is proportional to the number of filled cells, i.e.:
![Equation ([A5])](https://content.cld.iop.org/journals/1945-7111/163/4/H3014/revision1/d0024.gif)
that is, owing to Equations A1 and A4:
![Equation ([A6])](https://content.cld.iop.org/journals/1945-7111/163/4/H3014/revision1/d0025.gif)
which after introducing the time dependence of Rgel(t) predicted by Tanaka and Fillmore (i.e., Equation 1 in the main text) becomes identical to Equation 5 given in the main text.