Abstract
Performance and cost requirements for emerging storage applications challenge existing battery technologies and call for substantial improvements in cell energy and rate capability. Convection batteries can reduce mass transport limitations commonly observed during high current operation or with thick electrodes. In prior proof-of-concept work, while convection was shown to improve cell performance, its effectiveness was limited in the select cases studied. To understand the feasibility of the convection battery more comprehensively, we develop a mathematical model to describe convection in a Li-ion cell and evaluate performance as a function of a broad range of cell dimensions, component properties, as well as electrochemical and flow operating conditions. Qualitatively, we find that electrolyte flow enhances accessible capacity for cells with large electrolyte diffusive transport resistance and low initial amounts of electrolyte salt by reducing spatial concentration gradients and, thus, allowing for efficient high current operation. Quantitatively, by leveraging dimensional analysis that lumps >10 physical and cell parameters into representative dimensionless groups, we describe the efficacy, trade-offs, and upper performance bounds of convection in an electrochemical cell. Our analyses suggest that this format has the potential to enable high-power energy-dense storage which, in turn, may offer new application spaces for existing and emerging intercalation chemistries.
Export citation and abstract BibTeX RIS

This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 License (CC BY, http://creativecommons.org/licenses/by/4.0/), which permits unrestricted reuse of the work in any medium, provided the original work is properly cited.
List of symbols
| Symbol | Description |
| a | Active material particle surface area to volume |
| Acell | Cell cross-sectional area |
| Atube | Tube cross-sectional area |
| b | Bruggeman's coefficient |
| ce (x, t) | Anion concentration in the electrolyte |
| cinitial | Initial electrolyte concentration |
| ctank(t) | Tank concentration |
| cs,max | Maximum solid-phase concentration |
| Dbulk | Electrolyte diffusivity of a free solution |
| Deff | Effective electrolyte diffusivity |
| Ds | Solid-phase diffusivity |
| F | Faraday constant |
| Iapp | Applied current density |
| j(x, t) | Ionic flux |
| k | Reaction rate constant |
| L | Thickness |
| n | Number of control volumes used |
| QA | Areal capacity |
| R | Gas constant |
| Rp | Active material particle radius |
| T | Absolute temperature |
| tdis | Time to completely charge or discharge battery at a given Iapp |
| t+ | Li+ transference number |
| v | Superficial velocity in the cell |
| vtube | Superficial velocity in the tube |
| Vtank | Tank volume |
| ε | Porosity |
| εfiller | Filler fraction |
| Θ100% | Stoichiometry at 100% SoC |
| Θ0% | Stoichiometry at 0% SoC |
| κeff | Effective electrolyte conductivity |
| σ | Solid-phase conductivity |
| σeff | Effective solid-phase conductivity |
Ubiquitous in portable electronics and emergent in transportation and stationary applications, lithium (Li)-ion batteries arguably represent the state-of-the-art in electrochemical energy storage technology owing to their energy density, roundtrip efficiency, and cycle life. 1,2 While the past decade has seen a steady decline in battery price and concomitant increase in energy density due to a combination of materials development, manufacturing advances, and market scale, 3,4 current Li-ion batteries are challenged by the often incongruous requirements of emerging applications. 5,6 Of particular note is the need for rechargeable batteries with both high power and high energy density at a reasonable cost. 7 In the current cell format, sustained high power is frequently limited by diffusive transport losses, which necessitate the use of thin electrodes and separators. 5,8–10 This, in turn, leads to inactive components occupying a substantial fraction of the battery weight and volume, leading to higher subsequent energy storage costs. 11
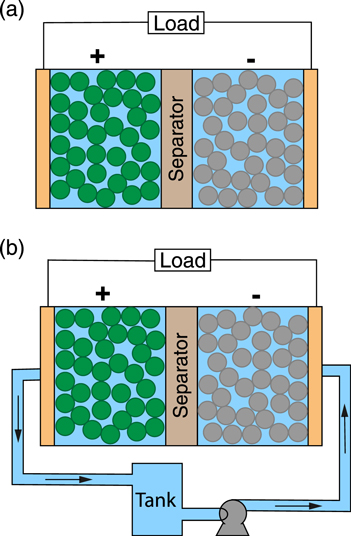
Most current research efforts focus on achieving performance improvements through material innovations including electrolyte formulations with reduced viscosity, increased conductivity, and high Li+ transference numbers; 12–14 charge-storage materials with surface coatings or structuring to enhance intercalation rates; 15,16 cell chemistries with higher energy density due to increased capacity and/or voltage; 17–19 and electrode microstructures with reduced tortuosity and increased pore connectivity. 20–22 In contrast, few have contemplated cell engineering as a means of unlocking new pathways to performance and cost targets. 23–25 One potentially promising approach is the convection battery, in which electrolyte is circulated through the device to overcome mass transport limitations (Fig. 1b). 26–29 Forced convection enables a more uniform electrolyte concentration throughout the cell, in principle allowing for the use of thicker electrodes or operation at high currents while maintaining high accessed capacity. 27 Compared to the traditional sealed cell configuration (Fig. 1a), the convection format can offer several advantages including (1) electrodes with an increased and controllable ion flux, (2) improved safety and maintenance, (3) simplified manufacturing, and, ultimately, (4) reduced system costs. 27 Suppes and co-workers demonstrated proof-of-concept convection cells, in a packed bed configuration, for both aqueous (Zn-MnO2) and non-aqueous (C-LiFePO4) chemistries. 26,27 Notably, for the C-LiFePO4 cell, which contained 6 mm-thick particle-bed-type electrodes, the authors observed an increase in accessed capacity from 10% to 25% for cells with stagnant and flowing electrolyte, respectively. 27 While these seminal experimental studies established that convection could improve cell performance, the prototype cell capacities were low, suggesting there are limits to this approach. To explain the impact of convection, Suppes and co-workers developed a simple electrolyte transport model that showed increasing the superficial velocity reduced the spatial concentration gradients within the cell, thereby increasing the limiting current density and energy efficiency. 28 These findings were further supported by theoretical analysis of electrolyte transport through a porous separator by Kim and Monroe. 30 While these works serve an important role in demonstrating convection-enhanced intercalation batteries, the results are limited to just a few cases of cell size, flow velocity, and operating current.
Figure 1. Intercalation battery configurations with (a) an enclosed cell design as is typical in most modern devices or (b) a novel flow-through design that attempts to improve the effective diffusivity of the electrolyte. The additional hardware required in (b) consists of an external storage tank and pump to provide forced convection through the porous intercalation materials and separator that compose the battery cell.
Download figure:
Standard image High-resolution imagePrevious studies leave key unanswered questions about the potential benefits of convection batteries in terms of ranges of geometric, physical, and operating parameters. It is critical to understand (1) the combinations of parameters that yield enhancement in convection battery performance relative to closed cells with no convection, (2) the upper limits to any enhancement, and (3) the transition behavior and output between these upper limits and corresponding closed cell cases. The intertwined nature of relationships between cell thickness, electrolyte flow rate, transport properties, and operating current and the resultant polarization, power output, and accessed capacity of the cell are unclear. Furthermore, there is no prior substantial body of results that could be used to understand these relationships. To this end, we refine a Li-ion electrochemical model, perform a systematic study using a range of parameters, and present comprehensive representations of cell performance as a function of these parameters. In doing so, we describe the key scaling relationships and introduce dimensionless groups that describe the conditional efficacy of convection batteries.
Despite a paucity of convection battery models beyond the works described above, there is a rich history of mathematical modeling in Li-ion batteries. 31–33 Arguably the most widely-used approach is the porous-electrode theory based pseudo-two-dimensional (P2D) model originally developed by Newman and co-workers. 34 The model describes thermodynamics, electrochemistry, and transport phenomena in the cell via a set of tightly coupled partial differential-algebraic equations (PDAEs) with variations in cell length (x), active material particle radius (r), and time (t). This model has since been reformulated using different numerical techniques and implemented in programs such as DUALFOIL, 35 COMSOL, 36 and Battery Design Studio. 37 More recently, Braatz and co-workers translated this model to MATLAB to increase usability, and have since termed their updated model the Li-ION SIMulation BAttery Toolbox (LIONSIMBA). 38 Here, we leverage and extend this pre-existing framework to describe convection in Li-ion cells.
In this paper, we seek to provide more comprehensive insight into the impact of convection on the cell-level performance of Li-ion batteries. Specifically, we modify the LIONSIMBA software to incorporate a convection term in the Nernst-Planck equation, amend the boundary conditions to allow for electrolyte flow into and out of the cell, and introduce an electrolyte tank. The new package, LIONSIMBA+c, is first validated against the original software and then used to generate more than 50,000 battery discharge curves as a function of cell dimensions, electrode, electrolyte, and separator properties, as well as electrochemical and fluid dynamic operating conditions. Through dimensional analysis, this simulation-based data set can be described compactly through relative scales of dimensionless groups, which both reveal cell-level performance trade-offs and indicate regions where convection is an effective means of boosting performance. While we focus only on cell-level performance enhancement and do not include discussion on system-level designs and trade-offs, we anticipate that the insights provided by this study will inform future cell engineering campaigns and may inspire further investigation of convection-enhanced energy storage systems.
Model Development
As discussed in the Introduction, LIONSIMBA has been previously validated against COMSOL MultiPhysics commercial software 39 and Newman's Fortran DUALFOIL 35 simulations to demonstrate the accuracy of its predictions to Li-ion battery operation. 38 LIONSIMBA uses a P2D model 34 to generate a set of PDAEs by assuming that the cell is perfectly mixed radially, but may contain spatial temperature, concentration, or potential gradients in the axial dimension. The set of PDAEs is subsequently reformulated into ordinary differential-algebraic equations (DAEs) using the finite volume method (FVM) by partitioning the spatial domain into discrete volumes or cells, each with constant properties due to the assumption of being perfectly mixed, and approximating the fluxes through the surfaces of these cells and the rate of generation within the cells in terms of the volume averages. Through the FVM formulation, as opposed to a finite difference solution, boundary conditions involving a specified external flux may be treated exactly, rather than as an approximation. This system of equations is solved numerically using the Implicit Differential Algebraic (IDA) solver produced by Lawrence Livermore National Laboratory, which uses a variable-order, variable-coefficient backwards differentiation formula. 40 To enable the desired extensions to LIONSIMBA, we needed to make the changes described in greater detail in the following paragraphs: (1) introduce the convection term to the Nernst-Planck equation, (2) modify the boundary conditions to the cell to account for forced convection at the boundaries, (3) gauge the conservation of anions within the external tank, and (4) calculate the electrode active area as a function of its porosity.
The convective flux term of the Nernst-Planck equation, while originally excluded from LIONSIMBA, is necessary to model electrolyte forced through the intercalation cell by an external pump. Although the heat transfer equations were also modified to account for electrolyte flow, for the remainder of this work we assume isothermal operation to limit our focus to the connection between mass transfer and cell performance. The effects of heat-transfer and the possibility for the use of convection to limit thermal excursions are beyond the scope of this initial study but will be contemplated in future work. Equation 1 shows the modified species conservation equation which includes the convective transport term (See Supplementary Note 5 for detailed derivation).
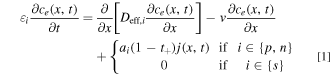
Here εi is the fractional porosity of domain i, where i ∈ {p, s, n} indicates the positive electrode (p), separator (s), or negative electrode (n) respectively, ce (x, t) is the anion concentration, which is equivalent to the cation concentration via the assumption of bulk electroneutrality, at position x and time t, Deff,i is the effective diffusion coefficient, v is electrolyte superficial velocity through the cell, which is constant by the assumption of constant fluid density within the cell, ai is the total particle surface area per unit volume of the electrode, t+ is the Li+ transference number, and j(x, t) is the ionic flux averaged over the interfacial area between the matrix and the pore solution. To avoid undue complication to the analyses, we neglect axial dispersion due to velocity variation in transverse directions. Based on estimations using Sherwood et al. for porous media flow, 41 this neglect is reasonable at the typical low velocities used in the model. For the fraction of high velocity cases, convection in the primary flow direction already dominates transport and causes spatial uniformity in concentration. Hence, we expect that axial dispersion from convective spreading only slightly enhances performance beyond the results of the present study. Another acceptable model approximation is the theory of dilute solutions rather than concentrated solutions. Although dilute solution treatment overlooks some effects, such as slight variations in density and velocity, importantly, the approach is particularly appropriate for major objectives of the work. In the identified upper limits of convection cell performance at high flow rates, concentrations remain relatively uniform and near inlet values. Then, to explain conditional convection cell performance enhancement, dilute solution theory enables the model to capture the trends and competition of transport modes.
The boundary conditions can be treated in a similar fashion to the original LIONSIMBA model, such that there is no diffusive flux entering or exiting the cell domain, but, due to forced electrolyte motion, convective fluxes now traverse these boundaries. This can be rationalized by considering a convection battery cell connected to the external tank with tubes that have cross-sectional area significantly smaller than that of the cell, the joints of which are thus dominated by strong convection and the diffusive fluxes are negligible in comparison. The cell boundaries specified by Eq. 2, as visualized in Fig. 2, result in a zero-derivative at the positions x =  0 = 0 and x =
0 = 0 and x =  n
= ΣLi
, where ΣLi
is the total thickness of the electrodes and separator.
n
= ΣLi
, where ΣLi
is the total thickness of the electrodes and separator.
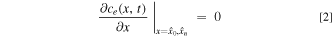
In addition to requiring the inclusion of the convection term, an open system with forced convection from an external holding tank with complete recycling requires a conservation equation on this feed material. By assuming the tank is well mixed, it can be treated as a fictitious node external to the battery cell components. When electrolyte flows from the negative electrode to the positive electrode, a material balance on the tank gives Eq. 3.

While the superficial electrolyte velocity in the tubes entering and exiting the tank, vtube, is unknown, at steady state and by assuming constant fluid density, the continuity equation simplifies to Atube vtube = Acell v, where Acell and Atube are the cross-sectional areas of the battery cell and the tube, respectively. Using this relationship, the unknown tube velocity can be substituted for known values, resulting in Eq. 4, which we use as the modeled conservation equation for anion concentration in the tank, ctank, while simultaneously solving for all other concentrations within the battery cell.
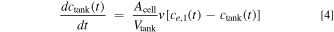
Figure 2. The finite volume discretization and domain used for simulations of the convection battery in the LIONSIMBA+c model. The nodes are numbered from the left, starting at x =  0 for the left boundary of N = 1 to x =
0 for the left boundary of N = 1 to x =  n
for the right boundary of N = np
+ ns
+ nn
. The diagram shown above is when the electrolyte flows from the negative electrode to the positive electrode such that the tank is located at a fictitious node N + 1; however, if the flow were reversed, the tank would be located at a fictitious node 0.
n
for the right boundary of N = np
+ ns
+ nn
. The diagram shown above is when the electrolyte flows from the negative electrode to the positive electrode such that the tank is located at a fictitious node N + 1; however, if the flow were reversed, the tank would be located at a fictitious node 0.
Download figure:
Standard image High-resolution imageLastly, whereas the original LIONSIMBA model allowed independent selection of the spherical radius of active material solid particles, Rp , electrode porosity, ε, and active material volumetric surface area, a, in reality these parameters will be interdependent, in accordance with Eq. 5, where εfiller is the fraction of the inactive materials. As such, we include this relationship in our updated model, to better reflect the physical limitations that are inherent to solid materials.
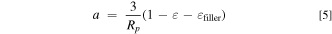
Additionally, while the original LIONSIMBA modeled solid electrolyte conductivity in isothermal operation, 42 it contained relationships for liquid electrolyte conductivity in the non-isothermal case, which we adapted for LIONSIMBA+c by fixing the temperature (Eq. A·1). Although dilute solution theory would predict correlation between the diffusivity, transference number, and conductivity, 43 in this work we treat these as independent parameters to provide a broad understanding of the device design space without limiting model applicability in concentrated solution conditions or alternate electrolytes.
Given the analytical modifications to the original np , ns , and nn control volumes in the positive electrode, separator, and negative electrode, respectively, the finite volume equations for interior points can be determined by assuming that each node is perfectly back-mixed, resulting in the set of equations shown in Eq. 6.
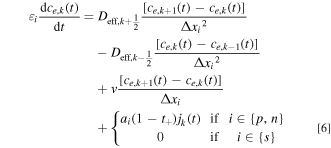
We discretize the convection term using upwind differencing scheme due to its stability and robust convergence behavior, and its accuracy is adequate for the purpose of this study. 44 Throughout this study, we assume that the electrolyte flows from the Li+-generating electrode (negative during discharge; solid arrow in Fig. 2) to the Li+-consuming electrode (positive during discharge) as this minimizes electrolyte salt depletion at low flow rates (Supplementary Note 3). In these equations, Δxi is the width of each node in domain i, and k the index of the node being considered. The boundary conditions given by Eq. 2 can similarly be discretized by considering anion conservation within nodes 1 and N assuming perfect mixing, resulting in Eqs. 7 and 8 respectively, where N = np + ns + nn .
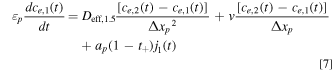
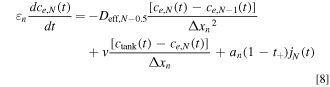
To ensure that the aforementioned changes made for LIONSIMBA+c did not generate unexpected deviations from the original model, we compare simulated discharge curves using both LIONSIMBA and LIONSIMBA+c with stagnant electrolyte at different C rates, defined as the applied current density normalized by areal capacity. Figure S1 (available online at stacks.iop.org/JES/167/140551/mmedia) shows no difference between the model outputs, indicating that the modifications did not introduce artificial changes to the expected behavior.
While the previous sections describe the modifications made to the LIONSIMBA toolkit to create LIONSIMBA+c, the task of effectively sampling the battery operating space to elucidate the regimes in which forced convection may be used to improve battery performance remains daunting given the number of possible engineering variables. To this end, for early investigations not shown, we leverage Monte Carlo methods which generate a random battery system with unique electrolyte properties and subsequently examine the impacts of stochastically selected applied current densities and forced flow velocities within the battery. Then, for the plots shown, we used dimensionless group values to generate simulation conditions that uniformly cover the entire space and then back calculate the electrolyte properties, applied current density, and forced flow velocity. Table I shows the critical parameter value ranges used for this sampling procedure, and the base parameter values selected for any un-sampled values, while Table A·I contains extraneous parameter values needed to repeat these simulations which are not relevant to further discussion. As we sought to understand the sensitivity of battery performance to electrolyte transport, we performed a number of galvanostatic simulations in LIONSIMBA+c using the original LIONSIMBA operating state of charge (SoC) range of 85.51% to 0.9% with a lower cutoff voltage of 2.5 V. In each simulation, we used a cell cross-sectional area of 1 cm2 and tank volume of 50 ml, where the tank contains electrolyte identical to that initially in the cell. We selected the higher-order polynomial approximation method provided by the original LIONSIMBA as the solid-phase diffusion model (Supplementary Note 1) for all our simulations. In total, we generated ca. 50,000 data sets with distinct combinations of cell parameters and operating conditions, with each simulation costing ca. 30 s of wall time.
Table I. A subset of the critical parameters used in LIONSIMBA+c simulations that define the battery operation in the positive electrode, which is limiting under all conditions studied throughout this study. a κeff is calculated through the electrolyte concentration, ce , and temperature, T, as shown in Eq. A·1.
| Symbol | Unit | Value |
|---|---|---|
| b | — | 2.5 |
| cinitial | [mol m−3] | 100–1500 |
| D | [m2 s−1] | 10−13–10−6 |
| Deff | [m2 s−1] | Dεb |
| F | [C mol−1] | 96487 |
| Iapp | [A m−2] | 10–300 |
| L | [m] | 8 × 10−5 |
| QA | [C m−2] | 96073 |
| R | [J/mol/K] | 8.314 |
| T | [K] | 298.15 |
| t+ | — | 0–1 |
| v | [m s−1] | 0–0.01 |
| ε | — | 0.4 |
| εfiller | — | 0.025 |
| σ | [S m−1] | 100 |
| σeff | [S m−1] | σ(1−ε−εfiller) |
| κeff | [S m−1] | varies with ce a |
| tdis | [s] | Q/Iapp |
To illustrate the potential effectiveness of convection-aided intercalation battery operation, we select a cell shown to access 60% of its theoretical capacity with a stagnant electrolyte (Fig. 3a). By introducing a flowing electrolyte with superficial velocities of 0.04 μm s−1 and 0.07 μm s−1, 83% and 98% of the theoretical capacity could be accessed, respectively, as the electrolyte mass transfer limitations originally occurring within the cell are eliminated. While increasing electrolyte flow rate beyond this point does not impact the accessed capacity, it results in greater power- and energy-density as a higher cell voltage is maintained across the discharge profile. Figure 3b suggests these performance benefits are caused by a smoothing of the concentration profile and are in qualitative agreement with prior models on this topic, 28 while any discrepancies are attributable to differences in cell parameters and operating conditions. Critically, the cell with a stagnant electrolyte experiences salt depletion in the positive electrode, causing the cell voltage to rapidly approach the cutoff voltage, whereas flowing electrolyte can be used to delay or altogether eliminate salt depletion. However, even when the flowing electrolyte can completely eliminate liquid-phase mass transfer resistances, an inability to access the theoretical capacity would suggest additional battery losses including ohmics, kinetics, or solid-phase mass transfer which cannot be rectified by improved liquid-phase transport (vide infra). Beyond enabling higher accessible capacities, more uniform concentration profiles lead to reduced concentration and activation overpotentials, and increased electrolyte conductivity (Fig. S2), thus greater power- and energy-density. However, the performance benefits achieved by increasing electrolyte flow rate are anticipated to plateau, resulting in optimal flow rates that may be selected to balance the improvements in electrochemical performance with the increased pumping losses needed to support electrolyte flow. Despite the hypothetical existence of such optima, for the conditions assessed here, the pumping losses through the cell constituted at most 0.006% of the energy gain on a per cell basis (Supplementary Note 4) and consequently will not be considered further. Pumping loss in components external to the cell require system design and are beyond the scope of the current work. Through this illustration, we can rationalize improvements in cell performance by a flattening concentration profile; however, as Fig. 3 is an extremely limited view of the overall parameter space, further simulations are needed to understand the broader trends.
Figure 3. The effect of convective mass transfer on (a) the discharge polarization curve and (b) the concentration profile of electrolyte at t = 380 s. Note the location of positive and negative electrodes is opposite to that in Figs. 1 and 2. These data show the positive impact of increasing flow rate on cell performance by minimizing electrolyte salt depletion in the positive electrode. Further discussions of the concentration profiles and the impacts of flow direction can be found in Supplementary Note 2 and Supplementary Note 3.
Download figure:
Standard image High-resolution imageModel Analysis
The development of LIONSIMBA+c enables assessment of cell performance via the simulation of individual discharge curves as a function of electrolyte properties and flow rate, electrode properties and dimensions, and applied current. With many adjustable and often interdependent system parameters, cell performance can be exhaustively characterized by full parametric sweeps (Table I) over multiple conditions as discussed above. The use of simulations, as opposed to experiments, enables the rapid identification of performance sensitivities, the evaluation of parameter-dependent tradeoffs, and the estimation of property sets required to achieve performance targets. However, compact and meaningful representation of cell performance as a function of individual variables is challenging as these outputs are based on coupled reaction and transport processes whose relative importance varies with different scales. Combining physical quantities into dimensionless groups can provide insight on the relative importance of different physical processes within the battery and, in turn, a large number of simulation results can be collapsed into a lower dimensional space. Here, we first report the derivation of relevant dimensionless groups, followed by data analyses using these dimensionless groups.
Because our focus is on the impact of convection on the electrolyte-phase transport during battery operation, it is natural to begin deriving relevant dimensionless groups from electrolyte transport equations. The anion conservation equation, Eq. 1, equates the time rate of change of anion concentration to the divergence of the total anion flux. By electing to non-dimensionalize this equation (Supplementary Note 5) through the thickness of the positive electrode, L, the full discharge time, tdis, applied current density, Iapp, and the initial concentration, cinitial, the order of magnitude of the resulting terms will be entirely defined by the coefficient groupings as shown in Eq. 9.
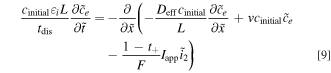
Based on this dimensionless form of the transport equation, several scales become immediately apparent: (1) electrolyte accumulation/depletion, cinitial εi Ltdis −1; (2) diffusion flux, Deff cinitial L−1; (3) convective flux, vcinitial; (4) electromigrative flux, (1-t+)Iapp F−1. Comparing the relative magnitudes of these fluxes, as shown in Table II, gives insight into the dominant transport phenomena and its relative importance on cell performance in the battery. In comparing the transport phenomena in an enclosed system, the diffusive and electromigrative fluxes, as determined by the dimensionless parameter γ, need to balance to prevent electrolyte salt depletion. A large value of γ indicates an increased likelihood for Li salt depletion in the cathode due to insufficient diffusive transport into the cathode. To include the effects of convection in our analysis, we introduce ξ, which is a measure of electromigrative flux compared to the sum of the diffusive and convective fluxes, such that in the absence of convection, ξ = γ. In the same manner, large values of ξ would indicate that the combined diffusive-convective fluxes are slower than the electromigrative flux removing ions from the cathode. Finally, any electrolyte initially present can be used to buffer against electrolyte salt depletion in the cathode, as measured by β, the ratio of electromigration to average flux required for electrolyte salt depletion. Importantly, the exact values of these parameters will change between the positive electrode, negative electrode, and separator. In this work, the dimensionless analyses presented are based on the positive electrode values, as, under the specific conditions contemplated, this is the most likely source of performance limitations. Note that the set of dimensionless quantities discussed above can also be derived using time constants as demonstrated in Supplementary Note 6.
Table II. Definitions of the dimensionless groups used throughout the remainder of this study to describe convection battery operation.
| Dimensionless Group | Expression | Meaning |
|---|---|---|
| γ |
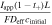
|

|
| ξ |
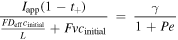
|

|
| Pe |
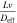
|

|
| β |
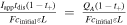
|

|
| δ' |
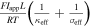
| dimensionless ohmic potential drop |
In addition to electrolyte transport limitations, other factors (electronic and ionic resistances, solid-phase transport, and kinetics) may also contribute to lower cell voltages or accessed capacity, and we identified ohmic losses to have the most dominant impacts on our own simulation results. As such, we include an additional dimensionless group, δ', to characterize the ohmic losses of a cell, similar to that defined by Newman and co-workers. 43 For this particular value, the electrolyte conductivity, κeff, is calculated through Eq. A·1 using the initial electrolyte concentration in the cell as opposed to the spatiotemporally varying concentration. While the solid-phase transport and kinetics may also limit cell performance, we focus our analysis on electrolyte phase transport limitations, as these other effects constitute minor contributions to performance under the conditions studied (Supplementary Note 7).
In this paper, simulations are performed with a wide range of input parameter values to identify overarching trends in convection cell performance. While all input parameter values used are grounded in the realm of physical possibility, not all combinations may be practically achievable based on current material sets. Even in such cases, the observations made provide guidance for future research opportunities. Additionally, while this study uses a LiCoO2/graphite redox chemistry, the qualitative understandings of the dimensionless groups gained from this work should be applicable to other battery chemistries.
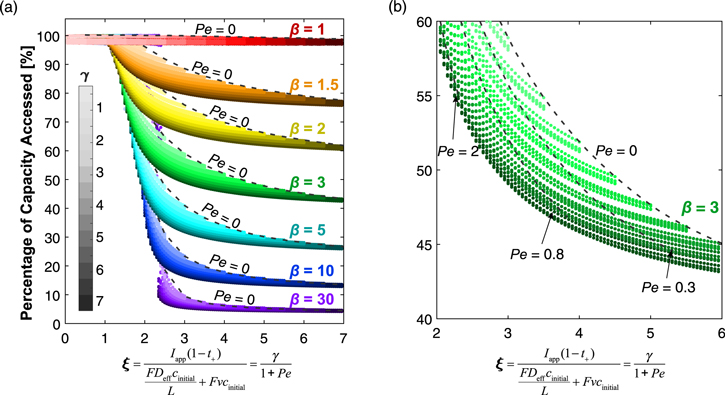
For the remainder of this work, we demonstrate the utility of these dimensionless groups through their ability to predict qualitative model behavior, in order to enhance the field's understanding of the critical points for convective mass transfer to improve battery performance. In all cases, we rely on the accessed capacity of charge stored within the battery as the metric of performance, although there are additional performance benefits to convection, because reducing inaccessible capacity is the first step towards improving overall energy density. To begin answering the question of the value of convective transport in an electrochemical cell, we examine a subset of the data of varying both γ and β. Under identical values of γ and β, we compare the capacity accessed in a cell containing a stagnant electrolyte vs a cell with a very high electrolyte velocity of 0.01 m s−1 (104 μm s−1). Note in Fig. 3, a velocity of just 10 μm s−1 yielded relatively uniform concentration and transport-optimized performance. We define the difference between the percentages of theoretical capacity accessed by the stagnant and 0.01m s−1 electrolyte as the accessed capacity enhancement, where a positive value indicates that a greater capacity is available when the electrolyte is flowing. The data contained in Fig. 4 show the regions where a flowing electrolyte can greatly improve the accessible capacity only existing in areas where both γ and β are large. Although quantitative differences exist for different initial electrolyte concentrations due to changing kinetic and solid-phase transport resistances, Fig. S3 shows the same qualitative trend as observed here. These trends can be rationalized by returning to the definitions of the dimensionless groups γ and β, where γ is the ratio of electromigration to diffusion, and β is the ratio of electromigration to the total flux that would cause electrolyte salt depletion. From these definitions, a cell with small γ has diffusion within the cell capable of balancing electromigration in the opposite direction, making electrolyte salt depletion highly unlikely. In practice, a small γ is the result of a thin electrode, an electrolyte with high diffusivity or large Li+ transference number, or a low discharge rate. Similarly, with a small value of β in the cathode, the initial amount of salt in the electrolyte is more than can be depleted by the electromigration of ions. For cells with low electrode porosity, small Li+ transference number, or high specific capacity active materials, both γ and β values are large, suggesting the accessed capacity for these cells can be significantly enhanced by including convective transport as a means of balancing electrolyte mass transfer.
Figure 4. Accessed capacity enhancement by 0.01 m s−1 of flow compared to a cell without flow. The figure is generated from 5166 data sets with varying Iapp, t+, and D, but the same initial electrolyte concentration, cinitial = 1000 mol m−3, and constant ohmic resistance, δ' = 3.89, corresponding to a dimensional ohmic potential drop of 0.1 V. A different initial electrolyte concentration will result in similar trends with slight variations in values, as illustrated in Fig. S3. "*" indicates conditions used for Fig. 3.
Download figure:
Standard image High-resolution imageBuilding on the analysis showing capacity enhancement with extremely high velocity, further analysis can help us to understand the degree to which intermediate flow rates and parameter combinations enable the convection cell to approach the theoretical maximum enhancement. As before, we select a subset of all collected data, choosing varying β, as indicated by different discrete colors, γ, as indicated by the saturation color bar, and ξ, as plotted on the abscissa in Fig. 5, to demonstrate any underlying patterns in these parameters' impact on cell performance. In addition to confirming the observations made in Fig. 4, this further analysis shows the clear existence of performance transition regimes where 1 ≲ ξ ≲ 3. In this range, the electromigration flux roughly balances the combined diffusion and convection fluxes. Interestingly, the transition region narrows with increasing β. This observation can be explained by a greater vulnerability to transport limitations with higher β due to decreased initial amount of salt to buffer any transport imbalance between electromigration vs diffusion and convection. By comparing these first two analyses (Figs. 4 and 5), there is clear analogy between ξ and γ as both parameters represent the ratios of fluxes in opposite directions within the intercalation cell. Interestingly, however, in Fig. 5, there is a broadening of the curves of each color that we otherwise expect to be individual traces collapsing all Pe values, with only β and ξ determining the behavior of cells with flowing electrolyte. Instead, the data presented suggests that the diffusional flux scale, Deff cinitial L−1, and convective flux scale, vcinitial, of the same magnitude do not counterbalance electromigration equally. A suspected cause is that the scales used to derive the dimensionless numbers are only estimates based on initial conditions and do not capture the dynamic behavior of the cell. When operated at intermediate ξ values, a concentration gradient develops during cell operation, resulting in different magnitudes of diffusion and convection terms in Eq. 1 due to their different dependence on the concentration gradient. This hypothesis is further supported by the diminution of the broadening at low ξ values when the concentration gradient becomes more uniform.
Figure 5. (a) Percentage of capacity accessed for convection cells with varying ξ values. The plot contains 29792 data sets with varying Iapp, t+, D, cinitial, and v, and a constant δ' value of 3.89 (0.1 V dimensional ohmic drop). Results for cinitial >1000 mol m−3 are not included in the plot as they lead to slightly different behaviors at intermediate ξ values shown in Fig. S4. (b) Enlarged view of data for β = 3 and contours of Pe values. For a particular γ value, the percentage of capacity accessed increases with increasing Pe.
Download figure:
Standard image High-resolution imageLastly, LIONSIMBA+c can be used to understand the impact of improved transport on non-transport resistances within the cell, such as low electrolyte conductivity or sluggish kinetics. For this study, we focus on the impacts of ohmic losses as shown in Fig. 6, but an analogous approach could be used to better understand the possible improvements in other areas of cell-design. With increasing ohmic resistance, the accessed capacity decreases monotonically from ca. 97% at δ' = 3.89 to ca. 54% at δ' = 31.2, despite including v = 0.01 m s−1 electrolyte flow to eliminate any sources of mass-transfer losses. Again, we see some spread in these data as individual simulations will have unique kinetic and solid-phase transport resistances, but the variance decreases with increasing δ' as fewer parameter combinations achieve the desired value. As previously discussed, by reducing the electrolyte salt concentration gradient, a convection cell offers opportunities for reduced concentration and activation overpotentials, and potentially improved electrolyte conductivity compared to a stagnant cell. Figures 6b and 6c compare the accessed capacity enhancement by convection for cells with low ohmic resistance (δ' = 3.89) and high ohmic resistance (δ' = 31.2). Both figures demonstrate the same qualitative trends seen in Fig. 4 but differ in the upper limit for enhancement, as discussed earlier. As such, while introducing convection can overcome cell limitations caused by diffusional resistances, this approach is not a panacea for limited accessed capacity.
Figure 6. (a) Percentage of capacity accessed during discharge for convection cells with v = 0.01 m s−1 (104 μm s−1), as a function of δ' values ranging from 3.89 to 31.2, which corresponds to dimensional ohmic drops ranging from 0.1 V to 0.8 V, respectively. The figure contains 560 data sets with varying Iapp, t+, D, and cinitial. Accessed capacity enhancement by 0.01 m s−1 of flow for data sets with cinitial = 100 mol m−3 is shown in (b) for δ' = 3.89 and (c) for δ' = 31.2.
Download figure:
Standard image High-resolution imageConclusions
Overcoming electrolyte mass transfer limits in intercalation-based battery chemistries would enable significant enhancements in accessible capacity and overall battery performance for many important applications. As such, we modified the open-source LIONSIMBA model of enclosed Li-ion batteries to incorporate electrolyte flow and, subsequently, simulated the impact of convection on isothermal cell performance over a broad range of conditions. For a cell operated under electrolyte-transport-limited conditions, such as high C-rate or low electrolyte diffusivity, electrolyte flow lessens concentration gradients across the cell, thereby preventing electrolyte salt depletion that adversely affects kinetic, ohmic, and transport resistances and, if uncontrolled, can result in hazardous conditions within the battery. This, in turn, can enable an expanded operating envelope for intercalation batteries by increasing the accessible capacity, but the effectiveness of this approach is dependent upon electrode properties, electrolyte composition, cell dimensions, and operating conditions. With the extension and description of physically meaningful dimensionless groups, we collapse > 10 physical parameters and thousands of cell discharge simulation results into insightful comprehensive plots (Figs. 4–6). These plots quantitatively address when convection enhances performance, how much flow is needed, and what is the upper bound of enhancement when convection is used. To summarize our key findings, convection is most helpful for a cell with high transport resistance from diffusion and insufficient salt in the electrolyte solution to compensate, which is represented by large γ and β values. Practical conditions with large γ and β include high applied current density, low electrode porosity, low Li+ transference number, and active materials with high specific capacity. The dimensionless group, ξ, represents the ratio of electromigrative flux to the sum of diffusion and convective fluxes, and can help determine whether a designed flow rate is high enough to access full capacity. The group δ' can help determine ohmic resistance, which is one of the factors that can limit the maximum capacity that a convection cell can access if the resistance is large. If significant, kinetic and solid-phase transport effects may also limit convection cell performance, and their impacts can be analyzed using an analogous approach to the one shown here for ohmic resistances.
Our simulation work suggests that compared to an enclosed cell, a convection cell provides opportunities for a wider range of operating conditions and electrode design parameters. Using the same or similar dimensionless plots presented here, the practitioner can readily calculate dimensionless group values for a cell and application of interest to estimate any benefit convection may offer. This approach could potentially lead to applications leveraging rate capability (e.g., fast charging) and enable high energy density (via larger electrode thicknesses). Further, by eliminating electrolyte salt depletion, convection could improve cell safety under extreme conditions. The evaluation of mass transport under isothermal conditions in this work lays the foundation to include convective heat transfer and to explore the anticipated benefit of thermal regulation in future modeling and experimentation.
Acknowledgments
The authors gratefully acknowledge funding from the MIT Deshpande Center. MJO gratefully acknowledges the National Science Foundation Graduate Research Fellowships Program under grant no. 1122374. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation. TJC gratefully acknowledges the National Defense Science and Engineering Graduate (NDSEG) Fellowship awarded by DoD, Air Force Office of Scientific Research. Finally, the authors thank Dr Robert Darling (RTRC) for his helpful suggestions.
Credit authorship contribution statement
Weiran Gao: Conceptualization, Methodology, Software, Validation, Formal Analysis, Investigation, Writing—Original Draft, Visualization, Writing—Review & Editing; Michael J. Orella: Conceptualization, Methodology, Software, Formal Analysis, Writing—Review & Editing; Thomas J. Carney: Conceptualization, Software, Writing—Original Draft, Writing—Review & Editing; Yuriy Roman-Leshkov: Supervision; Javit Drake: Conceptualization, Methodology, Formal Analysis, Writing—Review & Editing; Fikile R. Brushett: Conceptualization, Methodology, Formal Analysis, Resources, Writing—Review & Editing, Supervision, Project Administration.
Appendix
For both models, we used Eq. A·1 to calculate the effective electrolyte conductivity equation at T = 298.15 K. 45
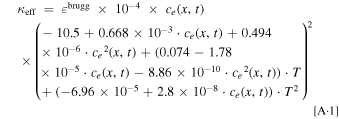
Table A·I. Other parameters used in modified LIONSIMBA.
| Units | Positive Electrode | Separator | Negative Electrode | |
|---|---|---|---|---|
| — | LiθCoO2 | — | LiθC6 | |
| a | m2 m−3 | 862500 | — | 851100 |
| b | — | 2.5 | 2.5 | 2.5 |
| cs max | mol m−3 | 51554 | — | 30555 |
| Ds | m2 s−1 | 1 × 10−14 | — | 3.9 × 10−14 |
| k | m2.5/(mol0.5 s) | 2.334 × 10−11 | — | 5.031 × 10−11 |
| L | m | 8 × 10−5 | 4 × 10−5 | 8 × 10−5 |
| n | — | 100 | 100 | 100 |
| Rp | m | 2 × 10−6 | — | 2 × 10−6 |
| ε | — | 0.4 | 0.4 | 0.4 |
| εfiller | — | 0.025 | — | 0.0326 |
| Θ100% | — | 0.4955 | — | 0.8551 |
| Θ0% | — | 0.9917 | — | 0.0066 |
| σ | [S m−1] | 100 | — | 100 |