Abstract
The development of non-uniform reaction current distribution within porous electrodes is a ubiquitous phenomenon during battery charging/discharging and frequently controls the rate performance of battery cells. Reaction inhomogeneity in porous electrodes is usually attributed to the kinetic limitation of mass transport within the electrolyte and/or solid electrode phase. In this work, however, we reveal that it is also strongly influenced by the intrinsic thermodynamic behavior of electrode materials, specifically the dependence of the equilibrium potential on the state of charge: the electrode reaction becomes increasingly non-uniform when the slope of the equilibrium potential curve is reduced. We employ numerical simulations and equivalent circuit model to elucidate such a correlation and show that the degree of reaction inhomogeneity and the resultant discharge capacity can be predicted by a dimensionless reaction uniformity number. For electrode materials that have equilibrium potentials insensitive to the state of charge and exhibit significant reaction non-uniformity, we demonstrate several approaches to spatially homogenizing the reaction current inside porous electrodes, including matching the electronic and ionic resistances, introducing graded electronic conductivity and reducing the surface reaction kinetics.
Export citation and abstract BibTeX RIS
List of Symbols

|
Volumetric surface area of cathode [m−1] |
| C | C rate |

|
Salt concentration in electrolyte [mol·m−3] |

|
Initial salt concentration in electrolyte [mol·m−3] |

|
Li concentration in electrode particles [mol·m−3] |

|
Normalized Li concentration in electrode particles |

|
Initial Li concentration in electrode particles [mol·m−3] |

|
Maximum Li concentration in electrode particles [mol·m−3] |

|
Ambipolar diffusivity of electrolyte [m2·s−1] |

|
Li diffusivity in active material [m2·s−1] |

|
Depth of discharge |

|
Final depth of discharge or normalized discharge capacity |

|
Rescaled final depth of discharge |
 / /
|
Predicted final depth of discharge of moving-zone reaction/uniform reaction |

|
Faraday constant (96485 C·mol−1) |

|
Li fraction in active material |

|
Applied current density [A·m−2] |
 / /
|
Current density in solid/liquid phase [A·m−2] |

|
Exchange current density of active material [A·m−2] |

|
Exchange current density on Li anode [A·m−2] |

|
Reaction flux on active material surface [mol·m−2·s−1] |

|
Reaction rate constant [mol·m−2·s−1·(mol·m−3)−1.5] |
 / /
|
Cathode/separator thickness [m] |

|
Salt penetration depth [m] |

|
Reaction zone length in the circuit model [m] |

|
Number of electrons in equation for electrode reaction |

|
Gas constant (8.314 J·mol−1·K−1) |
 / / / /
|
Resistance in liquid phase/in solid phase/on particle surface [Ω m−2] |
| rcat | Cathode particle radius [m] |

|
State of charge |

|
Temperature [298 K] |

|
Characteristic time before reaching steady state [s] |

|
Cation transference number in electrolyte |

|
Equilibrium (open-circuit) potential of active material [V] |

|
Slope of equilibrium potential [V] |

|
Potential difference between two regions at steady state [V] |

|
Scaled reaction zone width measured from P2D simulation |

|
Spatial coordinate [m] |

|
Spatial coordinate normalized by 
|

|
Thermodynamic factor |

|
Charge transfer coefficient |
 / /
|
Cathode/separator porosity |

|
Overpotential [V] |

|
Effective electrolyte conductivity [S·m−1] |

|
Reference electrolyte conductivity at 1 M [S·m−1] |

|
Reaction uniformity number |

|
Effective solid phase conductivity [S·m−1] |
 / /
|
Cathode/separator tortuosity |
 / /
|
Electrolyte/solid phase potential [V] |

|
Solid phase potential near current collector [V] |
Electrodes in rechargeable batteries usually take the form of porous electrodes, which consist of a porous matrix of active materials and additives with the void space filled by an electrolyte. Porous cathodes and anodes are typically prepared in the layer format and sandwiched between separators and current collectors to form a single battery cell. During charge/discharge, ions migrating within the electrolyte undergo redox reaction(s) with electrons transported in the solid matrix at the pore wall surface, which is represented by  for lithium-ion batteries. The reaction flux is often described by the Butler-Volmer equation:
for lithium-ion batteries. The reaction flux is often described by the Butler-Volmer equation:
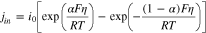
where the surface overpotential 
 and
and  are the electrical potentials of the electrolyte and solid matrix, respectively, and Ueq is the equilibrium or open-circuit potential of the active material. jin has also been described by other types of charge transfer kinetics1,2 but the difference does not qualitatively change the spatial distribution of jin within porous electrodes, which is the subject of this paper.
are the electrical potentials of the electrolyte and solid matrix, respectively, and Ueq is the equilibrium or open-circuit potential of the active material. jin has also been described by other types of charge transfer kinetics1,2 but the difference does not qualitatively change the spatial distribution of jin within porous electrodes, which is the subject of this paper.
Upon (dis)charging, jin is usually spatially inhomogeneous within porous electrodes due to the ionic and electronic resistances of electrolytic and solid matrix phases. Such reaction non-uniformity limits the power output and is a main cause for the under-utilization of battery capacity at high rates. With the ever-growing need for higher energy density and the improvement in battery fabrication processes, the use of thick electrodes in Li-ion batteries has attracted increasing interest in recent years. However, reaction inhomogeneity becomes more severe with increasing electrode thickness, which leads to the inferior rate performance, power loss, heating and cycling degradation of thick battery electrodes and presents a major barrier to their commercial applications. A rational understanding of the origins of the non-uniform reaction distribution is thus critical for the design and optimization of battery systems at the cell level.
The importance of reaction non-uniformity to electrode performance has long been recognized since the early study of porous electrodes.3–6 Newman and Tobias theoretically examined the reaction current distribution in porous electrodes by deriving analytical solutions to the one-dimensional porous electrode model.6 With the assumption of uniform electrolyte concentration, they show that the reaction distribution is controlled by two dimensionless numbers
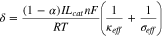
and  in the Tafel region (i.e. large overpotentials) of the charge transfer kinetics. Equation 2 is expressed in terms of anodic reactions and can be applied to cathodic reactions by changing
in the Tafel region (i.e. large overpotentials) of the charge transfer kinetics. Equation 2 is expressed in terms of anodic reactions and can be applied to cathodic reactions by changing  to
to  In the linear region (i.e. low overpotentials), they show that
In the linear region (i.e. low overpotentials), they show that  is replaced another dimensionless number
is replaced another dimensionless number
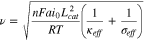
Reaction non-uniformity intensifies at large  or
or  i.e. when the system has low effective ionic (
i.e. when the system has low effective ionic ( ) and electronic (
) and electronic ( ) conductivities, large current (I) and/or exchange current density (i0). On the other hand, the ratio between the electronic and ionic conductivities
) conductivities, large current (I) and/or exchange current density (i0). On the other hand, the ratio between the electronic and ionic conductivities  controls the symmetry of the reaction distribution. The reaction occurs preferentially near the separator (or current collector) when
controls the symmetry of the reaction distribution. The reaction occurs preferentially near the separator (or current collector) when  ≫ 1 (or
≫ 1 (or  ), and develops on both sides of the electrodes when
), and develops on both sides of the electrodes when 
In their analysis, Newman and Tobias treated the open-circuit potential Ueq of electrodes in Eq. 1 as a constant. For electrode materials used in Li-ion batteries, however, it is common that Ueq depends on the extent of reaction or state of charge (SOC). A spatial gradient of Ueq will therefore result from the inhomogeneous reaction flux within porous electrodes, which will reversely influence the reaction distribution through the contribution of Ueq to jin in Eq. 1. In a recent study,7 we show that the reaction behavior of Li-ion porous electrodes is strongly affected by the SOC dependence of Ueq. When Ueq varies significantly with SOC, which is typical of compounds exhibiting solid-solution behavior upon (dis)charging such as Li(NiMnCo)O2 (NMC) and Li(NiCoAl)O2 (NCA), electrode particles tend to have a uniform reaction rate within the salt penetration region during discharge. We refer to this type of electrode materials as uniform-reaction-type electrodes. In contrast, many battery compounds such as LiFePO4 (LFP) and Li4Ti5O12 (LTO) undergo prominent first-order phase transitions upon Li composition swing and have wide voltage plateaus on their (dis)charge curves. For this group of electrodes whose Ueq is insensitive to SOC, reaction flux is instead confined to a narrow reaction zone, which propagates within the porous electrodes as (dis)charge continues. We refer to this type of compounds as moving-zone-reaction-type electrodes. It is discovered that uniform-reaction-type electrodes can deliver 1.7–2 times of the capacity utilization by moving-zone-reaction-type electrodes under otherwise same discharging conditions (electrode thickness and porosity, C rate, etc.).7 While reaction inhomogeneity in porous electrodes is usually considered a kinetic phenomenon, our study clearly reveals the important role of intrinsic thermodynamic properties of electrode materials, in particular the SOC dependence of Ueq.
In this work, we further the study on the thermodynamic origin of reaction non-uniformity in porous electrodes by considering a continuous spectrum of reaction behavior (uniform-reaction, moving-zone-reaction and their intermediates) modulated by the Ueq—SOC relation. The effect of the average slope of the Ueq(SOC) curve, or  on the reaction distribution and rate capability is examined by both pseudo-two-dimensional (P2D) porous electrode simulation8–12 and an equivalent circuit model. A dimensionless "reaction uniformity number,"
on the reaction distribution and rate capability is examined by both pseudo-two-dimensional (P2D) porous electrode simulation8–12 and an equivalent circuit model. A dimensionless "reaction uniformity number,"  is introduced to characterize the degree of reaction homogeneity.
is introduced to characterize the degree of reaction homogeneity.  provides quantitative predictions of the reaction zone width and discharge capacity of battery cells. Based on insights obtained from the analysis, we propose several approaches to improving the reaction uniformity of moving-zone-reaction-type electrodes and demonstrate their effectiveness in P2D simulations.
provides quantitative predictions of the reaction zone width and discharge capacity of battery cells. Based on insights obtained from the analysis, we propose several approaches to improving the reaction uniformity of moving-zone-reaction-type electrodes and demonstrate their effectiveness in P2D simulations.
Results and Discussion
P2D simulations of electrode reaction distribution
The two distinct types of reaction behaviors, uniform-reaction vs moving-zone-reaction, can be illustrated by the discharge process of NMC111 and LFP cathodes, respectively. Figs. 1a–1b displays the P2D simulation of an NMC111 half cell (i.e. with Li metal anode) discharged at 5 mA cm−2 in the electrolyte-transport-limited regime. Details on the implementation of the P2D model are described in Appendix. The NMC111 cathode is 200 μm thick and other simulation parameters are listed in Table A·I. Figure 1a shows that a large intercalation flux develops near separator at the beginning of discharge but is soon spatially uniform across the electrode before the depth of discharge (DoD) reaches 0.1 and then remains uniform until the end of discharge. Consequently, the entire electrode is uniformly lithiated and the in-plane-averaged SOC of electrode particles varies homogeneously within the porous electrode, see Fig 1b. Such uniform-reaction behavior as schematized in Fig. 1c is representative of electrode materials whose equilibrium potentials ( ) have a strong SOC dependence such as NMC and NCA.
) have a strong SOC dependence such as NMC and NCA.
Figure 1. Uniform-reaction and moving-zone-reaction behavior displayed by NMC111 and LFP half cells, respectively. In P2D simulations, both cells have a cathode thickness Lcat = 200 μm and are discharged at  = 5 mA cm−2. Other simulation parameters are listed in Table A·I. (a) and (d). Reaction flux
= 5 mA cm−2. Other simulation parameters are listed in Table A·I. (a) and (d). Reaction flux  on NMC111 and LFP particle surface, respectively. (b) and (d). Average Li concentration
on NMC111 and LFP particle surface, respectively. (b) and (d). Average Li concentration  in NMC111 and LFP particles, respectively. (c) and (f). Schematics of idealized uniform-reaction vs moving-zone-reaction behavior.
in NMC111 and LFP particles, respectively. (c) and (f). Schematics of idealized uniform-reaction vs moving-zone-reaction behavior.
Download figure:
Standard image High-resolution imageThe discharge process of an LFP half cell is shown in Figs. 1d–1e. While the LFP electrode has the same thickness as the NMC111 cathode and is discharged at the same current density of 5 mA cm−2, its reaction flux has a localized peak moving in the electrode during discharge. Fig. 1d shows that an intercalation flux peak first forms on the separator side and then migrates towards the current collector as discharging proceeds. The peak corresponds to a moving narrow reaction front, which separates a largely lithiated electrode region near the separator and an unreacted region near the current collector, see Fig. 1e. Such moving-zone-reaction behavior is idealized by the schematic shown in Fig. 1e. It is representative of electrode materials with SOC-independent  e.g. LFP and LTO that go through first-order phase transformation(s) upon (de)lithiation.
e.g. LFP and LTO that go through first-order phase transformation(s) upon (de)lithiation.
As the above simulations demonstrate, NMC111 and LFP half cells have very different reaction distributions during discharge, with the latter exhibiting much stronger inhomogeneity. Because the two cells have similar electrode thickness, porosity and conductivities, such difference results from the intrinsic properties of the two active materials and specifically, their different SOC dependence of Ueq. The thermodynamic difference between electrodes such as LFP, which undergo first-order phase transitions upon (dis)charging, and electrodes with extended solid solution regime such as NMC is known to result in qualitatively different solid-state lithium transport kinetics, which has been extensively studied including numerical simulations.13–15 However, there is little discussion in literature on the coupling between their thermodynamic phase behavior and the reaction distribution at the porous electrode level.
To illustrate the effect of the Ueq(SOC) curve on reaction uniformity, here we consider a model active material whose Ueq (unit: V) is given by
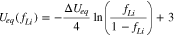
where  is the occupancy fraction of available Li sites and fLi = 1—SOC. As shown in Fig. 2a, parameter
is the occupancy fraction of available Li sites and fLi = 1—SOC. As shown in Fig. 2a, parameter  is equal the slope of Ueq at SOC = 0.5, which controls the steepness of the Ueq(SOC) curve. P2D simulations are performed with varied
is equal the slope of Ueq at SOC = 0.5, which controls the steepness of the Ueq(SOC) curve. P2D simulations are performed with varied  while all the other system properties are kept unchanged. Figs. 2b–2d present the evolution of the scaled Li concentration
while all the other system properties are kept unchanged. Figs. 2b–2d present the evolution of the scaled Li concentration  in electrode particles in a half cell discharged at 0.5 C when
in electrode particles in a half cell discharged at 0.5 C when  = 0.001, 0.01 and 1 V, respectively. The electrode thickness
= 0.001, 0.01 and 1 V, respectively. The electrode thickness  is 200 μm and other parameters are listed in Table A·I. The electronic conductivity
is 200 μm and other parameters are listed in Table A·I. The electronic conductivity  and surface reaction rate constant k0 used in the simulations are sufficiently large so that the discharging process is kinetically limited by electrolyte transport. The comparison shown in Figs. 2b–2d reveals that Li intercalation becomes more homogeneous as
and surface reaction rate constant k0 used in the simulations are sufficiently large so that the discharging process is kinetically limited by electrolyte transport. The comparison shown in Figs. 2b–2d reveals that Li intercalation becomes more homogeneous as  increases. Characteristics of moving-zone-reaction and uniform-reaction are evident at
increases. Characteristics of moving-zone-reaction and uniform-reaction are evident at  = 0.001 and 1 V, respectively. At the intermediate
= 0.001 and 1 V, respectively. At the intermediate  (0.01 V), electrode reaction exhibits a combination of moving-zone-reaction and uniform-reaction behaviors, where significant intercalation flux exists within a reaction zone of finite width. As illustrated in Fig. 2c, we may define a scaled reaction zone width WRZ as the inverse of the slope of
(0.01 V), electrode reaction exhibits a combination of moving-zone-reaction and uniform-reaction behaviors, where significant intercalation flux exists within a reaction zone of finite width. As illustrated in Fig. 2c, we may define a scaled reaction zone width WRZ as the inverse of the slope of  at
at  = 0.5 and SOC = 0.5:
= 0.5 and SOC = 0.5:  Fig. 2e shows that WRZ, which provides a measure of the reaction uniformity, increases monotonically with
Fig. 2e shows that WRZ, which provides a measure of the reaction uniformity, increases monotonically with  and should approach 0 and
and should approach 0 and  in the limiting moving-zone-reaction and uniform-reaction cases, respectively. The effect of
in the limiting moving-zone-reaction and uniform-reaction cases, respectively. The effect of  on the reaction distribution has direct consequence on the rate performance of the electrodes. As shown in Fig. 2f, increasing
on the reaction distribution has direct consequence on the rate performance of the electrodes. As shown in Fig. 2f, increasing  from 0.001 to 1 V significantly improves the discharge performance at high rates, with a 74% increase in the normalized discharge capacity DoDf at 2 C and a 103% increase at 5 C.
from 0.001 to 1 V significantly improves the discharge performance at high rates, with a 74% increase in the normalized discharge capacity DoDf at 2 C and a 103% increase at 5 C.
Figure 2. P2D simulations of a model electrode material in half cell configuration.  = 200 μm and other simulation parameters are listed in Table A·I (a) Ueq−fLi relation of the model electrode with different slope
= 200 μm and other simulation parameters are listed in Table A·I (a) Ueq−fLi relation of the model electrode with different slope  at fLi = 0.5. (b)–(d) Spatial distribution of
at fLi = 0.5. (b)–(d) Spatial distribution of  at different DoDs upon 0.5 C discharging for electrodes with
at different DoDs upon 0.5 C discharging for electrodes with  = 0.001 V (b), 0.01 V (c) and 1 V (d).
= 0.001 V (b), 0.01 V (c) and 1 V (d).  is the scaled distance to the current collector (separator at
is the scaled distance to the current collector (separator at  = 1). The dashed line and shaded area in (c) illustrate the scaled reaction zone width WRZ defined in the text. (e). Dependence of WRZ on
= 1). The dashed line and shaded area in (c) illustrate the scaled reaction zone width WRZ defined in the text. (e). Dependence of WRZ on  (f). Normalized discharge capacity vs C rate in half cells for electrodes with
(f). Normalized discharge capacity vs C rate in half cells for electrodes with  = 0.001, 0.01, 0.1 and 1 V.
= 0.001, 0.01, 0.1 and 1 V.
Download figure:
Standard image High-resolution imageThe effect of the slope of the Ueq(SOC) curve on the reaction uniformity in porous electrodes can be qualitatively understood as follows. Reaction flux at the electrode particle surface is controlled by the overpotential  where
where  and
and  are the electrical potentials of the electrolyte and active material, respectively. When discharging starts, Ueq is initially uniform across the porous electrode, but the presence of ionic/electronic resistances in electrolyte/solid phase generates spatial gradients in
are the electrical potentials of the electrolyte and active material, respectively. When discharging starts, Ueq is initially uniform across the porous electrode, but the presence of ionic/electronic resistances in electrolyte/solid phase generates spatial gradients in  and
and  which results in inhomogeneous η and therefore jin according to the Butler-Volmer equation (Eq. 1). When Ueq has a strong SOC dependence, non-uniform jin gives rise to an inhomogeneous spatial distribution of Ueq. Locations with higher jin see a larger decrease in Ueq, which in turn causes η and jin to drop more significantly than locations receiving lower jin. Therefore, the SOC-dependent Ueq serves as a "rectifier" to the non-uniform reaction distribution: it reduces the spatial gradient of jin until a constant reaction flux is reached within the porous electrode. The larger is the slope of Ueq(SOC), the stronger is such rectifying effect and the faster the electrode can establish a uniform reaction during discharging. On the other hand, SOC-insensitive Ueq such as in LFP and LTO is not able to compensate the spatial gradients of
which results in inhomogeneous η and therefore jin according to the Butler-Volmer equation (Eq. 1). When Ueq has a strong SOC dependence, non-uniform jin gives rise to an inhomogeneous spatial distribution of Ueq. Locations with higher jin see a larger decrease in Ueq, which in turn causes η and jin to drop more significantly than locations receiving lower jin. Therefore, the SOC-dependent Ueq serves as a "rectifier" to the non-uniform reaction distribution: it reduces the spatial gradient of jin until a constant reaction flux is reached within the porous electrode. The larger is the slope of Ueq(SOC), the stronger is such rectifying effect and the faster the electrode can establish a uniform reaction during discharging. On the other hand, SOC-insensitive Ueq such as in LFP and LTO is not able to compensate the spatial gradients of  and
and  to help homogenize the reaction flux. When discharging is electrolyte-transport-limited, reaction will first occur at the separator, where η is the largest, similar to the development of shunt current in flow batteries.16 When electrode particles near the separator are fully intercalated, the reaction front will move into the porous electrode like a traveling wave.
to help homogenize the reaction flux. When discharging is electrolyte-transport-limited, reaction will first occur at the separator, where η is the largest, similar to the development of shunt current in flow batteries.16 When electrode particles near the separator are fully intercalated, the reaction front will move into the porous electrode like a traveling wave.
In the next section, we analyze the dependence of reaction distribution on Ueq(SOC) in a more quantitative manner based on an equivalent circuit model.
Equivalent circuit model for reaction uniformity analysis
While P2D simulations provide detailed predictions of the reaction distribution within porous electrodes, its numerical nature makes it less straightforward to illuminate the general relation between the degree of reaction uniformity and various battery cell properties. As an alternative, we consider the discharge process in a considerably simplified circuit model, with the goal to derive a tractable expression to quantify the reaction uniformity in terms of the slope of Ueq(SOC) and other relevant parameters. Let LR be the dimension of the reaction zone in which the intercalation flux is non-zero during discharging. As illustrated in Fig. 3b, the model represents this portion of the electrode with an equivalent circuit, which divides the zone into two regions (region I and II). For simplicity, electrode particles in each region is assumed to undergo reaction uniformly and have the same SOC,  and
and  We treat the active material as a generalized capacitor, whose characteristic voltage–charge relation is given by Ueq(SOC). Its internal resistance is neglected as solid diffusion is assumed to be facile. The electronic resistance of the solid phase and ionic resistance of the electrolyte are represented by two resistors connecting region I and II,
We treat the active material as a generalized capacitor, whose characteristic voltage–charge relation is given by Ueq(SOC). Its internal resistance is neglected as solid diffusion is assumed to be facile. The electronic resistance of the solid phase and ionic resistance of the electrolyte are represented by two resistors connecting region I and II,  and
and  respectively.
respectively.
Figure 3. (a) Schematic of relevant kinetic processes during discharge and (b) their representation in a two-block equivalent circuit model.
Download figure:
Standard image High-resolution imageAssuming small surface overpotential η, we use the linearized Butler-Volmer equation to express the reaction current in region I and II:

where  is the volumetric surface area of the electrode particles and the exchange current density
is the volumetric surface area of the electrode particles and the exchange current density  is taken as a constant. Accordingly, the polarization caused by surface reaction is represented by a resistor
is taken as a constant. Accordingly, the polarization caused by surface reaction is represented by a resistor  in each region. For galvanostatic discharging, I1 and I2 are subject to the constraint:
in each region. For galvanostatic discharging, I1 and I2 are subject to the constraint:
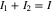
where I is the applied areal current density. Letting  at the current collector be
at the current collector be  and setting
and setting  at the cathode/separator interface to be 0, the surface overpotentials in region I and II are given by
at the cathode/separator interface to be 0, the surface overpotentials in region I and II are given by
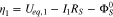
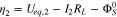
Ueq is assumed to vary linearly with SOC or 
 where
where  and
and  are the Li concentrations in the fully delithiated and lithiated states, respectively, and U0 is Ueq at SOC = 1. Accordingly, the evolution of Ueq in region I and II during discharge is governed by the following equations:
are the Li concentrations in the fully delithiated and lithiated states, respectively, and U0 is Ueq at SOC = 1. Accordingly, the evolution of Ueq in region I and II during discharge is governed by the following equations:
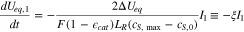
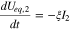
where  is electrode porosity. Applying Eqs. 5–8 to eliminate I1, I2 and
is electrode porosity. Applying Eqs. 5–8 to eliminate I1, I2 and  in Eqs. 9 and 10, we obtain
in Eqs. 9 and 10, we obtain
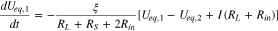

from which Ueq,1(t) and Ueq,2(t) can be solved:
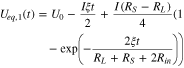
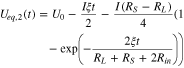
The equilibrium potential difference between region I and II, which quantifies the difference in the reaction degree, is thus
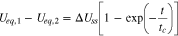
in which we define


The above result characterizes the time evolution of the reaction distribution within the reaction zone. As a main result of the circuit model, Eq. 15 shows that intercalation flux inside the reaction zone will reach a steady state distribution after a transient period with a characteristic time tc. In the steady state, region I and II have an equal reaction current (I1 = I2) so that their equilibrium potential difference  remains at a constant value
remains at a constant value 
 is negative when discharge is electrolyte-transport-limited, or
is negative when discharge is electrolyte-transport-limited, or  meaning that the active material near the separator will react first. For discharge limited by electronic transport (
meaning that the active material near the separator will react first. For discharge limited by electronic transport ( ),
),  is positive and the reaction will first occur near the current collector.
is positive and the reaction will first occur near the current collector.
Reaction uniformity number
In the last section, a steady-state equilibrium potential drop across the reaction zone,  is determined from the two-block circuit model. The fact that
is determined from the two-block circuit model. The fact that  cannot exceed
cannot exceed  places an upper limit on LR that can be maintained during discharge, which is given by
places an upper limit on LR that can be maintained during discharge, which is given by

We introduce a dimensionless reaction uniformity number and defined it as the ratio between  and the electrode thickness
and the electrode thickness 
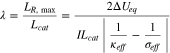
 bears the physical meaning of the maximum normalized reaction zone width. Its magnitude provides a measure of the degree of the reaction uniformity within the porous electrode. When
bears the physical meaning of the maximum normalized reaction zone width. Its magnitude provides a measure of the degree of the reaction uniformity within the porous electrode. When  the entire electrode can establish a homogeneous reaction distribution and exhibit uniform-reaction behavior. When
the entire electrode can establish a homogeneous reaction distribution and exhibit uniform-reaction behavior. When  reaction is confined to a narrow region much smaller than the electrode thickness, and so moving-zone-reaction-type behavior ensues.
reaction is confined to a narrow region much smaller than the electrode thickness, and so moving-zone-reaction-type behavior ensues.  reveals the roles of multiple factors (SOC dependence of Ueq,
reveals the roles of multiple factors (SOC dependence of Ueq, 

 I) in regulating the reaction distribution. Some electrode materials such as Li(Ni0.5Mn1.5)O4 undergo more than one first-order phase transitions upon (dis)charging with two plateaus on their Ueq(SOC). The discharge process of these electrodes is characterized by two separate reaction zones, which form and propagate within the electrodes in sequence. The same analysis can be applied to each reaction zone individually, in which the reaction uniformity number should be calculated based on the potential drop across each plateau.
I) in regulating the reaction distribution. Some electrode materials such as Li(Ni0.5Mn1.5)O4 undergo more than one first-order phase transitions upon (dis)charging with two plateaus on their Ueq(SOC). The discharge process of these electrodes is characterized by two separate reaction zones, which form and propagate within the electrodes in sequence. The same analysis can be applied to each reaction zone individually, in which the reaction uniformity number should be calculated based on the potential drop across each plateau.
To examine the predicative power of  given by Eq. 19, we compare it against the P2D simulations of the model electrode system presented above in Fig. 2. In Fig. 4a, we plot the reaction zone width WRZ, which is measured from the P2D simulations, against
given by Eq. 19, we compare it against the P2D simulations of the model electrode system presented above in Fig. 2. In Fig. 4a, we plot the reaction zone width WRZ, which is measured from the P2D simulations, against  estimated from the simulation parameters for electrodes with different
estimated from the simulation parameters for electrodes with different  In evaluating λ, we use the electrolyte conductivity at c = 1 M for
In evaluating λ, we use the electrolyte conductivity at c = 1 M for  although concentration-dependent
although concentration-dependent  is used in simulations. It can be seen that the calculated
is used in simulations. It can be seen that the calculated  agrees very well with the measured
agrees very well with the measured  over a wide range of values from 0.1 to 100, which shows that
over a wide range of values from 0.1 to 100, which shows that  can be used to accurately predict the extent of the reaction non-uniformity during discharge.
can be used to accurately predict the extent of the reaction non-uniformity during discharge.
Figure 4. (a) Comparison between  in Fig. 2e and
in Fig. 2e and  predicted by Eq. 19. Dashed line corresponds to
predicted by Eq. 19. Dashed line corresponds to  (b) Normalized discharge capacity
(b) Normalized discharge capacity  vs
vs  at 2 C, 3 C and 5 C. Dashed and dash-dotted lines are the predicted
at 2 C, 3 C and 5 C. Dashed and dash-dotted lines are the predicted  for moving-zone-reaction-type electrodes (
for moving-zone-reaction-type electrodes ( ) and uniform-reaction-type electrodes (
) and uniform-reaction-type electrodes ( ) based on the analytical model listed in Table I, respectively. (c). Rescaled discharge capacity
) based on the analytical model listed in Table I, respectively. (c). Rescaled discharge capacity 
 vs
vs  at 2 C, 3 C and 5 C. (d). Test of the sensitivity of the
at 2 C, 3 C and 5 C. (d). Test of the sensitivity of the  ∼
∼  relation to simulation parameters.
relation to simulation parameters. 

 and
and  are individually varied to 0.7
are individually varied to 0.7 and
and  of their default values (
of their default values ( = 2.95·10–10 m2 s−1,
= 2.95·10–10 m2 s−1,  = 200 μm,
= 200 μm,  = 0.25,
= 0.25,  = 2), and
= 2), and  is set to 2
is set to 2 and
and  of its default value (25 μm). Discharge rate is fixed at 3 C and other parameters are the same as in Table A·I. The black dashed line in (c) and (d) is the transition function
of its default value (25 μm). Discharge rate is fixed at 3 C and other parameters are the same as in Table A·I. The black dashed line in (c) and (d) is the transition function  (Eq. 20).
(Eq. 20).
Download figure:
Standard image High-resolution imageWhen the anion in the electrolyte has a non-zero transference number, local salt depletion (i.e. zero salt concentration) will occur in electrolyte near the current collector at high discharging rates or large electrode thickness7,17 and result in a large salt concentration gradient across the electrode, which will strongly influence the ionic conductivity. Although the simple circuit model does not take the concentration dependence of  into consideration, the reaction uniformity number
into consideration, the reaction uniformity number  still provides a reliable indication of the electrode performance in the presence of salt depletion. In Fig. 4b, we plot the normalized discharge capacity DoDf at 2 C, 3 C and 5 C from the P2D simulations of the model electrode system as a function of
still provides a reliable indication of the electrode performance in the presence of salt depletion. In Fig. 4b, we plot the normalized discharge capacity DoDf at 2 C, 3 C and 5 C from the P2D simulations of the model electrode system as a function of  It shows that DoDf increases monotonically with
It shows that DoDf increases monotonically with  and has two plateaus at small and large
and has two plateaus at small and large  values, which correspond to the moving-zone-reaction and uniform-reaction behavior, respectively. Previously, we developed a quantitative analytical model to predict the discharge performance of uniform-reaction- and moving-zone-reaction-type electrodes in the electrolyte-diffusion-limited regime.7 It gives the expressions of the width of the salt penetration zone LPZ (i.e. region with non-zero salt concentration and complementary to the salt depletion zone) as listed in Table I, and DoDf is evaluated as LPZ/Lcat. The dashed and dash-dotted lines in Fig. 4b represent DoDf predicted by the analytical model for moving-zone-reaction (
values, which correspond to the moving-zone-reaction and uniform-reaction behavior, respectively. Previously, we developed a quantitative analytical model to predict the discharge performance of uniform-reaction- and moving-zone-reaction-type electrodes in the electrolyte-diffusion-limited regime.7 It gives the expressions of the width of the salt penetration zone LPZ (i.e. region with non-zero salt concentration and complementary to the salt depletion zone) as listed in Table I, and DoDf is evaluated as LPZ/Lcat. The dashed and dash-dotted lines in Fig. 4b represent DoDf predicted by the analytical model for moving-zone-reaction ( ) and uniform-reaction (
) and uniform-reaction ( ) electrodes, respectively, which match the lower and upper limits of the simulated discharge capacity very well.
) electrodes, respectively, which match the lower and upper limits of the simulated discharge capacity very well.
Table I. Expressions of LPZ and DoDf for galvanostatic discharging of half cells predicted by an analytical model.7

|
Uniform-reaction (UR) electrodes |

|
| Moving-zone-reaction (MZR) electrodes |

|
|

|
||
While it is challenging to directly extend this analytical model to electrodes with the reaction behavior intermediate between uniform-reaction and moving-zone-reaction, we find that  serves as a very good descriptor of DoDf. When using Eq. 19 to calculate
serves as a very good descriptor of DoDf. When using Eq. 19 to calculate  in the presence of salt depletion, we replace
in the presence of salt depletion, we replace  with LPZ for uniform-reaction behavior, which is a more appropriate reference length scale as it represents the maximum thickness of the electrode region that can be fully discharged at the given discharge condition. In Fig. 4c, we replot Fig. 4b by rescaling DoDf as
with LPZ for uniform-reaction behavior, which is a more appropriate reference length scale as it represents the maximum thickness of the electrode region that can be fully discharged at the given discharge condition. In Fig. 4c, we replot Fig. 4b by rescaling DoDf as  which always varies between 0 and 1. It clearly shows that the
which always varies between 0 and 1. It clearly shows that the  ~
~  relations at different C rates collapse onto a single S-shaped curve, which can be fitted by an analytical function:
relations at different C rates collapse onto a single S-shaped curve, which can be fitted by an analytical function:
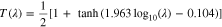
To test the generality of Eq. 20, we performed 100 additional simulations by varying different cell parameters (


 and
and  ) and compared the simulated
) and compared the simulated  against
against  As shown in Fig. 4d, overall the simulation results are in very good agreement with predictions by
As shown in Fig. 4d, overall the simulation results are in very good agreement with predictions by  which likely represents a universal
which likely represents a universal  ∼
∼ relation. The discharge capacity of electrodes with intermediate reaction behavior in the electrolyte-transport-limited regime may therefore be predicted as
relation. The discharge capacity of electrodes with intermediate reaction behavior in the electrolyte-transport-limited regime may therefore be predicted as
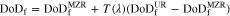
Approaches to homogenizing reaction distribution in moving-zone-reaction-type electrodes
Our work reveals that moving-zone-reaction-type electrodes, i.e. electrodes whose Ueq is insensitive to SOC, have inferior performance at high rates and/or large electrode thickness due to the strong reaction inhomogeneity during discharge. In addition, the highly localized intercalation flux within the narrow reaction front may accelerate battery degradation by causing excessive stress concentration and local heat generation. Based on the insights from the P2D simulation and circuit model, we discuss in this section how reaction in this type of electrodes can be homogenized to make them more suitable for high rate and thick electrode applications. Based on Eqs. 17 and 19 from the circuit model and somewhat counter-intuitively, we show that reducing the electronic conductivity and/or surface reaction rate is beneficial to improving the reaction uniformity in moving-zone-reaction-type electrodes.
Reduce electronic conductivity
The rate performance of today's Li-ion battery cells is typically limited by sluggish ionic transport in the electrolyte, whereas the electronic conductivity can be made sufficiently high with conductive additives or coatings on active materials. When  electrode reaction first occurs near the separator upon discharging,18,19 to which electrons travel a longer distance from the current collector to meet slow-moving Li ions from the anode. However, Eq. 19 predicts that the reaction uniformity can be improved by reducing the electronic conductivity to
electrode reaction first occurs near the separator upon discharging,18,19 to which electrons travel a longer distance from the current collector to meet slow-moving Li ions from the anode. However, Eq. 19 predicts that the reaction uniformity can be improved by reducing the electronic conductivity to  to render a large
to render a large  To test this prediction, a P2D simulation is performed for a model system with
To test this prediction, a P2D simulation is performed for a model system with  in which
in which  is set to
is set to  0.291 s m−1. As shown in Fig. 5a, two reaction fronts form on both sides of the electrode and propagate towards the electrode center during 0.5 C discharge. Accordingly, the intercalation flux is split into two peaks of lower intensities and does become more uniformly distributed compared to the higher
0.291 s m−1. As shown in Fig. 5a, two reaction fronts form on both sides of the electrode and propagate towards the electrode center during 0.5 C discharge. Accordingly, the intercalation flux is split into two peaks of lower intensities and does become more uniformly distributed compared to the higher  case, see Fig. 5b, although the reaction distribution is not entirely homogenized as predicted by the circuit model. This is because the model oversimplifies the situation by dividing the reaction zone into only two blocks and neglecting the non-uniformity within each block. Fig. 5c shows that DoDf increases monotonically with decreasing
case, see Fig. 5b, although the reaction distribution is not entirely homogenized as predicted by the circuit model. This is because the model oversimplifies the situation by dividing the reaction zone into only two blocks and neglecting the non-uniformity within each block. Fig. 5c shows that DoDf increases monotonically with decreasing  upon discharging at higher rate (1–3 C) and can even reach the discharge capacity of uniform-reaction-type electrodes (dash-dotted lines) when
upon discharging at higher rate (1–3 C) and can even reach the discharge capacity of uniform-reaction-type electrodes (dash-dotted lines) when  approaches
approaches  Upon further decreasing
Upon further decreasing  however, the discharge kinetics will be increasingly limited by the sluggish electronic transport, resulting in eventual deterioration in rate performance as indicated by the discharge capacity at 3 C. There exists an optimal ratio of
however, the discharge kinetics will be increasingly limited by the sluggish electronic transport, resulting in eventual deterioration in rate performance as indicated by the discharge capacity at 3 C. There exists an optimal ratio of  and
and  around 1.
around 1.
Figure 5. (a). Spatial distribution of  at different DoDs in a 200 μm-thick model electrode in a half cell discharged at 0.5 C with
at different DoDs in a 200 μm-thick model electrode in a half cell discharged at 0.5 C with  = 0.001 V and
= 0.001 V and  (b). Reaction current distributions at DoD = 0.5 for electrodes with
(b). Reaction current distributions at DoD = 0.5 for electrodes with  = 100 S m−1, 0.291 S m−1 and
= 100 S m−1, 0.291 S m−1 and  where X is the distance to the current collector. (c). Effect of
where X is the distance to the current collector. (c). Effect of  on the discharge capacity at 1 C, 2 C and 3 C discharging. Dashed and dash-dotted lines are
on the discharge capacity at 1 C, 2 C and 3 C discharging. Dashed and dash-dotted lines are  and
and  predicted by the analytical model, respectively. (d). Spatial distribution of
predicted by the analytical model, respectively. (d). Spatial distribution of  at different DoDs in a 200μm-thick model electrode with
at different DoDs in a 200μm-thick model electrode with  = 0.001 V and variable electronic conductivity
= 0.001 V and variable electronic conductivity  upon 0.5 C discharging.
upon 0.5 C discharging.
Download figure:
Standard image High-resolution imageGrade electronic conductivity
Further improvement in the reaction uniformity can be realized by allowing  to vary spatially within the electrode. This is because having a uniform reaction flux requires a constant surface overpotential everywhere, or
to vary spatially within the electrode. This is because having a uniform reaction flux requires a constant surface overpotential everywhere, or
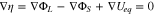
In Eq. 22, a significant  is usually present upon (dis)charging at relatively high rates due to the low ionic conductivity of the electrolyte, but
is usually present upon (dis)charging at relatively high rates due to the low ionic conductivity of the electrolyte, but  0 for moving-zone-reaction-type materials. Replacing
0 for moving-zone-reaction-type materials. Replacing  and
and  with the current densities in the solid phase (I1) and electrolyte (I2), respectively, Eq. 22 becomes:
with the current densities in the solid phase (I1) and electrolyte (I2), respectively, Eq. 22 becomes:

In the presence of a uniform flux, both  and
and  vary linearly with the distance to the current collector X:
vary linearly with the distance to the current collector X:  and
and  Therefore, Eq. 23 is satisfied if the following relation between
Therefore, Eq. 23 is satisfied if the following relation between  and
and  holds:
holds:
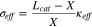
According to Eq. 24, the optimal  is a hyperbolic function and varies monotonically from infinity at the current collector (X = 0) to 0 at the separator (X =
is a hyperbolic function and varies monotonically from infinity at the current collector (X = 0) to 0 at the separator (X =  ). We confirm the effectiveness of such conductivity distribution via P2D simulation, in which
). We confirm the effectiveness of such conductivity distribution via P2D simulation, in which  is set as
is set as  and other parameters are the same as those for Fig. 5a. As shown in Figs. 5b and 5d, lithium intercalation indeed has a much more uniform distribution across the electrode throughout the discharge process than in systems with constant
and other parameters are the same as those for Fig. 5a. As shown in Figs. 5b and 5d, lithium intercalation indeed has a much more uniform distribution across the electrode throughout the discharge process than in systems with constant 
We note that Palko et al.20 recently describe a similar approach of tailoring spatially varied electrode matrix resistance to homogenize electrolyte depletion in electrical double layer capacitors (EDLC). The similarity in the derived  expressions in Ref. 20 and here demonstrates the analogy in the behavior of moving-zone-reaction-type battery electrodes and capacitors. On the other hand, uniform-reaction-type electrodes behave in a very different way and Eq. 22 highlights such difference. The ability of uniform-reaction-type compounds to sustain a non-zero spatial gradient in
expressions in Ref. 20 and here demonstrates the analogy in the behavior of moving-zone-reaction-type battery electrodes and capacitors. On the other hand, uniform-reaction-type electrodes behave in a very different way and Eq. 22 highlights such difference. The ability of uniform-reaction-type compounds to sustain a non-zero spatial gradient in  in porous electrodes makes it possible to offset
in porous electrodes makes it possible to offset  with
with  to maintain a uniform overpotential without the need for spatially varied
to maintain a uniform overpotential without the need for spatially varied  In the absence of a non-zero
In the absence of a non-zero  in moving-zone-reaction-type electrodes, however,
in moving-zone-reaction-type electrodes, however,  can only be balanced by the
can only be balanced by the  gradient to satisfy Eq. 22.
gradient to satisfy Eq. 22.
Experimentally, the electronic conductivity of porous electrodes can vary several orders of magnitude by adjusting the types and amount of conductive additives21–24 or applying coatings to active materials to either increase or decrease the conductivity. Electrodes with graded electronic conductivity may be prepared via layer-by-layer deposition processes. In Ref. 24, Zhang et al. fabricated layer-graded electrodes consisting of TiO2(B) and reduced graphene oxide (RGO) and varied the RGO:TiO2(B) ratio to control  in each layer. They report that graded TiO2(B)/RGO electrodes with the high
in each layer. They report that graded TiO2(B)/RGO electrodes with the high  layer placed adjacent to the current collector deliver more than 70% capacity at 20 C than uniform electrodes with the same average RGO weight fraction. The theoretical analysis presented here explains why such an approach is effective. In recent years, using heterogeneous architecture to enhance the rate performance of thick electrodes has been explored theoretically25,26 and experimentally.27–32 These studies focus on improving ionic transport in electrolyte by decreasing the electrode tortuosity or introducing graded porosity in electrodes. In contrast, the approach we consider here enhances the reaction uniformity by tailoring the electronic transport in the solid phase. The two different strategies could potentially be combined in the same electrode structures to achieve synergistic improvement to the battery rate performance.
layer placed adjacent to the current collector deliver more than 70% capacity at 20 C than uniform electrodes with the same average RGO weight fraction. The theoretical analysis presented here explains why such an approach is effective. In recent years, using heterogeneous architecture to enhance the rate performance of thick electrodes has been explored theoretically25,26 and experimentally.27–32 These studies focus on improving ionic transport in electrolyte by decreasing the electrode tortuosity or introducing graded porosity in electrodes. In contrast, the approach we consider here enhances the reaction uniformity by tailoring the electronic transport in the solid phase. The two different strategies could potentially be combined in the same electrode structures to achieve synergistic improvement to the battery rate performance.
Reduce surface reaction rate
The circuit model presented above shows that during discharge a battery cell first goes through a transient period with a characteristic time tc before establishing a steady-state reaction zone within the porous electrode. Since the active material has a uniform SOC at the beginning of discharge, another way to improve the reaction uniformity in moving-zone-reaction-type electrodes is to increase tc to delay the establishment of the narrow reaction front and let the system remain in the transient period for the majority of the discharge process. Eq. 17 shows that tc can be increased by reducing i0. We demonstrate this approach via P2D simulations of the model system with  = 0.001 V, in which the surface reaction rate constant k0 is decreased from the default value [10−8 mol·m−2·s−1·(mol·m−3)−1.5] to 10−11 and 10−13 mol·m−2·s−1·(mol·m−3)−1.5. The corresponding time evolution of
= 0.001 V, in which the surface reaction rate constant k0 is decreased from the default value [10−8 mol·m−2·s−1·(mol·m−3)−1.5] to 10−11 and 10−13 mol·m−2·s−1·(mol·m−3)−1.5. The corresponding time evolution of  is plotted in Figs. 6a and 6b, respectively. Compared to Fig. 3b, a smaller k0 indeed slows down the development of the sharp reaction front and results in a more uniform reaction across the electrode during discharge. As expected, decreasing k0 can increase the discharge capacity by 20%–35% at high rates (1–3 C), Fig. 6c, which is similar to the effect of reducing
is plotted in Figs. 6a and 6b, respectively. Compared to Fig. 3b, a smaller k0 indeed slows down the development of the sharp reaction front and results in a more uniform reaction across the electrode during discharge. As expected, decreasing k0 can increase the discharge capacity by 20%–35% at high rates (1–3 C), Fig. 6c, which is similar to the effect of reducing  although the improvement is not as pronounced. The reason that reducing the surface reaction kinetics is beneficial is that it prevents the localization of the intercalation flux and forces the reaction current to spread out over a larger electrode region. Like reducing
although the improvement is not as pronounced. The reason that reducing the surface reaction kinetics is beneficial is that it prevents the localization of the intercalation flux and forces the reaction current to spread out over a larger electrode region. Like reducing  having a too small k0 will lead to inferior discharge capacity because the induced large surface overpotential diminishes the capacity utilization before the cut-off potential is reached. An optimal k0 thus exists, which may be estimated by the criterion that the corresponding tc be comparable to the discharge time. Experimentally, surface reaction kinetics may be tailored by "artificial" SEI such as ALD coatings of various inorganic compounds (e.g. Al2O3, TiO2, ZrO233–35), whose insulating nature could retard the intercalation process and cause higher surface polarization.
having a too small k0 will lead to inferior discharge capacity because the induced large surface overpotential diminishes the capacity utilization before the cut-off potential is reached. An optimal k0 thus exists, which may be estimated by the criterion that the corresponding tc be comparable to the discharge time. Experimentally, surface reaction kinetics may be tailored by "artificial" SEI such as ALD coatings of various inorganic compounds (e.g. Al2O3, TiO2, ZrO233–35), whose insulating nature could retard the intercalation process and cause higher surface polarization.
Figure 6. P2D simulations of discharging a 200 μm-thick model electrode ( = 0.001 V) with low surface reaction rate constant k0 in a half cell at 1 C. Other simulation parameters are the same as those for Fig. 3b. (a) and (b). Spatial distribution of
= 0.001 V) with low surface reaction rate constant k0 in a half cell at 1 C. Other simulation parameters are the same as those for Fig. 3b. (a) and (b). Spatial distribution of  at different DoD during 0.5 C discharging with
at different DoD during 0.5 C discharging with  = 10–11 (a) and
= 10–11 (a) and  = 10−13 (b) mol·m−2·s−1·(mol·m−3)−1.5. (c). Discharge capacity vs k0 upon 1 C, 2 C and 3 C discharging. Dashed and dash-dotted lines are
= 10−13 (b) mol·m−2·s−1·(mol·m−3)−1.5. (c). Discharge capacity vs k0 upon 1 C, 2 C and 3 C discharging. Dashed and dash-dotted lines are  and
and  predicted by the analytical model (Table I).
predicted by the analytical model (Table I).
Download figure:
Standard image High-resolution imageWhile reducing  and k0 promotes the reaction uniformity, such approaches may lead to increased energy loss and degrade energy efficiency, the severity of which needs to be examined. Figure 7a shows the cell potential curves from the simulations of discharging four types of 200 μm-thick model electrodes (
and k0 promotes the reaction uniformity, such approaches may lead to increased energy loss and degrade energy efficiency, the severity of which needs to be examined. Figure 7a shows the cell potential curves from the simulations of discharging four types of 200 μm-thick model electrodes ( = 0.001 V) at 1 C: high
= 0.001 V) at 1 C: high  (100 s m−1, baseline), low and uniform
(100 s m−1, baseline), low and uniform  (0.291 s m−1), graded
(0.291 s m−1), graded  (Eq. 24), and low surface reaction rate k0 [10–13 mol·m−2·s−1·(mol·m−3)−1.5]. The electrodes with low and graded
(Eq. 24), and low surface reaction rate k0 [10–13 mol·m−2·s−1·(mol·m−3)−1.5]. The electrodes with low and graded  only see a small drop (∼0.02 V) in the discharge potential while delivering 30% more capacity than the baseline electrode at the same time. On the other hand, the electrode with reduced k0 has a larger depression in the discharge potential (∼0.1 V). In Fig. 7b, the total energy loss in a half cell upon 1 C discharging, which is the sum of losses due to the ionic, electronic and surface reaction resistances, is plotted as a function of DoD for the four cases. It can be seen that reducing or grading
only see a small drop (∼0.02 V) in the discharge potential while delivering 30% more capacity than the baseline electrode at the same time. On the other hand, the electrode with reduced k0 has a larger depression in the discharge potential (∼0.1 V). In Fig. 7b, the total energy loss in a half cell upon 1 C discharging, which is the sum of losses due to the ionic, electronic and surface reaction resistances, is plotted as a function of DoD for the four cases. It can be seen that reducing or grading  only slightly increases the energy loss by less than 15% compared to the baseline case while decreasing k0 doubles the energy loss. Therefore, tailoring the electronic conductivity of the solid electrode phase is a more attractive strategy to enhance the discharge performance of thick electrodes.
only slightly increases the energy loss by less than 15% compared to the baseline case while decreasing k0 doubles the energy loss. Therefore, tailoring the electronic conductivity of the solid electrode phase is a more attractive strategy to enhance the discharge performance of thick electrodes.
Figure 7. (a). Discharge potential curves of 200 μm-thick model electrodes ( = 0.001 V) with different electronic conductivity
= 0.001 V) with different electronic conductivity  or surface reaction rate constant k0 values as shown in the legend. Unit of
or surface reaction rate constant k0 values as shown in the legend. Unit of  is S m−1 and of k0 is mol·m−2·s−1·(mol·m−3)−1.5. Electrodes are discharged at 1 C in half cells. (b). Energy loss at the cell level vs DoD.
is S m−1 and of k0 is mol·m−2·s−1·(mol·m−3)−1.5. Electrodes are discharged at 1 C in half cells. (b). Energy loss at the cell level vs DoD.
Download figure:
Standard image High-resolution imageConclusions
In this work, we employ P2D simulations and equivalent circuit model to elucidate the important role of the SOC dependence of the open-circuit potential Ueq, an intrinsic thermodynamic property of battery compounds, in controlling the reaction uniformity within porous electrodes. Electrode reaction becomes increasingly homogeneous with the slope of the Ueq(SOC) curve, which has a direct impact on the battery discharge performance at high rates. The limiting cases can be described by the "uniform reaction" behavior for electrodes whose Ueq has strong SOC dependence (e.g. NMC and NCA), and the "moving-zone reaction" behavior for electrodes with SOC-independent Ueq (e.g. LiFePO4, Li4Ti5O12). A dimensionless "reaction uniformity" number,  is introduced to capture the effects of electrode and cycling parameters on the degree of reaction inhomogeneity. In the electrolyte-transport-limited regime,
is introduced to capture the effects of electrode and cycling parameters on the degree of reaction inhomogeneity. In the electrolyte-transport-limited regime,  accurately predicts the reaction zone width and exhibits a universal correlation with the rescaled discharge capacity, making
accurately predicts the reaction zone width and exhibits a universal correlation with the rescaled discharge capacity, making  a useful indicator of the electrode performance. We show that the reaction distribution in moving-zone-reaction-type electrodes can be homogenized by several approaches including (1) matching the ionic and electronic conductivities, (2) grading the electronic conductivity, and (3) slowing down the surface reaction kinetics, of which the first two do not significantly reduce the energy efficiency of the discharging process.
a useful indicator of the electrode performance. We show that the reaction distribution in moving-zone-reaction-type electrodes can be homogenized by several approaches including (1) matching the ionic and electronic conductivities, (2) grading the electronic conductivity, and (3) slowing down the surface reaction kinetics, of which the first two do not significantly reduce the energy efficiency of the discharging process.
Acknowledgments
FW is supported by DOE under project number DE-EE0006250. MT acknowledges support from DOE under project number DE-SC0019111. Simulations were partially performed on supercomputers at the Texas Advanced Computing Center (TACC) at The University of Texas and the National Energy Research Scientific Computing Center, a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231.
Appendix A
A.1. P2D simulations
detailed description of the P2D model can be found in literature.8–12 The governing equations implemented in the half cell simulations are summarized as follows.
The concentration  and ionic current
and ionic current  in a binary electrolyte are given by
in a binary electrolyte are given by
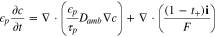

where the subscript  or
or  to represent cathode or separator. Let X = 0 be at the interface between the current collector and cathode. The boundary conditions are
to represent cathode or separator. Let X = 0 be at the interface between the current collector and cathode. The boundary conditions are
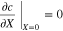
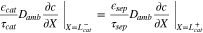
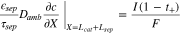
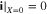
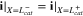
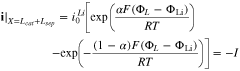
where superscripts (+ and −) denote the right and left side of the cathode/separator interface, respectively, and the potential of Li anode  is fixed at 0. The electronic current in solid electrode matrix
is fixed at 0. The electronic current in solid electrode matrix  is
is
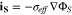
with the boundary conditions
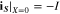
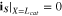
The ionic and electronic currents are coupled by surface reaction as
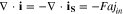
where  in cathode and reaction flux density
in cathode and reaction flux density  follows the Butler-Volmer equation (Eq. 1), in which
follows the Butler-Volmer equation (Eq. 1), in which  is given by
is given by
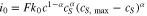
In the P2D simulations of NMC and LFP half cells, lithium diffusion in active materials is simplified as a radial diffusion in spherical particles as
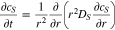
where the boundary conditions are
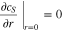
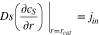
For the model electrode material, Li diffusion is assumed to be very facile so that  is constant within each electrode particle. All of the simulations are implemented in COMSOL Multiphysics® 5.3a.
is constant within each electrode particle. All of the simulations are implemented in COMSOL Multiphysics® 5.3a.
Table A·I. Parameters used in P2D simulations (unless otherwise stated).
| Parameter | Symbol | Value | ||
|---|---|---|---|---|
| Electrode properties | ||||
| NMC | LFP | Model cathode material | ||
| Cathode particle radius (μm) |

|
1 | 0.1 | 0.1 |
| Cathode porosity |

|
0.25 | 0.25 | 0.25 |
| Separator thickness (μm) |

|
25 | ||
| Separator porosity |

|
0.55 | ||
| Tortuosity |

|

|
||
| Maximum Li concentration in active materials (mol·m−3) |

|
49761 | 22806 | 20000 |
| Initial concentration in active materials (mol·m−3) |

|
22392 | 228 | 200 |
| Li diffusivity in active materials (m2·s−1) |

|
10–1436 | 10–1637 | — |
| Effective electrode conductivity (S·m−1) |

|
1038 | 10a) | 100 |
| Reaction rate constant (mol·m−2·s−1·(mol·m−3)−1.5) |

|
3·10–1138 | 3·10–11a) | 10−8 |
| Charge transfer coefficient |

|
0.5 | ||
| Exchange current density of Li anode (A·m−2) |

|
2038 | ||
| Equilibrium potential (V) |

|
See noteb) | ||
| Electrolyte (1 M LiPF6 in EC/DMC 50:50 wt%) properties | ||||
| Initial salt concentration (mol·m−3) |

|
1000 | ||
| Transference number of cations |

|
0.3939 | ||
| Ambipolar diffusivity (m2·s−1) |

|
2.95·10–1039 | ||
| Concentration-dependent ionic conductivity (S·m−1) |

|
0.00233  c) c) |
||
a)Assumed.
b)The equilibrium potential profiles of NMC and LFP are extracted from Fig. 2 in Ref. 40, and Fig. 2 in Ref. 41. The equilibrium potential of model cathode material is defined by Eq. 4.
c)Calculated by 









