Abstract
In recent work, we developed a set of equations that can be used to treat Li plating and subsequent electro-dissolution, and we analyzed how the equation system behaved for a particle of graphite, a fundamental unit of the negative electrode in lithium ion cells. In this work, we apply the same governing equations to the more realistic setting of a porous electrode consisting of many graphite particles. We propose a Li activity model wherein the activity of plated lithium differs from the activity of bulk Li in a thin layer (on the order of monolayers) at the interface with the graphite substrate and transitions smoothly to the activity of bulk Li at greater distances from the graphite interface. Since it is unclear at this point exactly how large this interfacial layer should be, we also show how to treat the limiting case, in which the interfacial layer thickness goes to zero and the activity of any deposited Li is that of bulk Li, which significantly complicates the porous-electrode analysis. We find the two approaches (i.e., finite thickness on the order of monlayers and zero thickness for the interfacial layer) yield very similar results.
Export citation and abstract BibTeX RIS

This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 License (CC BY, http://creativecommons.org/licenses/by/4.0/), which permits unrestricted reuse of the work in any medium, provided the original work is properly cited.
List of symbols

|
Surface to volume ratio of porous electrode, 1/cm |

|
Spherical particle radius in porous electrode, cm |

|
Activities of plated lithium, unoccupied and occupied sites of gallery j of the graphite |

|
Salt concentration in liquid phase, mol cm−3 |

|
Value of  at equilibrium, mol cm−3 at equilibrium, mol cm−3
|

|
Maximum concentration of lithium in electrode, mol cm−3 |

|
Diffusion coefficient in solid phase, cm2 s−1 |

|
Diffusion coefficient in liquid phase, cm2 s−1 |

|
Activity coefficient of electrolyte salt |

|
Faraday constant, Coulomb mol−1 |

|
current density in the solid or liquid phase, A cm−2 |

|
exchange current density, gallery j of graphite A cm−2 |

|
See Eq. 6, A cm−2 |

|
Total current density at 1-C rate |

|
Current density of lithium insertion or lithium plating reactions, A cm−2 |

|
Width of porous electrode or separator, cm |

|
Specific (volumetric) amount of plated and intercalated lithium, C cm−3 |

|
Dimensionless total charge of intercalated plus plated lithium, Eq. 17 |

|
Reaction rate of reaction 13, see also Eq. 16, mol cm−2-s−1 |

|
Radial coordinate in spherical particles, cm |

|
Gas constant, J cm−3-K−1 |

|
Electrode resistances, see Eq. 37, Ohm-cm2 |

|
transformation variable, Eq. 25 |

|
Time, s |

|
Diffusion time  s s
|

|
Transference number |

|
Temperature, K |

|
Open circuit voltage of intercalation reaction, V |

|
Open circuit voltage of plating reaction |

|
See Eq. 2, V |

|
Electrode voltage with respect to a lithium reference, V |

|
Total mole fraction of lithium, occupied and unoccupied site fraction in solid phase, respectively |

|
Maximum mole fraction of species j, see Eq. 2 |

|
Coordinate in porous electrode, cm |

|
Symmetry factor for the jth intercalation reaction 1 |

|
Symmetry factor for reaction 8 |

|
Dimensionless parameter, see Eq. 38 |

|
See Eq. 9, surface coverage of plated lithium, mol cm−2 |

|
See Eq. 9, mol cm−2 |

|
See Eq. 9 |

|
Tortuosities of the solid, and liquid phases in the electrode |

|
Porosity of the solid or liquid phase |

|
Surface overpotential of the intercalation reaction 1, V |

|
Surface overpotential of the Li plating reaction 8, V |

|
Conductivity in liquid phase, S cm−1 |

|
Potential in the solid or liquid phase, V |

|
Dimensionless time |

|
Thermodynamic parameters, see Eq. 2 |
Overbar 
|
Dimensionless form |
In the prior two publications associated with this work, major elements of the equation system to be described in this paper were used to examine a single-particle model of lithiated graphite along with Li plating and dissolution1 and to examine the influence of inhomogeneities along the graphite surface in terms of promoting localized Li plating.2 References 1 and 2 provide relevant literature reviews of models for Li plating as well. In this work, we extend the analyses to treat porous electrodes.
The first treatment of porous electrode models to consider Li plating during overcharge was provided by Arora, Doyle, and White.3 Several studies using variants of Ref. 3 have since appeared.4–14 Quite recently, Lin15 employed a trained "long short-term memory (LSTM) neural network" to predict the anode electrode potential so as to avoid Li plating; Lin also provides a brief review of relevant Li plating literature. Campbell et al.13 detail the use of differential voltage spectroscopy for determining the onset of Li plating, which we also employ in this work (cf. Figs. 2 and 9). Campbell et al.13 also provide a thorough review of the experimental literature associated with the electrochemical detection of Li plating.
References 1 and 2 focused on two new additions to the literature. First, the treatment of possible exchange reactions between plated Li and galleries in the graphite host were introduced, (cf. the reaction rate (16) below and the corresponding resistance  defined in Eq. 37). Second, previous studies of the lithium plating reaction3–14 assumed that the activity coefficient of plated lithium was the same as that of bulk Li; when this assumption is used in a conventional charge-transfer relation (a Butler–Volmer equation), it yields the paradoxical result that the reverse of lithium plating (electro-dissolution) can occur, even when no plated lithium is present. The paradox was resolved by recognizing that small amounts of plated lithium (on the order of monolayers) interact with the graphite host, giving rise to an activity expression differing from that of bulk lithium, of the form in Eq. 9 below. In particular, the open-circuit voltage (OCV) of plated lithium becomes nonzero for these small amounts of plating, which prohibits complete depletion of the plated lithium in the Butler-Volmer equation.
defined in Eq. 37). Second, previous studies of the lithium plating reaction3–14 assumed that the activity coefficient of plated lithium was the same as that of bulk Li; when this assumption is used in a conventional charge-transfer relation (a Butler–Volmer equation), it yields the paradoxical result that the reverse of lithium plating (electro-dissolution) can occur, even when no plated lithium is present. The paradox was resolved by recognizing that small amounts of plated lithium (on the order of monolayers) interact with the graphite host, giving rise to an activity expression differing from that of bulk lithium, of the form in Eq. 9 below. In particular, the open-circuit voltage (OCV) of plated lithium becomes nonzero for these small amounts of plating, which prohibits complete depletion of the plated lithium in the Butler-Volmer equation.
The above modification to the activity of plated lithium comes at a price in complexity. The small surface coverage  of plated lithium introduced in Eq. 9 dictates how large the surface coverage
of plated lithium introduced in Eq. 9 dictates how large the surface coverage  must be, before its activity tends to that of bulk lithium, and
must be, before its activity tends to that of bulk lithium, and  is presumed to be on the order of monolayers. The resulting OCV
is presumed to be on the order of monolayers. The resulting OCV  of plated lithium thus becomes near singular, where it is essentially equal to zero until
of plated lithium thus becomes near singular, where it is essentially equal to zero until  decreases to approach
decreases to approach  at which point it rises rapidly for values of
at which point it rises rapidly for values of  This near-singular behavior impacts solutions to the porous-electrode equations. In this work, we will consider lithiating a porous graphite electrode at constant current beyond the point at which plating starts to occur, followed by a period of open circuit, in which the plated lithium is re-absorbed into the graphite during equilibration. During constant lithiation, the plating first occurs on graphite particles at the electrode-separator interface. As the lithiation continues, the plating extends towards the copper current collector. This gives rise to two different regions of the electrode, separated by a moving boundary layer where, in the plated region,
This near-singular behavior impacts solutions to the porous-electrode equations. In this work, we will consider lithiating a porous graphite electrode at constant current beyond the point at which plating starts to occur, followed by a period of open circuit, in which the plated lithium is re-absorbed into the graphite during equilibration. During constant lithiation, the plating first occurs on graphite particles at the electrode-separator interface. As the lithiation continues, the plating extends towards the copper current collector. This gives rise to two different regions of the electrode, separated by a moving boundary layer where, in the plated region,  and
and  whereas in the un-plated region
whereas in the un-plated region  and
and  The boundary layer is the thin region of the electrode where
The boundary layer is the thin region of the electrode where  and
and  are approximately the same size. It is thus natural to consider solutions to the porous-electrode equations in the limiting case, for values of
are approximately the same size. It is thus natural to consider solutions to the porous-electrode equations in the limiting case, for values of  tending to zero.
tending to zero.
The next section describes the porous-electrode equations and gives them in a dimensionless form. The dimensionless surface coverage  (see Eq. 38) is the ratio of the amount of plating covering a spherical graphite particle of radius
(see Eq. 38) is the ratio of the amount of plating covering a spherical graphite particle of radius  divided by the lithium capacity of the same particle at full intercalation. For a spherical particle of 5 micron radius,
divided by the lithium capacity of the same particle at full intercalation. For a spherical particle of 5 micron radius,  which corresponds to 0.1 percent of the graphite capacity and about 2 monolayers of Li coverage. A set of equations is then derived for solutions to the limiting case, where
which corresponds to 0.1 percent of the graphite capacity and about 2 monolayers of Li coverage. A set of equations is then derived for solutions to the limiting case, where  In the section on Simulation Results and Discussion, solutions to the equations will be shown for the value
In the section on Simulation Results and Discussion, solutions to the equations will be shown for the value  These solutions are compared to solutions of the limiting case, where
These solutions are compared to solutions of the limiting case, where  Finally, an Appendix describes some details of the numerical solution process.
Finally, an Appendix describes some details of the numerical solution process.
Model Description
The porous electrode is modeled in a one-dimensional fashion using the coordinate  where the current collector is assumed to be at
where the current collector is assumed to be at  and the separator interface is assumed to be at
and the separator interface is assumed to be at  For simplicity, we assume that the separator has zero thickness and the reference and counter electrode are placed at
For simplicity, we assume that the separator has zero thickness and the reference and counter electrode are placed at  At each point
At each point  in the porous electrode, solid-phase diffusion occurs in a spherical graphite particle of radius
in the porous electrode, solid-phase diffusion occurs in a spherical graphite particle of radius  where both plating and lithium intercalation can occur at the interface between the electrolyte and the particle surface. As such, the geometric coordinates of this model correspond to
where both plating and lithium intercalation can occur at the interface between the electrolyte and the particle surface. As such, the geometric coordinates of this model correspond to  Figure 1 shows a schematic of the electrode and the coordinate system.
Figure 1 shows a schematic of the electrode and the coordinate system.
Figure 1. Schematic of the porous electrode. Dimensionless coordinates are  and
and 
Download figure:
Standard image High-resolution imageThermodynamics and kinetics of the intercalation of lithium into graphite
As was done in Refs. 1 and 2, the different galleries of intercalated lithium are assumed to be in thermodynamic equilibrium, so that their open-circuit potentials  for some common equilibrium potential
for some common equilibrium potential  of the graphite. A listing of parameters and properties can be found in Table I. The intercalation reaction in each gallery is represented as.
of the graphite. A listing of parameters and properties can be found in Table I. The intercalation reaction in each gallery is represented as.
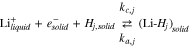
where  and
and  represent vacant and occupied sites for lithium in gallery j,
represent vacant and occupied sites for lithium in gallery j,  is a lithium ion in the electrolyte and
is a lithium ion in the electrolyte and  is an electron in the graphite. For each gallery j
is an electron in the graphite. For each gallery j
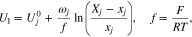

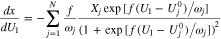
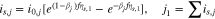
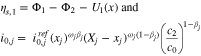
 is the solid-phase potential of the graphite,
is the solid-phase potential of the graphite,  is the potential of the adjacent electrolyte, both with respect to the lithium reference electrode, and
is the potential of the adjacent electrolyte, both with respect to the lithium reference electrode, and  is the salt concentration in the electrolyte. Equation 6 can become singular when
is the salt concentration in the electrolyte. Equation 6 can become singular when  is close to zero and
is close to zero and  tends to zero as well. To avoid this, we rewrite Eq. 6 using
tends to zero as well. To avoid this, we rewrite Eq. 6 using
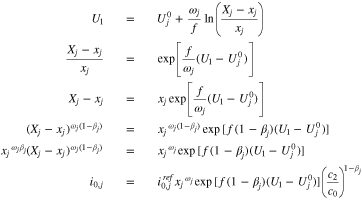
Table I. Parameters and properties.
| L, m | 1.20E-04 |

|
1 | ||||
| a, m | 5.00E-06 |
 A m−2 A m−2 |

|
||||
| T, K | 298 |
 mol m−2 mol m−2 |

|
||||
 mol m−3 mol m−3 |
1000 |
 V V |
0.6 | ||||
 A m−2 A m−2 |
1 |

|
0.4 | ||||

|
0.5 |
 m2 s−1 m2 s−1 |

|
||||

|
0.5 |
 A m−2 A m−2 |
1 | ||||
 mol m−3 mol m−3 |
30452 |

|
0.016757 | ||||

|
0.25 |
 s s |
1250 | ||||

|

|
Capacity, C m−2 |

|
||||

|

|
 Ohm-m2 Ohm-m2 |

|
||||
 S m−1 S m−1 |
1 |
 Ohm-m2 Ohm-m2 |

|
||||
 m2 s−1 m2 s−1 |

|
 Ohm-m2 Ohm-m2 |

|
||||
 S m−1 S m−1 |
50 |
 Ohm-m2 Ohm-m2 |

|
||||

|

|
 Ohm-m2 Ohm-m2 |

|
||||

|

|
||||||
| j= | 1 | 2 | 3 | 4 | 5 | 6 | 7 |

|
0.41336 | 0.23963 | 0.15018 | 0.05462 | 0.06744 | 0.05476 | 0.02 |
 (V) (V) |
0.08843 | 0.12799 | 0.14331 | 0.16984 | 0.21446 | 0.36325 | 0.088427 |

|
0.08611 | 0.08009 | 0.72469 | 2.53277 | 0.09470 | 5.97354 | 1 |
We assume that all  are equal, so one obtains from (5)
are equal, so one obtains from (5)

Note that the same problem can in principle arise when  becomes small, but this is less likely, as long as we stay away from zero intercalation. If it does occur, then one would have to use a special approximation for
becomes small, but this is less likely, as long as we stay away from zero intercalation. If it does occur, then one would have to use a special approximation for  in the limit as it becomes small:
in the limit as it becomes small:
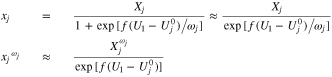
Thermodynamics and kinetics of the lithium plating reaction
Lithium in the electrolyte can either intercalate into the graphite or plate on the graphite surface. The plating reaction is represented as
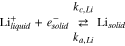
The plated lithium is assumed to consist of a film of negligible thickness on the surface of the graphite particle, which can be characterized by a surface concentration  of plated lithium. Substantial lithium plating only occurs at cell potentials below zero with respect to a lithium reference, but sub-monolayer amounts of plated lithium are assumed to exist in an equilibrium state with intercalated lithium, even at higher cell potentials. As described in Refs. 1 and 2, we express the activity of Li as
of plated lithium. Substantial lithium plating only occurs at cell potentials below zero with respect to a lithium reference, but sub-monolayer amounts of plated lithium are assumed to exist in an equilibrium state with intercalated lithium, even at higher cell potentials. As described in Refs. 1 and 2, we express the activity of Li as

Thus,  corresponds to the dilute-lithium, ideal-solution condition, and for
corresponds to the dilute-lithium, ideal-solution condition, and for 
 i.e., as the lithium surface concentration Γ grows larger than the reference value Γref, the activity of the deposited Li rapidly (exponentially) approaches unity, which is the activity of bulk Li. The value of Γref must be specified. For reasons outlined in Refs. 1 and 2, where the term relevant surface activity thickness is employed, we would expect Γref to be a couple of monolayers of Li; for deposits of Li greater than this, we would expect the deposited Li to have the activity of bulk Li. The open-circuit potential
i.e., as the lithium surface concentration Γ grows larger than the reference value Γref, the activity of the deposited Li rapidly (exponentially) approaches unity, which is the activity of bulk Li. The value of Γref must be specified. For reasons outlined in Refs. 1 and 2, where the term relevant surface activity thickness is employed, we would expect Γref to be a couple of monolayers of Li; for deposits of Li greater than this, we would expect the deposited Li to have the activity of bulk Li. The open-circuit potential  for plated lithium can now be expressed as
for plated lithium can now be expressed as
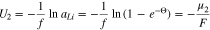
The chemical potential  is relative to lithium metal. Large surface coverages of plated lithium, corresponding to values
is relative to lithium metal. Large surface coverages of plated lithium, corresponding to values  have the same potential as lithium metal, and
have the same potential as lithium metal, and  tends to zero in this limit, but surface coverages less than
tends to zero in this limit, but surface coverages less than  develop positive potentials due to interactions with the graphite substrate. Based on formula 10,
develop positive potentials due to interactions with the graphite substrate. Based on formula 10,  can be roughly viewed as the coverage at which lithium plating starts to occur. For example, when the plated lithium is equilibrated with intercalated lithium,
can be roughly viewed as the coverage at which lithium plating starts to occur. For example, when the plated lithium is equilibrated with intercalated lithium,  thus, at an equilibrium voltage of 1 mV and room temperature, the surface coverage is about
thus, at an equilibrium voltage of 1 mV and room temperature, the surface coverage is about  whereas at 1 V, the surface coverage drops to about
whereas at 1 V, the surface coverage drops to about 
The kinetics of the lithium plating are given as
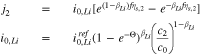
where 
If we use Eq. 10 to replace  with
with  in Eq. 11, we get
in Eq. 11, we get
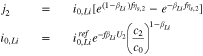
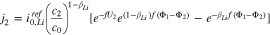
We turn now to the case when a third reaction is occurring between the plated and graphite phases. At the interface between the lithiated graphite and the Li plating,
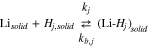
consistent with an elementary reaction when a Li deposit  is on top of the lithiated graphite:
is on top of the lithiated graphite:

where there is one such reaction for each gallery. The activities are given as  and
and  for vacant and occupied sites in gallery j. From Eq. 2,
for vacant and occupied sites in gallery j. From Eq. 2,
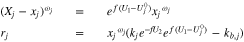
Note that at equilibrium,  so that
so that
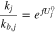
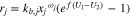
Summing all reactions together, one gets
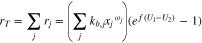
In what follows, for simplicity it is assumed that all  so that
so that
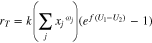
The relevant thermodynamics for the problem formulation are depicted in Fig. 2, where the abscissa  refers to
refers to
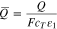
where  is the total charge (e.g., units of C cm−3) of plated and intercalated lithium. At equilibrium,
is the total charge (e.g., units of C cm−3) of plated and intercalated lithium. At equilibrium,  For
For  below 0.001, which (for a particle radius of 5 micron) corresponds to the reference surface coverage of Li being 0.1 percent of the specific areal capacity for deposited Li, further reductions in
below 0.001, which (for a particle radius of 5 micron) corresponds to the reference surface coverage of Li being 0.1 percent of the specific areal capacity for deposited Li, further reductions in  do not influence significantly the equilibrium results as plotted. The lower plot in Fig. 2 portrays the highly nonlinear behavior in
do not influence significantly the equilibrium results as plotted. The lower plot in Fig. 2 portrays the highly nonlinear behavior in  and the dimensionless effective diffusion coefficient, relevant to the diffusion of lithium in the graphite discussed below,
and the dimensionless effective diffusion coefficient, relevant to the diffusion of lithium in the graphite discussed below,  In addition, we see that differentiation of the OCV curve (
In addition, we see that differentiation of the OCV curve ( ) yields a sharp valley (a pronounced minimum) as (i) the graphite fills with Li and
) yields a sharp valley (a pronounced minimum) as (i) the graphite fills with Li and  leading to a sharp decline in the potential and
leading to a sharp decline in the potential and  followed by (ii) Li plating, causing
followed by (ii) Li plating, causing  a constant, and causing
a constant, and causing  to transition from a large, negative value to nearly zero. These observations underscore the relevance of evaluating
to transition from a large, negative value to nearly zero. These observations underscore the relevance of evaluating  to approximate the onset of Li plating (cf. Fig. 9).
to approximate the onset of Li plating (cf. Fig. 9).
Figure 2. Equilibrium potential (upper plot) and, in the lower plots, its differential vs dimensionless charge and the dimensionless, effective diffusion coefficient vs the fraction of Li-filled sites.
Download figure:
Standard image High-resolution imageCharge and material transport in a porous electrode
Plated lithium covers the surface of each graphite particle and a mass balance for this surface coverage implies that at 
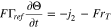
that is, the rate of growth of the surface coverage is the difference between the rate at which lithium is plated and the rate at which it transports into the graphite under reaction 13.
Diffusive transport of intercalated lithium in a spherical graphite particle is given as (Refs. 1 and 2)
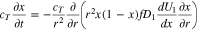
where  is the mole fraction of occupied lithium sites,
is the mole fraction of occupied lithium sites,  is a solid phase diffusion coefficient, and
is a solid phase diffusion coefficient, and  is the total concentration of sites (occupied and unoccupied) in the graphite. Because the relation
is the total concentration of sites (occupied and unoccupied) in the graphite. Because the relation  is given explicitly in Eq. 3, whereas the relationship
is given explicitly in Eq. 3, whereas the relationship  must be numerically inverted, it is convenient to reformulate Eq. 19 in terms of the dependent variable
must be numerically inverted, it is convenient to reformulate Eq. 19 in terms of the dependent variable 
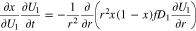
where  is given by Eq. 4. The boundary condition at the particle surface
is given by Eq. 4. The boundary condition at the particle surface  is given as
is given as
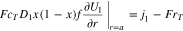
Of particular interest is the case when the reaction rate  is infinitely fast, that is,
is infinitely fast, that is,  In this case Eqs. 18 and 21 collapse and become redundant. The problem can be corrected replacing Eq. 18 by the difference of Eqs. 18 and 21:
In this case Eqs. 18 and 21 collapse and become redundant. The problem can be corrected replacing Eq. 18 by the difference of Eqs. 18 and 21:
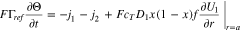
The boundary condition (21) continues to be valid, but in the limit  it reduces to the equilibrium condition
it reduces to the equilibrium condition
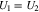
at 
Just as there is a choice between the variables  and
and  in the graphite, there is also a choice between the variables
in the graphite, there is also a choice between the variables  and
and  in Eq. 22, where the transformation (10) relates the two variables. Unfortunately, neither of these choices is optimal for numerical calculations. When starting to charge an empty cell, the variable
in Eq. 22, where the transformation (10) relates the two variables. Unfortunately, neither of these choices is optimal for numerical calculations. When starting to charge an empty cell, the variable  is very small, and caution must be taken to prohibit it from going negative during numerical iterations. It also becomes difficult to determine
is very small, and caution must be taken to prohibit it from going negative during numerical iterations. It also becomes difficult to determine  with enough accuracy to accurately determine
with enough accuracy to accurately determine  via Eq. 10. Similarly, when plating occurs, the variable
via Eq. 10. Similarly, when plating occurs, the variable  tends to zero and the amount of accuracy needed to back-calculate
tends to zero and the amount of accuracy needed to back-calculate  using Eq. 10 becomes prohibitive. In summary, it is desirable to use
using Eq. 10 becomes prohibitive. In summary, it is desirable to use  as the dependent variable during charging, but
as the dependent variable during charging, but  is the preferred choice when plating has occurred. There is a third alternative that contains the best of both choices, but it entails defining a new dependent variable, which we refer to as
is the preferred choice when plating has occurred. There is a third alternative that contains the best of both choices, but it entails defining a new dependent variable, which we refer to as  1,2 We define s by requiring it to satisfy the differential equation
1,2 We define s by requiring it to satisfy the differential equation
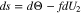
The idea behind Eq. 24 is that at small states of charge,  will be negligible so that s will be proportional to
will be negligible so that s will be proportional to  whereas when plating has occurred,
whereas when plating has occurred,  will be negligible and
will be negligible and  will be proportional to
will be proportional to  The different signs for
The different signs for  and
and  in Eq. 24 arise because the variable
in Eq. 24 arise because the variable  increases as
increases as  decreases. Eq. 24 can be solved as follows:
decreases. Eq. 24 can be solved as follows:
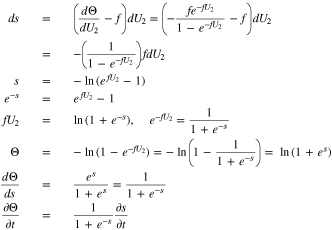
With these conventions, Eq. 22 becomes
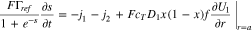
Equation 26, along with
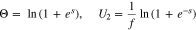
replace Eq. 22. In the limit of large k, when reaction 13 becomes facile, Eq. 21 becomes
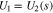
at 
The transport equations in the electrolyte of the porous electrode are well known1 and take the form

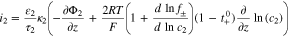
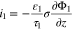
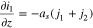
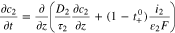
For charging at a constant current density  boundary conditions at the current collector
boundary conditions at the current collector  are
are
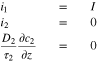
At the separator interface  the location of the reference electrode,
the location of the reference electrode,
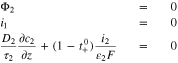
At the start of charging, we assume that all the graphite is at some high OCV, in our case,
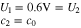
where  is the bulk value of salt concentration in the electrolyte.
is the bulk value of salt concentration in the electrolyte.
Dimensionless equations
We define the following resistances
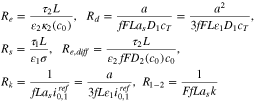
where one can view  as a characteristic electrolyte resistance,
as a characteristic electrolyte resistance,  as a solid-phase diffusion resistance,
as a solid-phase diffusion resistance,  as a solid phase electron resistance,
as a solid phase electron resistance,  as a salt diffusion resistance,
as a salt diffusion resistance,  as a charge transfer resistance for intercalation and
as a charge transfer resistance for intercalation and  as the resistance associated to the interface reaction between the plated and graphite phases. Additionally, define
as the resistance associated to the interface reaction between the plated and graphite phases. Additionally, define
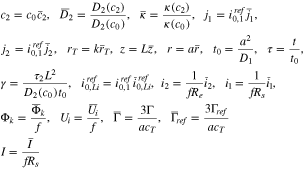
In dimensionless form, the electrode is in the region  with the separator at
with the separator at  and the current collector at
and the current collector at  (cf. Fig. 1). The solid phase diffusion equation becomes
(cf. Fig. 1). The solid phase diffusion equation becomes
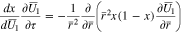
and equations for the unknowns  and
and  take the form
take the form
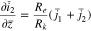
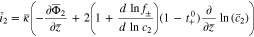
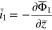
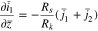
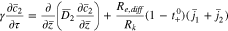
The plating reaction takes the form (at  )
)
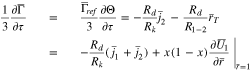
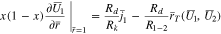
When  Eq. 46 is replaced with
Eq. 46 is replaced with
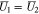
The dimensionless form of Eq. 26 becomes
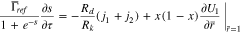
At the separator interface 

At the current collector 
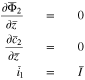
Equations in the limiting case 
In this limit, the variable  must be abandoned, and it must be replaced with the variable
must be abandoned, and it must be replaced with the variable  Note also from Eq. 10 that
Note also from Eq. 10 that  for any finite positive value of
for any finite positive value of  in this limit. We must consider three different situations.
in this limit. We must consider three different situations.
Case 1: No plating has occurred. In this case,  and Eq. 45 at the particle surface
and Eq. 45 at the particle surface  become
become
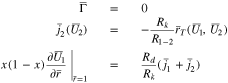
The second of Eq. 51 can be used to determine  as a function of
as a function of  and the other dependent variables. During charging at constant current, one must monitor the potential
and the other dependent variables. During charging at constant current, one must monitor the potential  at the separator interface
at the separator interface  continually while solving. Once
continually while solving. Once  plating will start and the equations in Case 2 must then be solved. When
plating will start and the equations in Case 2 must then be solved. When  the second of Eq. 51 becomes
the second of Eq. 51 becomes
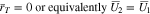
This condition should be understood as describing the situation when the rate constant  for the reactions 13 becomes infinite, and the plated and intercalated phases of lithium are always equilibrated.
for the reactions 13 becomes infinite, and the plated and intercalated phases of lithium are always equilibrated.
Case 2: Plating occurs, and the region of plating is expanding in time from the separator interface at  toward the current collector at
toward the current collector at  This situation holds once plating occurs during charging at a sufficiently large constant current
This situation holds once plating occurs during charging at a sufficiently large constant current  In this case, one must introduce an additional variable
In this case, one must introduce an additional variable  and Eqs. 45 and 46 become
and Eqs. 45 and 46 become
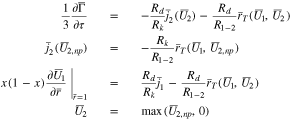
Note that only the second of the above equations depends on  the first and third equations are evaluated using
the first and third equations are evaluated using  instead. In this way, the entire electrode is automatically divided into a region where no plating has occurred, and
instead. In this way, the entire electrode is automatically divided into a region where no plating has occurred, and  and a region where plating is occurring, and
and a region where plating is occurring, and  After solving Eq. 53, the interface
After solving Eq. 53, the interface  between the plated and non-plated regions can be determined by using Newton iteration to find the zero of the function
between the plated and non-plated regions can be determined by using Newton iteration to find the zero of the function  however, this can be done as a post-processing step, and it is not necessary to determine
however, this can be done as a post-processing step, and it is not necessary to determine  in order to solve Eq. 53. This is the advantage of the above formulation: It solves a single set of equations in both the plated and un-plated regions, so that it is not necessary to treat each region separately. Note in addition that, in the region where no plating has occurred,
in order to solve Eq. 53. This is the advantage of the above formulation: It solves a single set of equations in both the plated and un-plated regions, so that it is not necessary to treat each region separately. Note in addition that, in the region where no plating has occurred,  so that the first and second of Eq. 53 imply that in this region
so that the first and second of Eq. 53 imply that in this region  and, assuming that
and, assuming that  is the initial condition,
is the initial condition,  will remain zero in the un-plated region.
will remain zero in the un-plated region.
When  Eq. 53 must be modified to
Eq. 53 must be modified to
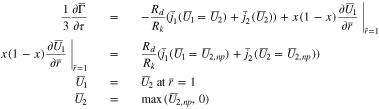
In this case, the flux condition (third of Eq. 53) becomes a Dirichlet condition (the third of Eq. 54), and the second equation, determining  now involves the flux at the particle surface. Eq. 53 assume that the function
now involves the flux at the particle surface. Eq. 53 assume that the function  is continuous at the interface
is continuous at the interface  between the plated and un-plated regions so that, in particular,
between the plated and un-plated regions so that, in particular,  As will be seen in Fig. 8, this assumption is not generally true when one switches from charging to open circuit (Case 3 below).
As will be seen in Fig. 8, this assumption is not generally true when one switches from charging to open circuit (Case 3 below).
Case 3: Plating exists, but the region of plating is decreasing in size over time, for example, when the cell goes to open circuit after charging. In this case, we introduce two new variables:  and
and  Equations 45 and 46 become
Equations 45 and 46 become

We assume in addition an initial condition for the first of the above equations at the time  when the cell is switched to open circuit.
when the cell is switched to open circuit.
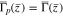
where  is determined from Case 2 at this initial time. The dependent variables solved for in Eq. 55 are
is determined from Case 2 at this initial time. The dependent variables solved for in Eq. 55 are  and the unknown flux
and the unknown flux  In the plated region,
In the plated region,  and the first equation above determines
and the first equation above determines  The third and fourth equations above set the value for
The third and fourth equations above set the value for  in the un-plated region (when
in the un-plated region (when  ). (Compare with the second of Eq. 53.) The fourth equation also insures that
). (Compare with the second of Eq. 53.) The fourth equation also insures that  in the plated region, but it allows for a discontinuity in
in the plated region, but it allows for a discontinuity in  at the interface
at the interface  between the plated and un-plated regions. (See Fig. 8.) After solving Eq. 55, the interface
between the plated and un-plated regions. (See Fig. 8.) After solving Eq. 55, the interface  between the plated and non-plated regions can be determined by using Newton iteration to find the zero of the function
between the plated and non-plated regions can be determined by using Newton iteration to find the zero of the function  although this is not necessary in order to solve Eq. 55. Again, the advantage of this formulation is that it gives a single set of equations that are valid in both the plated and un-plated regions.
although this is not necessary in order to solve Eq. 55. Again, the advantage of this formulation is that it gives a single set of equations that are valid in both the plated and un-plated regions.
In a similar fashion to Case 2, Eq. 55 must be modified when  to
to
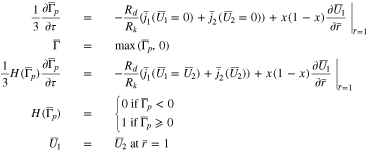
The dependent variables in Eq. 57 are  and the flux value
and the flux value  Again, the flux condition at
Again, the flux condition at  is replaced with a Dirichlet condition (the fourth of the above equations).
is replaced with a Dirichlet condition (the fourth of the above equations).
Equations 55 have a limited range of validity, as is the case for Eq. 53. To understand why, suppose one tried to use Eq. 55 in the situation given in Case 2, during charging, when the plated region is advancing toward the current collector. In such a situation, a point  might start out initially in the un-plated region, but over time become part of the plated region. In this situation,
might start out initially in the un-plated region, but over time become part of the plated region. In this situation,  would become negative for the initial time period until the plated region reached
would become negative for the initial time period until the plated region reached  These negative values would offset the resulting values for
These negative values would offset the resulting values for  at all subsequent times, leading to false values for
at all subsequent times, leading to false values for  This problem does not arise in Case 3, because any point
This problem does not arise in Case 3, because any point  that is initially un-plated remains un-plated for all subsequent times during which Eq. 55 are solved. The requirement that the plated region be receding in time is thus necessary for the validity of Eq. 55.
that is initially un-plated remains un-plated for all subsequent times during which Eq. 55 are solved. The requirement that the plated region be receding in time is thus necessary for the validity of Eq. 55.
Some parameter relationships
The following relationships were used in solving the model equations. (See Ref. 16 and the Notation Index of this document).
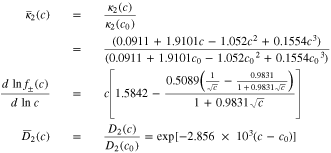
In the above formulas,  that is, the units of
that is, the units of  are mol L−1 where is the units of
are mol L−1 where is the units of  are mol cm−3.
are mol cm−3.
Simulation Results and Discussion
Table I shows the parameter values used in simulations. At time  the half-cell started in an equilibrium state, in which
the half-cell started in an equilibrium state, in which  and
and  A constant 1-C current was then applied to the cella for a period of 2900 s. At this point, the cell was switched to open circuit and allowed to relax. Since little is known about the interfacial reaction 13 between the plated and intercalated lithium phases, the two extreme situations
A constant 1-C current was then applied to the cella for a period of 2900 s. At this point, the cell was switched to open circuit and allowed to relax. Since little is known about the interfacial reaction 13 between the plated and intercalated lithium phases, the two extreme situations  were both simulated to explore how much of an impact this reaction can have on the onset of plating. The simulations were also done assuming a value of
were both simulated to explore how much of an impact this reaction can have on the onset of plating. The simulations were also done assuming a value of  b The equilibrium plots of Fig. 2 show the distinct near two-phase behavior of graphite associated with staging processes,17–19 which is reflected in the non-equilibrium (1-C) plots we shall now discuss.
b The equilibrium plots of Fig. 2 show the distinct near two-phase behavior of graphite associated with staging processes,17–19 which is reflected in the non-equilibrium (1-C) plots we shall now discuss.
For the values  Fig. 3a shows plots of the State of Charge (SOC)
Fig. 3a shows plots of the State of Charge (SOC)  vs time at both the particle surface and the particle center. Two different positions in the electrode are shown for these plots: the separator interface at
vs time at both the particle surface and the particle center. Two different positions in the electrode are shown for these plots: the separator interface at  and the current collector at
and the current collector at  In addition, the average state of charge over the entire particles at all positions
In addition, the average state of charge over the entire particles at all positions  within the electrode and the surface coverage of plated lithium
within the electrode and the surface coverage of plated lithium  at
at  are also shown. Figure 3b shows corresponding plots of the voltages
are also shown. Figure 3b shows corresponding plots of the voltages  (shown at the particle surface
(shown at the particle surface  and the particle center
and the particle center  for both the separator interface
for both the separator interface  and the current collector
and the current collector  ) as well as
) as well as  at both the separator interface and the current collector. Because
at both the separator interface and the current collector. Because  the plated and intercalated phases of lithium at the particle surface are equilibrated with each other and
the plated and intercalated phases of lithium at the particle surface are equilibrated with each other and  at the particle surface, consistent with Eq. 47. Plating first occurs at the separator interface and, over time, extends backwards toward the current collector. The start of plating can be seen from the plot of
at the particle surface, consistent with Eq. 47. Plating first occurs at the separator interface and, over time, extends backwards toward the current collector. The start of plating can be seen from the plot of  at the separator interface, which drops below 1 mV at about 2600 s; note, however, that the precise onset of plating is not well defined when
at the separator interface, which drops below 1 mV at about 2600 s; note, however, that the precise onset of plating is not well defined when  because
because  never completely becomes zero, but only tends exponentially to zero, as defined in Eq. 10. Equation 10 also implies that, at 1 mV,
never completely becomes zero, but only tends exponentially to zero, as defined in Eq. 10. Equation 10 also implies that, at 1 mV,  consistent with the plot of
consistent with the plot of  shown in Fig. 3a. Shown in Fig. 3b is the cell voltage
shown in Fig. 3a. Shown in Fig. 3b is the cell voltage  which rises sharply at 2900 s, when the cell goes to open circuit.
which rises sharply at 2900 s, when the cell goes to open circuit.
Figure 3. The various curves are labelled according to their position coordinates  (a) compositions x at various positions and
(a) compositions x at various positions and  at the separator-electrode interface for
at the separator-electrode interface for  , (b) cell voltage and potentials at various positions for
, (b) cell voltage and potentials at various positions for  , and (c) cell voltage and potentials at various positions for
, and (c) cell voltage and potentials at various positions for  vs time in s. The composition plot for
vs time in s. The composition plot for  was very similar to that of Fig. 3a and, hence, is not shown.
was very similar to that of Fig. 3a and, hence, is not shown.
Download figure:
Standard image High-resolution imageAt the start of open circuit,  still remains close to zero at the electrode-separator interface, because the amount of plated Li there is still significant. It is only at about 2964 s that
still remains close to zero at the electrode-separator interface, because the amount of plated Li there is still significant. It is only at about 2964 s that  starts to rise rapidly at the electrode-separator interface, indicating that the plating has entirely dissolved, either into the graphite, the electrolyte, or both. By 3500 s, all of the curves have reached an asymptote, indicating that the cell is approaching an equilibrium state near 0.1 V vs Li. Figure 3c shows the same type of plots as Fig. 3b, but
starts to rise rapidly at the electrode-separator interface, indicating that the plating has entirely dissolved, either into the graphite, the electrolyte, or both. By 3500 s, all of the curves have reached an asymptote, indicating that the cell is approaching an equilibrium state near 0.1 V vs Li. Figure 3c shows the same type of plots as Fig. 3b, but  Qualitatively, the plots are very similar, but the onset of plating occurs somewhat earlier, at around 2500 s, and the dissolution of the plating at open circuit takes somewhat longer, so that
Qualitatively, the plots are very similar, but the onset of plating occurs somewhat earlier, at around 2500 s, and the dissolution of the plating at open circuit takes somewhat longer, so that  at the separator interface only starts to rise from zero at about 2976 s. At 3500 s, the cell again appears to be close to a state of equilibrium.
at the separator interface only starts to rise from zero at about 2976 s. At 3500 s, the cell again appears to be close to a state of equilibrium.
Figure 4a (for  ) and Fig. 4b (for
) and Fig. 4b (for  ) show the distributions of
) show the distributions of  at different times prior to the onset of plating. For both plots,
at different times prior to the onset of plating. For both plots,  indicating that underpotential deposition is taking place, but no significant amounts of plating are occurring. When the graphite galleries and the Li deposit are equilibrated (Fig. 4a,
indicating that underpotential deposition is taking place, but no significant amounts of plating are occurring. When the graphite galleries and the Li deposit are equilibrated (Fig. 4a,  ),
),  reflects the staging behavior of the graphite substrate upon which the Li deposit resides. Conversely, when
reflects the staging behavior of the graphite substrate upon which the Li deposit resides. Conversely, when  (Fig. 4b), the graphite galleries and the Li deposit are not equilibrated, and the additional resistance yields smoother
(Fig. 4b), the graphite galleries and the Li deposit are not equilibrated, and the additional resistance yields smoother  curves.
curves.
Figure 4.
 profiles prior to the onset of plating, when
profiles prior to the onset of plating, when  for
for  (a) and
(a) and  (b). These profiles indicate that a certain amount of plating always occurs, even for OCVs
(b). These profiles indicate that a certain amount of plating always occurs, even for OCVs  but the amounts are minimal (in this case
but the amounts are minimal (in this case  ). When
). When 
 and, as a result, the multi-phase behavior in the graphite OCV is visible in the
and, as a result, the multi-phase behavior in the graphite OCV is visible in the  profiles.
profiles.
Download figure:
Standard image High-resolution imageFigure 5a (for  ) and Fig. 5b (for
) and Fig. 5b (for  ) show the surface coverages
) show the surface coverages  after the start of plating, but prior to going to open circuit, for the cases when
after the start of plating, but prior to going to open circuit, for the cases when  and
and  When
When  the value
the value  was plotted to enable better comparison with the
was plotted to enable better comparison with the  -values plotted when
-values plotted when  The plots give some idea of how close the values calculated for
The plots give some idea of how close the values calculated for  come to the limiting values when
come to the limiting values when  As previously noted, when
As previously noted, when  the onset of plating is not sharply defined, but when
the onset of plating is not sharply defined, but when  a clear boundary between plated and un-plated regions of the electrode can be seen, because in the un-plated regions
a clear boundary between plated and un-plated regions of the electrode can be seen, because in the un-plated regions 
Figure 5.
 profiles after the onset of plating but prior to open circuit at 2900 s, when
profiles after the onset of plating but prior to open circuit at 2900 s, when  and
and  for
for  (a) and
(a) and  (b). When
(b). When  there is a distinct boundary between the plated region
there is a distinct boundary between the plated region  and the unplated region
and the unplated region  but when
but when  no such clear delineation exists. However, the profiles for the two different
no such clear delineation exists. However, the profiles for the two different  -values are quite similar. For the cases shown when
-values are quite similar. For the cases shown when  the quantity
the quantity  is plotted to compare with
is plotted to compare with  when
when 
Download figure:
Standard image High-resolution imageFigures 6a and 6b are similar to Figs. 5a and 5b, except in Fig. 6 the  distributions are shown after the start of open circuit at 2900 s. Note that, whereas the plating occurred for 300 to 400 s before going to open circuit, the entire plated Li dissolves at open circuit within 70 to 80 s.
distributions are shown after the start of open circuit at 2900 s. Note that, whereas the plating occurred for 300 to 400 s before going to open circuit, the entire plated Li dissolves at open circuit within 70 to 80 s.
Figure 6.
 profiles after the start of open circuit at 2900 s, when
profiles after the start of open circuit at 2900 s, when  and
and  for
for  (a) and
(a) and  (b). In this figure, the boundary between the plated and unplated regions is receding in time, in contrast to Fig. 5. For the cases shown when
(b). In this figure, the boundary between the plated and unplated regions is receding in time, in contrast to Fig. 5. For the cases shown when  the quantity
the quantity  is plotted to compare with
is plotted to compare with  when
when 
Download figure:
Standard image High-resolution imageWhen  there is a sharp boundary point at
there is a sharp boundary point at  between the plated and un-plated regions of the electrode, which can be determined as the plating advances due to lithiation (Case 2 of the equations) by determining the zero-crossing of the function
between the plated and un-plated regions of the electrode, which can be determined as the plating advances due to lithiation (Case 2 of the equations) by determining the zero-crossing of the function  (see the second of Eq. 53). At open circuit, when the plating recedes,
(see the second of Eq. 53). At open circuit, when the plating recedes,  can be determined as the zero- crossing of
can be determined as the zero- crossing of  in the first of Eq. 55. Figure 7 shows plots of
in the first of Eq. 55. Figure 7 shows plots of  for the cases
for the cases  and
and  Note that plating first occurs at the separator interface at
Note that plating first occurs at the separator interface at  and then advances toward the current collector at
and then advances toward the current collector at  during lithiation. At 2900 s, when the cell goes to open circuit, the region of Li plating starts to recede toward the separator interface. Consistent with the prior discussion of Fig. 4, the results of Fig. 7 show that somewhat more lithium is plated when
during lithiation. At 2900 s, when the cell goes to open circuit, the region of Li plating starts to recede toward the separator interface. Consistent with the prior discussion of Fig. 4, the results of Fig. 7 show that somewhat more lithium is plated when  hence, for
hence, for  the plating starts earlier and takes longer to dissolve at open circuit.
the plating starts earlier and takes longer to dissolve at open circuit.
Figure 7. Plots of the boundary  between the plated and unplated regions when
between the plated and unplated regions when  In either case (
In either case ( ) plating always first starts at the electrode-separator interface
) plating always first starts at the electrode-separator interface  and progresses toward the current collector at
and progresses toward the current collector at  After open circuit (dashed lines) the plating recedes, and the boundary
After open circuit (dashed lines) the plating recedes, and the boundary  moves upward again toward the separator interface.
moves upward again toward the separator interface.
Download figure:
Standard image High-resolution imageWhen  and
and  there is a discontinuity in the function
there is a discontinuity in the function  when the cell switches to open circuit. The cell voltage jumps to a more positive value at the start of open circuit (see Figs. 3b and 3c at 2900 s), but the third and fourth of Eq. 55 imply that in the un-plated region of the electrode
when the cell switches to open circuit. The cell voltage jumps to a more positive value at the start of open circuit (see Figs. 3b and 3c at 2900 s), but the third and fourth of Eq. 55 imply that in the un-plated region of the electrode
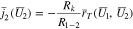
The plating current density  depends on the surface overpotential
depends on the surface overpotential  and the jump in cell voltage forces a corresponding jump in
and the jump in cell voltage forces a corresponding jump in  in the un-plated region in order to preserve Eq. 59. In contrast, in the plated region of the electrode,
in the un-plated region in order to preserve Eq. 59. In contrast, in the plated region of the electrode,  must remain zero, both before and after going to open circuit. This results in discontinuities for
must remain zero, both before and after going to open circuit. This results in discontinuities for  both in time (at the onset of open circuit) as well as at
both in time (at the onset of open circuit) as well as at  (the transition point between the plated and un-plated regions). Figure 8a shows plots of
(the transition point between the plated and un-plated regions). Figure 8a shows plots of  at various times after the onset of open circuit when
at various times after the onset of open circuit when  and
and  where these discontinuities can be clearly seen. Figure 8b shows the same plots, but for the case when
where these discontinuities can be clearly seen. Figure 8b shows the same plots, but for the case when  For any finite positive value of
For any finite positive value of  the curves for
the curves for  must be continuous, but they are clearly approaching a discontinuity for the small value
must be continuous, but they are clearly approaching a discontinuity for the small value  When
When  Eq. 59 no longer holds, because it is replaced with the equation
Eq. 59 no longer holds, because it is replaced with the equation  at
at  Since
Since  remains continuous in both
remains continuous in both  and
and  so must
so must 
Figure 8. If  whenever
whenever  the
the  profiles in the electrode become discontinuous at open circuit at the boundary between the plated and un-plated regions. The upper panel (a) shows the case when
profiles in the electrode become discontinuous at open circuit at the boundary between the plated and un-plated regions. The upper panel (a) shows the case when  . Whenever
. Whenever  the
the  profiles must be continuous, but one sees that at
profiles must be continuous, but one sees that at  (b) these profiles are tending toward the discontinuous behavior seen in the upper panel.
(b) these profiles are tending toward the discontinuous behavior seen in the upper panel.
Download figure:
Standard image High-resolution imageThe utility of differential voltage spectroscopy for determining the onset of Li plating,13 even at the 1-C charge rate, is demonstrated in Fig. 9. The peak associated with Li plating is less pronounced than for the equilibrium condition described in Fig. 2, but it is still quite evident. It is clear in Fig. 9 that when there is a sharp upturn in  at the electrode-separator interface, corresponding to Li plating, there is also a peak in
at the electrode-separator interface, corresponding to Li plating, there is also a peak in  The origins of the peak are identical to those first described in this work in the context of Fig. 2, but the resistances reduce the magnitude of the peak at the 1-C charge rate.
The origins of the peak are identical to those first described in this work in the context of Fig. 2, but the resistances reduce the magnitude of the peak at the 1-C charge rate.
Figure 9.
 and
and  Cell voltage
Cell voltage  its derivative
its derivative  with respect to the dimensionless charge
with respect to the dimensionless charge  and the Li plating concentration
and the Li plating concentration  at the electrode-separator interface. A key point in this figure is the peak in
at the electrode-separator interface. A key point in this figure is the peak in  reflecting the onset of Li plating, corresponding to the sharp upturn in
reflecting the onset of Li plating, corresponding to the sharp upturn in  at the electrode-separator interface.
at the electrode-separator interface.
Download figure:
Standard image High-resolution imageConclusions
We show how the model equations, previously developed in Refs. 1 and 2 for lithium plating, can be applied to examine a graphitic porous electrode and overcharge that leads to lithium plating. This previous work showed that the activity of plated Li on graphite cannot be set to one, as has been done up until now in previous literature,3–14 because the first couple of monlayers of plating interact with the graphite and are thus thermodynamically different from bulk Li metal.
- The resulting expression for the open-circuit voltage (OCV) as a function of surface coverage of plating, Eq. 10, is almost singular, that is, it is exponentially close to zero everywhere except for a very small surface coverage
 below which the OCV rises sharply. We illustrate the behavior of the near singular solutions to the porous-electrode equations, when
below which the OCV rises sharply. We illustrate the behavior of the near singular solutions to the porous-electrode equations, when  is very small, corresponding to a couple of monolayers of lithium, and in the limiting case when
is very small, corresponding to a couple of monolayers of lithium, and in the limiting case when  The latter case is of interest, because a precise value for
The latter case is of interest, because a precise value for  is unknown.
is unknown. - During lithiation at constant current, once plating starts, there are two different regions of the electrode: the plated region near the separator interface and the un-plated complementary region adjacent to the current collector. When
 different sets porous-electrode equations arise in each region. As the lithiation continues, the boundary between the plated and un-plated regions advances from the separator interface toward the current collector. A solution algorithm is given that simultaneously determines where this boundary is and solves the different sets of equations in each of these two regions.
different sets porous-electrode equations arise in each region. As the lithiation continues, the boundary between the plated and un-plated regions advances from the separator interface toward the current collector. A solution algorithm is given that simultaneously determines where this boundary is and solves the different sets of equations in each of these two regions. - If the Li plating process is abruptly interrupted, i.e., the cell is set to open circuit, the boundary starts to recede as plating is absorbed into the graphite. It turns out that the cases of advancing and receding boundary each require a different set of equations that must be solved when
 We derive these different equations and illustrate solutions.
We derive these different equations and illustrate solutions. - As was done in previous work,1,2 an exchange reaction between plated and intercalated lithium at the surface of the graphite particles is also considered and characterized by a resistance
 At this point in time, little is known about how large
At this point in time, little is known about how large  should be. We thus consider the two extreme cases, when
should be. We thus consider the two extreme cases, when  and the plated lithium is always equilibrated with intercalated lithium at the particle surface, and
and the plated lithium is always equilibrated with intercalated lithium at the particle surface, and  when the plated and intercalated lithium can only exchange indirectly through the electrolyte. Although differences are seen between these two cases, the solutions are qualitatively very similar.
when the plated and intercalated lithium can only exchange indirectly through the electrolyte. Although differences are seen between these two cases, the solutions are qualitatively very similar. - Solutions when
 are compared to solutions when
are compared to solutions when  is set to a small positive value, corresponding to about 2 monolayers of plated lithium. Here again, although differences between the two cases can be seen, they are qualitatively very similar.
is set to a small positive value, corresponding to about 2 monolayers of plated lithium. Here again, although differences between the two cases can be seen, they are qualitatively very similar. - Because of the singular nature of these equations, some details concerning the numerical solutions are included in an Appendix.
Appendix:: Some Details about the Numerical Simulations Shown
Figures 10a and 10b show the distributions of the local State of Charge  and
and  at the time
at the time  Both of these figures exhibit some of the multi-phase behavior that is seen in the equilibrium plots of Fig. 2. Of particular note is the sharp drop in both
Both of these figures exhibit some of the multi-phase behavior that is seen in the equilibrium plots of Fig. 2. Of particular note is the sharp drop in both  and
and  at about
at about  The drop is sharper at the particle center
The drop is sharper at the particle center  than at the surface
than at the surface  a trend which can also be seen in the plots of
a trend which can also be seen in the plots of  and
and  at the surfaces and particle centers in Figs. 3a and 3b, although in Fig. 3, these drops are occurring in time, not in the spatial coordinates. As the amount of plated and intercalated lithium increases in the cell, the locations
at the surfaces and particle centers in Figs. 3a and 3b, although in Fig. 3, these drops are occurring in time, not in the spatial coordinates. As the amount of plated and intercalated lithium increases in the cell, the locations  of the sharp changes move through the cell, and this requires a very fine grid to avoid oscillations in numerical solutions. We note that the primary cause of these sharp changes is the staging behavior of the open-circuit voltage
of the sharp changes move through the cell, and this requires a very fine grid to avoid oscillations in numerical solutions. We note that the primary cause of these sharp changes is the staging behavior of the open-circuit voltage  for graphite (cf. Fig. 2), and the same phenomena occur when charging at rates as high 1-C, even without the presence of plating.
for graphite (cf. Fig. 2), and the same phenomena occur when charging at rates as high 1-C, even without the presence of plating.
Figure 10. (a) Li filled sites in graphite as a function of position at  or 1435 s, about half way through the charge process and (b), the corresponding potential
or 1435 s, about half way through the charge process and (b), the corresponding potential  at the particle surfaces. From a numerical-computation perspective, the sharp gradients are of concern, as noted in the Appendix of this report.
at the particle surfaces. From a numerical-computation perspective, the sharp gradients are of concern, as noted in the Appendix of this report.
Download figure:
Standard image High-resolution imageThe equations were solved with the program Comsol using the Equation-Based Interface. A rectangular grid was used with 272 elements in the  -direction and 68 elements in the
-direction and 68 elements in the  -direction. A non-uniform mesh spacing in the
-direction. A non-uniform mesh spacing in the  -direction was used with a boundary layer near the particle surface. The BDF method21 for time stepping was used with a maximum BDF order of 5. For the case
-direction was used with a boundary layer near the particle surface. The BDF method21 for time stepping was used with a maximum BDF order of 5. For the case  the equations were also solved using a finite-difference code.16 The two different numerical solution methods produced results that were identical on the scales plotted in these figures.
the equations were also solved using a finite-difference code.16 The two different numerical solution methods produced results that were identical on the scales plotted in these figures.
Footnotes
- a
A current of 1-C is the constant current required to charge the electrode from zero to 100% State of Charge in 1 h.
- b
Assuming a BCC lattice structure for deposited Li with a 0.35 nm lattice parameter,20 for the particle radius
 and total concentration
and total concentration  given in Table I,
given in Table I,  corresponds to
corresponds to  monolayers of deposited Li. It should be recognized that the deposited Li is likely disordered, so the association of
monolayers of deposited Li. It should be recognized that the deposited Li is likely disordered, so the association of  with about 2 monolayers represents a rough approximation.
with about 2 monolayers represents a rough approximation.






























