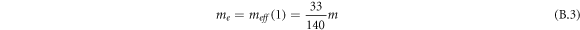Abstract
We present a detailed analysis on measurement sensitivity of dynamic acoustic forces via numerical simulation of the micro-cantilever responses. The rectangular micro-cantilever is regarded as a point mass in the dynamic model of forced and damped harmonic oscillator. We use single- and bimodal-frequency excitation schemes for actuation of the micro-cantilever in the presence of dynamic acoustic forces. In bimodal-frequency excitation scheme, the micro-cantilever is excited at its first two eigenmode frequencies simultaneously as opposed to single-frequency excitation. First, we numerically obtain micro-cantilever deflections by solving the equations of Motions (EOMs) constructed for the first two eigenmodes. Then, we determine oscillation amplitude and phase shift as a function of acoustic force strength within different frequency regions. Moreover, we relate amplitude and phase shift to virial and energy dissipation in order to explore the interaction between flexural modes in multifrequency excitation. The simulation results point out that bimodal-frequency excitation improves the measurement sensitivity of dynamic acoustic forces at particular frequencies. Herein, simultaneous application of driving forces enables higher sensitivities of observables and energy quantities as acoustic force frequencies become around the eigenmode frequencies. For our case, we obtain the highest phase shift (∼178°) for the acoustic force strength of 100 pN at the frequency of around 307.2 kHz. Therefore, this method can be easily adapted to improve measurement sensitivity of dynamic acoustic forces in a wider frequency window.
Export citation and abstract BibTeX RIS
1. Introduction
Acoustic emissions rely on energy release of elastic waves induced by localized stress-strain fields in materials [1]. Structural irregularities such as crack nucleation, phase transformation, dislocation in crystal lattice, and plastic deformation are some of the source mechanisms of acoustic emissions [2, 3]. By processing acoustic emission signals recorded from piezoelectric sensors, locations of surface defects and materials properties are determined [4]. In industrial applications, elastic acoustic waves are used to inspect the conditions of gas pipes, welds, and structures such as aircraft and storage tanks, which are under cycling loadings [3]. Moreover, acoustic emission signals possess information on the discrimination of failure modes for composite materials which are matrix cracking, fiber breakage, and debonding [5]. Acoustic emissions within the frequency range of 90-180kHz are released due to matrix cracking and the acoustic frequency range of 240-310 kHz due to debonding of carbon/epoxy material is detected using a spectrum analyser [6]. In the general case, each failure mechanism generates acoustic emissions within a particular range of frequency. Acoustic emissions exert forces on the surfaces of the micro-structures due to their energy contents [7]. This fact highlights the importance of achieving higher measurement sensitivity of acoustic forces in a broad frequency window using dynamics of micro-structures.
In this paper, a theoretical framework based on Atomic Force Microscopy (AFM) micro-cantilever dynamics is introduced to explore dynamic acoustic force sensitivity. Following works mentioned below deal with actuation of the micro-cantilever with acoustic forces and detection of acoustic emission. In our earlier work, static acoustic force sensitivity is investigated by using resonant AFM micro-cantilever under monomodal and bimodal operations [8]. In addition, a novel photo-acoustic excitation technique is implemented for effective non-contact actuation of micro-cantilever [9]. The thermal effect induced by photo-acoustic waves is eliminated through the innovative actuation method. In the work [7], oscillation characteristics of two resonant cantilevers excited by laser-induced photo-acoustic waves are investigated. In another work [10], effective responses of the micro-cantilever driven magnetically, acoustically, and thermally are explored for different environmental conditions. Theoretical and experimental differences between amplitude and phase responses are presented and evaluated for each excitation mechanism. Moreover, acoustic waves are detected by exciting the micro-cantilever at its resonance frequencies of 50, 100, and 150kHz for a variety of ambient air pressures [11]. Furthermore, micro-cantilever arrays with different resonance frequencies ranging between 0.1 and 1 MHz are utilized for the detection of acoustic signals [12].
In this current work, we utilize single- and bimodal-frequency excitation schemes for actuation of the micro-cantilever in the presence of dynamic acoustic forces. In the following studies, observables such as amplitude and phase shift and the energy quantities are determined based on dynamic responses of the micro-cantilever under tip-sample interaction forces in multifrequency AFM operations. Observable responses such as amplitudes and phase shifts are obtained in the presence of tip-sample interaction force by using tapping mode of Multi-frequency Atomic Force Microscopy (MF-AFM) [13–15]. Higher AFM observable sensitivities are achieved using bimodal-frequency excitation schemes [16–18]. Dynamic of the oscillating micro-cantilever is influenced by the tip-sample interaction force so that a larger phase shift is observed at higher mode [19, 20]. In view of virial theorem, energy stored by the oscillating micro-cantilever and dissipated power are the physical quantities emerging in conservative and non-conservative processes as a result of interaction with tip-sample force. In the work [21], oscillation observables such as amplitude and phase shift are related to these energy quantities analytically. In the study [22], a theory of phase contrast has been established and evaluated for bimodal AFM in terms of energy transfer between modes and dissipated energy. Phase shift transitions are discussed by relating them with signs of virials and average tip-sample interaction force. Furthermore, virials of the first two eigenmodes are determined as a function of amplitude ratio in bimodal AFM [23].
In our study, we develop a theoretical model which explains the use of oscillation observables to measure dynamic acoustic forces that is different from previous studies. The micro-cantilever experiencing dynamic acoustic forces at different frequencies is excited by using monomodal and bimodal excitation schemes. A multifrequency excitation scheme is applied to enhance the sensitivity of ultra-low dynamic acoustic forces. Changes in oscillation observables are explored with respect to acoustic force strength within different frequency regions. In addition, energy dissipation owing to the interaction of micro-cantilever with acoustic forces is evaluated from the point of view of virial theorem. Results of virial and dissipated power support the use of micro-cantilever dynamics to obtain highly significant sensitivities. Energy quantities such as supplied energy by external force, amount of energy transferred to the operating environment, and dissipated energy owing to acoustic forces are presented as a function of force strength for the critical acoustic force frequencies. The energy quantities are utilized to describe energy dissipation process in the measurement of dynamic acoustic forces. Therefore, the results are assessed in the light of energy conservation principle.
2. Theoretical framework and numerical studies
2.1. Single- and bimodal-frequency excitation schemes
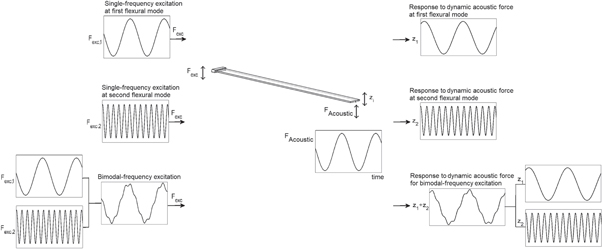
In numerical calculations, we obtain oscillations of a rectangular micro-cantilever excited at its resonance frequencies in measurement of dynamic acoustic forces. We introduce two excitation schemes for micro-cantilever actuation which are single- and bimodal-frequency excitation schemes (figure 1). In single-frequency excitation scheme, external driving force is applied to the micro-cantilever at a single frequency, that is its first or second eigenmode frequency. On the other hand, bimodal-frequency excitation scheme consists of application of driving forces at the first two eigenmode frequencies simultaneously. The EOMs are approximated by using point-mass object in consideration of the dynamic model of forced and damped harmonic oscillator [24]. The EOMs for instantaneous deflection zi (t) which are the second order differential equations are introduced below for single-frequency (Equation (1)) and bimodal-frequency (equation (2)) excitation schemes.
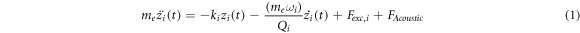
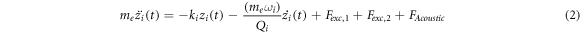
where me , ki , Qi , ωi are the effective mass, the spring constant, the quality factor and the angular resonance frequency (ωi = 2 π fei ) of the flexural mode i of the micro-cantilever. i is equal to 1 and 2 for the first and second eigenmode respectively. The micro-cantilever operates in air, whose influence on oscillation characteristic is represented by the quality factor [11]. Fexc,i is the excitation force at eigenmode frequency fei (equation 3). Since we investigate resonant dynamics of the micro-cantilever under dynamic acoustic force, frequency of external driving force is equal to eigenmode frequency of the micro-cantilever. In consideration of damping effect, maximum amplitude sensitivity to dynamic acoustic force is obtained by driving the micro-cantilever at its resonance frequencies.
Figure 1. Single- and bimodal-frequency excitation schemes and responses of the micro-cantilever under dynamic acoustic forces.
Download figure:
Standard image High-resolution imageIn our case, responses of the micro-cantilever to acoustic forces at different frequencies fAc are investigated for both excitation schemes. FAcoustic is formulated as cosine wave at angular frequency (ωAc = 2π fAc ) with acoustic force strength FAc (equation (4)).
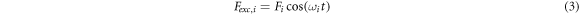
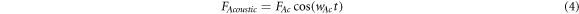
Deflections of the micro-cantilever zs (t) for single-frequency excitation scheme (equation 5) and zb (t) for bimodal-frequency excitation scheme (equation 6) are approximated as follows [24]:
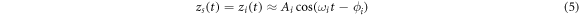
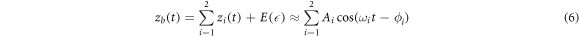
where Ai
is the oscillation amplitude and ϕi
is the phase shift of the ith eigenmode. The term E( ) contains contributions of oscillations at higher modes. More interestingly, since we explore the effect of multi-frequency excitation on measurement sensitivity, observables Ai
and ϕi
obtained using both excitation schemes are compared and evaluated in consideration of mode interaction. Different eigenmodes of the micro-cantilever under excitation forces at eigenmode frequencies are coupled by the virial of the excitation forces in the presence of dynamic acoustic forces. Moreover, observables of the second eigenmode are calculated in order to evaluate measurement sensitivity of acoustic forces at higher frequencies.
) contains contributions of oscillations at higher modes. More interestingly, since we explore the effect of multi-frequency excitation on measurement sensitivity, observables Ai
and ϕi
obtained using both excitation schemes are compared and evaluated in consideration of mode interaction. Different eigenmodes of the micro-cantilever under excitation forces at eigenmode frequencies are coupled by the virial of the excitation forces in the presence of dynamic acoustic forces. Moreover, observables of the second eigenmode are calculated in order to evaluate measurement sensitivity of acoustic forces at higher frequencies.
2.2. Virial theorem and power dissipation
Acoustic force acting on the micro-cantilever determines oscillation characteristic of the micro-cantilever under excitation force. Changes in time-varying observables such as amplitudes and phase shift are linked to energy conservation and dissipation processes via analytical expressions [21]. Therefore, dissipated power and stored energy of the micro-cantilever undergoing acoustic forces could be utilized as indicator parameters for measurement sensitivity. For both excitation schemes, energy is supplied externally to the micro-cantilever by excitation force in the steady-state. There exist energy losses due to dissipative interaction with the operating environment and acoustic forces. Phase shift between free oscillation and response in the presence of acoustic force is directly related to the amount of energy dissipation.
The external work done Eext,i
by the excitation force and energy exchange with the operating environment Eenv,i
per period (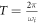 ) for ith
mode are described as follows [25]:
) for ith
mode are described as follows [25]:
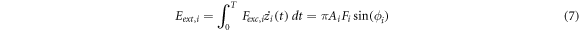
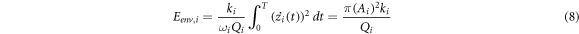
The energy dissipation per cycle is determined using energy conservation principle. The energy dissipation Ediss,i per period for ith mode is calculated by using following equations [25]:

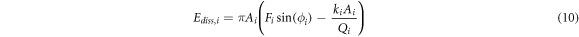
Dissipated power through interaction with acoustic force is also utilized as an indicator of energy dissipation. Since deflections of the micro-cantilever could be treated with diverse periods, dissipated power Pi is also defined beside the term of dissipated energy [21]. Alternatively, virial term Vi represents the stored energy of the micro-cantilever experiencing dynamic acoustic force and energy conservation process.
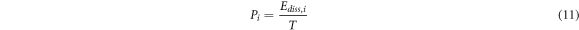
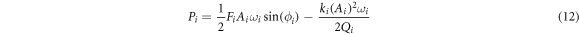
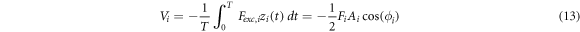
Dissipated power and virial per cycle for ith mode in single- and bimodal-frequency excitations are calculated using the analytical expressions ((Equation (12)) and (equation (13))) respectively [8].
2.3. Numerical simulation
In our calculations, the EOMs ((Equation (1)) and (equation (2))) are solved numerically using Fourth order Runge-Kutta method.
Acoustic force frequencies and their spectral regions with respect to the eigenmode frequencies are introduced in table 1. The acoustic force frequency in region A, fa is selected as quite lower than the first eigenmode frequency. The acoustic force frequency fi in region E is selected as higher than the second eigenmode frequency. The acoustic force frequency fe is set to the average value of the eigenmode frequencies fe1 and fe2. Region B and D indicate the frequency bands arranged around the first and second eigenmode frequencies respectively. Frequency region B contains three acoustic force frequencies which are fb , fc and fd . Besides, frequency region D possesses three acoustic force frequencies which are ff , fg and fh . In region B and D, fc and fg are equal to the first and second eigenmode frequency respectively. In our study, we explore responses of the micro-cantilever to acoustic forces at the frequencies around eigenmode frequencies. Because of that reason, diverse frequency regions with respect to the eigenmode frequencies are constructed. Even if the eigenmode frequencies are well-separate, we investigate the effect of multifrequency excitation on the observables and energy quantities by comparing its results with the ones obtained using a single-frequency excitation scheme. Accordingly, this allocation of the frequency bands improves assessment of the interaction of flexural modes in bimodal-frequency excitation.
Table 1. Frequencies of dynamic acoustic forces and spectral regions with respect to the first and second eigenmode frequencies of the micro-cantilever.
| Acoustic Force Frequencies—fAc (Hz) and Spectral Regions | ||||||||
|---|---|---|---|---|---|---|---|---|
| fa | fb | fc | fd | fe | ff | fg | fh | fi |
| 4,774 | 48,701 | 48,913 | 49,338 | 177,458 | 305,578 | 306,194 | 307,169 | 334,225 |
| Region A | Region B | Region B | Region B | Region C | Region D | Region D | Region D | Region E |
Micro-cantilever properties including dimensional parameters, i.e. length(l), width(w) and thickness(t), and coefficients of EOMs for both excitation schemes are presented in table 2 as given in [24].
Table 2. Micro-cantilever specification.
| k1 (N/m) | k2 (N/m) | Q1 | Q2 | fe1 (Hz) | fe2 (Hz) | l (μ m) | w (μ m) | t (μ m) |
|---|---|---|---|---|---|---|---|---|
| 0.9 | 35.2 | 255 | 1000 | 48,913 | 306,194 | 225 | 40 | 1.8 |
The effective mass of the micro-cantilever me is determined using the expression (equation (14)) as introduced in [26]. The mass density ρ of the micro-cantilever is equal to 2320kg m−3 as in [24].
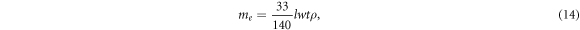
Acoustic force strengths are determined by multiplying the one-side surface area of the micro-cantilever (Asurface = lxw) with effective sound pressure levels (Pa) [7]. Sound pressure levels in the range of 34.9-54.9 dB correspond to acoustic force strengths, ranging between 10 pN to 100 pN [27]. The lower and upper limits of the range are determined based on degree of observable sensitivities in numerical simulations. Dynamic acoustic force is assumed to act on the free end of the micro-cantilever in consideration of validity of point-mass model (figure 1). Magnitudes of excitation forces at the first two eigenmode frequencies (F1 and F2) are set to 10.6 and 35.2 pN for single- and bimodal-frequency excitations respectively. The time interval of numerical simulation is between 19.0 and 19.20 ms. Initial conditions such as initial deflections and initial velocities are set to zero and applied to solve the second order differential equations ((Equation (1)) and (equation (2))) numerically in Matlab.
3. Results and evaluations
In this section, firstly, time-domain analysis on oscillations of the micro-cantilever experiencing acoustic forces is performed. In what follows, oscillation observables, i.e. amplitudes and phase shifts of the first and second flexural modes, are introduced for single- and bimodal-frequency excitations. Then, results of virial and dissipated power of the micro-cantilever dynamics are presented and evaluated by considering mode interactions in multifrequency excitation. Lastly, physical quantities such as energy supplied by external driving force, energy transferred to the operating environment, and dissipated energy triggered by acoustic force are given for the acoustic forces in critical regions.
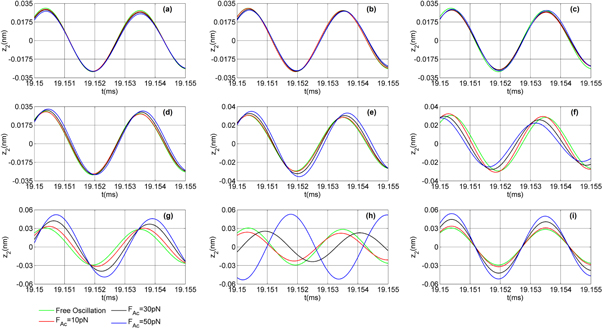
Figure 2 and figure 3 illustrate z1 and z2 oscillations of the micro-cantilever experiencing dynamic acoustic forces in the strength range of 10-50 pN for single- and bimodal-frequency excitation schemes respectively. Time-domain responses displayed in each subplot correspond to an acoustic force frequency given in table 1. Significant amplitude changes are prevalent for the acoustic forces in region B (figure 2(b-d)). Besides, remarkable phase shift is obtained for the acoustic force strength of 50 pN and the frequency fd (figure 2(d)). It is seen that z1 free oscillation is strongly influenced by the acoustic forces at the frequencies near the first eigenmode frequency of the micro-cantilever. For this case, as the acoustic force strength is increased from 10 to 50 pN, the amplitude increases notably. In addition, differences in phase shift responses among the frequencies in region B are quite notable with increasing acoustic force strength. This result indicates that phase shift response to acoustic force is much more significant to distinguish the acoustic force frequencies around the first eigenmode frequency. It is quite obvious that considerable change in an oscillation observable does not exist in other regions.
Figure 2. z1 oscillations at the first eigenmode frequency in single-frequency excitations in the presence of dynamic acoustic forces at the frequency (a) fa . (b) fb . (c) fc . (d) fd . (e) fe . (f) ff . (g) fg . (h) fh . (i) fi . Free oscillation is obtained owing to the application of external driving force at the first eigenmode frequency in the absence of dynamic acoustic force.
Download figure:
Standard image High-resolution imageFigure 3. z2 oscillations at the second eigenmode frequency in bimodal-frequency excitations in the presence of dynamic acoustic forces at the frequency (a) fa . (b) fb . (c) fc . (d) fd . (e) fe . (f) ff . (g) fg . (h) fh . (i) fi . Free oscillation is obtained owing to the application of external driving forces at the first and second eigenmode frequencies in the absence of dynamic acoustic force.
Download figure:
Standard image High-resolution imageBased on z2 oscillations depicted in figure 3, there exist higher amplitude changes and phase shifts for the acoustic forces in region D (figure 3(f-h)). Remarkable shifts in observables are not obtained for the other acoustic force frequencies (figure 3(a-e)). This result proves that the micro-cantilever responds considerably to acoustic force frequencies which are near its eigenmode in multifrequency excitation. We also remark that notable change in amplitude is observed for the acoustic force strength of 50 pN in region E (figure 3(i)). Response to higher frequencies beyond the second eigenmode frequency can be measured using resonant AFM micro-cantilever under multi-frequency operation. Moreover, we deduce that amplitudes change irregularly with respect to acoustic force strength in region D. Interaction of free oscillation with acoustic signals strongly depends on acoustic force frequency. Herein, optimization of excitation parameters such as magnitudes of driving forces could overcome the complexity of irregular responses. Additionally, remarkable phase shift becomes evident especially for the acoustic force strength of 50 pN as it is shown in figure 3(h). However, response to the acoustic force strength of 10 pN is less distinguishable for the frequencies in region D. These results point out that acoustic force strength in high-sensitivity frequency region determines amount of changes in oscillation observables.
3.1. Oscillation Observables
Time-dependent values of amplitude and phase shift are determined over a particular period of an oscillation [28]. In the algorithm, for z1 oscillations, we determine an amplitude by taking average of first two amplitudes of an oscillation in the time interval between 19.14 and 19.18 ms [24]. For z2 oscillations, we calculate an amplitude by taking average of first two amplitudes in the time interval between 19.15 and 19.16 ms. Besides, phase shift is determined using free oscillation and response of the micro-cantilever under acoustic force.
figures 4(a)–(d) depict the amplitude and phase shift curves as a function of acoustic force strength for the frequencies given in table 1. To visualize mode interactions in multifrequency excitations, results obtained using the excitation schemes are given in the same sub-plots in figure 4 for the critical frequencies. As the acoustic force strength is increased from 10 pN to 100 pN, gradual increase (approximately 2.2 nm) in A1 is obtained for the frequency fc for both excitation schemes (figure 4(a)). For the other frequencies in region B (fb and fd ), the same trend takes place in amplitude curves. Amplitude sensitivity does not exist for the acoustic force frequencies in the other regions. Moreover, phase shift becomes more evident for the frequency fd (ϕ1 of approximately 38.5° for the acoustic force strength of 100 pN in bimodal-frequency excitation) as it is seen from figure 4(b). Herein, amplitude response to acoustic force strength is much more significant than phase shift at the first eigenmode for measurement sensitivity.
Figure 4. Observable responses and energy quantities in the presence of dynamic acoustic forces at diverse frequencies for single- and bimodal-frequency excitations. (a) Amplitude curves for the first eigenmode. (b) Phase shift curves for the first eigenmode. (c) Amplitude curves for the second eigenmode. (d) Phase shift curves for the second eigenmode. (e) Virial curves for the first eigenmode. (f) Dissipated power curves for the first eigenmode. (g) Virial curves for the second eigenmode. (h) Dissipated power curves for the second eigenmode. Solid lines indicate parameters as a function of acoustic force strength obtained using bimodal-frequency excitation scheme. Dashed lines with asterisk markers indicate parameters as a function of acoustic force strength for the frequencies in regions B and D using single-frequency excitation scheme.
Download figure:
Standard image High-resolution imageAs acoustic force strength is increased gradually in the range of 10-100 pN, A2 increases steadily for the frequency fg and fi (figure 4(c)). There does not exist any notable phase shift sensitivity to acoustic force strength for the frequency fi , whereas maximum phase shift of around 60° is obtained for the frequency fg . For the frequency fi , resonant micro-cantilever under multifrequency operation responds to dynamic acoustic forces at the frequencies quite higher than second eigenmode frequency. Maximum phase shift ϕ2 of around 178° is obtained for the frequency fh (figure 4(d)). In addition, a steeper phase shift transition of around 148° in the acoustic force strength range of 25-50 pN is observed for the frequency fh in bimodal-frequency excitation. Herein, free oscillation has much more interaction conditions with the dynamic acoustic forces at the frequency fh leading to sharper and larger phase shifts. As it is seen from figure 4(c) and (d), A2 and ϕ2 sensitivities are enhanced notably for the acoustic force strength range of 35-65 pN at the frequency fh using bimodal-frequency excitation scheme. For this case, sensitivity improvement is achieved by driving the micro-cantilever at higher eigenmode frequency. Additionally, it should be noted that fluctuating behavior and lower amplitude sensitivity are observed for the acoustic force frequency ff as it is illustrated in figure 4(c). Based on these results, excitation parameters such as magnitudes of driving forces are to be optimized to increase observable sensitivities.
3.2. Virial and dissipated power
Virial and energy conservation theorems are used to explain energy dissipation process during measurement of dynamic acoustic forces. Results of dissipated power and virial with respect to acoustic force strength for the frequencies given in table 1 are plotted in figure 4(e-h). Virial at the first eigenmode V1 for both excitations decreases steadily for the acoustic force frequencies in region B as it is seen from figure 4(e). Negative values of virial represent energy dissipation from stored kinetic energy of the resonant micro-cantilever, which increases with interaction through larger acoustic force strength. Rates of dissipated powers at the first eigenmode P1 decrease in the negative range as acoustic force strength increases (figure 4(f)). Negative values of dissipated power indicate transferring energy from supplied energy to the dissipative operating environment in the presence of dynamic acoustic forces based on the energy conservation principle (equation (9)). Dissipated power P2 increases continuously for the frequency fg as acoustic force strength increases gradually (figure 4(h)). On the other hand, there does not exist any change in virial V2 with respect to acoustic force strength for the frequency fg . Dissipated energy of the micro-cantilever undergoing tip-sample interaction force is related with phase shift in AFM operations [29]. In our case, significant level of power dissipation due to dynamic acoustic forces is evident for the frequency fg at which considerable amount of amplitude and phase shift are obtained (figure 4(c)(d)(h)). On the other hand, dissipated power curve P2 for the frequency fh increases and decreases as acoustic force strength ascents (figure 4(h)). This erratic behavior is due to different dissipation grades of kinetic energy from the mechanically oscillating system. Moreover, except for the frequency fi , notable fluctuations in energy quantities are not observed for the acoustic force frequencies outside the region D.
3.3. Energy quantities
Analytical expressions of energy quantities such as supplied energy (Equation (7)), energy transferred to the operating environment (Equation (8)), and dissipated energy owing to dynamic acoustic force (equation (10)) are derived by using virial theorem and energy conservation principle. Using those equations, the energy quantities for the critical acoustic force frequencies in regions B and D are calculated and the results are plotted in figure 5. Phase shift is related to the amount of energy quantities for dynamical system of resonant micro-cantilever under tip-sample interaction force based on analytical expressions [30]. For our case, most of the supplied energy dissipates due to interaction with dynamic acoustic forces at the frequency fh
(figure 5(f)). On the other hand, as it is seen from figure 5(a), supplied energy is transferred to the operating environment for the frequency fb
in consideration of smaller phase shifts at the first eigenmode (figure 4(b)). Moreover, there do not exist considerable deviations among amounts of energy exchanged with the operating environment Eenv,i
for both excitation schemes (figure 5(a-f)). Unlike z-trajectories, velocities ( ) of the resonant micro-cantilever are not influenced by mode interaction in multi-frequency excitation. For the frequencies in region B, Eext,i
and Ediss,i
obtained using single- and bimodal-frequency excitation schemes deviate from each other as acoustic force strength increases (figure 5(a-c)). We would like to emphasize that interaction of flexural modes is evident in bimodal-frequency excitation based on energy levels for those frequencies. Ideally, energy levels at the first and second eigenmodes depend on amplitudes, influenced by acoustic force strengths.
) of the resonant micro-cantilever are not influenced by mode interaction in multi-frequency excitation. For the frequencies in region B, Eext,i
and Ediss,i
obtained using single- and bimodal-frequency excitation schemes deviate from each other as acoustic force strength increases (figure 5(a-c)). We would like to emphasize that interaction of flexural modes is evident in bimodal-frequency excitation based on energy levels for those frequencies. Ideally, energy levels at the first and second eigenmodes depend on amplitudes, influenced by acoustic force strengths.
Figure 5. Energy supplied by external driving force, energy transferred to the operating environment, and energy dissipation due to interaction with dynamic acoustic forces at the frequencies in regions B and D for single- and bimodal-frequency excitation schemes. Energy quantities for the acoustic force frequency (a) fb . (b) fc . (c) fd . (d) ff . (e) fg . (f) fh . Solid lines indicate energy quantities as a function of acoustic force strength obtained using bimodal-frequency excitation scheme. Dashed lines with square markers indicate energy quantities as a function of acoustic force strength obtained using single-frequency excitation scheme.
Download figure:
Standard image High-resolution image4. Conclusions
The present study is conducted to investigate measurement sensitivity of dynamic acoustic forces at diverse frequencies with respect to the eigenmode frequencies of the micro-cantilever. In view of all results mentioned so far, much higher observable and energy quantity sensitivities are obtained for the acoustic force frequencies near the eigenmode frequencies of the micro-cantilever as expectedly. In addition, it is possible to increase high-sensitivity frequency range using multifrequency excitation scheme. The results also prove that phase shift sensitivity at the second eigenmode is improved by driving the AFM micro-cantilever under bimodal operations. Herein, flexural mode interaction is evident in bimodal-frequency excitation. Alternatively, harmonic excitation schemes (e.g., biharmonic) could also be utilized to enhance measurement sensitivity. Since we use rectangular micro-cantilever, the ratio of the second eigenmode frequency to the first eigenmode frequency is equal to 6.27 [31]. The ratio could be tuned to span different frequency windows using micro-cantilevers with different geometrical shapes [32]. Furthermore, high phase shift sensitivities to acoustic forces are efficiently used in sensor applications. For our case, we obtain the highest phase shift response of around 178° at the second eigenmode, which is very useful in measurement of acoustic forces. In addition, the highest amplitude sensitivity of around 2.8 nm at the first eigenmode is considered to be beneficial in implications of sensor design. In view of virial theorem, phase shift is related to amount of energy dissipation at higher mode. Energy dissipation from mechanically oscillating micro-cantilever under acoustic force is affected by mode interaction in bimodal-frequency excitation which is a function of acoustic force strength. Therefore, the energy quantities depending on oscillation observables can be utilized to describe energy dissipation process in measurement of dynamic acoustic forces.
Data availability statement
All data that support the findings of this study are included within the article (and any supplementary files).
Appendix A.: Transformation into deflection for single- and bimodal-frequency excitations
Dynamics of a rectangular micro-cantilever beam is governed by one dimensional Euler-Bernoulli equation [33, 34]. The equation of motion for transversal deflections of the micro-cantilever is given as follows [35]:
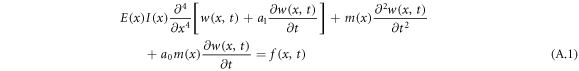
where w(x, t), m(x), I(x) and E(x) are the deflection, the mass density of the material, the moment of inertia, and Youngs modulus respectively. m(x), I(x), and E(x) are considered to be constant. a0 and a1 are the mass proportional damping and the stiffness proportional damping parameter respectively. For our case, f(x, t) is independent of x and equal to f(t), which is the total effective force as a summation of excitation and acoustic forces.
To explore dynamics of the driven micro-cantilever under excitation and acoustic forces, equation (A.1) is transformed into a set of decoupled harmonic oscillators. The deflection of the micro-cantilever is approximated as follows:
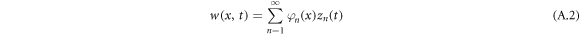
where φn (x) and zn (t) are the modal shape and the time-varying modal amplitude.
Substitution of equation (A.2) into equation (A.1) and subsequent application of the orthogonality relation yields as follows:
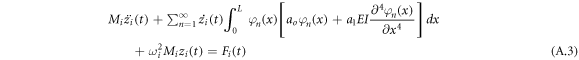
where Mi , and Fi are the generalized mass and the generalized external force respectively.
equation (A.3) can be transformed into the decouple differential equations as follows:
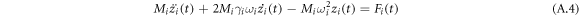
where γi is the modal damping parameter, which is formulated as follows:
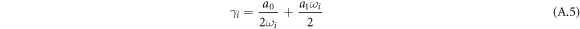
For our case, for single frequency excitation scheme, external force is formulated for eigenmode i as follows:
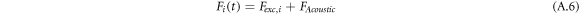
For bimodal-frequency excitation scheme:

Other coefficients of the equation of motion are given as follows:
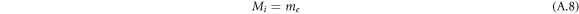
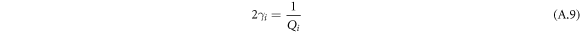
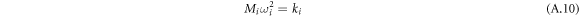
In consideration of point mass model, deflection of the micro-cantilever, which is independent of x, is approximated as follows.

Since the deflection is determined with respect to the equilibrium point (neutral position is equal to zero) of the effective point mass, the deflections for single- zs (t) and bimodal- zb (t) frequency excitation schemes are formulated as follows [18, 24]:
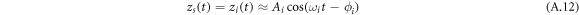
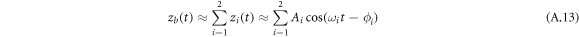
where Ai and ϕi are the amplitude of the deflection and phase shift for the ith eigenmode of the micro-cantilever. Since we obtain the deflections at the first two eigenmode frequencies, higher modes are ignored.
Appendix B.: Effective mass of the micro-cantilever
In our work, we determine the effective mass of the micro-cantilever based on Hollomons power law stress-strain equation for both modes. The effective mass for the micro-cantilever power-law beam of mass m is approximated as follows [26]:
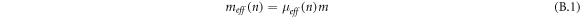
where μeff (n) is the effective mass coefficient for the strain-hardening exponent n. Effective mass coefficient is approximated as follows:
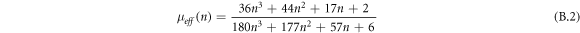
Here, the strain hardening component n is equal to 1 for linear elastic material of the micro-cantilever. Therefore, effective mass of the micro-cantilever is introduced in equation (B.3)