Abstract
The linear augmented-Slater-type-orbital (LASTO) method, as one of real-space band theories, is generalized to a spin-polarized Dirac-type density-functional in full potential scheme. Since the Bloch sum of Slater-type orbital can do the Fourier transformation analytically with a conditional convergence, it is not only easily extendable to a full-potential scheme, but also have a high compatibility to a four-component relativistic linear-augmented-plane-wave method. In this paper, the formulation of this full potential Dirac-type LASTO (DLASTO) method is presented in a self-contained manner. By applying it to a typical material for each of the 3d-, 4f- and 5f-electron systems, we discuss some of the cut-off parameters and orbital choices required in the DLASTO calculation and provide guidelines for their settings. In addition, the electronic structure and magnetism for each of these systems will be discussed.
Export citation and abstract BibTeX RIS
1. Introduction
In metals and alloys of the lanthanide and actinide series, a strong Coulomb interaction between electrons and nuclei causes 4f and 5f electrons to localize around nuclei with larger atomic numbers. As a byproduct, strong relativistic effects occur, which change the energy levels and distributions along with other inner core and valence electrons. In a first perturbation a 'direct' relativistic effect is described as the difference from the Schrödinger equation to the Dirac equation, resulting in an attraction force so that the energy levels or the centers of energy band shift lower than in the Schrödinger solution. The orbital wave functions have an orthogonality between different quantum numbers, and the electron distributions avoid overlapping as much as possible in space. Thus a cooperative effect between the relativistic effects and the orthogonality brings an 'indirect' relativistic effect that the f electrons spread away with other valence electrons distributed outside them [1] to cohere more by overlapping with valence electrons in the neighbor atoms.
In the metals and alloys, if the f electrons are contributed on the Fermi surface, the transport coefficients and superconducting properties are strongly influenced by them and the f electrons are behaved as itinerant electrons, or heavy electrons with the large effective mass. If so not, although they always keep a channel to overlap with other valence electrons as band electrons, they are usually called localized electrons. In such the case, the condensed matters have a small effective mass, because the Fermi level is crossed by non-f conduction bands. In any case, the magnetic properties stay connect to the atomic characters of the f electrons unlike 3d transition metals that the orbital moment dominants over the spin moment in most cases.
The lanthanide and actinide ions in solution are possible to exist with a different number of valence. In view of this, every element in itself has a variable degree of freedom in the valence number under its surrounding environment. For monoatomic metals, 'Wigner–Seitz (WS) radius', of which a hard sphere fills up a primitive cell as possible, is estimated from the measured crystal structure and lattice constants. In lanthanide metals, it is almost constant independence of increasing the atomic numbers, except for Eu and Yb metals having a different valence with others [2]. In lighter actinide metals than Pu or Am metals, however, the WS radius decreases in increasing the atomic numbers, that is equivalent to 'actinide contraction' due to the strong electron-nucleus Coulomb interaction. Beyond the boundary of Pu or Am, heavier actinide metals have constant WS radii like the lanthanide metals. It means to change some binding of the valence electrons, or to alter the valence number involved in changing an orbital configuration.
In a first-principles scheme, the density functional theory (DFT) with a local (spin-)density approximation (L(S)DA) [3] is still now an underlying principle, even including some expending theories. According to the Slater's transition state in the Hartree–Fock one-electron equation [4] and the Janak's theorem in the DFT [5], the band structure, Fermi surface, and other physical properties obtained from the L(S)DA calculations are all for intermediate valence states. For Ce and U nonmagnetic materials with small Sommerfeld coefficients (SC), if the electronic structure can be calculated self-consistently by LDA relativistic band theory, the resulting Fermi surface topology can explain the de Haas–van Alphen (dHvA) frequency-branches and/or ARPES measurements quite well, for example, in CeSn3 [6] and in UB2 [7, 8]. Therefore, such materials are considered to be in intermediate valence states. However, the first-principles band theory with L(S)DA has difficulty in predicting the electronic structure of lanthanides and actinides lying in other valence states than the intermediate valence state. Furthermore we recognize the unpredictability of valence fluctuation states, especially in lanthanide Eu and Yb compounds. One way to break the deadlock is to go back to the local atomic state as a principle and reconstruct it with the relativistic wave functions in the jj coupling of the fn configuration, for example, according to a concept of the relativistic Hartree–Fock (RHF) method [1, 9]. Therefore a relativistic band theory on orbitals in real space should be redeveloped to keep a direct connection between the atoms and the solids together with a high precision and a compatibility like the linear augmented-plane wave (LAPW) method.
In a purpose of this paper, the linear augmented-Slater-type-orbital (LASTO) method is generalized to a fully relativistic scheme with a spin-polarized Dirac-type density-functional and furthermore in a full potential scheme. In history the Slater-type orbitals (STO) are introduced as a simple analytical form of atomic orbitals to estimate an atomic shielding constants [10] and also have been used as one of a possible basis set in Hartree–Fock method for atoms [11]. The band theories of solids, as well-known, are categorized into two prominent classes by choosing a real-space or a reciprocal-space representation for the basis sets of Bloch functions [12]. Within the linear band theories [13], although there exits many other kinds of band theories, the LAPW method is a typical one represented by a basis set of plane waves in the reciprocal space, while another standard one is a linear muffin-tin orbital (LMTO) method with a basis set of atomic-like orbitals in real space [15, 16]. The LASTO basis set belongs to the real-space band theories like in the LMTO method, and their characteristics have been described in detail elsewhere [17–19] in a scalar-relativistic scheme, and the full-potential improvement to them has been done [20].
As a merit of the LASTO method, since the Bloch sum of the STO can do the Fourier transformation analytically with a conditional convergence, it is not only easily extendable to a full-potential scheme, but also have a high compatibility to a Dirac-type of relativistic LAPW (DLAPW) method [21–23], if the LASTO method is formulated by the spin-polarized coupled Dirac (SPCD) equation [24–26] and the Fourier components of the STO are expanded by using a relativistic plane wave [27]. Therefore the computational results of the Dirac-type LASTO (DLASTO) method are on the same precision as those of the DLAPW method, if the setting is correct, depending on the characteristics of it. Additionally, since the DLASTO method can be performed by diagonalizing some smaller matrices than in the DLAPW method, the rate-limitation step is improved while connecting from isolated atoms to the solids. In the real-space band theories, the LMTO method [28, 29], the KKR method [32–34], the LCAO method [30] and the ASW method [31] have already been extended to the SPCD-based band theory, but not yet to the LASTO method in spite of some specific merits.
This paper is organized as follows: in section 2, a basic relativistic Hamiltonian based on DFT is defined, and a formulation of the DLASTO method in this framework is given and expands to the full potential form. In section 3, we will show the details of the calculation method, including the setting of various parameters of the DLASTO method, and perform self-consistent calculations for Fe, Gd, and UN, which are representative materials of the 3d-, 4f-, and 5f-electron systems, and present the results of the calculations, such as the electronic structures of these materials. Finally, we will conclude and discuss the LDASTO method and the obtained results in section 4. In this paper, we describe all the expressions in units of Rydberg and with the same approximation for the relativistic APW method [35].
2. Formalism
2.1. Basic Hamiltonian
Let us establish a fundamental one-electronic equation, before the DLASTO method will be formulated. Here it is assumed that the spin-polarized relativistic density-functional is taken up to describe the electronic states in magnetic materials or atoms we are interested in. For such the systems the total energy in an external field ( ,
A
(
r
)) is defined as a functional of four-dimensional current (n(
r
),
J
(
r
)), and that the ground state is derived by taking a minimum of the functional so as to obtain a relativistic one-electronic equation [36]. In order to derive a numerical expression, the Gordon decomposition of the current is applied to this equation [37], thereby giving a useful equation of the 'spin-only' type [38–40] in units of Ry as,
,
A
(
r
)) is defined as a functional of four-dimensional current (n(
r
),
J
(
r
)), and that the ground state is derived by taking a minimum of the functional so as to obtain a relativistic one-electronic equation [36]. In order to derive a numerical expression, the Gordon decomposition of the current is applied to this equation [37], thereby giving a useful equation of the 'spin-only' type [38–40] in units of Ry as,

where c is the light velocity and p means the momentum operator (≡−i∇). This three operators, α , β and I represent the standard Dirac 4 × 4 matrices [27], and Σ signifies the 4 × 4 Pauli matrices. Then Eλ ( k ) is a band energy identified with band index λ and k vector in the first Brillouin zone, and Φλ ( k , r ) denotes the corresponding Bloch function.
In this formulation, a crystal structure is assumed to consist of na
different groups of atoms as a crystalline basis in the unit cell, and the basis contains np
atoms in the pth atomic group. The νth atom of the pth group (the pνth atom) is directed by vector  from an origin in the unit cell. As in the usual band theories, a real space of the unit cell is divided into the sphere region inside the spheres around each of the atoms and the interstitial region outside the spheres. Here a radius of the sphere denotes ap
for the atoms of the pth group.
from an origin in the unit cell. As in the usual band theories, a real space of the unit cell is divided into the sphere region inside the spheres around each of the atoms and the interstitial region outside the spheres. Here a radius of the sphere denotes ap
for the atoms of the pth group.
In (1), V( r ) and B ( r ) show the scalar potential and the magnetic field, respectively, each of which is defined by,

using the translation vector R and

with the charge density

and the magnetization

where θ(x) is the step function and ɛXC( r ) represents the exchange–correlation (XC) energy per a particle. In (4) and (5), EF stands for the Fermi energy, so that the sum or the integration is done over all the occupied states of λ and k in the first Brillouin zone. The first term described in the right side of (2) is the Coulomb potential between electrons and nuclei with atomic number Zp in the pth atomic group and the second term denotes the Coulomb potential between electrons. The third term of (2) and the expression of (3) indicate the scalar and the spin-dependent part of the XC potentials, respectively and the latter represents an internal magnetic field.
As in the full potential method, the scalar potential V(r) and the magnetic field B( r ) are expressed by a Fourier expansion in the interstitial region, while in the sphere region they are expanded by a spherical-harmonics. By taking account of the crystal symmetry, the interstitial scalar potential and magnetic field are explicitly described as

and

where G denotes a reciprocal-lattice vector, φs (r) are symmetrized plane-wave functions, or stars [14], which are invariant under rotational operators in the crystalline space group and Gs means a reciprocal modulus of generators to create the sth star φs (r). In the sphere region we can write down the scalar potential by
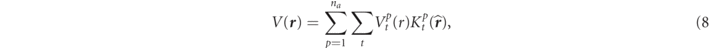
and the magnetic field as

where  means normalized lattice harmonics with the site symmetry of pth atomic group [14] that keep all the atomic positions invariant. The hat-notation of
means normalized lattice harmonics with the site symmetry of pth atomic group [14] that keep all the atomic positions invariant. The hat-notation of  stands for an angular part in a polar coordinate and it is henceforth used in formulation. The explicit definition of
stands for an angular part in a polar coordinate and it is henceforth used in formulation. The explicit definition of  used here is given in (A.11) of appendix
used here is given in (A.11) of appendix
2.2. Basis set
The Bloch function Φ(
k
,
r
) is expanded by DLASTO basis function  as follows,
as follows,

where the index N is an abbreviation for {nℓsμpν} and the band index λ is omitted here, though it is present in the expansion coefficients  .
.
In a non-relativistic case, the basis function in the interstitial region can be described using Fourier components of the Bloch sum of STO [17], that are atomic orbital functions simplified with principal quantum number n, angular momentum ℓ and screening factor ζ [10], expressed as,

As some analytically-derived results, a Dirac-type relativistic generalization to the interstitial basis function can be simply done to replace the STO or the plane waves with any four-component type of wave function. As a choice, here, we define the interstitial basis by use of the Fourier transformation of φnl ( r ) with relativistic plane waves [27], because it is highly compatibility to the DLAPW method [21]. If it is centered at the νth atom associated with the pth group and if its quantum state of orbital is in the principal n, the angular ℓ, the total angular J = ℓ + s and its z-component μ, then the basis function can be defined within the order of 1/c by,
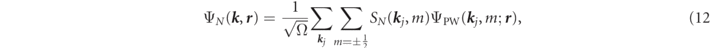
where ΨPW( k j , m; r ) are the relativistic plan waves, represented explicitly in units of Ry as,

Then SN ( k , m) are the envelop functions of ΨPW( k , m; r ),

where Ω is the volume of unit cell, and k j is defined using the reciprocal-lattice vector G j as k j = k + G j . In (13), ko is the relativistic energy
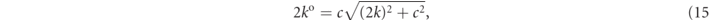
with a wavevector modulus k. In (13),
σ
are the usual Pauli matrices and χ(m) signifies the spinor function for  . In (14) here we use an index
. In (14) here we use an index  instead of J, and we should note that, for ℓ = 0, only
instead of J, and we should note that, for ℓ = 0, only  is available in the
is available in the  formulation.
formulation.
In (14),  corresponds to the main term for the Fourier components of relativistic STO, which is described as,
corresponds to the main term for the Fourier components of relativistic STO, which is described as,

with the Fourier component of radial STO for the pth group,

and the relativistic angular dependent term,

where jℓ
(x) is the spherical Bessel function of ℓ order. Practically the numerical calculation of  in (17) can be directly treated with terms of the Gauss hypergeometric function [41]. Then
in (17) can be directly treated with terms of the Gauss hypergeometric function [41]. Then 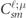 shows the Clebsch–Gordan (CG) coefficients, which are defined with the parameter
shows the Clebsch–Gordan (CG) coefficients, which are defined with the parameter  as the matrices
C
ℓμ
,
as the matrices
C
ℓμ
,

The STO screening factor ζp in (16) is determined from the boundary condition on the sphere surrounding any atom of the pth group by a common way of the linear band theories Dℓ = −ℓ − 1 [13] and ζp is derived from the following expression [17],

Inside the sphere at the pνth atom, the basis ΨN
(
k
,
r
) in (10) is augmented by a linear combination of wave function  and its corresponding energy-derivative wave function
and its corresponding energy-derivative wave function  , and is described by,
, and is described by,
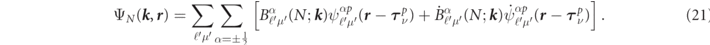
The wave function  , which is a solution of (1) around the pν atom with a spherically symmetric potentials
, which is a solution of (1) around the pν atom with a spherically symmetric potentials  of (8) and
of (8) and  of (9) along spin-quantized z-axis, is expressed as,
of (9) along spin-quantized z-axis, is expressed as,

where  and
and  are called the large and the small components of the relativistic radial functions, respectively. It should be noted that (22) is only validated by an approximation that breaks the orbital coupling with ℓ ± 2 [24, 32, 33]. The function
are called the large and the small components of the relativistic radial functions, respectively. It should be noted that (22) is only validated by an approximation that breaks the orbital coupling with ℓ ± 2 [24, 32, 33]. The function  represents a normalized spin-angular function,
represents a normalized spin-angular function,
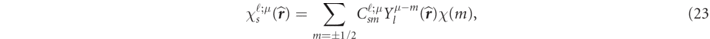
with the CG coefficients  in (19) and the spinor function χ(m).
in (19) and the spinor function χ(m).
In a spin-unpolarized case, α equals to  due to diagonalizing the states with j = ℓ + α and then
due to diagonalizing the states with j = ℓ + α and then  and
and  become a solution of the usual Dirac equation. If the radial magnetic field B(r) is nonzero, the spin polarization has
become a solution of the usual Dirac equation. If the radial magnetic field B(r) is nonzero, the spin polarization has  and
and  coupled between the j = ℓ + s states with
coupled between the j = ℓ + s states with  . With the parameter
. With the parameter  used in the CG coefficients (19), the simultaneous differential equations to (22) can be written down in a compact form as follows,
used in the CG coefficients (19), the simultaneous differential equations to (22) can be written down in a compact form as follows,


using  for
for  [24, 26]. By the presence of the last term in (25), we have to handle simultaneously the four differential equations for
[24, 26]. By the presence of the last term in (25), we have to handle simultaneously the four differential equations for  of (24) and (25). Here they are called SPCD equations and a computational algorithm to solve the SPCD equation is described in details elsewhere [26].
of (24) and (25). Here they are called SPCD equations and a computational algorithm to solve the SPCD equation is described in details elsewhere [26].
In a similar way the energy-derivative wave function  is defined by the style of (22), in which just only
is defined by the style of (22), in which just only  and
and  are replaced to
are replaced to  and
and  , respectively, and the corresponding SPCD equations for
, respectively, and the corresponding SPCD equations for  and
and  are given as,
are given as,


In (24)–(27),  is a fixed energy with respect to the (ℓνα) state in the pth atomic group [21].
is a fixed energy with respect to the (ℓνα) state in the pth atomic group [21].
The two coefficients of  and
and  in (21) are determined from the condition that the interstitial (12) and the sphere (21) of the basis set are continuous on the spheres. For N = {nℓsμpν}, the coefficients are obtained by solving the following simultaneous equations,
in (21) are determined from the condition that the interstitial (12) and the sphere (21) of the basis set are continuous on the spheres. For N = {nℓsμpν}, the coefficients are obtained by solving the following simultaneous equations,
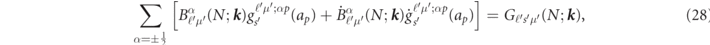

using

and

with the spherical-coordinate coefficients of

and

In (30) and (31),  is the m'm element of spin-rotational matrix,
is the m'm element of spin-rotational matrix,

with respect to the Euler angles,  and
and  , at the pνth atom. In non-collinear magnets that a local quantization axis of the spin in the sphere region is not along the z axis of a crystalline global coordinate, we can self-consistently calculate the local spin moment at the pνth atom by rotating the local axis by the angles
, at the pνth atom. In non-collinear magnets that a local quantization axis of the spin in the sphere region is not along the z axis of a crystalline global coordinate, we can self-consistently calculate the local spin moment at the pνth atom by rotating the local axis by the angles  and
and  from the global coordinate. Using a relativistic density-matrix, the Euler angles,
from the global coordinate. Using a relativistic density-matrix, the Euler angles,  and
and  can be determined also from a self-consistent calculation, but here we describe only the expressions to compute a fixed magnetic structure.
can be determined also from a self-consistent calculation, but here we describe only the expressions to compute a fixed magnetic structure.
In the derivation of (28)–(33), we use the same approximation of kj
≪ c as in the relativistic APW method [35]. It is to be noted that, although N contains p and ν, Gℓ's'μ'(N;
k
) in (30) and Fℓ's'μ'(N;
k
) in (31) are independent of the  vectors. Accordingly
vectors. Accordingly  and
and  have the same values for all the atoms of the pth group.
have the same values for all the atoms of the pth group.
2.3. Band energy
The band energies Eλ
(
k
) and the corresponding eigenvectors  for the band index λ are obtained by solving the set of equation,
for the band index λ are obtained by solving the set of equation,

with the Hamiltonian matrix elements

and the overlapping matrix elements

The Hamiltonian matrix elements HNN' in (36) are separated into a muffin-tin (MT) term  and a non-muffin-tin (NMT) term
and a non-muffin-tin (NMT) term  . The explicit expressions of
. The explicit expressions of  are casted in (A.1) of appendix
are casted in (A.1) of appendix  is expressed by
is expressed by

where VNMT(
r
) and
B
NMT(
r
) means the non-spherical terms in the scalar potential V(
r
) of (2) and the magnetic field
B
(
r
) of (3), respectively. In fact, VNMT(
r
) is obtainable from extracting the MT terms of  and Vp
(r) from V(
r
), and in the same manner
B
NMT(
r
) is given by subtracting
and Vp
(r) from V(
r
), and in the same manner
B
NMT(
r
) is given by subtracting  and Bp
(r) from
B
(
r
). The details of
and Bp
(r) from
B
(
r
). The details of  are in (A.8)–(A.18).
are in (A.8)–(A.18).
2.4. Densities
Once the energies and the eigenvectors for the band index λ are calculated from the general eigenvalue solutions of (35), the resulting eigenvectors  are transformed into
are transformed into  with a conversion equation
with a conversion equation

Thereby the Bloch function in the interstitial region is rewritten from (10) and (12) as

That is really the LAPW interstitial Bloch function, so that we can handle a prescription of a full-potential LAPW method [42] to develop the full potential scheme.
In obtaining the charge density (4) and the magnetization (5), the sums or the integrations over the occupied states are needed to perform, and to be more precise the tetrahedron method [43] is used on the assumption that any metallic system will be calculated here. For a semiconductor or an insulator the special point method is favorable to use [44]. From the tetrahedron method or the special point method, if the weights Wλ ( k ) are set out for the occupied states of λ and k in the irreducible wedge of the first Brillouin zone, the interstitial charge density n( r ) and magnetization m( r ) along the z axis of the global coordinate are calculated as follows,


using a spin-dependent density with  ,
,
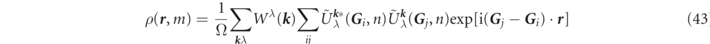

The right term of (43) is derived approximately from kj ≪ c and then it is transformed to (44) by symmetrization to the stars φs ( r ).
In an analogous way, the charge density in the sphere region is settled from (4) and (21) with the normalized lattice harmonics  as
as

where  is a radial contribution to the pth atomic group and the details are shown in (B.1)–(B.4) of appendix
is a radial contribution to the pth atomic group and the details are shown in (B.1)–(B.4) of appendix

where  is a radial contribution of magnetization in the pth atomic group, of which the expressions are written down in (B.5) and (B.6).
is a radial contribution of magnetization in the pth atomic group, of which the expressions are written down in (B.5) and (B.6).
2.5. Potentials
The interstitial and sphere scalar potentials V(
r
) of (6) and (8) are constructed from the densities of (41), (42), (45) and (46). As a routine application to the full-potential scheme we need a special procedure to yield the interstitial Coulomb potentials in the first and second terms of the right side in (2), that is known as the pseudo-charge method [42, 45]. In order to achieve a well convergence within a finite number of expansion, the interstitial charge density of (41) including the nuclear charges should be replaced to a pseudo-density, which varies with a smooth spatial distribution and conserves the same multipole moments. As a result the Fourier coefficients  of the pseudo-density for the stars are estimated instead of
of the pseudo-density for the stars are estimated instead of  in (41) and then the Coulomb potential part of
in (41) and then the Coulomb potential part of  in (6) is written for Gs
≠ 0 by
in (6) is written for Gs
≠ 0 by

As an origin of energy we choose the average of the interstitial Coulomb potential to  .
.
On the sphere boundaries for the pth atomic group, the Coulomb potentials  in (8) are estimated directly from the obtained
in (8) are estimated directly from the obtained  as
as

The above equation is derived, if  changes
changes  in (6) and then if the lattice-harmonics expansion of the stars,
in (6) and then if the lattice-harmonics expansion of the stars,

is used, where Lt
is an angular momentum for the tth non-zero lattice harmonics and 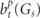 are the expansion coefficients to be obviously decided from (49).
are the expansion coefficients to be obviously decided from (49).
In the sphere region the Coulomb potentials of V(
r
) are solved on the boundary condition of  [45] and it can be expressed by
[45] and it can be expressed by
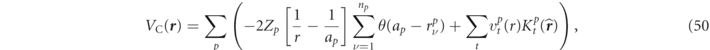
with

where  is a multipole moment of Lt
for any atom of the pth group,
is a multipole moment of Lt
for any atom of the pth group,

In the last term of the right side in (2), the interstitial XC potentials are calculated from n(
r
) of (41) and m(
r
) of (42). In order to manage them in practice, beforehand, we make a composite-transformation (CT) method that any function in a real space is transformed by the FFT algorithm to a reciprocal or plane-wave space and subsequently the resulting reciprocal-space functions are symmetrized to ones in a space of the stars. From  and
and  , the inverse CT method yields the numerical tables of n(
r
) and m(
r
) at grid-mesh points of the unit cell and hence the XC potentials are obtained at the same points. Furthermore the XC coefficients
, the inverse CT method yields the numerical tables of n(
r
) and m(
r
) at grid-mesh points of the unit cell and hence the XC potentials are obtained at the same points. Furthermore the XC coefficients  for the stars are calculated by the CT method, and the scalar potentials
for the stars are calculated by the CT method, and the scalar potentials  in (6) get from
in (6) get from  . The scalar magnetic fields
. The scalar magnetic fields  in (7), which are oriented along the z axis of the global coordinate, are calculated by the same procedure.
in (7), which are oriented along the z axis of the global coordinate, are calculated by the same procedure.
In the sphere region the XC potentials and the magnetic fields are evaluated using n(
r
) of (45) and m(
r
) of (46) at sampling points inside the spheres and the corresponding  and
and  for the lattice harmonics are estimated by the method of least squares so as to be the obtained values in the sampling points [46]. Finally the scalar potentials in the sphere region V(
r
) can be determined by adding
for the lattice harmonics are estimated by the method of least squares so as to be the obtained values in the sampling points [46]. Finally the scalar potentials in the sphere region V(
r
) can be determined by adding  into
into  in (51).
in (51).
3. Results
3.1. Computational details
In this section, we give the details of the DLASTO calculation formulated in the previous section. When one selects a solid to calculate, the input data for the crystal structure is usually set to lattice constants, crystal space group, and Wyckoff parameters including atom types. Using the symmetry operator of the space group, inequivalent atomic sites and their atomic numbers are identified in parallel with checking whether the input data matches the crystal structure, after which the pν atoms are numbered.
To start the DLASTO calculations, the initial crystal densities, which consist of the charge densities n(
r
) indicated by (41) and (45) and the magnetizations m(
r
) in (42) and (46), are estimated by solving the SPCD equations for (24) and (25). In the sphere region, the SPCD equations are calculated self-consistently under the atomic boundary condition to create the atomic densities for each of the inequivalent atoms. The obtained magnetizations are directly used as the spherically symmetric part 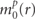 of m(
r
) in (46) and the other parts set zero, because of their atomic-like distributions in solids. While the spherically symmetric part
of m(
r
) in (46) and the other parts set zero, because of their atomic-like distributions in solids. While the spherically symmetric part  of n(
r
) in (41) are evaluated from overlapping the obtained charge densities by means of the Löwdin alpha expansion [35] according to the given
of n(
r
) in (41) are evaluated from overlapping the obtained charge densities by means of the Löwdin alpha expansion [35] according to the given  vectors and the translational vectors in the crystal structure. In the interstitial region,
vectors and the translational vectors in the crystal structure. In the interstitial region,  in (45) sets a constant so as to conserve the total charge in the solid and
in (45) sets a constant so as to conserve the total charge in the solid and  in (46) puts a zero constant as an initial value.
in (46) puts a zero constant as an initial value.
After these initial densities have been determined, the potentials in section 2.5 can be calculated. By numerically solving the generalized eigenvalue problem in (35), the energy eigenvalues and eigenvectors expected by these potentials can be obtained, and finally the Bloch function can be obtained. From this Bloch function, new densities can be estimated. The next self-consistent calculation is performed using the new input densities, until the input densities (or the initial densities) and this new output densities agree within a given tolerance. In general, the new input densities are estimated from the previous input and output densities. Here the Broyden's method is often used [47].
The DLASTO method has two cut-off parameters we have to set up in common with the LAPW method. One is an upper limit ℓmax for the sum of ℓ' in the sphere basis function (21) and another is kmax for the sum of k i in the interstitial basis function (12). Both of them make a decisive influence on the convergence for basis functions, and eventually for Bloch function. In the APW method, it has been indicated that ℓmax and kmax are related with values of function jℓ (kap ) [48], which traces back to the spherical-harmonics expansion of plane waves used to match on the boundaries between the sphere and interstitial regions. In the DLASTO method, it exists explicitly in (32) and (33). As an empirical rule, it is proposed that the d band energies are converged to the order of 0.001 Ry with a criterion kmax ap = 7 in APW method [48] and in the LAPW method it is a good convergence with kmax ap ranging from 7 to 9 for all the cases [14]. Although ℓmax is connected with Lt of the lattice harmonics (A.11) in the full potentials, ℓmax = 8 is a typical value in the LAPW method [14] or the DLAPW method [22], so as to obey the rule of kmax ap = ℓmax in the APW family.
Moreover the DLASTO method has yet another relationship to ζp
in 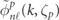 through
through  in (30) and (31). For the 3d orbital, the Fourier component of the radial STO in (17) can be expressed with n = 3, ℓ = 2 and k = kmax by
in (30) and (31). For the 3d orbital, the Fourier component of the radial STO in (17) can be expressed with n = 3, ℓ = 2 and k = kmax by

Thus the computational accuracy of the DLASTO method is partially determined by the choice of the cut-off values of kmax and ζp
. For the other orbitals, the relation between kmax and ζp
can be analytically derived from  in (17), but in the case of the 3d orbital the optimal solutions of kmax and ζp
cannot be identified from the function form of (53). Finally the DLASTO method becomes a conditional convergence for kmax and ζp
.
in (17), but in the case of the 3d orbital the optimal solutions of kmax and ζp
cannot be identified from the function form of (53). Finally the DLASTO method becomes a conditional convergence for kmax and ζp
.
As an empirical rule, it has been found that in the setting range of kmax
ap
= 9–14, the band structure can be well converged irrespective of the value of ζp
decided from the condition (20) and without a problem of incompleteness of the basis set that frequently occurs in the DLAPW method. It is a larger value than kmax
ap
= 8 in the APW family, but it does not increase the computing time, because the Hamiltonian HNN' and overlapping ONN' matrix elements in the interstitial region, which are the most time-consuming parts of the DLASTO method, are calculated by the FFT algorithm. Also, by empirically adjusting ζp
, a smaller value of kmax
ap
= 9 is in some cases sufficient to achieve a convergence. As increasing n and ℓ, the convergence tends to occur at small values of kmax
ap
due to the property of the function  .
.
For the spherical basis set (10) we have to choose orbitals {nℓsμ} to every pth atomic group in the solid. In the previous papers [20], it has been suggested that one choice is called 'single ζ' as using a single set composed of orbitals with a different ℓ, and the other is 'double ζ' which is a single ζ plus one more orbitals with an unoccupied states. In the LAPW method, the single and double ζ correspond to a concept of multiple windows. In each of the windows, a distinct set of fixed energies  is used to handle separate orbitals or semi-core states. Here we have chosen a minimum basis set with single ζ to give an overview of the qualities of the band structure obtained in the DLASTO calculation.
is used to handle separate orbitals or semi-core states. Here we have chosen a minimum basis set with single ζ to give an overview of the qualities of the band structure obtained in the DLASTO calculation.
3.2. Bcc Fe as a sample case of ferromagnets
As a test survey, we pick out a typical ferromagnet of body-centered-cubic (bcc) Fe and show the calculated results in the DLASTO method. From here on, we will proceed according to the exchange and correlation potentials of von Barth and Hedin [3]. For the basis set in the sphere region, total 18 orbitals of 3d2/3, 3d5/3, 4s1/2, 4p1/2 and 4p3/2 are set up and the other occupied states are calculated as core electrons by solving the SPCD equation or the Dirac equation. As an empirical rule in the 3d transition metals, it has been confirmed that unless the 3p electrons were calculated as valence band electrons, the DLAPW method could not make a spin polarized, as well as in the LAPW method [50]. In the DLASTO method, however, the final result yields the same spin polarization irrespective of whether the 3p states are core electrons or valence electrons. In order to show a wide energy range of the band dispersion, it seems better to add the unoccupied states 4p1/2 and 4p3/2, since their bands are distributed near above the Fermi level. The lattice constant 5.33aB is used in the same values of the previous paper [21] to compare with the DLAPW results, where aB is the Bohr radius. In the calculation, the value of ap is set out as 3.3aB to a certain maximum, and kmax ap = 12 and ℓmax = 8 are used. The integration of the densities in section 2.4 is executed by the tetrahedron method at 21 × 21 × 21 grid points in the first octant of the first Brillouin zone, namely at 505 points in the irreducible wedge.
Figure 1 shows the electronic band structure of bcc ferromagnet Fe calculated by the DLASTO method in the full potential scheme (FP-DLASTO), where the Fermi level is indicated in a dashed line. In figure 1, each blue and red color denotes the component intensities of the s and d orbitals, and the rest are represented by black. Thus, the change in color of red and blue reveals the strength of the hybridization between the d and s orbitals. The obtained FP-DLASTO band structure is well agree with the DLAPW one in bcc Fe [21] and also the Fermi surfaces have the same shape as in the DLAPW method. A common feature of the spin-polarized relativistic band structures of the DLASTO and DLAPW methods, other than the spin–orbit splitting, is that since the up- and down-spin states are not in good quantum numbers, a band-splitting occurs when the bands with these two spin states cross each other, which is different from the scalar relativistic band structure, especially in the Fermi-surface shapes. Hence the calculated Fermi surface can explain the angular dependence of the measured dHvA frequencies, though once more details are not given here on the analysis of the Fermi surface [21]. We can see that the FP-DLASTO method works well in the band structure of bcc Fe. If the similar settings were prepared for the 3d transition metals, the FP-LASTO method could determine the band structures within a similar accuracy.
Figure 1. Electronic band structure of bcc ferromagnet Fe along high-symmetry lines of bcc in DLASTO method. The dashed line denotes the Fermi level.
Download figure:
Standard image High-resolution imageTable 1 shows the spin moment μS, orbital moment μL and SC in bcc Fe in different methods. The spin moment is evaluated from a unit-cell-volume integral of m( r ) in (42) and (46) by

and it can be partitioned into the pth atomic group and angular momenta, though the detailed expressions are not given here. It is to be pressed that owing to an orthogonality of plane waves and a spatial symmetry of lattice harmonics, the main contribution of μS comes from the spherical term of Lt = 0 in the sphere region and the constant term of Gs = 0 in the interstitial region. Similarly the orbital moment is obtained from the sphere-region basis ΨN ( k , r ) in (21) as a projected quantity onto the z-axis of the local coordinate as follows:

where  is an operator for orbital angular momentum along the z-axis of the local coordinate. Practically, (55) can be computed using the matrix component of
is an operator for orbital angular momentum along the z-axis of the local coordinate. Practically, (55) can be computed using the matrix component of  as
as

where the ss' matrix elements for  and
and  are arranged in the same way as the CG coefficients in (19) using the parameter
are arranged in the same way as the CG coefficients in (19) using the parameter  .
.
Table 1. Spin moment, orbital moment and Sommerfeld coefficient in bulk bcc ferromagnet Fe.
| Method | Spin momentμS (μB) | Orbital momentμL (μB) | Sommerfeld coefficientγ (mJ K−2 mol−1) |
|---|---|---|---|
| FP-DLASTO | 2.19 | 0.069 | 2.377 |
| WM-DLASTO | 2.22 | 0.044 | 2.331 |
| MT-DLASTO | 2.21 | 0.043 | 2.299 |
| DLAPW [21] | 2.12 | 0.057 | 2.786 |
| DKKR [51] | 2.08 | 0.056 | — |
| FP-DKKR [34] | 2.24 | 0.050 | — |
| DLMTO [52] | 2.20 | 0.043 | — |
| LMTO [53] | 2.22 | 0.04 | — |
| FP-LMTO [54] | 2.19 | 0.049 | — |
| Experiment | 2.13 | 0.080 | 4.755 |
For the purpose of investigating a spatial dependence of potentials in the DLASTO method, three different types of potentials: the full (FP-), warped muffin-tin (WM-), and MT potentials are used to calculate the μS, μL and SC in the same lattice parameters, and the calculated results are shown in the top three lows of table 1. The WM-LASTO calculation uses a spherically-symmetric potential only in the sphere region, and namely it takes into account the same spatial distortion in the interstitial region as in the FP-LASTO one, while the MT-LASTO calculation further makes the interstitial potential constant. Comparing with the three potentials, the spin moments are in agreement within ±0.01 μB, while the orbital moment in the FP-DLASTO calculation is slightly larger than in the other ones. It could be seen that the non-spherical potentials in the sphere region are important to enhance the orbital moment in the DLASTO method, though the absolute values are generally small in bcc Fe.
In the four rows or less of table 1, the previous calculated results of the DLAPW method [21] or the other methods [34, 51–54] and the experimental results [55] are shown to compare with the DLASTO results on their calculation precision and trend. In other papers, the relativistic spin polarization theories based on the SPCD equation are often expressed in the abbreviated notation SPR, but note that here we use the same notation, D, for a unified representation. Although there are differences in the exchange potential and correlation potential formulas and lattice constants used, the spin moments have a magnitude of 2.22 μB as an average value. The DLASTO results show a spin polarization of about the average value, which is 0.09 μB larger than the experimental value. In the orbital moment, it appears that there is almost no change due to the potential shape and the relativistic spin polarization in the KKR and LMTO methods, though they cannot be compared in an exact sense because they were not performed under the same calculation conditions.
The SC of electronic specific heat γ is proportional to the density of states (DOS) at the Fermi level D(EF) as  , where kB is the Boltzmann constant. As can be seen from table 1, the SC of the DLASTO method is almost unchanged within the range of 0.08 mJ K−2 mol−1 with respect to the potential shape, which means that the dispersion of the bands at the Fermi level is unchanged to a corresponding magnitude. Moreover these SC values are about half smaller than the experimental values regardless of the calculation method. The DOS at the Fermi level, or the SC, needs to be improved by a magnitude of about 1 as a dimensionless enhancement factor (=γexp/γband − 1) in the exchange and correlation potentials or in the fundamental equations, where γband and γexp are the theoretical and experimental SC, respectively.
, where kB is the Boltzmann constant. As can be seen from table 1, the SC of the DLASTO method is almost unchanged within the range of 0.08 mJ K−2 mol−1 with respect to the potential shape, which means that the dispersion of the bands at the Fermi level is unchanged to a corresponding magnitude. Moreover these SC values are about half smaller than the experimental values regardless of the calculation method. The DOS at the Fermi level, or the SC, needs to be improved by a magnitude of about 1 as a dimensionless enhancement factor (=γexp/γband − 1) in the exchange and correlation potentials or in the fundamental equations, where γband and γexp are the theoretical and experimental SC, respectively.
3.3. Hcp ferromagnet Gd as lanthanide case
In most lanthanide compounds, Fermi surface studies of the dHvA effect have shown that the 4f electrons are localized in the ground state. In short, there are no 4f electrons on the Fermi surface. However the LSDA calculations in any case indicate a heavy-fermion electronic structure with 4f electrons on the Fermi surface: it is crucial to emphasize that the valence state is different from the one indicated by LSDA for the magnetic lanthanide system. Empirically, the angular dependence of the dHvA frequencies observed in magnetic lanthanide compounds can be usually extrapolated, as an alternative, from the topology of the Fermi surface calculated in the La or Y and Sr reference material, not containing 4f electrons, for example, in EuCo2Si2 [56]. Among lanthanide magnets, the elemental metal Gd is one of the ferromagnetic materials at room temperature and the only one in the lanthanide series. It crystallizes in the hexagonal-closed-packed (hcp) structure with a Curie temperature of 293.2 K [57]. A general discussion of first principles calculations for Gd metals has been summarized elsewhere [58]. At the onset, an attempt is made to calculate the ferromagnetic state of hcp Gd within LSDA in order to verify the accuracy and trend of the DLASTO method and the obtained results are compared with those of the DLAPW method previously calculated in the same framework [21].
In the LAPW calculation of Gd metal, it has been pointed out that fully occupied 5s and 5p orbitals should be treated as valence electrons including 4f, 5d and 6s orbitals. [50]. According to this criterion, we initially performed the DLASTO calculations with the same configuration of valence electrons as in the previous DLAPW calculations, but we encountered some problems: in the DLASTO method, if the STOs, obtained from ζp by (20), are connected to the wave functions of the 5s and 5p orbitals on the sphere, then the smearing contribution to the interstitial region tends to be larger for both orbitals than the one treated as core electrons. The electronic states of Gd metal have actually shown that the lost numbers of these 5s and 5p states from the sphere result in a change in the occupied number of 4f states, eventually giving a large change in the magnetic moment for the Gd ferromagnet. In order to avoid this problem in the DLASTO method, although it is possible to enlarge ζp manually to fit the current situation, as an option, it was to set a large radius ap = 3.2aB, as allowed by the crystal structure, so that the 5s and 6p orbitals would be spatially well localized inside the sphere as core electrons. In fact, since the 5p electron has only 0.02 electrons in the interstitial region, this is a permissible approximation that can be regarded as core electrons. Therefore we configured a total of 64 STO's in the interstitial region: 4f5/2, 4f7/2, 5d3/2, 5d5/2, 6s1/2, 6p1/2, and 6p3/2. The basis functions in the sphere region are expanded up to ℓmax = 8 and the cut-off to the interstitial plane waves is executed by kmax ap = 14. The lattice constants are set as a = 6.6389aB and c = 10.6024aB in the previous results of the DLAPW method [21], which are calculated in terms of the WS radius rWS = 3.642aB and c/a = 1.597. The integration of the densities is done by the tetrahedron method at 462 points in the irreducible triangular-prism of the first Brillouin zone of the hexagonal lattice.
Figure 2 shows the electronic structure of the hcp ferromagnet Gd in the DLASTO calculation within LSDA along high-symmetry axis of hexagonal Brillouin zone and the dashed line denotes the Fermi level. The red color in figure 2 illustrates the distribution intensity of the 4f electrons, while the blue color shows the distribution of the 5d electrons and the other contributions are drawn in black. Since the crystal structure of hcp contains two Gd atoms in the hexagonal Bravais lattice, the band structure involves a total of twenty-eight spin-splitting 4f bands, twice the occupation number of fourteen 4f-electrons. As can be seen from the band structure in figure 2, the 4f bands are split above and below the Fermi level into fourteen majority (up-spin) bands and fourteen minority (down-spin) bands with a size of about 4 eV. The magnitude of this splitting is called the magnetic exchange splitting δEex, which is of the size of 12 eV in experimental measurements [59, 60]. Although the value of δEex in the DLASTO method is very small compared to the experimental value, this band structure is justified by the LSDA calculations: below the Fermi level, there are the nearly dispersionless majority 4f bands at about 4 eV and the large bandwidth s band, and above the Fermi level, there are the minority 4f bands directly above and the widely distributed 5d bands [61]. In particular, for the band structure in the vicinity of the Fermi level, a detailed comparison can be made with the paper reported by Sticht and Kübler [62] using the ASW method including the spin–orbit interaction, and the dispersion of the 5d bands is found to be in very good agreement. The DLASTO method could be concluded to be sufficiently accurate even for the almost dispersionless 4f band if it is calculated with the above indicated cut-off parameters and STO's.
Figure 2. Electronic band structure of hcp ferromagnet Gd along high-symmetry axis of hexagonal Brillouin zone in DLASTO method within LSDA. The dashed line denotes the Fermi level.
Download figure:
Standard image High-resolution imageCompared with the previous band structure of the DLAPW method [21], the size of δEex is the same, but the differences are that majority and minority 4f bands of the DLAPW method have larger dispersion and bandwidth than those of the DLASTO method and in addition the DLAPW Fermi surfaces are formed by the 4f–5d hybridized bands with relatively large dispersion. As seen from figure 2, however, the DLASTO results show that the minority 4f bands are pinned just above the Fermi level, giving an itinerant electron contribution. The occupation number per atom for f orbitals in the sphere, nf , is shown to be 7.30 by the tetrahedron method. If it is a localized 4f electron with δEex = 12 eV as shown in the experiment, then nf = 7, which means that 0.3 f-electrons are supplied as itinerant electrons in the DLASTO calculations with LSDA. This is the cause of different quantitative values of physical quantities between the DLAPW and DLASTO methods for the Gd ferromagnet, for example magnetic moments, SC and so on.
Therefore, in table 2, the calculated magnetic moments, orbital moments, and SC for the hcp ferromagnet Gd are summarized together with the results from several band theories that can be compared with which the usual first-principles calculations with LSDA have been performed. In the 'method' column of table 2, the initial letter 'D' indicates a spin-polarized relativistic band theory based on the SPCD equation, while the letter '+SO' at the end indicates a relativistic band theory incorporating the spin–orbit interaction into the scalar-relativistic equation by perturbation. In the case of Gd ferromagnet, the magnetic moments are evaluated from the sum of the spin and orbital moments from all orbitals, not just the contribution from the 4f electrons. In the experiment, we only know the definite data that the g-factor is g = 2.00 ± 0.02 [64] and the magnetic moment is 7.63 μB [65]. Assuming that the rate of contribution in spin and orbital moments is equal for all orbitals, the magnitude of the orbital moment is estimated to be ±0.08 μB. On the other hand, under the condition that the 4f electrons are localized, the orbital moment from the 4f electrons would have disappeared since the seven occupied states are fully spin-polarized, so if we consider only the 0.63 μB contribution from non-4f electrons in the same way, the magnetic moment can be estimated to be as close to zero as possible, ±0.006 μB. The magnetic moment obtained by the DLASTO method is 7.51 μB, which appears to be a reasonable value, but the orbital moment is 0.80 μB, which is an extremely large value due to the itinerant contribution from the minority 4f electrons pointed out above. Furthermore, the value of SC is 31.65 mJ K−2 mol−1 in the heavy-fermion state, which is also a natural conclusion, and does not agree with the experimental results at all.
Table 2. Spin moment, orbital moment and Sommerfeld coefficient of hcp ferromagnet Gd in the LSDA calculations.
| Method | Magnetic moment (μB) | Orbital moment (μB) | Sommerfeld coefficient (mJ K−2 mol−1) |
|---|---|---|---|
| DLASTO | 7.51 | 0.80 | 31.65 |
| DLAPW [21] | 7.42 | 0.05 | 3.34 |
| ASW + SO [62] | 7.64 | 0.25 | 8.1 |
| DLCAO [30] | 7.71 | 0.22 | — |
| DASW [31] | 7.55 | 0.08 | — |
| FLAPW + SO [63] | 7.48 | 0.03 | — |
| Experiment | 7.63 [65] | ±0.08 | 3.7 [66] |
Although the electronic structure obtained from the with-LSDA-DLASTO calculation cannot be compared with the experimental results, the physical quantities related to the Fermi surface are shown below: the 19th, 20th, 21st, and 22nd bands, counting from the bottom of the valence band, cross the Fermi level and form the Fermi surface. The hole carrier numbers of the 19th and 20th bands are 0.013 and 0.091, and the electron carrier numbers of the 21st and 22nd bands are 0.102 and 0.002. These carrier numbers vary depending on the potential shape and calculation method, but it is clear that the Gd ferromagnet is a compensated metal with the same numbers in the holes and electrons.
Next, let us consider phenomenologically under what conditions we can upgrade the basic equation such as the SPCD equation of the DLASTO method in order to achieve an improvement in the magnitude of δEex. The x-ray photoemission spectroscopy of the Gd ferromagnet shows the occupied 4f-state at −7.44 eV from the Fermi level and the unoccupied 4f-state at +4.04 eV [59]. This indicates that for the band structure in figure 2 from the LSAD calculations, the occupied 4f band should be shifted to about 4 eV lower energy and the unoccupied 4f band should be moved to the same value of about 4 eV higher energy. Accordingly it means a localized 4f state in which there are no 4f electrons on the Fermi surface. The basic splitting structure inherent in the SPCD equation needs so as to be converted from a six-to-eight splitting between 4f5/2 and 4f7/2 states due to the relativistic spin–orbit interaction to a seven-to-seven splitting between 4f up-spin and 4f down-spin states. In lanthanide trivalent ions, it has been found that the magnetic ground states derived from the SPCD equation in the relativistic jμ representation reproduce the value of Landé g-factor in the LS coupling, where the spin–orbit interaction is negligibly small [26]. This unique feature is due to the Paschen–Back effect, which naturally shifts from the jj-coupling state to the LS-coupling state depending on the magnitude of the internal magnetic field, and is the reason why the DLASTO method can produce reasonable spin-splittings even for Gd ferromagnets, as well as in the DLAPW method.
Considering the spin-splitting structure of the SPCD equation and assuming that an additional constant potential is introduced only for the direct Coulomb term, it is sufficient to introduce a potential of the following form for the SPCD equation of (24) and (25),
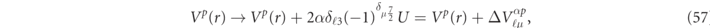
depending on the parity 2α = ±1 of 4f5/2 and 4f7/2. Here the factor δℓ3 means that this additional potential only acts on the 4f electrons, and the factor  is introduced according to the Paschen–Back effect. From the above discussion, it is clear that the parameter U in (57) should be set as U = 4 eV ≈ 0.3 Ry. Since the additional potential of
is introduced according to the Paschen–Back effect. From the above discussion, it is clear that the parameter U in (57) should be set as U = 4 eV ≈ 0.3 Ry. Since the additional potential of  is a constant value independent of real space, it is equivalent to replacing the band center of the fixed energy
is a constant value independent of real space, it is equivalent to replacing the band center of the fixed energy  with
with  , considering the structure of the SPCD equation between the energy
, considering the structure of the SPCD equation between the energy  and scalar potential Vp
(r). Therefore, in the DLASTO method, it is easy to perform the calculations by replacing only the energy term in the Hamiltonian matrix element
and scalar potential Vp
(r). Therefore, in the DLASTO method, it is easy to perform the calculations by replacing only the energy term in the Hamiltonian matrix element  of (36). Using the explicit expression for
of (36). Using the explicit expression for  described in (A.1) of appendix
described in (A.1) of appendix  for
for  . Here we will refer to this relativistic calculation method as LSDA + V. It should be noted here that the LSDA + V calculation is not in a self-consistent procedure, since the additional potential
. Here we will refer to this relativistic calculation method as LSDA + V. It should be noted here that the LSDA + V calculation is not in a self-consistent procedure, since the additional potential  in (57) is added only.
in (57) is added only.
Figure 3 shows the electronic structure of hcp ferromagnet Gd calculated by the DLASTO method with LSDA + V along hexagonal symmetry axis of the Brillouin zone. The dashed line denotes the Fermi level and clearly the 4f bands are moving away from the Fermi level, namely being the localized 4f electrons. The Fermi level is crossed mainly by highly dispersive 5d bands. Therefore, the SC value, which is estimated from the DOS of this band structure, is very small, 2.245 mJ K−2 mol−1, and the enhancement factor λ is very small, 0.64, based on comparison with the experimental value, 3.7 mJ K−2 mol−1 [66]. Counting from the bottom of the valence band, the 20th and 21st bands form the Fermi surface, which has a hole surface of 13% and an electron surface of 13% of the volume of the Brillouin zone, respectively. This indicates that the localization of the 4f electrons does not change the band index to produce the main Fermi surfaces or the fact that it is the compensated metal.
Figure 3. Electronic band structure of hcp ferromagnet Gd by the DLASTO method with LSDA + V along hexagonal symmetry axis of Brillouin zone. The dashed line denotes the Fermi level.
Download figure:
Standard image High-resolution imageAs shown in figure 3, the occupied 4f bands, which have almost flat energies with respect to wavenumber, exist from about 8 eV below the Fermi level in a region of about 2.5 eV width. In the unoccupied state, the flat 4f bands are centered about 4 eV above the Fermi level with about 3 eV width, and nevertheless they form some hybridized and/or mixed bands with the 5d electrons. The occupied 4f bands consist of 14 bands, although the band structure in figure 3 counts only 7 bands, almost flat at this energy scale, because one band in its appearance is actually consisted of two very slightly split states. Likewise, the unoccupied 4f states are made up of 14 bands. From the number of states calculated using the tetrahedron method, it can be confirmed that exactly seven 4f states are occupied per atom. Unfortunately, the magnetization density cannot be determined correctly, because it is not a self-consistent calculation.
Each of the seven apparent 4f bands in figure 3 is identified in terms of the z-component of total angular momentum μ, with the interband intervals widening in increasing energy order for the occupied states and narrowing for the unoccupied states. This splitting structure of the spacing pattern present in the DLASTO calculations is known as Landé interval rule, where the intervals increase in proportion to the magnitude of μ. It is shown that when the internal magnetic field is sufficiently larger than the spin–orbit interaction, this is effectively equivalent to a splitting of the LS coupling with a small spin–orbit interaction. As compared with the experiment [59], however, the calculated 4f interband intervals seem to be quite large. The interband intervals are related to the magnitude of the internal magnetic field in the DLASTO method so that in the practical sense the internal magnetic field allowed for the Gd ferromagnet should be determined in a self-consistent way to balance the large shifts of the 4f bands with LSDA + V. It is important to emphasize that a feasible first-principles reformulation of the underlying equations of relativistic spin polarization, rather than a perturbative approach, requires the introduction of a local potential with both parity and Pachen–Back effect symmetries, as in (57).
3.4. Paramagnet UN as actinide case
Among the actinide compounds, the uranium monopnictides UX (X = N, P, As, Sb and Bi) have a simple NaCl-type crystal structure and their unusual magnetic properties. The space group is Fm3m, and the Bravais lattice is a face-centered cubic (fcc) lattice. Uranium mononitride UN, with the lattice constant a = 4.89 Å, is an antiferromagnet of single- k type I with easy axis of ⟨001⟩ direction and the ordering temperature is 53 K [67]. The SC of the low-temperature specific heat is measured to be 49.6 mJ K−2 mol−1 [68], and therefore the 5f electrons in UN can be deduced to be itinerant electrons existing on the Fermi surface. First-principles calculations of the electronic structure of UN have been performed using various calculation methods, and detailed discussions of the results have been made elsewhere, including x-ray photoelectron spectroscopy measurements [69]. The application of the DLASTO method to uranium compounds requires caution in several respects. Since the information on band dispersion and Fermi surface of UN has been given by angle-resolved photoemission spectroscopy and the DLAPW calculation results in the paramagnetic state [70], we will restrict our discussion to the paramagnetic band calculation of UN in the actinide system.
Figure 4 shows the charge distributions of the outer orbitals 5f, 6p, 6d and 7s in an isolated uranium atom, where the horizontal axis denotes the distance from the nucleus in units of Bohr radius. These charge distributions are obtained by self-consistently calculating the Dirac equation with LDA, i.e. the equations in (24) and (25) with zero magnetic field, under atomic boundary conditions. The two contributions present in the charge distributions of 5f, 6p and 6d, respectively, illustrate the charge distribution of the two states split by the spin–orbit interaction. That is, for 5f, they are for the 5f5/2 and 5f7/2 states. In the case where the radius aU of the sphere region in the U atom for UN has a value of 3aB, the vertical solid line in figure 4 corresponds to it. This value of 3aB is almost the possible maximum value for the UN lattice constant by reducing the radius aN of the N atom. From this figure, it is clear that the 5f and 6p electrons are well localized and distributed inside the sphere, while the 6d and 7s are spread outside the sphere. Therefore, the 5f and 6p electrons make narrow bands in solids, respectively. On the contrary, the 7s electron is almost unoccupied in solids, and tends to become a band with a very large dispersion, although it is fully occupied in atom. In the DLASTO method, even if ζU is fixed at the condition of (20) and a rather large value of kmax is set, it has been confirmed that the band originating from the 7s orbital appears directly in the electronic structure near the Fermi level. Therefore, we extended (20) to include a parameter x as,

and we investigated the relationship between x and the electronic structure. If x is set to ℓ, we can return to the original value ζp (ℓ) = ζp . By comparing with the band structure of the DLAPW method calculated previously [70], as a rule of thumb, it is necessary to use an STO with a value of ζU around x = 2 or 3 for the 7s electron of U atom.
Figure 4. Relativistic charge distributions of the outer orbitals 5f, 6p, 6d and 7s in isolated uranium atom.
Download figure:
Standard image High-resolution imageNext, there is a question of whether to approach the 6p3/2 and 6p1/2 states of the U atom as core or valence electrons. As can be seen from figure 4, the charge distributions of the 6p3/2 and 6p1/2 states are smeared outside the sphere region with a radius of aU = 3. In fact, the numbers per electron outside the sphere are estimated to be about 0.25 and 0.04 for the 6p3/2 and 6p1/2 states, respectively. Therefore, the 6p3/2 state can only be treated as valence electrons. On the other hand, since the 6p1/2 state disappears from the sphere with a small amount of electrons, when the calculations are actually done with the 6p1/2 state treated as core and valence electrons, it is confirmed that there is a small change in the electronic states above and below the Fermi level. In the end, it is concluded that it is better to treat all the 6p states of actinide atoms as valence electrons in the DLASTO method as well as in the DLAPW method. For UN, therefore, the Bloch function is developed using 40 STOs as the basis set in the interstitial region, including 5f5/2, 5f7/2, 6p1/2, 6p3/2, 6d3/2, 6d5/2, and 7s1/2 in the U atom, and 2s1/2, 2p1/2, and 2p3/2 in the N atom.
Figure 5 shows the band structure of the DLASTO method for UN in the paramagnetic state along the symmetry axis of the fcc Brillouin zone. The settings in the calculation are ℓmax = 8 and kmax ap = 10. The radius of the sphere is aU = 2.8aB at the U atom, and aN = 1.7aB at the N atom. The integration of the densities is done by the tetrahedron method at 280 points in the irreducible wedge of the first Brillouin zone of the fcc lattice. The band structure of the DLASTO method closely reproduces the band dispersion of the DLAPW method, and furthermore it is qualitatively consistent with that of the FPLO minimum-basis calculation, except for a small value of SC [69]. The red and blue colors in figure 5 represent the distribution intensities of U-5f and N-2p electrons, respectively, and the other orbitals are shown in black. The 5f5/2 and 5f7/2 states of the U atom exist around the Fermi level, and the U-5f5/2 bands cross the Fermi level to form the Fermi surface. In addition, some of the U-5f5/2 states are found to form hybridized bands with the N-2p states. The very flat U-5f5/2-rich band crossing the Fermi level leads to a large DOS, and the SC of the low-temperature specific heat is estimated to be 18.56 mJ K−2 mol−1, thus the enhancement factor is relatively small at 1.67. Counting from the bottom of the valence band, the 9th and 10th bands cross the Fermi level and form the hole and electron surfaces of the Fermi surface, respectively. The hole surface occupies 54.5% of the Brillouin zone as holes, and the electron surface occupies 4.5% as electrons. This indicates that UN is an uncompensated metal in the paramagnetic state, and therefore there must be a large Fermi surface with about half the volume of the Brillouin zone.
Figure 5. Electronic band structure of DLASTO method for UN paramagnet along high-symmetry axis of fcc Brillouin zone. The dashed line denotes the Fermi level.
Download figure:
Standard image High-resolution imageThe bands of the occupied states on the symmetry axis Z connecting the symmetry points X and W in the Brillouin zone of the fcc in figure 5 were directly compared with the results measured by angle-resolved photoemission spectroscopy [70]. Although the calculated bandwidth appears to be narrower overall, the number and dispersion of the bands are in very good agreement. In particular, it is noteworthy that one band crosses the Fermi level on the Z axis around the X point. Although the shape of the Fermi surface is not shown here, it is very similar to that of the DLAPW method, and thus the shape of the Fermi surface around the X point is consistent with the Fermi surface mapping of angle-resolved photoemission.
4. Discussion and conclusion
In this paper, the LASTO method, which is one of the real space band theories, is extended to the full potential theory of relativistic spin polarization. By choosing the relativistic plane wave for the Fourier transformation, we were able to construct a Dirac-type relativistic band theory based on the SPCD equation while maintaining compatibility with the previously proposed DLAPW method. The full-potential augmentation is conceptually feasible by simply adapting the prescriptions that have been used previously in many other band theories, but since it is a Dirac-type relativistic extension, it is necessary to specify some special functions to calculate the full-potential matrix components and densities. In this paper we have presented the self-contained expressions for them. Since this is the first calculation in the full-potential relativistic extension of the LASTO method, we have limited the application to typical 3d-, 4f- and 5f-electron materials, and have given a detailed discussion on the accuracy and properties of the obtained results, which might provide some guidelines for the application to other material systems.
As an example of the 3d-electron system, we perform DLASTO calculations for the bcc ferromagnet Fe, which is considered to have small relativistic effects, and have shown the conditions for setting some of the cut-off parameters ℓmax and kmax required in this DLASTO method. It has been found that the DLASTO calculation gives the band structure comparable to those of the DLAPW method. The spin–orbit interaction makes a small but finite contribution to the orbital moment, and as a result the full-potential effect in the sphere region influences the orbital moment. From the applications to Fe, Gd and UN, generally, the selection of core and valence electrons was very dependent in the DLAPW method on the convergence of the electronic structure including the magnitude of the magnetic moment, but in the DLASTO method, the selection is less dependent, and thus, as one guideline, it might be better to treat the well-localized electrons in the sphere as core electrons. On the contrary, it is more difficult to treat the electrons confined already in the sphere as valence electrons in the DLASTO method, because the electronic structure depends on ζp , which represents the strength of screening for the basis functions in the interstitial region. Although there is a trade-off relationship in which the dependence of ζp becomes smaller as kmax becomes larger, in either case, the choice of orbitals for valence electrons and the cut-off parameters must be carefully set, taking into account the features of the DLASTO method and the characteristics of the materials.
As an example of the DLASTO calculation for the Lanthanide series, the electronic structure of the hcp ferromagnetism Gd induced by the scalar potential and the internal magnetic field within LSDA was investigated first-principles, and as a foregone conclusion it does not agree with the experimental results where the minority 4f bands are itinerant electrons on the Fermi surface. However the obtained results are comparable to the previous LSDA band calculations. It is demonstrated that the relativistic extension of the LASTO method by the relativistic plane wave expansion is a reasonable theoretical development even for very localized systems. The advantage of the DLASTO method is that the relativistic Wannier functions, which are the Fourier coefficients of the Bloch functions, can be directly computed in an analytical expression within the accuracy of the DLASTO method keeping the complementarity with the DLAPW method. A direct example for this was not given in this paper, but will be shown in detail in another paper.
As already explained in section 1, in order to obtain the correct electronic structure intrinsic to the 4f- or 5f-electron from first principles, it is necessary to be able to accurately represent and predict the valence in its f-occupied configuration. The SPCD equation is a zero-approximation for the relativistic fundamental equation including magnetic states, and it needs to be improved to include an intra-Coulomb interaction for jj-coupling states as shown in the RHF equation. It stems from the fact that the photoemission spectra of 4f-electron systems are well represented by the non-RHF LS coupling states [71]. The 5f-electron system has a larger spin–orbit splitting and a more broadening wave function than the 4f-electron system, so it can be considered as an intermediate coupling state approaching toward the jj-coupling state. From the SPCD equation, it can be deduced that the g-factor of the actinide trivalent ions deviates from the Landé g-factor of the LS-coupling state [26]. The DLASTO method based on the SPCD equation represents the LS-coupling from the jj-coupling through the intermediate-coupling states by the Pachen–Back effect, as explained in the Gd calculation of section 3.3. Therefore it is a highly versatile theory because it does not assume an LS-coupling state, so it could handle various coupling states in a fully relativistic form as well as with a magnetic polarization in the same theoretical scheme. It was pointed out for the Gd ferromagnet that the DLASTO calculated results are comparable to those of the LSDA band calculations which treat the spin–orbit interaction by a perturbative manner: the Gd ferromagnet is in a state close to the LS coupling with small spin–orbit coupling, as the same coupling state specified by the SPCD equation in lanthanide trivalent ions.
In order to make an improvement based on the SPCD equation, then, the intra-Coulomb potentials in the jj coupling have to be exactly described from the RHF equation so as to identify additional terms not included in the LSDA and to propose a computable and parameter-free potential. Then, all the information we need are the RHF matrix elements of the two-particle operator for the jn state of jj-coupling state and their coupling coefficients between the f orbitals. For the LS coupling, the coefficient tables in pn , dn and fn configurations have been published in the book [72], but it seems that there is no equivalent table of coefficients in fn configurations for the jj-coupling, though their calculation method has been given in Racah's series of papers [73]. At present, more research on the coupling coefficients might be needed.
As shown in the DLASTO calculations for the Gd ferromagnet, the LSDA + V was introduced phenomenologically, and it is regarded as being a parameter theory regressed from first-principles calculations. When a new relativistic potentials added for the SPCD equation with LSDA is derived from the RHF equation, unless it had the equivalent symmetry to (57) as a minimum condition, it could not be improved in the right direction to explain the experiment. Therefore, the LSDA + V provides a clear condition that should be improved in future studies. Although it might not make sense for the final purpose to extend LSDA + V to a self-consistent calculation method, it could be extended by applying the fixed-spin-moment method [74] to 4f-fixed energies to partially reveal the response of electrons other than 4f-electrons to the 4f intra-Coulomb interaction.
Finally, we would like to point out that further improvements in the lanthanide and actinide systems based on first-principles calculations are related to orbital magnetism. As a general feature, the orbital moment is more dominant than the spin moment in the magnetism of lanthanides and actinides. The SPCD equation is an approximation that neglects the potential terms dependent on the angular momentum. It is necessary to treat orbital current effects at local sites in a first-principles framework, and improvements will be presented in a future paper.
Acknowledgments
We really would like to thank Shin-ichi Fujimori for giving us the opportunity to write this paper. We are also grateful to Yuji Takada, Ikuto Kawasaki, and Kazuki Sumida in Electronic Structure Research Group at JAEA for fruitful discussions related to spectroscopy. Finally HY would also like to thank Jürgen Kübler for starting this research by providing me with the Alexander von Humboldt Stiftung, which allowed me to spend my research life at Technische Universität Darmstadt.
Data availability statement
All data that support the findings of this study are included within the article (and any supplementary files).
Appendix A.: Hamiltonian and overlapping matrix elements
In the explicit expressions of  of (36), it can be summarized as follows;
of (36), it can be summarized as follows;

In the case of the LSDA calculations, the energy  can be replaced by the fixed energy
can be replaced by the fixed energy  , while we merely insert
, while we merely insert  into
into  in the LSDA + V calculations. In the expression above,
in the LSDA + V calculations. In the expression above,  is an overlapping integral of the normalized radial wave functions
is an overlapping integral of the normalized radial wave functions  and
and  between α and β with the same (ℓ, μ) state at the center of the pth atom, which is explicitly given by
between α and β with the same (ℓ, μ) state at the center of the pth atom, which is explicitly given by
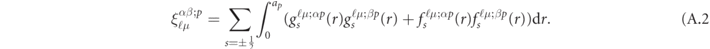
Since  and
and  are normalized, there are constraints of
are normalized, there are constraints of  for all of α = β. A dot-signed overlapping integral, for example
for all of α = β. A dot-signed overlapping integral, for example  is derived in (A.2) from the fact that
is derived in (A.2) from the fact that  and
and  are replaced with
are replaced with  and
and  , respectively.
, respectively.
In the first term of right side of (A.1),  denotes just the LAPW matrix element in the interstitial region as the follows,
denotes just the LAPW matrix element in the interstitial region as the follows,

where  is a constant scalar potential for V(
r
) with Gs
= 0 in (6) and
is a constant scalar potential for V(
r
) with Gs
= 0 in (6) and  are a constant magnetic field for B(
r
) in (7) along the z-axis in the crystalline global coordinate. Furthermore
are a constant magnetic field for B(
r
) in (7) along the z-axis in the crystalline global coordinate. Furthermore  means the definition
means the definition

using a total theta function projecting the interstitial region,

where θ(x) is the step function that θ(x) = 1 for x ≧ 0 and θ(x) = 0 for x < 0 and then  is an absolute value of
is an absolute value of  , which is the vector measured from the center of the pνth atom. Again
k
ij
is defined as
k
ij
=
k
j
−
k
i
=
G
j
−
G
i
and thus it is not dependent on any
k
in the first Brillouin zone. For the Θij
function, although we can obtain an analytical formula using the spherical Bessel function of order 1, j1(x) as,
, which is the vector measured from the center of the pνth atom. Again
k
ij
is defined as
k
ij
=
k
j
−
k
i
=
G
j
−
G
i
and thus it is not dependent on any
k
in the first Brillouin zone. For the Θij
function, although we can obtain an analytical formula using the spherical Bessel function of order 1, j1(x) as,

the FFT numerical technique should be anywise used in the Fourier transformation of the step function θ(x) of (A.4) to tabulate the values of Θij , since a rate-limiting process in all the calculations always occurs in calculating Θij . In doing so, what we should note is that the volume Ω of the unit cell in (A.4) can replaced into the volume V of the crystal, because of the translational symmetry in the real space of solids. In the above-mentioned expressions we use the approximation kj ≪ c as done in the relativistic APW method [35]. For (37), ONN' can be explicitly expressed by

The NMT term  in (38) is given by an explicit expression as
in (38) is given by an explicit expression as

where  corresponds to the interstitial contribution of the NMT terms in the LAPW method, which is written with Θ(
r
) of (A.5) as,
corresponds to the interstitial contribution of the NMT terms in the LAPW method, which is written with Θ(
r
) of (A.5) as,

and it can be tabulated numerically with the use of the FFT subroutine library. Here it is to be stressed that the constant scalar potential with Gs
= 0 is extracted from V(r) in (6). In (A.8),  is an integral of the NMT terms at the center of the pνth atom in the sphere region and if the local spin is oriented along the z axis in the local coordinate, it can be evaluated using
is an integral of the NMT terms at the center of the pνth atom in the sphere region and if the local spin is oriented along the z axis in the local coordinate, it can be evaluated using  of (22) as,
of (22) as,

where  is the normalized lattice harmonics,
is the normalized lattice harmonics,

where Lt
denotes an angular momentum for the tth non-zero lattice harmonics and  is an expansion coefficient at the pν atom. Once the angular integration of (A.8) is performed, we need the following formulas at the center of the pν atom as
is an expansion coefficient at the pν atom. Once the angular integration of (A.8) is performed, we need the following formulas at the center of the pν atom as

and

where σz
is z component of the standard Pauli matrices. In the above equations  and
and  can be called the spin-independent and spin-dependent relativistic Gaunt coefficients, respectively and each of them is defined by,
can be called the spin-independent and spin-dependent relativistic Gaunt coefficients, respectively and each of them is defined by,

and

where  are the CG coefficients of (19) and
are the CG coefficients of (19) and  are the Gaunt coefficients [49],
are the Gaunt coefficients [49],

The Gaunt coefficients are non-zero in M = m − m' and ℓ + L + ℓ' = even integer, and for ℓ, L and ℓ' they have the triangle inequality |ℓ − L| ≦ ℓ' ≦ ℓ + L. As a final formula  are rewritten down by,
are rewritten down by,

where the bra and ket representations, for example,  means that in an integral form
means that in an integral form

Similarly all the doted notations are shown directly from the corresponding non-doted notations, if the non-doted radial wave functions change the doted ones.
Appendix B.: Radial densities
The radial contributions  to the pth group of atoms in (45) are given by
to the pth group of atoms in (45) are given by

Here it is a significant point that the core-electron contribution  is added to
is added to  for t = 0 with a spherical symmetry in order that n(
r
) is the total density in the solid. In a self-consistent DLASTO procedure,
for t = 0 with a spherical symmetry in order that n(
r
) is the total density in the solid. In a self-consistent DLASTO procedure,  is obtained from solving the SPCD equation (25) under the atomic boundary conditions with the same potentials.
is obtained from solving the SPCD equation (25) under the atomic boundary conditions with the same potentials.
In (B.1),  , which are weights for the partial densities
, which are weights for the partial densities  , are calculated with terms of
, are calculated with terms of

for N' = {n'ℓ's'μ'p'ν'} by

where  is an expansion coefficients of
is an expansion coefficients of  , as shown in (A.11). The partial densities
, as shown in (A.11). The partial densities  are
are

where  are spin-independent relativistic Gaunt coefficients in (A.14). In the same rule as mentioned previously, for example, a dot notation
are spin-independent relativistic Gaunt coefficients in (A.14). In the same rule as mentioned previously, for example, a dot notation  of (B.1) for
of (B.1) for  is designated as the fact that in (B.2)
is designated as the fact that in (B.2)  is replaced into
is replaced into  and then in (B.3)
and then in (B.3)  is transformed into
is transformed into 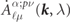 . While a dot notation
. While a dot notation  of (B.3) for
of (B.3) for  is associated with the replacement that
is associated with the replacement that  and
and  are changed into
are changed into  and
and  , respectively. The other single dot notation for
, respectively. The other single dot notation for  ,
,  , ... and double dot notation for
, ... and double dot notation for  and
and  are obtained from the same rule. Similarly, the radial contributions
are obtained from the same rule. Similarly, the radial contributions  in (46) are described by
in (46) are described by

and

where  are spin-dependent relativistic Gaunt coefficients in (A.16). It is to be noted that minus sign in the right side of (B.6) comes from the operator β in (38). Also the core-electron magnetization
are spin-dependent relativistic Gaunt coefficients in (A.16). It is to be noted that minus sign in the right side of (B.6) comes from the operator β in (38). Also the core-electron magnetization  , which is estimated from the atomic-like SPCD solution, is added to
, which is estimated from the atomic-like SPCD solution, is added to  , although it is vanishingly small for the closed shell of the core electrons. If an open shell is chosen at the core-electron configuration, the contribution of
, although it is vanishingly small for the closed shell of the core electrons. If an open shell is chosen at the core-electron configuration, the contribution of  is not necessarily small.
is not necessarily small.






