Abstract
Complete mathematical description on plasmas contains not only some coupled partial differential equations (PDEs) reflecting physics laws but also some inequalities reflecting physical reasonableness requirement. The phrase 'physical reasonableness' refers to that solutions should always correspond to non-negative-valued probability distribution function and non-negative-valued particle density. This work displays a universal strict method on the V-M system with a constraint inequality f ≥ 0∀ r, p, t. It treats the Vlasov equation as a recurrence formula relating expansion coefficient functions of the power series solution of the equation, and strictly demonstrates that the constraint determines the shape, or geometric characteristics, of space-time contours of the fluid velocity field. Consequently, the constraint inequality makes those PDEs reflecting physics laws to be expressed finally as an ordinary equation of the fluid velocity field with respect to its contour.
Export citation and abstract BibTeX RIS
1. Introduction
Complete mathematical description on a physics system should contain not only equations reflecting physics laws but also some physical reasonableness constraints. For example, plasma is acknowledged to be described by Vlasov-Maxwell (V-M) system which contains 5 partial differential equations (PDEs): a Vlasov equation (VE) of the probability distribution function (PDF) f and 4 Maxwell equations (MEs). According to acknowledged rule, there should be 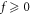 always. Therefore, strictly speaking, a complete mathematical description on plasmas contains 5 PDEs and an inequality (IE) f ≥ 0
always. Therefore, strictly speaking, a complete mathematical description on plasmas contains 5 PDEs and an inequality (IE) f ≥ 0
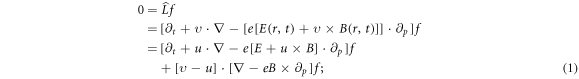

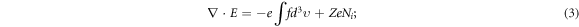
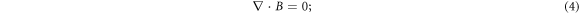
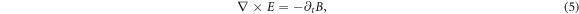
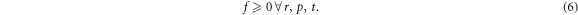
where p is the mono-variable function of υ: 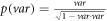 , and Ni and Z are ionic density and charge respectively. In this standard model, the VE, equation (1), is formally a 1st-order partial differential equation (PDE) defined over a 7-D space
, and Ni and Z are ionic density and charge respectively. In this standard model, the VE, equation (1), is formally a 1st-order partial differential equation (PDE) defined over a 7-D space 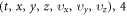 MEs are formally 1st-order PDEs defined over a 4-D space
MEs are formally 1st-order PDEs defined over a 4-D space 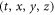 , the IE is also defined over the 7-D space.
, the IE is also defined over the 7-D space.
It is not trivial to emphasize these constraints. The IE (6) is not automatically valid. We introduce a mono-variable function 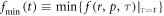 to denote the minimum-value of f at each time point. According to the VE equation (1), for
to denote the minimum-value of f at each time point. According to the VE equation (1), for 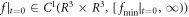 , there are
, there are 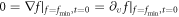 , which leads to, according to the VE equation (1),
, which leads to, according to the VE equation (1), 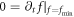 . Namely, for
. Namely, for  , if there is
, if there is  , there will be f > 0∀ r, p, t. But in many situations,
, there will be f > 0∀ r, p, t. But in many situations, 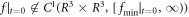 . For example,
. For example, 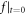 is often chosen by researchers to be of a ramped density profile linear dependent on the space distance
is often chosen by researchers to be of a ramped density profile linear dependent on the space distance 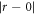 :
:  . Thus, there will be
. Thus, there will be

Moreover, if f meets the VE, any mono-variable, but not limited to be non-negative-valued, function whose variable is f, also meets the VE. For example, sin(f). Therefore, not all initial condition 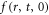 can warrant subsequently evolving f to meet the IE (6).
can warrant subsequently evolving f to meet the IE (6).
These examples well illustrate the necessity of basing investigation on plasmas on a complete mathematical description equations (1)–(6). Theoretical investigations on the V-M system (without the constraint) can be divided into two classes. One class is to apply analytic theories of PDE to the VE equation (1), which is taken as a 1st-order PDE defined over a 7-D space 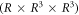 , and study uniqueness, existence, regularity and conservation of various solutions with specialized global mathematical properties [1–7]. The other class is to apply standard computational mathematical approaches for numerically solving equations (1)–(5) [8–21]. The later class is more popular because it can give detailed expression of solutions in terms of space-time coordinates, which is necessary for theoretical-experimental comparison.
, and study uniqueness, existence, regularity and conservation of various solutions with specialized global mathematical properties [1–7]. The other class is to apply standard computational mathematical approaches for numerically solving equations (1)–(5) [8–21]. The later class is more popular because it can give detailed expression of solutions in terms of space-time coordinates, which is necessary for theoretical-experimental comparison.
By now, all theoretical investigations are extension of differential equation theory, i.e. applying universal differential equation theoretical methods to PDEs reflecting physical laws. But the constraint IE reflecting physical reasonableness requirement is nearly untouched. Such an investigation style is logically sound: because PDEs with the constraint is a subset of PDEs, universal results valid for PDEs is also valid for PDEs with the constraint. But such universal results are too abstract to supply detailed solutions interested by physics community.
Such an investigation style is in a forward engineering manner: i.e., after obtaining universal results valid for PDEs and then picking out special results valid for PDEs with the constraint. Clearly, by now, such an forward engineering manner is still on the way (because the picking-out part is nearly not studied).
When there are multiple routes to achieve a same goal, the route with the highest efficiency is welcome. For studying such a complete mathematical description, beside above-mentioned forward engineering manner, there is a reverse engineering manner. That is, from the constraint IE, one can find allowed contour shapes which can warrant the IE to be fulfilled, and then based on these allowed contour shapes to study these PDEs. Compared with the forward engineering manner, the reverse engineering manner efficiently takes into account the constraint IE and targeted guides people attention being focused to some special results of PDEs. This makes finding detailed solutions interested by physics community to be in a short-cut, rather than in a long way.
Beside the VE, other equations of probability density function in many branches of applied sciences [22–25] should be also supplemented by a similar physical reasonable constraint inequality. Many authors [22–25] have noticed the importance of the non-negative-value constraint on the solved probability density functions and found a lot of solutions satisfying the constraint. Due to the difference between detailed forms of equations, those non-negative solutions cannot be transplanted to the V-M system, and hence efficiently finding non-negative solutions of f from the complete mathematical description on plasmas is worthy to be explored.
The purpose of this work is to display a strict, universal method, which is in such a reverse engineering manner, on equations (1)–(6). It is based on power series solution, and treats the VE equation (1) as a 'recurrence formula' relating many functions defined over 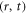 -space. These functions are expansion coefficient functions in the power series expression
-space. These functions are expansion coefficient functions in the power series expression
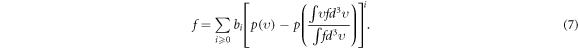
Especially, this method can, in the concrete, take the IE (6) into account.
2. Theory and method
An appropriate numerical experiment scheme on the complete mathematical description needs to re-consider the role of the VE and a more efficient expression of f. Strict theory has proven that any strict solution of the VE should have a spread over the υ-space [26]. This implies that f should be described by a set of functions 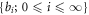 through power series [27–29]
through power series [27–29]
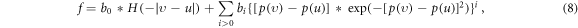
where H is Heaviside function 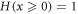 and
and 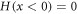 and
and 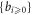 are continuous functions of
are continuous functions of  . Thus, f is described by many 4-D functions, including
. Thus, f is described by many 4-D functions, including 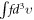 and
and 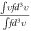 , those
, those 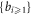 reflect how the f deviates from a Dirac-type distribution with respect to υ. Thus, one can view the VE as playing a role of recurrence formula relating these expansion coefficient functions
reflect how the f deviates from a Dirac-type distribution with respect to υ. Thus, one can view the VE as playing a role of recurrence formula relating these expansion coefficient functions 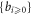 . Namely, this 1st-order 7-D PDE is equivalent to a set of 1st-order 4-D PDEs.
. Namely, this 1st-order 7-D PDE is equivalent to a set of 1st-order 4-D PDEs.
If further taking into account the mandatary constraint IE (6), one can find [28]
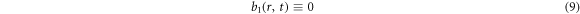
to be mandatary (otherwise, there will be f < 0 regime nearby the super surface υ − u = 0 in the 6-D phase space). Thus, substituting the power series expression equation (8) into the VE and comparing terms proportional to ![${\left[p\left(\upsilon \right)-p\left(u\right)\right]}^{i}$](https://content.cld.iop.org/journals/2516-1067/1/2/025005/revision2/prexab19f1ieqn27.gif) order-by-order, one can find that for terms proportional to
order-by-order, one can find that for terms proportional to ![${\left[p\left(\upsilon \right)-p\left(u\right)\right]}^{0}$](https://content.cld.iop.org/journals/2516-1067/1/2/025005/revision2/prexab19f1ieqn28.gif) , there should be
, there should be
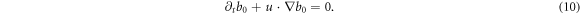
According to strict theory [26–29], equation (9) implies
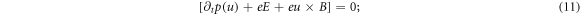
Thus, the V-M system exhibits a universal architecture: it is expressed by 1st-order PDEs in infinite number. In the PDEs corresponded by the VE, one couples with MEs
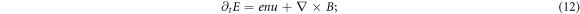
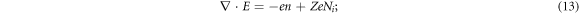
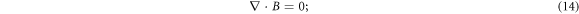
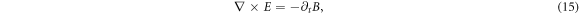
to form a closed equation set of 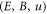 , other PDEs in infinite number are expressions of those {bi ≥ 0} in terms of
, other PDEs in infinite number are expressions of those {bi ≥ 0} in terms of 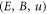 . Namely, one can determine 3 functions from equations (11)–(15), and then determine those {bi ≥ 0} from above-mentioned other PDEs. Then, constructing a f through these solved functions according to equation (8), one can easily prove such a constructed f satisfying the VE. These other PDEs imply each bi ≥ 2 to be a function of
. Namely, one can determine 3 functions from equations (11)–(15), and then determine those {bi ≥ 0} from above-mentioned other PDEs. Then, constructing a f through these solved functions according to equation (8), one can easily prove such a constructed f satisfying the VE. These other PDEs imply each bi ≥ 2 to be a function of 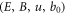 , and
, and  is determined through
is determined through
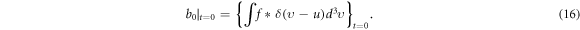
Namely, for f waiting to be solved, one can determine its two main features 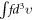 , or ∇ · E, and u through equations (11)–(15) then determine other features, such as
, or ∇ · E, and u through equations (11)–(15) then determine other features, such as 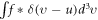 , from the VE. Thus, roles of the VE and the MEs are effectively separated to avoid conflict. Clearly, the architecture displays that few fluid functions govern a few fluid functions. This agrees with basic mathematical principle. Opposite situation where a few govern few corresponds to the number of equations being more than the unknown and hence no solution exists.
, from the VE. Thus, roles of the VE and the MEs are effectively separated to avoid conflict. Clearly, the architecture displays that few fluid functions govern a few fluid functions. This agrees with basic mathematical principle. Opposite situation where a few govern few corresponds to the number of equations being more than the unknown and hence no solution exists.
The constraint IE (6) has two direct deductions: one is equation (9) and the other is

Equations (11)–(15) is a 1-order PDE set of three functions 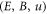 . It can also be expressed as the combination of the IE (17) and a 2-order PDE set of two functions
. It can also be expressed as the combination of the IE (17) and a 2-order PDE set of two functions  by expressing E in terms of p and B through equation (11) and substituting it into MEs equations (12)–(15) Note that the constraint equation (17) becomes to be in terms of p and B
by expressing E in terms of p and B through equation (11) and substituting it into MEs equations (12)–(15) Note that the constraint equation (17) becomes to be in terms of p and B
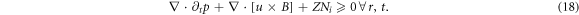
Now, what we dealt with is MEs equations (12)–(15)in terms of two functions p and B, which is an 2-order PDE set of 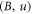 , and the constraint IE (18).
, and the constraint IE (18).
The role of the constraint IE of determining the shape of space-time contours of related physical fields has been not fully appreciated and utilized yet. For such a partial differential IE (PDIE) like equation (18), we can use independent variables, similar to those in [22, 23], constructed from 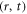
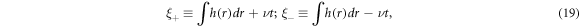
where the function h(r) represents the space shape of the static ionic density profile Ni ≡ Ni,0h(r) (Ni,0 is a constant), and ν is a constant, to rewrite the PDIE as a general form (where ci, j are constants)
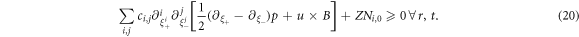
If expressing p and u × B as polynomials of ξ+ and ξ−, we can easily find that the IE (18) has confined p and u × B to be mono-variable functions of a same independent variable ξ+ or ξ−, i.e.
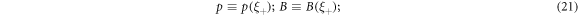
or
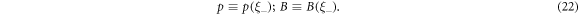
Otherwise, the IE cannot be valid ∀r, t because the equality 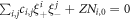 will define a super curve on the
will define a super curve on the 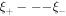 plane and hence divide the plane into two parts: one for > 0 and the other for < 0. In contrast, if the lefthand side of the IE (20) is mono-variable function and thus the PDIE is indeed an ordinary differential IE (ODIE), one can easily find that if the minimum of this mono-variable function is above the constant
plane and hence divide the plane into two parts: one for > 0 and the other for < 0. In contrast, if the lefthand side of the IE (20) is mono-variable function and thus the PDIE is indeed an ordinary differential IE (ODIE), one can easily find that if the minimum of this mono-variable function is above the constant 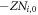 , the IE is valid ∀r, t. Namely, the IE has determined the shape of the space-time contours of the p-field and B-field. Moreover, why traveling wave solutions of other equations of probability density function are emphasized [22–25] might be reasonably attributed to the IE' requirement.
, the IE is valid ∀r, t. Namely, the IE has determined the shape of the space-time contours of the p-field and B-field. Moreover, why traveling wave solutions of other equations of probability density function are emphasized [22–25] might be reasonably attributed to the IE' requirement.
For 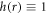 -case, equations (12)–(15) implies a 2nd-order PDE of W + u × B [27–30]
-case, equations (12)–(15) implies a 2nd-order PDE of W + u × B [27–30]
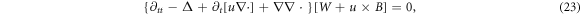
where
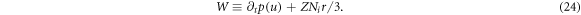
If denoting the angle between u and B as θ, we can find that W is θ-independent while u × B θ-dependent [30]. Because the allowed values of θ are over a broad regime, we thus obtain two same 2nd-order PDEs [27–30]
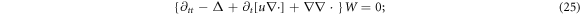
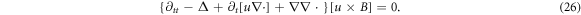
Applying  to this equation set, we can find that ∇ · W and
to this equation set, we can find that ∇ · W and ![${\rm{\nabla }}\cdot \left[u\times B\right]$](https://content.cld.iop.org/journals/2516-1067/1/2/025005/revision2/prexab19f1ieqn44.gif) also meet a same 2nd-order PDE and hence this fact implies a linear relationship between them [29, 30]
also meet a same 2nd-order PDE and hence this fact implies a linear relationship between them [29, 30]
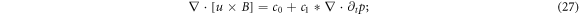

where c0 and c1 are constants. Because the linear relation should hold  (i.e., including t = 0), the values of c0 and c1 can be determined by initial condition
(i.e., including t = 0), the values of c0 and c1 can be determined by initial condition  [30, 31]:
[30, 31]:
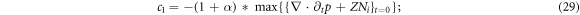
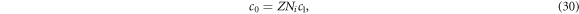
where α is a positive constant and the function max represents the maximum of allowed values of its variable. Thus, the constraint IE (18) becomes
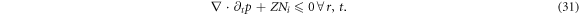
As above-mentioned, the IE (18) determines these PDEs to be finally converted to ODEs with respect to the independent variable ξ+ or ξ−. Note that equation (25) is a 2nd-order PDE of W or a 3rd-order PDE of p. A time-conservation law can be derived from this 3rd-order PDE [30]. Thus, equations (12)–(15), (18) is converted into a 2nd-order PDE of u and expressions of E and B in term of u [28, 30] and the constraint IE (18) (for simplicity, we do not write out their corresponding ODEs here):
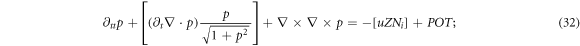
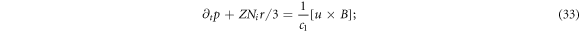

where POT is a vector determined by initial conditions of u, which is indeed determined by the initial condition of 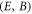 . This is because equation (25) is a 3rd-order PDE of p. Initial conditions for determining solutions of equation (25) include 3 terms:
. This is because equation (25) is a 3rd-order PDE of p. Initial conditions for determining solutions of equation (25) include 3 terms: 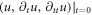 , and two of them
, and two of them 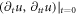 are affected by
are affected by 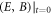 through equation (11).
through equation (11).
The positive-valued constant α is also determined by initial condition. The vector POT can be viewed as a constant if initially electromagnetic (EM) fields is of nearly uniform transverse intensity distribution. If initially the fields is a pure EM fields such as light, there will be 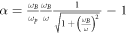 and
and 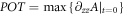 [30, 31], where A, ω, ωB are the vector potential, the frequency and the cyclotron frequency of the initial EM fields and ωp is the plasma frequency. For underdense plasmas, ωp < ω can warrant
[30, 31], where A, ω, ωB are the vector potential, the frequency and the cyclotron frequency of the initial EM fields and ωp is the plasma frequency. For underdense plasmas, ωp < ω can warrant 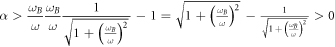 .
.
3. Conclusion
Complete mathematics description on plasmas is the V-M system constrained by an IE f ≥ 0∀r, υ, t . This is a model containing a 1st-order PDE and an IE defined over a 7-D space, four 1st-order PDEs over a 4-D space. Through the power series solution method, the constraint IE f ≥ 0∀ r, υ, t can be embodied through a mandatary fluid equation that expansion coefficient functions should satisfy and a macroscopic constraint IE n ≥ 0∀ r, t. The 7-D PDE plays a role of 'recurrence formula' relating these expansion coefficient functions (defined over the 4-D space). As a consequence, the complete mathematics description displays a universal architecture which refers to 3 fields functions defined over the 4-D space governing these expansion coefficient functions in infinite number. What 3 governing fields satisfy also contains the macroscopic constraint IE n ≥ 0∀ r, t. A strict method of solving fluid equations of 3 governing fields and the IE n ≥ 0∀ r, t is found. The IE n ≥ 0∀ r, t determines/affects the shape, or geometric characteristics, of contours of the space-time profile fluid velocity field.
In short, with increasing applications of statistics theory/viewpoint to various science disciplines, beside the detailed form of the evolution equation of the probability density function, (which might vary with respect to studied topics), non-negative-value constraint on the probability density function is mandatory to be satisfied. Beside directly seeking for non-negative solution of the probability density function [22–25], more in-depth treatment on the constraint is desired. Compared with the situation [22] where the probability density function is only space-time dependent, or a 4-D function, and its evolution equation is a PDE, the probability density function in plasma physics, a 7-D function, is more complicated and its evolution equation is indeed a differential-integral equation (because of MEs). Especially, the evolution equation involves in the definite integral over an independent variable (such as υ). In such a class of situations, directly seeking for non-negative solutions of the evolution equation is not an easy task, and the dependence of the probability density function on the integrated independent variables needs in-depth consideration. Therefore, it is necessary to analyze what the constraint implies and derive more concrete formulas from the constraint. This work displays an example of how to derive more concrete formulas from the constraint. Obviously, these concrete formulas are favorable to efficiently find non-negative solutions.
