Abstract
Quasi-distributed measurement of strain and/or temperature is often implemented using arrays of weakly reflecting fiber Bragg gratings (FBGs) whose reflection peaks are centered at the same nominal wavelength. The signals are obtained by measuring the phase difference between the reflections of consecutive FBGs. Typically, in such a system, the spatial resolution of the interrogator must be compatible with the spatial separation between consecutive FBGs. Insufficient resolution leads to an overlap of reflection peaks, a decrease in the differential-phase signal and poor sensitivity. In this paper, we study the use of two different sparsity based methodologies for improving the sensitivity of such quasi distributed acoustic sensing systems in the case where traditional signal processing approaches do not provide sufficient spatial resolution. These methods enable relaxing the requirements regarding the interrogator or, alternatively, reducing the needed separation between reflectors. Experimentally, these techniques were used to measure 1 kHz dynamic strain induced in a fiber segment between two discrete reflectors, located at the end of a 4 km long fiber. The separation between the reflectors was 18 m while the pulse (spatial) width was intentionally chosen bigger than that. It yielded approximately 5 dB increase in the measured signal compared to the traditional processing approach and an order of magnitude improvement in the sensitivity,  .
.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
One of the more notable applications of optical fiber sensing technology is distributed acoustic sensing (DAS). DAS has been drawing tremendous attention recently in both industry and academia, due to its diverse range of potential applications. These applications include intrusion detection, perimeter defense, monitoring oil and gas pipelines, monitoring transportation, structural health monitoring and more. It is characterized with: long range operation (tens of kilometers), immunity to electromagnetic interference, continuous coverage, reliability and cost-effectiveness. In common implementations of DAS, a conventional telecommunication type optical fiber cable is transformed into virtual array of thousands of microphones/geophones. This is achieved by connecting an interrogator at one end of the fiber cable. The interrogator launches light waveforms into a fiber and detects the backscattered light. The output of the optical detector is processed to yield spatially encoded acoustic signals.
There are two main techniques for implementing DAS: optical time domain reflectometry (OTDR [1]) and optical frequency domain reflectometery (OFDR [2]). Performance parameters, such as sensitivity and spatial resolution, are limited by system considerations in both techniques. For example, if the sensor is interrogated via OTDR, the width of the interrogation pulse determines the spatial resolution of the system and the pulse total energy directly affects its sensitivity. While the spatial resolution can be improved by using shorter pulses, the sensitivity will deteriorate due to the decrease in the pulse energy. Improving sensitivity by increasing the pulse peak power is limited due to nonlinear effects. On the other hand, in OFDR a linearly chirped continuous wave is used to interrogate the fiber. The backscattered raw signal is processed in the frequency domain to obtain the fiber profile. In this case, the spatial resolution is determined by the frequency range scanned by the interrogating waveform. Since more energy is launched into the fiber the method can potentially provide enhanced performance with respect to OTDR.
Reflectometric fiber-optic acoustic sensing systems can also be categorized according to the type of reflection which they use. One common approach is to use the fiber's intrinsic Rayleigh backscattering. In this approach, the sensing is truly distributed and despite rather low reflected power, impressive performance has been demonstrated [3–6]. Mechanical perturbations at the vicinity of the fiber (namely, acoustical signals or vibrations) affect the phase of the light in the fiber and induce variations in the backscatter profile.
Another approach is to use a sensing fiber with an array of weak discrete reflectors, e.g. fiber Bragg gratings (FBG) of the same nominal center wavelength. Such systems are often called quasi-distributed acoustic sensing (Q-DAS) systems. In this case, external perturbations modulate the differential phase between consecutive reflectors [7, 8]. Such configuration can provide better sensitivity than Rayleigh-based DAS due to the increase in backscattered power. This paper focuses on Q-DAS.
The backreflected response of a Q-DAS fiber, due to an optical impulse at its input, comprises discrete reflection peaks and low level noise-like signal due to Rayleigh backscattering. Neglecting Rayleigh backscattering, the backreflected impulse response can be represented as a K-sparse vector, where K is the number of reflectors. A vector of size n is called K-sparse if it has K ≪ n non-zero elements, which are sparsely positioned among many zeros. In this paper, sparse recovery techniques [9–11] are used to reconstruct the ideal sparse impulse response from low spatial resolution measurements and to demonstrate dynamic strain measurements.
While sparsity based techniques and related advanced signal processing methods were studied extensively in recent years, their use for processing backscatter data of FBG arrays is rare. Casagrande et al [12] and Apninder et al [13] studied the use of a genetic algorithm (GA) for analyzing FBG properties and presented a strain experiment for example. Weiss et al [14] described a comprehensive study on compressed sensing (CS) techniques and dictionary learning (DL) for WDM quasi-distributed data processing. Though learning the system's dictionary matrix increased the complexity, Weiss et al showed that their CS–DL methodology accurately estimated the FBGs time delays in static experiments, with efficient non-uniform sampling.
Sparsity-based algorithms facilitate solution of underdetermined linear system of equations via prior knowledge about the problem. There are numerous examples for applications where sparsity-based approaches outperform conventional algorithms [15]. To list just few examples, they were used for feature extraction [16, 17], denoising [18–20], super-resolution [21, 22] and more. Specifically, they have been extensively studied to reconstruct an unknown sparse signal from sub-Nyquist sampled data [23–25]. Several algorithms are available for such signal reconstruction [9, 26, 27]. This paper focuses on two of them. The first is the fast iterative shrinkage thresholding algorithm (FISTA [28]), which is a gradient-based iterative algorithm known for its good results in image denoising and deblurring [28, 29]. The second is the orthogonal matching pursuit (OMP [30]), a greedy algorithm that can recover sparse signals with a fast and efficient implementation.
In this paper, two common sparsity-based methodologies are described and implemented for phase sensitive OTDR (ϕ-OTDR) systems. The improvement they offer in both dynamic SNR and spatial resolution is experimentally analyzed, while addressing the runtime complexity of each method. The methods enabled measurement of 1 kHz dynamic strain, which was induced in a fiber segment between two discrete reflectors, at the end of a 4 km long fiber. The separation between the reflectors was approximately 18 m while the pulse spatial width was intentionally chosen bigger than that. It yielded more than 5 dB increase in the measured signal compared to the traditional processing approach and an order of magnitude improvement in the average sensitivity,  . The authors note that these techniques can be easily formulated for OFDR systems as well, as preliminary shown in [31]. Furthermore, this paper focuses on the theoretical development and experimental analysis of Q-DAS processing with sparsity-based techniques; therefore, the data used here is the originally uniformly sampled data. Follow-up research investigates the improvement in dynamic sensing capabilities together with significant hardware acquisition relaxations in the underdetermined case, where the raw-data is randomly sub-sampled, which leads to the CS setup [31, 32].
. The authors note that these techniques can be easily formulated for OFDR systems as well, as preliminary shown in [31]. Furthermore, this paper focuses on the theoretical development and experimental analysis of Q-DAS processing with sparsity-based techniques; therefore, the data used here is the originally uniformly sampled data. Follow-up research investigates the improvement in dynamic sensing capabilities together with significant hardware acquisition relaxations in the underdetermined case, where the raw-data is randomly sub-sampled, which leads to the CS setup [31, 32].
This paper is organized as follows: section 2 details Q-DAS measurement via ϕ-OTDR and sparsity-based recovery methodologies implementations for its processing, section 3 introduces the lab-built ϕ-OTDR experimental setup and section 4 presents the static and dynamic experimental results including comparison between all methodologies. Appendices A and B provide additional background on sparsity-based techniques that are used in this research.
2. Method
In this section, the optical Q-DAS theory and the chosen sparsity-based recovery methods for the optical data are detailed. Since the optical data have complex values, some nuances are emphasized for their mathematical derivation.
2.1. Q-DAS via coherent ϕ-OTDR
Consider an array of weak FBGs with the same nominal center wavelength. Monitoring the spectral shifts of the FBG's reflection peaks, or, alternatively, the phase difference between reflections from two consecutive peaks, may be used for measurement of the fiber's strain and/or temperature [33, 34].
In coherent phase-OTDR (ϕ-OTDR), an optical pulse with center frequency ω0 and complex envelope pulse(t), is launched into the fiber and the backscattered light is coherently detected. Assuming that nonlinear effects are negligible and that the induced phase variations are much slower than the scan rate, the system's response can be described as a weighted sum of the backscatter signals from all positions in the fiber. Accordingly, the receiver output can be expressed as a convolution of the response at the receiver output to a spatial impulse at z = 0, i.e. the system's impulse response pulse(t), and the complex reflection profile of the fiber  at ω0. Thus, we have
at ω0. Thus, we have
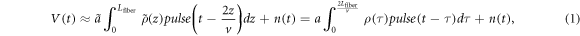
where  ,
,  , Lfiber is the fiber's length, v is the speed of light in the fiber, a is a constant describing the responsivity and gain of the receiver and n(t) denotes additive detection noise. Note that while the roundtrip delay is explicitly expressed in equation (1), the roundtrip phase is assumed to be part of the phase of ρ(τ). The expression for the receiver output can also be represented in a discrete form using the sampled versions of V(t), pulse(t), ρ(τ) and n(t), which reads as:
, Lfiber is the fiber's length, v is the speed of light in the fiber, a is a constant describing the responsivity and gain of the receiver and n(t) denotes additive detection noise. Note that while the roundtrip delay is explicitly expressed in equation (1), the roundtrip phase is assumed to be part of the phase of ρ(τ). The expression for the receiver output can also be represented in a discrete form using the sampled versions of V(t), pulse(t), ρ(τ) and n(t), which reads as:
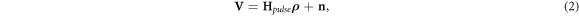
where  is the sampled signal,
is the sampled signal,  is the fiber's impulse response,
is the fiber's impulse response,  is the additive noise and
is the additive noise and  is a convolution matrix whose columns comprise shifted versions of pulse(t). The length of the measured signal, n, is determined by the optical sampling rate and the processing time (corresponding to the fiber length), while m can theoretically be larger, i.e. n ≤ m. However, there are limitations on m which reinforce the convergence of sparsity-based algorithms to reconstruct
is a convolution matrix whose columns comprise shifted versions of pulse(t). The length of the measured signal, n, is determined by the optical sampling rate and the processing time (corresponding to the fiber length), while m can theoretically be larger, i.e. n ≤ m. However, there are limitations on m which reinforce the convergence of sparsity-based algorithms to reconstruct  in such cases. They are elaborated under the CS theory.
in such cases. They are elaborated under the CS theory.
Neglecting Rayleigh scattering and assuming that the fiber comprises K discrete reflectors located at zk (k = 1, ..., K), the complex reflection profile of the fiber can be described as:  , where ρk is the reflectivity of the kth discrete reflector. Accordingly, the discrete version of the complex reflection profile,
, where ρk is the reflectivity of the kth discrete reflector. Accordingly, the discrete version of the complex reflection profile,  , is (approximately) a sparse vector with non-zero entries only at positions corresponding to zk.
, is (approximately) a sparse vector with non-zero entries only at positions corresponding to zk.
It is well known that OTDR-based sensing techniques inherently experience a trade-off between spatial resolution and SNR. Due to nonlinear effects, the pulse peak power cannot be increased beyond a given limit. Once the pulse peak power is set to its maximum value the only way to improve the SNR is to broaden the interrogating pulse but this comes at the expanse of spatial resolution. As shown in section 4, in the case of Q-DAS, an increase in the pulse width may lead to overlap of reflection peaks, a decrease in the differential phase signal and deterioration of the SNR. By using sparsity-based algorithms, however, it is possible to recover the high-resolution backscatter fiber profile from the low-resolution measured profile and improve the SNR in dynamic strain measurements.
2.2. Sparsity-based Q-DAS processing
The Q-DAS ϕ-OTDR measured data is a noisy complex-value signal that corresponds to the fiber's impulse response and the interrogating optical pulse. In order to reconstruct the fiber impulse response, denoted by  in equation (2), an underdetermined linear system of equations must be solved. Under the sparsity assumption of the Q-DAS fiber profile, this can be formalized using the following optimization problem:
in equation (2), an underdetermined linear system of equations must be solved. Under the sparsity assumption of the Q-DAS fiber profile, this can be formalized using the following optimization problem:
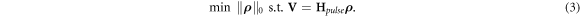
The ℓ0 norm in equation (3) is defined as the number of non-zero elements in its input, i.e. 
 [35]. The above equation is the fundamental CS problem formulation, where the matrix, here Hpulse, is termed the measurement matrix (see appendix A). In cases where the measurement matrix is invertible and well-conditioned, this optimization problem can be solved directly by multiplying both sides of
[35]. The above equation is the fundamental CS problem formulation, where the matrix, here Hpulse, is termed the measurement matrix (see appendix A). In cases where the measurement matrix is invertible and well-conditioned, this optimization problem can be solved directly by multiplying both sides of  with the inverse matrix
with the inverse matrix  . However, in many realistic cases, such as this, Hpulse is ill-conditioned and the measurement is noisy. In such cases, prohibitively large errors in the reconstructed signal may occur. Since equation (3) is non-convex, finding the solution by solving it directly is not computationally feasible [36]. Thus, various sparsity-based approaches have been developed to approximate its solution.
. However, in many realistic cases, such as this, Hpulse is ill-conditioned and the measurement is noisy. In such cases, prohibitively large errors in the reconstructed signal may occur. Since equation (3) is non-convex, finding the solution by solving it directly is not computationally feasible [36]. Thus, various sparsity-based approaches have been developed to approximate its solution.
In this paper, two approaches are studied and adapted for optical ϕ-OTDR data, i.e. to a complex-value form: (a) a convex-relaxation based iterative method named the fast iterative shrinkage algorithm (FISTA [28]) and (b) the greedy orthogonal matching pursuit method (OMP [30]); both detailed in appendix A.
For FISTA, the objective in equation (3) is relaxed using the following ℓ2-ℓ1 based optimization objective (see details in appendix A):
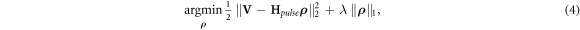
with λ being a weight parameter for balancing between the representation error and its sparsity. The FISTA approach is a fast version of the ISTA strategy (also known as proximal gradient). ISTA calculates the (complex) gradient step,  , of the ℓ2 term in equation (4) followed by an application of the complex proximal map of the ℓ1 norm, which is known as the soft thresholding operator, formulated in its complex form as [37]:
, of the ℓ2 term in equation (4) followed by an application of the complex proximal map of the ℓ1 norm, which is known as the soft thresholding operator, formulated in its complex form as [37]:
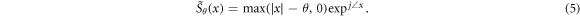
This leads to the following iterative approach, which is similar to that of the real-value case (see equation (A.3) in appendix A) with the distinction of a complex conjugate transposed operator performed on the measurement matrix:
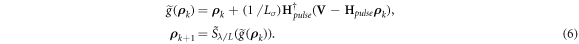
A full mathematical derivation for the complex-value gradient step appears in appendix B.
To accelerate the convergence of this technique, it has been suggested to use ISTA with an adaptive momentum step which leads to the FISTA strategy. Its implementation for Q-DAS is almost identical to its original real-value formulation, detailed in equation (A.5) in appendix A, only with the replacement of complex-value modified functions defined in equation (6). Namely, the transposition of the measurement matrix is replaced with a complex conjugate transpose, and the soft threshold operator is used in its complex form, as formulated in equation (5). The stopping criterion used is full-width-half-maximum (FHWM) of the reconstructed discrete reflectors. This allows control over the reconstructed fiber profile's spatial resolution. The computation time and its influence on dynamic SNR are elaborated in section 4.
The greedy OMP algorithm selects columns from the measurements matrix that are highly correlated to the currently approximated sparse signal. Its implementation for Q-DAS is identical to the detailed version in appendix A, where, again, the measurement matrix is Hpulse.
This paper focuses on the success of sparsity-based recovery techniques in ϕ-OTDR Q-DAS's dynamic signal reconstruction. Therefore, the measurement matrices are squared, i.e. n = m. Nonetheless, in both methods described above, the measurement matrix can be of a rectangular shape, i.e. n < m for applications of super resolution or randomly under-sampled signals (yielding a CS setup [31, 32]). In these cases, under some underlying restrictions, the sparse recovery can be employed for additional sensing system improvements [31, 32].
3. Experimental setup
The experimental tests were performed with the coherent ϕ-OTDR setup shown in figure 1. An ultra-coherent 1550 nm laser (NKT Adjustik E15) was split between a reference arm, containing a variable optical attenuator (VOA) to balance the optical power at the balanced photo detector (BPD), and a sensing arm. An acousto-optic modulator (AOM) in the sensing arm, with 200 MHz frequency shift, was used to create interrogation pulses at a scan rate (repetition rate) of 5 kHz. This necessitated a low-pass filter at the base-band, matching the pulse bandwidth. The pulses were created with an arbitrary waveform generator (AWG) feeding the AOM. The backscattered light from the fiber-under-test (FUT) was mixed with the reference to implement coherent detection. The mixed optical signals were detected with a balanced photo-detector and the result was sampled at a sampling rate of 0.5 GS/s. The FUT consisted of a 4 km fiber and 3 discrete reflectors. The discrete reflectors were implemented using unbalanced fiber couplers and FC-PC connectors (see figure 1), i.e. a discrete reflection from the Fresnel backscattering of the couplers' unconnected FC-PC connector. The first reflector consisted of a 90:10 fiber coupler and was used for determining the measurement matrix. The other two reflectors had 80:20 couplers and were connected to the FUT following the 4 km fiber. The separation between the reflecting FC-PC connectors of these reflectors was ∼18 m. A fiber stretcher between the distant pair of reflectors was used to induce strain equivalent to a phase shift of approximately 8.6 mrad peak-to-peak or 0.11n (using 10 mVpp) at a rate of 1 kHz. An additional 100 m fiber spool was added after the reflectors to distance the end-of-fiber reflection.
(using 10 mVpp) at a rate of 1 kHz. An additional 100 m fiber spool was added after the reflectors to distance the end-of-fiber reflection.
Figure 1. Optical ϕ-OTDR experimental setup.
Download figure:
Standard image High-resolution imageFor runtime comparison, all algorithms implementation and analysis were performed in Matlab on an i7-4720 2.6 GHz Intel core with 16 GB RAM.
4. Experimental results and discussion
Testing the proposed strategy comprises two parts. The first part are static tests which compared the spatial resolution between the analyzed methods and the second part are dynamic experiments oriented to test the dynamic SNR achieved by these approaches. The comparisons are performed between the mathematically reconstructed results of the FISTA and OMP methods and the experimental results obtained with ϕ-OTDR conventional processing. The conventional processing of the ϕ-OTDR raw-data is envelope detection to obtain the fiber profile and calculation of differential phase along the 'fast' time axis (namely, spatial phase difference) to obtain a linear measurement of the dynamic excitation signal of interest [38–40]. FISTA and OMP are mathematical methods which were developed to solve equations such as equation (2) for a sparse vector of unknowns. Accordingly, in this Q-DAS case, the fiber profiles they produce do not include other features of the original profile such as noise and Rayleigh scattering.
4.1. Static experiment
The proposed methodology was initially tested with the FUT described in section 3, with no perturbations. Interrogating pulses with durations of 350 and 60 ns were used. These durations correspond to spatial resolutions of 35 m and 6 m respectively. Out of the measured ∼4.1 km backscatter profile, a section of ∼140 m (690 sampling points) containing the two distant reflectors, was extracted and processed. Another section containing the reflection of the first reflector was used to construct a 690 × 690 convolution measurement matrix. The FISTA parameters (see section 2.2) were chosen as λ = 0.01 and (1/Lσ) = 0.5.
The results are presented in figure 2 for an interrogating pulse of width 350 ns (35 m spatial resolution). The measured profile is shown in black and is simply the envelope of the raw data. This is what we refer to as conventional ϕ-OTDR processing. It can be seen that the discrete reflectors are unresolved in this case. In contrast, the blue and the orange lines show, respectively, FISTA and OMP reconstructions of the FUT backscatter profile. The improvement in spatial resolution is evident. For reference, the measured ϕ-OTDR profile with the best spatial resolution achievable with the setup (60 ns pulse, i.e. 6 m spatial resolution) is shown in green.
Figure 2. Backscatter profiles using a 350 ns interrogation pulse—recorded optical data (black), processing with FISTA (blue) and processing with OMP (orange). Green curve displays a recorded optical data using a 60 ns interrogation pulse for reference.
Download figure:
Standard image High-resolution imageIt can be seen that implementing FISTA to process the Q-DAS data has improved the resolution from 35 m to 2 m, the stopping criterion is 177 iterations. On the other hand, the OMP algorithm identified pixel positions of the two reflectors,which can be considered as infinitesimal spatial resolution of one pixel in K = 2 iterations. In both sparsity-based methods the distance between the reconstructed reflectors was 18.6 m, as expected. Runtimes were 1.86 s in FISTA (until convergence to 2 m FWHM) and 0.012 s in OMP. The two orders of magnitude faster runtime for the OMP is due to the two iterations required to reconstruct only 2 reflectors (2 versus 177). For a scan rate of 5 kHz, real-time processing must be under 0.2 ms (assuming parallel processing of fiber segments). Efficient implementation with other programming languages, such as C or C++, can yield real-time OMP and FISTA processing operations. While this is straight forward for the fast OMP processing, it is also true for FISTA processing since its run time is strongly dependent on the number of iterations performed. As can be seen in figure 4, FISTA can be implemented with a factor of 10 less iterations with no significant decrease in dynamic performance, only in spatial resolution. This trade-off is discussed in the following section.
4.2. Dynamic experiment
To explore the potential of the methods for dynamical measurements, a fiber stretcher was placed between the two distant reflectors and was electrically driven to produce sinusoidal strain excitation between the reflectors, at a frequency of 1 kHz and strain of ∼0.11 n . 1024 consecutive measurements of the fiber profile were divided to 9 batches of 200 segments each, with 50% overlap (i.e. 40 ms per batch). Each segment was processed with OMP and FISTA (with a convergence condition of FWHM = 2 m), while the measurement matrix was calculated once for each batch. The algorithms configurations were the same as detailed in the static experiments, section 4.1.
. 1024 consecutive measurements of the fiber profile were divided to 9 batches of 200 segments each, with 50% overlap (i.e. 40 ms per batch). Each segment was processed with OMP and FISTA (with a convergence condition of FWHM = 2 m), while the measurement matrix was calculated once for each batch. The algorithms configurations were the same as detailed in the static experiments, section 4.1.
The dynamic strain signal was extracted from the phase difference between the two, now resolved, reflectors as a function of time. As a reference, differential phase signals were also extracted from the raw ϕ-OTDR signals. In this case, the reflectors were unresolved and the backscattered signal from each reflector undergoes a weighted convolution (both phase and amplitude) with non-ideal interrogating pulses. This prohibited a straight forward differential signal extraction since the points, from which the differential signal is the strongest, were unknown. However, since in this research the excitation frequency was known for the goal of comparing the sparsity-based methods, the excitation phase signal was exhaustively searched for between all possible location pairs. The target signal for the search was the highest dynamic SNR, defined as the ratio between the power of the phase signal at the excitation frequency (1 kHz) and the average power at neighboring frequency components.
The frequency spectrum shown in figure 3 corresponds to the differential phase signals extracted from the data along the fiber scan time axis. The black line represents the differential phase extracted from the raw ϕ-OTDR data with the highest dynamic SNR found, while the blue and orange lines represent the FISTA (FWHM = 2 m) and OMP extracted phases respectively. The excitation signal is clearly visible for the sparsity-based methods, at 1 kHz, and no prior knowledge of its frequency was required (compared to the conventional ϕ-OTDR signal processing which used prior knowledge to perform best SNR search).
Figure 3. Power spectral density of the differential phase, using 350 ns interrogation pulse. Best dynamic SNR extracted from unresolved reflectors in conventional ϕ-OTDR processing (black), processing with FISTA (blue) and processing with OMP (orange).
Download figure:
Standard image High-resolution imageTable 1 shows the average dynamic SNR for all three methodologies as a function of different pulse widths. The average dynamic SNR is calculated as the ratio between mean signal power and mean spectral noise over the 9 measurement batches. An improvement over the best available dynamic SNR, in the ϕ-OTDR unresolved profile, can be seen with respect to the sparsity-based methods. Approximately 5 dB and 6 dB improvement thanks to the use of FISTA and OMP processing respectively. The improvement in the dynamic SNR becomes more pronounced when the pulse width is larger than 275 ns. The abrupt increase in the SNR improvement is attributed to the fact that the interrogating pulse had sharp edges. Hence, the variation in the overlap of the backscatter responses from the two reflectors was not smooth.
Table 1. Average dynamic SNR comparison between ϕ-OTDR's original signal, FISTA (with 2 m FWHM) and OMP reconstructed signals, for different pulse width in dB.
| Pulse width (ns) | ϕ-OTDR (dB) | FISTA (dB) | OMP (dB) |
|---|---|---|---|
| 200 | 14.9 | 19.05 | 19.51 |
| 225 | 15.22 | 19.51 | 19.69 |
| 250 | 14.85 | 17.56 | 18.86 |
| 275 | 15.54 | 21.75 | 21.30 |
| 300 | 17.19 | 21.91 | 22.55 |
| 350 | 15.08 | 21.9 | 22.3 |
Moreover, the sensor's dynamic sensitivity was calculated corresponding to the measurements of the dynamic SNR as detailed above. The sensitivity is defined based on the noise floor of the calculated power spectral densities of the dynamic signal extracted from the differential phase. Table 2 presents all sensitivities for the two sparse reconstructed signals and the original signal with the best dynamic SNR found (as in table 1). Clear improvement in sensitivity is evident between the reconstructed signals and the original non-resolved signal. This can be attributed to the additional data, supplied by the interrogating pulse, and the sparsity-based methodologies that are used, which improve over conventional ϕ-OTDR processing.
Table 2. Average dynamic sensitivity comparison between ϕ-OTDR's original signal, FISTA (with 2 m FWHM) and OMP reconstructed signals, for different pulse width.
| Pulse width (ns) | ϕ-OTDR ![$\left[\tfrac{\mu \mathrm{rad}}{\sqrt{\mathrm{Hz}}}\right]$](https://content.cld.iop.org/journals/2515-7647/2/2/024002/revision2/jpphotonab72deieqn19.gif)
|
FISTA ![$\left[\tfrac{\mu \mathrm{rad}}{\sqrt{\mathrm{Hz}}}\right]$](https://content.cld.iop.org/journals/2515-7647/2/2/024002/revision2/jpphotonab72deieqn20.gif)
|
OMP ![$\left[\tfrac{\mu \mathrm{rad}}{\sqrt{\mathrm{Hz}}}\right]$](https://content.cld.iop.org/journals/2515-7647/2/2/024002/revision2/jpphotonab72deieqn21.gif)
|
|---|---|---|---|
| 200 | 2.33 ± 0.3 | 0.97 ± 0.06 | 0.97 ± 0.06 |
| 225 | 2.44 ± 0.1 | 0.96 ± 0.02 | 0.88 ± 0.05 |
| 250 | 2.56 ± 0.2 | 0.98 ± 0.03 | 0.83 ± 0.02 |
| 275 | 2.68 ± 0.3 | 0.90 ± 0.05 | 0.84 ± 0.05 |
| 300 | 3.59 ± 0.4 | 0.91 ± 0.05 | 0.75 ± 0.04 |
| 350 | 3.15 ± 0.5 | 0.89 ± 0.06 | 0.74 ± 0.05 |
In this FISTA implementation, the algorithm stopped when the peak width (FWHM) reached a given criterion (FWHM limit). Hence, the number of iterations, as well as the achieved dynamic SNR, depended on the choice of the FWHM limit. Figure 4 demonstrates this dependence between dynamic SNR, spatial resolution (FWHM) and FISTA run time (mean number of iterations over all 200 segments) for pulse width of 350 ns. A clear increase in convergence time for high spatial resolution (short FWHM) is evident. However, the increase in dynamic SNR, when going from spatial resolution of 7 m to spatial resolution of 1 m, is about ∼1 dB. Whether this improvement is cost effective or not is application dependent.
Figure 4. Dynamic SNR as a function of spatial resolution (bottom axis) and mean number of iterations (upper axis) to converge, using FISTA.
Download figure:
Standard image High-resolution image5. Conclusions
Quasi-distributed optical fiber sensors are frequently used in many applications. However, the trade-off between dynamic SNR and spatial resolution is often a factor which limits performance. In this paper, we proposed two processing algorithms to improve this limiting trade-off. Our proposed solution is based on the fact that the fiber profile can be considered sparse given that the discrete reflections are significantly stronger than the Rayleigh backscatter. The processing methods that were used, FISTA and OMP, are known in the field of sparse recovery and CS. We have demonstrated their ability to reconstruct unresolved discrete reflectors from a ϕ-OTDR system, showing experimentally that they improve both the spatial resolution and the dynamic SNR in a 4 km fiber.
It was previously shown [31] that a significant reduction in sampling rates can be achieved via random sampling and OMP reconstruction of Q-DAS static measurements. A small number of (uniformly distributed) samples from the measured data can be used for an efficient sparse fiber profile reconstruction. This significantly reduces the computational time and system hardware requirements. Future work will apply this under-sampled methodology to dynamic Q-DAS signals [32].
In addition, this paper focused, without loss of generality, on ϕ-OTDR interrogation. However, the same methodologies presented in it can be used with OFDR interrogation as well. In this case, the measurement matrix is the discrete fourier transform (DFT) matrix. The work in [31] demonstrates this possibility.
Acknowledgments
This research was supported by ERC-StG grant no. 757 497 (SPADE). The first author is partially supported by a scholarship from the Shlomo Shmeltzer Institute for Smart Transportation at Tel-Aviv University.
Appendix A.: Sparse recovery
Algorithms in the field of sparse recovery facilitate solution of underdetermined linear systems of equations given some prior knowledge about the measured data. Specifically, if the signal is known to be compressible by some transform, it is possible to recover it from data, which in the realm of classical signal processing is considered undersampled.
Consider the following minimization problem:
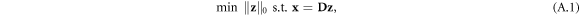
where  is the sparse representation of the measured vector
is the sparse representation of the measured vector  , and
, and  is a mathematical representation of the measurement process, termed the measurement matrix.
is a mathematical representation of the measurement process, termed the measurement matrix.
The ℓ0 norm in equation (A.1) is defined as the number of non-zero elements in its input [35], i.e.  . Though theoretically this problem can be solved directly if D is invertible and well-conditioned, in many realistic cases, D is ill-conditioned and the measurement is noisy. In such cases, the reconstructed signal may exhibit large errors. Since equation (A.1) is non-convex, finding the solution by solving it directly is time consuming. Thus, various sparsity based approaches have been developed to approximate its solution.
. Though theoretically this problem can be solved directly if D is invertible and well-conditioned, in many realistic cases, D is ill-conditioned and the measurement is noisy. In such cases, the reconstructed signal may exhibit large errors. Since equation (A.1) is non-convex, finding the solution by solving it directly is time consuming. Thus, various sparsity based approaches have been developed to approximate its solution.
One popular sparse recovery framework relaxes the minimization problem in equation (A.1) into a non-constrained convex minimization problem in terms of the ℓ1 and ℓ2 norms (rather than l0) as follows [41]:
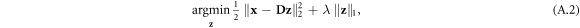
with λ being a weight parameter. While the two problems are not identical, under some conditions on D and the sparsity level, they produce similar solutions.
Notice that the relaxed form, equation (A.2), is convex and thus can be solved efficiently, e.g. using the fast iterative shrinkage algorithm (FISTA [28]), which we employ in this work. FISTA is an accelerated version of the iterative shrinkage thresholding algorithm (ISTA) [42], also known as the proximal gradient method. ISTA solves equation (A.2) iteratively by taking a step towards the gradient direction, equation (A.3), followed by a proximal mapping, which for the ℓ1-norm (our case) is the soft-threshold operator, Sθ(x), defined in equation (A.4)
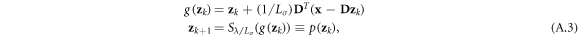
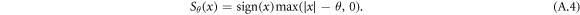
The sparse vector, z, is initialized with zeros in step k = 0, the matrix D has normalized columns and  , where σmax(A) is the largest eigenvalue of A. The use of the nonlinear function, Sθ (x) formulated in equation (A.4), compels the result to be sparse. In case of a complex valued input, the soft-threshold function multiplies its output by the inputs phase instead of sign, see equation (6). The procedure is complete when convergence is met using a stopping criterion, such as minimal error or maximum number of iterations.
, where σmax(A) is the largest eigenvalue of A. The use of the nonlinear function, Sθ (x) formulated in equation (A.4), compels the result to be sparse. In case of a complex valued input, the soft-threshold function multiplies its output by the inputs phase instead of sign, see equation (6). The procedure is complete when convergence is met using a stopping criterion, such as minimal error or maximum number of iterations.
In FISTA, a Nesterov momentum based acceleration is used, and thus the gradient step is defined as follows to accelerate convergence:
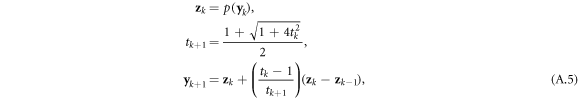
where t0 = 1 and y0 = x.
Another sparse recovery strategy solves equation (A.1) in a greedy way. A prominent method that relies on this approach is orthogonal matching pursuit (OMP [30]) that has a fast implementation especially for the cases of low sparsity levels. At each step k, a new non-zero element in the vector zk (initialized by z0 = 0) is chosen. This index is denoted as ik and selected as follows:
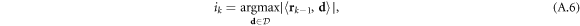
where rk = x − Dzk is the residual of the current solution, which is initialized by r0 = x, and  is the set of normalized column vectors from the measurement matrix, D. It can be seen from equation (A.6) that the index on step k is chosen to produce the best correlation between the residual part of the signal and a specific column in the measurement matrix. Denoting all the indices selected until step k as
is the set of normalized column vectors from the measurement matrix, D. It can be seen from equation (A.6) that the index on step k is chosen to produce the best correlation between the residual part of the signal and a specific column in the measurement matrix. Denoting all the indices selected until step k as  , the signal estimation is calculated with a least-squares approximation:
, the signal estimation is calculated with a least-squares approximation:
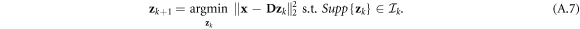
If the number of non-zero elements K is known, then K iterations are performed. Therefore, a fixed computation time is needed as opposed to the gradient-based methods, which do not assume the number of non-zero elements.
Appendix B.: Complex proximal gradient
In this appendix, the gradient step of the complex-value optimization problem, formulated in equation (4), is derived to its final expression, equation (6) [37].
Define  , where
, where  ,
,  and
and  , such that
, such that  ,
,  ,
,  . Therefore, a function
. Therefore, a function  can be defined as
can be defined as  . Wirtinger derivatives define the partial derivative of a complex function with respect to a complex number,
. Wirtinger derivatives define the partial derivative of a complex function with respect to a complex number,  and
and  as follows:
as follows:
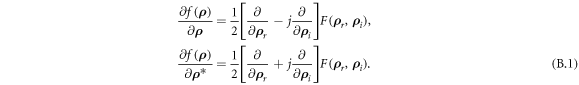
Windrow et al [43] have shown that the steepest descent direction for the complex least-square formulation, as stated above, is given by  and thus this expression is used to calculate the gradient step for equation (4). The function
and thus this expression is used to calculate the gradient step for equation (4). The function  can be written as
can be written as  for
for  . In this case, the Wirtinger derivative of
. In this case, the Wirtinger derivative of  with respect to
with respect to  (the first element in
(the first element in  ), is as follows:
), is as follows:
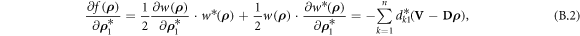
where dk1* is the kth element in the first column of D. Similarly, over all elements of  :
:
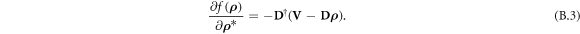
Thus, the gradient step should be formulated as shown in equation (6).





