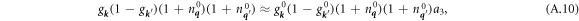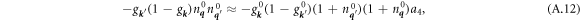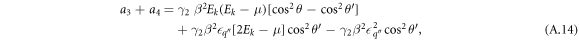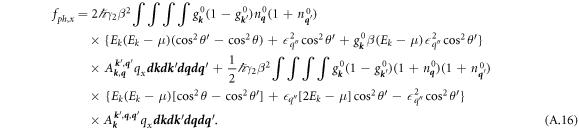Abstract
An electron-phonon Boltzmann transport equation is formulated which accounts for second order collisions with an electron-phonon vertex and a three-phonon vertex. This approach for electronic transport at second order reveals the existence of two forces perpendicular to the primary direction of electrical current, acting on the electrons and phonons. The force on electrons is equal and opposite to that on the phonons. Solutions for stationary states confirm that charge and thermal energy become separated. The force terms include both conservative and dissipative components, which for the phonons, lead to a modified Guyer-Krumhansl equation. The conservative components exist only when there exist explicit transverse gradients in the dissipated energy, and these terms may be incorporated into a Poisson kinematics. The dissipative force terms can cause threshold induced spontaneous symmetry breaking.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
While investigating electronic transport beyond first order calculations, a surprising pair of forces have been discovered that are perpendicular to the primary direction of electrical current. These forces act equally and opposit0ely on the electrons and phonons. This leads to a separation of charge and heat. This separation phenomenon builds on a previously discovered charge-spin separation that was predicted and eventually observed in one-dimensional systems [1–3].
The calculations presented here were performed up to second order scattering by incorporating both an electron-phonon vertex and a three-phonon vertex. The calculations also show that strong enough electrical current produces a bifurcation and spontaneous symmetry breaking. These results may be viewed within the context of nonlinear dynamics and pattern formation in nonequilibrium systems [4–7].
The first-principles scattering calculations are presented in sections 2 and 3. Discussion of these results in terms of phonon and electron dynamics is presented in sections 4 and 5. New terms are added to standard dynamical equations for electron and heat flow. Amongst these terms are both dissipative and conservative forces.
2. Electron-phonon Boltzmann transport equation
The microscopic approach presented here couples electrons and phonons through the quantum Boltzmann transport equation developed for electrons and for phonons [8–13], and is capable of dealing with second order scattering processes such as those depicted in figure 1. This is understood as a truncated approximation scheme under the BBGKY hierarchy [14]. This first principles approach leads to two equations for the electron and phonon distribution dynamics that can be called the electron-phonon Boltzmann transport equations (EPBTE). In particular a force equation for the phonon field is developed which displays the interesting heat induction effect.
Figure 1. Second order electron-phonon scattering diagrams, covering all cases with 3-phonon scattering. Two vertices are present, labeled W for electron-phonon and Q for phonon-phonon interaction. Diagrams (a) and (b) differ only in the direction of the virtual phonon q '' (similarly for c and d). Diagram (e) plays the dominant role in these calculations, when the current density is high.
Download figure:
Standard image High-resolution imageThe phonon Boltzmann equation has been used to derive the Guyer-Krumhansl equation for heat transfer. One application of the the Guyer-Krumhansl equation is towards successful understanding of the phenomenon of second sound in liquid helium. One of the results reported here is an additional term to the Guyer-Krumhansl equation.
The transport equation for the phonon distribution, n q , for a given wave vector, q , closely resembles the phonon BTE with the addition of an extra collision term. Accounting for the effect of both phonon-phonon collisions and electron-phonon collisions on n q gives an extension of the phonon BTE as

This constitutes the phonon part of the EPBTE. The collision terms are on the right hand side of (2.1). The phonon-phonon (pp) collision term is normally evaluated for a single vertex with 3 or 4 phonons involved. This term is responsible for providing thermal conduction as a response to a thermal gradient, but will not contribute to the transverse force discussed below in section 3. The spin quantum numbers are suppressed in the notation here as no spin-dependence will be discussed. The important collision integral is
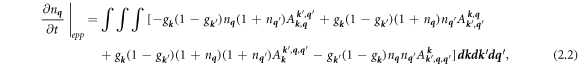
where g
k
is the electronic distribution function for electron wave vector
k
. The scattering diagrams of figure 1 represents the terms in (2.3). In particular diagrams a) and b) correspond to the first term, c) and d) to the second term, e) to the third term, and f) to the fourth and last term. Microscopic reversibility means that  and
and  . Swapping dummy indices
k
and
k
' in the 2nd and 4th terms gives
. Swapping dummy indices
k
and
k
' in the 2nd and 4th terms gives

Both momentum and energy conservation are built into the intrinsic transition factors 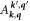 and
and 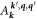 . The four terms in (2.3) cover the possibilities of phonons
q
and
q
' being created or annihilated. For electron sums
. The four terms in (2.3) cover the possibilities of phonons
q
and
q
' being created or annihilated. For electron sums  while for phonons
while for phonons  .
.
For the transition rate a cutoff time scale τ1 is required so that, for example, the second-order transition rate 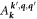 can be factored into the following 2-vertex form that goes like:
can be factored into the following 2-vertex form that goes like: 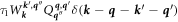 with an electron phonon vertex and a 3-phonon vertex connected by a virtual phonon
q
''. The
with an electron phonon vertex and a 3-phonon vertex connected by a virtual phonon
q
''. The 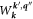 factor is an intrinsic transition probability and is associated with the electron-phonon scattering vertex while the other intrinsic transition probability
factor is an intrinsic transition probability and is associated with the electron-phonon scattering vertex while the other intrinsic transition probability  factor is associated with 3-phonon scattering. The time τ1, which will be calculated below, must be long enough for both (relatively fast) electron-phonon scattering and (relatively slow) phonon-phonon scattering to take place, i.e. long enough for the Dirac delta function for energy to form [9].
factor is associated with 3-phonon scattering. The time τ1, which will be calculated below, must be long enough for both (relatively fast) electron-phonon scattering and (relatively slow) phonon-phonon scattering to take place, i.e. long enough for the Dirac delta function for energy to form [9].
2.1. Detailed factorization of matrix element A
With a focus for a moment just on the three phonon processes then the textbook equation for the rate of change of n q is
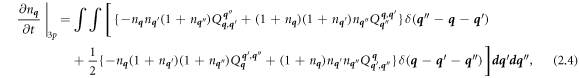
where the  is to avoid double-counting. By the principle of detailed balance, this rate is zero if all occupation factors n
q
take the equilibrium forms
is to avoid double-counting. By the principle of detailed balance, this rate is zero if all occupation factors n
q
take the equilibrium forms  . Because of electron-phonon scattering and the production of phonons
q
'', n
q
'' will not take the equilibrium form. For this specific factor a form
. Because of electron-phonon scattering and the production of phonons
q
'', n
q
'' will not take the equilibrium form. For this specific factor a form  is used. The physical reasoning is that one focuses only on 3-phonon scattering that occurs subsequently to the production of a phonon
q
'' by (first order) electron phonon scattering via
is used. The physical reasoning is that one focuses only on 3-phonon scattering that occurs subsequently to the production of a phonon
q
'' by (first order) electron phonon scattering via  .
.
For the remainder of this subsection it suffices to consider just one of the four terms in (2.4). It will be shown below in this section that the second term dominates the others so this is the term discussed immediately, which leaves:
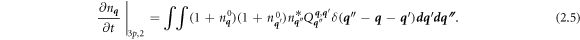
As mentioned above,  is produced by electron-phonon scattering. The phonons produced from these events will decay with a lifetime τq'' that is the lifetime of hot phonons produced from the electron-phonon scattering. The distribution
is produced by electron-phonon scattering. The phonons produced from these events will decay with a lifetime τq'' that is the lifetime of hot phonons produced from the electron-phonon scattering. The distribution  is described by
is described by

where the first order electron-phonon scattering rate is given by
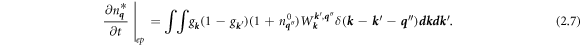
The steady-state solution to (2.6) is given by

which can be substituted into (2.5) to give:

Comparison to the (dominant) third term in (2.3) leads to the conclusion that 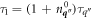 and
and

2.2. Useful result for phonon q '' lifetime
3. Transverse force terms for phonons and electrons
Returning to (2.3), for the phonons, the force per unit volume from collisions, is given by
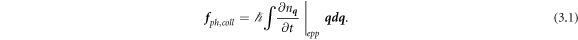
With electron flow directed along the longitudinal, or primary, z-axis the x-axis defines the transverse direction. The transverse force fph,x is the x-component of f ph,coll . This force is added in with all other contributions to the rate of change of phonon momentum density, ∂pph,x /∂t.
The phonon force is calculated from (2.3) and using an explicit nonequilibrium form of g k . The expression for fph,x is split into a sum fph,x = f1> + f1< + f2> + f2< + f3 + f4 such that
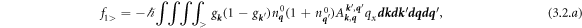
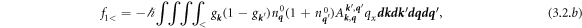




where it is explicit that equilibrium phonon distributions are used. The subscript > implies that only those processes with the virtual phonon
q
'' leaving the electron-phonon vertex W and entering the 3-phonon vertex Q are considered. The < denotes the opposite case. The  factors for f3 and f4 are included to avoid double-counting after considering the integration over both
q
and
factors for f3 and f4 are included to avoid double-counting after considering the integration over both
q
and 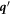 . The six terms are in the same order as in the corresponding diagrams of figure 1.
. The six terms are in the same order as in the corresponding diagrams of figure 1.
Utilizing a standard technique [8, 9] for offsetting with a drift velocity  , using the group velocity for electrons, ℏ
k
/m, one implements a drift or offset wave vector k0 = mv0/ℏ. Defining
, using the group velocity for electrons, ℏ
k
/m, one implements a drift or offset wave vector k0 = mv0/ℏ. Defining  , this offset is used to convert the equilibrium electron distribution
, this offset is used to convert the equilibrium electron distribution
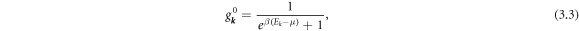
to a nonequilibrium form:
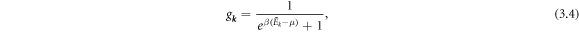
where β = 1/kB
T. Expanding in terms of small k0 gives:  . Defining, for convenience, b = β(Ek
− μ), γ1 = β
ℏ2
kz
k0/m and
. Defining, for convenience, b = β(Ek
− μ), γ1 = β
ℏ2
kz
k0/m and 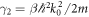 , such that
, such that ![${g}_{{\boldsymbol{k}}}={\left[{e}^{b}{e}^{({\gamma }_{2}-{\gamma }_{1})}+1\right]}^{-1}$](https://content.cld.iop.org/journals/2399-6528/5/9/095007/revision2/jpcoac2355ieqn27.gif) , allows for expansion up to second order in k0:
, allows for expansion up to second order in k0:

and
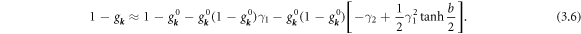
Note that 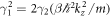 . With these results one shows that:
. With these results one shows that:
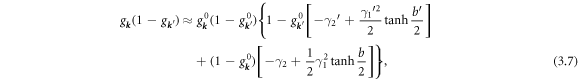
and
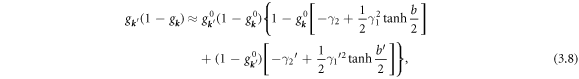
where terms linear and bilinear in kz
and  are dropped as these give zero when integrated.
are dropped as these give zero when integrated.
Details of this derivation are left for appendix A. The result for the lateral force per unit volume fph,x is

where  q'' is the energy of the virtual phonon, θ is the spherical polar angle for
k
, and
q'' is the energy of the virtual phonon, θ is the spherical polar angle for
k
, and  is the spherical polar angle for
is the spherical polar angle for  .
.
3.1. Dominant term for force
Since the main contribution to the
k
sums comes from electronic states near the Fermi level where 2Ek
− μ ≈ EF
, and the Fermi energy EF
always greatly exceeds  q'', the leading term in (3.9) comes from the
q'', the leading term in (3.9) comes from the ![${\epsilon }_{q^{\prime\prime} }\left[2{E}_{k}-\mu \right]{\cos }^{2}\theta ^{\prime} $](https://content.cld.iop.org/journals/2399-6528/5/9/095007/revision2/jpcoac2355ieqn32.gif) term. In the results below only this term is considered:
term. In the results below only this term is considered:
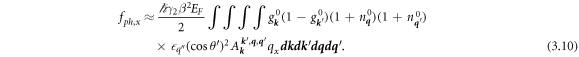
The third and fourth terms of (2.3) produce the major contributions to the phonon transverse force fph,x
. These main contributions occur because in the third and fourth terms  always holds. This is not the case in the first and second terms of (2.3) since in these processes the virtual phonons
q
'' can go both into and out of the W vertex. The plus sign in the front of (3.10) means that the third term in (2.3) represented by the scattering diagram in figure 1(e) is the dominant one. The physical interpretation of this is that the process emitting two phonons into the heat bath creates the most entropy and receives an extra statistical weight for this.
always holds. This is not the case in the first and second terms of (2.3) since in these processes the virtual phonons
q
'' can go both into and out of the W vertex. The plus sign in the front of (3.10) means that the third term in (2.3) represented by the scattering diagram in figure 1(e) is the dominant one. The physical interpretation of this is that the process emitting two phonons into the heat bath creates the most entropy and receives an extra statistical weight for this.
Bringing back the explicit integral over q '':
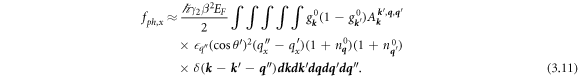
In the next subsection 3.2, spatial variation in the transverse direction is treated. Leading terms have an extra factor of  , producing a
, producing a 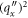 in the integrand and thus giving a non-zero result. A factor of
in the integrand and thus giving a non-zero result. A factor of  is also produced that gives zero upon integration. This allows the
is also produced that gives zero upon integration. This allows the  factor in (3.11) to be replaced by
factor in (3.11) to be replaced by  .
.
Substituting in for 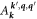 from (2.10) into (3.11), while also implementing (2.11), gives
from (2.10) into (3.11), while also implementing (2.11), gives
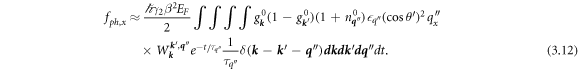
3.2. Spatial variation in the transition rate
The factor of qx
in (3.10) will make the integral zero by symmetry unless another qx
is produced. This can be accomplished if the transition rate  varies in the (transverse) x-direction. By (3.12) one way this can happen if the matrix element
varies in the (transverse) x-direction. By (3.12) one way this can happen if the matrix element 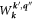 varies in the x-direction. This can also happen if occupation factors
varies in the x-direction. This can also happen if occupation factors  ,
,  ,
, 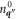 vary in the x-direction, and lastly, if τq'' varies in the x-direction.
vary in the x-direction, and lastly, if τq'' varies in the x-direction.
The two scattering vertices do not occur at the same time and place. The temporal separation is τq'' and the spatial separation is c
τq''. If
r
is the location of the midpoint of the electron-phonon collision and the 3-phonon collision then 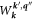 must be evaluated at
must be evaluated at  . So also must
. So also must 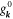 ,
,  , and
, and 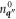 be evaluated at
be evaluated at 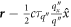 . In contrast, since the lifetime τq'' involves phonon-phonon scattering with vertex
. In contrast, since the lifetime τq'' involves phonon-phonon scattering with vertex  , it must be evaluated at position
, it must be evaluated at position 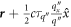 . Taking the first order expansion:
. Taking the first order expansion:

Completing the integral over t gives
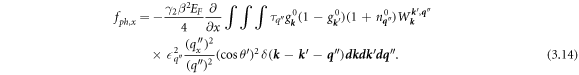
As mentioned, one way this force can be non-zero is if the matrix element 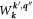 varies in the x-direction. The derivative
varies in the x-direction. The derivative  represents an explicit variation in the material composition in the x-direction. A simple example of this is an interface between two conventional metals, for example a gold-aluminum interface, either created by thin film growth in the x-direction or as a metallic superlattice [15]. In many models for electron-phonon interaction, using the deformation potential (including the Bardeen model), the square of the matrix element scales inversely with the lattice mass density [9, 13]. Near any of these interfaces one will find a sharp change in W in the direction perpendicular to the interface.
represents an explicit variation in the material composition in the x-direction. A simple example of this is an interface between two conventional metals, for example a gold-aluminum interface, either created by thin film growth in the x-direction or as a metallic superlattice [15]. In many models for electron-phonon interaction, using the deformation potential (including the Bardeen model), the square of the matrix element scales inversely with the lattice mass density [9, 13]. Near any of these interfaces one will find a sharp change in W in the direction perpendicular to the interface.
The following definition is made for an important time scale:
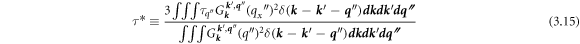
where 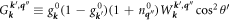 . The time τ* can be thought of as a nonequilibrium transport mean value of τq'' for a virtual phonon. The denominator in (3.15) closely resembles the Joule heating rate
J
el
·
E
which increases the phonon gas energy at rate
. The time τ* can be thought of as a nonequilibrium transport mean value of τq'' for a virtual phonon. The denominator in (3.15) closely resembles the Joule heating rate
J
el
·
E
which increases the phonon gas energy at rate  . Indeed, making use of (B.9) as derived in the appendix B allows (3.14) to be rewritten in a relatively concise form for the force per unit volume on the phonons as:
. Indeed, making use of (B.9) as derived in the appendix B allows (3.14) to be rewritten in a relatively concise form for the force per unit volume on the phonons as:

The force fph,x only exists while the electronic system is shifted away from equilibrium. In this case one may think of the phonons as being embedded in a nonequilibrium electronic system. This extra force term while being embedded will add onto any other force terms to dictate the phonon dynamics.
As expected from momentum conservation the transverse force on electrons is equal and opposite,
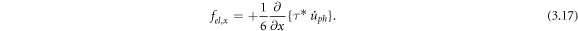
This force is not to be confused with the drag force in the 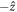 direction. The force fel,x
can also be explicitly derived by setting up equations similar to (3.2.a
)–(3.2.f
) while anticipating the
direction. The force fel,x
can also be explicitly derived by setting up equations similar to (3.2.a
)–(3.2.f
) while anticipating the  factor from the spatial variation, and following the minus signs carefully.
factor from the spatial variation, and following the minus signs carefully.
Together (3.16) and (3.17) constitute the main result presented here.
4. Heat transfer equation
The force in (3.16) can cause acceleration of the phonon field and change the phonon momentum. The phonon momentum density p ph is related to the heat flux vector λ by λ = c2 p ph . One term contributing to ∂ λ /∂t is represented by (3.16). This gives dynamics more complex than the Fourier heat law, λ = − κ∇T. Instead the Guyer-Krumhansl equation [11, 12, 16, 17] is invoked and the extra physics from (3.16) is added in to produce:
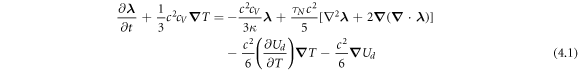
where cV is the volume specific heat, κ is the thermal conductivity, and the important quantity Ud is defined by

The first term on the right hand side of (4.1) comes from the thermal conduction, 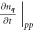 term, in (2.1). The main contributions to the thermal conductivity are umklapp processes with 3-phonon and 4-phonon collisions [9], whereas τN
is the relaxation time for normal processes. Given the approach described above, it is understood that
λ
has no component in the z-direction and the x and y components do not depend on z, i.e. (4.1) is effectively two-dimensional.
term, in (2.1). The main contributions to the thermal conductivity are umklapp processes with 3-phonon and 4-phonon collisions [9], whereas τN
is the relaxation time for normal processes. Given the approach described above, it is understood that
λ
has no component in the z-direction and the x and y components do not depend on z, i.e. (4.1) is effectively two-dimensional.
The quantity Ud has dimensions of an energy density but does not have its origins as a conventional energy does in physics. Indeed it can only be defined as the product of a time and a power (density). Since it arises from irreversible dissipation the term dissipation potential energy density might be apt for Ud . This potential energy density differs from the Rayleigh dissipation function which is implemented differently by taking a derivative with respect to velocity to produce a force [18].
It is important to point out that Ud may vary spatially because the temperature does, or explicitly when for example, the material properties change in the directions perpendicular to z. For example, for a uniform applied electric field, it could be the electrical conductivity that varies in the x and/or y directions and this would contribute to the last term in (4.1). This distinction is important since the ∂Ud /∂T term is dissipative whereas the ∇ Ud term contributes to reversible kinematics. The ∇ Ud term can induce phonons to flow even when there is no temperature gradient.
Taking the divergence of both sides of (4.1), while noting that ∇ · λ = − cV ∂T/∂t gives

where
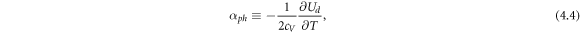
is a dimensionless parameter describing the temperature dependence of Ud . The partial differential equation (4.3) resembles the telegraph equation with an external driving function from the explicit variation of Ud . When Ud is expressed as τ* σel E2, one can readily see that αph is positive for materials for which the electrical conductivity σel decreases with increasing temperature, since the phonon lifetime is also expected to show the same trend. This should include all metals, while for the case of semiconductors having σel increasing with temperature, there is the possibility of negative αph . Defining the dimensionless number
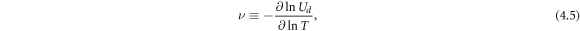
gives the following convenient form for αph :

4.1. Case with symmetry previously broken
The stationary state solution for (4.3) is readily found when Ud explicitly depends on transverse coordinates. In this case the solution is
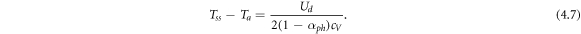
The result is a non-flat temperature profile superimposed on top of an otherwise uniform ambient temperature. Joule heating will raise the ambient temperature but in practice, effective external cooling can keep Ta close to what ambient is when there is no electrical flow. The profile exists even when αph = 0. In this case the profile is driven completely by any explicit spatial variation in Ud . The temperature profile becomes flat when the electrical current is turned off and Ud = 0. This profile is entirely a nonequilibrium effect and the effect will be small with the system near equilibrium. A trickle of current will not suffice; Rather, the system will likely have to pushed quite hard before the profile becomes detectable. For example, if an amount of energy equal to about 1% of the internal thermal energy is dissipated in what is typically a short time τ*, then a profile amplitude of about 1% of ambient could be observed. Thin samples with good heat-sinking would avoid excessive temperature rise from Joule heating and allow the opportunity for such profiles to be observed. Indeed, dissipated power levels need not be so high if ambient temperature is well below the Debye temperature where cV is small.
A good example system is an alternating ABAB electrically conductive superlattice with the A layers having larger ud than the B layers. Electrical current running along the conducting layers will produce the temperature and charge profiles. The A layers will be warmer than the B layers and as will be shown below, electrons will tend to be pushed into the B layers. An applied bias to this superlattice results in the same electric field E in each layer. Reexpressing (4.7) explicitly in terms of E gives

where it is understood that σel , cV , and αph have a spatial dependence, changing sharply at each AB interface.
In order to make specific calculations and predictions for the induced temperature profile a good estimate for the phonon lifetime τ* is required. The simplest approach is to use the lattice thermal conductivity expression  , which changes (4.8) to
, which changes (4.8) to
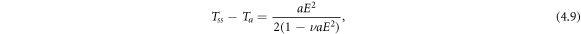
where
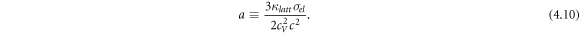
A good electrical conductor like silver would have a relatively large value for a and be more likely to give measurable values of Tss − Ta . The lattice thermal conductivity for conductors such as Ag can be calculated from first principles [19, 20]. At room temperature (RT) the value is κlatt = 5.2 W/mK and at 77 K the value is 12 W/mK. Making use of well-known values for the electrical conductivity, specific heat capacity and speed of sound, [8] allows for easy calculation of the parameter a and subsequent calculation of the curves shown in figure 2. If the AB superlattice consists of Ag and a relatively poor electrical conductor such as Bi, the result is square wave temperature profile with amplitude TAg − TBi . The RT plot in figure 2 (solid black curve) shows an upwards trend with TAg − TBi going as E2. Any effects from the (1 − ν aE2) factor in the denominator of (4.9) are not seen. A reasonable value for the minimum discernible temperature shift is 1 mK. For such a shift to be produced a 12.2 kV/m field would be required at RT. This is not easily achieved in practice as this temperature profile would be superimposed on top of significant Joule heating that would be difficult to heat sink, even for very thin, planar samples.
Figure 2. Calculated temperature profile amplitude for a Ag-Bi superlattice as a function of applied electric field. The field is applied in any direction parallel to the layers. These calculations were carried out for two temperatures: 295 K (solid black curve) and 77 K (dashed blue curve).
Download figure:
Standard image High-resolution imageMoving to lower temperature does make the task easier as indicated by the 77 K curve (dashed blue). For most of the range of electric fields shown the trend is similar to RT but with larger values of TAg − TBi . At fields above 2 × 105 V/m, the curve bends upwards because of the (1 − ν aE2) factor. A value of ν = 3 is used since σel goes approximately as T−1 and τ* is expected to go as T−2. At 77 K, the minimal discernible temperature of 1 mK is predicted to occur at a field of 2.1 kV/m. This is about 6 times less than at RT. Though these calculations indicate that detection of this temperature profile would not be easy, there does not seem to be any fundamental reason ruling out this detection. To date no electrical transport measurements have shown the effect predicted here. These preliminary investigations suggest that such a predicted temperature profile would be more easily detected at lower temperatures.
It may also be worthwhile for researchers to investigate other dissipative systems as well. The form of (3.16) suggests that any system in which the dissipated energy has a spatial gradient will result in forces on some particles, with the forces on the phonons to ensure momentum conservation. It may be the case that in such systems these forces are more readily detected. Examples of such systems include chemical reactions (reaction-diffusion dynamics) and front propagation (with dynamics) during phase transitions.
4.2. Case with spontaneous symmetry breaking
In the case where there is no explicit spatial dependence for Ud the material properties would be assumed to be uniform and (4.3) becomes
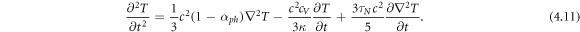
When the system is pushed very hard with high rates of dissipation such that at αph
≥ 1, (4.11) becomes unstable; There is a bifurcation, a solution would grow very quickly and would diverge if the system is strictly linear. Taking a spatial Fourier transform of ΔT to 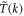 , and subsequently adding in an appropriate nonlinear term gives
, and subsequently adding in an appropriate nonlinear term gives
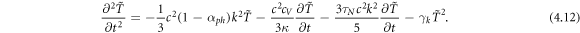
Adding the nonlinear term ensures a finite stationary solution of  , valid when αph
> 1. Nonlinear terms like
, valid when αph
> 1. Nonlinear terms like  can arise when the coefficient of thermal conductivity depends on temperature [21]. The details of these nonlinear terms, in particular how they depend on wavevector
k
, determine which wavelengths are the most prominent. It is possible that this stationary state solution is not spatially uniform, and would therefore constitute spontaneous symmetry breaking.
can arise when the coefficient of thermal conductivity depends on temperature [21]. The details of these nonlinear terms, in particular how they depend on wavevector
k
, determine which wavelengths are the most prominent. It is possible that this stationary state solution is not spatially uniform, and would therefore constitute spontaneous symmetry breaking.
The partial differential equation (4.12) bears some similarity to the Kuramoto-Sivashinsky (KS) equation, an important analysis tool used in the study of nonequilibrium systems that has been successfully utilized to model patterns formed in laminar flame fronts, certain types of Poiseuille flow, trapped ion modes in plasmas, and systems with Eckhaus instabilities such as Rayleigh-Bénard convection [4–6, 22–25]. Modeling with the KS equation can produce instabilities and interesting pattern formation when the diffusion coefficient is made negative. Though the KS equation has been used widely as a model, clear explanations are lacking in the literature for why a diffusion coefficient can be negative. The analysis presented here shows how a first principles approach can produce an effectively negative diffusion coefficient.
Observation of such an instability and/or pattern formation would likely require very high electrical current along the principal z-axis direction. Bringing the system near αph = 1 may dissipate so much energy such as to push the system near the point of irreparable damage, perhaps from melting, vaporization, or oxidation. Indeed, it may be the case that just before this threshold there is considerable channeling at short length scales with the higher temperature channels getting dangerously close to melting or vaporizing. This temperature channeling may be what happens just as the proverbial fuse blows. The above-mentioned positive feedback between channels may make it even more difficult to avoid blowing the fuse.
5. Electron dynamics and comparison
The electron gas motion (transverse to the drift velocity 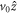 ) may be described by a mean velocity
v
and the momentum density
p
el
is related to the flux vector
j
by
j
=
p
el
/m. The force in (3.17) gives a term contributing to ∂
j
/∂t which otherwise is a simple equation taking into account the gradient in the electron chemical potential μ and ohmic drag. The modified dynamical equation is
) may be described by a mean velocity
v
and the momentum density
p
el
is related to the flux vector
j
by
j
=
p
el
/m. The force in (3.17) gives a term contributing to ∂
j
/∂t which otherwise is a simple equation taking into account the gradient in the electron chemical potential μ and ohmic drag. The modified dynamical equation is
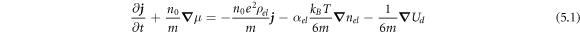
where nel is the electron number density with equilibrium value n0, ρel is the electrical resistivity, and

Again, the spatial variation of Ud is split into a purely dissipative part with the αel term because the dissipated energy depends on electron density, as well as the the direct spatial dependence giving the last (reversible) term in (5.1).
Taking the divergence of both sides of (5.1), and noting that ∇ · j = − ∂nel /∂t, gives
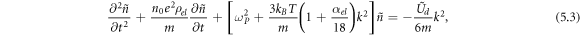
after the spatial Fourier transform to  and
and 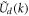 . The result is a modification of a plasma wave equation suitable for describing Langmuir waves, with the Bohm-Gross dispersion relation:
. The result is a modification of a plasma wave equation suitable for describing Langmuir waves, with the Bohm-Gross dispersion relation:

The stationary state solution is
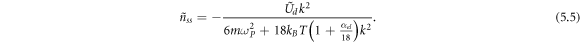
Unless αel is particularly large, the dependence of Ud on nel plays a minor role here. Also the general positive characteristic of αel means that any spontaneous symmetry breaking will not come directly from the electrons.
5.1. Comparison to phonon results
Comparing (4.7) to (5.5) for stationary states shows that the temperature profile is anticorrelated to the electron density profile. The occurs as the direct result of the opposing nature of the phonon and electron forces. This anticorrelation is stronger for electrons at shorter length scales, since the charge profile falls off at large length scales.
The interplay between phonon and electron displacements can be better understood in the case where a system that is initially uniform spatially, has enough electrical current applied such that the bifurcation point αph = 1 has been reached. The instability is expected to make some regions hotter than others. By the definition of αph this means that the relatively cooler regions will experience an increase in Ud , thus making Ud no longer uniform. This means that for the expected positive αel the cooler regions will receive extra electrons. Not only is a non-flat charge profile created spontaneously, but the direction of the electronic relaxation is such as to increase Ud even more. This positive feedback for electrons works in concert with that of the phonons to increase and amplify any spatially non-uniform features in Ud .
5.2. Impact on general nonequilibrium approaches
This has interesting implications on research approaches that have been developed for the general treatment of nonequilibrium systems. One such approach is GENERIC (general equation for the nonequilibrium reversible-irreversible coupling), in which the dynamical equations for dissipative fluids is described by two distinct terms, one for reversible Poisson kinematics and one for dissipative Ginzburg-Landau kinematics [26–28]. Produced here is are dissipative terms which might be expected, except that they are forces perpendicular to the principle axis of conduction of the main variable. The dissipation potential energy density Ud may be closely related to the dissipative potential function Ψ, used in the GENERIC scheme.
The function Ud cannot be the same as Ψ because also produced here, and perhaps not as expected, are conservative terms that fit in perfectly well into the Poisson kinematics, and having dissipation as their fundamental source. More precisely, it is pure dissipation in the one principle direction that produces reversible terms in the Hamiltonian that are perpendicular to that direction. Thus the same function Ud winds up contributing to both sides, reversible and irreversible, of the GENERIC formalism.
What has happened is that the z and x directions have become coupled when double vertex scattering has been taken into account. The result of the perpendicular conservative forces is quite surprising.
6. Conclusions
In summary, the theoretical approach presented here predicts the existence of forces, equal and opposite, on electrons and phonons, perpendicular to the primary flow direction of electrons. The force terms include both conservative and dissipative components. The conservative components exist only when there exist explicit transverse gradients in the dissipated energy. The dissipative force terms can cause spontaneous symmetry breaking when the dissipation exceeds a threshold. It is hoped that these results represent a step towards establishing a clear link between fundamental scattering physics and the study of pattern formation in nonequilibrium systems.
Acknowledgments
I thank Cathy J Meyer for her assistance in editing the manuscript.
Data availability statement
The data that support the findings of this study are available upon reasonable request from the authors.
Appendix A.:
Here the six force terms (3.2.a )-(3.2.f ) are explicitly evaluated when the electronic system is away from equilibrium.
A.1. Evaluation of f1> + f2> + f1< + f2<
Since states near the Fermi level are expected to make the most significant contributions to these integrals, one can assume b and  are small and one arrives at the method for replacing nonequlibrium electron occupancies g
k
and g
k
with equlibrium functions:
are small and one arrives at the method for replacing nonequlibrium electron occupancies g
k
and g
k
with equlibrium functions:
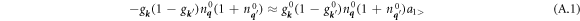
with
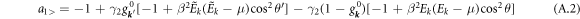
noting that 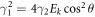 . Thus
. Thus

For a1< one simply replaces  q'' with −
q'' with −  q''. Proceeding similarly for the evaluation of f2>, while using the principle of detailed balance [9] in the form:
q''. Proceeding similarly for the evaluation of f2>, while using the principle of detailed balance [9] in the form:
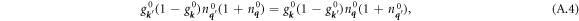
gives

with
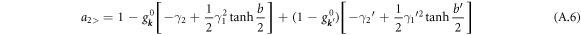
Next, accounting for the phonon energy  q'':
q'':

This is used with some algebra to give:
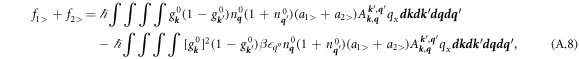
where the arrows on the integrals are now dropped. With some more algebra the first four force terms add to:

A.2. Evaluation of f3 + f4
A.3. f1> + f2> + f1< + f2< + f3 + f4
Appendix B.:
Here only first order electron-phonon scattering is considered, with electron wavevectors
k
and 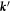 and phonon wavevector
q
'' that is either emitted or absorbed:
and phonon wavevector
q
'' that is either emitted or absorbed:
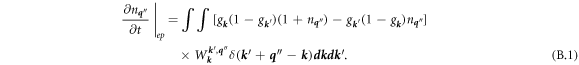
The rates ∂nph /∂t for phonon density increasing with time, and ∂uph /∂t for phonon energy density increasing with time, are then readily obtained:
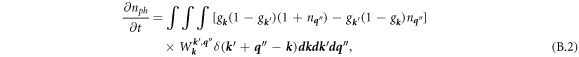
and
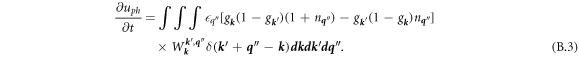
Making use of (3.7) and (3.8), the principle of detailed balance, while taking the Bloch assumption [9]  gives
gives

Next note that
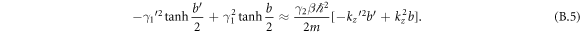
So

or

Using  gives
gives

This resembles the second term of the phonon x-force. Expecting the major contribution to the integral to come from states near Ek ≈ μ ≈ EF gives