Abstract
Weyl nodes are band degeneracy points with relativistic dispersion and topological properties arising in certain three-dimensional periodic systems with broken parity-time symmetry. Despite their fundamental importance, the intrinsic accidental nature of Weyl nodes makes the general endeavor of finding them a challenging task. In this work, we show how Weyl nodes can be generated in cubic crystal structures with a single orbital per site based on a systematic approach that combines a tight-binding analysis with general principles which can be applied to both fermionic and bosonic systems. The cubic Weyl systems generated here preserve time-reversal symmetry but break inversion symmetry hosting the minimum four Weyl points allowed. Laser assisted hopping techniques on cubic optical lattices can allow the artificial generation of such Weyl semimetals. Magnetic oscillation experiments can be used to probe the Weyl orbits along the Fermi arcs on opposite sides of the sample connected through the bulk Weyl nodes.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Weyl fermions—predicted around 90 years ago by H. Weyl [1]—are a fundamental building block of the standard model displaying their characteristic chiralities above the extremely high temperatures, T > 1016 K, reached at the early stages of the Universe after the Big Bang when the 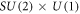 symmetry of the electroweak interaction was present. Despite their relevance, Weyl fermions have not yet been observed as individual particles in high-energy physics experiments. However, Weyl quasiparticles and the chiral anomaly have been found to be relevant to 3He-A superfluids [2], whose fermionic quasiparticle energy spectrum has point nodes, and more recently to solid-state systems. These provide a number of versatile platforms to observe and study Weyl physics, based on both fermionic [3, 4] and bosonic [5] systems. In the case of Weyl semimetals, despite the non-relativistic velocities of electrons, the crystal lattice potential leads to linear dispersions at the so-called Weyl points [6]. The associated non-trivial topological properties of Weyl semimetals have led to a variety of unusual physical phenomena such as the Adler-Bell-Jackiw chiral anomaly on a lattice [7–10] and the anomalous quantum Hall effect [11–13]. Similarly, artificially created bosonic platforms, such as nanophotonic systems [14–29] and cold atoms in optical lattices [30–33], can be tailored to host Weyl excitations and display unique phenomena such as robust photonic surface states, tunable axial gauge fields or long-range interactions between quantum emitters. Remarkably, fermionic and bosonic Weyl systems can often be described with a common physical picture, which has lead to a significant cross-fertilization between the two areas. A paradigmatic example of this common physical description are the characteristic Fermi arcs [3, 34–36]connecting the projection of Weyl points at the surfaces of both fermionic and bosonic Weyl systems, which reflect the topological origin of the corresponding surface bands.
symmetry of the electroweak interaction was present. Despite their relevance, Weyl fermions have not yet been observed as individual particles in high-energy physics experiments. However, Weyl quasiparticles and the chiral anomaly have been found to be relevant to 3He-A superfluids [2], whose fermionic quasiparticle energy spectrum has point nodes, and more recently to solid-state systems. These provide a number of versatile platforms to observe and study Weyl physics, based on both fermionic [3, 4] and bosonic [5] systems. In the case of Weyl semimetals, despite the non-relativistic velocities of electrons, the crystal lattice potential leads to linear dispersions at the so-called Weyl points [6]. The associated non-trivial topological properties of Weyl semimetals have led to a variety of unusual physical phenomena such as the Adler-Bell-Jackiw chiral anomaly on a lattice [7–10] and the anomalous quantum Hall effect [11–13]. Similarly, artificially created bosonic platforms, such as nanophotonic systems [14–29] and cold atoms in optical lattices [30–33], can be tailored to host Weyl excitations and display unique phenomena such as robust photonic surface states, tunable axial gauge fields or long-range interactions between quantum emitters. Remarkably, fermionic and bosonic Weyl systems can often be described with a common physical picture, which has lead to a significant cross-fertilization between the two areas. A paradigmatic example of this common physical description are the characteristic Fermi arcs [3, 34–36]connecting the projection of Weyl points at the surfaces of both fermionic and bosonic Weyl systems, which reflect the topological origin of the corresponding surface bands.
Although symmetry conditions for finding band touching points in solids have been studied thoroughly [37, 38], these studies have focused on band touchings at high symmetry points in the Brillouin Zone (BZ) i.e. symmetry enforced energy level degeneracies, rather than the special accidental degeneracies [39] we are interested here which typically lead to Weyl nodes in the complex band structure [36] of certain materials. The uncertainity of finding accidental band touching points implies a cumbersome search to identify materials in which such Weyl nodes could be realized. The alternative route we take here is the generation of Weyl nodes in artificially designed cubic crystal structures with desired properties. In this work, we show that Weyl nodes can be generated in three-dimensional (3D) cubic crystal structures by following a systematic approach which can be applied to both fermionic and bosonic systems. The proposed approach is based on the following two-step strategy: (i) First, a non-trivial in-plane nearest-neighbor (n.n.) hopping pattern is artificially tailored in certain 2D planes of the cubic crystal, respecting both parity (P) and time-reversal (T) symmetries which leads to Dirac nodes. (ii) Second, non-trivial next-nearest-neighbor (n.n.n.) hoppings are introduced which break parity (P) and induce the Weyl nodes. Our hopping construction is intended to produce the necessary accidental two-level degeneracies at certain k-points in the BZ zone so that Weyl fermions can emerge. Our work provides tight-binding hamiltonians which lead to Weyl points in cubic crystal structures. The actual form of these hamiltonians would be difficult to guess solely based on a symmetry group analysis.
Dirac [40, 41] and Weyl nodes [14, 30–32, 42] have been found in simple cubic lattices, AA-stacked honeycomb layers [43], and face-centered cubic (FCC) lattices [19], assuming that hoppings beyond n.n. sites can be neglected. In most of these constructions, Weyl nodes are generated by artificially imprinting phases on the original tight-binding hopping amplitudes: 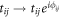 , leading to either broken T-symmetry [19, 31, 32, 42, 43] or broken P-symmetry [30] of the original lattice depending on the actual phases, ϕij, implemented. Cold atoms in optical lattices under shaking or laser assisted tunneling are proposed as ideal platforms to generate and analyze such Weyl points.
, leading to either broken T-symmetry [19, 31, 32, 42, 43] or broken P-symmetry [30] of the original lattice depending on the actual phases, ϕij, implemented. Cold atoms in optical lattices under shaking or laser assisted tunneling are proposed as ideal platforms to generate and analyze such Weyl points.
Dirac particles in simple cubic lattices [42] and Weyl points in T-symmetry broken FCC lattices have been also generated by applying tilted magnetic fields (real or synthetic) [44]. Weyl points occur in a model for BCC iron in which T-symmetry [45, 46] is broken. Our procedure is similar in spirit to previous proposals in which Weyl points have been generated from stacking 2D Chern insulators [43], 2D FCC lattices [31], 2D square lattices with Dirac cones or 1D chains with non-trivial topology [44]. The common denominator of these approaches is to first construct lower dimensional building blocks with topological properties which are then coupled through non-trivial hoppings which break either P or T symmetries. Our approach tries to channel these efforts into a unified framework which consists on singling out 2D building blocks of the original cubic lattice structure in which topological properties are artificially induced and couple them through non-trivial hoppings which generate 3D Weyl systems. Hence, our work tries to provide a generalization of previous approaches which is exemplified in the generation of a BCC Weyl semimetal with broken P-symmetry.
To illustrate the general character and relevance of the proposed approach, we apply it to a BCC lattice to show that it is possible to generate a T-symmetric BCC Weyl system featuring four Weyl points (the minimum number imposed by time reversal symmetry), as well as the intricate Fermi arcs connecting the projection of the Weyl points on different crystal faces. Our analysis also shows that the obtained Weyl system occurs as an intermediate state between a band insulator and a three-dimensional topological insulator. Finally, we discuss a possible experimental implementation of the proposed BCC Weyl system with cold atoms in an optical lattice using laser-assisted tunneling.
2. Generating Weyl nodes in cubic lattices
Our main aim is to generate Weyl nodes in a cubic crystal structure. We assume that the cubic crystal structure is adequately described by a tight-binding model with a single localized orbital per site. In principle, such tight-binding model not only includes n.n but also n.n.n hoppings extending the simple cubic lattice structure considered previously [30]. We would like to imprint a hopping pattern in the model which can lead to Weyl nodes in the band structure of the system. Hence, we assume that our unmodified crystal structure can be adequately described by a tight-binding Hamiltonian on a cubic crystal lattice [47, 48]:

where  are pairs of nearest-neighbor (n.n.) lattice sites whereas
are pairs of nearest-neighbor (n.n.) lattice sites whereas 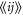 are pairs of next-nearest-neighbor (n.n.n.) sites. The Hamiltonian H0 can be used to model either a naturally-occurring non-interacting electronic material system featuring a single-s orbital per site (such an alkali metal), or an artificially created bosonic lattice (such a photonic crystal or cold atoms in an optical lattice, with a single bosonic mode per site). The operator
are pairs of next-nearest-neighbor (n.n.n.) sites. The Hamiltonian H0 can be used to model either a naturally-occurring non-interacting electronic material system featuring a single-s orbital per site (such an alkali metal), or an artificially created bosonic lattice (such a photonic crystal or cold atoms in an optical lattice, with a single bosonic mode per site). The operator  (ci) represents the corresponding fermionic or bosonic creation (anihilation) operator associated to the i-th site of the lattice (satisfying the corresponding commutation and anticommutation relations, respectively).
(ci) represents the corresponding fermionic or bosonic creation (anihilation) operator associated to the i-th site of the lattice (satisfying the corresponding commutation and anticommutation relations, respectively).
Since the hoppings are considered to be real and the crystal respects inversion symmetry, H0 respects PT symmetry. We consider modifications of the original hopping amplitudes from:  to
to  i. e. which only involve
i. e. which only involve  (mod 2π) hopping phases, that can be achieved by using laser assisted hopping techniques on optical lattices (see section 5). Since the modified hoppings are real, the final modified hamiltonian, H, will preserve T-symmetry but the modified hopping pattern will be chosen to break P-symmetry allowing for a Weyl system to emerge. Hence, the approach presented here differs somewhat from previous proposals such as the FCC Weyl system with T-breaking [44–46] but is similar in spirit to the approach performed in the simple cubic lattice [30] although the construction was restricted to n.n. hopping amplitudes only. In the present work we generalize this idea to any cubic lattice (SC, BCC, FCC) described by n.n. and n.n.n. hopping amplitudes going beyond approaches which consider n.n. hopping amplitudes only.
(mod 2π) hopping phases, that can be achieved by using laser assisted hopping techniques on optical lattices (see section 5). Since the modified hoppings are real, the final modified hamiltonian, H, will preserve T-symmetry but the modified hopping pattern will be chosen to break P-symmetry allowing for a Weyl system to emerge. Hence, the approach presented here differs somewhat from previous proposals such as the FCC Weyl system with T-breaking [44–46] but is similar in spirit to the approach performed in the simple cubic lattice [30] although the construction was restricted to n.n. hopping amplitudes only. In the present work we generalize this idea to any cubic lattice (SC, BCC, FCC) described by n.n. and n.n.n. hopping amplitudes going beyond approaches which consider n.n. hopping amplitudes only.
We note that the generation of the cubic lattice Weyl semimetals proposed here implies imprinting a desired hopping pattern with specially selected hopping signs. This seems in general very difficult to achieve in solid state materials through the application of anisotropic strain/elongations to the material. Although straightforward external irradiation can, in principle, be used to modify hoppings, the complex network of hopping signs in figure 1(a) implies a rather complicated laser setup which seems difficult to achieve in practice. However, laser assisted tunneling techniques can allow imprinting the desired hopping patterns in artificially generated cubic optical lattices as discussed in section 5. The laser setup and tilting potentials needed to generate the hopping pattern of figure 1(a) in a BCC lattice is summarized in table 2.
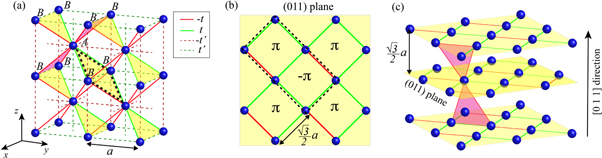
Figure 1. The crystal structure and modified hoppings leading to our T-invariant Weyl system on a BCC lattice. Both the nearest-neighbor hoppings (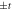 , solid lines), and next-nearest neighbor hoppings (
, solid lines), and next-nearest neighbor hoppings ( dashed lines) are shown. Red and green lines correspond to negative and positive hoppings, respectively. Four unit cells of the lattice are displayed for illustration. The top-left unit cell indicates the sites belonging to each of the sublattices characterizing the system (sublattices A and B). Thick black and gray dashed lines in the center and bottom-right of the panel correspond to instances of elementary plaquetes connecting nearest-neighbour and next-nearest-neighbour sites, respectively. (b) Elementary placquettes and corresponding flux-per-plaquette along the (0 1 1) plane of the lattice (marked in yellow (a)). The dashed rectangle marks the in-plane unit cell. (c) Sketch of the stacking of (0 1 1) planes forming the considered BCC structure. The pink-shadowed plaquettes correspond to the same color ones included in (a). For clarity, panels (b) and (c) only include nearest neighbor hoppings, and panel (c) only includes the lines associated to the interlayer hopping of one of the sites. Miller's indices convention has been used for labeling planes and directions.
dashed lines) are shown. Red and green lines correspond to negative and positive hoppings, respectively. Four unit cells of the lattice are displayed for illustration. The top-left unit cell indicates the sites belonging to each of the sublattices characterizing the system (sublattices A and B). Thick black and gray dashed lines in the center and bottom-right of the panel correspond to instances of elementary plaquetes connecting nearest-neighbour and next-nearest-neighbour sites, respectively. (b) Elementary placquettes and corresponding flux-per-plaquette along the (0 1 1) plane of the lattice (marked in yellow (a)). The dashed rectangle marks the in-plane unit cell. (c) Sketch of the stacking of (0 1 1) planes forming the considered BCC structure. The pink-shadowed plaquettes correspond to the same color ones included in (a). For clarity, panels (b) and (c) only include nearest neighbor hoppings, and panel (c) only includes the lines associated to the interlayer hopping of one of the sites. Miller's indices convention has been used for labeling planes and directions.
Download figure:
Standard image High-resolution imageTable 2. Characteristics of the different pairs of Raman lasers used in our approach.
| Lattice direction |
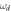
|
 (in units of (in units of  ) ) |
|---|---|---|
![$[1,0,0]$](https://content.cld.iop.org/journals/2399-6528/4/6/065006/revision2/jpcoab983cieqn14.gif)
|

|

|
![$[0,1,0]$](https://content.cld.iop.org/journals/2399-6528/4/6/065006/revision2/jpcoab983cieqn17.gif)
|

|

|
![$[0,0,1]$](https://content.cld.iop.org/journals/2399-6528/4/6/065006/revision2/jpcoab983cieqn20.gif)
|
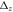
|
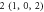
|
![$[1,-1,1]$](https://content.cld.iop.org/journals/2399-6528/4/6/065006/revision2/jpcoab983cieqn23.gif)
|

|

|
![$[-1,-1,1]$](https://content.cld.iop.org/journals/2399-6528/4/6/065006/revision2/jpcoab983cieqn26.gif)
|

|

|
![$[-1,1,1]$](https://content.cld.iop.org/journals/2399-6528/4/6/065006/revision2/jpcoab983cieqn29.gif)
|

|

|
![$[1,1,1]$](https://content.cld.iop.org/journals/2399-6528/4/6/065006/revision2/jpcoab983cieqn32.gif)
|

|

|
2.1. BCC lattice
To illustrate our systematic approach we now explain how to convert the original BCC lattice with say a single s-orbitals per site (so all the hoppings would have the same sign in the unmodified lattice) into a Weyl semimetal. Although our approach is not restricted to a particular lattice geometry, for definiteness, and due to its ubiquity in both electronic and bosonic platforms, we focus on the case of a BCC lattice (of lattice constant a, see figure 1(a)). It can be shown that in the case of a BCC lattice, the Bloch Hamiltonian associated to H0 produces a smooth single band with quadratic band edges. In the following, we show how that Hamiltonian can be systematically modified using a two-step strategy that allows transforming the original single band structure into a two-band structure with Weyl node degeneracies. In step (i) of our approach, we first inspect the original BCC crystal structure and realize that the set of (011) planes (marked in yellow in figures 1(a)–(c)) feature an in-plane n.n. hopping pattern that can be tailored to induce in-plane Dirac nodes. As seen in figure 1, each of these planes comprises a periodic lattice of square-shaped elementary plaquettes of side 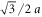 (see figure 1(a)). The in-plane hopping pattern shown in figure 1(b), introduces two different sublattices in the structure (sublattices A and B, see figure 1(a)) allowing for the presence of two bands in the system. On the other hand, the fact that the 2D lattice features a unit cell formed by two plaquettes (dashed line in figure 1(b)), with a flux-per-plaquette of π and −π, enables a Dirac point degeneracy between these two bands—note that this hopping pattern preserves parity and time reversal (PT) symmetry of the lattice. Explicitly, the Hamiltonian of the n.n. modified hopping pattern of the BCC crystal structure of figure 1(a) (neglecting by now n.n.n. hoppings) reads:
(see figure 1(a)). The in-plane hopping pattern shown in figure 1(b), introduces two different sublattices in the structure (sublattices A and B, see figure 1(a)) allowing for the presence of two bands in the system. On the other hand, the fact that the 2D lattice features a unit cell formed by two plaquettes (dashed line in figure 1(b)), with a flux-per-plaquette of π and −π, enables a Dirac point degeneracy between these two bands—note that this hopping pattern preserves parity and time reversal (PT) symmetry of the lattice. Explicitly, the Hamiltonian of the n.n. modified hopping pattern of the BCC crystal structure of figure 1(a) (neglecting by now n.n.n. hoppings) reads:
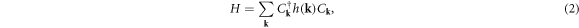
where: 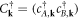 and with the n.n. Bloch hamiltonian:
and with the n.n. Bloch hamiltonian:

with 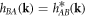 , where the relative positions between the n. n. sites read:
, where the relative positions between the n. n. sites read:  ,
, 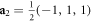 ,
,  , and
, and  . This hamiltonian can be re-expressed in terms of the Pauli matrices describing the pseudospin associated with the two inequivalent sites arising from the modified n.n. hopping pattern as:
. This hamiltonian can be re-expressed in terms of the Pauli matrices describing the pseudospin associated with the two inequivalent sites arising from the modified n.n. hopping pattern as:  , with:
, with: 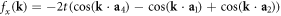 ,
, 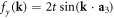 . The resulting dispersions:
. The resulting dispersions:  touch at four 3D Dirac points.
touch at four 3D Dirac points.
Thus, step (ii) adds a term proportional to σz to h(k) of equation (3):
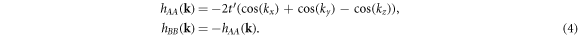
leading to the hamiltomnian:
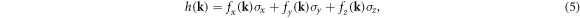
where:  , leading to the final band dispersions:
, leading to the final band dispersions: 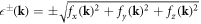 , plotted in figure 3, which touch at four Weyl points in the 3D momentum space. The two bands are non-degenerate since PT is not respected anymore due to breaking P-symmetry [49] but can still have accidental degeneracies [39] since:
, plotted in figure 3, which touch at four Weyl points in the 3D momentum space. The two bands are non-degenerate since PT is not respected anymore due to breaking P-symmetry [49] but can still have accidental degeneracies [39] since: 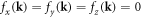 can be simultaneously satisfied in three dimensions [6]. This actually occurs in our BCC semimetal at the Weyl points given in table 1. Note that we have intentionally constructed the modified Hamiltonian (equation (5)) on a BCC lattice that preserves T-symmetry (
can be simultaneously satisfied in three dimensions [6]. This actually occurs in our BCC semimetal at the Weyl points given in table 1. Note that we have intentionally constructed the modified Hamiltonian (equation (5)) on a BCC lattice that preserves T-symmetry (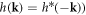 , but breaks spatial inversion symmetry (P) (
, but breaks spatial inversion symmetry (P) ( ). Hence, it is an example of a P-breaking Weyl semimetal [35, 49–51] in a BCC lattice which is in contrast to T-breaking BCC Weyl semimetals discussed previously [45, 46]. Regarding point group symmetries, although our BCC Weyl structure does not peserve the Oh point group symmetry of the cubic crystal structure, we find that the Bloch hamiltonian is invariant under reflection in the [011] direction (
). Hence, it is an example of a P-breaking Weyl semimetal [35, 49–51] in a BCC lattice which is in contrast to T-breaking BCC Weyl semimetals discussed previously [45, 46]. Regarding point group symmetries, although our BCC Weyl structure does not peserve the Oh point group symmetry of the cubic crystal structure, we find that the Bloch hamiltonian is invariant under reflection in the [011] direction ( ). Hence, our BCC Weyl system is a T-symmetry topological crystalline semimetal [52, 53] protected by the mirror (M) symmetry discussed.
). Hence, our BCC Weyl system is a T-symmetry topological crystalline semimetal [52, 53] protected by the mirror (M) symmetry discussed.
Table 1.
Weyl points generated in cubic crystal lattices based on our proposal. The position of the Weyl points in k-space ( ) and their chirality (χ) is independent of
) and their chirality (χ) is independent of  . Note that the chiralities of the Weyl points are related by T-symmetry retaining their chirality when
. Note that the chiralities of the Weyl points are related by T-symmetry retaining their chirality when  .
.
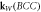
|

|

|
χ |
|---|---|---|---|
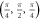
|
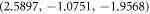
|
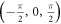
|
+ |
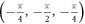
|

|
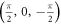
|
+ |
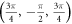
|
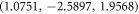
|
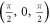
|
− |

|
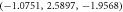
|

|
− |
2.2. FCC lattice
We now describe the generation of a FCC Weyl semimetal by first modifying the n.n. hopping network of the (100), (010) and (001) planes of the unmodified FCC crystal structure in the same way as we did for the (011) planes in the BCC lattice. The n.n. Bloch hamiltonian would read:
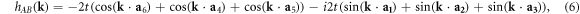
where the relative positions between n.n. sites are: 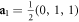 ,
, 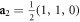 ,
, 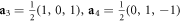 ,
, 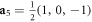 and
and 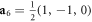 . This hamiltonian respecting PT-symmetry leads to 3D Dirac points. In order to obtain Weyl points we introduce the n.n.n. hopping amplitudes defined in equation (4). Figure 2(a) shows the resulting hopping pattern in real space for the considered crystal structure, including both n.n. and n.n.n. hopping amplitudes. The corresponding full hamiltonian, h(k) can be expressed in terms of the Pauli matrices (5) using:
. This hamiltonian respecting PT-symmetry leads to 3D Dirac points. In order to obtain Weyl points we introduce the n.n.n. hopping amplitudes defined in equation (4). Figure 2(a) shows the resulting hopping pattern in real space for the considered crystal structure, including both n.n. and n.n.n. hopping amplitudes. The corresponding full hamiltonian, h(k) can be expressed in terms of the Pauli matrices (5) using: 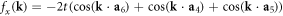 ,
,  and
and  . The new hamiltonian, h(k), generated in this way breaking P-symmetry leads to the four Weyl points in table 1.
. The new hamiltonian, h(k), generated in this way breaking P-symmetry leads to the four Weyl points in table 1.
Figure 2. Crystal structures and modified hopping patterns of the studied (a) FCC, and, (b) SC T-invariant Weyl lattices. Solid lines correspond to nearest-neighbor hoppings ( ), whereas dashed lines display next-nearest neighbor hoppings (
), whereas dashed lines display next-nearest neighbor hoppings ( ). Red and green lines represent negative and positive hoppings, respectively. For clarity in the visualization, the thickness of lines, as well as the color of the spheres marking the lattice positions, are different at the front and back of the displayed unit cell.
). Red and green lines represent negative and positive hoppings, respectively. For clarity in the visualization, the thickness of lines, as well as the color of the spheres marking the lattice positions, are different at the front and back of the displayed unit cell.
Download figure:
Standard image High-resolution image2.3. SC lattice
Weyl semimetals in SC lattices have been explored previously [30, 32]. Here, we propose a closely related implementation [30] but which now includes both n.n. and n.n.n. hoppings in a SC lattice (see figure 2(b)). First the n.n. hopping patterns of the (001) planes are modified to induce alternating ±π fluxes which leads to the n.n. Bloch hamiltonian:

which leads to four 3D Dirac points. The n.n.n. hoppings are modified to give the Bloch hamiltonian:
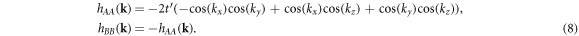
Hence, the full hamiltonian, h(k) can be expressed in terms of the Pauli matrices through: 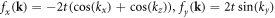 and
and  . This SC cubic lattice hosts the four Weyl points tabulated in table 1 related, as expected, by TRS symmetry.
. This SC cubic lattice hosts the four Weyl points tabulated in table 1 related, as expected, by TRS symmetry.
3. Bulk topological properties: Weyl nodes, chiralities and Berry curvatures
The generated Weyl system has characteristic topological properties associated with Weyl nodes [2, 6, 36]. The Nielsen-Nimoniya theorem [54] imposes that Weyl points in a lattice should always occur in pairs of opposite charges. In a T-symmetric system, the chiralities, 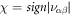 , where
, where 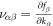 , (α, β = x, y, z), of the Weyl points at
, (α, β = x, y, z), of the Weyl points at  and
and 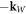 are equal. This is because T-symmetry implies:
are equal. This is because T-symmetry implies:  , leaving the products
, leaving the products 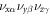 entering the chirality invariant under the interchange
entering the chirality invariant under the interchange 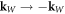 . Hence, we find the minimum four Weyl points [6] allowed in a T-symmetry system (see table 1) whose location is independent of
. Hence, we find the minimum four Weyl points [6] allowed in a T-symmetry system (see table 1) whose location is independent of 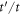 .
.
Weyl points can be considered hedgehogs of Berry curvature in momentum space [2, 55], behaving analogously to magnetic monopoles in real space. This is evident from calculations of the Berry curvature [56]:  , where
, where  is the eigenfunction of the occupied band. Figure 3 shows how Weyl points act as sources and drains of Berry curvature projected on the kx-kz plane in analogy with the magnetic field around magnetic monopoles in real space. Weyl points have a quantized Berry flux [57] given by:
is the eigenfunction of the occupied band. Figure 3 shows how Weyl points act as sources and drains of Berry curvature projected on the kx-kz plane in analogy with the magnetic field around magnetic monopoles in real space. Weyl points have a quantized Berry flux [57] given by: 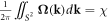 , so the chirality can be interpreted as a topological Chern number of the Weyl node. The expected chiralities of χ = ±1 of the four Weyl nodes found in our BCC Weyl semimetal are shown in table 1. Due to TRS the Berry curvature satisfies [57, 58]:
, so the chirality can be interpreted as a topological Chern number of the Weyl node. The expected chiralities of χ = ±1 of the four Weyl nodes found in our BCC Weyl semimetal are shown in table 1. Due to TRS the Berry curvature satisfies [57, 58]: 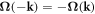 implying that there is no anomalous quantum Hall contribution to the Hall conductivity. However, an anomalous contribution to the electron velocity would arise under a weak uniform electric field [57]:
implying that there is no anomalous quantum Hall contribution to the Hall conductivity. However, an anomalous contribution to the electron velocity would arise under a weak uniform electric field [57]: 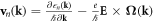 .
.
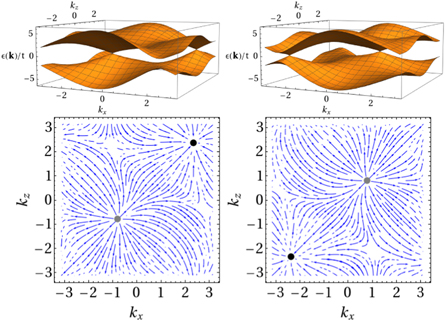
Figure 3. Weyl points and Berry curvatures of the BCC Weyl semimetal proposed. Two Weyl points with opposite chiralities in the kx-kz plane are shown in the top row for 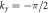 (left) and ky = π/2 (right). The corresponding projected Berry curvatures are shown in the bottom row. Inward and outward flows of Berry curvature indicate the presence of Weyl points with negative (black dot) and positive (grey dot) chiralities, respectively.
(left) and ky = π/2 (right). The corresponding projected Berry curvatures are shown in the bottom row. Inward and outward flows of Berry curvature indicate the presence of Weyl points with negative (black dot) and positive (grey dot) chiralities, respectively.
Download figure:
Standard image High-resolution imageA Weyl semimetal with broken P-symmetry can be viewed as an intermediate state between a trivial and a topological insulator [6, 49–51, 59–61]. Based on this fact, we explore the topological properties of our BCC Weyl semimetal by adding an external staggered mass term, mσz, to the Hamiltonian of equation (equation (5)). By tuning m from large negative to positive values we can drive the system from a band insulator to a topological insulator through an intermediate Weyl semimetallic phase. The Weyl nodes in this phase move around in k-space until at a critical mass, m, pairs of opposite chiralities meet at certain momenta anihilating each other as shown in figure 4 and opening a gap. For  , the Weyl points at (π/4, π/2, π/4) and (3π/4, −π/2, 3π/4) anihilate at
, the Weyl points at (π/4, π/2, π/4) and (3π/4, −π/2, 3π/4) anihilate at  whereas the Weyl points at
whereas the Weyl points at 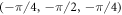 and
and  anihilate at
anihilate at  . Similarly, for
. Similarly, for 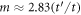 the Weyl points at
the Weyl points at 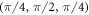 and
and 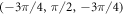 anihilate at (−1.1938, 0.7495, 1.943) whereas the Weyl points at
anihilate at (−1.1938, 0.7495, 1.943) whereas the Weyl points at  and
and  anihilate at
anihilate at 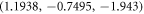 . The observed robustness of the Weyl points to the staggered mass term is due to the breaking of spatial inversion symmetry of our Hamiltonian. In particular, the BCC Weyl system with four Weyl nodes is stable for a staggered mass in the range:
. The observed robustness of the Weyl points to the staggered mass term is due to the breaking of spatial inversion symmetry of our Hamiltonian. In particular, the BCC Weyl system with four Weyl nodes is stable for a staggered mass in the range:  .
.
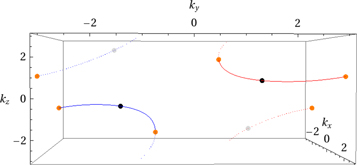
Figure 4. Effect of a staggered mass term on the location of Weyl points. A view along the x-direction of the first Brillouin zone of the BCC Weyl semimetal is shown. The m = 0 Weyl points with negative chirality are represented with a black dot while the Weyl points with positive chirality are represented with gray dots. The orange dots represent the momenta at which the Weyl nodes with opposite chiralities anihilate each other when the staggered mass term 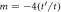 or
or  as described in the text.
as described in the text.
Download figure:
Standard image High-resolution image4. Topological surface bands and Fermi arcs
In gapped topological matter such as topological insulators [62] the bulk-boundary correspondence gives rise to gapless fermions on the surface of the system [55]. Similarly, in topological gapless materials such as Weyl semimetals, a crucial signature of Weyl fermions is the presence of gapless topological surface states. These surface states lead to exotic unclosed Fermi arcs [3, 36] in the surface Brillouin zone. We have computed the surface states on slabs which are cut along different crystal directions of the BCC Weyl semimetal. In figure 5 we show the Fermi arcs and surface bands on the (100) and (010) surfaces. We find Fermi arcs connecting the Weyl points with opposite chiralities at the surfaces of both sides of the slab. The Fermi arc shapes change depending on the termination of the surface i.e. whether the number of layers in the slab direction is even or odd.
Figure 5. Topological surface bands and Fermi arcs in a Weyl system on the BCC lattice. (a) Calculated Fermi arcs on the front (blue line) and back (red line) (100) surfaces of a slab with an odd number of layers. (b) Bulk (gray continuum) and surface band dispersions (red line) projected along the ky direction at kz = π/2 for the (100) slab of (a). (c), (d) same as (a), (b) respectively, but for a slab with an even number of layers. (e) Calculated Fermi arcs connecting Weyl points projected on the (010) surface of a slab with an even number of layers. (f) Bulk and surface band dispersions along the ky = kx direction for the (010) slab of (e). Note that the Fermi arcs on opposite sides of the slab coincide in the cases (c) and (e) for an even number of layers but not in (a) with an odd number of layers. The black (gray) dots represent the projection of the Weyl points on the different surface orientations with negative (positive) chiralities. The gray circle describes the edge of a cylinder along the x-direction cutting the (100) surfaces of the Brillouin zone which encloses a single Weyl point with positive chirality. Each edge of the cylinder sustains a topologically protected one-dimensional edge state contributing a state to the Fermi arc. The surface bands connecting the valence and conduction bulk bands lead to gapless metallic surfaces corroborating their topological nature.
Download figure:
Standard image High-resolution imageFermi arcs can be detected not only by ARPES experiments but also through standard quantum oscillation experiments in spite of the arcs being open. This is because under a magnetic field perpendicular to the surface of interest, electrons circulating along a Fermi arc on one side of the slab can traverse the bulk via the Weyl points to the Fermi arc on the opposite side of the slab leading to closed magnetic orbits [63]. These unusual closed orbits involving the bulk Weyl nodes can be detected in quantum oscillatory phenomena [64, 65]. At sufficiently strong magnetic fields, a quantum Hall effect occurs different from the standard 2D quantum Hall effect, involving chiral edge states along the direction of the applied magnetic field which intersect both the top and bottom surfaces. The dependence of the quantum Hall plateaus with the thickness of the samples indicates the existence of bulk chiral edge modes in contrast to the conventional 2D quantum Hall effect in layered semiconducting structures [66]. We may expect that the application of a magnetic field along the x-direction of our BCC Weyl semimetal lead to such sample thickness quantum Hall effect as a result of quantized orbits involving the top and bottom Fermi arcs in figure 5(a) connected through the bulk Weyl nodes. From our calculations we expect that for thicknesses of the sample larger than about 40 layers clear bulk-surface differentiation occurs and Fermi arcs on opposite surfaces would be only connected through the bulk Weyl nodes leading to the unusual Weyl orbits and associated magnetic oscillations as well as quantum hall effect phenomena.
We focus first on the results for the (100) surfaces shown in figures 5(a)–(d). The structure of the BCC crystal structure shown in figure 2 contains two types of atoms A and B. For a cut of the crystal with an even number of layers both surfaces contain atoms of the same type. On the other hand, for a cut involving an odd number of layers in the x-direction we have that one of the surfaces is formed by A(B)-sublattice atoms whereas the opposite side is formed by atoms of the B(A)-sublattice. In figures 5(a)–(b) we show the Fermi arcs and surface bands of the (100) surfaces of a slab with an odd number of layers along the x-direction. The Fermi arcs at the front and at the back surfaces are found to have very different shapes as shown in figure 5(a). This is in contrast to even number terminations in which the Fermi arcs on opposite surfaces coincide. The surface bands connect the valence and conduction bands closing the bulk gap leading to metallic surfaces.
Recent work suggests the possibility of realizing nontrivial knotting cyclotron orbits in a certain microscopic lattice model of a Weyl semimetal which breaks T-symmetry [67]. The band structure of such system hosts six Weyl nodes and the Fermi arcs on the two opposite surfaces cross without interference forming a trefoil knot together with the Weyl nodes. Under a magnetic field perpendicular to the surface electrons would circulate along the trefoil knotted orbit leading to observable topological effects not found in the unknotted orbits found in conventional Weyl semimetals. In our work, the Fermi arcs shown in figure 5(a) would lead to 'conventional' closed orbits formed by connecting the different Fermi arc shapes at the bottom and top surfaces, which do not cross, through the bulk Weyl nodes. Although our present BCC Weyl semimetal does not sustain knotted cyclotron orbits, other hopping patterns may be implemented along the lines proposed [67]. However, such hopping patterns previously considered in layered hexagonal structures [67] involve purely imaginary hoppings of alternating signs breaking T-symmetry. Hence, finding topologically non-trivial objects in P-breaking Weyl semimetals as discussed here will eventually require alternative proposals beyond the scope of the present work.
On the other hand, our calculations for the (010) surface of figure 5(e) show how two straight lines connect the two pairs of Weyl points with opposite chiralities along the diagonal (kz = kx direction) of the kx-kz surface. These open and disjoint Fermi lines result from the flat surface band located right at the Fermi energy shown in figure 5(f). Note that this flat band is similar to the one-dimensional surface band connecting two Dirac points in spinless graphene nanoribbons [52].
The topological protection of the surface states is guaranteed by the bulk-boundary correspondence. This can be explicitly illustrated by considering, for example, the (100) face by taking a cylinder which extends along the x-direction of the whole Brillouin zone and encloses a single Weyl point [36]. For example, the cylinder taken in figure 5(a) has a Chern number of +1 (since it contains a Weyl point with  ) giving rise to topologically protected edge states at the one-dimensional edges of the tube. Hence, this two-dimensional slice of the Brillouin zone behaves as a quantum Hall insulator with chiral states protected by a non-zero Chern number. The two edge states of the cylinder make slices of the Fermi arcs on the two (100) surfaces of the slab. By varying the radius of the cylinder the full Fermi arcs can be reconstructed.
) giving rise to topologically protected edge states at the one-dimensional edges of the tube. Hence, this two-dimensional slice of the Brillouin zone behaves as a quantum Hall insulator with chiral states protected by a non-zero Chern number. The two edge states of the cylinder make slices of the Fermi arcs on the two (100) surfaces of the slab. By varying the radius of the cylinder the full Fermi arcs can be reconstructed.
The character of the different insulating phases arising under the staggered mass term, m, discussed previously can be obtained by calculating their surface states [49, 51, 59]. In figure 6 we show the evolution of the Fermi arcs as the staggered mass m is changed from negative to positive values. For  the Weyl points anihilate and a gap opens up with no surface states so both the bulk and surface are gapped consistent with a conventional band insulator. In contrast, as m is increased with m > 0, the Fermi arcs change their shape until the Weyl points anihilate at
the Weyl points anihilate and a gap opens up with no surface states so both the bulk and surface are gapped consistent with a conventional band insulator. In contrast, as m is increased with m > 0, the Fermi arcs change their shape until the Weyl points anihilate at  giving way to a closed Fermi surface for
giving way to a closed Fermi surface for  . The surface bands leading to such Fermi surface have cone-like dispersions between the valence and conduction bands indicating the presence of a 3D topological insulator.
. The surface bands leading to such Fermi surface have cone-like dispersions between the valence and conduction bands indicating the presence of a 3D topological insulator.
Figure 6. Evolution of Fermi arcs on the (010) surface of the BCC Weyl lattice in the presence of a staggered mass term. In the Weyl semimetal the projected Fermi arcs on opposite sides of the slab with an even number of layers coincide. A band insulator with no surface states for 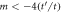 becomes a Weyl semimetal between
becomes a Weyl semimetal between 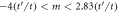 and finally a topological insulator for
and finally a topological insulator for  . The Weyl points with negative (positive) chiralities for the corresponding m are shown. The orange dots shown for reference are the projection of the anihilation of two Weyl points with opposite chiralities at
. The Weyl points with negative (positive) chiralities for the corresponding m are shown. The orange dots shown for reference are the projection of the anihilation of two Weyl points with opposite chiralities at 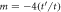 and
and 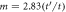 . We have taken
. We have taken 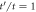 in all plots.
in all plots.
Download figure:
Standard image High-resolution image5. Implementation in optical lattices
In this section we describe a possible experimental implementation of the proposed Weyl lattices using ultracold atoms in optical lattices. In particular, we describe how the combination of laser-assisted tunneling and a linear potential energy gradient enables the realization of the tailored hopping patterns described in section 2. For concreteness, we focus on the case of the BCC lattice—a similar approach can be applied for the implementation of the FCC and SC crystal structures.
In the proposed implementation, we first create a canonical BCC optical lattice. We consider the laser configuration introduced in [68], which employs three pairs of lasers fields (of wavelength λ) and that can be implemented using retroreflected lasers. The electric field associated to each laser field is given by 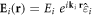 (where Ei, ki and
(where Ei, ki and 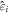 are the amplitude, propagation vector and polarization, respectively, of each field—with i = 1, ...,6 labelling each field). The six fields are counterpropagating in pairs along three orthogonal directions (
are the amplitude, propagation vector and polarization, respectively, of each field—with i = 1, ...,6 labelling each field). The six fields are counterpropagating in pairs along three orthogonal directions ( ), and feature the same field amplitude (Ei = E0) but three different non-orthogonal polarizations:
), and feature the same field amplitude (Ei = E0) but three different non-orthogonal polarizations:  ,
,  and
and  . The interference between these laser fields yields the following spatial-dependent electric field intensity, I(r):
. The interference between these laser fields yields the following spatial-dependent electric field intensity, I(r):
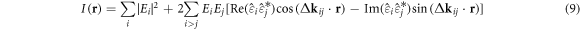
where 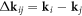 . The field intensity I(r) field intensity, in turn, leads the following potential [68]:
. The field intensity I(r) field intensity, in turn, leads the following potential [68]:

where V0 is the overall potential amplitude of the resulting potential. The real-space primitive vectors describing the periodicity of 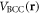 (
(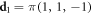 ,
,  and
and 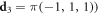 can be shown to expand a BCC lattice.
can be shown to expand a BCC lattice.
The second step of the proposed implementation involves placing the system under a tilted potential  (which can be achieved by using gravity or a magnetic field gradient [30, 69]). Specifically, in this case, we consider
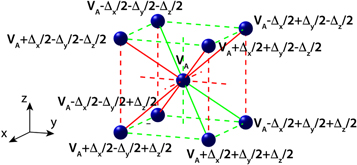
(which can be achieved by using gravity or a magnetic field gradient [30, 69]). Specifically, in this case, we consider 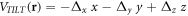 with Δx, Δy, Δz > 0. Figure 7 shows the potential energy distribution of
with Δx, Δy, Δz > 0. Figure 7 shows the potential energy distribution of  over the BCC sites (taking as reference the potential energy of an A-sublattice atom, VA). As observed, negative potential jumps of
over the BCC sites (taking as reference the potential energy of an A-sublattice atom, VA). As observed, negative potential jumps of 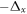 ,
,  and
and 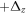 between consecutive sites are obtained along the x, y and z direction, respectively. Importantly, these potential jumps suppress completely both the n.n. and n.n.n. hoppings present in the original BCC lattice.
between consecutive sites are obtained along the x, y and z direction, respectively. Importantly, these potential jumps suppress completely both the n.n. and n.n.n. hoppings present in the original BCC lattice.
Figure 7. Schematic view of the energy potential distribution created by the tilted potential (described in the main text) on the considered BCC lattice.
Download figure:
Standard image High-resolution imageFinally, to realize the hopping pattern shown in figure 1 we restore and tailor both n.n. and n.n.n. hoppings of the lattice using laser assisted tunneling. In particular, following the approach of [30, 69], we propose to use suitably configured pairs of Raman lasers to modify the hopping phases along the relevant directions of the studied lattice (i.e., the three Cartesian directions and the four diagonals of the unit cell). On the one hand, the wavevector difference of each laser pair, 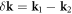 , introduces a phase
, introduces a phase  in the hopping between consecutive lattice sites (Ri and
in the hopping between consecutive lattice sites (Ri and 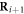 ) along the considered lattice direction. On the other hand, the frequency difference of each laser pair,
) along the considered lattice direction. On the other hand, the frequency difference of each laser pair,  is chosen so that its magnitude matches the potential energy jump between consecutive sites, with the important consideration that an additional phase
is chosen so that its magnitude matches the potential energy jump between consecutive sites, with the important consideration that an additional phase 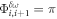 is added to the hopping amplitude whenever the sign of
is added to the hopping amplitude whenever the sign of  is opposite to the change of potential between
is opposite to the change of potential between  and
and 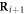 [69]. Thus, the combination of both
[69]. Thus, the combination of both 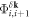 and
and 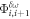 allows, for instance, to implement such involved patterns as the n.n.n. hopping configurations for A and B lattice sites shown in figure 7: A lattice sites feature an effective hopping of
allows, for instance, to implement such involved patterns as the n.n.n. hopping configurations for A and B lattice sites shown in figure 7: A lattice sites feature an effective hopping of 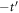 along
along  directions and
directions and 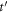 along the z direction, whereas for B sites we obtain the complementary distribution of surrounding n.n.n. hoppings (
along the z direction, whereas for B sites we obtain the complementary distribution of surrounding n.n.n. hoppings ( along the x, y directions and
along the x, y directions and 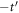 along the z direction). Table 2 summarizes the values of
along the z direction). Table 2 summarizes the values of  and
and  leading to the complete hopping pattern shown in figure 1. Finally, we note that in the described approach we assume that the cross-interference between lasers with different frequencies averages out in the timescales of interest (a condition readily accessible experimentally by using closely spaced laser wavelengths).
leading to the complete hopping pattern shown in figure 1. Finally, we note that in the described approach we assume that the cross-interference between lasers with different frequencies averages out in the timescales of interest (a condition readily accessible experimentally by using closely spaced laser wavelengths).
6. Conclusions
In summary, we have introduced a general systematic approach to generate Weyl nodes in cubic crystal structures which break P-symmetry but preserve T-symmetry. The approach can be applied to both fermionic and bosonic systems described by a tight-binding model on any cubic crystal (BCC,FCC,SC) with a single orbital per site. The Weyl semimetals generated have the minimum four Weyl nodes required by time-reversal symmetry. We have obtained the Fermi arcs on different crystal surfaces of our BCC crystal originating from the surface states topologically protected by non-zero Chern numbers of ±1. Under applied magnetic fields electrons could circulate along Weyl orbits traversing from one side to the opposite side of the samples via the Weyl nodes. Laser assisted hopping techniques applied on cold atoms in optical lattices appear to be a suitable procedure to experimentally implement our proposal. Our work complements the intense search of Weyl systems in complex materials providing a route to generate novel Weyl nodes with desired properties in cubic crystal structures.
Acknowledgments
We thank Hrvoje Buljan for helpful discussions. We acknowledge anonymous referee for insightful and helpful comments which have improved greatly our paper. We acknowledge financial support from RTI2018-098452-B-I00 (MINECO/FEDER, Unión Europea).
: Appendix. T-symmetry breaking Weyl semimetal
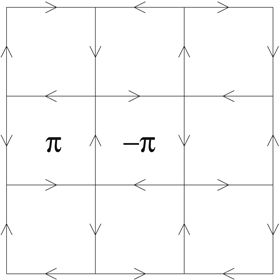
We illustrate here how to generate a Weyl semimetal which breaks T-symmetry for completeness. We now consider a tight-binding model on a square lattice with Peierls phases in the n.n. hoppings, 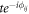 with phases:
with phases: 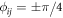 with each square plaquette pierced by alternating
with each square plaquette pierced by alternating 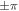 fluxes as shown in figure A1. This staggered flux arrangement can be described by the following n. n. hamiltonian:
fluxes as shown in figure A1. This staggered flux arrangement can be described by the following n. n. hamiltonian:
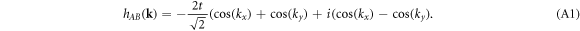
Since the hopping phases are different from ϕij = 0, π as in previous cases, the hamiltonian is complex breaking time-reversal symmetry: 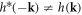 preserving inversion symmetry
preserving inversion symmetry 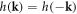 . This two-dimensional model has four Dirac points:
. This two-dimensional model has four Dirac points:  . In order to construct 3D Weyl points we consider a set of layers described by the hamiltonian above which are coupled through an interlayer hopping amplitude. This interlayer hopping is chosen to be real and is
. In order to construct 3D Weyl points we consider a set of layers described by the hamiltonian above which are coupled through an interlayer hopping amplitude. This interlayer hopping is chosen to be real and is 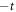 for the hopping between two A sites and
for the hopping between two A sites and 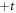 for the hopping amplitude between two B sites. Thus, the hopping along the z-axis leads to the diagonal matrix elements:
for the hopping amplitude between two B sites. Thus, the hopping along the z-axis leads to the diagonal matrix elements:

which effectively adds a σz term to the 2D hamiltonian above leading to the corresponding 3D hamiltonian:

with: 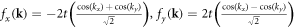 and
and 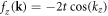 . The analysis of the model hamiltonian (A3) shows that there are 8 Weyl points with alternating chiralities as described in table A1.
. The analysis of the model hamiltonian (A3) shows that there are 8 Weyl points with alternating chiralities as described in table A1.
Figure A1. Hopping pattern in the (001) planes of the T-breaking 3D Weyl semimetal. A positive (negative) arrow in the x or y directions when going from site i to a nearest-neighbor site j means  (
( . An alternating flux of
. An alternating flux of 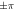 pierces the square plaquettes of the lattice.
pierces the square plaquettes of the lattice.
Download figure:
Standard image High-resolution imageTable A1. Weyl points in the 3D cubic lattice with broken time-reversal symmetry proposed.
| kW | χ |
|---|---|
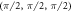
|
+ |
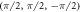
|
− |
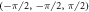
|
+ |

|
− |
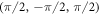
|
− |
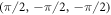
|
+ |
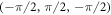
|
+ |
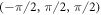
|
− |
Hence, we have generated a Weyl semimetal that breaks T symmetry but preserves the inversion symmetry of the lattice. We note that the Bloch hamiltonian, h(k) also has a C4 rotation point group symmetry since the Bloch hamiltonian satisfies: 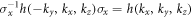 . Hence, Weyl nodes in the present T-symmetry breaking Weyl semimetal are protected by such crystalline symmetry.
. Hence, Weyl nodes in the present T-symmetry breaking Weyl semimetal are protected by such crystalline symmetry.