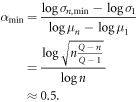Addendum: another explanation about the bounds of the Taylor exponent

Taylor's law describes the fluctuation characteristics underlying a complex system in which the variance of an event within a time span grows by a power law with respect to the mean. The previous paper, Taylor's Law for Linguistic Sequences and Random Walk Models (Tanaka-Ishii and Kobayashi 2018), appeared in Journal of Physics Communications and described a new way to apply Taylor analysis to texts. The method was applied to over 1100 texts across 14 languages. The results showed how the Taylor exponents of natural-language written texts were consistently around 0.58, thus being universal.

Experimentally, the Taylor exponent α is known to take a value within the range of 0.5 ≤ α ≤ 1.0 across a wide variety of domains, including finance, meteorology, agriculture, and biology. The previous paper shows how this is the case for language.

The Taylor exponent is analytically proven to be 0.5 for an independent and identically distributed (i.i.d.) process. The paper also shows a case when 1.0 is reached. This Addendum provides two additional cases of rare word alignment for α = 0.5 and α = 1.0. These cases provide an understanding to interpret the value of the exponent of a real text.

Consider dividing a text of length N into Q segments of length Δt, i.e., N = QΔt. Suppose that Q is sufficiently large.

First of all, if a word only appears once in the entire text, then μ₁ and σ₁ are calculated as follows.

$$\begin{eqnarray*}\begin{array}{rcl}{\mu }_{1} & = & \displaystyle \frac{1}{Q},\\ {\sigma }_{1} & = & \sqrt{\displaystyle \frac{1}{Q}\left((Q-1){\left(\displaystyle \frac{1}{Q}\right)}^{2}+{\left(1-\displaystyle \frac{1}{Q}\right)}^{2}\right)}\\ & = & \displaystyle \frac{\sqrt{Q-1}}{Q}.\end{array}\end{eqnarray*}$$

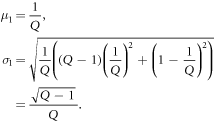
For words that appear n(≪Q) times in a text, there are two extreme possibilities: when the n words are all in the same segment, and on the other hand, when the n words are all in different segments.

When the n words all appear in the same segment, then σ becomes the largest for this case, as follows.

$$\begin{eqnarray*}\begin{array}{rcl}{\mu }_{n} & = & \displaystyle \frac{n}{Q},\\ {\sigma }_{n,\max } & = & \sqrt{\displaystyle \frac{1}{Q}\left((Q-1){\left(\displaystyle \frac{n}{Q}\right)}^{2}+{\left(n-\displaystyle \frac{n}{Q}\right)}^{2}\right)}\\ & = & \displaystyle \frac{n\sqrt{Q-1}}{Q}.\end{array}\end{eqnarray*}$$

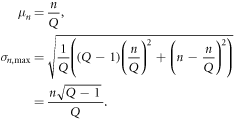
Because the extreme of such a case occurs when n = 1, α is 1, as follows.

$$\begin{eqnarray}\begin{array}{rcl}{\alpha }_{\max } & = & \displaystyle \frac{\mathrm{log}{\sigma }_{n,\max }-\mathrm{log}{\sigma }_{1}}{\mathrm{log}{\mu }_{n}-\mathrm{log}{\mu }_{1}}\\ & = & 1.\end{array}\end{eqnarray} \tag{ 1 }$$

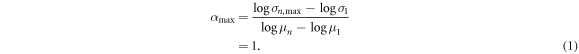
On the other hand, when the n words all appear in different segments, then σ becomes the smallest, as follows.

$$\begin{eqnarray*}\begin{array}{rcl}{\mu }_{n} & = & \displaystyle \frac{n}{Q},\\ {\sigma }_{n,\min } & = & \sqrt{\displaystyle \frac{1}{Q}\left((Q-n){\left(\displaystyle \frac{n}{Q}\right)}^{2}+n{\left(1-\displaystyle \frac{n}{Q}\right)}^{2}\right)}\\ & = & \displaystyle \frac{\sqrt{n(Q-n)}}{Q}.\end{array}\end{eqnarray*}$$

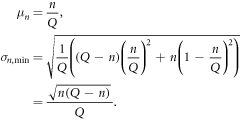
Because the extreme of such a case occurs when n = 1, α is 0.5, as follows.

$$\begin{eqnarray*}\begin{array}{rcl}{\alpha }_{\min } & = & \displaystyle \frac{\mathrm{log}{\sigma }_{n,\min }-\mathrm{log}{\sigma }_{1}}{\mathrm{log}{\mu }_{n}-\mathrm{log}{\mu }_{1}}\\ & = & \displaystyle \frac{\mathrm{log}\sqrt{n\tfrac{Q-n}{Q-1}}}{\mathrm{log}n}\\ & \approx & 0.5.\end{array}\end{eqnarray*}$$